Factors that impact fragility index and their visualizations

Abstract

Rationale aims and objectives:

As the recent literature has growing concerns about research replicability and the misuse and misconception of P-values, the fragility index (FI) has been an attractive measure to assess the robustness (or fragility) of clinical study results with binary outcomes. It is defined as the minimum number of event status modifications that can alter a study result’s statistical significance (or non-significance). Owing to its intuitive concept, the FI has been applied to assess the fragility of clinical studies of various specialties. However, the FI may be limited in certain settings. As a relatively new measure, more work is needed to examine its properties.

Methods:

This article explores several factors that may impact the derivation of the FI, including how event status is modified and the impact of significance levels. Moreover, we propose novel methods to visualize the fragility of a study’s result. These factors and methods are illustrated using worked examples of artificial datasets. Randomized controlled trials on antidepressant drugs are also used to evaluate their real-world performance.

Results:

The FI depends on the treatment arm(s) in which event status is modified, whether the original study result is significant, the statistical method used for calculating the P-value, and the threshold for determining statistical significance. Also, the proposed visualization methods can clearly demonstrate a study result’s fragility, which may be useful supplements to the single value of the FI.

Conclusion:

Our findings may help clinicians properly use the FI and appraise the reliability of a study’s conclusion.

Introduction

It is a common practice to report P-values for assessing statistical significance of treatment effects in clinical studies. However, the recent literature has arisen many concerns about research reproducibility and replicability.^1–7 It has been long recognized that P-values may be misused or misinterpreted as a measure of effect.^8–14 P-values less than the conventional significance level 0.05 may be more likely reported. This phenomenon is often termed as publication bias, selective reporting, or P-hacking, leading to substantial biased results and lack of replicability.^15–17

Recently, Walsh et al.¹⁸ proposed the fragility index (FI) to assess the robustness (or fragility) of a clinical study result’s significance for binary outcomes (i.e., events or non-events). It quantifies the minimal event status modifications that can alter the significance (or non-significance) of the result. It may be viewed as an extension of the concept introduced by Feinstein¹⁹ and Walter²⁰ dating back to 1990s; nevertheless, the FI considered by Walsh et al.¹⁸ has a more straightforward interpretation and regains researchers’ attention along with the growing concerns about research replicability. Clinicians may intuitively appraise the impact of certain events or non-events that play a critical role in the study result. In the past few years, the FI has become an attractive supplemental measure for evaluating the reliability of a study’s conclusion.^21,22

However, as a relatively new measure, cautions are needed when using the FI under certain settings. For example, the FI does not account for the times at which events occurred, so it may not be very suitable for time-to-event analyses.^23,24 Also, in some cases, the FI may be strongly associated with P-value, sample size, etc.^25–27; therefore, the FI might not provide much more additional information than the existing well-reported measures in such cases. Moreover, practical perspectives such as clinical importance may be taken into account when interpreting the FI.²⁸ These potential limitations stimulate further investigation on the FI’s properties.

This article explores and summarizes several factors that may impact the derivation of the FI. We also introduce novel methods to visualize a study’s fragility. These factors and visualization methods are illustrated by artificial datasets. Randomized controlled trials on antidepressant drugs are also used to show their real-world performance.

Methods

Fragility index

Table 1 demonstrates an illustrative 2×2 table of a study and event status modifications for deriving the FI. Suppose the study compares two treatments, denoted by 0 and 1. The association between the treatments and the binary outcome is of interest. The event status in both treatment arms can be potentially modified for deriving the FI, and the numbers of modified events are denoted by f₀ and f₁ accordingly in the two arms. If f₀=f₁=0, this corresponds to the original data. The calculation of the FI aims at finding the minimum number of modified events (i.e., the sum of the absolute values of f₀ and f₁) for altering the statistical significance (or non-significance).

Table 1.

Illustration of a 2×2 table, event status modifications, and three artificial datasets

Treatment	Event	Non-event	Sample size
Illustrative dataset:
Arm 0	e0	n0 − e0	n0
Arm 1	e1	n1 − e1	n1
Illustrative dataset with event status modifications:
Arm 0	e0 + f0	n0 − e0 − f0	n0
Arm 1	e1 + f1	n1 − e1 – f1	n1
Artificial dataset 1:
Arm 0	10	90	100
Arm 1	30	70	100
Artificial dataset 2:
Arm 0	25	75	100
Arm 1	30	70	100
Artificial dataset 3:
Arm 0	15	85	100
Arm 1	30	70	100

Note: n₀ and n₁ are sample sizes in treatment arms 0 and 1; e₀ and e₁ are event counts in the two arms in the original trial; and f₀ and f₁ are the numbers of modified events in the two arms for deriving the fragility index.

There are several factors that may impact the derivation of the FI. In the following, we will detail these factors and introduce methods to visualize them. Three artificial datasets, as shown in Table 1, will be used to demonstrate these. Each arm in each artificial dataset has 100 samples; arm 1 has 30 events across the three datasets, while the event count in arm 0 differs.

Treatment arm with event status modifications

Walsh et al.¹⁸ primarily considered studies with the balanced design (i.e., 1:1 treatment allocation ratio); therefore, they restricted the event status modifications to a single arm, rather than permitting them in both arms. In terms of our illustrative 2×2 table, either f₀ or f₁ is set to 0. This restriction may be arguably reasonable for the balanced design; that is, the modifications in the arm with fewer events would have a greater impact on the result and thus can alter the significance (or non-significance) faster. However, in practice, the two arms may not have exactly the same sample size; the restriction of modifications in a single arm may not guarantee to yield the minimal event status modifications. Our real data analysis will give several such cases. Even if the design is exactly balanced, the minimal event status modifications may not be restricted to a single arm; we will illustrate this using artificial dataset 1.

To visualize a study result’s fragility, we consider certain ranges for f₀ and f₁. For each pair of f₀ and f₁, the P-value is calculated using a specific statistical method (detailed later) with f₀ and f₁ modified events in arms 0 and 1, respectively. Consequently, the P-values in all cases of modifications may be presented in a matrix, whose columns correspond to the modifications in arm 0 and rows correspond to those in arm 1. We propose to visualize these P-values in a scatter plot with the modifications in arms 0 and 1 presented on the horizontal and vertical axes, respectively. Each point represents a P-value from each combination of modifications, and different colors indicate different magnitudes of the P-values.

Based on Fisher’s exact test at the significance level α=0.05, Figure 1A presents the derivation of the FI with all possible event status modifications in both arms in artificial dataset 1. The P-value of the original dataset is <0.001; as clearly shown in Figure 1A, the original result lies in the red area that represents statistical significance. The derivation of the FI is a process of searching for the shortest paths for moving the original result to the green area of non-significance. Such shortest paths correspond to the minimal event status modifications. For this artificial dataset, the FI is 8; that is, at least 8 event status modifications are needed to alter the significant result to be non-significant. Although the FI is a single value, the minimal modifications are not unique. Five different cases of minimal modifications could alter the significance. For example, these cases include changing 8 non-events to events in arm 0, or changing 4 non-events to events in arm 0 and 4 events to non-events in arm 1 (Figure 1A).

Figure 1. Fragility index of artificial dataset 1.

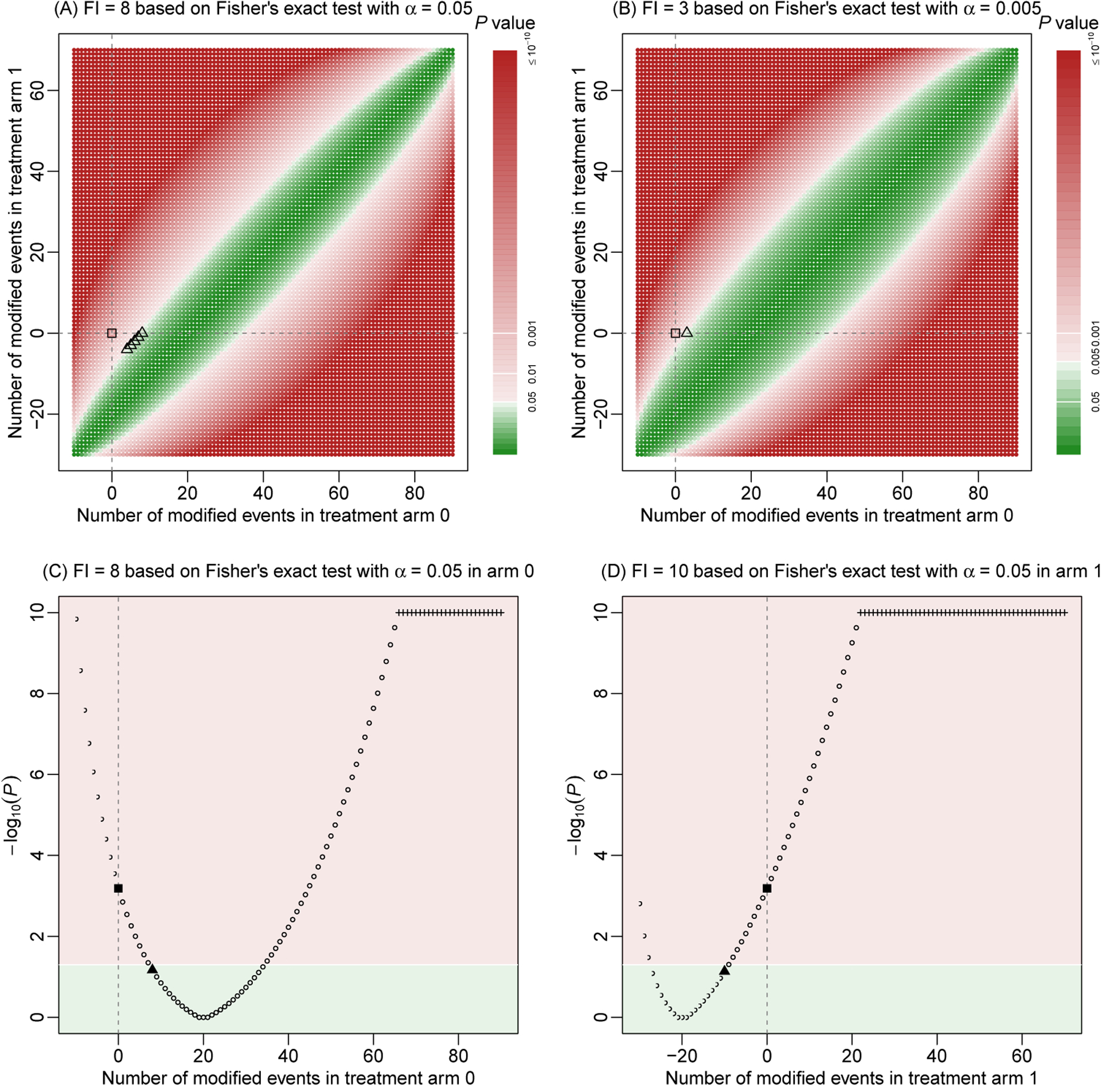
The fragility index is derived using Fisher’s exact test. Event status is modified in both treatment arms in (A) and (B); the modifications are restricted to arm 0 and arm 1 in (C) and (D), respectively. The significance level is 0.05, except in (B), where the level is lowered to 0.005. Each point represents a P-value based on specific event status modifications. P-values are presented on a base-10 logarithmic scale. Points or areas in green indicate non-significant results, and those in red indicate significant ones. Dashed lines represent no modifications in the corresponding arms. Square points represent the original P-value, triangle points indicate minimal modifications that alter the significance, and plus points represent truncated P-values at 10⁻¹⁰.

Figures 1C and 1D show the derivations of the FI when the modifications are restricted to a single arm. Essentially, these two plots are the projections of Figure 1A to each of the horizontal and vertical axes. If the modifications are restricted to arm 0 only, the significance could be still altered with 8 modifications, leading to the same FI=8. Indeed, as discussed above, this is one of the cases of minimal modifications when the modifications are permitted in both arms. If the modifications are restricted to arm 1 only, however, the FI increases to 10.

Direction of altering significance

Walsh et al.¹⁸ defined the FI for studies originally with significant results only. The FI can be similarly defined for originally non-significant results; the modifications aim at changing them to be significant.²⁹ Such a generalized FI will be considered in this article. The FI of a non-significant result may be as critical as that of a significant result. For example, some trials may want to show the equivalence of two treatments, and non-significant differences are of interest in such trials.

Based on Fisher’s exact test, artificial dataset 2 has a P-value of 0.527, indicating a non-significant result at α=0.05. Similar derivations of the FI can be applied to this non-significant result; Figure 2 shows the visualizations. Compared with artificial dataset 1, the major difference is that the original result is located in the green area of non-significance, and the aim is to find the minimal modifications that move the original result to the red area of significance. The FI is 8, which is achieved by changing 8 events to non-events in arm 0, or changing 7 events to non-events in arm 0 and 1 non-event to event in arm 1. If restricting the modifications to arm 1 only, the FI is 9.

Figure 2. Fragility index of artificial dataset 2.

The fragility index is derived using Fisher’s exact test. Event status is modified in both treatment arms (A), in arm 0 only (B), or in arm 1 only (C). The significance level is 0.05. Each point represents a P-value based on specific event status modifications. P-values are presented on a base-10 logarithmic scale. Points or areas in green indicate non-significant results, and those in red indicate significant ones. Dashed lines represent no modifications in the corresponding arms. Square points represent the original P-value, triangle points indicate minimal modifications that alter the non-significance, and plus points represent truncated P-values at 10⁻¹⁰.

Of note, when deriving the FI for an originally non-significant result, it is possible that the non-significance can never be altered to significance. This may occur when the study’s sample size is very small; even if all samples in one arm have events and all samples in another arm have non-events, the result may be still non-significant. In such cases, we may define the FI as not available (NA).

Statistical methods for assessing association

To assess the association between treatments and outcomes, Walsh et al.¹⁸ focused on Fisher’s exact test, regardless of the original statistical methods used in the real-world trials. This test is often used for small sample sizes, while in theory it is valid for all sample sizes. Besides this test, various alternative statistical methods are available.^30,31 Different methods lead to different P-values for the same dataset, which further influence the FI.

The chi-squared test is also commonly used. Unlike Fisher’s exact test, it is derived under the asymptotic large-sample setting; therefore, it may not be valid when some data cells in the 2×2 table are very small. In addition to making a binary decision about the association’s significance, many trials report certain effect measures, such as odds ratios (ORs), relative risks (RRs), and risk differences (RDs), to quantify treatment effects. The reported P-values in many published articles are frequently based on these measures. Of note, ORs and RRs are analyzed on a logarithmic scale. When zero event or non-event counts appear in one arm, the continuity correction of 0.5 is often applied to all four data cells in the 2×2 table, so that the ORs and RRs can be properly estimated. Also, without loss of generality, we focus on the two-sided alternative testing hypothesis when calculating the P-values using the various methods.

In the current practice, the FI is usually calculated based on inconsistent choices of statistical methods for calculating P-values, which may lead to FI=0.^18,32,33 For example, FI=0 is produced when a trial originally reports the OR with P-value<0.05 but a re-analysis of the same dataset using Fisher’s exact test leads to P-value>0.05. This inconsistent use of methods may reduce the interpretability of the FI, because the FI aims at describing a study result’s robustness, which is a property of a specific dataset, but the above case of FI=0 is more relevant to the properties of different statistical methods (e.g., type I error rates and statistical powers). Fisher’s exact test may not be uniformly powerful under all situations.^31,34 The statistical method used in a trial’s analysis may have been pre-specified and well-justified in its protocol. It might not be sensible to always use Fisher’s exact test for all trials when deriving their FIs. The significance’s change caused by using different methods may not be fully attributable to the result’s fragility; it could be also due to the low statistical power of Fisher’s exact test in certain cases. Therefore, we suggest to consistently use a specific statistical method when deriving the FI; under this rule, the FI should be at least 1.

Figure S1 in Supplemental Appendix A presents the FI derivation for artificial dataset 1 using the chi-squared test. The FI remains to be 8 as in the case of using Fisher’s exact test (Figure 1A). Figure S2 in Supplemental Appendix A gives the FI derivations using the effect measures of OR, RR, and RD. As depicted by the areas in different colors, these effect measures lead to some different trends of the P-values. Using the RR, the FI is 8, while it increases to 9 based on the OR and RD. Of note, here we apply all five methods described above to yield P-values of artificial dataset 1 for illustrative purposes. These examples do not suggest that researchers should try all methods to obtain P-values and compare FIs based on the different methods, because such practice may lead to P-hacking (i.e., reporting smaller P-values) or “fragility-hacking.” Instead, in real-world applications, researchers should use the statistical method specified in the protocol to derive the FI.

Significance level

The significance level α gives a cutoff of P-values, leading to the binary conclusions of significance or non-significance, so it has a great impact on the FI. Consequently, the FI should be always reported alongside the pre-specified significance level. For example, Figure 1B presents the fragility of artificial dataset 1 when α=0.005. Compared with Figure 1A when α=0.05, the green area of non-significance becomes wider, and thus the originally significant result can be more easily altered to be non-significant. Indeed, the new FI decreases to 3, much smaller than FI=8 when α=0.05.

As a statistical convention, the significance level is commonly set to 0.05. Alternative significance levels may be used in various research fields; they reflect the investigators’ attitudes toward acceptable false positives. Recently, to partly address the concerns about research replicability, some investigators recommend to lower the significance level from 0.05 to 0.005.^35,36 Therefore, the FI based solely on α=0.05 may not fully meet contemporary research needs.

To assess a study’s fragility from different investigators’ perspectives about statistical significance, we propose to derive the FIs based on a range of potential significance levels α (say, from 0.005 to 0.05) and present the FIs against the different levels. Figure 3 presents such plots for all three artificial datasets, based on a total of 100 significance levels equally spaced between 0.005 and 0.05; Fisher’s exact test is used to derive the FIs. Because FIs are integers by the definition, the plots of FIs vs. significance levels are step functions.

Figure 3. Fragility index against significance level in the three artificial datasets.

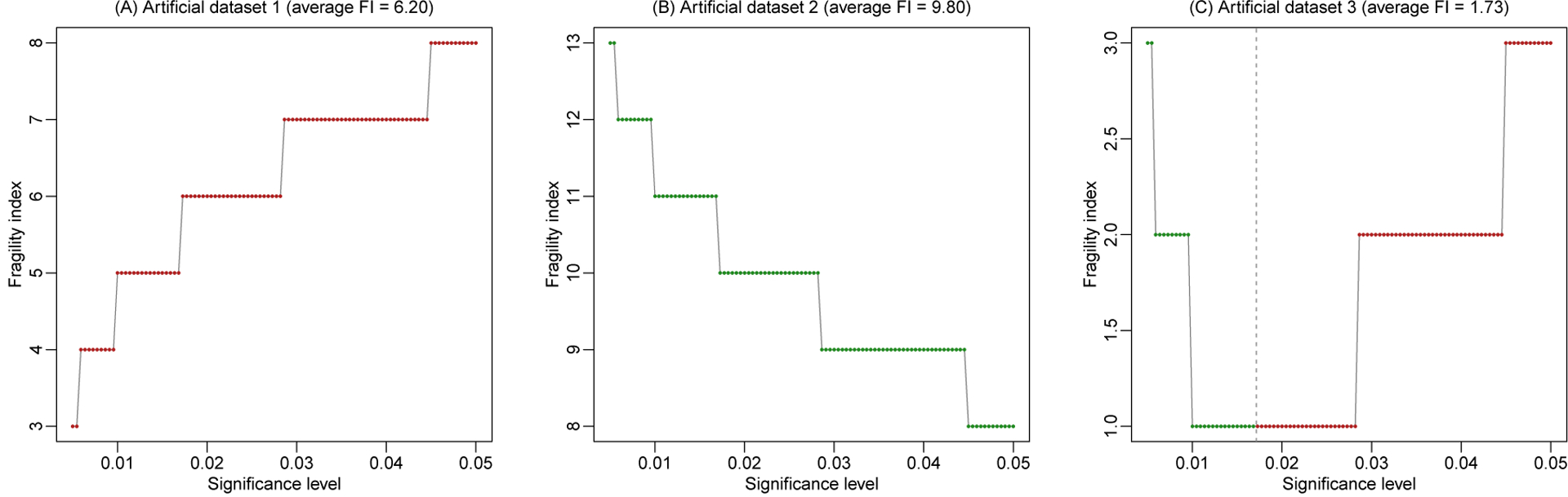
The fragility index is derived using Fisher’s exact test. Each point represents a fragility index derived at a specific significance level. Points in green indicate that originally non-significant results are altered to be significant, and those in red indicate that originally significant results are altered to be non-significant. The vertical dashed line (if shown) represents the P-value.

As the P-value of artificial dataset 1 is <0.001, the result is significant across all considered α between 0.005 and 0.05. As α decreases from 0.05 to 0.005, it is closer to the P-value, so that the significance can be altered with fewer event status modifications. Consequently, the FI decreases from 8 to 3 as α decreases (Figure 3A). For artificial dataset 2, the P-value is 0.527, so its result is non-significant for all α between 0.005 and 0.05. As α decreases from 0.05 to 0.005, more event status modifications are needed to alter the non-significant result to be significant, so the FI increases from 8 to 13 (Figure 3B). Artificial dataset 3 has a P-value of 0.017, which is within the range of α and is depicted by the vertical dashed line in Figure 3C. At α=0.05, the original result is significant with FI=3, which describes the minimal modifications needed to change the significance to non-significance. As α decreases toward the P-value, the FI decreases to 1. When α is less than the P-value, the original result becomes non-significant; in this case, the FI describes the minimal modifications needed to change the non-significance to significance. The FI increases back to 3 as α further decreases to 0.005.

In addition to the plot visualizing the trend of FIs vs. significance levels, we may calculate the average FI among the range of significance levels (i.e., 0.005–0.05 in the above examples). It assesses the overall fragility of the study result as the significance level varies. More specifically, the average FI reflects the (averaged) area under the FI curve in the plot; this idea is similar to the area under the receiver operating characteristic curve (AUC), which is commonly used in diagnostic decision making. Let FI(α) be the FI at the significance level α, where α is from α_L (e.g., 0.005) to α_U (e.g., 0.05); the (averaged) area under the curve is $\frac{1}{{\alpha }_{\text{U}}-{\alpha }_{\text{L}}}{\int }_{{\alpha }_{\text{L}}}^{{\alpha }_{\text{U}}}\text{FI}\left(\alpha \right)d\alpha$. Suppose that the FI curve is plotted at B equally-spaced values of significance levels (e.g., B=100 in the above example) between α_L and α_U, denoted by α_b (b = 1,…,B) with α₁ = α_L and α_B = α_U. Consequently, the (averaged) area under the curve can be approximated by the average FI when B is sufficiently large:

$$\frac{1}{{\alpha }_{\text{U}}-{\alpha }_{\text{L}}}{\int }_{{\alpha }_{\text{L}}}^{{\alpha }_{\text{U}}}\text{FI}\left(\alpha \right)d\alpha \approx \frac{1}{{\alpha }_{\text{U}}-{\alpha }_{\text{L}}}\times \frac{{\alpha }_{\text{U}}-{\alpha }_{\text{L}}}{B}{\sum }_{b=1}^B\text{FI}({\alpha }_b)=\frac{1}{B}{\sum }_{b=1}^B\text{FI}({\alpha }_b).$$

For example, the average FIs in the three artificial datasets are 6.20, 9.80, and 1.73, accordingly. The last artificial dataset has a fairly small average FI, indicating that its result’s significance or non-significance could be easily altered. Indeed, its P-value is 0.017, which is close to several commonly-used thresholds such as 0.05, 0.01, and 0.005.

Real data analysis

We use the randomized controlled trials collected in a systematic review by Cipriani et al.³⁷ to illustrate the real-world performance of the FI and the visualization methods. The original review contains a total of 522 trials comparing antidepressant drugs. We focus on two outcomes separately, i.e., responders (measured by the total number of patients who had a reduction of ≥50% of the total score on a standardized observer-rating scale for depression) and dropouts due to any cause; they reflect treatment efficacy and acceptability, respectively. We exclude trials with missing data or with more than two treatment arms. The FI is derived using each of the five statistical methods as discussed above. The significance level is pre-specified as 0.05; when assessing the FI at multiple significance levels, we consider their range from 0.005 to 0.05.

Research reproducibility

All analyses were performed using R (version 3.5.3). The real datasets and the R code for producing all results of the artificial and real data analyses are available in the Supplemental File. The methods proposed in this article can be also implemented via our R package “fragility.”

Results

We focus on presenting the results for the outcome of responders in the main content; those for dropouts are given in Supplemental Appendix B. A total of 356 trials with the outcome of responders were obtained. Among them, the median of arm-specific sample sizes was 71 with interquartile range (IQR) 35–126, and that of the arm-specific events (responders) was 34 with IQR 15–63. Moreover, 288 (81%) trials had sample size ratios (calculated as the ratio of the larger sample size divided by the smaller sample size within each trial) <1.1, while the remaining 68 (19%) trials had sample size ratios ≥1.1. Figure S3 in Supplemental Appendix C presents the distribution of the trials’ sample size ratios.

Figure 4 presents the distributions of the 356 trials’ FIs based on Fisher’s exact test and chi-squared test. Using Fisher’s exact test, 86 trials’ results were significant, while 270 were non-significant. The FIs ranged from 1 to 31, with a median 5 (IQR, 3–9). Among the 86 significant results, the median FI was 4 (IQR, 1–7); among the 270 non-significant results, the median FI was 6 (IQR, 3–9). Based on the chi-squared test, the numbers of trials with significant and non-significant results were 76 and 280, respectively. The bar plot (Figure 4B) had a roughly similar trend to that produced by Fisher’s exact test (Figure 4A), with an overall median FI (among all 356 trials) around 5. In both bar plots, more trials tended to have smaller FIs (indicating potentially more fragile results), while fewer trials tended to have larger FIs (indicating potentially more robust results). Despite of the similarity, noticeable differences existed between the FIs’ distributions produced by the two different tests. For example, Fisher’s exact test yielded more trials with very small FIs (say, <4) compared with the chi-squared test.

Figure 4. Bar plot of fragility indexes in the randomized controlled trials on antidepressant drugs with the outcome of responders.

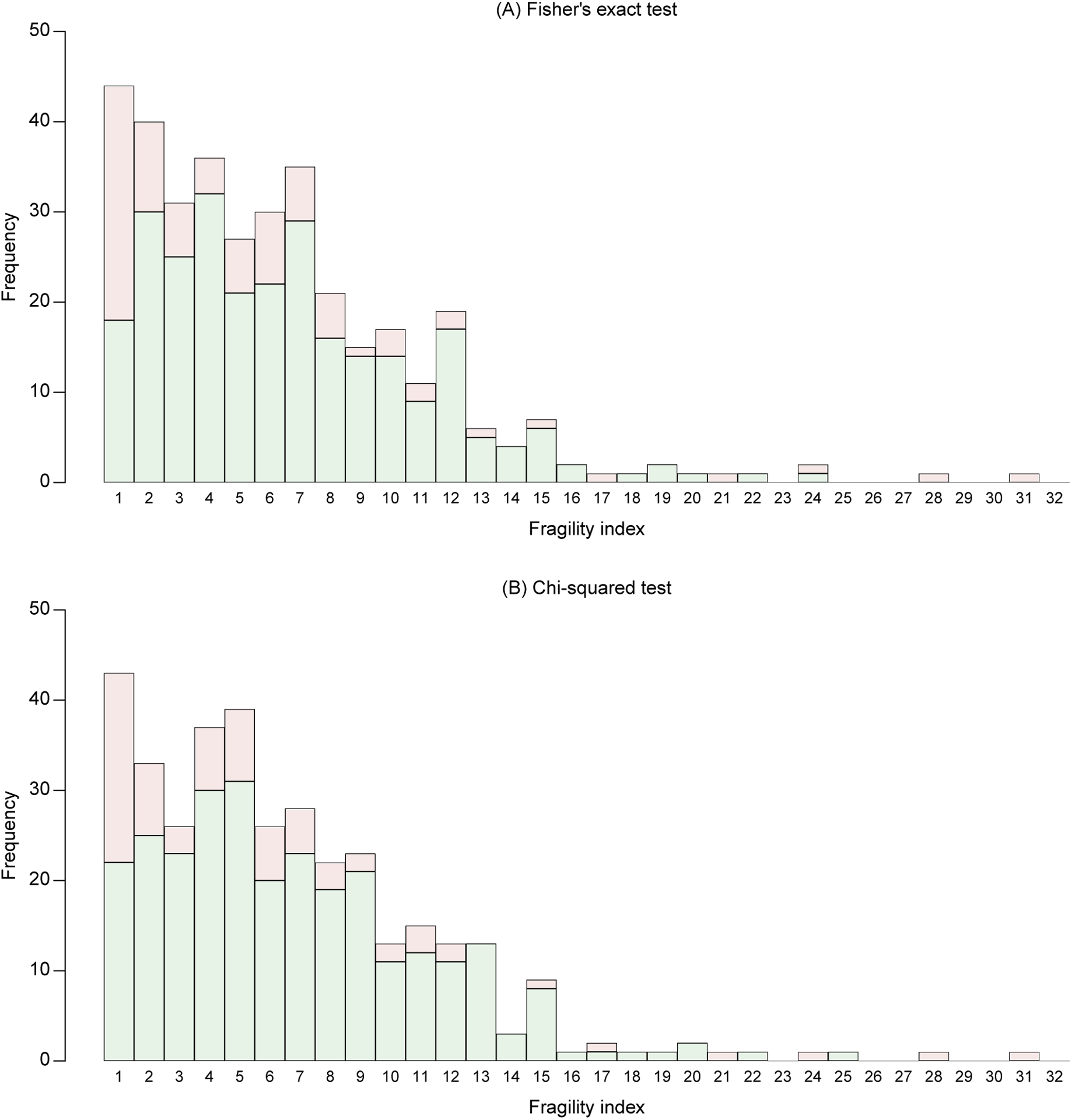
The fragility indexes are derived using Fisher’s exact test (A) and chi-squared test (B) at the significance level 0.05. Bars in green represent fragility indexes that alter non-significance to significance, and those in red represent fragility indexes that alter significance to non-significance.

Figure S4 in Supplemental Appendix C presents the distributions of FIs based on effect measures of OR, RR, and RD. The numbers of trials with significant and non-significant results were 91 and 265 using the OR, 88 and 268 using the RR, and 99 and 257 using the RD, respectively. Their bar plots also had roughly similar trends to those in Figure 4.

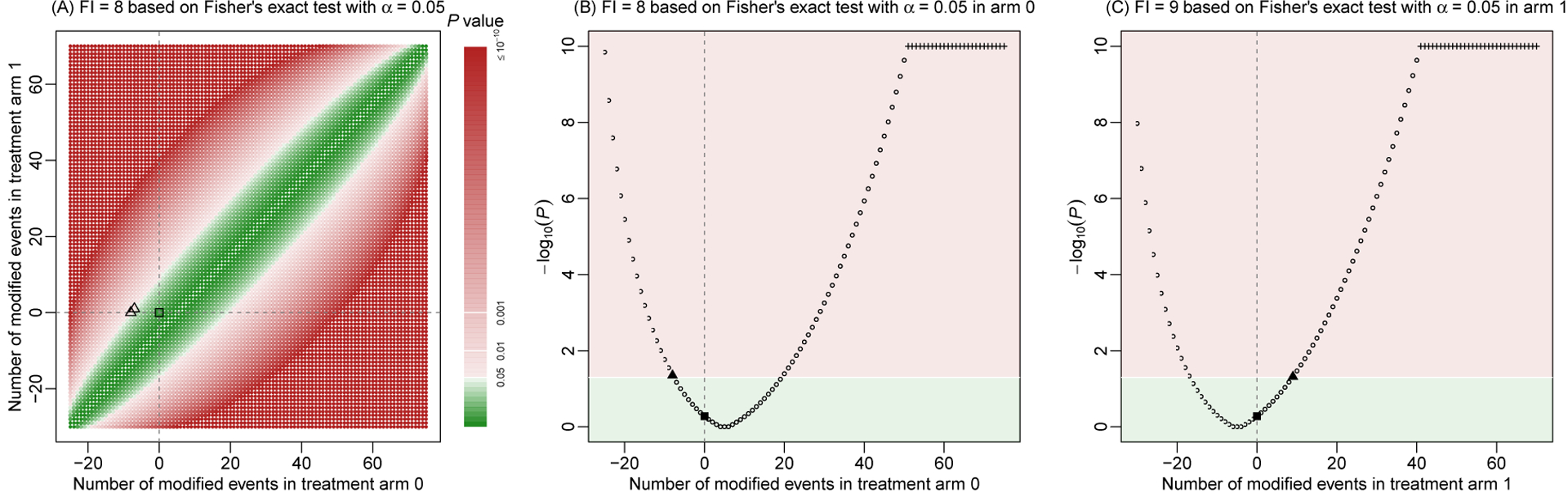
Moreover, when restricting event status modifications to either arm 0 or arm 1, the produced FIs of some trials were strictly larger than the FIs with modifications in both arms. Based on Fisher’s exact test, chi-squared test, OR, RR, and RD, the numbers of such trials were 8, 10, 7, 3, and 2, respectively. For example, Figure 5A shows the FI’s visualization of the trial by Cohn and Wilcox.³⁸ Using Fisher’s exact test, the FI was 17 with modifications in both arms, while it became 18 if modifications were restricted to arm 0 or arm 1.

Figure 5. Three examples from the randomized controlled trials on antidepressant drugs with the outcome of responders.

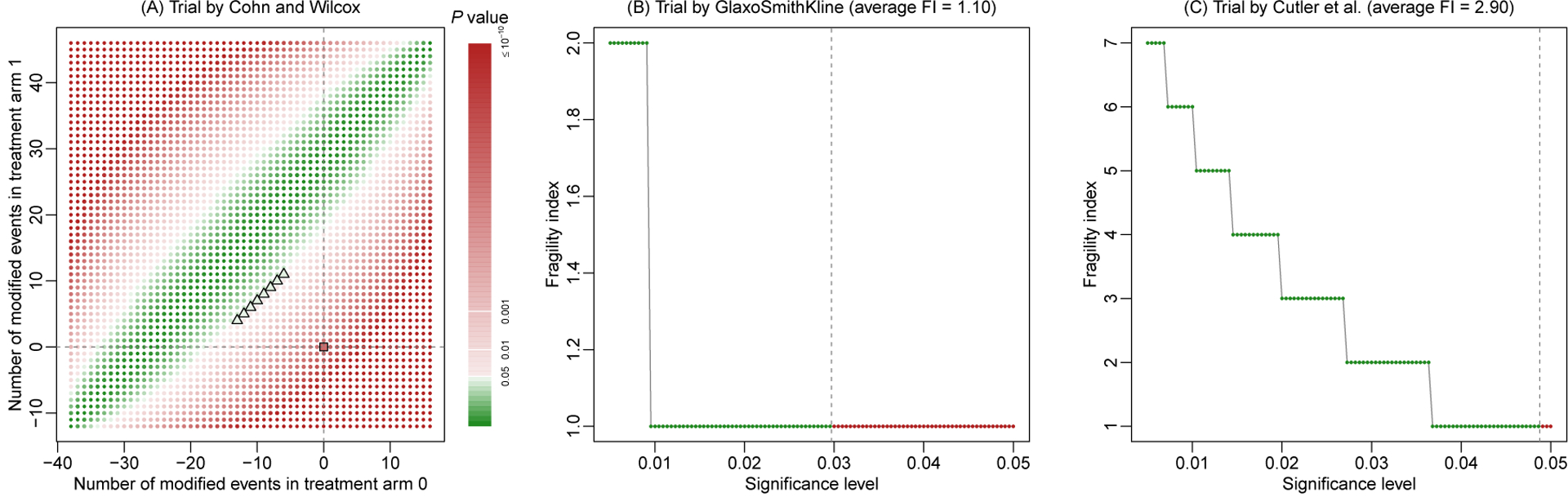
They include the trials by Cohn and Wilcox³⁸ (A), by GlaxoSmithKline (B), and by Cutler et al.³⁹ (C).

Figure S5 in Supplemental Appendix C presents the histograms of trial-specific average FIs based on Fisher’s exact test and chi-squared test when the significance level varied from 0.005 and 0.05. Figure S6 presents those based on effect measures of OR, RR, and RD. These histograms had some noticeable differences from the bar plots of FIs in Figures 4 and S4 at the significance level 0.05; the average FIs were generally larger than the FIs.

Figures 5B and 5C give two examples to illustrate the advantage of assessing FI at multiple significance levels. They are trials by GlaxoSmithKline and Cutler et al.³⁹ When the significance level was fixed at 0.05, both trials had FIs of 1 based on Fisher’s exact test. However, as the significance level decreased to 0.005, the FI of the trial by GlaxoSmithKline increased to 2 with an average FI of 1.10, while that of the trial by Cutler et al.³⁹ increased gradually to 7 with an average FI of 2.90. The average FIs indicated that the former trial tended to be more fragile than the latter trial.

Discussion

This article has explored several factors that impact the derivation of the FI. Specifically, the FI depends on the treatment arm(s) in which event status is modified, whether the original study result is significant, the statistical method used for calculating the P-value, and the threshold for determining statistical significance. All these factors should be carefully described when reporting the FI of a clinical study. Also, this article has proposed visualization methods to clearly demonstrate a study result’s fragility. They are potentially useful tools to help investigators better appraise the study conclusion’s reliability, in addition to using the single value of the FI.

By its definition, the FI may be considered as an absolute measure of fragility; it does not account for the sample size in the study. However, sample sizes may differ dramatically across studies; for example, among the trials on antidepressant drugs with the outcome of dropouts, the minimum and maximum trial-specific sample sizes are 7 and 1019, respectively. One event status modification is relatively large in the former trial (1/7=14.3%), while it may be negligible in the latter trial (1/1019<0.1%). Consequently, a relative measure, fragility quotient (FQ), may be used when researchers aim at comparing the fragility across different studies.⁴⁰ It is simply calculated as the FI divided by the study’s total sample size. Because the FQ is a linear transformation of the FI, the properties of the FI discussed in this article can be trivially extended to the FQ.

Moreover, this article focuses on the framework of individual studies. Recently, Atal et al.²⁹ extend the FI to the setting of meta-analyses that synthesize multiple independent studies on certain common topics. As meta-analyses have been increasingly used to aid medical decision making, it is also important to evaluate the certainty in their synthesized evidence.⁴¹ The replicability of meta-analyses has also been of great concern^7,42; the FI offers a potential tool to evaluate their results’ fragility. Nevertheless, meta-analyses involve more factors (e.g., between-study heterogeneity) that may impact the fragility than individual studies. Future work is needed to investigate the properties of meta-analyses’ FIs.