Accounting for the Central Role of Interfacial Water in Protein–Ligand Binding Free Energy Calculations

Abstract

Rigorous binding free energy methods in drug discovery are growing in popularity because of a combination of methodological advances, improvements in computer hardware, and workflow automation. These calculations typically use molecular dynamics (MD) to sample from the Boltzmann distribution of conformational states. However, when part or all of the binding sites is inaccessible to the bulk solvent, the time needed for water molecules to equilibrate between bulk solvent and the binding site can be well beyond what is practical with standard MD. This sampling limitation is problematic in relative binding free energy calculations, which compute the reversible work of converting ligand 1 to ligand 2 within the binding site. Thus, if ligand 1 is smaller and/or more polar than ligand 2, the perturbation may allow additional water molecules to occupy a region of the binding site. However, this change in hydration may not be captured by standard MD simulations and may therefore lead to errors in the computed free energy. We recently developed a hybrid Monte Carlo/MD (MC/MD) method, which speeds up the equilibration of water between bulk solvent and buried cavities, while sampling from the intended distribution of states. Here, we report on the use of this approach in the context of alchemical binding free energy calculations. We find that using MC/MD markedly improves the accuracy of the calculations and also reduces hysteresis between the forward and reverse perturbations, relative to matched calculations using only MD with or without the crystallographic water molecules. The present method is available for use in AMBER simulation software.

Graphical Abstract

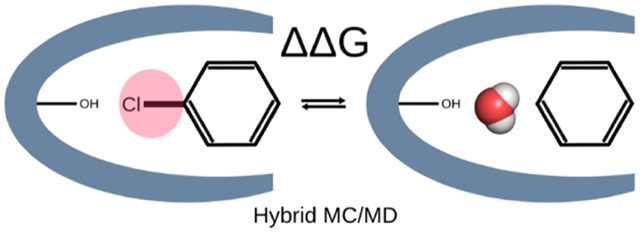
1. INTRODUCTION

The identification of a small organic molecule that binds a targeted protein with high affinity is a key early challenge in many drug discovery projects. A range of computational methods to estimate the affinity of candidate drug molecules for proteins have been developed to assist at this stage.^1–7 In recent years, advancements in both computer hardware and software^8–14 have enabled increasing application of relatively detailed molecular simulations to this problem. In particular, building on fundamental work on both theory and methods,^15–22 it is now feasible to integrate rigorous free energy methods into the drug design process.^23–27

Free energy methods require sampling the configurations of the aqueous protein–ligand complex from the Boltzmann distribution defined by a potential function, or force field.^28–31 These configurations are usually generated using molecular dynamics (MD) simulations,^32–35 but Monte Carlo (MC) methods may also be employed.^36–38 Given a method that provides correct sampling of a molecular system at equilibrium, one may choose among several methods of computing the difference in the free energy between two states of the system. These methods include thermodynamic integration (TI),³⁹ free energy perturbation (FEP),⁴⁰ Bennett acceptance ratio,⁴¹ and multistate Bennett acceptance ratio (MBAR).⁴² Perturbing all the way from the initial to the final state, although feasible in principle, usually leads to convergence problems, so it is common instead to compute the free energy difference by running equilibrium simulations at each of a series of small steps that interpolate between the initial and final states. Additional methods allow the calculation of free energy differences from nonequilibrium simulations, in which the progression from initial to final is forced to occur too fast for the simulations to generate equilibrium distributions.^43–47

In the context of computer-aided drug design, free energy methods may be used to compute the standard free energy of binding²⁰ by interpolating between the bound and unbound states with steps along a physical pathway, in which the ligand is stepwise removed from the binding site,^18,48,49 or a nonphysical, or alchemical, pathway, in which the ligand is artificially decoupled from the binding site and then recoupled with bulk solvent.^20,50,51 Standard binding free energy methods are often termed “absolute binding free energy” (ABFE) calculations to distinguish them from “relative binding free energy” (RBFE) calculations,^15,24,25 which provide the difference in binding free energy of two chemically similar ligands by perturbing one into the other within the binding site and then in bulk solution, and then using thermodynamic closure to connect these differences with the difference between their binding free energies (Figure 1). Because converting one ligand to another is a nonphysical process, RBFE calculations are also termed alchemical.

Figure 1.

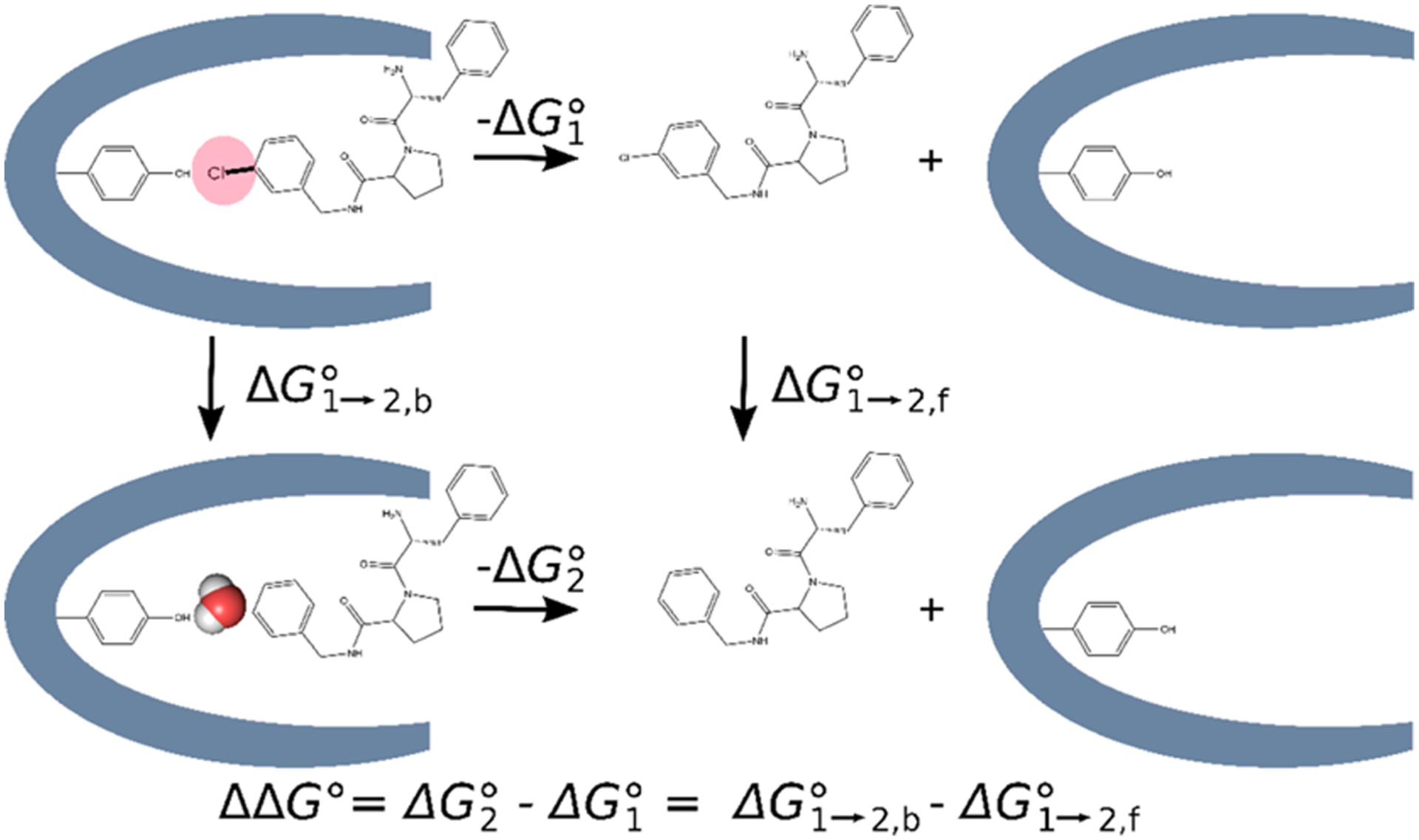
Thermodynamic cycle used in relative binding free energy (RBFE = ΔΔG°) calculations where the hydration of the binding site differs between the two ligands. The RBFE is calculated as the difference between the free energies of converting ligand 1 into ligand 2 in the binding site versus in solution.

In some drug design projects, the crystal structure of the targeted binding pocket reveals a buried cavity that has no channel through which water can enter or exit.⁵² Thus, water in the pocket can exchange with bulk water only through conformational fluctuations that open the binding pocket. Such fluctuations are generally infrequent relative to the time scales necessary to impact drug discovery projects using current simulation methods and accessible hardware. This situation poses a challenge for binding free energy calculations in which the hydration of the pocket requires change when going from the initial to the final state. Thus, in alchemical ABFE calculations, decoupling of the ligand from the binding site leaves an empty binding pocket which usually should become hydrated. Similarly, when one uses alchemical RBFE methods to compare the binding free energy of two ligands of different sizes and/or polarities, the number of waters bound along with the ligand often ought to change. Commonly used MD simulations cannot replicate these changes in the hydration of buried cavities, so the number of waters in the pocket remains constant, rather than adapting properly to changes in the ligand, and this structural error can lead to errors in computed free energies. In addition, if one runs the same perturbation in both directions—for example, going from ligand 2 to ligand 1 instead of ligand 1 to ligand 2—where the two starting states have different numbers of buried waters, the two free energies may be quite different. Such differences, termed hysteresis, are a sign of inadequate sampling in free energy calculations, as the free energy is a state function and the free energy change on going from state 1 to state 2 is the additive inverse of the free energy change on going from state 2 to state 1. Here the problem is inadequate sampling of water moves into and out of the binding site.

This problem can be addressed by including MC steps that can exchange water molecules into and out of the binding pocket without following a physically realizable path. When done with the correct Metropolis acceptance criterion,⁵³ the added MC steps should, like MD, sample from the desired thermodynamic distribution and thus rigorously yield the free energy. This approach is particularly valuable in the real-world situation in which one does not have advance knowledge of the numbers of buried waters, which is common in prospective drug discovery applications. Early work along these lines mixed regular MD sampling with grand canonical (GC) MC steps, which add or remove water molecules to or from the protein-solvent system in a manner that preserves the thermodynamic distribution for the appropriate chemical potential of water, and used this method to improve sampling in protein–ligand binding free energy calculations.⁵⁴ A recent preprint also shows that using a conceptually similar hybrid GC/MD approach during ligand perturbations in free energy calculations reduces hysteresis and somewhat lowers errors, relative to experiment, relative to pure MD, across a large number of test cases.⁵⁵ The use of GC to set up water occupancies along the perturbation steps of RBFE calculations, without sampling water occupancies during ligand perturbations, also has been shown to reduce hysteresis.⁵⁶ The GC method has been successfully applied to ligand binding free energies in the context of a pure MC algorithm,⁵⁷ which did not include full sampling of protein coordinates. However, the GC method adds complications related to setting the chemical potential of water and to fluctuations in the number of waters in the simulated system.

We recently reported a combined MC/MD approach that equilibrates water between buried cavities and the bulk without requiring the GC machinery and the resulting changes in particle number.⁵⁸ This method, which is available in the AMBER simulation package,^59,60 alternates blocks of standard MD steps with blocks of translational MC water move attempts executed within a rectangular region that overlaps with both the protein interior and the bulk solvent. The translational moves allow water molecules to exchange between bulk and buried cavities, while maintaining a Boltzmann distribution of states. In particular, water molecules can exit or enter the buried binding site as a ligand grows or contracts during the alchemical process of an RBFE calculation. The present MC/MD methodology thus should match the capability of GC/MD to enhance RBFE calculations, but in a less complex manner.

Here, we report the first application of the MC/MD method to the calculation of RBFEs for pairs of ligands that bind to buried protein cavities and that, when bound, are associated with different numbers of water molecules. We also compare this approach with other protocols for handling binding site hydration, including methods based on standard MD simulations. The MC/MD approach yields notably lower hysteresis and better agreement with experiment.

2. METHODS

2.1. Overview.

We compared four methods of treating binding site hydration in calculations of RBFEs between paired ligands that occupy buried protein cavities. For each pair, one ligand is smaller than the other, and crystallographic data drawn from the Protein Data Bank (PDB)^61–63 indicates that the extra space associated with the smaller ligand is occupied by at least one additional buried water molecule (Section 2.2). Two of the methods (methods 1 and 2) use our previously developed MC/MD code, which allows water molecules to equilibrate between bulk solvent and buried sites,⁵⁸ and two (methods 3 and 4) use only standard MD with different initial water configurations. All four methods (Figure 2) follow the same overall protocol, starting from a crystal structure of the protein with one of the two ligands. They all carry out an initial water placement by the usual method of superimposing a pre-equilibrated box of water on the protein–ligand system and discarding waters that clash with the solutes. This hydrated system is then replicated to generate a separate simulation for each of a series of windows along the alchemical change of the initial ligand to the final ligand, and the water structure in each of these simulations is allowed to relax with an equilibration simulation in which all nonhydrogen protein and ligand atoms are restrained to their initial coordinates. The progress from the initial to final window is scaled by the quantity λ, which goes from 0 to 1. Finally, production simulations with all atoms mobile are done for each λ window to compute the free energy change upon converting the initial ligand to the final ligand. Within this framework, the methods are distinguished as follows.

Figure 2.

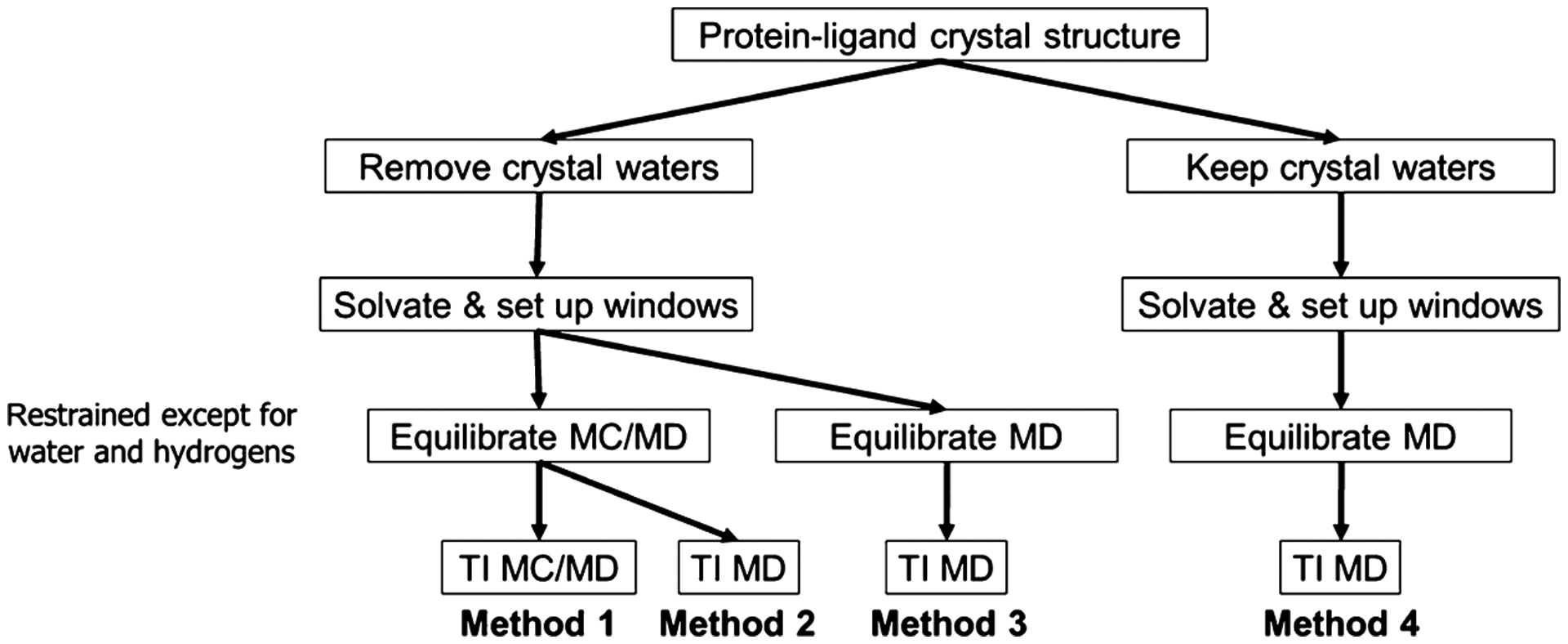
Four methods explored in this work for dealing with water molecules in the binding site. See text for details.

Method 1 strips out the crystallographic waters before the initial hydration step and then uses MC/MD during both the equilibration step and the free energy production step. Thus, water occupancy is customized to each λ window during equilibration and can continue to vary within each window during the production simulations.

Method 2 is the same as method 1, except that standard MD is used during the free energy production step. Thus, water occupancy is again customized to each λ window by the MC steps during equilibration but then may be effectively fixed during the production simulations, if the protein cavity is not open to allow direct exchange with the bulk.

Method 3 also strips out the crystallographic waters before the initial hydration step but uses only standard MD during both the equilibration and production phases. Thus, water occupancy is determined by the initial hydration step and is the same for all λ windows, rather than being allowed to equilibrate between the binding cavity and the bulk as in methods 1 and 2.

Method 4 is the same as method 3, except that crystallographic waters are retained.

2.2. Test Systems.

Our test systems are pharmaceutically relevant protein–ligand systems that meet the following criteria: (A) the binding pocket in crystal structures with bound ligand is a buried cavity; that is, it has no channel to the bulk large enough to allow a water molecule to enter or exit. (B) There are at least two inhibitors that share a chemical scaffold and differ from each other only by a small modification, and for which bound poses are available from crystal structures or could reasonably be constructed from existing cocrystal structures. (C) Of these, we could find two ligands with different numbers of buried water molecules trapped between the ligand and protein. (D) Experimentally measured binding free energies are available for both ligands. As detailed in Figure 3 and Table 1, the test systems are: Heat shock protein 90 (HSP90) with four ligands in two perturbations; Scytalone dehydratase and Bruton’s tyrosine kinase (BTK), each with two ligands in one perturbation; thrombin with four ligands in three perturbations; and OppA with four peptides in two perturbations. Prior free energy calculations have been reported for OppA with a different set of peptides;⁶⁴ the present cases were chosen for their large changes in water content. Here, we created ligand IDs comprising the first letter of the first author’s surname followed by the identifier used for the molecule in the publication. The peptides are named according to the one letter code of the amino acids (Figure 3; Table 1). Cocrystal structures are not available for inhibitors D13b and C3d, but cocrystal structures are available for the other compounds in their perturbations (D15b in 4FCP and C5d in 5STD, respectively). We constructed the required poses by docking D13b and C3d with the atoms they have in common with D15b and C5d, respectively, superimposed onto the available crystallographic coordinates.⁶⁵ Imposing requirements A–D led to a relatively small dataset designed to give a detailed picture of how the mechanics of the method play out in well-characterized systems. Larger scale benchmarking will be useful in the future to provide a statistical account of its performance.

Figure 3.

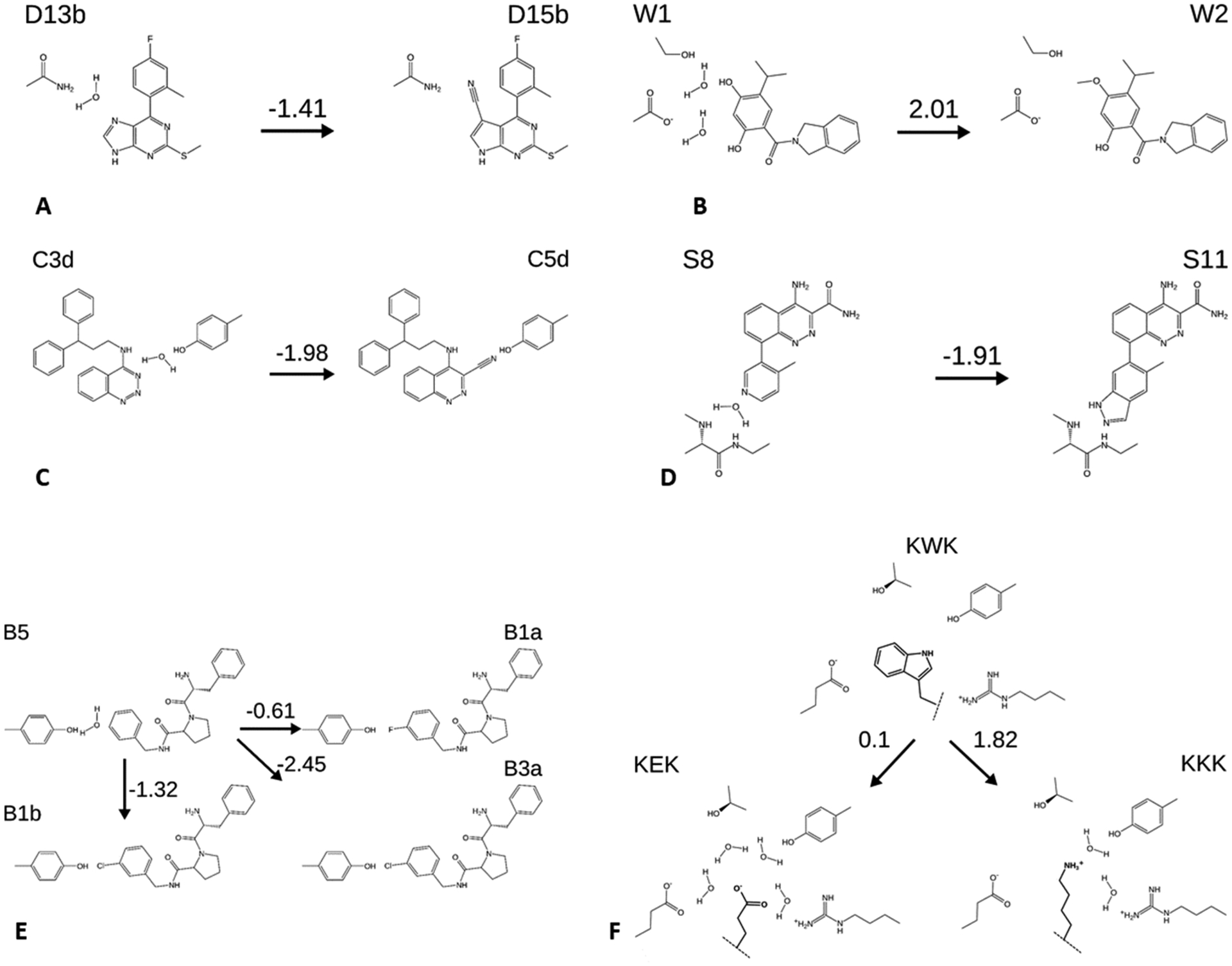
Perturbations considered in this study, with schematic representations of water displacements and selected neighboring side chains. Numbers above arrows are the experimental free energy changes (kcal mol⁻¹). (A,B) Ligands D13b and D15b and W1 and W2, all HSP90 inhibitors. (C) C3d and C5d, Scytalone dehydratase inhibitors. (D) S8 and S11, BTK inhibitors. (E) B1a, B1b, B3a, and B5, thrombin inhibitors. (F) peptides KEK, KKK, KWK, OppA inhibitors. Dashed lines indicate linkage to the rest of the peptide, which is not changed in these perturbations. Structures are shown with the charge states used in the simulations. Binding free energies are draw from the citations in Table 2.

Table 1.

Ligands and Proteins Used to Construct the Dataset in This Work^a

	ligand 1		ligand 2
protein	name	PDB ID	name	PDB ID	Ndisp; Figure 3 panel
HSP90	D13b	4FCP66*	D15b	4FCQ66	1; A
	W1	2XAB67	W2	2XJG67	2; B
Scytalone dehydratase	C3d	5STD68*	C5d	3STD68	1; C
BTK	S8	4ZLZ69	S11	4Z3V69	1; D
thrombin	B1b	2ZC970	B5	2ZFF70	1; E
	B3a	2ZF070			1; E
	B1a	2ZDV70			1; E
OppA	KKK	2OLB71	KWK	1JEV72	2; F
	KEK	1JEU72			4; F

^aN_disp: the number of buried waters displaced in each perturbation, based on the crystal structures. Figure 3 panel: panel in Figure 3 showing each perturbation.

^*indicates structures built from closely related ligands cocrystallized with the same protein. Citations provide both structural and binding affinity data.

2.3. Simulations and Free Energy Calculations.

All systems were constructed using the TIP3P water model,⁷³ the ff14SB^74,75 force field for the protein, and GAFF2⁷⁶ for the ligands. Ligands and protein–ligand complexes were solvated in rectangular boxes using tleap, with initial buffer sizes of 12 and 8 Å, respectively. The net charge of each system was neutralized by the addition of K⁺ or Cl⁻ ions as appropriate. The simulations were performed on graphics processor units (GPUs) with AMBER18’s GPU-accelerated PMEMD simulation code.^9,10,77,78 During equilibration, Cartesian restraints to the starting structure were applied to all ligand and protein heavy atoms, with a force constant of 5 kcal mol⁻¹ Å⁻². After a brief minimization (50 steps of steepest descent plus 450 steps of conjugate gradient), the system was sequentially heated at a fixed volume with linear ramps joining the temperatures 5, 100, 200, and 298.15 K, at 20 ps per ramp, with each ramp followed by an additional 20 ps with pressure coupling. The resulting setups then were converted to alchemical topologies by mapping the initial ligand’s atoms to the atoms of a new ligand, with a maximum common substructure algorithm as implemented in RDKit.⁷⁹ At this stage, the hydrogen masses were also increased to a target mass of 3.024 amu by repartitioning mass from the nearest bound heavy atom.^80,81 The heating steps were then repeated at each alchemical coupling value (λ window), and water structure was then equilibrated. Restraints were then removed, and the production simulations were conducted.

All simulations used a Langevin integrator with a 2 fs timestep for heating and equilibration and 4 fs for production with a friction coefficient of 2 ps⁻¹. Heating steps were run in NVT, while equilibration and production steps were run in NPT with pressure regulated at 1 atm with a MC barostat.⁸² The SHAKE algorithm^83,84 was used to constrain hydrogen bond lengths, except when the bond involves a softcore atom; that is, one that changes between the two end states.⁸⁵ The standard AMBER protocol for nonbonded interactions was followed. Thus, the particle mesh Ewald (PME) method⁸⁶ was used for periodic boundary conditions with an 8 Å cutoff for the short-ranged PME contribution as well as Lennard-Jones (LJ) interactions. A long-range continuum correction was used for the dispersive term.⁸⁷

The TI free energy calculations were done in three stages^88,89 following a previously described protocol:⁹⁰ decharge, LJ, and recharge. At the outset, a common set of atoms between the two ligands is established. The atoms in each ligand outside this set are then labeled as the two “softcore regions”. In the decharge stage, charge interactions only are removed from the first softcore region at λ windows of 0.0, 0.25, 0.5, 0.75, and 1.0. All interactions with the other ligand are neglected. During the LJ phase the repulsive/dispersive interactions on the first softcore region are turned off while those of the second region are turned on. The bonded and charge interactions in the common set of atoms are also switched at this time using λ windows of 0.0, 0.0479, 0.1151, 0.2063, 0.3161, 0.4374, 0.5626, 0.6839, 0.7937, 0.8849, 0.9521, and 1.0. The recharge stage uses the same protocol as the decharge stage except in reverse and using the second ligand. Note that, although we used TI,^39,91,92 other methods, such as MBAR,⁴² could also be used in this protocol.

The reported RBFEs are calculated by subtracting the free energy of alchemically mutating the free ligand from the free energy of alchemically mutating the bound ligand (Figure 1). For perturbations KWK–KKK and KEK–KWK, because they involve a change in the total charge of the molecule, we applied the finite box-size correction proposed by Rocklin et al. using a simple Poisson–Boltzmann approximation at the alchemical endpoints.^93,94 The final results are then compared to experimental values (Section 2.2). Each ligand pair was run in both directions, that is, with each ligand playing the role of the starting ligand and the final ligand, to enable evaluation of the hysteresis. In addition, each of these calculations was run five times with different random number seeds, to enable evaluation of the variance. The reported RBFEs (Table 2) are averages over all 10 runs both for the free and the bound states

$$\Delta \Delta G=\frac{1}{10}\left(\sum _{i=1}^5\left(\Delta G_{1\to 2,b,i}-\Delta G_{1\to 2,f,i}\right)-\sum _{i=1}^5\left(\Delta G_{2\to 1,b,i}-\Delta G_{2\to 1,f,i}\right)\right)$$

where ΔG_{1→2, x,i} is computed in the ith of the five forward perturbations for the bound and free state x = b and x = f, respectively, and ΔG_{2→1, x,i} is the corresponding backward perturbations, computed in the ith of the five. (Note that the two directions give free energy differences of opposite sign). The hystereses and variances for the perturbations of the ligands in solution were small (average of ~0.1 kcal mol⁻¹) relative to those of the bound ligands, so the hystereses and variances of the reported RBFEs trace almost entirely to the bound state calculations, and we focus on the hysteresis for the bound states

$$\text{hysteresis}=\frac{1}{5}\left(\sum _{i=1}^5\Delta G_{1\to 2,b,i}+\sum _{i=1}^5\Delta G_{2\to 1,b,i}\right)$$

Table 2.

Relative Binding Free Energies (kcal mol⁻¹) of all Perturbations Considered Here, and the RMSE for Each Method, Omitting the Perturbation of KEK–KWK, as Detailed in the Main Text^a

	experiment	method 1	method 2	method 3	method 4
D13b-D15b	1.41	3.13	3.19	3.34	3.11
W1-W2	2.01	0.93	0.51	−4.64	2.80
C3d-C5d	1.98	3.24	2.59	3.69	1.32
S8-S11	1.91	3.35	3.99	4.92	−0.11
B1b-B5	1.32	1.99	1.82	1.86	1.29
B3a-B5	2.45	1.08	1.04	0.93	0.85
B1a-B5	0.61	0.99	0.86	0.65	2.95
KWK-KKK	1.82	1.81	2.45	11.66	−5.73
KEK-KWK	0.10	15.61	16.46	18.16	13.63
RMSE*		1.13	1.27	4.46	3.02

^aThe values for the perturbations of KWK–KKK and KEK–KWK include the finite size corrections. Uncertainties over the five repetitions of each perturbation are presented in Table 3.

The reported standard deviations are computed separately for each group of five replicates (forward and backward) of the bound protein–ligand complex.

2.4. Equilibrating Buried Water Molecules.

The equilibration of buried water molecules was performed using our previously described MC/MD method which is implemented in AMBER.⁵⁸ In this method, the simulation alternates blocks of N_MC translational water move attempts with blocks of N_MD standard MDs time steps. As previously described, the MC moves occur only within a rectangular region that overlaps with the buried binding pocket and extends into bulk solvent (Figure 4). Here, the dimensions of this region were defined with a shift parameter of 8 Å as diagrammed in the figure. This is a conservative approach, which allows MC moves to translate water molecules into or out of any cavity that may exist or form throughout the protein. If one wishes to focus on equilibration of water between bulk and only the binding site, then a smaller box could be used. The rectangular region is filled with a steric grid that prevents move attempts into locations that are obviously blocked by existing protein or solvent atoms. The grid is recalculated prior to every MC cycle as described in ref 58. The MC blocks were performed at the same temperature as the MD and at constant volume.

Figure 4.

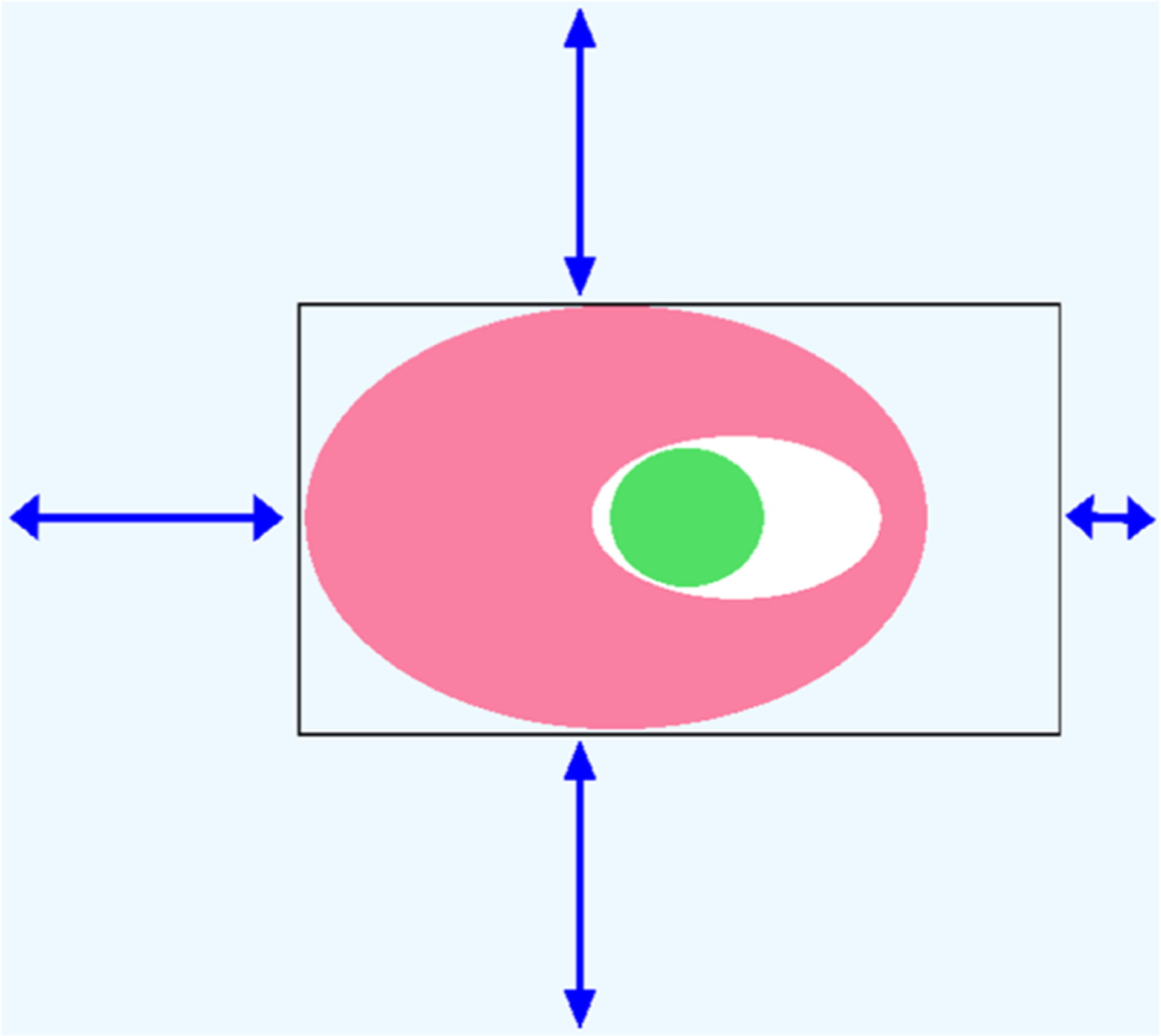
Schematic of the MC setup employed in this work. Light blue: simulation box. Black rectangle: perimeter of the rectangular MC exchange region, with its steric grid. Pink and green are the protein and ligand, respectively. The three longer arrows indicate the 8 Å shift of the grid from the edges of the simulation box. The short arrow on the right represents a smaller, 3 Å offset, which ensures that the box extends into bulk solvent and thus allows exchange between bulk and the interior of the protein.

Methods 1 and 2 (Section 2.1) used MC/MD during the equilibration stage. All heavy atoms of the protein and ligand were restrained, and alternating blocks of N_MD = 100 and N_MC = 1 × 10⁵ steps were carried out for a total of 25,000 MD time steps. Method 1 furthermore used MC/MD during the TI production calculations, with N_MD = 1000 and N_MC = 10,000 for a total of 500,000 MD time steps. Methods 3 and 4 were the same except that no MC steps were carried out (N_MC = 0). Thus, methods 2, 3, and 4 did not use MC/MD during the TI stage. This protocol was modified in two respects for the peptide ligands because of the large size of these compounds and the greater magnitude of the perturbations. First, for only the equilibration step, we increased the total number of MD steps from 25,000 to 250,000, maintaining N_MD = 100, N_MC = 1 × 10⁵. Second, to speed water sampling in the region of interest, we excluded only the softcore atoms from the steric grid, rather than the entire ligand as in the other perturbations. In this way, water moves into the binding pocket are attempted only at the specific site of the perturbation. The compute time effectively required for an MC step here is about the same as that for an MD step, so the extensive MC sampling, for the equilibration stage in particular, is time-consuming. However, the present protocol and grid specifications were not optimized for speed, and similar results may be obtainable with much fewer MC steps.

3. RESULTS AND DISCUSSION

3.1. Calculation Versus Experiment.

As indicated by the root-mean-square errors (RMSEs) in Table 2, methods 1 and 2, which both use the MC/MD technology to equilibrate water occupancy in the binding sites, yield notably better agreement with experiment than do methods 3 and 4, which do not allow waters to equilibrate between bulk and the binding sites. Note that the RMSE values exclude the results for KEK–KWK, for which all four methods yield errors of over 13 kcal mol⁻¹; this perturbation is examined separately in Section 3.3.3. As shown in the following subsection, the difference between methods [1, 2] and methods [3, 4] are large on the scale of the numerical uncertainties of the calculations. Thus, these results support the utility of the MC/MD procedure as a tool to improve the accuracy of free energy calculations involving buried binding sites.

Interestingly, the benefit from using MC/MD is obtained from the initial equilibration of water occupancy in each λ window (i.e. method 2). That is, on-going equilibration of water occupancy in the course of the production calculations, as done in method 1 but not method 2, does not afford more accuracy, at least for the present cases. The two methods that use only MD, and thus that do not equilibrate water between the binding site and the bulk, give quite different results when crystallographic waters are kept in place (method 4) versus when they are removed prior to initial solvation (method 3). Indeed, these two methods yield free energies that differ by up to 18 kcal mol⁻¹ (KWK–KKK, Table 2). Nonetheless, neither appears to be significantly more accurate than the other, based on their RMSE values of 4.1 and 3.6 kcal mol⁻¹ (Table 2). Across all methods, the finite-size correction contributed about −1.5 kcal mol⁻¹ to ΔΔG_KWK→KEK and about +1.5 kcal mol⁻¹ to ΔΔG_KWK→KKK, with standard deviations of 0.5–1.0 kcal mol⁻¹ across replicates.

3.2. Numerical Uncertainty and Hysteresis.

The mean standard deviations and hystereses of the FEPs, computed as given in Section 2.3, are almost all smaller than the scale of the differences in accuracy between the methods which use MC/MD (methods 1, 2) and those which use only MD (methods 3, 4). Thus, the mean standard deviations are all in the range 0.84–0.94 kcal mol⁻¹, and the mean hysteresis average 0.51–0.65 kcal mol⁻¹. (Note that KEK–KWK is again omitted from these statistics; see above). The only exception is method 4, whose mean hysteresis is larger, at 3.7 kcal mol⁻¹. This probably results from the fact that method 4 places different crystallographic waters for the two ligands, so the forward perturbation provides rather different results from the backward one. In contrast, the small hysteresis for method 3 probably results from the fact that the AMBER water placement procedure did not place any buried water molecules for either the ligand 1 or ligand 2 starting state. As a consequence, the forward and backward perturbations were both done without water in the binding site, producing low hysteresis but not a correct calculation. These results support the significance of the observations in Section 3.1. It is encouraging that most of the computed free energy differences are the same in both directions, as the free energy difference of a state change should be. However, it is worth emphasizing that low hysteresis does not imply good agreement with experiment. For example, the W1–W2 perturbation with method 3 has zero hysteresis (Table 3) but deviates from the experimental value by 6.7 kcal mol⁻¹ (Table 2).

Table 3.

Standard Deviations and Hystereses (kcal mol⁻¹) Associated with the RBFE Calculations Considered Here^a

	method 1		method 2		method 3		method 4
	SD	Hyst	SD	Hyst	SD	Hyst	SD	Hyst
D13b-D15b	0.49	0.39	0.60	0.26	0.36	0.16	0.72	0.3
W1-W2	0.99	0.59	0.97	0.78	0.56	0.00	0.73	6.61
C3d-C5d	1.31	1.41	1.4	0.47	1.51	0.11	1.4	1.48
S8-S11	1.13	0.18	1.02	0.36	1.07	0.98	0.91	0.25
B1b-B5	0.45	0.41	0.38	0.08	0.46	0.05	0.41	1.91
B3a-B5	0.44	0.01	0.44	0.03	0.4	0.33	0.3	1.14
B1a-B5	0.32	0.5	0.32	0.49	0.3	0.19	0.29	1.12
KWK-KKK	1.58	1.91	1.57	1.41	1.43	2.05	1.16	14.37
KEK-KWK	1.51	0.45	1.79	0.93	1.42	0.74	1.65	6.22
mean	0.91	0.65	0.94	0.53	0.83	0.51	0.84	3.71

^aSee Section 2.3 for definitions. The KEK–KWK perturbations are omitted from the means, as detailed in the main text.

3.3. Case Studies.

3.3.1. Changes in Water Occupancy along the W1–W2 Perturbation.

According to their respective cocrystal structures, going from ligand W1 (2XAB) to W2 (2XJG) is accompanied by displacement of two of three buried waters. We thus anticipated similar changes in the present perturbations. To check this, we examined how the water occupancy of the binding site varied with λ. As seen in Figure 5 (left), the final step of equilibration of W1 does start with an average of three water molecules, but as λ goes from 0 to 1, the mean number of waters fluctuates between about 1.5 and 3.0 in the early windows, falls to about 2.0 for most of the LJ windows, and then fluctuates between 1.5 and 2.0 as the charges become those of W2. Note that these equilibration runs are used by both method 1 and method 2, as diagrammed in Figure 2. The time- and replica-averaged number of waters shows a similar variation with λ during the TI production runs of method 1 (Figure 5, right), which are executed starting from the equilibrations. Thus, the water occupancies are similar to those at the end of the equilibration step Figure 5 (left), consistent with the observation (Section 3.1) that methods 1 and 2 give very similar free energies. The agreement between the water occupancy statistics between the two perturbation directions (red and blue in Figure 5, left and right panels) also helps explain the low hysteresis of these calculations.

Figure 5.

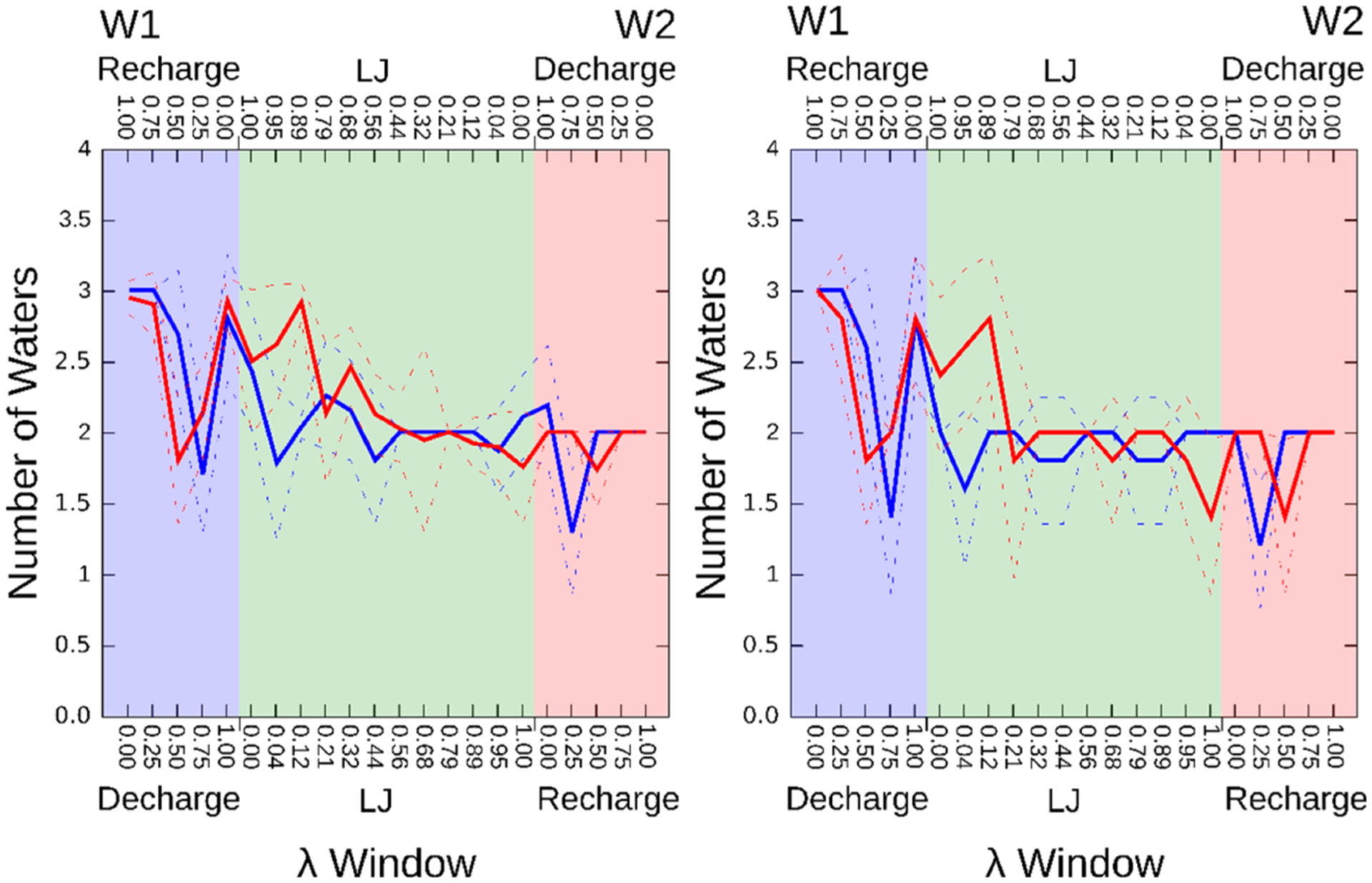
Computed mean water occupancies for each λ window in the W1–W2 perturbation. Blue: Perturbation W1 → W2 with the λ windows labeled at the lower X-axis. Red: Reverse perturbation, W2 → W1, with λ windows in reverse order as labeled at the upper X-axis. Dashed lines: show ranges defined by the standard deviations over the five repetitions. Left: Number of buried water molecules after the water equilibration step shared by methods 1 and 2 (see Figure 2), averaged over the five replicates. Right: Time- and replica-averaged number of buried water molecules for each λ window in the five TI production runs of method 1.

We examined the electron density of the W2 cocrystal structure and confirmed evidence for a single buried water associated with the ligand. Thus, the W2 simulations appear to overhydrate this structure. This could result from sampling issues, inaccuracies in the force field, and/or the fact that the crystallographic conditions (e.g., T = 100 K) differ from those at which the binding affinities were measured and under which these simulations were, accordingly, carried out. It is also conceivable that an alternative crystallographic refinement of this 2.25 Å resolution structure would accommodate another water molecule, in line with the simulations.

3.3.2. Water Sites in HSP90.

In contrast, the MC/MD calculations appeared to under-hydrate the structure of HSP90 with inhibitor D15b. Thus, the cocrystal structure (4FCQ⁶⁶) has three buried water molecules, while the simulations placed only waters 1 and 2 (Figure 6). In this case, however, examination of the electron density reveals that, although water sites 1 and 2 have distinct electron density, the electron density at water site 3 is less convincing, as shown in Figure 6. The electron density that was interpreted as a water appears to be continuous with the ligand density, rather than appearing as a discrete site. This might reflect partial occupancy by a different ligand, such as an impurity that may have been present in the mother liquor, or an alternate conformation of either a ligand or protein component. In this case, then, the MC/MD calculation may offer a more realistic picture of hydration in the buried cavity.

Figure 6.

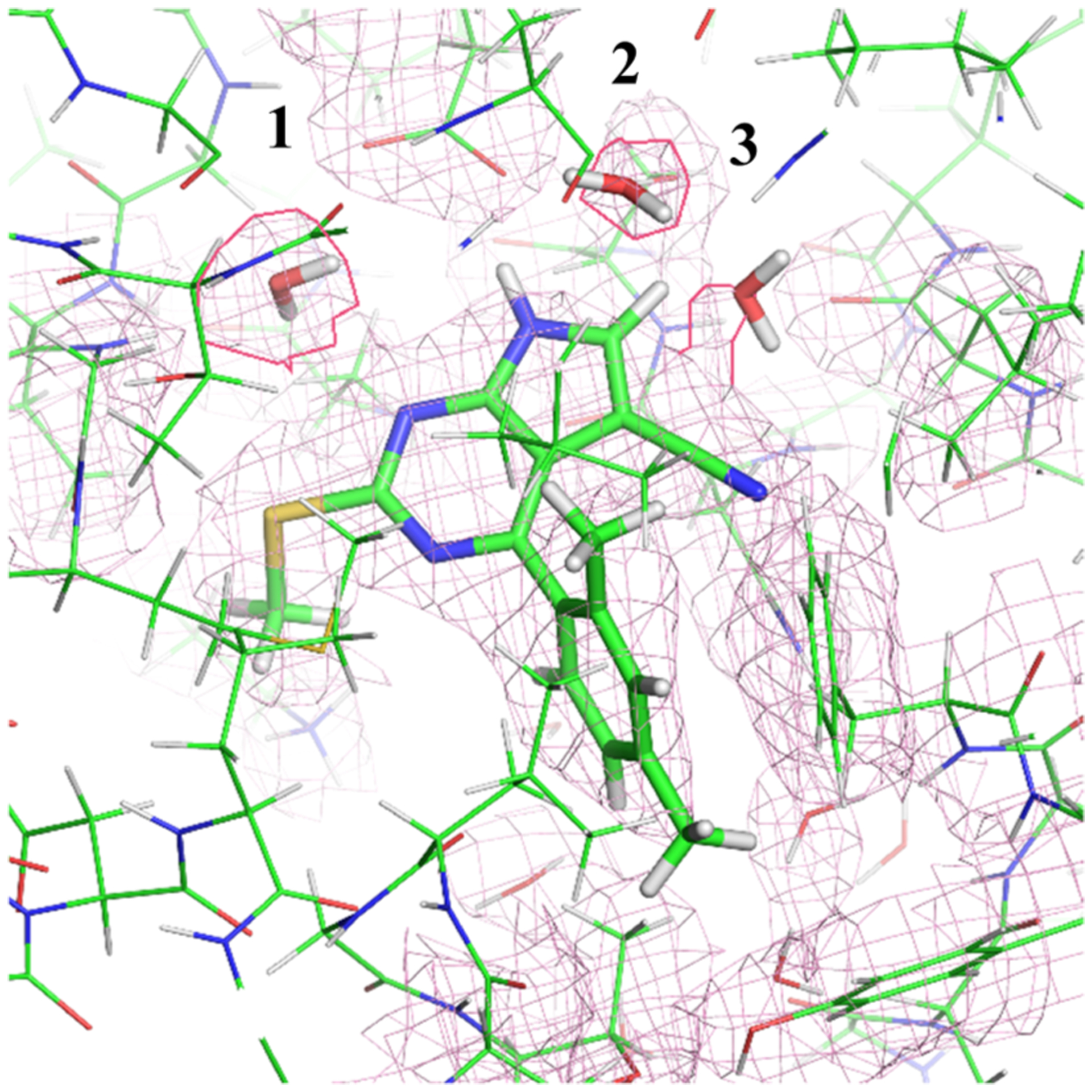
Examining the electron density map of the 4FCQ reveals that the right most water molecule displays a strange shape (as if it is a part of the ligand), suggesting it to not be a water molecule.

3.3.3. KEK–KWK Perturbation.

As noted in Section 3.1, the KEK–KWK perturbation is an extreme outlier, in the sense that none of the four water placement methods explored here leads to errors of less than 13 kcal mol⁻¹ relative to experiment. We, therefore, paid particular attention to how the MC/MD methods modeled the hydration. Going from KEK to KWK, the perturbation leads to displacement of four buried water molecules, according to the crystal structures (1JEU and 1JEV, respectively), and the electron density at the water sites appears to be well-resolved and distinct. We first examined the hydration states of the first decharge window (λ = 0.0) of KEK → KWK (Figure 7A) and the last recharge window (λ = 1.0) of KWK → KEK (Figure 7B). Both structures correspond to the fully present glutamic acid side chain and thus correspond to the cocrystal structure of KEK (1JEU).⁷² As shown in the figure, the four crystallographic water sites are reasonably well replicated by the simulations, although one water molecule is notably displaced in B. The hydration states of the first decharge window of KWK → KEK (Figure 7C) and the last recharge window of KEK → KWK (Figure 7D), which both correspond to the fully present tryptophan side chain, are compared with the cocrystal structure (1JEV, 2OLB) in panels C and D, respectively, of Figure 7. Here, two of three waters are properly placed.

Figure 7.

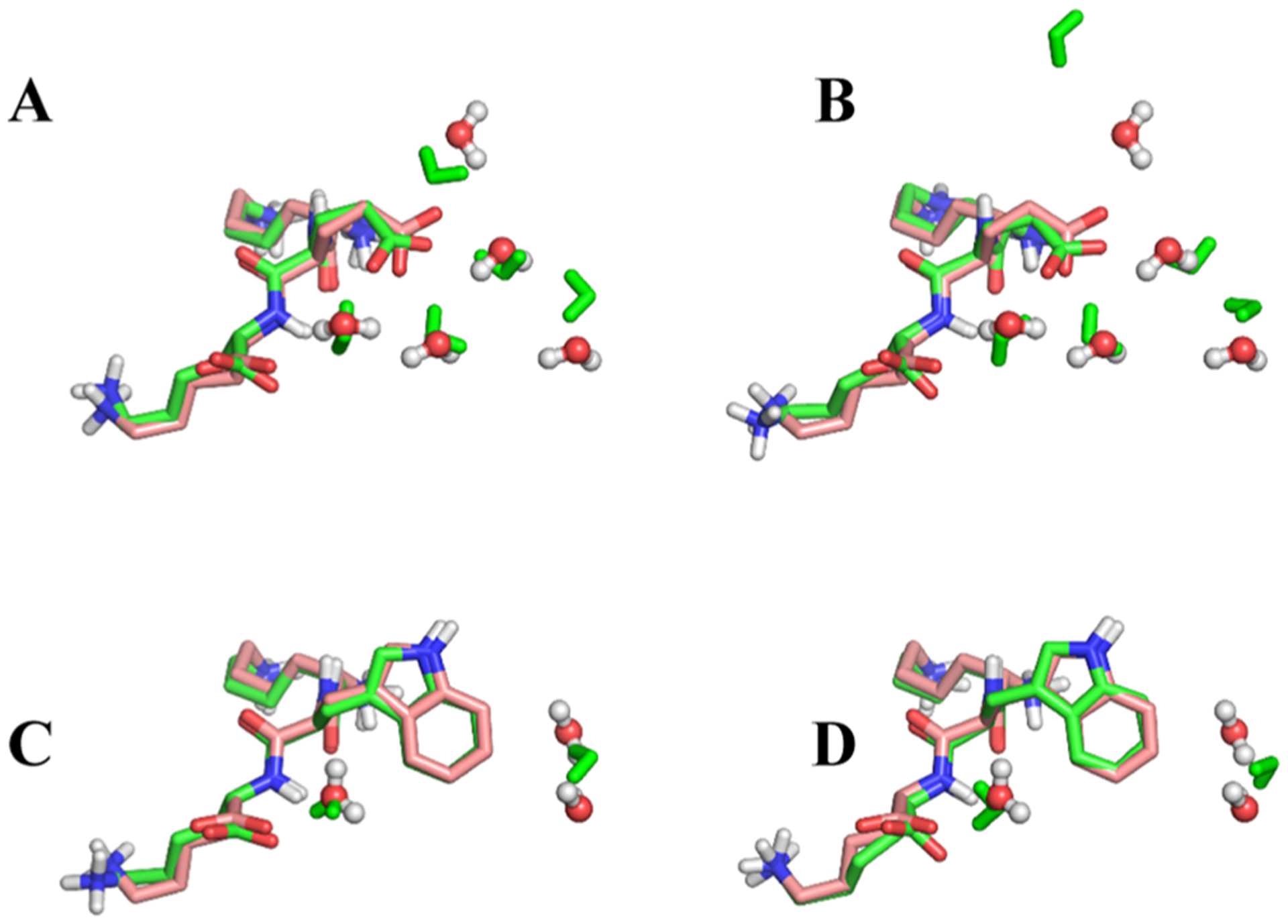
Crystal structures compared to the structures generated with MC/MD. For clarity, only the peptide KEK and the buried waters are shown. In A and B, the crystal structure of the 1JEU is compared to (A) first window of the perturbation KEK → KWK (decharge 0.0) and (B) last window of the perturbation KWK → KEK (recharge 1.0). In (C,D), the crystal structure of the 1JEV is compared to (C) first window of perturbation KWK → KEK (decharge 0.0), and (D) last window of the perturbation KEK → KWK (Recharge 1.0).

Thus, although water placement by the MC/MD method does not agree perfectly with experiment, the deviations are on a similar scale to those of other perturbations for which the RBFE calculations were far more accurate. We therefore considered whether inadequate sampling might be to blame. However, extending the λ window production simulations tenfold led to the same method 1 result to within 0.1 kcal mol⁻¹. This does not rule out sampling as the problem, but it makes this less probable. We also compared the simulated conformational preferences of the peptide and protein with the conformations in the respective crystal structures and did not observe any notable rearrangements. Given the change in the ligand’s net charge for this perturbation, and the potential for electrostatic interactions to make large energy contributions, it is natural to consider whether the treatment of electrostatics needs to be improved to reach a more accurate result. It is thus worth noting that the error for this perturbation is large both with and without the correction of electrostatic energies for the finite box size (Section 3.1). We conjecture that more accurate results might be obtained by use of an improved force field (e.g., with an explicit treatment of electronic polarizability), more extensive conformational sampling of the protein, or a more faithful representation of the biologically relevant system (e.g., inclusion of counterions around the perturbation). The fact that all four methods yield errors for this system that are similar in size and in the same direction suggests a shared source of error rather than random noise.

4. CONCLUSIONS

We find that allowing water molecules to equilibrate between the bulk solvent and protein interior, using the present hybrid MC/MD method leads to more accurate RBFE calculations for ligands that occupy buried binding sites. For the systems studied here, the improvement in RMS error, relative to pure MD, is ~2 kcal mol⁻¹, and the MC/MD results give an RMS error of ~1 kcal mol⁻¹, except for one case where all the methods fail. The MC/MD method also improves the internal consistency of the calculations, in the sense that it reduces the hysteresis of free energies obtained from forward and reverse perturbations, which should give identical results. These improvements presumably derive from the ability of this method to allow the number of buried waters associated with the ligand to change in concert with the alchemical perturbation of the ligand. Examination of the numbers and positions of the simulated waters shows the anticipated changes, although the agreement between simulation and crystallographic water sites remains imperfect. This likely reflects some combination of issues with sampling, force field, and the fact that the simulated conditions (e.g., temperature) were chosen to model the conditions of the binding assays rather than of the crystallography experiments. Interestingly, the accuracy of the calculations run with pure MD was not affected by whether crystallographic waters were retained or deleted during setup of the simulations.

With the present settings, the advantages of methods 1 and 2 relative to methods 3 and 4 come at a nontrivial cost in compute time. One reason is that we chose to err on the side of full convergence by using considerably more MC steps than we expected would be needed to equilibrate water occupancies, based on a prior study.⁵⁸ For practical applications, we would recommend a few initial trial calculations to get a sense for the number of MC steps needed for the system of interest, followed by production calculations using either method 1 or method 2 with this setting. Reductions in wall-clock time for a given number of MC steps should also be achievable by at least three algorithmic changes. First, running the MC steps on the GPU would save time by reducing communication between the GPU and the CPU. Second, one may compute the energy of a trial step as the change in the interaction energy of the moved water with all other atoms, instead of recomputing the full system energy. Third, the wall clock time needed for the MC steps can be reduced by taking advantage of algorithms that provide a valid Boltzmann distribution for MC trials run in parallel.^95,96

Although we focused on RBFE calculations, the present method is also expected to improve the accuracy of ABFE calculations involving ligands in buried binding sites, as recently highlighted.²⁷ In particular, double decoupling calculations²⁰ can leave the entire site empty without creating a channel to the bulk solvent. Allowing water to penetrate the site during the decoupling process may be essential to obtain accurate results. This is likely of less concern for ABFE calculations that follow physical pathways,^18,97 where forced removal of the ligand opens a channel to the bulk through which water can flow to reoccupy the site. However, there are cases where even these methods may benefit from the enhanced sampling of water, such as when a ligand is pulled from a deep, tunnel-like binding site that prevents water from back-filling until the ligand is entirely detached from the protein. Thus, there are a range of settings in which MC/MD and related methods should be of considerable value. The MC/MD implementation used here is available in current releases of the AMBER simulation package.