Abstract
A non-rigid MR-TRUS image registration framework is proposed for prostate interventions. The registration framework consists of a convolutional neural networks (CNN) for MR prostate segmentation, a CNN for TRUS prostate segmentation and a point-cloud based network for rapid 3D point cloud matching. Volumetric prostate point clouds were generated from the segmented prostate masks using tetrahedron meshing. The point cloud matching network was trained using deformation field that was generated by finite element analysis. Therefore, the network implicitly models the underlying biomechanical constraint when performing point cloud matching. A total of 50 patients’ datasets were used for the network training and testing. Alignment of prostate shapes after registration was evaluated using three metrics including Dice similarity coefficient (DSC), mean surface distance (MSD) and Hausdorff distance (HD). Internal point-to-point registration accuracy was assessed using target registration error (TRE). Jacobian determinant and strain tensors of the predicted deformation field were calculated to analyze the physical fidelity of the deformation field. On average, the mean and standard deviation were 0.94±0.02, 0.90±0.23 mm, 2.96±1.00 mm and 1.57±0.77 mm for DSC, MSD, HD and TRE, respectively. Robustness of our method to point cloud noise was evaluated by adding different levels of noise to the query point clouds. Our results demonstrated that the proposed method could rapidly perform MR-TRUS image registration with good registration accuracy and robustness.
Keywords: MR-TRUS, image registration, point cloud matching, finite element, deep learning
1. Introduction
Prostate cancer is the second most common malignant disease in men around the world. Prostate cancer accounts for about 28% of newly diagnosed cancers among men and is the leading cause of death from cancer (Weir et al., 2015). Transrectal ultrasound (TRUS) imaging is the standard imaging modality for cancer diagnosis and image-guided interventions, such as biopsy (Yacoub et al., 2012; Yang et al., 2011; Yang et al., 2015), brachytherapy (Reynier et al., 2004; Yang et al., 2014; Yang et al., 2017) and cryotherapy (Bahn et al., 2012) since TRUS is non-ionizing, widely accessible, inexpensive and real-time. Prostate brachytherapy is regularly used to treat prostate cancer using high-dose-rate (HDR), whole prostate gland irradiation (Challapalli et al., 2012). Dose escalation to the dominant intraprostatic lesion (DIL) after whole prostate irradiation was often used to improve tumor control in the initial site of DIL (Shaaer et al., 2019). However, it is difficult to delineate the tumor and DIL accurately on TRUS images due to the lack of soft tissue contrast.
Multiparametric MRI (mp-MRI) provides detailed anatomical and functional information which is unavailable on TRUS images (Bloom et al., 2018). Due to its superior soft-tissue contrast, mp-MRI has higher sensitivity and specificity for prostate cancer detection and characterization than TRUS (Shaaer et al., 2019; van de Ven et al., 2013). However, MRI is expensive, not as widely accessible as US and, most importantly, impractical to provide real-time image guidance for prostate interventions. It is beneficial to fuse TRUS and mp-MRI images to provide real-time image guidance with improved soft-tissue contrast (Dickinson et al., 2013; Zhang et al., 2015). MR-TRUS image registration could enable targeted biopsy and brachytherapy, which allow precise perineum biopsy needle insertion and brachytherapy catheter placement (Kadoury et al., 2010). In addition, it enables accurate DIL delineation which allows local radiation dose boost to DIL, leading to improved tumor control. Conventionally, MR-TRUS image registration is done manually by physicians. After rigid alignment of MR and US prostates, manual lesion delineation is performed to account for the complex prostate deformation (Shaaer et al., 2019). Prostate deformation could be induced by bladder and rectum filling, patient setup and TRUS probe. Manual registration allows only rigid registration and fails to account for the complex prostate deformation. In addition, manual registration process is physician dependent, time-consuming and irreproducible.
Single modality image registration such as CT-CT and MRI-MRI is often performed by minimizing image intensity differences between the fixed and moving images since images acquired with the same imaging modality have similar image intensities (Fu et al., 2018a). For multi-modality image registration such as CT-MRI registration, there is no direct image intensity correlation. As a result, statistical image texture similarities such as mutual information (MI) are often used in multi-modality image registration (Heinrich et al., 2012; Loeckx et al., 2010). For MRI-TRUS registration, it is very difficult to rely solely on image intensities due to the distinct image appearance between the two. Hence, the prostate shapes segmented from the MR and TRUS images should be utilized to facilitate the registration. Challenges are to segment the prostate with high accuracy and to regularize internal prostate deformation based on only surface-driven deformations. Spatial smoothing is commonly used to regularize the predicted deformation field. However, the over-simplified spatial smoothness constraint does not model the complex prostate deformation well. Accurate motion modelling is needed to account for the large prostate deformation induced by US probe. Therefore, it is important to develop an accurate MR-TRUS image registration method which overcomes the above-mentioned challenges simultaneously, including the lack of effective MR-TRUS image similarity metric and difficulties in accurate prostate segmentations and motion modeling.
2. Related works
Many methods have been proposed for MR-TRUS image registration (Hu et al., 2012; Hu et al., 2018b; Khallaghi et al., 2015a; Khallaghi et al., 2015b; Mitra et al., 2012; Sun et al., 2015; van de Ven et al., 2015; Wang et al., 2016; Wang et al., 2018; Yang et al., 2011; Yang et al., 2015). Generally, these methods can be categorized into three different groups, including intensity-based methods, surface-based methods and deep learning-based methods.
For intensity-based method, MI is often used as the image similarity measure between MR and TRUS. A variety of MI variants such as correlation ratio-based MI (Gong et al., 2017), contextual conditioned MI (Rivaz et al., 2014) have been proposed. However, MI does not model the spatial dependency of local structures well. Later, modality independent neighborhood descriptor (MIND) (Heinrich et al., 2012) was proposed by Heinrich et al. to calculate structural similarity across modalities. MIND accounts for the spatial structural dependency using local self-similarity measures. Sun et al. (Sun et al., 2015) used a multi-channel MIND as the image similarity measures for MR-TRUS image registration. Wang et al. (Wang et al., 2016) proposed to use MIND as a weighting factor for robust prostate surface point matching. Gabor wavelet was also used for feature extraction from MRI and TRUS images. Ou et al. (Ou et al., 2011) proposed to extract multi-scale and multi-orientation Gabor attributes which reflect the anatomical and geometric context around each voxel. The extracted Gabor attributes from MR and TRUS were then matched using a continuously-valued weighting function. Singh et al. (Singh et al., 2008) used manually identified landmarks to aid MR-TRUS image registration. Since TRUS provides very limited intraprostatic anatomical information other than the sparse calcifications and cysts, it is very difficult to achieve high MR-TRUS image registration accuracy based solely on image intensity.
For surface-based methods, prostate shapes on MR and TRUS are usually manually segmented in the first step. The shapes of the prostate were then meshed into 3D point cloud for surface matching. Commonly used point cloud matching methods include thin-plate spline robust point matching (TPS-RPM) (Chui and Rangarajan, 2003), iterative closest point (ICP) (Du et al., 2010), coherent point drifting (CPD) (Bernhard et al., 2007) and local feature statistics histogram (LFSH) (Yang et al., 2016). To constrain the deformation of point matching, Gaussian-mixture model (GMM) was used to compute probabilistic point correspondence to avoid binary point correspondence (Jian and Vemuri, 2011). CPD utilized a penalty term to constrain nearby points to move coherently as a group. Deformation of the point cloud could also be regularized by biomechanical models. For instance, Wang et al. developed a personalized statistical deformable model (PSDM) to guide prostate surface point matching (Wang et al., 2016). Then, interpolation-based models such as thin-plate spline (Bookstein, 1989) and elastic body splines (Kohlrausch et al., 2005) were utilized to calculate intraprostatic deformation. Though PSDM used in Wang et al.’s paper is a biomechanical model, intraprostatic deformation still needs to be interpolated from surface point deformation using thin-plate spline. Hu et al. (Hu et al., 2012; Hu et al., 2008) built a patient-specific statistical motion model using principal component analysis (PCA) by simulating the prostate-US probe interaction using finite element (FE) method. Different from Wang et al.’s model, Hu et al.’s model includes not only prostate surfaces points, but also intraprostatic points. Many FE models with various boundary conditions need to be performed for the same patient in order to build a specific/personalized motion model, which prevents the patient-specific model from being used in large scale. Later, Hu et al. (Hu et al., 2015) proposed a population-based prediction of patient-specific motion model. The idea was to utilize kernel regression analysis to describe a separate patient’s prostate motion using a multivariate combination of a pre-built population motion models. Khallaghi et al. proposed a biomechanically constrained surface-based MR-TRUS registration method by explicitly integrating a FE volumetric strain energy function into the surface point matching framework (Khallaghi et al., 2015b).
Deep learning-based methods have achieved the-state-of-art performance in many medical image applications, such as segmentation (Dong et al., 2019; Fu et al., 2018b; Fu et al., 2019) and registration (Fu et al., 2020; Haskins et al., 2019b). One advantage of deep learning-based registration is that it enables rapid prediction of the dense deformation vector field (DVF) in a single or a few forward predictions. Yan et al. (Yan et al., 2018) used an adversarial deep learning framework to predict an image similarity metric in terms of target registration error (TRE). In Yan et al.’s work, manually aligned images by experts were treated as the ground truth. A discriminator was used to tell whether an image was distorted using the ground truth deformation or the estimated deformation. Huskins et al. (Haskins et al., 2019a) predicted a deep-learning based MR-TRUS similarity metric, which outperformed MIND similarity metric in MR-TRUS image registration. Only rigid image registration was considered by both Yan et al. and Huskins et al. Onofrey et al. (Onofrey et al., 2016) proposed to synthesize TRUS images from MR images so that the MR-TRUS registration could be cast into TRUS-TRUS single modality registration. Hu et al. (Hu et al., 2018b) trained a weakly supervised network for MR-TRUS image registration using label correspondences. Only MR-TRUS image pairs were required in the inference stage since labels were used in the training stage for loss calculation. Deep learning network learns through gradient back propagation of the loss with respect to the network learnable weights. The label correspondence loss represents only a portion of the true loss that should be defined on the whole prostate. As a result, the network needs to infer the whole prostate deformation based on an under-constrained loss definition. Hu et al. (Hu et al., 2018a) recently proposed an adversarial network to distinguish between the network-predicted DVF and the FE-generated DVF. Their results showed that the adversarial network was able to generate physically plausible deformation with only prostate gland segmentations and without any other deformation smoothness regularization.
Due to the unique challenges of MR-TRUS registrations, it is not optimal to directly apply the commonly used convolutional neural networks (CNN) to MR-TRUS image registration. The TRUS images provide very sparse reliable anatomical markers such as urethra, seminal vesicles, cysts and calcifications. It is very challenging to automatically detect and segment these markers on both MRI and US to establish correspondences. In addition, some cases may not show these anatomical markers due to image noise and artifacts. Therefore, it is not effective to train a CNN to directly predict the dense DVF from the MR-TRUS image intensities. In this study, we proposed a shape-based registration where prostate shapes are represented by 3D point clouds. Traditional CNN can only take regular voxel grids dataset such as images as input and cannot directly consume irregular data structures such as 3D point cloud. Fortunately, Qi et al. (Qi et al., 2016; Qi et al., 2017) proposed a deep learning framework, PointNet, for classification and segmentation of 3D point cloud. The PointNet was designed to directly consume irregular geometric dataset such as 3D point clouds. Based on PointNet, Liu et al. (Liu et al., 2018) proposed a network called FlowNet3D to predict 3D scene flow from 3D points that were generated from stereo and RGB-D images. Meanwhile, Aoki et al. (Aoki et al., 2019) proposed a network called PointNetLK to combine PointNet and Lucas & Kanade (LK) algorithm for 3D point cloud rigid registration. Rigid transformations were calculated iteratively in PointNetLK. Inspired by these methods, we proposed a new point cloud matching method for MR-TRUS prostate image registration. Different from FlowNet3D, the proposed ProRegNet utilized a weighted surface and volume point cloud loss to balance surface and intraprostatic point cloud matching. For the ease of description, the proposed MR-TRUS prostate registration network is referred to ‘ProRegNet’. Prostate shapes from both MR and TRUS were first automatically segmented using our previously developed deep learning-based segmentation networks. The segmented prostate volumes were then meshed into 3D tetrahedron elements to generate volumetric point clouds. Surface point correspondences were established using non-rigid ICP. FE analysis was performed for every case in our datasets using surface nodal correspondence as FE boundary condition. Dense DVFs were generated based on the results of the FE simulation. The dense DVFs were considered as the ground truth deformation for MR-TRUS prostate registration. Volumetric point cloud correspondences were then established based on the dense DVFs. ProRegNet was trained using the prostate volumetric point clouds and their correspondences, which implicitly encoded biomechanical constraints. Compared to previous studies, the contributions of our study include
A novel MR-TRUS image registration network, ProRegNet, was proposed to directly predict volumetric point cloud motion that deforms the MR prostate shape to the TRUS prostate shape.
Trained with FE-simulated point correspondences, ProRegNet was able to predict volumetric prostate point cloud motion with implicit biomechanical constraints.
Deep learning-based MR and TRUS prostate segmentations were adopted to enable fully automatic MR-TRUS image registration.
3. Materials and Methods
The proposed registration framework consists of 1) volumetric point cloud generation, 2) FE-based training datasets preparation, and 3) ProRegNet training and testing. Detailed workflow of the proposed method is shown in Figure 1. In the first step, volumetric point cloud was generated from automatically segmented MR and TRUS prostate masks using tetrahedron meshing. In the second step, FE models were created to simulate the prostate deformation. Ground truth (GT) volumetric point cloud correspondence was established using the deformation field calculated by the FE models. In the last step, the proposed ProRegNet was trained to perform point cloud matching by directly taking the two prostate volumetric point clouds as input.
Fig. 1.
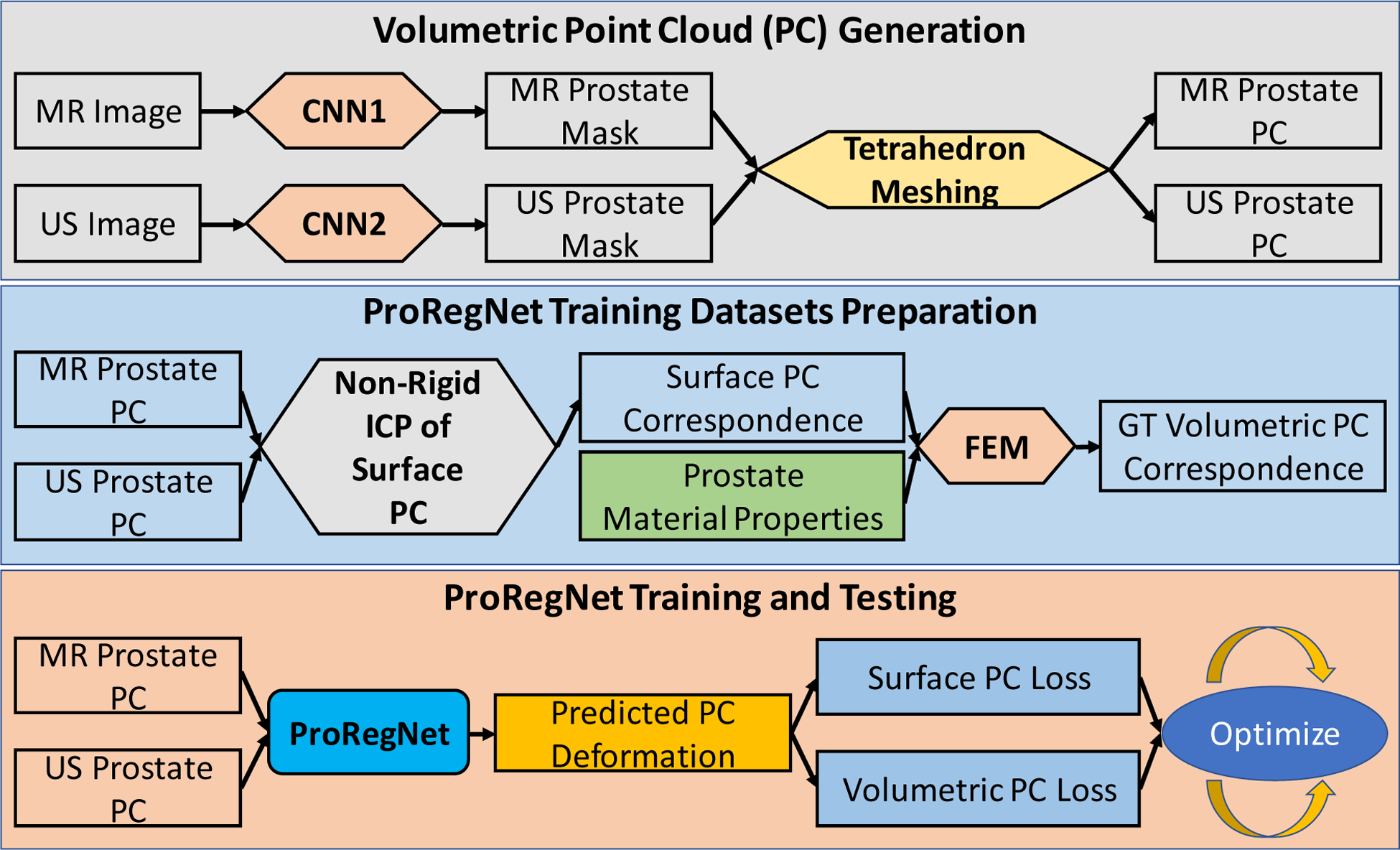
Flowchart of the proposed method. The proposed framework consists of three major steps which are volumetric point cloud generation, training datasets preparation, network training and testing.
3.1. Data Acquisition
A total of 50 pairs of T2-weighted MR and TRUS images were collected from 50 prostate cancer patients who underwent HDR brachytherapy at our clinic. The 3D TRUS images were captured with a clinical ultrasound scanner (HI VISION Avius, Hitachi Medical Group, Japan) and a transrectal 7.5 MHz prostate biplane probe (UST-672-5/7.5) in the operating room before catheter placement. To scan over the longitudinal axis, a mechanical SurePoint stepper (Bard Medical, Inc., GA) was used to guide the stepwise movement of the US probe along the longitudinal axis. Multiple parallel scans in the transverse plane were captured from the patient, with a 1mm step size from the apex to the base. The patient was scanned in lithotomy position. The size of a typical prostate is ~60–80 mm in the longitudinal axis. A margin of 5–10 mm anterior and posterior to the prostate was scanned to ensure whole prostate coverage. The T2-weighted MR images were acquired using a 1.5T scanner (MAGNETOM Avanto, Siemens, Germany) with repetition time of 1200ms and echo time of 123ms. MR images were acquired using a body coil. The original voxel sizes of the MR and TRUS images were 0.63×0.63×2.00 mm3 and 0.12×0.12×1.00 mm3 respectively. For consistency, all MR and TRUS images were resampled to an isotropic voxel size of 0.5×0.5×0.5 mm3 prior to image registration. Institutional review board approval was obtained with no informed consent required for this HIPAA-compliant retrospective analysis.
3.2. Volumetric Point Cloud Generation
Prostate can be represented by volumetric point cloud. It is crucial to have accurate prostate segmentation for shape-based MR-TRUS image registration. Ghavami et al. reported that all top five prostate segmentation methods in PROMISE12 challenge were based on CNN (Ghavami et al., 2019; Litjens et al., 2014). The top DSC on whole MRI prostate segmentation was 0.90. Yuan et al. proposed a global optimization approach to delineate 3D endfiring TRUS prostate and achieved a DSC of 0.93 (Yuan et al., 2013) Yang et al. improved TRUS prostate segmentation in brachytherapy with TRUS-CT registration and achieved an average DSC of 0.91 (Yang et al., 2017). In this study, we developed two separate CNN networks for MR and TRUS prostate segmentations. The DSC of our automatic segmentation results were 0.88±0.05 and 0.92±0.03 for MR and TRUS images, respectively. The mean surface distance (MSD) of our automatic segmentation results were 1.02±0.35mm and 0.6±0.23mm for MR and TRUS images, respectively. Our prostate segmentation methods have been published. Readers are referred to Lei et al. (Lei et al., 2019) and Wang et al. (Wang et al., 2019) for details regarding our segmentation methods.
The segmented prostate masks were then meshed into first order tetrahedron elements for volumetric prostate point cloud generation. First order tetrahedron elements were used to be consistent with our following FE analysis. Second order tetrahedron elements could be used if the element type in the meshing is consistent with the element type used in the FE. The volumetric MR and TRUS prostate point cloud were subsequently used as the input for the point cloud matching and image registration. Surface triangular meshes were obtained from the tetrahedron meshes after mesh analysis to facilitate calculation of surface-based loss function, which is described in detail later. For robust mesh generation, it is not required for the MR and TRUS mesh to have the same number of vertices, elements, faces or patterns.
3.3. Training Datasets Generation
For many surface-based methods, the shape of the prostate was represented using 3D surface point cloud. The final voxel-wise dense DVF was generated from surface point cloud deformation using interpolation-based models such as spline interpolations. The interpolation-based models may generate inaccurate intraprostatic deformation due to the lack to internal control points and biomechanical constraints. To address this issue, we aim to train a network that can predict dense volumetric point cloud motion with biomechanical constraints for MR-TRUS registration. To this end, we need to generate dense volumetric point cloud pairs with FE-calculated point correspondences between the dense volumetric point cloud pair for the network training. The patient-specific FE models proposed by Hu et al. (Hu et al., 2012) and Wang et al. (Wang et al., 2016) cannot be easily applied to our case since the prostate shapes segmented from MR and TRUS images are usually different from each other. Instead of using US probe-prostate interactions as boundary conditions, using nodal displacement between MR and TRUS prostate shapes as boundary conditions ensures that the FE-deformed MR prostate shape match the TRUS prostate shape. Population-based training datasets could be prepared by performing such FE analysis for every case in our datasets. To build FE models with such boundary condition, we need to first establish surface point correspondence. In the next section, surface point registration process is described in detail to establish point correspondence.
3.3.1. Prostate Surface Registration
Unless otherwise stated, MR prostate point cloud and source point cloud are used interchangeably while TRUS prostate point cloud and target point cloud are used interchangeably. A modified iterative closest point (ICP) based non-rigid surface registration algorithm was used to establish surface point cloud correspondence. The input of the non-rigid ICP algorithm is the prostate surface mesh which include 3D surface point cloud and triangular element connectivity. As an initialization step, the MR and TRUS surface meshes were aligned by overlapping their geometrical centers. Rigid alignment was then performed by optimizing a global bidirectional point cloud correspondence loss (Besl and McKay, 1992). The bidirectional point cloud correspondence includes forward vertex correspondence (source vertex to target vertex) and backward vertex correspondence (target vertex to source vertex).
For computational efficiency, a sparse set of source vertices with even spatial distribution were sampled from the original dense source vertices so that target vertices have a higher spatial density than that of the sampled source vertices. As a result, for the ith vertex on the sampled source surface, there are one nearest neighbor vertex on the target surface and multiple vertices on target surfaces for which their nearest neighbor vertex is the same ith vertex on the sampled source surface. Forward vertex correspondence is defined as the nearest neighbor of one source vertex on the target surface:
| (1) |
where represents the ith vertex on source surface, represents the jth vertex on the target surface, the source and target surfaces have a total number of Ns and Nt vertices. denote the Euclidean distance between the two spatial vertices and .
Backward vertex correspondence is defined as the vertices on the target surface for which the same ith vertex on the source surface is their nearest neighbor. Backward vertex correspondence can be expressed as one or more vertices:
| (2) |
Rotation, translation and scaling are solved iteratively by minimizing a weighted forward closest point distance and backward closest point distance (Audenaert et al., 2019). Scaling was not used in our study as the voxel sizes of the resampled MR and US images were consistent prior to meshing.
| (3) |
where the first term minimizes the forward closest point distance and the second term minimizes the backward closest point distance. The inclusion of the second term is to introduce extra force to warp the source surface to the target surface with high curvatures since the second term puts more weight on the target surface. Final rigid alignment was achieved using:
| (4) |
To account for the complex prostate deformation, additional non-rigid transformation was needed. The distances between the source and target point cloud were modeled as a sum of Nc Gaussian Radial Basis Functions (G-RBF) (Kim et al., 2016). For computational efficiency, Nc is usually a much smaller subset of Ns The distances vector could be modeled using G-RBF as:
| (5) |
where wk is the deformation coefficient to be determined, ck is located at the source surface point location . The width of the Gaussian function is controlled by r. ε is the distance between the ck and . The deformation coefficient wk could be calculated by minimizing:
| (6) |
where is the distance mapping to be approximated using G-RBF. Given the distance mapping δ(vs) between the source and target surface during iteration, the deformation coefficient wk can be calculated as:
| (7) |
A final step to refine the surface point matching was performed by locally aligning the two surface point clouds as a weighted local rigid transformation (Audenaert et al., 2019; Li et al., 2008).
3.3.2. Finite Element Simulation of Prostate Deformation
FE simulations were performed using the established surface point correspondences as boundary condition to calculate intraprostatic deformations. Commercial FE software (ANSYS 2019 R2, Oxfordshire, UK) was used to construct FE models. The FE models were configured as a static structural job in ANSYS. Throughout our experiments, the initial material properties of prostate were modeled as Young’s modulus E = 5kPa and Poisson’s ratio v = 0.49, same as that used in Khallaghi et al.’s work (Khallaghi et al., 2015a). Prostate material behavior was simulated by an isotropic and homogeneous hyper-elastic material, represented by Neo-hookean hyper-elastic model (Shahzad et al., 2015). According to continuum mechanics, we have:
| (8) |
where G is the initial shear modulus, which was calculated to be 14.9kPa, K is the bulk modulus, which was calculated to be 83kPa. Compressible Neo-hookean material has a strain energy function of (Pence and Gou, 2015):
| (9) |
where C10 is the material constant that control the shear behavior, which was calculated to be C10 = G/2 = 7.45kPa, D1 is the material constant that control the bulk compressibility, which was calculated to be D1 = 2/K = 2.4 × 10−5Pa−1. denotes the first strain invariant, Jel denotes the elastic volume strain.
There are around 1000 nodes and 5000 tetrahedral elements in the FE models. A template ANSYS input file was generated for each patient using ANSYS Workbench. Subsequently, these input files were modified to apply the surface point correspondences as nodal displacement boundary conditions. Large deflection checkbox in ANSYS was switched on to account for the material stiffness change due to prostate shape change. The FE models were solved using ANSYS Mechanical APDL with 10 sub-steps with equal time interval. Nodal directional displacements of each sub-step were recorded. One example of the FE meshing and final nodal displacement contour were shown in Fig. 2.
Fig.2.
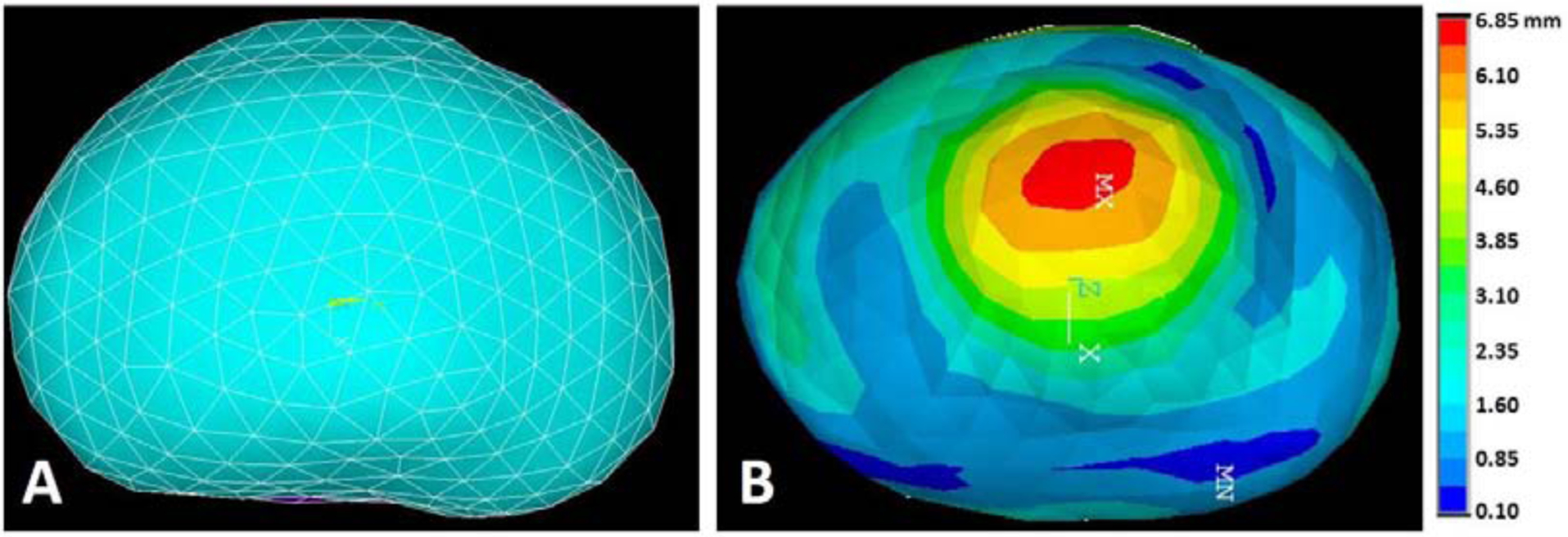
A: Prostate meshing in FE model, representing MR prostate, B: Contour of prostate displacement magnitude after deformation, representing US prostate.
The proposed network took two prostate point clouds generated from MR and TRUS, respectively. The network predicted the MR prostate points motion vector to align the prostate shape of MRI to that of the TRUS. The inputs of the network have two characteristics. First, there is no one-to-one point correspondence between the two point clouds. Second, the numbers of points in the two point clouds are not necessarily the same. Nevertheless, the two point clouds before and after deformation in the FE simulation have such correspondence and the same number of points. Therefore, the network cannot be directly trained using the two point clouds and nodal displacements in the FE simulation. To generate the MR prostate points motion vectors for network training, we first generated voxel-wise DVF images from the FE volumetric nodal displacements using thin-plate-spline interpolation. The voxel-wise DVF images were considered as the ground truth deformation between the MR and TRUS prostate. Then, MR prostate points motion vectors were sampled from the voxel-wise DVF images. For 50 patients, we generated a total of 500 FE results which include ten FE sub-steps per patient. Each training dataset contains a MR prostate volumetric point-cloud set, a TRUS prostate volumetric point-cloud set, and the ground truth motion vector of MR point-cloud set. Each point cloud set contains around 25,000 points.
3.4. ProRegNet
3.4.1. Network design
Fig.3 shows the goal of ProRegNet, which is to directly match the MR prostate shape to the TRUS prostate shape. Point cloud data structure is represented by a group of spatially distributed 3D points. Compared to image data structure, point cloud data structure is highly irregular. Point cloud data structure has several important properties, which are 1) points in the point cloud are unordered, meaning that the geometrical representation and interpretation should not change regardless of the order of the points in the point cloud. The network should be immune to any permutation of the points in the point cloud; 2) despite being unordered, point cloud is spatially organized. The interaction among points locally or globally forms its own signature that uniquely features the underlying geometric representation; 3) the meaning of the point cloud should be invariant under rigid transformations, such as rotation and translation. A rotated prostate represented by a rotated point cloud with vertices at different spatial locations should have the same meaning as the original prostate. A network that directly consumes point cloud needs to consider all the above-mentioned properties. The vertices number discrepancy between the source point cloud and target point cloud imposes additional challenge to the network design.
Fig. 3.
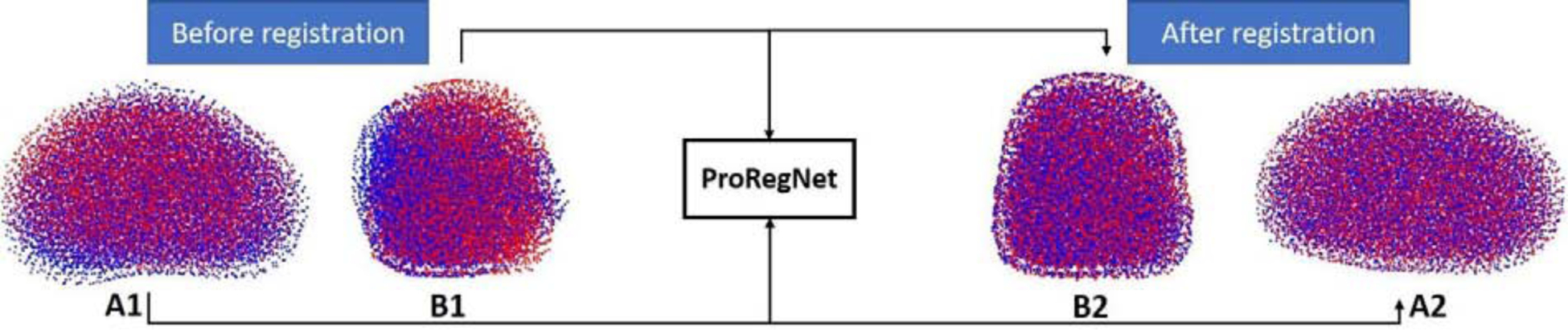
ProRegNet aims to predict volumetric point cloud motion from a point cloud pair. Red point cloud represents the TRUS prostate shape while blue point cloud represents the MR prostate shape. A1 and A2 show the point clouds in axial plane while B1 and B2 show the point clouds in sagittal plane.
The source point cloud has Ns vertices, expressed as ,. The target point cloud has Nt vertices, expressed as ,. As an initialization step, rigid ICP of surface points were performed to roughly align the point clouds. Then, the centroids of the source and target point clouds were calculated as the geometrical centers and expressed as and , respectively. The input vectors of the network were then rearranged as a matrix of size Ns × 7 and Nt × 7 for the source and target point clouds, respectively. The ith point in the source point cloud was rearranged as , where are the ith point location in the source point cloud relative to are the ith point location in the source point cloud relative to , and is a binary indicator of whether the point belongs to the prostate surface. The was introduced to incorporate surface point loss to the network. Similarly, the ith point in the target source point cloud is expressed as , where are the ith point location in the target point cloud relative to are the ith point location in the target point cloud relative to , and is a binary indicator of whether the point belongs to the target prostate surface. The reason to spatially encode each point with respect to both and is to provide two frames of reference for network point cloud motion prediction.
In ProRegNet, N points were randomly sampled from the original point cloud pair. Two types of convolutional layers specific to point cloud were introduced, one for convolution and the other for de-convolution. The point cloud convolutional layer first samples n regions from the input point cloud with farthest point sampling. The centers of the n regions were at . For each region with radius of r around , features were extracted using function:
| (10) |
where function h(·) was realized as a multi-layer perceptron (MLP) network. The MAX operation is element-wise max pooling. Max pooling was used here as a symmetric operation which is suitable for the unordered point cloud and invariant to point cloud rigid transformations. With varying value of radius r, the MLP network could learn multi-scale local point cloud features. For the point cloud de-convolutional layer, features of n input points were computed on specified locations on the target points with n′ points, where n′ > n. The point cloud convolutional and de-convolutional layers solve the problem of end-to-end feature learning of a single point cloud. However, they did not address the problem of point cloud motion prediction between two point-clouds. Liu et al. (Liu et al., 2018) proposed a point cloud embedding layer to address this issue. Due to the lack of one-to-one point correspondence, the point cloud embedding layer used multiple softly corresponding points in the target point cloud near a source point within radius of re. The point cloud embedding layer learnt to use both feature similarities and spatial relationships to predict a weighted point correspondence.
Fig. 4 shows the architecture of the ProRegNet. N was set to 4096 in our network. Each input point cloud first went through a separate PC conv operator, which includes two-point cloud convolutional layers with r = 5mm, n = 1024, c = 64 and r = 10mm, n = 265, c = 128, respectively. Then, the learnt features from both point clouds were fed into a point cloud embedding layer with re = 2.5mm, c = 256. The last point cloud conv operator includes two point-cloud convolutional layers with r = 17.5mm, n = 64, c = 256 and r = 25mm, n = 16, c = 512, respectively. The point cloud up-conv operator includes three point-cloud de-convolutional layers to resample the number back to its original size of N.
Fig. 4.
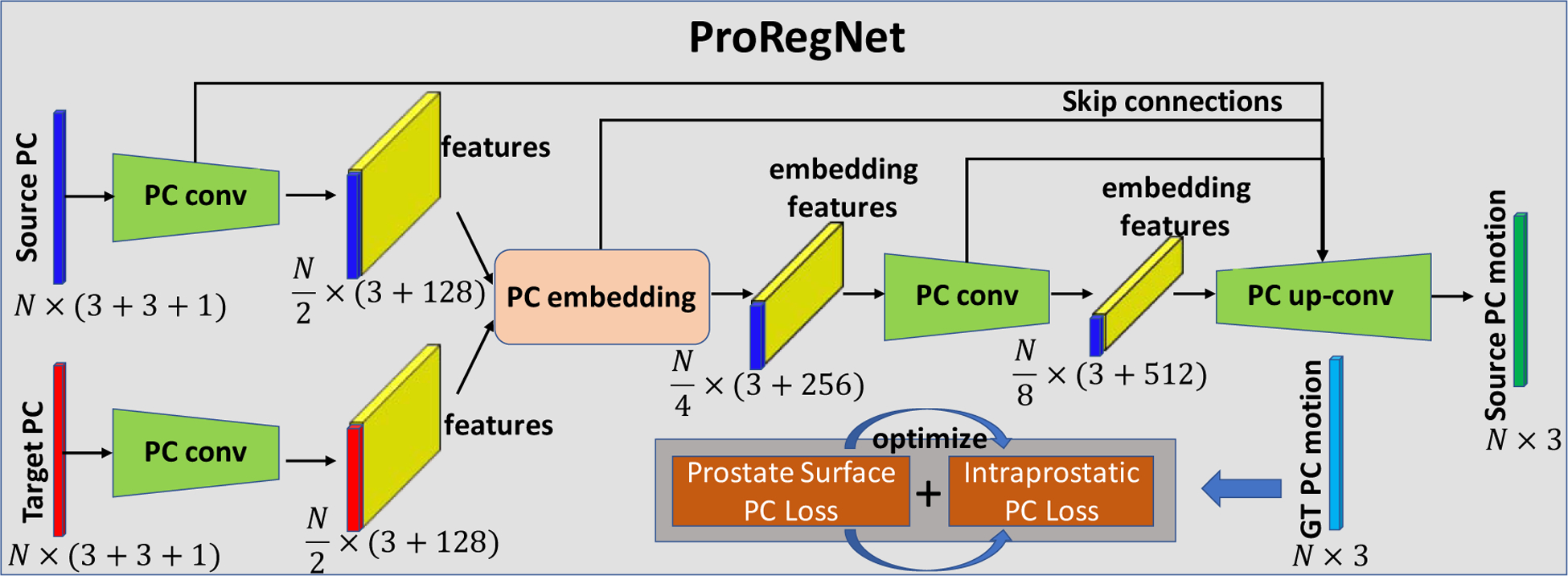
Network design of ProRegNet. The network consists of PC conv, PC embedding and PC up-conv operations. The loss function is a weighted sum of prostate surface PC loss and intraprostatic PC loss.
3.4.2. Loss functions
The loss of the ProRegNet was a weighted sum of surface point cloud loss and volumetric point cloud loss. Mean square error was used as the loss function between the predicted motion and ground truth motion. The volumetric point cloud loss put equal weight on every point in the point cloud. Surface point cloud loss was added to promote the point correspondence between prostate surface points. Therefore, was encoded into to distinguish the surface points from the intraprostatic points. Challenges to design a suitable surface loss function include 1) the function needs to be differentiable with respect to point locations; 2) the function needs to be computationally efficient since the loss needs to be calculated repeatedly throughout the optimization process; 3) the function needs to be robust to outliers. Fan et al. (Fan et al., 2016) studied two distance metrics, which are the Chamfer distance and Earth Mover’s distance. We adopted the Chamfer distance (CD), which is defined as:
| (11) |
where and represent the surface points from the source point cloud and target point cloud. and are the number of surface points for source and target, respectively. For each point, the Chamfer distance algorithm finds the nearest neighbor in the other point cloud and adds the squared distance of each points together. The Chamfer distance is continuous and piecewise smooth with respect to point locations. The final loss for ProRegNet is:
| (12) |
where the first term is the mean square error between the predicted motion vector and the ground truth motion vector. The second term is the surface distance loss. The weighting factor was set to 10 because the ratio between the number of volumetric and surface points was around 10.
3.4.3. Training and Testing
ProRegNet was implemented in Python 3.6 and TensorFlow on a NVIDIA TITAN XP GPU with 12GB of memory. Adam gradient optimizer with learning rate of 1e-3 was used in optimization. Ten FE results per patient were used to generate nine training datasets by pairing up the first step with each subsequent sub-step. In total, we have 450 training datasets for 50 patients. Five-fold cross validation was used to train and test the network. During training and testing, 4096 points were first randomly sampled from the original point cloud. For 4096 volumetric points, there were around 400 surface points. Since the network was trained to be invariant to point permutations, the sampled 4096 points were randomly shuffled ten times in testing stage. Final motion results were obtained by averaging the ten motion predictions. Voxel-wise DVF image was obtained from the network motion prediction using thin-plate-spline interpolation. MR image was then deformed using the voxel-wise DVF to register with the TRUS image.
The training datasets preparation is time-consuming. However, once trained, the network can make the point matching prediction very rapidly in less than 3 seconds. The ProRegNet took around 2 hours to train. The prostate can be segmented on MR and US images using our previously trained segmentation networks in less than 2 seconds (Lei et al., 2019; Wang et al., 2019). The whole MR-TRUS image registration procedures, including segmentation, meshing, network prediction and DVF image calculation took 3 to 5 mins on average.
3.5. Comparison Methods
To demonstrate the superiority of the proposed method, it was compared with another two MR-TRUS image registration methods. The first method was a surface-based method, which performed prostate surface registration same as Section 3.3.1. Voxel-wise DVF image was then obtained from the surface point cloud motion using thin-plate-spline interpolation. The other method was to use CNN for MR-TRUS image registration. From the 450 point-cloud training datasets, we created another 450 image training datasets. Each image training dataset includes a MR prostate mask, a TRUS prostate mask and a ground truth DVF image obtained using FE models. Fig.5. shows the network structure of the CNN network. The CNN has 12 convolutional layers and 3 max pooling layers. Bicubic resampler was used to resample the predicted DVF to its original image size. Deformed MR masks were generated using spatial transformers. DICE coefficient loss, DVF mean absolute error (MAE) loss and DVF regularization smoothness loss were minimized for network training. To provide spatial information to the input mask images, three spatially-encoded masks in the x, y, z directions were generated from one input mask. There was a total of 6 spatially-encoded masks, three masks for MR and another three masks for TRUS. For fair comparison, the CNN was trained in the same way as ProRegNet. For the ease of description, the surface-based method was referred to ‘SurfReg’. The CNN-based method is referred to ‘CnnReg’.
Fig. 5.
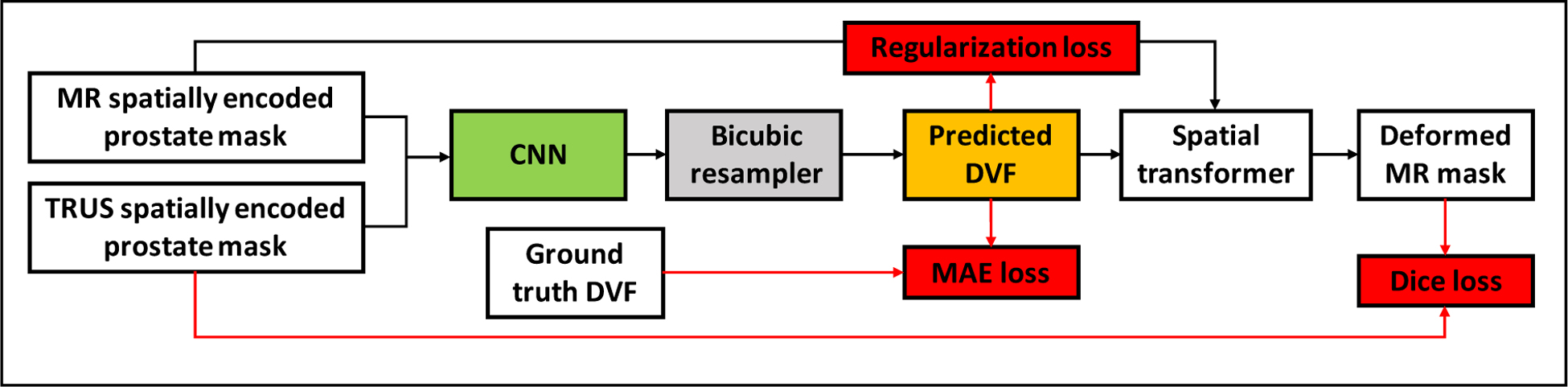
Network design of CnnReg. The CNN network consists of 12 convolutional layers and 3 max pooling layers. The loss function contains DVF regularization loss, DVF mean absolute error loss and Dice loss.
3.6. Evaluation of Registration Accuracy
Target registration error (TRE) were calculated to evaluate the registration accuracy. Landmarks such as centers of small nodules, cysts, calcifications were carefully selected manually by an experienced physician. For each patient, around 3 to 5 landmarks were selected. DSC coefficient was calculated to evaluate the volume overlap ratio between the deformed MR and TRUS prostate. To evaluate the surface similarity between the deformed MR and TRUS prostate, we used Hausdorff distance (HD) and mean surface distance (MSD). The HD measures the local maximum distance between the deformed MR prostate shape and the TRUS prostate shape. The MSD is the mean surface distance between the two surfaces. Jacobian determinants (JD) and normal strains Exx, Eyy, Ezz of the deformation field were calculated to assess the physical fidelity of the predicted deformation. The Jacobian determinant is defined as:
| (13) |
where ε is the strain tensor calculated from the deformation field, I is the identity matrix, det(·) is the determinant of the matrix.
4. Results
4.1. Registration accuracy
To evaluate the registration accuracy, we calculated eight metrics, including DSC, MSD, HD, TRE, JD, Exx, Eyy and Ezz, for SurfReg, CnnReg and ProRegNet, respectively. The results were compared and analyzed. Table 1 shows the mean and standard deviation of DSC, MSD, HD and TRE for the three different methods. Boxplot of these metrics were shown in Fig. 6 and Fig. 7. The central mark in the boxplot is the median, the top and bottom edges of the box indicate the 75th and 25th percentiles, respectively. The dashed line in boxplot extends to the most extreme data points that are not outliers. Outliers are shown as red ‘+’ symbol. As evidenced by its DSC, MSD and HD values, SurfReg has the best performance on surface matching and volume matching among the three methods. This is reasonable since SurfReg focused solely on the surface point matching. As described in Section 3.3.1, SurfReg utilized G-RBF to calculate general deformation for rough point matching and a weighted rigid deformation for local fine point matching. Therefore, SurfReg enforced the two prostate shapes to match well both globally and locally. CnnReg generated the second-best surface matching and volume matching performance in terms of DSC, MSD and HD. However, volume overlapping (DSC) and surface distance (MSD, HD) metrics are not accurate or adequate to evaluate the point-to-point MR-TRUS registration accuracies. The reasons are 1) intraprostatic deformation is not considered in DSC, MSD or HD; 2) exact shape matching could sometimes generate adverse effect due to inaccurate local segmentations as a result of either poor contrast, low slice resolution or tissue ambiguities. To evaluate the intraprostatic registration accuracy, TRE were calculated and reported in Table 1. Paired student t-test was performed to analyze the statistical significance for all four metrics. Contrary to DSC, MSD and HD values, the TRE values suggested that ProRegNet was the most accurate among the three methods, with an average improvement of 0.91mm over CnnReg and 1.13 mm over SurfReg. Multiple comparisons were made with the same null hypothesis using DSC, MSD, HD. Bonferroni correction suggests a threshold significance level of 0.05/3=0.017 to account for the familywise type I error. The p-values (1 vs. 3) in Table 1 are greater than 0.017, which suggests that SurfReg has the same performance as ProRegNet in terms of DSC, MSD and HD.
Table 1.
DSC, MSD, HD and TRE for SurfReg, CnnReg and ProRegNet. Values: Mean±Std
| DSC | MSD (mm) | HD (mm) | TRE (mm) | |
|---|---|---|---|---|
| SurfReg (1) | 0.98±0.01 | 0.58±0.04 | 1.86±1.24 | 2.70±1.15 |
| CnnReg (2) | 0.96±0.03 | 0.73±0.19 | 2.51±1.21 | 2.48±1.05 |
| ProRegNet (3) | 0.94±0.02 | 0.90±0.23 | 2.96±1.00 | 1.57±0.77 |
| p-value (1 vs. 3) | 0.11 | 0.02 | 0.09 | 0.005 |
| p-value (2 vs. 3) | <0.001 | <0.001 | <0.001 | 0.002 |
Fig.6.
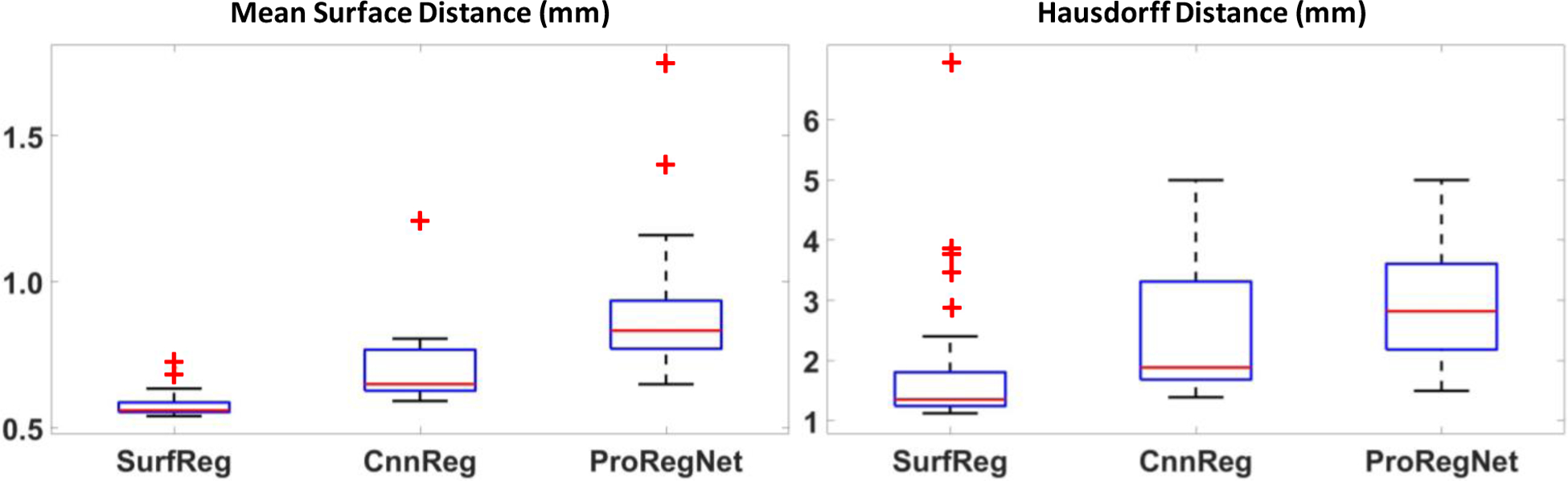
Boxplots of MSD and HD for SurfReg, CnnReg and ProRegNet. The central mark in the boxplot is the median, the top and bottom edges of the box indicate the 75th and 25th percentiles, respectively. The dashed line in boxplot extends to the most extreme data points that are not outliers. Outliers are shown as red ‘+’ symbol.
Fig.7.
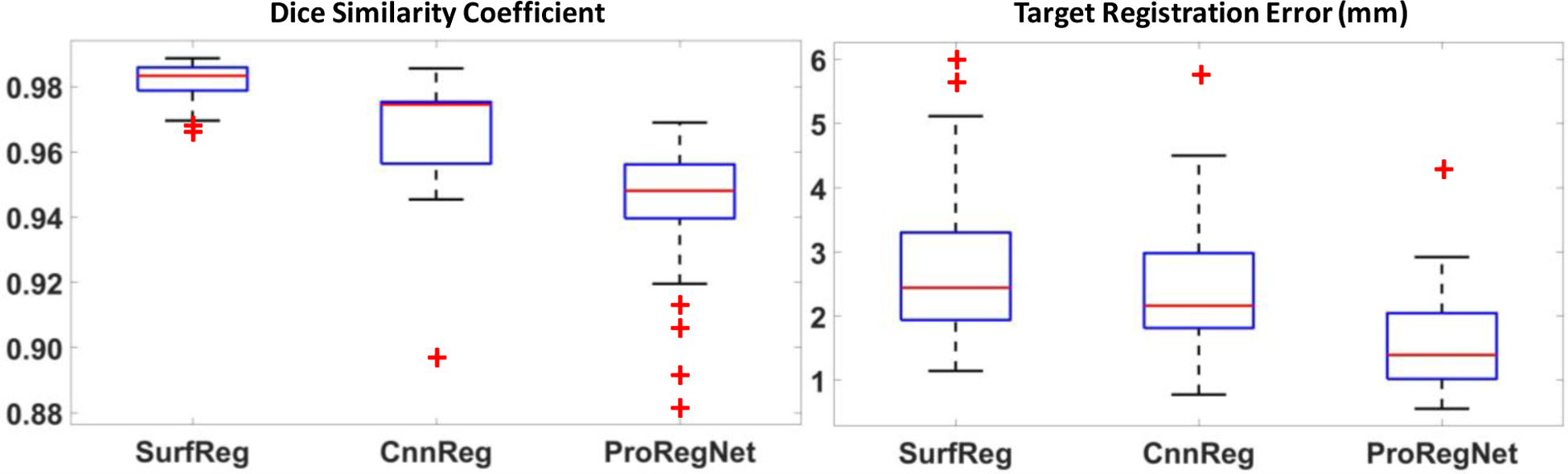
Boxplots of DSC and TRE for SurfReg, CnnReg and ProRegNet. The central mark in the boxplot is the median, the top and bottom edges of the box indicate the 75th and 25th percentiles, respectively. The dashed line in boxplot extends to the most extreme data points that are not outliers. Outliers are shown as red ‘+’ symbol.
Registration results of two cases are shown in Fig. 8 and Fig. 9 in the transverse, coronal and sagittal planes. In Fig. 8 and Fig. 9, first column shows the original TRUS and MR images. Second column shows the images after rigid registration in checkboard and red-green fusion. Third, fourth and fifth columns show the registration results for SurfReg, CnnReg and ProRegNet, respectively. Blue dashed contour indicates TRUS prostate shape while red dashed contour indicates MR prostate shape. The cyst within prostate was highlighted by arrows. Arrows were not plotted in fused images to avoid occlusion. The checkboards were placed so that the checkboard edges crossed the cyst of interest for better visualization. Fig.8 and Fig. 9 shows that the prostate shape matching after registration was the best for SurfReg than the other two methods. However, as illustrated by the arrows in Fig. 8 and Fig. 9, ProRegNet has the best cyst matching among the three methods. This phenomenon could be explained by the fact that SurfReg lacks biomechanical constraint for intraprostatic deformation regularization. For SurfReg, TPS interpolation was used to calculate intraprostatic deformation, leading to under-constrained deformation. Despite trained using ground truth DVFs, the CnnReg only achieved limited improvement over SurfReg in terms of TRE. The results show that CnnReg could not efficiently learn how to perform registration from the spatially-encoded prostate mask pair. This could be explained by the fact that MR-TRUS masks lack enough intensity-based features for the registration task. As a result, CnnReg which is good at extracting intensity-based textural features from images failed to significantly outperform SurfReg. On the contrary, ProRegNet has managed to learn the underlying point matching pattern directly from the point cloud pair and its correspondences. Despite of some contour discrepancies between the deformed MR shape and TRUS shape, the ProRegNet generated the best cyst matching among the three methods. Therefore, we claim that it is sometimes necessary to tolerate certain level of prostate surface mismatch and preserve the underlying biomechanical constraints, given possible inaccurate local contours. Similar concept was found in Khallaghi et al.’s work (Khallaghi et al., 2015a), where the authors proposed to use statistical shape models to account for prostate contour inaccuracies for consistent surface registration.
Fig.8.
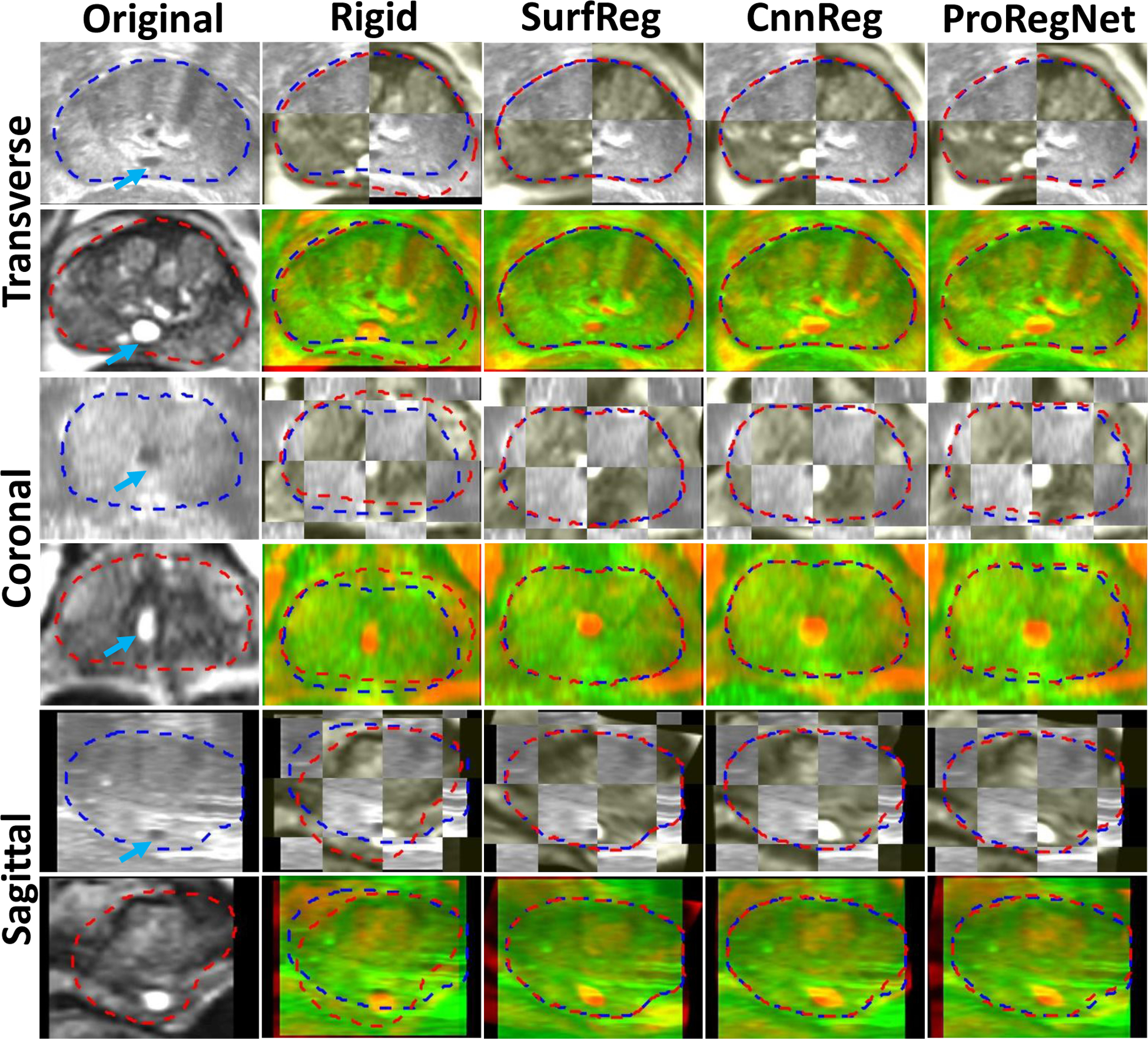
Example image slices from one case. Results are shown in the transverse, coronal and sagittal planes. First column shows the original TRUS and MR images. Second column shows the images after rigid registration in checkboard and red-green fusion. Third, fourth and fifth columns show the registration results for SurfReg, CnnReg and ProRegNet, respectively. Blue dashed contour indicates the TRUS prostate shape while red dashed contour indicates MR prostate shape. The cyst within prostate were highlighted by arrows on the original images.
Fig.9.
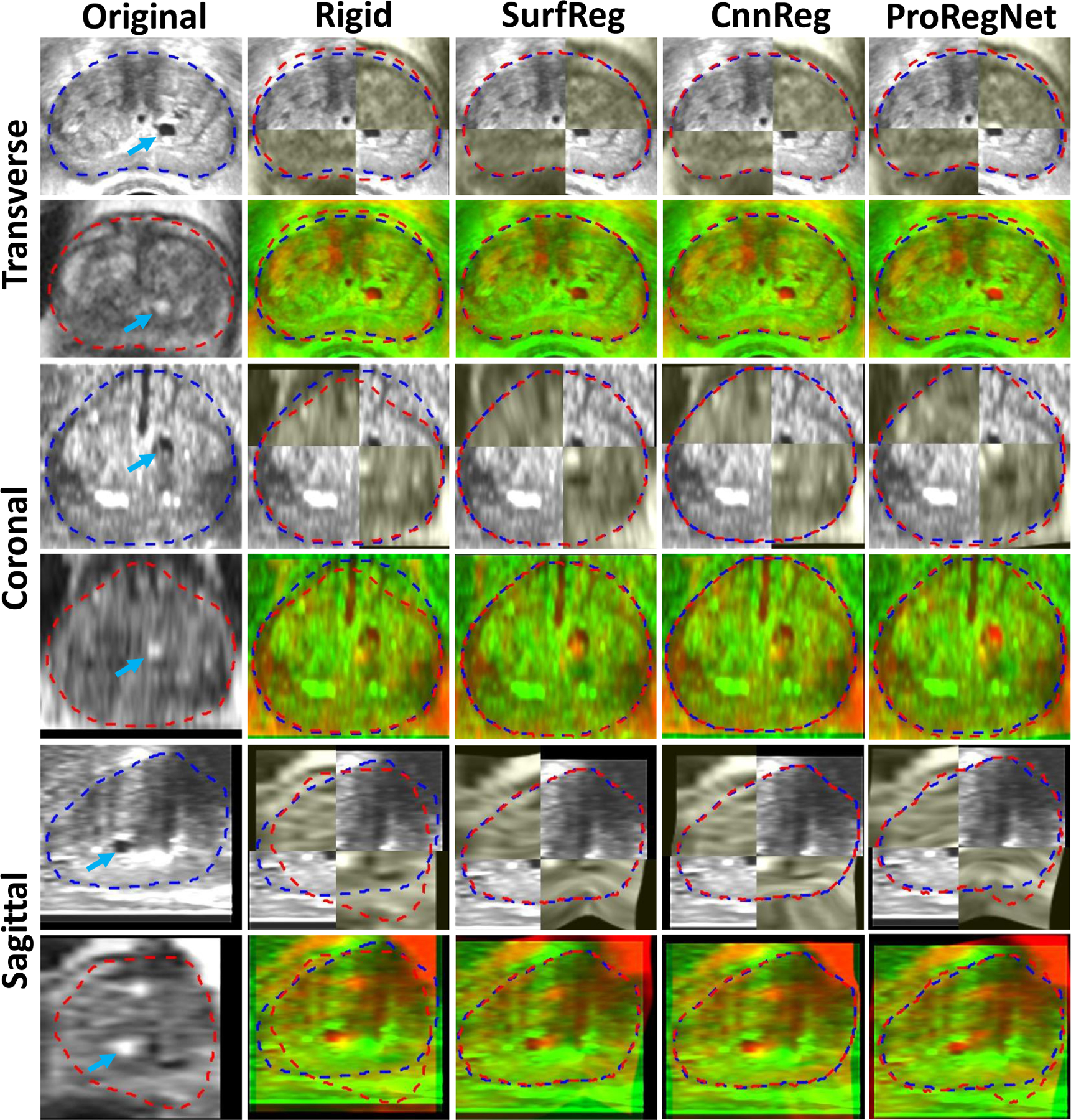
Example image slices from another case. Results are shown in the transverse, coronal and sagittal planes. First column shows the original TRUS and MR images. Second column shows the images after rigid registration in checkboard and red-green fusion. Third, fourth and fifth columns show the registration results for SurfReg, CnnReg and ProRegNet, respectively. Blue dashed contour indicates the TRUS prostate shape while red dashed contour indicates MR prostate shape. The cyst within prostate were highlighted by arrows on the original images.
Strain tensor images were obtained from the predicted DVF. JD, Exx, Eyy and Ezz images were calculated from the strain tensor images to evaluate the physical fidelity of the predicted DVF. JD of the predicted DVF calculated by Eq. 13 represents the volumetric strain. JD value greater than one means volumetric expansion while JD value less than one means volumetric shrinkage. Negative JD value means deformation singularity, indicating ‘folding’ in the DVF. Fig. 10 shows that the ranges of JD are all positive, which means the predicted DVF is free from singularities for all three methods. Since SurfReg enforced strong surface matching, SurfReg was more likely to generate inaccurate JD near the surface, as evidenced by the arrows in Fig. 10. Though trained using the ground truth DVF, CnnReg generated JD images that were not smooth enough near the prostate surface. In comparison, ProRegNet generated JD images that were in best agreement to the ground truth. To evaluate the JD error quantitatively, we calculated the mean absolute error between the ground truth and the predicted JD within the prostate mask for all three methods. Results were reported in Table 2. The proposed ProRegNet had the smallest mean and standard deviation error for JD, Exx, Eyy and Ezz. P-values were calculated using two-sample t-test for (ProRegNet, SurfReg) and (ProRegNet, CnnReg). P-values show that the improvement of ProRegNet over SurfReg was statistically significant for JD, Eyy and Ezz. However, the improvement of ProRegNet over CnnReg was statistically significant for only Ezz. This could be explained by the fact that both the ProRegNet and CnnReg were trained using the ground truth DVF, resulting in statistically insignificant differences for JD, Exx and Eyy. Nevertheless, Fig. 10 suggests that the CnnReg had significant JD error, especially outside the prostate mask, which was not included in the JD error calculation in Table 2.
Fig.10.
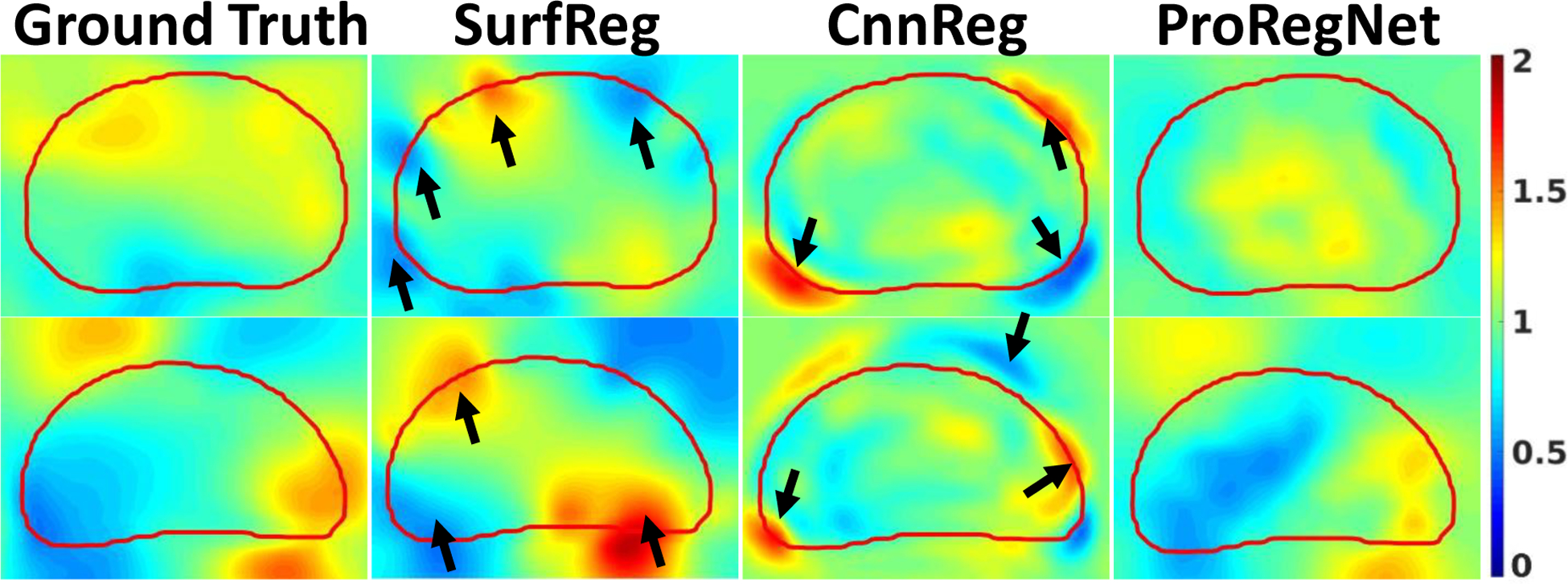
Example slices of JD comparison for SurfReg, CnnReg and ProRegNet from two different cases. Red contour indicates the TRUS prostate shape. Arrows indicate high JD errors.
Table 2.
Mean absolute error between the ground truth and prediction for Jacobian determinant, normal strain in the x, y, z directions. Values: Mean±Std.
| JD | Exx | Eyy | Ezz | |
|---|---|---|---|---|
| SurfReg (1) | 0.18±0.04 | 0.10±0.02 | 0.12±0.03 | 0.10±0.02 |
| CnnReg (2) | 0.17±0.05 | 0.10±0.01 | 0.10±0.02 | 0.12±0.04 |
| ProRegNet (3) | 0.14±0.02 | 0.09±0.01 | 0.09±0.01 | 0.09±0.01 |
| p-value (1 vs 3) | 0.01 | 0.05 | 0.01 | 0.01 |
| p-value (2 vs 3) | 0.09 | 0.14 | 0.19 | 0.02 |
Fig. 11 shows one example slice before and after registration for all three methods. Fig.11 (A2–A4) shows the deformed MR, with the TRUS contours shown in blue and deformed MR contours shown in red. Fig.11 (B2–B4) shows the absolute JD error with same TRUS contours shown in blue. We have found out that the SurfReg sometimes generated unrealistically deformed MR image after registration, such as Fig.11(A2). This phenomenon was more likely to happen near the prostate surface for patients whose prostate has undergone significant shape changes during TRUS. Such phenomenon did not occur for any patient using ProRegNet. Indicated by the arrows in Fig.11 (A3), there may be large contour shape discrepancies after registration for CnnReg. We aligned the JD error image vertically with the deformed MR images to analyze the correlation. As indicated by the arrows, poor registration results occurred at locations where JD errors were large. Fig. 11 (B4) shows that JD error was minimal for ProRegNet. Fig.11 demonstrated that the biomechanical constraints learnt by ProRegNet was effective in regularizing the deformation prediction.
Fig.11:
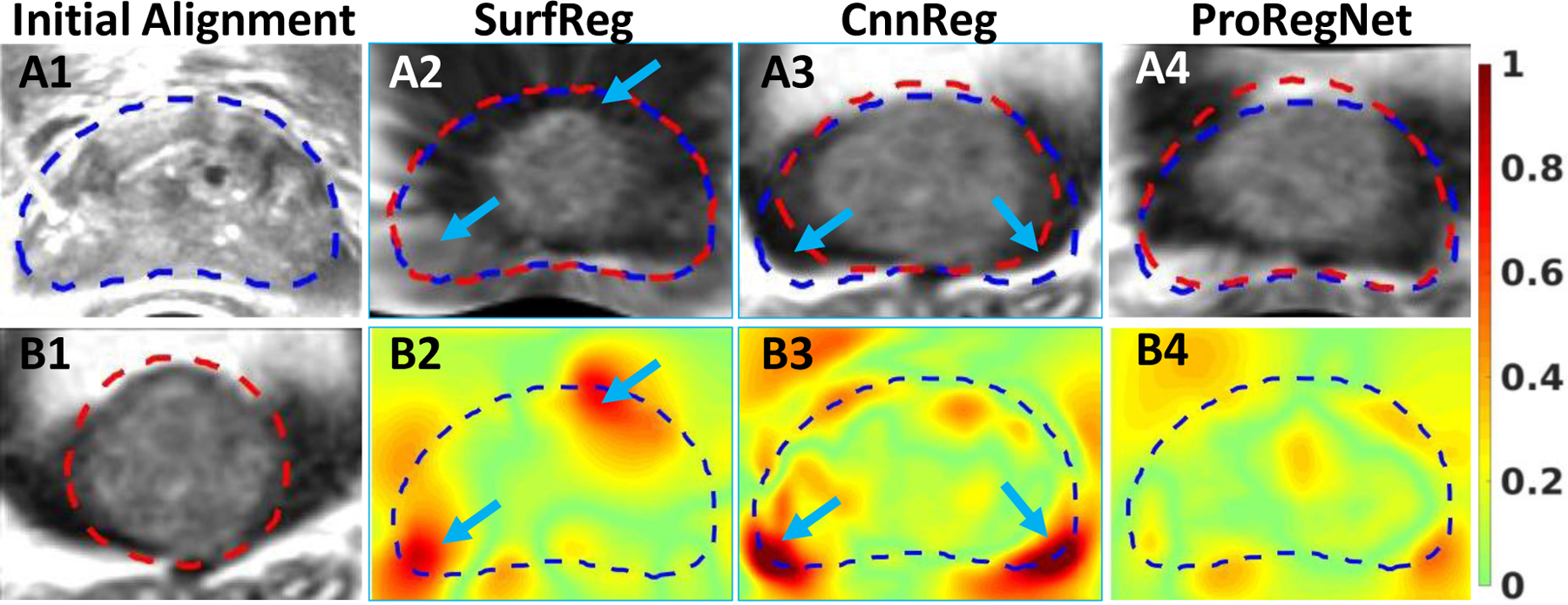
TRUS image. B1: MR image. A2–A4: Deformed MR images after registration by SurfReg, CnnReg and ProRegNet, respectively. B2-B4: JD absolute error for SurfReg, CnnReg and ProRegNet, respectively. Blue contours indicate the TRUS prostate shapes while the red contours indicate MR prostate shapes. Poor registration was observed at regions where JD error was large, as indicated by arrows.
Besides the numerical evaluations, qualitative assessments of registration uncertainties were also performed by one experienced medical physicist with more than 10 years of experience on MR-TRUS fusion. To assess the uncertain levels of registration results, we have followed the guidelines recommended by AAPM Task Group 132 (Brock et al., 2017), which defines uncertainty level of 0 to 4 as ‘whole scan aligned’, ‘locally aligned’, ‘usable with risk of deformation’, ‘usable for diagnosis only’, ‘alignment not acceptable’, respectively. Fig. 12 shows the grouped bar plot of the uncertainty levels for all three methods. The mean uncertainty levels were 2.08, 2.04 and 1.50 for SurfReg, CnnReg and ProRegNet, respectively. The unacceptable cases were caused by large prostate shape discrepancies at regions such as lateral prostate, prostate apex and base, resulting in unrealistically stretched or compressed prostate.
Fig. 12.
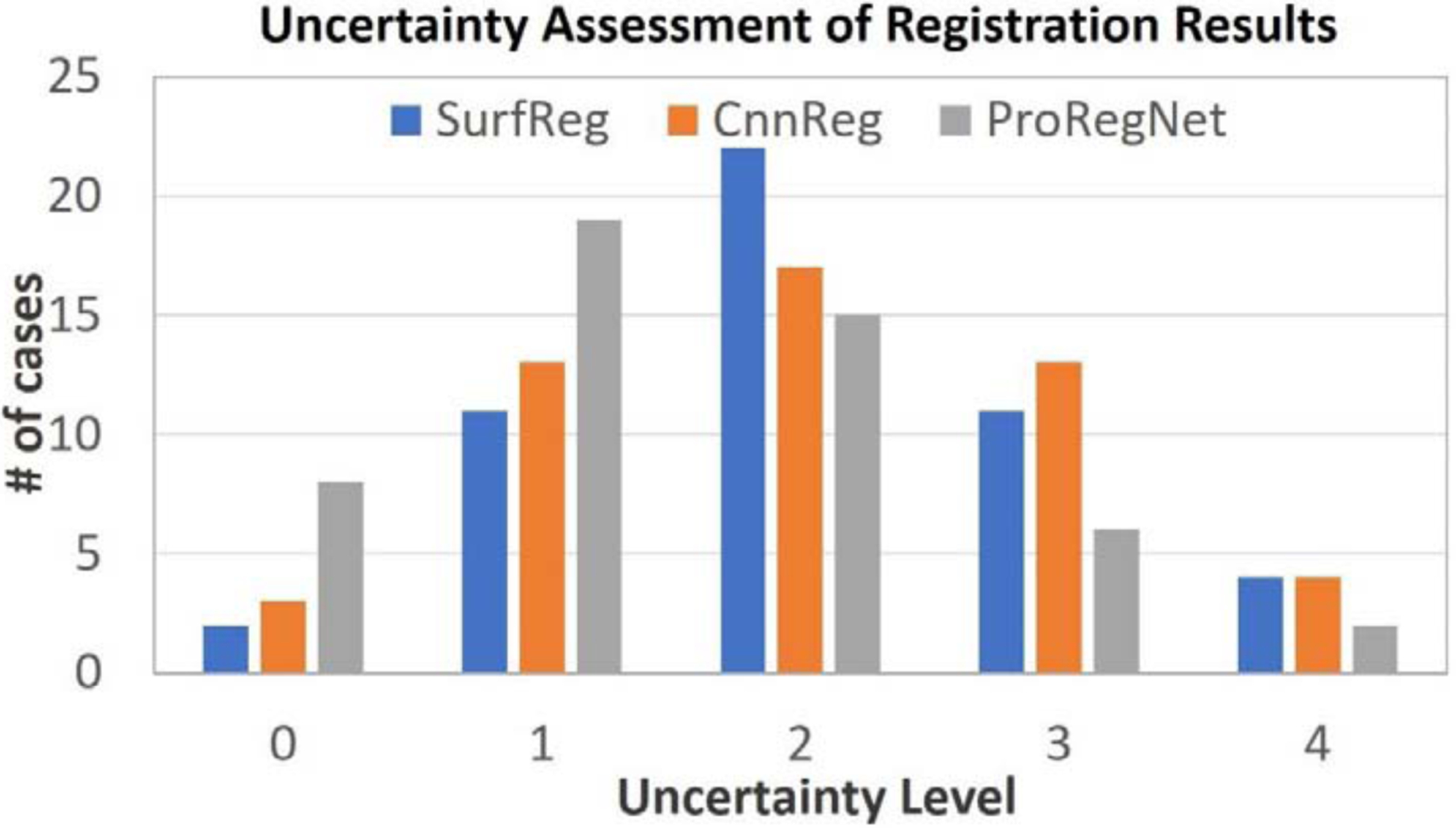
Qualitative expert uncertainty assessments of MR-TURS image registration results.
4.2. Robustness of ProRegNet to Inaccurate Segmentation
In practice, the prostate shapes might be corrupted due to inaccurate segmentations. We studied the robustness of ProRegNet to inaccurate segmentations and meshing perturbations by adding random noise to the locations of the points in both MR and TRUS point cloud. The original point clouds were perturbed by adding noise with four levels of amplitude on selected points with five percentages. The four spatial noise amplitude levels were [−2.5, 2.5], [−5.0, 5.0], [−7.5, 7.5] and [−10.0, 10.0] mm with random uniform distribution. The five percentages were 20%, 40%, 60%, 80% and 100%. Experiments of registration were conducted on these noisy prostate shapes. TRE was calculated using the same landmarks and reported in Table 3. It can be observed from Table 3 that the TRE generally increased from 1.51mm to 1.97mm as the noise level increased from 2.5mm on 20% points to 10mm on 100% points.
Table 3.
Noise sensitivity of ProRegNet in terms of TRE in mm. Values: Mean±Std. Statistical significance is indicated in bold.
| Noise Amplitude (mm) | Point Percentage | ||||
|---|---|---|---|---|---|
| 20% | 40% | 60% | 80% | 100% | |
| [−2.5,2.5] | 1.51±0.62 | 1.54±0.59 | 1.53±0.65 | 1.55±0.59 | 1.53±0.58 |
| [−5,5] | 1.54±0.56 | 1.53±0.59 | 1.57±0.56 | 1.55±0.60 | 1.57±0.59 |
| [−7.5,7.5] | 1.65±0.61 | 1.69±0.62 | 1.67±0.57 | 1.70±0.63 | 1.73±0.66 |
| [−10,10] | 1.74±0.58 | 1.79±0.65 | 1.87±0.60 | 1.94±0.77 | 1.97±0.79 |
To further study the statistical significance of the TRE results between using original shapes and using noisy shapes, we calculated the p-values using two-sample t-test. The p-values were shown in Table 4. For visual comparison, we plotted noisy shapes with its original shapes on both TRUS and MR prostate shapes in Fig. 13. Blue point clouds represent original shapes while red point clouds represent noisy shapes. Fig.13 (A1–A4) show TRUS prostate shapes with noise amplitude of ±2.5, ±5, ±7.5, ±10 mm on 100% of points, respectively. Fig. 13 (B1–B4) show MR prostate shapes with noise amplitude of ±2.5, ±5, ±7.5, ±10 mm on 100% of points, respectively. Table 4 shows that only shapes of Fig. 13 (A4 and B4) in Fig. 13 caused the ProRegNet to generate TRE values that were statistically significantly different than the original shapes. Both Table 3 and Table 4 demonstrated that our ProRegNet was able to perform robustly under severe noisy contamination on the original point clouds. One reason for the good robustness to noise is that the point clouds of prostate shapes in the training datasets had no specific spatial patterns. The spatial pattern of the point clouds could easily be destroyed by the added noise, which would significantly degrade the network performance. The robustness of ProRegNet could also be attributed to the fact that noise was added uniformed to all the points which did not perturb the overall shapes of the prostate much. Nevertheless, this proved that the ProRegNet was able to retrieve important shape representative features and discard inaccurate outlier points.
Table 4.
P-values between TREs calculated using original shapes and TREs calculated using noisy shapes. Statistical significance is indicated in bold.
| Noise Amplitude (mm) | Point Percentage | ||||
|---|---|---|---|---|---|
| 20% | 40% | 60% | 80% | 100% | |
| [−2.5,2.5] | 0.91 | 0.78 | 0.84 | 0.71 | 0.84 |
| [−5.0,5.0] | 0.78 | 0.81 | 0.58 | 0.72 | 0.60 |
| [−7.5,7.5] | 0.29 | 0.18 | 0.21 | 0.18 | 0.12 |
| [−10.0,10.0] | 0.09 | 0.05 | 0.01 | 0.01 | 0.01 |
Fig.13.
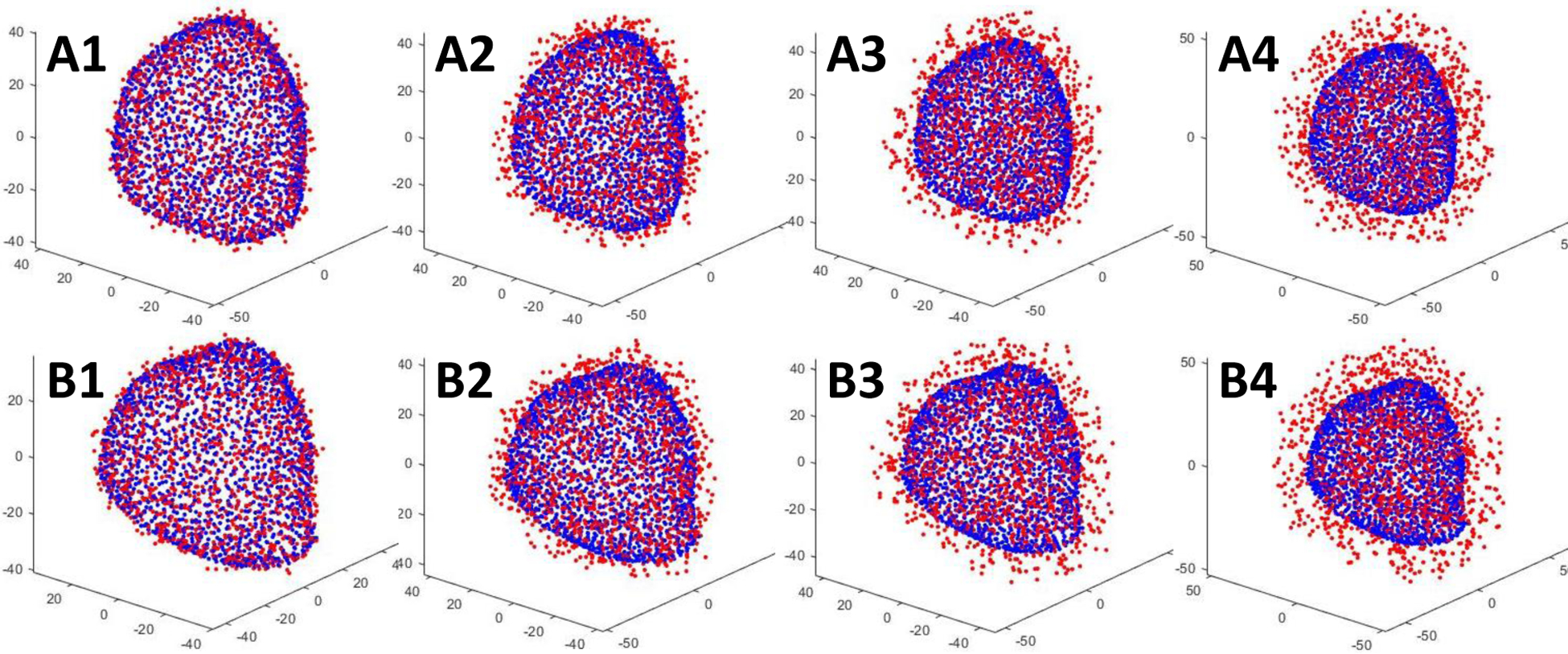
Point clouds contaminated with different level of noise. Blue point clouds represent original shapes while red point clouds represent noisy shapes. A1–A4: TRUS prostate shapes with noise amplitude of ±2.5, ±5, ±7.5, ±10 mm on 100% of points, respectively. B1–B4: MR prostate shapes with noise amplitude of ±2.5, ±5, ±7.5, ±10 mm on 100% of points, respectively.
Since the automatically prostate segmentation may have errors, we performed an additional experiment to investigate the robustness of our method to such segmentation errors. For the ease of evaluation, we have chosen the case in Fig.9 as the experiment subject as the cyst in this case is clearly visible. Manual contour was carefully prepared for this patient. MR-TRUS registration was performed using the manual segmentation and compared to that using the automatic segmentation results. In Fig. 14, we can see that there are very minimal differences between the registration results. The registration results using manual contours appear to be slightly better as judged by the cyst matching indicated by the arrows in Fig. 14.
Fig. 14.
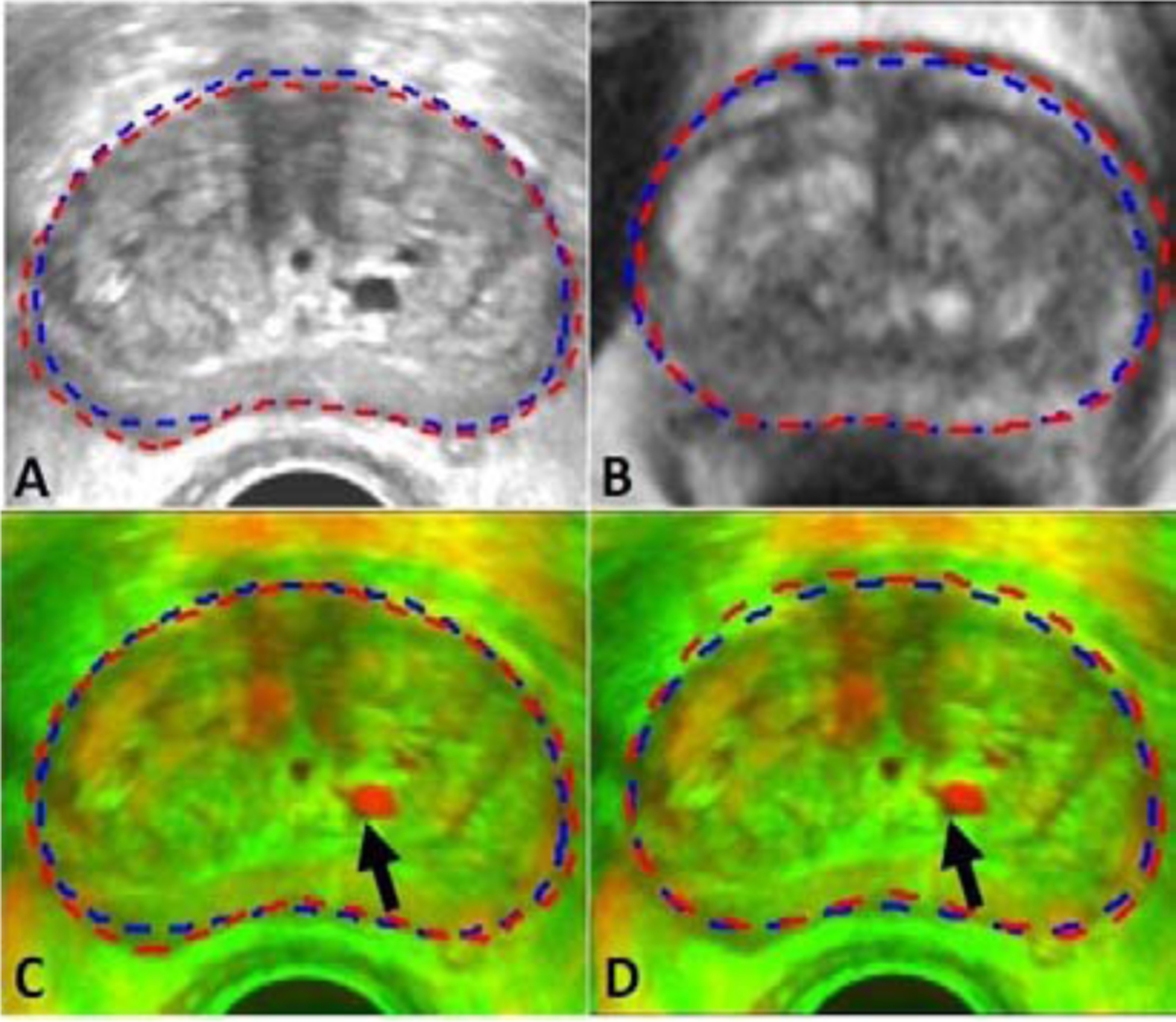
A–B: Manual contours and automatic contours on TRUS and MR images, respectively. Manual contours are shown in red and automatic contours are shown in blue. C–D: Fused images of registration results using manual contours and automatic contours, respectively.
5. Discussions
In this study, a novel deep learning-based point cloud matching method was proposed for MR-TRUS image registration. Due to the vast appearance difference between MR and TRUS images, image intensity-based similarity metrics have very limited success in MR-TRUS image registration. To bypass the need for an accurate similarity metric, the segmented prostate shapes were utilized to drive the registration process. The prostate shapes are the reliable features that are available in both MR and TRUS images. However, it is difficult to propagate the prostate surface-driven deformation to intraprostatic deformation. Intraprostatic deformation was usually calculated from surface-driven deformation using interpolation-based models, such as radial basis functions, free-form deformations and Gaussian-basis functions. These interpolation-based models may result in implausible interior deformation field due to the lack of intraprostatic control points and deformation regularization. To address this issue, we have used volumetric point could with many intraprostatic points. The proposed ProRegNet was able to directly consume irregular 3D point cloud and predict the motion between the MR and TRUS volumetric point clouds without iterations. Biomechanical models have been proven to be superior to interpolation-based models (Khallaghi et al., 2015a; Khallaghi et al., 2015b; van de Ven et al., 2015). However, it is impractical to build a patient-specific FE model for every patient who underwent TRUS in the operating room given that FE modeling is very time-consuming and resource-intensive. Recently, Liang et al. (Liang et al., 2018) published a paper on a first attempt to use deep learning as a fast and accurate surrogate for the time-consuming FE modeling on aorta stress calculation. Inspired by this work, we proposed to train a deep learning network to replace FE modeling that deforms the MR prostate shape to TRUS prostate shape. A total of 500 training datasets, 10 datasets per patient, were generated by FE modeling of MR-TRUS deformation for 50 patients. The proposed ProRegNet was trained to learn the biomechanical constraints that were encoded in the FE-generated point correspondence.
It is important to ensure the segmentation accuracy of the prostate for surface-driven registrations. Manual contour is too time-consuming to be performed for every patient in real time. In addition, human contour is prone to error under time-constraint and fatigue. To address this issue, we proposed to use deep learning-based methods for prostate segmentation in the first step. The deep learning-based methods could achieve an average DSC of 0.86 and 0.92 for MR and TRUS, respectively. To avoid large segmentation errors, physicians are encouraged to check and make necessary corrections prior to registration. We have found out that the most extreme outlier case in Fig. 6 and Fig. 7 for ProRegNet was from the same patient. To further analyze the cause, we plotted the prostate shapes of this outlier case in Fig. 15 (B1 and B2). For comparison purpose, another case with good registration accuracy was shown in Fig. 15 (A1 and A2). The cause of the outlier could be two-fold, 1) the large shape discrepancy could be caused by segmentation inaccuracies, especially at the apex and base slices along the transverse axis. Though the prostate boundary is usually more visible in MR than TRUS, MR prostate segmentation is prone to error because MR usually has a large slice thickness. The large slice thickness would introduce errors especially at the apex and base of the prostate since the prostate may end between slices. To avoid such an outlier, we could ask physicians to check the contours and make necessary corrections quickly prior to registration; 2) the prostate shape in TRUS has undergone large deformation compared to MR, leading to significant prostate shape difference. The small training datasets could not cover this extreme case, resulting in poor generalization to this extreme case. We could collect more datasets to include such cases into the training datasets in the future.
Fig. 15.
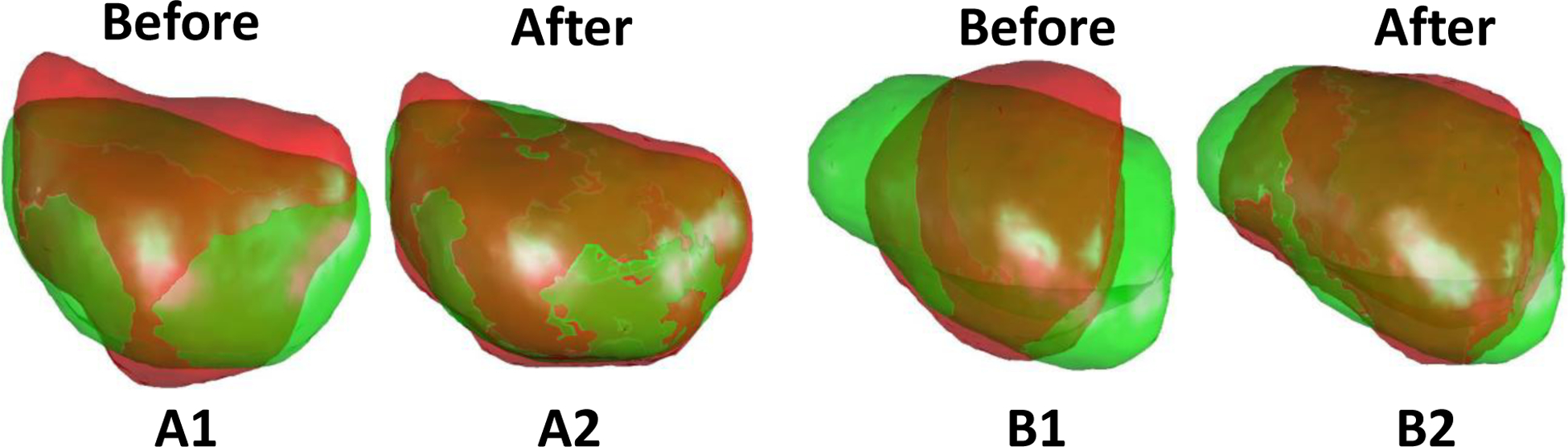
MR-TRUS prostate shapes before and after ProRegNet registration in the sagittal plane. Green shape represents TURS prostate shape while red shape represents MR prostate shape. A1–A2: Prostate shapes before and after registration for one good case. B1–B2: Prostate shapes before and after registration for the outlier case.
In this study, we utilized nodal displacement boundary conditions instead of US probe-prostate interaction modeling to drive the prostate deformation. The US probe-prostate interaction modelling may be advantageous at modelling the actual US imaging process. However, it is very difficult to accurately define other FE boundary conditions that require not only precise surrounding organs modelling such as shapes, stiffnesses but also proper interactions handling between them such as nodal coupling, friction or frictionless sliding. In addition, the level of elastic support the prostate gets from its surrounding tissues directly affects how much rigid translation the prostate could undergo when the prostate is pressed by the US probe. More importantly, the FE simulation driven by different US probe-prostate tissue interactions could hardly deform the MR prostate in a way that exactly replicate the prostate shape of the US. This is undesired in our study since our goal is to replicate the prostate shape correspondence between MR and US, before and amid the US imaging, so that we can predict the prostate motion from the two shapes. On the contrary, nodal displacement boundary condition could ensure that the FE-deformed MR prostate shape matches that of the US prostate shape. Being aware that the nodal displacement correspondence generated by surface registration could lead to errors in FE simulation, we only generated training datasets based on the surface registration method to bootstrap our biomechanical modelling and network training. Once the network was trained, one-to-one point correspondence was not required to predict the motion vector field of one volumetric point cloud to match the other. It was further shown in Fig. 14 that the proposed method is tolerable to certain levels of prostate segmentation errors.
We used the sum of volumetric points motion error and surface Chamber distance as loss function. The volumetric points motion error which measures the differences between the predicted motion and the FE-generated motion enables the network to learn the biomechanically constrained motion patterns. The surface Chamber distance encourages the network to match prostate shapes at the same time. We have trained another model without the surface distance loss to test its importance. The DSC, MSD, HD and TRE for the network trained without surface distance loss were 0.93±0.02, 0.97±0.17 mm, 3.40±1.06 mm and 1.61±0.55 mm, respectively. All four metrics were worse without surface distance loss, demonstrating the usefulness of surface distance loss.
One limitation of this study is that only one set of material parameters was used in the FE modeling. Hu et al. (Hu et al., 2012) simulated the prostate using a range of parameters. Wang et al. (Wang et al., 2016) obtained the prostate material parameter using US shear wave elastography. The accuracy of the US elastography needs to be carefully studied before its precision can be trusted. All tissues were assumed to behave as isotropic, homogeneous and elastic material in both studies, which is another source of error in biomechanical modeling. It is difficult to justify the importance of absolute accuracy of patient-specific material elasticity given other uncertainties, such as material anisotropy, heterogeneity and boundary condition precision. On the other hand, it is reasonable for Wang et al. to measure individual material elasticity since they aimed to build a patient-specific model. On the contrary, we aimed to build a population-based model using FE. Fu et al. (Fu et al., 2013) reported that soft tissue is highly inhomogeneous with nondeterministic material parameters. Soft tissue of the same subject could vary across different days. Hence, it is reasonable to use the mean prostate elasticity for population-based simulations.
Our method was trained and tested using datasets from brachytherapy which has a similar US probe-tissue interaction, US image acquisition and needle/catheter placement orientation as perineum biopsy. On the other hand, end-fired biopsy widely used today has different processes, which may cause different prostate deformation pattern. Therefore, the proposed method may not be readily applicable to end-fired biopsy. The segmentation networks were trained and tested using images from our department. They are likely to generate sub-optimal segmentation results on images from different commercial systems. In the future, we plan to investigate our networks using multi-institutional datasets from different imaging systems.
We have investigated our method via comparison with the traditional surface-based methods and CNN-based method using eight different metrics. To study the robustness of our method to noise, many experiments were conducted with prostate shapes contaminated with different level of noise. Though we have investigated our method from different perspectives, there are many other experiments that we could conduct to further improve our understanding. Currently, we paired only the first step with the subsequent sub-steps of FE results to prepare the training datasets. In the future, we will try to pair up any two sub-steps of the FE results in the training dataset. In this manner, we could have 2250 training datasets instead of the current 450 training datasets, which should increase the network’s ability to generalize well on new patients. In addition, the network could learn the point matching as a multi-step temporal procedure by pairing up each sub-step with its subsequent sub-step. Despite not available across all patients, corresponding anatomical landmarks inside the prostate have been demonstrated to be helpful in MR-TRUS image registration. We plan to develop an automatic algorithm to detect and establish landmarks correspondences prior to registration to further improve the registration accuracy.
6. Conclusions
A novel deep learning-based 3D point cloud matching method was proposed for MR-TRUS image registration. Population-based FE models were conducted to simulate prostate deformations between MR and TRUS. The FE-generated deformation field was used to train the proposed network to apply biomechanical constraint on the 3D point matching. Our results demonstrated that the proposed method was able to accurately and rapidly register MR and TRUS prostate images for image-guided prostate intervention.
Highlights.
Volumetric point cloud motion was predicted by network for MR-TRUS prostate registration.
FE-simulated point correspondences were used to model biomechanical constraints.
Surface Chamber distance loss was used to promote prostate shape registration.
Acknowledgement
This research is supported in part by the National Cancer Institute of the National Institutes of Health under Award Number R01CA215718 (XY), the Department of Defense (DoD) Prostate Cancer Research Program (PCRP) Award W81XWH-17-1-0438 (TL) and W81XWH-17-1-0439 (AJ) and Dunwoody Golf Club Prostate Cancer Research Award (XY), a philanthropic award provided by the Winship Cancer Institute of Emory University.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures
The authors declare no conflicts of interest.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Audenaert EA, Van Houcke J, Almeida DF, Paelinck L, Peiffer M, Steenackers G, Vandermeulen D, 2019. Cascaded statistical shape model based segmentation of the full lower limb in CT. Comput Methods Biomech Biomed Engin 22, 644–657. [DOI] [PubMed] [Google Scholar]
- Bahn D, de Castro Abreu AL, Gill IS, Hung AJ, Silverman P, Gross ME, Lieskovsky G, Ukimura O, 2012. Focal cryotherapy for clinically unilateral, low-intermediate risk prostate cancer in 73 men with a median follow-up of 3.7 years. Eur Urol 62, 55–63. [DOI] [PubMed] [Google Scholar]
- Bernhard S, John P, Thomas H, 2007. Non-rigid point set registration: Coherent Point Drift, Advances in Neural Information Processing Systems 19: Proceedings of the 2006 Conference. MITP, p. 1. [Google Scholar]
- Besl PJ, McKay ND, 1992. A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence 14, 239–256. [Google Scholar]
- Bloom JB, Gold SA, Hale GR, Rayn KN, Sabarwal VK, Bakhutashvili I, Valera V, Turkbey B, Pinto PA, Wood BJ, 2018. “Super-active surveillance”: MRI ultrasound fusion biopsy and ablation for less invasive management of prostate cancer. Gland Surg 7, 166–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bookstein FL, 1989. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence 11, 567–585. [Google Scholar]
- Brock KK, Mutic S, McNutt TR, Li H, Kessler ML, 2017. Use of image registration and fusion algorithms and techniques in radiotherapy: Report of the AAPM Radiation Therapy Committee Task Group No. 132. Med Phys 44, e43–e76. [DOI] [PubMed] [Google Scholar]
- Challapalli A, Jones E, Harvey C, Hellawell GO, Mangar SA, 2012. High dose rate prostate brachytherapy: an overview of the rationale, experience and emerging applications in the treatment of prostate cancer. Br J Radiol 85 Spec No 1, S18–S27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chui H, Rangarajan A, 2003. A new point matching algorithm for non-rigid registration. Computer Vision and Image Understanding 89, 114–141. [Google Scholar]
- Dickinson L, Hu Y, Ahmed HU, Allen C, Kirkham AP, Emberton M, Barratt D, 2013. Image-directed, tissue-preserving focal therapy of prostate cancer: a feasibility study of a novel deformable magnetic resonance-ultrasound (MR-US) registration system. BJU Int 112, 594–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong X, Lei Y, Wang T, Thomas M, Tang L, Curran WJ, Liu T, Yang X, 2019. Automatic multiorgan segmentation in thorax CT images using U-net-GAN. Med Phys 46, 2157–2168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du S, Zheng N, Ying S, Liu J, 2010. Affine iterative closest point algorithm for point set registration. Pattern Recognition Letters 31, 791–799. [Google Scholar]
- Fan H, Su H, Guibas LJ, 2016. A Point Set Generation Network for 3D Object Reconstruction from a Single Image. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2463–2471. [Google Scholar]
- Fu Y, Lei Y, Wang T, Curran WJ, Liu T, Yang X, 2020. Deep learning in medical image registration: a review. Phys Med Biol. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y, Liu S, Li HH, Li H, Yang D, 2018a. An adaptive motion regularization technique to support sliding motion in deformable image registration. Med Phys 45, 735–747. [DOI] [PubMed] [Google Scholar]
- Fu Y, Mazur TR, Wu X, Liu S, Chang X, Lu Y, Li HH, Kim H, Roach MC, Henke L, Yang D, 2018b. A novel MRI segmentation method using CNN-based correction network for MRI-guided adaptive radiotherapy. Med Phys 45, 5129–5137. [DOI] [PubMed] [Google Scholar]
- Fu Y, Wu X, Thomas AM, Li HH, Yang D, 2019. Automatic large quantity landmark pairs detection in 4DCT lung images. Med Phys 46, 4490–4501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu YB, Chui CK, Teo CL, 2013. Liver tissue characterization from uniaxial stress–strain data using probabilistic and inverse finite element methods. Journal of the Mechanical Behavior of Biomedical Materials 20, 105–112. [DOI] [PubMed] [Google Scholar]
- Ghavami N, Hu Y, Gibson E, Bonmati E, Emberton M, Moore CM, Barratt DC, 2019. Automatic segmentation of prostate MRI using convolutional neural networks: Investigating the impact of network architecture on the accuracy of volume measurement and MRI-ultrasound registration. Medical Image Analysis 58, 101558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong L, Wang H, Peng C, Dai Y, Ding M, Sun Y, Yang X, Zheng J, 2017. Non-rigid MR-TRUS image registration for image-guided prostate biopsy using correlation ratio-based mutual information. Biomed Eng Online 16, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haskins G, Kruecker J, Kruger U, Xu S, Pinto PA, Wood BJ, Yan P, 2019a. Learning deep similarity metric for 3D MR–TRUS image registration. International Journal of Computer Assisted Radiology and Surgery 14, 417–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haskins G, Kruger U, Yan P, 2019b. Deep Learning in Medical Image Registration: A Survey. ArXiv abs/1903.02026. [Google Scholar]
- Heinrich MP, Jenkinson M, Bhushan M, Matin T, Gleeson FV, Brady SM, Schnabel JA, 2012. MIND: Modality independent neighbourhood descriptor for multi-modal deformable registration. Medical Image Analysis 16, 1423–1435. [DOI] [PubMed] [Google Scholar]
- Hu Y, Ahmed HU, Taylor Z, Allen C, Emberton M, Hawkes D, Barratt D, 2012. MR to ultrasound registration for image-guided prostate interventions. Med Image Anal 16, 687–703. [DOI] [PubMed] [Google Scholar]
- Hu Y, Gibson E, Ahmed HU, Moore CM, Emberton M, Barratt DC, 2015. Population-based prediction of subject-specific prostate deformation for MR-to-ultrasound image registration. Medical image analysis 26, 332–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y, Gibson E, Ghavami N, Bonmati E, Moore CM, Emberton M, Vercauteren T, Noble JA, Barratt DC, 2018a. Adversarial Deformation Regularization for Training Image Registration Neural Networks, MICCAI. [Google Scholar]
- Hu Y, Modat M, Gibson E, Li W, Ghavami N, Bonmati E, Wang G, Bandula S, Moore CM, Emberton M, Ourselin S, Noble JA, Barratt DC, Vercauteren T, 2018b. Weakly-supervised convolutional neural networks for multimodal image registration. Med Image Anal 49, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y, Morgan D, Ahmed HU, Pendse D, Sahu M, Allen C, Emberton M, Hawkes D, Barratt D, 2008. A statistical motion model based on biomechanical simulations for data fusion during image-guided prostate interventions. Med Image Comput Comput Assist Interv 11, 737–744. [DOI] [PubMed] [Google Scholar]
- Jian B, Vemuri BC, 2011. Robust Point Set Registration Using Gaussian Mixture Models. IEEE Transactions on Pattern Analysis and Machine Intelligence 33, 1633–1645. [DOI] [PubMed] [Google Scholar]
- Kadoury S, Yan P, Xu S, Glossop N, Choyke P, Turkbey B, Pinto P, Wood BJ, Kruecker J, 2010. Realtime TRUS/MRI Fusion Targeted-Biopsy for Prostate Cancer: A Clinical Demonstration of Increased Positive Biopsy Rates. Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 52–62. [Google Scholar]
- Khallaghi S, Sanchez CA, Rasoulian A, Nouranian S, Romagnoli C, Abdi H, Chang SD, Black PC, Goldenberg L, Morris WJ, Spadinger I, Fenster A, Ward A, Fels S, Abolmaesumi P, 2015a. Statistical Biomechanical Surface Registration: Application to MR-TRUS Fusion for Prostate Interventions. IEEE Trans Med Imaging 34, 2535–2549. [DOI] [PubMed] [Google Scholar]
- Khallaghi S, Sánchez CA, Rasoulian A, Sun Y, Imani F, Khojaste A, Goksel O, Romagnoli C, Abdi H, Chang S, Mousavi P, Fenster A, Ward A, Fels S, Abolmaesumi P, 2015b. Biomechanically Constrained Surface Registration: Application to MR-TRUS Fusion for Prostate Interventions. IEEE Transactions on Medical Imaging 34, 2404–2414. [DOI] [PubMed] [Google Scholar]
- Kim Y, Na YH, Xing L, Lee R, Park S, 2016. Automatic deformable surface registration for medical applications by radial basis function-based robust point-matching. Comput Biol Med 77, 173–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohlrausch J, Rohr K, Stiehl HS, 2005. A New Class of Elastic Body Splines for Nonrigid Registration of Medical Images. Journal of Mathematical Imaging and Vision 23, 253–280. [Google Scholar]
- Lei Y, Tian S, He X, Wang T, Wang B, Patel P, Jani AB, Mao H, Curran WJ, Liu T, Yang X, 2019. Ultrasound prostate segmentation based on multidirectional deeply supervised V-Net. Med Phys 46, 3194–3206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Sumner RW, Pauly M, 2008. Global Correspondence Optimization for Non-Rigid Registration of Depth Scans. Computer Graphics Forum 27, 1421–1430. [Google Scholar]
- Liang L, Liu M, Martin C, Sun W, 2018. A deep learning approach to estimate stress distribution: a fast and accurate surrogate of finite-element analysis. J R Soc Interface 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litjens G, Toth R, van de Ven W, Hoeks C, Kerkstra S, van Ginneken B, Vincent G, Guillard G, Birbeck N, Zhang J, Strand R, Malmberg F, Ou Y, Davatzikos C, Kirschner M, Jung F, Yuan J, Qiu W, Gao Q, Edwards PE, Maan B, van der Heijden F, Ghose S, Mitra J, Dowling J, Barratt D, Huisman H, Madabhushi A, 2014. Evaluation of prostate segmentation algorithms for MRI: the PROMISE12 challenge. Med Image Anal 18, 359–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Qi CR, Guibas LJ, 2018. FlowNet3D: Learning Scene Flow in 3D Point Clouds, CVPR. [Google Scholar]
- Loeckx D, Slagmolen P, Maes F, Vandermeulen D, Suetens P, 2010. Nonrigid image registration using conditional mutual information. IEEE Trans Med Imaging 29, 19–29. [DOI] [PubMed] [Google Scholar]
- Mitra J, Kato Z, Marti R, Oliver A, Llado X, Sidibe D, Ghose S, Vilanova JC, Comet J, Meriaudeau F, 2012. A spline-based non-linear diffeomorphism for multimodal prostate registration. Med Image Anal 16, 1259–1279. [DOI] [PubMed] [Google Scholar]
- Onofrey JA, Oksuz I, Sarkar S, Venkataraman R, Staib LH, Papademetris X, 2016. MRI-TRUS Image Synthesis with Application to Image-Guided Prostate Intervention. Springer International Publishing, Cham, pp. 157–166. [Google Scholar]
- Ou Y, Sotiras A, Paragios N, Davatzikos C, 2011. DRAMMS: Deformable registration via attribute matching and mutual-saliency weighting. Med Image Anal 15, 622–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pence TJ, Gou K, 2015. On compressible versions of the incompressible neo-Hookean material. Mathematics and Mechanics of Solids 20, 157–182. [Google Scholar]
- Qi C, Su H, Mo K, Guibas LJ, 2016. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 77–85. [Google Scholar]
- Qi CR, Yi L, Su H, Guibas LJ, 2017. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space, NIPS. [Google Scholar]
- Reynier C, Troccaz J, Fourneret P, Dusserre A, Gay-Jeune C, Descotes JL, Bolla M, Giraud JY, 2004. MRI/TRUS data fusion for prostate brachytherapy. Preliminary results. Med Phys 31, 1568–1575. [DOI] [PubMed] [Google Scholar]
- Rivaz H, Karimaghaloo Z, Fonov VS, Collins DL, 2014. Nonrigid registration of ultrasound and MRI using contextual conditioned mutual information. IEEE Trans Med Imaging 33, 708–725. [DOI] [PubMed] [Google Scholar]
- Shaaer A, Davidson M, Semple M, Nicolae A, Mendez LC, Chung H, Loblaw A, Tseng CL, Morton G, Ravi A, 2019. Clinical evaluation of an MRI-to-ultrasound deformable image registration algorithm for prostate brachytherapy. Brachytherapy 18, 95–102. [DOI] [PubMed] [Google Scholar]
- Shahzad M, Kamran A, Siddiqui MZ, Farhan M, 2015. Mechanical Characterization and FE Modelling of a Hyperelastic Material. [Google Scholar]
- Singh AK, Kruecker J, Xu S, Glossop N, Guion P, Ullman K, Choyke PL, Wood BJ, 2008. Initial clinical experience with real-time transrectal ultrasonography-magnetic resonance imaging fusion-guided prostate biopsy. BJU Int 101, 841–845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y, Yuan J, Qiu W, Rajchl M, Romagnoli C, Fenster A, 2015. Three-Dimensional Nonrigid MR-TRUS Registration Using Dual Optimization. IEEE Trans Med Imaging 34, 1085–1095. [DOI] [PubMed] [Google Scholar]
- van de Ven WJ, Hu Y, Barentsz JO, Karssemeijer N, Barratt D, Huisman HJ, 2015. Biomechanical modeling constrained surface-based image registration for prostate MR guided TRUS biopsy. Med Phys 42, 2470–2481. [DOI] [PubMed] [Google Scholar]
- van de Ven WJ, Hulsbergen-van de Kaa CA, Hambrock T, Barentsz JO, Huisman HJ, 2013. Simulated required accuracy of image registration tools for targeting high-grade cancer components with prostate biopsies. Eur Radiol 23, 1401–1407. [DOI] [PubMed] [Google Scholar]
- Wang B, Lei Y, Tian S, Wang T, Liu Y, Patel P, Jani AB, Mao H, Curran WJ, Liu T, Yang X, 2019. Deeply supervised 3D fully convolutional networks with group dilated convolution for automatic MRI prostate segmentation. Med Phys 46, 1707–1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Cheng JZ, Ni D, Lin M, Qin J, Luo X, Xu M, Xie X, Heng PA, 2016. Towards Personalized Statistical Deformable Model and Hybrid Point Matching for Robust MR-TRUS Registration. IEEE Trans Med Imaging 35, 589–604. [DOI] [PubMed] [Google Scholar]
- Wang Y, Zheng Q, Heng PA, 2018. Online Robust Projective Dictionary Learning: Shape Modeling for MR-TRUS Registration. IEEE Transactions on Medical Imaging 37, 1067–1078. [DOI] [PubMed] [Google Scholar]
- Weir HK, Thompson TD, Soman A, Moller B, Leadbetter S, 2015. The past, present, and future of cancer incidence in the United States: 1975 through 2020. Cancer 121, 1827–1837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yacoub JH, Verma S, Moulton JS, Eggener S, Aytekin O, 2012. Imaging-guided prostate biopsy: conventional and emerging techniques. Radiographics 32, 819–837. [DOI] [PubMed] [Google Scholar]
- Yan P, Xu S, Rastinehad AR, Wood BJ, 2018. Adversarial Image Registration with Application for MR and TRUS Image Fusion. Springer International Publishing, Cham, pp. 197–204. [Google Scholar]
- Yang J, Cao Z, Zhang Q, 2016. A fast and robust local descriptor for 3D point cloud registration. Information Sciences 346–347, 163–179. [Google Scholar]
- Yang X, Akbari H, Halig L, Fei B, 2011. 3D Non-rigid Registration Using Surface and Local Salient Features for Transrectal Ultrasound Image-guided Prostate Biopsy. Proc SPIE Int Soc Opt Eng 7964, 79642v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Rossi P, Mao H, Jani AB, Ogunleye T, Curran WJ, Liu T, 2015. A MR-TRUS Registration Method for Ultrasound-Guided Prostate Interventions. Proc SPIE Int Soc Opt Eng 9415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Rossi P, Ogunleye T, Marcus DM, Jani AB, Mao H, Curran WJ, Liu T, 2014. Prostate CT segmentation method based on nonrigid registration in ultrasound-guided CT-based HDR prostate brachytherapy. Med Phys 41, 111915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Rossi PJ, Jani AB, Mao H, Zhou Z, Curran WJ, Liu T, 2017. Improved prostate delineation in prostate HDR brachytherapy with TRUS-CT deformable registration technology: A pilot study with MRI validation. J Appl Clin Med Phys 18, 202–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J, Qiu W, Rajchl M, Ukwatta E, Tai X, Fenster A, 2013. Efficient 3D Endfiring TRUS Prostate Segmentation with Globally Optimized Rotational Symmetry, 2013 IEEE Conference on Computer Vision and Pattern Recognition, pp. 2211–2218. [Google Scholar]
- Zhang S, Jiang S, Yang Z, Liu R, 2015. 2D Ultrasound and 3D MR Image Registration of the Prostate for Brachytherapy Surgical Navigation. Medicine (Baltimore) 94, e1643. [DOI] [PMC free article] [PubMed] [Google Scholar]


