Triple diffusion encoding MRI predicts intra-axonal and extra-axonal diffusion tensors in white matter

Abstract

Purpose:

To demonstrate how triple diffusion encoding (TDE) MRI can be applied to separately estimate the intra-axonal and extra-axonal diffusion tensors in white matter (WM).

Methods:

Using a TDE pulse sequence with an axially symmetric b-matrix, diffusion MRI data were acquired at 3 T for three healthy adults with an axial b-value of 4000 s/mm², a radial b-value of 307 s/mm², and 64 diffusion encoding directions. This acquisition was then repeated with the radial b-value set to zero. A previously proposed theory was applied to this data in order to estimate the intra-axonal diffusivity and axonal water fraction for each WM voxel. Conventional single diffusion encoding data were also obtained with b-values of 1000 and 2000 s/mm², which provided additional information sufficient for determining both the intra-axonal and extra-axonal diffusion tensors.

Results:

From the TDE data, the average intra-axonal diffusivity in WM was found to be 2.24 ± 0.18 μm²/ms, and the average axonal water fraction was found to be 0.60 ± 0.11. From the two diffusion tensors, average WM values were estimated for several compartment-specific diffusion parameters. In particular, the extra-axonal mean diffusivity was 1.09 ± 0.19 μm²/ms, the intra-axonal fractional anisotropy was 0.50 ± 0.14, and the extra-axonal fractional anisotropy was 0.23 ± 0.13.

Conclusion:

By employing a simple TDE pulse sequence with an axially symmetric b-matrix, the diffusion tensors for the intra-axonal and extra-axonal spaces can be separately estimated in adult WM. This allows one to determine compartment-specific diffusion properties for these two water pools.

1 |. INTRODUCTION

The most familiar diffusion MRI (dMRI) parameters, such as the mean diffusivity (MD) and fractional anisotropy (FA), often include contributions from multiple microenvironments within a tissue.^1–3 For example, in white matter (WM), the MD and FA reflect water mobility of both the intra-axonal and extra-axonal compartments. The biophysical interpretation of changes associated with disease or aging of such amalgamated dMRI parameters can be challenging, since it is often unclear which tissue compartments are most affected.

In order to help alleviate this source of ambiguity, a variety of microstructural models have been proposed, particularly for brain tissue, in which the free parameters correspond to compartment-specific diffusion properties of interest.^4–14 The parameters are estimated by fitting dMRI data, often using nonlinear optimization methods. In WM, one such parameter, the intrinsic intra-axonal diffusivity (D_a), has proven especially challenging to measure.^12,15,16 This is because D_a estimates are sensitive to modeling assumptions and tend to be only loosely constrained by the data, although some recently proposed approaches seem to be more promising.^10,12–14

Tissue modeling of this sort has typically employed data acquired with single diffusion encoding (SDE), in which only one diffusion-sensitizing gradient direction is used for each spin excitation, as this is the simplest and most widely available type of dMRI sequence. However, by supplementing SDE data with triple diffusion encoding (TDE) data, it is possible to estimate D_a and the axonal water fraction (f) in a remarkably direct manner that involves only mild assumptions and avoids complex fitting procedures.¹⁷ An essential feature of the TDE sequence is that it have an axially symmetric b-matrix with nonzero eigenvalues, which is not possible to achieve with either SDE or double diffusion encoding (DDE). Prior work has illustrated this method with numerical simulations.¹⁷ The major purpose of this paper is to demonstrate its application for in vivo data from adult human brain.

Given values for D_a and f, one can then use fiber ball imaging (FBI)^18,19 and diffusional kurtosis imaging (DKI),^20,21 which are both SDE techniques, to further estimate the individual diffusion tensors for the intra-axonal (D_a) and extra-axonal (D_e) spaces. In this way, TDE MRI may be combined with more conventional methods to provide a fairly comprehensive description of diffusion for both the intra-axonal and extra-axonal water pools. In particular, the two individual diffusion tensors allow for a variety of compartment-specific diffusion properties to be determined, such as the fractional anisotropy for the intra-axonal space (FAA) and the mean diffusivity for the extra-axonal space (${\overline{D}}_e$).

Four key assumptions underlie this approach: 1) water exchange between the intra-axonal and extra-axonal water pools can be neglected over time scales comparable to the diffusion time of the dMRI pulse sequence, which is typically tens of milliseconds; 2) the dMRI signal from water within myelin can be neglected; 3) axons can be idealized as thin, straight cylinders; and 4) the applied diffusion weighting is sufficiently strong to largely suppress the dMRI signal from extra-axonal water relative to the intra-axonal dMRI signal. Assumption 1 is justified by the long water exchange times of about 1 s measured in WM.²² Assumption 2 is valid provided the T2 of myelin water, which is about 10 to 20 ms,²³ is short in comparison to the echo time for the sequence, as is usually true for dMRI sequences implemented on clinical MRI systems. Assumption 3 is strongly supported by recent work on the scaling of the dMRI signal for b-values greater than about 4000 s/mm².^19,24,25 There is also substantial evidence that Assumption 4 holds to a reasonable approximation, at least in healthy adults, for b-values greater than 4000 s/mm².¹⁹ Importantly, it is not necessary to assume a specific model for diffusion in the extra-axonal space (e.g., Gaussian diffusion). This is a crucial distinction between the TDE method described here and several SDE methods^{4–7,9,10,12–14} for separately quantifying intra-axonal and extra-axonal diffusion properties.

In this first experimental demonstration, we focus on the details of the TDE pulse sequence and present preliminary data for three healthy adult subjects. We also compare and contrast our results to those of a closely related alternative approach for estimating estimate D_a that combines data obtained using a TDE pulse sequence and a DDE pulse sequence.²⁶

2 |. METHODS

2.1 |. TDE pulse sequence

A TDE pulse sequence has, in general, diffusion weighting along three distinct directions for each spin excitation. In this work, these directions are all taken to be orthogonal. One of these directions has the largest diffusion weighting and will be referred to as the axial direction. The b-value associated with the axial direction is indicated by b_∥. The other two directions, with smaller diffusion weightings, will be called the radial directions. The b-values for the two radial directions, denoted by b_⊥, are assumed to be equal.

A pulse sequence diagram for the TDE sequence is shown in Figure 1 with the axial gradients oriented in the x-direction and with the radial gradients oriented in the y- and z-directions. This sequence is similar to the one proposed in our previous work,¹⁷ but differs here in two respects. First, one set of radial gradients is placed after the axial gradients, and one set of radial gradients is placed before. In our previous work, both sets of radial gradients were played out prior to the axial gradients. This change allows us to reduce the minimum TE for the sequence substantially and thereby improve the SNR. The other difference is to incorporate finite rise times. The TDE pulse sequence code was developed by adding radial gradients to a single-shot EPI SDE pulse sequence (provided by Siemens Healthineers, Erlangen, Germany).

1).

Schematic for the triple diffusion encoding (TDE) pulse sequence used in this study. The axial gradients are oriented in the x-direction while the radial gradients are oriented in the y- and z-directions. By design, the diffusion weighting in the axial direction is higher than for the radial directions, and the axial direction defines the diffusion encoding direction for the sequence. The amplitude of the axial gradient pulses is indicated by g_∥, and the amplitude of the radial gradient pulses is indicated by g_⊥. The diffusion time of each direction corresponds to the interval between the centers of the gradient pulses, and it is indicated by Δ_∥ for the axial direction and by Δ_⊥ for the radial directions. The gradient pulse durations correspond to the interval during which a gradient is at its maximum amplitude plus the rise time, and these are indicated by δ_∥ for the axial direction and by δ_⊥ for the radial directions. The b-matrix for the sequence is axially symmetric since the radial pulses have identical amplitudes and timings. Not shown in this schematic are the imaging gradients, which were implemented as a single shot EPI acquisition

In terms of the sequence parameters, the axial b-value is given by^27,28

$$b_{\parallel }={\gamma }^2{g}_{\parallel }^2\left[{\delta }_{\parallel }^2{\left({\Delta }_{\parallel }-\frac{1}{3}{\delta }_{\parallel }\right)}^2-\frac{1}{6}{\epsilon }_{\parallel }^2{\delta }_{\parallel }+\frac{1}{30}{\epsilon }_{\parallel }^3\right],$$ (1)

where γ is the proton gyromagnetic ratio, g_∥ is the axial gradient amplitude, Δ_∥ is the axial diffusion time, δ_∥ is the axial pulse duration, and ε_∥ is the axial rise time. For ε_∥ = 0, Eq. 1 reduces to the well-known b-value formula for the Stejskal-Tanner sequence.²⁹ Similarly, the radial b-value is given by

$$b_{\perp }={\gamma }^2{g}_{\perp }^2\left[{\delta }_{\perp }^2{\left({\Delta }_{\perp }-\frac{1}{3}{\delta }_{\perp }\right)}^2-\frac{1}{6}{\epsilon }_{\perp }^2{\delta }_{\perp }+\frac{1}{30}{\epsilon }_{\perp }^3\right],$$ (2)

where g_⊥ is the radial gradient amplitude, Δ_⊥ is the radial diffusion time, δ_⊥ is the radial pulse duration, and ε_⊥ is the radial rise time.

If we ignore the contributions from the imaging gradients, the b-matrix for our TDE sequence is simply

$$\mathbf{b}=\left(\begin{array}{ccc}{b}_{\parallel }& 0& 0\\ 0& b_{\perp }& 0\\ 0& 0& b_{\perp }\end{array}\right)$$ (3)

for the orientation of the gradients depicted in Figure 1. It is crucial for our method that this be axially symmetric. In general, the principal eigenvector of the b-matrix will be defined as the diffusion encoding direction for the sequence.

2.2 |. Imaging

Three healthy adult volunteers (ages 28 to 31 yr) were scanned on a 3 T Prisma^fit MRI system (Siemens Healthineers, Erlangen, Germany) equipped with 80 mT/m gradients, a slew rate of 200 T/m/s and VE11c software. Data were obtained using a 32-channel head coil under a protocol approved by the institutional review board of the Medical University of South Carolina.

For each subject, single-shot full Fourier TDE data were acquired with the following imaging parameters: TE = 122 ms, TR = 3900 ms, FOV = 222 × 222 mm², acquisition matrix = 74 × 74, slice thickness = 3 mm, number of slices = 42, phase encoding acceleration factor (GRAPPA) = 2, slice acceleration factor = 2, coil combine mode = adaptive combine, bandwidth = 1536 Hx/px, and number of diffusion encoding directions = 64. The gradient pulse timing parameters were Δ_∥ = 37.04 ms, δ_∥ = 18.55 ms, ε_∥ = 1.52 ms, Δ_⊥ = 12.0 ms, δ_⊥ = 9.48 ms, and ε_⊥ = 1.52 ms.

The main TDE acquisition had axial and radial b-values of b_∥ = 4000 s/mm² and b_⊥ = 307 s/mm². This corresponds to g_∥ ≈ g_⊥ ≈ 73 mT/m. The choice of these b-values was informed by considerations discussed in our previous work.¹⁷ An additional 10 images were acquired with both the axial and radial b-values set to zero (b0 images). The total acquisition time was 5 min 8 s. We then repeated this main acquisition except with the radial gradients switched off so that b_⊥ = 0 s/mm², which corresponds to conventional SDE with a b-value of 4000 s/mm². In nulling the radial gradients, a dead time was incorporated into the sequence so that the timing of the other gradients and the TE were unchanged. This secondary acquisition also included 10 b0 images and had the identical acquisition time of 5 min 8 s. Because of cross-terms between the diffusion and imaging gradients, the exact b-values, as determined from the b-matrices, differed slightly from the nominal values cited above and varied with diffusion encoding direction. Specifically, the axial b-values varied between 3988 and 4012 s/mm² with a standard deviation of 7 s/mm², and the radial b-values varied between 306 and 307 s/mm² with a standard deviation of 0.3 s/mm². These small variations were neglected in our data analysis.

In order to estimate the total diffusion and kurtosis tensors, the same pulse sequence was used to obtain data with b_∥ = 1000 and 2000 s/mm² for b_⊥ = 0 s/mm², which corresponds to low b-value SDE. A dead time in place of the radial gradients was again used to keep all of the other imaging parameters unchanged. Another set of 10 b0 images were obtained in this scan, and the total acquisition time was 9 min and 15 s.

For anatomical reference, MPRAGE data were obtained from each subject with the following imaging parameters: TE = 2.26 ms, TR = 2300 ms, TI = 900 ms, flip angle = 8°, FOV = 256 × 256 mm², acquisition matrix = 256 × 256, slice thickness = 1 mm, number of slices = 192, and phase encoding acceleration factor (GRAPPA) = 2. The acquisition time was 5 min and 21 s.

As a simple test of our TDE pulse sequence, we also acquired data for a spherical water bottle phantom using the same imaging parameters as for the human scans except with TR set to 10 s and the gradient pulse timings adjusted to generate smaller b-values. A longer TR was chosen since free water has a much larger T1 than brain, and smaller b-values were used since the diffusivity of free water is much higher than for water in brain. Three sets of b-values were tested: (b_∥ = 640 s/mm², b_⊥ = 0 s/mm²), (b_∥ = 198 s/mm², b_⊥ = 197 s/mm²), and (b_∥ = 49 s/mm², b_⊥ = 302 s/mm²).

2.3 |. Data analysis

For each subject, all diffusion weighted images were denoised using a Marchenko-Pastur principal components analysis approach.³⁰ These denoised images were then co-registered with standard techniques, including correction of image distortion due to eddy currents (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/eddy).^31,32 We also applied Gibbs ringing³³ and Rician noise bias³⁴ corrections.

A diffusional kurtosis imaging (DKI) analysis was applied to the dMRI data obtained with b_∥ = 1000 and 2000 s/mm² in order to find the total diffusion and kurtosis tensors in each voxel.^20,21,35 From these two tensors, several standard diffusion parameters were determined, including MD, FA, and mean kurtosis (MK). WM was defined as all voxels of the cerebrum with MD < 1.5 μm²/ms and MK > 1.³⁶

The dMRI signal for the two acquisitions with b_∥ = 4000 s/mm² were individually averaged in each voxel over the 64 diffusion encoding directions. The intra-axonal diffusivity in WM was then calculated from¹⁷

$$D_a=\frac{1}{b_{\perp }}\text{ln}\left(\frac{{\overline{S}}_1}{{\overline{S}}_2}\sqrt{\frac{b_{\parallel }}{b_{\parallel }-b_{\perp }}}\right)$$ (4)

where ${\overline{S}}_1$ is the direction-averaged signal when b_⊥ = 0 s/mm² and ${\overline{S}}_2$ is the direction-averaged signal when b_⊥ = 307 s/mm². We also calculated the axonal water fraction in each voxel from¹⁷

$$f=2\sqrt{\frac{D_a{b}_{\parallel }}{\pi }}\cdot \frac{{\overline{S}}_1}{{\overline{S}}_0}$$ (5)

where ${\overline{S}}_0$ is the average signal for the b0 images. The validity of Eqs. 4 and 5 requires that b_∥ be about 4000 s/mm² or greater and that b_⊥ ≪ b_∥. The different ordering of the radial and axial gradient pulses used here, in comparison to our previous work,¹⁷ does not affect the accuracy of these two equations.

The fiber orientation density function (fODF) for each WM voxel was estimated from the dMRI data with b_∥ = 4000 s/mm² and b_⊥ = 0 s/mm² by applying the FBI method.^18,19 Specifically, the spherical harmonic expansion coefficients, $a_{2l}^m$, of the dMRI data were used to estimate the spherical harmonic expansion coefficients, $c_{2l}^m$, of the fODF from the formula

$$c_{2l}^m=\frac{a_{2l}^m}{2\pi P_{2l}(0)g_{2l}\left(b_{\parallel }{D}_a\right)}\cdot \sqrt{\frac{b_{\parallel }{D}_a}{\pi }},$$ (6)

where P_2l(x) is the Legendre polynomial of degree 2l, and

$$g_{2l}\left(b_{\parallel }{D}_a\right)\equiv \frac{l!{\left(b_{{}_{\parallel }}{D}_a\right)}^{l+\frac{1}{2}}}{\Gamma \left(2l+\frac{3}{2}\right)}{}_{1}F{}_1\left(l+\frac{1}{2};2l+\frac{3}{2};-b_{\parallel }{D}_a\right)$$ (7)

with ₁F₁(a;b;z) indicating the confluent hypergeometric function of the first kind and Γ(x) indicating the gamma function. Only spherical harmonic coefficients of even degree were needed because of the antipodal symmetry of the dMRI signal.³⁷ The diffusion tensor for the intra-axonal space, D_a, was then obtained from¹³

$${\mathbf{D}}_a=\frac{D_a}{c_0^0\sqrt{30}}\left(\begin{array}{ccc}\frac{\sqrt{30}}{3}{c}_0^0-\frac{\sqrt{6}}{3}{c}_2^0+c_2^2+c_2^{-2}& i{c}_2^2-i{c}_2^{-2}& -c_2^1+c_2^{-1}\\ i{c}_2^2-i{c}_2^{-2}& \frac{\sqrt{30}}{3}{c}_0^0-\frac{\sqrt{6}}{3}{c}_2^0-c_2^2-c_2^{-2}& -i{c}_2^1-i{c}_2^{-1}\\ -c_2^1+c_2^{-1}& -i{c}_2^1-i{c}_2^{-1}& \frac{\sqrt{30}}{3}{c}_0^0+\frac{2\sqrt{6}}{3}{c}_2^0\end{array}\right).$$ (8)

This diffusion tensor is for the entire intra-axonal compartment taken as a whole rather than for just an individual axonal fiber.

The total diffusion tensor, D, is related to the intra-axonal diffusion tensor and the extra-axonal diffusion tensor, D_e, by the formula

$$\mathbf{D}=f{\mathbf{D}}_a+(1-f){\mathbf{D}}_e.$$ (9)

The validity of Eq. 9 only requires that the intra-axonal and extra-axonal spaces are distinct compartments having negligible water exchange on time scales comparable to the diffusion time and that the contribution of myelin water to the dMRI signal can be ignored. Importantly, it holds even if diffusion in the extra-axonal space is non-Gaussian. To find the extra-axonal diffusion tensor, we rearranged Eq. 9 into the form

$${\mathbf{D}}_e=\frac{\mathbf{D}-f{\mathbf{D}}_a}{1-f}.$$ (10)

This allowed us to determine D_e, since the total diffusion tensor was found with DKI, the intra-axonal diffusion tensor was obtained from Eq. 8, and the axonal water fraction was calculated from Eq. 5.

From the eigenvalues of D_a and D_e, several compartment-specific diffusion properties were obtained using standard expressions. In particular, the mean diffusivity of the extra-axonal space is given by

$${\overline{D}}_e=\frac{1}{3}\left({\lambda }_{e,1}+{\lambda }_{e,2}+{\lambda }_{e,3}\right),$$ (11)

the fractional anisotropy of the intra-axonal space is given by,

$$\text{FAA}=\sqrt{\frac{{\left({\lambda }_{a,1}-{\lambda }_{a,2}\right)}^2+{\left({\lambda }_{a,1}-{\lambda }_{a,3}\right)}^2+{\left({\lambda }_{a,2}-{\lambda }_{a,3}\right)}^2}{2\left({\lambda }_{a,1}^2+{\lambda }_{a,2}^2+{\lambda }_{a,3}^2\right)}},$$ (12)

and the fractional anisotropy of the extra-axonal space is given by,

$$\text{FAE}=\sqrt{\frac{{\left({\lambda }_{e,1}-{\lambda }_{e,2}\right)}^2+{\left({\lambda }_{e,1}-{\lambda }_{e,3}\right)}^2+{\left({\lambda }_{e,2}-{\lambda }_{e,3}\right)}^2}{2\left({\lambda }_{e,1}^2+{\lambda }_{e,2}^2+{\lambda }_{e,3}^2\right)}}$$ (13)

where (λ_a,1 ≥ λ_a,2 ≥ λ_a,3) are the eigenvalues of D_a and (λ_e,1 ≥ λ_e,2 ≥ λ_e,3) are the eigenvalues of D_e.^38,39

For the water bottle phantom data, the same preprocessing steps as for the human data were employed except that the co-registration step was skipped. Then a standard diffusion tensor imaging analysis^38,39 was performed to obtain the MD and FA in which the total b-value was taken as b ≡ b_∥ + 2b_⊥.

3 |. RESULTS

Parametric maps of MD and FA for the water bottle phantom are shown in Figure 2 for a single slice through the middle of the bottle. Similar maps are obtained with all three sets of b-values. For b_∥ = 640 s/mm² and b_⊥ = 0 s/mm², we find MD = 2.11 ± 0.03 μm²/ms and FA = 0.015 ± 0.017; for b_∥ = 198 s/mm² and b_⊥ = 199 s/mm², we find MD = 2.13 ± 0.05 μm²/ms and FA = 0.018 ± 0.023; for b_∥ = 49 s/mm² and b_⊥ = 302 s/mm², we find MD = 2.12 ± 0.05 μm²/ms and FA = 0.009 ± 0.012. All the MD estimates are comparable to literature values for the room temperature diffusivity of free water.⁴⁰ In each case, the FA is close to zero as expected for an isotropic phantom. These results provide a basic check for the accuracy of the data generated by our TDE pulse sequence.

2).

Mean diffusivity (MD) and fractional anisotropy (FA) maps for a spherical water bottle phantom as determined with the TDE pulse sequence. Three different combinations of axial and radial gradients were tested, and all the maps are from the same imaging slice. The MD maps are similar in all cases, while the FA values are close to zero as expected for an isotropic phantom. The calibration bar for the MD is in units of μm²/ms, the calibration bar for the FA is unitless, and the indicated b-values have units of s/mm²

Using the TDE pulse sequence, diffusion-weighted images were obtained with reasonably good SNR throughout the WM. The average SNR for the ${\overline{S}}_0$, ${\overline{S}}_1$, and ${\overline{S}}_2$ in WM were 113 ± 4, 20 ± 1, and 10 ± 1, respectively, where the uncertainties are inter-subject standard deviations. In calculating the SNR, we employed noise maps generated by the denoising algorithm. Examples of ${\overline{S}}_0$, ${\overline{S}}_1$, and ${\overline{S}}_2$ images from one subject are shown in Figure 3.

3).

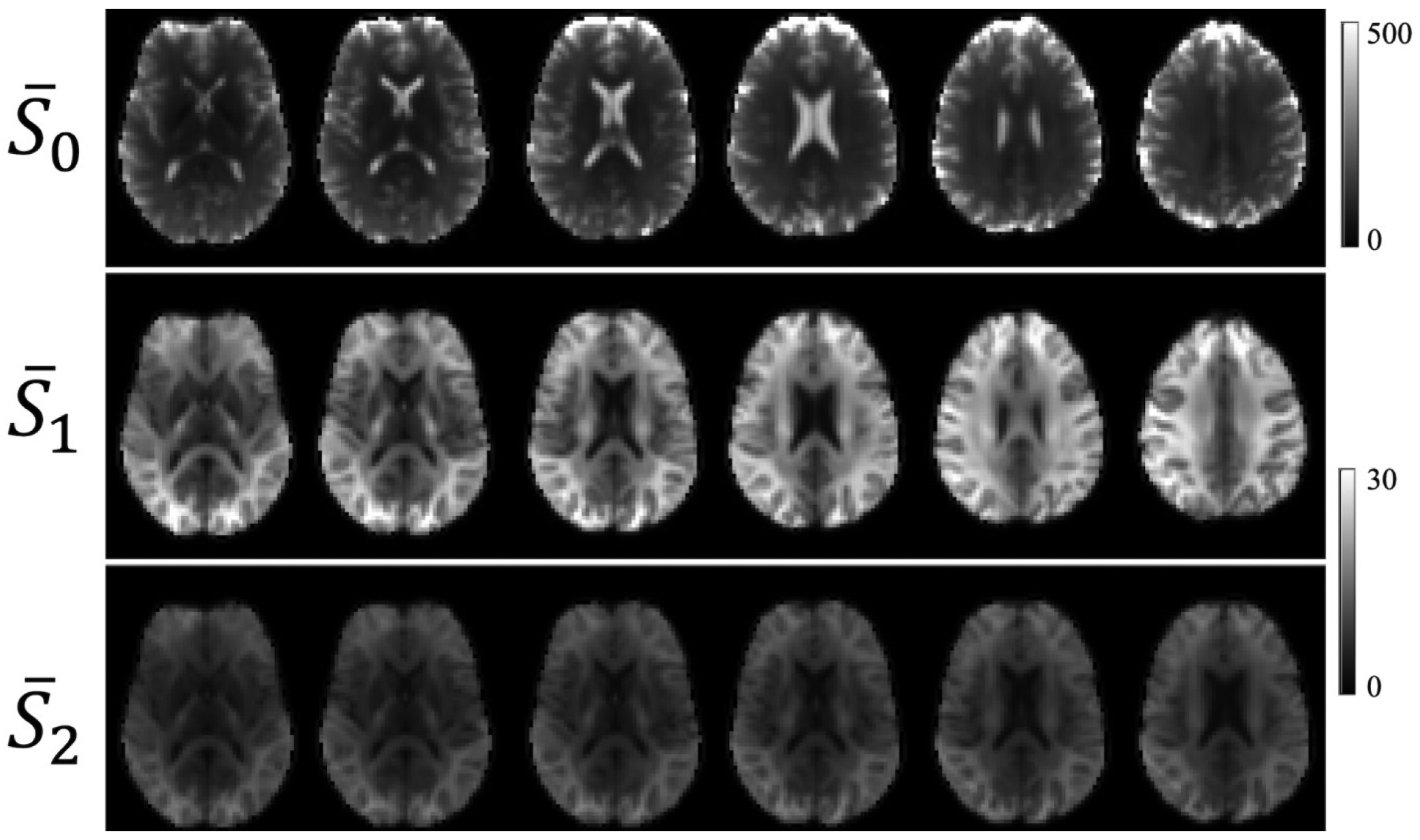
Average TDE images for six consecutive anatomical slices from one subject. The average of all of the b0 images (${\overline{S}}_0$) is shown in the first row. The average over the 64 diffusion encoding directions obtained with b_∥ = 4000 s/mm² and b_⊥ = 0 s/mm² (${\overline{S}}_1$) is shown in the second row. The average over the 64 diffusion encoding directions obtained with b_∥ = 4000 s/mm² and b_⊥ = 300 s/mm² (${\overline{S}}_2$) is shown in the third row. The calibration bars are labeled in relative units. To aid visualization, the intensity range for the ${\overline{S}}_1$ and ${\overline{S}}_2$ images is smaller than for ${\overline{S}}_0$ images

Parametric maps of D_a, ${\overline{D}}_e$, and f for the same subject and anatomical slices are given by Figure 4. The WM has been colored to emphasize that our method for calculating these parameters is only valid in this region. Average WM values of all three parameters for all three subjects are listed in Table 1. As a reference, the MD is also listed. Combining the data from all three subjects gives D_a= 2.24 ± 0.18 μm²/ms, ${\overline{D}}_e=1.09\pm 0.19$ μm²/ms, and f = 0.60 ± 0.11. In Figure 5, D_a, ${\overline{D}}_e$, and f are plotted as functions of FA. Both D_a and ${\overline{D}}_e$ vary weakly with FA, but f grows by almost a factor of two as FA increases from 0.1 to 0.8. This suggests that axons are substantially more tightly packed in high FA regions than in low FA regions.

4).

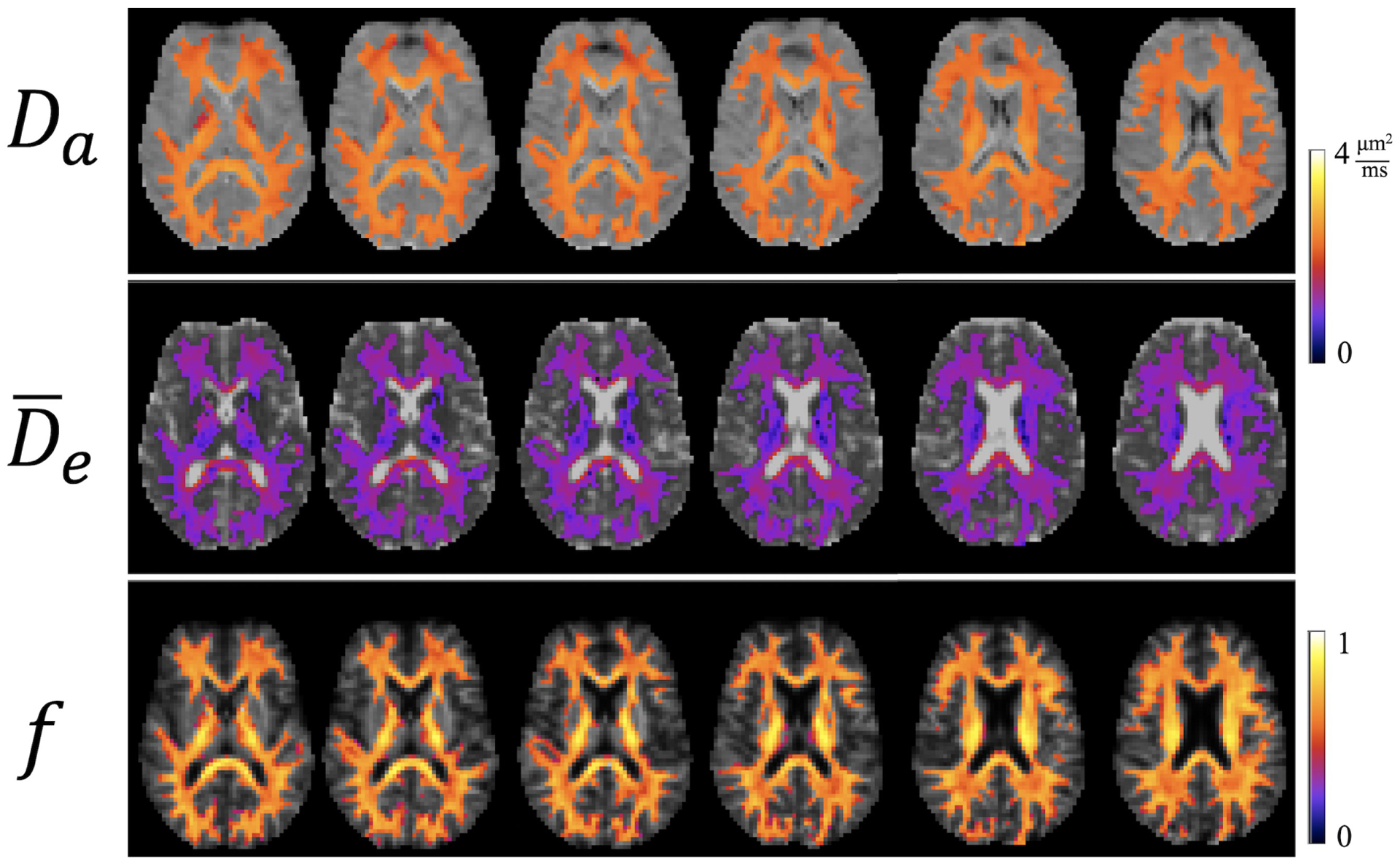
Parametric maps of intra-axonal diffusivity (D_a), mean extra-axonal diffusivity (${\overline{D}}_e$) and axonal water fraction (f) for the same subject and slices as in Figure 3. These estimates are only valid in white matter (WM) regions (shown in color). The calibration bars for the two diffusivities are in units of μm²/ms, while the calibration bar for f is unitless

TABLE 1.

Average values over all white matter (WM) voxels of mean diffusivity (MD), intra-axonal diffusivity (D_a), extra-axonal diffusivity (${\overline{D}}_e$), and axonal water fraction (f) for three healthy, adult subjects. The uncertainties are standard deviations

	MD [μm2/ms]	Da[μm2/ms]	${\overline{D}}_e$ [μm2/ms]	f
Subject 1	0.90 ± 0.10	2.31 ± 0.23	1.09 ± 0.21	0.59 ± 0.11
Subject 2	0.87 ± 0.10	2.21 ± 0.14	1.08 ± 0.18	0.60 ± 0.11
Subject 3	0.89 ± 0.10	2.21 ± 0.15	1.11 ± 0.18	0.60 ± 0.10

5).

The averages over all white matter voxels of D_a, ${\overline{D}}_e$, and f as functions of fractional anisotropy (FA) for all three subjects. D_a and ${\overline{D}}_e$ are fairly insensitive to FA, but f increases monotonically. The bin size is 0.1, and the error bars indicate intra-subject standard deviations. The data points for Subjects 2 and 3 have been displaced slightly in the horizontal direction to improve readability

Figure 6 gives parametric maps of FA, FAA, and FAE for the same subject and slices as in Figures 3 and 4. For FAA and FAE, the WM is again colored to indicate the region of validity for these parameters. The FA map, however, is not colored as this parameter is meaningful throughout the brain. In most WM voxels, the FAA exceeds the FAE, showing that diffusion anisotropy of water inside axons is usually higher than for extra-axonal water. Table 2 lists the WM average values of FA, FAA, and FAE for all three subjects. Combining the data from the three subjects gives FAA = 0.50 ± 0.14 and FAE = 0.23 ± 0.13. The dependencies of FAA and FAE on FA are depicted in Figure 7 showing that both of these compartment specific parameters are monotonically increasing functions of FA.

6).

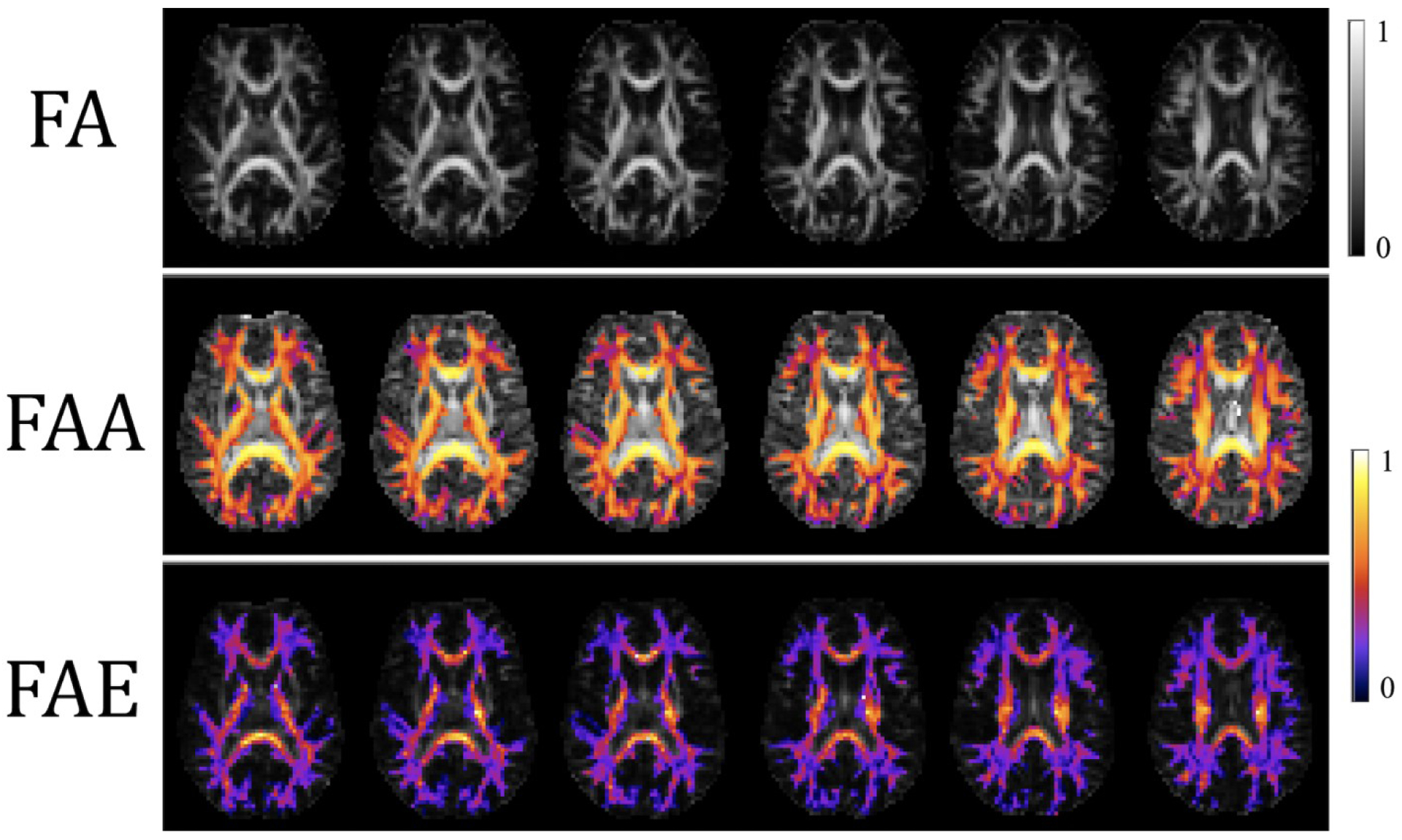
Parametric maps of FA, fractional anisotropy axonal (FAA) and fractional anisotropy extra-axonal (FAE) for the same subject and slices as in Figures 3 and 4. The FA is meaningful in all tissues, but the FAA and FAE estimates are only valid in WM regions (shown in color). The calibration bars are both unitless

TABLE 2.

Average values over all WM voxels of fractional anisotropy (FA), fractional anisotropy axonal (FAA), and fractional anisotropy extra-axonal (FAE) for three healthy, adult subjects. The uncertainties are standard deviations

	FA	FAA	FAE
Subject 1	0.34 ± 0.13	0.49 ± 0.14	0.22 ± 0.13
Subject 2	0.37 ± 0.14	0.51 ± 0.14	0.24 ± 0.13
Subject 3	0.37 ± 0.14	0.51 ± 0.14	0.24 ± 0.12

7).

The average over all white matter voxels of FAA and FAE as functions of FA for all three subjects. Both FAA and FAE increase monotonically with FA. In most cases, FAA > FA > FAE, which suggests that diffusion of water inside axons is more anisotropic than the diffusion of water within the extra-axonal space. The diagonal lines through the origin have a slope of one. The bin size is 0.1, and the error bars indicate intra-subject standard deviations. The data points for Subjects 2 and 3 have been displaced slightly in the horizontal direction to improve readability

Since one of the key assumptions underlying our TDE method is that the diffusion weighting is sufficiently strong to suppress the dMRI signal from extra-axonal water, it is of interest to consider the quantity

$$C=\text{exp}\left(-b_{\parallel }{\lambda }_{e,3}-\Delta R_{2}TE\right)$$ (14)

where λ_e,3 is the smallest eigenvalue for the extra-axonal diffusion tensor and ΔR₂ is the difference between the extra-axonal and intra-axonal transverse relaxation rates. This gives a rough estimate of the relative suppression factor with respect to the intra-axonal dMRI signal, because the direction-averaged intra-axonal signal will generally have a component, corresponding to axons aligned perpendicular to the axial gradients, that is minimally affected by the diffusion weighting. Typical values for the extra-axonal and intra-axonal transverse relaxation times are 60 ms and 80 ms,⁴¹ respectively, which leads to ΔR₂TE = 0.51 for our experiment. From the measured values of λ_e,3, we then find that C ≤ 0.1 in 96.7%, 95.2%, and 96.7% of WM voxels for Subjects 1, 2, and 3. In the small fraction of the WM voxels in which the suppression factor exceeds 0.1, the accuracy of our method may be reduced.

Formulae giving the expected standard deviation and bias due to noise for D_a and f as estimated from Eqs. 4 and 5 are provided in Ref. 17 (equations 15, 16, 18, 19). For our experiment, we have D_a ≈ 2.24 μm²/ms, f ≈ 0.6, b_∥ = 4000 s/mm², b_⊥ = 307 s/mm², SNR (for b0 images) ≈ 113, number of diffusion encoding directions = 64, and number of b0 images = 20. The formulae of Ref. 17 then yield δD_a ≈ 0.04 μm²/ms, ΔD_a ≈ 0.0002 μm²/ms, δf ≈ 0.008, and Δf ≈ 0.0001, where δD_a is the standard deviation for D_a, ΔD_a is the bias for D_a, δf is the standard deviation for f, and Δf is the bias for f. These are likely overestimates as they do not incorporate the beneficial effects of Marchenko-Pastur denoising. Therefore, the impact of signal noise on our results for these two parameters should be minor.

4 |. DISCUSSION

The main purpose of this study is to present an experimental demonstration of a previously proposed method for estimating both the intra-axonal and extra-axonal diffusion tensors in WM. This method requires that dMRI data be obtained with a TDE pulse sequence that has an axially symmetric b-matrix.¹⁷ The TDE sequence was implemented through modification of a standard SDE sequence by adding a pair of radial diffusion-sensitizing gradients that are mutually orthogonal as well as orthogonal to the original SDE gradients, which are then regarded as the axial gradients. The b-value for the axial gradients is assumed to be much larger than for the two sets of radial gradients. A notable feature of the sequence is that one set of radial gradient pulses precedes the axial gradient pulses while the other follows it. With this arrangement, we were able to attain a TE of 122 ms and adequate SNR for obtaining images with 3 mm isotropic voxels.

The method requires the axial b-value, b_∥, to be sufficiently strong to suppress the dMRI signal from the extra-axonal water pool. Specifically, previous studies indicate the condition b_∥ ≥ 4000 s/mm² should be satisfied.^19,24 For this reason, we choose b_∥ = 4000 s/mm² in our experiments as this was considered to be the smallest feasible axial diffusion weighting. The estimated suppression factor of Eq. 14 confirms that this is indeed a sufficiently high axial b-value for more than 95% of WM voxels. It should be emphasized, however, that this criterion for b_∥ has only been established for healthy adults. In the presence of pathology, it may not be adequate, likely leading to overestimates for the axonal water fraction along with biases in other parameters. Acute stroke is one example for which diffusion properties are altered markedly and our method might therefore not apply.

The radial b-value, b_⊥, should be much less than b_∥, but a too small b_⊥ would result in low precision parameter estimates. For a fixed TE, the optimal value for the radial b-value is about b_⊥ ≈ 1.1/D_a.¹⁷ For our measured average of D_a = 2.24 ± 0.18 μm²/ms, this gives b_⊥ = 491 ± 39 s/mm². Experimentally, we found the best precision was obtained for b_⊥ ≈ 300 s/mm² when the minimum possible TE was used (data not shown), which determined our choice for this parameter.

The TDE data must be acquired in a sufficiently large number of diffusion encoding directions to allow for an accurate estimate of the direction-averaged dMRI signal. Here we used 64 diffusion encoding directions, which was motivated by results obtained for the closely related FBI imaging technique.¹⁹ The diffusion encoding direction is defined, for our TDE sequence, as being aligned with the axial gradients. While the radial gradients must be orthogonal to the axial gradients and to each other, their orientations are otherwise not constrained. In particular, the results of our method should not change substantially if the radial gradients were all rotated by an arbitrary angle about the diffusion encoding direction, provided the assumptions upon which our method relies are all justified. This is a consequence of the b-matrix being axially symmetric and is reflected in Eq. 4 by the dependence on the diffusion weighting entering only through b_∥ and b_⊥.

The direction-averaged TDE data (i.e., ${\overline{S}}_2$) are utilized in Eq. 4, along with direction-averaged data acquired with identical imaging parameters other than b_⊥ being set to zero (i.e., ${\overline{S}}_1$), to estimate the intra-axonal diffusivity. An advantage of our method, in contrast to alternative SDE techniques,^{5–7,10,12–14} is the simplicity with which the intra-axonal diffusivity is obtained. In fact, with the TDE approach, D_a is the easiest parameter to determine rather than, as other studies have found, one of the most difficult.^15,16 Once D_a is known, then the axonal water fraction, f, can be readily calculated from Eq. 5, which also requires data for the average b0 signal (i.e., ${\overline{S}}_0$).

To find the intra-axonal diffusion tensor, D_a, we use the fact that a standard FBI analysis of the same multi-direction data obtained using the TDE sequence with b_⊥ = 0 is sufficient to estimate D_a/D_a.¹³ Since D_a is known, the full D_a follows immediately. Finally, provided Eq. 9 holds, the extra-axonal diffusion tensor, D_e, can be calculated from f, D_a, and the total diffusion tensor. The validity of Eq. 9 is quite broad, requiring only that water exchange between the intra-axonal and extra-axonal compartments is negligible and that myelin water can be ignored. Here the total diffusion tensor was obtained by using DKI with low b-value SDE data.

To illustrate this TDE-based approach for determining the intra-axonal and extra-axonal diffusion tensors, we applied it to estimate several compartment-specific parameters for three healthy adult subjects. We found that D_a and ${\overline{D}}_e$ did not vary strongly with diffusion anisotropy, but that f, FAA, and FAE all had substantial regional variations and increased monotonically with FA. These results suggest that axonal fiber bundles are more tightly packed in high FA regions than in low FA regions.

There is a close relationship between the TDE method considered here and one proposed by Dhital and coworkers.²⁶ Both are based on similar physical principles, but with important technical differences. First, the Dhital method uses TDE data with b_⊥ > b_∥ instead of with b_⊥ < b_∥. Also, rather than combining TDE data with SDE data, Dhital and coworkers combine TDE data with DDE data. This may be why their TE (140 ms) and voxel size (4 mm isotropic) were somewhat larger than for our experiment. The analysis procedure for the Dhital method is also more complicated than for ours (which is in part due to the different choices of axial and radial b-values), and it was implemented only in “single bundle” WM voxels (i.e., voxels with a single predominant fiber orientation). Nonetheless, the value for D_a of 2.25 ± 0.03 μm²/ms obtained by Dhital and coworkers is indeed similar to our estimate for the intra-axonal diffusivity. The standard deviation for our value is considerably larger, but this could be a consequence of our result representing all WM voxels rather than just single bundle WM.

Our TDE method also has connections to the fiber ball white matter (FBWM) technique.¹³ In particular, FBWM employs versions of Eqs. 5–10 in a similar manner. However, FBWM uses only SDE data, which means that D_a cannot be found from Eq. 4. Instead, FBWM numerically fits a specific model for water diffusion in WM to SDE data over a range of b-values to determine the axonal water fraction, which together with Eq. 5 implies a value for D_a. In contrast to the TDE approach, which allows for unspecified non-Gaussian water diffusion in the extra-axonal space, FBWM treats extra-axonal diffusion as Gaussian. Thus, an advantage to acquiring TDE data is that the number of modeling assumptions can then be reduced. It would be of interest to directly compare TDE and FBWM predictions for compartment-specific diffusion properties, which could help to assess to the accuracy of FBWM.

One limitation of this study is that we did not include a correction for the different transverse relaxation rates of the intra-axonal and extra-axonal water pools. As a consequence, our estimate for the axonal water fraction has some T2 weighting. The estimates of the compartmental diffusion tensors should, however, be largely unaffected by this. For most WM voxels, the T2 of extra-axonal water is believed to be shorter than for intra-axonal water.^14,41,42 Therefore, we expect our f values to be overestimates. Our average value of f = 0.60 ± 0.11 may be compared to histologic data obtained by Stikov and coworkers,⁴³ who measured the axonal volume fraction (AVF) and the myelin volume fraction (MVF) of the corpus callosum in macaque. Using the relationship

$$f=\frac{AVF}{1-MVF},$$ (15)

where the denominator reflects the fact that the myelin water signal is negligible for our experiment, the data of Stikov and coworkers then yield f = 0.52 ± 0.08, which is indeed somewhat below our TDE estimate. To determine a T2 correction for f, one could acquire additional multi-direction SDE data with a second TE and apply the method of McKinnon and Jensen.⁴¹

Although the assumptions upon which the TDE method are based have good empirical support, it should be emphasized that they are nonetheless approximations and that their accuracy will depend on the choice of imaging parameters. For example, deviations from the predications of the thin, straight axon approximation may be apparent at very high b-values (>7000 s/mm²),⁴⁴ which could reflect axon curvature or finite radius effects. Another open question is whether the intra-axonal water pool, as quantified here, corresponds to water in all axons or just in myelinated axons. It is plausible that the water exchange time for unmyelinated axons is substantially shorter than for myelinated axons to an extent that water within unmyelinated axons is in rapid exchange with extra-axonal water and thus effectively merged with this compartment as far as diffusion properties are concerned. While the observed scaling behavior of the direction-averaged dMRI signal with b-value,^19,24,25 does strongly support our basic picture of it being dominated by contributions from intra-axonal water for the large axial b-value used in our experiments, possible contributions from other WM components, such as glial cells, also cannot be definitively excluded and further investigations exploring the direction-averaged dMRI signal’s specificity to intra-axonal water would be of value. Finally, an important caveat is that prior work supporting the required assumptions for the TDE method has mainly been performed in healthy adult human brain at a field level of 3 T. Their validity for young children, neuropathologies, animal models, fixed tissue, and other field levels is not well known and should be examined in future studies. Of particular interest would be preclinical experiments that both test the b-value scaling behavior of the direction-averaged dMRI signal and directly compare TDE estimates of axonal water fraction to histology.

5 |. CONCLUSIONS

We demonstrated the application of a TDE pulse sequence with an axially symmetric b-matrix to estimate the intra-axonal and extra-axonal diffusion tensors in WM. Data acquired with this sequence allow the intra-axonal diffusivity to be calculated in a simple and direct way. From this parameter and additional data obtained with conventional SDE MRI, the diffusion tensors for the intra-axonal and extra-axonal water pools are then straightforward to determine, along with several compartment-specific diffusion measures. A notable feature of this TDE approach is that detailed assumptions regarding water diffusion in the extra-axonal space are not needed.