A three-dimensional modeling method for quantitative photoacoustic breast imaging with handheld probe

Abstract

By providing complementary functional information, photoacoustic (PA) breast imaging based on the handheld ultrasound (US) probe has demonstrated promising potential for breast cancer diagnosis. However, the quantitative PA imaging primarily relies on the knowledge of the optical fluence distribution in the three-dimensional (3D) heterogeneous breast tissue. Previous studies based on the handheld system generally provided two-dimensional (2D) B-scan results, which contains limited anatomical information of the tissue and the lesion. This study proposed a method to perform 3D modeling of the photon transportation for dual-modality PA/US system based on the local 3D breast anatomical information by scanning US probe. Then the calculated optical fluence distribution can be used for PA imaging. Our phantom and clinical pilot study results demonstrated that this method has potential to improve the accuracy of the quantitative PA breast imaging, and it can also be used in other clinical implementations.

1. Introduction

Photoacoustic imaging (PAI) is an emerging technique that constructs images of biological tissues based on the contrast which is determined by the characteristics of their optical absorptions [1]. Since the hemoglobin in blood has strong and unique optical absorption in comparison to other tissues, blood vessels are considered as superior endogenous targets for imaging. Therefore, PAI has been utilized in clinical implementations to assist with diseases diagnosis when abnormal vasculature behavior is observed, especially in cancer diagnosis [2,3]. Breast cancer is a world-wide threat that takes up 30 % of all new cancer diagnosis among women [4], hence much attentions are attracted to the PA breast imaging [5]. Among many developed PA breast imaging systems, the handheld PA/US dual-modality system based on the clinical US system is preferred by physicians due to its familiarity [6]. Besides, the traditional B-scan ultrasound (US) imaging can also provide important complementary anatomical information [7]. Up to now, several PA/US handheld systems have been developed for clinical study and the results showed great potential in breast cancer diagnoses [[8], [9], [10], [11], [12]].

One of the important physiological parameters for breast cancer is the oxygen saturation (SO₂), which can be derived from quantitative PA imaging based on the spectral differences in optical absorption between the oxygenated and the de-oxygenated hemoglobin [13]. Since the PA signal is proportional to the multiplication of the tissue optical absorption coefficient with the local optical fluence and the Grüneisen parameter, the quantitative PA breast imaging requires compensation for the fluence difference at different light wavelengths. However, it becomes a very challenging job because of the high heterogeneity in living tissue that heavily increases the complexity in fluence distribution. Several approaches are being explored, including the direct calculation of the fluence based on numerically solving the radiative transfer equation [[14], [15], [16]], spectral unmixing methods [17,18], and most recently machine learning algorithms [[19], [20], [21]]. In this work, we employed the first approach.

The optical fluence could be calculated once the anatomical structure in human breast with corresponding optical properties were known. For instance, the finite element forward model is used for the optical fluence compensation [22], and several researches employed this way for the handheld PA/US 2D imaging [23,24]. However, the breast tissue, especially when there is a lesion, has an optically heterogeneous 3D structure, leading to non-negligible variation of optical properties for different types of normal tissues and lesions. Therefore, the lack of important 3D morphology of the tissue in 2D imaging, the accuracy of the optical fluence compensation would be affected.

In this study, based on a dual-modality PA/US system that used a linear probe, we proposed a 3D modeling method to calculate the optical fluence distribution, and then used this information to compensate the PA imaging results. In this method, we scanned a US probe over the entire suspicious breast lesion, from where different types of tissues (such as skin, adipose tissue, and fibroglandular tissue), as well as the tumor, were identified based on US B-scan serial images. Their optical properties were assigned accordingly, which enabled personalized 3D modeling of human breasts. We quantitatively studied fluence compensation model on heterogeneous phantom and breast tumor patients, and calculated SO₂ with and without fluence compensation. Our results demonstrated 3D modeling could improve the accuracy of quantitative PA breast mapping.

2. Methods and material

2.1. PA/US dual-modality imaging system

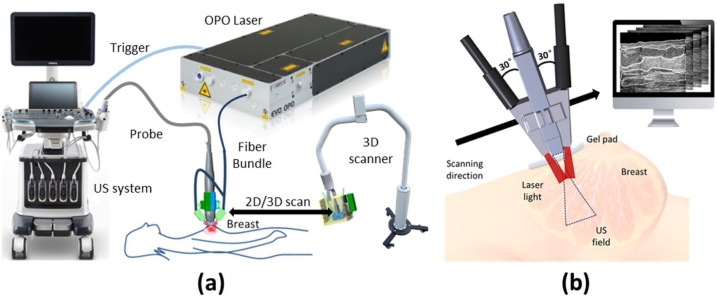
A clinical US system (Resona7, Mindray Bio-Medical Electronics, Shenzhen, China), which is connected with a 192 elements linear probe (L9-3U, Mindray Bio-Medical Electronics, Shenzhen, China) of 5.8 MHz-central-frequency was modified to perform US/PA dual-modality imaging which provides FOV of $4.4\text{c}\text{m}\times 5\text{c}\text{m}$. The laser source is an optical parameter oscillation (OPO) laser (SpitLight EVO 200, InnoLas Laser GmbH, Krailling, Germany) with a repetition rate of 10 Hz. The laser was delivered via a one-two fiber bundle (made by CeramOptec GmbH, Bonn, Germany), and the two bundle terminals were mounted on both sides of the US handheld probe to illuminate the tissue at an incident angle of 30° for less direct illumination under the probe. This incident angle is refracted to 21° after the light entering a transparent custom-made ultrasound gel pad of 1.0 cm thickness from the air. The refractive-index-matched boundary condition was employed between gel pad and tissue. To measure the SO₂, we used two wavelengths, 750 nm and 830 nm, for the PA phantom and human breast imaging. The measured fluence onto the skin surface from each laser beam is 10 mJ/cm², which is within the safety limit according to the ANSI standard. The output energy of each laser pulse is constantly monitored and was used to compensate the PA results via normalization. Fig. 1(a) shows the setup of the US/PA dual-modality system. A zoomed-in diagram illustrates the dual-modality hand-held probe and the scanning process, as shown in Fig. 1(b).

Fig. 1.

(a) A diagram of the US/PA dual-modality system; (b) An illustration of US/PA dual-modality probe setup, the scanning process will produce a series of B-scan images along the scanning direction.

During the clinical pilot study, the physician first held the handheld probe to locate the tumor by US, then the probe was mounted onto a scanner which automatically conveyed the probe at a speed of 0.1 cm/s for a total 4.0 cm range, covering the entire suspicious lesion region found by US. The gel pad was put between the scanner and patient to reduce the unwanted PA signal at the probe surface. Physician applied force on the gel pad to flatten the human breast surface to avoid surface tissue deformation when scanning the probe. Since we only applied slight force, it won’t cause obvious tissue deformation.

Our study protocol was approved by the institutional ethics committee of Peking Union Medical College Hospital. All research was performed in accordance with relevant regulations. Written informed consent was obtained from all participants. Biopsy and surgical resection were performed on all the enrolled patients with pathological diagnoses. Frozen section and paraffin section results confirmed that the first patient had breast fibroadenoma while the second patient had breast papilloma.

2.2. Theory of blood oxygen saturation correction by optical fluence compensation

The initial pressure ${\mathit{p}}_0$ generated by PA effect is proportional to the local absorbed photon energy density ${\mathit{A}}_e$ (J/m³), which is described by [Eq. (1)]:

$${\mathit{p}}_0=\Gamma {\eta }_{th}{\mathit{A}}_e,$$ (1)

where $\text{Γ}$ is the Grüneisen parameter which is a temperature sensitive dimensionless parameter, ${\eta }_{th}$ is the percentage of the absorbed photon energy that is converted into heat. The absorption coefficient ${\mu }_a$ (cm⁻¹) has the relationship to the ${\mathit{A}}_e$, as follows,

$${\mu }_a\left(\mathit{\lambda },\mathit{r}\right)=\frac{{\mathit{A}}_e\left(\mathit{\lambda },\mathit{r}\right)}{\mathit{F}\left(\mathit{\lambda },\mathit{r}\right)}\propto \frac{{\mathit{p}}_0\left(\mathit{\lambda },\mathit{r}\right)}{\mathit{F}\left(\mathit{\lambda },\mathit{r}\right)},$$ (2)

where F(λ,r) (J/m²) is the optical fluence that is used to describe the local density of the laser photons. Since the blood vessel absorption coefficient depends on the concentrations of both oxygenated hemoglobin and deoxygenated hemoglobin, the SO₂ can be calculated by measuring PA signals from at least two wavelengths [25].

Because the optical parameters in different tissue types are also wavelength dependent, local optical fluence compensation need to be calculated at corresponding wavelengths. To assess the effectiveness of fluence compensation later, we defined the ΔSO₂ representing the SO₂ difference between compensated (cSO₂) value based on our 3D modeling and the un-compensated (uSO₂) value which is derived directly from the 2D PA/US imaging results:

$$\Delta {SO}_2={u{SO}_2-cSO}_2$$ (3)

As a simpler approximate compensation approach, the bulk tissue is also sometime assumed to be an optically homogenous with uniform background absorption and scattering properties (with spectral difference). For comparison with our method, we also define the hSO₂ as compensated SO₂ value when breast tissue or phantom is considered as 3D homogeneous material. The difference between hSO₂ and cSO₂ is therefore depending on whether tissue or phantom is compensated based on homogeneous model (hSO₂) or heterogeneous model (cSO₂).

2.3. 3D modelling of photon transportation in breast tissue

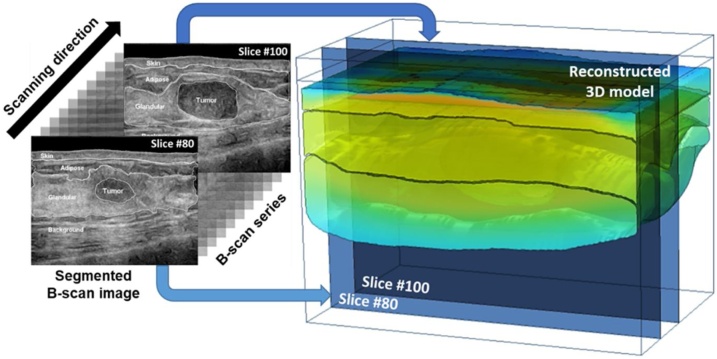
According to the real conditions, the illumination pattern is modelled as two identical rectangles by the size of $4.7\text{c}\text{m}\times 0.8\text{c}\text{m}$ located at 0.93 mm below skin surface where photons have passed one transport mean free path. For 3D study in which the probe scans, the lateral position of the light source will move together with the probe. The fluence calculation is based on the light diffusion model which demands 3D breast structure. In this study, we reconstructed the 3D breast model through a series of 2D US B-scan slices. Then, we can identify different types of tissues (i.e. skin, adipose tissue, and fibroglandular tissue) and tumor according to their US characteristics and anatomical features to do image segmentation. The identified tumor and tissues were segmented separately and fused into a complete 3D breast model. In this pilot study, we only chose patient whose tumor has a distinguished boundary in US imaging to avoid ambiguity and the segmentation is done manually under the guidance from experienced physicians. A diagram of this process is shown in Fig. 2, where two B-scan slices are selected to illustrate the 3D reconstruction mechanism.

Fig. 2.

The 3D breast model is reconstructed from a series of US B-scan images in which two slices are selected to further explain the reconstruction mechanism.

After segmentation, the 3D model is constructed by integrating slices with tumor and normal tissues individually using the function ‘loft’ in the COMSOL Multiphysics (COMSOL Inc., Stockholm, Sweden), and then optical parameters of each segmented region are imported to the corresponding domain, where we can set optical diffusion equations and boundary conditions to calculate the optical fluence. The COMSOL solves the diffusion equation in the breast tissue regime and the source is quantified using current density S at the illumination site [26]:

$$\left\{\begin{array}{c}-\frac{1}{{\mu }_{eff}^2}{\nabla }^2\mathbf{\Phi }(\mathit{\lambda },\mathit{r})+\mathbf{\Phi }(\mathit{\lambda },\mathit{r})=0\\ \frac{1}{{\mu }_{eff}^2}\nabla \mathbf{\Phi }(\mathit{\lambda },\mathit{r})\bullet \mathbf{n}=S(r)\end{array}\right)$$ (4)

where Φ is the optical fluence, n is a unit vector normal to the illumination spot and the effective attenuation coefficient ${\mu }_{\text{e}\text{f}\text{f}}$ is defined as:

$${\mu }_{eff}=\sqrt{3{\mu }_a\left({\mu }_a+{\mu }_s^{\text{'}}\right)}$$ (5)

where ${\mu }_a$ and ${\mu }_s^{\text{'}}$ are the absorption coefficient and the reduced scattering coefficient, respectively. To build a breast model that based on the anatomical structure, we allocate specific ${\mu }_{\text{e}\text{f}\text{f}}$ to each segmented tissue for the simulation of photon distribution.

In this study, we used two wavelengths (750 nm and 830 nm) for the quantitative PA imaging. The optical properties of skin, adipose tissue, fibroglandular tissue, tumor, and background tissues at these two wavelengths was used according to previous reported literature studies [[27], [28], [29], [30], [31]], as listed in Table 1. The background tissues cover the regions outside the segmented tissues (see Fig. 2). The optical parameters that describe the background tissue comes from literature when the optical properties of human breast are measured in vivo and the entire human breast is considered as homogeneous material.

Table 1.

Optical parameters of different tissue layers [[27], [28], [29], [30], [31]].

Tissue type	Wavelength(nm)	${\mathit{\mu }}_{\mathit{a}}$ (cm−1)	${\mathit{\mu }}_{\mathit{s}}^{\text{'}}$ (cm−1)	${\mathit{\mu }}_{\mathit{e}\mathit{f}\mathit{f}}$(cm−1)
Skin	750	0.63	20.8	6.36
	830	0.59	18.4	5.8
Adipose tissue	750	0.036	11	1.09
	830	0.034	10.2	1.02
Fibroglandular tissue	750	0.084	12.8	1.8
	830	0.096	11.2	1.81
Background	750	0.03	11	1.01
	830	0.038	10.4	1.09
Tumor	750	0.12	8.3	1.74
	830	0.13	7.2	1.69

2.4. Tissue mimicking phantom

Since it is still challenging to know the actual SO₂ values in human breast vessels via non-invasive method, so we designed a phantom study to evaluate the performance of our method. The breast tumor mimicking phantom is in ellipsoidal ($2\text{c}\text{m}\times 1.4\text{c}\text{m}\times 1.4\text{c}\text{m}$) shape, which consists of 2 % agar (Sigma-Aldrich, Missouri, United States), 1 % intralipid (KeLun Industry Group, Szechuan, China) and 0.005 % indocyanine green (Fisher Scientific, Pittsburgh, United States). The agar to make the tumor phantom was first heated to 100 $℃$ which is above its melting point, then intralipid and indocyanine green were added to the solution when the temperature was dropping to 50 $℃$. The mixed solution was poured into an ellipsoidal mold for solidification. To mimic the blood vessel, we used a silicon tube (outer diameter $1\text{m}\text{m},\text{i}\text{n}\text{n}\text{e}\text{r}\text{d}\text{i}\text{a}\text{m}\text{e}\text{t}\text{e}\text{r}0.5\text{m}\text{m}$) which pierced through the ellipsoid along its long axis and hung horizontally at 1.6 cm depth. Following the reported procedure of ref [32], the bulk breast tissue phantom is consisted of 0.1 % TiO₂ (Sigma-Aldrich, Missouri, United States) and gel wax (Yaley Enterprises, California, United States). The gel wax was heated to a liquid state at 170 $℃$ and put into a sonicator (KQ3200ES, KunShan Ultrasonic Instruments, JiangSu, China) which sustained a water bath at 100 $℃$. TiO₂ was then added into the gel wax solution during sonication for mixing and degassing. When there were no TiO₂ particles or bubbles visualized, the mixed solution was slowly poured into the acrylic container at 70 $℃$.

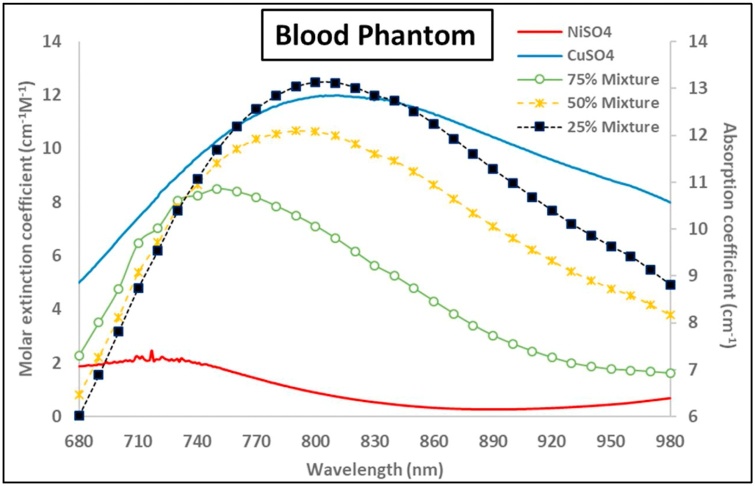
Because we were not accessible to instruments to measure SO₂ of real blood sample, so we used pseudo-blood material instead according to ref [33]. The pseudo blood is a mixture of NiSO₄ (pseudo-oxygenated hemoglobin) and CuSO₄ (pseudo-deoxygenated hemoglobin) solution. Therefore, the value of pseudo-SO₂ is calculated using the molar concentration of NiSO₄ divided by the summation of the molar concentrations of both NiSO₄ and CuSO₄. Three distinct pseudo-SO₂ values of blood mimicking phantoms were selected for the experiment, which are 75 %. 50 % and 25 % respectively. The absorption spectrum of those two chemicals were measured using a spectrophotometer (UV-3600 Plus, SHIMADZU, Kyoto, Japan), as shown in Fig. 3 in red and blue lines, and the absorption coefficient of the mixture 75 %, 50 % and 25 % are represented by green line with hollow dots, yellow dashed line with crosses and black dotted line with boxes, respectively.

Fig. 3.

Optical parameters of the pseudo-blood phantom: red line and blue line are the molar extinction coefficients of NiSO₄ and CuSO₄; green line with hollow dots, yellow dashed line with crosses and black dotted line with boxes are the absorption coefficient of 75 %, 50 % and 25 % pseudo-SO₂ blood phantom, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).

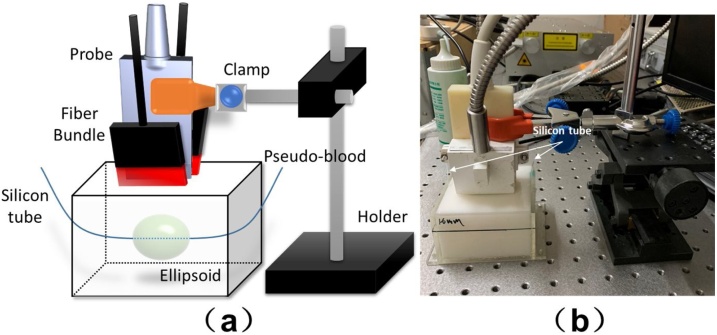
The experiment setup is shown in Fig. 4(a) and (b). The US probe was first held vertically to locate the ellipsoid and the maximum longitudinal section of the silicon tube via US imaging, and then kept the probe steady during the experiment. Lasers with 750 nm and 830 nm wavelengths were employed for PA imaging. After the PA/US dual imaging, the phantom was dissected to measure the actual size and position of the ellipsoid, which is used for 3D reconstruction of the anatomical structure. The optical parameters that involved in the phantom model are shown in Table 2.

Fig. 4.

(a) A schematic diagram of the phantom experiment setup; (b) A photograph of actual setup during phantom experiment.

Table 2.

Optical parameters of phantom [32,[34], [35], [36]].

Phantom	Wavelength(nm)	${\mathit{\mu }}_{\mathit{a}}$ (cm−1)	${\mathit{\mu }}_{\mathit{s}}^{\text{'}}$ (cm−1)	${\mathit{\mu }}_{\mathit{e}\mathit{f}\mathit{f}}$(cm−1)
Substrate	750	0.02	5.5	0.57
	830	0.02	5	0.55
Ellipsoid	750	0.09	11	1.73
	830	0.07	10	1.52

3. Results

3.1. Phantom study

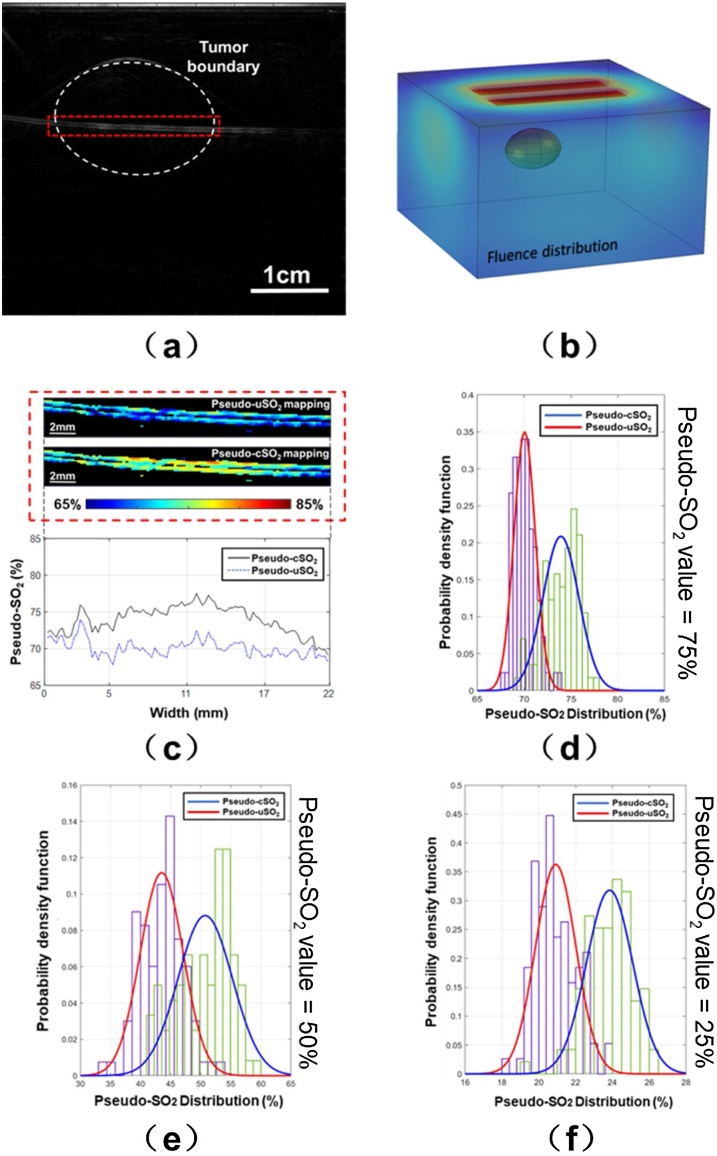
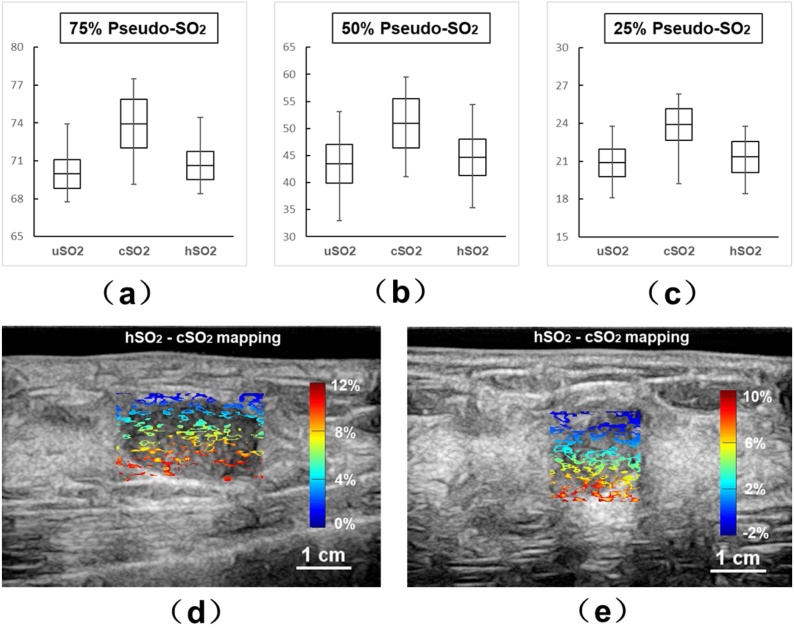
Fig. 5(a) shows the results of the PAI imaging of the phantom with 75 % pseudo-SO₂ level at 750 nm wavelength. The white dashed contour line represents the boundary of the tumor. The corresponding fluence distribution of the phantom is modelled and presented in Fig. 5(b) at 750 nm wavelength. When 75 % pseudo-SO₂ solution was in the tube, the measured pseudo-uSO₂ (without fluence compensation) and the pseudo-cSO₂ (with fluence compensation) mapping are shown in the upper section of Fig. 5(c). The exhibited region enclosed in the red dashed box in Fig. 5(c) is corresponding to the same region in the red dashed box in Fig. 5(a). The averaged pseudo-uSO₂ and pseudo-cSO₂ values along the vessel are presented in dashed blue line and solid black line in the lower section of Fig. 5(c). According to the SO₂ mapping, the pseudo-cSO₂ is overall larger than the uncompensated counterpart. We also calculated the probability density function of pseudo-uSO₂ (purple bars) and pseudo-cSO₂ (green bars) for 75 %, 50 % and 25 % pseudo-SO₂ level of the area inside the red dashed box. The distributions of their probability density functions are introduced by histogram shown in Fig. 5(d–f). The red and blue lines in Fig. 5(d–f) are the normal fitting curve to the probability density function of pseudo-uSO₂ and pseudo-cSO₂, respectively. In Fig. 5(d), The red fitting curve is centered at 70.0 % and the blue fitting curve is centered at 74.0 % when the actual pseudo-SO₂ value is 75 %. In Fig. 5(e), the pseudo-uSO₂ is centered at 43 % while the pseudo-cSO₂ is centered at 51 % for 50 % pseudo-SO₂ value. Finally, for the 25 % pseudo-SO₂ value, the mean pseudo-uSO₂ is 21 % and the mean pseudo-cSO₂ is 24 %. Two more results with different pseudo-SO₂ values (0% and 100 %) are provided in the supplementary note 1 (Fig. S.1), and they both show the increase in accuracy. Therefore, the phantom study results indicate that the fluence compensation based on 3D modeling would increase the measurement accuracy.

Fig. 5.

(a) Normalized PA signal of the phantom at 750 nm wavelength (75 % actual pseudo-SO₂ value); (b) Fluence distribution of 3D model at 750 nm wavelength; (c) upper: Pseudo-uSO₂ and pseudo-cSO₂ mapping inside the same red dashed box in (a); lower: the averaged pseudo-uSO₂ and pseudo-cSO₂ values distribution along the horizontal vessel (75 % actual pseudo-SO₂ value); (d-f) The purple and green bars are the probability density function of pseudo-uSO₂ and pseudo-cSO₂ distribution of 75 %, 50 % and 25 % actual pseudo-SO₂ values. The red and blue lines are normal fitting curve to pseudo-uSO₂ and pseudo-cSO₂ distribution, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).

3.2. Pilot clinical study

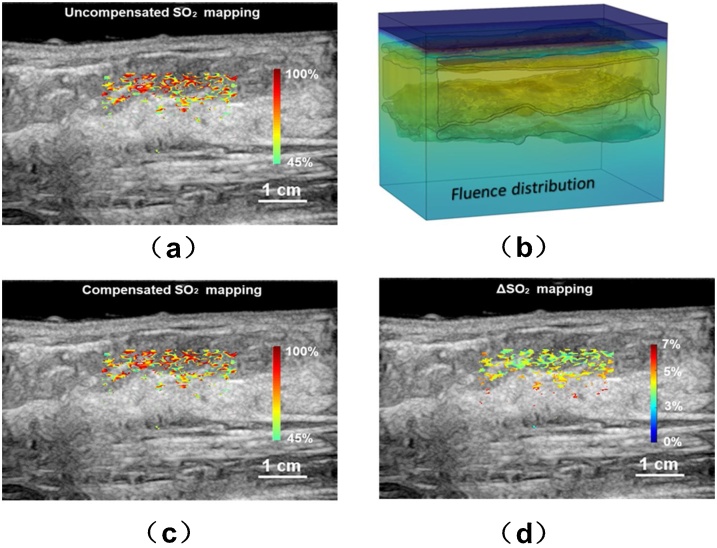
We also investigated the effect of fluence compensation on SO₂ measurement on one healthy volunteer and two patients with benign tumors. As aforementioned, for the patient study, the physician first located the suspicious lesion via routine US examination, then the probe was mounted on a scanner to scan over the lesion. We first constructed the 3D breast modeling based on US B-scan results. Then the optical fluence can be calculated. For the healthy volunteer, Fig. 6(b) represented the imaging result at 785 nm wavelength when the probe was at the center position during scanning. We chose a $2.5\text{c}\text{m}\times 2.0\text{c}\text{m}$ ROI that centered at 1.6 cm depth to show the mapping of uSO₂ (Fig. 6a), cSO₂ (Fig. 6c) and ΔSO₂ (Fig. 6d), respectively. The ΔSO₂ value is primarily around 3% in superficial region and over 5% in deeper area.

Fig. 6.

Study results for the healthy volunteer. (a) The uncompensated SO2 distribution; (b) the 3D modeling of the fluence distribution; (c) the compensated SO2 distribution based on the 3D modeling; (d) the $\Delta {SO}_2$ mapping.

For the breast tumor cases, the tumors in this study have fairly regular shapes with their center positions situated in the fibroglandular layer at about 1.6 cm below skin surface. The majority of breast tumors are located in this layer where blood vessels are relatively abundant. The first patient (right breast) has a tumor size $2.0\text{c}\text{m}\times 1.4\text{c}\text{m}\times 1.1\text{c}\text{m}$ centered at 1.58 cm in depth while the second patient (left breast) has a smaller one with a size of $1.1\text{c}\text{m}\times 0.9\text{c}\text{m}\times 0.9\text{c}\text{m}$ centered at 1.59 cm in depth. For both patients, we chose the ROI of ΔSO₂ distribution in a rectangular box that concentric with the tumor while each side of the box is 1.0 mm broader than the tumor. The tumor and its surrounding area we presented are the most interested region by physicians.

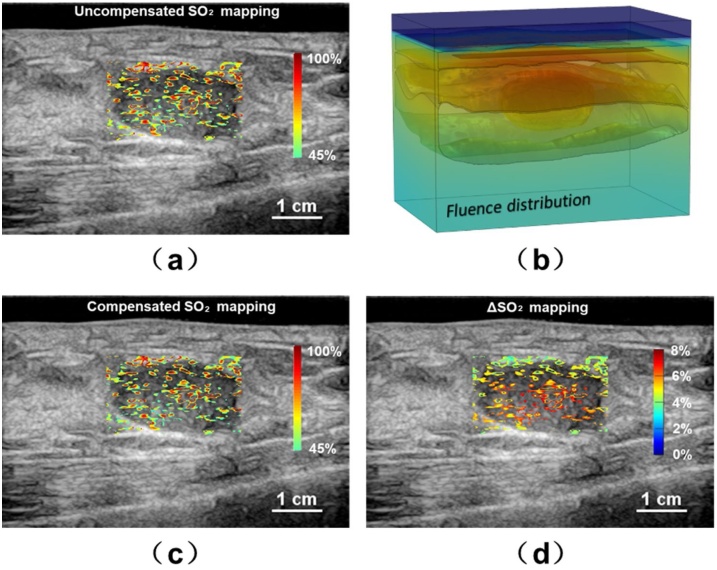
The uSO₂ map of the first patient is shown in Fig. 7(a) without the optical fluence compensation. As aforementioned, a 3D local breast model with the tumor can be constructed based on US B-scan results, and the corresponding fluence distribution map exhibited under 785 nm laser illumination is shown in Fig. 7(b). Fig. 7(c) and (d) showed the cSO₂ map and the ΔSO₂ mapping, respectively. It can be seen that the compensation based on 3D model can rectify the absolute SO₂ value up to 7.8 % (58.24 % in cSO₂ and 65.32 % in uSO₂) at the central areas of the tumor and 4% in the surrounding areas. This correction would be important for physicians to assess the blood SO₂ level inside/around the tumor.

Fig. 7.

Study results for the first patient. (a) The uncompensated SO2 distribution; (b) the 3D modeling of the fluence distribution; (c) the compensated SO2 distribution based on the 3D modeling; (d) the $\Delta {SO}_2$ mapping.

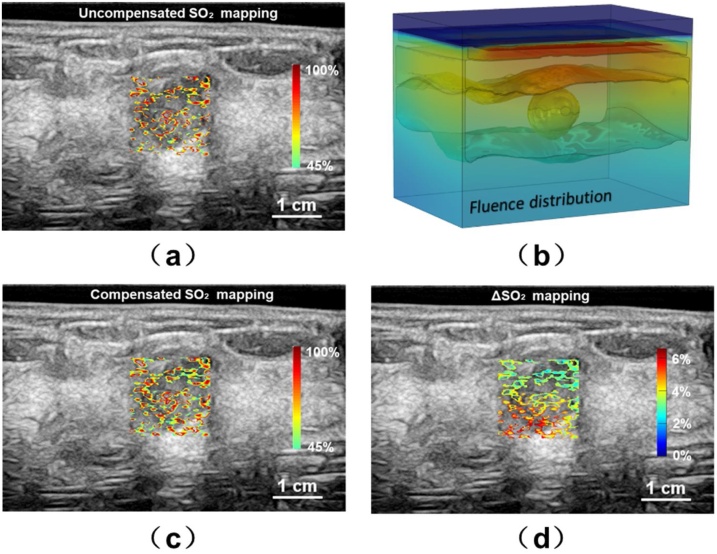
Fig. 8(a–d) shows the results for the second patient whose tumor size is smaller. The ΔSO₂ mapping indicates the most difference is no longer located at the central area of tumor but rather distributed along the top and bottom surface. The cSO₂ around bottom left corner is 6% lower than the uSO₂ value while 3% lower than the uSO₂ value near the top surface.

Fig. 8.

Study results for the second patient. (a) The uncompensated SO2 distribution; (b) the 3D modeling of the fluence distribution; (c) the compensated SO2 distribution based on the 3D modeling; (d) the $\Delta {SO}_2$ mapping.

3.3. Comparison with homogeneous model

To further validate the effectiveness of our method, we compared our method to a 3D compensation method in which the breast tissue or phantom are considered as a homogeneous scattering material. As defined earlier, we use hSO₂ minus cSO₂ values to show the differences between those two methods. Fig. 9(a–c) shows the comparison of pseudo-uSO₂, pseudo-cSO₂ and pseudo-hSO₂ values in the phantom study at 75 %, 50 % and 25 % pseudo-SO₂ level, respectively. The horizontal line in the middle of the black boxes in Fig. 9(a–c) represents the mean value of the pseudo-SO₂ in the silicon tube. The top and bottom edge of the black box represents the standard deviation (S.D.) of the pseudo-SO₂ values. Upper and lower error bars represent maximum and minimum pseudo-SO₂ values. From the results, although the pseudo-hSO₂ values can be slightly more accurate by 1–2 % than the uncompensated results, our method significantly increased the accuracy. Fig. 9(d–e) shows the mappings of SO₂ differences between hSO₂ and cSO₂ values of the first and the second patient. The SO₂ differences between these two methods are more significant at deeper tumor region in the human breast.

Fig. 9.

(a-c) pseudo-uSO₂, pseudo-cSO₂ and pseudo-hSO₂ values in the phantom study at 75 %, 50 % and 25 % actual pseudo-SO₂ levels. Mean value is represented by horizontal line in the black box; S.D. values are represented by the top and bottom edges of the black box; error bars indicate maximum and minimum values of the pseudo-SO₂ values; (d-e) Difference mapping between pseudo-hSO₂ and pseudo-cSO₂ values for the first and second patients.

4. Discussions and conclusion

In this work, we developed a method to locally compensate the spectral fluence difference for quantitative PA breast imaging. Based on a serial of US B-scan results, the reconstructed 3D anatomical structure, together with corresponding spectral-dependent optical parameters, can be used to calculate the optical fluence, which is essential for the quantitative PA imaging, such as the SO₂ mapping. The phantom study indicated that our method could increase the accuracy of the SO₂ mapping. For pilot clinical study, we imaged two tumors with different size. According to the ΔSO₂ mapping from Fig. 6, Fig. 7, Fig. 8, the magnitude of the compensation indicates non-negligible influence of optical fluence compensation by 3D modeling on quantitative PA breast imaging. Meanwhile, to effectively increase the SO2 accuracy with our method, it is desired to have accurate optical parameters of different tissue types for each patient.

We also compared the results of our 3D structure-based compensation with 3D model where only a homogenous tissue is considered for both human and phantom cases. In Fig. 9(a–b), up to 10 % SO₂ differences between two methods can be observed in human cases especially in deeper regions. For the phantom study results shown in Fig. 9(c–e), although the difference between two methods is less significant than human cases, the compensation using our method is still more effective than homogeneous 3D compensation. The pseudo-cSO₂ values are not only closer to the actual pseudo-SO₂ values, but also showing more potentials of improvement than pseudo-hSO₂ compare to pseudo-uSO₂ values.

However, the accuracy of the calculated SO₂ highly depends on the imported optical parameters of different tissue types in the 3D modeling. In practice, these parameter values vary from person to person. Therefore, finding a robust method to accurately measure these personalized optical parameters is crucial for the implementation of our method (supplementary note.2). In addition, the diffusion approximation used in our model requires the condition that there is no bulky strong optical absorption regions. In our clinical studies, the subjects are either healthy or earlier stage benign tumor, which satisfied this condition. However, for breast cancers of later stage, prominent angiogenesis or necrosis tissue inside lesion may contain strong optical absorbers, which will potentially impair the effectiveness of diffusion approximation. Besides, tissue segmentation is also a crucial factor which needs to be assured by experienced physicians.

We also evaluated the effect of breathing motion which is shown in the supplementary video. According to the clinical imaging results shown in Fig. 7, the thickness of the imaged human breast is over 4 cm from the skin surface to the chest wall. Based on the mechanical properties of the soft tissue, which is not a rigid matter, the breathing motion will cause more serious tissue deformation in the deeper region close to the chest wall. While, both tumors in this study are located primarily within 2 cm below the skin surface. We didn’t notice prominent tissue deformation around the tumor. Therefore, the breathing motion can be neglected in our reported cases.

Besides, several future works should be carried out. First, more clinical study cases are needed, including more types, size, and locations of breast tumor/cancer to provide a comprehensive statistical analysis for clinical use. In our previous work, the un-compensated results have already showed prominent differences in statistical SO₂ for benign and malignant breast tumors [37]. Second, the whole modelling process is still time-consuming by manually segmentation of tumor boundaries from US results. We expect to have more clinical cases, then we can use machine learning to speed up the segmentation. Third, we will quantitatively evaluate the effectiveness of our method on new locations where a large artery can be identified in the ROI, so we can use the SO₂ value as reference. Finally, we will improve the sensitivity of our imaging system. At this moment, there are still SO₂ variations that can be observed in the red dashed box in Fig. 5(c). Although there are several reasons contributing to this phenomenon, including the non-uniform phantom manufacturing, low SNR, and strong optical absorption inside the “phantom blood”, we believe the relatively low SNR (or contrast to noise ratio (CNR) $\approx 9.1$ in the reconstructed images) is the primary cause.

Finally, by developing this diffusion model, we are aiming to provide a promising tool for clinical use. We expect our method could increase the accuracy of local SO₂ value which can help physicians to diagnosis of breast tumors. Moreover, this method can be straightforwardly implemented to other clinical PA imaging studies, such as the thyroid imaging.

Declaration of Competing Interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work. there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled “A three-dimensional modeling method for quantitative photoacoustic breast imaging with handheld probe”.

Biographies

Tao Han received his Ph.D. degree in the Chemical Engineering Department from Loughborough University in 2016. He is currently a postdoctoral research fellow at Department of Biomedical Engineering in Peking University. His research interest includes photoacoustic imaging, multi-modality imaging, and currently focuses on quantitative photoacoustic breast imaging.

Meng Yang is senior physician and associate professor in Ultrasonography Department, Peking Union Medical College Hospital. She received her M.D. degree in Medical Imaging and Nuclear Medicine from Peking Union Medical College Hospital in 2013. She is an expert in superficial, musculoskeletal, Obstetric and Gynecologic ultrasonography. Her research interest focuses on the clinical translation of photoacoustic functional imaging, molecular imaging and multi-modality imaging for clinical diagonsis.

Fang Yang received her Ph.D. degree in the Biomedical Engineering Department, Tianjin University, 2006. She is currently a senior engineer in Mindray Bio-Medical Electronics Co.,Ltd., Shenzhen. She is focusing on the development of ultrasound/photoacoustics dual modality imaging system for clinical use.

Lingyi Zhao is a PhD candidate in the Peking University/Georgia Tech/Emory BME joint PhD program. She focuses on developing medical imaging device and processing imaging data from clinical studies, particularly in photoacoustic imaging and shear wave imaging.

Yuxin Jiang is chief physician and professor in Ultrasonography Department, Peking Union Medical College Hospital. He is the vice president of Chinese Medical Doctor Association, chairman of the Chinese Medical Association (Ultrasonography branch) and committee member of International Society of Ultrasound in Obstetrics and Gynecology (ISUOG). Professor Yuxin Jiang is also the vice president of Asian Federation of Societies for Ultrasound in Medicine and Biology (AFSUMB). He has authored over 100 peer-review journal articles and served as the chief editor of Chinese Journal of Ultrasonography and Chinese Journal of Medical Imaging Technology. His research is focused on ultrasonic contrast, intravenous ultrasound, early stage diagnosis of breast cancer, ultrasound in obstetrics and gynecology.

Changhui Li is an associate professor in the department of Biomedical Engineering of Peking University. He received his B.Sc. degree in 1997 from Peking University and Ph.D. degree in 2006 from Texas A&M University. Prior to joining Peking University, he worked at Washington University, St. Louis as a post doctor from 2006 to 2010. His research focuses on developing novel biomedical imaging methods, including photoacoustic imaging and fluorescence imaging.

Appendix A. Supplementary data

The following are Supplementary data to this article: