Abstract
Purpose
Variation in retinal thickness with eye size complicates efforts to estimate retinal ganglion cell number from optical coherence tomography (OCT) measures. We examined the relationship among axial length, the thickness and volume of the ganglion cell layer (GCL), and the size of the optic chiasm.
Methods
We used OCT to measure GCL thickness over 50 degrees of the horizontal meridian in 50 healthy participants with a wide range of axial lengths. Using a model eye informed by individual biometry, we converted GCL thickness to tissue volume per square degree. We also measured the volume of the optic chiasm for 40 participants using magnetic resonance imaging (MRI).
Results
There is a positive relationship between GCL tissue volume and axial length. Given prior psychophysical results, we conclude that increased axial length is associated with increased retinal ganglion cell size, decreased cell packing, or both. We characterize how retinal ganglion cell tissue varies systematically in volume and spatial distribution as a function of axial length. This model allows us to remove the effect of axial length from individual difference measures of GCL volume. We find that variation in this adjusted GCL volume correlates well with the size of the optic chiasm.
Conclusions
Our results provide the volume of ganglion cell tissue in the retina, adjusted for the presumed effects of axial length upon ganglion cell size and/or packing. The resulting volume measure accounts for individual differences in the size of the optic chiasm, supporting its use to characterize the post-retinal visual pathway.
Translational Relevance
Variations in ametropia can confound clinical measures of retinal features. We present a framework within which the thickness and volume of retinal structures can be measured and corrected for the effects of axial length.
Keywords: retinal ganglion cells, optical coherence tomography, spatial acuity, model eye
Introduction
The retinal ganglion cells receive signals that originate in the photoreceptors and transmit information to the central nervous system. These cells are located within the retinal ganglion cell layer (GCL) of the eye, along with displaced amacrine cells and supportive tissue. The technique of optical coherence tomography (OCT) has been regularly used to measure the thickness (in mm) of the GCL and other retinal layers. There is some interest in characterizing the GCL in healthy eyes, both to understand the contribution of these cells to normal vision and as a point of reference for measurements in ophthalmologic diseases that damage the retinal ganglion cells. A confounding property of OCT measurements in healthy control participants, however, is that the thickness of retinal tissue systematically varies with the size of the eye under study: the larger and more myopic the eye,1 the thinner the retina tends to be.2,3
It may seem at first that this systematic variation of GCL thickness in eyes of different sizes should have an impact upon visual perceptual ability. The GCL is a relative bottleneck in the visual pathway, as the retinal ganglion cells are outnumbered over 100-to-1 by both the photoreceptors and by the neurons of the primary visual cortex. Retinal ganglion cell density has been linked to the limit of grating acuity in the periphery of the visual field.4–8 Specifically, the systematic decline in spatial acuity from parafoveal vision to the periphery follows very closely the corresponding decline in midget retinal ganglion cell receptive field density.6
Given that the retina is thinner in larger eyes, we might therefore expect people with myopia, even with refractive correction, to have worse peripheral spatial acuity than emmetropes. This, however, is not the case. Measured with laser interference fringes, angular spatial acuity does not vary significantly as a function of individual differences in spherical refractive error.9,10 Because the limit of peripheral spatial acuity is plausibly linked to the density of retinal ganglion cells on the retina, these psychophysical findings suggest that eyes of different sizes nonetheless have, on average, the same number of retinal ganglion cells.
It is possible that the OCT and psychophysical measurements can be reconciled by considering the relationship between tissue thickness and volume in eyes of different sizes. The equivalence of spatial acuity across eyes of different sizes is only obtained when acuity is expressed in cycles per degree of visual angle (and when avoiding the effects of spectacle magnification from corrective lenses11). In larger eyes, a greater surface area of retina (in square mm) subtends a given portion of the visual field (in square degrees of visual angle). It may be the case that eyes of different sizes have, on average, the same number of retinal ganglion cells, but that these cells are simply spread over a larger surface area in myopic eyes, resulting in a thinner retina. If we further assume that tissue thickness reflects only the number of cells present, with no changes in cell size or packing, then a prediction of this “stretching” model11–14 is that measurements of the GCL in eyes of different sizes should be rendered equivalent when expressed as the volume of tissue that subtends a square degree of visual angle. An examination of this prediction, and a characterization of its failure, can contribute to efforts to derive estimates of retinal ganglion cell counts from OCT measures of the retinal layers.15,16
Here, we examine the relationship between axial length and the properties of the GCL. We collected OCT measurements of GCL thickness along the horizontal meridian in 50 normally sighted participants, and used biometric measurements from each participant to generate a model eye that allowed us to convert GCL thickness into tissue volume. Our goal is to test the relationship between GCL tissue volume and axial length, as predicted by the stretching model. We then designed a model using principal component analysis to remove the effect of axial length from the measure of GCL tissue volume to better evaluate the contribution of individual variation in the total number of retinal ganglion cells present in the eye. Last, to test the efficacy of this model for characterizing the post-retinal visual pathway, we investigated the relationship between volumetric representations of GCL tissue and individual variation in the size of the optic chiasm.
Methods
Ethics Statement
This study was approved by the University of Pennsylvania Institutional Review Board, and all participants provided written consent.
Participants
We studied 50 normally sighted participants, recruited from the University of Pennsylvania and the surrounding Philadelphia community. This number of subjects was the targeted enrollment for the funding period of the study. Brain imaging data for each participant were collected following a preregistered protocol (https://osf.io/ervrh). Participants were required to be at least 18 years of age, have no history of ophthalmologic disease, and have corrected visual acuity of 20/40 or better. There were multiple sessions of data collection for each participant, typically across multiple days. These sessions included several retinal imaging studies, as well as structural and functional magnetic resonance imaging (MRI). After measurement of distance acuity and autorefraction, participants underwent pharmacologic dilation of the pupil prior to collection of biometric measures and retinal imaging.
Measurement of Visual Acuity
Best corrected distance visual acuity was measured for both eyes for every participant using the Early Treatment of Diabetic Retinopathy Study (ETDRS) chart.17 The logarithm of the minimum angle of resolution (logMAR) acuity for each eye was calculated, with interpolation between lines based upon number correct.18 For 48 of 50 participants, acuity between the 2 eyes was within 1 line. We therefore report the average acuity of the two eyes.
Biometry
All 50 participants underwent autorefraction of both eyes using an auto kerato-refractometer (Canon RK-F1 Full Auto Ref-Keratometer; Canon Medical Systems, Ōtawara, Tochigi, Japan). We measured the axial length of both eyes in all 50 participants using the IOLMaster 500 (Carl Zeiss Meditec, Jena, Germany). This instrument was also used to obtain keratometric measurements of both eyes in 40 of 50 participants.
There was a high correlation of these measurements between eyes across participants (all Pearson's correlation values > 0.95). Therefore, we took the average of the values across eyes in creating a model eye for each participant (after mirroring the measure of corneal torsion). For the 10 participants who did not undergo keratometry, we used mean imputation to estimate the model values from the remainder of our population.
Optical Coherence Tomography
We imaged both eyes of every participant using the Heidelberg Spectralis OCT (Heidelberg Engineering, Heidelberg, Germany; software version: 6.8.0.1) The imaging session included several measurements. We describe here the measurements made on the horizontal meridian. In the Supplementary Materials we describe the results of a parallel set of analyses performed upon measurements made on the vertical meridian. For each eye, 3 overlapping acquisitions of 30 degrees width were made along the horizontal meridian. Each acquisition was a high-resolution horizontal line scan that included the fovea. Retinal tracking was enabled on the device and the operator saved the scans after 100 individual B-scans were automatically aligned and averaged using the built-in Spectralis software. The images were exported from the instrument in DICOM format for further analysis, and retained their original x-axis position values in units of degrees of visual angle. For one participant, these data were not collected for the left eye. For this participant, only the images of the right eye were used in the subsequent analyses. Images from both eyes were used in the analyses of the remaining 49 participants.
OCT Montage
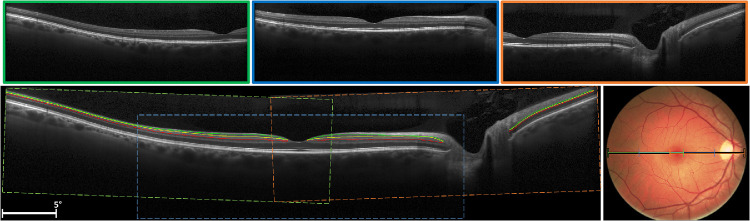
For each eye for each participant, we created a montage of the three, overlapping horizontal line scans. Using the central fovea scan as a reference, we performed a global rigid registration between the other two scans onto the central scan. Our registration approach used a standard scale-invariant feature transform (SIFT)19 feature detection on the intensity of each image. This technique attempts to locate and match similar patterns of intensity between the images, and then estimate the pixel displacement for each image needed to align the image structures. RANSAC20 was used to improve this alignment by detecting and removing outlier matches between the intensity features found by SIFT. Figure 1 shows the individual B-scans on the top row, and the montaged full scan on the bottom row.
Figure 1.
Example horizontal line scans. Three images (top row) each covering 30 degrees of retina were acquired for each eye for each subject and then montaged together into a single image (bottom row, left). The relative scales of the montaged scans are shown overlaid on a color fundus photograph from the same subject (bottom row, right). The GCL and IPL in each montaged image were manually labeled. The borders (shown as yellow, green, and red) defined by these labels were smoothed with a spline.
GCL Segmentation and Measurement
We performed manual segmentation to identify the GCL and inner plexiform layer (IPL). The montaged horizontal line images were viewed using ITKSNAP.21 One of the authors (J.N.) labeled pixels on the image as corresponding to the GCL or IPL, following a written protocol developed for this study. A third category (“indistinct”) was assigned to regions of the GCL and IPL where the boundary between the two could not be discerned, typically as the result of “shadow” artifacts from overlying retinal blood vessels. The three aligned images in each montage were observed simultaneously, and the best defined layer in the three images was used for the segmentation.
The manual segmentation defined three boundaries in the montaged images: (1) the boundary between the retinal nerve fiber layer and the GCL; (2) the boundary between the GCL and the IPL; and (3) the boundary between the IPL and the inner nuclear layer. We fit 15th order cubic splines to each of these boundaries, allowing us to interpolate across short patches in which the boundary between the GCL and IPL was indistinct. The spline order was determined empirically after experimenting with different values for 20 of the eyes. As each boundary is discontinuous at the fovea and optic nerve, three disjoint splines were individually fit to three sections of the retina: (1) from the temporal extent of the image to the fovea center, (2) from the fovea center to the optic nerve, and (3) from the optic nerve to the nasal extent of the image.
Using the smoothed delineations, we obtained the thickness of the GCL and IPL at equal eccentricity positions along the GCL/IPL boundary. At each location, we calculated the closest Euclidean distance from the GCL/IPL boundary to the inner GCL and outer IPL boundaries, thus providing the thickness (in mm) of each layer.
The layer measurements showed a high degree of similarity between left and right eyes for each participant. We found that the Pearson's correlation of the mean thickness (across eccentricity) of the GCL + IPL, between left and right eyes across participants, was R = 0.89 (P < 1e-6). This high correlation indicates that measurements from each eye are not independent, and suggests that combining the measurements from the two eyes within participant will yield a better estimate of individual participant variation. Therefore, in subsequent analyses, we averaged the measurements between the two eyes for each participant. To do so, we mirror-reversed the GCL and IPL thickness profiles from the left eye, aligned the measurements between the two eyes at the fovea, and averaged the values.
Calculation of Retinal Area Per Square Degree
A software model eye22 was used to calculate the relationship between the retinal surface and visual field. The model was customized for each participant using their biometric information, including axial length, spherical refractive error, and keratometry values (when available). Variation in the overall size and dimensions of the vitreous chamber was derived largely from David Atchison's work.23 Ray tracing through the model provided an estimate of mm2/degree2 at positions along the horizontal meridian, passing through the fovea. These values were then used to convert the thickness profiles into the volume of tissue per square degree of visual angle.
Principal Component Analysis Approach
We applied a principal component analysis (PCA) to the profiles of GCL tissue volume across participants. Due to individual differences in the extent of the fovea and position of the optic disc, some eccentricity points had measurements from a subset of the 50 participants studied. We confined the PCA analysis to those eccentricity locations at which 45 of 50 participants had a thickness measurement. The PCA was conducted in MATLAB using the alternating least squares algorithm to impute the values at those locations with measurements from > 45 but < 50 participants. The resulting PCA scores were observed to have small areas of high variation that were suspected to reflect noise. To reduce the influence of these, we conditioned the scores with a cubic smoothing spline (smoothing parameter = 0.1). All subsequent calculations of variance explained and fits to the data were conducted with these smoothed scores.
Measurement of Optic Chiasm Volume
We collected structural brain MRI images from 40 of the participants. MRI scanning made use of the Human Connectome Project LifeSpan protocol (VD13D) implemented on a 3-Tesla Siemens Prisma with a 64-channel Siemens head coil. A T1-weighted, 3D, magnetization-prepared rapid gradient-echo (MPRAGE) image was acquired for each participant in axial orientation with 0.8 mm isotropic voxels, repetition time (TR) = 2.4 seconds, echo time (TE) = 2.22 ms, inversion time (TI) = 1000 ms, and field of view (FOV) = 256 mm, flip angle = 8 degrees.
The MRI data were processed using the Human Connectome Project minimal processing pipeline.24 This pipeline includes application of the FreeSurfer version 5.3 toolbox, which performs tissue segmentation of the anatomical data.25–28 The optic chiasm was automatically identified and demarcated in the MPRAGE image for each participant in their native anatomic space based on registration to a probabilistic atlas in FreeSurfer.29
Statistical Analysis and Model Fitting
The relationship between measures was examined across the population using Pearson's correlation. Confidence intervals on the observed correlation were estimated across 1000 boot-strap resamples (with replacement) of the studied population. For those correlations used to test for the presence of a non-zero relationship between retinal measures and the optic chiasm volume, we report P values derived from tabular values given the Pearson score. We examined the combined ability of two retinal measures (ganglion cell tissue volume with and without adjustment for axial length) to account for variation in optic chiasm volume across the population. To do so, the mean-centered retinal measures served as covariates (along with an intercept term) in a linear model of optic chiasm volume, implemented using the MATLAB fitlm function.
Data and Code Availability
The code used to analyze the data and produce the figures is publicly available (https://github.com/gkaguirrelab/retinaTOMEAnalysis). The raw and processed data used in this study are also available for download (https://doi.org/10.6084/m9.figshare.c.5117903.v1).
Results
We obtained OCT and eye biometric measurements from 50 normally sighted participants. Table 1 provides the demographic and biometric information for this group. There was a strong negative correlation between axial length and spherical refractive error across our participants (R = –0.83, P < 1e-6). Despite this marked variation in refractive error, all participants had a best-corrected visual acuity (BCVA) of 0.07 logMAR (decimal equivalent 20/23) or better. There was no significant correlation across the participants between the axial length and BCVA (R = –0.07, P = 0.629). For the 10 participants who did not undergo keratometry and whose corneal curvature values were estimated using mean imputation, we assumed the mean value of 43.40 diopters at 0 degrees, and 44.34 diopters at 90 degrees, obtained from measurements of the remaining participants.
Table 1.
Demographic and Biometric Data
| Age, y | # Male / # Female | BCVA, log MAR | SR, Diopters | Axial Length, mm | K1, Diopters | K2, Diopters |
|---|---|---|---|---|---|---|
| 26 ± 10.1 | 26/24 | −0.05 ± 0.07 | −1.125 ± 4.25 | 24.1 ± 2.03 | 43.4 ± 2.32 | 44.0 ± 2.05 |
We studied 50 subjects. The median and interquartile range are provided for several measures. SR = spherical refractive error obtained by auto refraction.
Relationship Among GCL Thickness, Volume, and Axial Length
We collected horizontal OCT line scans through the fovea from both eyes of our participants (see Fig. 1, top). These acquisitions were montaged, segmented, and combined across eyes to obtain the thickness profile of the GCL for each participant across a 50 degree extent (see Fig. 1, bottom).
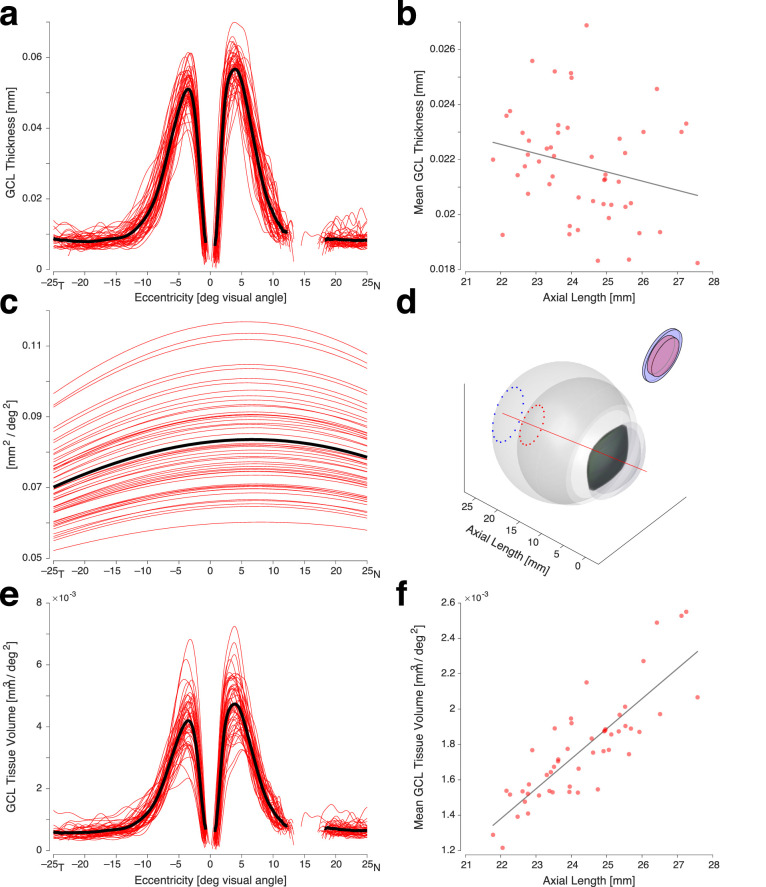
Figure 2a presents the GCL thickness profiles for each of the 50 participants, along with the group mean. As expected, the nasal parafoveal region is, on average, thicker than the temporal region. There is substantial individual variation in the profiles, most notably in the peak thickness of the temporal parafoveal region, which ranged from 0.04 to 0.06 mm. We obtained the mean thickness of the GCL profile across eccentricity for each participant, and compared this mean thickness value to axial length (Fig. 2b) and found a modest negative correlation (R = –0.24, P = 0.093).
Figure 2.
Relationship among GCL thickness, volume, and axial length. (a) GCL thickness profiles for 50 subjects (red) and the population mean (black), extending from –25 degrees (temporal) to 25 degrees (nasal). (b) The relationship between axial length and the mean GCL thickness from each participant. (c) The calculated retinal surface area (in mm2) that subtends a square degree of visual angle as a function of horizontal position on the retina. The function varies across subjects (red) primarily due to differences in axial length. The population mean is shown in black. (d) Rendering of the model eyes generated for the participants with the shortest and longest axial length. The dotted circles subtend 30 degrees diameter of the visual field in each eye around the visual axis (red line). Illustrated inset is a patch of retina from these two eyes that each have a diameter of 30 degrees, have the same tissue volume, and correspondingly have different thickness. (e) The volume of GCL tissue per square degree of visual angle as a function of retinal eccentricity for the 50 participants (red) and the population mean (black). (f) The relationship between axial length and the mean GCL tissue volume per square degree across eccentricity from each participant.
One source of variation in retinal thickness may simply be differences in the retinal surface area in eyes of different sizes. This possibility has been described as the “stretching” account of retinal development (e.g., Refs. 11–14). To evaluate this, we used a software model eye,22 informed by individual biometric measurements, to simulate vitreous chamber size and the optics of the eye for each participant. The simulation provides the retinal area (in mm2) that subtends the visual field (in degrees2) as a function of position along the horizontal meridian of the eye (Fig. 2c). The form of this conversion across eccentricity for the emmetropic eye is in good agreement with the equations of Drasdo and Fowler (1974),30 and as updated by Watson (2014).31 As expected, substantial variation in the conversion factor is present across participants, attributable to variation in axial length (Fig. 2d).
We applied the conversion functions to the GCL thickness profile from each participant. The result is a profile of the volume of GCL tissue (in mm3) that subtends a square degree of visual angle (Fig. 2e), expressed as a function of eccentricity in visual degrees. The general form of the profile is unaltered by this conversion, although we observe that the variation in the overall tissue volume across participants is greater than the variation that was observed in layer thickness.
We examined the relationship between the mean (across eccentricity) tissue volume and axial length. We find that the conversion to tissue volume has introduced a strong, positive correlation with axial length (R = 0.84, P < 1e-6; Fig. 2f). This finding diverges from the simple stretching model, which predicts that a volumetric representation of the data should no longer be related to axial length.
Characterization Model for GCL Volume Profiles
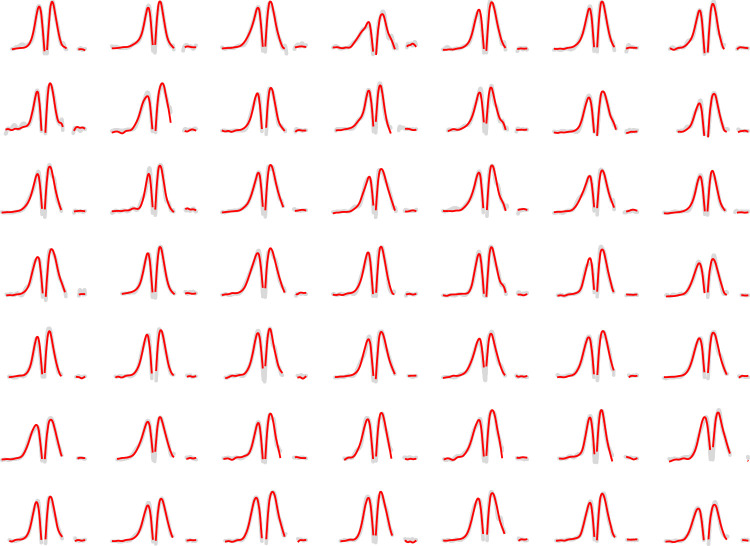
Using the derived GCL volume measurements, we conducted a PCA upon the tissue volume profiles of our 50 participants (Fig. 3). To reduce the influence of noisy measurements at some eccentricity locations, we conditioned the principal components with a cubic smoothing spline. We found that the first 6 components were sufficient to explain 99.5% of the variance in the data. The first component primarily represents the mean tissue volume profile. Subsequent components capture variation in the distribution of GCL tissue across eccentricity. For example, components two and four characterize the relative tendency of tissue to be crowded toward the parafoveal hills or pushed more toward the periphery. Figure 4 shows the reconstruction of individual participant tissue volume profiles using only the first six, smoothed, principle components. We find that this low-dimension representation well represents the original profiles of GCL tissue volume.
Figure 3.
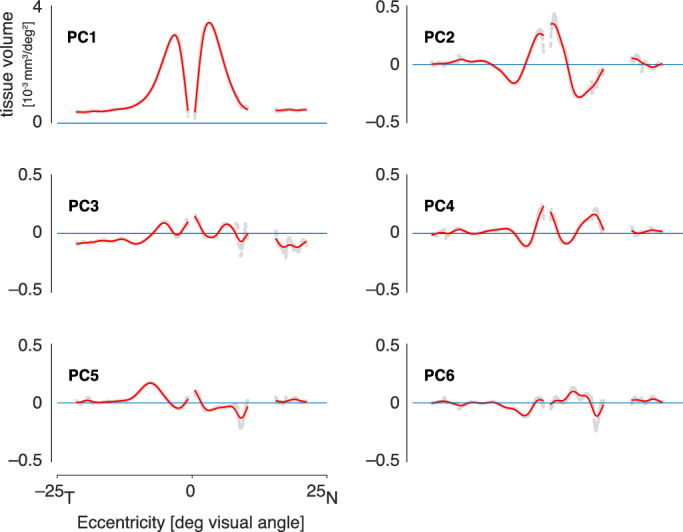
The first six principal components derived from an analysis of GCL tissue volume profiles across the 50 participants. The initial (gray) components were smoothed (red) to reduce the influence of noisy regions of the measurement.
Figure 4.
Original (gray) and reconstructed (red) GCL tissue volume profiles for the first 49 participants, using the first 6 smoothed principle components, demonstrating the accuracy of the low dimensional representation of the data.
The GCL tissue volume profile for each participant can be described by the loading on the six components. We examined if variation in axial length produces systematic variation in these weights. We performed a regression of each principal component loading with respect to axial length, which creates a hyperplane whose normal vector describes the direction and magnitude that axial length has on each principal component. We find a significant and substantial relationship with axial length for PC1 and PC2. Table 2 summarizes the properties of the principal components.
Table 2.
Properties of the Principal Components Derived From the GCL Tissue Volume Profiles Across Subjects
| Shape | Correlation | |
|---|---|---|
| Variance | w/Axial | |
| PC | Explained | Length |
| 1 | – | 0.85*** |
| 2 | 40% | 0.75*** |
| 3 | 12% | 0.11 |
| 4 | 10% | 0.25 |
| 5 | 8% | –0.16 |
| 6 | 5% | –0.13 |
The first 6 principal components were found to explain 99.5% of the total variance in the data. The first principal component primarily accounts for variation across subjects in the mean tissue volume across the profile. Components 2 to 6 account for 75% of the remaining variation in the shape of the profile across subjects. The Pearson correlation of axial length with the weights on each of the components is also given (*** indicate correlations with significance P < 0.001; the remaining coefficients were found to be nonsignificant).
These results may be used to visualize the effect of axial length upon the GCL. Figure 5 presents (in green) the GCL profile for an emmetropic eye, and then how that profile is altered with variation in axial length for each of the six principal components. As can be seen, variation in axial length scales the overall tissue volume (PC1), but also adjusts the distribution of tissue across eccentricity (PC2). In myopic eyes, retinal ganglion cell tissue is crowded more closely toward the fovea.
Figure 5.
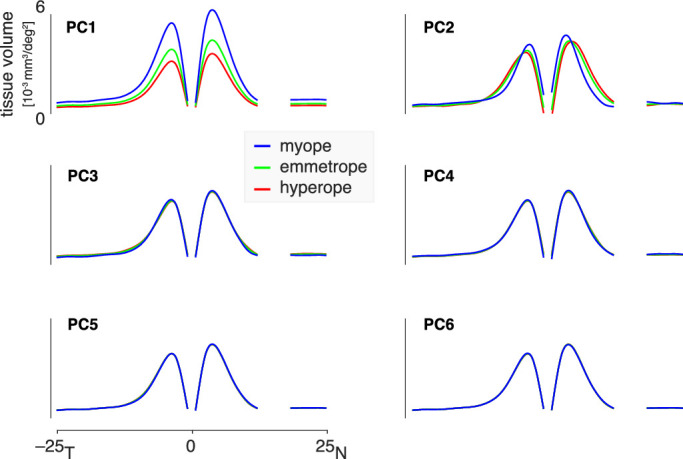
The influence of axial length on the GCL tissue volume profile, as reflected in each of the first six principal components. Each plot shows how one of the principal components varies with axial length from myopic (blue, 27.57 mm), to emmetropic (green, 23.58 mm), to hyperopic (red, 21.79 mm).
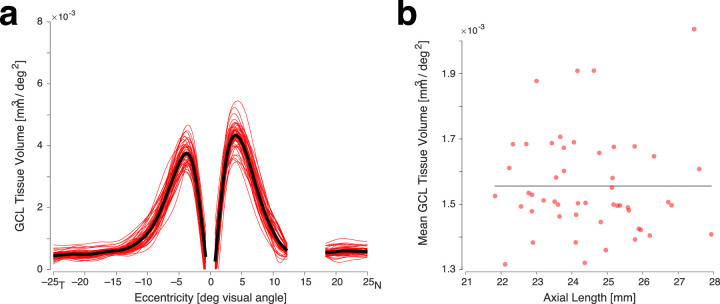
Having characterized the effect of axial length upon the GCL tissue volume profile, it is now possible to adjust the profile obtained for any one participant to remove the influence of axial length. In effect, we can express the GCL tissue volume profile for each participant, projected to the emmetropic eye. Figure 6a presents the individual and mean profiles following this adjustment. Although individual differences remain, the extreme variation seen in Figure 2e has been removed. Figure 6b confirms that the effect of axial length in the data has been removed.
Figure 6.
(a) GCL tissue volume profiles for the 50 subjects after removing the effect of axial length by projecting each profile to the emmetropic eye. (b) The relationship between axial length and the mean GCL tissue volume per square degree across eccentricity from each participant following correction for variation in axial length.
Individual differences in the overall volume of the GCL tissue remain after adjustment for the effect of axial length. We next asked if this adjusted measurement may be related to other properties of the visual pathway that reflect the influence of retinal ganglion cells.
Relation to Optic Chiasm Volume
The retinal ganglion cells give rise to axons that form the optic nerve and decussate at the optic chiasm. We considered that individual differences in the size of the optic chiasm would reflect individual differences in the number of retinal ganglion cells in the retina. We obtained a high resolution, T1-weighted image of the brain in 40 of the 50 participants, and derived from this image the volume of the optic chiasm. We then examined the correlation across participants between optic chiasm volume and retinal measures.
We first examined the relationship between mean GCL thickness (see Fig. 2b) and optic chiasm volume, and found a significant relationship (R = 0.37 ± 0.20 SEM obtained by bootstrap resampling across the participants, P = 0.0173). Next, we examined this relationship for mean GCL tissue volume, unadjusted for axial length (Fig. 2f). This correlation was substantially higher (R = 0.51 ± 0.11 SEM, P = 6.8e-4), indicating that the volume of ganglion cell tissue is a better predictor of the size of the optic chiasm than is the thickness of this retinal layer. We then examined individual differences in the volume of ganglion cell tissue, after adjusting for the modeled effects of axial length (Fig. 6b), and found that this measure is also strongly related to optic chiasm size (R = 0.53 ± 0.16 SEM, P = 4.5e-4).
The adjusted and unadjusted volume measures are correlated with one another (R = 0.50, P = 2.1e-4), but presumably reflect different properties of the GCL. By appeal to results from psychophysics, we propose that the GCL volume measure after adjustment for axial length reflects the number of retinal ganglion cells. In contrast, the unadjusted volume is dominated by variation in cell size and packing. We find that both volume measures (adjusted and unadjusted) are well correlated with the size of the optic chiasm. We therefore examined if the adjusted and unadjusted volume measures each make an independent contribution to the prediction of optic chiasm size. We included both measures in a linear model of optic chiasm size. Overall, this model explained significant variance in the optic chiasm measurements (F[2,37] = 10.9, P = 1.9e-4). Further, both the adjusted and unadjusted GCL volume measures made significant, independent contributions to the model (P = 0.022 and P = 0.029, respectively). The relative weighting of the two GCL measures was effectively equal. Figure 7 presents the performance of this combined model. On the x-axis is the combined score for each participant of the two GCL volume measures (expressed as the deviation of each subject from the across-participant mean of this score), and on the y-axis the optic chiasm volume. Those subjects who tended to have a greater volume of GCL tissue, tended to have a larger optic chiasm.
Figure 7.
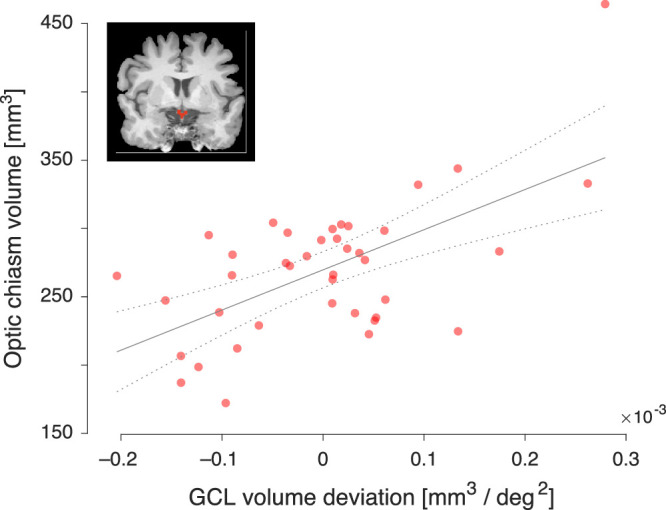
Relation of modeled GCL tissue volume to optic chiasm volume. Optic chiasm volume was measured from an anatomic MRI image in each of forty participants (example coronal MRI image inset; optic chiasm indicated in red). The optic chiasm volume (y-axis) for each participant was related to individual variation in measured GCL tissue volume (x-axis). Variation in GCL tissue volume was modeled as the weighted and combined influence of measured mean GCL tissue volume, with and without adjustment for the effects of variation in axial length. The best fit line (with 95% confidence intervals) of the model is shown.
Finally, we examined how well other biometric measures account for optic chiasm size. We find that height (R = 0.36, P = 0.010), weight (R = 0.28, P = 0.049), axial length (R = 0.27, P = 0.058), and age (R = 0.12, P = 0.406) all have a weaker relationship with optic chiasm volume than did measures of GCL tissue volume.
Replication for the Vertical Meridian
We conducted a parallel analysis of data obtained from the vertical meridian. As detailed in the Supplementary Materials, we replicated our findings in these data, including demonstrating that the volume of ganglion cell tissue is the best predictor of individual variation in optic chiasm volume.
Discussion
Several neurologic32,33 and ophthalmologic34,35 diseases are associated with the loss of retinal ganglion cells. In these conditions, OCT measures of retinal structures have been pursued as imaging biomarkers of the health of retinal cells.36–39 Existing analyses, however, rarely account for the effect that variation in eye size has upon OCT measures. In this study, we measured normal variation in the profile of the GCL of the human retina and related that variation to individual differences in axial length and to the size of the optic chiasm. Our goal is to understand the properties of different measurement units and coordinate frames in characterizing the GCL, and how these choices may be related to counts of the underlying ganglion cell population.
Our study provides a basic empirical result: the population-average profile of the thickness and volume of the GCL along the horizontal and vertical meridians. There are limited prior reports of the thickness of the isolated GCL in healthy human eyes, perhaps due to the challenge of segmenting the GCL and IPL in OCT images. Curcio and colleagues (2011)40 measured the thickness of the GCL along the horizontal meridian in postmortem histology from the eyes of 18 older donors (ages 40–92 years). Raza and Hood (2015)15 presented the average, segmented, two-dimensional GCL profile from macular volume scans in 36 healthy participants. Woertz and colleagues (2020)41 measured the thickness of the segmented GCL along the horizontal and vertical meridians in 25 control participants. All of these measurements identify a peak thickness of approximately 60 microns in the nasal parafoveal region, and a slightly lower peak thickness on the temporal side. Our measurements are in good agreement with this prior work. The current measurements extend further into the periphery of the retina, reaching to 25 degrees eccentricity, as compared to approximately 10 degrees eccentricity in prior work. We find that the GCL thickness plateaus beyond approximately 20 degrees.
It seems reasonable to presume that variation in the size of the GCL is related to variation in the total number of retinal ganglion cells. This presumption is well supported for variation across eccentricity. The profile of GCL thickness matches well the profile of retinal ganglion cell counts measured from histological section by Curcio and Allen (1990).4 Raza and Hood (2015)15 used this insight to link their two-dimensional map of GCL thickness to an interpolated map of retinal ganglion cell density. Their method provides an estimate of differences in regional ganglion cell count by examining individual differences in relative GCL thickness.
Thickness and Volume
Variation in eye size, however, complicates efforts to relate GCL thickness to retinal ganglion cell count. A larger eye uses a greater retinal surface area to represent the same size visual field. It may be the case that the same number of retinal ganglion cells are spread over a larger surface area, causing the resulting layer to be thinner. Indeed, we find in our data that the GCL is slightly thinner in larger eyes, consistent with similar, prior measurements of the GCL + IPL.3,42–45
If the only effect of variation in axial length upon the GCL is to vary the area over which a fixed number of ganglion cells are distributed, then a measurement of tissue volume will correct for this effect. Specifically, there would be no variation by axial length in a measure of cubic mm of GCL tissue per degree square of visual field. We might call this a “volume naïve” version of the stretching model, and we hasten to add that this naivety is used here to motivate a modeling approach for OCT data, but is not to be found in the thoughtful, prior psychophysical work by other investigators. Regardless, our results reject this simple account, as we find instead that larger eyes have a far greater volume of ganglion cell tissue than would be predicted.
One explanation for this effect is that larger eyes have more ganglion cells, and that this greater number of cells results in a greater volume. Psychophysical data argue against this possibility, as angular peripheral spatial acuity is found to not differ across variation in spherical error.9,10 A related, supportive finding is that, beyond approximately 1 degrees eccentricity, the density of cones in eyes of different sizes is invariant with axial length when expressed relative to square degrees of the visual field.46 Therefore, it seems that variation in spherical refractive error and associated axial length acts to distribute photoreceptors and ganglion cells over different surface areas, but not to alter markedly their numbers.
If the number of cells does not differ in myopic eyes, then either the individual cells are larger, or they are packed less densely, or both. In histologic studies of the central and peripheral nervous system, there is a relationship among number, size, and packing of cells across species, and across differences in body size within species.47 Although these relationships vary substantially by cell type,48 there is a general finding that in larger organs, neural soma size is larger, and the cells are less densely packed.
Individual Differences in Cell Count and Cell Size
We modeled the empirical relationship between axial length and GCL tissue volume in our cohort of 50 participants, and then removed this effect from the data. The residuals of this analysis represent individual variation in GCL tissue volume that cannot be explained by variation in axial length. This residual variation could be the result of further individual differences in cell packing—unrelated to axial length—or the consequence of individual differences in the number of retinal ganglion cells in the GCL, or both.
There is evidence that people differ substantially in the total number of retinal ganglion cells present in their eyes. Estimates derived from histology of the human retina suggest that the total number of retinal ganglion cells in an eye varies from 0.75 to 1.5 million across individuals.4 Counts of the axons in the optic nerve of human eyes are in good agreement, finding the total number of fibers varies between roughly 0.6 and 1.4 million in healthy eyes.49 Variation in the mean diameter of these axons was substantially less across people than was the variation in total axon number.
We find that GCL tissue volume, adjusted for axial length, is the best single predictor of individual differences in the size of the optic chiasm in our population. To the extent that GCL and optic chiasm volume reflect the number of retinal ganglion cells and their axons, respectively, this finding identifies axial length-adjusted GCL tissue volume as a measure related to ganglion cell number.
We find an independent and additive prediction of optic chiasm volume by the unadjusted GCL tissue volume. As discussed above, the unadjusted GCL volume measure is dominated by variations in cell size and / or packing that accompany differences in axial length. The correlation with optic chiasm volume suggests that the enlargement of GCL volume in bigger eyes is accompanied by an enlargement of axonal size. This is consistent with myopic eyes having retinal ganglion cells with larger cell bodies, and accompanying larger axons, as has been observed in other neural tissue.50
Although we find GCL tissue volume to be a promising measure to relate to properties of the post-retinal visual pathway, several unanswered questions remain. Even after adjustment for the volumetric effects of axial length, individual differences in adjusted GCL tissue volume combine true variation in cell number with variation in incidental features of cell density. Ideally, we would relate our OCT measures of GCL structure to a more direct measure of retinal ganglion cell count, either through imaging with adaptive optics,51 or through individual difference psychophysical measures that may be related to ganglion cell number.52
Another important limit is that we have measured only a portion of the retinal surface, and it may be the case that the peripheral retina varies across subjects in a manner that is distinct from the center. By montaging multiple line scans, we have examined 50 degrees extent of the horizontal meridian (and 25 degrees of the vertical meridian; see Supplementary Materials). If we assume that our measurement of the horizontal meridian captures individual differences at all polar angle locations, we still have measured only 9.4% of the retinal surface (i.e., of the 2π steradians in a hemisphere, we have sampled 2π × [1-cos(25°)] = 0.59 steradians). This limited window into retinal variation remains true even if we consider the uneven distribution of ganglion cells across the retinal surface. Using the Curcio and Allen measures,4 we calculate that the central 25 degrees eccentricity of the retina contains only 14–15% of the total retinal ganglion cell endowment of the eye. Nonetheless, we find a substantial correlation between optic chiasm size and our measure of ganglion cell tissue volume. Therefore, individual differences in the central and peripheral retina are shared to some extent.
Distinctions Between Units for Retinal Measurement
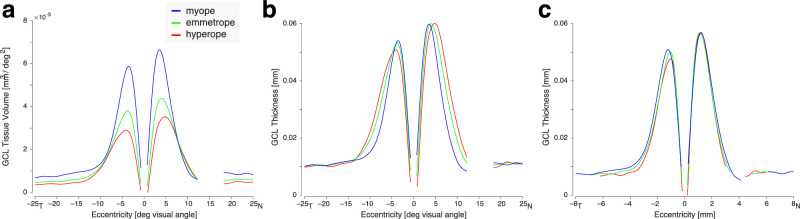
As has been explored previously for photoreceptor density and angiography,46,53 the current study illustrates the effect of different units of representation for measurements of the GCL, and how these choices interact with variation in the axial length of the eye. Figure 8 presents the modeled GCL profile for three eyes of varying ametropia, in three different measurement frames. We were motivated by theoretical considerations to examine tissue volume per square degree of visual field, expressed as a function of visual field position (Fig. 8a). We propose that this coordinate frame is well suited to relate properties of the GCL to visual perception and the post-retinal pathway. The post-retinal visual pathway has a retinotopic organization that is remarkably consistent across individuals when expressed in degrees of polar angle and eccentricity of the visual field.54,55 Although eyes may vary in shape and size, they have the shared property of representing a fixed amount of the visual field (in degrees) using a collection of retinal ganglion cells of a given volume. A challenge for this coordinate representation is the confounding effect of changes in cell size and packing across axial length. We present here a model of this effect, which allows us to remove its influence.
Figure 8.
The retinal ganglion cell layer considered in different coordinate frames. The profile of the GCL along the horizontal meridian is modeled for eyes of varying axial lengths (myope 27.57 mm; emmetrope 23.58 mm; and hyperope 21.79 mm). This same set of profiles is plotted for three different choices of unit and coordinate frames. (a) GCL tissue volume per square degree of visual angle as a function of eccentricity in degrees of visual angle; (b) GCL thickness in mm as a function of eccentricity in degrees of visual angle; (c) GCL thickness in mm as a function of eccentricity in mm of retina. For the last of these, the extent of the plotted functions along the x-axis varies with eye size.
Measurements of the GCL and related structures have traditionally been made as thickness (in mm or microns), expressed as a function of retinal distance in degrees of visual angle (Fig. 8b) or mm (Fig. 8c). The choice of x-axis units obviously interacts with spherical ametropia, as the size of the vitreous chamber influences the conversion of degrees to mm. Prior work has carefully characterized normal variation in the shape of the foveal pit, and how that variation is related to axial length.56–58 As the morphology of the foveal pit is influenced by multiple retinal layers, the GCL thickness profiles we report here cannot be directly related to these prior studies. Indeed, we note that Woertz and colleagues (2020)41 found that the GCL and IPL had quite variable relative thicknesses across individuals, leading us to be cautious in attempting to relate our measurements of a single retinal layer to larger properties of retinal morphology.
Conclusion
In the current study, we characterize the relationship between variation in axial length and measurements of the GCL. Based upon an assumption that eyes of different sizes do not systematically vary in their total number of retinal ganglion cells, we introduce a measure of the volume of ganglion cell tissue relative to the visual field, and an adjustment for axial length to remove variation in cell size and packing. The resulting measure accounts for individual differences in the size of the optic chiasm, supporting its use to characterize the post-retinal visual pathway.
Supplementary Material
Acknowledgments
Supported by National Institutes of Health Grant U01EY025864: Human Connectomes in Low Vision, and P30 EY001583: Core Grant for Vision Research. Thank you to Edda B. Haggerty for carefully labeling the vertical meridian images.
Disclosure: M. Chen, None; J. Nofziger, None; R. Datta, None; J.C. Gee, None; J. Morgan, None; G.K. Aguirre, None
References
- 1. Atchison DA, Jones CE, Schmid KL, et al. Eye shape in emmetropia and myopia. InvestOphthalmolVisSci. 2004; 45(10): 3380–3386. [DOI] [PubMed] [Google Scholar]
- 2. Jonas JB, Xu L, Wei WB, et al. Retinal thickness and axial length. InvestOphthalmolVisSci. 2016; 57(4): 1791–1797. [DOI] [PubMed] [Google Scholar]
- 3. Takeyama A, Kita Y, Kita R, Tomita G. Influence of axial length on ganglion cell complex (GCC) thickness and on GCC thickness to retinal thickness ratios in young adults. JpnJOphthalmol. 2014; 58(1): 86–93. [DOI] [PubMed] [Google Scholar]
- 4. Curcio CA, Allen KA. Topography of ganglion cells in human retina. JCompNeurol. 1990; 300(1): 5–25. [DOI] [PubMed] [Google Scholar]
- 5. Dacey DM. The mosaic of midget ganglion cells in the human retina. JNeurosci. 1993; 13(12): 5334–5355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Thibos LN, Cheney FE,, Walsh DJ. Retinal limits to the detection and resolution of gratings. JOSA A. 1987; 4(8): 1524–1529. [DOI] [PubMed] [Google Scholar]
- 7. Thibos LN, Walsh DJ,, Cheney FE.. Vision beyond the resolution limit: aliasing in the periphery. VisRes. 1987; 27(12): 2193–2197. [DOI] [PubMed] [Google Scholar]
- 8. Wang YZ, Thibos LN,, Bradley A.. Effects of refractive error on detection acuity and resolution acuity in peripheral vision. InvestOphthalmolVisSci. 1997; 38(10): 2134–2143. [PubMed] [Google Scholar]
- 9. Coletta NJ,, Watson T. Effect of myopia on visual acuity measured with laser interference fringes. VisRes. 2006; 46(5): 636–651. [DOI] [PubMed] [Google Scholar]
- 10. Atchison DA, Schmid KL, Pritchard N. Neural and optical limits to visual performance in myopia. VisRes. 2006; 46(21): 3707–3722. [DOI] [PubMed] [Google Scholar]
- 11. Chui TY, Yap MK, Chan HH, Thibos LN. Retinal stretching limits peripheral visual acuity in myopia. VisRes. 2005; 45(5): 593–605. [DOI] [PubMed] [Google Scholar]
- 12. Curtin BJ, Karlin DB. Axial length measurements and fundus changes of the myopic eye. AmJOphthalmol. 1971; 71(1): 42–53. [DOI] [PubMed] [Google Scholar]
- 13. Romano PE, Von Noorden GK. Knapp's law and unilateral axial high myopia. 1970. BinoculVisStrabismus Q. 1999; 14(3): 215–222. [PubMed] [Google Scholar]
- 14. Vera-Diaz FA, McGraw PV, Strang NC, Whitaker D. A psychophysical investigation of ocular expansion in human eyes. InvestOphthalmolVisSci. 2005; 46(2): 758–763. [DOI] [PubMed] [Google Scholar]
- 15. Raza AS, Hood DC. Evaluation of the structure–function relationship in glaucoma using a novel method for estimating the number of retinal ganglion cells in the human retina. InvestOphthalmolVisSci. 2015; 56(9): 5548–5556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Hood DC, Kardon RH. A framework for comparing structural and functional measures of glaucomatous damage. ProgRetinEye Res. 2007; 26(6): 688–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Bailey IL, Lovie-Kitchin JE. Visual acuity testing. From the laboratory to the clinic. VisRes. 2013; 90: 2–9. [DOI] [PubMed] [Google Scholar]
- 18. Holladay JT. Proper method for calculating average visual acuity. JRefractSurg. 1997; 13(4): 388–391. [DOI] [PubMed] [Google Scholar]
- 19. Lowe DG. Object recognition from local scale-invariant features. In Proceedings of the seventh IEEE international conference on computer vision, 1999, September; 2: 1150–1157. [Google Scholar]
- 20. Fischler M.A, Bolles RC. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM. 1981; 24(6): 381–395. [Google Scholar]
- 21. Yushkevich PA, Piven J, Hazlett HC, et al. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006; 31(3): 1116–1128. [DOI] [PubMed] [Google Scholar]
- 22. Aguirre GK. A model of the entrance pupil of the human eye. SciRep. 2019; 9(1): 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Atchison DA, Pritchard N, Schmid KL, Scott DH, Jones CE, Pope JM. Shape of the retinal surface in emmetropia and myopia. InvestOphthalmolVisSci. 2005; 46(8): 2698–2707. [DOI] [PubMed] [Google Scholar]
- 24. Glasser MF, Sotiropoulos SN, Wilson JA, et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 2013; 80: 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage. 1999; 9(2): 179–194. [DOI] [PubMed] [Google Scholar]
- 26. Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis: II: inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999; 9(2): 195–207. [DOI] [PubMed] [Google Scholar]
- 27. Fischl B, Sereno MI, Tootell RB, Dale AM. High‐resolution intersubject averaging and a coordinate system for the cortical surface. HumBrain Mapp. 1999; 8(4): 272–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. ProcNatl AcadSci. 2000; 97(20): 11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Fischl B, Salat DH, Busa E, et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002; 33(3): 341–355. [DOI] [PubMed] [Google Scholar]
- 30. Drasdo N, Fowler CW. Non-linear projection of the retinal image in a wide-angle schematic eye. BrJOphthalmol. 1974; 58(8): 709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Watson AB. A formula for human retinal ganglion cell receptive field density as a function of visual field location. JVis. 2014; 14(7): 15–15. [DOI] [PubMed] [Google Scholar]
- 32. Blanks JC, Hinton DR, Sadun AA, Miller CA. Retinal ganglion cell degeneration in Alzheimer's disease. Brain Res. 1989; 501(2): 364–372. [DOI] [PubMed] [Google Scholar]
- 33. Kerrison JB, Flynn T, Green WR. Retinal pathologic changes in multiple sclerosis. Retina (Philadelphia, Pa.). 1994; 14(5): 445–451. [DOI] [PubMed] [Google Scholar]
- 34. Quigley HA, Nickells RW, Kerrigan LA, Pease ME, Thibault DJ, Zack DJ. Retinal ganglion cell death in experimental glaucoma and after axotomy occurs by apoptosis. InvestOphthalmolVisSci. 1995; 36(5): 774–786. [PubMed] [Google Scholar]
- 35. Kerrigan LA, Zack DJ, Quigley HA, Smith SD, Pease ME. TUNEL-positive ganglion cells in human primary open-angle glaucoma. ArchOphthalmol. 1997; 115(8): 1031–1035. [DOI] [PubMed] [Google Scholar]
- 36. Tian T, Zhu XH, Liu YH. Potential role of retina as a biomarker for progression of Parkinson's disease. IntJOphthalmol. 2011; 4(4): 433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Alonso R, Gonzalez-Moron D, Garcea O. Optical coherence tomography as a biomarker of neurodegeneration in multiple sclerosis: a review. MultSclerRelatDisord. 2018; 22: 77–82. [DOI] [PubMed] [Google Scholar]
- 38. Valenti DA. Alzheimer's disease and glaucoma: Imaging the biomarkers of neurodegenerative disease. Int J Alzheimers Dis. 2010; 2010:793931, 9, 10.4061/2010/793931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Kim EK, Park HYL, Park CK. Segmented inner plexiform layer thickness as a potential biomarker to evaluate open-angle glaucoma: dendritic degeneration of retinal ganglion cell. PLoS One. 2017; 12(8): e0182404, 10.1371/journal.pone.0182404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Curcio CA, Messinger JD, Sloan KR, Mitra A, McGwin G, Spaide RF. Human chorioretinal layer thicknesses measured in macula-wide, high-resolution histologic sections. InvestOphthalmolVisSci. 2011; 52(7): 3943–3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Woertz EN, Omoba BS, Dunn TM, et al. Assessing ganglion cell layer topography in human albinism using optical coherence tomography. InvestOphthalmolVisSci. 2020; 61(3): 36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Hirasawa K, Shoji N. Association between ganglion cell complex and axial length. JpnJOphthalmol. 2013; 57(5): 429–434. [DOI] [PubMed] [Google Scholar]
- 43. Mwanza JC, Durbin MK, Budenz DL, et al. Profile and predictors of normal ganglion cell–inner plexiform layer thickness measured with frequency-domain optical coherence tomography. InvestOphthalmolVisSci. 2011; 52(11): 7872–7879. [DOI] [PubMed] [Google Scholar]
- 44. Seo S, Lee CE, Jeong JH, Park KH, Kim DM, Jeoung JW. Ganglion cell-inner plexiform layer and retinal nerve fiber layer thickness according to myopia and optic disc area: a quantitative and three-dimensional analysis. BMC Ophthalmol. 2017; 17(1): 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Szigeti A, Tátrai E, Varga BE, et al. The effect of axial length on the thickness of intraretinal layers of the macula. PLoS One. 2015; 10(11): e0142383, 10.1371/journal.pone.0142383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Li KY, Tiruveedhula P, Roorda A. Intersubject variability of foveal cone photoreceptor density in relation to eye length. InvestOphthalmolVisSci. 2010; 51(12): 6858–6867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Herculano‐Houzel S. Brains matter, bodies maybe not: the case for examining neuron numbers irrespective of body size. AnnNYAcadSci. 2011; 1225(1): 191–199. [DOI] [PubMed] [Google Scholar]
- 48. Wang SSH, Ambrosini AE, Wittenberg GM. Evolution and scaling of dendrites. Dendrites. Oxford University Press; 2016: 47–75. [Google Scholar]
- 49. Mikelberg FS, Drance SM, Schulzer M, Yidegiligne HM, Weis MM. The normal human optic nerve: axon count and axon diameter distribution. Ophthalmology. 1989; 96(9): 1325–1328. [DOI] [PubMed] [Google Scholar]
- 50. Cullheim S. Relations between cell body size, axon diameter and axon conduction velocity of cat sciatic α-motoneurons stained with horseradish peroxidase. NeurosciLett. 1978; 8(1): 17–20. [DOI] [PubMed] [Google Scholar]
- 51. Liu Z, Kurokawa K, Zhang F, Lee JJ, Miller DT. Imaging and quantifying ganglion cells and other transparent neurons in the living human retina. ProcNatl AcadSci. 2017; 114(48): 12803–12808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Kwon M, Liu R. Linkage between retinal ganglion cell density and the nonuniform spatial integration across the visual field. ProcNatl AcadSci. 2019; 116(9): 3827–3836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Llanas S, Linderman RE, Chen FK, Carroll J. Assessing the use of incorrectly scaled optical coherence tomography angiography images in peer-reviewed studies: a systematic review. JAMA Ophthalmol. 2020; 138(1): 86–94. [DOI] [PubMed] [Google Scholar]
- 54. Benson NC, Butt OH, Datta R, Radoeva PD, Brainard DH, Aguirre GK. The retinotopic organization of striate cortex is well predicted by surface topology. CurrBiol. 2012; 22(21): 2081–2085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Benson NC, Butt OH, Brainard DH, Aguirre GK. Correction of distortion in flattened representations of the cortical surface allows prediction of V1-V3 functional organization from anatomy. PLoS ComputBiol. 2014; 10(3): e1003538, 10.1371/journal.pcbi.1003538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Tick S, Rossant F, Ghorbel I, Gaudric A, Sahel JA, Chaumet-Riffaud P, Paques M. Foveal shape and structure in a normal population. InvestOphthalmolVisSci. 2011; 52(8): 5105–5110. [DOI] [PubMed] [Google Scholar]
- 57. Kim MS, Kim JS, Choi J, Kim JH, Oh WH. A study of foveal shape in emmetropia and myopia using spectral domain optical coherence tomography. JKorean OphthalmolSoc. 2014;55(6): 833–839. [Google Scholar]
- 58. Dubis AM, McAllister JT, Carroll J. Reconstructing foveal pit morphology from optical coherence tomography imaging. BrJOphthalmol. 2009; 93(9): 1223–1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code used to analyze the data and produce the figures is publicly available (https://github.com/gkaguirrelab/retinaTOMEAnalysis). The raw and processed data used in this study are also available for download (https://doi.org/10.6084/m9.figshare.c.5117903.v1).