NADH-driven poly-3-hydroxybutyrate accumulation in Escherichia coli: Data from enzymatic assays and oxygen-limited continuous cultures

Abstract

Biosynthesis of poly-3-hydroxybutyrate (PHB) as a fermentation product enables the coupling of growth and product generation. Moreover, the reduction of oxygen supply should reduce operative cost and increase product yield. Generation of PHB as a fermentation product depends on the in vivo activity of an NADH-preferring acetoacetyl-CoA reductase. Proof of this concept requires (i) quantification of the cofactor preference, in physiologically relevant conditions, of a putative NADH-preferring acetoacetyl-CoA reductase and (ii) verification of PHB accumulation using an NADH-preferring acetoacetyl-CoA reductase in a species naturally incapable of doing so, for example, Escherichia coli. This dataset contains kinetic data obtained by spectrophotometry and data from a continuous culture of an engineered E. coli strain accumulating PHB under oxygen-limiting conditions. In this dataset it is possible to find (1) enzyme stability assays; (2) initial rates and progress curves from reactions catalyzed by two acetoacetyl-CoA reductases; (3) estimations of the relative use of NADH and NADPH by two acetoacetyl-CoA reductases; (4) estimations of the flux capacity of the reaction catalyzed by an acetoacetyl-CoA reductase; (5) biomass composition of an engineered E. coli strain transformed with a plasmid; (6) calculation of reconciled specific rates of this engineered strain growing on sucrose as the sole carbon source under oxygen limitation and (7) metabolic fluxes distributions during the continuous growth of this engineered strain. Because a relatively small number of acetoacetyl-CoA reductases have been kinetically characterized, data and scripts here provided could be useful for further kinetic characterizations. Moreover, the procedure described to estimate biomass composition could be interesting to estimate plasmid and protein burden in other strains. Application of data reconciliation to fermentations should help to obtain specific rates consistent with the principle of mass and electron conservation. All the required data and scripts to perform these analyses are deposited in a Mendeley Data repository. This article was co-submitted with the manuscript entitled “An NADH preferring acetoacetyl-CoA reductase is engaged in poly-3-hydroxybutyrate accumulation in Escherichiasia. coli”.

Specifications Table

Subject	Biological Sciences. Biotechnology
Specific subject area	Continuous production of poly-3-hydroxybutyrate as a fermentation product under oxygen limitation.
Type of data	Figure: Product concentration versus Enzyme concentration times Time.
	Figure: Initial rates versus acetoacetyl-CoA concentration
	Figures: Progress curves of reactions catalyzed by acetoacetyl-CoA reductases.
	Figure: Relative consumption of NADH and NADPH in the reactions catalyzed by two acetoacetyl-CoA reductases.
	Figure: Flux capacity of a reaction catalyzed by an acetoacetyl-CoA reductase at different NADH/NAD+ ratios.
	Table: Biomass composition of the E. coli strain ((F– λ– ilvG– rfb-50 rph-1 (DE3) ΔadhE ΔadhP ΔldhA Δpta ΔmhpF)) transformed with the plasmid pCOLA-phaCAphaB-cscABK.
	Table: Non-balanced and reconciled specific rates during the continuous growth of that engineered strain, using sucrose as the sole carbon source, at a dilution rate of 0.1 h−1, and oxygen limitation.
	Table: Metabolic fluxes distributions during the continuous growth of that engineered strain, using sucrose as the sole carbon source, at a dilution rate of 0.1 h−1, and oxygen limitation.
How data were acquired	In the case of kinetic data, product concentrations were estimated by spectrophotometry and enzyme concentrations were estimated using the Biorad Protein Assay kit. Time and initial rates were automatically recorded/calculated by the spectrophotometer Synergy HTX plate-reader (Biotek) with the software Gen5 (Biotek). Scripts to read and analyze the kinetic data were written and tested with the software DYNAFIT [1] version 4 for Windows (Biokin).
	Other scripts were written and tested with MATLAB 2020a.
Data format	Data from the Selwyn tests are available as Microsoft Excel files where the columns corresponding to Product concentrations and to Enzyme concentration times Time are clearly identified.
	Data from reaction progress curves are available as .txt files where the first column contains the time (in seconds) and the second column contains the corresponding substrate concentrations (in micromolar).
	Initial rates are available as a .txt file where the first column contains the concentrations of acetoacetyl-CoA (in micromolar) and the second column contains the initial rates (in micromole of product/micromole of enzyme/second).
	Data from biomass composition is provided as a Microsoft Excel file.
Parameters for data collection	Kinetic data were recorded at 30 °C. Continuous cell cultures were studied at 37 °C. Further details are explained in the section Experimental Design, Materials and Methods.
Description of data collection	Kinetic data were obtained by spectrophotometry in a plate reader equipped with monochromator, temperature control and a built-in software controlled by the user through the software Gen5. Data from continuous cultures were obtained by the integration of data obtained by different means. More details in the section Experimental Design, Materials and Methods.
Data source location	Institution: Department of Biotechnology, Delft University of Technology
	City/Town/Region: Delft, Zuid Holland
	Country: Netherlands
Data accessibility	Repository name:
	NADH-driven polyhydroxybutyrate accumulation in E. coli dataset 2
	Data identification number: 10.17632/954dxdncrv.1
	Direct URL to data: http://dx.doi.org/10.17632/954dxdncrv.1
	Instructions for accessing these data: Freely available in Mendeley Database.
Related research article	Olavarria K., Carnet A., van Ranselaar J., Quakkelaar C., Cabrera R., Guedes da Silva L., Smids A.L., Villalobos P., van Loosdrecht M.C.M., and Wahl S.A.. An NADH preferring acetoacetyl-CoA reductase is engaged in poly-3-hydroxybutyrate accumulation in E. coli. Journal of Biotechnology. Accepted on October 18, 2020. https://doi.org/10.1016/j.jbiotec.2020.10.022

Value of the Data

• •Open available data from kinetic characterizations of acetoacetyl-CoA reductases are scarce. Here-provided data enable a comparison between the performances using NADH or NADPH. On the other hand, the vast majority of the available PHB accumulation data were obtained in batch. Here we show PHB accumulation rates obtained with continuous cultures, using sucrose as the sole carbon source, and under oxygen limitation.
• •The provided data could be useful for colleagues working in artificial operon design, protein engineering, enzyme kinetics, genetic modifications, cell factory design, bioreactor operation and strain physiological characterization.
• •The provided data and scripts enable the reproduction of the results reported in the main manuscript linked to this article. Moreover, they also enable to explore different outcomes if the input data is different. For example, NAD(P)(H) concentration ranges, enzyme concentration/activity, kinetic parameters, bioenergetic parameters or biomass composition can be changed.
• •Input data and scripts are open and freely available. We provided scripts to perform kinetic parameter estimations, kinetic model discrimination, estimation of cofactor preference, calculation of flux capacity, data reconciliation, elaboration of in silico metabolic models considering plasmid and protein burden. Moreover, we provided DNA sequence maps from different plasmids.

1. Data Description

Kinetic data of reactions catalyzed by two acetoacetyl-CoA reductases are presented. One of these enzymes was obtained from a Candidatus Accumulibacter phosphatis-enriched mix culture (AAR^CAp). The other enzyme, AAR^Chimera, was derived from the acetoacetyl-CoA reductases from Cupriavidus necator (AAR^Cn): the original residues N37-S38-P39-R40-R41 from AAR^Cn were replaced by the residues E37-F38-D39-K40-P41 from AAR^CAp.

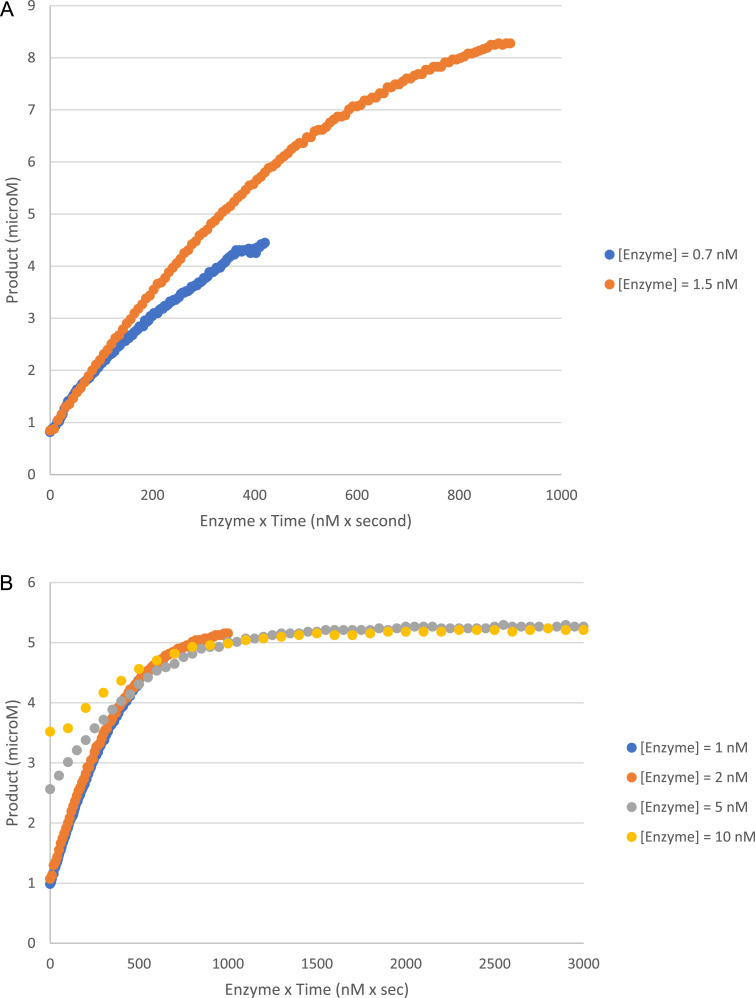
The online freely available Mendeley Data repository “NADH-driven polyhydroxybutyrate accumulation in E. coli dataset 2″ contains the folder “Enzyme Kinetics data”. Inside that folder, it is possible to find the data and conditions from two enzyme stability assays (Selwyn test), performed with AAR^CAp (Fig. 1).

Fig. 1.

Selwyn plots of reactions catalyzed by AAR^CAp. Two experiments were performed with different concentration of NADH (A: 10 mM; B: 5 mM). In both experiments, the reaction buffer was 50 mM Tris (pH 8), 5 mM MgCl₂, 5 mM NaCl. Temperature was set at 30 °C. Initial acetoacetyl-CoA concentration was 100 mM in both experiments.

Inside the folder “Enzyme kinetics data”, it is also possible to find the folder “Data and analysis in DYNAFIT”, which contains the following folders:

• (1)data_AARCAp_varying_AcAcCoA_NADH
• (2)data_AARCAp_varying_AcAcCoA_NADPH
• (3)data_AARCAp_varying_NADH
• (4)data_AARCAp_varying_NADPH
• (5)data_AARChimera_varying_NADH
• (6)data_AARChimera_varying_NADPH

These folder contains “.txt” files with data from kinetic experiments.

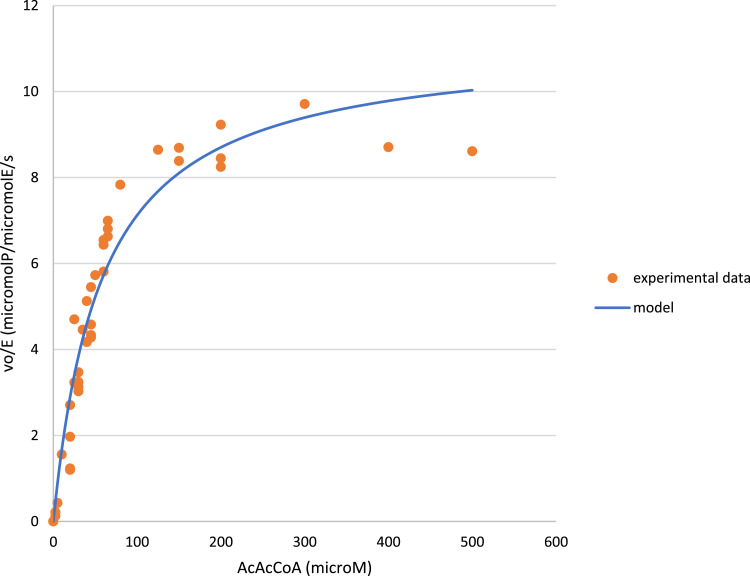
Inside the folder named “data_AARCAp_varying_AcAcCoA_NADH”, it is possible to find the file “data.txt”. This file contains initial rates of reactions catalyzed by AAR^CAp, at different concentrations of acetoacetyl-CoA, and NADH concentration fixed at 300 μM. Data from this experiment are arranged, in the file “data.txt”, in two columns. The first column has the assayed acetoacetyl-CoA concentrations (in micromolar) and the second column has the measured initial rates (in micromol of product/ micromol of enzyme/ second) (Fig. 2).

Fig. 2.

Specific initial rates of reactions catalyzed by AAR^CAp at different concentrations of acetoacetyl-CoA. Concentration of the cofactor NADH was fixed at 300 mM. The reaction buffer was 50 mM Tris (pH 8), 5 mM MgCl₂, 5 mM NaCl. Temperature was set at 30 °C. Best fit curve was obtained with a simple Michaelian model.

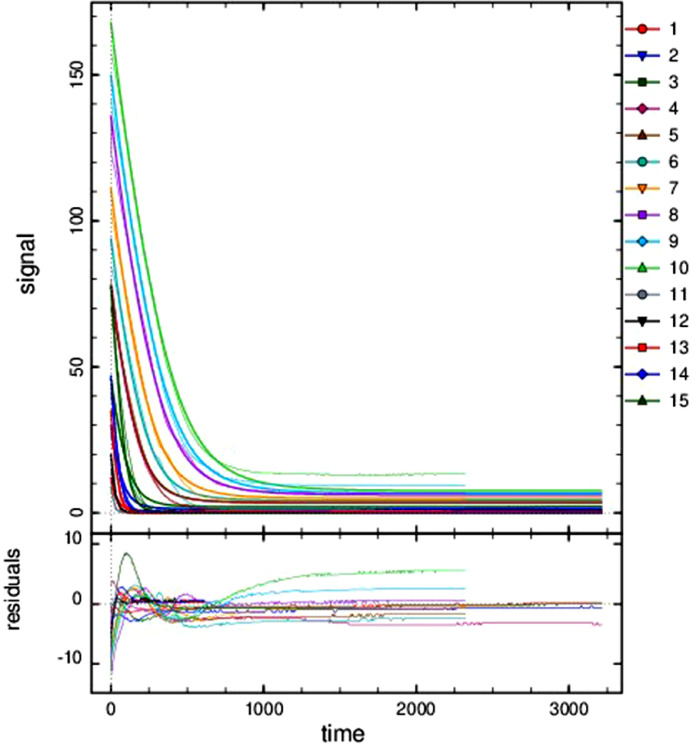
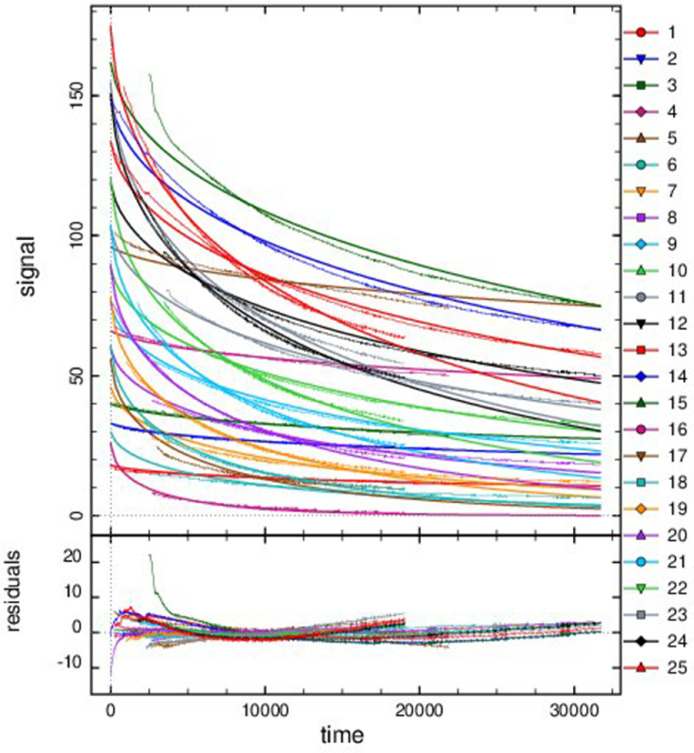
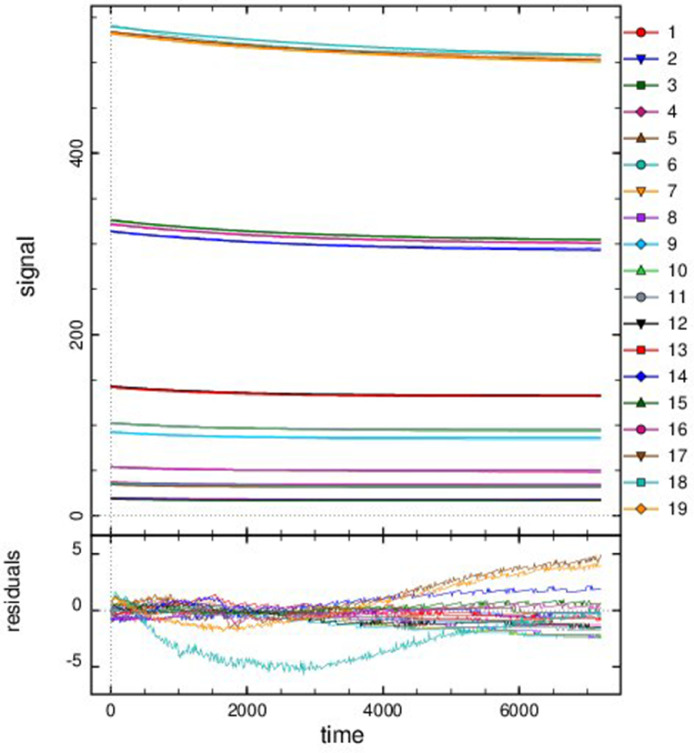
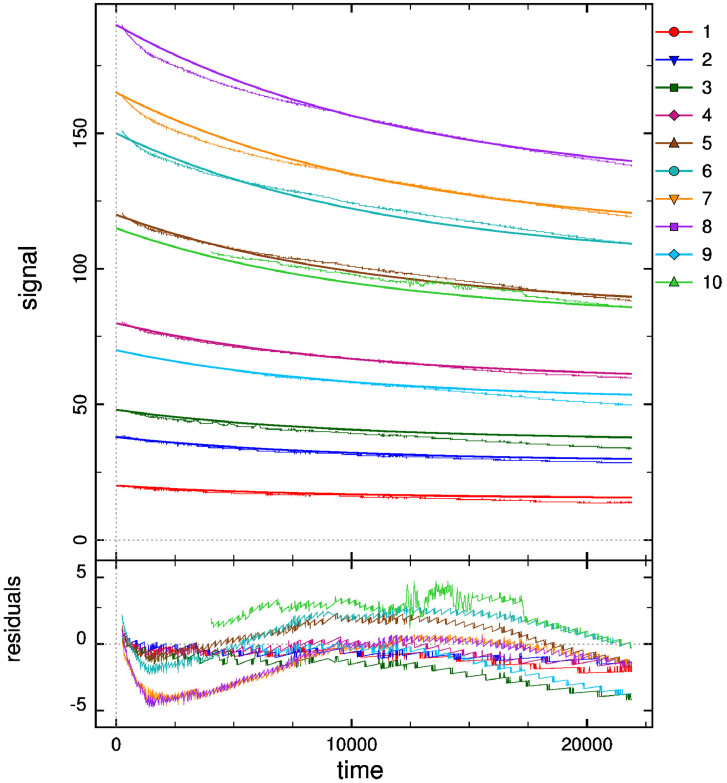
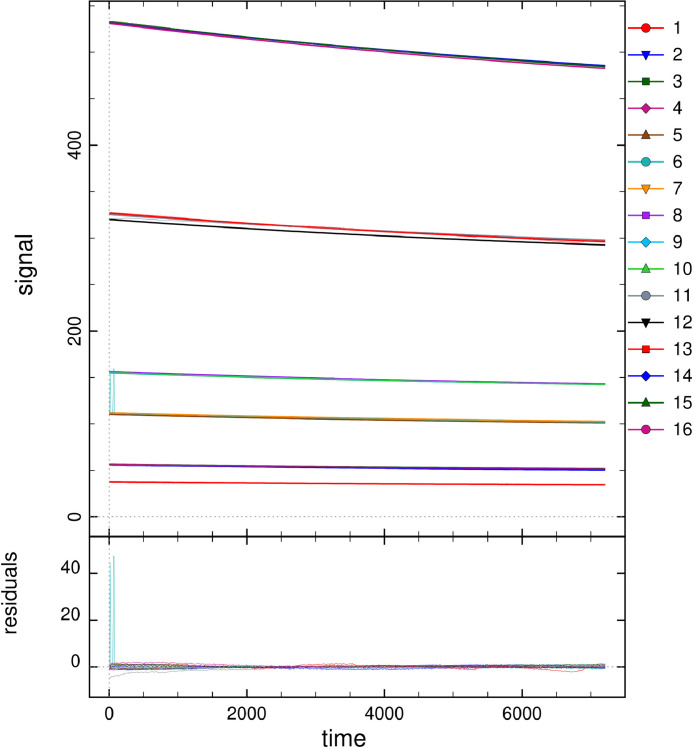
For the other five data folders inside the folder “Data and analysis in DYNAFIT”, groups of reaction progress curves are reported. Inside these groups, individual reaction progress curves were reported in separated “.txt” files. Experimental data of reaction progress curves were arranged in two columns. One column has the time (in seconds) and the second column has the varying substrate/cofactor concentration (in micromolar). For each reaction progress curve, the corresponding initial cofactor/substrate and enzyme concentrations are reported in the corresponding “.rtf” file, placed in the same folder “Enzyme kinetics data”. These files with the conditions of each assay were named with the format “conditions_XXXXX.rtf”. These progress curves were recorded for reactions catalyzed by AAR^CAp and AAR^Chimera. The substrate, cofactor and enzyme concentrations are indicated in each case (Figs. 3–7).The model that best explain each dataset is also indicated in each case. DYNAFIT scripts to analyze the kinetic data are also available in the folder “Enzyme kinetics data”.

Fig. 4.

Progress curves of reactions catalyzed by AAR^CAp at different NADH concentrations. The acetoacetyl-CoA concentration was fixed at 400 mM. Time scale is in seconds. The thick lines represent the global fitting, while thinner lines represent the experimental data. Best fit curves were obtained with a competitive product inhibition model. The initial concentrations of NADH and enzyme were: (1) NADH = 12 mM, Enzyme = 0.05 mM. (2) NADH = 30 mM, Enzyme = 0.05 mM. (3) NADH = 46 mM, Enzyme = 0.05 mM. (4) NADH = 77 mM, Enzyme = 0.05 mM. (5) NADH = 78 mM, Enzyme = 0.05 mM. (6) NADH = 94 mM, Enzyme = 0.05 mM. (7) NADH = 111 mM, Enzyme = 0.05 mM. (8) NADH = 136 mM, Enzyme = 0.05 mM. (9) NADH = 150 mM, Enzyme = 0.05 mM. (10) NADH = 168 mM, Enzyme = 0.05 mM. (11) NADH = 9 mM, Enzyme = 0.1 mM. (12) NADH = 20 mM, Enzyme = 0.1mM. (13) NADH = 35 mM, Enzyme = 0.1 mM. (14) NADH = 47 mM, Enzyme = 0.1 mM. (15) NADH = 78 mM, Enzyme = 0.1 mM.

Fig. 5.

Progress curves of reactions catalyzed by AAR^CAp at different NADPH concentrations. The acetoacetyl-CoA concentration was fixed at 400 mM. Time scale is in seconds. The thick lines represent the global fitting, while thinner lines represent the experimental data. Best fit curves were obtained with a competitive product inhibition model. The initial concentrations of NADPH and enzyme were: (1) NADPH = 18 mM, Enzyme = 0.05 mM. (2) NADPH = 33 mM, Enzyme = 0.05 mM. (3) NADPH = 40 mM, Enzyme = 0.05 mM. (4) NADPH = 66 mM, Enzyme = 0.05 mM. (5) NADPH = 96 mM, Enzyme = 0.05 mM. (6) NADPH = 30 mM, Enzyme = 0.5 mM. (7) NADPH = 46 mM, Enzyme = 0.5 mM. (8) NADPH = 60 mM, Enzyme = 0.5 mM. (9) NADPH = 76 mM, Enzyme = 0.5 mM. (10) NADPH = 89 mM, Enzyme = 0.5 mM. (11) NADPH = 103 mM, Enzyme = 0.5 mM. (12) NADPH = 119 mM, Enzyme = 0.5 mM. (13) NADPH = 134 mM, Enzyme = 0.5 mM. (14) NADPH = 149 mM, Enzyme = 0.5 mM. (15) NADPH = 162 mM, Enzyme = 0.5 mM. (16) NADPH = 26 mM, Enzyme = 1.5 mM. (17) NADPH = 56 mM, Enzyme = 1.5 mM. (18) NADPH = 61 mM, Enzyme = 1.5 mM. (19) NADPH = 78 mM, Enzyme = 1.5 mM. (20) NADPH = 90 mM, Enzyme = 1.5 mM. (21) NADPH = 104 mM, Enzyme = 1.5 mM. (22) NADPH = 121 mM, Enzyme = 1.5 mM. (23) NADPH = 155 mM, Enzyme = 1.5 mM. (24) NADPH = 151 mM, Enzyme = 1.5 mM. (25) NADPH = 175 mM, Enzyme = 1.5 mM.

Fig. 6.

Progress curves of reactions catalyzed by AAR^Chimera at different NADH concentrations. The acetoacetyl-CoA concentration was fixed at 400 mM. Time scale is in seconds. The thick lines represent the global fitting, while thinner lines represent the experimental data. Best fit curves were obtained with a simple Michaelian model. The initial concentrations of NADH and enzyme were: (1) NADH = 19.6 mM, Enzyme = 0.002 mM. (2) NADH = 19.4 mM, Enzyme = 0.002 mM. (3) NADH = 18.6 mM, Enzyme = 0.002 mM. (4) NADH = 37.2 mM, Enzyme = 0.002 mM. (5) NADH = 34.6 mM, Enzyme = 0.002 mM. (6) NADH = 36.1 mM, Enzyme = 0.002 mM. (7) NADH = 54 mM, Enzyme = 0.002 mM. (8) NADH = 54 mM, Enzyme = 0.002 mM. (9) NADH = 92.5 mM, Enzyme = 0.002 mM. (10) NADH = 102.5 mM, Enzyme = 0.002 mM. (11) NADH = 102.5 mM, Enzyme = 0.002 mM. (12) NADH = 143 mM, Enzyme = 0.002 mM. (13) NADH = 142 mM, Enzyme = 0.002 mM. (14) NADH = 314 mM, Enzyme = 0.002 mM. (15) NADH = 326 mM, Enzyme = 0.002 mM. (16) NADH = 322 mM, Enzyme = 0.002 mM. (17) NADH = 534 mM, Enzyme = 0.002 mM. (18) NADH = 540 mM, Enzyme = 0.002 mM. (19) NADH = 532 mM, Enzyme = 0.002 mM.

Fig. 3.

Progress curves of reactions catalyzed by AAR^CAp at different acetoacetyl-CoA concentrations. The NADPH concentration was fixed at 300 mM. Time scale is in seconds. The thick lines represent the global fitting, while thinner lines represent the experimental data. Best fit curves were obtained with a simple Michaelian model. The initial concentrations of acetoacetyl-CoA and enzyme were: (1) AcAcCoA = 20 mM, Enzyme = 0.07 mM. (2) AcAcCoA = 38 mM, Enzyme = 0.07 mM. (3) AcAcCoA = 48 mM, Enzyme = 0.07 mM. (4) AcAcCoA = 80 mM, Enzyme = 0.08 mM. (5) AcAcCoA = 120 mM, Enzyme = 0.09 mM. (6) AcAcCoA = 150 mM, Enzyme = 0.1 mM. (7) AcAcCoA = 165 mM, Enzyme = 0.1 mM. (8) AcAcCoA = 190 mM, Enzyme = 0.1 mM. (9) AcAcCoA = 70 mM, Enzyme = 0.08 mM. (10) AcAcCoA = 115 mM, Enzyme = 0.09 mM.

Fig. 7.

Progress curves of reaction catalyzed by AAR^Chimera at different NADPH concentrations. The acetoacetyl-CoA concentration was fixed at 400 mM. Time scale is in seconds. The thick lines represent the global fitting, while thinner lines represent the experimental data. Best fit curves were obtained with a simple Michaelian model. The initial concentrations of NADPH and enzyme were: (1) NADPH = 38 mM, Enzyme = 0.0015 mM. (2) NADPH = 56 mM, Enzyme = 0.0018 mM. (3) NADPH = 56 mM, Enzyme = 0.0015 mM. (4) NADPH = 56 mM, Enzyme = 0.0015 mM. (5) NADPH = 110 mM, Enzyme = 0.0015 mM. (6) NADPH = 112 mM, Enzyme = 0.0016 mM. (7) NADPH = 112 mM, Enzyme = 0.0015 mM. (8) NADPH = 155 mM, Enzyme = 0.0016 mM. (9) NADPH = 155 mM, Enzyme = 0.0015 mM. (10) NADPH = 155 mM, Enzyme = 0.0015 mM. (11) NADPH = 325 mM, Enzyme = 0.0018 mM. (12) NADPH = 320 mM, Enzyme = 0.0018 mM. (13) NADPH = 327 mM, Enzyme = 0.002 mM. (14) NADPH = 532 mM, Enzyme = 0.0021 mM. (15) NADPH = 533 mM, Enzyme = 0.0022 mM. (16) NADPH = 531 mM, Enzyme = 0.0022 mM.

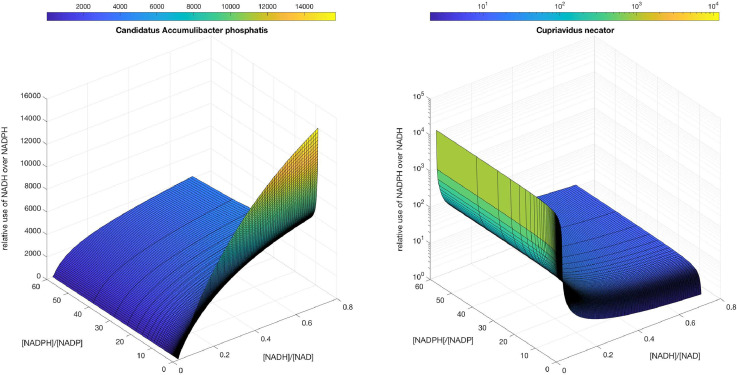
Inside the folder “Enzyme kinetics data”, it is also possible to find a MATLAB script named “Relative_consumption_NADH_NADPH.m”. This script enables to calculate and plot the relative use of NADH and NADPH by two acetoacetyl-CoA reductases, at different NADH/NAD⁺ and NADPH/NADP⁺ ratios. In the available example, it is possible to make these calculations for the reactions catalyzed by AAR^CAp and AAR^Cn (Fig. 8). In that calculation, the input data are:

• -the equilibrium constant of the reaction catalyzed by the acetoacetyl-CoA reductases (Keq = 92)
• -the assumed concentrations of acetoacetyl-CoA (AcAcCoA=22) and 3-hydroxybutyryl-CoA (HBCoA=60) in micromolar.
• -the total sums of NAD⁺ plus NADH concentrations (moiety_size_NAD) and NADP⁺ plus NADPH (moiety_size_NADP), in micromolar.
• -the more oxidized and the more reduced values for the NADH/NAD⁺ and NADPH/NADP⁺ concentration ratios (NADH_over_NAD_ratio_oxidized, NADH_over_NAD_ratio_reduced, NADPH_over_NADP_ratio_oxidized and NADPH_over_NADP_ratio_reduced).
• -The main kinetic parameters of the enzymes under comparison.

Fig. 8.

Relative use of NADH over NADPH (or vice versa) by the acetoacetyl-CoA reductases from Ca. A. phosphatis and C. necator.

For the ratios shown in Fig. 8, values of moiety_size_NAD = 1570 [2]; NADH_over_NAD_ratio_oxidized = 0.03 [3], NADH_over_NAD_ratio_reduced = 0.71 [3], moiety_size_NADP = 122 [2] and the extreme values of NADPH_over_NADP_ratio_oxidized = 0.32 [4] and NADPH_over_NADP_ratio_reduced ratios = 60 [2] were used. Regarding the kinetic parameters, they were obtained with the data contained in the folder “Enzyme kinetics data” or obtained from literature. The source of each kinetic parameter is declared in the script.

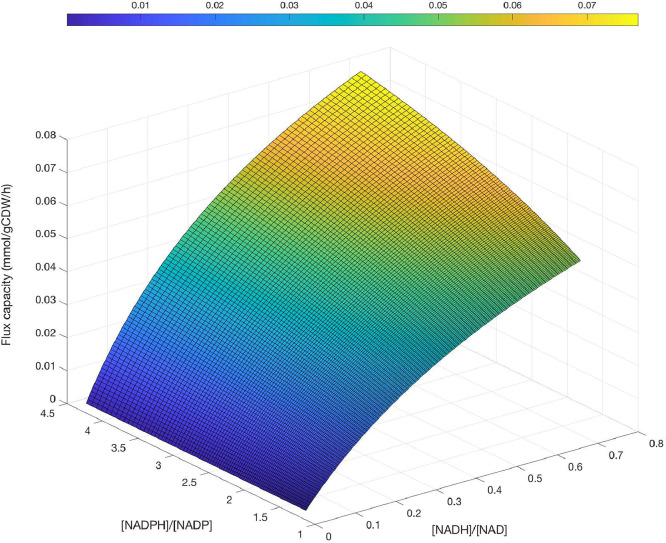
Finally, in the folder “Enzyme Kinetics data”, it is possible to find a MATLAB script to calculate the flux capacity of the reaction catalyzed by AAR^CAp. Clearly, the same calculation can be applied for another enzyme, provided the corresponding kinetic data be employed as input. This script uses the same input employed to calculate the relative use of NADH and NADPH, plus an estimate of the specific acetoacetyl-CoA reductase activity registered/expected in cells expressing this enzyme. In the specific case shown in the MATLAB script, a specific acetoacetyl-CoA reductase activity of 11.3 nmol/min/mg was employed as input. Convenient conversion factors were introduced in the calculations to express the flux capacity in units of mmol/gCDW/h (Fig. 9).

Fig. 9.

Flux capacity of the reaction catalyzed by AAR^CAp at different NADH/NAD+ and NADPH/NADP⁺ concentration ratios.

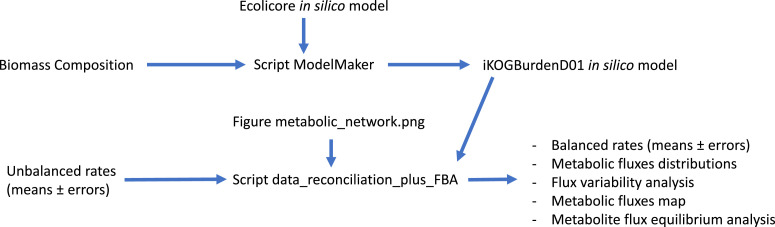
Beyond the kinetic analyses, in the same Mendeley Data repository “NADH-driven polyhydroxybutyrate accumulation in E. coli dataset 2″ it is possible to find a folder named “Fermentations”. In that folder, there are different files required to analyze experimental data from a continuous growth of an engineered E. coli strain (((F– λ– ilvG– rfb-50 rph-1 (DE3) ΔadhE ΔadhP ΔldhA Δpta ΔmhpF)) transformed with the plasmid pCOLA-phaCAphaB-cscABK). That engineered strain grew with a dilution rate D = 0.1 h ^− 1, under oxygen limitation, and using sucrose as the sole carbon source. Details about how the input information was obtained are described in the section Experimental Design, Materials and Methods. A workflow explaining the interactions among the files present in the folder “Fermentations” is presented in Fig. 10.

Fig. 10.

Workflow to reproduce the analysis of the continuous cultures. As output, it will be possible to calculate balanced specific rates, metabolic fluxes distributions, flux variability analysis, generate a metabolic fluxes map and calculate the fluxes contributing to the maintenance of the steady-state of a given metabolite.

Starting with an estimation of the biomass composition (Table 1) and the in silico model “Ecolicore.mat” (provided in the repository and also available at the BiGG database, University of California San Diego), the MATLAB script “ModelMaker.m” generates a new in silico model (iKOGBurdenD01.mat) with a biomass formation “reaction” including the recombinant DNA and protein burdens (the obtained in silico model can be found in the Mendeley Data repository). To run this MATLAB script, the freely available COBRA Toolbox for MATLAB [5] version 2.0 or higher, has to be previously installed.

Table 1.

Biomass composition of the engineered strain after considering plasmid and heterologous protein contributions. Relative elemental composition for each component is below the columns identified with the symbol of the elements carbon, hydrogen, nitrogen, oxygen, sulfur and phosphorous. After considering recombinant DNA and protein burdens, 1 carbon-mol of biomass (CmolX) has a “molecular” weight of 23.1840 gCDW/CmolX, and its reduction degree is γ=4.2920.

Biomolecules	Percent of weight (%)	C	H	N	O	S	P	mol per CmolX
Protein	64.68	1.000	1.580	0.288	0.309	0.009	0.00	0.656327
DNA	1.04	1.00	1.05	0.39	0.62	0.00	0.10	0.007682
Ethanolamine	2.59	2.00	8.00	1.00	1.00	0.00	0.00	0.009683
Glycerol	4.31	3.00	8.00	0.00	3.00	0.00	0.00	0.010852
Glycogen	0.59	6.00	10.00	0.00	5.00	0.00	0.00	0.000842
Hexadecanoate	2.96	16.00	31.00	0.00	2.00	0.00	0.00	0.002691
Hexadecenoate	2.28	16.00	29.00	0.00	2.00	0.00	0.00	0.002086
Lipopolysaccharide	0.81	171.00	297.00	4.00	88.00	0.00	2.00	0.000048
Octadecenoate	1.65	18.00	33.00	0.00	2.00	0.00	0.00	0.001362
Peptidoglycan	0.59	40.00	62.00	8.00	21.00	0.00	0.00	0.000138
Putrescine	0.28	4.00	14.00	2.00	0.00	0.00	0.00	0.000709
RNA	6.89	1.00	1.02	0.41	0.73	0.00	0.10	0.047476
Spermidine	0.09	7.00	22.00	3.00	0.00	0.00	0.00	0.000149
Heterologous proteins	5.02	1.00	1.58	0.29	0.31	0.01	0.00	0.050939
Plasmid	0.13	1.00	1.05	0.39	0.62	0.00	0.10	0.000946
Ash	6.10

Once the model iKOGBurdenD01 is constructed, the script “data_reconciliation_plus_FBA.m”, which includes the unbalanced rates (Table 2) manually introduced, can perform a flux balance analysis and generates different output files. COBRA Toolbox is also required to run this script. However, we are also including in the repository a script to perform data reconciliation without the participation of the COBRA Toolbox (data_reconciliation_only). Different output options are available in the script “data_reconciliation_plus_FBA.m”: Balanced (reconciled) rates with their associated errors; optimum, maximum and minimum feasible fluxes (Table 3); a visual representation of the metabolic fluxes and the calculation of the fluxes contributing to the formation and consumption of any given metabolite included in the in silico model. Clearly, under steady-state, the sum of the fluxes contributing to the formation of a given metabolite must be equal to the sum of the fluxes consuming that metabolite.

Table 2.

Specific unbalanced and reconciled rates for the engineered strain growing in a continuous culture, under oxygen limitation, using sucrose as the sole carbon source.

Steady-state 1
	Raw data			unbalanced means	unbalanced SD	renconciled means	reconciled SD
qx (h−1)	0.0978	0.0952	0.1055	0.100	0.005	0.1098	0.0041
qsucrose (mmol/gCDW/h)	−0.718	−0.6857	−0.6501	−0.685	0.0343	−0.7906	0.0155
qacetate (mmol/gCDW/h)	0.0074	0.0073	0.0042	0.0063	0.002	0.0062	0.002
qlactate (mmol/gCDW/h)	0.0454	0.0564	0.049	0.0503	0.006	0.0495	0.006
qsuccinate (mmol/gCDW/h)	0.0467	0.0391	0.0381	0.0413	0.005	0.0377	0.005
qCO2 (mmol/gCDW/h)	4.57	4.616	4.619	4.600	0.027	4.4285	0.0183
qO2 (mmol/gCDW/h)	−3.97	−3.996	−4.011	−4.000	0.021	−4.1004	0.0174
qPHB (mmol/gCDW/h)	0.0022	0.00219	0.0025	0.0023	0.0001	0.0023	0.0001
qformate (mmol/gCDW/h)	b.d.l.	b.d.l.	b.d.l.	0	0	0	0
Steady-state 2
	Raw data			unbalanced means	unbalanced SD	renconciled means	reconciled SD
qx (h−1)	0.1057	0.0977	0.096	0.100	0.005	0.0939	0.0041
qsucrose (mmol/gCDW/h)	−0.8191	−0.8148	−0.8231	−0.819	0.041	−0.6675	0.0163
qacetate (mmol/gCDW/h)	0.1622	0.207	0.1992	0.1893	0.024	0.198	0.0239
qlactate (mmol/gCDW/h)	0.00386	0.00425	0.00471	0.0043	0.0004	0.0043	0.0004
qsuccinate (mmol/gCDW/h)	0.0247	0.01715	0.01904	0.0203	0.004	0.0222	0.004
qCO2 (mmol/gCDW/h)	2.971	2.919	2.961	2.95	0.03	3.1196	0.0158
qO2 (mmol/gCDW/h)	−2.867	−2.846	−2.855	−2.86	0.011	−2.8381	0.0105
qPHB (mmol/gCDW/h)	0.0714	0.06834	0.06507	0.0683	0.0034	0.0676	0.0034
qformate (mmol/gCDW/h)	0.059	0.0761	0.0662	0.0673	0.008	0.0736	0.0079

b.d.l.: below detection level.

Table 3.

Metabolic fluxes distributions for the engineered strain during the two studied steady-states. The feasible minimal and maximal fluxes for each reaction is also reported. Metabolites labelled with the symbol [e] are considered extracellular while the symbol [c] signal the intracellular metabolites.

		Steady-state 1			Steady-state 2
Reaction name	Reaction	Optimal flux (mol/CmolX/h)	Minimum flux (mol/CmolX/h)	Maximum flux (mol/CmolX/h)	Optimal flux (mol/CmolX/h)	Minimum flux (mol/CmolX/h)	Maximum flux (mol/CmolX/h)
EX_ac(e)	ac[e] ->	0.0002	0.0002	0.0002	0.0051	0.0051	0.0051
EX_acald(e)	acald[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_akg(e)	akg[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_co2(e)	co2[e] <=>	0.1028	0.1028	0.1028	0.0721	0.0721	0.0721
EX_etoh(e)	etoh[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_for(e)	for[e] ->	0.0000	0.0000	0.0000	0.0019	0.0019	0.0019
EX_fru(e)	fru[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_fum(e)	fum[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_glc(e)	glc-D[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_gln_L(e)	gln-L[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_glu_L(e)	glu-L[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_h(e)	h[e] <=>	0.0282	0.0282	0.0282	0.0291	0.0291	0.0291
EX_h2o(e)	h2o[e] <=>	0.1442	0.1442	0.1442	0.1082	0.1082	0.1082
EX_lac_D(e)	lac-D[e] ->	0.0013	0.0013	0.0013	0.0001	0.0001	0.0001
EX_mal_L(e)	mal-L[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_nh4(e)	nh4[e] <=>	−0.0266	−0.0266	−0.0266	−0.0223	−0.0223	−0.0223
EX_o2(e)	o2[e] <=>	−0.0955	−0.0955	−0.0955	−0.0660	−0.0660	−0.0660
EX_pi(e)	pi[e] <=>	−0.0007	−0.0007	−0.0007	−0.0006	−0.0006	−0.0006
EX_pyr(e)	pyr[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_succ(e)	succ[e] ->	0.0010	0.0008	0.0010	0.0006	0.0004	0.0006
EX_so4[e]	so4[e] <=>	−0.0007	−0.0007	−0.0007	−0.0006	−0.0006	−0.0006
EX_glyc[e]	glyc[e] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
GlucosePTS	glc-D[e] + pep[c] -> g6p[c] + pyr[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
PGI	g6p[c] <=> f6p[c]	0.0114	0.0114	0.0114	0.0055	0.0055	0.0055
PFK	f6p[c] + atp[c] -> adp[c] + fdp[c] + h[c]	0.0313	0.0313	0.0313	0.0249	0.0249	0.0249
ALD	fdp[c] <=> dhap[c] + g3p[c]	0.0313	0.0313	0.0313	0.0249	0.0249	0.0249
TPI	dhap[c] <=> g3p[c]	0.0301	0.0301	0.0301	0.0239	0.0239	0.0239
GAPDH	g3p[c] + nad[c] + pi[c] <=> h[c] + 13dpg[c] + nadh[c]	0.0636	0.0636	0.0636	0.0521	0.0521	0.0521
PGK	adp[c] + 13dpg[c] <=> atp[c] + 3pg[c]	0.0636	0.0636	0.0636	0.0521	0.0521	0.0521
PGlycerateM	3pg[c] <=> 2pg[c]	0.0575	0.0575	0.0575	0.0469	0.0469	0.0469
ENO	2pg[c] <=> pep[c] + h2o[c]	0.0575	0.0575	0.0575	0.0469	0.0469	0.0469
PYK	pep[c] + adp[c] + h[c] -> pyr[c] + atp[c]	0.0468	0.0468	0.0469	0.0383	0.0383	0.0383
PDH	pyr[c] + nad[c] + coa[c] -> nadh[c] + accoa[c] + co2[c]	0.0380	0.0380	0.0380	0.0316	0.0316	0.0316
AKGDH	nad[c] + coa[c] + akg[c] -> nadh[c] + co2[c] + succoa[c]	0.0273	0.0273	0.0273	0.0147	0.0147	0.0147
Aconitase	cit[c] <=> icit[c]	0.0309	0.0309	0.0309	0.0177	0.0177	0.0177
CS	h2o[c] + accoa[c] + oaa[c] -> h[c] + coa[c] + cit[c]	0.0309	0.0309	0.0309	0.0177	0.0177	0.0177
FUM	h2o[c] + fum[c] <=> mal-L[c]	0.0280	0.0280	0.0280	0.0155	0.0155	0.0155
ICDH	icit[c] + nadp[c] -> co2[c] + akg[c] + nadph[c]	0.0309	0.0309	0.0309	0.0177	0.0177	0.0177
MDH	nad[c] + mal-L[c] <=> h[c] + nadh[c] + oaa[c]	0.0280	0.0280	0.0280	0.0155	0.0155	0.0155
SUCDH	fadh[c] + succ[c] -> fum[c] + fadh2[c]	0.0263	0.0263	1000	0.0141	0.0141	1000
SCS	adp[c] + pi[c] + succoa[c] -> atp[c] + coa[c] + succ[c]	0.0259	0.0259	0.0259	0.0135	0.0135	0.0135
DHFRd	h[c] + nadph[c] + dhf[c] -> nadp[c] + thf[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
PPihydrolase	h2o[c] + ppi[c] -> h[c] + 2 pi[c]	0.0119	0.0119	0.0119	0.0088	0.0088	0.0088
PEPC	pep[c] + h2o[c] + co2[c] -> h[c] + pi[c] + oaa[c]	0.0081	0.0081	0.0081	0.0065	0.0065	0.0065
G6PDH	g6p[c] + nadp[c] -> h[c] + nadph[c] + 6pgl[c]	0.0065	0.0065	0.0065	0.0096	0.0096	0.0096
6PGlactonase	h2o[c] + 6pgl[c] -> h[c] + 6pgc[c]	0.0065	0.0065	0.0065	0.0096	0.0096	0.0096
GND	nadp[c] + 6pgc[c] -> co2[c] + nadph[c] + ru5p-D[c]	0.0065	0.0065	0.0065	0.0096	0.0096	0.0096
RibIso	r5p[c] <=> ru5p-D[c]	−0.0045	−0.0045	−0.0045	−0.0051	−0.0051	−0.0051
RibEpi	ru5p-D[c] <=> xu5p-D[c]	0.0020	0.0020	0.0020	0.0044	0.0044	0.0044
TALA	g3p[c] + s7p[c] <=> f6p[c] + e4p[c]	0.0016	0.0016	0.0016	0.0027	0.0027	0.0027
TKT1	r5p[c] + xu5p-D[c] <=> g3p[c] + s7p[c]	0.0016	0.0016	0.0016	0.0027	0.0027	0.0027
TKT2	xu5p-D[c] + e4p[c] <=> f6p[c] + g3p[c]	0.0004	0.0004	0.0004	0.0017	0.0017	0.0017
ATPase	4 h[e] + adp[c] + pi[c] <=> atp[c] + 3 h[c] + h2o[c]	0.2528	0.2528	0.2528	0.1769	0.1769	0.1769
ETC_FADH2	fadh2[c] + q8[c] -> fadh[c] + q8h2[c]	0.0263	0.0263	1000	0.0141	0.0141	1000
ETOH	2 h[c] + 2 nadh[c] + accoa[c] <=> 2 nad[c] + coa[c] + etoh[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
ACK	adp[c] + actp[c] -> atp[c] + ac[c]	0.0000	0.0000	0.0000	0.0037	0.0037	0.0037
LDH	pyr[c] + h[c] + nadh[c] <=> nad[c] + lac-D[c]	0.0013	0.0013	0.0013	0.0001	0.0001	0.0001
PTA	pi[c] + accoa[c] <=> coa[c] + actp[c]	0.0000	0.0000	0.0000	0.0037	0.0037	0.0037
PGlucoseM	g1p[c] <=> g6p[c]	−0.0001	−0.0001	−0.0001	−0.0001	−0.0001	−0.0001
CarbonicAnhydrase	h2o[c] + co2[c] <=> h[c] + hco3[c]	0.0066	0.0066	0.0066	0.0055	0.0055	0.0055
ATPM	atp[c] + h2o[c] -> adp[c] + h[c] + pi[c]	0.1572	0.0750	0.1572	0.0919	0.0750	0.0919
GlycerolKinase	atp[c] + glyc[c] -> adp[c] + h[c] + glyc3p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
FBPase	fdp[c] + h2o[c] -> f6p[c] + pi[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
PEPCK	atp[c] + oaa[c] -> pep[c] + adp[c] + co2[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
ICL	icit[c] -> succ[c] + glx[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
MALS	h2o[c] + accoa[c] + glx[c] -> h[c] + coa[c] + mal-L[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
pntAB	2 h[e] + nadh[c] + nadp[c] -> 2 h[c] + nad[c] + nadph[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
UdhA	nad[c] + nadph[c] -> nadh[c] + nadp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
ED1	6pgc[c] -> h2o[c] + KDPG[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
ED2	KDPG[c] -> pyr[c] + g3p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
FUMDHq8	fum[c] + q8h2[c] -> succ[c] + q8[c]	0.0000	0.0000	1000.0	0.0000	0.0000	1000
PFL	pyr[c] + coa[c] -> accoa[c] + for[c]	0.0000	0.0000	0.0000	0.0002	0.0002	0.0002
Hydrogenase	h[c] + for[c] -> co2[c] + H2[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_H2[c]	H2[c] ->	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
DHAPred	h[c] + dhap[c] + nadh[c] -> nad[c] + glyc3p[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
DHAPred2	h[c] + dhap[c] + nadph[c] -> nadp[c] + glyc3p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r49	0.333333 atp[c] + 0.666667 h[c] + 0.333333 h2o[c] + ac[c] -> ac[e] + h[e] + 0.333333 adp[c] + 0.333333 pi[c]	0.0002	0.0002	0.0002	0.0051	0.0051	0.0051
r53	0.333333 atp[c] + 0.666667 h[c] + 0.333333 h2o[c] + lac-D[c] -> h[e] + lac-D[e] + 0.333333 adp[c] + 0.333333 pi[c]	0.0013	0.0013	0.0013	0.0001	0.0001	0.0001
r55	0.333333 atp[c] + 0.666667 h[c] + 0.333333 h2o[c] + for[c] -> for[e] + h[e] + 0.333333 adp[c] + 0.333333 pi[c]	0.0000	0.0000	0.0000	0.0019	0.0019	0.0019
r60	0.333333 atp[c] + 0.666667 h[c] + 0.333333 h2o[c] + succ[c] -> h[e] + succ[e] + 0.333333 adp[c] + 0.333333 pi[c]	0.0010	0.0010	0.0010	0.0006	0.0006	0.0006
r51	co2[c] -> co2[e]	0.1028	0.1028	0.1028	0.0721	0.0721	0.0721
r50	nh4[e] -> nh4[c]	0.0266	0.0266	0.0266	0.0223	0.0223	0.0223
r54	etoh[c] -> etoh[e]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r11	atp[c] + h[c] + g1p[c] -> ppi[c] + adpglc[c]	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
r12	adpglc[c] -> adp[c] + h[c] + glycogen[c]	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
r37	h[c] + nadph[c] + trdox[c] -> nadp[c] + trdrd[c]	0.0025	0.0025	0.0025	0.0021	0.0021	0.0021
r42	ru5p-D[c] <=> ara5p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r43	2dr5p[c] -> g3p[c] + acald[c]	0.0017	0.0017	0.0017	0.0014	0.0014	0.0014
r46	r1p[c] <=> r5p[c]	−0.0017	−0.0017	−0.0017	−0.0014	−0.0014	−0.0014
r47	2dr1p[c] <=> 2dr5p[c]	0.0017	0.0017	0.0017	0.0014	0.0014	0.0014
r48	acald[e] <=> acald[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r56	glyc[c] <=> glyc[e]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r57	h2o[e] <=> h2o[c]	−0.1442	−0.1442	−0.1442	−0.1082	−0.1082	−0.1082
r58	o2[e] <=> o2[c]	0.0955	0.0955	0.0955	0.0660	0.0660	0.0660
r59	h[e] + pi[e] <=> h[c] + pi[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r61	so4[e] + atp[c] + h2o[c] -> adp[c] + h[c] + pi[c] + so4[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r62	ala-L[c] <=> ala-D[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r63	atp[c] + nh4[c] + asp-L[c] -> h[c] + ppi[c] + amp[c] + asn-L[c]	0.0009	0.0009	0.0009	0.0007	0.0007	0.0007
r64	akg[c] + asp-L[c] <=> oaa[c] + glu-L[c]	−0.0052	−0.0052	−0.0052	−0.0043	−0.0043	−0.0043
r65	akg[c] + ala-L[c] <=> pyr[c] + glu-L[c]	−0.0019	−0.0019	−0.0019	−0.0016	−0.0016	−0.0016
r66	3 h2o[c] + dkmpp[c] -> 6 h[c] + pi[c] + for[c] + 2kmb[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r67	glu-L[c] + 2kmb[c] -> akg[c] + met-L[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r68	5mdru1p[c] -> h2o[c] + dkmpp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r69	atp[c] + 5mtr[c] -> adp[c] + h[c] + 5mdr1p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r70	5mdr1p[c] <=> 5mdru1p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r71	atp[c] + acglu[c] -> adp[c] + acg5p[c]	0.0009	0.0009	0.0009	0.0008	0.0008	0.0008
r72	h2o[c] + acorn[c] -> ac[c] + orn[c]	0.0009	0.0009	0.0009	0.0008	0.0008	0.0008
r73	akg[c] + acorn[c] <=> glu-L[c] + acg5sa[c]	−0.0009	−0.0009	−0.0009	−0.0008	−0.0008	−0.0008
r74	h[c] + amet[c] <=> co2[c] + ametam[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r75	argsuc[c] <=> fum[c] + arg-L[c]	0.0008	0.0008	0.0008	0.0007	0.0007	0.0007
r76	atp[c] + asp-L[c] + citr-L[c] -> h[c] + ppi[c] + amp[c] + argsuc[c]	0.0008	0.0008	0.0008	0.0007	0.0007	0.0007
r77	2 atp[c] + h2o[c] + hco3[c] + gln-L[c] -> 2 adp[c] + 2 h[c] + pi[c] + glu-L[c] + cbp[c]	0.0011	0.0011	0.0011	0.0009	0.0009	0.0009
r78	atp[c] + glu-L[c] -> adp[c] + glu5p[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r79	h[c] + nadph[c] + glu5p[c] -> pi[c] + nadp[c] + glu5sa[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r80	glu5sa[c] -> h[c] + h2o[c] + 1pyr5c[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r81	h2o[c] + 5mta[c] -> 5mtr[c] + ade[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r82	pi[c] + nadp[c] + acg5sa[c] <=> h[c] + nadph[c] + acg5p[c]	−0.0009	−0.0009	−0.0009	−0.0008	−0.0008	−0.0008
r83	accoa[c] + glu-L[c] -> h[c] + coa[c] + acglu[c]	0.0009	0.0009	0.0009	0.0008	0.0008	0.0008
r84	orn[c] + cbp[c] <=> h[c] + pi[c] + citr-L[c]	0.0008	0.0008	0.0008	0.0007	0.0007	0.0007
r85	h[c] + orn[c] -> co2[c] + ptrc[c]	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
r86	2 h[c] + nadph[c] + 1pyr5c[c] -> nadp[c] + pro-L[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r87	ametam[c] + ptrc[c] -> h[c] + 5mta[c] + spmd[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r88	h2o[c] + pap[c] -> pi[c] + amp[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r89	atp[c] + aps[c] -> adp[c] + h[c] + paps[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r90	acser[c] + h2s[c] -> h[c] + ac[c] + cys-L[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r91	trdrd[c] + paps[c] -> 2 h[c] + trdox[c] + pap[c] + so3[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r92	accoa[c] + ser-L[c] <=> coa[c] + acser[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r93	atp[c] + h2o[c] + so4[c] + gtp[c] -> pi[c] + ppi[c] + aps[c] + gdp[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r94	5 h[c] + 3 nadph[c] + so3[c] -> 3 h2o[c] + 3 nadp[c] + h2s[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r95	h[c] + akg[c] + nadph[c] + nh4[c] -> h2o[c] + nadp[c] + glu-L[c]	0.0231	0.0231	0.0231	0.0194	0.0194	0.0194
r96	atp[c] + nh4[c] + glu-L[c] -> adp[c] + h[c] + pi[c] + gln-L[c]	0.0037	0.0037	0.0037	0.0031	0.0031	0.0031
r97	thf[c] + ser-L[c] -> h2o[c] + gly[c] + mlthf[c]	0.0035	0.0035	0.0035	0.0029	0.0029	0.0029
r98	nad[c] + 3pg[c] -> h[c] + nadh[c] + 3php[c]	0.0061	0.0061	0.0061	0.0052	0.0052	0.0052
r99	h2o[c] + pser-L[c] -> pi[c] + ser-L[c]	0.0061	0.0061	0.0061	0.0052	0.0052	0.0052
r100	glu-L[c] + 3php[c] -> akg[c] + pser-L[c]	0.0061	0.0061	0.0061	0.0052	0.0052	0.0052
r101	prfp[c] -> prlp[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r102	atp[c] + prpp[c] -> ppi[c] + prbatp[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r103	2 nad[c] + h2o[c] + histd[c] -> 3 h[c] + 2 nadh[c] + his-L[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r104	h2o[c] + hisp[c] -> pi[c] + histd[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r105	glu-L[c] + imacp[c] -> akg[c] + hisp[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r106	gln-L[c] + prlp[c] -> h[c] + glu-L[c] + aicar[c] + eig3p[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r107	eig3p[c] -> h2o[c] + imacp[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r108	h2o[c] + prbamp[c] -> prfp[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r109	h2o[c] + prbatp[c] -> h[c] + ppi[c] + prbamp[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r110	atp[c] + r5p[c] <=> h[c] + amp[c] + prpp[c]	0.0011	0.0011	0.0011	0.0010	0.0010	0.0010
r111	h2o[c] + cyst-L[c] -> pyr[c] + nh4[c] + hcys-L[c]	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004
r112	succoa[c] + hom-L[c] -> coa[c] + suchms[c]	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004
r113	atp[c] + h2o[c] + met-L[c] -> pi[c] + ppi[c] + amet[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r114	hcys-L[c] + 5mthf[c] -> thf[c] + met-L[c]	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004
r115	cys-L[c] + suchms[c] -> h[c] + succ[c] + cyst-L[c]	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004
r116	atp[c] + asp-L[c] <=> adp[c] + 4pasp[c]	0.0014	0.0014	0.0014	0.0012	0.0012	0.0012
r117	pi[c] + nadp[c] + aspsa[c] <=> h[c] + nadph[c] + 4pasp[c]	−0.0014	−0.0014	−0.0014	−0.0012	−0.0012	−0.0012
r118	h[c] + 26dap-M[c] -> co2[c] + lys-L[c]	0.0010	0.0010	0.0010	0.0008	0.0008	0.0008
r119	26dap-LL[c] <=> 26dap-M[c]	0.0010	0.0010	0.0010	0.0008	0.0008	0.0008
r120	h[c] + nadph[c] + 23dhdp[c] -> nadp[c] + thdp[c]	0.0010	0.0010	0.0010	0.0008	0.0008	0.0008
r121	pyr[c] + aspsa[c] -> h[c] + 2 h2o[c] + 23dhdp[c]	0.0010	0.0010	0.0010	0.0008	0.0008	0.0008
r122	nadp[c] + hom-L[c] <=> h[c] + nadph[c] + aspsa[c]	−0.0004	−0.0004	−0.0004	−0.0004	−0.0004	−0.0004
r123	h2o[c] + sl26da[c] -> succ[c] + 26dap-LL[c]	0.0010	0.0010	0.0010	0.0008	0.0008	0.0008
r124	akg[c] + sl26da[c] <=> glu-L[c] + sl2a6o[c]	−0.0010	−0.0010	−0.0010	−0.0008	−0.0008	−0.0008
r125	h2o[c] + succoa[c] + thdp[c] -> coa[c] + sl2a6o[c]	0.0010	0.0010	0.0010	0.0008	0.0008	0.0008
r126	thr-L[c] <=> acald[c] + gly[c]	−0.0017	−0.0017	−0.0017	−0.0014	−0.0014	−0.0014
r127	3dhq[c] <=> h2o[c] + 3dhsk[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r128	2dda7p[c] -> pi[c] + 3dhq[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r129	pep[c] + h2o[c] + e4p[c] -> pi[c] + 2dda7p[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r130	pep[c] + skm5p[c] <=> pi[c] + 3psme[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r131	prpp[c] + anth[c] -> ppi[c] + pran[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r132	gln-L[c] + chor[c] -> pyr[c] + h[c] + glu-L[c] + anth[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r133	chor[c] -> pphn[c]	0.0011	0.0011	0.0011	0.0009	0.0009	0.0009
r134	3psme[c] -> pi[c] + chor[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r135	h[c] + 2cpr5p[c] -> h2o[c] + co2[c] + 3ig3p[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r136	akg[c] + phe-L[c] <=> glu-L[c] + phpyr[c]	−0.0006	−0.0006	−0.0006	−0.0005	−0.0005	−0.0005
r137	pran[c] -> 2cpr5p[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r138	h[c] + pphn[c] -> h2o[c] + co2[c] + phpyr[c]	0.0006	0.0006	0.0006	0.0005	0.0005	0.0005
r139	nad[c] + pphn[c] -> nadh[c] + co2[c] + 34hpp[c]	0.0005	0.0005	0.0005	0.0004	0.0004	0.0004
r140	h[c] + nadph[c] + 3dhsk[c] <=> nadp[c] + skm[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r141	atp[c] + skm[c] -> adp[c] + h[c] + skm5p[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r142	3ig3p[c] -> g3p[c] + indole[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r143	h2o[c] + trp-L[c] <=> pyr[c] + nh4[c] + indole[c]	−0.0002	−0.0002	−0.0002	−0.0002	−0.0002	−0.0002
r144	akg[c] + tyr-L[c] <=> glu-L[c] + 34hpp[c]	−0.0005	−0.0005	−0.0005	−0.0004	−0.0004	−0.0004
r145	pyr[c] + h[c] + 2obut[c] -> co2[c] + 2ahbut[c]	0.0008	0.0008	0.0008	0.0007	0.0007	0.0007
r146	h2o[c] + 2ippm[c] <=> 3c3hmp[c]	−0.0009	−0.0009	−0.0009	−0.0007	−0.0007	−0.0007
r147	h2o[c] + accoa[c] + 3mob[c] -> h[c] + coa[c] + 3c3hmp[c]	0.0009	0.0009	0.0009	0.0007	0.0007	0.0007
r148	h[c] + 3c4mop[c] -> co2[c] + 4mop[c]	0.0009	0.0009	0.0009	0.0007	0.0007	0.0007
r149	3c2hmp[c] <=> h2o[c] + 2ippm[c]	−0.0009	−0.0009	−0.0009	−0.0007	−0.0007	−0.0007
r150	nad[c] + 3c2hmp[c] -> h[c] + nadh[c] + 3c4mop[c]	0.0009	0.0009	0.0009	0.0007	0.0007	0.0007
r151	h[c] + nadph[c] + alac-S[c] -> nadp[c] + 23dhmb[c]	0.0021	0.0021	0.0021	0.0018	0.0018	0.0018
r152	2 pyr[c] + h[c] -> co2[c] + alac-S[c]	0.0021	0.0021	0.0021	0.0018	0.0018	0.0018
r153	23dhmb[c] -> h2o[c] + 3mob[c]	0.0021	0.0021	0.0021	0.0018	0.0018	0.0018
r154	23dhmp[c] -> h2o[c] + 3mop[c]	0.0008	0.0008	0.0008	0.0007	0.0007	0.0007
r155	akg[c] + ile-L[c] <=> glu-L[c] + 3mop[c]	−0.0008	−0.0008	−0.0008	−0.0007	−0.0007	−0.0007
r156	h[c] + nadph[c] + 2ahbut[c] -> nadp[c] + 23dhmp[c]	0.0008	0.0008	0.0008	0.0007	0.0007	0.0007
r157	glu-L[c] + 4mop[c] -> akg[c] + leu-L[c]	0.0009	0.0009	0.0009	0.0007	0.0007	0.0007
r158	thr-L[c] -> nh4[c] + 2obut[c]	0.0008	0.0008	0.0008	0.0007	0.0007	0.0007
r159	akg[c] + val-L[c] <=> glu-L[c] + 3mob[c]	−0.0012	−0.0012	−0.0012	−0.0010	−0.0010	−0.0010
r160	pep[c] + h2o[c] + ara5p[c] -> pi[c] + kdo8p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r161	ckdo[c] + lipidA[c] -> h[c] + cmp[c] + kdolipid4[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r162	ckdo[c] + kdolipid4[c] -> h[c] + cmp[c] + kdo2lipid4[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r163	ctp[c] + kdo[c] -> ppi[c] + ckdo[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r164	h2o[c] + kdo8p[c] -> pi[c] + kdo[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r165	atp[c] + ACP[c] + ttdcea[c] -> ppi[c] + amp[c] + tdeACP[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r166	atp[c] + ACP[c] + hdca[c] -> ppi[c] + amp[c] + palmACP[c]	0.0013	0.0013	0.0013	0.0011	0.0011	0.0011
r167	atp[c] + ACP[c] + hdcea[c] -> ppi[c] + amp[c] + hdeACP[c]	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
r168	atp[c] + ACP[c] + ocdcea[c] -> ppi[c] + amp[c] + octeACP[c]	0.0021	0.0021	0.0021	0.0018	0.0018	0.0018
r169	atp[c] + ACP[c] + ttdca[c] -> ppi[c] + amp[c] + myrsACP[c]	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
r170	adphep-D,D[c] -> adphep-L,D[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r171	atp[c] + 2 ala-D[c] <=> adp[c] + h[c] + pi[c] + alaala[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r172	atp[c] + h[c] + gmhep1p[c] -> ppi[c] + adphep-D,D[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r173	h2o[c] + gmhep17bp[c] -> pi[c] + gmhep1p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r174	atp[c] + gmhep7p[c] -> adp[c] + h[c] + gmhep17bp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r175	atp[c] + 0.02 12dgr_EC[c] -> adp[c] + h[c] + 0.02 pa_EC[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r176	kdo2lipid4[c] + ddcaACP[c] -> ACP[c] + kdo2lipid4L[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r177	myrsACP[c] + kdo2lipid4L[c] -> ACP[c] + lipa[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r178	h[c] + cmp[c] + 0.02 pe_EC[c] <=> 0.02 12dgr_EC[c] + cdpea[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r179	accoa[c] + gam1p[c] -> h[c] + coa[c] + acgam1p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r180	glu-D[c] <=> glu-L[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r181	f6p[c] + gln-L[c] -> glu-L[c] + gam6p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r182	h2o[c] + g3pe[c] -> h[c] + glyc3p[c] + etha[c]	0.0011	0.0011	0.0011	0.0009	0.0009	0.0009
r183	h2o[c] + g3pg[c] -> h[c] + glyc[c] + glyc3p[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r184	lipidX[c] + u23ga[c] -> h[c] + lipidAds[c] + udp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r185	3 ckdo[c] + 3 adphep-L,D[c] + lipa[c] + 2 cdpea[c] + 2 udpg[c] -> 3 adp[c] + 10 h[c] + 3 cmp[c] + 2 udp[c] + 2 cdp[c] + lps_EC[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r186	h2o[c] + 0.02 agpe_EC[c] -> h[c] + 0.05 ttdcea[c] + 0.36 hdca[c] + 0.07 hdcea[c] + 0.5 ocdcea[c] + 0.02 ttdca[c] + g3pe[c]	0.0011	0.0011	0.0011	0.0009	0.0009	0.0009
r187	h2o[c] + 0.02 agpg_EC[c] -> h[c] + 0.05 ttdcea[c] + 0.36 hdca[c] + 0.07 hdcea[c] + 0.5 ocdcea[c] + 0.02 ttdca[c] + g3pg[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r188	uaagmda[c] -> h[c] + peptido_EC[c] + udcpdp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r189	h2o[c] + 0.02 pe_EC[c] -> h[c] + 0.05 ttdcea[c] + 0.36 hdca[c] + 0.07 hdcea[c] + 0.5 ocdcea[c] + 0.02 ttdca[c] + 0.02 agpe_EC[c]	0.0011	0.0011	0.0011	0.0009	0.0009	0.0009
r190	gam1p[c] <=> gam6p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r191	h2o[c] + 0.02 pg_EC[c] -> h[c] + 0.05 ttdcea[c] + 0.36 hdca[c] + 0.07 hdcea[c] + 0.5 ocdcea[c] + 0.02 ttdca[c] + 0.02 agpg_EC[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r192	udcpp[c] + ugmda[c] -> uagmda[c] + ump[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r193	s7p[c] -> gmhep7p[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r194	atp[c] + lipidAds[c] -> adp[c] + h[c] + lipidA[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r195	3hmrsACP[c] + u3hga[c] -> h[c] + ACP[c] + u23ga[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r196	h2o[c] + u3aga[c] -> ac[c] + u3hga[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r197	h[c] + nadph[c] + uaccg[c] -> nadp[c] + uamr[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r198	pep[c] + uacgam[c] -> pi[c] + uaccg[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r199	3hmrsACP[c] + uacgam[c] <=> ACP[c] + u3aga[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r200	h[c] + acgam1p[c] + utp[c] -> ppi[c] + uacgam[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r201	uagmda[c] + uacgam[c] -> h[c] + udp[c] + uaagmda[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r202	atp[c] + ala-L[c] + uamr[c] -> adp[c] + h[c] + pi[c] + uama[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r203	atp[c] + glu-D[c] + uama[c] -> adp[c] + h[c] + pi[c] + uamag[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r204	atp[c] + 26dap-M[c] + uamag[c] -> adp[c] + h[c] + pi[c] + ugmd[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r205	atp[c] + alaala[c] + ugmd[c] -> adp[c] + h[c] + pi[c] + ugmda[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r206	h2o[c] + u23ga[c] -> 2 h[c] + lipidX[c] + ump[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r207	h2o[c] + udcpdp[c] -> h[c] + pi[c] + udcpp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r208	h[c] + g1p[c] + utp[c] <=> ppi[c] + udpg[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r209	h[c] + nadh[c] + mlthf[c] -> nad[c] + 5mthf[c]	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004
r210	h2o[c] + 10fthf[c] -> h[c] + thf[c] + for[c]	0.0020	0.0020	0.0020	0.0017	0.0017	0.0017
r211	h2o[c] + methf[c] <=> 10fthf[c]	0.0031	0.0031	0.0031	0.0026	0.0026	0.0026
r212	nadp[c] + mlthf[c] <=> h[c] + nadph[c] + methf[c]	0.0031	0.0031	0.0031	0.0026	0.0026	0.0026
r213	2 h[c] + nadph[c] + ddcaACP[c] + malACP[c] -> co2[c] + nadp[c] + ACP[c] + 3hmrsACP[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r214	atp[c] + accoa[c] + hco3[c] <=> adp[c] + h[c] + pi[c] + malcoa[c]	0.0051	0.0051	0.0051	0.0043	0.0043	0.0043
r215	h[c] + accoa[c] + malACP[c] -> coa[c] + co2[c] + actACP[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r216	h[c] + ctp[c] + 0.02 pa_EC[c] <=> ppi[c] + 0.02 cdpdag1[c]	0.0023	0.0023	0.0023	0.0019	0.0019	0.0019
r217	14 h[c] + 10 nadph[c] + 4 malACP[c] + actACP[c] -> 5 h2o[c] + 4 co2[c] + 10 nadp[c] + 4 ACP[c] + ddcaACP[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r218	17 h[c] + 12 nadph[c] + 5 malACP[c] + actACP[c] -> 6 h2o[c] + 5 co2[c] + 12 nadp[c] + 5 ACP[c] + myrsACP[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r219	20 h[c] + 14 nadph[c] + 6 malACP[c] + actACP[c] -> 7 h2o[c] + 6 co2[c] + 14 nadp[c] + 6 ACP[c] + palmACP[c]	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003
r220	19 h[c] + 13 nadph[c] + 6 malACP[c] + actACP[c] -> 7 h2o[c] + 6 co2[c] + 13 nadp[c] + 6 ACP[c] + hdeACP[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r221	22 h[c] + 15 nadph[c] + 7 malACP[c] + actACP[c] -> 8 h2o[c] + 7 co2[c] + 15 nadp[c] + 7 ACP[c] + octeACP[c]	0.0002	0.0002	0.0002	0.0001	0.0001	0.0001
r222	ACP[c] + malcoa[c] <=> coa[c] + malACP[c]	0.0051	0.0051	0.0051	0.0043	0.0043	0.0043
r223	glyc3p[c] + 0.1 tdeACP[c] + 0.72 palmACP[c] + 0.14 hdeACP[c] + octeACP[c] + 0.04 myrsACP[c] -> 2 ACP[c] + 0.02 pa_EC[c]	0.0023	0.0023	0.0023	0.0019	0.0019	0.0019
r224	h2o[c] + 0.02 pgp_EC[c] -> pi[c] + 0.02 pg_EC[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r225	glyc3p[c] + 0.02 cdpdag1[c] <=> h[c] + cmp[c] + 0.02 pgp_EC[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r226	h[c] + 0.02 ps_EC[c] -> co2[c] + 0.02 pe_EC[c]	0.0011	0.0011	0.0011	0.0009	0.0009	0.0009
r227	ser-L[c] + 0.02 cdpdag1[c] <=> h[c] + cmp[c] + 0.02 ps_EC[c]	0.0011	0.0011	0.0011	0.0009	0.0009	0.0009
r228	h2o[c] + damp[c] -> pi[c] + dad-2[c]	0.0017	0.0017	0.0017	0.0014	0.0014	0.0014
r229	atp[c] + adn[c] -> adp[c] + h[c] + amp[c]	0.0017	0.0017	0.0017	0.0014	0.0014	0.0014
r230	atp[c] + amp[c] <=> 2 adp[c]	0.0112	0.0112	0.0112	0.0081	0.0081	0.0081
r231	atp[c] + cmp[c] <=> adp[c] + cdp[c]	0.0022	0.0022	0.0022	0.0018	0.0018	0.0018
r232	atp[c] + dcmp[c] <=> adp[c] + dcdp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r233	atp[c] + damp[c] <=> adp[c] + dadp[c]	−0.0017	−0.0017	−0.0017	−0.0015	−0.0015	−0.0015
r234	atp[c] + dgmp[c] <=> adp[c] + dgdp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r235	atp[c] + gmp[c] <=> adp[c] + gdp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r236	atp[c] + cdp[c] <=> adp[c] + ctp[c]	0.0022	0.0022	0.0022	0.0018	0.0018	0.0018
r237	atp[c] + dudp[c] <=> adp[c] + dutp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r238	atp[c] + gdp[c] <=> adp[c] + gtp[c]	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
r239	atp[c] + udp[c] <=> adp[c] + utp[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r240	pi[c] + adn[c] <=> r1p[c] + ade[c]	−0.0017	−0.0017	−0.0017	−0.0014	−0.0014	−0.0014
r241	pi[c] + dad-2[c] <=> 2dr1p[c] + ade[c]	0.0017	0.0017	0.0017	0.0014	0.0014	0.0014
r242	adp[c] + trdrd[c] -> h2o[c] + trdox[c] + dadp[c]	0.0017	0.0017	0.0017	0.0015	0.0015	0.0015
r243	trdrd[c] + cdp[c] -> h2o[c] + trdox[c] + dcdp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r244	trdrd[c] + gdp[c] -> h2o[c] + trdox[c] + dgdp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r245	trdrd[c] + utp[c] -> h2o[c] + trdox[c] + dutp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r246	mlthf[c] + dump[c] -> dhf[c] + dtmp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r247	atp[c] + ump[c] <=> adp[c] + udp[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r248	atp[c] + dump[c] <=> adp[c] + dudp[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r249	25aics[c] <=> fum[c] + aicar[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r250	asp-L[c] + gtp[c] + imp[c] -> 2 h[c] + pi[c] + gdp[c] + dcamp[c]	0.0005	0.0005	0.0005	0.0004	0.0004	0.0004
r251	dcamp[c] <=> fum[c] + amp[c]	0.0005	0.0005	0.0005	0.0004	0.0004	0.0004
r252	asp-L[c] + cbp[c] -> h[c] + pi[c] + cbasp[c]	0.0003	0.0003	0.0003	0.0002	0.0002	0.0002
r253	atp[c] + h2o[c] + gln-L[c] + utp[c] -> adp[c] + 2 h[c] + pi[c] + glu-L[c] + ctp[c]	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
r254	q8[c] + dhor-S[c] -> q8h2[c] + orot[c]	0.0003	0.0003	0.0003	0.0002	0.0002	0.0002
r255	h2o[c] + dhor-S[c] <=> h[c] + cbasp[c]	−0.0003	−0.0003	−0.0003	−0.0002	−0.0002	−0.0002
r256	h2o[c] + gln-L[c] + prpp[c] -> ppi[c] + glu-L[c] + pram[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r257	atp[c] + h2o[c] + gln-L[c] + xmp[c] -> 2 h[c] + ppi[c] + amp[c] + glu-L[c] + gmp[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r258	h2o[c] + imp[c] <=> fprica[c]	−0.0007	−0.0007	−0.0007	−0.0006	−0.0006	−0.0006
r259	nad[c] + h2o[c] + imp[c] -> h[c] + nadh[c] + xmp[c]	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
r260	ppi[c] + orot5p[c] <=> prpp[c] + orot[c]	−0.0003	−0.0003	−0.0003	−0.0002	−0.0002	−0.0002
r261	h[c] + orot5p[c] -> co2[c] + ump[c]	0.0003	0.0003	0.0003	0.0002	0.0002	0.0002
r262	atp[c] + hco3[c] + air[c] -> adp[c] + h[c] + pi[c] + 5caiz[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r263	5aizc[c] <=> 5caiz[c]	−0.0004	−0.0004	−0.0004	−0.0003	−0.0003	−0.0003
r264	atp[c] + fpram[c] -> adp[c] + 2 h[c] + pi[c] + air[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r265	aicar[c] + 10fthf[c] <=> thf[c] + fprica[c]	0.0007	0.0007	0.0007	0.0006	0.0006	0.0006
r266	atp[c] + asp-L[c] + 5aizc[c] <=> adp[c] + h[c] + pi[c] + 25aics[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r267	atp[c] + h2o[c] + gln-L[c] + fgam[c] -> adp[c] + h[c] + pi[c] + glu-L[c] + fpram[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r268	10fthf[c] + gar[c] <=> h[c] + thf[c] + fgam[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r269	atp[c] + gly[c] + pram[c] <=> adp[c] + h[c] + pi[c] + gar[c]	0.0004	0.0004	0.0004	0.0003	0.0003	0.0003
r278	q8[c] + glyc3p[c] -> dhap[c] + q8h2[c]	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
r283	atp[c] + coa[c] + ac[c] -> accoa[c] + ppi[c] + amp[c]	0.0015	0.0015	0.0015	0.0000	0.0000	0.0000
Protein_ amino_acids	0.113 ala-L[c] + 0.0532 asp-L[c] + 0.0532 asn-L[c] + 0.0599 glu-L[c] + 0.0259 met-L[c] + 0.0512 arg-L[c] + 0.0599 gln-L[c] + 0.0416 pro-L[c] + 0.0176 cys-L[c] + 0.0501 ser-L[c] + 0.0872 gly[c] + 0.0182 his-L[c] + 0.0605 lys-L[c] + 0.0545 thr-L[c] + 0.035 phe-L[c] + 0.0114 trp-L[c] + 0.029 tyr-L[c] + 0.0493 ile-L[c] + 0.0541 leu-L[c] + 0.0752 val-L[c] -> Aaprot[c]	0.0165	0.0165	0.0165	0.0138	0.0138	0.0138
Protein_ translation	4 atp[c] + 3 h2o[c] + Aaprot[c] -> 4 adp[c] + 4 h[c] + 4 pi[c] + 4.77 Biom_Prot[c]	0.0153	0.0153	0.0153	0.0128	0.0128	0.0128
DNA	2 atp[c] + h2o[c] + 0.246 damp[c] + 0.254 dcmp[c] + 0.254 dgmp[c] + 0.246 dtmp[c] -> 2 adp[c] + 2 h[c] + 2 pi[c] + 9.75 DNA[c]	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
RNA	2 atp[c] + h2o[c] + 0.262 amp[c] + 0.2 cmp[c] + 0.216 ump[c] + 0.322 gmp[c] -> 2 adp[c] + 2 h[c] + 2 pi[c] + 9.58 RNAtot[c]	0.0006	0.0006	0.0006	0.0005	0.0005	0.0005
ETC_O2	2.98 h[c] + q8h2[c] + 0.5 o2[c] -> 2.98 h[e] + h2o[c] + q8[c]	0.1909	0.1909	0.1909	0.1321	0.1321	0.1321
ETC_NADH	3.98 h[c] + nadh[c] + q8[c] -> 2.98 h[e] + nad[c] + q8h2[c]	0.1623	0.1623	0.1623	0.1178	0.1178	0.1178
ETC_FOR	2.49 h[c] + q8[c] + for[c] -> 1.49 h[e] + co2[c] + q8h2[c]	0.0020	0.0020	0.0020	0.0000	0.0000	0.0000
LeanBiomass	0.011447 glyc[c] + 0.000888 glycogen[c] + 0.000747 ptrc[c] + 0.000157 spmd[c] + 0.002838 hdca[c] + 0.002201 hdcea[c] + 0.001436 ocdcea[c] + 0.010214 etha[c] + 5.1e-05 lps_EC[c] + 0.000145 peptido_EC[c] + 0.692337 Biom_Prot[c] + 0.008103 DNA[c] + 0.050081 RNAtot[c] -> BuildingBlocks	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
EX_Biomass	Biomass ->	0.1112	0.1112	0.1139	0.0932	0.0932	0.0980
EX_sucrose[e]	sucrose[e] ->	−0.0180	−0.0180	−0.0180	−0.0151	−0.0151	−0.0151
EX_HB[c]	HB[c] ->	0.0001	0.0001	0.0001	0.0016	0.0016	0.0016
SucroseSimporter	h[e] + sucrose[e] -> h[c] + sucrose[c]	0.0180	0.0180	0.0180	0.0151	0.0151	0.0151
SucroseHydrolase	h2o[c] + sucrose[c] -> fru[c] + glucose[c]	0.0180	0.0180	0.0180	0.0151	0.0151	0.0151
FruKin	atp[c] + fru[c] -> f6p[c] + adp[c] + h[c]	0.0180	0.0180	0.0180	0.0151	0.0151	0.0151
GluKin	atp[c] + glucose[c] -> g6p[c] + adp[c] + h[c]	0.0180	0.0180	0.0180	0.0151	0.0151	0.0151
sintPHB	h[c] + nadh[c] + 2 accoa[c] -> nad[c] + 2 coa[c] + HB[c]	0.0001	0.0001	0.0001	0.0016	0.0016	0.0016
Plasmid	2 atp[c] + h2o[c] + 0.228 damp[c] + 0.272 dcmp[c] + 0.272 dgmp[c] + 0.228 dtmp[c] -> 2 adp[c] + 2 h[c] + 2 pi[c] + 9.75 Plasmid	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
RecombinantP	4 atp[c] + 3 h2o[c] + Aaprot[c] -> 4 adp[c] + 4 h[c] + 4 pi[c] + 4.77 RP	0.0012	0.0012	0.0012	0.0010	0.0010	0.0010
Joining_Building_ Blocks	0.010852 glyc[c] + 0.000842 glycogen[c] + 0.000709 ptrc[c] + 0.000149 spmd[c] + 0.002691 hdca[c] + 0.002086 hdcea[c] + 0.001362 ocdcea[c] + 0.009683 etha[c] + 4.8e-05 lps_EC[c] + 0.000138 peptido_EC[c] + 0.656327 Biom_Prot[c] + 0.007682 DNA[c] + 0.047476 RNAtot[c] + 0.000946 Plasmid + 0.050939 RP -> BuildingBlocksBurden	0.1112	0.1112	0.1112	0.0932	0.0932	0.0932
Biomass_ Formation	0.46 atp[c] + 0.46 h2o[c] + BuildingBlocksBurden -> 0.46 adp[c] + 0.46 h[c] + 0.46 pi[c] + Biomass	0.1112	0.1112	0.1112	0.0932	0.0932	0.0932

2. Experimental Design, Materials and Methods

2.1. DNA manipulations

For routine procedures, cells were grown on Lysogenic Broth (LB) medium (10 g tryptone, 5 g yeast extract and 5 g NaCl per liter of deionized water) supplemented with ad hoc antibiotics. The characteristics of the primers, plasmids and strains employed in this research are summarized a supplementary material of the accompanying paper “An NADH preferring acetoacetyl-CoA reductase is engaged in poly-3-hydroxybutyrate accumulation in E. coli”.

DNA amplification, restriction and ligation as well as bacterial transformation, selection and identification were executed according to the standard procedures described elsewhere [6]. When amplifying DNA for cloning purposes, Q5 High-Fidelity DNA Polymerase (New England Biolabs) was used. GoTaq Green Master Mix (Promega) was used for colony PCR. Plasmid purification from cultures was done using the QIAprep Spin Miniprep Kit (Qiagen). For plasmid propagation and long-term storage of constructions, introduction of the plasmids in E. coli One Shot® TOP10 (ThermoFisher Scientific) was implemented. All DNA modifying enzymes employed in this study were purchased from New England Biolabs.

AAR^CAp is encoded by the phaB^CAp6 gene. The phaB^CAp6 gene was isolated from a metagenomic DNA sample obtained from a Ca. A. phosphatis-enriched mix culture. This gene has a very high DNA identity with the annotated phaB gene from Ca. A. phosphatis (locus KEGG CAP2UW1_3919). To amplify and clone phaB^CAp6 gene, a sample of total DNA from the mix culture was obtained with the commercially available PowerSoil® DNA isolation Kit (MO BIO Laboratories), following the instructions of the manufacturer. The enrichment of that mix culture was done using an enhanced biological phosphorus removal procedure [7], starting with crushed granular sludge from the Garmerwolde Nereda plant, The Netherlands. A sample of the obtained DNA (30 ng) was used as template in a PCR reaction using the primers PAOphaB_BamUpCrt and PAOphaB_XbaDwCrt. Those primers were designed to hybridize with the reference phaB^CAp (GenBank: Genome CP001715.1, locus_tag="CAP2UW1_3919″) and they added target sequences for the restriction enzymes BamHI and XbaI in the extremes of the amplified DNA. The PCR product was cleaned (NucleoSpin® Gel and PCR clean-up (Macherey-Nagel)) and restricted with BamHI and cloned into the pMiniT vector using a PCR Cloning Kit (New England Biolabs, #E1202). Before perform the ligation into the pMiniT vector, 5′ four base overhangs resulting from restriction with BamHI were filled using reagents included in the PCR Cloning Kit. The ligation product was employed to transform NEB-10 beta cells (New England Biolabs, #C3019), included as part of the PCR Cloning Kit. By colony PCR, four colonies bearing plasmids carrying inserts of the expected size were detected. The recombinant plasmids from those clones were isolated and the insertions were amplified using primers provided with the PCR Cloning Kit. The resulting PCR products were sequenced (Baseclear, Netherlands) and the plasmid carrying the insert with the highest identity respect to the annotated phaB^CAp gene was named pMiniT-phaBCAp. The open reading frame present in pMiniT-phaBCAp was employed for further cloning procedures aiming the recombinant expression of the encoded protein and the construction of an artificial operon together with the phaCA genes from C. necator (see below).

On the other hand, an artificial DNA sequence, was designed and purchased (IDT, Integrated DNA Technologies, Belgium). This artificial sequence encodes for a version of the acetoacetyl-CoA reductases from C. necator (AAR^Cn) where the original residues N37-S38-P39-R40-R41 were replaced by the residues E37-F38-D39-K40-P41 from AAR^CAp. This artificial enzyme was named AAR^Chimera. The amino acid encoding sequences of AAR^CAp and AAR^Chimera were cloned in the vector pCOLA-duet-1, in frame with a vector DNA sequence encoding for a poly-histidine tail. The relevant DNA sequences of the plasmids pCOLA-His-phaBCAp6 and pCola-phaB-Chimera were checked by sequencing, and these plasmids were introduced in E. coli BL21(DE3) cells.

To verify the ability of phaB^CAp to encode for a protein capable to catalyze in vivo the conversion of acetoacetyl-CoA to 3-hydroxybutyryl-CoA, an artificial operon was constructed joining the genes phaC and phaA from C. necator (encoding for a PHB synthase and a β-ketothiolase respectively) and phaB^CAp. The fragment embracing the open reading frames of phaCA genes plus the intergenic space between phaA and phaB (including the Shine-Dalgarno sequence upstream of phaB) from C. necator was amplified from the plasmid pBBRMCS-2-phaCABCnecator using the primers phaCABRalsXhoUPCrt and phaPCARalsBamDwCrt. After restriction (XhoI and BamHI) of the PCR product, it was cloned into the pTrcMCS vector to obtain the resultant plasmid pTrc-phaCACnecator. Then, phaB^CAp was amplified from the plasmid pMiniT-phaB^CAp using the primers phaB-PAO-nat_Bam2.FOR and phaBPAOHind.REV. The obtained PCR product was restricted (BamHI and HindIII) and ligated downstream of the fragment phaCA in pTrc-phaCACnecator. The obtained plasmid was named pTrc-phaCACnecatorphaBCAp. Finally, a fragment embracing the genes phaCA^CnecatorphaB^CAp was amplified using the primers phaCABRals_NdeUpCrt and PAOphaB_XhoDwCrt, restricted with NdeI and XhoI, and ligated into the pCOLA-duet vector. The resultant plasmid was named pCola-phaCACnecatorphaBCAp and carried the artificial operon phaCA^CnecatorphaB^CAp under the control of the T7 promoter.

Finally, to avoid the use of antibiotics in the planned continuous cultures, we transferred the genes cscB, cscK and cscA from E. coli W to the plasmid pCola-phaCACnecatorphaBCAp. The cscABK genes encodes for the sucrose hydrolase, the sucrose:proton symporter and the fructose kinase from E. coli W, respectively. E. coli strains from the K-12 group are naturally unable to grow on sucrose as the sole carbon source, but the introduction of cscABK genes confers this ability [8]. Therefore, the resultant plasmid with the genes cscB, cscK, cscA, phaC, phaA and phaB becomes essential for the growth of an E. coli K-12 derived strain on sucrose as the sole carbon source. The resultant plasmid was named pColaphaCABcscABK. For its construction, a DNA fragment embracing the genes cscB, cscK, cscA was amplified by PCR using as the template genomic DNA from E. coli W and the primers XhoIcrtcscBFW and cscAXhoIcrtRV. The resultant PCR product was restricted with the enzyme XhoI and ligated into the plasmid pCola-phaCACnecatorphaBCAp, who was previously restricted also with XhoI and treated with alkaline phosphatase to minimizes recircularization.

After transformation and plasmid propagation in E. coli One Shot® TOP10, the plasmid pColaphaCABcscABK was purified and introduced, by electroporation, in cells of the E. coli strain MG1655(DE3)∆5, kindly donated by professor Isabel Rocha (CEB-Centre of Biological Engineering, University of Minho, Portugal). That strain was previously modified to express the T7 RNA polymerase upon induction with Isopropyl β-D-1-thiogalactopyranoside (IPTG) [9]; and its genes adhE, adhP, ldhA, pta and mhpF were previously deleted.

The DNA sequence maps of all the plasmids involved in this research project can be found in the repository “NADH-driven polyhydroxybutyrate accumulation in E. coli dataset 2″ in Mendeley Data.

2.2. Protein purification

Cells of E. coli BL21(DE3) transformed with the plasmid pCOLA-His-phaBCAp6 and pCola-phaB-Chimera were aerobically grown on LB supplemented with Kanamycin (180 rpm, 37 °C) up to an optical density (600 nm) of 0.5. Over-expression of AAR^CAp and AAR^Chimera was induced with IPTG 200 (0.5 mM) and temperature was decreased to 25 °C. Induced cultures were grown for 16 h and the cells were harvested by centrifugation (2500 g, 4 °C, 20 min). To wash the cells, the resultant pellets were suspended in ice-cold Buffer A (50 mM Tris, 100 mM NaCl, 5 mM MgCl₂, pH 8) up to 10% of the original culture volume and centrifuged (2500 g, 4 °C, 10 min). The resultant pellets were suspended again in 10% of the original culture volume using ice-cold Buffer A but supplemented with DL-Dithiothreitol 2 mM and cOmplete™ EDTA-free Protease Inhibitor Cocktail (Roche) prepared according with the instructions of the manufacturer. Cells were broken by sonication and the cell-free extracts were obtained rescuing the supernatant after centrifugation (45 min, 4 °C, 15,000 g). The His-tagged proteins were purified from the obtained cell-free extracts using 5 ml HisTrap FF columns (GE Healthcare), following the instructions of the manufacturer. Buffer A supplemented with a basal concentration of imidazole (20 mM) and NaCl (100 mM) was employed to equilibrate the columns. The obtained cell-free extracts were spiked with NaCl and imidazole to achieve the same concentration present in the equilibration buffer. After the cell-free extracts were loaded, columns were washed with equilibration buffer, passing through them at least 20 times the volume of the loaded cell-free extracts. For the elution of his-tagged proteins, volumes of buffer A equivalent to 20 times the loaded cell-free extracts were injected in the columns, but buffer A was supplemented with a steadily increasing concentration of imidazole, conforming a gradient from 20 mM to 500 mM. Fractions of 2 ml were harvested in Eppendorf tubes. The NADH-linked acetoacetyl-CoA reductase activities were spectrophotometrically measured in the fractions (NADH 100 μM, acetoacetyl-CoA 100 μM in buffer A). Those fractions with acetoacetyl-CoA reductase activities ranking in the upper quartile were pooled. Imidazole was washed out from the pools and proteins were concentrated by centrifugation using a Millipore® Amicon® Ultra-Centifugal Filter Concentrator with a cut-off of 10 kDa. The resultant pools were stored at −20 °C, with 50% glycerol, until perform the enzymatic assays. The purity of the obtained protein samples was assessed by SDS-PAGE.

2.3. Enzymatic assays

The substrates employed for the enzymatic assays were purchased from Sigma (NADH and NADPH) and Santa Cruz Biotechnology (acetoacetyl-CoA) and had analytical grade quality. NADH and NADPH were freshly prepared by dissolving them in Buffer A. Acetoacetyl-CoA, NAD⁺ and NADP⁺ were freshly dissolved in des-ionized water (resistivity 18.2 MΩ*cm at 25 °C). Substrate concentration in these stock solutions was estimated by spectrophotometry, dissolving samples taken from the stocks in 50 mM MOPS (pH 7), 5 mM MgCl₂, 5 mM NaCl. The concentrations of the resultant solutions were determined by spectrophotometry, using apparent molar extinction coefficients obtained in conditions similar to ours (ε^app at 340 nm for NAD(P)H = 6220 M⁻¹ cm⁻¹; for acetoacetyl-CoA at 310 nm, ε^app = 11,000 M⁻¹ cm⁻¹). The protein concentration was determined using the Protein assay reagent (Bio-Rad) and Bovine Serum Albumin (Bio-Rad) as standard.

To calculate the acetoacetyl-CoA reductase activity, the consumption of acetoacetyl-CoA and NAD(P)H was monitored following the changes in the absorbances at 310 nm or 360 nm. The apparent molar extinction coefficients were ε^AcAcCoA,310 = 11,000 M⁻¹ cm⁻¹, ε^NAD(P)H,310 = 3340 M⁻¹ cm⁻¹, ε^AcAcCoA,360 = 900 M⁻¹ cm⁻¹, and ε^NAD(P)H,360 = 4275 M⁻¹ cm⁻¹. We did not register the changes in absorbance at 340 nm to avoid optical artefacts.

Initial rates and reaction progress curves were studied in the Buffer A at 30 °C. All the spectrophotometric measurements were performed in a Biotek Synergy HTX plate reader, using the in-build path length correction option to estimate the heights of the columns of liquid where the reactions happened. To estimate the initial rates estimations, pseudo-linear temporal changes in the absorbance were considered inside the time frame where less than 5% of the substrate had been consumed.

2.4. Analysis of the kinetic data

The reactions catalyzed by acetoacetyl-CoA reductases (E.C. 1.1.1.36) are bi-substrate bi-product (BiBi) reactions. However, for the kinetic parameter estimation, those BiBi reactions were modeled as pseudo-mono-substrate mono-product reactions. The initial concentration of the substrate not explicitly considered in each experiment is reported in each case.

Parameter estimations were performed with the software DYNAFIT [1]. For the analysis of initial rates, a simple Michaelian model (rapid-equilibrium) was assumed. Reaction progress curves were analyzed with steady-state models. DYNAFIT enables to do global fittings, i.e., it fits simultaneously data obtained using different concentrations of substrate and/or enzyme and/or modifiers. DYNAFIT enables to find the best fitted values for the parameters of a given model and it also enables to compare different models, finding which model best explains the observed results (model discrimination).

When modeling with DYNAFIT, it is not necessary to know the rate equation describing the chemical reaction(s) under study. What the user must provide is a (bio)chemical mechanism representing the meaningful interactions. For example, product inhibition can be mechanistically represented in the following way, where k₁, k_-1, k_off and k_cat are the rate constants characterizing the elemental interactions:

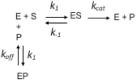
This mechanism can be written in DYNAFIT code as follows:

$$\mathrm{E}+\mathrm{S}<===>\text{ES}:\mathrm{k}1\text{kminus}1;$$ (1)

$$\text{ES}-->\mathrm{E}+\mathrm{P}:\text{kcat};$$ (2)

$$\mathrm{E}+\mathrm{P}<===>\text{EP}:\mathrm{k}1\text{koff};$$ (3)

The semicolon (;) is used in DYNAFIT to comment the lines. Therefore, in a line, DYNAFIT is “blind” to everything written after the symbol “;”.

Note that rate constant k₁ could have different values in the elemental interaction (1) and in the elemental interaction (3). Why using the same constant k₁? We have four unknown parameters (k₁, k_-1, k_off and k_cat) to describe three chemical transformations. To solve this mathematical problem, an arbitrary value could be assigned to k₁. Certainly, the best fitted values for k_-1 and k_off obtained by this method will be arbitrary as well, but they are not independent of the arbitrary value assigned to k₁.

Anyways, for many practical applications, it is enough to know the constants K_M, K_i and k_cat. The kinetic constants K_M and K_i are more or less complex functions of elemental rate constants, depending on the mechanism. For the specific case of product inhibition shown in the scheme above, K_M and K_i are defined as:

$$K_M=\frac{k_{-1}+k_{cat}}{k_1}$$

$$K_i=\frac{k_{off}}{k_1}$$

The enzyme stability tests showed that partial enzyme inactivation could happen. Therefore, in the analysis of the reaction progress curves, enzyme degradation was considered. It was modeled as a first order decay process:

$$\mathrm{E}-->\text{InactiveE}:\text{kdeg}$$

The value of the degradation constant (k_deg) was estimated by DYNAFIT.

The required scripts are provided in the repository “NADH-driven polyhydroxybutyrate accumulation in E.coli dataset 2″ in Mendeley Data. To run these scripts, it is necessary to download and activate DYNAFIT (freely available for academic institutions). Note that DYNAFIT scripts contain a line indicating the route to the data containing folder. These are the data that will be processed by the script. This route is usually written with reference to the folder where DYNAFIT itself is installed (annotated as ./). For example, in the script to analyze the data corresponding to the experiment named “AARCAp_varying_AcAcCoA_NADH”, it is possible to find the following lines (function of each line is commented after the semicolon):

• [data]; keyword in DYNAFIT announcing the section where data will be declared

• directory ./results/VovsS/AARCAp;data are in folder AARCAP, inside folder VovsS, inside the folder results, placed in the same folder where DYNAFIT was installed.

• extension txt; indicates that the data are in a “.txt” file

• variable S; indicates that the independent variable is the substrate concentration, represented in the chemical mechanism as S

• file data; indicates that the file with the experimental data is named “data.txt”

• [output]; keyword in DYNAFIT announcing the section dealing with the results of the analyses

• directory ./results/VovsS/AARCAp/output1; indicates that the folder named “output1” will be created in this route

Another important information contained in DYNAFIT scripts is the so called “Response”. The Response or molar Response is a proportionality constant to express the output parameters in convenient units. In this specific case, we were interested in expressing the values of K_M and K_i in micromolar (μM) and the values of k_cat in micromole of product generated, per micromole of active sites, per second (s⁻¹ for simplicity). In the case of the progress curves, in the input files, the concentration of the substrate was already in units of micromolar and the time was in seconds. Therefore, the molar Response in the scripts was S = 1.

In the case of initial rates versus substrate concentrations, the initial rates were expressed in units of micromolProduct(Substrate)/micromolEnzyme/s, then the molar response was P = 1. On the other hand, if the initial rates were in units of micromolP/mgEnzyme/min (U/mg), then it would be necessary to calculate the conversion factor. Considering the molecular weight of the poly-histidine-tagged form of the protein encoded by phaB^CAp6 (27,554 g/mol), the molar Response would be:

$$\frac{1\mu mo{l}_{product}}{m{g}_{enzyme}*min}=\frac{1\mu mo{l}_{product}}{\frac{{10}^{-3}{g}_{enzyme}*{10}^6\mu mo{l}_{enzyme}}{27554g_{enzyme}}*60s}=0.459s^{-1}$$

These instructions should be enough to run the scripts with DYNAFIT. However, for better understanding of all the lines in the scripts, and eventually modify these scripts for other applications, we strongly recommend to check the DYNAFIT scripting rules, freely available in the website of the developer (http://www.biokin.com/dynafit/).

Estimation of the relative cofactor usage and flux capacity of a reaction catalyzed by an acetoacetyl-CoA reductase

To quantify the relative use of NADH over NADPH (or vice versa) by a given acetoacetyl-CoA reductase, we calculated the ratio of the activities with NADH and NADPH. These activities were calculated adapting a generic BiBi equation described by Rohwer and co-workers [10] to the reactions catalyzed by acetoacetyl-CoA reductases:

$$v^{NADH}=\frac{k_{cat}^{NADH}*E*\frac{NADH*AcAcCoA}{K^{NADH}*K^{AcAcCoA}}*\left(1-\frac{NAD*3HBCoA}{NADH*AcAcCoA*K_{eq}}\right)}{\left(1+\frac{NADH}{K^{NADH}}+\frac{3HBCoA}{K^{3HBCoA}}\right)*\left(1+\frac{AcAcCoA}{K^{AcAcCoA}}+\frac{NAD}{K^{NAD}}\right)}.$$

where $K^{NADH},K^{AcAcCoA},$ $K^{3HBCoA}$ and $K^{NAD}$ are dissociation constants associated to the interactions between the corresponding ligands and different forms of the enzyme. The experimentally determined K_M and K_ic were considered good approximations of the dissociation constants of the generic equation. The constants not directly available from our experimental data were estimated taking advantage of the Haldane relationships.

Another important detail was the consideration of NADPH and NADP⁺ as competitive inhibitors of NADH and NAD⁺binding. This way, the terms $K^{NADH}$ and $K^{NAD}$ were multiplied by the factor (1 + NADPH/K^NADPH + NADP/K^NADP). A similar analysis was applied to the reactions catalyzed by NADPH.

Different to other approaches, we considered the cofactor specificity as a dynamic property, i.e., it is not a fixed value, it changes depending on the NAD⁺, NADH, NADP⁺ and NADPH concentrations. With the scripts available in the repository “NADH-driven polyhydroxybutyrate accumulation in E. coli dataset 2″ in Mendeley Data, individual NAD⁺, NADH, NADP⁺ and NADPH concentrations are calculated by solving a simple system of algebraic equations. These equations reflect two physiologically relevant principles: (i) cofactor concentrations have to fulfill the thermodynamic constraints enabling the operation of the Embden-Meyerhof pathway and (ii) the concentration sums (NAD⁺ + NADH) and (NADP⁺ + NADPH) were considered conserved moieties.

It should be noticed that the ratios of the activities with NADH and NADPH R = v^NADH/v^NADPH is independent of the enzyme concentration because the terms “E” in the numerator and denominator cancel each other. On the other hand, the flux capacity does depends on the enzyme (AAR^CAp) concentration, and this dependency is linear:

$$\begin{array}{ccc}& & Fluxcapacity\hfill \\ & & =\frac{k_{cat}^{NADH}*AA{R}^{CAp}*\frac{NADH*AcAcCoA}{K^{NADH}*\left(1+\frac{NADPH}{K^{NADPH}}+\frac{NADP}{K^{NADP}}\right)*K_{NADH}^{AcAcCoA}}*\left(1-\frac{NAD*3HBCoA}{NADH*AcAcCoA*K_{eq}}\right)}{\left(1+\frac{NADH}{K^{NADH}*\left(1+\frac{NADPH}{K^{NADPH}}+\frac{NADP}{K^{NADP}}\right)}+\frac{3HBCoA}{K_{NADH}^{3HBCoA}}\right)*\left(1+\frac{AcAcCoA}{K_{NADH}^{AcAcCoA}}+\frac{NAD}{K^{NAD}*\left(1+\frac{NADPH}{K^{NADPH}}+\frac{NADP}{K^{NADP}}\right)}\right)}\hfill \end{array}$$

Therefore, besides the kinetic parameters and the ligands concentrations, enzyme concentration is required. If the kinetic parameters of the enzyme are known, it is possible to have an estimate of the enzyme concentration using as input an initial rate measured in defined conditions. During our initial rate measuring, the concentrations of the products were negligible, and the competitors NADP⁺ and NADPH were not present; therefore, the generic equation can be simplified to:

$$initialrate=\frac{k_{cat}^{NADH}*AA{R}^{CAp}*\frac{NADH*AcAcCoA}{K^{NADH}*K^{AcAcCoA}}}{\left(1+\frac{NADH}{K^{NADH}}\right)*\left(1+\frac{AcAcCoA}{K^{AcAcCoA}}\right)}$$

With concentrations of acetoacetyl-CoA 50 μM and NADH 50 μM, an initial rate of specific acetoacetyl-CoA reductase activity of 11.3 nmol/min/mg_cytoplasmic_proteins was measured in cell-free extracts from the engineered E. coli strain (((F– λ– ilvG– rfb-50 rph-1 (DE3) ΔadhE ΔadhP ΔldhA Δpta ΔmhpF)) transformed with the plasmid pCOLA-phaCAphaB-cscABK. With these data, enzyme concentration was estimated:

$$AA{R}^{CAp}=\frac{initialrate*K_M^{NADH}*K_M^{AcAcCoA}*\left(1+\frac{NADH}{K_M^{NADH}}\right)*\left(1+\frac{AcAcCoA}{K_M^{AcAcCoA}}\right)}{k_{cat}*NADH*AcAcCoA}=0.00135\frac{mgAA{R}^{CAp}}{mgcytoplasmicprotein}$$

where, k_cat = 8.9 mol NADH/mol_AAR^CAp/s; NADH in the assay = 50 µM; AcAcCoA in the assay = 50 µM; K_M^NADH = 7.7 µM; K_M^AcAcCoA = 56.7 µM; Molecular weight AAR^CAp = 25,896 gr_AAR^CAp/mol_AAR^CAp; acetoacetyl-CoA reductase specific activity = 11 nmol NADH/min/mg_cytoplasmic_protein.

Using the appropriate conversion factors, this enzyme abundancy can be expressed in units of mol AAR^CAp per gram of cell dry weight:

$$\begin{array}{ccc}& & \frac{0.00135gAA{R}^{CAp}}{gcyt.protein}*\frac{1molAA{R}^{CAp}}{25896gAA{R}^{CAp}}*\frac{0.8gcyt.protein}{1gtotalprotein}*\frac{0.68gtotalprotein}{1gCDW}\hfill \\ & & =0.0283\frac{\mu molAA{R}^{CAp}}{gCDW}\hfill \end{array}$$

Finally, converting micromole to millimole, and second to hours; the flux capacity can be expressed in units of mmol/gCDW/h.

Biomass composition of the engineered E. coli strain (((F– λ– ilvG– rfb-50 rph-1 (DE3) ΔadhE ΔadhP ΔldhA Δpta ΔmhpF)) transformed with the plasmid pCOLA-phaCAphaB-cscABK.

As reference for the lean biomass composition, we took the values reported by Taymaz-Nikerel and co-workers for E. coli K-12 MG1655 aerobically growing on glucose as the sole carbon source, at a dilution rate of 0.1 h⁻¹ [11]. Considering the elemental composition and the relative contributions to the weight of the different biomass components, we calculated: (1) the molar proportion of the different biomass components in the lean biomass, (2) the relative atomic composition of the total biomass (C₁H_1.681N_0.253O_0.3471S_0.0067P_0.0066), (3) the molecular weight of the virtual molecule representing the total biomass (M_wx = 23.195), and (4) the corresponding degree of reduction (4.301).

Given the fact that the genes enabling the PHB accumulation and the genes enabling the sucrose consumption were introduced via the plasmid pCOLA-phaCAphaB-cscABK, some modifications were introduced to the biomass composition to account for the plasmidial DNA and the heterologous proteins encoded by the genes carried by this plasmid.

To calculate the contribution of the plasmid to the cellular weight, some assumptions were done. In E. coli, it has been previously shown that the cell volume decreases with the dilution rate following a second degree polynomial equation [12]. Therefore, the published data of plasmid weights at different dilution rates [13] were fitted to a second degree polynomial equation to calculate the weight of the plasmids at 0.1 h⁻¹. The result was 0.0013 g_plasmid/gCDW (0.13%). Because available reports about the change in the copy number are contradictory, it was assumed that the number of plasmids per cell does not change with the dilution rate. The analyses of the GC content of the plasmid (54%) showed that the relative atomic composition of this molecule do not diverge significantly from the average E. coli chromosomal DNA. This way, the same relative atomic composition of the chromosomal DNA (C₁H_1.05N_0.385O_0.616P_0.103) was assigned for this plasmid.

On the other hand, to calculate the contribution to the cellular weight of the heterologous proteins encoded by the episomal genes carried by the plasmid, further assumptions were made. Because the DNA sequences of the episomal genes is known, it was possible to calculate the molecular weight of the encoded proteins. The contribution of the plasmid-encoded aminoglycoside acetyltransferase (KanR, protein responsible for resistance to kanamycin) to the E. coli proteome was calculated using the specific aminoglycoside acetyltransferase activities reported for E. coli C600 expressing the plasmid pWP701 and the activity of the aminoglycoside acetyltransferase purified from this strain [14]:

$$\mathrm{E}={\mathrm{V}}^{\text{max}}/{\mathrm{k}}_{\text{cat}}=\left(0.032\text{katal}/\text{mg}\_\text{cytoplasmic}\_\text{protein}\right)/\left(2\text{katal}/\text{mg}\_\text{KanR}\right)=0.0160\text{mg}\_\text{KanR}/\text{mg}\_\text{cytoplasmic}\_\text{protein}$$

Assuming that cscABK and KanR genes were expressed with similar strength, the relative contributions of the proteins encoded by the operon cscABK were calculated based on their molecular mass ratios respect to the molecular weight of the aminoglycoside acetyltransferase.

On the other hand, the specific AAR^CAp activity measured in cells of the engineered strain under initial rates conditions (0.011 µmol NADH/min/mg_cytoplasmic_protein) was taken to calculate the contribution of this enzyme to the pool of cytoplasmic proteins, as explained above:

$$AAR=\frac{AARsp.activity*K_M^{NADH}*K_M^{AcAcCoA}*\left(1+\frac{NADH}{K_M^{NADH}}\right)*\left(1+\frac{AcAcCoA}{K_M^{AcAcCoA}}\right)}{k_{cat}*NADH*AcAcCoA}=0.00135\left(\frac{mgAAR}{mgcytoplasmicprotein}\right)$$

Using the same approach applied to calculate the contributions to the proteome of the proteins encoded by the cscABK genes, the contributions of the proteins encoded by the phaCA^Cnecator genes to the E. coli proteome were calculated considering their protein molecular mass ratios respect to the molecular weight of AAR^CAp. Knowning that around 80% of the E. coli proteome are soluble proteins and proteins constitute 68% of the cell dry weight, it was estimated that heterologous proteins should represent 0.0502 g/gCDW (5% of the cell dry weight) (Table 4).

Table 4.

Contribution of the heterologous proteins to the biomass composition.

	Elemental composition						M (g/mol)	Individual contributions to cytoplasmic proteins pool
	C	H	N	O	S	P
KanR	1387	2124	376	406	13	0	30,944	0.0160*
cscA	2430	3619	685	707	21	0	54,353	0.0281*
cscB	2249	3354	512	545	20	0	46,870	0.0242*
cscK	1447	2305	407	442	17	0	32,983	0.0171*
phaB	1142	1828	306	344	18	0	25,896	0.00135*
phaA	1774	2906	502	538	21	0	40,502	0.0021*
phaC	2900	4452	800	836	13	0	64,244	0.0033*
Sum of individual contributions								0.0920*
Protein content in Biomass (g_protein/gCDW)								0.6819
Cytoplasmic proteins in total protein (%)								80
contribution of heterologous protein to Biomass (g_heterologous_proteins/gCDW)								0.0502

^⁎expressed in units of g_heterologous_protein/g_cytoplasmic_protein.

The analyses of the elemental composition of the heterologous proteins pool (C₁H_1.515N_0.264O_0.279S_0.009) showed that it does not diverge significantly from the average E. coli chromosomally-encoded protein (C₁H_1.58N_0.288O_0.309S_0.009). This way, the same relative atomic composition of the chromosomally-encoded protein was assigned for the heterologous proteins pool.

Knowing the contributions of plasmid and heterologous proteins to the cellular weight, the contributions of other biomolecules were re-scaled. With the relative contributions of the lean biomass, the plasmid and the heterologous proteins to 1 gCDW of total biomass; and considering the relative atomic compositions of the lean biomass, the plasmid and the heterologous proteins, we calculated:

• •The proportion between the virtual molecules representing the lean biomass, the plasmid and the heterologous proteins: 1 Lean Biomass: 0.0011 Plasmid: 0.0574 Heterologous proteins.
• •The relative atomic composition of the biomass including plasmid and heterologous proteins (C₁H_1.6749N_0.255O_0.3453S_0.0069P_0.0063), the molecular weight of the virtual molecule representing the total biomass (M_wx = 23.184) and the corresponding degree of reduction (4.292).

The final result appears in Table 1. In the folder “Fermentations”, in the repository “NADH-driven polyhydroxybutyrate accumulation in E. coli dataset 2″ in Mendeley Data, it is possible to find an Excel file named “Biomass composition” with all the above described calculations. Moreover, it is also possible to find a MATLAB script to generate an in silico metabolic model of the engineered strain.

It should be noticed that the bioenergetic parameters P/O ratio (δ), growth dependent maintenance (K_X) and growth independent maintenance (mATP) are explicit (modifiable) in the script generating the in silico model, enabling the exploration of the effects of changing those parameters.

Funding

This work was supported by the joint research program NWO (BRAZIL.2013.018) – FAPESP (2013/50,357-2). The contributions of Karel Olavarria and Mark C.M. van Loosdrecht were also supported by a SIAM Gravitation Grant (024.002.002) from the Netherlands Ministry of Education, Culture and Science (OCW) and NWO.

Ethics Statement

Authors confirm that this article follows the ethical requirements established by Data in Brief and the Elsevier. This work does not involved the use of human subjects, animal experiments or data collected from social media platforms.

CRediT authorship contribution statement

Karel Olavarria: Validation, Formal analysis, Investigation, Resources, Writing - original draft, Funding acquisition. Caspar Quakkelaar: Investigation. Joachim van Renselaar: Investigation. Dennis Langerak: Investigation. Mark C.M. van Loosdrecht: Supervision, Funding acquisition. S.A. Wahl: Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships which have or could be perceived to have influenced the work reported in this article.

Data Availability

• NADH-driven polyhydroxybutyrate accumulation in E. coli dataset 2 (Original data) (Mendeley Data)