Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Nov 23;5(48):31432–31439. doi: 10.1021/acsomega.0c05049

Complementary Base Lowers the Barrier in SuFEx Click Chemistry for Primary Amine Nucleophiles

Jan-Niclas Luy 1, Ralf Tonner 1,*
PMCID: PMC7726939  PMID: 33324855

Abstract

graphic file with name ao0c05049_0008.jpg

The sulfur(VI) fluoride exchange (SuFEx) reaction is an emerging scheme for connecting molecular building blocks. Due to its broad functional group tolerance and rather stable resulting linkage, it is seeing rapid adoption in various fields of chemistry. Still, to date the reaction mechanism is poorly understood, which hampers further development. Here, we show that the mechanism of the SuFEx reaction for the prototypical example of methanesulfonyl fluoride reacting with methylamine can be understood as an SN2-type reaction. By analyzing the reaction path with the help of density functional theory in vacuo and under consideration of solvent and co-reactant influence, we identify the often used complementary base as a crucial ingredient to lower the reaction barrier significantly by increasing the nucleophilicity of the primary amine. With the help of energy decomposition analysis at the transition state structures, we quantify the underlying stereoelectronic effects and propose new avenues for experimental exploration of the potential of SuFEx chemistry.

Introduction

The sulfur(VI) fluoride exchange reaction (SuFEx) was introduced as a new member of the “click chemistry” family1 by Sharpless et al.,2 thus significantly extending the previous work on organosulfur fluorides.3,4 The method has recently seen a surge in research interest due to its excellent functional group tolerance, robustness, and reliability in diverse applications such as drug design,5−7 polymer chemistry,8,9 and materials science.10−12 The SuFEx scheme is mainly used for linking molecular building blocks by substituting the fluoride atom of sulfonyl fluorides with a suitable nucleophile (see Scheme 1 for a typical example investigated here).

Scheme 1. Typical Example of SuFEx Chemistry Investigated in this Study Reaction of Methanesulfonyl Fluoride 1 with Nucleophile Methylamine 2 Yields Sulfonylamine 3 and Hydrogenfluoride.

Scheme 1

Open in a new tab

From the wealth of available nucleophiles, aryl silyl ethers have so far received most attention since they lead to high yields and show a broad substrate scope.13 An alternative to aryl silyl ethers that promises simpler protocols and stronger (S–N) links while providing good yields are amine-based nucleophiles.5,14 These characteristics explain the interest in SuFEx chemistry far beyond the realm of organic synthesis, e.g., in surface chemistry. But how can this reaction scheme lead to progress in these fields?

Controlled organic functionalization of semiconductor surfaces is a major research goal in materials science with applications ranging from sensors to molecular devices.15 Functionalization can be carried out with solvent being present and also under ultrahigh vacuum (UHV) conditions more typical for surface science or even a combination of both.16

Our long-term goal in this research field is the identification of suitable reaction schemes for controlled functionalization in a layer-by-layer fashion from a computational perspective.17,18 In this context, single-step reaction procedures like SuFEx are strongly preferred due to the synthetic constraints added by the surface.19 Furthermore, optimization of reaction conditions in UHV chemistry is limited since variation of, e.g., solvent or pH values are not possible. Thus, a “click”-type reaction is sought for. Suitability of SuFEx for surface functionalization and the “click”-character under typical reaction conditions has been shown recently in several studies.19−21 It has also been noted that for surface functionalization, amine-based nucleophiles (Scheme 1) are preferred over the standard SuFEx route since no prior installation of silyl ethers on the surface is necessary.19 We thus set out to understand the reaction mechanism of SuFEx in vacuum as well as wet chemical conditions to test its feasibility for the scenarios of surface functionalization mentioned above.

The main factor limiting the potential of SuFEx chemistry is the lack of mechanistic insight, e.g., concerning the role of co-reactants and solvents.22 The current understanding of the reaction mechanism based on experimental observations states that stabilization of the fluoride ion in intermediates and products is the determining factor in achieving high reaction rates.2 There are also suggestions regarding the role of the base as either attacking the fluorosulfonate moiety to displace fluorine or act as a fluorine shuttle.10,23 Overall, it is observed that strong bases and H2F– can act as catalysts for the reaction but the exact role is unclear up to now.10,19,24,25

We challenge and extend this understanding in the present study. Very recently, the mechanism of the Si-free SuFEx reaction with phenolate anions was investigated with the help of density functional theory (DFT), and an addition–elimination mechanism with very low barriers and early transition states was found while an SN2-type reaction could not be excluded under experimental conditions.26 The authors also concluded that the very high reactivity of the phenolate anion probably leads to a different mechanism compared to less strong nucleophiles, as investigated here.

As a suitable model system comprising all the essential elements of SuFEx chemistry suitable for surface functionalization, we chose the reaction of methanesulfonyl fluoride 1 with methylamine 2 (reaction (1), Scheme 1). The results should be transferable to other aliphatic amines and further nucleophiles, as shown below. The article is structured as follows: We start with an in-depth analysis of the gas phase reaction mechanism, including thermodynamic and kinetic aspects. Following this, the influence of solvent and co-reactant is investigated with the aid of implicit solvation modeling and microsolvation approaches.27,28 Finally, the electronic structure of the product and transition state structure are analyzed with the help of energy decomposition analysis (EDA) to provide a rationale for the observations.

Results and Discussion

First, we discuss gas phase reaction energies (ΔE°) and energy barriers (ΔE‡) for the most plausible mechanism proposed in the literature: nucleophilic substitution at the sulfur atom (Figure 1).2 Reaction (1) proceeds via a weakly-bound pre-complex 1-2 (dispersion interactions contribute ∼50% to the bonding energy) through a high-lying transition-state structure (TS) toward a post-complex with hydrogen-bonded HF (3-HF) that can dissociate in the final reaction step to yield product 3. The total reaction is computed (PBE0-D3/def2-TZVPP//PBE-D3/def2-TZVPP) to be slightly exothermic (ΔE° = −8 kJ/mol), while the activation energy to the TS is high (ΔE‡ = 159 kJ/mol). Considering thermodynamic and entropic corrections leads to a slight increase in barrier (ΔG° = −4 kJ/mol, ΔG‡ = 170 kJ/mol). But these correction terms have a significant influence on pre- and post-complexes, which are significantly destabilized due to the unfavorable entropic term TΔS for association reactions (loss of translational freedom). The reaction might indeed proceed without these pre- and post-complexes under typical lab conditions, similar to the difference in SN2 reaction profiles between gas-phase and solution-phase chemistry.29 This will be further discussed below when solvent effects are presented.

Figure 1.

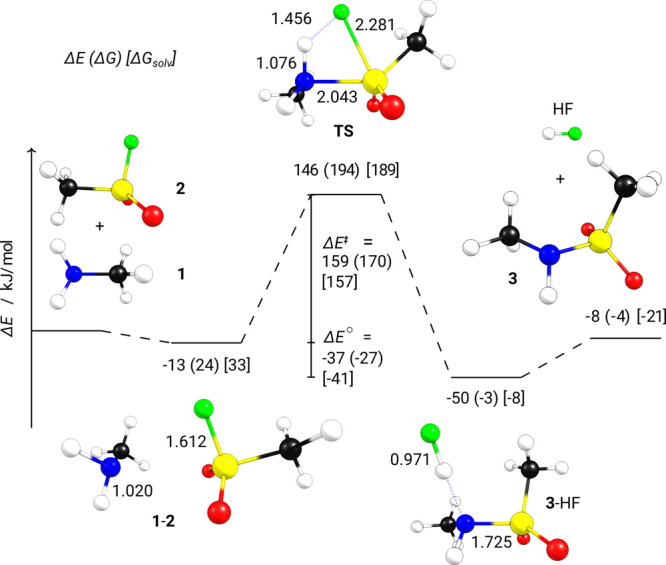
Figure 1

Open in a new tab

Reaction profile of 1 with 2 yielding 3 and HF. The reaction energy ΔE° (PBE0) is the difference between energies of pre-complex 1-2 and post-complex 3-HF. The barrier ΔE‡ (PBE0) is the difference between 1-2 and TS. Gibbs energies ΔG (PBE) are given in parentheses and the energies with implicit solvent correction for water ΔGsolv (PBE) in square brackets. All calculations with def2-TZVPP basis set.

The high barriers computed are in line with the long reaction times and low yields reported in some studies for reactions at room temperature.2,5,7 In comparison, the frequently utilized Cu-catalyzed azide–alkyne cycloaddition “click” reaction shows much more favorable thermodynamic and kinetic signatures (ΔE° = −254 kJ/mol, ΔE‡ = 62 kJ/mol30). The strain-promoted azide–alkyne cycloaddition shows an even lower reaction barrier of ΔE‡ = 33 kJ/mol,31 highlighting the need for further optimization of the amine SuFEx reaction scheme. We will outline some possibilities for this optimization in the following.

Next, we analyze the nature of the TS with the help of reaction force analysis of the potential energy surface (PES) from 1-2 to 3-HF. This approach based on a fine-grained intrinsic reaction coordinate (IRC) calculation starting at the TS yields the reaction force (F, blue line in Figure 2) and the force constant (κ, green line in Figure 2) along the IRC. The roots of κ separate the IRC path into regions resembling TS (gray), reactants (yellow), and products (red) whose shape and size characterize the phases of a reaction.32,33 It thus allows to characterize the nature of transition states and provides a microscopic picture on the crucial changes in the molecule along the minimum energy path with the largest influence on the reaction barrier.34

Figure 2.

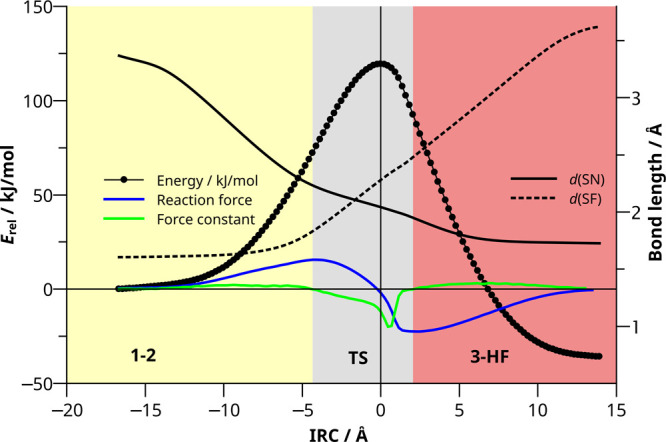
Figure 2

Open in a new tab

Result of reaction force analysis for reaction (1). The Euclidean distance between steps is tracked on the x axis and energy relative to 1-2 on the left axis. The reaction force, F (blue) and force constant, κ (green) are the first and second derivative of the energy with respect to atomic positions, respectively. Changes in the bond lengths d(SN) (solid) and d(SF) (dotted) are tracked on the right axis.

The first finding is an asymmetric profile of the transition region (gray area). The TS is positioned rather close to the product, and the minimum of the force constant curve (green) does not coincide with the maximum of the energy (black circles). Those characteristics are indicative of a non-concerted reaction where bond-breaking and bond-making do not happen simultaneously along the reaction path as has been found before for the β-H elimination of group 15 alkyls.34 An analysis of the bond lengths along the reaction path (Figure 2) confirms that the S–F bond is only slightly elongated at the beginning of the transition region (deviation from value in 2, Δd(SF) = +0.227 Å) while the S–N bond is already close to its value at the TS (deviation from value at TS: Δd(SN) = +0.190 Å, see also the animated IRC in the Video S1). At the TS, the N–H bond is only moderately elongated (Δd(NH) = +0.056 Å, see Figure 1) and cannot be considered broken, yet. However, after the TS, cleavage of the N–H bond together with H–F bond formation proceeds fast and simultaneously. It becomes evident that around TS, the fluorine atom is already dissociated from S but not yet bound to H. As supported by partial charge analysis (natural population analysis, NPA), we have a nearly “naked” fluorine anion at the TS, which explains the high barrier (q(F): −0.47 (1); −0.70 (TS); −0.54 e (3-HF)). This seemingly supports the findings in the literature that stabilization of F– should lead to a decreased barrier and in turn, an increase in the reaction rate. We will now show that the picture is more complex.

Effects of Solvent, Side Product, and Co-Reactant

After the examination of the gas-phase reaction, we now include solvent effects by means of (i) a continuum solvation model (conductor-like screening model, COSMO)35 and (ii) microsolvation approaches. Initially, we look at the effect of H2O since it is a typical solvent for the SuFEx reaction, e.g., for in vivo studies and biphasic solvent approaches.2,7 Furthermore, we investigate the effects of the side product HF and of N(CH3)3 as a typical example for the base often used in SuFEx reactions as co-reactant.2,5 The results are summarized in Table 1.

Table 1. Reaction Free Energies and Barriers of the SuFEx Reaction Showing the Influence of Solvent (H2O), Side Product (HF) and Base (N(CH3)3)a.

solvent description ΔG° (ΔΔG°) ΔG‡ (ΔΔG‡)
in vacuo –27 (0) 170 (0)
+H2O (implicit) –41 (−14) 157 (−13)
+H2O (explicit) –32 (−5) 165 (−5)
+HF –2 (+25) 175 (+5)
+N(CH3)3 –60 (−33) 143 (−27)
+HF and N(CH3)3 –33 (−6) 143 (−27)
Open in a new tab
a

All energies in kJ/mol at PBE0/def2-TZVPP//PBE/def2-TZVPP. Solvent correction at PBE/def2-TZVPP. Gibbs free energies (ΔG°, ΔG‡) are given with respect to the pre- and post-complexes with the shortest Euclidian distance to the TS (see Figure S2 in the Supporting Information for product structures) and changes w.r.t. the in vacuo value are given in parentheses (ΔΔG°, ΔΔG‡). Electronic energies (ΔE) are listed in the Supporting Information (Table S2) as well.

First, we investigate the influence of H2O on thermodynamic and kinetic signatures of reaction (1) (Table 1). The stabilizing electrostatic effect of water due to its high dielectric constant (ε = 80) is already found with the COSMO approach (which is not able to capture hydrogen bonding effects), and the numbers are given in Figure 1 (ΔGsolv in square brackets). We discuss the values relative to the Gibbs energy reference (ΔG, in round brackets). Notably, the pre-complex 1-2 is destabilized (ΔΔG = +9 kJ/mol) while the post-complex 3-HF is slightly stabilized (ΔΔG = −5 kJ/mol). The polar transition state is stabilized leading to a slightly lower barrier (ΔΔG‡ = −13 kJ/mol, Table 1).

Next, we look at the effect of microsolvation by including one H2O molecule explicitly in the calculation. The effect on the barrier is small (ΔΔG‡ = −5 kJ/mol, Table 1), and the thermodynamic driving force is also less strong (ΔΔG° = −5 kJ/mol) compared to the implicit solvent treatment (ΔΔG° = −14 kJ/mol). Both methods show qualitatively the same trends, but for a quantitative answer a comprehensive modeling of several explicit solvation shells (possibly in addition to an implicit treatment) is needed, which is beyond the scope of this study. An improved estimate of the reaction barrier in water is given by combining implicit solvent modeling and three explicit water molecules in a trimer structure,36 leading to a barrier of ΔE‡ = 153 kJ/mol. This value is only 6 kJ/mol smaller compared to the gas-phase value (Table S2), supporting the notion of small solvent influence.

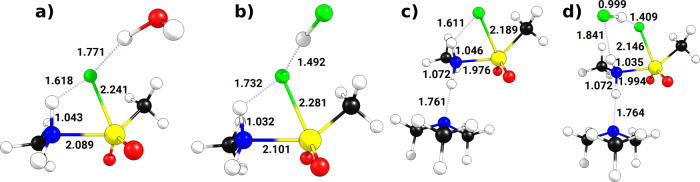
It is likely that the implicit solvation model overestimates the stabilization of TS and post-complex 3-HF in aqueous solution when compared to the explicit treatment since structural changes induced by hydrogen bonds are not accounted for. Those structural changes can be large, as shown in Figure 3. Coordination of H2O to the leaving group fluorine (Figure 3a) leads to longer F–H (+0.162 Å), S–N (+0.040 Å) distances and shorter N–H (−0.033 Å) and S–F bonds (−0.040 Å) with respect to the in vacuo values (Figure 1). This stabilization thus leads to an earlier transition state, in accordance with the Hammond–Leffler postulate and the slightly lower barrier.

Figure 3.

Figure 3

Open in a new tab

Optimized transition state structures with selected structural parameters under consideration of (a) explicit solvent (H2O), (b) side product (HF), (c) base (N(CH3)3), and (d) side product and base combined (HF + N(CH3)3). Bond lengths are given in Å.

Next, we consider the influence of side product HF taking part in the reaction, which is rather likely due to the stoichiometric amounts being formed in reaction (1). The reaction becomes considerably less favorable (ΔΔG° = +25 kJ/mol, Table 1), and the barrier increases slightly (ΔΔG‡ = +5 kJ/mol). The changes in bond lengths for the transition state structure are puzzling at first sight (Figure 3b). While the longer F–H (+0.276 Å) and S–N (+0.058 Å) bonds as well as the short N–H (−0.044 Å) bond indicate an even earlier transition state, the S–F distance is unchanged wrt the in vacuo calculation. This can be understood by the exceptionally high stability of the 4e3c bond (1.492 Å) in [FHF]−, which leads to a stabilized and almost detached fluorine leaving group rather early on the IRC.37 The apparent destabilization of TS comes as a result of choosing the pre-complex where HF is coordinated to the amine as the reference. When calculating the barrier with respect to the reactants, a stabilization of 24 kJ/mol is found compared to the gas-phase reaction. Ultimately, an HF dimer is formed, which has a weaker hydrogen bond compared to [FHF]−.

Common co-reactants in SuFEx chemistry are tertiary amine bases.5 Thus, we consider next the reaction including N(CH3)3. The added base has the strongest influence on the reactivity among the additives considered here and leads to a stronger exergonic reaction (ΔΔG° = −33 kJ/mol, Table 1) as well as a significantly lower reaction barrier (ΔΔG‡ = −27 kJ/mol). The base coordinates to the nucleophile (Figure 3c) and leads to an unusual transition state structure where the S–F bond is rather short (−0.092 Å) and the F–H distance long (+0.155 Å), indicating an early transition state but the N–S bond is quite short already (−0.067 Å). This can be understood through the increased nucleophilicity of the attacking amine as evidenced by the HOMO being higher in energy with added base compared to the free nucleophile (ΔEHOMO = +0.63 eV).

After traversal of the transition region, structural reorganization of the post-complex takes place (see Figure S2). The thermodynamic driving force of this reorganization is the formation of a HF/N(CH3)3 acid/base adduct. This reaction thus removes the base from the reaction mixture and helps to rationalize the experimental finding that the base is necessary in stoichiometric amounts to achieve good yields.2,5

Finally, we investigate the effect of side product HF and amine base being present at the same time. The barrier lowered by the base is not affected by HF being present (ΔΔG‡ = −27 kJ/mol), and the transition state structure (Figure 3d) shows similar features compared to base alone (Figure 3c). The difference is found for two additional hydrogen bonds being formed by HF with fluorine and the amine group, respectively. The hydrogen bond between the fluorine atom and amine group present in all other transition state structures is thus broken but there is no net energetic penalty (ΔΔG‡ is the same for the last two lines in Table 1). The final structure is less stable compared to the pure base adduct (ΔΔG° = −6 kJ/mol) due to an extended H–bond network (see Figure S2 in the Supporting Information).

From these investigations, we conclude that the largest influence on the reaction barrier is found for the amine base increasing the nucleophilicity of CH3NH2. The stabilization of the leaving group fluorine has a much smaller effect on the reaction barrier. The solvent effect at the example of water is moderate and seems to be well captured by an implicit solvation model.

Bonding Analysis

Concerning the reaction mechanism, two questions remain which cannot be answered by total energy calculations alone: What are the details of bond formation providing the driving force for the SuFEx reaction? Which (electronic) effect causes the added base to lower the barrier? The energy decomposition analysis (EDA) is an ideal tool to address both questions as it decomposes the interaction energy (ΔEint) between two molecular fragments into quantities that can be correlated to chemical bonding concepts.38−40 First, ΔEint is decomposed into an electronic interaction term (ΔEint(elec)) and a dispersion contribution (ΔEint(disp)) that is derived by semiempirical approximations (DFT-D3).41 The actual EDA procedure then breaks down ΔEint(elec) into a quasiclassical electrostatic contribution (ΔEelstat), orbital interaction comprising charge transfer and polarization (ΔEorb), and Pauli repulsion (ΔEPauli).40,42 After including the energy that is required to deform the fragments into the structure (and electronic state) they have in the molecule (ΔEprep), the total bonding energy (ΔEbond) can be written as

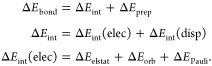graphic file with name ao0c05049_m001.jpg

The orbital interaction term (ΔEorb) can be further decomposed with the help of natural orbitals for chemical valence (NOCV).43 Here, the major orbital interactions can be visually identified and their energy contribution quantified.

Table 2 shows the EDA results of 3 and TS with and without base. First, we note that the best description of the newly formed S–N bond changes along the reaction path. This finding is in line with chemical intuition but can now be quantitatively supported by EDA. The TS is best described as a donor–acceptor complex between closed shell molecules. Here, the role of the donor is adopted by the nucleophile methylamine, and the electron poor sulfur atom of the sulfonylfluoride is the acceptor. Product 3 on the other hand shows a shared electron S–N bond, which is a consequence of cleaving the bond homolytically assigning one electron to each of the fragments. The EDA allows for different fragmentations favoring either a donor–acceptor or shared electron description. It is well established that the best description of a system is given by the EDA fragmentation with the lowest orbital energy value.44 The EDA can thus help in deciding which bonding picture is more appropriate. As shown in Table S3 in the Supporting Information, the alternative fragmentation scheme for 3 as a donor–acceptor complex shows a significantly higher ΔEorb value and is thus the less suitable description.

Table 2. Bonding Analysis (EDA) of 3 and TS with and without N(CH3)3a.

bonding analysis (EDA) 3 TS TS + N(CH3)3
ΔEint –308   –152   –193  
ΔEint(disp)b –12 4% –13 9% –21 11%
ΔEint(elec)b –296 96% –138 91% –172 89%
ΔEPauli 1742   852   957  
ΔEelstatc –885 43% –479 48% –560 50%
ΔEorbc –1153 57% –511 52% –569 50%
ΔEorb(S–N)d –971 84% –402 79% –466 82%
ΔEorb(NH--F)d     –55 11% –34 6%
ΔEorb(rest)d –182 16% –54 11% –69 12%
ΔEprep 15   260   266  
ΔEbond –293   108   72  
Open in a new tab
a

All energies in kJ/mol at PBE/TZ2P. Fragments for 3 are generated from homolytic cleavage at N–S into neutral doublets. For the TS, the reactants are used as fragments in a neutral, singlet configuration.

b

Percentage values: Relative contributions of dispersion and electronic effects to the interaction energy ΔEint.

c

Percentage values: Relative contributions between the attractive EDA terms ΔEelstat and ΔEorb.

d

Percentage values: Relative contributions to the orbital interaction ΔEorb. The character of the orbital contribution as S–N bond or NH--F hydrogen bond is revealed by NOCV analysis, as shown below. Non-assignable contributions are summed in the “rest” term.

The shared electron S–N bond in 3 is strong (ΔEbond = −293 kJ/mol) and shows only very small contributions from dispersion interaction; the interaction energy is governed by large EDA terms ΔEelstat, ΔEorb, and ΔEPauli. The major stabilizing term (57%) is the orbital interaction energy (ΔEorb), which is typical for bonds with a strong covalent character found in orbital-driven reactions.42 The ΔEorb term is largely governed by contributions from the S–N bond (84% of ΔEorb) as indicated by deformation densities (Δρ) derived from the NOCV analysis (Figure 4). The unequal contributions from the sulfonyl group (Figure 4a; Δρα1, ΔEα1 = −637 kJ/mol) and the amine group (Figure 4b; Δρβ1, ΔEβ1 = −334 kJ/mol) together with the difference in eigenvalues (να1 = ±0.83, νβ1 = ±0.55) are characteristics for a shared-electron bond polarized toward nitrogen, in line with the higher electronegativity of this element.

Figure 4.

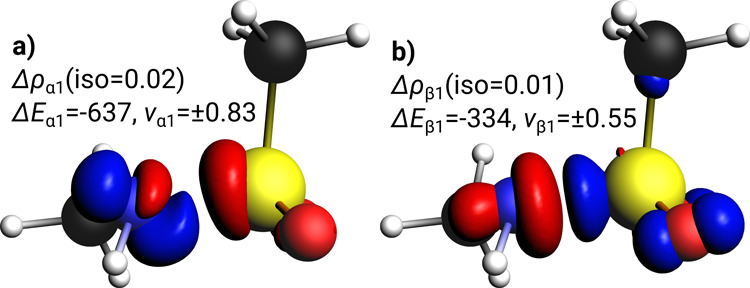
Figure 4

Open in a new tab

Deformation density Δρ1 shows charge flow between NOCVs of 3 and associated contributions to the total orbital energy (ΔE1 in kJ/mol) for α- and β-electrons, respectively. Eigenvalues ν1 quantify the amount of transferred electron density (red: charge depletion, blue: charge accumulation). Iso-values are chosen for visual clarity. Bonding character of Δρ1 is a polar shared-electron N–S bond with contributions from the (a) sulfonyl fragment and from the (b) amine fragment.

In contrast to the product, the S–N bond in the TS with and without base can be described as a donor–acceptor interaction (Table 2). Although, fluorine could in principle be described as being an independent fragment (leading to a three-fragment EDA), we chose to describe the former sulfonylfluoride as one fragment based on previous experience with transition state analysis in similar systems.34 The interaction energy in the TS is much lower (ΔEint = −152 kJ/mol) as expected for a state where the bond formation process is still ongoing. Again, the major bonding contributions are of covalent nature, and dispersion interactions play a minor role. The nearly equal contribution of electrostatic (48%) and orbital interaction (52%) to the attractive energy terms are typical for a donor–acceptor interaction.45 The bonding energy is positive here due to a high preparation energy (ΔEprep = +260 kJ/mol) in line with the high energy barrier described earlier. The major contribution to the orbital interaction (79%) is given by the charge donation of the non-bonded electron pair at nitrogen into the acceptor orbital at the sulfonyl fragment (ΔE1 = −402 kJ/mol, Figure 5a). A further significant stabilization comes from the already forming hydrogen bond NH---F delivering a further 55 kJ/mol to the orbital energy term (Figure 5b). In line with the partial charge at the fluorine atom discussed above, we find charge flow in Δρ1 to F, which is not compensated by the reverse, much smaller, charge flow in Δρ2.

Figure 5.

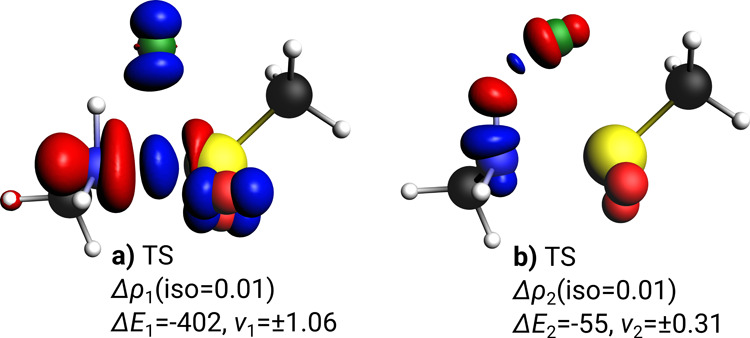
Figure 5

Open in a new tab

Selected deformation densities Δρi show charge flow between NOCVs of TS and associated contributions to the total orbital energy (ΔEi in kJ/mol). Eigenvalues νi quantify the amount of transferred electron density (red: charge depletion, blue: charge accumulation). Iso-values are chosen for visual clarity. Bonding character of Δρi is (a) LP(N) → p*(S) donor–acceptor bond, (b) NH---F hydrogen bond.

Adding the amine base changes the bonding picture only gradually (Table 2). But the value of the interaction energy increases significantly (ΔΔEint = −41 kJ/mol), in line with the lowering of the barrier discussed above. The resulting shorter S–N distance in the transition state structure leads to all three EDA terms rising in total value. The resulting balance between orbital (50%) and electrostatic (50%) energy contributions indicates an increased significance of the latter term compared to TS without base. We can reveal the nature of the increased orbital interaction by NOCV analysis. The deformation densities are unaltered compared to TS without base and are thus shown in the Supporting Information (Figure S3). Significant change is found for the donor-acceptor bond, where the orbital contribution (ΔEorb(S–N)) increases by 64 kJ/mol, and the NH---F hydrogen bond (ΔEorb(NH--F)) is weakened by 21 kJ/mol.

Thus, it appears that the major effect of the added base is a strengthening of the dative S–N bond in the transition state structure by increasing the nucleophilicity of the amine base. This local effect should be found in other reactants as well since it depends only on a local bonding interaction.

Conclusions

Our computational investigations of the mechanism for the SuFEx reaction for a prototypical case of fluoride substitution by a primary amine at the density functional theory level revealed that the reaction shows a high energy barrier that can be lowered significantly by an added base. The reaction proceeds via a non-synchronous one-step mechanism with initial weakening of the S–F bond and slightly delayed nucleophilic attack of the amine. The major effect of the base is to increase the nucleophilicity of the amine. The influence of a typical solvent (water) and side product HF on the reaction barrier is small. But HF can decrease the reactivity by destabilizing the product and should therefore be scavenged. As an added side effect, scavenging might reduce the risk of racemization.46

The results indicate further possibility for experimentally improving the scope of SuFEx chemistry by adjusting the strengths and stoichiometry of the base added. Tertiary amine bases are favorable since they cannot act as nucleophiles in this reaction scheme themselves due to lack of acidic protons, thus avoiding side reactions. Possibly, steric effects of the added base have to be considered when the transition state structure becomes crowded. Polar solvents that stabilize the leaving group F– are able to lower the reaction barrier further. This study gives some indication from a microsolvation approach but for a quantitative result, large-scale solvent-shell simulations are a possible next step.

Our hypothesis can be experimentally probed by kinetic measurements, testing a dependency of the reaction rate on the base concentration in SuFEx schemes. Since the main effect of the base is an increase in nucleophilicity while not changing the bonding at the transition state structure, this conclusion can be extended to other typical nucleophiles in SuFEx chemistry that probably follow the same mechanism (e.g., other amines, alcohols).

We show that electronic structure analysis of a prototypical system via energy decomposition analysis can reveal the determining factor for an important class of organic reactions.

Computational Methods

Structure optimizations were performed with TURBOMOLE 7.247 using the generalized gradient approximation (GGA)-based exchange–correlation density functional PBE,48 including DFT-D3 dispersion correction with a Becke–Johnson (BJ) type damping function.41,49 After careful benchmarking against high-precision wave function-based methods (see Table S1 in the Supporting Information), the hybrid functional PBE0-D350 was employed for total energy calculations. Throughout this work, the def2-TZVPP basis set51 together with a fine integration grid (m4) was used and the self-consistent field (SCF) energy convergence criteria set to 10–8Eh. All generated minima (transition states) were verified to have zero (one) imaginary frequency modes via analytic computation of the Hesse matrix.

Additionally, the implicit solvation model COSMO35 was used to compare the response of the solute to the explicit “microsolvation” method. Default values were taken for cavity construction. Solvation energies are reported, including the outlying charge correction.

Gibbs free energies (ΔG) were calculated at the PBE-D3(BJ) level. For this purpose the interactive program “freeh” included in the TURBOMOLE suite was used. The partition sums were computed in the rigid rotor, harmonic oscillator, and ideal gas approximations. Vibrational energies were not scaled and imaginary vibrational modes (at transition states) were excluded from the analysis. Standard ambient temperature (298.15 K) and pressure (0.1 MPa) (SATP) values were chosen. Calculated chemical potentials were then added to the total electronic energy at the hybrid-DFT PBE0-D3 level to yield Gibbs free energies.

The reaction force F(ζ) = – ∂E/∂ζ and force constant32,33 κ(ζ) = ∂E2/∂2ζ were calculated by numerical differentiation (centered finite differences) of a high-resolution intrinsic reaction coordinate (IRC) ζ with PBE-D3. The IRC connects stationary points on the potential energy surface (PES). Points of inflection along the IRC separate the reaction into reactant, product, and transition regions. A symmetrical transition region indicates a concerted mechanism. The IRC was generated with the Gaussian16 (A.03) program52 (CalcAll, MaxPoints = 150, Tight). Settings used with Gaussian16 were set to resemble those of TURBOMOLE as close as possible. While the basis set and functional are identical to those used with TURBOMOLE, the numerical integration grid was set to “UltraFine”, and the quadratically convergent SCF procedure was used.

The energy decomposition analysis (EDA)53 was performed with the Amsterdam density functional (ADF 2019.301) package.54−56 Again, the PBE-D3 functional was used in conjunction with the triple-zeta Slater-type basis set TZ2P57 and the frozen core was set to “large”. Scalar relativistic effects were treated with the zeroth order regular approximation.58 Within the EDA scheme, the interaction energy between molecular fragments is decomposed into electrostatic contribution, Pauli repulsion, orbital relaxation, and dispersion. Together with the fragment preparation energy the bonding energy is derived as outlined in the manuscript.

The natural orbitals for chemical valence (NOCV)43 scheme is an extension to this method. Here, the orbital relaxation is further separated into individual deformation densities Δρ and corresponding eigenvalues ±ν that quantify the electron flow. This allows for the interpretation of interactions between fragments by visual inspection of the most important deformation densities.

Acknowledgments

The authors thank the German Research Foundation (DFG) for funding via SFB 1083 and also acknowledge computational resources provided by HRZ Marburg and CSC Frankfurt.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c05049.

  • Additional structural data, energies, and computational raw data (PDF)

  • Video showing IRC animations (MP4)

The authors declare no competing financial interest.

Supplementary Material

ao0c05049_si_001.pdf (787KB, pdf)
ao0c05049_si_002.mp4 (78.6KB, mp4)

References

  1. Kolb H. C.; Finn M. G.; Sharpless K. B. Click Chemistry: Diverse Chemical Function from a Few Good Reactions. Angew. Chem., Int. Ed. 2001, 40, 2004–2021. . [DOI] [PubMed] [Google Scholar]
  2. Dong J.; Krasnova L.; Finn M. G.; Sharpless K. B. Sulfur (VI) fluoride exchange (SuFEx): another good reaction for click chemistry. Angew. Chem. Int. Ed. 2014, 53, 9430–9448. 10.1002/anie.201309399. [DOI] [PubMed] [Google Scholar]
  3. Steinkopf W. Über Aromatische Sulfofluoride. J. Prakt. Chem. 1927, 117, 1–82. 10.1002/prac.19271170101. [DOI] [Google Scholar]
  4. Krutak J. J.; Burpitt R. D.; Moore W. H.; Hyatt J. A. Chemistry of ethenesulfonyl fluoride. Fluorosulfonylethylation of organic compounds. J. Org. Chem. 1979, 44, 3847–3858. 10.1021/jo01336a022. [DOI] [Google Scholar]
  5. Bogolubsky A. V.; Moroz Y. S.; Mykhailiuk P. K.; Pipko S. E.; Konovets A. I.; Sadkova I. V.; Tolmachev A. Sulfonyl Fluorides as Alternative to Sulfonyl Chlorides in Parallel Synthesis of Aliphatic Sulfonamides. ACS Comb. Sci. 2014, 16, 192–197. 10.1021/co400164z. [DOI] [PubMed] [Google Scholar]
  6. Liu Z.; Li J.; Li S.; Li G.; Sharpless K. B.; Wu P. SuFEx Click Chemistry Enabled Late-Stage Drug Functionalization. J. Am. Chem. Soc. 2018, 140, 2919–2925. 10.1021/jacs.7b12788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Wang N.; Yang B.; Fu C.; Zhu H.; Zheng F.; Kobayashi T.; Liu J.; Li S.; Ma C.; Wang P. G.; Wang Q.; Wang L. Genetically Encoding Fluorosulfate-l-tyrosine To React with Lysine, Histidine, and Tyrosine via SuFEx in Proteins in Vivo. J. Am. Chem. Soc. 2018, 140, 4995–4999. 10.1021/jacs.8b01087. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Oakdale J. S.; Kwisnek L.; Fokin V. V. Selective and Orthogonal Post-Polymerization Modification using Sulfur(VI) Fluoride Exchange (SuFEx) and Copper-Catalyzed Azide–Alkyne Cycloaddition (CuAAC) Reactions. Macromolecules 2016, 49, 4473–4479. 10.1021/acs.macromol.6b00101. [DOI] [Google Scholar]
  9. Brendel J. C.; Martin L.; Zhang J.; Perrier S. SuFEx – a selectively triggered chemistry for fast, efficient and equimolar polymer–polymer coupling reactions. Polym. Chem. 2017, 8, 7475–7485. 10.1039/C7PY01636K. [DOI] [Google Scholar]
  10. Brooks K.; Yatvin J.; Kovaliov M.; Crane G. H.; Horn J.; Averick S.; Locklin J. SuFEx Postpolymerization Modification Kinetics and Reactivity in Polymer Brushes. Macromolecules 2018, 51, 297–305. 10.1021/acs.macromol.7b02372. [DOI] [Google Scholar]
  11. Fan H.; Ji Y.; Xu Q.; Zhou F.; Wu B.; Wang L.; Li Y.; Lu J. Sulfur (VI) Fluoride Exchange Polymerization for Large Conjugate Chromophores and Functional Main-Chain Polysulfates with Nonvolatile Memory Performance. ChemPlusChem 2018, 83, 407–413. 10.1002/cplu.201800067. [DOI] [PubMed] [Google Scholar]
  12. Park S.; Song H.; Ko N.; Kim C.; Kim K.; Lee E. SuFEx in Metal–Organic Frameworks: Versatile Postsynthetic Modification Tool. ACS Appl. Mater. Interfaces 2018, 10, 33785–33789. 10.1021/acsami.8b14065. [DOI] [PubMed] [Google Scholar]
  13. Gao B.; Zhang L.; Zheng Q.; Zhou F.; Klivansky L. M.; Lu J.; Liu Y.; Dong J.; Wu P.; Sharpless K. B. Bifluoride-catalysed sulfur(VI) fluoride exchange reaction for the synthesis of polysulfates and polysulfonates. Nat. Chem. 2017, 9, 1083–1088. 10.1038/nchem.2796. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Li C.; Zheng Y.; Rakesh K. P.; Qin H.-L. But-3-ene-1,3-disulfonyl difluoride (BDF): a highly selective SuFEx clickable hub for the quick assembly of sultam-containing aliphatic sulfonyl fluorides. Chem. Commun. 2020, 56, 8075–8078. 10.1039/D0CC03248D. [DOI] [PubMed] [Google Scholar]
  15. Wolkow R. A. Controlled molecular adsorption on silicon: Laying a Foundation for Molecular Devices. Annu. Rev. Phys. Chem. 1999, 50, 413–441. 10.1146/annurev.physchem.50.1.413. [DOI] [PubMed] [Google Scholar]
  16. He C.; Abraham B.; Fan H.; Harmer R.; Li Z.; Galoppini E.; Gundlach L.; Teplyakov A. V. Morphology-Preserving Sensitization of ZnO Nanorod Surfaces via Click-Chemistry. J. Phys. Chem. Lett. 2018, 9, 768–772. 10.1021/acs.jpclett.7b03388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Pecher L.; Schober C.; Tonner R. Chemisorption of a Strained but Flexible Molecule: Cyclooctyne on Si(001). Chem. – Eur. J. 2017, 23, 5459–5466. 10.1002/chem.201605952. [DOI] [PubMed] [Google Scholar]
  18. Pecher L.; Tonner R. Computational analysis of the competitive bonding and reactivity pattern of a bifunctional cyclooctyne on Si(001). Theor. Chem. Acc. 2018, 137, 48. 10.1007/s00214-018-2212-5. [DOI] [Google Scholar]
  19. Gahtory D.; Sen R.; Pujari S.; Li S.; Zheng Q.; Moses J. E.; Sharpless K. B.; Zuilhof H. Quantitative and Orthogonal Formation and Reactivity of SuFEx Platforms. Chem. – Eur. J. 2018, 24, 10550–10556. 10.1002/chem.201802356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Liu S.; Cao Y.; Wu Z.; Chen H. Reactive films fabricated using click sulfur(vi)–fluoride exchange reactions via layer-by-layer assembly. J. Mater. Chem. B 2020, 8, 5529–5534. 10.1039/D0TB00908C. [DOI] [PubMed] [Google Scholar]
  21. Randall J. D.; Eyckens D. J.; Stojcevski F.; Francis P. S.; Doeven E. H.; Barlow A. J.; Barrow A. S.; Arnold C. L.; Moses J. E.; Henderson L. C. Modification of Carbon Fibre Surfaces by Sulfur-Fluoride Exchange Click Chemistry. ChemPhysChem 2018, 19, 3176–3181. 10.1002/cphc.201800789. [DOI] [PubMed] [Google Scholar]
  22. Barrow A. S.; Smedley C. J.; Zheng Q.; Li S.; Dong J.; Moses J. E. The growing applications of SuFEx click chemistry. Chem. Soc. Rev. 2019, 48, 4731–4758. 10.1039/C8CS00960K. [DOI] [PubMed] [Google Scholar]
  23. Gembus V.; Marsais F.; Levacher V. An Efficient Organocatalyzed Interconversion of Silyl Ethers to Tosylates Using DBU and p-Toluenesulfonyl Fluoride. Synlett 2008, 2008, 1463–1466. 10.1055/s-2008-1078407. [DOI] [Google Scholar]
  24. Smedley C. J.; Zheng Q.; Gao B.; Li S.; Molino A.; Duivenvoorden H. M.; Parker B. S.; Wilson D. J. D.; Sharpless K. B.; Moses J. E. Bifluoride Ion Mediated SuFEx Trifluoromethylation of Sulfonyl Fluorides and Iminosulfur Oxydifluorides. Angew. Chem., Int. Ed. 2019, 58, 4552–4556. 10.1002/anie.201813761. [DOI] [PubMed] [Google Scholar]
  25. Mahapatra S.; Woroch C. P.; Butler T. W.; Carneiro S. N.; Kwan S. C.; Khasnavis S. R.; Gu J.; Dutra J. K.; Vetelino B. C.; Bellenger J.; am Ende C. W.; Ball N. D. SuFEx Activation with Ca(NTf2)2: A Unified Strategy to Access Sulfamides, Sulfamates, and Sulfonamides from S(VI) Fluorides. Org. Lett. 2020, 22, 4389–4394. 10.1021/acs.orglett.0c01397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Liang D.-D.; Streefkerk D. E.; Jordaan D.; Wagemakers J.; Baggerman J.; Zuilhof H. Silicon-Free SuFEx Reactions of Sulfonimidoyl Fluorides: Scope, Enantioselectivity, and Mechanism. Angew. Chem., Int. Ed. 2020, 59, 7494–7500. 10.1002/anie.201915519. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Bachrach S. M. Microsolvation of Glycine: A DFT Study. J. Phys. Chem. A 2008, 112, 3722–3730. 10.1021/jp711048c. [DOI] [PubMed] [Google Scholar]
  28. Flörez E.; Acelas N.; Ibargüen C.; Mondal S.; Cabellos J. L.; Merino G.; Restrepo A. Microsolvation of NO3–: structural exploration and bonding analysis. RSC Adv. 2016, 6, 71913. 10.1039/C6RA15059D. [DOI] [Google Scholar]
  29. Vayner G.; Houk K. N.; Jorgensen W. L.; Brauman J. I. Steric Retardation of SN2 Reactions in the Gas Phase and Solution. J. Am. Chem. Soc. 2004, 126, 9054–9058. 10.1021/ja049070m. [DOI] [PubMed] [Google Scholar]
  30. Himo F.; Lovell T.; Hilgraf R.; Rostovtsev V. V.; Noodleman L.; Sharpless K. B.; Fokin V. V. Copper(I)-Catalyzed Synthesis of Azoles. DFT Study Predicts Unprecedented Reactivity and Intermediates. J. Am. Chem. Soc. 2005, 127, 210–216. 10.1021/ja0471525. [DOI] [PubMed] [Google Scholar]
  31. Ess D. H.; Jones G. O.; Houk K. N. Transition States of Strain-Promoted Metal-Free Click Chemistry: 1,3-Dipolar Cycloadditions of Phenyl Azide and Cyclooctynes. Org. Lett. 2008, 10, 1633–1636. 10.1021/ol8003657. [DOI] [PubMed] [Google Scholar]
  32. Politzer P.; Toro-Labbé A.; Gutiérrez-Oliva S.; Herrera B.; Jaque P.; Concha M. C.; Murray J. S. The reaction force: Three key points along an intrinsic reaction coordinate. J. Chem. Sci. 2005, 117, 467–472. 10.1007/BF02708350. [DOI] [Google Scholar]
  33. Inostroza-Rivera R.; Herrera B.; Toro-Labbé A. Using the reaction force and the reaction electronic flux on the proton transfer of formamide derived systems. Phys. Chem. Chem. Phys. 2014, 16, 14489–14495. 10.1039/c3cp55159h. [DOI] [PubMed] [Google Scholar]
  34. Stegmüller A.; Tonner R. β-Hydrogen elimination mechanism in the absence of low-lying acceptor orbitals in EH2(t-C4H9) (E = N–Bi). Inorg.Chem. 2015, 54, 6363–6372. 10.1021/acs.inorgchem.5b00687. [DOI] [PubMed] [Google Scholar]
  35. Schäfer A.; Klamt A.; Sattel D.; Lohrenz J. C. W.; Eckert F. COSMO Implementation in TURBOMOLE: Extension of an efficient quantum chemical code towards liquid systems. Phys. Chem. Chem. Phys. 2000, 2, 2187. 10.1039/b000184h. [DOI] [Google Scholar]
  36. Xantheas S. S.; Dunning T. H. Jr. The structure of the water trimer from ab initio calculations. J. Chem. Phys. 1993, 98, 8037–8040. 10.1063/1.464558. [DOI] [Google Scholar]
  37. Wenthold P. G.; Squires R. R. Bond Dissociation Energies of F2– and HF2–. A Gas-Phase Experimental and G2 Theoretical Study. J. Phys. Chem. 1995, 99, 2002–2005. 10.1021/j100007a034. [DOI] [Google Scholar]
  38. Ziegler T.; Rauk A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chim. Acta 1977, 46, 1–10. 10.1007/BF02401406. [DOI] [Google Scholar]
  39. Kitaura K.; Morokuma K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. 10.1002/qua.560100211. [DOI] [Google Scholar]
  40. Bickelhaupt F. M.; Nibbering N. M. M.; Van Wezenbeek E. M.; Baerends E. J. Central bond in the three CN. indicating radical species NC-CN, CN-CN and CN-NC: electron pair bonding and Pauli repulsion effects. J. Phys. Chem. 1992, 96, 4864–4873. 10.1021/j100191a027. [DOI] [Google Scholar]
  41. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  42. von Hopffgarten M.; Frenking G. Energy decomposition analysis. WIREs Comput. Mol. Sci. 2011, 2, 43–62. 10.1002/wcms.71. [DOI] [Google Scholar]
  43. Mitoraj M. P.; Michalak A.; Ziegler T. On the nature of the agostic bond between metal centers and β-hydrogen atoms in alkyl complexes. An analysis based on the extended transition state method and the natural orbitals for chemical valence scheme (ETS-NOCV). Organometallics 2009, 28, 3727–3733. 10.1021/om900203m. [DOI] [Google Scholar]
  44. Frenking G.; Matthias Bickelhaupt F.. The Chemical Bond; John Wiley & Sons, Ltd: 2014; Chapter 4, pp. 121–157. [Google Scholar]
  45. Pecher L.; Laref S.; Raupach M.; Tonner R. Ethers on Si(001): a prime example for the common ground between surface science and molecular organic chemistry. Angew. Chem., Int. Ed. 2017, 56, 15150–15154. 10.1002/anie.201707428. [DOI] [PubMed] [Google Scholar]
  46. Greed S.; Briggs E. L.; Idiris F. I. M.; White A. J. P.; Lücking U.; Bull J. A. Synthesis of highly enantioenriched sulfonimidoyl fluorides and sulfonimidamides by stereospecific sulfur–fluorine exchange (SuFEx) reaction. Chem. – Eur. J. 2020, 26, 12533–12538. 10.1002/chem.202002265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. TURBOMOLE V7.2 2017; a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com, last accessed 21.08.2020.
  48. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  49. Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  50. Ernzerhof M.; Scuseria G. E. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. 10.1063/1.478401. [DOI] [PubMed] [Google Scholar]
  51. Weigend F.; Ahlrichs R. CC2 excitation energy calculations on large molecules using the resolution of the identity approximation. Phys. Chem. Chem. Phys. 2000, 7, 3297–3305. 10.1039/b508541a. [DOI] [Google Scholar]
  52. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16; Revision A.03, Gaussian, Inc.: Wallingford CT, 2016. [Google Scholar]
  53. Mitoraj M. P.; Michalak A.; Ziegler T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962. 10.1021/ct800503d. [DOI] [PubMed] [Google Scholar]
  54. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Guerra C. F.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931. 10.1002/jcc.1056. [DOI] [Google Scholar]
  55. Guerra C. F.; Snijders J. G.; te Velde G.; Baerends E. J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391. 10.1007/s002140050353. [DOI] [Google Scholar]
  56. ADF2019, SCM Theoretical Chemistry; Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com, last accessed 21.08.2020.
  57. van Lenthe E.; Baerends E. J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
  58. van Lenthe E.; Baerends E. J.; Snijders J. G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. 10.1063/1.466059. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c05049_si_001.pdf (787KB, pdf)
ao0c05049_si_002.mp4 (78.6KB, mp4)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES