Probabilistic forecasting of surgical case duration using machine learning: model development and validation

Abstract

Objective

Accurate estimations of surgical case durations can lead to the cost-effective utilization of operating rooms. We developed a novel machine learning approach, using both structured and unstructured features as input, to predict a continuous probability distribution of surgical case durations.

Materials and Methods

The data set consisted of 53 783 surgical cases performed over 4 years at a tertiary-care pediatric hospital. Features extracted included categorical (American Society of Anesthesiologists [ASA] Physical Status, inpatient status, day of week), continuous (scheduled surgery duration, patient age), and unstructured text (procedure name, surgical diagnosis) variables. A mixture density network (MDN) was trained and compared to multiple tree-based methods and a Bayesian statistical method. A continuous ranked probability score (CRPS), a generalized extension of mean absolute error, was the primary performance measure. Pinball loss (PL) was calculated to assess accuracy at specific quantiles. Performance measures were additionally evaluated on common and rare surgical procedures. Permutation feature importance was measured for the best performing model.

Results

MDN had the best performance, with a CRPS of 18.1 minutes, compared to tree-based methods (19.5–22.1 minutes) and the Bayesian method (21.2 minutes). MDN had the best PL at all quantiles, and the best CRPS and PL for both common and rare procedures. Scheduled duration and procedure name were the most important features in the MDN.

Conclusions

Using natural language processing of surgical descriptors, we demonstrated the use of ML approaches to predict the continuous probability distribution of surgical case durations. The more discerning forecast of the ML-based MDN approach affords opportunities for guiding intelligent schedule design and day-of-surgery operational decisions.

INTRODUCTION

Costs of surgery account for roughly a third of all health-care spending in the United States.¹ Operating room (OR) cost is a significant contributor to high surgical costs and is estimated to be approximately $36 per minute.² The cost-effective utilization of OR time is often impaired by uncertainties in the surgical case duration. OR underutilization leads to idle staff, whose wages are among the biggest contributor to OR costs;² meanwhile, OR overutilization leads to cancellations of impending surgeries,³ medical errors, fatigue and burnout,^4,5 and increased staff turnover.⁶

Scheduled case duration is often based on a surgeon’s estimate, which is frequently inaccurate.^7–9 Statistical and machine learning (ML) approaches have been used for estimating case durations. For example, a Bayesian statistical method used a weighted combination of the surgeon’s estimate with historical data to forecast the duration of surgery.¹⁰ Similarly, ML approaches have demonstrated improvements to prediction accuracy, compared to traditional institutional estimates.^11–13 These methods have also been applied in predicting case durations for pediatric surgeries,^14,15 with 1 study showing between 75% and 85% accuracy in predicting cases that overrun their scheduled time by a predefined percentage.¹⁵

Prior studies using ML techniques for predicting case durations have several limitations. First, studies were often small in scale, with approximately 1000 patients.^11,12 Second, studies primarily evaluated only a favorable subset of cases, such as the 10 most common procedures¹⁵ or procedures that were performed more than 30 times.¹³ Third, most studies have used the mean surgical case duration as the predicted outcome.^11–15 Prior research suggests that schedule creation informed by case duration variance, rather than a mean case duration, may be less likely to result in overutilization. This advantage arises from the identification of case sequences that have high cumulative variance and are likely to overrun their scheduled time.¹⁶ Furthermore, many operational decisions on the day of surgery depend on knowledge of both the mean and variance of case durations. For example, answers to the question “what is the probability that an OR will run past 5pm?” may motivate decisions such as releasing or retaining staff, opening an additional room for a surgeon, or determining the placement of an add-on case.

Finally, current prediction approaches rely on structured data elements as input for the prediction models (ie, categorical and continuous variables). However, such data elements are highly heterogenous and can vary considerably between institutions. For example, some electronic health records (EHRs) encode procedure name as a single category, some as multiple categories, and others as free text. Furthermore, the categories themselves can be heterogenous (eg, “Adenotonsillectomy” and “Tonsillectomy and Adenoidectomy” describe identical procedures). As such, ML approaches that can be generalized must be able to semantically decode a common version of heterogenous data structures, such as free text.

We developed a novel approach for predicting surgical case durations by training ML models that utilize both structured variables and free text. In addition, we characterized surgical case duration as a continuous probability distribution, rather than using mean duration, to inform perioperative decision making. We discuss the pragmatic applications of this approach for accurately predicting surgical case durations, enabling intelligent schedule design, and guiding day-of-surgery operational decisions.

MATERIALS AND METHODS

Study setting and data sources

Data used in this study included all cases that were performed in a central operating location at St. Louis Children’s Hospital (Saint Louis, MO), a free-standing, tertiary-care, pediatric hospital, between 2 April 2013 and 31 December 2017. The start date reflects the deployment of the SIS (Surgical Information Systems, Alpharetta, GA) EHR at our institution. This data set included data on surgeries performed by various surgical services, including General, Cardiothoracic, Orthopedic, Otolaryngology, Ophthalmology, Plastic, Urology, Gynecology, Transplant, and Neurosurgery. Procedures performed by non-surgical services in the central operating location, such as Gastroenterology, Hematology/Oncology, Dentistry, and Pain Medicine, were also included.

The institutional review board of Washington University approved this study with a waiver of consent (IRB #201910015). The model development adhered to the “Transparent Reporting of a Multivariate Prediction Model for Individual Prognosis or Diagnosis” (TRIPOD) guidelines.¹⁷

Variable definitions and feature extraction

Models in this study were trained to predict actual surgical case duration, which was defined as the time between patient entry into the OR to patient exit (“wheels-in to wheels-out”) and extracted from SIS. This definition was chosen because of its importance to all perioperative stakeholders, as opposed to “skin incision to skin closure,” or “anesthesia start time to anesthesia stop time.” Prior research indicates that the actual duration follows a log-normal distribution for most types of surgeries.^8,18 As such, the actual duration was log-transformed and normalized to have a mean of 0 and a standard deviation of 1 for its treatment in the ML models.

Surgeries are allocated a block of time in the OR schedule based on their anticipated duration (henceforth “scheduled duration”). At our institution, the scheduled duration is primarily based on the surgeon’s estimate. The scheduled duration is sometimes modulated by historical data, but this is not a standardized or a consistent process. In rare cases, a “placeholder” scheduled duration is entered for emergent cases. Scheduled duration was extracted from SIS, then log-transformed and normalized.

Other predictor variables extracted from SIS included the day of the week of a surgery and the operating location. Additional predictor variables were extracted from the corresponding anesthesia record in the MetaVision electronic medical record (iMDSoft, Tel Aviv, Israel), including procedure name, surgical diagnosis, surgeon name, patient age, inpatient status, and American Society of Anesthesiologists (ASA; Schaumburg, IL) Physical Status (ASA-PS). All extracted variables were used by all predictive models.

The surgeon name, day of the week of surgery, operating location, inpatient status, and ASA-PS were categorical variables. Surgeon name refers to the first attending surgeon or proceduralist associated with the case. The day of the week of surgery was defined relative to the time a patient entered the OR. Operating locations referred to the specific operating room or anesthetizing location in which the procedure occurred; there were 14 general ORs, 1 dedicated cardiac OR, and 1 procedure room. Inpatient status was treated as a binary categorical variable, where “true” was assigned to patients that were an inpatient at the time of surgery. Each ASA-PS was treated as its own category (“1” and “1E” were treated as separate categories). Categorical variables were encoded as a one-hot vector after extraction.

Procedure name and surgical diagnosis were unstructured free-text variables. Procedure name was a short free-text description of the surgery or procedure(s) intended to be performed. Billing codes (eg, Common Procedure Terminology) for procedures or diagnoses were not utilized in this analysis, as they were not consistently available at the time of surgery. Surgical diagnosis was a free-text description of the principal diagnosis necessitating the surgery or procedure. After extraction from the medical record, procedure name and surgical diagnosis were stripped of common English stop words (eg, “a,” “the”) and punctuations. The final step of free-text preprocessing was model dependent, and options are described below.

Patient age in days was recorded in the medical record and was extracted as a continuous variable and normalized. If patient age was missing, the mean age across all patients in the training data set was used. Missing categorical variables were represented with an empty vector. Missing text data was represented with an empty string.

Model development

We developed multiple tree-based and neural network–based ML approaches. Data between 1 January and 31 December 2017 were sequestered and used for evaluation of predictive models (henceforth, “test data”). The remaining data (henceforth, “training data”) were randomized and used for training and validation. Five-fold cross-validation was used to tune model hyper-parameters. A detailed description of the implementation of each model, hyperparameters, and performance metrics on validation data can be found in Supplementary Appendix 1. Performance metrics on test data were evaluated only once for each finalized model.

Three tree-based models were trained: simple decision tree (DT), random forest (RF), and gradient boosted decision tree (GBT). For all trees, unigrams and bigrams were extracted from free-text variables and encoded in a term frequency-inverse document frequency sparse vector. For a given tree-based model, a pair of trees were used to predict the mean and standard deviation of the output probability distribution.

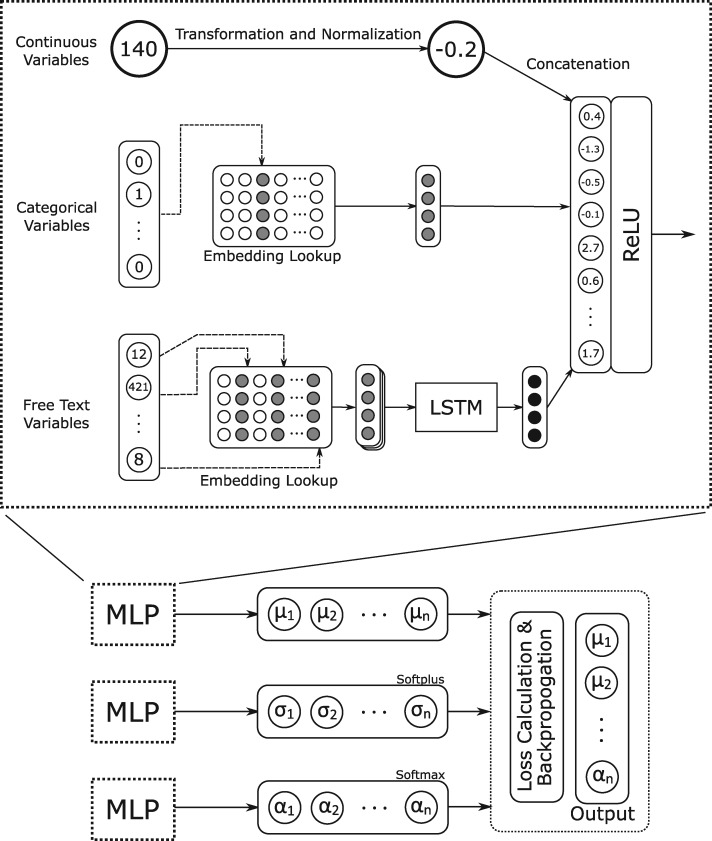
One neural network was trained: a mixture density network (MDN).¹⁹ For this approach, free-text inputs were tokenized and each word token was embedded into a vector. The tensor representing each phrase was used as input for a long short-term memory (LSTM) recurrent neural network. The output of the LSTM was then concatenated with the other input vectors and used as an input for a multi-layer perceptron (MLP) with 1 hidden layer and a vector output. Three iterations of this MLP were trained simultaneously, with their vector outputs corresponding respectively to the means, standard deviations, and mixing coefficients of a mixture of Gaussian distributions. This mixture of Gaussian distributions was the output of the MDN, representing a forecast of surgical case duration as a continuous probability distribution.

The loss function used to train model parameters was the negative log likelihood of observing the actual duration. Given a training case where x is the actual duration; n is the number of Gaussian distributions in the MDN output; and µ_i, σ_i, and α_i refer to the mean, standard deviation, and mixing coefficient of the ith distribution, respectively, this loss function was formalized as:

$$L=\mathrm{ }-\log \left[\sum _{i=1}^n{\alpha }_i\left(\frac{e^{\frac{-{\left(x-{\mu }_i\right)}^2}{2{\sigma }_i^2}}}{{\sigma }_i\sqrt{2\pi }}\right)\right]$$

The number of normal distributions contributing to the mixture was set prior to training, and we tuned this parameter along with other hyperparameters.

Given the propensity of MDNs to overfit, particularly for rare combinations of input parameters,^20,21 we employed a training strategy to limit overfitting in which all 3 MLP components of the MDN were trained with early stopping, the MLPs corresponding to mixing weight and standard deviation were frozen, and the remaining MLP corresponding to the means was trained for additional epochs. The architecture of our MDN implementation is shown in Figure 1.

Figure 1.

Architecture of the Mixture Density Network. LSTM: long short-term memory; MLP: multilayer perceptron; ReLU: rectified linear unit.

ML models were compared against a non-ML statistical method. We chose a specific Bayesian statistical method developed by Dexter et al¹⁰ that shared input variables with the ML models (procedure name, surgeon name, and scheduled duration) and also predicted a continuous probability distribution of the outcome variable. The performance of the Bayesian method can be measured using the same metrics as the ML models. This method produces a normal distribution from a weighted combination of historical case data and an empirical distribution centered on the case’s scheduled duration. Three key values—α, β, and τ—were computed from the training data: α and β are parameters of an inverse gamma function that serves as the conjugate prior for variance and τ is a weighting parameter with units of cases. When the number of historical cases is equal to τ, then the historical distribution and empirical distribution are weighted equally.

Performance measures

The primary performance measure in this study is the accuracy of each model, measured by the continuous ranked probability score (CRPS). CRPS is a measure of accuracy for probabilistic forecasts of continuous outcomes.^22–24 CRPS is formalized by the following equation, where F is the cumulative distribution function (CDF) of a forecast, H denotes the Heaviside step function representing the CDF of the observed outcome, and x is the observed outcome:

$$\mathit{CRPS}\left(F,x\right)=\mathrm{ }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\left(F\left(y\right)-\mathcal{ }\mathcal{H}\left\{y\ge x\right\}\right)}^{2}dy$$

We chose to report CRPS as our primary outcome for several reasons. First, it is a global measure that combines all predictive qualities into a single value. Models are rewarded for accurately representing the hypothetical underlying distribution from which observations are sampled, and also for incorporating predictors that enable more precise (ie, narrow) predictive distributions. Second, it is measured in units of the predicted variable (minutes, in this study) and has a finite ideal score of 0, making it easier to interpret as a measure of distance from truth that has similarities to the root mean squared error and mean absolute error (MAE). Third, it can be calculated for any forecast for which the cumulative probability distribution is known, including deterministic forecasts, for which it simplifies to MAE. For these reasons, CRPS has been described as a generalized MAE.²³

We used CRPS to compare all ML algorithms against the Bayesian statistical method. We also evaluated CRPS of the scheduled duration, which is a deterministic forecast of actual duration, to contextualize the performance of the statistical and ML models. Although all models were trained in log space, their predictive normal distributions were first transformed back into their corresponding lognormal counterparts for the calculation of CRPS, so that an accurate value of minutes could be reported.

CRPS does not evaluate performance at specific quantiles. As such, as part of a secondary analysis, we computed the pinball loss (PL) function to evaluate the performance of each model at specific quantiles. The PL is a measure of quantile accuracy and, like CRPS, has a numerical range of [0, inf], where 0 is the perfect score and can only be achieved by a deterministic prediction with 0 absolute error. It is calculated separately for any quantile (0,1).²⁵ For each algorithm, we compared the PL at the 0.05, 0.25, 0.50, 0.75, and 0.95 quantiles.

We also evaluated the performance of each model on common versus rare surgeries. Subgroups of common and rare surgeries were taken from the test data. The procedure name and surgeon were used to determine the rarity of a surgery as follows: if p was a specific combination of a procedure name and surgeon, and n_p is the number of cases by p, then the common surgical group was defined as cases with n_p > 20 and a rare surgical group was defined as cases with n_p = 1.

Feature importance was evaluated on the best-performing model by calculating the permutation importance (PI). PI (also known as model class reliance) is an algorithm-agnostic measure of feature importance.^26,27 To calculate the PI of a feature f, PI_f, the values of f in the test data set are first randomly shuffled. Then, the performance of the model is calculated on the test data set containing shuffled f. If f is important to the model, then we would expect the performance to degrade significantly when f is shuffled, whereas if f is not important, then the performance should be preserved. PI_f was calculated as CRPS (shuffled f)/CRPS (unshuffled), where a high PI denotes high feature importance.

Python 3.7.4 was used for all feature extraction, algorithm implementation, and performance testing. The sci-kit learn library was used for the implementation of DT, RF, and GBT. Google’s Tensorflow library²⁸ was used to implement mixture density networks. The properscoring Python package was used to compute CRPS.²⁹

RESULTS

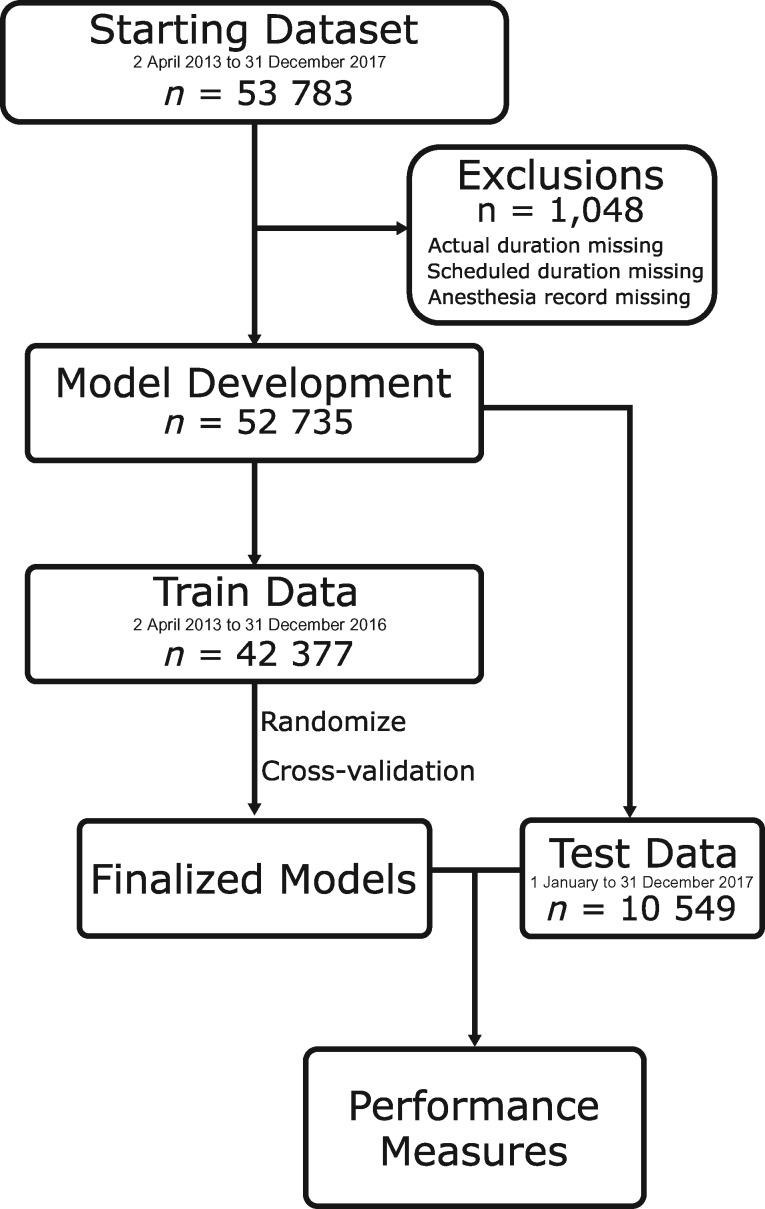
A total of 53 783 surgical cases were retrieved; 1048 cases were excluded either because they did not have a scheduled or actual surgical time documented or because they did not have a corresponding anesthesia record with case details. A total of 52 735 cases were included in the model development and evaluation (see Figure 2). There were 15 068 unique procedure names and 304 unique surgeons. Test data were comprised of 10 358 cases, or 19.6% of the total data set. The common and rare subgroups were comprised of 2381 and 4109 cases, respectively. See Table 1 for a summary of patient and procedure characteristics for each group. For detailed characteristics for each cross-validation fold, see Supplementary Appendix 1. See Table 2 for the most common procedure names.

Figure 2.

Construction of train and test data sets.

Table 1.

Patient and procedure characteristics

Feature	Total	Train	Test	Common	Rare
Number of cases	52 735	42 377	10 358	2381	4109
Mean age, years	7.8	7.8	8.1	7.7	8.4
Number of inpatients	15 254 (28.9)	12 377 (29.2)	2877 (27.8)	449 (18.9)	1411 (34.3)
ASA Physical Status
1	17 707 (33.6)	14 667 (34.6)	3040 (29.3)	672 (28.2)	1139 (27.7)
1E	1456 (2.8)	1075 (25.4)	381 (3.7)	109 (4.6)	191 (4.6)
2	20 846 (39.5)	16 618 (39.2)	4228 (40.8)	1178 (49.5)	1523 (37.1)
2E	723 (1.4)	554 (1.3)	169 (1.6)	31 (1.3)	93 (2.3)
3	10 241 (19.4)	8070 (19.0)	2171 (21.0)	378 (15.9)	978 (23.8)
3E	388 (0.7)	290 (0.7)	98 (0.9)	3 (0.1)	59 (1.4)
4	1062 (2.0)	879 (2.1)	183 (1.8)	6 (0.3)	87 (2.1)
4E	254 (0.5)	184 (0.4)	70 (0.7)	1 (0)	35 (0.9)
5	12 (0)	11 (0)	1 (0)	0 (0)	1 (0)
5E	22 (0)	17 (0)	5 (0)	0 (0)	2 (0)
6	3 (0)	3 (0)	0 (0)	0 (0)	0 (0)
Unknown	21 (0)	9 (0)	12 (0.1)	3 (0.1)	1 (0)
Unique procedure names	15 068	12 470	3932	29	3612
Unique diagnoses	20 225	17 027	4738	598	2764
Number of surgeons	304	271	171	30	165
Mean actual duration, min	103.7	102.9	107.1	72.9	131.6
Mean scheduled duration, min	104.6	104.1	106.7	82	124.1
Day of week
M-F	50 702 (96.1)	40 772 (96.2)	9930 (95.9)	2325 (97.6)	3863 (94.0)
Sat	1059 (2.0)	828 (2.0)	231 (2.2)	28 (1.2)	127 (3.1)
Sun	974 (1.8)	777 (1.8)	197 (1.9)	28 (1.2)	119 (2.9)
OR location
Main OR	40 975 (77.7)	32 895 (77.6)	8080 (78.0)	1816 (76.3)	3300 (80.3)
Cardiac OR	1286 (2.4)	1001 (2.4)	285 (2.8)	0 (0)	139 (3.4)
Procedure room	3705 (7.0)	2876 (6.8)	829 (8.0)	384 (16.1)	99 (2.4)
Unknown	6769 (12.8)	5605 (13.2)	1164 (11.2)	181 (7.6)	571 (13.9)

Note: OR locations and days of the week have been grouped for readability. Individual ORs and days of the week were treated as distinct values. Counts are expressed as: count (percentage of group number of cases).

ASA: American Society of Anesthesiologists; OR: operating room.

Table 2.

Most common raw procedure names

Procedure Name	Number
Bilateral myringotomy with tube insertiona	1849
Upper endoscopy	1690
Eye muscle correction/2 muscles—bilateral	1473
Dorsal rhizotomy selective	1164
Laparoscopic appendectomy	1031
Full mouth restorative dentistry	811
Colonoscopy	626
T and Ab	492
Bilateral adenotonsillectomyb	483
Bilateral myringotomy with tube insertion—bilaterala	459

Note: Procedures denoted with matching superscripts represent groups of procedure names that are semantically equivalent.

Model performance

The scheduled case duration had a CRPS (ie, MAE) of 32.1 minutes in the test data. The MDN had the lowest CRPS (18.1 minutes). This is compared to the GBT (19.5 minutes), RF (19.6 minutes), Bayesian method (21.2 minutes), and DT (22.1 minutes; see Table 3). Model outputs for a given set of inputs can be seen in Figure 3.

Table 3.

Continuous ranked probability score

	Overall Test Data	Common Subgroup	Rare Subgroup
DT	22.1	10.8	30.4
GBT	19.5	9.5	26.9
RF	19.6	10.0	27.0
MDN	18.1	9.1	24.8
Bayes	21.2	10.2	30.7
SD	32.1	19.5	41.2

Note: Data are in minutes.

Bayes: Bayesian statistical method; DT: decision tree; GBT: gradient boosted decision tree; MDN: mixture density network; RF: random forest; SD: scheduled duration.

Figure 3.

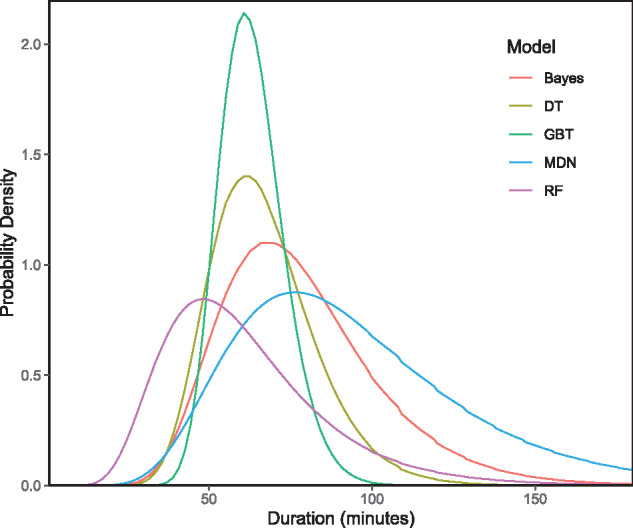
Sample model output. Model inputs: {Procedure Name: “Exam Under Anesthesia Eye Bilateral/Glaucoma Valve w/EUA”, Surgical Diagnosis: “Glaucoma”, Surgeon: “SurgeonID##”, Location: “OR#5”, Inpatient: false, ASA-PS: “II”, Age: 4.3 years, Day-of-week: “Tuesday”, Scheduled Time: 60 minutes}. ASA-PS: American Society of Anesthesiologists Physical Status; Bayes: Bayesian statistical method; DT: decision tree; GBT: gradient boosted decision tree; MDN: mixture density network; RF: random forest.

In our secondary analysis, MDN had the lowest PL in all quantiles for all subgroups. For both the common and rare subgroups, the MDN also had the lowest CRPSs (9.1 and 24.8 minutes, respectively). All algorithms except for DT outperformed the Bayesian method at all quantiles in the overall test data and the rare subgroup. In the common subgroup, the Bayesian method outperformed all ML models except for GBT and MDN (see Table 4).

Table 4.

Pinball loss

	Quantile
	0.05	0.25	0.5	0.75	0.95
Overall test data
DT	0.049	0.139	0.174	0.147	0.055
GBT	0.043	0.124	0.155	0.128	0.046
RF	0.047	0.127	0.156	0.130	0.051
MDN	0.040	0.116	0.146	0.120	0.042
Bayes	0.049	0.134	0.169	0.143	0.059
Common subgroup
DT	0.039	0.107	0.135	0.120	0.045
GBT	0.033	0.101	0.129	0.108	0.038
RF	0.039	0.108	0.136	0.112	0.043
MDN	0.031	0.098	0.125	0.102	0.035
Bayes	0.033	0.101	0.131	0.111	0.043
Rare subgroup
DT	0.057	0.162	0.201	0.168	0.064
GBT	0.050	0.142	0.177	0.144	0.051
RF	0.054	0.143	0.176	0.147	0.057
MDN	0.047	0.132	0.164	0.133	0.046
Bayes	0.065	0.163	0.204	0.174	0.077

Note: Bayes: Bayesian statistical method; DT: decision tree; GBT: gradient boosted decision tree; MDN: mixture density network; RF: random forest.

Feature importance

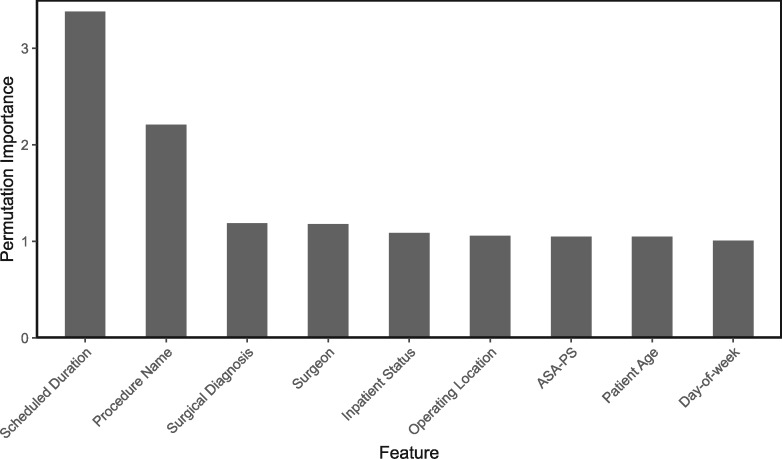
Permutation importance (PI) was calculated for the MDN on all included features (see Figure 4). Scheduled duration was the most important feature, with a PI of 3.38, followed by procedure name (PI 2.21). The PIs of all other predictor variables were comparatively low.

Figure 4.

Permutation importance of mixture density network features. ASA-PS: American Society of Anesthesiologists Physical Status.

DISCUSSION

We used a machine learning approach to predict a continuous probability distribution of actual surgical case durations from a combination of unstructured text, categorical variables, and continuous preoperative variables. Multiple tree-based approaches and an MDN were compared against a Bayesian statistical method. For our primary performance metric (ie, CRPS), the MDN outperformed all the other algorithms in the overall test data, with a 15% improvement in CRPS over the Bayesian method. The MDN also had the best performance in both the common and rare surgical groups, where its advantages over the Bayesian method were 11% and 19%, respectively. For our secondary outcome measure (ie, pinball loss), the MDN had the best PL across all quantiles. Of all the models that were evaluated, only the MDN could approximate non-parametric probability distributions, giving it an edge in surgery types that do not follow lognormal distributions.

These findings provide pragmatic opportunities for translation in real-world OR settings. First, surgical descriptors in realistic operational settings are often unstructured, incomplete, and unfiltered, and contain errors and idiosyncrasies. In addition, they are often encoded in different data structures between different EHRs or institutions. For example, some EHRs may use only a single category to encode the procedure description. Others use a combination of primary and secondary procedure(s). Most allow a free-text option or allow the modulation of existing categories with free-text modifiers. Different surgeons may have different names for procedures that are similar or identical. We approach the imperfect nature of these data by transforming all data structures to a free-text string and performing natural language processing techniques. As such, information pertaining to duration can be extracted from atypically written procedure names, procedure names containing typographic errors, or uncommon combinations of common procedures. Our methodology can also be applied regardless of how a specific EHR encodes surgical descriptors, assuming they can be collapsed as free text. As a result, meaningful predictions can be made on all cases performed, rather than on a favorable subset as presented by existing ML techniques.^13,15

Second, our approach estimates a continuous probability distribution of surgical case durations. We foresee that this type of prediction will have more applicability than a prediction of mean surgical duration. Sequences of cases with higher variance in case duration are more likely to result in under- or overutilization, compared with cases that have identical mean durations but lower variance. Predictions that account only for the mean case duration cannot avoid combinations of cases with high variance that lead to a higher rate of misutilization. Providing a probabilistic forecast of the duration for each surgical procedure allows for the identification of putative schedules at risk for misutilization, and suggests alternatives that potentially minimize this risk.¹⁶

In addition to the improved schedule design, knowing the variance of a surgical case duration can aid in day-of-surgery operational decisions. For example, a charge anesthesiologist or nurse manager may want to know the probability of an OR running past a specific time for making staffing or operational decisions, such as retaining or releasing available anesthesia providers, offering a second operating location to a surgeon to maximize OR utilization, or deciding which room to use for an add-on procedure. Such decisions are frequently made with limited information regarding the variance of case durations, and oftentimes are significant cognitive burdens that distract from effective patient care. The deployment of an accurate predictive model for surgical case duration could effectively assimilate important information from disparate sources, aid in operational decision-making, and ultimately lead to more efficient OR utilization and more cognitive focus on patient care tasks. Further research is needed to quantify such benefits for operational endpoints, such as OR utilization, staff satisfaction scores, and overtime pay.

The scheduled time and procedure name were the most important features (as measured by PI) related to surgical case duration in the best-performing model. Conversely, surgeon identity, patient age, operative diagnosis, day of the week, inpatient status, and ASA-PS had comparatively low PIs and conferred only small benefits to performance. The relative importance of these predictor variables is consistent with existing literature.¹⁸ A more nuanced set of predictors, such as patient factors specific to the surgery type (eg, apnea-hypopnea index) or operationally contextual factors (eg, whether a surgeon is running multiple ORs), may allow for a more discerning forecast. Even with an exhaustive search of preoperative predictors, however, error and uncertainty in the prediction model will still exist. A significant portion of the information encoding surgical case duration is discovered intraoperatively. As such, to make a prediction algorithm more useful for solving day-of-surgery operational problems, real-time values from the EHR must be extracted and evaluated.

Study limitations

This study had several limitations. This was a single-center, retrospective study. We used a large, multi-year data set that included 15 068 unique procedures, representing a wide variety of surgical subspecialties at an academic pediatric institution. Determinants of surgical case duration may differ for adult populations or for community hospitals. Further research is needed to ascertain whether our models are effective in systems of hospitals with more disparate procedure data. Although we used natural language processing to enable semantic decoding of procedure names and surgical diagnoses, some sophisticated techniques were not utilized, such as typographical error detection and acronym expansion. It is possible that in rare cases, data leakage can occur if the case is booked after it has started or completed. This may occur in certain situations; for example, a trauma patient arriving after hours in critical condition with little to no advance warning, and perioperative staff not having sufficient time to create a patient record prior to the surgery. When this occurs, the scheduled case duration may be assigned with knowledge of the actual duration. However, we believe this to be extremely rare, and all models would be affected equally. We did not consider concept drift in training our models. Over time, the accuracy of a trained model will degrade without some scheme for retraining, as new surgeons and procedure names are introduced. Furthermore, relationships between predictor variables may differ between the beginning and end of the study period, particularly over years of data. For example, surgeons may become more efficient at performing certain procedures or become better at estimating their duration. Turnover time was not addressed in this study. Turnover time is an important component of OR utilization and is affected by an array of predictor variables. As such, deployment of our model would only allow predictions of end time to be made if the start time is known or assumed. This reduces the accuracy of predictions of later procedures when several procedures are serially performed.

Future directions

Opportunities for future work include the application of our methodology to a generalized patient population, such as a multi-hospital network; the incorporation of real-time variables; and the prediction of turnover time, as well as modeling concept drift. We focused on surgical cases in this study; however, the techniques described in this study could potentially be extended to provide predictions for other types of scheduled patient encounters, which include non-surgical procedures and office visits. Potential improvements in operational endpoints, such as percent utilization and staff overtime cost, could be measured following the deployment of a predictive model.

Conclusions

We demonstrated a novel ML technique using unstructured text descriptions of procedure names combined with other preoperative variables to predict a continuous probability distribution of the surgical case duration. Our approach to model input allows for the treatment of realistically unstructured preoperative data, which allows for surgeries of all types and rarities to be evaluated. Our approach to model output informs an intelligent schedule design and provides actionable information for day-of-surgery operational decisions. Overall, this study demonstrates a substantial advancement in the application of machine learning techniques to an important operational problem in medicine.

FUNDING

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

AUTHOR CONTRIBUTorS

YJ conceived of the project idea and devised and implemented all models. TK extracted project data from the local electronic health record and helped refine models. All authors discussed the results and contributed to the final manuscript.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST

None declared.