Determining sample size and length of follow-up for smartphone-based digital phenotyping studies

Abstract

Objective

Studies that use patient smartphones to collect ecological momentary assessment and sensor data, an approach frequently referred to as digital phenotyping, have increased in popularity in recent years. There is a lack of formal guidelines for the design of new digital phenotyping studies so that they are powered to detect both population-level longitudinal associations as well as individual-level change points in multivariate time series. In particular, determining the appropriate balance of sample size relative to the targeted duration of follow-up is a challenge.

Materials and Methods

We used data from 2 prior smartphone-based digital phenotyping studies to provide reasonable ranges of effect size and parameters. We considered likelihood ratio tests for generalized linear mixed models as well as for change point detection of individual-level multivariate time series.

Results

We propose a joint procedure for sequentially calculating first an appropriate length of follow-up and then a necessary minimum sample size required to provide adequate power. In addition, we developed an accompanying accessible sample size and power calculator.

Discussion

The 2-parameter problem of identifying both an appropriate sample size and duration of follow-up for a longitudinal study requires the simultaneous consideration of 2 analysis methods during study design.

Conclusion

The temporally dense longitudinal data collected by digital phenotyping studies may warrant a variety of applicable analysis choices. Our use of generalized linear mixed models as well as change point detection to guide sample size and study duration calculations provide a tool to effectively power new digital phenotyping studies.

INTRODUCTION

The rise of biomedical research involving smartphones and wearable sensors has created new opportunities to study human behavior in naturalistic settings and to quantify the lived experiences of patients.^1,2 This new methodology of digital phenotyping has been defined as the moment-by-moment quantification of the individual-level human phenotype in situ using data from smartphones and other personal digital devices.³ The data available from these devices, in particular smartphones, enable scientists to define and measure a rich set of granular social, behavioral, and cognitive markers, many of which have been traditionally obtained using surveys or clinician-administered tests. The potential of gathering such temporally dense longitudinal data is broad and ranges from predicting relapse in psychotic disorders using smartphone-based geolocation and call/text logs⁴ to understanding social withdrawal in Alzheimer’s disease using communication and social media logs.⁵ However, despite the growing popularity of the approach and the vast quantities of smartphone sensor and log data gathered with digital phenotyping, there are no existing sample size or power calculations in the published literature for these types of studies. Note that in the special case of an N-of-1studies, a type of crossover design where each individual is given a minimum of 2 treatments so as to act as their own control, a sample size framework has been developed.⁶

When designing a digital phenotyping study, there are 2 necessary decisions to make. First, what sample size is needed to draw statistically sound scientific conclusions of the phenomenon of interest? The invasive nature of digital phenotyping may be a barrier to recruitment and recruitment efforts are often 1 of the most important limiting factors in any research study involving human subjects. Thus, understanding the minimal number of research participants is extremely important. Second, what is the ideal follow-up duration needed to obtain sufficient information for each study participant? Many smartphone-based digital phenotyping studies collect some combination of active data and passive data, where the former often takes the form of phone-based surveys. In these settings, a meaningful measure of adherence considers jointly surveying adherence and volume of passively collected smartphone data. Of these 2 categories, surveys are typically the more important limiting factor, as survey adherence tends to decline with study duration as research participants become fatigued. Adherence to passive data collection can also decline if individuals turn off their phones more frequently over time, disable smartphone sensors (mainly GPS), or uninstall the study app. Within our data, the level of missingness in smartphone accelerometer and GPS data, averaged over several cohorts, increased 0.5%–1% per week. In general, mental health smartphone applications have a large amount of attrition in engagement and use.⁷ While study incentives, such as monetary payments, may boost adherence, they also limit the generalizability of studies and underscore the importance of designing studies of appropriate duration (ie, studies that are sufficiently long to have adequate power to answer the questions of interest but are not too long to waste resources or cause unnecessary burden on subjects). Traditional methods for study power calculations are not useful and may even be misleading if the longitudinal nature of the data is ignored by assuming independence. Thus, there is a need for new methods to guide study design and sample size for digital phenotyping research.

MATERIALS AND METHODS

The small sample sizes of most current digital phenotyping studies limit the ability to develop new methods, including sample size calculations. Thus, to create a larger sample we pooled 2 digital phenotyping studies that utilize the same digital phenotyping platform, Beiwe.³ The first study utilized Beiwe for up to 3 months in 17 patients with schizophrenia³ and the second for up to 30 months in 15 patients with bipolar disorder.⁸ Both studies received IRB approval from their respective institutions and all participants signed written informed consent. In both studies similar digital phenotyping data was gathered, including smartphone GPS and communication logs. For the purposes of this article, we focus solely on sample size.

In this article, we address 2 different types of analyses: change point detection and association testing. Change point detection identifies, at the level of individuals, a point in time when there is a shift in behavior. Association testing identifies population-level longitudinal relationships between an outcome of interest and behavioral features across the sample. When designing a digital phenotyping study, we suggest utilizing individual-level change point detection models to select an appropriate target for the minimum effective length of follow-up ($T$) as a first step. Effective length of follow-up for association testing refers to the number of days where both the outcome and features are observed. In contrast, for change point detection the effective length of follow-up refers to the number of days where only the features are observed. Once $T$ has been selected, we then use a population-level association model to select an appropriate sample size ($N$). The intuition behind this ordering is that population-level models require both $N$ and $T$ to compute power, so first using an individual-level model to identify an appropriate $T$ allows for the population-level model to solve for the only remaining unknown variable, $N$.

In the following, we refer to sample size, or the total number of study participants, as N, and we refer to the duration of follow-up (in days) as T. Both N and T are important factors in the design of a digital phenotyping study. When considering suitable values of N and T, it is important to distinguish between population-level studies and individual-level studies. Larger sample sizes increase the accuracy of population-level models and the power of population-level tests of association. However, individual-level models (ie, models that use data from each individual separately) do not benefit from increasing N because data in these models are not aggregated across the sample.

Individual-level analysis: determining $\mathit{T}$ (length of follow-up)

The goal of a typical individual-level analysis is to detect a change point in the behavior of an individual from passively collected data. Let ${\mathit{X}}_{ij}=(X_{ij1},\dots ,X_{\mathit{ijp}})$ be the vector of p digital phenotyping features observed for individual i on day j of follow-up, where these features summarize different aspects of passive data, such as time spent at home derived from GPS sensor samples or the number of received phone calls derived from communication logs. Let ${\mathit{\mu }}_{ij}=({\mu }_{ij1},\mathrm{ }\dots ,\mathrm{ }{\mu }_{\mathit{ijp}})$ be the mean of ${\mathit{X}}_{ij}$, ${ϵ}_{ij}$ be a multivariate normal random variable with mean 0 and covariance $\mathbf{\Sigma }$, and let ${\mathit{\delta }}_{\mathit{i}}=({\delta }_{i1},\dots ,{\delta }_{ip})$ be the shifts in the behavioral features at the change point that occurs $m$ days prior to day $T$. In the case where the behavioral features are not normally distributed, we can first apply a nonparametric rank transformation to achieve normality. This, along with any scaling of the features, needs to be accounted for prior to any model interpretation. The standard model for the change point in the mean of the behavioral features assuming normalized, unit variance residuals ${ϵ}_{ij}$ is:

$${\mathit{X}}_{ij}={\mathit{\mu }}_{ij}+\mathrm{I}\left(\mathrm{j}>\mathrm{T}-\mathrm{m}\right){\mathit{\delta }}_{\mathit{i}}+{ϵ}_{ij}\mathrm{ }$$ (1)

where $\mathrm{I}\left(\cdot \right)$ is the indicator function. Testing for a change point is equivalent to testing the null hypothesis of ${\mathit{\delta }}_{\mathit{i}}=0$ against the alternative of ${\mathit{\delta }}_{\mathit{i}}\ne 0$. Let $Q_{im}={\sum }_{k=1}^p{Q}_{\mathit{imk}}^2$ be the likelihood-ratio test statistic⁹ for this hypothesis where:

$$Q_{\mathit{imk}}=\frac{\frac{\sum _{l=T-m+1}^T{X}_{\mathit{ilk}}}{m}-{\stackrel{-}{X}}_{i\cdot k}}{\sqrt{\frac{T-m}{Tm}}}$$

Assuming a constant ${\mu }_{\mathit{ijk}}$ over time (j) for notational simplicity the distribution of $Q_{\mathit{imk}}\sim N({\delta }_{ik}\sqrt{\frac{(T-m)m}{T}},\mathrm{ }1)$. This implies, under independence of features, that under the null distribution $Q_{im}$ is chi-squared with $p$ degrees of freedom, while under the alternative distribution $Q_{im}$ follows a noncentral chi-square distribution with $p$ degrees of freedom and with noncentrality parameter ${\mathit{\delta }}_{\mathit{i}}^T{\mathit{\delta }}_{\mathit{i}}\cdot m(T-m)/T$. Because the timing of the change (here, $m$) in behavior is not known a priori, we must instead consider the test statistic $Q_i=\underset{1\le \mathrm{m} \le \mathrm{D}}{\max }{Q}_{im}$, where $D$ is the lag, or number of days in the past where we are searching for change points. Recall that T is the follow-up time, so $Q_i$ searches for a change point starting at the most recent time point as well as up to $D$ days prior.

The distribution of $Q_i$ is difficult to ascertain analytically for the purposes of sample size and power calculations. Explicit derivations for cov$(Q_{im},Q_{iq})$ are possible, but $Q_i$ represents the maximum of a $D$-dimensional multivariate noncentral chi-square distribution which has no closed-form distribution function despite having an easily estimable covariance matrix. In addition, the assumption independence between features is unrealistic. To avoid these issues and allow for correlation between features, we approximate power by simulating both the null and alternative distributions through the sieve bootstrap.¹⁰

Detecting behavioral changes is of primary use mainly if the change in behavior is detected soon after it occurs. Consider, for example, a patient with suicidal ideation who has identifiable behavioral changes that manifest themselves in reduced sociability, poor quality sleep, and not leaving their home, all of which can be quantified from the smartphone and thus captured in $\mathit{X}$. These behavioral changes could be used to prompt an intervention, but only if the change is detected in a timely fashion. In a situation like this, it may only be useful to identify recent changes in behavior, say in the most recent week, for which $D=7$ would be relevant. This procedure of finding an appropriate follow-up time T will identify the minimum number of days required to detect a change in behavior, so practical study designs should aim to overshoot the T that gives sufficient power for this test.

Population-level analysis: determining N (sample size)

While individual-level models can inform the choice of T, the minimum required length of follow-up to be able to detect behavioral change points, these models do not help in choosing an appropriate sample size, N. Population-level models, or models that aggregate information across a sample to make inferences about the population they represent, gain strength with increases in N in addition to increases in T. A recommended family of population-level models capable of finding associations between digital phenotyping features and clinical outcomes that takes the longitudinal nature of the data into account is the family of generalized linear mixed models (GLMMs).^11,12 Letting $Y_{ij}$ be an outcome measured for participant i on day j of follow-up which, in digital phenotyping, is typically a smartphone survey score but could represent any clinical outcome of interest, we consider the following model for the association between $Y_{ij}$ and the digital phenotyping features ${\mathit{X}}_{ij}$:

$$g\left(E\left(Y_{ij}\right|{\mathit{b}}_{\mathit{i}})\right)={\mathit{X}}_{ij}^T\mathit{\beta }+{\mathit{Z}}_{ij}^T{\mathit{b}}_i.\mathrm{ }$$ (2)

where $E(\cdot )$ represents the expectation of a random variable, $g(\cdot )$ is the appropriate link function chosen based on the nature of the outcome variable (eg, binary vs. continuous), ${\mathit{b}}_{\mathit{i}}$ are the normally distributed random effects for participant i with corresponding design matrix ${\mathit{Z}}_{ij}$, and $\mathit{\beta }$ is the vector of regression coefficients for the digital phenotyping features. This model accommodates a variety of exponential family distributions that the outcome, $Y_{ij}$, can take. We consider using the likelihood ratio test of the null hypothesis of ${\mathit{C}}^{\mathit{T}}\mathit{\beta }=0$ against the alternative of ${\mathit{C}}^{\mathit{T}}\mathit{\beta }\ne 0$ for any linear contrast matrix $\mathit{C}$. Questions of power and sample size for GLMMs have been well explored¹³ with multiple solutions and software packages developed such as the R package sim.glmm, a simulation-based solution.¹⁴ Similarly, for a fine grid of values over both N and T, we simulate power in a random intercept model for a variety of effect sizes, missing data patterns, variances in the random intercept, sampling rates, and significance levels. When a value of T is known based on other information, say, the minimum duration of follow-up to power change point detection sufficiently, then N may be the only parameter that needs to be selected to achieve sufficient power in the GLMM analysis.

Given that most new digital phenotyping studies are for discovery with no prior knowledge about which of the variables to include in the model (2), here we consider modeling each digital phenotyping feature separately to identify significant marginal associations with the outcome. We therefore fit model (2) a total of 31 times, once for each digital phenotyping feature taking turns as the lone predictor. We use a conservative Bonferroni correction to the 0.05 significance level in order to account for multiple testing. Of note, multiple testing is a larger problem for change point detection than it is for association testing due to the repeated daily tests that change point detection requires. This explains our choice of a smaller significance level for change point detection.

RESULTS

Individual-level analysis: Determining $\mathit{T}$ (length of follow-up)

We consider simulation of behavioral change points in the case of a typical digital phenotyping study. We simulated daily behavioral digital phenotyping features ($p=31$) and estimated $\mathbf{\Sigma }$ across all subjects in both the schizophrenia and bipolar studies and standardized the features to have unit variance. Large behavioral changes ($\tau =1.4)$ and small behavioral changes ($\tau =1.1)$ were considered where ${\delta }_k\sim N(0,\tau )$, where change points occur at $m=2,\mathrm{ }4,\mathrm{ }6$, (ie, at 2, 4, or 6 days) prior to the end of follow-up. A more conservative significance level than the commonly used $\alpha =0.05$ should be used in these types of settings to account for multiple comparisons, though each study should select a significance level so as to balance false positives/false negatives appropriately, depending on the context. Here we use a significance level of $\alpha =0.01$. In Figure 1, we show results for simulated power using 10 000 iterations for varying follow-up durations, $T$. Power increases as the number of data post-change point increases (ie, as $T-m$ increases). This is because having more data post-change point provides more information and therefore increases our certainty that the changes in the features are significant and not due to random chance. Also, power increases as the length of follow-up increases (ie, as $T$ increases). This is because having a longer history for a study participant allows us to more firmly establish their behavioral baseline, hence making changes from that baseline easier to detect.

Figure 1.

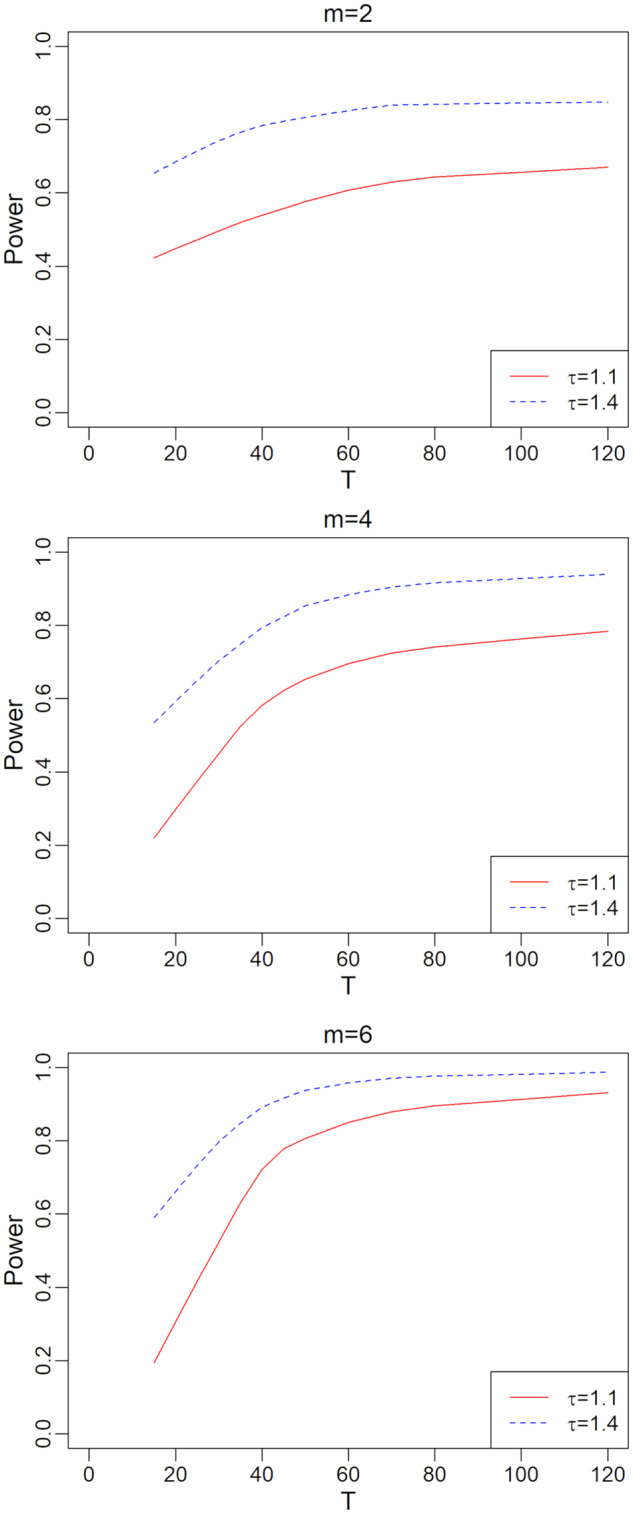
Length of follow-up in relation to the power to detect change points in individual-level analysis. Power to detect a change point in the $p$ daily behavioral digital phenotyping features that occurs $m$ days in the past (ie, only $m$ days of data post-change point, are simulated using 10 000 iterations for each point on the $T$ axis). The dotted line represents large behavioral changes and the solid line represents smaller behavioral changes.

Note that power does not tend to 1 as the length of follow-up tends to infinity ($T\to \mathrm{\infty })$. This is because even if the duration of follow-up is ever-increasing, the amount of data post-change point remains fixed. In other words, even if we have a lifetime of data to establish a person’s specific routine with great accuracy, it may be near impossible to detect a change in that routine with any statistical certainty if the change occurred only yesterday. Sufficient time needs to pass for us be sure that any change is real and not a random anomaly.

For reference, we provide a few example interpretations of Figure 1: 40 days/120 days of follow-up is sufficient to detect a large/small change in behavior that occurs 4 days before the end of follow-up with 80% power; and 30 days/50 days of follow-up is sufficient to detect a large/small change in behavior that occurs 6 days before the end of follow-up with 80% power.

Population-level analysis: determining N (sample size)

To simulate the power of the population-level association GLMMs under realistic settings, we estimate effect sizes from the digital phenotyping study of schizophrenia^3,4 and the digital phenotyping study of bipolar disorder.⁸ The 4 cases we consider, each a random intercept model, are:

1. Bernoulli outcome, strong association: A person’s self-report of them taking their medication ($Y_{ij}$) on a given day is positively associated with how closely they have followed their routine ($X_{ij}$) on that day. Schizophrenia study.

   $${\beta }_0=-4.86,\mathrm{ }{\beta }_1=0.68,\mathrm{ }\tau =18.35$$
2. Bernoulli outcome, weak association: A person leaving their home ($Y_{ij}$) on a given day is positively associated with the number of individuals they contact (either via calls or text messages) on their phone ($X_{ij}$) on that day. Bipolar study.

   $${\beta }_0=-0.27,\mathrm{ }{\beta }_1=0.21,\mathrm{ }\tau =2.06$$
3. Normal outcome, strong association: Self-report of anxiety ($Y_{ij}$) on a given day is negatively associated with the amount of time spent at home ($X_{ij}$) that day. Schizophrenia study.

   $${\beta }_0=-0.27,\mathrm{ }{\beta }_1=-0.06,\mathrm{ }\tau =1.14,\mathrm{ }{\sigma }^2=0.24$$
4. Normal outcome, weak association: Self-report of depression ($Y_{ij}$) on a given day is negatively associated with a person’s in-degree of their social network ($X_{ij}$) on that day. Schizophrenia study.

   $${\beta }_0=0.40,\mathrm{ }{\beta }_1=-0.03,\mathrm{ }\tau =1.41,\mathrm{ }{\sigma }^2=0.24$$

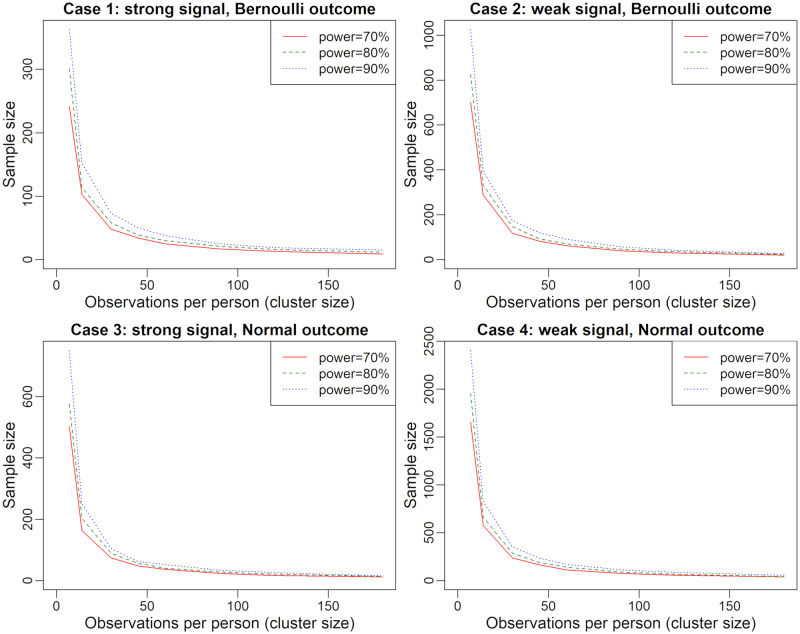
Power and sample size simulations based on these model parameters and effect sizes are demonstrated in Figure 2. As sample size ($N$) decreases, the length of follow-up ($T$) for each participant must increase in order to sustain power. Similarly, studies with very short follow-up periods require large sample sizes in order to sustain power. In particular, studies with follow-up periods that tend to be shorter than a month per participant require disproportionately large sample sizes in order to be well-powered to detect these associations.

Figure 2.

Sample size and follow-up duration in relation to the power of association tests in population-level analysis. Simulations based on the number of days where both predictor and outcome are collected. For each power level and each fixed $T$, sample size was varied using a binary search with 500 iterations at each step in order to identify the sample size that led to the desired power.

DISCUSSION

The temporally dense longitudinal data produced in digital phenotyping studies can be analyzed in a variety of ways. Classical statistical models for longitudinal associations between phenotypes, often collected via self-report, and passively collected behavioral features, can be used. While we present generalized linear mixed models here, one could also consider generalized estimation equations¹⁵ or functional linear models.¹⁶ Similarly, there are a variety of time series modeling choices that can be made.¹⁷

Although we acknowledge that there may be context-specific modeling choices for the analysis of digital phenotyping data, missing data can play an important role in limiting analysis choices. Many time series models require complete data or require imputation to be performed prior to model fitting. Imputation can be a useful tool when missing data is infrequent and unrelated to the outcome of interest, but both criteria are often not met in practice. Especially in studies with long duration of follow-up, it is not uncommon for missing data to be frequent enough to render imputation inadvisable. There is a well developed literature for accounting for missing data in statistical models for longitudinal data, such as for mixed models^18,19 and for generalized estimating equations,²⁰ but these approaches work only for censored data where the censoring mechanism is jointly modeled with the observed data, and so the intermittent missingness present in most digital phenotyping studies cannot be aided by these classical treatment of missing data.

CONCLUSIONS

We present 2 specific and traditional statistical models for longitudinal data, change point detection and generalized linear mixed models, which we use to find the minimum length of follow-up and the appropriate sample-size for a well-powered digital phenotyping study. We provide examples of reasonable effect sizes that were obtained from our existing digital phenotyping studies so that researchers new to this area have a general sense of the magnitude of effect sizes in these types of studies. This procedure for identifying an appropriate sample size and length of follow-up through power simulations has been implemented in an R package, DPsamplesize, so that any researcher can conduct their own simulations to determine length of follow-up and sample size for their specific study. In addition, we have developed an interactive Shiny R application to make this approach to sample size and study duration calculation accessible to the practitioner. The interactive Shiny application for calculating appropriate sample size and study duration is available at: https://onnela-lab.shinyapps.io/digital_phenotyping_sample_size_calculator/.

FUNDING

This work is supported by R01MH116884 (Barnett), K23MH116130 (Torous), DP2MH103909 (Onnela), and U01MH116925 (Baker).

AUTHOR CONTRIBUTIONS

IB and JPO conceived of the manuscript design. JB, JT, and JPO collected the data. IB performed the analyses and wrote the manuscript. JPO, JB, HR, JT contributed to writing the manuscript.

CONFLICT OF INTEREST STATEMENT

None delcared.