Automated Gleason grading of prostate cancer using transfer learning from general-purpose deep-learning networks

Abstract

Two deep-learning algorithms designed to classify images according to the Gleason grading system that used transfer learning from two well-known general-purpose image classification networks (AlexNet and GoogleNet) were trained on Hematoxylin–Eosin histopathology stained microscopy images with prostate cancer. The dataset consisted of 439 images asymmetrically distributed in four Gleason grading groups. Mean and standard deviation accuracy for AlexNet derivate network was of 61.17±7 and for GoogleNet derivate network was of 60.9±7.4. The similar results obtained by the two networks with very different architecture, together with the normal distribution of classification error for both algorithms show that we have reached a maximum classification rate on this dataset. Taking into consideration all the constraints, we conclude that the resulted networks could assist pathologists in this field, providing first or second opinions on Gleason grading, thus presenting an objective opinion in a grading system which has showed in time a great deal of interobserver variability.

Introduction

Prostate cancer is the second most common cancer diagnosed in men, with over 10% of the male population being diagnosed during their lifetime [1].

Despite the advances in all imaging medical fields [ultrasound, computed tomography (CT), magnetic resonance imaging (MRI)], the “gold standard” for diagnosis remains the microscopic tissue examination performed by a pathologist.

Developed in 1966, the Gleason grading system (GGS), together with more recent revisions [2,3], stratifies prostate cancers based on architectural patterns as a reflection of their biology. GGS remains the most powerful predictor of prognosis in almost all prostate cancer studies, being widely used in standardized patient management [4]. The GGS classifies prostate cancer growth patterns in five grades (some having sub-grades), and summing up the two most common grades results the final Gleason score, which ranges between two and 10, and which is supposed to stratify patient’s outcome.

Without any intention to alter the role of GGS in prognostic and patient management, different studies have shown that the system suffers from two major drawbacks: the first being related to the grading itself, while the second is related to the quantity of the biological product that is being analyzed. The first drawback refers to the suboptimal interobserver and intraobserver variability, with reported discordance ranging from 30% to 53% [5,6,7,8,9,10], and with imprecise differences between classes on standard feature extraction algorithms, such as fractal analysis [11,12,13]. The second drawback refers to the fact that the score is computed using the dominant and subdominant patterns of the cancer. In healthy subjects, the size of the prostate is approximately 3×4×5 cm, whereas in pathological conditions the size increases three times. The size of the prostate, combined with the possible transurethral resection of the prostate, produce a considerable sample size thus requiring a careful assessment of first and second most frequent patterns.

Taking into consideration the mentioned drawbacks, the GGS proves that these tasks are time-consuming if they are performed by the pathologist, and also that they imply material cost with high interobserver and intraobserver variability. Hence, this task is suitable for computer-aided medical diagnosis systems.

Multiple computer-aided diagnosis (CAD) systems have been proposed for GGS automatization with different approaches, from standard artificial intelligence (AI) algorithms [14,15,16] to the newer deep-learning (DL) approaches [17,18,19].

Aim

The aim of current research was to develop a DL algorithm that uses transfer learning from well-known pre-trained networks capable of classifying histological images according to the GGS with high accuracy (ACC).

Patients, Materials and Methods

Patient inclusion, ethical data and image retrieval

We prospectively included 439 images from 83 patients who underwent total prostate resection, following a diagnosis of prostate cancer, between January 2013 and December 2015 at the Municipal Clinical Hospital of Cluj-Napoca, Romania. All presumptive diagnoses were made by combining clinical and imaging data and confirmed through pathology. All patients signed informed consent forms and agreed to tissue harvesting for research purposes, as per usual Hospital Guidelines. We ascertained that our study did not interfere with therapeutic or diagnostic procedures. We harvested tissue from whole-organ resection specimens for usual diagnosis and staging by two expert pathologists; afterwards, images were obtained as per the below protocol.

In the original GGS, revised several times by the author himself [20,21,22,23], the architectural patterns of tumor proliferation were labeled based on the five main classes and subtypes. Thus, the Gleason pattern 1 (very rare) is characterized by a very well-differentiated proliferation, consisting of medium-sized, round or oval, uniform glands, arranged very compactly but separated from each other. Compared to pattern 1, the glands from pattern 2 have a greater variability in size and shape and are separated by stromal bays, with an average distance of interglandular separation smaller than the diameter of a gland. Pattern 3 is considered the form with moderate differentiation. Gleason described this pattern as having three distinct architectural morphological aspects, designated as patterns 3A, 3B, and 3C. The 3A subtype is characterized by the presence of isolated glands of medium size, with a variable shape, consisting of elongations, twists and angles that can also have sharp angles. Subtype 3B has, in principle, the same architectural appearance as pattern 3A, with the only difference that the tumor glands are smaller. Subtype 3C is composed of ducts or ducts expanded with sieve or intraluminal papillary tumor masses which, in accordance with the hypothesis that this pattern would really represent an intraductal proliferation, have smooth, rounded contours, as of relaxed ductal profiles. Pattern 4 is considered a poorly differentiated high-grade proliferation. Gleason described this pattern as having two distinct morphological aspects – patterns 4A and 4B. Subtype 4A – tumor proliferation is composed of cells that may have either a fused micro-acinar arrangement or a cribriform or a papillary one. Tumor cells form either infiltrative masses with a totally irregular appearance or strings or cords of epithelial malignant cells. Subtype 4B – carcinomatous proliferation of this type is identical in terms of architectural appearance to the other subtype of pattern 4, with the only difference that the cells that form it have a clear cytoplasm. Pattern 5 is the weakest differentiated form of prostate cancer and was also divided by Gleason into two subtypes: 5A and 5B. Subtype 5A resembles the “comedo” type of intraductal breast carcinoma, presenting as tumor masses in which the cells have a chordal or cylindrical arrangement, with a cribriform, papillary appearance (as in subtype 3C) or solid, with smooth, rounded edges, whose central area is typically occupied by necrotic detritus. Subtype 5B consists of tumor areas with irregular edges formed by anaplastic tumor cells.

The recent revisions simplified somehow the original system. Thus, pattern 3 remained with only two subtypes mainly (original 3A and 3B). Pattern 4 included cribriform glands larger than benign glands and with an irregular border, finally consisting of poorly formed glands of either cribriform or fused architecture [2,3, 24].

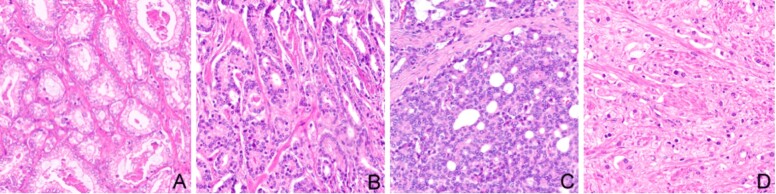
We included in our study 439 Hematoxylin and Eosin (HE) images with monotonous patterns that were classified according to GGS by two pathologists in four groups: Gleason pattern 2 (n=57), Gleason pattern 3 (n=166), Gleason pattern 4 (n=182), and Gleason pattern 5 (n=34). The dataset had no image with pattern 1. The images, 32-bit red, green, blue (RGB) color space, were cropped at 512-by-512 pixels from whole slide images scanned with Leica Aperio AT2, using a 20× apochromatic objective. A sample of each pattern is presented in Figure 1.

Figure 1.

Samples from the dataset (HE staining, ×200): (A) Gleason pattern 2; (B) Gleason pattern 3; (C) Gleason pattern 4; (D) Gleason pattern 5

Deep neural network algorithms and methods

Two DL algorithms were developed using transfer learning from AlexNet [25] and GoogleNet [26] networks.

AlexNet is a convolutional neural network that has been trained on more than a million images from the ImageNet database available free of charge on http://www.image-net.org. The network is eight layers deep and classifies images into 1000 categories of objects from the real world. The network has an input image size of 227-by-227 pixels, with a 32-bit RGB color space. In order to fit the input layer of the network, we resized the images at 227-by-227 pixels keeping the 32-bit RGB color space. The last layers of the network were replaced in order to classify the input images in four classes according to the GGS patterns.

GoogleNet is a convolutional neural network that is 22 layers deep, also trained on ImageNet. The network classifies images in the same 1000 object categories as AlexNet. The network has an input image size of 224-by-224 pixels, with a 32-bit RGB color space. In order to fit the input layer of the network, the images processed for AlexNet were resized at 224-by-224 pixels keeping the 32-bit RGB color space. The last layers of the network were replaced in order to classify the input images in four classes according to the GGS patterns.

We used 85% of the images for training and the remaining 15% for testing.

We performed the algorithm implementation and the statistical assessment in MATLAB (MathWorks, USA).

Results

DL being a stochastic algorithm, a certain number of runs is needed to be performed in order to obtain robust and trustworthy results. A suitable statistical power (two-tailed type of null hypothesis with default statistical power goal p≥95% and type I error α=0.05 – level of significance) can be achieved through 100 independent computer runs. When designing an experiment, one needs to perform statistical power analysis together with sample size. Precision and ACC may lack due to a low sample size, whereas a high sample size may lead to an increase of computational and time costs, without a gain in performance. The standard 10-fold cross-validation has been used in our study. The DL algorithms have been independently run 100 times in a complete 10-fold cross-validation cycle.

When running multiple times a stochastic algorithm, we encounter differences between ACCs, hence we need to compute also the standard deviation (SD) of the ACCs obtained. If we obtain low value SD, then our model is more stable.

In order to perform different statistical tests, we first need to verify whether the sample data has a normal distribution or not. If the data does not have a normal distribution, the results might be affected, due to the existence of outliers. In our study, we applied the Kolmogorov–Smirnov and the Shapiro–Wilk W tests.

Mean and SD on 100 algorithm runs for the ACC was of 61.17±7 and of 60.9±7.4 for AlexNet and GoogleNet, respectively.

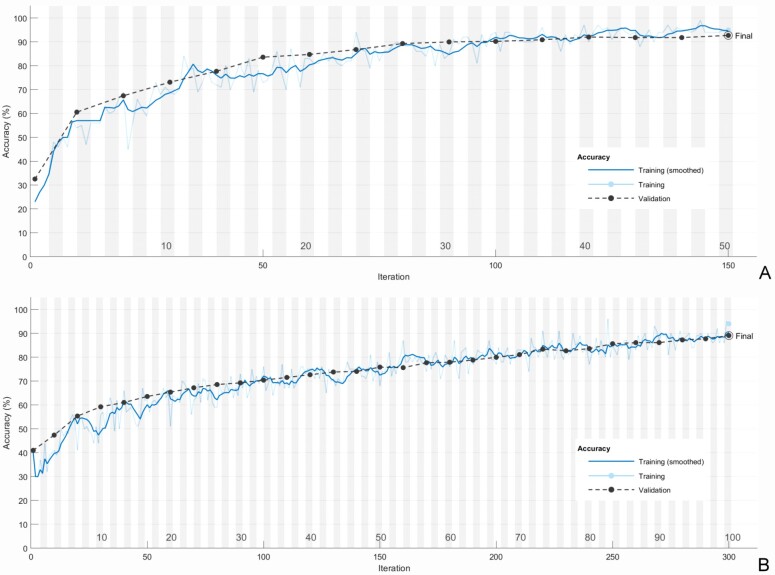
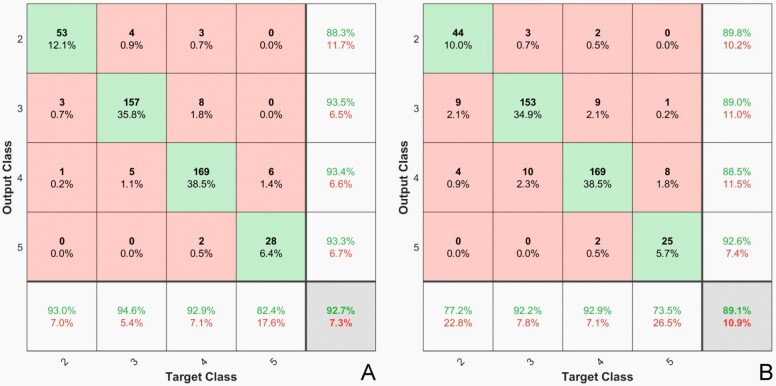
Samples of the training sequences are presented in Figure 2 and the confusion matrix from the same runs, applied to the whole dataset in Figure 3.

Figure 2.

Training process: (A) AlexNet; (B) GoogleNet

Figure 3.

Confusion matrix heatmap: (A) AlexNet; (B) GoogleNet

Due to its simpler architecture, we packed the resulted algorithm from AlexNet in a standalone application (Microsoft Windows) capable of learning on new image datasets, transferring knowledge form pre-trained networks, and classifying new images. A preview of the application is presented in Figure 4.

Figure 4.

Standalone prostate cancer image classifier application interface

The results of the Kolmogorov–Smirnov and Shapiro–Wilk W tests are displayed in Table 1.

Table 1.

Normal distribution assessment

Algorithm	Kolmogorov–Smirnov (K–S)		Shapiro–Wilk (S–W) W
	K–S max D	Lilliefors p	S–W W	p-level
AlexNet	0.107	0.2	0.976	0.41
GoogleNet	0.122	0.1	0.977	0.46

From Table 1, we can see that regardless the algorithm, the sample data is normally distributed. Hence, we can proceed to compare how the two algorithms perform using the t-test for independent samples. The results could be objectively compared because both algorithms have been run in the same conditions (100 computer-runs/10-fold cross validation).

The results from the t-test are displayed in Table 2.

Table 2.

Statistical assessment the means of the two algorithms

Variable	t-test / p-level
AlexNet vs. GoogleNet	0.62 / 0.53

As shown in Table 2, there is no significant difference in means (p-level >0.05) between the two networks concerning the testing performances. Thus, both algorithms perform the same on this dataset.

Discussion

When using the GGS to stratify the aggressiveness of prostate cancer, pathologists are often confronted with a classification problem pertaining to the varying nature of tissue loss and resulting morphology. Thus, it is imperative that common morphological descriptors should be identified and applied in medical practice, in order to unify the opinions of different clinician pathologists and provide a closer-to-accurate prognosis. Survival as well as different approaches for treatment depend on this step. Diagnosis between malignant and benign histological tissue is possible by using semi-automated computer-assisted methods [27,28]. Previous approaches relied on identifying distinctive features [29,30,31] and training neural networks to identify and quantify such pre-determined and operator-dependent markers. Recently, DL greatly reduced this effort, at the expense of transparency – basically, the technique can be labeled as a “black box” approach, since the operator is “blinded” to the way, the computer identifies the significant features. As previous authors stated, this may be a serious impediment towards widespread acceptance and regulatory approval [32].

In our study, we used digitized images of prostate cancer microscopy, classified as Gleason patterns 2 to 5. We have proven here that it is feasible to use a DL approach to tackle this medical classification problem, irrespective of the network architecture – either using AlexNet or GoogleNet, which produced comparable results. This computerized approach may lead to successful implementation of medical-grade tools aimed to both second the opinion of a medical expert, or to provide intermediate diagnosis in tertiary medical centers that lack immediate access to a pathologist expert or which can rely on telemedicine for faster decision making. In our opinion, it is not, however, advisable to not involve a human specialist in the process, since the algorithms also have specific limitations that are inherent due to the imperfect nature of the Gleason scoring system.

A common observed problem of the GGS scoring is that score 7 (grades 4+3) cancers were associated with a three-fold increase in prostate cancer outcome compared with grades 3+4 cancers [95% confidence interval (CI), 1.1 to 8.6) [33]. The same conclusion was reported by Chan et al. (2000) [34]; the authors have concluded that Gleason score 4+3 tumors had an increased risk of progression independent of stage and margin status (p<0.0001). They also reported that the 5-year actuarial risk of progression was 15% for Gleason score 3+4 and 40% for 4+3 tumors. A close look to the data in Figure 4 shows a higher error rate of the classification exactly between pattern 3 and pattern 4. Thus, AlexNet incorrectly labeled five images with pattern 4 as pattern 3 and eight images with pattern 3 as pattern 4. GoogleNet incorrectly labeled nine images with pattern 4 as pattern 3, and 10 images with pattern 3 as pattern 4. This represents 25% of all the errors of the AlexNet classifier and 40% of GoogleNet. This can be explained on one hand by the fact the classifier was trained on images labeled by pathologists and is thus subjected to their subjectivity and, on the other hand, it could show a problem related to the GGS itself as reports show higher interobserver variability between these classes. In a similar report [35], the 24 cases that had score changes, five cases were upgraded from grade 3 to 4 and 15 were downgraded from grade 4 to 3, this representing 80% of the reported changes.

This study has limitations that would need to be addressed to prior to clinical usage, and these will need future work and improvements. However, based on its performance, the resulted application could be used for research purposes.

First, the specimens that were used to develop the DL algorithms originated from a single medical center, the slides were stained in one laboratory, using only the HE staining, the digital data were acquired using a single slide scanner, and, the classes are unbalanced. Only after the results would be confirmed on multi-center studies, with different staining protocols, the images would be digitalized using slide scanners from different vendors and the dataset would be large enough and balanced, then the proposed method could be considered for clinical deployment.

Second, the study focuses on classifying images of acinar prostatic adenocarcinoma excluding other types of prostate cancer or invading nearby tumors, and there were no normal glands available as reference. Used incorrectly, it could generate miss classification and miss understanding.

Last, a more serious limitation is the subjective nature of the GGS. Inter-pathologist variability is a non-negligible aspect, as also shown in other studies [18], and it can be overcome considering two different approaches. One possible approach would be to replace the “gold standard” classification – GGS – with a simpler and more objective one. This is unlikely due to the large usage of the GGS in practice. From our experience [36,37], a possible alternative could be the Srigley grading system, which, at least, has more clearly defined classes. Another possible approach could be the use of a large trading set, thus reducing the error probability.

We conducted our study on resection specimens; however, CAD on needle core biopsies would have a higher clinical impact. Since there is no difference on the GGS training and functionality for core biopsies [19], we expect a constant behavior for the classifiers, but the theory remains to be proved in further work.

Different from other approaches, this study describes the transfer learning from general-purpose DL networks to a diagnostic system of prostate cancer grading through GGS using routine histopathology images. The technique has been successfully used on ultrasound and MRI images [38,39,40,41].

Conclusions

In this paper, we present two DL algorithms design to classify images according to GGS. The algorithms use transfer learning from two well-known general-purpose image classification DL networks – AlexNet and GoogleNet –, and are further trained on histopathology images of prostate cancer. With a reported ACC of 61.17±7 for AlexNet and of 60.9±7.4 for GoogleNet, with a small dataset of only 439 asymmetrically distributed cases in four GGS classes, we find the result to be promising. The similar results obtained by the two networks with very different architecture, together with the normal distribution of classification error for both algorithms show that we have reached a maximum classification rate on this dataset. With further evaluation, the resulted networks could assist pathologists by presenting an objective first or second opinion in a grading system with high interobserver and intraobserver variability.

Conflict of interests

The authors declare that they have no conflict of interests.