A fast and high-quality charge model for the next generation general AMBER force field

Abstract

The General AMBER Force Field (GAFF) has been broadly used by researchers all over the world to perform in silico simulations and modelings on diverse scientific topics, especially in the field of computer-aided drug design whose primary task is to accurately predict the affinity and selectivity of receptor–ligand binding. The atomic partial charges in GAFF and the second generation of GAFF (GAFF2) were originally developed with the quantum mechanics derived restrained electrostatic potential charge, but in practice, users usually adopt an efficient charge method, Austin Model 1-bond charge corrections (AM1-BCC), based on which, without expensive ab initio calculations, the atomic charges could be efficiently and conveniently obtained with the ANTECHAMBER module implemented in the AMBER software package. In this work, we developed a new set of BCC parameters specifically for GAFF2 using 442 neutral organic solutes covering diverse functional groups in aqueous solution. Compared to the original BCC parameter set, the new parameter set significantly reduced the mean unsigned error (MUE) of hydration free energies from 1.03 kcal/mol to 0.37 kcal/mol. More excitingly, this new AM1-BCC model also showed excellent performance in the solvation free energy (SFE) calculation on diverse solutes in various organic solvents across a range of different dielectric constants. In this large-scale test with totally 895 neutral organic solvent–solute systems, the new parameter set led to accurate SFE predictions with the MUE and the root-mean-square-error of 0.51 kcal/mol and 0.65 kcal/mol, respectively. This newly developed charge model, ABCG2, paved a promising path for the next generation GAFF development.

I. INTRODUCTION

In computer-aided drug design (CADD) efforts, especially at the stages of lead-identification and lead-optimization, a major task is to accurately predict the binding affinities of receptors (proteins or nucleic acids) and ligands.^1–4 The prediction quality generally depends on the free energy calculation algorithm and force field (FF).⁵ The former includes various efficient end-point free energy methods, such as LIE and MM-PBSA/GBSA,^6–12 and rigorous alchemical free energy methods, such as TI, FEP, λ-dynamics, and other advanced-sampling-based methods.^13–18 The latter includes specific macromolecular force fields (FFs)^19–23 and general FFs for arbitrary compounds, which may be encountered as ligands.^24–27 In the past, the accuracy and transferability issues have challenged the general FF development. One thought has been moving from additive fixed-charge models to polarizable models^28–33 because the latter allow the electrostatic effect across different dielectric environments (from polar to nonpolar) to be naturally handled. While polarizable FFs are currently undergoing active development, so far they have been seldom applied on simulating and calculating protein-ligand binding interactions.^30–32 Due to the efficiency requirement, particularly burdened by the need of a comprehensive description of the enormous chemical space, classical pair-wise additive FFs based on fixed point charge models not only are the current main-stream but also are expected to prevail in the near and a perceivable future. With the above thought, this work explores whether additive general FFs can be further optimized to meet the accuracy and transferability requirement, for instance reliably treating a range of polar and nonpolar environments.

The general AMBER force field (GAFF)^24,25 is the first general FF developed in academia, primarily to model arbitrary organic molecules. It has been widely applied on a variety of scientific topics by researchers all over the world. So far it has been cited more than 7600 times according to the databases of Web of Sciences (https://www.webofknowledge.com, accessed on June 3, 2020) and more than 9600 times according to Google Scholar Citation (https://scholar.google.com, accessed on June 3, 2020). Since 2015, the second generation of GAFF (GAFF2) has been released to the public via the AMBER program and AmberTools. Related description can be found in the footer of the released gaff2.dat file and with the completion of the remaining work on representative chemical space expansion and some parameter improvement, the development detail is soon to be submitted for publication. In a very brief summary, compared to GAFF, GAFF2 has updated the bonded parameters to reproduce molecular geometries, vibrational spectra, and potential energy surfaces from higher level quantum mechanics (QM) calculations on more model compounds, and updated the non-bonded parameters to better reproduce ab initio interaction energies and experimental neat liquid properties. Positive feedback from users (in private communications and in literature³⁴) also revealed the encouraging performance of GAFF2 in various aspects. For example, Slochower et al.³⁴ performed a free energy calculation study on 43 α and β-cyclodextrin (CD) host–guest pairs with different FFs: GAFF, GAFF2, and SMIRNOFF99Frosst.³⁵ It was found that GAFF2 “has statistically significant(ly) better correlation with the experimental data” on the binding free energy and enthalpy, “excellent agreement with experiment on predicted binding entropy,” and “better model for the flexibility of the CD cavity” compared to GAFF and SMIRNOFF99Frosst, although the latter two are “arguably better than GAFF v2.1 on estimated binding free energies … based on the mean signed error relative to experiment.”

Originally, GAFF was developed based on the restrained electrostatic potential (RESP)^36,37 charge model to assign atomic charges, which fits atomic charges against the electrostatic potential (ESP) from the QM calculation at the HF/6-31G^* level of theory, just like the AMBER biomolecular FFs^21,22 for the biomolecules. For the fact that ab initio calculations are expensive, in practice, GAFF users usually adopt the fast semiempirical method of Austin Model 1 with bond charge corrections (AM1-BCC)^38,39 to generate atomic charges. AM1-BCC charges could be efficiently and conveniently obtained via the ANTECHAMBER⁴⁰ module of the AMBER program tools. The basic idea of AM1-BCC is to use AM1 Mulliken charges to capture primary electronic structural features of a molecule and then apply a set of additive bond charge corrections (BCCs) upon AM1 Mulliken charges to emulate the HF/6-31G^* ESP. The advantages of AM1-BCC lie in that not only the process is convenient and efficient (because ab initio calculations are not necessary) but also the produced atomic charges are less dependent on the input molecular conformation. GAFF2 was also developed based on the RESP charge model. It is reasonable to expect that many users would still prefer employing the AM1-BCC charge scheme instead of RESP. Therefore, in this work, we sought to develop an optimized AM1-BCC set for GAFF2. Specifically, we employed a solvation free energy (SFE) based strategy for this optimization. In our previous development of GAFF and GAFF2, this important physiochemical property was not directly targeted in the parameterization process but only employed for later validation, mostly due to the fact that the SFE calculation is much more computationally costly than the calculation of density or heat of vaporization. Indeed, the SFE based strategy has not been commonly adopted except for GROMOS 53A6²³ and 53A6OXY,⁴¹ which considered the SFEs of amino acid analogues and functional groups containing oxygen, respectively, also as the parameterization target.

SFE is a critical property in physical, chemical, and biological processes. SFE is closely related to many other important properties, such as solubility, partition coefficient, membrane permeability, and protein-ligand binding free energy in drug-discovery projects.⁴² Generally, the accuracy level of the SFE calculation limits the accuracy expectation for the prediction of the above properties. For example, the absolute or relative SFE calculation is an elementary step in the thermodynamic cycle used for the absolute or relative protein-ligand binding free energy calculation.¹⁵ Moreover, a ligand binding process can be viewed as a special dissolution process; both involve the conformation rearrangement of the small molecule and relaxation of the environment (solvent or protein). In certain aspect, the difference between these two processes only lies in complexity and dielectrics of the corresponding environment. Therefore, the SFE calculation is often utilized to test sampling algorithms and potential energy functions, as the basic benchmark for binding free energy prediction.⁵ As a popular force field, GAFF has also been extensively validated in the aspect of SFE in water [i.e., hydration free energy (HFE)].^43–54 Test studies have been performed across the diverse categories of the organic molecules, on different charge models (RESP, or AM1-BCC, or the commercial Merck-Frosst version of AM1-BCC^52–55), and through various free energy methods in different molecular dynamics (MD) programs.^43–55

In principle, both van der Waals (VDW) parameters and atom charges can be optimized against SFEs. For instance, Nerenberg et al.⁵⁵ and Jämbeck and Lyubartsev⁵⁶ tried specifically tuning the VDW interactions between the solute atoms and the oxygen atom in water with the Lorentz–Berthelot combination rules kept or abandoned.⁵⁶ Based on our experience and general expert understanding in the field, we prefer to focus on the charge adjustment because SFEs are more sensitive to atomic partial charges, whilst neat liquid properties are more sensitive to VDW parameters. Therefore, the VDW parameters in both GAFF and GAFF2 were mainly calibrated against pure liquid properties, such as density and heat of vaporization. In terms of charge optimization, upon the initial atomic charge assignment, three options can be taken: (1) reassigning charges based on the higher level of QM theories and basis sets, (2) applying scale factors, and (3) specifically tuning BCCs. Previous studies revealed that the atomic charges directly derived from the higher level of the QM methods can only introduce marginal improvement to the SFE calculation.^57–60 A scale factor applied on the QM derived atomic charges could improve the overall performance on the SFE calculation, but different optimal scale factors may be needed for different solvents.⁶¹ In this study, we chose the strategy of optimizing the specific BCC terms in the AM1-BCC model to focus the reduction of the systematic errors of SFEs on certain functional groups, which were identified as the bottleneck of achieving accurate transfer free energy or binding free energy prediction. In this work, we (1) for the first time tested the performance of the original AM1-BCC charge model with GAFF2 on the HFEs of a large dataset of more than 400 neutral molecules, (2) developed a new set of AM1-BCC parameters, which significantly improves the accuracy of the HFE calculations in explicit TIP3P water, and (3) verified that the new AM1-BCC charge model also has an outstanding performance on the SFE calculation in various nonpolar and polar organic solvents, which have different dielectric constants. The results not only enhanced the capability of the quantitative prediction of key properties in CADD but also paved a feasible way for the development of the next generation general AMBER force field.

II. METHODS

A. Dataset preparation

The experimental data of SFEs of the neutral molecules in water (HFEs) were taken from the FreeSolv v0.52 database,⁵⁴ and the experimental data of SFEs in organic solvents were obtained from the Minnesota Solvation Database v2012.⁶² The initial structures of solutes/solvents were taken from the mol2 files in the FreeSolv v0.52 database or from the xyz files in Minnesota Solvation Database v2012, then were imported to Schrödinger Maestro v11.2⁶³ for visual check and necessary manual modification, such as setting correct bond types for the molecule structures from the xyz files, and then all the structures were saved in the mol2 format.

B. Force fields and preparation of systems

Geometry optimization in the gas phase was performed for all mol2 structures by Gaussian 16⁶⁴ at the Hartree–Fock (HF) level of theory with 6-31G^* basis. The Gaussian output files were directed to ANTECHAMBER⁴⁰ to generate the corresponding topology files (containing AM1-BCC atomic charges) and parameter files (including bonded terms and VDW terms) using the GAFF2 force field. The SQM module in Amber Tools was called by ANTECHAMBER to produce AM1 charges, which was further modified by the predefined BCC terms (either original ones or adjusted ones in this study) to produce the final AM1-BCC atomic charges. When parameterizing the specific BCC terms, the corresponding values in the file $AMBERHOME/dat/antechamber/BCCPARM.DAT were tuned. The organic solvent molecules were processed in the same procedure as the solute molecules. Water was treated with the TIP3P⁶⁵ model.

For each solvent–solute pair system, a single solute molecule was solvated in a cubic box of pure solvent molecules with the TLEAP module in AMBER18.⁶⁶ The size of the simulation box varies depending on the size of solute and the type of solvents. The rule of thumb is that the minimum solute-box distance should be larger than the short-range cutoff (10 Å here) to avoid image violations. For water solvent, the minimum distance between any solute atom and an edge of the box was set to 12 Å. For organic solvents, the initial solution box generated by TLEAP often have a vacuum space due to the size of solvent molecules and the need of deleting solvent molecules to avoid steric conflicts (Fig. S4 in supplementary material). The solution box would shrink after equilibrium runs. Therefore, the input of the initial thickness of the solvent shell provided to TLEAP was set individually for different solvent–solute pairs to ensure the side sizes of cubic boxes after equilibration were ∼39 Å, which is enough to get a solvent shell of at least 10 Å for all of the considered solutes in this study.

C. Simulation protocols

The thermodynamic integration (TI) modules of both central processing unit (CPU) and graphic processing unit (GPU) versions^67–69 implemented in AMBER18⁶⁶ were adopted to carry out simulations and calculate the SFEs. Periodic boundary condition and the isothermal-isobaric NPT ensemble were produced in all simulations, including both the equilibration and production phases. The temperature was kept at 298 K using Langevin dynamics with the collision frequency gamma_ln being set to 2.0 ps⁻¹. The pressure was kept at 1.013 25 bar with Monte Carlo barostat and the pressure relaxation time being set to 2.0 ps. Because the bond constraint SHAKE algorithm is disabled for TI mutations in AMBER GPU-TI module pmemdGTI, a time step of 1 fs was used for all MD simulations. The whole solute molecule was incorporated into the soft-core region for both VDW and electrostatic interactions.^70,71 The default soft-core potential implemented in AMBER18 package⁶⁶ was applied. The single-step decoupling protocol⁷¹ was performed at nine discrete λ windows (0.015 92, 0.081 98, 0.193 31, 0.337 87, 0.5, 0.662 13, 0.806 69, 0.918 02, and 0.984 08). The energy information was saved every 0.5 ps for post-analysis. The Gaussian quadrature rule was adopted to integrate ∂V/∂λ (marked as “DV/DL” in AMBER output files) as described by Eqs. (1)–(3) and the weights (w_i) corresponding to the λ_i values were 0.040 64, 0.090 32, 0.130 31, 0.156 17, 0.165 12, 0.156 17, 0.130 31, 0.090 32, and 0.040 64 according to Table 21.1 in the AMBER18 manual,⁶⁶

$$V\left(\lambda \right)=\left(1-\lambda \right)V_0+\lambda V_1,$$ (1)

$$\mathrm{\Delta }G=G\left(\lambda =1\right)-G\left(\lambda =0\right)={\int }_0^1⟨{\frac{\partial V}{\partial \lambda }}_{\lambda }⟩d\lambda \approx \sum w_i{⟨\partial V/\partial \lambda ⟩}_i,$$ (2)

$$\frac{\partial V}{\partial \lambda }=V_1-V_0,$$ (3)

where Hamiltonian V(λ) is the mixed potential of the initial state, V₀, and the final state, V₁.

After setting-up of the systems, initial equilibrations were conducted at λ = 0.5 with CPU-TI for 200 ps before switching to GPU-TI runs because AMBER CPU-TI has more tolerance for the changes in the size of the simulation box than AMBER GPU-TI in the NPT ensemble simulations. Five snapshots were extracted at even intervals from the last 100 ps of the CPU-TI equilibration trajectory as the starting configurations of five individual GPU-TI runs at λ = 0.5. A 2-ns simulation was conducted for each individual GPU-TI run, and the final snapshot was used as the starting configuration for the two neighboring λ windows, i.e., λ = 0.337 87 and 0.662 13, and their final snapshots of these two λ windows were used as the starting configurations of their neighboring λ windows toward two λ endpoints, respectively (Fig. S1). Similarly, for each independent run of a λ window, a 2-ns MD simulation was conducted and the beginning 0.5 ns simulation was considered as further equilibration steps, and therefore, excluded for post-analysis. The above TI protocol is shown in Fig. S1. The SFE values were separately calculated from five replicas starting with different randomly generated initial velocities (run1 to run5) at all λ windows. Then the arithmetic average was used as the final SFE for each solvent–solute pair, and the associated standard deviation was used to indicate the precision.

D. Strategy and procedure of parameterizing BCC terms

The HFEs of various solutes with single or multifold functional groups in TIP3P water were calculated with the GAFF2 force field parameters and AM1-BCC charges. The BCC terms for those functional groups with mean unsigned errors (MUEs) of >0.6 kcal/mol were adjusted, and new AM1-BCC charges were re-generated, followed by a new round of HFE calculations. The BCC terms were verified and adjusted if needed in a sequential manner according to the scheme shown in Fig. S2. In brief, the parameters for alkanes and aromatic hydrocarbons were first evaluated and adjusted if necessary, followed by alkenes, alkynes, and other chemical functional groups. The adjusted BCC parameters in earlier steps will be applied directly in the subsequent steps. After all optimizations targeting HFEs were done, the updated BCC terms were directly applied to the calculations of SFEs in various organic solvents to test their performance and transferability in different dielectric environments. The overall procedure of developing and validating the new AM1-BCC charge model is demonstrated in Fig. S3.

III. RESULTS

For most solvent–solute pairs, the standard deviation of the calculated SFE from five individual TI replicas in this study is usually <0.2 kcal/mol. Considering the uncertainty of individual experimental measurements of SFEs can be up to ∼0.6 kcal/mol,⁵⁴ the precision of our TI protocol is sufficient for the parameterization process.

A. Performance of GAFF2 with the original and new AM1-BCC charge models on hydration free energies

Just as GAFF, GAFF2 has been developed with the RESP charge model for atomic partial charge assignment and the TIP3P water model for studying the molecular properties in aqueous solution, following the similar force field parameterization strategy in the AMBER biomolecule force field development in order to maximize the compatibility between the biomolecular and organic molecular force fields.^21,22 The HFEs and other SFEs have not been utilized as the targets of parameterization. The overall better performance of GAFF2/RESP on the HFE in TIP3P water than that of GAFF/RESP has been validated by us, and will be demonstrated in another manuscript of GAFF2 description. In this study, we focus on the performance of the original AM1-BCC (interchangeable as the old AM1-BCC in this manuscript) charge model with the GAFF2 parameters on HFEs of a variety of organic solute molecules, and the corresponding improvement after we optimize certain BCC parameters.

As presented in Fig. 1 and Table I, the mean unsigned error (MUE) of hydration free energies for 27 linear and branched alkanes is 0.34 kcal/mol, and the MUE of nine cycloalkanes is 0.51 kcal/mol both less than the default uncertainty (0.6 kcal/mol) of experimental measurements in the FreeSolv database.⁵⁴ Therefore, the BCC terms for alkanes were considered as good enough and were kept unchanged. Except for alkanes, the rest of the functional groups shown in Fig. 1 and Table I involved more or less adjustment of the related BCC parameters. 12 types of functional groups with original AM1-BCC charges show systematic errors >1.0 kcal/mol, including chlorinated aliphatic and aromatic hydrocarbons, brominated hydrocarbons, alcohols, amines, pyrazines and pyridines, nitriles, nitro hydrocarbons, nitrooxy alkanes, amides, and thioethers. After the optimization of the BCC terms, all functional groups have the MUE ≤ 0.6 kcal/mol for the benchmarked molecules. For most benchmarked functional groups shown in Table I, the new AM1-BCC charge model makes the predictive index PI^72,73 and Pearson’s correlation coefficient R increase, the slope k value closer to 1.0, and the intercept b value closer to 0.0, except for several functional groups with very few data points and a narrow range of the experimental data. For the tested 442 neutral solutes in total, the MUE from the original AM1-BCC charge model is 1.03 kcal/mol, and the MUE from the new AM1-BCC charge model is significantly decreased to only 0.37 kcal/mol. The predictive index PI increases from 0.91 to 0.98. Pearson’s correlation coefficient R increases from 0.92 to 0.98. When fitting the calculated data (y) vs the experimental data (x) with function y = kx + b, the slope k value increases from 0.86 to 0.98, and the intercept b value changes from 0.27 kcal/mol to −0.06 kcal/mol. Figure 2 shows the overall performance of the original and the newly proposed AM1-BCC charges on the hydration free energies calculated with GAFF2 parameters.

FIG. 1.

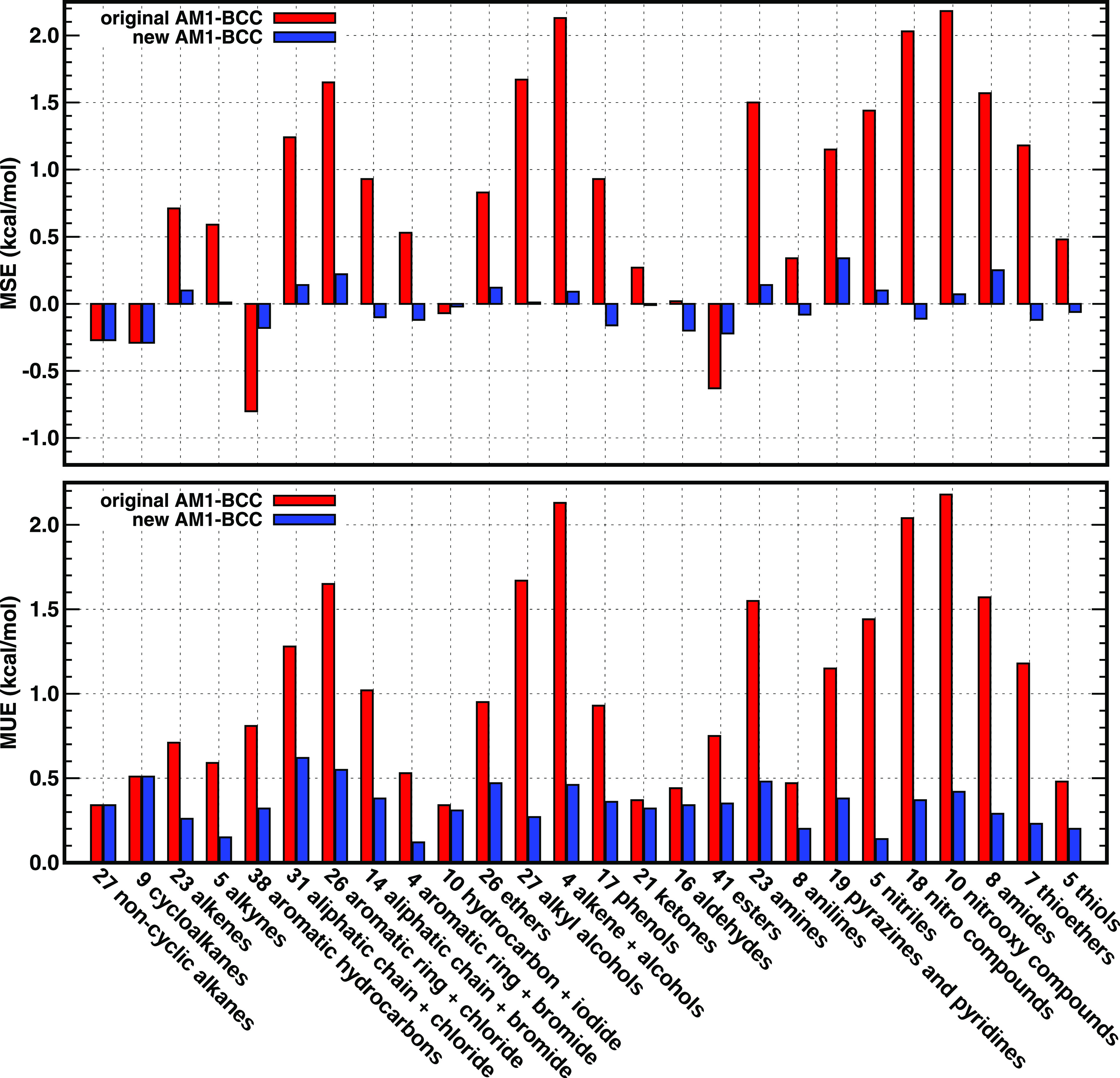
Performance of the original and the proposed new AM1-BCC charge models on the hydration free energies of 442 neutral solutes with different functional groups.

TABLE I.

The performance of the original and the proposed new AM1-BCC atomic charges in combination with the GAFF2 parameters on the hydration free energies of neutral organic solutes in TIP3P water. Expt. stands for experimental; MSE stands for mean signed error; MUE stands for mean unsigned error; PI stands for predictive index; R stands for Pearson’s correlation coefficient; k and b stand for the slope and intercept values when fitting the calculated data (y) vs experimental data (x) with function y = kx + b.

	Expt. data		Original AM1-BCC						New AM1-BCC (ABCG2)
	Data	range	MSE	MUE				b	MSE	MUE				b
Solutes	No.	(kcal/mol)	(kcal/mol)	(kcal/mol)	PI	R	k	(kcal/mol)	(kcal/mol)	(kcal/mol)	PI	R	k	(kcal/mol)
Non-cyclic alkanes	27	1.33	−0.27	0.34	0.56	0.61	0.40	1.27	−0.27	0.34	0.56	0.61	0.40	1.27
Cycloalkanes	9	1.80	−0.29	0.51	0.35	0.36	0.20	1.04	−0.29	0.51	0.35	0.36	0.20	1.04
Alkenes	23	1.92	0.71	0.71	0.79	0.80	0.74	1.02	0.10	0.26	0.88	0.86	1.02	0.07
Alkynes	5	0.87	0.59	0.59	0.43	0.60	0.27	0.80	0.01	0.15	0.95	0.96	0.49	0.16
Aromatic hydrocarbons	38	4.68	−0.80	0.81	0.96	0.98	1.36	−0.21	−0.18	0.32	0.97	0.98	1.20	0.15
Aliphatic chain + chloride	31	4.53	1.24	1.28	0.83	0.84	0.75	1.03	0.14	0.62	0.71	0.76	1.17	0.29
Aromatic ring + chloride	26	3.83	1.65	1.65	0.24	0.17	0.13	−0.31	0.22	0.55	0.89	0.84	0.81	−0.22
Aliphatic chain + bromide	14	3.17	0.93	1.02	0.73	0.83	0.34	0.57	−0.10	0.38	0.80	0.88	0.53	−0.36
Aromatic ring + bromide	4	0.99	0.53	0.53	0.08	0.46	0.47	−0.47	−0.12	0.12	1.00	0.99	1.02	−0.08
Hydrocarbon + iodide	10	2.76	−0.07	0.34	0.91	0.91	0.53	−0.39	−0.02	0.31	0.84	0.90	0.64	−0.27
Eithers	26	5.20	0.83	0.95	0.92	0.90	0.97	0.73	0.12	0.47	0.95	0.94	1.01	0.14
Alkyl alcohols	27	5.66	1.67	1.67	0.88	0.95	0.75	0.51	0.01	0.27	0.86	0.95	0.90	−0.45
Alkene + alcohols	4	0.59	2.13	2.13	0.10	0.05	0.09	−5.67	0.09	0.46	0.21	0.14	0.23	−2.97
Phenols	17	2.90	0.93	0.93	0.73	0.84	0.83	−1.25	−0.16	0.36	0.86	0.92	0.91	0.39
Ketones	21	4.35	0.27	0.37	0.97	0.94	0.74	−0.68	−0.01	0.32	0.96	0.93	0.82	−0.65
Aldehydes	16	2.20	0.02	0.44	0.90	0.81	1.16	0.53	−0.20	0.34	0.96	0.83	0.85	−0.68
Esters	41	7.82	−0.63	0.75	0.97	0.95	0.87	−1.11	−0.22	0.35	0.97	0.98	1.07	0.04
Amines	23	6.10	1.50	1.55	0.82	0.78	0.90	1.02	0.14	0.48	0.96	0.94	1.09	0.57
Anilines	8	4.02	0.34	0.47	0.85	0.89	0.80	−1.47	−0.08	0.20	0.98	0.98	0.95	−0.34
Pyrazines and pyridines	19	2.83	1.15	1.15	0.67	0.60	0.94	0.86	0.34	0.38	0.71	0.89	1.09	0.75
Nitriles	5	0.58	1.44	1.44	1.00	0.90	2.00	5.23	0.10	0.14	1.00	0.90	1.12	0.56
Nitro compounds	18	9.13	2.03	2.04	0.94	0.94	0.90	1.44	−0.11	0.37	0.98	0.98	0.94	−0.47
Nitrooxy compounds	10	6.52	2.18	2.18	0.92	0.95	0.58	0.45	0.07	0.42	0.96	0.97	0.88	−0.41
Amides	8	3.19	1.57	1.57	0.98	0.98	0.90	0.63	0.25	0.29	0.95	0.95	0.93	−0.46
Thioethers	7	0.62	1.18	1.18	0.42	0.60	0.62	0.61	−0.12	0.23	0.34	0.26	0.37	−1.06
Thiols	5	1.56	0.48	0.48	0.85	0.98	0.90	0.33	−0.06	0.20	0.85	0.97	0.66	−0.54
Sum	442	15.11	0.65	1.03	0.91	0.92	0.86	0.27	−0.03	0.37	0.98	0.98	0.98	−0.06

FIG. 2.

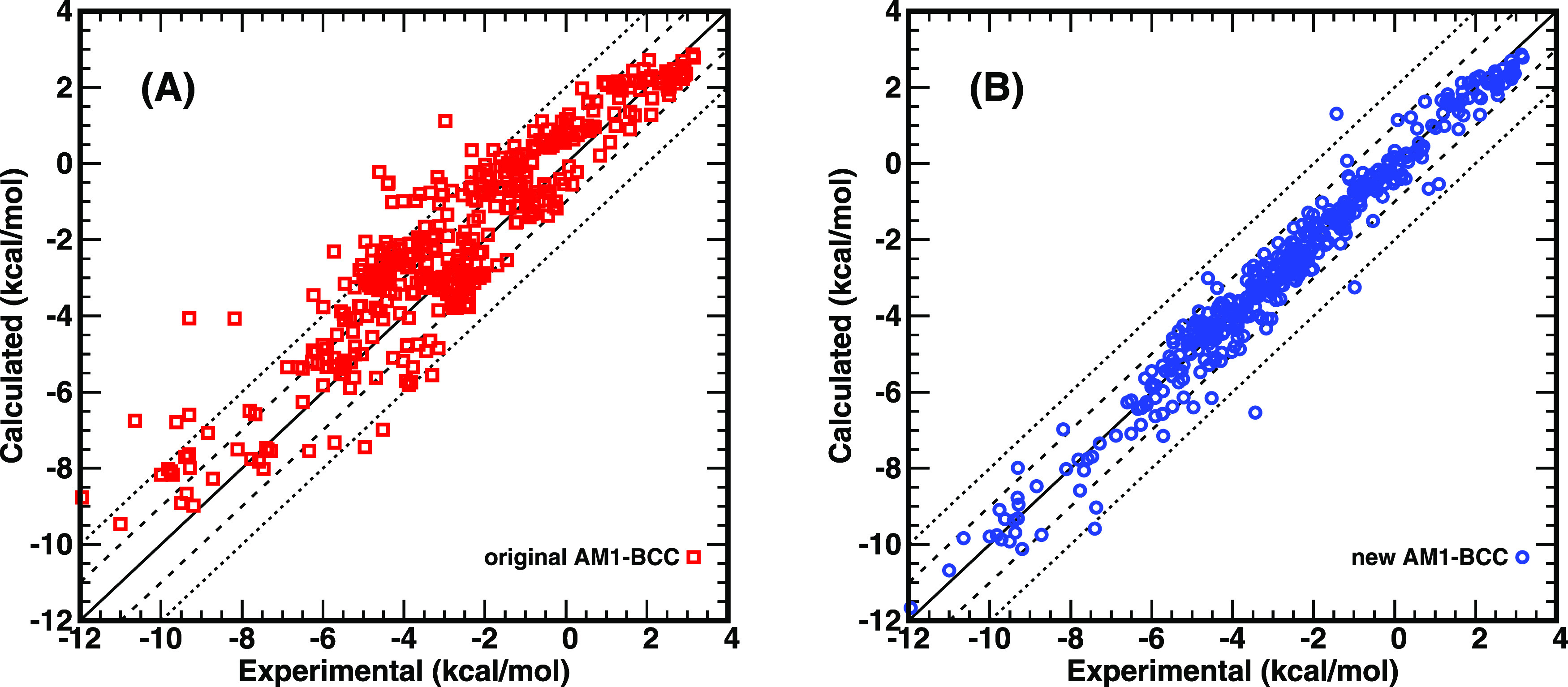
Predicted vs experimental data of hydration free energies of various organic solutes calculated with the GAFF2 parameters combined with (A) original AM1-BCC and (B) new AM1-BCC (ABCG2, an abbreviation of AM1-BCC-GAFF2) proposed in this study.

B. Performance of the two AM1-BCC models on solvation free energies in organic solvents

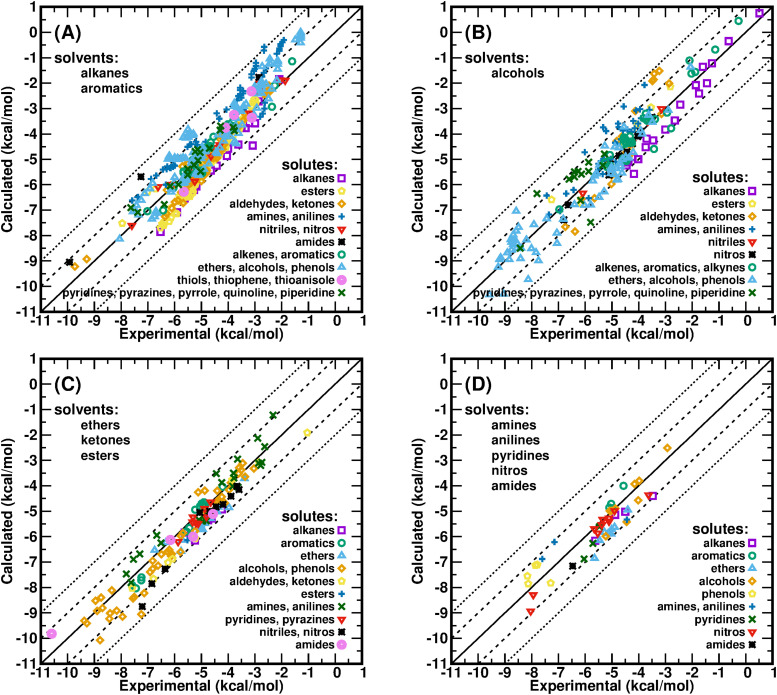
The updated BCC terms targeting HFEs were applied to the calculations of SFEs in various organic solvents without adjusting any BCC parameters. The calculated results compared to the experimental data of 895 neutral organic solvent–solute pairs are shown in Fig. 3. Encouragingly, the BCC terms optimized in the polar solvent TIP3P water work very well for a variety of polar and nonpolar organic solvents with different dielectric constants. Among the 895 calculated data, 66.9% have unsigned errors (UEs) <0.6 kcal/mol, 21.5% have UEs between 0.6 kcal/mol and 1.0 kcal/mol, and 12.4% of the data have UEs >1.0 kcal/mol. The MUE of all 895 neutral organic solvent–solute pairs is only 0.51 kcal/mol, and the root mean square error (RMSE) is only 0.65 kcal/mol, both close to the experimental uncertainty of SFE. The predictive index PI for all 895 pairs is 0.95, and Pearson’s correlation coefficient is 0.94 (Table II); when fitting the calculated data (y) vs the experimental data (x) of all 895 pairs with function y = kx + b, the slope k is 1.06, and the intercept b is 0.31 kcal/mol (Table II).

FIG. 3.

Calculated results vs the experimental data of solvation free energies of various organic solute compounds in different organic solvents: (a), saturated alkanes and aromatic hydrocarbons as solvents; (b), alcohols as solvents; (c), ethers, ketones, and esters as solvents; and (d), nitrogen-containing solvents.

TABLE II.

The performance of new AM1-BCC charges with GAFF2 parameters on the solvation free energies of neutral organic solvent–neutral organic solute pairs. Expt. stands for experimental; MSE stands for mean signed error; MUE stands for mean unsigned error; RMSE stands for root mean square error; PI stands for predictive index; R stands for Pearson’s correlation coefficient; k and b stand for the slope and intercept values, respectively, when fitting the calculated data (y) vs experimental data (x) with function y = kx + b.

		Data	Expt. data	MSE	MUE	RMSE				b
Solvents	Solutes	No.	range (kcal/mol)	(kcal/mol)	(kcal/mol)	(kcal/mol)	PI	R	k	(kcal/mol)
CH	CH	54	5.41	−0.26	0.46	0.57	0.93	0.93	1.09	0.16
CH	CHO	295	8.44	−0.01	0.50	0.62	0.93	0.93	1.12	0.58
CH	CHN	83	5.77	0.71	0.81	0.96	0.95	0.95	1.11	1.21
CH	CHON	20	7.12	0.31	0.41	0.58	0.98	0.97	0.97	0.15
Alkanes	CHS	5	2.54	0.17	0.51	0.54	0.89	0.95	1.36	1.59
Alkanes	CHCl	14	2.95	−0.13	0.26	0.29	0.99	0.97	0.91	−0.56
Alkanes	CHF, CHI, CHBr	13	4.07	−0.23	0.31	0.46	0.91	0.94	0.91	−0.69
Ethers	CH	16	3.04	−0.21	0.35	0.42	0.89	0.93	1.12	0.45
Ethers	CHO	39	11.03	−0.23	0.46	0.58	0.98	0.97	0.98	−0.38
Ethers	CHN	23	4.35	0.03	0.44	0.53	0.96	0.94	1.11	0.51
Ethers	CHON	10	6.93	−0.45	0.61	0.73	1.00	0.96	0.90	−1.00
Alcohols	CH	54	7.48	−0.16	0.43	0.54	0.93	0.95	1.07	0.08
Alcohols	CHO	96	10.30	−0.08	0.59	0.73	0.97	0.95	1.03	0.10
Alcohols	CHN	55	5.28	0.45	0.59	0.75	0.91	0.89	1.04	0.68
Alcohols	CHON	16	8.26	−0.10	0.22	0.31	1.00	0.99	0.96	−0.34
Ketones	CH	5	3.21	−0.26	0.46	0.50	0.67	0.94	1.06	0.03
Ketones	CHO	9	5.26	−0.59	0.60	0.69	0.98	0.98	1.00	−0.61
Ketones	CHN, CHON	6	4.68	−0.11	0.32	0.37	1.00	0.99	0.79	−1.11
Esters	CH	3	2.87	−0.23	0.34	0.38	0.89	0.98	1.03	−0.08
Esters	CHO	26	6.24	−0.42	0.45	0.53	0.98	0.98	0.99	−0.48
Esters	CHN, CHON	6	2.75	0.12	0.23	0.30	0.98	0.97	0.93	−0.32
CHN	CH	8	2.14	−0.12	0.43	0.50	0.65	0.66	0.67	−1.71
CHN	CHO	22	5.23	−0.26	0.55	0.63	0.97	0.92	0.85	−1.07
CHN	CHN, CHON	9	3.98	−0.21	0.59	0.66	0.85	0.87	0.58	−2.55
CHON	CHON	8	3.14	−0.31	0.32	0.44	0.99	0.99	1.20	0.94
Summary		895	12.87	0.01	0.51	0.65	0.95	0.94	1.06	0.31

IV. DISCUSSION

Although the first generation of GAFF was developed based on the RESP charge model rather than the AM1-BCC charge model, and the SFE was not utilized in the parameter calibration, the studies had shown that in terms of the SFE calculation accuracy, the combination of GAFF and AM1-BCC was competitive in comparison with other FFs. For instance, an average unsigned error (AVE) of 1.03 kcal/mol to the reference experimental values was obtained for the nitrogen-containing polar functional groups with GAFF/AM1-BCC,^46,52 while the OPLS2005 parameters and charges led to errors greater than 1.3 kcal/mol, as revealed in the studies by Shivakumar et al.^43,46 In SFE calculation related to function groups like branched alkanes, cycloalkanes, alkynes, some polar groups, and most of the halogenated molecules, Shivakumar et al. found that GAFF/AM1-BCC was superior to most force fields and on par with OPLS2005.^43,44 To OPLS2005 based SFE, amides were the biggest outlier with an AUE of 2.4 kcal/mol, while GAFF led to an AUE of 1.6 kcal/mol. Notably, based on the above, Shivakumar et al. specifically incorporated the SFEs of 153 molecules as the training set to adjust the CM1A-BCC charge model for their new OPLS2.0 force field.⁴⁴

As aforementioned, GAFF2/RESP has achieved better performance over GAFF/RESP on various physicochemical properties including SFE; the details on GAFF2/RESP will be described in another manuscript. The current study was motivated by our observation, as shown in the RESULTS section, that when GAFF2 was directly combined with the original AM1-BCC charge model, it could lead to a systematic error greater than 1.0 kcal/mol for the HFE calculation related to a range of functional groups, especially certain polar groups. Such a systematic error could be the major obstacle limiting the accuracy of calculating important properties, such as solubility, transfer/partition free energy, membrane permeability, and most importantly protein–ligand binding free energy. Based on the hypothesis that further BCC term optimization may provide a feasible way to greatly improve the performance of GAFF2/AM1-BCC charge model, we employed the HFE as the guiding target, conducted BCC reparameterization, and successfully obtained a new set of BCC parameters. As shown, this new ABCG2 charge model greatly reduced the MUE of HFE prediction for a set of 442 neutral molecules from 1.03 kcal/mol to 0.37 kcal/mol, which is even less than the default uncertainty of individual experimental measurement, 0.6 kcal/mol, in the FreeSolv database v0.52. Moreover, the new ABCG2 charge model also performed excellently for the SFE calculation in various polar and nonpolar organic solvents, demonstrating a very good transferability among different dielectric environments. The MUE of SFE prediction for 895 neutral organic solvent–solute systems is as small as 0.51 kcal/mol, which is still less than the aforementioned uncertainty of individual experimental measurement, 0.6 kcal/mol. Such a significant improvement is expected to drastically boost the accuracy for the future protein–ligand binding free energy calculation, which is a primary task in CADD. In summary, this new ABCG2 charge model offers not only efficiency and convenience but also the accuracy and transferability to future in silico drug development effort in either high-throughput screening or alchemical free energy prediction.

Certainly, charge model optimization based on SFE alone does not guarantee universal accuracy for all the properties or suitability of molecular dynamics simulation on all the systems because the FF parameters, including atomic charges, VDW, and other parameters are more or less correlated. They should be adjusted together in an iterative manner to get a physically faithful and reliable FF. Here, we propose an immediate feasible application of this new AM1-BCC charge model: using GAFF2/ABCG2 to re-evaluate properties, such as SFE and binding free energy, employing simulation trajectories generated based on GAFF/RESP, GAFF/old-AM1-BCC, GAFF2/RESP, or other combinations of FF and charge model. For the purpose of binding free energy prediction, we have achieved BCC parameter optimization for carboxylic and ammonium ions, which are frequently encountered in both proteins and ligands. Specifically, the MUE of hydration free energy prediction on 15 ammonium ions was reduced from 2.85 kcal/mol to 0.89 kcal/mol, and the HFE MUE of three carboxylic ions was reduced from 5.30 kcal/mol to 0.43 kcal/mol. The BCC parameter optimization work on other organic ions are currently in progress, and the corresponding new BCC parameters (together with the updated BCCs in this study) will be released to the public via the future release of the AMBER program. In addition, we would also like to test this new AM1-BCC charge model with other water models, such as the explicit OPC water model,⁷⁴ since it has been recommended for the latest AMBER ff19SB protein force field.⁷⁵ It is worth pointing out that such an improved AM1-BCC charge model with good performance on SFE prediction, as demonstrated in this study, also paves a feasible path to the development of the next generation of GAFF. With the astonishing progress in the computing power, including GPU computing in the recent years, it is time to incorporate the computationally intensive SFE as one of the primary targets in FF parameterization. This is also the future plan for us as a development team of the AMBER family.

V. CONCLUSION

GAFF2 has been released to the public through the AMBER program and the AMBER Tools since 2015, and has been continuingly enriched and improved. Currently, GAFF2 is in the final packing stage and the detailed description about its development is soon to be submitted for publication. In this study, we focused on the GAFF2 performance when combined with the AM1-BCC charge model in terms of the solvation free energy calculation. We found that TI calculations with GAFF2/original AM1-BCC on the HFE of 442 neutral organic solutes in TIP3P water produced a MUE of 1.03 kcal/mol. So, we optimized the BCC parameters to achieve a new set of AM1-BCC parameters, which significantly reduced the MUE of HFEs of the aforementioned 442 neutral organic solutes to only 0.37 kcal/mol. We further found that this new set of AM1-BCC charge model also led to a low MUE of 0.51 kcal/mol for SFEs of 895 pairs of neutral organic solutes in a variety of neutral organic solvents. This result demonstrated that the newly derived AM1-BCC model (ABCG2) has the capability of treating different dielectric environments. Such encouraging dielectric transferability ensures the suitability of the new force field model for quantitatively predicting the important properties in CADD such as solvation, transferring, and binding free energies. Moreover, the excellent results achieved in this study point out a feasible way of developing next generation GAFF, i.e., including the computationally intensive SFE as one of the primary parameterization targets. The new BCC parameters optimized in this study will be released to the public in the near future via a new version of the AMBER program.

SUPPLEMENTARY MATERIAL

See the supplementary material for the protocol of initial equilibration and later λ expanding in the TI calculation (Fig. S1), the detailed scheme of adjusting bond charge correction (BCC) parameters for various chemical functional groups, sequentially (Fig. S2), the overall flow chart of conducting BCC parameterization using hydration free energies and validation using solvation free energies of a large number of solutes in various organic solvents (Fig. S3), the rule and steps of setting initial box for the organic solvent–solute systems (Fig. S4), and the adjusted BCC terms with their original and new values.

DATA AVAILABILITY

The new BCC parameters of the ABCG2 charge model along with the atom type definition file will be released to the public via the future release of the AMBER program.