Biased transformation erases traditions sustained by conformist transmission

Abstract

Conformist transmission is a cognitively simple decision-making process by which observers are disproportionately likely to follow the majority. It has been studied in multiple species because theory suggests it can create stable cultural variation. However, the current theory assumes that while conformist transmission favours the majority, it is otherwise unbiased and does not systematically transform information, even though such biases are widely documented. Here, we relax this assumption, requiring conformist observers to infer the size of the majority from finite observations of their group mates. Because such inference can be subject to bias, it can lead to the biased transformation of transmitted information. We find that when individuals are biased (even weakly) the capacity of conformist transmission to sustain traditions is reduced and, in many cases, removed entirely. This suggests that the emphasis on conformist transmission as a source of stable cultural variation may be misplaced.

1. Introduction

Cultural evolutionary theory makes predictions about who, when and what individuals copy, as well as the cultural dynamics produced by this evolved psychology [1]. Supporting this work, experimental studies of humans, fishes, rats, primates, flies and birds have confirmed that social learning behaviours match theoretical predictions [2,3]. Nonetheless, long-term cultural dynamics remain challenging to observe empirically.

One behaviour predicted by cultural evolutionary theory is conformist transmission [1,4]: a disproportionate tendency to adopt majority beliefs, where the probability that an individual adopts the majority option exceeds the proportional size of the majority. Conformist transmission has been studied extensively because theory suggests it is broadly favoured by selection [5–8] and causes popular behaviours to spread, creating stable traditions and between-group differences [8,9]. Moreover, conformist transmission is cognitively simple and does not rely on the payoffs associated with different behaviours being readily observable or even different. As such, conformist transmission offers a plausible mechanism for stable cultural traditions, including functionless traditions, across multiple species and empirical studies have found evidence for it in adults, children, chimpanzees, birds and fruit flies [10–14].

The theoretical basis of conformist transmission, along with cultural evolutionary theory more generally, draws heavily from population genetics, leading to an emphasis on selection between variants as the key source of cultural change. However, other approaches, drawing from cognitive science, place greater emphasis on how individual cognition transforms transmitted information. Such ‘biased transformation' creates cultural evolution towards ‘cultural attractors' [15]. Proponents of this approach have noted the simplistic approach to information transmission typical of cultural evolutionary models [16] wherein beliefs are transferred instantaneously, with occasional random errors. In reality, beliefs are transmitted through behaviours, perceptual systems and material artefacts [17] and must be reconstructed by the observer. This raises the possibility of subtle and systematic transmission errors. Dramatic population-level consequences of biased transformation during transmission have been documented [18,19], yet this has not been integrated into models of conformist transmission. As such, it is unclear whether the conclusions of cultural evolutionary theory, including the ability of conformist transmission to sustain cultural traditions, hold when a more realistic description of transmission is included. Here, we use Bayes‘ rule to provide such a model, with prior beliefs acting as distorting factors that transform transmitted information. Contradicting existing theory, we find that under many conditions conformist transmission cannot stabilize traditions. This suggests that the current emphasis on conformist transmission as a source of cultural stability may be misplaced.

2. Results

(a). A binary decision

Consider an infinitely large group of individuals who choose between two options: A and B. The frequency of A is q. Individuals are conformist and they first use Bayes' rule to estimate q, and then conform to their estimate. Individuals start with a prior belief about q, which is described as a beta distribution with parameters a and b. When a = b = 1 the prior is uniform. Increasing a favours higher values of q; increasing b favours lower values. We assume a = 1, but define the bias, β, such that b = 1 + β.

Individuals update their belief about q by observing N other individuals (henceforth ‘models') sampled at random. The average numbers of models who choose A and B are Nq and N(1 − q), respectively. The resulting ‘posterior' belief is a beta distribution with parameters a' and b’, where

$$a^{\mathrm{\prime }}=a+Nq=1+Nq$$ 2.1

and

$$b^{\mathrm{\prime }}=b+N(1-q)=1+\hspace{0.17em}\beta +N(1-q).$$ 2.2

Individuals take the most likely value (i.e. the mode) of the posterior distribution, q′, as their estimate of q, where

$$q^{\mathrm{\prime }}=\frac{a^{\mathrm{\prime }}-1}{a^{\mathrm{\prime }}+b^{\mathrm{\prime }}-2}=\frac{Nq}{\beta +N}\hspace{0.17em}.$$ 2.3

When N ≫ β, this reduces to q′ = q and individuals accurately perceive q. When β ≫ N, this approaches q′ = 0 and individuals conclude B is popular regardless of the data.

Individuals then engage in conformist transmission, adopting A with probability p_A where

$$p_A=\frac{q^{\mathrm{\prime }c}}{q^{\mathrm{\prime }c}+{(1-q^{\mathrm{\prime }})}^c}$$ 2.4

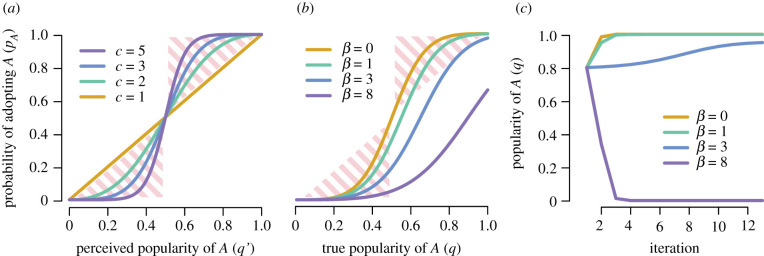
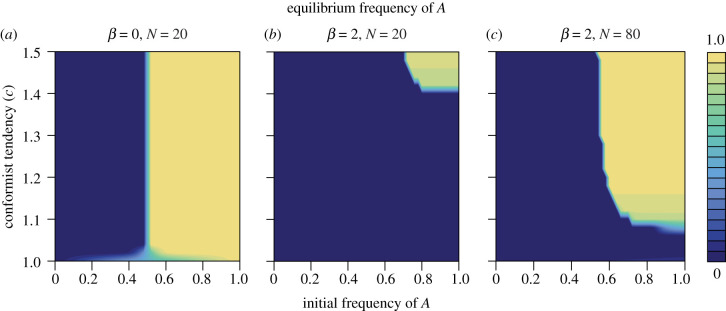
with c controlling the strength of the conformist tendency (figure 1a). Once all individuals conform, q will equal p_A and repeating this process produces cultural evolution. However, because individuals conform to q′ and not q, biased priors distort their response and established traditions may be unstable (figure 1b,c). When β = 0, the majority behaviour always spreads to fixation, thus replicating the findings of prior work. However, when β > 0 traditions will erode if (i) the conformist tendency is weak, (ii) the initial size of the majority is small or (iii) the number of models is small (figure 2). The effect of the bias can either be complete or partial, in which case, a mixed equilibrium is reached.

Figure 1.

(a–b) Response curves (equation (2.4)) for different values of c and β, given (a) β = 0, and (b) c = 3 and N = 10. Traditions are stable to the extent the curves fall in the shaded area. (c) Cultural evolution given the curves in panel b, starting at q = 0.8. The tradition is stable when β < 2, unstable when β = 8, and a mixed equilibrium is reached when β = 3.

Figure 2.

Equilibria reached for different values of c, β and N. (a) In the absence of a biased prior, popular behaviours spread to fixation. (b) With little data a biased prior has a large effect unless the conformist tendency is large and in opposition to the prior. (c) With more observations, the data tend to win out against a biased prior unless the conformist tendency is weak or the initial majority slim.

(b). A continuous decision

Consider the same situation above, but where individuals choose a value along a continuous dimension. Conformist transmission has not previously been considered in such a case, and we define it as a tendency to adopt the mean trait value in a population with an expected squared error less than the population variance (thereby causing the population to homogenize). The rate at which variance decreases is the strength of the conformist tendency.

Let q be the mean value in the population, and w the variance, with individuals' prior belief about q being a normal distribution with mean u and variance v. For simplicity, we assume individuals are aware of the value of w. Individuals observe N models to update their beliefs about q. The expected average observed value is q, and the expected posterior [20] is a normal distribution with mean u’ where

$$u^{\mathrm{\prime }}=\frac{(N/w)q+(u/v)}{(N/w)+(1/v)}.$$ 2.5

This reflects the competing influence of the prior (weighted by 1/v) and data (weighted by N/w): when N/w ≫ 1/v, inferences are accurate (i.e. u′ = q). When 1/v ≫ N/w, the prior determines the posterior (i.e. u′ = u).

Once all individuals conform, the new values of q and w are u′ and w′, respectively (where w′ = w/c and c is the strength of the conformist tendency). As such, variation (w) will endlessly dwindle, while an equilibrium in the mean arises when u′ = q. Provided that w > 0, this has a single solution: q = u. This means that populations will converge on the mean of their prior regardless of the amount of data collected (N) or the strength of the conformist tendency (c). The only exception is when w = 0 (i.e. there is no variation), in which case all values of q are stable.

3. Discussion

The models presented here have assessed the capacity of conformist transmission to stabilize binary and continuous traditions in the context of the biased transformation of transmitted information. The results suggest this capacity is limited for binary traditions and absent for continuous traditions.

Discrete traditions are stable only when (i) there are sufficient models, (ii) the conformist tendency is sufficiently strong, and (iii) the prior is sufficiently unbiased. How often are these conditions met? Data suggest that the conformist tendency in human cultural transmission can be quite strong [10,11], even more so in birds [13], and pronounced, if truncated, in flies [14]. However, other studies of humans [21], chimpanzees [12] and flies [22] found weaker effects, suggesting it likely varies across species, individuals and contexts. Biased priors, however, appear widespread: a study of conformist transmission in great tits found that when two foraging methods were equally popular, observer birds were twice as likely to adopt method A than method B [13], while female flies showed a strong preference for laying eggs on a banana- versus strawberry-flavoured substrate [22]. Similarly, human participants who were shown two novel shapes—one spikey, one smooth—and asked to assign them names from a set of two possibilities (‘kiki’ and ‘bouba' [23]) showed a very strong preference (approx. 95%) for assigning the spikey shape the sharper name. While the ontogeny of these biases likely varies, our results are not mechanism–specific and should apply generally.

In some cases, the instability of discrete traditions can be empirically observed, with traditions decaying across experimental timeframes, as was the case with the strong conformist response in fruitflies [14]. Where traditions outlast experiments, their stability can be assessed by estimating the relevant parameters (β, N, c), or by inspection of response curves (figure 1). The latter approach can readily be applied to existing work. For example, this approach suggests that experimentally induced foraging traditions in great tits [13] are stable. This is because the birds' bias is counteracted by a very strong conformist tendency, but also because a majority of greater than 60% is required for stability and the groups were seeded with unanimous demonstrators. However, the opposite conclusion is reached when applying this approach to the weaker tendency observed in a human study that manipulated the magnitude of prior information (effectively an experimentally induced bias in the prior) as well as the number of models [10]. In this case, stable traditions are only likely when the prior information is very weak, and the number of models is high.

Thus, the ability of conformist transmission to stabilize discrete traditions may be quite narrow. Moreover, our results suggest it is impossible for continuous traditions. Nonetheless, culturally inherited traditions, both discrete and continuous are widespread in human societies and have been documented in non-human species too, for instance, the wake-up times of meerkat troops [24], or mating site preferences in blue-headed wrasse [25]. This work suggests these traditions cannot be underpinned by conformist transmission alone, and alternative mechanisms must be involved. One possibility is that these traditions already match individuals' biases, and so are being stabilized by the biases themselves. However, while this would produce stable behaviour, it would not produce stable between-group variation unless the biases themselves also varied between groups. Alternatively, asocial learning or payoff-biased transmission could respond to either external fitness functions or punishment of norm violators to stabilize rewarded behaviours. This can be seen in great tits: when the payoffs to experimentally induced traditions were reduced, birds quickly switched to other methods [26]. Alternatively, highly influential individuals may also be able to shape culture according to their personal preferences; for instance, a leader may (selfishly) foster cooperation among their followers [27]. Further work could build on the theory presented here to include these factors. Other limitations of this work include the assumption that the prior biases are stable across both individuals and time. Both are unlikely to hold if the biases are themselves learnt (even if only partially). Even where biases are under genetic influence, selection may act to reduce them if they consistently favoured suboptimal behaviours.

This work argues that the current emphasis on conformist transmission as a source of stable cultural variation needs revisiting. Only when traits are (i) discrete, with (ii) a strong conformist tendency, (iii) plentiful data and (iv) a weakly biased prior is this likely, and it is unlikely that these conditions are broadly satisfied. These results are produced by incorporating a more detailed account of transmission into a cultural evolutionary framework. The approach adopted here, Bayes' rule, is a general-purpose mechanism that could be applied to many other cultural evolutionary questions. Such work can bridge the gap between cultural evolution and cognitive science and provide a more comprehensive account of pan-species cultural change.

Ethics

This work did not require ethical approval.

Data accessibility

This work does not involve data.

Authors' contributions

T.J.H.M. executed the formal analysis. Both authors conceived of the project, wrote and approve of the manuscript, and accept responsibility for its accuracy.

Competing interests

We declare we have no competing interests.

Funding

This work was not supported by any external funds.