Abstract
Interactions among individuals in natural populations often occur in a dynamically changing environment. Understanding the role of environmental variation in population dynamics has long been a central topic in theoretical ecology and population biology. However, the key question of how individuals, in the middle of challenging social dilemmas (e.g. the ‘tragedy of the commons’), modulate their behaviours to adapt to the fluctuation of the environment has not yet been addressed satisfactorily. Using evolutionary game theory, we develop a framework of stochastic games that incorporates the adaptive mechanism of reinforcement learning to investigate whether cooperative behaviours can evolve in the ever-changing group interaction environment. When the action choices of players are just slightly influenced by past reinforcements, we construct an analytical condition to determine whether cooperation can be favoured over defection. Intuitively, this condition reveals why and how the environment can mediate cooperative dilemmas. Under our model architecture, we also compare this learning mechanism with two non-learning decision rules, and we find that learning significantly improves the propensity for cooperation in weak social dilemmas, and, in sharp contrast, hinders cooperation in strong social dilemmas. Our results suggest that in complex social–ecological dilemmas, learning enables the adaptation of individuals to varying environments.
Keywords: reinforcement learning, evolutionary game theory, stochastic game, adaptive behaviour, social dilemma
1. Introduction
Throughout the natural world, cooperating through enduring a cost to endow unrelated others with a benefit is evident at almost all levels of biological organisms, from bacteria to primates [1]. This phenomenon is especially true for modern human societies with various institutions and nation-states, in which cooperation is normally regarded as the first choice to cope with some major global challenges, such as curbing global warming [2,3] and governing the commons [4]. However, the mechanism underlying cooperative behaviour has perplexed evolutionary biologists and social economists for a long time [5,6]. Since according to the evolutionary theory of ‘survival of the fittest’ and the hypothesis of Homo economicus, this costly prosocial behaviour will be definitively selected against and should have evolved to be dominated by selfish act [7].
To explain how cooperation can evolve and be maintained in human societies or other animal groups, a large body of theoretical and experimental models have been put forward based on evolutionary game theory [6,8,9] and social evolution theory [10]. Traditionally, the vast majority of the previous work addressing this cooperative conundrum concentrates on the intriguing paradigm of a two-player game with two strategies, Prisoner’s Dilemma [6,11]. Motivated by abundant biological and social scenarios where interactions frequently occur in a group of individuals, its multi-person version, the public goods game, has attracted much attention in recent years [12]. Meanwhile, it also prompts a growing number of researchers to devote to studying multi-player games and multi-strategy games [13–18]. However, these prominent studies implicitly assume, as most of the canonical work does, that the game environment is static and independent of players’ actions. In other words, in these models, how players act by choosing game-play strategies only affects the strategic composition in the population, but the game environment itself is not influenced. As a result, a single fixed game is played repeatedly. Of course, this assumption is well grounded, if the timescale of interest (e.g. the time to fixation or extinction of a species) is significantly shorter than that of the environmental change. For most realistic social and ecological systems, however, it seems to be too idealized. Hence, an explicit consideration of environmental change is needed. A prototypical instance is the overgrazing of common pasture lands [19], where the depleted state may force individuals to cooperate and accordingly the common-pool resources will increase, whereas the replete state may induce defection and the common-pool resources will decrease [20,21]. Other examples also exist widely across scales from small-scale microbes to large-scale human societies [22]. A common feature of these examples is the existence of the feedback loop where individual behaviours alter environmental states, and are influenced in turn by the modified environment [20,23].
Although the effect of environmental variations on population dynamics has long been recognized in theoretical ecology and population biology [24–26], it is only recently that there has been a surge of interest in constructing game–environment feedbacks [20,21,23,27,28] to understand the puzzle of cooperation, especially in structured populations [29–31]. Different from the conventional set-up in evolutionary game theory [8,9], the key conceptual innovation of these works is the introduction of multiple games [32,33], evolving games [34,35], dynamical system games [36] or stochastic games [37,38]. By doing so, the players’ payoff depends on not only strategic interactions but also the environmental state, and meanwhile, the fluctuation of the environment will be subject to the actions adopted by players. In this sense, the consideration of a dynamic game environment for the evolution of cooperation has as least two significant implications. First, it vastly expands the existing research scope of evolutionary game theory by adding a third dimension (multiple games) to the prior two-dimension space (multiple players and multiple strategies) [33]. That is, this extension generalizes the existing framework to encompass a broader range of scenarios. Second, the new key component, environmental feedbacks [20,23], is integrated seamlessly into the previous theoretical architecture.
While these promising studies primarily focused on pre-specified or pre-programmed behavioural policies to analyse the interdependent dynamics between individual behaviours and environmental variations, the key question of how individuals adjust their behaviours to adapt to the changing environment has not yet been sufficiently addressed. In fact, when confronting complex biotic and abiotic environmental fluctuations, how organisms adaptively modulate their behaviours is of great importance for their long-term survival efforts [25,39]. For example, those plants growing in the lower strata of established canopies can adjust their stem elongation and morphology in response to the spectral distribution of radiation, especially the ratio of red to far-red wavelength bands [40]; in arid regions, bee larvae, as well as angiosperm seeds, strictly comply with a bet-hedging emergence and germination rule such that reproduction activities are only limited to a short period of time following the desert rainy season [41]. Particularly, as an individual-level adaptation, learning through reinforcement is a fundamental cognitive or psychological mechanism used by humans and animals to guide action selections in response to the contingencies provided by the environment [42–44]. Employing the experience gained from historical interactions, individuals always tend to reinforce those actions that will increase the probability of rewarding events and lower the probability of aversive events. Although this learning principle has become a central method in various disciplines, such as artificial intelligence [44,45], neuroscience [43], learning in games [46] and behavioural game theory [47], there is still a lack of theoretical understanding of how it guides individuals to make decisions in order to resolve cooperative dilemmas.
In the present work, we develop a general framework to investigate whether cooperative behaviours can evolve by learning through reinforcement in constantly changing multi-player game environments. To characterize the interplay between players’ behaviours and environmental variations, we propose a normative model of multi-player stochastic games, in which the outcome of one’s choice relies on not only the opponents’ choices but also the current game environment. Moreover, we use a social network to capture the spatial interactions of individuals. Instead of using a pre-specified pattern, every decision-maker in our model learns to choose a behavioural policy by associating each game outcome with reinforcements. By doing so, our model not only considers the environmental feedback, but also incorporates a cognitive or psychological feedback loop (i.e. players’ decisions determine their payoffs in the game, and in turn are affected by the payoffs). When selection intensity is so weak that the action choices of players are just slightly influenced by past reinforcements, we derive the analytical condition that allows for cooperation to evolve under the threat of the temptation to defection. Through extensive agent-based simulations, we validate the effectiveness of the closed-form criterion in well-mixed and structured populations. Also, we compare the learning mechanism with two non-learning decision rules, and interestingly, we find that learning markedly improves the propensity for cooperation in weak social dilemmas whereas it hinders cooperation in strong social dilemmas. Furthermore, under non-stationary conditions, we analyse how cooperation coevolves with the environment and the effect of external incentives on the cooperative evolution by agent-based simulations.
2. Model and methods
2.1. Model
We consider a finite population of N individuals living in an evolving physical or social environment. The population structure describing how individuals interact with their neighbours is characterized by a network, where nodes represent individuals and edges indicate interactions. When individuals interact with their neighbours, only two actions, cooperation (C) and defection (D), are available, and initially, every individual is initialized with a random action in the set with a certain probability. In each time step, one individual is chosen randomly from the population to be the focal player, and then d − 1 of its neighbours as co-players are selected at random to form a d-player (d ≥ 2) stochastic game [37,38]. To ensure that the game can always be organized successfully, we assume that each individual in the population has at least d − 1 neighbours. Denote the possible number of C players among d − 1 co-players by the set , and possible environmental states by the set , where si, i = 1, 2, …, M, represents the environmental state of type i. Then, depending on the co-players’ configuration and the environmental state in the current round, each player will gain a payoff given in table 1. Players who take action C will get a payoff , whereas those who take action D will get a payoff , where represents the set of real numbers. Players update their actions asynchronously; that is, in each time step, only the focal player updates its action, and other individuals still use the actions in the previous round. Furthermore, to prescribe the action update rule, we define the policy with two parameters θ and β to specify the probability that action a is chosen by the focal player when there are j opponents taking action C among d − 1 co-players in the environmental state . Therein, is the column vector of L-dimension used for updating the policy by learning through reinforcement, and β ∈ [0, + ∞) is the selection intensity [48], also termed the adaptation rate [49], which captures the effect of past reinforcements on the current action choice.
Table 1.
Payoff table of the d-player stochastic game.
| no. C co-players | d − 1 | … | j | … | 0 |
|---|---|---|---|---|---|
| C | ad−1(s) | … | aj(s) | … | a0(s) |
| D | bd−1(s) | … | bj(s) | … | b0(s) |
After each round, players’ decisions regarding whether to cooperate or defect in the game interaction will not only influence their immediate payoffs but also the environmental state in the next round. That is to say, the probability of the environmental state in the next round is conditioned on the action chosen by the focal player and the environmental state in the current round. Without loss of generality, we here assume that the dynamics of environmental states {st} obey an irreducible and aperiodic Markov chain, which thus possesses a unique stationary distribution. Also, from table 1, it is clear that the payoff of each player is a function of the environmental state. Therefore, when the environment transits from one state to another, the type of the (multi-player) normal-form game defined by the payoff table may be altered accordingly.
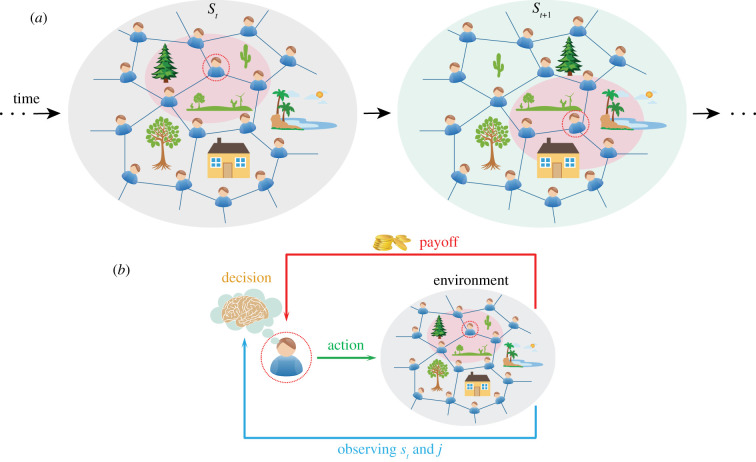
The emergence of the new environmental state in the next round, apart from influencing the game type, may also trigger players to adjust their behavioural policies. This is because those previously used decision-making schemes may no longer be appropriate in the changed environment. We here consider a canonical learning mechanism, the actor–critic reinforcement learning [42–44], to characterize the individual adaptation to the fluctuating environment. Specifically, after each round, the players’ payoffs received from the game interaction will play a role of the incentive signal of the interactive scenario. If one choice gives rise to a higher return in a certain scenario, then it will be reinforced with a higher probability in the future when encountering the same situation again. By contrast, those choices resulting in lower payoffs will be weakened gradually. Technically, this process is achieved via updating the learning parameter θ of the policy after each round (see Methods for more details). In the successive round, the acquired experience will be shared within the population and the updated policy will be reused by the newly chosen focal player to determine which action to be taken. In a similar way, this dynamical process of game formation and policy updating is repeated infinitely (figure 1).
Figure 1.
Illustration of evolutionary dynamics for 4-player stochastic games in the structured population. (a) At a time step t, a random individual is chosen as the focal player (depicted by the dashed red circle), and then three of its neighbours are selected randomly as co-players to form a 4-player game (because the focal player only has three neighbours, all of them are chosen), which is depicted by the light magenta shaded area. Conditioned on the focal player’s action and the environmental state st at time t, the environmental state at time t + 1 will be changed to st+1 with a transition probability. Similarly, a new round of the game will be reorganized at time t + 1. This process is repeated infinitely. (b) At time t, after perceiving the environmental state st and the co-players’ configuration j, the focal player uses policy π to determine which action to be taken, whereas its co-players still use their previous actions in the past round. At the end of this round, each player will gain a payoff, which will play a role of the feedback signal and will assist the focal player to update its policy.
2.2. Methods
2.2.1. Actor–critic reinforcement learning
As the name suggests, the architecture of the actor–critic reinforcement learning consists of two modules. The actor module maintains and learns the action policy. Generally, there are two commonly used forms, ε-greedy and Boltzmann exploration [44,45]. Here, we adopt the latter for convenience, and consider the following Boltzmann distribution with a linear combination of features:
| 2.1 |
where is the column feature vector with the same dimension of θ, which is handcrafted to capture the important features when a focal player takes action a given the environmental state s and the number of C players j among its d − 1 co-players. Moreover, the dimension of the feature vector will in general be chosen to be much smaller than that of environmental states for the computational efficiency, i.e. L ≪ M. For the construction of the feature vector, there are many options, such as polynomials, Fourier basis, radial basis functions and artificial neural networks [44]. As mentioned in the Model, β controls the selection intensity, or equivalently the adaptation rate. If β → 0, it defines a weak selection and the action choice is only slightly affected by past reinforcements. When β = 0, in particular, players choose actions with uniform probability. By contrast, if β → +∞, the action with the maximum θTϕs,j,a will be exclusively selected.
Another module is the critic, which is designed to evaluate the performance of the policy. In general, the long-run expected return of the policy per step, ρ(π), will be a good measurement of the policy’s performance, which is defined by
| 2.2 |
where rt+1 ∈ {ad−1(s), … , a0(s), bd−1(s), … , b0(s)} is a random variable which denotes the payoff of the focal player at time t ∈ {0, 1, 2, … }. In particular, if one denotes the probability that the environmental state at time t is st under the policy π when starting from the initial state s0 by Pr{st = s|s0, π}, and the average probability that all possible individuals chosen as the focal player encounter j opponents taking action C among d − 1 co-players by p·j, then ρ(π) can be computed by
| 2.3 |
where is the stationary distribution of environmental states under the policy π; is the payoff of the focal player when it takes action a given the environmental state s and the number of C players j among its d − 1 co-players, which is given by
| 2.4 |
Moreover, to measure the long-term accumulative performance of the policy, we define a Q-value function,
| 2.5 |
which is a conditional value depending on the initial environmental state s0 = s, the number of C players j0 = j among d − 1 co-players, and action a0 = a at time t = 0. Since the space of the environmental state is usually combinatorial and extremely large in many game scenarios, it is in effect impossible to calculate the Q-value function exactly for every environmental state within finite time with given computational resources [44]. Typically, one effective way to deal with this problem is to find a good approximation of the Q-value function. Let fw(s, j, a) be the approximation to the Q-value function and satisfy the compatibility condition [50,51]
| 2.6 |
where is the column vector of weight parameters. To effectively approximate the Q-value function, it is natural to learn fw(s, j, a) by updating w via the least mean square method under the policy π. After acquiring the approximated measurement of the policy’s performance fw(s, j, a), policy π can be then improved by following the gradient ascent of ρ(π). Thus, the full algorithm of the actor–critic reinforcement learning can be given by (see electronic supplementary material SI.1 for details)
| 2.7 |
where is the estimation of ρ(π), and iterates through and , t = 0, 1, 2, … ; αt and γt are learning step-sizes which are positive, non-increasing for , and satisfy , and , and . These conditions required for the learning step-sizes guarantee that the policy parameter θt is updated at a slower timescale than that of the function approximation wt, and thus ensure the convergence of the learning rule [51,52].
2.2.2. Evolution of cooperative behaviours
To capture the evolutionary process of cooperation, we first denote the number of C players in the population by nt at time t. Since there is only one individual to revise its action per step in our model, all possible changes of nt in each time step will be limited to increasing by one, decreasing by one, or keeping unchanged. It implies that the evolutionary process of cooperation can be formulated as a Markov chain {nt} defined over the finite state space . Meanwhile, the transition probability from to can be calculated by
| 2.8 |
where pC = u/N (respectively, pD = (N − u)/N) is the probability that an individual who previously took action C (respectively, D) is chosen as the focal player at time t; pC,j (respectively, pD,j) is the average probability that players who previously took action C (respectively, D) encounter j opponents taking action C among d − 1 co-players at time t. It is clear that the Markov chain is non-stationary because the transition probabilities change with time.
To find the average abundance of cooperators in the population, we first note that the actor–critic reinforcement learning converges [50,51] and the environmental dynamics have been described by an irreducible and aperiodic Markov chain. As such, we denote the limiting value of the policy parameter θt for t → ∞ by θ* (a local optimum of ρ(π); see electronic supplementary material SI.1 for details), and the unique stationary distribution of environmental states by . It follows that the probability transition matrix P(t) = [pu,v(t)](N+1)×(N+1) will converge to for t → ∞, where
| 2.9 |
Moreover, it is noteworthy that the Markov chain described by the probability transition matrix P* will be irreducible and aperiodic. This is because based on the matrix P*, any two states of the Markov chain are accessible to each other and the period of all states is 1. Hence, one can conclude that the non-stationary Markov chain {nt} is strongly ergodic [53,54], and there exists a unique long-run (i.e. stationary) distribution . Therein, X can be obtained by calculating the left eigenvector corresponding to eigenvalue 1 of the probability transition matrix P*, i.e. the unique solution to X(P* − I) = 0N+1 and , where I is the identity matrix with the same dimension of P* and 0N+1 is the row vector with N + 1 zero entries. When the system has reached the stationary state, the average abundance of C players in the population can be computed by . If 〈xC〉 > 1/2, it implies that C players are more abundant than D players in the population.
3. Results
3.1. Conditions for the prevalence of cooperation
We first study the condition under which cooperation can be favoured over defection, and restrict our analysis in the limit of weak selection (β → 0) given that finding a closed-form solution to this problem for arbitrary selection intensity is usually NP-complete or # P-complete [55]. In the absence of mutations, such a condition can be obtained in general by comparing the fixation probability of cooperation with that of defection [48]. In our model, however, how players update their actions is conducted by the policy with an exploration–exploitation trade-off, which possesses a property similar to the mutation–selection process [56]. Thus, in this case, we need to calculate the average abundance of C players when the population has reached the stationary state, and determine whether it is higher than that of D players [57]. Using all aj(s) to construct the vector A = [a(s1), a(s2), … , a(sM)]T, and all bj(s) to construct the vector B = [b(s1), b(s2), … , b(sM)]T, where a(sk) = [a0(sk), a1(sk), … , ad−1(sk)] and b(sk) = [bd−1(sk), bd−2(sk), … , b0(sk)], k = 1, 2, … , M, it follows that under weak selection the average abundance of C players in the stationary state is (see electronic supplementary material SI.2 for details)
| 3.1 |
and thus it is higher than that of D players if and only if
| 3.2 |
where Φs is the coefficient matrix corresponding to the environmental state s, and needed to be calculated for the given population structure, but independent of both aj(s) and bj(s) for and .
To obtain an explicit formulation of condition (3.2), we further consider two specific population structures, well-mixed populations and structured populations. In the former case, the interactive links of individuals are described by a complete graph, whereas in the latter case, they are described by a regular graph with node degree d − 1. When the population size is sufficiently large, we find that in the limit of weak selection, condition (3.2) in these two populations reduces to an identical closed form (see electronic supplementary material SI.3 for details):
| 3.3 |
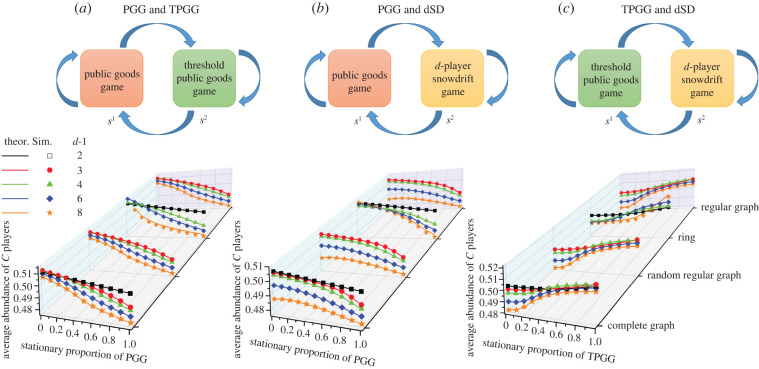
Through extensive agent-based simulations, we validate the effectiveness of this criterion. As illustrated in figure 2,we calculate the average abundance of C players in the population with two distinct environmental states, s1 and s2, which, for instance, can represent the prosperous state and degraded state of a social–ecological system [20,58], respectively. To specify the type of the (multi-player) normal-form game defined by the payoff table 1 for each given environmental state, in figure 2, we consider that one of the three candidates, the public goods game (PGG) [19], threshold public goods game (TPGG) [3,59] and d-player snowdrift game (dSD) [60], is played in each state. In these three kinds of games, the implication of defection is unambiguous and it means not to contribute. However, in defining cooperation and calculating payoffs, there are some differences. In the PGG, action C means contributing a fixed amount c to the common pool. After a round of donation, the sum of all contributions from the d-player group will be multiplied by a synergy factor rs > 1 and then allotted equally among all members, where rs depends on the current game environment s. In this case, the payoffs of cooperators and defectors are computed by aj(s) = (j + 1)rsc/d − c and bj(s) = jrsc/d, , respectively. The aforementioned setting is also true for the TPGG, except that there exists a minimum contribution effort, T, for players to receive benefits. More specifically, only when the number of C players in the d-player game is not smaller than T can each player receive a payoff from the common pool; otherwise, everyone gets nothing. It then follows that a C player will receive a payoff aj(s) = (j + 1)crs/d − c for j ≥ T − 1 and aj(s) = 0 otherwise, whereas a D player will receive bj(s) = jcrs/d for j ≥ T and bj(s) = 0 otherwise. Different from the PGG and TPGG, in the dSD, action C means endowing everyone with a fixed payoff and simultaneously sharing a total cost evenly with the other C players, where depends on the environmental state s. In this case, the payoffs of cooperators and defectors are then changed to for , and for j > 0 and b0(s) = 0, respectively. As shown in figure 2, the theoretical predictions for the average abundance of C players are highly consistent with simulation results, which suggests that criterion (3.3) is effective for determining whether cooperation can outperform defection.
Figure 2.
Average abundance of C players in the population as a function of the stationary proportion of different games. In each homogeneous environmental state, s1 or s2, one of the three normal-form games, PGG, TPGG and dSD, is played. In the top row, three transition graphs are depicted to describe how the environment transits from one state to another. Corresponding to these three transition graphs, the bottom row shows the average abundance of C players in various population structures, based on theoretical calculations and simulations. All simulations are obtained by averaging 40 network realizations and 108 time steps after a transient time of 107, and θ is normalized per step to unify the magnitude. The feature vector ϕs,j,a is chosen to be the one-hot vector. Parameter values: N = 400, β = 0.01, , rs = 3 in the PGG while rs = 4 in the TPGG, in (b) while in (c), and T = [d/2] + 1 ([ · ] represents the integer part).
Moreover, conditions (3.2) and (3.3) offer us an intuitional theoretical interpretation of why the environment can mediate social dilemmas [22]. As shown in figure 2, in an identical scenario, the average abundance of C players is always less than 1/2 in the homogeneous state where the PGG is played, whereas it is greater than 1/2 in some homogeneous states where a TPGG or dSD is played. The reason is that the social dilemma in the TPGG and dSD is weaker than that in the PGG. Thus, cooperation in these two kinds of games is easier to evolve. Namely, if the environment is homogeneous, condition (3.2) or (3.3) in the PGG is more difficult to be satisfied in contrast to the TPGG or dSD. Due to the existence of the underlying transition of the environment, however, the population may have some opportunities to extricate itself from those hostile environmental states where defection is dominant (e.g. the state of the PGG). This case is especially likely after some prosocial behaviours have been implemented by players [21,29,58]. As such, the population will spend some time staying in the states where defection is not always favourable (e.g. the TPGG or dSD). Consequently, the changing environment balances the conditions that favour versus undermine cooperation, and meanwhile the social dilemma that the population is confronted with is diluted. Such an observation is also in line with the fact that the final condition of whether cooperation can prevail is a convex combination of those results in each homogeneously environmental state, as shown in conditions (3.2) and (3.3).
3.2. Learning versus non-learning
Here, we exclude the effect of reinforcement learning, and apply our model framework to study two prototypical non-learning processes of action choices, the smoothed best response [11] and the aspiration-based update [59,61]. For the former, in each time step, the focal player chosen in our model revises its action by comparing the payoff of cooperation with that of defection, and the more profitable action will be adopted. Instead of doing this in a deterministic fashion, in many real-life situations, it is more reasonable to assume that the choice of the best response is achieved smoothly and influenced by noise. One typical form to model this process is the Fermi function [11]:
| 3.4 |
which specifies the probability for the focal player to choose action . For the latter, however, the focal player determines whether to switch to a new action by comparing the action’s payoff with an internal aspiration level. If the payoff is higher than the aspiration level, the focal player will switch to that action with a higher probability. Otherwise, its action is more likely to keep unchanged. Similarly, the commonly used form to quantify the probability that the focal player switches to the new action is still the Fermi function [59,61]:
| 3.5 |
where a constant aspiration level is adopted because heterogenous aspirations [61] or time-varying aspirations (see electronic supplementary material SI.4) cannot result in altering the evolutionary outcome under weak selection. Using these two non-learning update rules as the decision-making policy of the focal player, under our model framework, we find that in the limit of weak selection, cooperation is more abundant than defection if and only if
| 3.6 |
where σj, , are some coefficients needed to be calculated for the given population structure, but independent of both aj(s) and bj(s). In either well-mixed populations or structured populations, we find that the coefficients are for the smoothed best response and for the aspiration-based update (see electronic supplementary material SI.4 for details). In particular, if the population consistently stays in a fixed environment, condition (3.6) will reduce to the ‘sigma-rule’ of multi-player normal-form games [15].
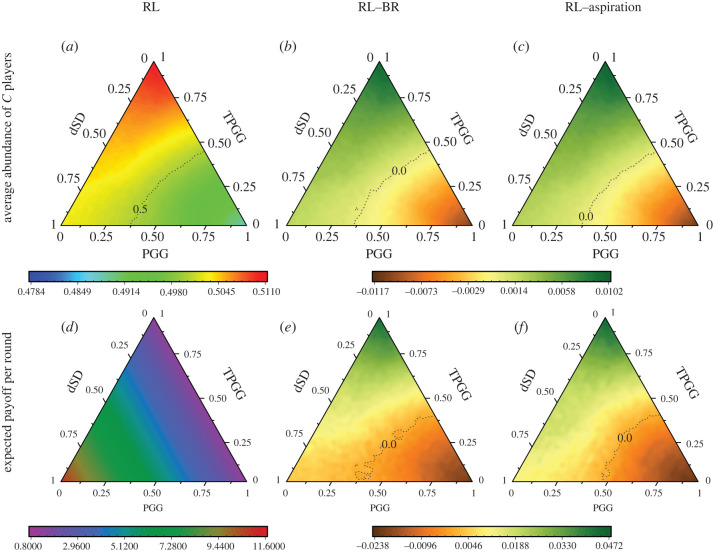
In a population where there are three distinct environmental states and in each state one of the PGG, TPGG and dSD is played, we compare the results obtained by learning through reinforcement with those obtained from the two non-learning updates. As illustrated in figure 3, we calculate the average abundance of C players and the expected payoff of focal players per round for all possible stationary distributions of environmental states. Intriguingly, one can find that learning enables players to adapt to the varying environment. When the population stays in the environment where players are confronted with a weak social dilemma (i.e. the TPGG or dSD will be more likely to be played than the PGG), learning players will have a higher propensity for cooperation than those non-learning players. Meanwhile, they will reap a higher expected payoff per step. By contrast, when the population stays in the environment where the social dilemma is strong (i.e. the PGG will be more likely to be played than the TPGG and dSD), learning players will have a lower propensity for cooperation and accordingly they will get a lower expected payoff per step than non-learning players. Once again, we demonstrate that the analytical results are consistent with the agent-based simulations (see electronic supplementary material, figure S5).
Figure 3.
Differences in the average abundance of C players and the expected payoff of players per round between the reinforcement learning (RL) and two non-learning updates. In (a,d), we show the average abundance of C players and the expected payoff per round when players update actions via the RL, respectively. Taking them as the benchmark, (b,e) illustrate the differences between the RL and the smoothed best response (BR), while (c,f) show the gaps between the RL and the aspiration-based rule (aspiration). The population structure is a lattice network (see electronic supplementary material, figures S1–S4, for other population structures with different network degrees). Parameter values: N = 400, d = 5, β = 0.01, , T = [d/2] + 1, , rs = 3 in the PGG while rs = 4 in the TPGG.
3.3. Evolutionary dynamics under non-stationary conditions
The aforementioned analysis mainly focuses on the stationary population environment, i.e. the dynamics of environmental states have a unique stationary distribution and the payoff structure of the game does not change in time. Here, we relax this set-up to study the evolutionary dynamics of cooperation under two kinds of non-stationary conditions by agent-based simulations.
3.3.1. Non-stationary environmental state distribution
The first case that we are interested in is that the probability distribution of environmental states changes with time. In a population with two environmental states, s1 and s2, we denote the average proportion of the time that the environment stays in state s1 (i.e. the average probability that the environment stays in s1 per step) by z ∈ [0, 1]. Then, the average fraction of time in state s2 is 1 − z. To describe the type of game played in each environmental state, let s1 be the prosperous state where environmental resources are replete and players are at the risk of the ‘tragedy of the commons’ (i.e. a PGG is played), whereas s2 be the degraded state where environmental resources are gradually depleted. In both environmental states, cooperation is an altruistic behaviour that will increase the common-pool resources, whereas defection is a selfish behaviour that will lead the common-pool resources to be consumed. Furthermore, the state of common-pool resources (i.e. the environmental state) will conversely affect individual behaviours. To characterize this feedback relation, we here adopt the difference form of the replicator dynamics with environmental feedbacks [20,23] to describe the evolution of the average time proportion of state s1:
| 3.7 |
where η denotes the positive step-size, xC(t) is the proportion of C players in the population at time t, and is the tipping point of the proportion of C players. If the proportion of C players xC(t) is above the tipping point , it means that the number of cooperators is competent to sustain the supply of common-pool resources. At the same time, the environment will be more likely to stay in the prosperous state s1, leading z(t) to increase. Otherwise, cooperators are insufficient and the public resources will be continuously consumed. In this case, z(t) will decrease as the environment will more frequently stay in the degraded state s2.
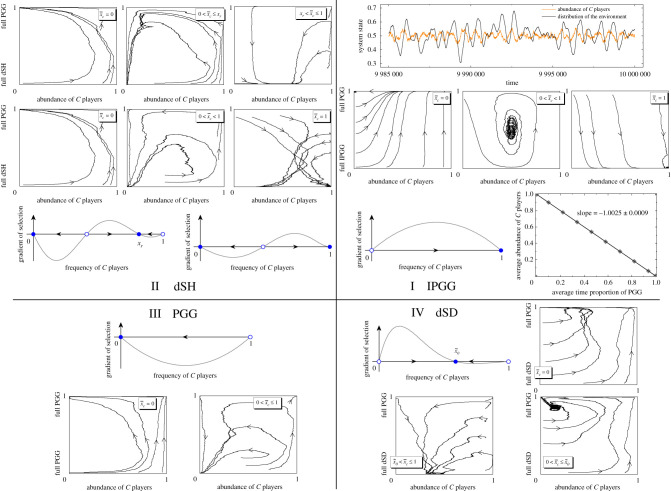
We consider that in the prosperous state s1 players play a PGG. However, in the degraded state s2, one of four different games, the PGG, IPGG (inverse public goods game, which reverses the payoffs of action C and D in the PGG), dSH (d-player stag hunt game, which is a variant of the TPGG, and whose only difference from the TPGG is that cooperators always entail a cost c even if j < T), and dSD, is played. The reason that we select these four types of games is twofold. On the one hand, they are commonly used to mimic the essence of a vast number of real-life group interactions [12]; on the other hand, they encompass all possible evolutionary behaviours for the frequency-dependent selection between C and D under the classic replicator dynamics [9]: D dominance, C dominance, bistability, and coexistence (figure 4). Through agent-based simulations, in figure 4, we show the co-evolutionary dynamics of cooperation and the environment under moderate selection intensity. Depending on the game type and the value of the tipping point , the population emerges various dynamic behaviours. Particularly, although our model is stochastic and incorporates the effect of environment and learning, we can still observe those dominance, bistability and coexistence behaviours analogously obtained under the deterministic replicator dynamics. In addition, when replicator dynamics predict that cooperation will be the dominant choice in the degraded state s2, our results show some persistent oscillations between cooperation and the environment (panel I in figure 4).
Figure 4.
Co-evolutionary dynamics of cooperation and the environment under moderate selection intensity. From panel I to panel IV, the PGG is fixed to be played in state s1, while in state s2, the IPGG, dSH, PGG and dSD are played, respectively. Under replicator dynamics [12,60,62], the gradients of selection in these four games are shown in each panel, respectively. Blue solid circles are used to depict stable equilibria, while open blue circles are used to depict unstable equilibria. The direction of evolution is indicated by arrows. The phase graphs in each panel show the co-evolutionary dynamics of the time proportion of the PGG and the average proportion of C players for different value intervals of the tipping point . Corresponding to the value interval , the first row in panel I shows the persistent oscillations of cooperation and the environment. The bottom right sub-figure in panel I shows the linear relation between the average abundance of C players and the average time proportion of the PGG, which suggests that condition (3.3) is still valid for relatively moderate selection intensity. The first row in panel II uses the parameter condition [62] under which there is a stable and an unstable interior equilibrium for the dSH under replicator dynamics (the bottom left), whereas the second row uses that under which there is a unique interior unstable equilibrium (the bottom right). The population structure is a complete graph. Parameter values: N = 400, d = 5, β = 2, , , rs = 3 for all panels, except in panel II, where rs = 4 and T = 3 for the first row, and rs = 5.01 and T = 4 for the second row.
3.3.2. External incentives
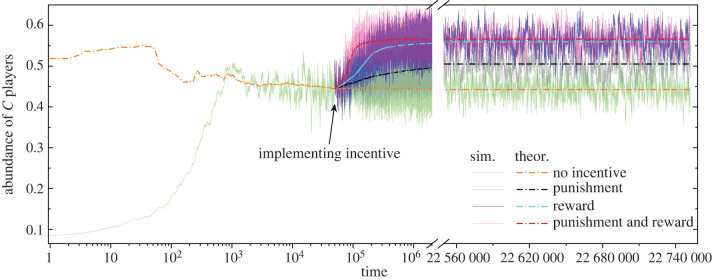
Another interesting case is the existence of external incentives, which will undermine the stationarity of the payoff structure of the game. Like two sides of a coin, reward and punishment are two diametrically opposed external incentives for sustaining human cooperation [63,64]. The former is a type of positive incentives where players who cooperate will get an additional bonus, while the latter is a kind of negative incentives where those who defect will be sanctioned and need to pay a fine. At a certain moment during the evolution of cooperation, we separately implement punishment and reward, or jointly enforce them to all players in the population with four environmental states. One can observe that both punishment and reward are effective tools in promoting cooperation, even if the game environment may change (figure 5).
Figure 5.
Evolution of cooperation under the influence of external incentives. Light solid lines indicate simulations whereas dash dot lines are theoretical results. During the evolution, we separately implement punishment (the fine is 0.4) and reward (the bonus is 0.65), or jointly enforce them in a population where the IPGG, dSH, PGG and dSD are played in each state with probability distribution (0.05, 0.05, 0.85, 0.05), respectively. The population structure is a lattice network. Parameter values: N = 400, d = 5, β = 0.05, for all games, except rs = 3 in the PGG and TPGG, rs = 5 and T = [d/2] + 2 in the dSH, and in the dSD.
4. Discussion
In natural populations, the biotic and abiotic environment that organisms are exposed to varies persistently in time and space. To win the struggle for survival in this uncertain world, organisms have to timely adjust their behaviours in response to the fluctuation of their living environments [25,39]. For the longstanding conundrum of how cooperation can evolve, however, the majority of the existing evolutionary interpretations has been devoted to understanding the static interactive scenarios [1,6]. Therefore, when individual interactions, especially involving multiple players at a time, occur in the changing environment, determining whether cooperation can evolve will become fairly tricky. Here, we developed a general model framework by introducing the adaptation mechanism of reinforcement learning to investigate how cooperation can evolve in the constantly changing multi-player game environment. Our model not only considers the interplay between players’ behaviours and environmental variations, but also incorporates a cognitive or psychological feedback loop where players’ choices determine the game outcome, and in turn are affected by it. Such a setting is, to some extent, analogous to the human decision in the context of the hybrid human–machine cooperation [65], a key research theme in the emerging interdisciplinary field of machine behaviour [66], in which humans can use algorithms to make decisions and subsequently the training of the same algorithms is affected by those decisions.
The importance of environmental variations in population dynamics has long been recognized in theoretical ecology and population biology [24–26]. In a realistic social or ecological system, individual behaviours and environmental variations are inevitably coupled together [24,25]. By consuming, transforming, or producing common-pool resources, for example, organisms are enabled to alter their living environments, and consequently, such modification may consequentially be detrimental or beneficial to their survival [22]. Our analytical condition for determining whether cooperation can be favoured over defection indeed provides us a plausible theoretical explanation for this phenomenon. If mutual actions of individuals lead the environment to transit from a preferable state where cooperation is more profitable to a hostile one where defection is more dominant, cooperation will be suppressed. By contrast, cooperation will flourish if the transition order is reversed. In particular, if the population has access to switching among multiple environmental states, the environment will play the role of intermediates in social interactions and the final outcome of whether cooperation can evolve will be the synthesis of results in each environmental state. Such an observation is different from the recent findings where game transitions can result in a more favourable outcome for cooperation even if all individual games favour defection [21,29]. One important reason for this is that we do not follow the scheme to explicitly assign a specific rule to prescribe the update of environmental states (i.e. model-specific methods), but rather simply assuming the ergodicity for the environmental dynamics (i.e. model-free methods). Thus, in this sense, our model is general and can be applied to a large variety of environmental dynamic processes.
Moreover, compared with the existing studies on the evolution of cooperation in the changing environment [20,21,23,27–29], another striking difference is that, apart from the environmental feedback, our model introduces the learning mechanism of reinforcement. Since, when the environment changes, the previous decision-making scheme adopted by individuals may fail to work, they must learn how to adjust their behaviours in response to the contingencies given by the environment, in order to obtain a higher fitness. Such a scenario is also closely related to some recent work across disciplines, including complexity science [49,67–70], artificial intelligence [44,56,71], evolutionary biology [72,73] and neuroscience [43]. However, their dominant attention has been paid to learning dynamics, the deterministic limit of the learning process, the design of new learning algorithms in games, or neural computations. In comparison, our model is discrete and stochastic, and focuses on multi-player stochastic games. In particular, our analysis for the game system is systematic and encompasses a variety of factors, such as group interactions, spatial structures and environmental variations. In addition, our work may offer some new insight into the interface between reinforcement learning and evolutionary game theory from the perspective of function approximation [44,50], because most existing progress in combining tools from these two fields to explore the interaction of multiple agents is based on value-based methods [49,56,70,71].
In the present work, one of the main limitations is that the strategic update is restricted to the asynchronous type and the learning experience is required to be shared among individuals. Although such a setting is appropriate in those scenarios where individuals modify their strategies independently, and typical in economics applications and for overlapping generations [11], it has been suggested that the unanimous satisfactory decisions reached by all asynchronous update individuals cannot always be guaranteed by synchronous updates [74]. In particular, if individuals are able to communicate with each other via a network or leverage the perceived information to model and infer the choices of others [45,47], the asynchronous update will suffer from some difficulties. Thus, further work on synchronously strategic revisions is worth exploring in the future. Of course, such an extension will also be full of challenges, because updating strategies concurrently for multiple agents will inevitably give rise to some complications, such as the curse of dimensionality, requirement for coordination, non-stationarity and exploration–exploitation trade-off [45]. Moreover, some further efforts should be invested in the partial observability of the Markov environmental states and relaxing the perfect environmental information required in our model to the unobservable or unpredictable type [75].
Acknowledgements
The simulations were performed on the High-performance Computing Platform of Peking University.
Data accessibility
This article has no additional data.
Authors' contributions
F.H., M.C. and L.W. participated in the design of the study and drafted the manuscript.
Competing interests
We declare we have no competing interest.
Funding
This work was supported by the National Natural Science Foundation of China (grant nos. 61751301 and 61533001). F.H. acknowledges the support from China Scholarship Council (grant no. 201906010075). M.C. was supported in part by the European Research Council (grant no. ERC-CoG-771687) and The Netherlands Organization for Scientific Research (grant no. NWO-vidi-14134).
References
- 1.West SA, Griffin AS, Gardner A. 2007. Evolutionary explanations for cooperation. Curr. Biol. 17, R661–R672. ( 10.1016/j.cub.2007.06.004) [DOI] [PubMed] [Google Scholar]
- 2.Gardiner SM, Caney S, Jamieson D, Shue H (eds). 2010. Climate ethics: essential readings. Oxford, UK: Oxford University Press. [Google Scholar]
- 3.Milinski M, Sommerfeld RD, Krambeck H-J, Reed FA, Marotzke J. 2008. The collective-risk social dilemma and the prevention of simulated dangerous climate change. Proc. Natl Acad. Sci. USA 105, 2291–2294. ( 10.1073/pnas.0709546105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ostrom E. 1990. Governing the commons: the evolution of institutions for collective action. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 5.Colman AM. 2006. The puzzle of cooperation. Nature 440, 744–745. ( 10.1038/440744b) [DOI] [Google Scholar]
- 6.Nowak MA. 2006. Five rules for the evolution of cooperation. Science 314, 1560–1563. ( 10.1126/science.1133755) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dawkins R. 2016. The selfish gene. Oxford, UK: Oxford University Press. [Google Scholar]
- 8.Smith JM. 1982. Evolution and the theory of games. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 9.Hofbauer J, Sigmund K. 1998. Evolutionary games and population dynamics. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 10.Hamilton WD. 1964. The genetical evolution of social behaviour I and II. J. Theor. Biol. 7, 1–52. ( 10.1016/0022-5193(64)90038-4) [DOI] [PubMed] [Google Scholar]
- 11.Szabó G, Fath G. 2007. Evolutionary games on graphs. Phys. Rep. 446, 97–216. ( 10.1016/j.physrep.2007.04.004) [DOI] [Google Scholar]
- 12.Archetti M, Scheuring I. 2012. Game theory of public goods in one-shot social dilemmas without assortment. J. Theor. Biol. 299, 9–20. ( 10.1016/j.jtbi.2011.06.018) [DOI] [PubMed] [Google Scholar]
- 13.Gokhale CS, Traulsen A. 2010. Evolutionary games in the multiverse. Proc. Natl Acad. Sci. USA 107, 5500–5504. ( 10.1073/pnas.0912214107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tarnita CE, Wage N, Nowak MA. 2011. Multiple strategies in structured populations. Proc. Natl Acad. Sci. USA 108, 2334–2337. ( 10.1073/pnas.1016008108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wu B, Traulsen A, Gokhale CS. 2013. Dynamic properties of evolutionary multi-player games in finite populations. Games 4, 182–199. ( 10.3390/g4020182) [DOI] [Google Scholar]
- 16.Pena J, Wu B, Traulsen A. 2016. Ordering structured populations in multiplayer cooperation games. J. R. Soc. Interface 13, 20150881 ( 10.1098/rsif.2015.0881) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.McAvoy A, Hauert C. 2016. Structure coefficients and strategy selection in multiplayer games. J. Math. Biol. 72, 203–238. ( 10.1007/s00285-015-0882-3) [DOI] [PubMed] [Google Scholar]
- 18.Huang F, Chen X, Wang L. 2019. Evolutionary dynamics of networked multi-person games: mixing opponent-aware and opponent-independent strategy decisions. New J. Phys. 21, 063013 ( 10.1088/1367-2630/ab241b) [DOI] [Google Scholar]
- 19.Hardin G. 1968. The tragedy of the commons. Science 162, 1243–1248. ( 10.1126/science.162.3859.1243) [DOI] [PubMed] [Google Scholar]
- 20.Weitz JS, Eksin C, Paarporn K, Brown SP, Ratcliff WC. 2016. An oscillating tragedy of the commons in replicator dynamics with game-environment feedback. Proc. Natl Acad. Sci. USA 113, E7518–E7525. ( 10.1073/pnas.1604096113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hilbe C, Šimsa Š, Chatterjee K, Nowak MA. 2018. Evolution of cooperation in stochastic games. Nature 559, 246–249. ( 10.1038/s41586-018-0277-x) [DOI] [PubMed] [Google Scholar]
- 22.Estrela S, Libby E, Van Cleve J, Débarre F, Deforet M, Harcombe WR, Peña J, Brown SP, Hochberg ME. 2019. Environmentally mediated social dilemmas. Trends Ecol. Evol. 34, 6–18. ( 10.1016/j.tree.2018.10.004) [DOI] [PubMed] [Google Scholar]
- 23.Tilman AR, Plotkin JB, Akçay E. 2020. Evolutionary games with environmental feedbacks. Nat. Commun. 11, 915 ( 10.1038/s41467-020-14531-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.MacArthur R. 1970. Species packing and competitive equilibrium for many species. Theor. Popul. Biol. 1, 1–11. ( 10.1016/0040-5809(70)90039-0) [DOI] [PubMed] [Google Scholar]
- 25.Levins R. 1968. Evolution in changing environments: some theoretical explorations. Princeton, NJ: Princeton University Press. [Google Scholar]
- 26.Rosenberg NA. 2020. Fifty years of theoretical population biology. Theor. Popul. Biol. 133, 1–12. ( 10.1016/j.tpb.2020.04.001) [DOI] [PubMed] [Google Scholar]
- 27.Chen X, Szolnoki A. 2018. Punishment and inspection for governing the commons in a feedback-evolving game. PLoS Comput. Biol. 14, e1006347 ( 10.1371/journal.pcbi.1006347) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hauert C, Saade C, McAvoy A. 2019. Asymmetric evolutionary games with environmental feedback. J. Theor. Biol. 462, 347–360. ( 10.1016/j.jtbi.2018.11.019) [DOI] [PubMed] [Google Scholar]
- 29.Su Q, McAvoy A, Wang L, Nowak MA. 2019. Evolutionary dynamics with game transitions. Proc. Natl Acad. Sci. USA 116, 25 398–25 404. ( 10.1073/pnas.1908936116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Szolnoki A, Chen X. 2018. Environmental feedback drives cooperation in spatial social dilemmas. Europhys. Lett. 120, 58001 ( 10.1209/0295-5075/120/58001) [DOI] [Google Scholar]
- 31.Szolnoki A, Perc M. 2019. Seasonal payoff variations and the evolution of cooperation in social dilemmas. Sci. Rep. 9, 12575 ( 10.1038/s41598-019-49075-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hashimoto K. 2006. Unpredictability induced by unfocused games in evolutionary game dynamics. J. Theor. Biol. 241, 669–675. ( 10.1016/j.jtbi.2006.01.003) [DOI] [PubMed] [Google Scholar]
- 33.Venkateswaran VR, Gokhale CS. 2019. Evolutionary dynamics of complex multiple games. Proc. R. Soc. B 286, 20190900 ( 10.1098/rspb.2019.0900) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ashcroft P, Altrock PM, Galla T. 2014. Fixation in finite populations evolving in fluctuating environments. J. R. Soc. Interface 11, 20140663 ( 10.1098/rsif.2014.0663) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Stewart AJ, Plotkin JB. 2014. Collapse of cooperation in evolving games. Proc. Natl Acad. Sci. USA 111, 17 558–17 563. ( 10.1073/pnas.1408618111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Akiyama E, Kaneko K. 2000. Dynamical systems game theory and dynamics of games. Physica D 147, 221–258. ( 10.1016/S0167-2789(00)00157-3) [DOI] [Google Scholar]
- 37.Shapley LS. 1953. Stochastic games. Proc. Natl Acad. Sci. USA 39, 1095–1100. ( 10.1073/pnas.39.10.1953) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Neyman A, Sorin S (eds). 2003. Stochastic games and applications. Dordrecht, The Netherlands: Kluwer Academic Press. [Google Scholar]
- 39.Meyers LA, Bull JJ. 2002. Fighting change with change: adaptive variation in an uncertain world. Trends Ecol. Evol. 17, 551–557. ( 10.1016/S0169-5347(02)02633-2) [DOI] [Google Scholar]
- 40.Ballaré CL, Scopel AL, Sánchez RA. 1990. Far-red radiation reflected from adjacent leaves: an early signal of competition in plant canopies. Science 247, 329–332. ( 10.1126/science.247.4940.329) [DOI] [PubMed] [Google Scholar]
- 41.Danforth BN. 1999. Emergence dynamics and bet hedging in a desert bee, perdita portalis. Proc. R. Soc. B 266, 1985–1994. ( 10.1098/rspb.1999.0876) [DOI] [Google Scholar]
- 42.Thorndike EL. 1911. Animal intelligence: experimental studies. New York, NY: Macmillan. [Google Scholar]
- 43.Niv Y. 2009. Reinforcement learning in the brain. J. Math. Psychol. 53, 139–154. ( 10.1016/j.jmp.2008.12.005) [DOI] [Google Scholar]
- 44.Sutton RS, Barto AG. 2018. Reinforcement learning: an introduction. Cambridge, MA: MIT Press. [Google Scholar]
- 45.Busoniu L, Babuska R, De Schutter B. 2008. A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man Cybernet. C 38, 156–172. ( 10.1109/TSMCC.2007.913919) [DOI] [Google Scholar]
- 46.Fudenberg D, Levine D. 1998. The theory of learning in games. Cambridge, MA: MIT Press. [Google Scholar]
- 47.Camerer CF. 2011. Behavioral game theory: experiments in strategic interaction. Princeton, NJ: Princeton University Press. [Google Scholar]
- 48.Nowak MA, Sasaki A, Taylor C, Fudenberg D. 2004. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650. ( 10.1038/nature02414) [DOI] [PubMed] [Google Scholar]
- 49.Sato Y, Akiyama E, Crutchfield JP. 2005. Stability and diversity in collective adaptation. Physica D 210, 21–57. ( 10.1016/j.physd.2005.06.031) [DOI] [Google Scholar]
- 50.Sutton RS, McAllester DA, Singh SP, Mansour Y. 1999. Policy gradient methods for reinforcement learning with function approximation. In Proc. 12th Int. Conf. on Neural Information Processing Systems, pp. 1057–1063. Cambridge, MA: MIT Press.
- 51.Konda VR, Tsitsiklis JN. 1999. Actor-critic algorithms. In Proc. 12th Int. Conf. on Neural Information Processing Systems, pp. 1008–1014. Cambridge, MA: MIT Press.
- 52.Borkar VS. 1997. Stochastic approximation with two time scales. Syst. Control Lett. 29, 291–294. ( 10.1016/S0167-6911(97)90015-3) [DOI] [Google Scholar]
- 53.Isaacson DL, Madsen RW. 1976. Markov chains theory and applications. New York, NY: John Wiley & Sons. [Google Scholar]
- 54.Bowerman BL. 1974. Nonstationary Markov decision processes and related topics in nonstationary Markov chains. PhD thesis, Iowa State University.
- 55.Ibsen-Jensen R, Chatterjee K, Nowak MA. 2015. Computational complexity of ecological and evolutionary spatial dynamics. Proc. Natl Acad. Sci. USA 112, 15 636–15 641. ( 10.1073/pnas.1511366112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Tuyls K, Verbeeck K, Lenaerts T. 2003. A selection-mutation model for q-learning in multi-agent systems. In Proc. 2nd Int. Conf. on Autonomous Agents and Multiagent Systems (AAMAS 2003), pp. 693–700. New York, NY: ACM ( 10.1145/860575.860687) [DOI]
- 57.Tarnita CE, Ohtsuki H, Antal T, Fu F, Nowak MA. 2009. Strategy selection in structured populations. J. Theor. Biol. 259, 570–581. ( 10.1016/j.jtbi.2009.03.035) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Barfuss W, Donges JF, Vasconcelos VV, Kurths J, Levin SA. 2020. Caring for the future can turn tragedy into comedy for long-term collective action under risk of collapse. Proc. Natl Acad. Sci. USA 117, 12 915–12 922. ( 10.1073/pnas.1916545117) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Du J, Wu B, Altrock PM, Wang L. 2014. Aspiration dynamics of multi-player games in finite populations. J. R. Soc. Interface 11, 20140077 ( 10.1098/rsif.2014.0077) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Souza MO, Pacheco JM, Santos FC. 2009. Evolution of cooperation under n-person snowdrift games. J. Theor. Biol. 260, 581–588. ( 10.1016/j.jtbi.2009.07.010) [DOI] [PubMed] [Google Scholar]
- 61.Wu B, Zhou L. 2018. Individualised aspiration dynamics: calculation by proofs. PLoS Comput. Biol. 14, e1006035 ( 10.1371/journal.pcbi.1006035) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pacheco JM, Santos FC, Souza MO, Skyrms B. 2009. Evolutionary dynamics of collective action in n-person stag hunt dilemmas. Proc. R. Soc. B 276, 315–321. ( 10.1098/rspb.2008.1126) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fehr E, Fischbacher U. 2003. The nature of human altruism. Nature 425, 785–791. ( 10.1038/nature02043) [DOI] [PubMed] [Google Scholar]
- 64.Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. 2017. Statistical physics of human cooperation. Phys. Rep. 687, 1–51. ( 10.1016/j.physrep.2017.05.004) [DOI] [Google Scholar]
- 65.Crandall JW, Oudah M, Ishowo-Oloko F, Abdallah S, Bonnefon JF, Cebrian M, Shariff A, Goodrich MA, Rahwan I. 2018. Cooperating with machines. Nat. Commun. 9, 233 ( 10.1038/s41467-017-02597-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Rahwan I. et al. 2019. Machine behaviour. Nature 568, 477–486. ( 10.1038/s41586-019-1138-y) [DOI] [PubMed] [Google Scholar]
- 67.Macy MW, Flache A. 2002. Learning dynamics in social dilemmas. Proc. Natl Acad. Sci. USA 99 (Suppl. 3), 7229–7236. ( 10.1073/pnas.092080099) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sato Y, Akiyama E, Farmer JD. 2002. Chaos in learning a simple two-person game. Proc. Natl Acad. Sci. USA 99, 4748–4751. ( 10.1073/pnas.032086299) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Galla T, Farmer JD. 2013. Complex dynamics in learning complicated games. Proc. Natl Acad. Sci. USA 110, 1232–1236. ( 10.1073/pnas.1109672110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Barfuss W, Donges JF, Kurths J. 2019. Deterministic limit of temporal difference reinforcement learning for stochastic games. Phys. Rev. E 99, 043305 ( 10.1103/PhysRevE.99.043305) [DOI] [PubMed] [Google Scholar]
- 71.Bloembergen D, Tuyls K, Hennes D, Kaisers M. 2015. Evolutionary dynamics of multi-agent learning: a survey. J. Artif. Intell. Res. 53, 659–697. ( 10.1613/jair.4818) [DOI] [Google Scholar]
- 72.Dridi S, Lehmann L. 2014. On learning dynamics underlying the evolution of learning rules. Theor. Popul. Biol. 91, 20–36. ( 10.1016/j.tpb.2013.09.003) [DOI] [PubMed] [Google Scholar]
- 73.Dridi S, Akçay E. 2018. Learning to cooperate: the evolution of social rewards in repeated interactions. Am. Nat. 191, 58–73. ( 10.1086/694822) [DOI] [PubMed] [Google Scholar]
- 74.Ramazi P, Riehl J, Cao M. 2016. Networks of conforming or nonconforming individuals tend to reach satisfactory decisions. Proc. Natl Acad. Sci. USA 113, 12 985–12 990. ( 10.1073/pnas.1610244113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Kaelbling LP, Littman ML, Cassandra AR. 1998. Planning and acting in partially observable stochastic domains. Artif. Intell. 101, 99–134. ( 10.1016/S0004-3702(98)00023-X) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.