An ecophysiological model of plant–pest interactions: the role of nutrient and water availability

Abstract

Empirical studies have shown that particular irrigation/fertilization regimes can reduce pest populations in agroecosystems. This appears to promise that the ecological concept of bottom-up control can be applied to pest management. However, a conceptual framework is necessary to develop a mechanistic basis for empirical evidence. Here, we couple a mechanistic plant growth model with a pest population model. We demonstrate its utility by applying it to the peach–green aphid system. Aphids are herbivores which feed on the plant phloem, deplete plants’ resources and (potentially) transmit viral diseases. The model reproduces system properties observed in field studies and shows under which conditions the diametrically opposed plant vigour and plant stress hypotheses find support. We show that the effect of fertilization/irrigation on the pest population cannot be simply reduced as positive or negative. In fact, the magnitude and direction of any effect depend on the precise level of fertilization/irrigation and on the date of observation. We show that a new synthesis of experimental data can emerge by embedding a mechanistic plant growth model, widely studied in agronomy, in a consumer–resource modelling framework, widely studied in ecology. The future challenge is to use this insight to inform practical decision making by farmers and growers.

1. Introduction

Chemicals have been widely used in agriculture to control pests since the middle of the twentieth century, particularly in more economically developed countries [1]. However, widespread application of agrochemicals carries an inherent environmental cost. There is also the significant challenge of declining efficacy owing to the emergence and spread of insecticide resistance in pest populations [2]. In recent decades, agroecology has developed as a discipline which aims to provide alternatives to the use of chemicals in agronomy to control pests. The rationale is that ecological concepts and principles can be applied to control pest populations while reducing the use of chemicals [3]. The concept of ‘bottom-up’ control, according to which population dynamics are driven by the quantity and quality of resources, is particularly highlighted by agroecologists. There are a number of agricultural practices that can affect plant physiology and that alter resources offered by plants to pests [4,5]. For example, fertilization modifies the nutrient balance in plants, enhancing plant tissue nutritional status, and influences the synthesis of defence compounds [6]. Similarly, irrigation controls plant vigour and phloem nutritional quality and viscosity, possibly regulating pest abundance [7–11].

Unfortunately, how pests might be affected by plant nutrient and irrigation status is far from obvious. Empirical evidence is ambiguous, potentially supporting diametrically opposed hypotheses. On the one hand, the plant vigour hypothesis (PVH) [12] argues that pest populations should increase most rapidly on vigorously growing plants (or organs), since these habitats provide more resources. In support of this hypothesis, there is some experimental evidence suggesting that practices such as fertilization and irrigation, or favourable conditions for plant growth such as increased organic soil fertility, can be associated with abundant pest populations [13,14]. On the other hand, the plant stress hypothesis (PSH) [15] argues that pests perform better on stressed plants that would not have resources to deploy defences and/or whose nutritional quality might be enhanced. This has been determined experimentally to be the case for some aphid species feeding on plants subjected to controlled irrigation deficit [16,17].

In order to efficiently use the concepts of bottom-up control in agroecology, it is necessary to shed light on the mechanisms that are responsible for the observed patterns. We require a unified conceptual framework that is sufficiently flexible for both the PVH and PSH hypotheses to find support. Developing and validating such a framework requires integration of information from field experiments with mathematical modelling. Experimental data are clearly necessary to test the validity of theoretical hypotheses, but are often extremely costly and time consuming to obtain. Mathematical modelling, particularly mechanistic models, represent a useful tool to investigate which processes can be responsible for the observed patterns and to explore the consequences of different agricultural practices [18].

Here, we present an original, explicitly agroecological, model synthesizing elements of models as commonly used within the disciplines of agronomy and ecology. Agronomic models tend to empirically parametrize the detrimental effects of pests on plant biological rates (e.g. photosynthetic, growth, solute transport). However, such models invariably neglect the dynamical interaction between the plant (or some of its component parts) and the pest (e.g. [19–21]). That is, the impact of a pest on the plant is modelled by varying one or more plant parameters, according to the pest disturbance level with no further interaction or feedback. On the other hand, in ecology, there is a very broad literature of models on interactions (e.g. predation, consumption, competition etc.) between different species or organisms. These types of models have been widely used to study temporal and spatial dynamics in plant–pest (e.g. [22–24]) and particularly plant–pathogen systems (e.g. [25–27]). However, these types of model usually present a simplistic description of the plant (but see [28]), which in turn limits the possibility to consider the effects of agronomic practices. Some authors attempted to bridge the gap between agronomy and ecology by explicitly integrating pest dynamics in crop models [29,30]. However, and arguably, past works have over-emphasized realism and precision at the cost of parsimony, meaning that general principles cannot be revealed.

Here, focusing on parsimony, we couple a relatively simple plant growth model, which describes carbon and nitrogen assimilation and allocation to the shoot and root compartments of a plant, with a pest population model. With regard to the plant, we use the modelling framework proposed by Thornley in the early 1970s [31], and refined in the following decades [32–35], which represents a cornerstone in plant and crop modelling. With regard to the pest, we propose a novel population model that includes intraspecific competition in which pest birth and mortality rates depend on resource availability and quality. Moreover, we assume that the presence of the pest can induce the plant to produce defensive traits or compounds [36]. We demonstrate the utility of our model by applying it to the peach (Prunus persica)–green aphid (Myzus persicae) system. Aphids are specialized herbivores which feed on the phloem of vascular plants. This depletes plants’ resources, affecting growth and reproduction, as well as eventually impacting upon yield [37]. Moreover, aphids are the most common vector of plant viral diseases and so can often cause indirect damage far exceeding direct impacts via herbivory [38]. We use likelihood-based techniques to calibrate model parameters and select model assumptions against field data obtained under different conditions of irrigation and fertilization. The resulting model has the ability to reproduce different system properties observed in field studies, as well as showing under which conditions the PVH and PSH find more support. Our model also provides insights to conceive new targeted experiments to better understand this class of system and rethink the control of plant–aphid systems.

2. Material and methods

2.1. Model outline and assumptions

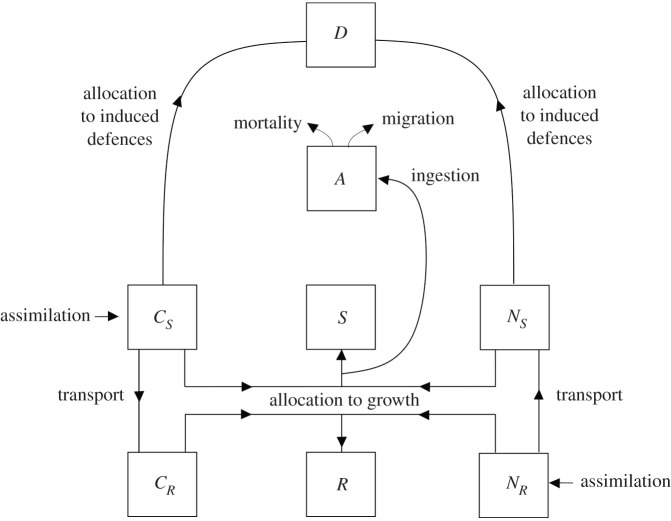
The model, which describes the temporal variation, during a growing season, of plant dry mass (partitioned into shoots and roots, in turn composed of structural mass, carbon and nitrogen substrates), its induced defensive level and the aphid population dwelling on the plant, is schematically represented in figure 1. According to Thornely and Johnson's seminal works [18,31–33], carbon is assimilated from the atmosphere via photosynthesis and stored in shoots, as shoot carbon substrate (C_S), or transported and then stored in roots as root carbon substrate (C_R). Similarly, nitrogen is assimilated from the soil, stored in roots as root nitrogen substrate (N_R), or transported and then stored in shoots as shoot nitrogen substrate (N_S). Carbon and nitrogen substrates are used, in a fixed ratio, to constitute structural shoot (S) and root (R) dry mass. With respect to the original model of Thornley, we added the assumption that the constitution of new plant mass is regulated by changes in the photo-period [39]. Such an assumption permits us to model the fact that perennial plants suspend growth, in favour of reserve constitution, before entering winter dormancy [40]. The assimilation of substrate (C_S or N_R) per unit of plant organ (S or R) decreases with organ mass because of shoot self-shading and root competition for nitrogen and it is inhibited by substrate concentration in the organ [33].

Figure 1.

Schematic representation of the plant–aphid model where the plant is constituted by shoot (S) and root (R) structural dry mass and carbon (C_i) and nitrogen (N_i) substrates in shoots (i = S) and roots (i = R). The aphid population (A) intercepts a fraction of substrates allocated to constitute shoot structural mass and the plant diverts shoot substrates (carbon and nitrogen) to produce defensive compounds (D). More details are given in the main text.

We coupled the plant model of carbon and nitrogen assimilation and partitioning with an aphid population model by assuming that aphids, which penetrate growing shoots of the host plant with a stylet and feed on the phloem [41], intercept a fraction of the substrates (C_S and N_S) directed towards the shoot structural mass compartment (S) to support their growth [42]. We assume that aphids act in a scramble competition context [43] and therefore any aphid ingests its maximum daily amount of food when the per capita available resource is sufficient, but that otherwise the resource is evenly shared among all the individuals: all other things being equal, the larger the aphid population gets, the lower the per capita ingested resource. The aphid birth rate depends on the per capita ingested food [44]: it is maximum when aphids have access to their maximum daily amount of food and decreases when aphids evenly share the limited resource. Whenever the aphid birth rate becomes lower than the mortality rate the aphid population declines. We assume that crowding can induce aphids to leave the plant [45].

We assumed that the infested plant can be induced to use carbon and nitrogen substrates to defend itself, to the detriment of growth [41,46,47]. This can result in the production of chemical and/or morphological and physiological changes that can reduce aphid accessibility to the resource (e.g. by phloem sealing) [48,49] and/or decrease the rate at which ingested food is converted into progeny, e.g. by releasing toxic components in the sieve that can even repel or kill the aphid [36]. We assumed that the production of induced defence compounds increases with the abundance of aphids [41].

2.2. Model equations

In quantitative terms, we describe the temporal variation of the plant–aphid system with the following system of ordinary differential equations.

In our model C_S, N_S, S, C_R, N_R and R are expressed in grams (g); D is expressed in an arbitrary defence unit (DU) and A in individuals (ind.); and t represents the number of days (d) that have passed since 1 January of the year of the considered growing season. In equation (2.1a), ${\sigma }_{\mathrm{C}}S{[(1+S/\nu )(1+C_S/(S{\iota }_{\mathrm{C}}))]}^{-1}$ is the carbon substrate assimilated in shoots; ${\phi }_{\mathrm{C}}\kappa (C_S/S)(N_S/S)S$ is the shoot carbon substrate allocated to shoot growth or reserves; (C_S/S − C_R/R)(S R)^q · (S^q + R^q)⁻¹ is the shoot carbon substrate transported towards roots; and α(C_S/S)A is the shoot carbon substrate diverted to defences, in a unit of time. In equation (2.1b), (N_R/R − N_S/S) (SR)^q · (S^q + R^q)⁻¹ is the nitrogen substrate transported from roots towards shoots; ${\phi }_{\mathrm{N}}\kappa (C_S/S)(N_S/S)S$ is the shoot nitrogen substrate allocated to shoot growth or reserves; and α(N_S/S)A is the shoot nitrogen substrate diverted to defences, with each of these quantities being measured as rates per unit of time. In equation (2.1c), the time-dependent parameter Φ = λ^η/(λ^η + t^η) determines the suspension of plant growth-driven changes in the photo-period. The term Φκ(C_S/S)(N_S/S)S is the increase in structural shoot dry mass in the absence of any phloem withdrawal by the aphids, with κ being the maximum rate of utilization of the substrates. The term θA/(Φκ(C_S/S)(N_S/S)S) represents the fraction of substrates diverted from the allocation to plant growth, because of ingestion by aphids, when aphid per capita intake is limited by aphid maximum daily food intake, θ, and not by resource availability. The term ${\beta }_1({(D/S)}^{{\delta }_1}/({\pi }_1^{{\delta }_1}+{(D/S)}^{{\delta }_1}))$ indicates the fraction of phloem that is protected by plant defences and that is therefore inaccessible to aphids. When aphid per capita intake is limited by the resource availability, aphids ingest all the phloem they can access and the per capita intake is reduced. The dynamics of the variables in the root compartments (C_R, N_R, R) follow similar rules to those for assimilation of substrates, transport and allocation to root growth and we assumed that they are not directly affected by the presence of aphids. In equation (2.1h), we assume that the aphid birth rate is proportional to the per capita food intake (θ or $\mathit{\Phi }\kappa (C_S/S)(N_S/S)S(1-{\beta }_1({(D/S)}^{{\delta }_1}/({\pi }_1^{{\delta }_1}+{(D/S)}^{{\delta }_1})))1/A$) and that it can decrease as a result of a possible action of the defences. In other words, we assume that plant defences can determine an extra mortality rate, per unit of ingested food, modelled as ${\beta }_2({(}^{D/S){\delta }_2}/({\pi }_2^{{\delta }_2}+{(D/S)}^{{\delta }_2}))$. We modelled both the fraction of the phloem that can be protected and the phloem ‘toxicity’ as an increasing function of the concentration of defences, D/S. The shape of this function is given by the value of parameter δ_i. Namely, if δ_i > 1 it is convex for D/S < π_i and concave for D/S > π_i; if 0 < δ_i < 1, it is strictly concave. The parameter ω is the strength of possible density-dependent mechanisms inducing aphid migration. Details of the model variables and parameters are reported in table 1.

Table 1.

Model variables and parameters. For those parameters calibrated in the present work the calibrated 99% confidence intervals are reported in brackets. Cal, calibrated in the present work; Fix, fixed in the present work; see electronic supplementary material.

variable		dim.	description
S		g	shoot structural dry mass
R		g	root structural dry mass
CS		g	shoot carbon substrate
CR		g	root carbon substrate
NS		g	shoot nitrogen substrate
NR		g	root nitrogen substrate
D		DU	plant-induced defences
A		ind.	aphid population
parameter	value	dim.	description	source
C and N assimilation
${\sigma }_{\mathrm{C}}$	0.1	d−1	assimilation rate of C	[33]
${\sigma }_{\mathrm{N}}$	6.70–17.08 10−3 [1.76–19.54] [4.56–43.04] 10−3 a	d−1	assimilation rate of N	Cal
ν	1000	g	shoot (root) mass halving substrate assimilation due to self-shading (competition)	[33]
${\iota }_{\mathrm{C}}$	0.1	/	semi-saturation C concentration	[33]
${\iota }_{\mathrm{N}}$	0.01	/	semi-saturation N concentration	[33]
C and N substrate allocation to plant growth
${\phi }_{\mathrm{C}}$	0.50	/	unit of substrate C per unit of structural dry mass	[33]
${\phi }_{\mathrm{N}}$	2.50 10−2	/	unit of substrate N per unit of structural dry mass	[33]
κ	142–223 [56–601] [48–876]b	d−1	maximum rate of substrate utilization	Cal
η	73	/	switch-off function of plant growth: steepness	Fix
λ	169	d	switch-off function of plant growth: date of equal partitioning between growth and reserves	Fix
transport
q	0.86 [0.84–0.89]	/	plant architecture scaling parameter	Cal
defences development
α	0.02 [0.01–0.03]	g d−1 ind−1	allocation of substrates to defences per unit of aphid	Cal
${\epsilon }_{\mathrm{C}}$	5 10−2	DU g−1	conversion efficiency of C substrate in defences	[50]
${\epsilon }_{\mathrm{N}}$	1	DU g−1	conversion efficiency of N substrate in defences	[50]
aphid
θ	1.12 10−3	g d−1 ind−1	maximum food intake per aphid	[51]
ξ	171	ind g−1	maximum conversion efficiency of ingested food into descendants	[52]
μ	0.04	d−1	aphid natural mortality rate	[53]
π1	8.52 10−3 [3.70–23.12] 10−3	DU g−1	swich-on function of defences protected phloem fraction: concentration of defences at which the defence effect is half-saturated	Cal
δ1	0.65 [0.55–0.73]	/	swich-on function of defences protected phloem fraction: steepness	Cal
${\pi }_2$	0.05 [0.03–0.08]	DU g−1	swich-on function of defences induced mortality/repulsion rate: concentration of defences at which the defence effect is half-saturated	Cal
${\delta }_2$	118 [27–251]	/	swich-on function of defences induced mortality/repulsion rate: steepness	Cal
β1	1	/	swich-on function of defences protected phloem fraction: asymptotic value	Fix
${\beta }_2$	28 [13–76]	/	swich-on function of defences induced mortality/repulsion rate: asymptotic value	Cal

^aValues refer to different fertilization treatments. ^bValues refer to different irrigation treatments.

2.3. Model calibration

We apply the model to a system composed of 44 peach plants infested by green aphid subjected to four different treatments obtained by combining two levels of fertilization and irrigation. The shoot growth and the aphid infestation level were measured weekly on each plant: details of the experiment and of the observations are reported in Rousselin et al. [9] and in the electronic supplementary material. According to available data, we set the initial conditions of the system at the first observation date (i.e. 29 April, which was the 119th day of the year 2013) (see electronic supplementary material). We set the value of model parameters according to information available from peer-reviewed literature or experimental data whenever possible (table 1; electronic supplementary material). On the other hand, no information was available to a priori derive reliable estimates for parameters ${\sigma }_{\mathrm{N}}$ (net N assimilation rate) and κ (maximum rate of utilization of the substrates), which depend on environmental conditions that possibly varied in the different treatments: parameter q, affecting substrate transport within the plant and depending on the plant architecture [33], and six parameters relevant to the production of defences (α) and their effect (π₁, δ₁, β₂, π₂, δ₂). We estimated these unknown parameters by minimizing a cost function expressed as the sum of two negative log-likelihood functions, computed with respect to observations of shoot dry mass and aphid abundance (see the electronic supplementary material for details). We assessed the empirical distributions of calibrated parameters by making use of the moving block bootstrap [54]. In particular, we reconstructed bootstrapped time series for each of the observed variables and we fitted the values of the unknown parameters. We repeated this process 1000 times and we generated the 99% confidence intervals (CI) for each parameter via the percentile method [55].

2.4. Model selection

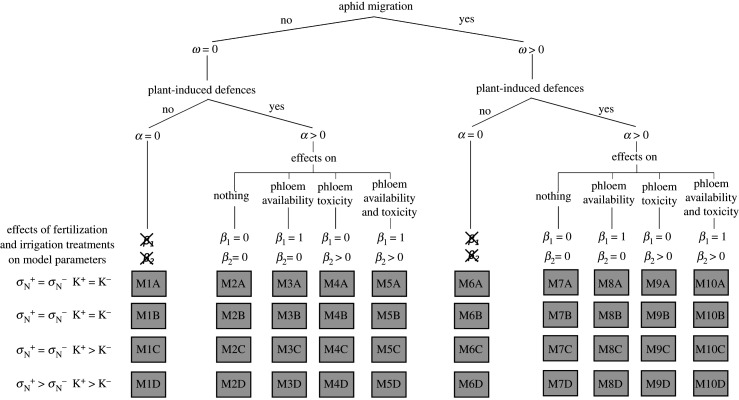
To account for possible different mechanisms regarding aphid ecology, the plant response to aphid infestation and its consequences, we contrasted the ‘full’ model reported in equation (2.1) with a set of nested models lacking some processes (figure 2). Namely, the full model (M10) assumes that aphid crowding promotes aphid migration and that the plant produces defences that make a fraction of resources inaccessible to aphids and kill, or repel, aphids if ingested. Three models nested in M10 assume a crowding effect on aphid migration and the induced production of defences. Yet, they can differ regarding the effect of defences: killing/repulsion effect (M9), reduction of phloem accessibility (M8) or no effect (M7). There is also a simpler model that neglects the production of defences (M6). We also considered five analogous models ignoring the effect of aphid crowding, ω = 0 (M1, M2, M3, M4, M5).

Figure 2.

Schematic representation of the mechanisms considered in the different models Mi (i ∈ [1, 10]) nested in equation (2.1): (i) density-dependent aphid migration (ω), (ii) plant-induced defences development (α) and (iii) effect of induced defences on phloem availability to aphids (β₁) and on phloem toxicity (β₂). When the model parameter is set to zero, the relevant mechanism is ignored. Each model can be based on different hypotheses about the variation in the nitrogen assimilation rate σ_N (equal (A,C) or different (B,D) across fertilization treatments) and the substrate utilization rate k (equal (A,B) or different (C,D) across irrigation treatments).

We tested if the effect of irrigation and fertilization can be represented in the models through a variation in some parameters κ and ${\sigma }_{\mathrm{N}}$. The rationale is that the rate of utilization of the substrates (parameter κ) and the nitrogen assimilation rate (parameter σ_N) are expected to decrease in water [8,56] and nutrient [35,57] stress conditions, respectively. We then contrasted each of the 10 models assuming that (i) κ and ${\sigma }_{\mathrm{N}}$, respectively, vary with irrigation and fertilization treatments; (ii) κ varies with irrigation and ${\sigma }_{\mathrm{N}}$ does not vary with fertilization; (iii) κ does not vary with irrigation and ${\sigma }_{\mathrm{N}}$ varies with fertilization; (iv) neither ${\sigma }_{\mathrm{N}}$ nor κ vary with fertilization and irrigation. Therefore, we calibrated two values for nitrogen assimilation rate per unit of root (${\sigma }_{\mathrm{N}}^{+}$, ${\sigma }_{\mathrm{N}}^{-}$) in cases (i) and (iii) and a unique value (${\sigma }_{\mathrm{N}}^{\pm }$) in cases (ii) and (iv). Analogously, we calibrated two values for the allocation of substrates to plant growth (κ⁺ and κ⁻) in cases (i) and (ii) and a unique value (κ^±) in cases (iii) and (iv).

Overall, we compared 40 different models (figure 2), obtained by incorporating five hypotheses on plant defences, two on density dependence of aphid migration and four on the effect of irrigation and fertilization, with one another. We selected the best model, that is, the one providing the best compromise between the goodness of fit to observed data and parsimony, through a model selection procedure based upon the Akaike information criterion [58]. For each model, we computed a value of AIC = 2C + 2n_p, where C is the minimum of the log-likelihood-based cost function estimated for the model and n_p is the number of calibrated parameters. Then, we ranked the models according to their AIC values and we computed the AIC differences (ΔAIC_i) between the AIC value of the ith model and the minimum AIC among all considered models (table 2). Models with ΔAIC_i < 2 can be considered as equivalent [59,60] and, among equivalent models, we selected the simplest one (i.e. the one with fewest estimated parameters) as the best.

Table 2.

Comparison among candidate models for the plant–aphid system. For each model, we give its identifier ID (see text and figure 2 for details); its complexity assessed by the number of calibrated parameters n_p; its Akaike score AIC; its ΔAIC_i computed as the difference between its AIC and the lowest obtained from all the models, i.e. AIC = 6519.0.

ID	np	AIC	ΔAICi	ID	np	AIC	ΔAICi
M10D	12	6519.0	0.0	M8A	7	6751.6	232.6
M5D	11	6520.8	1.8	M2D	6	6756.2	237.2
M8D	9	6570.8	51.8	M4D	9	6762.2	243.2
M10B	11	6576.1	57.1	M3C	7	6773.4	254.4
M5B	10	6590.5	71.5	M2B	5	6775.4	256.4
M3D	8	6624.5	105.5	M4B	8	6781.3	262.3
M7D	7	6628.4	109.4	M4C	8	6785.0	266.0
M6D	6	6632.1	113.1	M3A	6	6786.7	267.7
M9D	10	6634.2	115.2	M6C	5	6794.0	275.0
M3B	7	6641.5	122.5	M7C	6	6795.5	276.5
M8B	8	6641.9	122.9	M6A	4	6798.5	279.5
M7B	6	6646.4	127.4	M7A	5	6800.5	281.5
M9B	9	6651.6	132.6	M2C	5	6865.2	346.2
M6B	5	6696.0	177.0	M2A	4	6871.9	352.9
M9C	9	6708.6	189.6	M4A	7	6877.0	358.0
M10C	11	6712.6	193.6	M9A	8	6878.7	359.7
M8C	8	6721.6	202.6	M1B	4	7216.0	697.0
M5C	10	6727.9	208.9	M1D	5	7228.4	709.4
M10A	10	6742.9	223.9	M1A	3	7241.7	722.7
M5A	9	6746.8	227.8	M1C	4	7262.4	743.4

2.5. Sensitivity analysis

To assess the robustness of the model outputs to uncertainty affecting model parameters, we performed a sensitivity analysis of the model to (small) perturbations of the default parameter values reported in table 1. According to Thornley & Johnson [18], we computed the sensitivity of the variable Y (where for Y we considered the maximum value of S, of A and of their ratio A/S over the growing season) to small variations of parameter p_i as

$$\psi (Y,p_i)=\frac{\mathrm{\partial }Y}{\mathrm{\partial }{p}_i}\frac{\hspace{0.17em}{p}_i}{Y}\simeq \frac{\delta Y}{Y}\frac{\hspace{0.17em}{p}_i}{\delta p_i}.$$ 2.2

In practice, after having changed the value of each parameter by +5% [18], we computed the value of ψ; if ψ(Y, p_i) > 1 we concluded that the parameter has a more-than-linear effect on the variable.

2.6. The role played by fertilization and irrigation

After having ascertained that parameters κ and ${\sigma }_{\mathrm{N}}$ are likely to vary with irrigation and fertilization treatments, respectively, we used the selected model to simulate the temporal dynamics of the system for different values of these parameters. This allowed us to perform an in silico experiment to explore whether or not the model was able to reproduce the observed empirical patterns that claimed support for the plant vigour or the plant stress hypotheses. The in silico experiment is intended to test if the aphid density is affected by the fertilization (or irrigation) treatment. We considered five levels for the fertilization treatment (i.e. ${\sigma }_{\mathrm{N}}$ equal to 0.0012, 0.0024, 0.012, 0.06 and 0.12 d⁻¹) and five levels for the irrigation treatment (i.e. κ equal to 18, 36, 182, 910 and 1820 d⁻¹) corresponding to very low–low–average–high–very high levels of fertilization (or irrigation). We varied the level of one treatment while keeping the other fixed at its average value, thus obtaining nine different combinations of factorial levels. Since in real factorial experiments the number of replicates (i.e. different plant individuals) is limited, we chose to simulate 10 replicates for each combination of factors, which corresponds to a realistic experiment with 90 plants being monitored. We simulated 10 possible trajectories of the system variables, for the same combination of factors, by running the model with 10 different parameter sets drawn from the empirical distribution obtained in the calibration process.

3. Results

3.1. Model calibration and selection

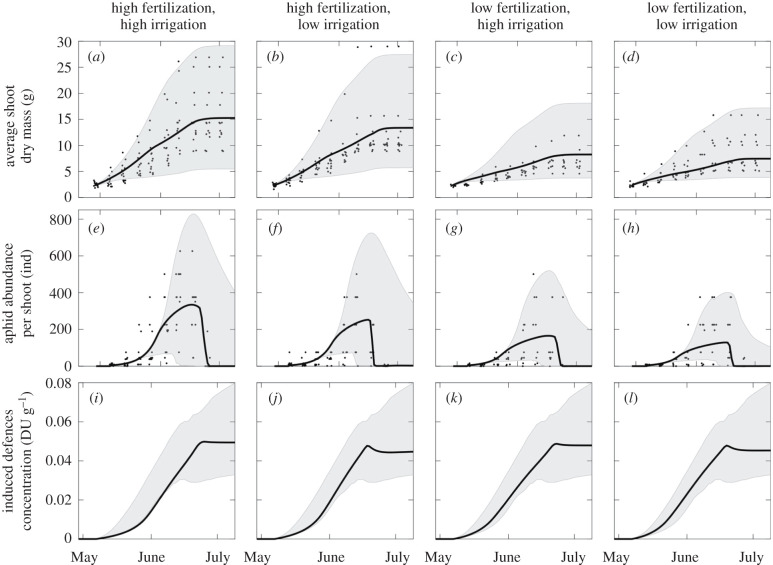
The best model (‘the model’, hereafter) assumes that (i) aphid migration due to crowding can be neglected; (ii) aphid presence induces the plant to divert resources from growth to defence; (iii) defences reduce phloem accessibility to aphids and, at higher concentrations, make the phloem sufficiently toxic to kill or repel aphids (electronic supplementary material, figure S1); (iv) the rates of nitrogen assimilation and substrate utilization differ for different levels of fertilization and irrigation, respectively.

The model fitted all four datasets, reproducing the main observed temporal patterns and differences between treatments (figure 3). Shoot growth is enhanced in high fertilization treatments while the water treatment considered here plays only a relatively minor role. The time course for shoot mass is linear and was followed by a stop towards the end of June. This is consistent with a potential exponential course, in the first part of the season [61], which has been prevented by the presence of the aphids. On the other hand, the stop in shoot growth at the end of June is induced by changes in the day-length. Note that parameter ϕ(t) = 0.5 for t = λ = 169, corresponding to 18 June. Aphid population growth is initially sigmoidal, followed by a decay towards the end of June when the plant growth is halted (figure 3) and the concentration of defences attains the critical value of ${\pi }_2=0.03-0.08$, which makes ingestion from the phloem detrimental rather than beneficial to aphids. The initial phase of aphid growth is enhanced in high fertilization treatments characterized by more vigorous plants.

Figure 3.

Observed (black points) and predicted (black lines) values of average shoot dry mass (a–d), average aphid abundance per shoot (e–h) and induced defences concentration (i–l) under different fertilization and irrigation treatments: high fertilization and irrigation (a,e,i), high fertilization and low irrigation (b,f,j), low fertilization and high irrigation (c,g,k), low fertilization and irrigation (d,h,l). Grey shaded areas indicate the predicted 99% confidence bands.

The model gives biologically plausible parameter estimates (table 1) and the estimated variability in parameters permits most of the variability observed in the data to be captured. The calibrated values of σ_N, κ and q are consistent with previously published values (i.e. σ_N = 0.02 d⁻¹, κ = 200 d⁻¹ and q = 0.67 − 1 in [33]). The estimated values of parameters δ₁ < 1 and δ₂ > 1 suggest that the fraction of phloem that is protected from aphid withdrawal quickly increases for low concentrations of defences, whereas the phloem toxicity is switched on when the concentration of defences exceeds a threshold value (electronic supplementary material, figure S1). On the other hand, the model parameters relevant to the production of defences and their effect on aphids have no equivalent in the literature for a direct comparison.

3.2. Sensitivity analysis

Ranked values of the sensitivity, ψ, of shoot production and maximum aphid abundance and density to small changes in the parameter values are reported in electronic supplementary material, table S1. Negative values of ψ indicate a negative correlation between a change in a parameter value and the corresponding variable of interest. As expected, increasing the parameter λ results in an increase in shoot production, as it determines an increase in the growing season of 8.45 d, being 0.05 λ = 8.45, and consequently more resources to sustain a bigger aphid population, maintaining similar aphid densities. Similarly, an increase in q results in an increase both in shoot production and in the peak of aphid abundance and density, as it determines a more efficient transport of substrates C and N between roots and shoots. This translates into bigger plants able to sustain higher peaks of aphid population densities.

With the exception of q and λ, our sensitivity analysis indicates that none of the model parameters has important (e.g. ψ > 1) consequences, indicating that the model is robust. However, our sensitivity analysis nevertheless provides some interesting insights. For instance, it shows that an increase in all those parameters positively related to the plant growth (${\sigma }_c,{\sigma }_n,{\iota }_C,{\iota }_N,k,\nu$) determine an increase in the maximum aphid abundance and, to a lesser extent, in maximum aphid density. If the aphids were more efficient in converting food into progeny (higher ξ), aphid density would increase but the overall population abundance would diminish as the resource would be over-exploited. An increase in the parameter α, determining a higher rate of resources devoted to defences, would have almost no effect on the shoot production but it would decrease aphid abundance and density. Yet, the plant could take advantage of a lower aphid abundance, since aphids are important vectors of viral diseases [41].

3.3. The role played by fertilization and irrigation

Shoot growth follows a sigmoidal pattern and it increases with fertilization and irrigation (figure 4a,b). The concentration of carbon substrates in shoots varies between 3% and 23% during the growing season with peaks at its beginning, when plant growth is limited by the nitrogen supply, and at its end, when plant growth halts in response to day length decreases, but carbon assimilation continues. Carbon concentration is enhanced in stressful conditions (very low to low fertilization/irrigation treatments) that limit plant growth rather than carbon assimilation (figure 4c,d). The concentration of nitrogen substrates varies between 0.1% and 1.4% during the growing season (figure 4e,f). It decreases in the first weeks of growth, but, in the case of very high/high fertilization or very low irrigation, it increases until the second week of May. In fact, for high fertilization treatments, nitrogen is not initially consumed by plant growth, which is limited by carbon supply, and, for low watering, nitrogen concentration increases as plant growth is impaired while N assimilation is not. The peak concentration of defences is delayed in time for higher fertilization and irrigation (figure 4g,h). When the plant is well watered, the time of the peak aphid population density is delayed by one week. This is due to the fact that defences need more time to reach significant concentrations in bigger plants (figure 4i,j). The positive effect of fertilization and irrigation upon aphid abundance becomes evident at the end of May. In the first part of the season, aphid density is enhanced by a low/average value of fertilization (or irrigation) while later in the season aphid density is higher in a well-fertilized (irrigated) plant (figure 4k,l).

Figure 4.

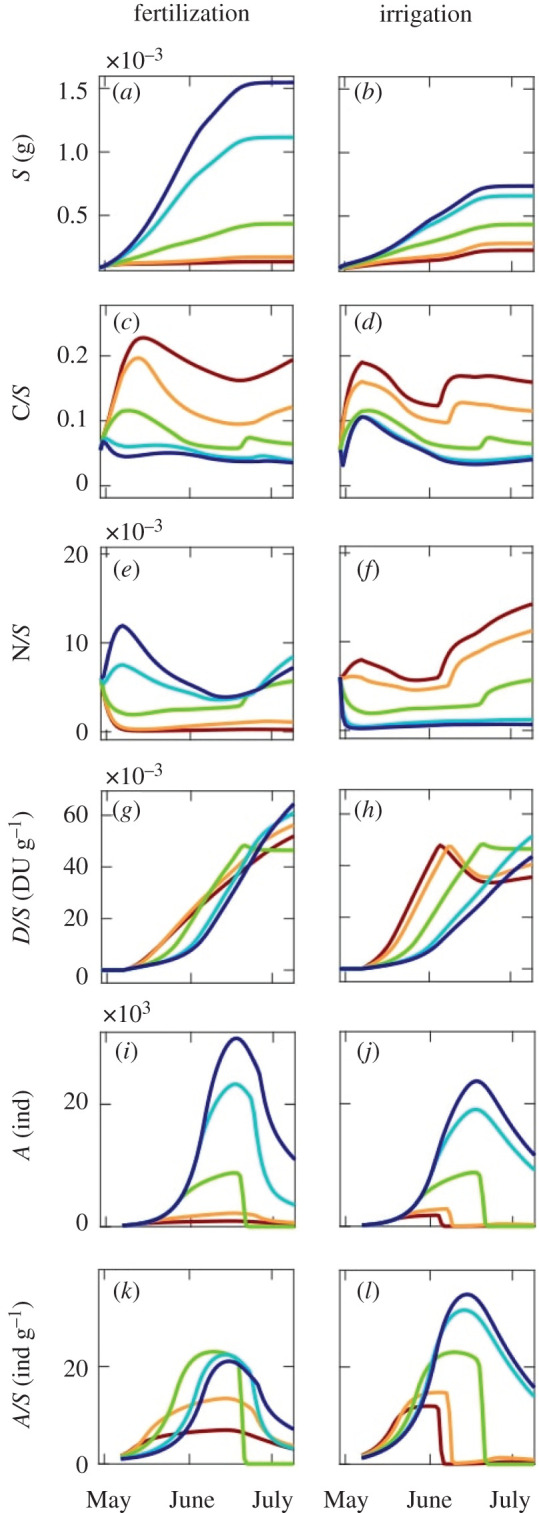
Simulated effect of fertilization (left column) and irrigation (right column) on the plant–aphid system: average shoot dry mass S (a,b), carbon C/S (c,d) and nitrogen N/S (e,f) substrate concentration in shoots, defences concentration in shoot D/S (g,h), aphid abundance A (i,j) and density A/S (k,l). Lines—colour identifies fertilization (or irrigation) level: very low (red), low (orange), average (green), high (light blue) and very high (blue).

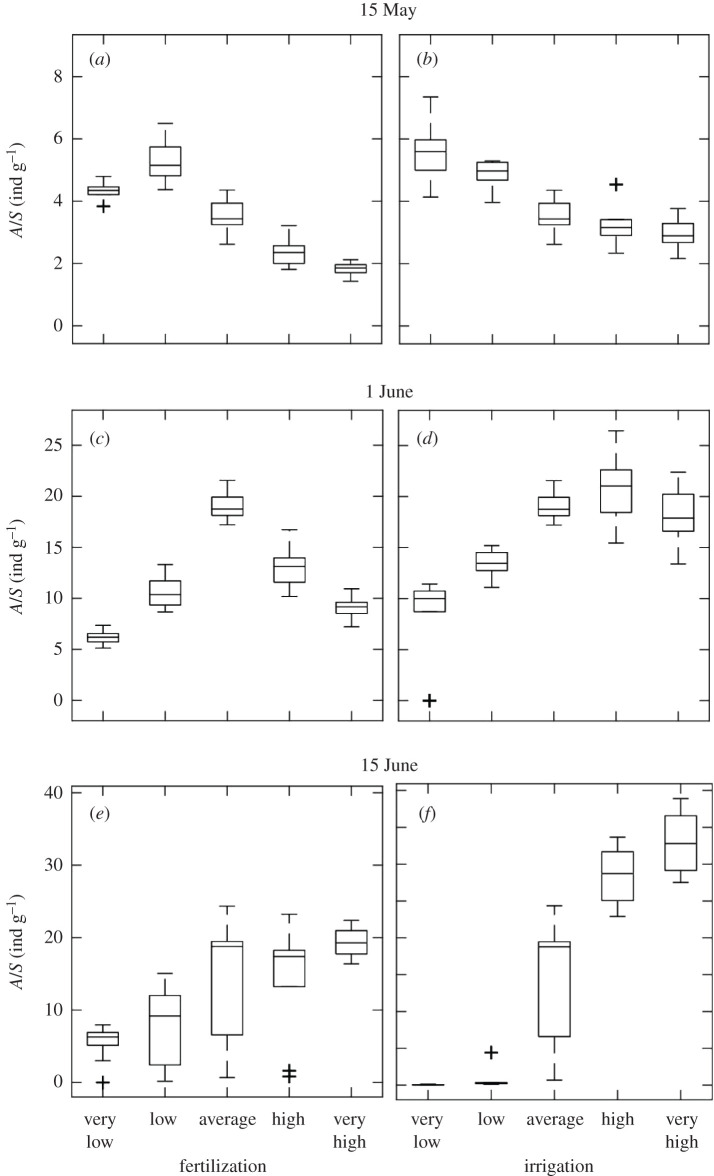
The results of our virtual experiment show that one can draw very different conclusions depending on the considered fertilization/irrigation levels and the date of observations. For instance, one could infer that fertilization (i) enhances aphid population by observing aphid density in the mid- to late part of the season for very low to average values of fertilization (figure 5c–e); (ii) decreases it, by observing aphid density in the early to mid-season for average to very high values of fertilization (figure 5a–c); (iii) has no effect, by observing aphid density early and late in the season, for high to very high values of fertilization (figure 5a–e). Similarly, different conclusions can be drawn regarding the effect of irrigation: positive (figure 5f), negative (figure 5b) or null (figure 5d, from average to very high values of irrigation). The explicit consideration of inter-individual variability in growth trajectories shows that patterns emerging from a limited (i.e. 10) number of replicates per treatment become less clear at the end of the growing season (see longer boxes in figure 5e,f). We purposefully avoided performing statistical tests on our results because the number of replicates, which can be easily varied in a virtual experiment, would have increased the statistical power to detect changes in aphid density (see [62] for a similar exercise).

Figure 5.

Simulated effect of fertilization (a,c,e) and irrigation (b,d,f) on aphid density on 15 May, 1 June and 15 June. Boxes represent the first and third quartiles (25% and 75%) with a line inside indicating the median of 10 simulated replicates of each treatment. The whiskers extend ±1.5× the interquartile range (75th percentile—25th percentile) from the third and first quartiles. Values outside the whiskers are considered outliers and plotted individually using the ‘+’ symbol.

4. Discussion

In this work, we showed that embedding a mechanistic plant growth model, widely studied in agronomy, in a consumer–resource modelling framework, widely studied in ecology, might be a promising approach for agroecology. We demonstrated the ability of such a novel approach in understanding the consequences of irrigation and fertilization treatments in a plant–aphid system. Yet, the proposed model has the ambition of being physiologically rigorous and general enough to be applied to different plant–pest systems and to incorporate the description of other agronomic practices.

4.1. The selected model and model calibration and selection

A recent review [41] suggested that infested plants can put in place phloem-sealing mechanisms to interfere with aphids’ access to plant resources and produce a number of secondary metabolites (e.g. cardenolides, glucosinolates and benzoxazinoids), which, if ingested, impair aphid viability [41]. Our study suggests that both defensive mechanisms are at play in the peach–green aphid system. According to our calibration, impairing phloem accessibility is the most effective at low concentrations of defences, while ‘intoxicating’ aphids is the most effective at higher concentrations. This is in accordance with works on the Arabidopsis-Myzus persicae system, for which reductions in aphid fecundity, up to 100%, have been reported in response to high concentrations of some plant defensive compounds [63,64]. The model application to a real study case subjected to different irrigation×fertilization treatments indicates that parameters relevant to plant nitrogen assimilation (${\sigma }_{\mathrm{N}}$) and plant utilization of substrates (κ), originally proposed within a theoretical framework [31], can be linked to agronomic practices and then manipulated by the grower. However, in order to effectively use the proposed model to define effective agronomic recommendations, further studies on the response of the model parameters to effective practices are clearly required.

One of the main features of the peach–green aphid system is that, at the beginning of summer, aphid populations dwelling on peach trees drop. This occurs because aphids die, or abandon their primary host, or give birth to winged newborns that migrate to secondary herbaceous hosts [65]. However, the underlying mechanisms triggering these processes are far from being clear. Our findings suggest that the reduction in resource availability, due to the investment in defensive traits and to photo-period-driven interruption of shoot growth, along with the reduction of the phloem nutritional value, due to the accumulation of defensive compounds possibly toxic to the aphid, are the mechanisms most likely to be responsible for the observed patterns. In principle, the crash in aphid population could be due to other factors such as the arrival of predators attracted by high aphid density [66] or the possible reduction of the phloem nutritional value due to plant ageing [6]. However, if the aphid population drop were driven by density-dependent mechanisms, one would probably expect to observe fluctuations in the aphid population rather than a constant decline [67]. Moreover, in previous modelling works, it has been shown that observed population trends in different aphid species could be reproduced by considering a per capita death rate positively related to the aphid cumulative population size [68–70]. Such a relationship coherently emerges as a property of our model if the pest presence induces the plant to produce defences that accumulate, and not if the phloem nutritional value declines throughout the season, independently from aphid presence.

Performing experiments to find correct numerical values for parameters of biological models is virtually impossible because many parameters cannot be directly measured. For this reason, we were forced to numerically calibrate nine parameters via our likelihood-based model fitting procedure. However, biologically plausible parameter estimates and good fitting do not guarantee that parameter estimates are correct, because of possible correlations among the parameters [71] and model identifiability problems that can arise from an imbalance between model complexity and available data [72]. The proposed modelling framework would therefore benefit enormously from experimental works dedicated to the measurement, or at least a sound assessment, of some model parameters. Despite the importance of the parameter q in Thornley’s models, we found no studies on its assessment. Similarly, although it is well known that a plant can divert resources from growth to defence [73], we found no quantitative relationships relevant to the cost of making defences (parameter α in our model) in terms of growth loss, nor between the presence of defences and pest performances. Our exercise provides a preliminary assessment of these parameters that needs to be confirmed or confuted by dedicated field and/or laboratory works.

4.2. The role played by fertilization and irrigation

Variations in plant growth, and in the concentrations of C and N substrates in plant tissues, for different levels of fertilization and/or irrigation are well acknowledged [56,74] and they have already been shown to be emerging properties of the original model for plant growth used in this work [31]. Our pest–plant model maintains these properties (figure 4a–f) and allows further insights regarding the variations observed in an aphid population. The aphid population response to fertilization and irrigation has been explored in a number of empirical works not providing a straightforward picture. Some authors observed no effect of fertilization in the wheat–Russian wheat aphid system [75], or negative effects of irrigation in the apple–rosy apple aphid and in the cotton–cotton aphid systems, respectively [76,77]. Other authors observed the highest aphid abundance at an average level of fertilization, and no effect of irrigation, in the chrysanthemum–cotton aphid system [78]. The intrinsic rate of oat aphid population increase in three grass species was observed to be favoured by irrigation in [79]. On the other hand, aphid population was observed to be maximal for moderate water stress in the cabbage–green aphid and cabbage–cabbage aphid systems [17], and in one out of three genotypes tested for the poplar–woolly poplar aphid system [80]. Our model, parametrized for the peach–green aphid system, shows that all this apparently contrasting empirical evidence can emerge from the same biological principles governing plant–pest dynamics and that both plant vigour and plant stress hypotheses can find support when observing a plant–pest system evolving in time and subject to different levels of changes in the environmental conditions. The aphid population dynamics reproduced by our model (figure 5) indicate that the effect of fertilization and irrigation on the pest population cannot be simply reduced to positive or negative. In fact, its sign and strength depends on the considered levels of fertilization/irrigation and on the date of observation along the growing season. The contribution of our work is to show how a new synthesis of the experimental data can emerge by using mechanistic modelling. The challenge for our future work is to show how this insight—as well as the model developed here—can be used to inform practical decision making by farmers and growers.

Data accessibility

Datasets for this research are included in Rousselin et al. [9] and are reported in the electronic supplementary material.

Authors' contributions

D.B. conceived the study. D.B. and M.Z. designed and implemented the study. All three authors discussed the results and their implications throughout the study, and wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

The fieldwork to create the dataset used in this work was funded by the ARIMNET (ANR-12-AGR-0001) ‘APMed’ project (Apple and Peach in Mediterranean orchards) and the ‘RegPuc’ project (Quelles stratègies d’irrigation et de fertilisation pour règuler les populations de pucerons verts en vergers de pêcher). The PhD grant to M.Z. is funded by the PACA (Provence-Alpes-Côtes d’Azur) region and INRAE Agroècosistèmes department.