Chiral Spin Spirals at the Surface of the van der Waals Ferromagnet Fe₃GeTe₂

Abstract

Topologically protected magnetic structures provide a robust platform for low power consumption devices for computation and data storage. Examples of these structures are skyrmions, chiral domain walls, and spin spirals. Here, we use scanning electron microscopy with polarization analysis to unveil the presence of chiral counterclockwise Néel spin spirals at the surface of a bulk van der Waals ferromagnet Fe₃GeTe₂ (FGT) at zero magnetic field. These Néel spin spirals survive up to FGT’s Curie temperature of T_C = 220 K, with little change in the periodicity p = 300 nm of the spin spiral throughout the studied temperature range. The formation of a spin spiral showing counterclockwise rotation strongly suggests the presence of a positive Dzyaloshinskii–Moriya interaction in FGT, which provides the first steps towards the understanding of the magnetic structure of FGT. Our results additionally pave the way for chiral magnetism in van der Waals materials and their heterostructures.

Magnetism in layered systems has proven to be a fertile ground for emergent magnetic phenomena. The absence of inversion symmetry combined with large spin-orbit coupling in some of these structures can give rise to an asymmetric exchange interaction known as the Dzyaloshinskii–Moriya interaction (DMI).¹⁻⁴ Systems with a large DMI offer a huge playground for the exploration of topologically protected magnetic structures such as skyrmions and chiral domain walls, which have dimensions in the order of tens of nanometers and are promising elements for low-power consumption electronics.^3,5 Long-range non-collinear magnetic structures can also arise in materials with large DMI, where the magnetization continuously varies in the material in a sinusoidal fashion.^1,3,6,7 These structures, named spin spirals, carry important information on the magnetic properties of the system through their periodicity and handedness. Moreover, spin spirals have been shown to evolve into skyrmions in the presence of a sufficiently large magnetic field for various material systems.^3,8,9

The recent discovery of magnetic ordering in van der Waals (vdW) materials down to the monolayer limit^10,11 has opened a new direction in the field of two-dimensional materials, allowing researchers to explore magnetism in lower dimensions in simple crystal systems.¹²⁻¹⁵ Particularly, the metallic vdW ferromagnet Fe₃GeTe₂ (FGT) shows large out-of-plane magnetic anisotropy and high Curie temperature (T_C = 220 K),^16,17 which can be pushed above room temperature upon doping¹⁸ or patterning.¹⁹ The large out-of-plane magnetic anisotropy of FGT indicates a high spin-orbit coupling and opens the possibility to form interesting magnetic textures, such as skyrmions or spin spirals. These magnetic textures in vdW magnets are still largely unexplored and are currently a topic to which significant research efforts are devoted.²⁰⁻²³ Unveiling these spin structures in two-dimensions can give a significant push towards a deeper understanding of magnetism in lower dimensions, along with the prospect of using vdW magnets for future applications.

In this Letter, we image the magnetic texture at the surface of FGT to identify the underlying interactions. We reveal the presence of a spin spiral rotating out-of-plane in a counterclockwise fashion by scanning electron microscopy with polarization analysis (SEMPA).²⁴⁻²⁶ The stabilization of these magnetic textures indicates that a positive DMI is present in FGT. Additionally, from temperature-dependent measurements we find that the periodicity of the magnetization textures remains constant in the studied temperature range from 60 K up to T_C, even though a large temperature-dependent anisotropy is reported for these systems.²⁷ These observations allow for a further understanding of the FGT magnetic structure, paving the way for chiral magnetism using vdW materials.

Our samples are obtained by mechanical exfoliation of a bulk FGT crystals (HQ Graphene) on a Si wafer. The sample preparation was performed in high vacuum, with pressures lower than 10^–7 mbar to avoid oxidation of the exfoliated FGT crystals. A dusting layer of Co (0.3 nm) was deposited using sputtering deposition, and the samples were then loaded into the SEMPA microscope chamber while keeping the sample in ultra-high vacuum (2 × 10^–10 mbar). The Co dusting layer was found to enhance the SEMPA signal while maintaining the same magnetic pattern as in pristine flakes,^28,29 and this is discussed in more detail in the Supporting Information Section SII. An Atomic Force Microscopy scan of the flake can be found in the Supporting Information SI.

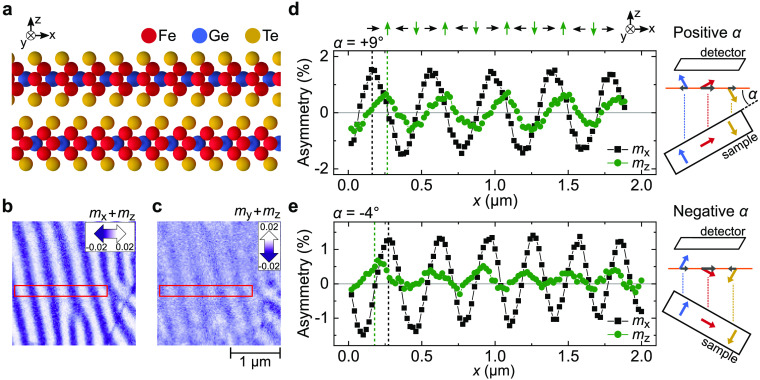
A side view of the crystal structure of FGT is schematically depicted in Figure 1a. The individual FGT layers are arranged in an AB stacking sequence, where each layer is rotated by 180° around the out-of-plane (z-) axis with respect to the adjacent layers. FGT has a space symmetry group P6₃/mmc, with the inversion symmetry point located in the space between the layers.¹⁶ The magnetic properties of FGT become apparent when the sample is cooled below T_C = 220 K, and a perpendicular magnetic anisotropy along the z-axis is found.^16,17

Figure 1.

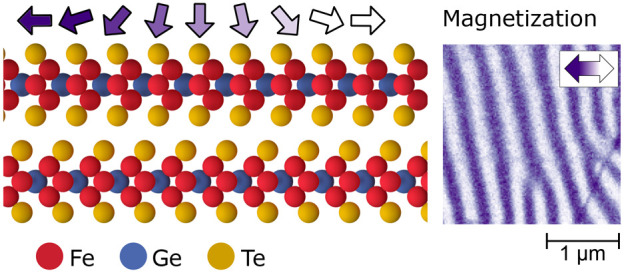
Spin spirals at the surface of a d = 185 nm thick FGT flake at T = 150 K. (a) Crystal structure of two FGT layers. (b, c) SEMPA images measured at the surface of FGT for α = +9°. Panel (b) shows m_x contrast and panel (c) m_y for the exact same area, with the color scale (in arbitrary units) indicated by the arrows in the top right-hand corner. Additionally, in both SEMPA images an out-of-plane magnetization m_z can be present, which is adjustable in panel (c) only. (d, e) Averaged magnetization profiles obtained from SEMPA measurements for the same area. In black and green we depict the average magnetization profile in the red rectangle of panels (b) and (c), respectively. The sample tilt, illustrated on the right, was α = +9° in panel (d) and α = −4° in panel (e). The phase shift reverses from +π/2 in panel (d) to −π/2 in panel (e), which is expected for a m_z magnetization contrast in the SEMPA image in panel (c). Overall, we observe a counterclockwise rotating Néel spin spiral as is indicated schematically by the arrows above panel (d).

We use SEMPA to obtain vectorial information on the surface magnetization of FGT.²⁴⁻²⁶ In SEMPA, the detector for the secondary electrons in a regular scanning electron microscope is modified to provide spin sensitivity. This is done by accelerating spin-polarized secondary electrons, emitted by the sample, towards a W(100) target. Depending on the spin polarization direction, the secondary electrons are scattered from the target to different diffraction spots. The difference in intensities between these diffraction spots provides a quantitative measurement of the in-plane spin polarization of the secondary electrons coming from the sample. The lateral spatial resolution of our system is about 30 nm,^30,31 and due to the high surface sensitivity of SEMPA, we probe only the magnetic texture of the top FGT layer (see the Supporting Information SI SI for a schematic setup).²⁶Figure 1b and c show SEMPA images of the surface of a d = 185 nm thick FGT flake (flake A) at T = 150 K. Both images are measured simultaneously and probe the exact same area of the flake. Figure 1b shows magnetization contrast in the x-direction (m_x), where a dark (light) purple contrast indicates a magnetization pointing towards the left (right), as is indicated by the arrow in the top right-hand corner. The m_y contrast is shown in Figure 1c. A strong magnetization contrast is present in Figure 1b, and a vertical stripe-like pattern is observed, revealing an alternating in-plane magnetization from left to right. Only a slight magnetization contrast is observed in Figure 1c, but a similar vertical stripe-like pattern is present.

Even though SEMPA is in principle sensitive only to the in-plane magnetization component, we are able to detect the out-of-plane direction through a projection technique.²⁹ Here, we tilt the sample by an angle α with respect to the measurement axis of the detector, as is schematically depicted on the right side of Figure 1d and e. It results in an adjustable mixing of the out-of-plane magnetization m_z component in the m_y channel. As we will demonstrate later on, the main component in the m_y SEMPA image is given by the out-of-plane m_z contrast. We note that a contribution from m_z can also be added to the m_x signal by an accidental tilt from the sample mount in that direction. However, we expect this contribution to be small as discussed in SI Section SII.

The spatial variation of the magnetization on the surface of FGT can be better quantified by averaging the signal along the vertical direction in the region highlighted by the red rectangles in Figure 1b and c. The averaged signals for Figure 1b and c are shown in black and green in Figure 1d, respectively, where a positive tilting angle of α = +9 was used. Here, the magnetization contrast, or asymmetry, is plotted as a function of position where a positive asymmetry corresponds to the light purple coloring in the SEMPA images. A sinusoidal variation in the magnetization contrast is clearly observed in both data sets with the same periodicity but different amplitudes. The absence of plateaus in the line traces demonstrates the presence of a spin spiral at the surface of FGT, rather than a domain pattern. Moreover, we find that the two data sets are phase shifted by +π/2, indicating a continuous spatial change in the magnetization direction.

The higher amplitude for the m_x signal is expected if the signal in the m_y detector measures only a projection of the out-of-plane magnetization. We confirm this by disentangling the in-plane (m_y) and out-of-plane (m_z) magnetic component in the SEMPA image shown in Figure 1c by performing sample-tilt-controlled experiments. When we vary α from positive to negative values, the projection of the m_z signal changes sign, whereas the m_x and m_y magnetization remains (approximately) constant. This is schematically illustrated in the insets on the right side of Figure 1d and e. We expect to find the same behavior for the phase shift; upon a sign change of α the phase shift reverses (from +π/2 to −π/2) if the magnetization contrast is out-of-plane (m_z), and it remains constant if the magnetization contrast is in-plane (m_y). In Figure 1e we show the magnetization profile for the same region as in Figure 1d, but with a negative tilt angle of α = −4°. We clearly observe that the black and green data sets are now phase shifted by −π/2, which indicates that the signal in Figure 1c primarily consists of m_z contrast. Moreover, for α = 0° the out-of-plane contrast vanishes as can be seen in SI Section SIII. When we combine the magnetization profiles of Figure 1d (and e), we are able to reconstruct the magnetic texture in the top layer of our FGT flake. This is depicted schematically by the arrows on top of Figure 1d and illustrates a magnetization that continuously rotates in the xz-plane. The reconstruction therefore reveals the presence of a counterclockwise rotating Néel spin spiral with a period of p = 407 nm on the surface of FGT, which is rather surprising as will be explained below.

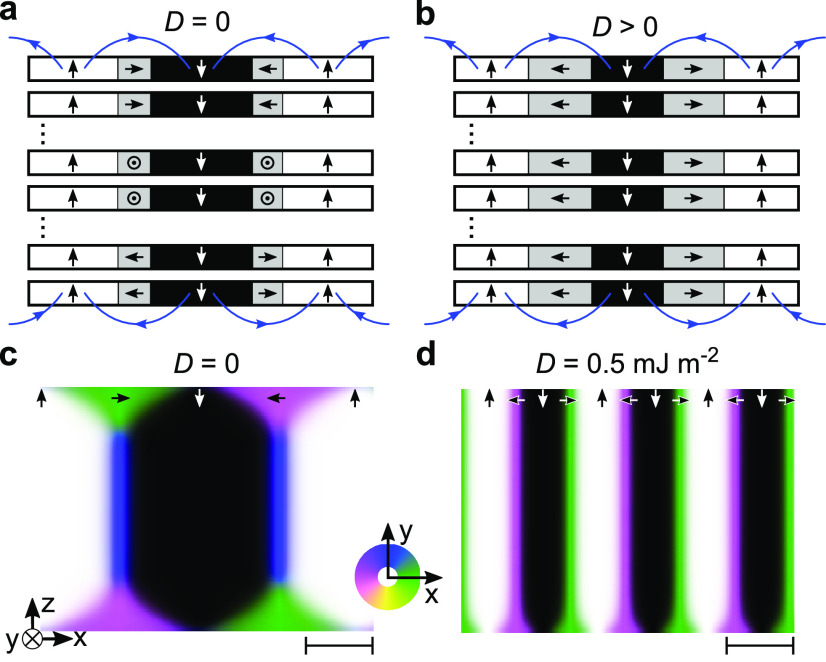
In the following we take a closer look at the interactions at play in FGT to understand in more detail why the formation of the counterclockwise spin spiral is peculiar and in addition indicates the presence of a positive DMI. FGT is known to exhibit a strong ferromagnetic exchange stiffness¹⁶ and a strong (temperature-dependent) perpendicular magnetic anisotropy.²⁷ In Figure 2a we schematically depict the expected magnetic texture when including these interactions without a DMI (D = 0), and it consists of magnetic domains separated by narrow domain walls. The out-of-plane magnetized domains are indicated in white and black for up and down domains, respectively, and the domains are aligned for each FGT layer due to the interlayer exchange interaction and dipolar stray fields (blue arrows). In grey we indicate the domain walls, where the magnetization rotates in-plane. As depicted in Figure 2a, the magnetization in the domain walls aligns with the direction given by the dipolar fields, which results in the formation of a clockwise rotating Néel wall in the top FGT layer, a Bloch wall in intermediate FGT layers, and a counterclockwise Néel wall in the bottom FGT layer. This is analogous to the spin textures found in cobalt-based magnetic multilayers without a DMI.^30,32 Therefore, in case dipolar fields are the dominant interaction, we would expect to measure a clockwise rotating spin texture with SEMPA, since the surface sensitivity of the SEMPA probes only the top FGT layer (highlighted in red).

Figure 2.

(a, b) Schematic representation of the magnetic texture in FGT, showing a side view of six FGT layers. The white and black area correspond to up and down magnetized domains, and the grey areas correspond to an in-plane magnetization, with the arrows denoting the direction. The blue arrows indicate the dipolar fields. With SEMPA only the top layer of FGT is imaged. In panel (a) the DMI is zero and the magnetization in the domain walls aligns with the dipolar fields, resulting in clockwise Néel domain wall in the top layer, Bloch walls in intermediate layers, and a counterclockwise Néel wall in the bottom FGT layer. In panel (b) the DMI is positive in each layer and large compared to the dipolar fields. The magnetic texture consists of an out-of-plane rotating spin spiral in a counterclockwise direction throughout all FGT layers. (c, d) Side view of micromagnetic simulation results for 128 layers of FGT and K = 40 kJ m^–3. The in-plane magnetization direction is indicated by the color wheel in the xy-plane. In (c) D = 0 and in (d) D = 0.5 mJ m^–2, and for the top FGT layer a clockwise and counterclockwise rotating spin texture is found, respectively. The scale bars on the lower right hand side indicate 25 nm.

The discrepancy between the measured counterclockwise spin spiral discussed in Figure 1 and the predicted clockwise rotation of the magnetization for dipolar dominated systems (Figure 2a) for the top FGT layer indicates that additional interactions need to be considered.

As mentioned earlier, a known interaction to influence the chirality of the magnetization is the DMI, which we propose to be present in FGT alongside recently published studies.²⁰⁻²² From our SEMPA measurements alone we cannot conclude if the DMI originates from the FGT/Co interface or if it is a bulk property of FGT. Considering a DMI to be present only at the FGT/Co interface, all intermediate FGT layers should have a Bloch texture due to the dipolar fields, as is schematically indicated in Figure 2a. However, this contradicts the results of recently published Lorentz TransmissionElectronMicroscopy studies,²⁰⁻²² where Néel domain walls in 60 nm thick FGT samples throughout all FGT layers are measured. Here, we provide direct evidence on the specific rotation of the Néel walls which could not be determined earlier, resolving the sign of the DMI term to be positive. The supporting evidence of the LTEM measurements and the findings in this work therefore indicate the presence of a bulk DMI in FGT with a positive sign, as it imposes the counterclockwise rotation of the magnetic spin texture, which is schematically depicted in Figure 2b.

We verify the validity of the schematic images depicted in Figure 2a and b with micromagnetic MuMax³ simulations.³³ A side view of the simulation results are depicted in Figure 2c and d for K = 40 kJ m^–3, and other simulation details are specified in SI Section V. In Figure 2c, D = 0 and the up and down domains are separated by domain walls with a varying width across the FGT thickness. The in-plane magnetization direction is indicated by the color wheel depicted in the lower right-hand corner. At the surface of FGT (highlighted by the red border) a clockwise rotating spin texture is found. In Figure 2d, on the other hand, D = 0.5 mJ m^–2 in each FGT layer and a counterclockwise Néel spin spiral in all magnetic layers is obtained.

A lower bound of the DMI D_thres can be calculated from the transformation of the domain wall textures observed in Figure 2. From Figure 2c we find that the majority of the domain walls consists of a Bloch wall texture (indicated in blue), and upon increasing the DMI a counterclockwise Néel texture is stabilized for each layer in Figure 2d. Following ref (34), the threshold DMI value for this system is then given by

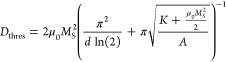1

with M_S the saturation magnetization, d the thickness of the flake, A the exchange stiffness, and K the anisotropy, which is strongly temperature dependent for FGT. Reported values for the anisotropy range from K = 1.5 MJ m^–3 for bulk FGT at 5 K¹⁶ to K = 0.23 MJ m^–3 for 10 nm FGT flakes at 120 K.²⁷ This results in a lower bound for the DMI term of D > 0.09–0.2 mJ m^–2, respectively, using M_S = 0.38 MA m^–1 and A = 1 pJ m^–1 as reported in ref (16).

So far, the presented data indicate the presence of a positive DMI in FGT, but the exact origin of this DMI remains elusive. The inversion symmetry of FGT, as shown in Figure 1a, in principle suggests an absence of a net DMI. However, the local inversion symmetry breaking in a single FGT layer combined with a low interlayer coupling between the layers could give rise to a measurable DMI term.^35,36 As of the writing of the article a first theoretical study investigated the origin of DMI in FGT.³⁷ In future work changes in the DMI strength as a function of layer thickness and Fe composition of FGT could be experimentally investigated by, for example, mapping the thickness-dependent handedness of the Néel walls by X-ray techniques, e.g., circular dichroism X-ray resonance magnetic scattering, CD-XRMS.

At this point we would like to note that besides the counterclockwise rotating Néel spin spiral an additional spin texture is simultaneously present in the experiments, where the magnetization rotates mainly in the xy-plane. The SEMPA measurements are depicted in SI Section SIV, and both a clockwise and counterclockwise rotation of this spin texture is observed. We suspect that local fluctuations in strain or Fe atom concentration deficiency caused variations in the magnetic parameters (e.g. magnetic anisotropy and DMI), allowing both the out-of-plane and in-plane spin textures to stabilize.^38,39 A qualitative agreement between micromagnetic simulations including a positive DMI and these SEMPA measurements is found and discussed in SI Section SV.

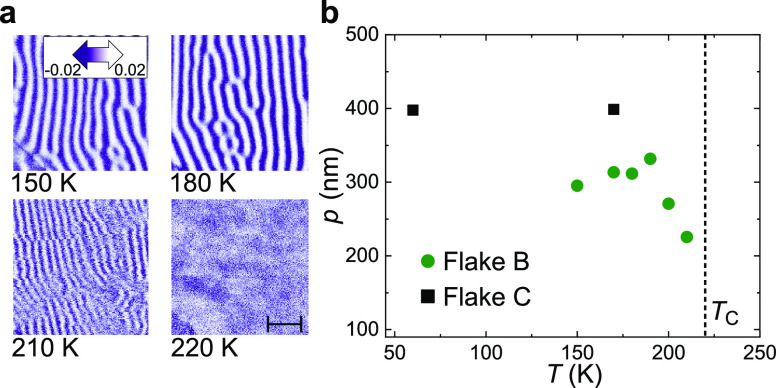
Finally, we turn our attention to the temperature dependence of the magnetic texture. Figure 3a shows m_x SEMPA images for the same area on a different flake (flake B) at various temperatures. A similar magnetization pattern to the one discussed previously is observed for temperatures below the Curie-temperature of FGT (e.g., T = 150 and 180 K). The periodicity of the spin texture is almost independent of temperature in this range and shows a period (p) of approximately 300 nm for Flake B, which is plotted in Figure 3b. Upon increasing the temperature towards T_C the period of the magnetization rapidly decreases, showing a period of approximately 225 nm at T = 210 K, where fluctuations in the magnetization pattern are also observed due to the local heating induced by the electron beam. Above 220 K the Curie-temperature is reached (indicated by the dashed line) and the magnetic contrast completely vanishes. A different FGT flake (flake C) was also investigated using a larger temperature range by cooling the setup with liquid helium. We find that for flake C the period of the magnetic texture (here p ≈ 400 nm) also remains constant when varying the temperature from 60 to 170 K.

Figure 3.

Temperature dependence of the magnetic texture on the surface of FGT. (a) SEMPA images showing the m_x contrast for T = 150, 180, 210, and 220 K on flake B. The in-plane magnetization direction is indicated by the arrow in the top left-hand image. The scale bar in the bottom right-hand image indicates 1 μm and holds for all images. (b) The period of the magnetization in m_x is plotted as a function of temperature for flakes B and C, and T_C is indicated by the dashed line.

The periodicity of the magnetic texture is determined by the interplay between the micromagnetic parameters, e.g., exchange, anisotropy, and DMI, and the dipolar interactions. Although the anisotropy shows a strong temperature dependence in FGT for thin samples²⁷ and for thicker flakes of similar van der Waals materials, e.g., Cr₂Ge₂Te₆,⁴⁰ a change in the periodicity of the magnetic texture is expected only if this change is significant compared to other interactions. In our samples, due to the thickness (>60 nm) of the FGT layers, the dipolar interactions are dominant¹⁹ and the anisotropy contribution is therefore small compared to other interactions. Future works could explore a temperature-dependent study of the domain size in thinner FGT samples, providing insights on the temperature dependence of magnetic parameters, such as the DMI.

In summary, we have investigated the magnetic texture in the top layer of FGT using SEMPA. Our measurements revealed the presence of out-of-plane spin spirals rotating in a counterclockwise fashion, which indicates the presence of a positive DMI in FGT, although the origin of the DMI remains elusive, with a possible explanation being a local inversion symmetry breaking in single FGT layers. We find the spin spiral pattern to be nearly temperature independent, indicating that the magnetic structure is not dominated by the anisotropy in these thicker FGT flakes. Our work provides an important starting point for the use of (bulk) magnetic van der Waals materials for chiral magnetism. We note that the value for the DMI estimated here for bulk FGT could possibly be further increased by enhancing the spin-orbit interaction through proximity effects from other vdW materials,⁴¹ similarly to what is done in sputtered thin metallic layers such as Pt/Co systems. The demonstration of chiral magnetic structures at the surface of bulk vdW materials is a crucial step towards more complicated vdW heterostructures with engineered magnetic properties.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c03111.

• SI is for a schematic setup of the SEMPA and additional SEM and AFM images, SII discusses the magnetic contrast in SEMPA images, SIII shows additional α-dependent measurements, and SIV shows the in-plane spin spiral and SV the micromagnetic simulations (PDF).

Author Contributions

M.J.M. and M.H.D.G. conceived the idea and initiated the project. M.J.M. prepared the samples and performed the experiments and data analysis with M.H.D.G.’s assistance. M.J.M. performed the micromagnetic simulations with assistance from J.L., R.A.D., H.J.M.S., B.K., and R.L., and M.H.D.G. supervised the project. M.J.M. wrote the manuscript with assistance from M.H.D.G. All authors commented on the final version of the manuscript.

The authors declare no competing financial interest.