Performance Budget Planning: The Case of a Research University

Abstract

We describe a performance budget planning model developed for a research university, comprised of a set of 88 key variables and 38 non-linear structural equations that describe interactions among them. These equations, based on the knowledge of research university’s financial working and theoretical considerations, relate expenditures and revenues to teaching and research operations. We demonstrate the value of this model for developing insight into the financial structure of the university. In particular, we show how the model aids in (1) comparing the effect of various policy alternatives on the performance of the university, (2) performing comparative statics analysis of any subset of variables of interest, (3) choice of policy variables and policy alternatives, and (4) gaining insight into the structure of the interactions for a given policy alternative in terms of the causal chain between policy variables and outcome variables. We also describe a computer implementation of the model and discuss a class of mathematical tools for policy planning analysis that facilitate the use and manipulation of models based on sets of nonlinear constraints.

1 Introduction

The causal ordering algorithm, as described by Herb Simon in his seminal 1953 paper [3], has numerous applications in areas such as engineering, finance, causal discovery, or artificial intelligence. In this paper, we describe one such application proposed by Herb himself in early 1990s. Herb felt that a lot of the contentious discussions around university budgets were not sufficiently informed by structural constraints, which he expressed in his 1967 paper on the challenges facing a college president [4]. The work on capturing the financial constrains facing the job of a university president started during Kalagnanam’s post-doc at CMU, where he worked with Herb on a “structural model of the university budget” to help in his role as an advisor to the university president. The idea was that this would make explicit the actual policy levers and how different budget decisions would impact outcomes, especially with respect to the goals of the university, such as maintaining a given faculty/student ratio. This was an excellent experience from the perspective of (i) being able to observe an administrative and management aspect of faculty (especially that of academic deans), (ii) actually informing ensuing discussions by means of analysis using models coded in Mathematica that highlighted the impact of various scenarios on university policy parameters, and (iii) being able to observe the respect that Herb’s knowledge and intuition commanded from Carnegie Mellon’s deans and presidents. It was around 1992 that the idea and the first draft of this paper came to being. Druzdzel joined Simon and Kalagnanam in mid-1990s, embedding the model in a decision support system that allowed for visualizing the model’s causal structure and how it changed as a function of different choice of policy variables. The model was at some point adopted by the Office for Planning and Budget at Carnegie Mellon University but this is the first time that we are presenting it before a wider audience.

Universities are like most economic units concerned with production, finance, and marketing [4]. Even though the product of a university is knowledge and skill, something that may seem unusual when compared to the products of a steel mill or an automobile manufacturer, university management faces the same responsibilities, challenges, and economic constraints. The president of a university, similarly to the executives of business, industry, or government, is subject to the pecuniary calculus required to justify its claims on societal resources. The functions of a university president (or of any other executive) involve raising money, performance budget planning, and developing a suitable university environment to achieve its goal. In this paper, we focus our attention on the specific function of budget planning which involves managing the cash flows encountered in the administration of a university. A budget is concerned with where dollars come from and what they are used for and can be thought of as a plan of action that is expressed in dollar terms. However, a budget that is expressed as a list of salaries and miscellaneous expenses is not very useful for managing a university. The university president requires a performance budget described in terms of key variables that relate the expenditures and revenues to the operations.

The performance budget planning model presented in this paper consists of structural equations capturing individual mechanisms acting in the system, which, as shown by Simon [3], capture causal information that is explicated when these equations are embedded in a model. The model allows for deriving the causal structure among its variables once a choice has been made of the policy drivers. It supports both structural and numerical analysis that directly aids key tasks within the domain of strategic budget planning. We examine a key policy question that seems to repeatedly appear in university discussions: Does teaching subsidize research or is it the other way round? With the use of the performance budget model, we make explicit the key variables that are relevant to answering such questions and provide a concrete basis for informing such (often contentious) discussions.

The remainder of this paper is divided into two major parts. Section 2 describes the performance budget model, along with its structure, variables, and equations, and Section 3 illustrates various ways in which the model can be used in exploring policy alternatives. We show how the model supports the choice of policy variables, evaluation of policy options, comparative statics, and structural analysis. Finally, Section 4 discusses the implications of this work for strategic policy planning and for the design of strategic decision support systems.

2 The Performance Budget Model

2.1 Model Structure

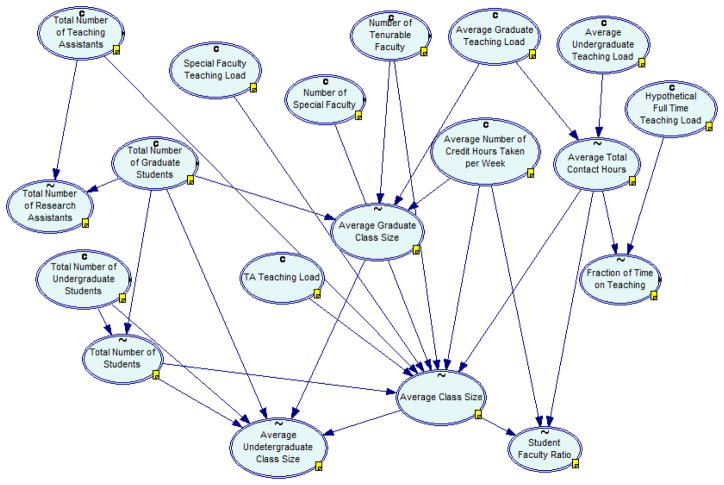
The Performance Budget Model (PBM) consists of 88 variables describing key university budget elements such as the number of faculty, the number of students, class size, teaching loads, student-faculty ratio, tuition amounts, instructional and research expenditures, direct and indirect research costs, and space costs. These variables are divided into seven submodels: Teaching Operations, Teaching Expenditures, Research Expenditures, Income, Space Cost, Total Expense, and Surplus (see Figure 1). Each of these contains variables capturing the submodel’s essential quantities (see Figure 2 for the details of the Teaching Expenditures submodel). We account separately in PBM for research units (ru) and academic units (au), since the research units are relatively independent of the academic funds and the research staff is separate from faculty. The current model represents aggregate, university level relationships. It does not capture inter-college effects such as increasing enrollment in one college while decreasing it in another. The model does not address curriculum or program issues and also excludes such issues as administrative staffing and auxiliary units.

Fig. 1.

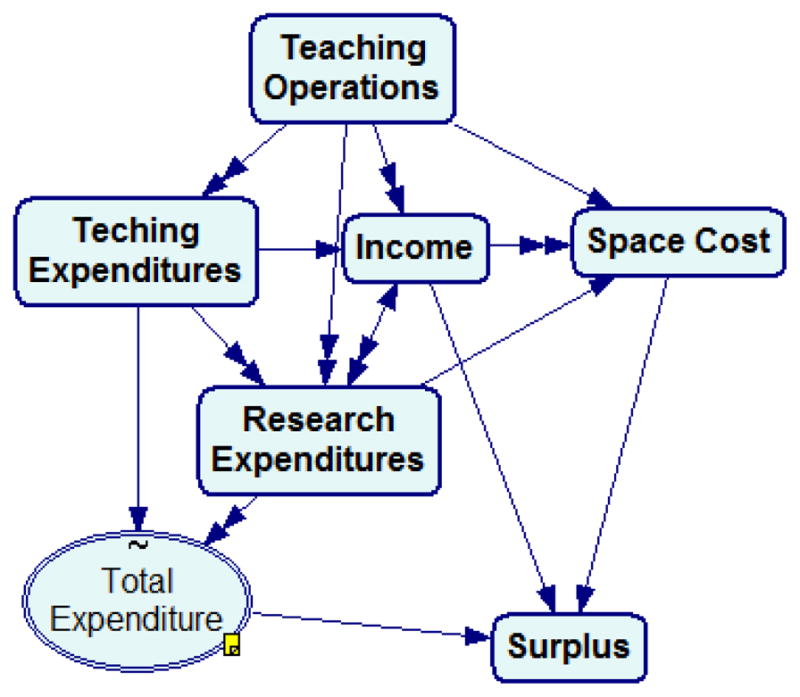
The structure of submodels in the Performance Budget Model.

Fig. 2.

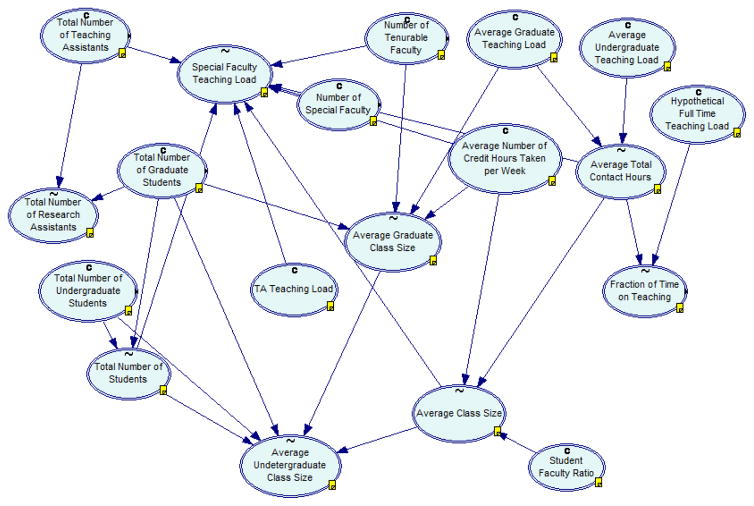
Details of the Teaching Operations submodel.

Interactions between PBM variables are described by 38 non-linear algebraic equations, each of which represents an independent financial mechanism acting in the university environment. The following equation, for example, describes the interaction between class size (clsze), the number of students (stud), their average weekly credit hour load (credhrs), the number of tenurable faculty, teaching assistants, and special faculty (facten, tasst, and facspec), and their corresponding average weekly teaching loads (tloadten, tloadasst, and tloadsp).

$$\mathit{clsze}=\frac{\mathit{stud}\times \mathit{credhrs}}{\mathit{facten}\times \mathit{tloadten}+\mathit{tasst}\times \mathit{tloadasst}+\mathit{facspec}\times \mathit{tloadsp}}$$

This equation is listed as Equation 4 in Appendix along with 37 other equations and their brief descriptions.

The 38 equations form basic constraints on the system. Providing values for any 50 of the 88 variables allows for deriving the values of the remaining 38 variables, provided that the resulting system of equations has a solution. These 38 variables are the system’s dependent variables. The 50 independent variables, whose values are specified a-priori, are of two types: (1) policy variables that are readily controlled by the university administration, such as the number of tenure track faculty or their teaching load, and (2) variables that are determined externally, outside the control of university’s decision makers, such as federal overhead rates or average grant research income per faculty member. The distinction between independent and dependent variables is not permanently fixed. It is under user’s control which variables are independent and what their values should be: PBM permits interchange between independent and dependent variables provided that the consistency of the equations is maintained. By changing the set of independent variables and/or changing their values, one can examine the consequences both of policy changes and changes in the University’s environment. Once we have chosen a set of independent variables, the causal ordering algorithm derives the graphical structure of the model and determines how the model variables depend on the independent variables.

2.2 Parameter Estimation and Validation

The equations of PBM describe the budget structure of a research-oriented university and with some minor modifications should be applicable to most academic institutions. The first step in applying PBM at Carnegie Mellon University consisted of estimating the values of independent variables. Many of these, but not all of them, were obtained directly from the university’s financial records and records of student enrollment. Others were based on special reports on university operations prepared by the Carnegie Mellon University’s Office of Planning and Budget. The numbers underlying all pictures included in this paper were derived from the 1989/1990 financial reports, although they have been randomly distorted to preserve the confidentiality of the university’s financial data. Hence, they only serve an illustrative purpose.

PBM equipped with the values of 50 exogenous variables predicted the 1990/1991 performance statistics with a reasonable accuracy (all values for the base case as predicted by PBM were within a few percent of the true values), giving some assurance that PBM is within the ballpark of reality. The staff of Carnegie Mellon University’s Office of Planning and Budget has amended PBM with the data for later fiscal years obtaining similarly precise output. What we consider a small error, say $200K error in surplus on a total budget of $100M, worried some of the staff used to administrative accounting procedures. We should stress that PBM is not designed for use in accounting, but rather for long-term analysis of university policies. It is not intended to predict the specific figures associated with the university budget, but rather to illustrate the magnitude and direction of change in output variables given changes in policy variables. Hence high accuracy of the parameters and the mode outcomes is not essential. This could be achieved at the expense of model simplicity.

This modeling approach stands in contrast with more conventional approaches that use regression analysis to estimate functional relation for each structural equation. The data required for such modeling is seldom available, and the nonlinearity of most of the equations greatly increases its complexity. In contrast, our approach provides a way of validating PBM by examining it’s gross behavior against actual accounting data and data from special studies over a number of years.

3 Strategic Planning Analysis

The discussion in this section is organized around illustrative questions posed in the context of university operations. We provide selected graphical outputs of our system along with a brief discussion of the insight that resulted from them. Since this section is aimed at illustrating the usefulness of such modeling approaches to strategic planning and the facilitating role of computer support systems towards this end, we have removed the details of PBM to Appendix in order to keep our discussion focussed on illustrating the support system. To help the reader in identifying the variables referred to in this section in the equations listed in Appendix, we report the variable names in parentheses.

3.1 Policy Analysis

The first example consists of evaluating how changes in a typical policy (independent) variable affect the magnitude of a goal (dependent) variable. In university operations, teaching generates certain revenues (tuition) and requires various expenditures. The algebraic difference between these two quantities is the surplus (or, if the value turns out to be negative, deficit) from teaching operations. Similarly, research generates grant and contract revenues and requires expenditures and, hence, has its own surplus or deficit. Typically, a university has other sources of revenues (e.g., endowment income, annual gifts, etc.) that are used to finance teaching and research beyond what could be supported by the revenues generated directly from those activities. We may wish to determine, for our university, whether these other sources of revenue are being used mainly to support teaching, research, or both.

The question turns out not to have an easy answer. Who is supporting whom depends on how we allocate faculty salaries and other indirect costs associated with them. We propose the following framing of this problem. Let flload be a variable expressing the hypothetical full time teaching load, i.e., the number of hours that we would expect each faculty to teach if they were doing no research. flload is a purely hypothetical variable, since almost everyone in a research university is doing some research. Still, it is critical in determining who is subsidizing whom. After all, the main reason why a university decreases the teaching load from what one might expect in such a hypothetical situation, is to compensate for the time spent on research.

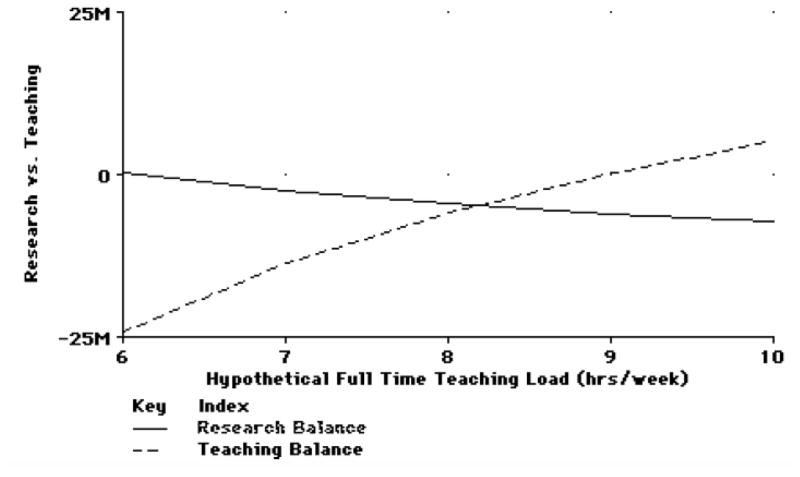
Suppose that the average actual teaching load of tenure-track faculty (tloadten) is 5 hours, while the postulated full-time load (flload) is 8 hours. Then 5/8 of faculty salaries will be charged to teaching, the rest to research. In Figure 3 below, the net surplus from research activities is the difference between research income (incres) and research expenditures (exptch). Correspondingly, the surplus from teaching is the difference between tuition income (inctuit) and expenditures for teaching (exptch). We plot the research surplus and the teaching surplus (actually both are negative over almost the entire domain of interest of possible full time teaching load, and, hence, should be rather called deficits) against the policy variable, flload.

Fig. 3.

Impact of flload on teaching and research surplus.

It is clear from the figure that for high values of the assumed full teaching load (say flload = 10 hours), tuition revenue covers instructional costs, while research has a deficit, presumably covered by other sources of income, such as gifts and endowments, of about $8M. On the other hand, for a lower teaching load (say flload = 6 hours), research has no deficit, while instruction has a deficit of $25M. For a hypothethical full teaching load of a little higher than 8 hours/week both teaching and research have an equal deficit of about four million dollars which is covered by other sources. Of course, these particular numbers depend on the values of other variables in PBM — salaries, tuition rate, sizes of faculty and student bodies, etc. These are, as we mentioned, not real Carnegie Mellon University’s data.

3.2 Comparative Statics

One of the intended uses of PBM is to examine how the values for certain dependent variables (e.g., the surplus or deficit of the university budget, the average class size, etc.) vary with changes in independent variables, the latter representing either environmental or policy variables. An enhancement in this analysis is studying how such relations change when another independent variable changes. Analyses that answer such questions are usually known in econometric literature as comparative statics.

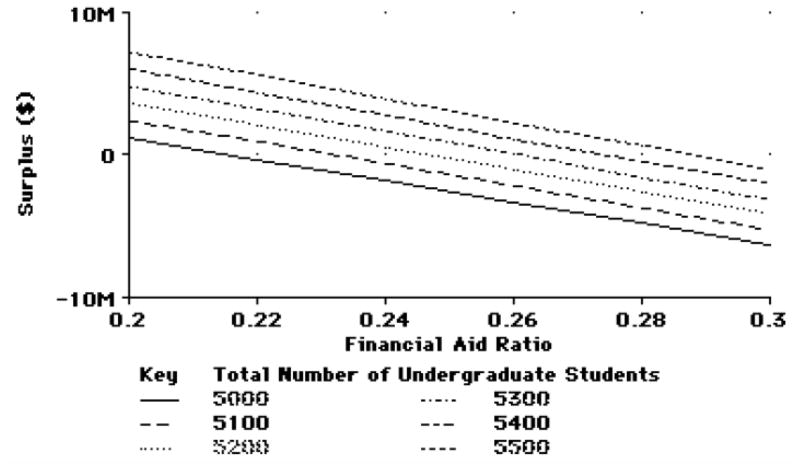
Our second policy example is based on comparative statics analysis and illustrates the dependence of an outcome variable on an independent (policy or environmental) variable changes with different values of a second independent variable. PBM allows the change in any dependent variable to be plotted as a function of another independent variable of interest. For example, Figure 4 measures on the y-axis how the university surplus (sur) decreases with increase in student aid (aid), expressed as the ratio of student aid to tuition income; showing along the x-axis the rate of this decrease for different sizes of the undergraduate student body (studu). The user can focus on a fragment of this graph and find out that increasing the student aid from 20% to 21% of tuition would cost about $650,000 with 5,000 students, but $700,000 with 5,400 students.

Fig. 4.

A comparative statics example: Surplus as a function of the ratio of student aid to tuition income (aid) and the size of the undergraduate student body (studu).

3.3 Changes in Structure

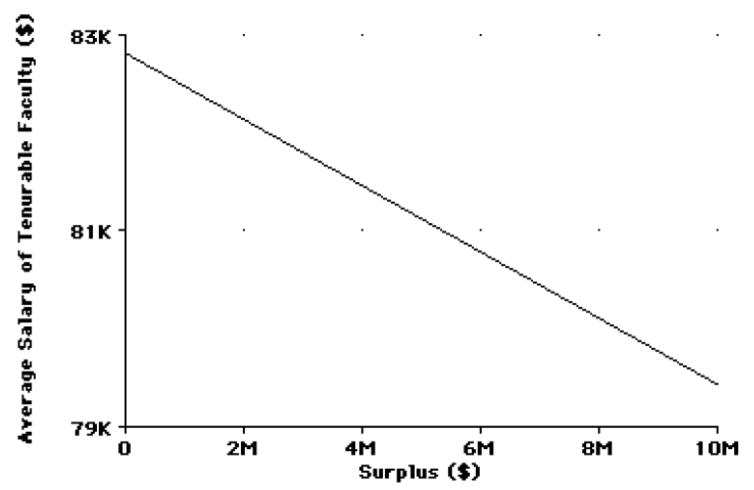
Most variables in a performance budget planning context are potential policy variables and the difference between policy variables, environmental constraints, and endogenous variables is to some degree a matter of choice. Section 2.1, for instance, cited average faculty salary as an example of an environmental constraint. This is the case, for example, when the university decides that its salaries will be competitive with those of a specified comparison group of universities or when strong faculty unions dictate the salary ranges. On the other hand, average salary could be taken as a policy variable and the average teaching load as a constraint (again, for example, determined by the “competition” for faculty or union negotiations). Alternatively, both these independent variables could be viewed as constraints. Similarly, a common concern is to keep the net surplus (sur) constrained within a certain range, possibly at the expense of salaries of tenurable faculty (salten), and examine how these would be affected at different levels of the surplus. In Figure 5 below, we plot how the salary of tenurable faculty (salten) need to be adjusted to keep the surplus (sur) at different values.

Fig. 5.

Tenurable faculty salary (salten) as a function of surplus (sur).

Decisions concerning which variables are the policy variables are known in econometrics as changes in structure. Changes in structure in a model amount to replacing one or more equations in the model by other equations. Please, note that an exogenously assigned value of a policy variable is an equation; for example, a policy decision to set the average salary of tenurable faculty to $60,000 is represented by an equation salten = 60000. Models that are based on structural equations support changes in structure directly in the sense that the solution of the system of equations after the replacement will be the predicted state of the system after the change in structure [2,1].

We believe that supporting changes in structure is essential for strategic planning systems and the user interface to such systems should make changes in structure easy and efficient. Often a policy maker confronted with a complex system does not know what actions should be taken to achieve a strategic goal — the set of policy variables and their optimal values may become clear only in the course of the analysis. Typical systems require the user to decide before-hand which variables are policy variables and which are intermediate or goal variables. A change in the set of policy variables has often to be followed by rebuilding the model, a process too cumbersome to be of exploratory nature. One of the strengths of our model is that it allows a simple switching between dependent and independent variables, provided the overall system remains consistent. The system then rebuilds the model by resolving functional references in the desired direction and draws the new model structure. Figures 1 and 2 show the causal ordering among the variables of PBM for the base-case choice of policy variables. Figure 6 shows the causal ordering within the teaching operations submodel when student/faculty ration (ratio) is made a policy variable and special faculty teaching load (tloadsp) a dependent variable.

Fig. 6. Teaching Operations.

submodel when student/faculty ration (ratio) is made a policy variable and special faculty teaching load (tloadsp) a dependent variable.

3.4 Structural Analysis

For a model to be influential in practice it very important that the user is able understand the results of the analysis performed by the support system. Insight into a model can be increased greatly by an explanation of the interactions among its components. When solving systems of nonlinear constraints, the explanations that are useful pertain to how information propagates from the independent variables to the dependent variables of interest. The interface to PBM shows this by means of directed graphs, examples of which have been given in Figures 1, 2, and 2. These directed graphs are retrieved from a system of simultaneous equations using the theory of causal ordering and an associated algorithm proposed by Simon [3]. We will give an illustrative example of how this is accomplished. Readers interested in the theory of causal ordering are directed to Herb original paper [3].

Consider Figure 3 which graphs the effect of the hypothetical full time teaching load (flload) on research and teaching balance. Although this clearly illustrates the effect flload on surplus, it is not clear as to how flload affects intermediate dependent variables, nor is it apparent as to which constraints are actively responsible the behavior shown in Figure 3. By using the theory of causal ordering we can identify the order in which dependent variables are solved. For example, for the set of independent variables assumed to produce Figure 3, the dependent variables are solved in the order shown in Table 1.

Table 1.

Causal ordering: solution order of the model for the set of independent variables producing Figure 3.

Causal Order	Complete Subsets of Variables	Complete Subsets of Equations
1	(stud), (rasst), (tloadten), (clszeg), (expresru), (inctuit), (space)	(1), (2), (3), (5), (15), (22), (29)
2	(clsze), (tchfrac), (capspace)	(4), (8), (30)
3	(clszeu), (ratio), (exptdir), (ot), (exprdirac), (or), (incresac)	(6), (7), (10), (11), (18), (19), (28)
4	(ovrhdtamt), (exptch), (exprdir), (expdoc), (incres)	(9), (12), (13), (21), (23)
5	(expres), (inc), (resdir), (costother), (costspace), (costda), (costga)	(20), (24), (25), (27), (31), (35), (36)
6	(expresac), (ovrhdramt), (resind), (spacebd), (spaceed), (spaceom), (exptot)	(14), (16), (26), (32), (33), (34), (37)
7	(ovrhdramtac), (sur)	(17), (38)

The variables of Order 3 are such that they can be determined once the variables of Order 1 and 2 are determined. In this sense, the variables of Order 3 are causally dependent on variables of Order 1 and 2. Note, however, that the dependencies of a specific variable of Order 3 is through the equations that it appears in and, hence, it does not necessarily depend on all variables of Order 1 or 2. The complete subsets of equations indicate those equations that can be explicitly solved for the variables that appear in them. For example, Equation 6 (Appendix) can be solved for variable clszeu (Order 3) once the variables clsze (Order 2) and stud (Order 1) are determined (the rest are independent variables).

We should note that it is not always possible to derive the solution order that can be drawn as a directed graph with interactions among pairs of variables. Some systems of simultaneous equations contain subsets of equations that need be solved simultaneously without any apparent order among their variables. For example, when starting from the base case model (Figures 1 and 2) surplus (sur) is chosen to be an independent variable and the number of tenurable faculty (facten) is chosen to be a dependent variable, a subset of 26 equations with 26 variables (clsze, clszeg, costda, costga, costother, costspace, expdoc, exprdir, exprdirac, expres, expresac, exptch, exptdir, exptot, facten, inc, incres, incresac, or, ot, ovrhdramt, ovrhdramtac, ovrhdtamt, resdir, space, and spacebd) needs to be solved simultanously. Table 2 shows the order in which equations are solved in this case.

Table 2.

Causal ordering for the base case model with surplus (sur) chosen to be an independent variable and the number of tenurable faculty (facten) chosen to be a dependent variable.

Causal Order	Complete Subsets of Variables	Complete Subsets of Equations
1	(stud), (rasst), (tloadten), (clszeg), (expresru), (inctuit), (space)	(1), (2), (3), (5), (15), (22), (29)
2	(clsze), (tchfrac), (capspace)	(4), (8), (30)
3	(clszeu), (ratio), (exptdir), (ot), (exprdirac), (or)	(6), (7), (10), (11), (18), (19)
4	(ovrhdtamt), (exptch), (exprdir)	(9), (12), (13)
5	(incres, costother, incresac, costga, costspace, expres, expresac, inc, resdir, costda, ovrhdramt, spacebd, ovrhdramtac, quoten, expdoc, exptot)	(14, 16, 17, 20, 21, 23, 24, 25, 27, 28, 31, 32, 35, 36, 37, 38)
6	(spaceed), (spaceom), (resind)	(26), (33), (34)

4 Concluding Remarks

We have introduced a modeling approach to policy planning in the context of university operations. Our Performance Budget Model is based on a system of simultaneous structural equations encoding basic mechanisms underlying the functioning of a research university. This approach allows a complete and holistic description of a complex institution in mathematical terms. It provides a natural support for changes in structure and by this allows for counterfactual predictions that involve not only manipulation of policy variables but also their choice. Moreover, its demands on data for parameter estimation and validation are modest as compared to the conventional econometric methods, where the functional relation describing each mechanism is estimated by regression methods. Our analysis with PBM indicated that it provided fairly accurate predictions of the statistics from university financial reports. The university model was met with a lot of interest at Carnegie Mellon University’s Office of Planning and Budget in support of university-level strategic policy making. The PBM has been developed for Carnegie Mellon University but we believe that it is applicable to any research university after verifying the mechanisms involved and their parameters.

The modeling approach discussed in this paper, is universal in the sense that it’s only domain dependent part is the description of mathematical equations and policy variables. It can be viewed as a domain independent shell for supporting strategic decisions and is applicable to modeling environments that are based on structural equations. We believe that our modeling approach can be easily generalized to other business contexts and complements existing analytical tools for policy planning. Our model presents a glimpse of a new generation of powerful visual spreadsheets. It provides the ability to solve systems of nonlinear equations using standard and well studied numerical algorithms used in the sciences. It also allows the independent variables to be changed at will without having to reformulate the model each time. This provides immense flexibility in evaluating alternate policy options that is not afforded by present day models. We presented two examples (Section 3.4) that illustrated the flexibility of this support system. When we changed the set of independent variables, the structure of the model changed, as is apparent from Tables 1 and 2. The initial model was in a form in which all endogenous variables could be explicitly expressed in terms of the exogenous variables or other endogenous variables that preceded them in the causal order. However, with the change of structure we may encounter systems of equations that need to be solved simultaneously, as is apparent from Table 2. The power of the approach presented here is twofold: (1) it automatically computes the new structure, and (2) it brings to bear appropriate numeric/symbolic methods to solve for systems of simultaneous equations when needed. In order to examine such structural changes in present day spreadsheets, we would have to go through the laborious task of rebuilding the new spreadsheet and their equations. Moreover, our system incorporates symbolic methods (for differentiation and equation solving) to evaluate mathematical entities such as Jacobians which facilitate the automation of tasks such as comparative statics. The integration of numerical and symbolic methods, as demonstrated here, provides exciting opportunities for the development of support systems that can drastically improve problem solving ability in the business workplace.

Appendix: PBM Variables and Equations

The 88 model variables are divided into seven submodels: Teaching Operations, Teaching Expenditures, Research Expenditures, Income, Space Cost, Total Expense, and Surplus, each described in detail in the following sections. We would like to point out that some equations describe interactions among variables within a submodel. Others, involve variables from two or more submodels. Where an equation of the latter type will be represented in a causal graph depends on the causal ordering of the variables and this, in turn, which 50 of the 88 model variables are exogenous. Faced with the task of structuring our presentation so as to maximize clarity, we decided to discuss each of the equations within a submodel and chose the most typical submodel that it relates to. To help the reader navigate through the model, we report for each model variable the equation number where it appears.

Teaching Operations Submodel

The Teaching Operations Submodel relates student and faculty numbers to class size, teaching loads, and student-faculty ratio. The variables included in this model are: studu (1, 6, 22), studg (1, 2, 5, 6, 21, 22), stud (1, 4, 6), tasst (2, 4, 12, 21), rasst (2), facten (4, 5, 10, 11, 18, 19, 20, 28, 29), facspec (4, 10, 11), tloadsp (4), tloadg (3, 5), tloadu (3), tloadasst (4), tloadten (3, 4, 7, 8), credhrs (4, 5, 7), flload (8), tchfrac (8, 10, 11, 18, 19), clsze (4, 6, 7), clszeg (5, 6), clszeu (6), ratio (7).

The total number of students (stud) is the sum of the total number of undergraduate students (studu) and the total number of graduate (doctoral) students (studg).

$$\mathit{stud}=\mathit{studu}+\mathit{studg}.$$ (1)

The following equation ties the number of teaching assistantships (tasst) and the number of research assistantships (rasst) to the total number of graduate students (studg). It expresses the assumption that all doctoral students hold either a teaching assistantship or a research assistantship. (The variable rasst is not used in any other equation. However, it is used indirectly in Equation 21 through the term (studg – tasst).

$$\mathit{studg}=\mathit{tasst}+\mathit{rasst}.$$ (2)

The average teaching load for tenurable faculty (in terms of semester hours per week) (tloadten) is the sum of the load of undergraduate (tloadu) and graduates (tloadg) courses,

$$\mathit{tloadten}=\mathit{tloadu}+\mathit{tloadg}.$$ (3)

Class size (clsze) is expressed by the number of students (stud, this is multiplied by the average credit hours taken, credhrs) per semester credit hour taught (this is expressed in terms of the numbers of tenurable faculty, TAs, and special faculty times their respective teaching loads),

$$\mathit{clsze}=\frac{\mathit{stud}\times \mathit{credhrs}}{\mathit{facten}\times \mathit{tloadten}+\mathit{tasst}\times \mathit{tloadasst}+\mathit{facspec}\times \mathit{tloadsp}}.$$ (4)

Average graduate class size (clszeg) is expressed as the total credit hours taken by graduate students (studg × credhrs) divided by total semester hours taught by regular faculty (facten×tloadg). (Note: This implies that only regular faculty teach graduate students.)

$$\mathit{clszeg}=\frac{\mathit{studg}\times \mathit{credhrs}}{\mathit{facten}\times \mathit{tloadg}}$$ (5)

$$\mathit{clszeu}=\frac{\mathit{studu}\times \mathit{clsze}\times \mathit{clszeg}}{\mathit{stud}\times \mathit{clszeg}-\mathit{studg}\times \mathit{clsze}}$$ (6)

The student to faculty ratio (ratio) is the ratio of total credit hours taught by tenurable faculty (their teaching load, tloadten, times the average class size, clsze) and the total credit hours taught (by all faculty and TAs),

$$\mathit{ratio}=\frac{\mathit{tloadten}\times \mathit{clsze}}{\mathit{credhrs}}.$$ (7)

The average fraction of tenurable faculty time allocated to teaching (tchfrac) is simply expressed as the ratio of the actual teaching load of tenurable faculty to a hypothetical full-time teaching load (flload) that assumes only modest research activity,

$$\mathit{tchfrac}=\frac{\mathit{tloadten}}{\mathit{flload}}.$$ (8)

Teaching Expenditures Submodel

The Teaching Expenditures Submodel describes expenditures for instruction. The variables included in this model are: frng (9, 12, 20), tuitg (12, 21, 22), salten (10, 18), salspec (10), ovrhdt (9, 11, 12), ot (11), exptch (12, 37), exptdir (9, 10, 12), ovrhdtamt (9).

Only Equation 9, computing the dollar amount for overhead on instruction (ovrhdtamt) from the total direct teaching expenditures (exptdir), describes internal interactions within the Teaching Expenditures submodel

$$\mathit{ovrhdtamt}=\mathit{exptdir}\times \mathit{ovrhdt}(1+\mathit{frng}).$$ (9)

Equations 10, 11, and 12 describe interactions between the Teaching Operations and Teaching Expenditures submodels.

Direct teaching expense (exptdir) is calculated as the sum of the salaries for special teaching faculty (facspec × salspec) and the portion of regular faculty assigned to teaching by the teaching fraction term (tchfrac). (Note: The salaries for teaching assistants are not included as a direct expense, so they are automatically excluded from the base upon which overhead is computed.)

$$\mathit{exptdir}=\mathit{facten}\times \mathit{salten}\times \mathit{tchfrac}+\mathit{facspec}\times \mathit{salspec}$$ (10)

The following equation calculates an overhead rate for teaching (ovrhdt) which is based on the fraction of tenurable faculty time allocated to teaching plus special faculty (full time). (Note: TAs are excluded from this calculation.)

$$\mathit{ovrhdt}=ot\times (\mathit{facten}\times \mathit{tchfrac}+\mathit{facspec})$$ (11)

The following equation computes total teaching expenses (exptch). Overhead is applied to total faculty compensation (salaries plus fringe). TA salaries ($12,000 per annum) are added to direct and indirect expenses for regular and special faculty. This assumes the same fringe rate for regular and special faculty.

$$\mathit{exptch}=\mathit{exptdir}\times (1+\mathit{frng})\times (1+\mathit{ovrhdt})+\mathit{tasst}\times (\mathit{tuitg}+12000)$$ (12)

Research Expenditures Submodel

The Research Expenditures Submodel contains equations that determine expenditures for research. The variables included in this model are: exprdirru (13, 15, 17, 20), ovrhdrru (15, 17, 20), exprdir (13, 16), ovrhdramt (16, 17), ovrhdramtac (17), expresru (14, 15), salgradpc (21), mo (18), facres (18, 19, 28, 29), salres (18), facpcsub (18), expdoc (21, 37), exprdirac (13, 18, 20), expresac (14), pcquosal (20), ovrhdr (19, 20), govovh (20), expres (14, 16, 20, 37), or (19).

The following five equations describe internal interactions within the Research Expenditures submodel.

Similar to Equation 23, total direct research expenses (exprdir) are the sum of direct research in academic units (exprdirac) plus direct research expenditures in the research units (exprdirru)

$$\mathit{exprdir}=\mathit{exprdirac}+\mathit{exprdirru}.$$ (13)

Total research-related expenditures by academic units (expresac) is the difference between the total research related expenditures (expres) and the research expenditures of the research units (expresru)

$$\mathit{expresac}=\mathit{expres}-\mathit{expresru}.$$ (14)

The following equation shows total research expenses for various research units as the direct research expenses (exprdirru) (defined here as all expenses for research units, since all of their output is research oriented) plus the associated indirect expenses. The overhead rate (ovrhdrru) is computed as the proportion of indirect costs recovered over total expenses (not just direct expenses).

$$\mathit{expresru}=\mathit{exprdirru}\times (1+\mathit{ovrhdrru})$$ (15)

Overhead amount (in dollars) of research expenditures (ovrhdramt) is equal to difference between total research expenditures (expres) and direct research expenditures (exprdir),

$$\mathit{ovrhdramt}=\mathit{expres}-\mathit{exprdir}.$$ (16)

Research overhead (in dollars) associated with academic units (ovrhdramtac) is equal to the difference between total research overhead (ovrhdramt) and research overhead attributed to research units (exprdirru),

$$\mathit{ovrhdramtac}=\mathit{ovrhdramt}-\mathit{exprdirru}\times \mathit{ovrhdrru}.$$ (17)

The remaining four equations describe interactions between the Research Expenditures submodel with other submodels.

The following equation calculates the direct expenditure for research in academic units (exprdirac). Direct academic research expenses are equal to the proportion of regular faculty academic year salaries charged to research (1 – tchfrac), plus the salary expense for research faculty, plus the direct expense for summer research. The last term assumes that all faculty activity during the summer is research oriented. The component $(\mathit{facpcsub}+\mathit{facpcact})\times \frac{mo}{9}$ computes the research salary amounts for the summer term.

$$\mathit{exprdirac}=\mathit{facres}\times \mathit{salres}+\mathit{facten}\times \mathit{salten}\times \left((1-\mathit{tchfrac})+(\mathit{facpcsub}+\mathit{facpcact})\times \frac{mo}{9}\right)$$ (18)

With Teaching Operations and Teaching Expenditures submodels:

The following equation calculates an overhead rate for research (ovrhdr), which is based on research faculty (doing full time research) (facres) and the fraction of regular faculty allocated to research (1–tchfrac). Note that research assistants are not included in this calculation.

$$\mathit{ovrhdr}=or\times (\mathit{facres}+(1-\mathit{tchfrac})\times \mathit{facten})$$ (19)

With Teaching Operations, Teaching Expenditures, and Income submodels:

Total research expenditures are equal to direct research expenditures (see Equation 13) times their benefit expense (frng), plus the total active contract expenditures for regular faculty, plus the portion of indirect expense that is actually spent but not recovered (due to federal constraints/regulations), plus the direct and indirect expenses of the research units,

$$\mathit{expres}=(\mathit{exprdirac}+\mathit{exprdirru})\times (1+\mathit{frng})-\mathit{exprdirac}\times \mathit{govovh}+\mathit{incres}\times \mathit{ovrhdr}+\mathit{exprdirru}\times \mathit{ovrhdrru}+\mathit{facpcact}\times \mathit{facten}\times (1-\mathit{pcquosal})\times \mathit{quoten}.$$ (20)

Equation 21 calculates the non-research funded expenses for graduate research assistants as the total salary expense for all research assistants minus the portion of salaries charged to sponsored projects. The equation assumes $1,000 per month stipend for 12 months.

$$\mathit{expdoc}=(\mathit{studg}-\mathit{tasst})\times (\mathit{tuitg}+12000)-\mathit{salgradpc}\times \mathit{incresac}$$ (21)

Income Submodel

The Income Submodel contains equations that determine income, including distinction between “direct” and “indirect” income. The variables included in this model are: quores (28), quoten (28, 20), facpcact (28, 18, 20), incresac(21, 23, 28), incresru (23), incres (20, 23, 24, 25, 27, 31, 35, 36), indrat (25, 26), resdir (25, 26), tuitu (22), aid (22), inctuit (22, 24), incmisc (24), incgift (24), incend (24), inc (24, 38).

Income from tuition (inctuit) is the sum of the tuition income from graduate students (studg × tuitg, total number graduate students times graduate tuition) and the tuition income from undergraduate students (studu × tuitu, total number of undergraduate students times undergraduate tuition) the latter reduced by the fraction of tuition income that is devoted to financial aid (aid),

$$\mathit{inctuit}=\mathit{tuitu}\times \mathit{studu}\times (1-\mathit{aid})+\mathit{studg}\times \mathit{tuitg}.$$ (22)

Research income is the sum of research-related income from academic units (incresac) and all income from the research units (incresru),

$$\mathit{incres}=\mathit{incresac}+\mathit{incresru}.$$ (23)

Total income is the sum of five income categories: tuition income (inctuit), draw on endowment (incend), research income (incres), gift income (incgift), and miscellenous income (incmisc),

$$\mathit{inc}=\mathit{inctuit}+\mathit{incend}+\mathit{incres}+\mathit{incgift}+\mathit{incmisc}.$$ (24)

Research income comes from direct (resdir) and indirect income. The latter is expressed as indirect research ratio (indrat),

$$\mathit{incres}=\mathit{resdir}\times (1+\mathit{indrat}).$$ (25)

Another relationship between direct and indirect research income is expressed by the following equation:

$$\mathit{resind}=\mathit{resdir}\times \mathit{indrat}.$$ (26)

The following equation computes a dollar amount associated with the other (e.g., Faculty Administration Allowance, Sponsored Projects Administration, Library, Student Services) portion of indirect costs. The sum of costspace, costda, costga, and costother should equal total indirect costs associated with research.

$$\mathit{costother}=\mathit{incres}\times \mathit{rlother}$$ (27)

Research income from academic units (incresac) is the sum of the average dollar amounts of active research contracts per type of researcher times the total number of researchers of that type,

$$\mathit{incresac}=\mathit{quores}\times \mathit{facres}+\mathit{quoten}\times \mathit{facten}\times \mathit{facpcact}.$$ (28)

Space Cost Submodel

The Space Cost Submodel contains equations describing space costs. The variables included in this model are: rlspace (31), costspace (31, 32, 33, 34), rlda (35), costda (35), rlga (36), costga (36), rlother (27), costother (27), edfactor (33), bdfactor (32), omfactor (34), spaceed (33), spacebd (32, 38), spaceom (34), spaceru (29), spaceres (29), spacetch (29), space (29, 30), spchge (30), leased (30), capspace (30).

The following equation assigns manpower usage of space (Note: it is not tied to expenditures.)

$$\mathit{space}=\mathit{facten}\times \mathit{spacetch}+\mathit{facres}\times \mathit{spaceres}+\mathit{spaceru}.$$ (29)

The followingh equation calculates a “cost of space” charge (Note, it is not tied to expenditures.)

$$\mathit{capspace}=(\mathit{space}-\mathit{leased})\times \mathit{spchge}.$$ (30)

The cost of space (in dollars) is set up as a factor of total research income. This variable is tied back to surplus (sur), but still needs to be tied to manpower. Equations 29 and 30 should be expanded and related to Equations 31, 32, 33, and 34. One possibility would be to create four space components: classroom space as a function of students, teaching space as a function of regular and special faculty, research space as a function of research faculty, and other space as a function of overhead/total staff,

$$\mathit{costspace}=\mathit{incres}\times \mathit{rlspace}.$$ (31)

There are three components of Costspace. Equations 32, 33, and 34 compute the dollar amounts associated with each component. Equation 32 computes the portion of space costs associated with building depreciation.

$$\mathit{spacebd}=\mathit{bdfactor}\times \mathit{costspace}$$ (32)

Equation 33 computes the portion of space costs associated with equipment depreciation.

$$\mathit{spaceed}=\mathit{edfactor}\times \mathit{costspace}$$ (33)

Equation 34 computes the portion of space costs associated with operations and maintenance of plant.

$$\mathit{spaceom}=\mathit{omfactor}\times \mathit{costspace}$$ (34)

Equation 35 computes a dollar amount associated with the Departmental Administration portion of indirect costs. Interactions with Research Expenditures submodel.

$$\mathit{costda}=\mathit{incres}\times \mathit{rlda}$$ (35)

Equation 36 computes a dollar amount associated with the General and Administrative portion of indirect costs.

$$\mathit{costga}=\mathit{incres}\times \mathit{rlga}$$ (36)

Total Expenditures Submodel

Only one variable: exptot (37, 38).

Total expenditures are the sum of instructional expenditures (exptch), research expenditures (expres), and expenditures for doctoral students (expdoc),

$$\mathit{exptot}=\mathit{exptch}+\mathit{expres}+\mathit{expdoc}.$$ (37)

Surplus Submodel

Only two variables: captran (38), sur (38).

Budget surplus (sur) is equal to the difference between total income (inc) and total expenditures (exptot) and transfers to capital (captran). spacebd is added to surplus.

$$\mathit{sur}=\mathit{inc}-\mathit{exptot}-\mathit{captran}+\mathit{spacebd}$$ (38)