Performance Characteristics of Profiling Methods and the Impact of Inadequate Case-mix Adjustment

Abstract

Profiling or evaluation of health care providers involves the application of statistical models to compare each provider’s performance with respect to a patient outcome, such as unplanned 30-day hospital readmission, adjusted for patient case-mix characteristics. The nationally adopted method is based on random effects (RE) hierarchical logistic regression models. Although RE models are sensible for modeling hierarchical data, novel high dimensional fixed effects (FE) models have been proposed which may be well-suited for the objective of identifying sub-standard performance. However, there are limited comparative studies. Thus, we examine their relative performance, including the impact of inadequate case-mix adjustment.

1. Introduction

Unplanned hospital readmission is considered an indicator of the quality and efficiency of patient care. Many hospital readmissions are potentially preventable and contribute substantially to the cost of patient care with costs to Medicare estimated at more than $17 billion annually (Jencks et al. 2009). In particular, the burden of hospitalization is high for patients receiving dialysis, with an unadjusted rate of 30-day unplanned readmission of approximately 30% (United States Renal Data System [USRDS] 2015). Profiling or evaluation of health care providers, e.g., hospitals, nursing homes, dialysis facilities, with respect to a patient outcome such as 30-day unplanned hospital readmission is important to ensure adequate and safe health care delivery to patients. Profiling analyses serve several purposes, including 1) identifying providers with performance below standard by government agencies for regulatory or payment purposes; 2) conveying information to patients regarding the quality of care of providers; and 3) providing feedback to providers for quality improvement among others. Although profiling dates back to nearly a century (Codman 1916), more systematic reporting of patient outcomes among providers has only appeared directly to consumers in the last decade by the Centers for Medicare & Medicaid Services (CMS). This includes condition-specific 30-day mortality (e.g., acute myocardial infarction, heart failure, pneumonia) and 30-day (all-cause) readmission rates; see Keenan et al. (2008), Krumholz et al. (2011), Lindenauer et al. (2011), Horwitz et al. (2011) and Horwitz et al. (2014).

The specific inferential goal of profiling is to accurately report estimates of provider effects relative to a reference, such as a national rate, and in the process, identify providers that are exceptionally high/“worse,” low/“better” or “not different” relative to the reference. Patient outcomes vary across providers due to variation in providers quality of care (provider effects) and variation in patient case-mix (patient-level factors including demographics, comorbidities, and types of index hospitalization). Because patients are nested within providers, profiling models are hierarchical logistic regressions of the form outcome = provider effects + case-mix effects. In addition to the nested structure of the data, sparse outcome data have naturally led to the adoption of modeling provider effects as random effects (RE). In fact, RE model is an approach adopted by CMS for readmission (CMS 2014; Ash et al. 2012; Horwitz et al. 2011; Krumholz et al. 2011); see also Normand and Shahian (2007) and Normand et al. (1997) for further motivation of the RE model. Throughout this work, we refer to the terms “RE model” and “CMS model” interchangeably and they refer to the CMS adopted model with random intercepts for providers.

Subsequently, Kalbfleisch and Wolfe (2013) and He et al. (2013) have proposed modeling provider effects as fixed effects (FE). The FE model of He et al. (2013) is a high-dimensional parameter model with a unique fixed intercept for each provider. Based on the high-dimensional FE methodology developments by the University of Michigan Kidney Epidemiology and Cost Center (UM-KECC; Kalbfleisch and Wolfe (2013) and He et al. (2013)) for CMS, a CMS dry-run of the FE model for hospital readmission for dialysis facilities was conducted in 2014 and a report on SRR was submitted to CMS in 2014 and subsequently updated in 2017 (CMS 2017). Because CMS had already implemented RE profiling models for hospitals with respect to 30-day readmission (and in-hospital mortality as well), e.g. see Ash et al. (2012), the issue of whether to adopt FE vs. RE for dialysis facilities is a pertinent consideration. Research from UM-KECC and the recently updated CMS report on SRR for dialysis facilities (CMS 2017) suggest potential adoption of FE model for SRR for profiling dialysis facilities. However, we note that the choice of FE vs. RE models is a relevant issue for profiling other providers, such as hospitals (and not just dialysis facilities; Kalbfleisch and Wolfe (2013)), and warrants more systematic assessments because of the emerging research on FE models. Thus, in this work, we considered simulation studies to compare the performance (inferential procedure) of FE vs. RE/CMS profiling models.

Although RE models can provide stable provider effect estimates (through shrinkage), they are biased toward the overall provider average and the bias is larger for smaller facilities and in the presence of confounding between patient risk factors and provider effects (Kalbfleisch and Wolfe 2013). Also, as reported in Kalbfleisch and Wolfe (2013), the overall average error in estimation of provider effects is smaller since mean square error is minimized over the full set of provider effects in the RE approach; however, the FE estimates have smaller error for outlier ‘providers whose effects are exceptionally large or small’.

Despite these intriguing results, no study to our knowledge has been conducted to provide a direct comparison of the CMS/RE model and the high-dimensional FE model, utilizing the precise inferential procedures in the current practice for profiling providers. Thus, in this work we conduct extensive simulation experiments to further elucidate the inferential performances of the RE (CMS) model and the FE model. As part of this study we examine how low provider volume affects the relative performance of the two methods. We also consider the impact of inadequate case-mix adjustment on the ability of the RE and FE method to identify truly under-performing (and over-performing providers). Our study here aims to provide insights into these important practical issues. We note that our comparative simulation studies here differs from those in Kalbfleisch and Wolfe (2013) which focused on estimation accuracy and the inherent estimation bias from the RE model using simple linear regression models.

We provide a historical note here that there is another use of the term “fixed effects” models in the profiling literature, where a FE model refers to a standard logistic regression model (with one overall intercept) which has been used for 30-day mortality following admission for acute myocardial infarction and mortality following coronary artery bypass (e.g, see Austin, Alter and Tu 2003). This is different from the high-dimensional FE model with a unique fixed intercept for each provider. Other studies have also considered variations in the provider-specific measures (e.g., see Yang et al. 2014) and inference under more flexible hierarchical Bayesian (RE) models (e.g., see Paddock et al. 2006), which is not the objective of our study. None of these prior studies considered the CMS model specifically nor compared the RE model to the high-dimensional FE model of He et al. (2013). Also, we note that our paper focuses on the currently implemented RE/CMS model. However, extensions to the current RE/CMS model have been proposed (e.g., Silber et al. 2016; George et al. 2017), which incorporates providers characteristics, including volume, infrastructure (e.g. technology) and staffing to improve prediction. The idea of potentially extending the RE/CMS model to incorporate provider characteristics was suggested earlier by Ash et al. (2012).

2. Methods

2.1. RE and FE Models

The RE model implemented by CMS for (30-day unplanned) all-cause or condition-specific hospital readmission (Horwitz et al. 2011; Ash et al. 2012) is the following RE logistic regression model,

$$g\left({\mu }_{ij}\right)={\gamma }_i+{\mathit{\beta }}^{\text{T}}{\mathbf{\text{Z}}}_{ij},{\gamma }_i~N\left({\gamma }_0,{\sigma }^2\right),$$ (1)

where μ_ij = p_ij = Pr(Y_ij = 1|β,γ_i,Z_ij) is the expected readmission for patient index discharge j = 1,2,…,n_i in provider i = 1,2,…,F, and g(p_ij) = log{p_ij/(1−p_ij)} is the logit function. In (1) β^T = (β₁,…,β_r) adjusts for case-mix effects where the patient case-mix (baseline and admission characteristics) is denoted by the vector of r covariates Z_ij = (Z_ij1,Z_ij2,…,Z_ijr).

In contrast, in the context of providers as dialysis facilities, Kalbfleisch and Wolfe (2013) and He et al. (2013) proposed modeling providers’ effects with fixed effects (γ₁,…,γ_F) in the FE model

$$g\left({\mu }_{ij}\right)={\gamma }_i+{\mathit{\beta }}^{\text{T}}{Z}_{ij},i=1,\dots ,F.$$ (2)

For clarity, we emphasize that the FE model (2) is a single simultaneous model for all F facilities/providers with a high-dimensional parameter space (where F is several thousands) and not a separate logistic regression model for each provider. Furthermore, it is also not a single logistic regression with an overall intercept term which is often referred to as a fixed effects model in early literature on profiling. Note that when F is large as in model (2), e.g. with F = 6,000 dialysis facilities across the U.S. and 30 case-mix parameters, the dimension of the parameter space is 6,030 and standard software fails. To be able fit such a model with that many parameters, the novel alternating one-step Newton-Raphson alogirithm proposed by He et al. (2013) is used.

We further note that the RE model (1) may be generalized, such as inclusion of provider-level characteristics (Ash et al. 2012), although our focus here is on the nationally implemented relevant RE model (1). For the FE model (2) in the context of performance assessment of dialysis facilities, further adjustment through inclusion of a hospital RE was considered in He et al. (2013), although it was found that the contribution of the hospital effect was small. In order to compare RE and FE models and for the results to be more applicable to different provider settings, we consider the FE model in (2).

Given the provider and case-mix effect estimates, denoted by $\widehat{{\gamma }_i}$ and $\widehat{\mathit{\beta }}$, respectively, the estimated standardized readmission ratio (SRR) for provider i is

$$SR{R}_i=\frac{{\sum }_{j=1}^{n_i}{\widehat{p}}_{ij}}{{\sum }_{j=1}^{n_i}{\widehat{p}}_{M,ij}},$$ (3)

where ${\widehat{p}}_{ij}=g^{-1}\left(\widehat{{\gamma }_i}\text{ +}{\widehat{\mathit{\beta }}}^{\text{T}}{Z}_{ij}\right)$ is the estimated probability of readmission for patient j in provider i and ${\widehat{p}}_{M,ij}=g^{-1}\left({\widehat{\gamma }}_M+{\widehat{\mathit{\beta }}}^{\text{T}}{Z}_{ij}\right)$. For the FE model, ${\widehat{\gamma }}_M$ in the denominator is taken to be the median of the ${\left\{{\widehat{\gamma }}_i\right\}}_{i=1}^F$ and for the RE model it is the estimated mean of the distribution of γ_i (namely ${\widehat{\gamma }}_0$). The numerator of SRR_i is the expected total number of readmissions for facility i and the denominator is the expected total number of readmissions for an “average” facility (taken over the population of all facilities), adjusted for the particular case-mix of the same patients in facility i. Note that SRR_i estimates the true/theoretical quantity ${\widetilde{SRR}}_i={\sum }_{j=1}^{n_i}{p}_{ij}/{\sum }_{j=1}^{n_i}{p}_{M,ij}$, where p_ij = g⁻¹(γ_i + β^TZ_ij) and p_M,ij = g⁻¹(γ_M + β^TZij).

2.2. Estimation, Inference and Available Software

The RE model is a standard generalized linear mixed effects model and available software, including SAS PROC GLIMMIX or R library lme4 function glmer, can be used to fit it. The CMS implementation uses SAS PROC GLIMMIX (Ross et al. 2010; Horwitz et al. 2011; Ash et al. 2012). A bootstrap resampling of facilities with replacement (500 samples) is used to obtain a 95% confidence interval (CI) for each ${\widetilde{SRR}}_i$ The random effects sampled from the posterior distribution of γ_i are used to estimate ${\widetilde{SRR}}_i$ in each bootstrap sample. (Details are provided in the Supplemental Appendix Section.) Provider i is flagged as performing worse than expected relative to the national reference if the lower confidence limit is above 1; and similarly, a provider is identified as performing better than the national reference when the upper confidence limit is below 1. Facilities with CI for SRR_i containing 1 are considered not different compared to the national reference.

For the FE model estimation, He et al. (2013) proposed an iterative algorithm that alternates between estimation of {γ_i} given β and estimation of β given {γ_i} using one-step Newton-Raphson updates. Iteration terminates when max $\Vert p_{ij}^{(\mathcal{l}+1)}-p_{ij}^{(\mathcal{l})}\Vert <{10}^{-6}$ on successive steps l. (See He et al. (2013) and the Appendix section for details.) Inference for ${\widetilde{SRR}}_i$, accounting for the high-dimensional FE parameters, is based on testing the null hypothesis $H_0:{\gamma }_i={\gamma }_M\left(\text{i.e., }{\widetilde{SRR}}_i=1\right)$. A method based on resampling under the null hypothesis is used to evaluate the p-value, the “probability that a given provider would experience a number of readmission as least as extreme as that observed if the null hypothesis is true, accounting for the provider’s patient case-mix”.

We implemented the RE (CMS) model in SAS PROC GLIMMIX and R, and the results coincide. R codes for both RE and FE models are provided as supplemental materials. These are publicly available along with documentation on a step-by-step tutorial for implementation using a sample dataset with 1,000 providers. See supplemental materials for R codes and www.http://faculity.sites.uci.edu/nguyen/supplement/ for details. In this work, references to ‘RE’ and ‘FE’ methods refer specifically the models described by (1) and (2) together with the estimation and inference procedures described in the Supplemental Appendix section.

3. Simulation Studies

We designed the simulation studies to address the three specific aims: A1) assess the overall relative inferential performance of RE and FE in identifying “extremely” under- (or over-) performing providers; A2) examine how the inferential performance of the methods depends on (i) patient case-mix complexity (correlation/dependence structure), (ii) provider volume, the number of patients within a provider, (iii) baseline readmission rate (BRR), and (iv) the relative provider signal (i.e. effect size, P-EF) relative to the patient case-mix effect size (CM-ES). A3) determine the impact of inadequate case-mix adjustment on profiling performance. We note that in the context of the current models, the baseline readmission rate is essentially the effective sample size or outcome sparsity level, which generally affects estimation and inference. (The selected range of BRR of 14%–40% was chosen to be broad, but still capture realistic baseline hospitalization rates in the dialysis population.) Also, for the simulation models below, we expanded the simulation model from He et al. (2013) to allow for correlation among case-mix variables and incorporated USRDS data/case-mix characteristics.

3.1. Simulation Setting 1 - General Set-Up

The basic data generating model we considered was

$$g\left({\mu }_{ij}\right)={\gamma }_i+{\gamma }_0+{\beta }_1{Z}_{ij1}+\cdots {\beta }_{15}{Z}_{ij15}$$ (4)

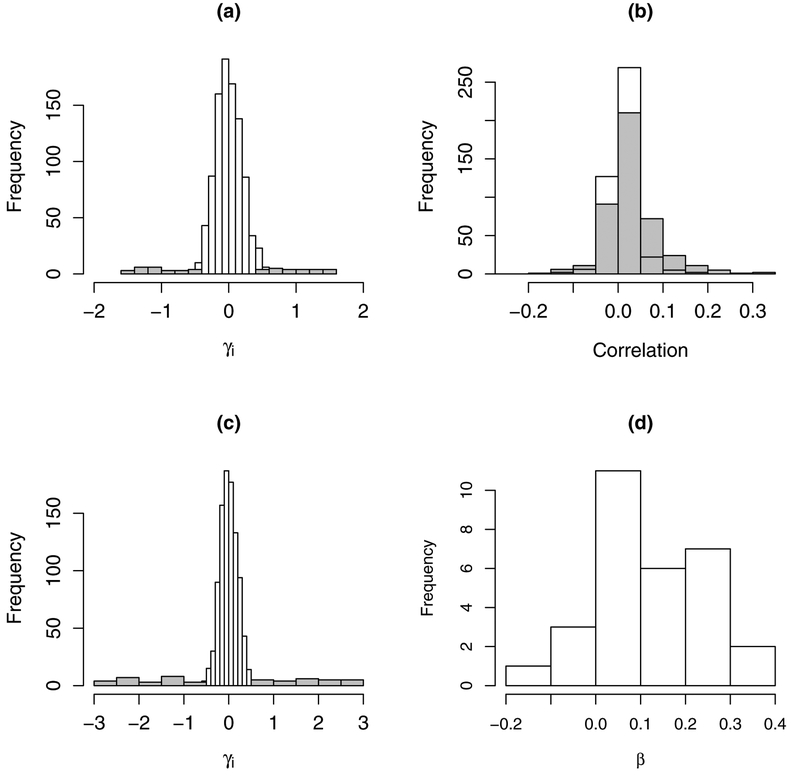
with i = 1,…,F = 1,000 providers. Among the providers, 2.5% were under-performers and 2.5% were over-performers whose effects were generated as γ_i ~ Uniform(0.4,1.5) and γ_i ~ −Uniform(0.4,1.5), respectively. The remaining 95% of providers, with effects not different from the national reference, were generated from a N(0,σ²) distribution with σ² = 0.2². Figure 1(a) displays the distribution of provider effects for one dataset (1,000 providers). Baseline rates of readmission (BRR) considered were 14.3%, 27.3%, and 41.7% (referred to as low, medium and high) corresponding to γ₀ = log(1/6), log(3/8), and log(5/7), respectively.

Figure 1:

(a) Distribution of provider effects, γ_i, for simulation setting 1 (Section 3.1); gray indicates truly better and worse providers. (b) Distribution of observed correlations among case-mix variables based on USRDS data (gray) and correlations in simulated data (white). (c) Distribution of provider effects from simulated data, γ_i, informed by characteristics of USRDS dialysis facility data (Section 3.2). (d) Distribution of case-mix effect estimates $\left({\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{30}\right)$ from USRDS dialysis facilities data used to inform simulation study.

The patient case-mix vector, Z_ij, was generated from a multivariate normal distribution with means 0, variances 1, and correlation ρ_rr′ ≡ ρ(Z_ijr,Z_ijr′), 1 ≤ r,r′ ≤ 15. To assess how case-mix complexity affects the performance of RE and FE methods, we considered five case-mix dependence settings: uncorrelated case-mix with ρ_rr′ = 0 and various levels of correlated case-mix with ρ_rr′ = 0.2,0.5, and 0.8. For the fifth setting that mimics correlations between the USRDS case-mix, case-mix variables with more general dependence were generated in three blocks with different correlation structures: 0.01 ≤ ρ_rr′ ≤ 0.05 in block 1 for variables Z₁ to Z₅; 0.05 ≤ ρ_rr′ ≤ 0.1 in block 2 for variables Z₆ to Z₁₀; 0.1 ≤ ρ_rr′ ≤ 0.25 in block 3 for variables Z₁₁ to Z₁₅; correlations of variables across blocks were also correlated in the range of 0.01 ≤ ρ_rr′ ≤ 0.25.

To examine the impact of the provider effect size (P-ES), relative to the patient case-mix effect size (CM-ES), we considered two P-ES and two CM-ES settings: (P-ES 1): γ_i ~ Uniform(0.4,1.5), γ_i ~ −Uniform(0.4,1.5), and N(0,0.2²) for facilities under-performing, over-performing, and not different from the national reference, respectively; (P-ES 2): γ_i ~ Uniform(0.6,1.5), γ_i ~ −Uniform(0.6,1.5), and N(0,0.2²) for facilities under-performing, over-performing and not different from the national reference, respectively, where provider signals have been increased. For patient case-mix effect size (CM-ES) we considered the following two settings: (CM-ES 1) β_A ≡ (β₁,…,β₁₅)^T such that β₁ = ⋯ = β₁₀ = 0.5 and β₁₁ = ⋯ = β₁₅ = 1; (CM-ES 2) β_B is increased to 2 × β_A. More specifically, we considered the following three combinations of settings: (i) P-ES 1 (“smaller”) with CM-ES 1 (“smaller”); (ii) P-ES 1 (“smaller”) with CM-ES 2 (“larger”); and (iii) P-ES 2 (“larger”) with CM-ES 1 (“smaller”). Comparison of (i) vs. (ii) allows assessment of the impact of larger patient case-mix signal relative to a given (fixed) provider signal. For instance, in the case where patient case-mix contributes predominantly to the risk of readmission compared to providers’ contribution to patient readmission, the efficacy of all methods to identify extreme providers should be diminished. On the other hand, comparison of (i) vs. (iii) will assess the basic principle that for a fixed patient case-mix contribution to readmission, increasing the providers’ contribution to patient readmission should result in improved profiling performance.

Also, the generated data consisted of provider volume ranging from 42 to 210 patients on average. More specifically, the number of patients were generated from a truncated Poisson distribution following He et al. (2013), where the number of patients was taken to be $n_i={\sum }_{h=1}^{1000}{m}_{ih}1\left\{m_{ih}\le 7\right\}$ with m_ih ~ Poisson(15). This process mimics the sparse data structure of hospital h and dialysis facility (provider) i in practice. We defined small, medium and large sized providers by tertile (small: 42–103; medium: 104–126: large: 127–210 patients on average). Two hundred datasets, each with 1,000 providers, were generated for each simulation study scenario, defined by a) provider effect size (γ_i distribution), b) patient case-mix effect size (β); c) case-mix complexity; and d) baseline readmission rates as summarized in Supplemental Table S1.

To study the impact of inadequate case-mix adjustment, the following nested sequence of models were fitted to each simulated dataset: (1) ${\mathcal{M}}_0:$ intercept only (no case-mix adjustment); (2) ${\mathcal{M}}_1:$ adjustment for {Z₁,Z₂}; (3) ${\mathcal{M}}_2:$ adjustment for {Z₁,…,Z₁₀}; (4) ${\mathcal{M}}_3:$ adjustment for {Z₁₁,…,Z₁₅}; and (5) ${\mathcal{M}}_f:$ full model with complete case-mix adjustment. The full model provides a useful benchmark to evaluate how the performance deteriorates with increasing inadequate case-mix adjustment.

3.2. Simulation Setting 2 - USRDS Data Characteristics

We also considered a simulation study more tailored to the assessment of dialysis facilities (providers). Paralleling works for profiling all-cause readmission for hospitals (CMS 2014; Horwitz et al. 2011), assessment of dialysis facilities included the following 30 patient case-mix covariates: age, body mass index (BMI), length of index hospitalization (days), time on dialysis (years), high risk index hospitalization, diabetes as the cause of ESRD, sex and 23 past-year comorbidities: amputation status; chronic obstructive pulmonary disease; cardiorespiratory failure/shock; coagulation defects and other specified hematological disorders; drug and alcohol disorders; endstage liver disease; fibrosis of lung or other chronic lung disorders; hemiplegia, paraplegia, paralysis; hip fracture/dislocation; major organ transplants; metastatic cancer; other hematological disorders; other infectious disease and pneumonias; other major cancers; pancreatic disease; psychiatric comorbidity; respirator dependence; rheumatoid arthritis and inflammatory connective tissue disease; seizure disorders; septicemia/shock; severe cancer; severe infection; and ulcers (CMS 2014).

Using the USRDS data, the observed 30 × 30 correlation matrix and sample variances were used to generate W_ij ~ N₃₀(μ_W,Σ_W), with Σ_W = (σ_r,r′) and μ_W = (μ₁,…,μ₃₀) chosen to be the observed means or prevalences for binary covariates based on USRDS data. Letting W_ijr denote the underlying continuous latent variables, the observed binary covariates Z_ijr were generated through the process: Z_ijr = 1{W_ijr < z_rσ_r,r + μ_r}, where 1{A} is the indicator function for event A, z_r = Φ⁻¹(μ_r) and Φ⁻¹( ) is the standard normal inverse CDF. Note that this process generates binary covariates with prevalences equal to the observed prevalences in the USRDS data (μ_W). The distribution of the correlations among case-mix variables were similar to the observed distribution of correlation values in the USRDS data (Figure 1(b)). The distribution of facility effect sizes (distribution of γ_i) was modeled as γ_i ~ N(0,0.2²) for facilities not different from the reference and outlying facilities were generated as ±Uniform(0.6,3) (Figure 1(c)). The patient case-mix effects, β^T = (β₁,…,β₃₀) were set to be proportional to the estimates based on the USRDS data (Figure 1(d)).

We simulated 200 datasets, each with 1,000 facilities. Similar to the first simulation study above, for each dataset, we fitted the sequence of models: (1) ${\mathcal{M}}_0^{*}:$ intercept only (no case-mix adjustment); (2) ${\mathcal{M}}_1^{*}:$ adjustment for adjustment for {Z₁,…,Z₁₅}; (3) ${\mathcal{M}}_2^{*}:$ adjustment for adjustment for {Z₁,…,Z₁₅}; (4) ${\mathcal{M}}_3^{*}:$ adjustment for {Z₁,…,Z₂₅}; and (5) ${\mathcal{M}}_f^{*}:$ full model with complete case-mix adjustment.

4. Results

4.1. Overall Performance and Effect of Case-Mix Complexity

The overall performance of FE and RE models are described in terms of sensitivity (SEN) to correctly identify providers that under-perform (W: “worse”), over-perform (B: “better”) relative to the reference standard (e.g., national reference), and specificity. Specificity (SPEC) refers to the correct identification/flagging of providers that do not differ compared to the reference standard (ND: “not different”). Because provider assessment policies focus on identifying under-performing providers, we focus on the results for SEN-W and SPEC-ND (although the performance of SEN-B are similar to SEN-W in our studies due to symmetry).

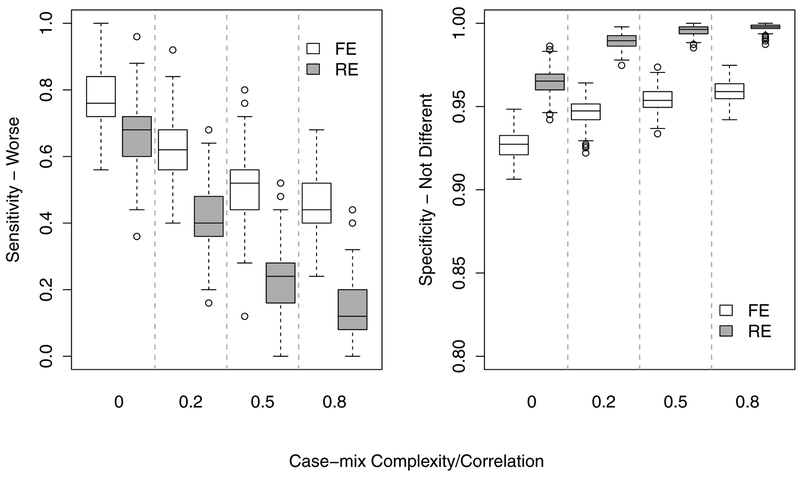
To assess the overall performance of FE and RE models, we first describe the results for the full model where covariates/case-mix variables were correctly/fully specified in the models. Figure 2 summarizes the performance of FE vs. RE for identifying providers that performed worse than the reference (SEN-W) and providers with performance not different from the reference (SPEC-ND) for the case of readmission rate of 27%. Several salient and informative patterns of model performance are clear from Figure 2. First, the overall SEN-W across all providers was substantially higher for FE compared to RE models for all settings of case-mix complexity/correlation (e.g., mean 76.6% vs. 66.8% at ρ = 0). Second, the ability of both FE and RE models to flag extreme under-performing providers declined with increasing case-mix complexity; and the performance of RE models deteriorated rapidly as case-mix complexity increased. For example, at ρ = 0.8 the SEN-W for RE deteriorated to an average of only 13.3% compared to 44.6% for FE. Thus, the performance (sensitivity) for the RE model (for the case-mix ρ = 0.8 setting) declined by 80.3% from the uncorrelated case-mix setting, while the FE model dropped by only 41.8%.

Figure 2:

Overall performance of the full (benchmark) RE and FE models: (Left) overall sensitivity for identifying truly under-performing (worse) providers and (Right) specificity, i.e., providers with standardized readmission rate not different from the reference rate.

The specificity (SPEC-ND), i.e., rate of correctly identifying the providers that do not differ from the reference standard, increased slightly with increasing case-mix complexity; e.g., 92.7% to 96.5% for ρ = 0 to ρ = 0.8, respectively, for the FE model. As expected, the SPECND is higher for the RE model (95.9% to 99.8% for ρ = 0 to ρ = 0.8, respectively). The extreme conservatism of the RE model to not flag providers as under-performing resulted in high SPEC-ND rates, because the majority (190,000 = 200 × 1000 × 0.95) of providers are truly ND relative the reference standard. In fact, under any setting that may resemble real data (ρ > 0) the SPEC-ND for the RE model is > 98% because the vast majority of the 5,000 truly under-performing providers were categorized as ND. In short, it poorly discriminated truly under-performing providers and classified nearly all providers as ND.

4.2. Effect of Provider Volume

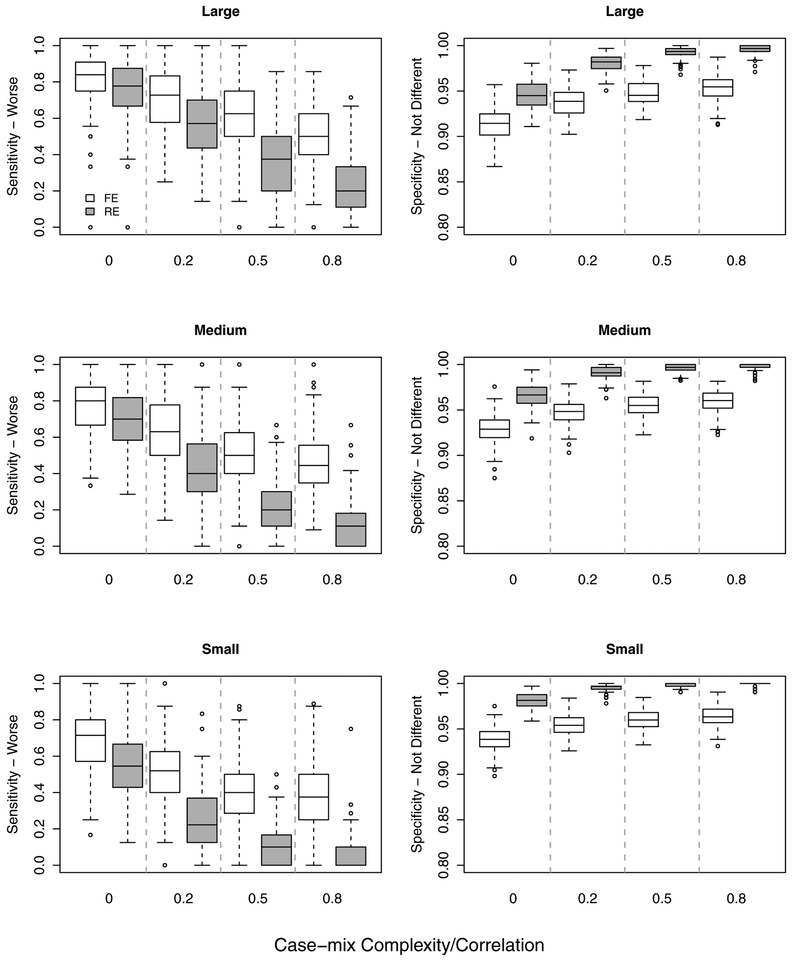
For large providers with 127–210 patients (defined as the third tertile), the relative performance patterns for RE vs. FE models were similar to the overall pattern across all providers, except with nominal SEN-W and SPEC-ND rates higher for both methods (Figure 3).

Figure 3:

Overall performance of the full (benchmark) RE and FE models by provider volume/size: Small, medium and large providers defined by tertiles: (Left) Sensitivity, (Right) Specificity.

Of particular interest in practice is understanding the performance characteristics of RE and FE methods for small providers with low patient volume. For the purpose of this study, small providers were defined as those with 23–103 patients (the first tertile). Although small providers in practice actually have lower numbers of patients, our definition of small providers in these simulation studies is adequate to illustrate the relative performance characteristics for RE and FE models for smaller providers. As expected, the nominal SEN-W rates were lower for both models across case-mix complexity/correlation settings. However, the already rapidly deteriorating SEN-W rate for the RE described above was further accelerated for small volume providers. More specifically, the average SEN-W was 54.0% for ρ = 0 and 5.3% for ρ = 0.8, which is a 90.1% decline in sensitivity. The relative SEN-W rate (e.g., ρ = 0.8 relative to ρ = 0) for the FE model also further declined for small providers, although the average decline was lower for the FE model compared to the RE model.

4.3. Relative Effect of Patient Case-Mix Contribution

Two competing factors that affect the ability of methods to accurately identify truly under performing providers are the 1) magnitude of the providers’ contributions and 2) magnitude of the patient case-mix effect on the risk of readmission (magnitude of {γ_i} and β, respectively). We fixed the magnitude (and distribution) of the providers’ effect size (P-ES) for contribution to patient readmission and considered two patient case-mix effect sizes (CM-ES): β_A = β vs. β_B = 2 × β (CM-ES 1 vs. CM-ES 2). Because the larger patient case-mix effect, namely β_B, reduces the relative signal attributable to the providers’ contribution to patient readmission in the regression model, it is expected that the ability to detect under-performing providers would be diminished. This is illustrated in Table 1, comparing (a) CM-ES 1 (β) to (b) CM-ES 2 (2×β) for baseline readmission of 27%. Under higher signal attributable to patient case-mix, the ability to detect under-performing providers was decreased for both models. However, the RE model was relatively ineffective at detecting the under-performing providers, even for large providers. It clearly failed to detect under-performing providers across all reasonable case-mix scenarios for small providers as well as medium volume providers, where SEN-W rates were less than 1.0% for ρ ≥ 0.5 and for ρ = 0.2 SEN-W rates were 7.1% and 3.1% for medium and small providers, respectively,

Table 1:

(a) vs. (b): Impact of low and higher patient case-mix effect size (CM-ES 1: β vs. CMS-ES 2: 2×β) on performance of the full (benchmark) RE and FE models across provider volume (large, medium, small). (a) vs. (c): Impact of low and higher provider effect size (P-ES 1 vs. P-ES 2) on performance at a fixed patient case-mix effect size (β). Presented are results for the case of baseline readmission rates of 27%). Simulation settings, design parameters, and models.

	(a) P-ES 1 & CM-ES 1		(b) P-ES 1 & CM-ES 2		(c) P-ES 2 & CM-ES 1
ρ	FE	RE	FE	RE	FE	RE
Overall
0	69.9	49.4	61.5	37.0	86.2	78.9
0.2	62.3	41.2	39.0	8.7	71.2	49.5
0.5	51.2	23.2	30.7	2.4	60.0	28.9
0.8	44.6	13.2	25.4	1.3	51.9	18.5
Large
0	82.7	77.5	55.2	24.9	92.3	89.2
0.2	70.8	56.7	47.7	16.0	79.4	65.7
0.5	60.9	36.7	38.2	5.7	69.9	44.4
0.8	52.1	22.1	31.6	2.9	61.9	32.1
Medium
0	77.7	68.8	44.5	13.6	87.0	80.9
0.2	64.0	43.2	40.8	7.1	71.5	51.5
0.5	51.3	22.4	29.9	<1.0	61.6	29.7
0.8	45.5	12.7	26.8	<1.0	52.2	16.9
Small
0	69.3	54.0	36.3	5.5	79.4	66.9
0.2	52.5	24.4	29.4	3.1	63.4	32.7
0.5	41.7	11.0	24.6	<1.0	49.2	13.6
0.8	36.7	5.3	18.2	<1.0	41.9	7.0

Finally, as a basic verification that if P-ES increases, for a fixed level of CM-ES (i.e., low P-ES 1 vs. higher P-ES 2), the ability to detect truly under-performing providers should improve because the provider signal level is increasing. As expected, the simulation results confirmed this (Table 1, compare (a) vs. (c)). For example, at ρ = 0.2, the average overall SEN-W’s for the FE model for low vs. higher P-ES were 62.3% vs. 71.2%; for the RE model the SEN-W’s were 41.2% vs. 49.5% for low vs. higher P-ES.

4.4. Varying Baseline Readmission Rate

We briefly note that the overall patterns of performance (SEN-W and SPEC-ND) across providers and by facility volume were similar for the low, medium and higher baseline readmission rates (results not shown). This also holds under different levels of facility contribution to patient readmission ({γ_i} settings P-ES 1 and P-ES 2) and the two levels of patient case-mix effect (β settings CM-ES 1 and CM-ES 2).

4.5. Impact of Inadequate Case-Mix Adjustment

We next examine the impact of inadequately adjusting for patient case-mix. Recall that β₁ = ⋯ = β₁₀ = 0.5 and β₁₁ = ⋯ = β₁₅ = 1 so that the case-mix variables Z₁₁ – Z₁₅ have larger effects on patient readmission than Z₁ – Z₁₀. The different levels of inadequate case-mix adjustment include: (i) no adjustment, i.e., intercept only model; (ii) inclusion of Z₁ and Z₂; (iii) inclusion of Z₁ – Z₁₀; and (iv) inclusion of Z₁₁ – Z₁₅. The full FE and RE models that include all variables represent the benchmarks.

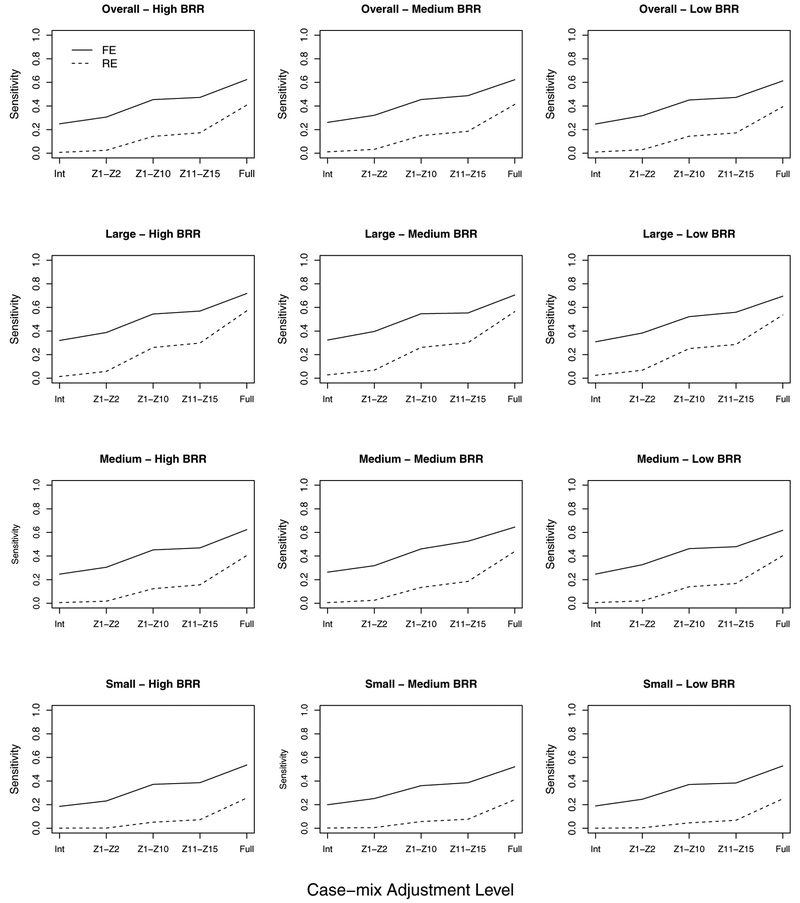
We will describe the impact of inadequate case-mix adjustment using the overall sensitivity for medium baseline rate (Figure 4, middle column), although the relative patterns of results were similar for other cases. Sub-optimal case-mix adjustment degraded both methods’ abilities to accurately identify under-performing providers as expected. This overall characteristic is well-known and was confirmed (see Figure 4). However, several informative novel results can be gleaned from Figure 4. First, it is clear that, nominally, the impact of inadequate case-mix on RE model is substantial. With no adjustment (intercept only model), the RE and FE model sensitivity rates were 1.1% and 25.9% (baseline), respectively; and the benchmark rates were 41.2% and 62.3%. Second, with higher inadequate case-mix adjustments (i.e., models (ii) and (iii)), the impact of the model choice (RE vs. FE) is on the same order as the impact of inadequate case-mix adjustment. For example, the average difference in sensitivity between methods (FE − RE) is 28.6%, while the average difference in sensitivity between benchmark and minimal adjustment using only {Z₁,Z₂} were 37.9% and 30.4% for the RE and FE models, respectively. Similarly, the average sensitivity difference between benchmark and expanded case-mix adjustment with {Z₁,…,Z₁₀} were 38.0% and 30.4% for the RE and FE models, respectively; the average difference between the two models (with {Z₁,…,Z₁₀}) was of similar order at 36.8%. We note that the conservative specificity for the RE models with inadequate case-mix adjustment (Figure S1) was similar to the full model.

Figure 4:

Impact of inadequate case-mix (CM) adjustment levels (Int: Iintercept only, Z₁ − Z₂, Z₁ − Z₁₀, Z₁₁ − Z₁₅, Full: Full model) on sensitivities of RE and FE models. Given are sensitivities to detect under-performing providers for CM correlation ρ = 0.2 across low, medium, and high baseline readmission rates (BRR). Results are presented across all providers (overall) and stratified by provider volume (large, medium, small).

4.6. More General Dependence/Correlation Structure

The patterns of results were similar for the more general correlation structure within and across blocks with unequal correlation among patient case-mix variables (0.01 ≤ ρ_rr′ ≤ 0.25) selected to be similar to USRDS data described in Section 3.1. Nominal SEN-W and SPEC-ND rates were similar to the case with equal correlation of ρ = 0.2. For example, results for the case of medium baseline readmission rate of ~ 27% are provided in Figure S2. Also, the pattern of results for inadequate case-mix adjustment on performance was similar under this more general dependence structure (Figure S3).

4.7. Simulation Studies Based on USRDS Data

Results for simulated data modeled after USRDS data in terms of the observed distribution of the effect of patient-level case-mix (absolute magnitude of β), correlation structure among case-mix risk variables and approximate distribution of γ_i’s (see Figure 1 (b)–(d)) are summarized in Figure S4 across the different levels of baseline readmission rates. Even though differences in performance between FE and RE were expectedly smaller under the larger provider effect size (distribution of γ_i’s); the overall pattern that FE is better able to flag under performing providers also holds in this simulation study. Similarly, the impact of inadequate case-mix adjustment described earlier also holds (see Figure S5).

4.8. Empirical Null Adjustment for Overdispersion

In the RE model, natural variation among facilities is model through a N(0,σ²); however, the FE model does not allow for potential overdispersion. As illustrated by Kalbfleisch and Wolfe (2013), the distribution of the test-statistics (Z-scores) deviate from the theoretical null N(0,1) distribution, and, when conditioned on the facility size, increased variance was observed with increasing facility size. To address this overdispersion, the use of the empirical null distribution was proposed for FE inference, where a robust M-estimation method was fitted to the distribution of Z-scores to obtain variance estimates. The issue was also recently examined in the context of longitudinal monitoring of dialysis facilities (Estes et al. 2018). In this empirical null adjustment approach, each p-value in the FE model is converted into a Z-score. The means and variances of the distributions of the Z-score, stratified by facility volume, are estimated using a robust M-estimation method (implemented using the rlm R function in the MASS library). The empirical null distribution is used to assess a targeted percent of outlier providers, stratified by provider volume. We applied the empirical null adjustment to flag 2.5% of under performing providers. Sensitivity for flagging under-performing providers and specificity for identifying ND providers are summarized in Figure 5 for the case of ρ = 0.2 case-mix correlation (results for other scenarios were similar). With the empirical null adjustment, SEN-W was lower and with an improvement in SPEC-ND compared to flagging based on nominal p-values (unadjusted), as expected. Overall performances of these flagging procedures for the FE model were better than the RE model (e.g., compare to Figure 3 at ρ = 0.2). For example, under the setting ρ = 0.2, the SEN-W for RE and FE based on nominal p-values (Figure 3 - medium) was 62.3% vs. 41.2% (FE-nominal vs. RE) and SPEC-ND was 94.6% vs. 98.9%, respectively. With FE flagging based on the empirical null distribution (Figure 5 - medium), the SEN-W was 50.7% and SPEC-ND was 97.9%. Thus, the SPEC-ND improved (97.9% vs. 98.9% for FE-empirical vs. RE), but the SEN-W for FE-empirical was still substantially better than the RE model (50.7% vs. 41.2%).

Figure 5:

Comparison of overall flagging performance based on (gray) empirical null distribution/adjustment vs. (white) nominal p-values (unadjusted) for FE models. Given are sensitivity and specificity by provider volume (small, medium, and large) and for varying baseline readmission rates (BRR, low, medium and high).

We note that the empirical null adjustment is applied at the correct percent of underperforming providers in the above comparison. Hence, the results obtained from the empirical null adjustment may be optimistic. In addition, multiple testing adjustments could potentially improve flagging results of RE models as well, however the empirical null adjustment cannot directly be applied to the CMS inference of RE in the above comparison, since the inference is not a hypotheses testing procedure that involves a p-value, and is rather based on bootstrap confidence intervals. However, we note that empirical null adjustment is useful when targeting fixed percentage of providers in practice (e.g., 1% or 5%).

5. Discsussion

Our works here present the first direct comparison of RE and FE models, specifically comparing the CMS implementation with inference based on bootstrap CI for SRR and the hypothesis testing approach of the high-dimensional FE. The results showed that the RE models were relatively ineffective at identifying under-performing providers and that the choice between the RE and FE models contributed a large influence on the sensitivity to flag truly underperforming providers, similarly to the impact of extremely inadequate case-mix adjustment. This conclusion applies across provider volumes and various baseline rates of readmission examined. We note that although our focus is on SRR, the same models are applicable to SMR (standardized mortality ratio), SIR (standardized infection ratio) or other condition-specific hospital readmission ratio.

Although one of the conceptual merits of the RE approach is its ability to handle sparse outcome data or providers with very few patients (through shrinkage), the results here suggested that RE models were relatively ineffective at identifying under-performing providers with lower volume. Even in the case of high frequency of readmissions (e.g., baseline readmission rate of ~ 42%) and for providers with large volume, RE models were found to be less effective at identifying under-performing providers for all levels of case-mix complexity/correlation. These results underscore the findings of Kalbfleisch and Wolfe (2013) that although RE models have lower overall estimation error (mean square error, as a result of Stein estimation and empirical Bayes (Efron and Morris 1973)), this average gain does not necessarily translate into improvement in power to identify under-performing (“exceptional”) providers. As noted out by Kalbfleisch and Wolfe (2013), the gain in precision for RE models is achieved in the center of the distribution of outcomes, while FE models have smaller error for “exceptional” providers, which is a main focus of profiling analysis.

We also note that the RE models assume that the provider effects are independent from patient case-mix (risk factors). This may not hold in practice such as when the risk factors may have unbalanced distribution across providers which induces correlation with provider effects. This leads to biased estimates as have been examined in some details in Kalbfleisch and Wolfe (2013). The FE models are not contrained by this assumption. We also note that the computational burden of the RE model, via bootstrapping, is substantial (orders of magnitude higher compared to FE models) and is a relative disadvantage in practice.

Although we have conducted a fairly extensive study, it is certainly not exhaustive in addressing the myriad of issues in profiling analysis. With respect to issues of modeling, estimation and inference, we hope the work here encourages additional studies to further examine the merits and limitations of both the RE and FE approaches in order to improve guidance for practitioners and to develop novel improvements to the methods. We also note that our study here of the impact of inadequate case-mix adjustment on inference (flagging extreme facilities) is limited in scope. The process of case-mix adjustment in practice is complex and often incorporates inputs from diverse stakeholders (e.g., patients, dialysis providers, government regulatory agencies etc.) and policy objectives. For the interested readers, an introductory to the importance of case-mix adjustment in practice can be found in Ash et al. (2012), and for the dialysis population, see CMS (2017) and Estes et al. (2018b) and references therein.