Multicategory Outcome Weighted Margin-based Learning for Estimating Individualized Treatment Rules

Abstract

Due to heterogeneity for many chronic diseases, precise personalized medicine, also known as precision medicine, has drawn increasing attentions in the scientific community. One main goal of precision medicine is to develop the most effective tailored therapy for each individual patient. To that end, one needs to incorporate individual characteristics to detect a proper individual treatment rule (ITR), by which suitable decisions on treatment assignments can be made to optimize patients’ clinical outcome. For binary treatment settings, outcome weighted learning (OWL) and several of its variations have been proposed recently to estimate the ITR by optimizing the conditional expected outcome given patients’ information. However, for multiple treatment scenarios, it remains unclear how to use OWL effectively. It can be shown that some direct extensions of OWL for multiple treatments, such as one-versus-one and one-versus-rest methods, can yield suboptimal performance. In this paper, we propose a new learning method, named Multicategory Outcome weighted Margin-based Learning (MOML), for estimating ITR with multiple treatments. Our proposed method is very general and covers OWL as a special case. We show Fisher consistency for the estimated ITR, and establish convergence rate properties. Variable selection using the sparse l₁ penalty is also considered. Analysis of simulated examples and a type 2 diabetes mellitus observational study are used to demonstrate competitive performance of the proposed method.

1. Introduction

One important goal in precision medicine is to develop effective statistical methods for evaluating treatments with heterogeneous effects among patients. In particular, a treatment that works for patients with certain characteristics may not be effective for others (Simoncelli, 2014). To maximize the overall benefits that patients can receive from the recommended therapy, one popular direction is to look for proper individual treatment rules (ITRs), which are functions that map patient characteristics into the treatment space.

In the recent literature, important developments have been made in building the ITRs for binary treatment cases. In particular, some existing work studied the ITR problem and subgroup analysis using regression approaches (Tian et al. (2014)). Qian and Murphy (2011) formulated the ITR detection into an optimization problem based on a conditional expectation that contains an indicator function. Zhao et al. (2012) used a weighted classification framework and proposed outcome weighted learning (OWL) that used a surrogate loss to replace the indicator function. Zhou et al. (2017) proposed using the residuals produced by linear regression between the outcome and the covariates to improve the finite sample performance of Zhao et al. (2012). Zhang et al. (2012) proposed a robust ITR method to handle potential regression model misspecification in modeling the outcome.

Despite the successful developments in ITR estimation for binary treatments, how the idea should be adapted to multicategory treatment scenarios is still not fully explored. Generally speaking, some regression based methods can be applied for this purpose under parametric assumptions such as certain model mean structures (Robins et al., 2008). However, violation of such assumptions can lead to misleading results. In this paper, we develop a statistical learning framework that can conduct optimal ITR detection for nominal multicategory treatment cases. For simplicity, for the rest of the paper, we use the term multicategory to represent “nominal multicategory” when there is no confusion.

In the classification literature, large-margin classifiers have been popular and often used in practice. Well known examples include the support vector machine (SVM) and penalized logistic regression (PLR) (Hastie et al. (2009)). Among various large-margin classifiers, there are two main types, soft and hard classifiers (Liu et al., 2011). The essential difference is whether obtaining the classifier requires estimating the conditional probability of each class. Soft classifiers such as PLR estimate the class conditional probability, while hard classifiers such as the SVM only target on the classification boundary. Liu et al. (2011) showed that the performance of soft and hard classifiers can vary for problems with different settings. They further proposed the large-margin unified machine (LUM) loss family which covers both soft and hard classifiers through a tuning parameter and can work well for different problems.

To solve k-class multicategory problems, one direct approach is to use sequential binary classifiers. In particular, there are two common approaches in the literature, namely, one-versus-one and one-versus-rest approaches (Allwein et al., 2001). However, these sequential binary classifiers can be suboptimal. One common approach to handle a k-class problem simultaneously is to estimate k functions with the sum-to-zero constraint (Lee et al., 2004; Liu and Yuan, 2011; Zhang and Liu, 2013). Recently, Zhang and Liu (2014) pointed out that this approach can be inefficient because one needs to add an extra sum-to-zero constraint in the optimization problem to guarantee the identifiability and desirable properties of the classifiers. In this way, extra computational cost is needed in solving the corresponding constrained optimization problem. To overcome this drawback, Zhang and Liu (2014) proposed an angle-based large-margin classification technique using k −1 functions without the sum-to-zero constraint. This angle-based method was shown to perform well in terms of both prediction accuracy and computational efficiency.

With the success of large-margin classifiers in conducting standard classification, it is desirable to adapt it into the OWL framework to help find the ITR for multicategory treatments. In this paper, we propose a new technique named Multicategory Outcome-weighted Margin-based Learning (MOML) to solve this problem. We start with the binary treatment scenario, and then generalize the methods into the muticategory treatment case. In particular, we use the vertices of a k-vertex simplex with the origin as its center in a k−1 Euclidean space to represent the k treatments. Then we construct k−1 functions to map the covariates of each patient into a k−1 dimensional vector, and the prediction rule is defined as the treatment that has the smallest angle between this vector and the corresponding vertex of the simplex. Motivated by Zhao et al. (2012), we design the objective function in the loss+penalty form. The loss part is the weighted expectation of a loss function, ℓ(·), of the angle between the (k − 1)-dimensional function vector and the vertex of the actual treatment. The penalty term is used to control the model complexity. In this paper, we compare two options of the penalty terms: l₁ and l₂ penalties. Note that the former option can lead to sparse models and hence can be used for variable selection. According to the loss term introduced, how MOML detects ITR can be understood as follows: for the patients who have a good clinical outcome, the estimated optimal treatment is supposed to be the one that has a small angle to the actual treatment; on the other hand, for the patients who have poor clinical results, the estimated optimal treatments should have large angles with the actual treatments.

The main contributions of this paper are summarized as follows: (1) We propose the Outcome-weighted Margin-based Learning (OML) to achieve ITR estimation for binary treatments. This learning technique produces a flexible class of decision functions that covers both soft and hard classifiers to obtain additional information and better prediction performance. (2) We propose the weighted angle-based method to adapt OML to multicategory treatment scenarios. Under soft classifiers, we discuss how one can obtain the estimated ratio of clinical rewards for each treatment pair so that one can determine the balance between cost and gain. We show the consistency properties and convergence rates of excess risks for MOML. In addition, we compare MOML with the one-versus-one and one-versus-rest extensions of OWL. (3) For the case of linear decision boundaries, we propose using an l₁ penalty to achieve variable sparsity. We further show that this technique leads to variable selection consistency under certain assumptions.

The remainder of the paper is organized as follows. In Section 3, we first review the OWL method and illustrate how OML is introduced for ITR estimation under the binary treatment setting. Then we explain how to extend OML to multicategory cases and give insights on how to maintain Fisher consistency by choosing the loss function. We also point out how the fitted decision functions can be connected to the ratios of the predicted clinical rewards under soft classifiers. In Sections 4 and 5, we provide six simulated examples and an application to a type-2 diabetes mellitus observational study to evaluate the finite sample performance of MOML. Discussions and conclusions are provided in Section 6. Some additional theories, including the excess risk convergence rate and selection consistency, and all the technical details and proofs, are left in the supplemental material.

2. Methodology

In this section, we first introduce the concepts and notations of ITRs in Section 3.1, and then discuss how to use binary margin-based classifiers to find the optimal ITR for two treatments in Section 3.2. In Section 3.3, we demonstrate how to extend the proposed method to the case of multiple treatments.

2.1. Individualized Treatment Rules and Outcome Weighted Learning

Suppose we observe the training datadatasetset {(x_i, a_i, r_i); i = 1, …, n} from an underlying distribution P(X, A,R), where X ∈ ℝ^p is a patient’s covariate vector, A ∈ {1, …, k} is the treatment, and R is the observed clinical outcome, namely, the reward. In particular, P(x, a, r) = f₀(x)pr(a|x)f₁(r|x; a), where f₀ is the unknown density of X, pr(a|x) is the probability of receiving treatment a for a patient with covariates x, and f₁ is the unknown density of R conditional on (X;A). We assume that larger values of R are more desirable. In this paper, we focus on k-arm trials. An ITR D is a mapping from the covariate space ℝ^p to the treatment set {1, …, k}.

Before discussing multicategory treatments, we first introduce the binary optimal ITR and illustrate how it can be formulated as an outcome-weighted binary classification problem. To better understand ITRs, we use E to denote the expectation with respect to P. For any ITR D(·), we let P^D be the distribution of {X, A,R} under which the treatment A is decided by D(X) with P^D(x, a, r) = f₀(x)I(a = D(x))f₁(r|x; a), and let E^D be the corresponding expectation. Therefore, P^D is the distribution with the same X-marginal as P and given X = x, the conditional distribution of R is P(r|X = x;A = D(x)). We assume pr(A = a|x) > 0 for any a ∈ {1, …, k}. One can verify that P^D is absolutely continuous with respect to P, and the Radon-Nikodym derivative dP^D/dP = I{a = D(x)}/π_a(x), where I(·) is the indicator function, and π_a(x) = pr(A = a|x). Consequently, the expected reward for a given ITR D is:

$$E^D(R)=\int Rd{P}^D=\int R\frac{d{P}^D}{dP}dP=\int R\frac{I\{A=D(\mathit{X})\}}{{\pi }_A(\mathit{X})}dP.$$

An optimal ITR D* is defined as $D^{*}={\mathrm{argmax}}_D{E}^D(R)={\mathrm{argmax}}_{D}E\left[R\frac{I\{A=D(\mathit{X})\}}{{\pi }_A(\mathit{X})}\right]$. An equivalent expression of D* is that, for any x, D*(x) = argmax_{a∈{1,...,k}} E(R|X = x;A = a). In other words, D* is an optimal ITR if for any x, the expected reward that corresponds to D*(x) is larger than that of any treatment in {1, …, k}\D*(x). The optimal rule D*(x) is estimated based on the observed training data from the joint distribution of (X, A,R). For a future patient with observed covariate x, the optimal treatment is predicted based on the estimated D*(x).

In the literature, a common approach to find D* is to estimate E(R | A = a;X = x) for each treatment, using parametric or semiparametric regression models (Robins, 2004; Moodie et al., 2009; Qian and Murphy, 2011). For a new patient with covariates x, the treatment recommendation is based on which $\widehat{E}\{R|A=a;\mathit{X}=\mathit{x}\}$ is the maximum.

When there are two treatments, one can relabel them as A ∈ {+1,−1}. Qian and Murphy (2011) showed that in this case, finding D* can be formulated as a binary classification problem. In particular, one can verify that D* is the minimizer of

$$\int \frac{R}{{\pi }_A(\mathit{X})}I\{A\ne D(\mathit{X})\}dP.$$ (2.1)

An important observation is that (3.1) can be viewed as a weighted 0–1 loss in a weighted binary classification problem. To see this, note that with the training dataset {(x_i, a_i, r_i); i = 1, …, n}, one aims to minimize the following empirical loss that corresponds to (3.1)

$$\frac{1}{n}\sum _{i=1}^n\frac{r_i}{{\pi }_{a_i}\left({\mathit{x}}_i\right)}I\left\{a_{i}D\left({\mathit{x}}_i\right)\ne 1\right\}.$$ (2.2)

However, because the indicator function is discontinuous, solving (3.2) can be NP-hard. To overcome this difficulty, one can use a surrogate loss function ℓ(·) for binary margin-based classification. Zhao et al. (2012) proposed the OWL, which employed the hinge loss in the SVM for the optimization. In particular, they assumed that r_i ≥ 0 for all i, and used a single function f(x) for classification, as is typical in binary margin-based classifiers. The treatment is assigned by D(x) = sign{f(x)}. The corresponding optimization problem in Zhao et al. (2012) can be written as

$$\underset{f}{\mathrm{argmin}}\frac{1}{n}\sum _{i=1}^n\frac{r_i}{{\pi }_{a_i}\left({\mathit{x}}_i\right)}{\left\{1-a_{i}f\left({\mathit{x}}_i\right)\right\}}_{+}+\lambda J(f),$$ (2.3)

where (1−u)₊ = max(0,1−u) is the hinge loss function, J(f) is a penalty on f to prevent overfitting, and λ is the tuning parameter.

As a remark, we note that Zhao et al. (2012) only considered nonnegative rewards so that the corresponding problem remains to be convex optimization. When there are negative rewards, they recommended to shift all rewards by a constant. Chen et al. (2017) showed that the performance of OWL varies with the choice of the shifting constant. To address this problem, they modified the loss to handle negative rewards directly.

2.2. Outcome Weighted Margin-based Learning for Binary Treatments

As discussed in Section 2, there are many open problems despite the seminal progress in Zhao et al. (2012). In particular, many choices of margin-based loss functions have not been fully studied in the literature. To investigate this problem, we propose our Outcome weighted Margin-based Learning (OML) method. In Section 2.2, we focus on the case where k = 2 and A ∈ {+1,−1}, and propose the optimization problem of OML as follows

$$\underset{f}{\mathrm{argmin}}\frac{1}{n}\sum _{i=1}^n\frac{r_i}{{\pi }_{a_i}\left({\mathit{x}}_i\right)}\ell \left\{a_{i}f\left({\mathit{x}}_i\right)\right\}+\lambda J(f),$$ (2.4)

where ℓ(·) is a loss function in margin-based classification. Different ℓ(·)’s correspond to different classification methods. For example, SVMs use the hinge loss as in (3.3), and logistic regression uses the deviance loss ℓ(u) = log{1 + exp(−u)}. See the supplementary material for a plot of several commonly used loss functions. We generalize our OML method to handle problems with multiple treatments in Section 3.3.

To explore different soft and hard classifiers, we need to define the theoretical minimizer of a classifier. To begin with, we first assume that r_i ≥ 0. Consequently, (3.4) is convex if ℓ(·) and J(f) are convex, and can then be solved by standard optimization methods, such as those in Boyd and Vandenberghe (2004). We defer the discussion of negative rewards until after Theorem 1. Define the conditional expected loss with respect to (3.4) to be $S(\mathit{x})=E\left[\frac{R}{{\pi }_A(\mathit{X})}\ell \{Af(\mathit{X})\}|\mathit{X}=\mathit{x}\right]$, where the expectation is taken with respect to the marginal distribution of (R,A) for a given x. We define the theoretical minimizer of S(x) as

$$f*(\mathit{x})=\underset{f}{\mathrm{argmin}}S(\mathit{x})=\underset{f}{\mathrm{argmin}}E[\frac{R}{{\pi }_A(\mathit{X})}\ell \{Af(\mathit{X})\}|\mathit{X}=\mathit{x}].$$

Note that f^* depends on the loss function ℓ.

With f* introduced, we can first explore consistency of a classifier. In the standard margin-based classification literature, Fisher consistency (Lin, 2002; Liu, 2007), also known as classification calibration (Bartlett et al., 2006), is a fundamental requirement of classifiers. For problems of finding optimal ITRs using classification, the method is said to be Fisher consistent if the predicted treatment based on f* leads to the best expectation of the outcome rewards (Zhao et al., 2012). In other words, for binary problems, the method is Fisher consistent if sign{f*(x)} = argmax_a R(x, a), where R(x, a) = ∫(R | X = x,A = a)dP is the expected reward for a given treatment a at a fixed x. Zhao et al. (2012) proved that the OWL method using the hinge loss is Fisher consistent for non-negative rewards. In the next proposition, we provide a more general result that is applicable for various loss functions.

Proposition 1

For finding optimal ITRs using binary margin-based classifiers, assume that the rewards are non-negative. Then the method is Fisher consistent if ℓ(·) is differentiable at 0, and ℓ(u) < ℓ(−u) for any u > 0.

Proposition 1 shows that in ITR problems, many binary margin-based classifiers are Fisher consistent. For instance, both soft and hard classifiers in the LUM loss family (Liu et al., 2011) are Fisher consistent. Note that the LUM family uses a parameter c to control whether the classification is soft (c = 0) or hard (c → ∞). See the appendix for more details of the LUM loss functions.

In standard margin-based classification, besides Fisher consistency, f* can also be used to estimate the class conditional probabilities. This approach has been widely used in the literature. See, for example, Hastie et al. (2009), Liu et al. (2011), among others. For completeness, we include a brief explanation on how to estimate probabilities using f* in the appendix. For problems that employ binary classifiers to find optimal ITRs, we show in the next theorem that when one uses certain loss functions, f* can be used to find the ratio between R(x,+1) and R(x,−1).

Theorem 1

For finding optimal ITRs using binary margin-based classifiers, assume that the rewards are non-negative. Furthermore, assume that the loss function ℓ(·) is differentiable with ℓ′(u) < 0 for all u. Then we have that

$$\frac{R(\mathit{x},+1)}{R(\mathit{x},-1)}=\frac{{\ell }^{\prime }\left(-f*\right)}{{\ell }^{\prime }\left(f*\right)}.$$ (2.5)

As a result, for any new observation x, once we obtain the fitted classification function $\widehat{f}(\mathit{x})$, we can estimate the ratio of R(x,+1) to R(x,−1) using ${\ell }^{\prime }\{-\widehat{f}(\mathit{x})\}/{\ell }^{\prime }\{\widehat{f}(\mathit{x})\}$, which provides more information than the ITR itself.

Remark 1

From Theorem 1, one can see that estimation of the ratio of expected rewards in ITR problems is similar to the class conditional probability estimation in standard margin-based classification. In particular, let P₊₁(x) and P₋₁(x) be the conditional class probabilities for classes +1 and −1 respectively in binary classification (see the appendix for more details). One can verify that with similar conditions on ℓ, we can use ${\ell }^{\prime }(-\widehat{f})/{\ell }^{\prime }(\widehat{f})$ to estimate P₊₁(x)/P₋₁(x). For example, in standard logistic regression, estimating P₊₁(x)/P₋₁(x) by ${\ell }^{\prime }(-\widehat{f})/{\ell }^{\prime }(\widehat{f})$ is equivalent to using the logit link function for probability estimation. Similar discussions on class probability estimation for standard multicategory classification problems were made in Zou et al. (2008), Zhang and Liu (2014), and Neykov et al. (2016).

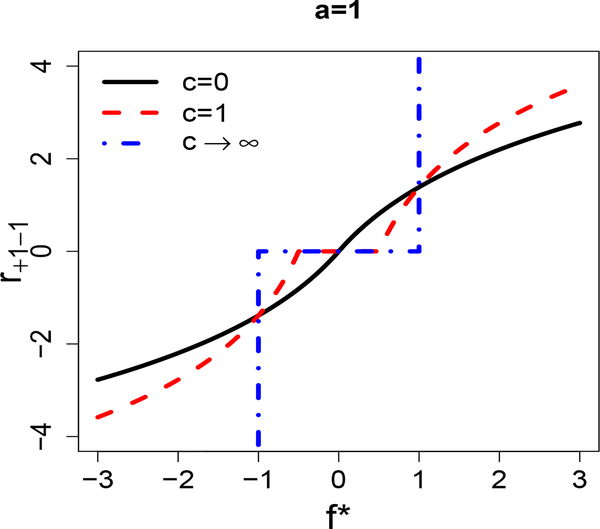
With Theorem 1, we can explore the difference between soft and hard classifiers for finding optimal ITRs. In particular, we plot log{R(x,+1)/R(x,−1)}, denoted by r₊₁₋₁, against f* for some loss functions in the LUM family in Figure 1. We can see that with soft classifiers (c = 0), there is a one-to-one correspondence between r₊₁₋₁ and f*. In other words, we can estimate the ratio between expected rewards for any new patients, using the estimated $\widehat{f}$. This ratio information can be important in practical problems as discussed in Section 1. As we will see in Section 4, if the underlying ratios are smooth functions, soft classifiers tend to perform better than hard classifiers, by accurately estimating the ratios.

Figure 1:

Plot of log{R(x,+1)/R(x,−1)} (r₊₁₋₁ on the y axis) against f* for some LUM loss functions. Here c = 0 corresponds to the soft LUM loss, and c → ∞ corresponds to the SVM hinge loss, which is a hard classifier. Note that a is another parameter in the LUM family (see the appendix), and a = 1, c = 1 correspond to the loss function for distance-weighted discriminant analysis (Marron et al., 2007).

For c > 0, the flat region of r₊₁₋₁ makes estimation of this ratio more difficult. In particular, if $\widehat{f}\in [-c/(1+c),c/(1+c)]$, then the method cannot provide an estimate of r₊₁₋₁. As c increases, the flat region enlarges. In the limit (c → ∞), the hard classifier provides little information about r₊₁₋₁. In other words, hard classifiers bypass the estimation of r₊₁₋₁ and focus on the boundary (that is, R(x,+1) = R(x,−1) in binary problems) estimation only. We demonstrate in the supplemental material that, when the underlying ratios are close to step functions, hard classifiers can perform better than soft ones, because accurate estimation of r₊₁₋₁ can be very difficult.

Next, we discuss how to address negative rewards in our OML method. Recall that when all r_i ≥ 0, one can use a surrogate loss function ℓ that is a convex upper bound of the 0–1 loss, as from (3.2) to (3.4). When r_i < 0, the corresponding 0–1 loss is equivalent to −|r_i|I{a_iD(x_i) ≠ 1}, which can be regarded as a −1–0 loss (Chen et al., 2017). In this case, because the reward is negative, it is desirable to consider the other treatment rather than a_i. Based on these observations, we propose the following optimization of binary problems for both positive and negative rewards,

$$\underset{f}{\mathrm{argmin}}\frac{1}{n}\sum _{i=1}^n\frac{\left|r_i\right|}{{\pi }_{a_i}\left({\mathit{x}}_i\right)}{\ell }_{r_i}\left\{a_{i}f\left({\mathit{x}}_i\right)\right\}+\lambda J(f),$$ (2.6)

where ${\ell }_{r_i}(u)=\ell (u)$ if r_i ≥ 0, and ${\ell }_{r_i}(u)=\ell (-u)$ if r_i < 0 (the inverted loss). Note that ℓ(−u)−1 is the tight convex upper bound of the −1–0 loss as long as ℓ is convex, and minimizing ℓ{−a_if(x_i)} − 1 and ℓ{−a_if(x_i)} with respect to f are equivalent. The treatment recommendation rule for negative rewards is still D(x) = sign{f(x)}.

The next theorem shows that our binary OML method with negative rewards can also enjoy Fisher consistency with mild conditions on the loss function.

Theorem 2

For finding optimal ITRs using binary OML classifiers (3.6), the method is Fisher consistent if ℓ(·) is differentiable at 0, and ℓ(u) < ℓ(−u) for any u > 0.

From Theorem 2 we can see that by including the inverted loss functions for negative rewards, our OML method can still be asymptotically consistent. In contrast, estimation of the rewards ratio gets more involved if R can be negative. The next theorem shows that our OML method is able to provide an upper or lower bound for the corresponding rewards ratios, under some mild assumptions.

Theorem 3

For finding optimal ITRs using binary margin-based classifiers, assume that the expected rewards satisfy that R(x,a) > 0 for all x and a. Furthermore, assume that the loss function ℓ(·) is differentiable with ℓ′(u) < 0 for all u. Then we have that

$$\{\begin{array}{ll}\frac{R(\mathit{x},+1)}{R(\mathit{x},-1)}\ge \frac{{\ell }^{\prime }\left(-f*\right)}{{\ell }^{\prime }\left(f*\right)},\hfill & \text{if}R(\mathit{x},+1)>R(\mathit{x},-1),\hfill \\ \frac{R(\mathit{x},+1)}{R(\mathit{x},-1)}\le \frac{{\ell }^{\prime }\left(-f*\right)}{{\ell }^{\prime }\left(f*\right)},\hfill & \text{if}R(\mathit{x},+1)<R(\mathit{x},-1).\hfill \end{array}$$ (2.7)

Theorem 3 shows that ${\ell }^{\prime }(-\widehat{f})/{\ell }^{\prime }(\widehat{f})$ can be used as a lower bound for the rewards ratio when treatment +1 is better, and an upper bound if −1 is better. The condition that R(x, a) > 0 for all x and a can be satisfied, for example, when patients with no treatments have zero expected rewards, and all treatments under study have preliminary results to show that they are overall effective. Note that when there are negative rewards, our OML method cannot provide an accurate estimation of the rewards ratio but a bound (see the proof of Theorem 3 in the supplemental material for more details), yet the method is still Fisher consistent. Hence, we can see that in ITR problems, rewards estimation can be more difficult than treatment recommendation. This is analogous to standard classification, in which probability estimation can be more difficult than label prediction.

In the next section, we generalize our OML method to handle problems with multiple treatments.

2.3. Multicategory Outcome Weighted Margin-based Learning

To find D* in a practical problem with k > 2 treatments, one can employ sequential binary classifiers, such as the one-versus-one and one-versus-rest approaches. However, these ideas can lead to inconsistent ITR estimators (see the supplemental material for a proof on the inconsistency of the one-versus-rest SVM approach). As discussed in Section 2, it can be desirable to have a multicategory classifier that considers all k treatments simultaneously in one optimization problem.

In the literature, many commonly used simultaneous multicategory margin-based classifiers employ k classification functions for the k classes, and impose a sum-to-zero constraint on the k functions to reduce the parameter space and to ensure some theoretical properties such as Fisher consistency. Recently, Zhang and Liu (2014) showed that this approach can be redundant, and suboptimal in terms of computational speed and classification accuracy. To overcome these difficulties, Zhang and Liu (2014) proposed the angle-based classification method. In this paper, we propose to find the optimal ITRs with multiple treatments in the angle-based classification framework.

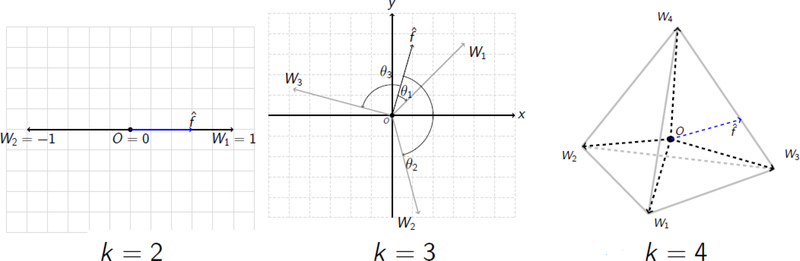
The standard angle-based classification can be summarized as follows. Let {(x_i, y_i); i = 1, …, n}, be the training dataset, where y represents the class label. Define a simplex W with k vertices {W₁, …,W_k} in a (k − 1)-dimensional space, such that

$${\mathit{W}}_j=\{\begin{array}{ll}{(k-1)}^{-1/2}{\mathbf{1}}_{k-1},\hfill & j=1,\hfill \\ -\left(1+k^{1/2}\right)/\{{(k-1)}^{3/2}\}{\mathbf{1}}_{k-1}+{\{k/(k-1)\}}^{1/2}{e}_{j-1},\hfill & 2\le j\le k,\hfill \end{array}$$

where 1_k−1 is a vector of 1’s with length k − 1, and e_j ∈ ℝ^k−1 is a vector with the jth element 1 and 0 elsewhere. This simplex has symmetry with all vertices being equal distances to each other. The anglebased classifier uses a (k − 1)-dimensional classification function vector f = (f₁, …, f_k−1)^T, which maps x to f(x) ∈ ℝ^k−1. Note that f introduces k angles with respect to W₁, …,W_k, namely, ∠(f,W_j); j = 1, …, k. The prediction rule is based on which angle is the smallest. In particular, $\widehat{y}(\mathit{x})={\mathrm{argmin}}_{j\in \{1,\dots ,k\}}\angle \left(\mathit{f},W_j\right)$, where $\widehat{y}(\mathit{x})$ is the predicted label for x. Figure 2 illustrates how to make predictions using this angle based classification idea when k = 2, 3, and 4. When k = 3, for example, the mapped observation $\widehat{f}$ is predicted as the class corresponding to W₁ because θ₁ is the smallest angle. Based on the observation that argmin_{j∈{1,...,k}} ∠(f,W_j) = argmax_{j∈{1,...,k}}〈f,W_j〉, Zhang and Liu (2014) proposed the following optimization problem for the angle-based classifier

$$\underset{f}{\mathrm{argmin}}\frac{1}{n}\sum _{i=1}^n\ell \left\{\langle {\mathit{W}}_{y_i},\mathit{f}\left({\mathit{x}}_i\right)\rangle \right\}+\lambda J(\mathit{f}),$$ (2.8)

where ℓ(·) is a binary margin-based surrogate loss function which is typically non-negative and satisfies ℓ(u) < ℓ(−u) for any u > 0, J(f) is a penalty on f to prevent overfitting, and λ is a tuning parameter to balance the goodness of fit and the model complexity. One advantage of the angle-based classifier is that it is free of the sum-to-zero constraint, and can be more efficient for learning with big datasets.

Figure 2:

Illustration for the angle-based classification with k = 2,3, and 4. For example, when k = 3 (as the plot in the middle shows), the mapped observation $\widehat{f}$ is predicted as the class corresponding to W₁ because θ₁ < θ₃ < θ₂.

To generalize our OML method from the binary setting to handle multicategory problems, we propose the following optimization

$$\underset{f}{\mathrm{argmin}}\frac{1}{n}\sum _{i=1}^n\frac{\left|r_i\right|}{{\pi }_{a_i}\left({\mathit{x}}_i\right)}{\ell }_{r_i}\left\{\langle {\mathit{W}}_{a_i},\mathit{f}\left({\mathit{x}}_i\right)\rangle \right\}+\lambda J(\mathit{f}),$$ (2.9)

where ${\ell }_{r_i}$ is defined as in (3.6). As to the penalty term J(f), we discuss two options in this paper: the l₂ and l₁ penalties. When applying the l₁ penalty, one can remove the covariates that have zero coefficient estimates in all k − 1 components of the fitted f. We show in Section 4 that such a sparse penalty can have selection consistency under linear learning. For a new patient with the covariate vector x, once the fitted classification function vector $\widehat{\mathit{f}}$ is obtained, the corresponding treatment recommendation is ${\mathrm{argmax}}_{a\in \{1,\dots ,k\}}\langle W_a,\widehat{\mathit{f}}(\mathit{x})\mathrm{\rangle }$. One can verify that when k = 2, (3.9) reduces to (3.6). Hence, for the statistical learning theory (see the supplemental material), we focus on multicategory classification, and the results can be applied to binary cases directly.

Next, we study Fisher consistency of MOML for multicategory treatments. In the literature of standard margin-based classification, Fisher consistency is more involved in multicategory problems than in binary settings. For example, it is known that the binary SVM is Fisher consistent (Lin, 2002). However, its direct generalization to the multicategory classifier is inconsistent, both in the framework of using k functions and a sum-to-zero constraint (Liu, 2007), and in the framework of angle-based classification (Zhang and Liu, 2014). To overcome these challenges, many new multicategory SVMs have been proposed. See, for example, Lee et al. (2004), Liu and Yuan (2011), among others. For finding optimal ITRs, we have the following result for Fisher consistency of our MOML method in multicategory treatment problems.

Before presenting our main result, we introduce an important assumption. First, recall that the expected reward for a given treatment j at x is R(x, a) = ∫ (R | X = x,A = a)dP. Define the positive part of a conditional reward to be $R_j^{+}(\mathit{x})=\int (R|\mathit{X}=\mathit{x},A=j)I(R>0)dP$, and the negative part to be $R_j^{-}(\mathit{x})=\int (R|\mathit{X}=\mathit{x},A=j)I(R<0)dP$. One can verify that $R(\mathit{x},j)=R_j^{+}(\mathit{x})+R_j^{-}(\mathit{x})$. Here $R_j^{-}(\mathit{x})$ can be used to measure the possibility and severeness of adverse effects for treatment j on patients with the covariate vector x. The next assumption requires that R⁻(x) of the best treatment for a given patient should not be small.

Assumption 1

For a patient with the covariate vector x, denote the best treatment by j (i.e., R(x, j) > R(x, i) for any i ≠ j). Then, $R_j^{-}(\mathit{x})\ge R_i^{-}(\mathit{x})$ for any i ≠ j.

Assumption 1 is desirable, and often necessary for practical problems. In particular, for any patient, we should expect that the best treatment does not have a large probability of adverse effects, and its adverse effects are relatively mild. Assumption 1 can be satisfied, for example, when the rewards are all positive, or the marginal distributions of rewards for different patients and treatments are the same except for a constant shift (e.g., normal distributions with a common variance). With Assumption 1, we are ready to present the next theorem for Fisher consistency of our MOML method.

Theorem 4

For finding optimal ITRs using MOML classifiers (3.9), suppose Assumption 1 is valid, then the method is Fisher consistent if ℓ(·) is convex and strictly decreasing. Moreover, the MOML with the hinge loss is not Fisher consistent.

Note that Theorem 4 provides a sufficient condition for the MOML classifier to be Fisher consistent. In the literature, there are some classifiers whose loss functions do not satisfy the condition in Theorem 4, yet one can still verify that the corresponding MOML method is Fisher consistent. For example, one can use a similar approach as in the proof of Theorem 4 to show that our MOML method using the proximal SVM loss is Fisher consistent. On the other hand, our MOML SVM (i.e. using the standard hinge loss) is not Fisher consistent. To overcome this challenge, we propose to use the LUM loss function with a large but finite c. This loss function is very close to the SVM hinge loss which corresponds to c → ∞, and it can preserve Fisher consistency. Note that a similar approach was previously used in Zhang and Liu (2014) to obtain a Fisher consistent angle-based classifier.

To estimate the ratio of the expected rewards for different treatments, we have the following theorem.

Theorem 5

Suppose the loss function ℓ(u) is convex and differentiable with ℓ′(u) < 0 for all u. If the random reward satisfies R ≥ 0, then for any i ≠ j ∈ {1, …, k}, we have

$$\frac{R(\mathit{x},i)}{R(\mathit{x},j)}=\frac{{\ell }^{\prime }\left(\langle \mathit{f}*,{\mathit{W}}_j\rangle \right)}{{\ell }^{\prime }\left(\langle \mathit{f}*,{\mathit{W}}_i\rangle \right)}.$$

From Theorem 5, once $\widehat{\mathit{f}}(\mathit{x})$ is obtained for a new patient with x, we can estimate the rewards ratio between the ith and jth treatments by ${\ell }^{\prime }\{\langle \widehat{\mathit{f}}(\mathit{x}),{\mathit{W}}_j\rangle \}/{\ell }^{\prime }\{\langle \widehat{\mathit{f}}(\mathit{x}),W_i\rangle \}$. Additional discussions on soft and hard classifiers are provided in the supplemental material.

We also develop some additional theoretical results of MOML such as the convergence rate of excess risks. In addition, we show that MOML enjoys variable selection consistency under linear ITRs with J(f) to be the l₁ penalty. More details are included in the additional statistical learning theory section of the supplemental material.

3. Numerical Studies

In this section, we use six simulation studies with both linear and nonlinear ITR boundaries to assess the finite sample performance of the proposed MOML method. For all examples, we fit MOML with the l₂ penalty and compare it with standard outcome weighted learning (OWL, Zhao et al. (2012)) with extensions of one-versus-rest (OWL-1) and one-versus-one (OWL-2). Furthermore, to evaluate the performance of variable selection as discussed in Section 3.2, we implement MOML with the l₁ penalty (MOML-l₁) for all linear ITR boundary examples. When fitting OWL, we replace the hinge loss with the modified loss in (7) to improve its performance for a fair comparison. For the one-versus-rest extension, we conduct sequential one-versus-rest binary optimal treatment estimation (i.e. 1 vs others, 2 vs others, · · ·, k vs others) and then pick the treatment recommended by the classifier ${\widehat{\mathit{f}}}_j$ with the largest magnitude among j = 1, · · · , k. For the one-versus-one extension, we first estimate the decision function ${\widehat{\mathit{f}}}_l$, for l = 1, · · · , k(k − 1)/2, based on each pair of treatments (i.e. 1 vs 2, 1 vs 3, · · ·, k − 1 vs k), and then pick the treatment suggested by the ${\widehat{\mathit{f}}}_l$ with the largest magnitude. Note that the one-versus-one extension only uses a subset of the data to fit each ${\widehat{\mathit{f}}}_l$. For a meaningful comparison, we restrict f to be linear functions of x for all the models in linear ITR boundary examples, and apply Gaussian kernel learning to fit f in non-linear ITR boundary examples.

When we generate the datasets, we first simulate a training set which is used to fit the model. We also generate an independent and equal-size tuning set to find the best combination of tuning parameters as well as a much larger testing set to evaluate the model performance (10 times as big as the training set). As to the tuning parameter range, we choose a from {0.1, 1, 10}, let c vary in {0.1, 10, 100, 1000}, and let λ vary in {0.001, 0.01, 0.1, 1, 10}. We report the averages and standard deviations of the mis-classification rates and empirical value functions of testing sets as the criteria for model assessment. The empirical value function is defined as ${\mathbb{P}}_n^{*}\left[I(A=D(\mathit{X}))R/{\pi }_A(\mathit{X})\right]/{\mathbb{P}}_n^{*}\left[I(A=D(\mathit{X}))/{\pi }_A(\mathit{X})\right]$, where ${\mathbb{P}}_n^{*}$ denotes the empirical average of the testing dataset (Zhao et al., 2012). The value function is treated as a more comprehensive measure on how close the estimated ITR is to the true optimal ITR. We repeat the simulations for 50 times in each example.

In the first four examples, we generate the datasets in which the optimal treatment boundaries are linear functions of the covariates. We add additional covariates as random noises in Examples 3 and 4. In the last two examples, we discuss non-linear ITR scenarios and perform Gaussian kernel learning classifiers. We let the dimensions of the covariates x vary in p ∈ {10, 50} for all examples. The kernel bandwidth τ is fixed to be $1/\left(2{\widehat{\sigma }}^2\right)$ where $\widehat{\sigma }$ is the median of the pairwise Euclidean distance of the simulated covariates (Wu and Liu, 2007). The details of each setting are presented as below:

Example 1

We consider three points (c₁, c₂ c₃) of equal distances from the p-dimensional space to represent the cluster centroids of the true optimal treatments. For each c_j where j = 1, 2, 3, we generate its covariate X_i from a multivariate normal distribution N(c_j, I_p), where I_p is a p-dimensional identity matrix. The actually assigned A_i follows a discrete uniform distribution U{1, 2, 3}. The reward R_i follows a Gaussian distribution N(μ(X_i,A_i, d_i), 1), where $\mu \left(X_i,A_i,d_i\right)=X_i^T\mathit{\beta }+5\cdot I(A_i=d_i)$, ${\mathit{\beta }}^T=({\mathbf{1}}_{p/2}^T,-{\mathbf{1}}_{p/2}^T)$ and d_i is the optimal treatment for X_i determined by the cluster centroids. The training dataset is of size 300.

Example 2

We define a five-treatment scenario in which the five centroids (c₁, · · ·, c₅) form a simplex in ℝ⁴. The marginal distribution X_i|c_j follows a normal distribution with mean c_j and covariate matrix as 0.1I_p. The treatment A_i follows a discrete uniform U{1, · · ·, 5}. The reward R_i ~ N(μ(X_i,A_i, d_i), 0.1), where $\mu \left(X_i,A_i,d_i\right)=X_i^T\mathit{\beta }+3\cdot I\left(A_i=d_i\right)+1$ and ${\mathit{\beta }}^T=0.1\times ({\mathbf{1}}_{p/2}^T,-{\mathbf{1}}_{p/2}^T)$. The training dataset is of size 500.

Example 3

This is an example with ten treatments and the optimal ITR boundary depends on the first two covariates, i.e. (X₁,X₂). The ten corresponding centroids (c₁, · · · , c₁₀) spread out evenly on the unit circle $X_1^2+X_2^2=1$ and the marginal distribution of (X₁,X₂)^T is a normal distribution with mean c_j and covariate matrix 0.03I₂. Similar to Example 2, A_i ~ U{1, · · ·, 10} and R_i ~ N(μ(X_i,A_i, d_i),1), where $\mu \left(X_i,A_i,d_i\right)=X_i^T\mathit{\beta }+5\cdot I\left(A_i=d_i\right)-2$ and ${\mathit{\beta }}^T=\left({\mathbf{1}}_5^T,-{\mathbf{1}}_5^T,{\mathbf{0}}_{p-10}^T\right)$. The training dataset is of size 600.

Example 4

All the settings are the same as Example 2 except that ${\mathit{\beta }}^T=0.1\times \left(1,1,-1,-1,{\mathbf{0}}_{p-4}^T\right)$.

Example 5

This is a three class example with each centroid c_j for j = 1, 2, 3 distributed on two mess points with equal probabilities. The marginal distribution of (X₁,X₂)^T is a mixture normal 0:5N[(cos(jπ/3), sin(jπ/3))^T, 0:08I₂]+0:5N[(cos(π+jπ/3), sin(π+jπ/3))^T, 0:08I₂]. The treatment A_i ~ U{1, 2, 3} and the reward R_i ~ N(μ(X_i,A_i, d_i), 1), where $\mu \left(X_i,A_i,d_i\right)=X_i^T\mathit{\beta }+5\cdot I\left(A_i=d_i\right)-1$ and ${\mathit{\beta }}^T=({\mathbf{1}}_{p/2}^T,-{\mathbf{1}}_{p/2}^T)$. The training dataset is of size 300.

Example 6

In this example, the optimal treatment d_i for each X_i is determined with probability 95% by the signs of two underlying non-linear functions $f_1(X)=X_1^2+X_2^2+\exp \left\{0.5X_3\right\}$ and $f_2(X)=X_4^2-X_5^3-X_6$ while a random noise is added to d_i with probability 5% to create a positive Bayes error. In particular, we have d_i defined as

$$d_i=d\left(X_i\right)=\{\begin{array}{cc}1+{\left[\mathrm{sign}\left(f_1\left(X_i\right)-m_1\right)\right]}_{+}+2\times {\left[\mathrm{sign}\left(f_2\left(X_i\right)-m_2\right)\right]}_{+}& \text{with}\text{prob.}0.95\\ U_i& \text{with}\text{prob.}0.05\end{array},$$

where m₁ and m₂ are the medians of f₁ and f₂ respectively, and U_i follows a discrete U{1, 2, 3, 4} which is independent of (A_i,X_i). The covariate X_i follows a continuous uniform distribution U(0, 1), A_i ~ U{1, · · ·, 4}, and R_i ~ N(μ(X_i,A_i, d_i), 1), where $\mu \left(X_i,A_i,d_i\right)=X_i^T\mathit{\beta }+5\cdot I\left(A_i=d_i\right)-1$ and ${\mathit{\beta }}^T=({\mathbf{1}}_{p/2}^T,-{\mathbf{1}}_{p/2}^T)$. The training dataset is of size 500.

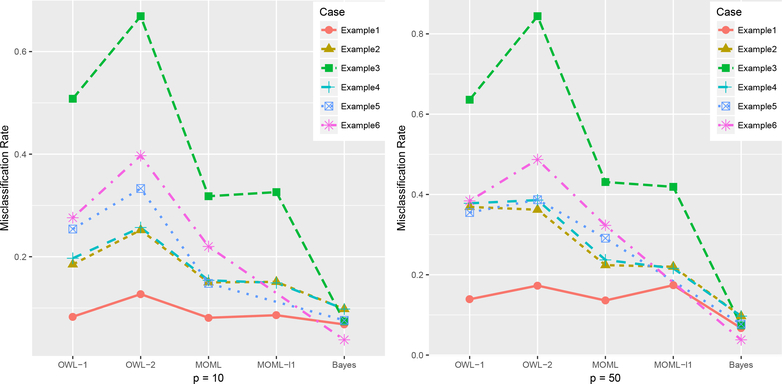
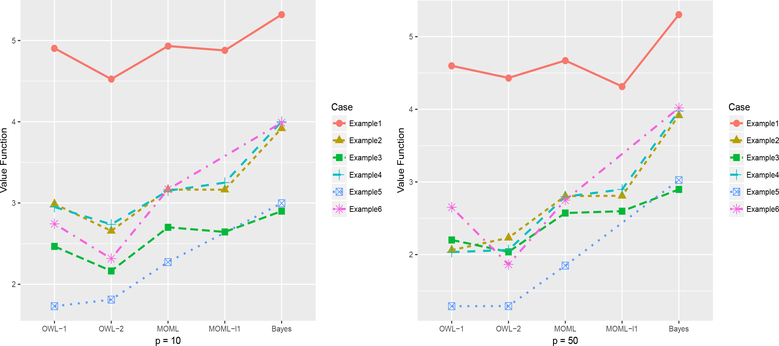
Figures 3 and 4 plot the sample means of the misclassification rates and the empirical value functions produced by all the models. The numerical results with standard deviations are reported in tables in the supplemental material. From the results, MOML with the l₂ penalty, MOML with the l₁ penalty and OWL-1 (with one-versus-rest extension) perform equivalently when the underlying ITR is not very complex and the treatment effect is strong enough as Example 1 shows when p = 10. Example 2 represents the situations when the linear ITR becomes more complex and the treatment effect is intermediate. Under this circumstance, MOML can produce much larger empirical value function results than the two simple OWL extensions. Example 4 has a similar setting as Example 2 while some noise variables are added to the covariate set. Under this scenario, MOML with the l₁ penalty can outperform MOML with the l₂ penalty because it is able to remove many unnecessary noise variables. Such an improvement of prediction accuracy becomes more clear under the case with higher covariate dimensions, i.e. p = 50. As to the selection result, when p = 10, MOML-l₁ removes 64.6% noises on average while keeping all the useful variables; when p = 50, about 57.6% noises are removed and all the useful ones are kept. Example 3 represents a difficult ITR detection scenario with a large number of treatments involved (k = 10). In this case, the two MOML methods can have much smaller misclassification rates than the two OWL extensions and this implies that MOML can produce stable estimation results. The variable selection results show that MOML-l₁ succeeded in removing 68.8% and 60.2% noises under p = 10 and p = 50 respectively. All the true variables are all kept under both cases. Examples 5 and 6 are two representatives of nonlinear ITRs. In Example 5, MOML can maintain a low misclassification rate when the covariate dimension is not large (i.e. p = 10). As more variables are added into the covariate space, all the methods produce significantly worse prediction performance even though MOML can still outperform the two OWL extensions. In this way, one is recommended to take actions to reduce the covariate dimension before applying nonlinear MOML in practice. In Example 6, we intentionally include some outliers into the samples to assess models’ robustness. All the methods are affected while MOML can still produce better prediction results than other methods.

Figure 3:

Plots of misclassification rates of simulation studies. OWL-1 and OWL-2 represent the two extensions of outcome weighted learning (one-versus-rest and one-versus-one), MOML and MOML-l₁ represent outcome weighted margin-based learning with l₂ and l₁ penalties respectively, and Bayes represents the empirical Bayes error.

Figure 4:

Plots of value functions of simulation studies. OWL-1 and OWL-2 represent the two extensions of outcome weighted learning (one-versus-rest and one-versus-one), MOML and MOML-l₁ represent outcome weighted margin-based learning with l₂ and l₁ penalties respectively, and Bayes represents the empirical Bayes error.

Finally, we explore the advantages of soft and hard classifiers using Examples 1 and 6. We try different values of c, and show that a properly tuned classifier performs very well. The details are left in the supplemental material.

4. Application to a Type 2 Diabetes Mellitus Study

In this section, we apply the proposed method to a type 2 diabetes mellitus (T2DM) observational study to assess its performance in real life data applications. This study includes people with T2DM during 2012–2013, from clinical practice research datalink (CPRD) (Herrett et al. (2015)). Four anti-diabetic therapies have been considered in this study: glucagon-like peptide-1 (GLP-1) receptor agonist, long-acting insulin only, intermediate-acting insulin only and a regime including short-acting insulin. The primary target variable is the change of HbA1c before and after the treatment, and seven clinical factors are used including age, gender, ethnicity, body mass index, high-density lipoprotein cholesterol (HDL), low-density lipoprotein cholesterol (LDL) and smoking status. In total, 634 patients satisfy aforementioned requirements and around 5% have complete observations. Considering the large missing proportion, we perform the following steps to deal with the issue. First, all the factors that have a missing rate larger than 70% are removed. Second, a standard t test is implemented for each remained factor to check whether its missing indicator affects the response. If the test result is statistically significant, we keep the variable in while removing all its missing observations. Otherwise we delete the variable. We have 230 observations left after this cleaning process.

We apply the same methods with linear and Gaussian kernels to the cleaned T2DM dataset as in the simulation analysis. We use the negative value of HbA1c change as the reward because the treatment goal is to decrease HbA1c. The prosperity score π_A(X) is calculated based on a fitted multinomial logistic regression between the assigned treatment and all the covariates. We use the 5-fold cross-validation to choose the best tuning parameter over 50 replications. In particular, we randomly divide the clean data into five equal-sized subsets and train the model based on every four of them (training sets) in turn and make prediction using the remaining one (validation sets). The means and standard deviations of the empirical value functions for training and validation sets are presented in Table 1.

Table 1:

Analysis Results for the T2DM Dataset. Estimated averages and standard deviations (in parenthesis) of the value function are reported using 5-fold cross-validation with 50 replications. OWL-1 and OWL-2 represent two extensions of OWL (one-versus-rest and one-versus-one), MOML and MOML-l₁ represent the outcome weighted margin-based learning with l₂ and l₁ penalties respectively. The observed average reward for the cleaned dataset is 2.246.

	Training	Validation
OWL-1-Linear	2.712 (0.329)	2.371 (0.483)
OWL-2-Linear	2.487 (0.233)	2.221 (0.561)
OWL-1-Gaussian	4.118 (0.401)	3.285 (0.490)
OWL-2-Gaussian	4.003 (0.374)	3.221 (0.468)
MOML-Linear	2.610 (0.130)	2.440 (0.320)
MOML-l1-Linear	2.813 (0.138)	2.533 (0.182)
MOML-Gaussian	4.105 (0.221)	3.612 (0.328)

Table 1 shows that the proposed MOML with the Gaussian kernel gives the best predicted value function results with its standard deviation smaller than that of OWL with the Gaussian kernel. MOML-l₁ suggests keeping all the variables over the 50 replicates, which indicates that the covariates remained in the clean data can be all potentially important when a linear function is chosen to fit the ITR. In terms of the estimated optimal treatment assignment results, the one-versus-rest extension of OWL with

Gaussian kernel (OWL-1-Gaussian) assigns around 32% patients into the short-acting insulin and the rest into the other three treatment groups in a relatively even way. MOML with the Gaussian kernel recommends approximate 40% patients to take the short-acting insulin, around 25% and 23% patients to take intermediate and long-acting insulin respectively and less than 12% to take the GLP-1. This conclusion is consistent to some literature on short-acting insulins, which shows the benefit of reducing HbA1c (Holman et al., 2007). On the other hand, prandial insulins can also increase the risk of hypo and weight gain. In this way, it can be worthwhile to treat some composite metric as the outcome, including HbA1c change, hypo events, and weight gain information together, to find the corresponding optimal treatment rules.

5. Discussion

In this paper, we propose a margin-based loss function to solve the optimal individual treatment estimation problem for binary treatments and then extend it into multicategory treatment scenarios. For binary treatments, we develop the loss based on the LUM family so that the proposed method can cover a wide range of ITRs varying from soft to hard classifiers. The standard OWL is one special case of the proposed margin-based learning methods because the LUM family loss becomes the hinge loss when c → ∞ and a = 1. For multiple treatments, we formulate the loss as a weighted sum of angles between the estimated decision function f and the actual treatment A. We show that MOML enjoys desirable theoretical properties and has higher prediction accuracy under both linear and nonlinear treatment assignment boundaries. Our method can produce well-understood ITR results with clear geometric interpretation. Moreover, the optimization problem of MOML is unconstrained and hence can be more efficient to compute when compared to other multicategory methods with the sumto-zero constraint. We also showed that the proposed MOML can have selection consistency using the l₁ penalty for the case with linear decision boundaries. This idea can be extended for nonlinear boundaries as well. One possibility is to use the idea of weighed kernels and impose a weight vector w in front of the covariate x in the standard kernel definition (Chen et al., 2017).