Using Cure Models to Estimate the Serial Interval of Tuberculosis With Limited Follow-up

Abstract

Serial interval (SI), defined as the time between symptom onset in an infector and infectee pair, is commonly used to understand infectious diseases transmission. Slow progression to active disease, as well as the small percentage of individuals who will eventually develop active disease, complicate the estimation of the SI for tuberculosis (TB). In this paper, we showed via simulation studies that when there is credible information on the percentage of those who will develop TB disease following infection, a cure model, first introduced by Boag in 1949, should be used to estimate the SI for TB. This model includes a parameter in the likelihood function to account for the study population being composed of those who will have the event of interest and those who will never have the event. We estimated the SI for TB to be approximately 0.5 years for the United States and Canada (January 2002 to December 2006) and approximately 2.0 years for Brazil (March 2008 to June 2012), which might imply a higher occurrence of reinfection TB in a developing country like Brazil.

Abbreviations:

SI

serial interval

TB

tuberculosis

The serial interval (SI), defined as the time between symptom onset of an infector and infectee pair, is commonly used to understand infectious disease transmission dynamics (1). It is typically used as an approximation of the more biologically relevant generation interval—the time between the (unobserved) point of infection in an infector and infectee. Assuming that the time between infection and onset of symptoms is independent and identically distributed for the infector and the infectee, the SI is an unbiased estimator of the generation interval (1). This value, coupled with the reproductive number (the average number of secondary cases generated per case), is important in understanding how rapidly an infectious disease might spread through a population and is frequently used in modeling studies of infectious diseases (2–8).

The SI is often estimated from observed data as the mean or median of the observed (or reported) time between symptom onset in infector and infectee pairs (2), which is often determined using contact tracing. Genetic information is frequently incorporated to increase the probability of identifying a correct linkage (9). In diseases with a relatively short infectious period, it is reasonable to assume that all SIs can be observed with adequate follow-up and detailed contact tracing. Then one can estimate the entire SI distribution using basic maximum likelihood estimation and model fit criteria (such as the Akaike information criterion) to choose among potential parametric distributions, such as the gamma, lognormal, or Weibull (7, 10, 11). Modifications to account for truncation (10), the discreteness of data traditionally collected (11), and interval censoring (12) have been described elsewhere. Additionally, nonparametric methods have been proposed to estimate survival curves and are readily applicable to this problem (10, 13, 14).

Estimation of the SI for tuberculosis (TB) is complicated by 2 factors. First, in contrast with diseases such as influenza, there can be a long latent period (of potentially years) between infection with Mycobacterium tuberculosis, the causative agent of TB, and the development of TB symptoms (“TB disease”). Due to the long disease latency, it is not feasible to follow all contacts of an infectious case long enough to determine whether they develop disease, and one should consider infected contacts of a TB case as right censored (i.e., having left the study before the outcome event occurred). Second, the lifetime risk of developing symptomatic TB disease, given initial infection, is estimated to be 5%–10% in an immunocompetent host (15) and is greater in younger age groups and less in older ones (16). However, survival analysis methods assume that all the “censored” individuals will eventually experience the event of interest, which is clearly not the case when the outcome of interest is development of TB disease. This assumption is therefore violated and could lead to substantial bias in the resulting estimate of the SI for TB (15, 17, 18).

A systematic review (19) showed that existing approaches to estimate the SI of TB mostly use only observed SIs. Here, we show how one can use cure models, first proposed by Boag in 1949 (20), to estimate the SI (or any parametric survival curve) when those who have not experienced disease by the end of follow-up are not all still at risk of developing disease. We illustrate through simulations the limitations of this approach and the assumptions needed to implement it and apply these methods to TB study data.

METHODS

Statistical methods

We first describe a naive approach using only the observed SIs and discarding information on all individuals who did not develop disease. Denote the observed SIs by 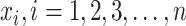. The joint likelihood function is:

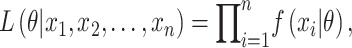(1)

where 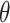is the parameter space in a parametric distribution and 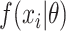is the probability density function for the observed SIs. We consider either the gamma or lognormal distribution (7, 10, 19, 21–23). To estimate 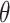, we can either use a maximum likelihood estimation approach or a Bayesian approach using Markov chain Monte Carlo sampling.

The limitation of the naive method is the assumption of having observed all the SIs, which is unlikely due to insufficiently long follow-up, as described previously. The standard approach for accounting for this censoring in the data is to modify the likelihood by dividing the entire data set between those who had an observed SI and those who did not, which assumes that all individuals eventually develop the disease of interest (24) but, due to follow-up being too short or individuals being lost to follow-up, we fail to observe all the SIs. Here, we let 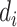be the censoring indicator for person 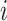where 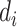= 1 if the SI is observed, and 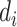= 0 if the SI is censored. The joint likelihood function is:

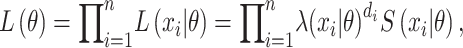(2)

where 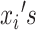are either the observed SIs for those who develop TB disease before the end of the study or the total time that a censored individual is followe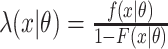d, and 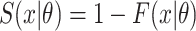. Here, and 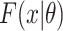are the probability density function and cumulative distribution function for the SIs. Again maximum likelihood estimation or Markov chain Monte Carlo approaches to estimation are appropriate.

As noted, a key assumption that all individuals will eventually experience the event of interest is violated in TB studies. A similar situation occurs in cancer where many individuals experience cure after treatment, and survival models to describe the time to relapse must incorporate the probability of cure (25). The “cure model” was developed for this problem. It divides the population into those who will have the event and those who will not (hence have infinite survival time) and adds an additional parameter to capture the probability of a person having the event of interest (e.g., developing active disease), p, to the likelihood function which becomes

(3)

with 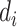, 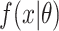and 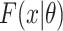are defined as before. Because censoring is present in the data, the 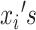are either the observed SIs for those who develop TB disease before the end of the study or the total time that a censored individual is followed. The parameter p is for the probability of developing disease and 1 − p is the probability of being “cured.” The introduction of this parameter creates a problem of identifiability and without additional data, standard maximum likelihood estimation will struggle to simultaneously estimate this parameter and the parameters of the SI estimation accurately. One approach to this problem is to use existing literature and fix p at a value, for instance 0.10 for TB. However, without strong information on this parameter, we risk biasing the estimate. Because this quantity is not observable, in the past it has been estimated using the expectation-maximization—EM—algorithm (26). A less heavy-handed approach is to use Bayesian estimation techniques, where we create an informative prior for p, based on the literature. Given that 0 ≤ P ≤ 1, a beta distribution is appropriate and can be centered at a value that is identified from existing literature. For the case of TB, we might use a beta distribution for the prior centered around a value between 0.05 and 0.10, based on Horsburgh (15).

Othus et al. (25) suggested that a survival curve that plateaus toward the end of study might suggest that a certain fraction of the study population is “cured” and therefore never experiences the event of interest, indicating the appropriateness of a cure model. We evaluated the survival curve in both simulated and real data to determine the appropriateness of the cure model.

Household contact studies are popular for studying TB transmission and might contain information that can be used to estimate the SI (17). The exact time of symptom development is not easily observed so the diagnosis date of TB disease is used as a surrogate. TB cases diagnosed proximate to their index case are sometimes defined as “coprevalent,” meaning that transmission between the index case and the secondary case is questionable due to the short time period and therefore that SI might be excluded (27). We conducted sensitivity analysis when analyzing the real data by excluding coprevalent cases within 30 days or 90 days of their index cases. When excluding coprevalent cases using 30 days, the SI, denoted by 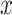, is defined as:

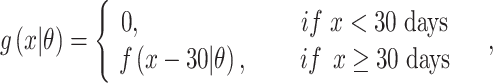(4)

where 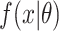is the parametric density (for example, γ) we use to estimate the SI. A similar strategy is applied using 90 days.

Simulation study

We simulated data to mirror TB household contact studies and to test the performance of the cure model under a variety of circumstances. Within each simulation, we simulate 3%, 10%, 50%, and 80% of the entire population developing TB disease. The first 2 of these 4 scenarios are consistent with TB, while the latter 2 are included to better understand the behavior of cure models more generally. Based on the limited estimates for the SI of TB (19), the SI for each simulated individual who is not cured is drawn from a gamma distribution with a mean of 1.4 years and a median of 1.1 years. For sensitivity analysis, we also consider a lognormal distribution with a mean of 3.0 years and a median of 1.8 years, which might be more similar to the distributions suggested by Behr et al. (28) with a heavier tail in the distribution. For those who develop active TB disease, we use 3 censoring mechanisms: 1) SIs are all censored at year 1; 2) SIs are all censored at year 2; and 3) SIs are censored randomly over 2–5 years. This means that an individual who is not cured and has a simulated SI of 2.5 years would be censored in scenarios 1 and 2 but might (or might not) be censored in scenario 3. We performed 1,000 simulations using STAN (29) in R (R Foundation for Statistical Computing, Vienna, Austria), using the “rstan” package for each scenario.

We estimate the SI in the simulated data using 3 methods: 1) the naive approach using the likelihood function in equation 1; 2) the traditional survival approach using the likelihood function in equation 2; and 3) the cure model approach using the likelihood in equation 3. In all 3 approaches, the SI estimates are summarized by posterior distributions of the parameters, which are approximated by Markov chain Monte Carlo sampling. In the cure model approach, the additional parameter p is estimated using different prior distributions (see Web Table 1, available at https://doi.org/10.1093/aje/kwaa090). For example, when the true disease rate is 3%, a flat prior for p is beta (1, 1) (mean = 0.5, median, 0.5), which puts equal weights on probabilities between 0 and 1; an informative prior for p is beta (0.2, 5) (mean = 0.04, median, 0.005) which puts more weights on lower probabilities; a misspecified prior for p is beta (5, 1) (mean = 0.8, median, 0.8) which puts more weights on higher probabilities.

To evaluate the performance of the different approaches for estimation, we evaluated the bias of each estimator as well as the mean squared error. More details on the simulations are provided in the Web Material.

Data sets

The first data set is from Vitoria, Brazil, 2008–2013 (30). It enrolled 160 index cases who had sputum acid-fast bacilli smear and culture-positive TB disease, identified through a prospective household contact study, and 958 individuals living in the same households as these index cases. Of the 958 household contacts, 47 developed active TB disease during follow-up, ranging from 2 to 6 years.

The second data set is from the United States and Canada, 2002–2006 (31). It enrolled 718 index cases and 4,490 contacts, of whom 158 developed active TB disease during the 4-year follow-up period.

Both studies assumed that all TB disease was transmitted from the index cases to diagnosed contacts and used diagnosis date as a surrogate for disease onset. We assumed that the time from onset to diagnosis is independent and identically distributed for index cases and household contacts in order to estimate the SI.

RESULTS

Simulation results

In the simulations, the traditional survival-model estimates were extremely biased when the disease rate was low (Figure 1, Web Table 2). The naive approach consistently underestimated the SI, although the underestimation was minimal with adequate follow-up (Figure 1). The cure model produced relatively unbiased results when the disease rate was low and censoring occurred relatively late (Figure 1). The bias for the cure model decreased as the disease rate increased from 3% to 80%, regardless of the specification of the prior for p.

Figure 1.

Bias of mean serial interval in a simulation study of cases with tuberculosis and their household contacts. A) Censored at year 1; B) censored at year 2; C) censored during years 2–5. Red is the survival approach, blue is for a misspecified prior in the cure model, green is a flat prior in the cure model, purple is an informative prior in the cure model, and orange is the naive approach. Large biases not shown in this figure are: 1) censor at year 1, 3% disease rate, the survival approach with bias 4,826; 2) censor at year 2, 3% disease rate, the survival approach with bias 15,215, and a misspecified prior in the cure model with bias 12,224; 3) censor at year 2, 10% disease rate, the survival approach with bias 5,875; 4) censor at years 2–5, 3% disease rate, the survival approach with bias 65,862, and a misspecified prior in the cure model with bias 37,671; 5) censor at year 2–5, 10% disease rate, the survival approach with bias 19,149.

The survival curves appear to be a useful indicator of the applicability of the cure model. The survival curve tended to plateau toward the end of follow-up when censoring occurred between 2 and 5 years, for all disease rates (Web Figure 1). This phenomenon was most apparent for lower disease rates (3% and 10%), which was consistent with the cure model performing well in these scenarios. Similar patterns were observed in the sensitivity analysis where we used a lognormal distribution instead of a gamma distribution for the true underlying SI distribution.

For an example of simulated SI data, see Web Figure 2. For complete simulation details and results, refer to Web Appendixes 1 and 2, as well as Web Figures 3–5. For R code to fit the cure models, see Web Appendix 3.

Real data results

For the Brazil data, the naive approach yielded an estimated SI of 1.5 years (95% credible interval: 1.1, 2.1), and with the traditional survival approach, the SI was estimated at 584 years (95% credible interval: 244, 2,016). The survival curve appeared to plateau toward the end of the study, suggesting the appropriateness of a cure model (Web Figure 6). Using the cure model approach with a flat prior (beta (1, 1), which put equal weights between 0 and 1 for p, the probability of disease, the SI was estimated at 2.2 years (95% credible interval: 1.2, 17.1), and p was estimated at 0.06 (95% credible interval: 0.05, 0.14). Using the same approach with an informative prior for p (beta (0.2, 5) with mean = 0.04 and median, 0.005), the SI was estimated at 2.1 years (95% credible interval 1.3, 9.4), and p was estimated at 0.06 (95% credible interval: 0.05, 0.10). Sensitivity analysis showed that when excluding cases with short SIs (either less than 30 or 90 days), the cure model yielded similar estimated SIs and probability of disease (Web Table 3).

For the US/Canada data, the naive approach yielded an estimated SI of 0.52 years (95% credible interval: 0.43, 0.64) and with the traditional survival approach, the SI was estimated at 28,496 years (95% credible interval: 10,033, 129,651). The survival curve did not appear to plateau toward the end of the study, suggesting that the cure model might not be necessary (Web Figure 7) and the naive approach was sufficient. Using the cure model with a flat prior for the probability of disease p, the SI was estimated at 0.51 years (95% credible interval: 0.41, 0.62), and p was estimated at 0.03 (95% credible interval: 0.02, 0.03). Using the same approach with an informative prior for p did not alter the results (mean SI = 0.51 years, 95% CI: 0.41, 0.64; p = 0.03, 95% CI: 0.02, 0.04). Sensitivity analysis showed that when excluding cases with short SIs (either less than 30 or 90 days), the cure model yielded a lower estimated rate of disease and a longer estimated SI (Web Table 4).

DISCUSSION

When estimating SIs for an infectious disease, one must consider issues with incomplete follow-up and the potential for infected individuals to never develop disease. In simulation studies, we show that results from the naive approach are biased, tending to underestimate the mean of the SI. Traditional survival techniques are inappropriate; they assume that all individuals are at risk of the disease, which is not the case if the survival curve plateaus before reaching zero. The cure model modifies the likelihood function in survival analysis by dividing the study population into those who will have the event and those who will not have the event (hence have infinite survival time). We show that cure models, when used in the presence of credible information on the cure rate (the proportion of individuals who never experience the event of interest) can lead to less biased estimates in scenarios where the cure rate ranges from 20% to 97%, while simultaneously estimating the probability of disease. We showed the impact of applying these models to estimation of the SI using real data from Brazil and from the United States and Canada.

We found via a simulation study that in the setting of TB, the naive approach, which only analyzed the observed SIs, consistently underestimated the SI, although the underestimation was minimal with sufficient follow-up. We included this approach to make a case for the use of the cure model, given that the naive approach is currently the common approach to estimate the SI for TB (19, 21, 22). To address issues of inadequate follow-up and censoring, we proposed to use a cure model and tested this approach with multiple disease rates and multiple censoring mechanisms. We found that when the disease rate was low, the cure model performed well (lower bias, mean squared error) when the censoring occurred relatively late to allow sufficient observed SIs or when we had correct prior information on the probability of disease. We also found that, when the disease rate increased from 3% to 80%, the cure model performed well regardless of the censoring mechanisms.

Othus et al. (25) suggested that a survival curve that plateaus toward the end of study might indicate the appropriateness of a cure model, which agrees with what we found in the simulations: When the disease rate was low and censoring occurred later, the cure model performed well with low bias and mean squared error (Figure 1). This is also consistent with the real data results. In the Brazil (30) data set, the survival curve indicated that the cure model might be appropriate, and therefore the cure model approach yielded a larger estimated SI compared with the naive approach, which analyzed only observed SIs. In the US/Canada (31) data set, the survival curve did not show a need for the cure model. In this case, the cure model yielded results similar to those of the naive approach. We recommend that in the presence of prior information on the disease rate, especially when the disease rate is low, one should consider using a cure model instead of a traditional survival approach, with an informative prior being used for the cure rate. The survival curve can be a useful tool to determine whether a cure model should be used.

The US/Canada data set yielded a lower SI (0.5 years) than the Brazil data set (approximately 2 years). This might imply a higher occurrence of reinfection TB in a higher-TB-burden country such as Brazil (28). In the case of reinfection TB, latently infected individuals can become infected again by another strain of M. tuberculosis and develop active disease, resulting in what appears to be longer SIs. It is currently not possible to differentiate between different strains of latent TB, thus limiting our ability to understand the SI and true dynamics of transmission.

Accurate estimates of the SI are important for understanding the transmission dynamics of an infectious disease, informing modeling studies, and understanding the length of time that a latently infected individual is most likely to be at risk of developing active disease. Our understanding of this quantity is limited for TB (19), which could be problematic in estimating the reproductive number for TB given that these 2 quantities have been used jointly to describe infectious disease dynamics (19). In the present work, we provide not only estimates of this quantity for 2 geographic settings but also a general approach for obtaining estimates of the SI that can be applied to other settings.

There are important limitations in this work. First, the SI we consider is only an unbiased estimator for the generation interval when the time between infection and onset of symptoms is independent and identically distributed for the infector and the infectee, and has been shown to have a larger mean than the generation interval in the presence of asymptomatic infection (32). Next, we do not have access to molecular data, which would potentially allow us to better determine whether cases are in fact linked by transmission. We make a simplifying assumption that those who are in a household did in fact transmit to each other. However, even this data would not necessarily clarify issues from reinfection. This is a clear limitation because substantial transmission outside the household, particularly in high-burden settings, has been demonstrated (33). In addition, due to limitations in TB diagnostics, we are unable to determine whether individuals are being reinfected with TB or developing active disease due to an infection that was contracted long ago (termed reactivation TB). This could either elongate the SI estimates if the true infector developed symptoms after the index case in the study data we use or could shrink it if an individual was infected again after the index-case exposure. The results we present using data from the United States and Canada, where TB burden is low, would seem to indicate that we are likely overestimating the SI in higher-burden settings. Further molecular testing and improved diagnostics will increase our understanding of this important transmission dynamic.

As we approach 2035—the year designated by the World Health Organization’s End TB Strategy as the goal for reducing TB incidence by 90% (34)—we must urgently rethink how we measure progress toward this goal. Few studies have estimated the SI, and those that have attempted this have focused on naive methods (19). Improved methods to estimate the SI could help identify locations that require focused interventions to reduce TB incidence, meet the End TB Strategy goals, and inform TB modeling studies, providing better understanding of the efficacy of potential interventions and policies.