Hidden Imputations and the Kaplan-Meier Estimator

Abstract

The Kaplan-Meier (KM) estimator of the survival function imputes event times for right-censored and left-truncated observations, but these imputations are hidden and therefore sometimes unrecognized by applied health scientists. Using a simple example data set and the redistribution algorithm, we illustrate how imputations are made by the KM estimator. We also discuss the assumptions necessary for valid analyses of survival data. Illustrating imputations hidden by the KM estimator helps to clarify these assumptions and therefore may reduce inappropriate inferences.

Abbreviations

AIDS

acquired immunodeficiency syndrome

KM

Kaplan-Meier

Applied health scientists will sometimes express inconsistent views regarding survival analyses, such as “I don’t want to impute, or make up, any data. Please just show me the Kaplan-Meier estimator!” However, statisticians have recognized for decades (1) that the Kaplan-Meier (KM) estimator (2) implicitly imputes event times for right-censored observations. Likewise, the KM estimator extended to account for late entry (3) implicitly imputes event times for left-truncated observations.

To review briefly, the survival function is the probability of remaining event-free. Formally, 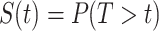for some follow-up time , where is the time from the origin to the event (4). The KM estimator is the product, taken over the ordered set of distinct event times, of the complement of the number of events divided by the number at risk. Formally,

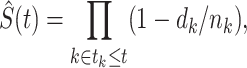where 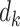is the number of events and 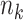is the number at risk, both at tim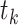e , the 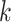th distinct event time.

In the setting we discuss here, where we have both right-censored and left-truncated observations, the number at risk excludes persons who have already experienced the event or been censored before time 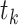, as well as those who enter follow-up at or after time 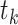. The extended (to late entries) KM (5), or Lynden-Bell (3), estimator of the survival function is appropriate for data which include right-censoring and left-truncation. This extension to the original KM estimator simply define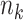s as

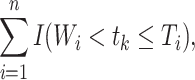where 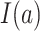is the indicator function (i.e., returns 1 if 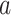is true, 0 if false) and 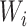is the time after the origin at which participant i entered the study.

The KM estimator of the survival function is widely used because it is a nonparametric maximum likelihood estimator (and is therefore asymptotically consistent and efficient) (6) and because it is algorithmically simple. But the simplicity of the KM estimator hides the fact that right-censored and left-truncated events are imputed. Here, we make 2 things explicit: 1) how right-censored observations are redistributed via proportions to future event times after the censoring times (i.e., following Efron’s redistribution algorithm (1)); and 2) how late entries require imputing the unseen (due to truncation) individuals via odds of the probabilities (i.e., jumps in the KM) at events before the late entries relative to the event probabilities past the late entries. We illustrate, using redistribution algorithms, how hidden imputations are made in the KM estimator, and we then discuss the critical assumptions necessary for valid analyses of survival data subject to right-censoring and late entries.

HIDDEN IMPUTATIONS

Say that we wish to study the time from diagnosis of acquired immunodeficiency syndrome (AIDS) to death (7), but a participant’s data can be right-censored at time 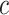years from the origin of AIDS diagnosis, due to dropout from the study. Additionally, a participant’s data can be left-truncated at time 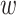years from the origin, due to entry into the study at 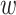years from the origin of interest (e.g., AIDS diagnosis), often referred as “late entries.” In an alternate setting, we might wish to study the time from initiating attempts at pregnancy (i.e., the origin) to conception, where women’s data can be right-censored due to dropout or left-truncated due to late entry.

Consider the data for 10 individuals shown in Figure 1A, with the case identifier as the y-axis and time from AIDS diagnosis to death as the x-axis. The data include the number of years between the origin (i.e., AIDS diagnosis) and study entry, denoted as 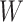, and the number of years between this same origin and study exit, denoted as 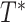, where 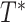is the minimum of 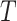(i.e., years between AIDS diagnosis and death) and 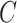(i.e., years between AIDS diagnosis and censoring). Solid black lines denote time under follow-up, from 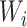to 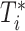. Death before censoring is denoted by 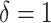, and in Figure 1A by lines ending with solid dots. Participants 1, 4, 5, and 8 enter the study at AIDS diagnosis (i.e., 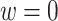), while participants 2, 3, 6, 7, 9, and 10 enter the study late, at a known time after AIDS diagnosis (i.e., ).

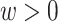Figure 1.

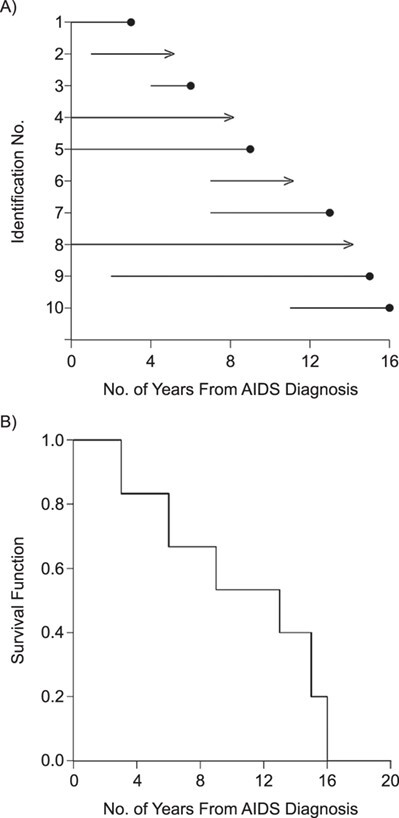
A) Data from 10 hypothetical study participants who were diagnosed with acquired immunodeficiency syndrome (AIDS) during (n = 4) or before (n = 6) study entry and were followed up to 16 years for death. B) Extended Kaplan-Meier estimator of the survivor function.

Turnbull extended Efron’s redistribution algorithm to allow for left-truncation (8), and this extended redistribution algorithm is equivalent to the extended KM estimator detailed above. In Figure 1B, we show the extended KM estimator for the data in part A. In the example, the extended KM estimate of the survival function at t = 10 years is

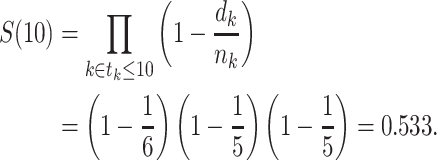In Figure 2 we illustrate the redistribution of all 10 participants. The upper portion (i.e., top 5 rows) of Figure 2 details the 6 distinct event times 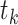, the number of events 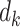, the size of the risk sets 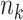, the extended KM estimator, and the jumps (i.e., step sizes) in the estimator, say 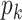. The kernel of Figure 2 consists of the central shaded 10 × 6 rectangle. Each row in this rectangle represents a participant, and each column represents an event time. The third and fourth columns in Figure 2 (labeled 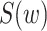and “No. Truncated,” respectively) provide information on the number of truncated events. Here we detail only the most illustrative case, the case of participant 6, who enters the study late and is censored. In Web Appendix 1 (available at https://doi.org/10.1093/aje/kwaa086), we provide details for the remaining 9 participants.

Figure 2.

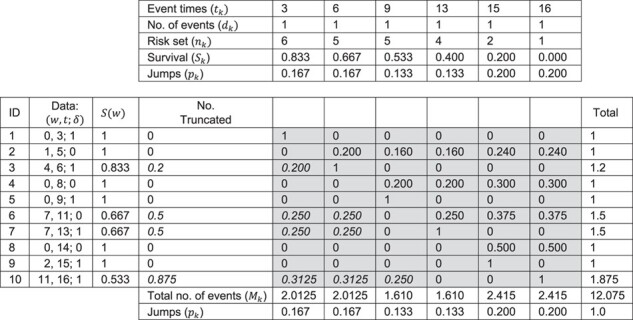
Redistribution of right-censored and left-truncated observations among 10 hypothetical study participants who were diagnosed with acquired immunodeficiency syndrome (AIDS) during (n = 4) or before (n = 6) study entry and were followed up to 16 years for death. ID, identification.

Hidden imputations for censoring

What is hidden in the KM algorithm is that right-censored observations are allocated as (partial) events in proportion to all events that occur after the observation’s censoring time. Specifically, if 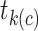is the first event time after an individual is censored at time 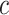, the KM estimator imputes 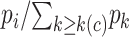events at the ith event time after c, which corresponds to the probability that the individual censored at c will develop the event at the ith event time after c. For example, participant 6 was censored at 11 years after AIDS diagnosis and therefore has their unit mass distributed among the 3 remaining events occurring at 13, 15, and 16 years after AIDS diagnosis. This censored observation is distributed proportionally given the jumps in the extended KM estimator, which are 0.133 (i.e., ), 0.2 (i.e., 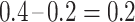), and 0.2 (i.e., 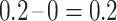), respectively. Therefore, this censored observation is distributed (or imputed) as 1/4, 3/8, and 3/8, respectively. For example, the first allocation is obtained as .

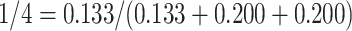Hidden imputations for left-truncation

Also hidden in the extended KM algorithm is that left-truncated events are allocated as odds of the event probabilities at events before the late entries relative to the sum of the probabilities past the late entries. For a late entry at time w, we first determine the number of unseen truncated events, which is calculated as 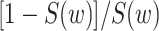(see Web Appendix 2 for derivation). Then, we allocate these “ghosts” (8) proportional to all events that occurred before time w. This 2-step algorithm is equivalent to imputing 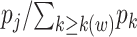events at the jth event time before w (i.e., 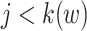), where 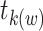is the first event time after an individual enters the study at time w. This number of imputed events corresponds to the number of unseen individuals who are peers of the recruited individuals but were truncated (not enrolled) because they developed the event before the recruited individual at 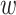years since origin. For example, using the 2-step algorithm, participant 6 entered follow-up at 7 years after AIDS diagnosis, when the survival function is 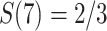. Consequently, participant 6 contributes 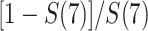, or 1/2 of a truncated event. This 1/2 truncated event is distributed to the 2 observed event times between the origin and 7 years after AIDS diagnosis, which occur at years 3 and 6 for participants 1 and 3, respectively. In effect, the step sizes in the risk function at times 3 and 6 will account for the unobserved risk contributed by the truncated “ghosts” of participant 6 prior to their late entry. This 1/2 truncated event is distributed proportionally given the jumps in the extended KM curve at times 3 and 6 years, which are both 0.167. Because the jump sizes are the same at times 3 years and 6 years, the truncated event is divided equally as 0.250 and 0.250. In this way, the extended KM estimator is able to “impute” events due to truncated observations by redistributing them in proportion to the size of the jumps in the survival function.

To complete Figure 2, we sum across and down the central 10 × 6 rectangle. Taking the column totals (2.0125, 2.0125, 1.610, 1.610, 2.415, and 2.415) and dividing by the sum of the row totals (12.075) yields the bottom row in Figure 2, which is identical to the jumps from the extended KM estimator given in the top portion of Figure 2. The completed Figure 2 provides an explicit picture of how the extended KM estimator of the survival function imputes right-censored and left-truncated events. Discussion of the standard errors and confidence intervals using the total number of events after the imputations are completed is provided in Web Appendix 3.

ASSUMPTIONS

The extended KM estimator is simple and succinct, but it does not make apparent that right-censored and left-truncated events are imputed in the manner illustrated above by redistribution. The validity of the extended KM estimator rests on the dual conditions that right-censoring and left-truncation are both random, conditional on any variables used to stratify the curves. The explicit imputation shown in Figure 2 helps to make clear the assumptions necessary for valid estimation of the survival curve. For example, we allocate a censored observation proportionally to all events after the censoring time as a direct consequence of the assumption that the individual was censored at random. If the individual was instead censored at random conditional on some set of measured covariates, that person’s unit mass ought to be redistributed proportionally, but only to those events with the same covariate set. If the individual was instead censored conditional on some set of unmeasured covariates, then we do not know how to redistribute them, and the survival curve is not identifiable or computable given the observed data. Likewise, we allocate any unseen events proportionally to all events before the late entry time as a direct consequence of the assumption that the individual entered the study at random. If the individual instead entered at random conditional on some set of measured covariates, then their unseen events should be redistributed proportionally, but only to those events with the same covariate set. If the individual instead entered conditional on some set of unmeasured covariates, then we do not know how to redistribute them, and the survival curve is again not identifiable given the observed data.

The characterization of the hidden imputation used by the extended KM estimator presented here for the case of uninformative censoring and truncation can also be used to arrive at unbiased estimates of the survival function for cases of interval-censored data and for data with informative censoring where the informative mechanism is known. The key is to redistribute not to all event times after censoring, or to all event times before late entries, but to only the pertinent subsets (e.g., if an individual’s event occurs in the interval , it should only be redistributed to event times observed in that interval).

In summary, methods with which to appropriately account for right-censoring and left-truncation in epidemiologic studies impute right-censored and left-truncated events, to the chagrin of those who wish to avoid imputations. These or any method used to recover right-censored or left-truncated events must operate under assumptions. While epidemiologists are generally aware that assumptions are required for valid estimation of the survival function, illustrating hidden imputations in survival analyses helps to clarify these assumptions and may reduce unnecessary violations.