The Surface and Hydration Properties of Lipid Droplets

Abstract

Lipid droplets (LDs) are energy storage organelles composed of neutral lipids, such as triacylglycerol (TG) and sterol esters, surrounded by a phospholipid (PL) monolayer. Their central role in metabolism, complex life cycle, and unique lipid monolayer surface have garnered great attention over the last decade. In this article, results from the largest and longest all-atom simulations to date suggest that 5–8% of the LD surface is occupied by TG molecules, a number that exceeds the maximal solubility reported for TGs in PL bilayers (2.8%). Two distinct classes of TG molecules that interact with the LD monolayer are found. Those at the monolayer surface (SURF-TG) are ordered like PLs with the glycerol moiety exposed to water, creating a significant amount of chemically unique packing defects, and the acyl chains extended toward the LD center. In contrast, the TGs that intercalate just into the PL tail region (CORE-TG) are disordered and increase the amount of PL packing defects and the PL tail order. The degree of interdigitation caused by CORE-TG is stable and determines the width of the TG-PL overlap, whereas that caused by SURF-TG fluctuates and is highly correlated with the area per PL or the expansion of the monolayer. Thus, when the supply of PLs is limited, SURF-TG may reduce surface tension by behaving as a secondary membrane component. The hydration properties of the simulated LD systems demonstrate ∼10 times more water in the LD core than previously reported. Collectively, the reported surface and hydration properties are expected to play a direct role in the mechanisms by which proteins target and interact with LDs.

Significance

Long (10 μs) all-atom molecular dynamics simulations herein suggest that lipid droplets (LDs) have several unique and previously unknown physical properties. First, after a long equilibration process (>5 μs), many triacylglycerol molecules (neutral fats in the LD core) transition to the LD surface, where they adopt phospholipid-like structure and dynamics, thereby creating chemically distinct defect types from bilayer membranes. Second, additional triacylglycerols intercalate into the phospholipid tails but retain core-like disorder. Finally, the amount of water in the LD core region shows a slight preference for the phospholipid-core interface and is significantly larger than previously reported. Each of these properties is expected to influence the nature by which proteins target and interact with LDs.

Introduction

The phospholipid (PL) monolayer surrounding lipid droplets (LDs) is a distinguishing feature from other organelles, which are generally surrounded by PL bilayers. LDs play a crucial role in cellular metabolic processes as they store excess energy in the form of neutral lipids such as triacylglycerols (TGs) and sterol esters (1, 2, 3). The proteins that associate with LD surfaces regulate lipogenesis and lipolysis to store and use energy when necessary, modulating the size of the LD depending on the metabolic status of the cell. Therefore, investigating the mechanisms of how proteins target and interact with LD surfaces is central to understanding the biology of LDs and related metabolic diseases (4, 5, 6).

LD proteins are classified into two types based on their origin (6). The first type (class I proteins) involves proteins embedded in the endoplasmic reticulum (ER) bilayer membrane that relocalize to LD via LD-ER membrane contact points (7, 8, 9). This mechanism of LD protein targeting requires membrane continuity and occurs either when LDs bud from the ER membrane or when LDs rebind to the ER via ER-LD bridges, in which the cytosolic leaflet of the ER membrane is continuous with the monolayer surface of LDs (8,9). Type I proteins typically contain a hydrophobic, membrane-embedded hairpin structure that has been shown to be sufficient for LD localization in a sequence-sensitive manner (6,8,10). Examples of type I proteins include enzymes involved in TG synthesis, such as glycerol-3-phosphate acyltransferase 4 (GPAT4) (8,11) and diacylglycerol O-acyltransferase 2 (DGAT2) (12, 13, 14). The second type (class II proteins) targets LDs from the cytosol and is generally characterized by one or more amphipathic helices (6,15). For example, the perilipin family binds to the surface of LDs via their 11 mer repeat amphipathic region and regulate lipolysis (16, 17, 18). In S2 cells, CTP:phosphocholine cytidylyltransferase associates with LDs via its amphipathic M domain and catalyzes the synthesis of phosphatidylcholine to augment the surface monolayer of growing LDs (5,15,19).

Many LD proteins can bind to both bilayer membranes and monolayer surfaces but have a preference for one over the other. Given that LDs have the same PL composition as the ER bilayer (ERbil), it is likely that the physical properties of monolayers versus bilayers influence preferential LD targeting. For example, the hydrophobic residues in class I proteins, initially embedded in the ER membrane, were recently shown to gain thermodynamic stabilization because of interactions with the LD monolayer and particularly with intercalated TG molecules (10). Similarly, it has been suggested that LDs have bigger, more persistent packing defects than bilayer membranes (6,15,20) and that class II proteins may preferentially associate with these defects via interactions with large hydrophobic residues in their amphipathic helices (15). However, this general packing defect model is only valid when describing nonspecific adsorption of amphipathic helices; it cannot explain LDs’ differential recruitment. For instance, each perilipin family member targets different LDs depending on their distinct neutral lipid composition (21). Also, the binding affinity of an amphipathic helix was recently shown to depend on the neutral lipid composition of the LD, despite having the same PL composition and density (22). Yet, how the neutral lipids, thought to be below the PL monolayer, are involved in protein recruitment is largely unknown. For these reasons, characterizing the physical properties of LDs is not only an intriguing question in LD biology but is central to understanding the mechanisms of proteins targeting to LDs.

Despite their biological importance and partially because of their more recent discovery, the physical properties of LD systems have not yet been studied as much as those of bilayer membranes. The solubility of neutral lipids in bilayers has been measured experimentally (23,24) but has yet to be measured in LD monolayers. It is challenging to characterize lipids at the molecular scale using experimental techniques. Computational methods can complement experimental findings by providing molecular-level insight. For example, coarse-grained (CG) simulations of bilayer membranes with the addition of the small amount of neutral lipids have suggested how the spontaneous accumulation of neutral lipids between two PL monolayers could occur during the early stages of the LD biogenesis (25, 26, 27). All-atom simulations have helped describe low-density lipoproteins and high-density lipoproteins, which have similar structures to LDs once they have matured to their spherical shape, despite being much smaller and sterol-ester abundant (28, 29, 30, 31, 32, 33, 34, 35). LDs, in contrast, are TG abundant and larger (100 nm to 100 μm in diameter) (1), resulting in a surface that is close to planar as opposed to the highly curved low-density lipoproteins/high-density lipoproteins surface. Finally, a few simulation studies have focused directly on the surface properties (15,20), physicochemical properties (36), and the inner lipid distribution (37,38) of LDs. However, many of these previous studies used CG models, which may not describe hydration, dynamical properties, or entropy-driven processes correctly (39, 40, 41, 42). Those that were all-atom simulations (15,20,35) involved simulation durations (<1 μs) that may not be sufficient to reach equilibration for LD systems.

In this work, all-atom molecular dynamics (MD) simulations of the largest reported LD systems (8- and 16-nm thick TG layers) and longest reported simulation time (10 μs) are analyzed. Three novel facets are found: 1) 5–8% of the LD surface is occupied by TG molecules, which is substantially larger than previous suggestions for monolayers and exceeds the experimentally reported solubility of TG in a pure 3-palmitoyl-2-oleoyl-D-glycero-1-phosphatidylcholine (POPC) PL bilayer (2.8%) (23); 2) there are two types of PL-intercalated TG molecules, those closer to the core (CORE-TG) and those on the LD surface (SURF-TG), which have the same structure and order as PLs and thereby act as a secondary membrane component, creating chemically unique defects in LD surfaces; and 3) the LD core contains 0.008 g of water per g TG, which is approximately 10-fold higher than previously reported (20). Implications for how the reported properties could influence protein-LD interactions and targeting are discussed.

Methods

System setup and simulation details

Five systems were studied: three bilayer systems with various PL compositions of POPC, 2,3-dioleoyl-D-glycero-1-phosphatidylethanolamine (DOPE), and phosphatidylinositol (SAPI) and two LD systems with 8- and 16-nm thick TG layers. The bilayer systems were prepared using the CHARMM-GUI membrane builder (43, 44, 45, 46) and included a homogeneous POPC bilayer (POPCbil), a homogeneous DOPE bilayer (DOPEbil), and a heterogeneous bilayer of 88:37:10 POPC:DOPE:SAPI, representative of the ER membrane (ERbil) (47). We note that DOPE is a nonlamellar lipid that forms the inverse hexagonal phase at room temperature (48). The force field used for DOPE properly reproduces this behavior but, for finite simulation times starting in the lamellar phase and under periodic boundary conditions, remains in a lamellar phase (49,50). The mechanical properties of two different DOPE phases were described by Sodt and Pastor (51). The lamellar DOPEbil simulations were included herein only to demonstrate the influence of both PL composition and environment (bilayer versus monolayer) on the degree of order of the lipid tails. We further benchmarked our POPCbil simulation against reference data. Our computed area per lipid headgroup (APL) of POPCbil (64.5 ± 0.4 Å²) is equal within statistical uncertainty to the reported value (64.7 ± 0.2 Å²) (50). We also confirmed that the order parameters of POPC are in good agreement with reference data (50).

Given that LDs are thought to have a comparable composition to the ER, our LD monolayers were also composed of 88:37:10 POPC:DOPE:SAPI (47). Similar to previous studies (28,35), the LDs were modeled with trilayer structures that were constructed by separating the two leaflets of a bilayer membrane (ERbil) and then inserting a relaxed TG layer (8-nm or 16-nm thick) between them. We denote the resulting LD systems as 8 nm LD or 16 nm LD, reflective of their TG layer thickness. The experimentally measured surface tension of LDs containing TG was determined to be 1.63 mN/m (22). This low surface tension justifies approximating a LD as a trilayer structure simulated in the zero-surface tension NPT ensemble, although the influence of surface tension will be the focus of future work. The detailed procedure of building a trilayer structure is as follows. The initial bilayer membrane was constructed with the CHARMM-GUI membrane builder (43, 44, 45, 46). Independently, a 4-nm thick (in the z dimension) TG layer was prepared using Packmol (52) and was equilibrated for 50 ns in the NPT ensemble, resulting in a final density of 0.9040 g/cm³. The final structure of the TG layer and the bilayer membrane had the same x and y dimensions of 9.5 nm. The 4-nm thick TG layer was duplicated in the z dimension to build the 8- and 16-nm thick TG layer. The two leaflets of ERbil were separated, and the TG layer was inserted with an extra 1-nm spacing along the z dimension between the TG layer and each of the PL leaflets. Any TG molecules that were within 2 Å of PLs were removed. The extra space was reduced with 0.1 ns of NPT simulation. All systems were solvated in TIP3P water (53) and 0.15 M NaCl solution. A detailed description of the systems is provided in Table 1.

Table 1.

A Detailed Description of the Systems Used in This Work

	Bilayer Membranes			LDs
	POPCbil	DOPEbil	ERbil	8 nm LD	16 nm LD
POPC:DOPE:SAPIa	40:0:0	0:40:0	88:37:10	88:37:10	88:37:10
TGb	0	0	0	429	866
Simulation length (μs)	0.2	0.2	1	10	10

^aThe number of molecules per leaflet.

^bThe number of TG molecules.

The TG topology was obtained from DOPE by replacing its headgroup with its sn-1 tail (the structures of POPC, DOPE, and TG are shown in Fig. S1). The TG topology used in this study is available in https://github.com/ksy141/TG. The same TG topology has been used in the other articles (10,15). To validate our TG model, we performed a bulk TG simulation (35 ns) and a water-TG-water interfacial simulation (50 ns). Our bulk TG simulation shows the density to be 0.9034 ± 0.0005 g/cm³ at 310 K, which is very close to experimental data (0.8991 g/cm³ at 313 K) (54). In the interfacial simulation, the calculated interfacial tension, 29.7 ± 1.7 mN/m at 310 K, is in good agreement with the experimentally measured 32 mN/m (55) at 298 K.

The MD simulations were performed using the GROMACS (version 2018) simulation engine (56) with the CHARMM36 lipid force field (50,57). Simulations were evolved with a 2-fs timestep. The particle mesh Ewald algorithm (58) was used to evaluate long-range electrostatic interactions with a real space cutoff of 1.0 nm. Lennard-Jones interactions were cutoff at 1.0 nm with the potential-shift function. Long-range dispersion was corrected for energy and pressure. The pressure was maintained semi-isotropically using the Parrinello-Rahman barostat (59) at a pressure of 1.0 bar, a compressibility of 4.5 × 10⁻⁵ bar⁻¹, and a coupling time constant of 2.0 ps. Bonds to hydrogen atoms were constrained using the LINCS algorithm (60). The temperature was maintained at 310 K using the stochastic velocity rescaling thermostat (61) with a coupling time constant of 0.1 ps. The trajectories of POPCbil and DOPEbil were extracted every 100 ps, whereas those for the ERbil, 8 nm LD, and 16 nm LD were extracted every 1 ns. The total durations of simulations of POPCbil, DOPEbil, ERbil, 8 nm LD, and 16 nm LD were 0.2, 0.2, 1, 10, and 10 μs, respectively. When computing the time-averaged quantities, the first 100 ns and 5 μs were considered to be an equilibration process and discarded for the bilayer and LD simulations, respectively. For time series results, the running average of 100 data points were shown instead of instantaneous values. All error bars were estimated by dividing the equilibrated trajectory into five blocks, computing the quantity for each block, and then determining the standard deviation (SD) of the block quantities (i.e., block averaging). Molecular images included in this work were rendered using Visual Molecular Dynamics (VMD) (62), and the trajectories were analyzed with MDAnalysis (63).

Classification of TG

TG molecules were categorized into two groups: SURF-TG and CORE-TG for those on the surface and in the core of the LD, respectively. The designation was based on the distance between the TG oxygen atoms and the average position of PL tails (along the z axis) of the closer leaflet. If all six of a given TG’s oxygen atoms were above the average z position of the PL tails (z_avg) of the upper leaflet or below the average z position of the PL tails of the lower leaflet, it was classified as SURF-TG. Otherwise, it was considered CORE-TG. Although there were some occurrences of only one to five TG oxygen atoms above/below the average z position of the PL tails, these were transient species that either returned to the core region or stabilized as SURF-TG.

Lipid-packing defects

For the bilayer membranes, we used a Cartesian-based algorithm to evaluate lipid-packing defects (20,64, 65, 66). For each PL located in a leaflet, the atoms whose z positions were greater than a certain threshold value (z_thr) were chosen (we use greater here in reference to the upper leaflet, but the opposite applies to the lower leaflet throughout). In this work, the z position of a PL’s central C2 atom minus a chosen value, d_PL = 1 Å, was used as the threshold (z_thr = z_C2 − d_PL) to be consistent with the previous work (20,64, 65, 66). Then, we created a three-dimensional grid with a spacing of 1 Å on the surface of the membrane with z coordinates ranging from z_thr to the highest z position of all PL atoms (z_max). The scalar value of the grid point is associated with the surrounding atoms that are closer than half of the diagonal of the grid ($\sqrt{3}/2$ Å) plus the atom’s radius. The radii were taken from the CHARMM36 parameter set (50). Different values were added to the grid point based on the types of overlapping atoms. Polar atoms (headgroups or glycerol moieties) added a value of 10⁶, whereas acyl chain atoms only add 10³. After looping over all the PL molecules, the three-dimensional grid is reduced to a two-dimensional grid by summing up the scalar values along the z axis.

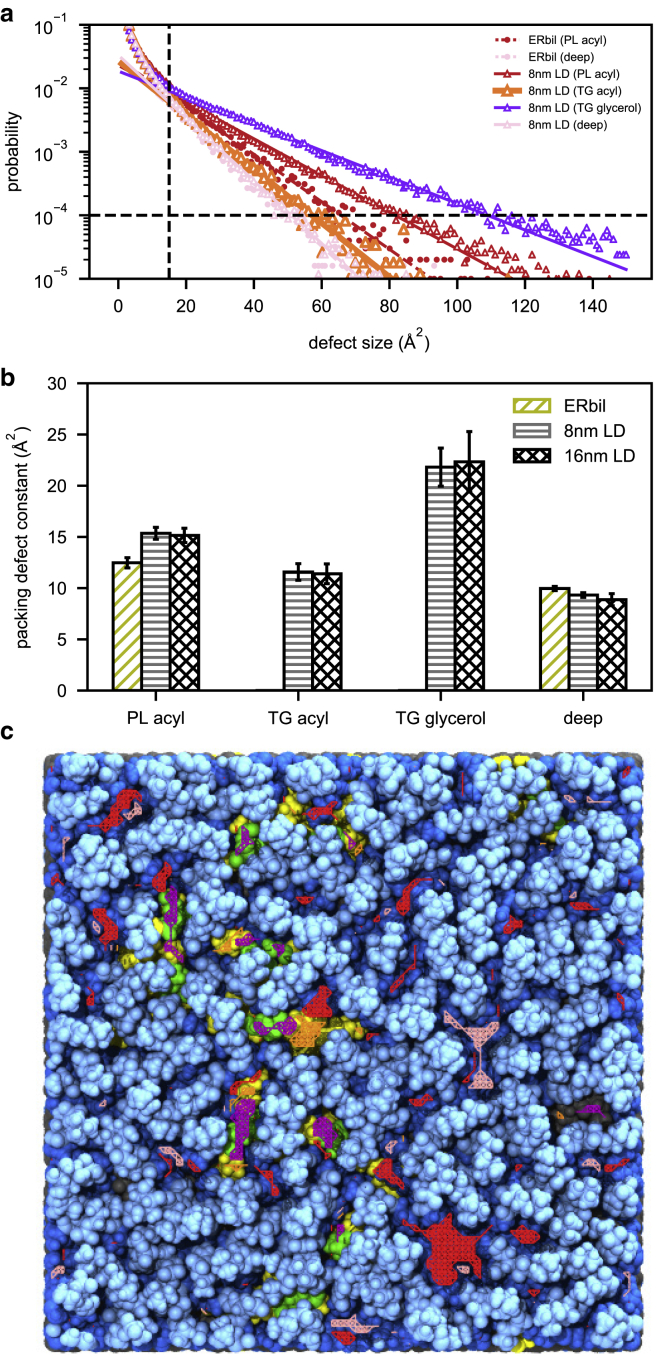
In this two-dimensional grid, a point with the scalar value of 0 has no atoms near it and is assigned to an elementary “deep” defect. On the other hand, a grid point with the value equal to or greater than 10⁶ is assigned to no defect as this grid point overlaps with at least one of the headgroup or glycerol atoms. A grid point with the value ranging from 10³ to 10⁶ (exclusive) is defined as an elementary “shallow” defect, which will be referred to in this work as an elementary “PL acyl” defect. For each defect type, neighboring elementary defects were clustered. If a clustered defect contains N elementary defects, this cluster is considered to have a defect size of N Ų. We computed the packing defect distribution with 400 bins, ranging from 0 to 150 Å². Then, the probability of finding a defect with the size of N Ų was fit to an exponential decay function (20,64,66,67): P(N) = ce^−N/π. If a defect has a size smaller than 15 Å² or a probability lower than 10⁻⁴, it was not used in the fitting, consistent with previous work (66). The packing defect constant (π), as shown in Fig. 2 b, is a helpful comparative number indicative of how quickly the decay function falls off; thus, larger packing defect constants are obtained when there is a higher probability of larger packing defects. We confirmed that the locations of PL acyl defects and deep defects found of a 1,2-dioleoyl-sn-glycero-3-phosphocholine/DOPE bilayer membrane using our analysis script and the PackMem script (66) are exactly the same except for edges (data not shown). The differences at edges resulted from a different consideration of a box boundary, and this will go away if a system is big enough.

Figure 2.

Packing defects of ERbil and LDs. (a) Packing defect distribution of heterogeneous ERbil (circle marker and dashed line) and 8 nm LD (triangle marker and solid line) for PL acyl (red), TG acyl (orange; thicker than other lines), TG glycerol (purple), and deep (pink) defects. (b) The packing defect constants for PL acyl, TG acyl, TG glycerol, and deep defects. The error bars were obtained using the block averaging method with five blocks. (c) Co-localization of defects and the last snapshot of 8 nm LD. Color coding for defects is as in (a). The light and dark blue indicate polar groups (headgroups and glycerol moieties) and acyl chains of PLs, respectively. The green and yellow indicate glycerol moieties and acyl chains of SURF-TG, respectively, and the black CORE-TG. To see this figure in color, go online.

This algorithm was extended to evaluate the packing defects of LD systems. First, the PL acyl defects and deep defects were calculated by only considering PL molecules (not including TGs). Therefore, the locations in which TGs were exposed to the LD surface were considered to have a deep defect, even though TG atoms may have overlapped with a grid point ranging from z_thr to z_max. These “pseudo” deep defects were then further specified into three different categories based on their overlap with TG molecules: TG acyl defects, TG glycerol defects, and “real” deep defects. An additional parameter, z_avg, which is defined to be the average z position of the PL tails, was introduced to set the z range of a new three-dimensional grid. A three-dimensional grid with spacing of 1 Å, ranging from z_avg to z_max, was constructed. If a grid point that was formerly a pseudo-deep defect overlaps with TG acyl atoms, it is considered to be a TG acyl defect, adding a value of 10⁻³. Similarly, if an elementary pseudo-deep defect grid point overlaps with a TG glycerol atom, it is considered to be a TG glycerol defect, adding a value of 1. When no TG atoms overlap, this is finally considered a deep defect. There are grid points whose values are contributed by different types of defects. The priority is ranked with a value added to a grid point. For instance, when a grid point overlaps both with a PL acyl atom (adding a value of 10³) and a TG acyl atom (adding a value of 10⁻³), as the sum of those two is within the range from 10³ to 10⁶ (exclusive), this grid point is considered an elementary PL acyl defect. In this way, the algorithm differentiates the packing defects caused by PLs and TGs. An illustration of the algorithm is shown in Fig. S2.

Order parameters

Order parameters (68) were calculated using second-order Legendre polynomials of cosθ: $S_{CD}=\frac{1}{2}\left|\langle 3{\text{cos}}^2\theta -1\rangle \right|$. The angle (θ) between the position vector of a carbon atom of an acyl chain to a bonded hydrogen atom with the z axis was used. The bracket represents the ensemble average.

Interdigitation

The degree of interdigitation between TGs and PLs was calculated consistently with previous studies (20,69); the density profiles of TGs and PLs with respect to the z axis (ρ_TG(z) and ρ_PL(z), respectively) were first used to define an overlap parameter, ρ_ov(z):

$${\rho }_{\mathit{ov}}\left(z\right)=4\frac{{\rho }_{TG}\left(z\right)\times {\rho }_{PL}\left(z\right)}{{\left({\rho }_{TG}\left(z\right)+{\rho }_{PL}\left(z\right)\right)}^2}.$$

The overlap parameter can range from 0 to 1; it is 0 when one of density profiles is equal to zero and 1 when ρ_TG(z) = ρ_PL(z). In essence, it reflects how the two density profiles (TG and PL) differ at each z position. The amount of interdigitation (λ_ov) was then obtained by integrating the overlap parameter along the z axis over the whole box such that

$${\lambda }_{ov}=\underset{0}{\overset{L}{\int }}{\rho }_{ov}\left(z\right)dz,$$

where L is the z dimension of the simulation box. The quantity reflects the area common to the two density profiles.

Water permeation potential of mean force

Replica-exchange (70) umbrella sampling (71) simulations were run to compute the permeation potential of mean force (PMF) for a water molecule through the LD monolayer. The collective variable used as the reaction coordinate was the z distance between the center of mass of one randomly selected water molecule and the center of mass of the phosphorous atoms of the upper leaflet. Harmonic restraints with a force constant of 700 kJ/mol/nm² were placed in each of the 40 umbrella sampling windows with a 0.15 nm spacing over a range of −3.4 to 2.45 nm (0 nm is the average z position of the upper phosphorous atoms; (+) moves toward water, whereas (−) moves toward the LD core). An initial structure for each window was prepared by running a steered MD simulation, biasing the same collective variable, with a force constant of 500 kJ/mol/nm² for 40 ns. The exchange between windows was attempted every 1000 steps. The PMF was calculated using the weighted histogram analysis method (WHAM) (72,73) with a bin spacing of 0.03 nm. The replica-exchange umbrella sampling simulations were run for 100 ns, and the trajectories were divided into five blocks to calculate error bars with block averaging. The external plugin, PLUMED2, was used for the biased simulations (74).

At each window, the coordination number between the chosen water molecule and the oxygen atoms of PL or TG was computed: $s=\sum _{i\in A}1-{\left(\frac{r_i}{r_0}\right)}^6/1-{\left(\frac{r_i}{r_0}\right)}^{12}$, where A is the oxygen atoms of the glycerol moiety of either PL or TG, r_i is the distance from the oxygen atom i included in A to the oxygen atom of the chosen water molecule, and r₀ is set to 0.25 nm. The normalized coordination number for PL was obtained by dividing the coordination number by the number of PL in the upper leaflet, which is 135. The normalized coordination number for SURF-TG was computed by first selecting the SURF-TG oxygen atoms, computing the coordination number with the biased water molecule and dividing it by the number of SURF-TG at each timeframe. Here, a broader definition of SURF-TG was used; TG molecules with at least one of six oxygen atoms above than the average z position of the PL acyl chain of the upper leaflet are considered SURF-TG. This was done to incorporate the effects of TG glycerol moieties located at the center of the PL monolayer (e.g., deeply intercalated CORE-TG or those transitioning to/from SURF-TG), which have significant interactions with the biased water molecule.

Results and Discussion

Reshaping landscapes of LD surfaces

LD structures and lipid-packing defects

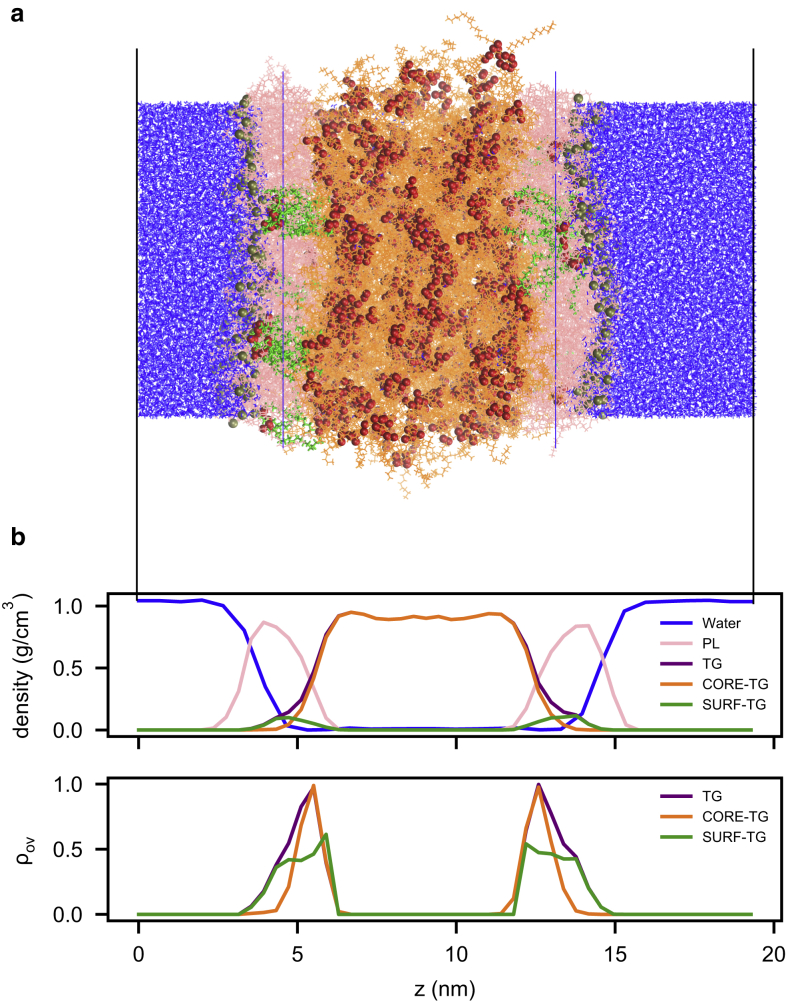
10-μs long MD simulations of the LD-mimicking trilayer systems were performed to study the structural and physical properties of LDs. After a long equilibration time (5 μs), the LD surfaces clearly demonstrate partial occupancy by TG molecules (SURF-TG) (Figs. 1, S3, and S4). The glycerol moieties of SURF-TG are predominantly aligned with the glycerol moieties of the PLs but more inserted toward the core. Thus, our simulations demonstrate much more active intercalation of TGs than did the previous packing defect model of LDs, in which the intrusion of TG tails results in the increased packing defects of the LD surface (15,20). The intercalation of CORE-TG in this study corresponds to the intrusion of TG tails in the previous packing defect model as SURF-TG was not reported. As shown in Figs. 1, S3, and S4, the dominant TG class on the LD surface is SURF-TG. Although there is significant overlap of CORE-TG and the PL tails, little of it is exposed at the surface.

Figure 1.

LD structure. (a) The last snapshot of 8 nm LD simulation. Water molecules are shown in blue and PLs in pink. Gray and red space-filling representations indicate phosphorous atoms of PLs and oxygen atoms of TG molecules, respectively. SURF-TG is shown in green and CORE-TG in orange. Blue lines indicate the average z position of PL tails. (b) The corresponding density profiles (top) and overlap parameter profiles (bottom) along the z coordinate of the snapshot of (a). The black lines are for the alignment between (a) and (b). The time-averaged density and overlap profiles of 8 nm LD are shown in Fig. S4a. To see this figure in color, go online.

It has been suggested that lipid-packing defects play a key role in protein targeting of LDs (15,65), making them potentially an important surface property. We therefore quantified the packing defects for both the bilayer membrane and LD systems (Fig. 2). Each defect type was evaluated, and the probability of finding a defect size was fitted to the exponential curve (details are shown in the Methods) to compute a packing defect constant (Fig. 2 a). Previous studies have reported the packing defect constant (π) of deep defects or PL acyl defects for a bilayer membrane to be within the range of 6–10 or 7–15 Å², respectively (66). Consistent with literature values, the results from our simulations show the packing defect constant of ERbil for deep defects and PL acyl defects to be 10.0 ± 0.2 and 12.5 ± 0.5 Å², respectively (Fig. 2 b). Although the LD systems have comparable deep defects with ERbil, the PL acyl defects did increase (∼15.3 Å²), and TG acyl defects and TG glycerol defects were significant additions, ∼11.5 and ∼22.0 Å, respectively (Fig. 2 b). As shown in Fig. 2 c, each molecular group type is covered with the corresponding defect type. Overall, the LD systems contain substantially more packing defects compared with the bilayer membrane, and the packing defects caused by TGs are predominantly created by SURF-TG. Our simulation results also show that the LD systems contain bigger PL acyl packing defects than the bilayer membrane, potentially contributed to by the intrusion of CORE-TG to the PL tails of the monolayer (Figs. 1 b and 2 b). Last, it should be noted that the PL and TG packing defect constants are comparable, suggesting that the two defects could compete with each other for interacting with proteins on LD surfaces. Investigating the relationship between the two types of defects on LD surfaces and protein interactions will be pursued in future research.

Characterizing the molecular properties of SURF-TG

Order parameters

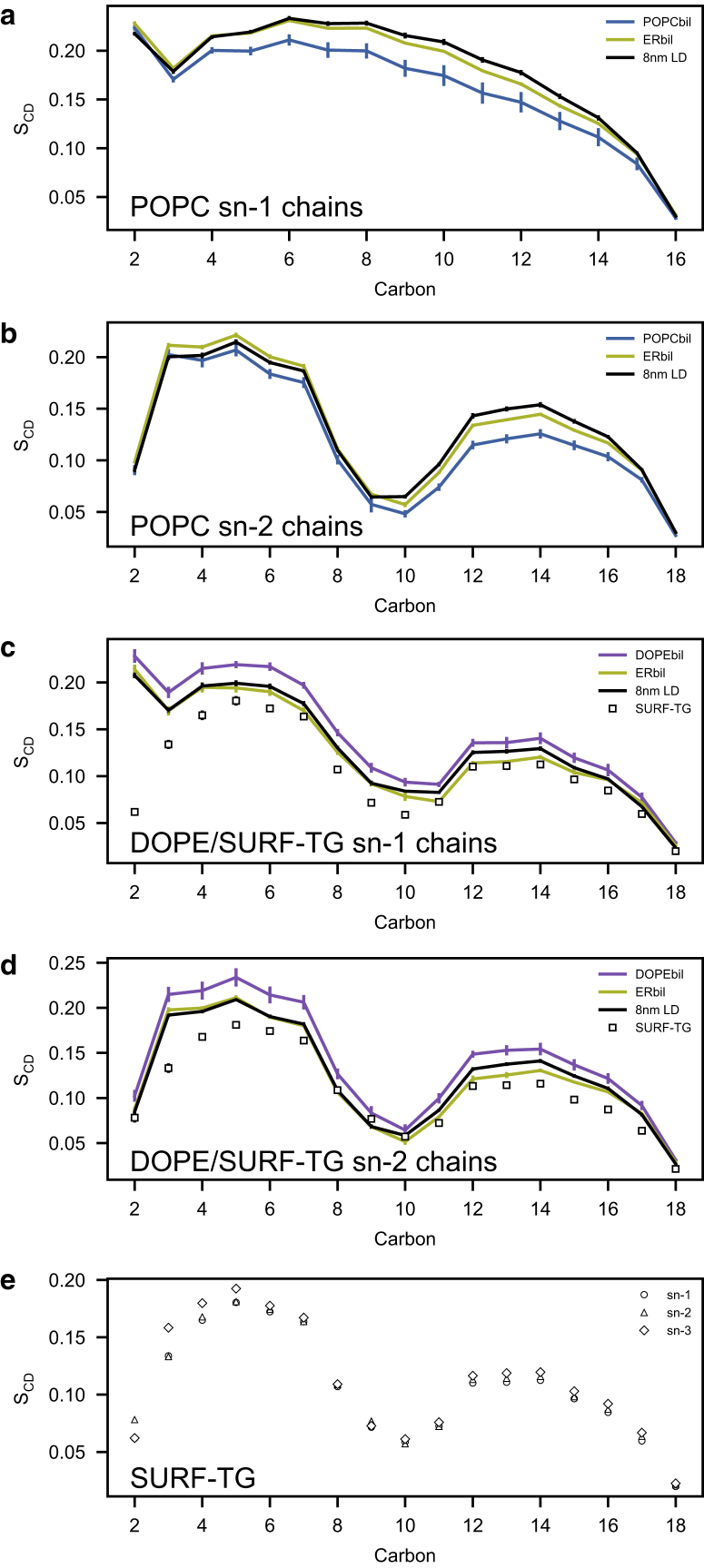
To characterize the molecular properties of SURF-TG, we calculated tail order parameters of the PLs and SURF-TG (Fig. 3) in the bilayer and LD systems. (The molecular structures of POPC, DOPE, and TG are shown in Fig. S1). As shown in Fig. 3, a and b, the addition of DOPE in the ERbil increases the order of POPC molecules compared with the pure POPCbil. In contrast, the order of the DOPE molecules decreases in the ERbil compared with that in the pure DOPEbil trapped in the lamellar phase (see Methods) (Fig. 3, c and d). The changes in order correlate well with the changes in lipid-packing density, which can be inferred from the APL values. For instance, the APL of POPCbil, DOPEbil, and ERbil was 0.645, 0.615, and 0.628 nm², respectively. Thus, the average room for each POPC molecule becomes smaller in the ERbil compared with the POPCbil, resulting in higher packing and increased order. In contrast, DOPE was more highly packed in the DOPEbil (trapped in the lamellar phase) but becomes more loosely packed in the ERbil, resulting in decreased order.

Figure 3.

The order parameters of POPC, DOPE, and TG molecules in POPCbil, DOPEbil, ERbil, and 8 nm LD. The error was estimated by taking the SD from the five blocks of the equilibrated trajectories. (a) POPC sn-1 chains. (b) POPC sn-2 chains. (c) DOPE (lines) and SURF-TG (marker) sn-1 chains. (d) DOPE (lines) and SURF-TG (marker) sn-2 chains. (e) SURF-TG sn-1, sn-2, and sn-3 chains. To see this figure in color, go online.

Interestingly, the LD systems track the ERbil quite well, with a slight increase in order in the lower tail order parameters (c12–c16) for both POPC and DOPE. This increased ordering of POPC tails has been previously reported, although not explained, for lipoprotein trilayer systems (35). As described below, the lower PL tails are more densely packed, and thus more ordered, in the LD systems because of intercalated TG molecules.

We then calculated the order parameter of the SURF-TG molecules. All the acyl chains within a TG molecule are identical except for the glycerol moiety (The sn-1 and sn-3 chains have α carbon, whereas the sn-2 chain has β carbon; see Fig. S1). Therefore, we expected the order parameters of each TG acyl chain to be comparable to one another. We further expected the order parameters of SURF-TG to be comparable to those for DOPE because they have identical acyl chains. Consistent with these expectations, the order parameters of all of the acyl chains on SURF-TG molecules were comparable (Fig. 3 e). Furthermore, the order parameters of sn-1 and sn-2 chains of SURF-TG were comparable with that of DOPE except for the first several carbon atoms (Fig. 3, c and d). It is worth noting that the order parameters of the CORE-TG molecules were zero, meaning that they do not have any order in their structure. Even those CORE-TG that are transiently intercalated with the PL tails are highly dynamic and thus have order parameters very close to zero. The transient behavior of CORE-TG and the PL-like behavior of SURF-TG are shown in Video S1.

Video S1. The Trajectory of 8nm LD from 9 μs to 10 μs, Showing the Transient Behavior of CORE-TG and PL-Like Behavior of SURF-TG

Two CORE-TG molecules are shown in black and two SURF-TG molecules in green. Phospholipids are shown in pink and phosphorus atoms in pink space-filling representation.

Collectively, the order parameter results demonstrate that SURF-TG are ordered in an analogous manner to DOPE with their glycerol moieties exposed to water and acyl chains extended toward the LD center. This suggests that SURF-TG serves as a secondary membrane component in the LD PL monolayer, a finding that could be tested experimentally by probing TG tail order as a function of depth from the LD surface.

Influence of intercalated TG molecules

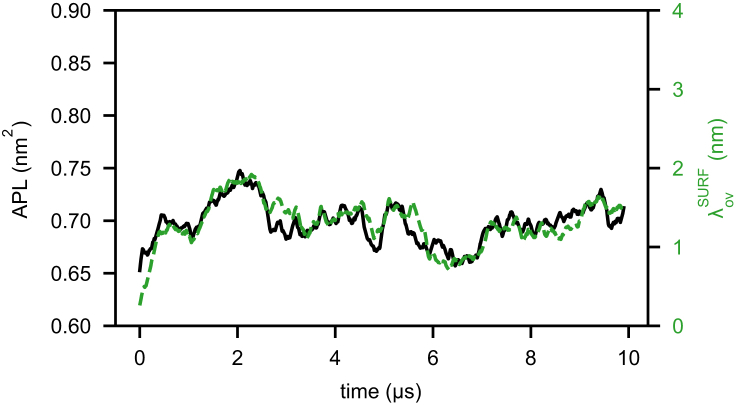
To better understand how the two types of TGs influence LD properties, we quantified their intercalation into the PL monolayer. The overlap parameter (ρ_ov(z)) profiles (Figs. 1 b and S4) show the expected dominance of SURF-TG closer to the surface of the monolayer, whereas CORE-TG dominates in the lower PL tail region. In tracking the total amount of interdigitation (λ_ov) (the spatial integration of the overlap) over time, there are clear differences between SURF-TG and CORE-TG. As shown in Fig. 4, ${\lambda }_{ov}^{SURF}$ fluctuates over time in a manner that is highly correlated with the APL. These fluctuations are also highly correlated with the molar ratio of SURF-TG with respect to PLs, calculated as N_SURF-TG/(N_SURF-TG + N_PL) (Fig. S5). This further explains why LD systems have higher APLs than bilayer membranes; SURF-TG molecules cause system expansion in the x and y dimensions. In contrast, ${\lambda }_{ov}^{CORE}$ is fairly stable over time, converging to a value of ∼1.83 nm (Fig. S5). Previously reported values of interdigitation varied from 0.73 to 1.48 nm, depending on force fields and the resolution of the simulations (20). Our simulations, therefore, already suggest a greater degree of interdigitation than previous reports based on CORE-TG alone.

Figure 4.

The area per PL (black line) and the amount of interdigitation of PLs by SURF-TG (green dashed line) for 8 nm LD. For comparison, the APLs of POPCbil, DOPEbil, and ERbil were 0.645, 0.615, and 0.628 nm², respectively. To see this figure in color, go online.

To support our findings on the intercalation of SURF-TG, we have compared the APL of our systems with experimental data and previous simulations. The results from our simulations show the APL of ERbil, 8 nm LD, and 16 nm LD to be 62.8 ± 0.1, 69.4 ± 1.4, and 69.5 ± 1.9 Å², respectively. This 11% increase in the APL from ERbil to LDs agrees well with the recent experimentally measured 15% increase in the APL from a POPCbil to a POPC monolayer surrounding an LD (22). A possible explanation for the slight difference between the experiment and our simulations is surface tension. The same work reported the surface tension of a TG-containing LD to be 1.63 mN/m (22), whereas our simulations were conducted at zero-surface tension. We expect a larger APL increase for simulations run with an applied surface tension. Thus, we argue an 11% increase of the APL at zero-surface tension agrees well with a 15% increase at 1.63 mN/m. A more detailed study on the influence of surface tension on APL and the amount of SURF-TG will be the focus of future work. On the other hand, a previous short LD simulation, performed for 100 ns, reported only a 2% increase in the APL, which is most likely because of early interdigitation with CORE-TG (35). In contrast, reported united-atom and MARTINI simulations reported nearly identical APL between a bilayer membrane and a LD (20), likely because limitations in the force field and CG representation. Taken together, the APL analysis shows agreement between our simulations and experiments and further validates the existence (and amount) of SURF-TG.

To better understand the impact of intercalated CORE-TG on PL ordering, we consider the four-region model of a bilayer membrane by Marrink and Berendsen (75), wherein the lower PL tail region (with the width of 0.55 nm for each leaflet) is the low-density region, with density comparable to liquid hexane. Overall, our ERbil tracks the four-region model well, as shown in Fig. S6. The low-density region (−1.5 to −2 nm) was apparent in ERbil (black solid line). The 8 nm LD system, however, shows higher density (red solid line) because of interdigitated CORE-TG. The increased density in this region results in higher PL ordering (c12–c16) for both POPC and DOPE (Fig. 3). Taken together, the two types of intercalated TG molecules have a different physical impact on the monolayer properties, with SURF-TG directly influencing surface properties like APL, whereas CORE-TG consistently, although dynamically, intercalates with the PL tail region, resulting in a slightly higher density and order in the lower tail region.

Hydration of LDs

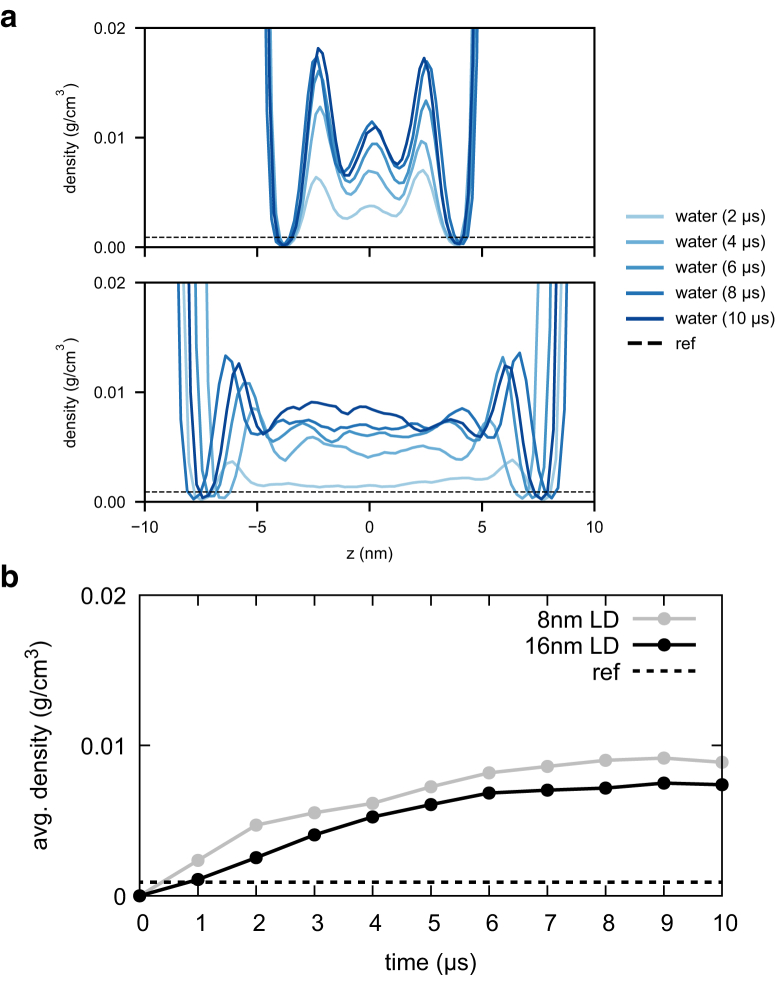
Finally, we focused on the hydration of our LD simulations. Recent work has noted a significant number of water molecules below the LD PL monolayer in the presence of proteins (10). We computed the water density profiles at various simulation times (Fig. 5 a) and observed significantly more water in the LD core (∼8 g water/1 kg oil or 0.8% kg/kg) than previously reported (∼1 g water/1 kg oil or 0.1% kg/kg) (20). Different from alkanes, a TG molecule has a polar glycerol moiety (see TG structure in Fig. S1), which can stabilize water molecules via hydrogen bonding. Consistent with this explanation, the calculated water density in the LD core is clearly proportional to the density of the TG glycerol moieties (Fig. S7).

Figure 5.

The water density profiles at simulation times. (a) The water density profiles, shown every 2 μs, of 8 nm LD (top) and 16 nm LD (bottom). The center of the phosphorus atoms (similar to the center of a LD) was zeroed. (b) The (spatially) average water density in the LD core, shown every 1 μs. The reference value of water (dashed) was from Bacle et al. (20). To see this figure in color, go online.

To verify convergence of the amount of water in the LD core, we first computed the average water density in the LD core by integrating the water density profile between two monolayers and dividing by the core height (z dimension). The resulting average water density (Fig. 5 b) converges at ∼8 μs for both the 8 and 16 nm LD systems. The middle peak in 8 nm LD (Fig. 5 a, top) results from a clustering of glycerol moieties and is indicative of short-range order because of the system size (Fig. S7, top). This residual structure mostly disappears in the larger 16 nm LD system (Fig. 5 a, bottom and Fig. S7, bottom) and explains the slightly higher water content in 8 nm LD (Fig. 5 b). To further validate our hydration results, we next calculated the water permeation PMF (a free energy profile) with replica-exchange umbrella sampling (see Methods). The resulting PMF is consistent with the free energy profile computed from the water density profile, F(z) = −k_BTlogρ(z)/ρ₀, where ρ(z) is the water density with respect to z, and ρ₀ is the bulk water density (Fig. 6 a). Together with the convergence of water density with simulation time (Fig. 5 b), the enhanced sampling results (Fig. 6 a) confirm our hydration results are converged and reliable within the limits of the force field. TIP3P has been shown to underestimate permeation into hydrophobic regions because of overpolarization (76), and future efforts to develop polarizable models may shift the quantification we report herein.

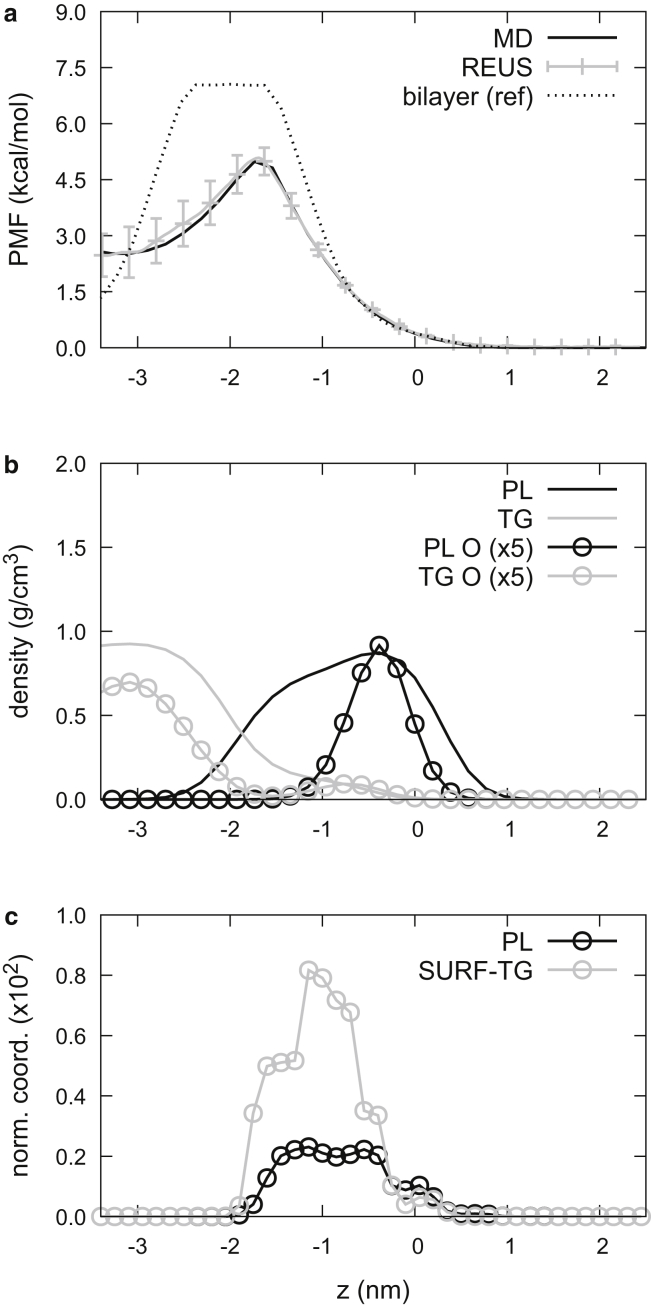
Figure 6.

Water permeation. (a) PMFs obtained from the last 2 μs of the 8 nm LD simulation (black line) and from replica-exchange umbrella sampling (gray). The error bars were obtained using the block averaging method. PMF for water permeation into a bilayer membrane (dashed black line) was obtained from (77). (b) Density of PL (black line), TG (gray line), and respective oxygen glycerol atoms (circles) from the last 2 μs of the 8 nm LD simulation. For visual clarity, the oxygen density was multiplied by 5. (c) The normalized coordination number between the water molecule and a PL glycerol (black circles) or SURF-TG glycerol (gray circles). For visual clarity, the normalized coordination was multiplied by 100.

For comparison, we include the PMF for water permeation into a POPCbil membrane from the work by Venable et al. (77). Both the bilayer and LD PMFs peak around −1.6 nm, in which the PL density is shifting from high to the lower density and in which the density of oxygen atoms is lowest in the LD (Figs. 6, a and b and S6). However, the energy barrier to partition from the water phase to the center of the LD is significantly less (by 2.5 kcal/mol) than that to the bilayer center. Given this discrepancy occurs around −0.8 nm, where the glycerol moieties of SURF-TG are located, we hypothesized the reduction could be due to water hydrogen bonding with SURF-TG glycerols. Unlike PL, SURF-TG can transition to CORE-TG or CORE-TG to SURF-TG, which extends the region where the water molecule can form hydrogen bonds. As discussed above, the glycerol moieties of SURF-TG are also closer to the LD core by ∼0.4 nm, additionally extending the hydrogen bonding region. We confirmed our hypothesis by computing the normalized coordination number (Fig. 6 c) between the oxygen atom of the biased water molecule and the oxygen atoms in the glycerol moieties of PL or SURF-TG (see Methods). Interestingly, the normalized coordination analysis shows that the water molecule preferentially interacts with the SURF-TG glycerols (gray circles in Fig. 6 c) over the PL glycerols (black circles). We expect this is because pulling the PL glycerol moiety toward the LD core accompanies membrane deformations, whereas pulling CORE-TG to SURF-TG or SURF-TG to CORE-TG has a much lower energy penalty.

Another comparison that can be made is with the experimentally measured water moisture of olive oil, whose main component is TG. Although a water-in-oil emulsion is fundamentally different from an oil-PL-water LD because of the lack of amphiphiles (PL) and different sizes, this comparison offers a rough idea of the range of expected hydration. Depending on the origin of olive oil, reports of the moisture content vary greatly, from less than 0.2% kg/kg (78,79) to up to 0.8% kg/kg (80). Our hydration value is within this range at ∼0.8% kg/kg.

Taken together, the results presented herein demonstrate significant hydration within the LD core with a slight increase just below the PL tails because of increased concentration of TG glycerol moieties from intercalated CORE-TG. The water density at the PL/TG interfacial region is expected to be important in the stabilization of class I LD proteins that have charged residues near their hairpin kink (10). More generally, this degree of hydration may be an important factor to consider not only class I and II protein-LD interactions but also in the association of amphipathic molecules with LD cores.

Conclusions

LDs are distinct from other bilayer-bound organelles because of their monolayer surface of PLs and neutral lipid core. Using the largest reported LD models (8 and 16 nm TG layers) and the longest reported simulation times (10 μs) for all-atom resolution, the simulations presented herein provide new perspectives on the surface and hydration properties of LDs. Two types of TG molecules are found, SURF-TG and CORE-TG, which interact with, and influence, the PL monolayer in distinct ways. The SURF-TG occupy 5–8% of LD surfaces, which is greater than the solubility reported for TG in a POPC PL bilayer (2.8%) (23). The glycerol moieties in SURF-TG are largely exposed to water, and the tail order parameters, which are indicative of structure and order, are very similar to those found in PLs, especially DOPE. Thus, SURF-TG seem to behave as a membrane component, substantially increasing the amount of packing defects at the monolayer-water interface and creating chemically unique defects over neutral glycerol moieties. In contrast, the CORE-TG intercalate into the PL tails, retaining the disorder expected in the LD core and potentially contributing to the increase in PL packing defects found in our simulations. We also demonstrate that the APL, which is representative of expansion of the membrane, fluctuates in a highly correlated manner with the amount of interdigitation by SURF-TG (the number of SURF-TG), whereas the amount of interdigitation by CORE-TG is stable and does not influence the size of the membrane. Finally, we observe water density in the LD core to be 0.008 g of water per g TG, which is an order of magnitude higher than previously reported (20).

Equilibration across the LD monolayer was a slow process (>5 μs) during which TG molecules diffuse into the PL monolayer, whereas water diffuses into the LD core. Although previous atomistic studies did report some degree of intercalation of TG from the LD core (one can see the intrusion of TG tails into the PL tails), the presence of SURF-TG was not observed (15,20,35). This was likely the result of limited simulation time (<1 μs). Consistent with this, the SURF-TG in our simulations did not become evident until after 1 μs. In contrast, CG studies performed long MD simulations of large LD systems or oil lenses (the initial stage of the LD formation); however, no observation of SURF-TG or significant LD hydration was reported (20,25,26,37,38). We suspect that this is due to the challenging limitations of accuracy, transferability, and entropy in CG modeling (39, 40, 41).

The presented results provide new perspectives on LD surfaces in the context of protein targeting mechanisms. A previous study proposed that proteins containing amphipathic helices can bind to the packing defects of LDs, which were therein reported to be slightly larger and more persistent than bilayer membranes (15). Our results, however, suggest that there are markedly larger packing defects than previously reported, in addition to chemically unique defects created by SURF-TG. We anticipate the targeting mechanisms will be significantly influenced by these SURF-TG defects. For example, the first step and rate-limiting step of lipolysis is carried out by adipose triglyceride lipase, which converts a triglyceride into a diglyceride and fatty acid (81, 82, 83). However, how adipose triglyceride lipase resting on LD surfaces can reach the glycerol moiety of TG across the PL monolayer is unknown. With this new model, the SURF-TG molecules, and especially the carbonyl carbons, are exposed to the cytosol, easily accessible and in close proximity to the second hydrolysis substrate, water. This targeting model in which neutral lipids exposed at LD surfaces interact with a protein is further supported by the recent findings of LDs’ differential protein recruitment. Chorlay and Thiam found different targeting preferences by amphipathic peptides to LDs with different neutral lipid compositions but the same PL composition and density (22). This differential recruitment was maintained with different surface tension, although the binding levels changed. Our results suggest that a quite significant exposure of neutral lipids at the LD surface is a likely explanation of differential recruitment.

We also anticipate that SURF-TG may play an active role in modulating the surface tension in LDs. It is an outstanding curiosity how LDs, which shrink with lipolysis and grow with TG synthesis, maintain similar growth/shrinkage in their monolayer structures. For a given LD size, there is an optimal number of PLs in the monolayer (84). Our finding suggests that in the case of too few PLs, TGs can shift to SURF-TG to act as a secondary monolayer component and thereby reduce the monolayer surface tension. This is consistent with experimental data that report the surface composition of water/(PL + TG)/air as a function of surface tension (55). When the surface is under expansion, both TGs and PLs are mixed and surface active. However, when it is compressed, TGs demix from the PL layer and form a separate phase in air because PLs are more surface active than TGs. Thus, we predict that SURF-TG can reduce surface tension by being a secondary monolayer component when the supply of PLs is limited or during the initial stages of the LD formation (1,85). In turn, we also anticipate that the percentage of exposed SURF-TG may influence the LD life cycle, e.g., recruiting proteins to synthesize more PLs.

Finally, increased water density is found in the LD core. Even though it is present in a relatively small quantity, water in the LD core can play a crucial role in stabilizing charged or polar residues embedded in the LD monolayer. For example, proteins that target LDs from the ER often contain a hydrophobic hairpin motif, which has been proven to be sufficient for LD localization (8,10). These hairpin motifs include highly conserved charged residues at hinge, and mutation of those residues to hydrophobic residues cause the defects to LD targeting (10). In the ER membrane, those charged residues are stabilized by interacting with the phosphate group of the lower leaflet; water can do the corresponding work in LD core. Future work will explore the influence of mixing sterol esters into the pure TG core studied here, the influence of surface tension, and the ways in which the reported properties influence LD protein targeting.

Author Contributions

S.K. and J.M.J.S. designed the research. S.K. performed the simulations. S.K. and J.M.J.S. analyzed the results and wrote the article.

Editor: Sarah Veatch.