Abstract
Single-particle tracking is an important technique in the life sciences to understand the kinetics of biomolecules. The analysis of apparent diffusion coefficients in vivo, for example, enables researchers to determine whether biomolecules are moving alone, as part of a larger complex, or are bound to large cellular components such as the membrane or chromosomal DNA. A remaining challenge has been to retrieve quantitative kinetic models, especially for molecules that rapidly switch between different diffusional states. Here, we present analytical diffusion distribution analysis (anaDDA), a framework that allows for extracting transition rates from distributions of apparent diffusion coefficients calculated from short trajectories that feature less than 10 localizations per track. Under the assumption that the system is Markovian and diffusion is purely Brownian, we show that theoretically predicted distributions accurately match simulated distributions and that anaDDA outperforms existing methods to retrieve kinetics, especially in the fast regime of 0.1–10 transitions per imaging frame. AnaDDA does account for the effects of confinement and tracking window boundaries. Furthermore, we added the option to perform global fitting of data acquired at different frame times to allow complex models with multiple states to be fitted confidently. Previously, we have started to develop anaDDA to investigate the target search of CRISPR-Cas complexes. In this work, we have optimized the algorithms and reanalyzed experimental data of DNA polymerase I diffusing in live Escherichia coli. We found that long-lived DNA interaction by DNA polymerase are more abundant upon DNA damage, suggesting roles in DNA repair. We further revealed and quantified fast DNA probing interactions that last shorter than 10 ms. AnaDDA pushes the boundaries of the timescale of interactions that can be probed with single-particle tracking and is a mathematically rigorous framework that can be further expanded to extract detailed information about the behavior of biomolecules in living cells.
Significance
Fluorescence-based single-particle tracking is an important tool to study the dynamics of biological systems. The rate at which biomolecules move and interact is ideally inferred from their positional trajectories. Currently, however, extraction of these kinetic parameters remains challenging, especially with short trajectories. We have developed an analytical framework (analytical diffusion distribution analysis (anaDDA)) that extracts transition rates directly from the distribution of apparent diffusion coefficients. AnaDDA outperforms existing tools, especially in regimes in which transition rates approach the data acquisition rate. We demonstrate its general applicability by reanalyzing previously published data on DNA polymerase diffusion and find fast DNA interactions previously unobserved. AnaDDA is computationally fast, easy to use, and allows researchers to reveal detailed information about the behavior of biomolecules in living cells.
Introduction
Single-molecule studies have greatly expanded our knowledge of the mode of action and kinetics of DNA-protein interactions at the nanoscale (1). Single-molecule Förster resonance energy transfer (FRET) and optical/magnetic tweezers, for example, are well suited techniques to study forces, conformational changes, and displacements of DNA binding proteins such as DNA and RNA polymerases (2,3), helicases (4,5), and CRISPR-Cas proteins (6,7) in vitro with high spatiotemporal resolution (8, 9, 10, 11). In vivo, however, single-particle tracking (SPT) remains the most convenient choice to study dynamic interactions (12). For performing SPT, a gene of interest is fused to a gene expressing either a fluorescent protein or a protein tag (HaloTag/SnapTag) that can be later labeled with an organic fluorophore (13,14). To avoid the temporal overlapping of emitters moving in the confined volume of (bacterial) cells, two strategies can be pursued. Either the expression level of the protein of interest is kept sufficiently low, or the emission signal from different proteins has to be separated in time, which can be achieved using photoswitchable or photoactivatable fluorescent proteins or the equivalent organic fluorophores, enabling single-particle tracking photoactivation light microscopy (sptPALM) (15, 16, 17, 18). After linking subsequent localizations of tagged proteins into tracks, the apparent diffusion coefficient for each track j is calculated from the average of n squared displacements , where n represents a given step number. Summing overall tracks j will lead to a distribution of D∗ values, even if the motion of each particle is governed by a single diffusive state with diffusion coefficient D (19).
The different mobilities of proteins switching between a DNA-bound state, in which proteins diffuse very slowly, and a DNA-free state, in which proteins diffuse through the cytoplasm, can provide kinetic information on the frequency and longevity of DNA-protein interactions.
For tracking applications in which the number of localizations per track is large (>50 localizations), previous studies have demonstrated the reliable extraction of diffusion and transition kinetics (20,21). For sptPALM with fluorescent proteins, however, the ability to extract this information is severely compromised by premature photobleaching, often limiting the length of each track to a few localizations (22). Furthermore, the limited localization precision increases the apparent diffusion of immobile states. Therefore, measured displacements cannot be unambiguously assigned to either a bound or a diffusing state. As a consequence, histograms of D∗ values are often rather broad, making a clear distinction between two diffusional states of a single species impossible. For the special case of noninterconverting D∗ distributions, the shape of distributions can be calculated for a fixed number of analyzed steps (23,24) and, via fitting of the experimental data, used to extract the fractions of mobile and immobile proteins.
Another factor that can increase the overlap between two states in D∗ distributions are state transitions occurring within single tracks. Using a typical frame time of 10 ms and a typical track length of 40 ms, any transition occurring within that track length will average out (Fig. 1 A). The framework described in (23,24) does not account for the possibility of transitions within a track. Consequently, the overlap can lead to overfitting as an increase of intermediate values would necessitate the addition of more states, which are not necessarily biologically relevant. In vitro single-molecule FRET measurements have encountered a similar challenge, in which the interchanging of conformational states within single bursts or within single frames resulted in the averaging of FRET values. By implementing probability distribution analysis (PDA) (25,26), previous studies were able to extract kinetic information and fit the entire FRET distribution (27, 28, 29).
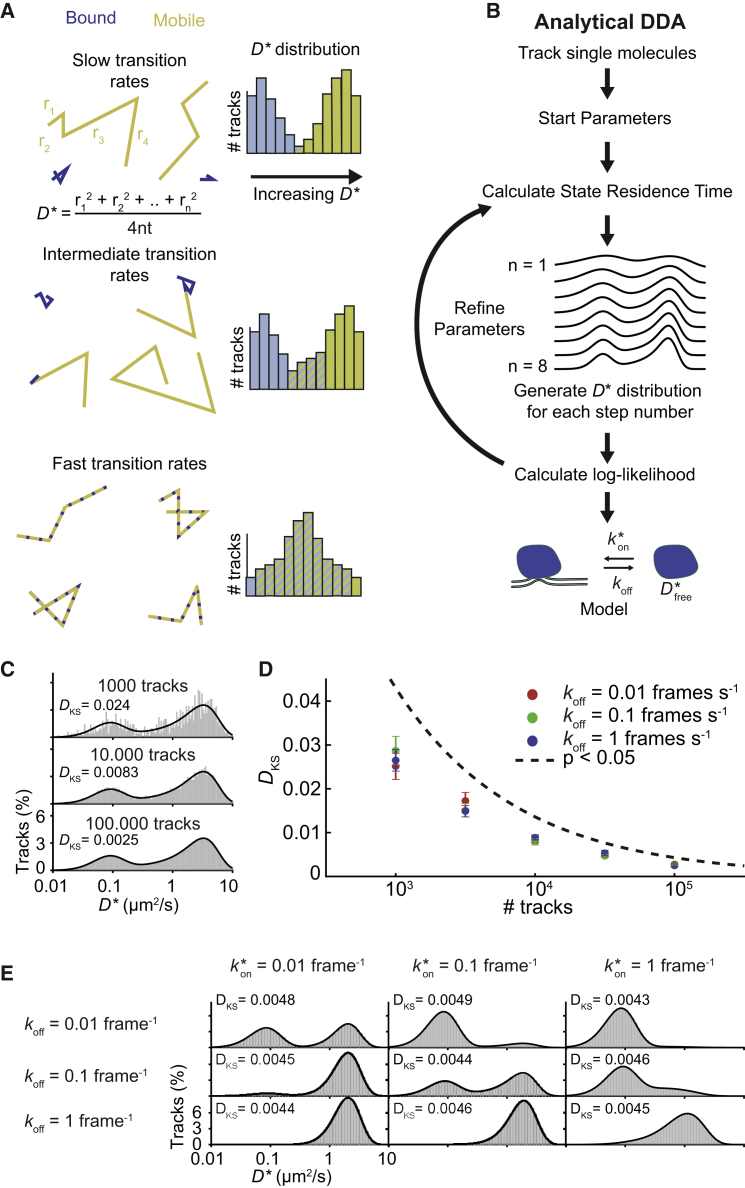
Figure 1.
AnaDDA. (A) The effect of transition rates on D∗ distributions is depicted with simulated tracks of four steps and different transition rates. With increasing transition rates relative to the frame rate, the bound and unbound distributions start merging toward an intermediate apparent diffusion speed diffusivity (right). The distribution of apparent diffusion coefficients D∗, calculated from the mean jump distances of a track, originates from the finite number of steps (n) that are measured for each particle and allows the extraction of the underlying diffusion coefficient and transition kinetics of the states. (B) Procedure of anaDDA is as follows: the D∗ values from tracked single particles are run into an MLE optimization program that refines a set of start parameters based on the likelihood to find a certain value given the number of steps (all tracks longer than eight are reduced to the first eight steps). (C) Shown is a comparison of simulated (gray bars) and theoretically predicted (black line) distribution with different amount of tracks and the following starting parameters: = 0.2 frame−1, = 0.2 frame−1, Dfree = 4 μm2/s, σ = 30 nm (localization precision), and step number = 4 steps. Tracks are simulated without any confinement boundaries. The Kolmogorov-Smirnov test statistic (DKS) is indicated at each histogram. (D) Shown is the Kolmogorov-Smirnov test statistic compared with the threshold for statistically distinguishable distributions. Values above the threshold line indicate that two distributions significantly differ from each other. Error bars indicate SEM of three independent simulations. (E) Shown is a comparison of simulated D∗ distributions (gray) and the distributions calculated with anaDDA for different transition rates (black). The shape of the distributions depends on both the ratio between and koff and the absolute values of these parameters. In this example, Dfree = 4 μm2/s, and σ = 30 nm. For more tested parameters, see Fig. S1. To see this figure in color, go online.
In this study, we aim to incorporate the statistical framework of PDA into D∗ fitting based on averaging single frame displacements in individual sptPALM tracks, which will allow us to directly extract biologically relevant parameters such as on- and off-rate next to the free diffusion coefficient and the total DNA-bound fraction. This method, which we call analytical diffusion distribution analysis (anaDDA), finds the kinetic parameters by implementing maximal likelihood estimation (MLE) and uses the probability to find D∗ for all tracks between one to eight steps long (where step number is the number of localizations, 1), present in the data set (Fig. 1 B). We benchmark this analysis method, with a simulation of transitioning particles, and implement modifications that account for specific experimental challenges, such as varying tracking windows and confinement effects within the cell. Furthermore, we compare anaDDA to a different kinetic analysis tool that use Bayesian statistics or unsupervised Gibbs sampling to infer state transitions from the data (30,31). We study the effects of confinement and tracking parameters on the fitting of the distribution coefficient distribution, and although anaDDA was not designed to automatically determine the number of states, we discuss ways to manually assess the number of states required to fit the data. We furthermore reanalyze previously published sptPALM data of DNA interacting proteins, obtain their kinetic parameters, and reveal that fast DNA probing interactions were hidden in the published data. Using anaDDA on short trajectories, we demonstrate the fast and accurate analysis of transient DNA-protein interactions in the millisecond time range, a range that was previously only accessible in slimfield microscopy (32). In addition, anaDDA allows users to quickly check whether any tracking data that would imply the existence of either many static states or non-Brownian diffusion can be reduced to a simple Brownian diffusion model with dynamic state transitions.
Methods
D∗ fitting with transitioning states
Distributions of D∗ have been fitted in numerous studies of DNA binding proteins (33,34) using a formalism derived by Qian et al. (23) from repeated convolution of the exponential distribution of displacement, resulting in a γ function for each state. The formalism was later expanded by Michalet to account for localization errors (35), leading to
| (1) |
where x is the measured displacement, D is the diffusion coefficient, n is the number of steps per track, is the frame time, σ is the localization error, and fD(x;D,n) is the probability to find a measured displacement given D and n. For multistate (or multispecies) systems, terms can be added with different values of Di and normalized by probability coefficients Ai. The goal is to find the distribution of apparent D∗ values (x) for a certain number of underlying states that each have a probability Ai and a diffusion coefficient Di. These distributions assume, however, that there is no dynamic transitioning occurring between diffusional states of one species.
To account for the dynamics of state transitions in a two-state system, we incorporated a statistical framework derived for PDA that is used to analyze single-molecule FRET distributions (25,26,36). This method describes the distribution of time spent in each state given a certain , koff, and the integrated time tint.
The probability of staying in an initially occupied state S1 for an occupation time tS1 without transition is
| (2) |
The probability density functions describing tS1 for an odd or an even number of transitions starting from state S1 are given by (26)
| (3) |
| (4) |
Here, tS1 and tS2 are times spent in state S1 and state S2, and I0 and I1 are Bessel functions of order zero and one, respectively. Note that tS1 + tS2 = tint. Equations for starting in state S2 (WcontS2, WoddS2, and WevenS2) can be found by exchanging koff for and tS1 for tS2 and vice versa in Eqs. 2, 3, and 4.
To correctly describe the distribution over a certain number of frames, we first calculated the distribution over a single time frame tf. Within a single frame, a particle started in that state can either end in the same state or in a different state. Therefore, in a two-state system, the probability functions for four scenarios have to be calculated as follows:
| (5) |
| (6) |
| (7) |
| (8) |
for i = 1,2.
To link the distribution of times spent in a state to the distribution of measured displacements (x), we can convert the time spent in each state and its diffusion coefficient to the average diffusion coefficient by the following equation:
| (9) |
In the case of the transition between an immobile bound state S1 (DS1 = 0) and a mobile state with diffusion coefficient DS2 = Dfree, we can modify the above equation to
| (10) |
AnaDDA is able to fit systems with two mobile states, but for the rest of the article (Fig. S3), we analyze systems with an immobile state and use Eq. 10.
Using Eq. 10, the probability distribution function (Eq. 1) can be modified according to
| (11) |
Subsequently, the probability to find a certain diffusion coefficient (x) for a single time step given the time spent in the mobile state is given by . We can then find the distribution of measured diffusion coefficients for a single frame by integrating overall possible times spent in the mobile state:
| (12) |
Now that we have the distribution for a single time step, we need to find the distribution for the average of multiple frames. For this, we use the same method as Qian et al. (23), namely repeated convolution of the distribution for a single frame while keeping track of the start and end state. The probability distributions are therefore
| (13) |
| (14) |
| (15) |
| (16) |
For a track consisting of four frames, the distributions found for two frames can be convoluted again. The full distribution is then found by summing up each of the partial distributions multiplied by the chance they start in S1 or S2:
| (17) |
with pS1 and pS2 defined in Eqs. 18 and 19, respectively:
| (18) |
| (19) |
Localization error
As two consecutive steps share at least one localization, the localization error of this localization leads to a correlation between the measured displacements (35). Only in the special case of the localization error being zero, the measured displacements are uncorrelated. The distribution of the sum of displacements for a certain number of steps is therefore not described by a γ distribution, which is the sum of independent variables. However, as each step separately is a γ random variable, we calculate the summation of correlated γ random variables to describe the distribution of localization error analytically for different number of steps. For derivations, see Supporting Materials and Methods, Derivation of D∗ distributions of localization error.
Tracking window
To the prevent the accidental linking of different diffusing particles, many tracking algorithms use a certain cutoff, in which steps longer than a certain distance are not allowed (37, 38, 39). However, this tracking window can influence the distribution of D values recovered. In anaDDA, we correct for this by setting = 0, where maxD is the maximal D∗ value that can be obtained given the tracking window.
Confinement
To take the effects of geometrical confinement within the cell into account, we implemented an analytical way to calculate the effective diffusion coefficient given the geometry and the real diffusion coefficient. Most boundary geometries encountered in in vivo settings are either spherical or rod shaped. For a spherical geometry, the effective measured mean squared displacement given a diffusion coefficient D and a timestep Δt have been previously derived for multiple dimensions (40). We have used these equations to find Dobs = fboundary(r,t,D), which is the observed diffusion coefficient given a certain boundary condition (spherical/rod shaped), the boundary radius r, the frame time t, and the real diffusion coefficient D. For derivations, see Supporting Materials and Methods, Derivation of confinement corrections.
MLE
To find the underlying parameters of experimental data and simulations, we use MLE, which maximizes the joint probability of observing by iteration through the parameter space. Generally, MLE requires a probability density function to calculate and sum up all probabilities of each observed data point. The benefit of the method is that it does not require any binning compared with other optimization methods. However, MLE does require the exact probability for each data point to be calculable. Because we use numerical convolution (for increasing the performance of the algorithm, we implemented a fast Fourier transform (FFT) convolution (41)), we will only get the probability at discrete points within the probability density function. Therefore, to calculate the probabilities for the points of our data set, we use spline interpolation.
Because MLE is known to be affected by local minima (42), we use a number of cycles (generally four) in which we generate random starting parameters and run the algorithm several times, after which we select the end parameter set with the maximal likelihood. Those parameters are then used as starting parameters for bootstrapping in which we run the analysis through a number of subsets of the data to get an estimate of the SDs of our parameter estimates.
Plotting of diffusion distribution histograms
With the parameter sets used in our simulations, the diffusion histograms are visually more distinguishable when log(D∗) is plotted compared to D∗. We therefore integrated the linear density function with widths specified by the bin size of the logarithmic scale to calculate the probability density function for log(D∗) instead of D∗.
Software
The latest version of the software is available on GitHub: https://github.com/HohlbeinLab/anaDDA.
Results
AnaDDA generates D∗ distributions equal to the ground truth of simulated distributions
AnaDDA allows for calculating the shape of the D∗ distribution, depending on the free diffusion coefficient (the diffusion coefficient in the absence of binding interactions) and the transition rates. As this shape depends on the number of localizations per track, we separate the tracks according to their respective length and fit each data point to the distribution that matches their step length. To benchmark our new analysis method, we first compared our theoretical predictions of the D∗ distribution to data in which we simulated the diffusional characteristics of a particle that dynamically switches between a (DNA-) bound state and a freely diffusing state without including any boundary conditions for diffusion (see section below for confinement within cells). With an increasing number of tracks, the predicted D∗ distribution increasingly resembles the predicted theoretical distribution (Fig. 1 C). To test whether our theoretical distributions differed from the simulated ground truth, we performed Kolmogorov-Smirnov tests. We found that the test statistic DKS converged to zero for larger number of tracks analyzed and was on average smaller than the critical value required to reject the null hypothesis (DKS = 0.004 for p < 0.05), indicating that the ground truth simulations and our theoretical predictions come from the same distribution (Fig. 1 D).
We varied the range of transition timescales (Fig. 1 E) ranging from 0.01 to 10 transitions per frame (at 0.01 s frame time) at all different step numbers per track included in this analysis (1–8; Fig. S1 A) and compared a range of frame times (20–100 Hz) and experimentally realistic localization errors (20–50 nm) (Fig. S1 B). Under all these conditions, the ground truth simulations (n = 100,000 tracks) and the anaDDA-generated distributions showed very close agreement (DKS < 0.004). As this analysis involved a direct comparison between the predicted and simulated distribution without fitting the data or any optimization of parameters, it can be concluded that our theoretically predicted distributions are similar to the ground truth distributions.
AnaDDA can extract transition rates from tracks with more than one transition per frame
With data from experimental measurements, the ground truth is unknown, and parameters have to be inferred by fitting. First, we tested via simulations how reliably parameters can be extracted over a large dynamic range of transitions. We compared the input parameters to the extracted ones with MLE. To benchmark the performance of extraction, we calculate the accuracy through the geometric mean and the precision through the geometric SD of 10 independent simulations. For all tested data sizes (5000–100,000 tracks) and transition rates (0.001–10 transitions per frame), the analysis method is accurate (±5% of input parameters). The precision decreased slightly with decreasing data size and for small/large transition rates (Fig. 2). Furthermore, the precision at high transition rates (>1 transition per frame) is lower for than koff (Fig. 2, A and B). In general, the highest precision is found for tracks between 0.1 and 1 transition per frame. With 50,000 tracks per simulation, the transition rates over three orders of magnitude (0.002–2 transitions per frame) were determined with an error smaller than 20% of the actual value (Fig. 2, A–C).
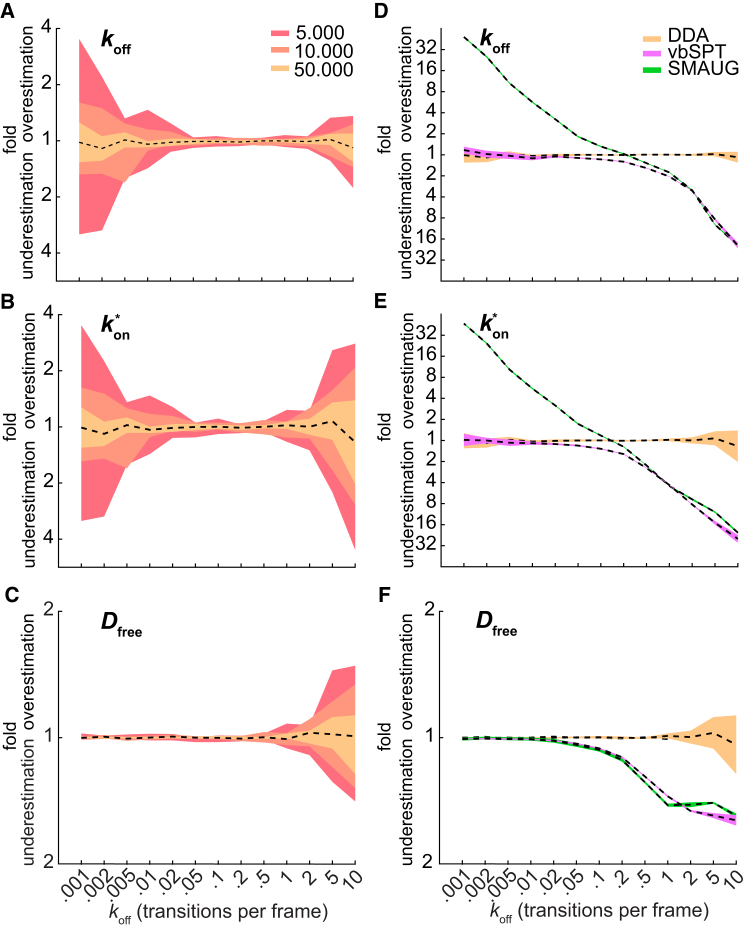
Figure 2.
MLE extraction of parameters. The accuracy is calculated through the value of the geometric mean (dashed black line), and the precision is calculated through the geometric SD of 10 independent simulations. The step number per track was exponentially distributed with a mean of three steps and a cutoff at eight steps (Dfree = 4 μm2/s, σ = 30 nm). (A–C) Shown is the effect of data size on the accuracy and precision of extraction of (A) koff, (B) , and (C) Dfree for n = 5,000 tracks (red), 10,000 tracks (orange), and 50,000 tracks (yellow). (D–F) Shown is a comparison of anaDDA versus vbSPT and SMAUG on the accuracy and precision of extraction of (D) koff, (E) , and (F) Dfree. 50,000 tracks were used for both methods. To see this figure in color, go online.
We compared our method with a previously published framework that used Bayesian statistics to infer transition and diffusion dynamics (variational Bayes single-particle tracking (vbSPT)) (30) and a framework that used unsupervised Gibbs sampling for similar purposes (single-molecule analysis by unsupervised Gibbs sampling (SMAUG)) (31). As vbSPT and SMAUG deduce the number of states from the data, we limited the amount of states in this analysis software to two to achieve a fair comparison. For slow transitions (<0.01 transition per frame), both anaDDA and vbSPT were able to extract the correct kinetic parameters for data sets containing 50,000 tracks (<20% error; Fig. 2, D–F), whereas SMAUG overestimated the transition rates. At faster transitions (>0.02 transitions per frame), however, we observed a decrease in the extracted free diffusion coefficient and a decrease in the extracted on- and off-rates for both vbSPT and SMAUG. A similar trend was observed for data sets containing only 1000 tracks (Fig. S2 A).
We furthermore compared the different analysis methods in the presence of tracking errors, arising from high density measurements, in which tracks from different particles are erroneously linked. We simulated tracks occurring simultaneously in increasing densities (0.01–0.25 particles per μm2). Subsequently, we linked the localizations using a previously described tracking algorithm that uses minimization of the total squared displacement of all possible trajectories within a given tracking window (43). For most timescales, anaDDA can still extract the correct parameters, but for low and high transition rates, the extraction is sensitive to the tracking errors occurring at high densities (0.1–0.25 particles per μm2; Fig. S2 B). At low transition rates (0.001–0.05 transitions per frame), the transition rates were overestimated, and at high transition rates (210 transitions per frame), the on-rate and free diffusion coefficient were overestimated. When vbSPT and SMAUG were tested with simulations at the highest densities (0.25 particles per μm2), the extracted kinetic parameters were even further away from the ground truth. Our simulation shows that to robustly extract kinetic parameters, localization densities should be kept low (<0.1 per μm2).
When we removed the restriction of a two-state model, vbSPT started introducing multiple false states (Fig. S3 A). Already at low transition rates (0.01 transitions per frame), vbSPT suggests the presence of a false third state. At this transition rate, two states (0.06 and 0.11 μm2/s) were close to the expected average diffusion coefficient of the simulated immobile state (σ2/t = 0.09 μm2/s). The highest number of predicted states (four states) was found for transition rates between 0.05 and 0.5 transitions per frame. To see whether anaDDA also would fit more false states, we tried to force a second dynamic species (Fig. S3 B). In this case, the second species fraction was found to have zero amplitude, indicating that under the tested conditions, anaDDA would not introduce a false state.
So far, we have limited the analysis to systems for which one of the states is immobile, but anaDDA can also be applied to systems with two mobile states. We expected that the extraction of parameters would be less accurate for these systems, first because a new parameter needs to be extracted from the data and second because the overlap of D∗ distributions from two mobile distributions tend to overlap more than distributions of a mobile and an immobile state (Fig. S3 C). We found that under these conditions, anaDDA still performs well in the range 0.01–2 transitions per frame (less than 20% error with 50,000 tracks) but that parameters extracted from lower or higher transition rate simulations are less accurate compared with systems with an immobile state (Fig. S3, D–G). Under the same simulation conditions, vbSPT and SMAUG overestimate the transition rates at low transition rates (>4× at 0.001 transitions per frame) and underestimate at high transition rates (>20× at 10 transitions per frame).
Our findings suggest that vbSPT and SMAUG fail to account for the increasing occurrence of multiple transitions within a single frame at fast transition rates. Our analysis software is distinctive in its ability to extract kinetic parameters when multiple transitions are likely to occur within a single track. In fact, anaDDA can validate whether a simple two-state model with fast transitions is sufficient to explain the data, whereas vbSPT and SMAUG would introduce virtual static or slowly interconverting states. To further improve the applicability of anaDDA to real experimental sptPALM data, we wanted to correct for artifacts that can influence DDA, namely confined diffusion within cells and application of tracking windows.
AnaDDA corrects for confinement within cells and restricted tracking windows
To study the effect of geometrical confinement, we simulated diffusive particles within the confined boundaries of different cell shapes. We previously showed that confinement only has a very small effect on observed transition rates in bacterial cells (44). However, as the measured diffusion coefficient can be greatly affected by confinement, we implemented an algorithm based on previously developed derivations (40) (for details see Methods) to account for confinement in both rod-shaped (e.g., Escherichia coli cells) and spherical-shaped boundaries (e.g., eukaryotic nuclei) (Fig. 3 A).
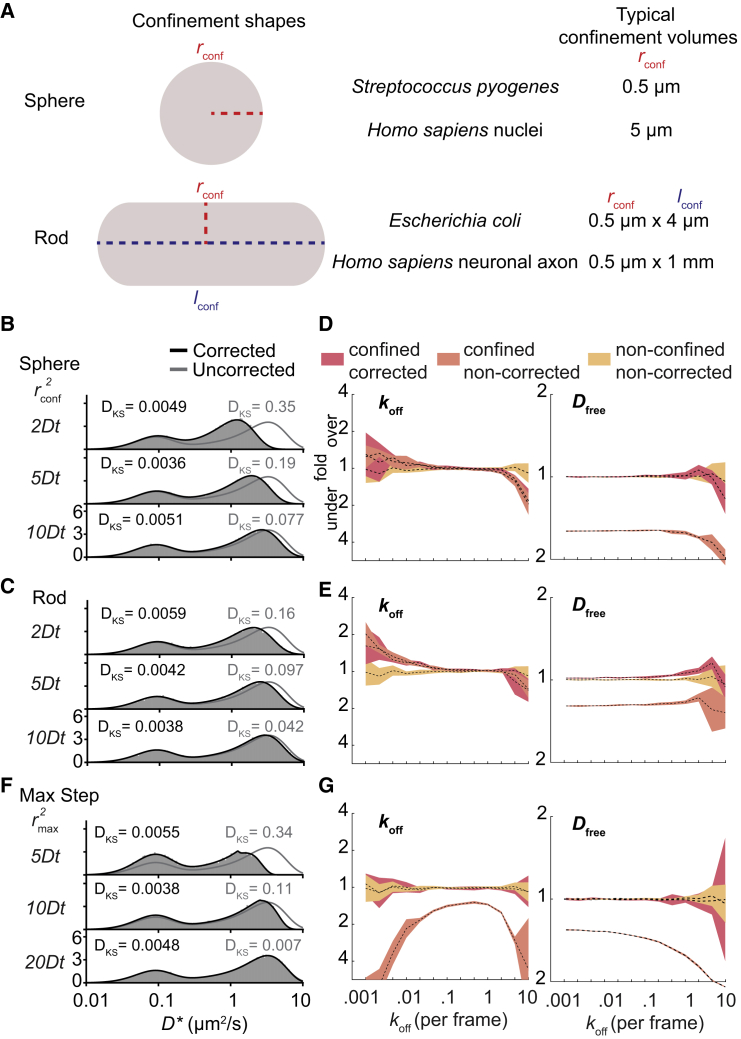
Figure 3.
Effects of geometrical confinement and the length of the tracking window. (A) Typical confinement shapes within cells are shown. The boundary shape of spherical cells is defined by a single parameter (radius; rconf.), whereas rod-shaped cells are defined by two parameters (radius and length; rconf and lconf). (B and C) Shown is the influence of spherical- and rod-shaped boundaries on the distribution of simulated (gray box) and uncorrected DDA (gray line) and corrected DDA (black line) distributions (koff = 0.2 frame−1, = 0.2 frame−1, step number = 4 steps). (D and E) Shown is the influence of spherical- and rod-shaped cells on the estimation of parameters of DDA on unconfined simulated trajectories (yellow), uncorrected DDA on confined simulated trajectories (orange), and corrected DDA on confined trajectories (red). (F and G) Shown is the same as (B–E) except for simulated trajectories with a maximal step size. Simulation parameters are as follows: Dfree = 4 μm2/s, σ = 30 nm (localization precision), and n = 50,000 tracks. The Kolmogorov-Smirnov test statistic (DKS) is indicated in each histogram. To see this figure in color, go online.
For both spherical and rod-shaped cells (cell length/radius = 8:1), we found that our theoretical predictions for varying cell sizes (r2 = (2, 5, or 20)Dfreet) match well with simulated data (Fig. 3, B and C; DKS < 0.006) in contrast to uncorrected distributions for which the predicted distributions are statistically different from the simulated distributions (DKS > 0.04). In an E. coli cell (r = 0.5 μm) and under standard measurement frame times (0.01 s), these confinement regimes (Dfreet) would be reached with Dfree values of 12.5 μm2/s, respectively, which matches the values found for small single fluorescent proteins (45). In a eukaryotic nucleus (r = 5 μm), these regimes would correspond to Dfree values up to 750 μm2/s, which is generally much faster than any reported literature values. This finding indicates that geometrical confinement by cell boundaries is mostly limiting in prokaryotic studies. However, at longer frame times (0.1 s), confinement effects will play a role when studying diffusion within eukaryotic nuclei.
As not every cell in a population is the same size, the distribution might be further affected by a variation of cell sizes. We therefore analyzed a mixture of three different simulated cell sizes and found that the distributions remained statistically indistinguishable from a uniform population of the same cell size (Fig. S4; DKS < 0.006). This shows that the correction method remains valid as long as the average dimensions of the cell boundaries are known.
To further test our ability to infer parameters from the data in a system in which diffusion is geometrically confined, we performed MLE with and without corrections for confinement. We observe that the incorporation of our confinement corrections increases the accuracy and precision of the estimation of Dfree (Fig. 3, D and E). Compared with unconfined diffusion, there is a bias in recovered transition rates at very small and large transition rates as these regimes are most sensitive to small deviations of the predicted distribution to the ground truth. These minor deviations are most likely caused by a correlation that occurs for diffusing particles within boundaries, in which particles that are close to the boundary in one frame are again likely to encounter the boundary in the next frame. That effect is not taken into account in our current implementation. However, for most transition regimes (0.01–2 transitions per frame), the error of the estimated parameters falls within 20%.
Another type of analysis artifact comes from the settings for tracking windows. When the density of labeled fluorophores is higher than one per cell, different molecules can be falsely assigned to the same track. To prevent this effect, multiple tracking software algorithms set a limit to the maximal step length that individual tracks are allowed to have. Although this is sometimes unavoidable, the absence of the largest steps can severely affect the MLE fitting parameters. AnaDDA is able to correct for this by integrating this maximal displacement in the probability distribution (see Methods). The effect of this correction was tested for a range of radii of tracking windows (r2 = (5, 10, or 20)Dfreet), and in all cases, the DKS of the corrected distributions were below the threshold for significantly different distributions (DKS = 0.006), whereas for small and intermediate tracking windows (r2 = (5 and 10)Dfreet), uncorrected distributions were significantly different (DKS = 0.34 and DKS = 0.11; Fig. 3, F and G). The tracking window also had a large effect on both the predicted transition rates and free diffusion coefficients from MLE, in which in the absence of corrections, all parameters were significantly underestimated (>1.5×). With the correction, the estimations were again unbiased and very similar to the accuracy and precision of estimations in the absence of tracking windows.
Taken together, anaDDA can correct the distributions for measurements that are affected by confinement within spherical- and rod-shaped boundaries and by the application of a maximal step size within tracking algorithms. Because these artifacts cause a nonlinear relationship between the mean-squared displacement and the time step in a similar fashion as anomalous diffusion (46), it allows the user to validate whether a simple Brownian model with confinement is able to explain the data before assuming more complex modes of diffusion.
AnaDDA can be expanded for multiple states and can integrate multiple frame times
So far, we have discussed the presence of one diffusing species converting between two diffusional states. In the following, we will expand the DDA fitting to account for more species and states.
Many DNA binding proteins contain both non- and target-specific interactions with DNA. Therefore, it is likely that the kinetics of these two interactions are different, which would require the model to be expanded beyond a two-state model. PDA statistical analysis currently does not incorporate more than two dynamic states. However, it is possible to incorporate more states by assuming that their dynamics are much slower than the nonspecific DNA interactions, which would result in a negligible amount of transitions in the time frame studied. Then, these states can be approximated by separate static (noninterchanging) species (Fig. 4 A). Generally, the specific interactions are much longer lasting than the nonspecific interactions (47), so in many cases, this assumption would be valid.
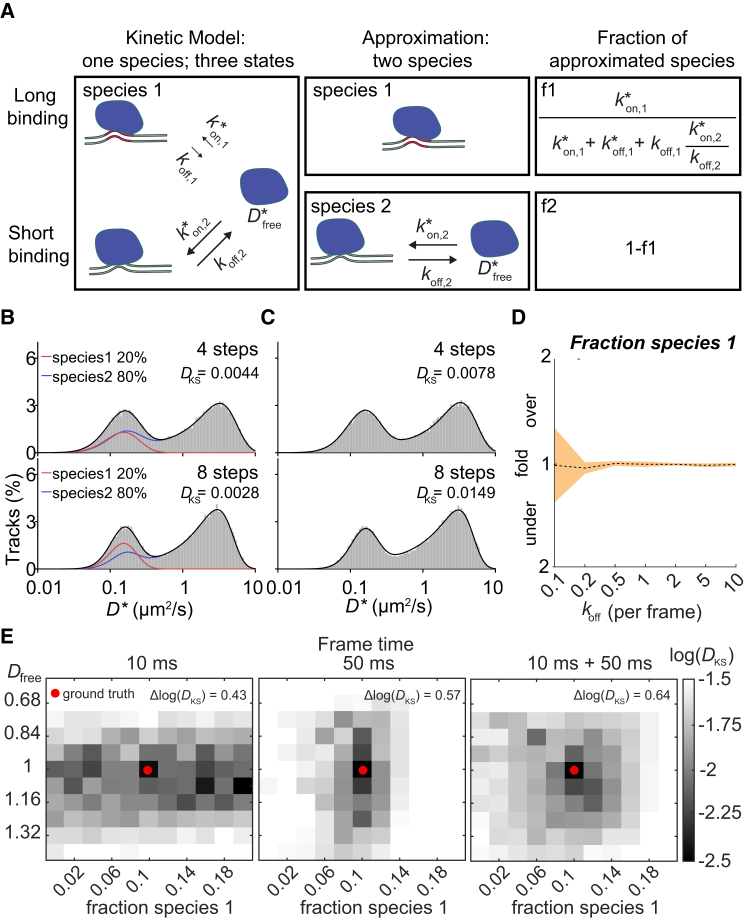
Figure 4.
Three-state models and multiple frame times. (A) Three-state models cannot be directly described with PDA statistics. If some interactions are slower than the typical frame time, however, the approximation can be made that they belong to a nontransitioning separate species. The expected fraction of each of these species can be calculated from the on- and off-rates of all states (right). (B) Shown is a comparison of a simulated three-state model (koff,1 = 0.01 frame−1, = 0.005 frame−1, koff,2 = 0.2 frame−1, = 0.2 frame−1) with a predicted theoretical approximated two species model, in which the slower transitioning state is approximated as a separate immobile species (red), and the other species (blue) still contains two states with koff,2and as transition rates. Upper panel shows a step number of four steps, and lower panel shows a step number of eight steps. (C) Shown is the best fit of the simulated three-state model from (B) with a single species two-state model. (D) Shown is the MLE extraction of the expected fraction of the first approximated species for different values of koff,2. (E) Shown is a heat map of the log(DKS) between a simulated distribution (Dfree= 1, fraction immobile = 0.1; ground truth (red dot)) and a theoretical predicted distribution with varying parameters around the parameters used for the simulation, in which the simulation consisted either of 100,000 tracks at 10-ms frame time (left), 100,000 tracks at 50-ms frame time (middle), or 50,000 tracks at 10-ms frame time and 50,000 tracks at 50-ms frame time, respectively (right). The discrete Laplacian Δlog(DKS) calculated from the ground truth coordinate is the sum of the second derivatives in both dimensions and indicates how quickly log(DKS) increases with parameter values slightly different than the ground truth. The Kolmogorov-Smirnov test statistic (DKS) is indicated in each histogram. To see this figure in color, go online.
To test how well this approximation works and how well the method can distinguish this model from a simple two-state model, we simulated a linear (A ⇄ B ⇄ C) three-state model containing one slow transitioning bound state ( = 0.005 frame−1, koff,1 = 0.01 frame−1) and one fast transitioning bound state ( = 0.2 frame−1, koff,2 = 0.2 frame−1). We compared this simulation to our theoretically predicted distribution in which we approximated the slower transitioning state as a separate immobile species and the faster transitioning state as a separate species (Fig. 4 B). The fraction of the approximated immobile species (20%) and transitioning species (80%) can be calculated from the ratio of the on- and off-rates (Fig. 4 B). We found very good agreement between the theoretical prediction and the simulation (DKS < 0.006), indicating that this approximation can be applied in this case.
We then tried to find whether a single species two-state model could also fit the distribution of the three-state model (Fig. 4 C). We found that although for smaller tracks, there are parameters that can fit the distribution quite well (DKS = 0.0078 for step number of four steps), the distribution for larger tracks significantly deviated from the ground truth (DKS = 0.0149 for step number of eight steps). Therefore, with a sufficient number of longer tracks, two-state and three-state models are clearly distinguishable.
We then tested under which conditions the parameters can be reliably extracted from the data. To this end, we varied the transition rates of the fast-bound state ( and koff,2) while keeping the slower bound state fixed. We observed that under all transition rates tested (0.1–10 transitions per frame), the error of the estimated parameters falls within 25% and that with increasing rates of the fast-bound state, the extraction of the fraction parameter became more reliable (Fig. 4 D). This finding indicates that as long as the transition rates associated with the different bound states are different enough (>10 fold), with one of them being significantly slower than the frame time used in the measurements, parameters for three-state models can be reliably extracted with anaDDA.
More complex models with larger number of species, each having up to three states and meeting the requirements described above, can also be fitted using anaDDA but are prone to increased uncertainty and under- or overfitting as many parameters in these models could give rise to similar distributions. We therefore advise users to fit models with a maximum of four free parameters when the data was recorded using a single frame time. To overcome this limitation, we implemented the ability to use data acquired at different frame times into a single global fit. By fitting data from multiple frame times simultaneously, the number of potential parameters that can fit all the data decreases, leading to more accurate and precise fitting for more complex models.
As an example, we simulated a two species (one immobile and one transitioning) model and calculated the Kolmogorov-Smirnov test statistic (DKS) for a range of parameters around the input parameters for a simulated data set consisting of tracks either measured at a single frame time (10 or 50 ms) or a combined set in which half of the data set contained simulated tracks from each frame time (Fig. 4 E). If there are other closely related parameters with similar DKS values to the ground truth, the fit can converge to these values as well. Therefore, the uncertainty is linked to the parameter space with DKS similar to the DKS of the ground truth. We observed that different frame times perform better on different parameters. In particular, short frame times led to more uncertainty in the determination of the fraction of each species, whereas long frame times gave more uncertainty in the determination of the free diffusion coefficient. When data recorded at different frame times are combined, there is only a single set of parameters that give rise to a similar DKS as the ground truth. To quantify the benefit of the combination of frame times, we calculated the discrete Laplacian score (Δlog(DKS)) from the ground truth coordinate. The score is the sum of the second derivatives in both dimensions and indicates how quickly log(DKS) increases when moving away from the ground truth. We found that the combined frame times of 10 and 50 ms data had a higher score (0.64) compared with data sets from either frame time alone (0.57 for 50 ms and 0.43 for 10 ms data sets), indicating that data sets with more than one frame time outperform data sets recorded at a single frame time. In conclusion, the benefit of gathering data with different frame times is that it reduces the parameter space that can simultaneously fit multiple distributions and therefore offers better performance with the same number of data points.
E. coli DNA polymerase I undergoes rapid DNA interactions
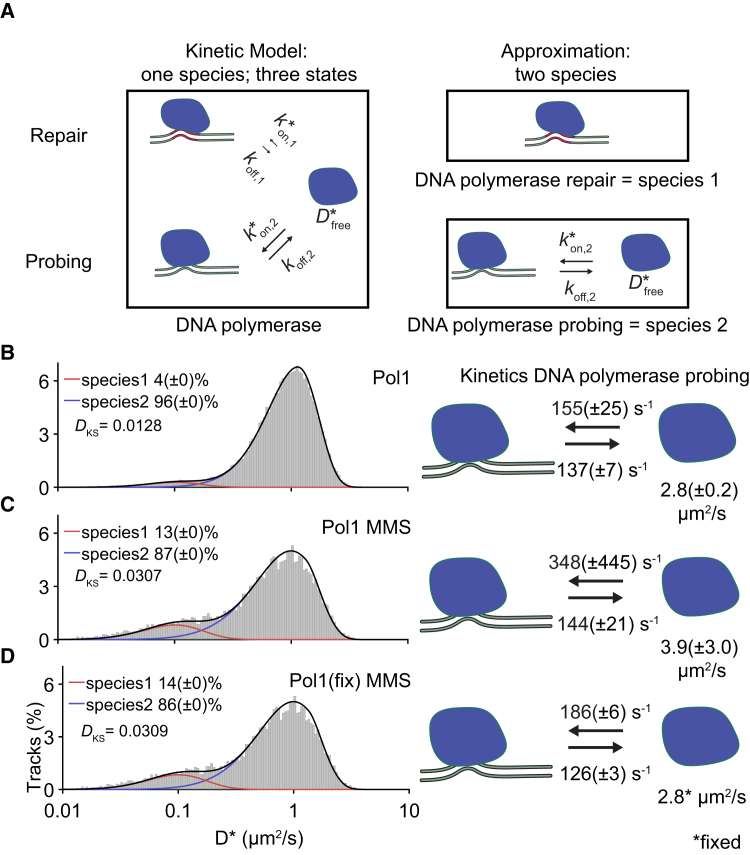
To test the applicability of our analysis method to experimental data, we reanalyzed previously published data on the diffusion of DNA polymerase I in E. coli (17). In this study, the diffusion distribution of PAmCherry-Pol1 was grouped into immobile and mobile diffusing particles by simple thresholding without determination of any transition kinetics. The authors found that under normal conditions only 4–5% of the proteins were immobile. However, they found that even the mobile tracks were mostly located within the nucleoid, which may suggest that these tracks represent transient DNA binding, probably probing the DNA for repair sites. We therefore hypothesized that the previously assigned mobile fraction is also undergoing rapid transitions between DNA-bound and freely diffusing states.
We decided to fit the data with two species, one belonging to proteins involved in repair (a species with a single bound state) and one to probing (a species with a bound and a freely diffusing state). When we fitted this model (two species and three states; Fig. 5 A), we found a similar percentage of proteins involved in repair as described in the previous study (4%; Fig. 5 B). Furthermore, we found that the probing species had a free diffusion speed of 2.8 (±0.2) μm2/s in the cytoplasm and that it is involved in very rapid DNA probing events (koff 137 ± 7 s−1; 155 ± 25 s−1). Based on the on- and off-rates, we calculated that the probing species spends more than half the time (∼55%) bound to DNA. Altogether, DNA polymerase spends ∼60% bound to DNA either in repair (4%) or probing for mismatch sites (55%).
Figure 5.
Extracting kinetic information of DNA polymerase I diffusing in live E. coli cells. (A) Shown is an approximated model of the kinetic model of DNA polymerase diffusion containing a DNA repair and DNA probing state (left). These states were separated into a single-state repair species (species one; right) and a probing species with two states (species two; right). (B) Shown is the fit of DNA polymerase I in untreated cells (n = 179.511 tracks). The D∗ was fit with two species, one species involved in repair (red line) with a single state (immobile) and one species involved in scanning DNA with two states (mobile and immobile; blue line). The transition between the latter two states and the free diffusion coefficient of the mobile state are depicted. Fit was performed on all different step numbers (one to eight steps), and histograms are only shown for a single step number (four steps). Tracks with eight or more steps were truncated to eight steps for the entire fit. For the histogram, D∗ calculated from tracks truncated to four steps are shown. (C) Shown is the same as (B) but performed on the data of DNA polymerase in cells treated with MMS. (D) Shown is the same as (C) except that the free diffusion coefficient of the mobile state was fixed to the same value as was found for polymerase in untreated cells (B). The Kolmogorov-Smirnov test statistic (DKS) is indicated in each histogram, and uncertainty in parameters were estimated with bootstrapping (±SD). Experimental data were taken from a previous study (17). To see this figure in color, go online.
The study also measured the diffusivity of DNA polymerase in the presence of the DNA damaging agent methyl methanesulfonate (MMS). Using anaDDA, we found that the immobile species increased to 13%, which matches the findings in the publication (13 ± 0.2%; Fig. 5 C). The transition rates and diffusion coefficients under this condition could not be assigned with confidence based on the bootstrap values (koff 137 ± 7 s−1; 348 ± 25 s−1). We hypothesized that this is caused by the lower number of available tracks (41,415 tracks) compared with the untreated data set (142,178 tracks).
To quantitatively assess the transition kinetics in the presence of DNA damage, we made the assumption that DNA damage would not alter the free diffusion behavior of DNA polymerase in the cytoplasm but only the kinetics of the interactions with DNA. We therefore fixed Dfree to the value found for DNA polymerase in untreated cells (2.8 μm2/s; Fig. 5 D), which caused the fitting to converge to a narrow range of transition rates. We observed that although the koff remained the same (126 ± 3 s−1), the on-rate increased in the presence of damaged DNA (185 ± 6 s−1), indicating that more DNA polymerases were bound to DNA in long-term repair events (from 4 to 13%) and that also the polymerases engaged in probing spent more time bound to DNA. Altogether, these numbers would indicate that DNA polymerase in the presence of MMS spent ∼75% of its time to DNA either at a repair site (13%) or while probing the DNA (60%).
We further found that the maximal step size of five pixels used in the original analysis significantly affected the distribution of observed D∗ values (Fig. S5). AnaDDA was able to correctly predict and take this effect into account. Overall, the transition rates between bound and unbound polymerase found under both conditions are high compared to the frame rate (>1 transition per frame), which demonstrates the applicability of anaDDA to quantify very fast transition kinetics in vivo.
Discussion
anaDDA is able to accurately extract kinetics occurring within four orders of magnitude with around 10 to 0.01 transitions per frame. With conventional camera frame rates of 100 Hz, this range translates to interaction kinetics of 1 ms to 1 s, even if the mean track length is as short as three to four frames. Furthermore, anaDDA is able to account for confinement and tracking window effects and has the possibility to fit data acquired at multiple frame times into a single global model. The reanalysis of previously published data on DNA polymerase I in E. coli suggests that this protein complex uses rapid probing of DNA and therefore spends more than 50% of its time bound to DNA, a value previously hypothesized based on its preferred localization in the nucleoid but not quantified up to now. These new insights into the biology of DNA polymerase in vivo can experimentally be further tested. The predicted times spent on DNA in the absence (60%) and presence of MMS (75%) can be independently quantified by measuring the ratio of polymerases in DNA-containing and DNA-free segments of cells elongated by cephalexin as was done previously for CRISPR-Cas complexes in E. coli (44).
Compared with other simulation-based frameworks for estimating transition rates (19,48,49), anaDDA holds several advantages. First, the distributions of simulations are not exact as they are generated from a limited number of particles and therefore do not allow for using an MLE approach, which requires convergence based on exact probability even for small changes in the parameter space. Second, because analysis methods can only be verified by knowing the ground truth, these algorithms can only be tested with and against simulations itself. Consequently, the analysis and verification data are not independent, which could lead to unobservable errors. Furthermore, our analysis method is computationally significantly faster. MLE takes just around 15 s to find the optimal parameter set for a global fit to a 50,000 tracks data set with a step number range of one to eight steps (Intel Core i7), whereas a simulation estimating three parameters with a global fit of all step numbers required around 10 h to find an optimal set of parameters.
Despite the new possibilities that anaDDA offers to analyze complex sptPALM data, a number of challenges remain. First, our transition rate analysis is limited to Markovian processes, which assume that the transition rates are independent of past events. This assumption seems to be valid for protein binding kinetics in vivo (30,47,50) but might not be generalizable for all biological systems (51,52). Second, macromolecules such as DNA binding proteins potentially have many different binding sites and therefore would have many different kon and koff values. The transition rates extracted with anaDDA do not fully capture this complex biological behavior and therefore should be interpreted as an average timescale at which these transitions take place. Third, the number of states cannot, unlike Bayesian methods, be automatically extracted from the data set. However, given the complexity of sptPALM data, Bayesian algorithms are prone to overfit the data (Fig. S3 A). A more robust way for model selection can be achieved by incorporating experimental controls (e.g., mutants or subunits that reduce complexity) and measurements at multiple frame times (Fig. 4 B). Fourth, potential effects of finite exposure times (53,54) on the measured displacements have not been yet incorporated in anaDDA. These effects, however, can be minimized by using stroboscopic illumination (38,55). Fifth, anaDDA assumes Brownian motion and does not incorporate anomalous diffusion, which has been observed in some in vivo systems (56,57). Our method can be adapted to incorporate anomalous diffusion once it is clear which of the many potential models (58) is suited best for the observed anomalous diffusion (59). Again, care should be taken as these more complex models are more easily overfitted. Last, for performance reasons, the tracks that we analyze in anaDDA are currently limited to a maximal step number of eight steps, which under most experimental conditions represent more than 90% of the tracks and longer tracks are truncated to the maximal step number of eight.
In our current implementation, it is possible to include two transitioning states into the direct fitting. We have shown, however, that when transition rates are slow compared with the frame time of the measurement, states can be treated as separate species. Further development of the underlying master equations of PDA statistics could allow direct implementation of multistate models.
With the increasing use of brighter and more stable organic fluorophore (14,60) or low photon flux measurements (61) for single-particle tracking, the resulting increase of the step number per track and the decrease of the localization error will enable further improvements in the precision of extracted kinetic parameters. Currently, we have implemented the software for tracking in two dimensions, but the algorithms can be further modified toward tracking in three dimensions. Using the estimated error for each individual localization can further improve the robustness of the analysis as has been demonstrated previously (62). Another improvement that can be incorporated in our framework and has already been developed is to take the effect of particles moving out of focus and the recovery of localizations depending on diffusion coefficients into account (19,38).
Our analysis method allows the quantification of fast kinetic transitions inside living cells with state lifetimes in the 1 ms to 1 s range, opening a temporal range at which many DNA screening interactions are expected to take place (55). So far, however, quantifying these interactions has been limited because of a lack of appropriate analytic and experimental methods. We are convinced that anaDDA will offer the means to determining fast kinetics in vivo, which will be the key to uncover and understand the behavior of biomolecular complexes in cells.
Author Contributions
S.J.J.B. and J.H. conceived and supervised the project. J.H. provided the initial idea. J.N.A.V. developed the framework, derived the equations, and wrote the analysis scripts. J.N.A.V. and J.H. wrote the manuscript. S.J.J.B. provided feedback on the manuscript.
Acknowledgments
The authors thank Dr. S. Uphoff for supplying the experimental data on DNA polymerase, Dr. K. Martens for feedback and co-development of the Monte Carlo DDA implementation, and all members of the Hohlbein and the Brouns groups for input during group discussions.
This work was supported by the European Research Council starting grant 639707 and by the Netherlands Organisation for Scientific Research as part of the Frontiers of Nanoscience program.
Editor: Gerhard Schuetz.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.09.033.
Contributor Information
Stan J.J. Brouns, Email: stanbrouns@gmail.com.
Johannes Hohlbein, Email: johannes.hohlbein@wur.nl.
Supporting Citations
References (63, 64, 65) appear in the Supporting Material.
Supporting Material
References
- 1.Miller H., Zhou Z., Leake M.C. Single-molecule techniques in biophysics: a review of the progress in methods and applications. Rep. Prog. Phys. 2018;81:024601. doi: 10.1088/1361-6633/aa8a02. [DOI] [PubMed] [Google Scholar]
- 2.Hohlbein J., Aigrain L., Kapanidis A.N. Conformational landscapes of DNA polymerase I and mutator derivatives establish fidelity checkpoints for nucleotide insertion. Nat. Commun. 2013;4:2131. doi: 10.1038/ncomms3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hodges C., Bintu L., Bustamante C. Nucleosomal fluctuations govern the transcription dynamics of RNA polymerase II. Science. 2009;325:626–628. doi: 10.1126/science.1172926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rothenberg E., Ha T. Single-molecule FRET analysis of helicase functions. Methods Mol. Biol. 2010;587:29–43. doi: 10.1007/978-1-60327-355-8_3. [DOI] [PubMed] [Google Scholar]
- 5.Craig J.M., Laszlo A.H., Gundlach J.H. Revealing dynamics of helicase translocation on single-stranded DNA using high-resolution nanopore tweezers. Proc. Natl. Acad. Sci. USA. 2017;114:11932–11937. doi: 10.1073/pnas.1711282114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rutkauskas M., Krivoy A., Seidel R. Single-molecule insight into target recognition by CRISPR–Cas complexes. Methods Enzymol. 2017;582:239–273. doi: 10.1016/bs.mie.2016.10.001. [DOI] [PubMed] [Google Scholar]
- 7.Blosser T.R., Loeff L., Joo C. Two distinct DNA binding modes guide dual roles of a CRISPR-Cas protein complex. Mol. Cell. 2015;58:60–70. doi: 10.1016/j.molcel.2015.01.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Heller I., Hoekstra T.P., Wuite G.J.L. Optical tweezers analysis of DNA-protein complexes. Chem. Rev. 2014;114:3087–3119. doi: 10.1021/cr4003006. [DOI] [PubMed] [Google Scholar]
- 9.Blouin S., Craggs T.D., Penedo J.C. Functional studies of DNA-protein interactions using FRET techniques. Methods Mol. Biol. 2015;1334:115–141. doi: 10.1007/978-1-4939-2877-4_8. [DOI] [PubMed] [Google Scholar]
- 10.Hohlbein J., Craggs T.D., Cordes T. Alternating-laser excitation: single-molecule FRET and beyond. Chem. Soc. Rev. 2014;43:1156–1171. doi: 10.1039/c3cs60233h. [DOI] [PubMed] [Google Scholar]
- 11.Lerner E., Cordes T., Weiss S. Toward dynamic structural biology: two decades of single-molecule Förster resonance energy transfer. Science. 2018;359:eaan1133. doi: 10.1126/science.aan1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kapanidis A.N., Lepore A., El Karoui M. Rediscovering bacteria through single-molecule imaging in living cells. Biophys. J. 2018;115:190–202. doi: 10.1016/j.bpj.2018.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jradi F.M., Lavis L.D. Chemistry of photosensitive fluorophores for single-molecule localization microscopy. ACS Chem. Biol. 2019;14:1077–1090. doi: 10.1021/acschembio.9b00197. [DOI] [PubMed] [Google Scholar]
- 14.Banaz N., Mäkelä J., Uphoff S. Choosing the right label for single-molecule tracking in live bacteria: side-by-side comparison of photoactivatable fluorescent protein and Halo tag dyes. J. Phys. D Appl. Phys. 2019;52:064002. doi: 10.1088/1361-6463/aaf255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Manley S., Gillette J.M., Lippincott-Schwartz J. High-density mapping of single-molecule trajectories with photoactivated localization microscopy. Nat. Methods. 2008;5:155–157. doi: 10.1038/nmeth.1176. [DOI] [PubMed] [Google Scholar]
- 16.English B.P., Hauryliuk V., Elf J. Single-molecule investigations of the stringent response machinery in living bacterial cells. Proc. Natl. Acad. Sci. USA. 2011;108:E365–E373. doi: 10.1073/pnas.1102255108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Uphoff S., Reyes-Lamothe R., Kapanidis A.N. Single-molecule DNA repair in live bacteria. Proc. Natl. Acad. Sci. USA. 2013;110:8063–8068. doi: 10.1073/pnas.1301804110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Garza de Leon F., Sellars L., Kapanidis A.N. Tracking low-copy transcription factors in living bacteria: the case of the lac repressor. Biophys. J. 2017;112:1316–1327. doi: 10.1016/j.bpj.2017.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rocha J., Corbitt J., Gahlmann A. Resolving cytosolic diffusive states in bacteria by single-molecule tracking. Biophys. J. 2019;116:1970–1983. doi: 10.1016/j.bpj.2019.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Akimoto T., Yamamoto E. Detection of transition times from single-particle-tracking trajectories. Phys. Rev. E. 2017;96:052138. doi: 10.1103/PhysRevE.96.052138. [DOI] [PubMed] [Google Scholar]
- 21.Lanoiselée Y., Grebenkov D.S. Unraveling intermittent features in single-particle trajectories by a local convex hull method. Phys. Rev. E. 2017;96:022144. doi: 10.1103/PhysRevE.96.022144. [DOI] [PubMed] [Google Scholar]
- 22.van Beljouw S.P.B., van der Els S., Hohlbein J. Evaluating single-particle tracking by photo-activation localization microscopy (sptPALM) in Lactococcus lactis. Phys. Biol. 2019;16:035001. doi: 10.1088/1478-3975/ab0162. [DOI] [PubMed] [Google Scholar]
- 23.Qian H., Sheetz M.P., Elson E.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991;60:910–921. doi: 10.1016/S0006-3495(91)82125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Saxton M.J. Single-particle tracking: the distribution of diffusion coefficients. Biophys. J. 1997;72:1744–1753. doi: 10.1016/S0006-3495(97)78820-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kalinin S., Felekyan S., Seidel C.A.M. Characterizing multiple molecular States in single-molecule multiparameter fluorescence detection by probability distribution analysis. J. Phys. Chem. B. 2008;112:8361–8374. doi: 10.1021/jp711942q. [DOI] [PubMed] [Google Scholar]
- 26.Palo K., Mets U., Kask P. Calculation of photon-count number distributions via master equations. Biophys. J. 2006;90:2179–2191. doi: 10.1529/biophysj.105.066084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nir E., Michalet X., Weiss S. Shot-noise limited single-molecule FRET histograms: comparison between theory and experiments. J. Phys. Chem. B. 2006;110:22103–22124. doi: 10.1021/jp063483n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Santoso Y., Torella J.P., Kapanidis A.N. Characterizing single-molecule FRET dynamics with probability distribution analysis. ChemPhysChem. 2010;11:2209–2219. doi: 10.1002/cphc.201000129. [DOI] [PubMed] [Google Scholar]
- 29.Farooq S., Hohlbein J. Camera-based single-molecule FRET detection with improved time resolution. Phys. Chem. Chem. Phys. 2015;17:27862–27872. doi: 10.1039/c5cp04137f. [DOI] [PubMed] [Google Scholar]
- 30.Persson F., Lindén M., Elf J. Extracting intracellular diffusive states and transition rates from single-molecule tracking data. Nat. Methods. 2013;10:265–269. doi: 10.1038/nmeth.2367. [DOI] [PubMed] [Google Scholar]
- 31.Karslake J.D., Donarski E.D., Biteen J.S. SMAUG: analyzing single-molecule tracks with nonparametric Bayesian statistics. Methods. 2020;S1046-2023:30029–30033. doi: 10.1016/j.ymeth.2020.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Plank M., Wadhams G.H., Leake M.C. Millisecond timescale slimfield imaging and automated quantification of single fluorescent protein molecules for use in probing complex biological processes. Integr. Biol. 2009;1:602–612. doi: 10.1039/b907837a. [DOI] [PubMed] [Google Scholar]
- 33.Stracy M., Lesterlin C., Kapanidis A.N. Live-cell superresolution microscopy reveals the organization of RNA polymerase in the bacterial nucleoid. Proc. Natl. Acad. Sci. USA. 2015;112:E4390–E4399. doi: 10.1073/pnas.1507592112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vrljic M., Nishimura S.Y., McConnell H.M. Translational diffusion of individual class II MHC membrane proteins in cells. Biophys. J. 2002;83:2681–2692. doi: 10.1016/S0006-3495(02)75277-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Michalet X. Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;82:041914. doi: 10.1103/PhysRevE.82.041914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Antonik M., Felekyan S., Seidel C.A.M. Separating structural heterogeneities from stochastic variations in fluorescence resonance energy transfer distributions via photon distribution analysis. J. Phys. Chem. B. 2006;110:6970–6978. doi: 10.1021/jp057257+. [DOI] [PubMed] [Google Scholar]
- 37.Lee B.H., Park H.Y. HybTrack: a hybrid single particle tracking software using manual and automatic detection of dim signals. Sci. Rep. 2018;8:212. doi: 10.1038/s41598-017-18569-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hansen A.S., Woringer M., Darzacq X. Robust model-based analysis of single-particle tracking experiments with Spot-On. Elife. 2018;7:e33125. doi: 10.7554/eLife.33125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Uphoff S., Sherratt D.J., Kapanidis A.N. Visualizing protein-DNA interactions in live bacterial cells using photoactivated single-molecule tracking. J. Vis. Exp. 2014;10:51117. doi: 10.3791/51177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bickel T. A note on confined diffusion. Phys. A Stat. Mech. its Appl. 2007;377:24–32. [Google Scholar]
- 41.Smith S.W. The Scientist and Engineer’s Guide to Digital Signal Processing. California Technical Publishing; 2003. FFT convolution; pp. 311–318. [Google Scholar]
- 42.Myung I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003;47:90–100. [Google Scholar]
- 43.Crocker J.C., Grier D.G. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 1996;179:298–310. [Google Scholar]
- 44.Vink J.N.A., Martens K.J.A., Brouns S.J.J. Direct visualization of native CRISPR target search in live bacteria reveals cascade DNA surveillance mechanism. Mol. Cell. 2020;77:39–50.e10. doi: 10.1016/j.molcel.2019.10.021. [DOI] [PubMed] [Google Scholar]
- 45.Woodside M.T., Anthony P.C., Block S.M. Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science. 2006;314:1001–1004. doi: 10.1126/science.1133601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Robson A., Burrage K., Leake M.C. Inferring diffusion in single live cells at the single-molecule level. Philos. Trans. R. Soc. B Biol. Sci. 2013;368:20120029. doi: 10.1098/rstb.2012.0029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Slutsky M., Mirny L.A. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophys. J. 2004;87:4021–4035. doi: 10.1529/biophysj.104.050765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wieser S., Axmann M., Schütz G.J. Versatile analysis of single-molecule tracking data by comprehensive testing against Monte Carlo simulations. Biophys. J. 2008;95:5988–6001. doi: 10.1529/biophysj.108.141655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Martens K.J.A., van Beljouw S.P.B., Hohlbein J. Visualisation of dCas9 target search in vivo using an open-microscopy framework. Nat. Commun. 2019;10:3552. doi: 10.1038/s41467-019-11514-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ho H.N., Zalami D., Ghodke H. Identification of multiple kinetic populations of DNA-binding proteins in live cells. Biophys. J. 2019;117:950–961. doi: 10.1016/j.bpj.2019.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Talaga D.S. COCIS: markov processes in single molecule fluorescence. Curr. Opin. Colloid Interface Sci. 2007;12:285–296. doi: 10.1016/j.cocis.2007.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Morimatsu M., Takagi H., Sako Y. Multiple-state reactions between the epidermal growth factor receptor and Grb2 as observed by using single-molecule analysis. Proc. Natl. Acad. Sci. USA. 2007;104:18013–18018. doi: 10.1073/pnas.0701330104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Goulian M., Simon S.M. Tracking single proteins within cells. Biophys. J. 2000;79:2188–2198. doi: 10.1016/S0006-3495(00)76467-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Berglund A.J. Statistics of camera-based single-particle tracking. Phys. Rev. E. 2010;82:011917. doi: 10.1103/PhysRevE.82.011917. [DOI] [PubMed] [Google Scholar]
- 55.Elf J., Li G.W., Xie X.S. Probing transcription factor dynamics at the single-molecule level in a living cell. Science. 2007;316:1191–1194. doi: 10.1126/science.1141967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Höfling F., Franosch T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013;76:046602. doi: 10.1088/0034-4885/76/4/046602. [DOI] [PubMed] [Google Scholar]
- 57.Bohrer C.H., Xiao J. Complex diffusion in bacteria. In: Duménil G., van Teeffelen S., editors. Physical Microbiology. Springer International Publishing; 2020. pp. 15–43. [Google Scholar]
- 58.Metzler R., Jeon J.H., Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014;16:24128–24164. doi: 10.1039/c4cp03465a. [DOI] [PubMed] [Google Scholar]
- 59.Barkai E., Garini Y., Metzler R. Strange kinetics of single molecules in living cells. Phys. Today. 2012;65:29–35. [Google Scholar]
- 60.Los G.V., Encell L.P., Wood K.V. HaloTag: a novel protein labeling technology for cell imaging and protein analysis. ACS Chem. Biol. 2008;3:373–382. doi: 10.1021/cb800025k. [DOI] [PubMed] [Google Scholar]
- 61.Balzarotti F., Eilers Y., Hell S.W. Nanometer resolution imaging and tracking of fluorescent molecules with minimal photon fluxes. Science. 2017;355:606–612. doi: 10.1126/science.aak9913. [DOI] [PubMed] [Google Scholar]
- 62.Lindén M., Elf J. Variational algorithms for analyzing noisy multistate diffusion trajectories. Biophys. J. 2018;115:276–282. doi: 10.1016/j.bpj.2018.05.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Paris J.F. A note on the sum of correlated gamma random variables. arXiv. 2011 arXiv:1103.0505. [Google Scholar]
- 64.Martos-Naya, E., J. M. Romero-Jerez, …, J. F. Paris. 2016. A MATLAB TM program for the computation of the confluent hypergeometric function ϕ 2. https://core.ac.uk/download/pdf/62909374.pdf.
- 65.Bausch J. On the efficient calculation of a linear combination of chi-square random variables with an application in counting string vacua. J. Phys. A Math. Theor. 2013;46:505202. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.