Water Loss in Aging Erythrocytes Provides a Clue to a General Mechanism of Cellular Senescence

Abstract

Experimental evidence for age-dependent loss of intracellular water content as a widespread concomitant of cellular senescence is reviewed. Quantitative models are presented, indicating that an age-dependent increase in macromolecular crowding resulting from water loss may be responsible for three observed phenomena: a general age-dependent loss of intracellular protein solubility, a delayed and rapid appearance of high molecular weight aggregates, and an age-dependent transfer of intracellular protein from dilute to concentrated or condensed phases.

Significance

The hypothesis that cells in many organisms and tissues gradually lose water with aging, suggested by experimental studies on erythrocytes, provides a unified explanation for several general markers of cellular senescence.

Introduction

A casual search of online bibliographic databases such as PubMed reveals that the rate of publication of studies of mechanisms underlying senescence is currently at an all-time high, motivated in part by the search for possible treatments of age-related neurodegenerative diseases. Physical and chemical changes associated with aging have been studied in a wide variety of eukaryotic organisms, ranging from yeast to humans. An almost universal concomitant of aging seems to be an increase in the propensity of a wide variety of proteins to aggregate or precipitate (1, 2, 3, 4, 5, 6). It has recently been reported that age-dependent protein aggregation in Caenorhabditis elegans is cooperative and detected only after a significant lag time (6), and the onset of symptoms of age-related neurodegenerative diseases linked to protein aggregation in normal humans does not appear until the individual is typically above 60 years of age (7, 8, 9). Finally, it has been recently reported that reproductive aging in yeast is accompanied by a substantial increase in the size of cytoplasmic vesicles (10). The nonspecific nature of these varied phenomena suggests that all of these observations may be attributed to a general physico-chemical mechanism that is modulated by but not qualitatively dependent upon specific interactions between intracellular constituents. In this report, we propose such a mechanism based upon the hypothesis that the water content of cells decreases with aging. This hypothesis derives from experimental measurements of the water content of aging erythrocytes.

Age-dependent water loss: specific or general?

Human erythrocytes have a lifetime of ∼120 days in circulation (11). By pulse labeling reticulocytes, it is possible to measure the properties of labeled erythrocytes as a function of the time in circulation (“age”). It was shown that the density of these cells increases with age (11,12). Concurrent measurements of cell density and cell volume (11) indicate that with increasing cell density, the average intracellular hemoglobin (Hb) concentration increases from 280 to 410 g/L, and the average cell volume decreases from 106 to 70 fL. However, the mass of contained Hb (= concentration × volume) remains constant to within 4%, indicating that the cell membrane remains essentially impermeable to Hb as the cell shrinks with age. Thus, as a first approximation, we may regard the cell membrane as semipermeable and the intact erythrocyte as a miniature osmometer.

As the cell ages and intracellular Hb concentration increases, the osmotic pressure of the Hb increases from ∼200 to ∼500 torr (13,14), rendering the cell interior extremely hypertonic with respect to the external medium. If the membrane were passive with respect to water transport, water would be entering the cell rather than leaving it, a process that would ultimately lead to lysis, i.e., cell destruction. The counterintuitive loss of intracellular water may be linked to age-dependent changes in the activity of ion transporters, leading to disruption of the mechanism of volume regulation (15).

Under physiological conditions, wild-type Hb (HbA) exists predominantly as a stable heterotetramer with a molar mass of ∼65 kg (16). We shall henceforth refer to this species as the Hb “monomer.” HbA is possibly the most soluble protein in nature. In solutions at neutral pH and moderate ionic strength, such as phosphate-buffered saline, sedimentation equilibrium experiments indicate that HbA remains essentially entirely monomeric at concentrations up to over 300 g/L (17,18) and temperatures of up to 37°C (19). However, data obtained from other types of measurement have been interpreted as evidence for the existence of oligomers or condensates of HbA at an elevated temperature (20,21). The deoxygenated form of an inherited mutant Hb (deoxyHbS), which differs from HbA in a single mutation in each β-chain, exhibits a markedly lower solubility, leading to the formation of rodlike fibrils of indefinite size via an essentially first-order phase transition (13,22). The formation of these fibrils within deoxygenated erythrocytes containing HbS is the proximate cause of sickle cell disease (23).

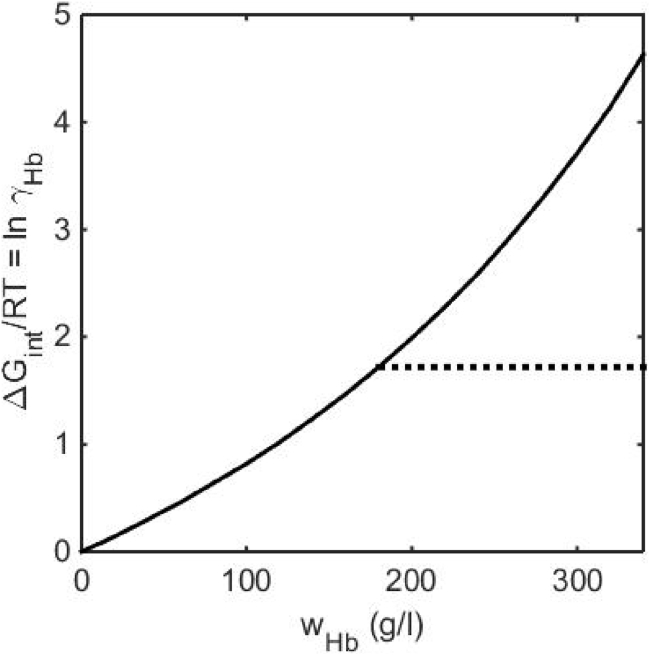
The concentration-dependent free energy of interaction between molecules of deoxyHbA, oxyHbA, and oxyHbS in solutions of moderate ionic strength and neutral pH, denoted by ΔG_int, has been quantified over a wide range of concentrations via measurement of the concentration dependence of sedimentation equilibrium (19,24) and osmotic pressure (13,14). The results obtained from these experiments under one set of conditions are plotted in Fig. 1. Results obtained for deoxyHbA, (carbonmonoxy) COHbA, COHbS, and oxyHbS are identical to within the precision of measurement over the entire range of measured concentrations—up to 350 g/L (19,24). Results obtained for deoxyHbS are identical to those of the other Hbs up to its solubility limit, ∼180 g/L under these conditions (24). To within the precision of measurement, the concentration dependence of the free energy of interaction of soluble Hb is independent of temperature between 2 and 37°C (19). To a very good approximation, the polymerization of deoxyHbS may be described as a first-order phase transition (13,22). Therefore, when the total concentration of deoxyHbS exceeds its solubility limit and soluble Hb is in equilibrium with the condensed phase (fiber), the thermodynamic activity of Hb is constrained to remain constant and independent of total concentration, as indicated by the dashed line in Fig. 1. It follows that condensation provides an effective means of substantially reducing the entropic work associated with increasing Hb concentration at high concentration.

Figure 1.

ΔG_int per mole of deoxy HbA, carbonmonoxy HbA and carbonmonoxy HbS (solid), and deoxyHbS (dashed) as functions of w/v Hb concentration in 0.1 M phosphate buffer (pH 7.4) at 37°C.

We recognize that erythrocytes represent a highly specialized cell type. Although erythrocyte senescence may take place over a period of months, aging processes occur over both shorter and longer periods of time, depending upon the organism and tissue within the organism. However, there exists a significant body of evidence that a variety of tissues in a variety of organisms lose water over time, as evidenced by a substantially increasing ratio of dry weight/wet weight (25, 26, 27) and other experimental measurements (28, 29, 30, 31). Because it is difficult if not impossible to rationalize tissue water loss without concomitant intracellular water loss, we suggest that there exist general cause-and-effect relationships between a progressive loss of water in cells and tissues and 1) widespread age-dependent loss of protein solubility, 2) a delayed onset of protein aggregation in C. elegans and aggregation-linked symptoms of degenerative disease in humans, and 3) age-dependent transport of protein from more dilute to more concentrated intracellular compartments. These relationships are illustrated using quantitative models presented below that take into account the influence of excluded volume on biochemical equilibria and kinetics.

Methods

Numerical calculations based upon the models described below were carried out using user-written scripts and functions in MATLAB (R2019a; The MathWorks, Natick, MA) that are available upon request.

Models for the effect of time-dependent water loss on intracellular protein aggregation and phase transitions

Because these models are didactic in nature and intended to provide qualitative rather than quantitative comparison with experimental data, we employ the following simplifying assumptions:

• 1)Globular proteins are represented as equivalent spherical particles, the size of which is determined by the nature and magnitude of the long-range interactions between them: long-range repulsion increases the effective radius, and long-range attraction decreases the effective radius. The equivalent particles so defined are presumed to interact with each other via steric repulsion only (32, 33, 34). The equivalent hard particle model has successfully accounted for a variety of thermodynamic properties of different globular proteins in highly nonideal solution (35,36).
• 2)Although it is recognized that physiological fluids generally contain many species of macromolecule, the models presented here contain either a single solute species or a single dilute species and a single concentrated species of macromolecule. This simplification is justifiable on the grounds that condensation and liquid-liquid phase separation in multisolute solution mixtures parallels that of solutions containing one or two solute species (13).
• 3)We assume, for simplicity, that the decrease in cellular or tissue water is linear in time (which is approximately what is observed in the experimental studies cited above) and that the total amount of each macromolecular solute per unit volume remains roughly constant. The total weight or volume concentration w of each solute species then varies with time as

$$w_i=\frac{w_i^0}{1-\alpha t},$$ (1)

where $w_i^0$ denotes the initial concentration of solute species i, t denotes elapsed time, and α is a constant of proportionality that may vary with organism and tissue type. So that the models introduced below will apply independent of the particular tissue or organism modeled (i.e., the particular value of α defining the actual rate of water loss in that tissue or organism), we shall subsequently utilize the unitless elapsed time denoted by t^∗ = αt.

Model 1: Time-dependent decrease of solubility and accumulation of condensate

The following model is a simplified and slightly modified special case of a more general treatment presented earlier (37). Consider a dilute (i.e., non-self-interacting) protein, called the trace species, in a medium containing a concentration w_C of a second unrelated protein, called crowder, which varies with time according to Eq. 1. Let the ratio of the effective radii of the trace to the crowder species be given by

$$R={\left(M_T/M_C\right)}^{1/3},$$ (2)

where M_T and M_C denote the molar masses of trace and crowder species, respectively. The effective fraction of solution volume occupied by the crowder is ϕ = v_excw_C, where v_exc denotes the specific exclusion volume in units of inverse w/v concentration (33). According to the scaled particle theory of hard sphere fluids (38,39), the thermodynamic activity coefficient of the trace species will vary with the concentration of the crowder species according to

$$\ln {\gamma }_T=-\ln \left(1-\varphi \right)+A_{1}z+A_2{z}^2+A_3{z}^3,$$ (3)

where z = ϕ/(1 − ϕ), A₁ = R³ + 3R² + 3R, A₂ = 3R³ + 4.5R², and A₃ = 3R³. For a first-order condensation reaction, the thermodynamic activity of the solution phase is held constant equal to that of the condensed phase, which is independent of concentration

$$a_{sol}=w_{sol}{\gamma }_T=\text{constant.}$$ (4)

The solubility of the trace species is then given by

$$w_{sol}\left(\varphi \right)=w_{sol}^0/{\gamma }_T\left(\varphi \right),$$ (5)

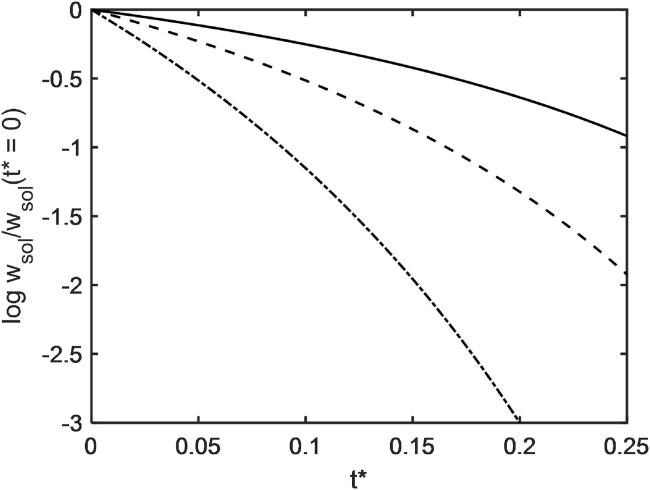
where $w_{sol}^0$ denotes the solubility of the trace species in the limit ϕ → 0. The dependence of w_sol/w_sol(t^∗ = 0) upon elapsed time, calculated using Eqs. 1, 2, 3, and 5 with parameter values given in the figure caption, is plotted in Fig. 2. It may be seen that as elapsed time and crowder concentration increase, the solubility of tracer may decrease by as much as one or more orders of magnitude, and the larger the tracer species relative to crowder, the more rapidly its solubility decreases.

Figure 2.

Logarithm of w_sol/w_sol(t^∗ = 0) as a function of t^∗, calculated using Eqs. 1, 2, 3, and 4 with v_exc = 0.001 L/g (34), $w_C^0$ = 300 g/L, and M_T/M_C = 1/3 (solid), 1 (dash), and 3 (dot-dash).

It follows from Eq. 5 that the equilibrium constant for condensation, denoted by K, is given by

$$K\equiv 1/w_{sol}=K_0{\gamma }_T,$$ (6)

where K₀ denotes the value of K in the ideal limit (ϕ → 0). Excluded volume theory predicts that in the transition-state kinetic limit, the enhancement of association equilibria in solution due to volume exclusion derives predominantly from the enhancement of association rates relative to dissociation rates (39,40). It follows from Eq. 6 that

$$k/k_0\cong K/K_0={\gamma }_T,$$ (7)

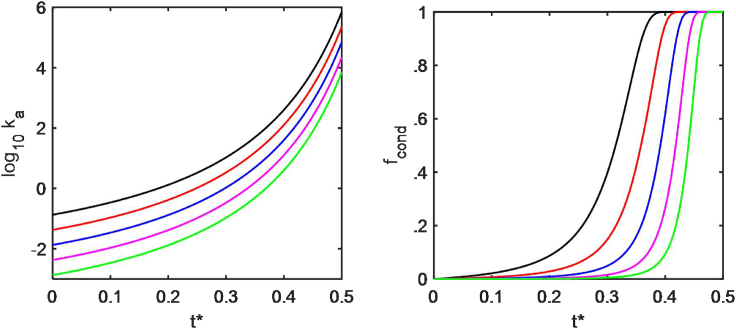
where k₀ denotes the value of k in the ideal limit. Plots of the association rate constant k as a function of time, calculated using parameter values given in the figure caption, are shown in the left panel of Fig. 3. Assuming that the rate of dissolution (dissociation from the condensed phase) is negligible relative to the rate of condensation (incorporation into the condensed phase), the rate of growth of the condensed phase may be written as

$$d{f}_{cond}/dt=-d{f}_{sol}/dt=k{f}_{sol},$$ (8)

where f_cond and f_sol denote the mass fractions of tracer present as condensed and soluble species, respectively. The dependence of f_cond on time may be calculated via numerical integration of Eq. 8 with a time-dependent value of k calculated using Eqs. 3 and 7. Plots of f_cond vs. t^∗, calculated using the parameter values given in the figure caption, are shown in the right panel of Fig. 3.

Figure 3.

Left panel: time dependence of the association rate constant for condensation. Right panel: shown is the time dependence of the mass fraction of trace protein in the condensed phase. Shown are curves calculated for M_T/M_C = 3, ϕ(t^∗ = 0) = 0.2, f_cond(t^∗ = 0) = 0, and log k(ϕ = 0) = −3 (black), −3.5 (red), −4 (blue), −4.5 (magenta), and −5 (green). To see this figure in color, go online.

Model 2: Time-dependent increase in the size of a concentrated liquid phase

Consider a total volume v_tot containing a total concentration c_tot of a macromolecular solute distributed between two immiscible solution phases at equilibrium, one of which contains a high weight/volume concentration of protein w₂ and a second containing a lower concentration of protein w₁. When w₁ < w_tot < w₂, the fraction of volume occupied by the concentrated phase 2 at equilibrium is given by (41):

$$f_2=\frac{w_{tot}-w_1}{w_2-w_1},$$ (9)

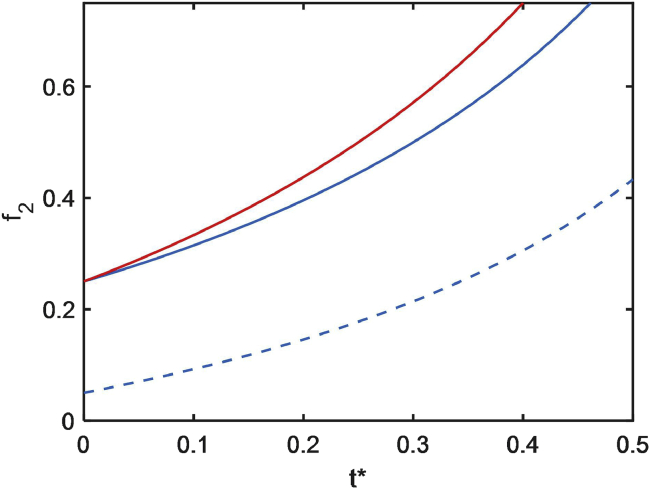
where the time-dependent value of w_tot varies with elapsed time as indicated in Eq. 1. In Fig. 4, f₂, calculated using Eqs. 1 and 9 with the values of w₁ and w₂ given in the figure caption, is plotted as a function of the scaled time t^∗.

Figure 4.

Volume fraction of concentrated phase as a function of elapsed time. Shown are blue curves calculated with w₁ = 25 and w₂ = 100 and a red curve calculated with w₁ = 25 and w₂ = 75. The value of $w_{tot}^0$ for each curve is determined by the specified value of f₂ at t^∗ = 0 according to text Eq. 9. To see this figure in color, go online.

Discussion

As indicated in Fig. 2, model 1 predicts that with increasing age of an organism, the solubility of those proteins whose solubility is affected by excluded volume will decrease at an increasing rate. As the cell ages, the total concentration of each of these proteins in a particular intracellular compartment will exceed its solubility by an ever-greater amount, and the amount of that protein that is condensed (insoluble) at equilibrium will increase correspondingly. This prediction is consistent with the observations reported in (1, 2, 3, 4, 5, 6).

Model 1 also predicts that the rate of condensation is highly dependent on elapsed time (Fig. 3 left panel). Because of this, the accumulation of condensed protein is highly cooperative in time (Fig. 3 right panel). The appearance of the aggregated protein and/or the symptoms of aggregation-linked neurodegenerative disease may not become evident until the organism has reached an advanced age. These predictions are consistent with the observations reported in (6, 7, 8, 9).

As indicated in Fig. 4, model 2 predicts that when the total concentration of a protein distributed between immiscible dilute and concentrated solution phases increases, the volume fraction of the concentrated phase will increase, but the concentrations of protein in each of the phases will remain constant. This is qualitatively consistent with the observation that as yeast ages, the volume fraction of intracellular vesicles increases markedly but that “crowding” (total protein concentration) in the extravesicular compartment is relatively constant (10).

It has been proposed that the breakdown of cellular function begins when the rate and extent of protein aggregation exceeds the ability of a chaperone and other rescue systems, collectively referred to as the proteostasis network, to process and remove pathogenic aggregates from cells (42,43). The highly cooperative appearance of aggregates after a considerable delay in elapsed time, predicted by model 1, indicated by the blue, magenta, and green curves in the right-hand panel of Fig. 3, suggests that the elapsed time corresponding to overloading of the proteostasis network will be insensitive to the specific amount of aggregation of a particular protein that can be tolerated by this network.

This investigation was motivated by well-documented studies of water loss in aging erythrocytes. In normal erythrocytes, cellular shrinkage accompanying aging is not expected to induce aggregation of intracellular HbA because of its exceedingly high solubility. However, enhanced crowding-induced aggregation or self-association of some intracellular metabolic enzymes (44), that may lead to age-dependent changes in metabolic activity (see (45) for an example), is a distinct possibility worthy of further inquiry. The models introduced here also strongly suggest that the propensity of an HbS-containing erythrocyte to sickle when deoxygenated will increase in a cooperative fashion with increasing age or time in circulation of the erythrocyte.

The models presented above are based upon the assumption that steric repulsion (volume exclusion) provides the dominant source of the free energy of interaction between cytoplasmic macromolecules. Although attractive interactions clearly also contribute to the total interaction free energy (46,47), both theory (47) and experiment (48, 49, 50, 51, 52) indicate that repulsive interactions provide the major influence upon the formation of large aggregates (as opposed to small oligomers) in crowded solutions. The use of scaled particle theory to estimate the effect of excluded volume upon thermodynamic activity has been used previously to account for the effect of excluded volume upon the rate and extent of fiber formation in highly volume-occupied solutions of sickle Hb (13,53), FtsZ (50), and amyloid-forming proteins and polypeptides (54,55). Therefore, we believe that these models and calculations provide a reasonable qualitative or semiquantitative description of the underlying phenomena.

Although it is unrealistic to expect that organelles or aggregates observed within cells are formed via mechanisms as elementary as those postulated here, the fact that diverse age-dependent phenomena observed in a variety of organisms are qualitatively recapitulated by these simple models suggests that the observed phenomena may be attributed, at least in part, to the thermodynamic and kinetic consequences of age-dependent macromolecular crowding. Detailed studies of the concentration and distribution of water and intracellular proteins and other macromolecules in a variety of organisms and cell types as a function of age will be necessary to validate or invalidate the underlying assumptions.

Editor: Madan Babu.