Diurnal Variations in the Motility of Populations of Biflagellate Microalgae

Abstract

The motility of microalgae has been studied extensively, particularly in model microorganisms such as Chlamydomonas reinhardtii. For this and other microalgal species, diurnal cycles are well known to control the metabolism, growth, and cell division. Diurnal variations, however, have been largely neglected in quantitative studies of motility. Here, we demonstrate using tracking microscopy how the motility statistics of C. reinhardtii are modulated by diurnal cycles. With nine independently inoculated cultures synchronized to the light-dark cycle at the exponential growth phase, we repeatedly observed that the mean swimming speed is greater during the dark period of a diurnal cycle. From this measurement, using a hydrodynamic power balance, we infer the mean flagellar beat frequency and conjecture that its diurnal variation reflects modulation of intracellular ATP. Our measurements also quantify the diurnal variations of the orientational and gravitactic transport of C. reinhardtii. We use this to explore the population-level consequences of diurnal variations of motility statistics by evaluating a prediction for how the gravitactic steady state changes with time during a diurnal cycle. Finally, we discuss the consequences of diurnal variations of microalgal motility in soil and pelagic environments.

Significance

We report tracking microscopy measurements that demonstrate that the mean swimming speed of Chlamydomonas reinhardtii is significantly greater during the dark period of a diurnal cycle. Using hydrodynamic (low Reynolds number) power balance, we also inferred the mean flagellar beat frequency from the swimming speed, hypothesizing that the observed variations in this frequency correlate with the diurnal regulation of flagellar ATP. Diurnal variations of the orientational and gravitactic transport of C. reinhardtii were also quantified and used in a continuum model to predict that at the population scale, the steady-state vertical distribution of C. reinhardtii is broader during the dark period. Our findings could have significant implications for the biology and ecology of microalgae in soil and pelagic environments.

Introduction

Many microorganisms experience changes in light and darkness corresponding to the regular alternation of day and night and have evolved circadian clocks to adapt to these environmental rhythms (1). The effect of these diurnal cycles is particularly important for photosynthetic microorganisms, such as the model unicellular microalga Chlamydomonas reinhardtii, for which light is only available for growth during the day. For C. reinhardtii, diurnal cycles have been shown to set endogenous circadian clocks (2), allowing for the optimal distribution of metabolic processes (3), growth, and division (4) between light and dark phases.

C. reinhardtii swims by beating a pair of flagella. The study of its motility, from the molecular details of flagellar motion through to the collective behavior of whole populations (5, 6, 7), continues to be a very active area of study. Although it is known that the circadian clock of C. reinhardtii regulates phototaxis (8) and chemotaxis in zoospores (9), the swimming motility of C. reinhardtii has not been comprehensively quantified as a function of diurnal cycles, to our knowledge, as we do in this study.

In previous studies measuring the swimming speed of C. reinhardtii (10, 11, 12, 13, 14, 15, 16), cells were usually sampled at a single time point in the cell cycle under growth conditions (temperature, growth medium, and illumination) not corresponding to those necessary for obtaining diurnally synchronized cultures. Similar considerations apply to quantitative measurements of motility in other microalgal species. For example, swimming speed, rotational diffusivity, and gravitactic reorientation time (the time it takes a cell to gravitactically reorient to the vertical) have recently been measured for the marine species Dunaliella salina (17) and Heterosigma akashiwo (18,19). However, like in the studies of C. reinhardtii, these microalgae were not synchronized to diurnal cycles.

C. reinhardtii flagella are resorbed during mitosis (20), so it is expected that the number of motile cells will change when cells divide. However, it is not a priori clear how other statistical measures of motility, such as mean swimming speed, rotational diffusivity, and gravitactic reorientation time, will change diurnally. In this study, we use tracking microscopy augmented by individual-based simulations to obtain these motility statistics as a function of time during the cell cycle of C. reinhardtii cells synchronized to light-dark cycles.

Materials and Methods

Culturing conditions and synchronization of cell division

C. reinhardtii CC-125 wild-type cells were transferred from slant cultures to 130 mL Tris-minimal medium and grown photoautotrophically and axenically in 250 mL of conical flasks in a shaking incubator (Infors Minitron; Infors AG, Bottiminger, Switzerland). Cultures were constantly shaken at 100 rpm and bubbled with air at constant temperature 25°C. Cultures were exposed to a 14:10 light-dark cycle with 300 μmol (m² ⋅ s) photosynthetically active radiation. At the beginning of each light period, each culture was diluted to 5 × 10⁵ cells/mL with Tris-minimal medium to keep cultures in the exponential growth phase (21). Experiments were carried out after cells had reproduced over five or more light-dark cycles. On an experiment day, aliquots were drawn from an independent culture at different hours of the days over a maximal span of 18 h. After being sampled, the independent culture was immediately placed back into the incubator. After the experiments were finished for the day, the culture was disposed of and not reused. There were a total of 9 days of experiments with nine independently inoculated cultures over a span of two months.

Sampling, cell enumeration, and imaging

At various times during the 24-h light:dark cycle, an aliquot sample was extracted from a culture flask, and motility counts and density measurements were performed in sequences I–V, as below, lasting at most 1.5 h. Experiments were repeated over several light:dark cycles with nine independent flask cultures, each sampled at random time points to give a total of 31 data sets. Sequence I, cell counts, included a 0.5-μL suspension that was diluted in 10 mL of ISOTON buffer solution (Beckman Coulter, Brea, CA) and measured with a Z2 Coulter (Beckman Coulter, Brea, CA) counter. Measurements were repeated three times for each sample. Each cell number density and volume measurement corresponded to more than 2500 particles. In sequence II, microscopy of swimmers, to avoid any phototactic response, procedures II–IV were performed in a dark room. In addition, blackout fabric (Thorlabs, Newton, NJ) was used to block any stray light from the computer screen. The cells were imaged using a vertical-stage microscope via a 4× objective (UPlanFL; N, 0.13 NA; Olympus, Tokyo, Japan) with bright-field deep red illumination (peaking at 660 nm to avoid eliciting a phototactic response (12,22)); see Fig. 2 a. Suspensions of cells were transferred using a micropipette to a 0.4 × 8 × 50 mm rectangular capillary, which was then loaded onto the microscope stage. The suspension was allowed to rest for 10 s so that fluid motion could dissipate and the distribution of the cell orientations could equilibrate, as confirmed by tracking analysis. Videos of swimming cells, each 20 s long, were captured at 50 or 162 frames per second with a CMOS camera (Pointgrey, Grasshopper3 GS3-U3-23S6M), with a spatial resolution of 1.5 μm/pixel for the magnification employed. We recorded 10 individual videos at a cell number densities approximately 5 × 10⁵ cells/mL during the light period and five individual videos at densities of 1 × 10⁶ cells/mL and above in the postdivision dark period. In sequence III, recording nonswimmers, the capillary was transferred to a horizontal stage microscope (IX73; Olympus) with a 600-nm-long pass filter (Cokin, Leavenworth, KS) applied to the light source to avoid eliciting responses to white light. For times greater than or approximately equal to 2 min, nonswimmers (settling speed ∼5μm/s) settled to the bottom of the capillary (depth of 400 μm). Focusing on the bottom of the capillary, videos containing static and swimming cells were recorded at one frame per second at five different locations. For sequence IV, recording cell sedimentation, see Supporting Materials and Methods. For sequence V, cell shape and condition, a few images of the immobilized cells were taken with the horizontal stage microscope using a 60× objective (LUCPlanFL; N, 0.70 NA; Olympus) to examine the shape and the physiological state of the cells.

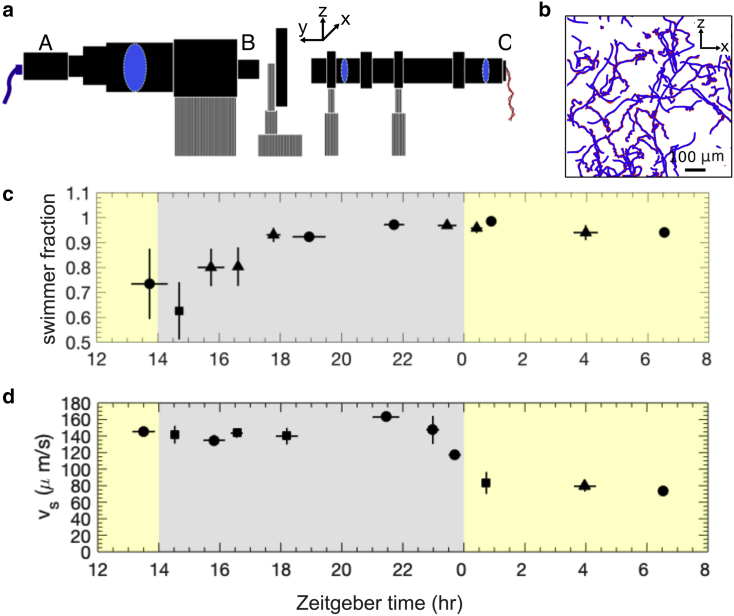
Figure 2.

(a) An illustration of the vertical-stage microscope with Köhler illumination (side view). “A” is the camera; “B” is a 4× objective lens; “C” is LED illumination. (b) Original trajectories (red) were reduced to the large-scale motility dynamics by a median filter that removes the helical swimming oscillations (blue). (c) Fraction of the cell population that are swimmers is shown. (d) Swimming speed is shown. The solid cirlce, solid triangle, and solid square symbols, respectively, represent a sample size of two, three, and four. Error bars indicate the standard error of the mean. To see this figure in color, go online.

Quantifying motile fraction, swimming speed, and shape parameters

Swimmer fraction

A median filter was applied to videos containing nonswimmers; this removes swimming cells. Static nonswimming cells were then counted using the particle identification function in the tracking algorithm (23). The number density of nonswimmers was calculated in the volume defined by the capillary depth and the area of the field of view. Finally, the swimmer fraction is evaluated as the ratio between the nonswimmer density and the total number density obtained from Coulter countermeasurements. For the mean swimming speed, a background image obtained by median filtering the time sequence of the swimming cells was subtracted from image sequences to remove static cells. Cell tracking was performed with a MATLAB (The MathWorks, Natick, MA) implementation of the Crocker and Grier algorithm (23). From each set of videos, between 1550 and 54,000 trajectories were acquired, with the higher end corresponding to the postmitotic period. Chlamydomonas is known to swim helically, turning counterclockwise at a frequency of 2 Hz (24), which manifests itself as small oscillations in the two-dimensional (2D) projected trajectories. These oscillations were removed using a median filter at 0.25-s intervals. Consequently, 0.25-s segments were truncated from the two ends of each trajectory (Fig. 2 b). Trajectories tracked originate from a volume 200 μm in depth of the same order of magnitude as the average trajectory length, and therefore, the trajectories are 2D projections of the three-dimensional trajectories (25). The true swimming speed is evaluated assuming that swimming speeds have a sufficiently narrow distribution, in which case, $\langle v_{\text{s}}{\rangle }^2\approx \langle v_{\text{s}}^2\rangle =2\langle v_{\text{x}}^2\rangle +\langle v_{\text{z}}^2\rangle$, where in the last step, we reasonably assume that for a gravitactic species such as C. reinhardtii, the speed is isotropic in the horizontal plane (26). The assumption is reasonable for C. reinhardtii CC-125; for this strain, Fujita et al. (15) observed that the variation of swimming speed is ∼23% of the mean and is mainly a result of cell-to-cell variation. The decorrelation time of the swimming speed in either direction was estimated to be 6 s (see Supporting Materials and Methods); therefore, v_x and v_z were evaluated at 6-s intervals along the trajectories to ensure the mean evaluated is unbiased. Each data set consists of 5–10 repeated recordings, and the error is evaluated as the standard error (SE) of mean in the data set. When cells are undergoing mass division, they become nonmotile and appear as settling cells in videos. In analysis (see below), nonmotile cells were identified and removed. To assess cell shape, the major and minor axes were manually measured from the high-resolution images in MATLAB. For the Zeitgeber time (ZT) assignment, after analysis, the final data sets were grouped according to the time intervals in which they were acquired and represented and assigned an average time and parameter values. Sampling during the light period caused growth to be interrupted as cells were transferred to microscopy under red light. Data sets acquired under these conditions were assigned the time corresponding to sampling from the flask culture to represent the hours of light exposure more accurately. On the other hand, data sets acquired during the dark period were assigned the time of video recording.

Gravitactic parameters, rotational diffusivity, and mass density

Assuming steady-state gravitactic swimming statistics, the bias parameter λ can be evaluated from $\langle v_{\text{z}}\rangle /v_{\text{s}}=\text{coth}\left(\lambda \right)-1/\lambda$, where $\langle v_{\text{z}}\rangle$ is the ensemble average of the vertical component of the swimming velocities, obtained from tracking as above, and v_s is the swimming speed (26). The rotational diffusivity D_r was inferred from the direction correlation function of the tracked data. We carried out three-dimensional individual-based simulations, which allowed us to properly deduce the value of D_r from the 2D projections available in the tracked data (see Supporting Materials and Methods). The gravitactic reorientation B was inferred indirectly from the definition of λ = 1/(2BD_r). The mass density of cells was deduced from the settling speed of ultraviolet-immobilized C. reinhardtii cells (see Supporting Materials and Methods).

Theoretical prediction of vertical gravitactic distribution

In the absence of background flow, the concentration n(r, t) of a population of gravitactic algae obeys (26,27)

$$\frac{\partial n}{\partial t}=-\nabla \cdot \left[v_{\text{s}}\langle \mathbf{p}\rangle n-\frac{v_{\text{s}}^2}{D_r}\mathbf{D}\cdot \nabla n\right],$$ (1)

where $\langle \mathbf{p}\rangle$ = (0, 0, K₁) is the mean cell orientation, D = diag(K₁/λ, K₁/λ, K₂) is the anisotropic diffusivity tensor, and K₁(λ) = coth(λ) − 1/λ and K₂(λ) = 1− coth²(λ) + 1/λ² are functions of the bias parameter λ (see (26,28)). As previously discussed in this study, v_s is the cell mean swimming speed and D_r is the rotational diffusivity. We seek the steady state (∂n/∂ = 0), so that Eq. 1 becomes

$$\frac{\text{d}n}{\text{d}z}=\frac{K_1}{K_2}\frac{D_r}{v_{\text{s}}}n,$$ (2)

which, with a background concentration n_b and a free surface at z = h and requiring $\left(1/h\right){\int }_0^{h}n\left(z\right)\text{d}z=n_b$, is solved by

$$n\left(z\right)=n_b\frac{h}{l}\frac{e^{\left(z-h\right)/l}}{1-e^{-h/l}},$$ (3)

where we have defined the characteristic length scale $l=\left(K_2/K_1\right)\left(v_{\text{s}}/D_{\text{r}}\right)$. This can be evaluated using swimming parameters from different ZT values. For the prediction in the discussion we have used for ZT4, v_s = 80 μm/s, D_r = 0.4/s, and λ = 0.1. For ZT18, v_s = 140 μm/s, D_r = 0.4/s, and λ = 0.1.

Results

Growth and division of synchronized swimmers

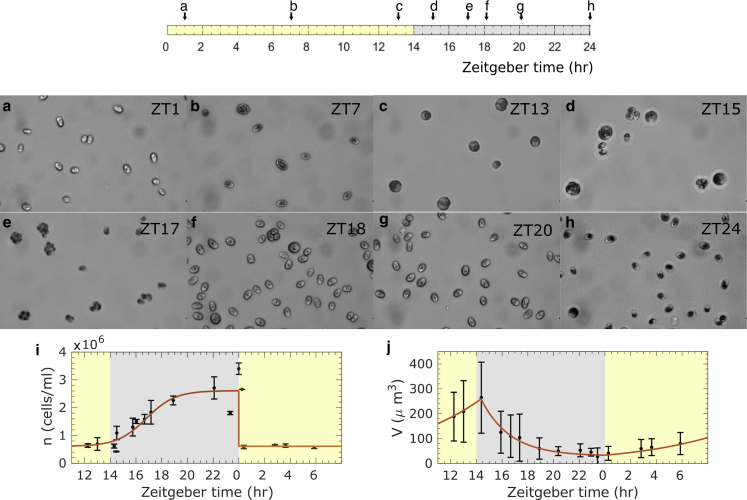
Cells of C. reinhardtii CC125, a model wild-type strain for flagellated motility (15,29,30), were entrained to a 14:10 light-dark cycle, as detailed in Materials and Methods. Images taken at different time points throughout the cell cycle, indicated as Zeitgeber times in hours after the onset of illumination, confirm qualitatively the synchronization of growth and reproduction of cells to the light-dark cycle (Fig. 1, a–h). These were further quantified by measurements of cell size and number (see Materials and Methods). During the light period, cells grow photosynthetically, increasing in size (Fig. 1 j) and becoming more spherical in shape (Fig. S3 b). The cell number density in this period is stationary (Fig. 1 i). Subsequently, 3–4 h into the dark period, cells undergo mitotic division and rapidly proliferate (Fig. 1 a). This is indicated by a sharp reduction of average cell volume between ZT14 to ZT15 (Fig. 1 j). In the late dark period, whereas the cell number density approaches a steady level (Fig. 1 i), cell volume continues to decrease. These observations reflect the canonical behavior of synchronized microalgal cells. Next, we consider how motility changes through the diurnal cycle.

Figure 1.

(a–h) Images of C. reinhardtii cells at different time points in a 14:10 light-dark cycle. Note that variation in cell opacity is due to different optical contrast. (i) Cell number density is fitted to a logistic function n = n_max/(1 + exp(−k(t − t_c))) + n₀, where n_max = 2 × 10⁶ cells/mL, k = 0.885 h⁻¹, t_c = 16.8 h, and n₀ = 6.11 × 10⁵ cells/mL. Error bars represent SE of mean. (j) Cell volume is fitted to exponential growth and decay trends V = V₁ exp(k(t − t_c)) + V₂, respectively, with V₁ = 33.2 μm³, k = 0.143 h⁻¹, t_c = 0, V₂ = 0, V₁ = 227 μm³, k = −0.445 h⁻¹, t_c = 14.4 h, and V₂ = 30.0 μm³. Error bars represent standard deviations of the volume distribution. To see this figure in color, go online.

Diurnal changes in swimming speed

We used tracking microscopy to characterize the diurnal variations in swimming motility of C. reinhardtii (see Materials and Methods). During the light period, the swimmer fraction, shown in Fig. 2 c, is constant and high (∼96%). Its value then decreases at the onset of the dark period, during which the fraction of swimmers reaches a minimum at around ZT15. Subsequently, the swimmer fraction grows back to its light period value at ZT22. This pattern reflects the well-known cessation of motility of mother cells due to flagellar resorption preceding mitosis and followed by hatching of newly flagellated motile daughter cells. The average postmitosis cell number density, n = 2.61 × 10⁶, derives from an average of 2.28 divisions of 5 × 10⁵ mother cells. Assuming 30 min for flagella resorption (31) and 30 min for each division cycle (4), the total division time is estimated to take ∼90–150 min. This estimate is in good agreement with the temporal trends of the cell number density and volume discussed above and is also consistent with the description of synchronized Chlamydomonas mitosis in existing studies (32). Swimming fraction results thus reflect the expected cellular dynamics of synchronized cells.

Measurements of mean swimming speed, however, reveal an unexpected and surprising quantitative trend; the speed falls from 140 to 160 μm/s during the dark period to 80 μm/s at the onset of the light period (Fig. 2 d). Although the order of magnitude of the swimming speed is comparable with that of previous studies (10,14,15), the intriguing quantitative diurnal change we have here observed has not, to the best of our knowledge, previously been reported.

Flagellar beat frequency and power

By a simple hydrodynamic argument, we can connect the diurnal variation of measured mean speed with the associated variation in mean flagellar beat frequency, which, as discussed below, can be connected to cellular bioenergetics. The beating flagella of C. reinhardtii transmit power to the surrounding fluid and translate the cell against the resistive drag force exerted by the fluid on the cell body. Because this swimming motion occurs at low Reynolds number (Re = v_sa/ν ∼ 10⁻⁴, with values of v_s and a from Figs. 2 and S3, respectively, and ν ≈ 10² μm/s² is the dynamic viscosity for water at 25°C), we can write the propulsive power balance as follows:

$$wf=F_{\text{d}}{v}_{\text{s}},$$ (4)

where w is the work per beat performed by flagella, f is the flagellar beat frequency, v_s is the swimming speed, and F_d is the drag force. All quantities are averages over the beat cycle, and we assume a fixed average flagellar waveform. The drag force is given by Stokes’ law,

$$F_{\text{d}}=6\pi \mu a{C}_{\text{F}}{v}_{\text{s}},$$ (5)

where μ is the kinematic viscosity of the growth medium and the drag coefficient is given by $C_{\text{F}}=\left(8/3\right)e^3{\left[-2e+\left(1+e^2\right)\text{ln}\left(1+e/1-e\right)\right]}^{-1}$, where $e=\sqrt{1-b^2/a^2}$ is the mean eccentricity of the cell, assumed to have the shape of a spheroid with semimajor and semiminor axes a and b, respectively. Substituting the expression for F_d from Eq. 5 into Eq. 4, we then obtain

$$f=f_0+k{v}_{\text{s}}^2,$$ (6)

where we have defined k = 6πμaC_F/w and f₀, an experimental threshold frequency defined below. Fujita et al. (15) have measured swimming speed as a function of flagellar beat frequency of C. reinhardtii, including CC-125, the wild-type strain used in this study, and four outer dynein arm mutants, oda1, oda11, suppf1, and suppf2. These mutants have a breastroke motion similar to the wild-type but beat at different (lower) frequencies (15). Here, we introduce a threshold frequency f₀ to account for the fact that, at low beating frequencies, the translational displacement of mutants falls below resolution of the tracking method used to measure swimming (15). Fitting the Fujita et al. (15) data using Eq. 6 gives f₀ = 29 Hz and k = 9.6 × 10⁻⁴ s/μm².

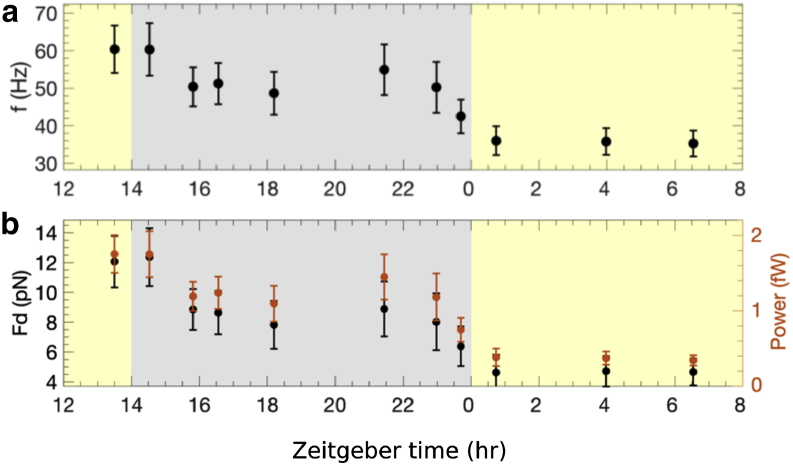
The diurnal variation of average beat frequency thus inferred from our speed data is shown in Fig. 3 a. The order-of-magnitude values of the beat frequencies agree with previously reported values (10,15,30); however, to our knowledge, the diurnal variation in the frequency is reported here for the first time. Furthermore, using Eqs. 4 and 5, we can also obtain the variation in mean drag force and power, respectively. These are shown in Fig. 3 a. The power is of the same order of magnitude as the mean power inferred by Guasto et al. from analysis of the flow field around swimming C. reinhardtii (33). As in other studies, however, this study did not investigate diurnally synchronized cells.

Figure 3.

Diurnal variation of (a) average beating frequency and (b) average drag force and power are shown. Error bars are propagated errors evaluated using Eqs. 5 and 6 and the errors in the measured swimming parameters. To see this figure in color, go online.

Gravitactic parameters, rotational diffusivity, and mass density

Aside from mean speed and flagellar frequency, we measured other motility and hydrodynamic parameters important for the transport and dispersion of suspensions. These measurements are important for allowing the parameterization of mathematical models of cell suspensions, as has been done for other species, but ignoring diurnal variations (17). The parameters measured include the gravitactic reorientation time B, rotational diffusivity D_r, and bias parameter λ = 1/(2BD_r), which quantifies the ratio of rotational diffusive/gravitational reorientation times. The diurnal variation of these parameters is plotted in Fig. S4, c and d and Fig. S4 a, respectively. The data for these parameters are noisier than for the swimming speed, and it is harder to identify trends. The bias parameter λ is approximately constant in value during the light period and into the dark period, except for an apparent dip in value before the start of the light period. The reorientation time B appears to grow during the dark phase, falling at the start of the light phase, and growing again during the day. The rotational diffusivity D_r also grows in the dark but then appears to fall during the day. The largest values of B we have measured are four times larger than what has been previously reported (10) for C. reinhardtii. The values for D_r are larger but of the same order of magnitude as reported in previous studies (14,34). To our knowledge, the bias parameter λ has not been previously measured for C. reinhardtii and, across the diurnal variations, is measured to be smaller than that quantified for other gravitactic species (e.g., λ = 0.21 for D. salina (17) and λ = 2.2 for C. augustae (25)).

Tracking settling heat-immobilized cells, we were also able to quantify the mean mass density ρ of cells, an important parameter for the analysis of suspension bioconvective instabilities (26) and for coupling the gyrotactic dynamics of cells to flow (e.g., in pipe flows (17)). As shown in Fig. S5, the density appears 10% larger than the surrounding fluid, with a slight reduction in its value during the light period.

Discussion

We have characterized the motility of C. reinhardtii through light-dark cycles using tracking microscopy. Our results, to our knowledge, reveal a previously unobserved diurnal variation in the mean swimming speed of this model species. Furthermore, using a hydrodynamic power balance, we were able to infer from the speed the corresponding diurnal variation in mean beat frequency.

It would be interesting to connect the variation of beat frequency we infer with intracellular levels of ATP. This has not yet been done for C. reinhardtii. However, a study of demembraned Lytechinus pictus sea urchin sperm flagella has demonstrated that ATP concentration correlates positively with flagellar beat frequency (35). With the caveat that this is a different organism, we can appeal to the fact that eukaryotic flagella are strongly conserved organelles (36) to hypothesize that a similar correlation between frequency and ATP levels will apply qualitatively for C. reinhardtii. If this hypothesis is correct, then changes in flagellar frequency shown in Fig. 3 a would reflect changes in flagellar ATP. In particular, our data could be interpreted as suggesting that the amount of ATP available to flagella is lower at the end of the dark phase than at the end of the light phase. We emphasize that this is speculation based on our hypothesis. Future experiments and mathematical modeling will be necessary to test the prediction from our results that flagellar frequency does indeed chart the variation of flagellar ATP. It would be, for example, very interesting to carry out experiments similar to (35), assaying the diurnal variation of ATP in the flagella of C. reinhardtii.

Our results also quantify the power exerted by the cell on the fluid when swimming, as shown in Fig. 3 b. This power, like the frequency, broadly decreases during the dark phase to a lower light-phase value. Across the diurnal variation, its value, ∼1 fW, is an order of magnitude smaller than the minimal mechanistic power required for flagellar motility, which was estimated by Raven from the reaction rate of dynein molecules along the flagella to be 22 fW for freshwater microalgae with the same broad characteristics as C. reinhardtii (37). This power, in turn, was estimated to be half of the minimal cell maintenance power (37). These estimates demonstrate that swimming is energetically affordable to photosynthetic microalgae, as opposed to other microorganisms such as bacteria, for which it represents a much more prohibitive metabolic cost (26,38). However, such order-of-magnitude estimates are unable to shine light on the variations in cellular bioenergetics that underly the diurnal variations in swimming that we have observed.

The flagellar beat is powered by ATP in the flagellar compartment (39), which has either arrived there by diffusion from the cytosol or has been generated in situ by reactions with the metabolite 3-phosphoglycerate. During the photosynthetic light period, ATP and 3-phosphoglycerate molecules are produced by the central carbon metabolism in reactions compartmentalized in the chloroplast, mitochondria, or cytosol (40). Synthesis of energy-storing metabolites (starch, lipids), nutrient uptake, cell maintenance, and growth all consume ATP during the light period. We can assume that flagellar motion also consumes a small fraction of the ATP budget. If the hypothesis above, on the connection between flagellar frequency and ATP levels, is correct, then our results would suggest that ATP available to flagella surges at the onset of division. This is associated with the transition from photosynthetic growth to mitotic division powered by respiration. During the dark period, in the absence of photosynthesis, only mitochondria and the cytosol, by degrading storage products using respiration and fermentation (3), are active in producing ATP to power cell division and flagellar beating. The balance of these intracellular processes will determine how much ATP is available to flagella. Plausibly, as the total pool of ATP diminishes with the degradation of storage products, there will be less ATP available for flagella, qualitatively accounting for the decline toward the end of the dark period that we infer from our results. It will be interesting in future experiments and modeling to quantify the intracellular energy budget and connect it with swimming measurements such as those we have carried out.

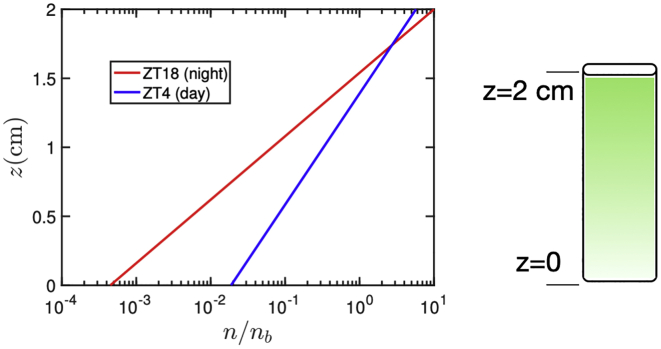
The observed diurnal variation in the motility statistics of C. reinhardtii has interesting consequences for its population-scale behavior. Consider, for example, a C. reinhardtii suspension in a vertically oriented container that does not support large-scale flows, (e.g., a capillary (see Fig. 4)). The transport in such a suspension is driven by fluxes due to gravitactic swimming, which drive cells to the top of the container, and anisotropic diffusion, which homogenizes the distribution of cells (preferentially in the vertical direction). At long times, these fluxes balance, and the steady-state distribution of cells can be shown to be given by n(z) ∼ e^z/l, where z is the vertical coordinate and l = v_s/D_rf(λ) is the characteristic length scale of the distribution, with v_s being the swimming speed, D_r the rotational diffusivity, and f(λ), a function of the bias parameter λ, derived from the biases in direction and diffusivity (see Materials and Methods for a detailed derivation). In previous studies (e.g., (14,17,25)), these parameters have been considered fixed and independent of patterns of illumination during culture. Here, instead, we account for diurnal variation of illumination and evaluate the length l with parameters measured in the light and dark phases of a diurnal cycle. For example, taking values from ZT4 and ZT18, we find l_light/l_dark = 0.6. That is to say, C. reinhardtii distributes vertically more broadly during the light than in the dark phase. This is clear from a plot of the steady-state distributions plotted for ZT4 and ZT18 (see Fig. 4). It will be interesting to test these predictions in future laboratory experiments, carried out under red light illumination, as in this study, and (14) to initially avoid the complications of phototaxis.

Figure 4.

Predicted vertical distribution for C. reinhardtii in a capillary of height h = 2 cm, using motility parameters measured at ZT4 (light phase) and ZT18 (dark phase) are shown. To see this figure in color, go online.

The predictions for C. reinhardtii in a capillary illustrate how diurnal variations in motility can quantitatively affect the spatial distribution of a population microalgae. In the environment, diurnal changes in this distribution could have important biological and ecological consequences because the location of cells determines their access to light and nutrients and thus the growth of the microalgae. As mentioned, our study has neglected biased swimming toward light (phototaxis). In future studies of photosynthetic species such as C. reinhardtii, it will be important to quantitate diurnal variations of phototaxis, revisiting the classic work by Bruce (8). This could be achieved through microfluidic and “mesofluidic” experiments, such as the capillaries above. It will then be possible to theoretically and experimentally address the question of how microalgae such as C. reinhardtii, with diurnally varying motility, optimally utilize light where and when it is available, as well as spatially distributed dissolved nutrients. This will depend on microalgal species and habitat. Photosynthetic soil dwellers, such as C. reinhardtii, generally reside in the first few millimeters of topsoil, where light can penetrate (41). The quantitative study of the dynamics of these populations over daily and seasonal cycles remains an open question (42). In future work, complementing field studies, it would be very interesting to design laboratory studies to elucidate how the behavior of C. reinhardtii and other soil species (both established laboratory strains and isolates from the soil) changes diurnally in artificial soils, which could be patterned microfluidically. For example, our prediction for the capillary indicates a larger spread of the population during the dark phase. Will this spread be mirrored in soil-like porous structures, and does it allow microalgae to access more nutrients in the soil at night?

Another important habitat for microalgae is the pelagic environment of lakes, seas, and oceans. C. reinhardtii has not been reported in lakes, but related species of Chlamydomonas spp have (43). Motility is thought to confer advantage to microalgae in stratified lakes because they can thrive by migrating to the well-lit surface during the day and down the water column at night to find nutrients (42). Similar considerations are made for oceanic environments (44), for which mathematical models have been developed in which vertical migration speeds are proportional to the swimming speeds, which are assumed constant (45). If the swimming of marine species changes significantly during the dark phase, as reported here for C. reinhardtii, this could have a big impact on the predictions of migration models.

By affecting motility, diurnal variations also affect gyrotaxis, the orientational bias on swimming microalgae caused by a combination of gravitational and viscous torques, the latter due to shear in a flow. In related work, inspired by biotechnological applications, we use a combination of experiment and numerical modeling to study how the distribution of C. reinhardtii cells in a downwelling pipe flow changes as a function of shear and Zeitgeber time in a diurnal cycle (unpublished data). Whether in the laboratory, biotechnological applications, or the field, the light history of microalgae will have a strong, quantitative impact on their motility and will need to be considered more carefully in future studies.

Author Contributions

O.A.C., D.J., and J.K. conceived the experiments. D.J. and E.S. developed the data analysis. D.J. conducted the experiment, data analysis, and simulations. All authors reviewed the manuscript.