The Accidental Ally: Nucleosome Barriers Can Accelerate Cohesin-Mediated Loop Formation in Chromatin

Abstract

An important question in the context of the three-dimensional organization of chromosomes is the mechanism of formation of large loops between distant basepairs. Recent experiments suggest that the formation of loops might be mediated by loop extrusion factor proteins such as cohesin. Experiments on cohesin have shown that cohesins walk diffusively on the DNA and that nucleosomes act as obstacles to the diffusion, lowering the permeability and hence reducing the effective diffusion constant. An estimation of the times required to form the loops of typical sizes seen in Hi-C experiments using these low-effective-diffusion constants leads to times that are unphysically large. The puzzle then is the following: how does a cohesin molecule diffusing on the DNA backbone achieve speeds necessary to form the large loops seen in experiments? We propose a simple answer to this puzzle and show that although at low densities, nucleosomes act as barriers to cohesin diffusion, beyond a certain concentration they can reduce loop formation times because of a subtle interplay between the nucleosome size and the mean linker length. This effect is further enhanced on considering stochastic binding kinetics of nucleosomes on the DNA backbone and leads to predictions of lower loop formation times than might be expected from a naive obstacle picture of nucleosomes.

Significance

The spatial organization of the genome occurs through multiple looped conformations, forming a complex structure called chromatin. The formation of these loops is driven by a process known as loop extrusion by proteins such as cohesin and condensin. The cohesin protein, in particular, diffuses through a rugged landscape of DNA covered with dynamic protein complexes known as nucleosomes. Although individual nucleosomes act as barriers to cohesin diffusion, in this work we show that the size of these nucleosome barriers plays a nontrivial role in loop formation. Counterintuitively, at high densities, nucleosomes can accelerate loop formation by cohesin. Our work proposes a possible resolution to the puzzling question of how passively diffusing cohesin can form large chromosomal loops on biologically relevant timescales.

Introduction

The principles behind the organization of chromatin into a three-dimensional folded structure inside the nucleus remain an important open question (1, 2, 3, 4). A ubiquitous structural motif, as observed through Hi-C (5, 6, 7, 8) and other experiments (9, 10, 11), is the formation of large loops, ranging from kilobases to megabases. These loops play both a structural as well as functional roles, bringing together regions of the DNA that are widely spaced along the backbone (12, 13, 14). In recent years, much work has been done in trying to understand the mechanism of formation of these large loops. There is now a significant body of experimental observations that implicate a class of proteins called the structural maintenance of chromosome (SMC) protein complexes, such as cohesin and condensin, in the formation and maintenance of these large chromosomal loops (15, 16, 17, 18, 19, 20, 21, 22, 23). SMC protein complexes are known to play a major role in chromosome segregation in interphase and mitosis. Both cohesin and condensin consist of SMC subunits and share structural similarities. SMC subunits (SMC1 and SMC3 in cohesin and SMC2 and SMC4 in condensin) fold back on themselves to form an approximately 50-nm-long arm. These two arms are then connected at one end by a hinge domain, and the other two ends that have ATPase activity are connected by a kleisin subunit (RAD21 in cohesin and condensin-associated protein H2 (CAPH2) in condensin) to form a ring-like structure of the whole complex (24, 25, 26, 27, 28, 29, 30). This ring-like structure has been hypothesized to form a topological association with the DNA backbone (31,32). In particular, experiments on cohesin have shown that such topological association with the DNA can lead to very long residence times of cohesin (33). The SMC ring can then embrace two chromosome strands, either within a single cohesin ring (embrace model) (30) or within two cohesin rings mediated by an external protein (handcuff model) (34,35). These two chromatin strands, bound topologically to the cohesin ring, can then extrude loops of chromosome, with the loop formation process ending at CTCF markers on the chromosome (30,36, 37, 38, 39). There have been previous attempts to model this loop formation process through the action of SMC proteins. A common feature of these models is that the motion of these SMC proteins on the DNA backbone was assumed to be active, driven by the consumption of ATP (40, 41, 42, 43, 44) and motivated by the presence of ATPase activity in the SMC proteins and the fast timescales for the formation of these large loops. Such active SMC proteins have been theoretically shown to compact the chromosome effectively, with stable loops formed by stacks of SMC proteins at the base of the loops (40,41). Indeed, multiple experiments have shown that the SMC protein condensin is responsible for active, directed loop formation across species (21,22,45). The role of CTCF proteins in stopping the loop extrusion process has also been modeled and has successfully reproduced the occurrence of topologically associated domains (TADs) in the simulated contact maps (39,44). Active extrusion of loops coupled with topoisomerase activity has also been suggested to lead to disentanglement of sister chromatids and corresponding simplification of genome topology (41,46, 47, 48). Nonequilibrium effects and the role of an osmotic pressure gradient have also been hypothesized to play a role in the loop formation process (49, 50, 51). A full review of existing models for loop extrusion can be found in (52).

Recent experiments have, however, called into question this picture of active loop extrusion by cohesin. In vitro experiments using yeast cohesin (purified from Schizosaccharomyces pombe) on DNA curtains have elucidated the nature of the motion of the cohesin protein on the DNA backbone. These experiments show that although the loading of the cohesin molecule on to the DNA is assisted by the ATP activity, the motion of the cohesin protein itself on the DNA strand is a purely diffusive process and does not depend on ATP (33). Analysis of the trajectory of cohesin on the DNA yields a time exponent of 0.97, in excellent agreement with diffusive motion (33). The measured diffusion coefficient of cohesin on bare DNA curtains is found to be D $\simeq$ 1 μm²/s at physiological salt concentrations of c_KCl ∼100 mM (33). Similar results were also observed in single-molecule in vitro experiments using purified human cohesin, with trajectories consistent with passive diffusion rather than active, directional motion (53). The measured diffusion coefficient at physiological salt concentration was found to be D $\simeq$ 0.16 μm²/s. Interestingly, these experiments found although the motion of the cohesin is diffusive, the diffusion coefficient itself was a function of the ATP concentration, with ATP depletion resulting in reduced diffusivities, possibly as a result of structural changes (53). Further, the size of the cohesin ring implies that obstacles in the path of this diffusive trajectory can slow down the motion of cohesin. In particular, nucleosomes were found to act as obstacles to the diffusion of cohesin and lowered the effective diffusion coefficient (33). In vitro experiments with a dense array of static nucleosomes have observed that the cohesin becomes almost static, and the estimated diffusive loop formation speed at these high nucleosome densities was 7 kb per hour (33), entirely too slow for the formation of the large loops that are seen in Hi-C experiments (10,54, 55, 56). In addition, although there exist certain external active proteins such as FtSz that can drive cohesin actively along the backbone, the lifetime of these proteins are very small, unlike the topologically bound cohesin, and hence, they cannot lead to persistent active motion of cohesin (33).

These experimental observations posit an interesting puzzle. Cohesin motion along the DNA appears to be purely diffusive, and the estimated diffusion coefficient seems incompatible with the formation of large loops. We investigate whether we can recover the fast loop formation times observed in experiments within the framework of passive, diffusive motion of cohesin. We show that the finite size of the nucleosome obstacles introduces an additional length scale in the system, and an interplay of this with the linker length can lead to nonmonotonic looping times with varying nucleosome density. We report a regime in which addition of nucleosomes can speed up the looping process, and we estimate looping times that explain how large loops may be formed even by a passively diffusing cohesin.

Materials and Methods

Model

We consider only the one-dimensional diffusion of cohesin on chromatin. A comprehensive understanding of the timescales of the looping process requires taking into account the full three-dimensional nature of the problem. The chromatin fiber is a three-dimensional object that lies embedded in an extremely crowded environment (57,58). The local properties of the chromatin fiber (39,50) and the presence of DNA-binding proteins can also alter the dynamics of the looping process (59). Further, the thermodynamics of the opening and closing of the cohesin ring has also been conjectured to play an important role in loop formation (60). However, the mechanism we discuss in this manuscript is distinct from these proposed mechanisms and may be understood simply via the one-dimensional diffusion of cohesin on chromatin. Other determinants of loop formation can then be added as additional ingredients to the model.

We model the DNA backbone as a one-dimensional lattice of length L. The two subunits of the cohesin-chromatin complex are modeled as two random walkers (RWs) that perform diffusive motion on this 1D lattice (Fig. 1). Note that these two subunits could either be part of the same cohesin protein (embrace model) (30) or two different cohesins linked by a mediating protein (handcuff model) (34,35). The two cohesin subunits initially bind at neighboring sites on the DNA and then start to drift apart because of diffusion. The length of the DNA between the subunits corresponds to the instantaneous size of the loop extruded. The two subunits cannot occupy the same site, with a loop of size zero corresponding to the situation in which the subunits occupy neighboring sites. The two ends of the DNA lattice correspond to the terminal points of the loop and can biologically correspond to CTCF motifs, which are known to act as endpoints for loop formation (30,36, 37, 38, 39). In the context of our model, this is represented by absorbing boundary conditions at x = 0 and x = L.

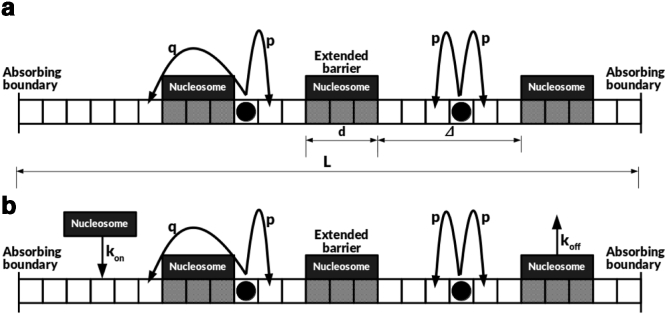
Figure 1.

(a) Schematic of cohesin rings diffusing on DNA lattice. Nucleosomes form extended barriers covering d lattice sites. A cohesin ring traverses a nucleosomal barrier with a hopping rate q as compared to the bare lattice hopping rate p, with q << p. Δ is the mean linker length between two nucleosomes. (b) For the case of dynamic nucleosomes, nucleosomes can bind to the DNA lattice with a rate k_on and unbind with rate k_off.

Nucleosomes are modeled as extended objects in one dimension that cover and occlude d = 150 sites on the DNA lattice. Motivated by the experimental characterizations of motion of cohesin on nucleosome-bound DNA, we consider nucleosomes as barriers that reduce the local hopping rate of the cohesin rings. For a cohesin subunit present at a bulk site (no nucleosome on either side), the discrete master equation can then be written as

$$\frac{\partial P\left(n,t\right)}{\partial t}=pP\left(n-1,t\right)\left(1-{\delta }_{m,n}\right)+pP\left(n+1,t\right)\left(1-{\delta }_{m,n}\right)-pP\left(n,t\right)\left(2-{\delta }_{m,n-1}-{\delta }_{m,n+1}\right),$$

where P(n, t) denotes the probability for the cohesin subunit to be at site n at time t. The position of the second cohesin subunit is denoted by m, and the Kronecker delta functions δ_ij implement the constraint that both of the cohesin subunits cannot occupy the same site. The hopping rate for cohesin in the bulk is denoted by p. At a site r that has a nucleosome to its right, the time evolution of the occupation probability can be written as

$$\frac{\partial P\left(r,t\right)}{\partial t}=pP\left(r-1,t\right)\left(1-{\delta }_{m,r}\right)+qP\left(r+d+1,t\right)\left(1-{\delta }_{m,r}\right)-pP\left(r,t\right)\left(1-{\delta }_{m,r-1}\right)-qP\left(r,t\right)\left(1-{\delta }_{m,r+d+1}\right),$$

whereas for a site l that has a nucleosome to its left, we have

$$\frac{\partial P\left(l,t\right)}{\partial t}=qP\left(l-d-1,t\right)\left(1-{\delta }_{m,l}\right)+pP\left(l+1,t\right)\left(1-{\delta }_{m,n}\right)-pP\left(l,t\right)\left(1-{\delta }_{m,l+1}\right)-qP\left(l,t\right)\left(1-{\delta }_{m,l-d-1}\right),$$

where q denotes the reduced barrier crossing rate of the cohesin ring in the presence of a nucleosome (q << p). We are interested in determining the time taken by the cohesin molecule to form a loop of length L. The two rings absorb at the two boundaries at different times (t_L and t_R), and the time taken to form the loop is defined as the maximum of these two times, t_loop = max{t_L, t_R}; this corresponds to the time when both the cohesin rings have reached the CTCF sites (at the lattice boundaries). This corresponds to the first passage time for this stochastic problem of two random walkers in the presence of absorbing boundaries. We simulate the looping process on the discrete DNA lattice of length L using stochastic simulations (see Materials and Methods). Recent experiments on cohesin diffusion on DNA curtains have provided accurate estimates of the cohesin diffusion constant, D. We choose D = 1 μm²/s, corresponding to the experimental measurements at physiological salt concentrations (33). This yields a hopping rate in the bulk of p = 9.1 × 10⁶/s. The reduced hopping rate when a cohesin ring has to pass through a nucleosomal barrier is estimated from experimental measurements of the permeability of nucleosomes to a cohesin, and yields a value of q = 114/s (33). Note that because a cohesin hopping across a nucleosome leads to a hop of size d along the 1D DNA backbone, the condition for nucleosomes to be barriers implies that qd² ≤ p, which yields an upper bound of q ≤ 400/s for the chosen value of the bulk hopping rate.

Static nucleosomes

In the case of static nucleosomes, nucleosomes are placed on the DNA lattice maintaining a certain constant linker length (Δ) between two consecutive nucleosomes. We verified that our results do not change if the nucleosomes are positioned randomly while keeping the mean linker length the same (Fig. S1). The two cohesin subunits, modeled as two RWs, are initialized at two consecutive lattice sites near the middle of the lattice. We use an algorithm with equal time updates with a sufficiently small time increment to ensure that the cohesin subunits cannot take more than a single step during this time interval. At each time step, we first choose one of the two subunits randomly and update its position in accordance with the appropriate hopping rates. If the subunit is adjacent to a nucleosome, it can hop across the nucleosome with a rate q or hop away from the nucleosome with a rate p, whereas if the subunit is not adjacent to a nucleosome, it can hop to either of the two adjacent sites with a rate p. We then repeat this for the other cohesin subunit. The two subunits are not allowed to occupy the same lattice site. We record the times t_L and t_R when the left and right RWs get absorbed at the boundaries. The looping time t_loop is the maximum of these two times. The simulation is repeated for 1000 ensembles to obtain the mean looping time.

Dynamic nucleosomes

In the case of dynamic nucleosomes, nucleosomes bind and unbind to the DNA lattice stochastically. We choose a fixed binding rate (k_on) = 12/s (61, 62, 63), whereas the unbinding rate (k_off) is varied to achieve different mean linker lengths. An unbound nucleosome binds to the DNA at a rate k_on if there is sufficient space available between the two nearest neighboring nucleosomes and if the cohesin is not already bound to any of the d sites. We first allow the system to reach a steady state nucleosomal occupancy in the absence of cohesin. Once the system reaches steady state, we position the cohesin subunits near the midpoint of the lattice. At each timestep, we choose the N + 2 entities (N number of nucleosomes and two RWs) in random order. If a bound nucleosome is picked, it can unbind from the DNA with a rate k_off; if an unbound nucleosome is picked, it can bind to the DNA with a rate k_on. If either of the cohesin subunits are picked, they hop to an adjacent empty lattice site with a rate p or hop across a nucleosome with a rate q. The system evolves until both of the cohesin subunits are absorbed at the two lattice boundaries. We again note the looping time t_loop, and the mean looping time is obtained after averaging over ∼1000 such ensembles, as before.

Ensemble cloning

To access the tails of the first passage (and survival probability) distributions, we use an ensemble cloning scheme, which can access these regions to a high degree of accuracy (64,65). We start with 1000 distinct initial configurations at t = 0 and then allow all the 1000 systems to evolve for a time T. After this time T, in some systems both the RWs reach the end points of the lattice and are absorbed, yielding a looping time t_loop. In the remaining systems, at least one of the RWs survives. We then clone these surviving systems to bring back the total number of systems to 1000 and again evolve for a time T. We repeat this procedure until we reach a desired accuracy for the survival probability.

At t = 0, the survival probability is S(0) = 1. Let M(T) denote the number of systems that survive after evolving for time T. Then, the survival probability at time T is S(T) = S(0)(M(T)/1000). At this point, we clone these M(T) surviving systems to bring back the number of systems to 1000 and allow the systems to evolve for another interval of time T. After this second iteration, let the number of surviving systems be M(2T). Hence, the survival probability after this second iteration becomes S(2T) = S(T) × (M(2T)/1000). The prefactor of S(T) in the previous expression ensures that the resulting survival probabilities are not biased toward longer waiting times. The time T is chosen such that roughly half the number of systems survive after each iteration. Thus, the survival probability after k iterations is of the order of ∼2^−k, and hence, this procedure allows one to access the tails of the survival probability distribution.

Results

Nucleosomal barriers can accelerate cohesin looping

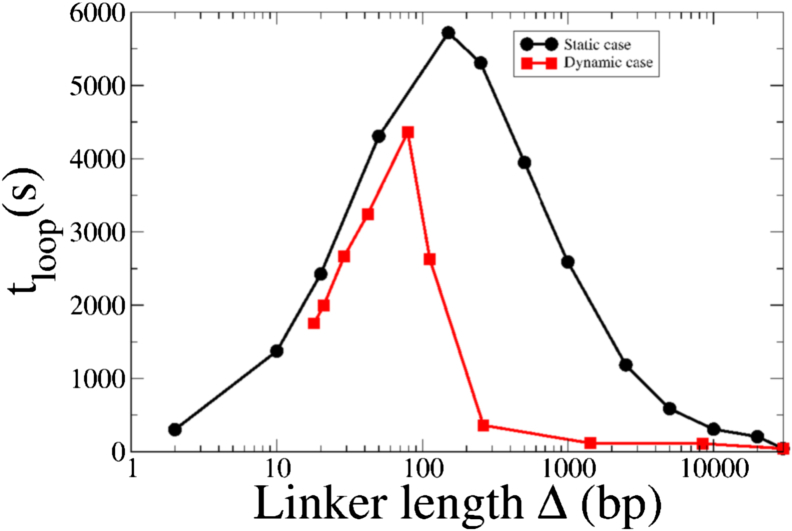
We first consider the case of static nucleosomes, i.e., when the nucleosomes occupy fixed random positions on the DNA lattice. The results for the looping time t_loop as a function of the linker length (Δ) are shown in Fig. 2 for a lattice of length L = 30 kbp. Starting from the completely empty lattice (Δ = L = 30 kbp), as we increase the number of nucleosomes (and hence decrease Δ), the loop formation time slowly increases (Fig. 2, black curve). This is expected because the nucleosomes act as extended barriers to the diffusion, and hence, increasing the number of nucleosomes increases the time taken to form a loop. Contrary to naive expectations, however, this increase in t_loop does not continue beyond a certain number of nucleosomes. Remarkably, beyond the point at which the linker length becomes comparable to the nucleosome size itself, Δ $\simeq$ d, reducing the nucleosome spacing Δ decreases the loop formation time and hence increases the effective diffusivity. At the densest configuration of nucleosomes, the first passage time can reduce by two orders of magnitude from the slowest case at Δ = d, and correspondingly, the effective diffusion coefficient can increase by two orders of magnitude.

Figure 2.

The loop formation time as a function of linker length for two cohesin subunits on a lattice with L = 30 kbp. The black curve (circles) corresponds to results for cohesin subunits in the presence of static nucleosomes. The red curve (squares) shows the result for cohesin subunits in the presence of dynamic nucleosomes. Both cases show a nonmonotonic dependence of the looping time on mean linker length, with a regime in which looping times decreases with increasing nucleosome density. To see this figure in color, go online.

This nontrivial behavior arises because introducing nucleosomes of finite sizes has a twofold effect—they not only introduce slower sites into the DNA backbone but, because of their finite size, also reduce the entropic cost of exploring a finite section of DNA. Physically, this can be understood as follows—the extended barriers pose an effective energy barrier that the cohesin subunit must overcome. Competing with this energy cost, there is also the entropic cost that is associated with the hopping of cohesin on the linker region between two nucleosomes. The effective free-energy barrier is highest when the length of the nucleosome is comparable to the mean length of the linker DNA, leading to large escape times in this region. For linker lengths smaller than this critical value, the attempt rate for barrier crossing increases as the linker region shrinks, leads to faster barrier crossings and hence smaller looping times. This was verified explicitly by changing the nucleosome size in our simulations (Fig. S2) and also varying the hopping rates p and q (Fig. S3), and the largest loop formation time was always obtained when the mean linker length was equal to the assumed nucleosome size. In addition, to confirm that this effect was not due to the interactions between the two cohesin subunits, we also verified this nonmonotonic nature of the looping time for a single RW on the 1D lattice (Fig. S4).

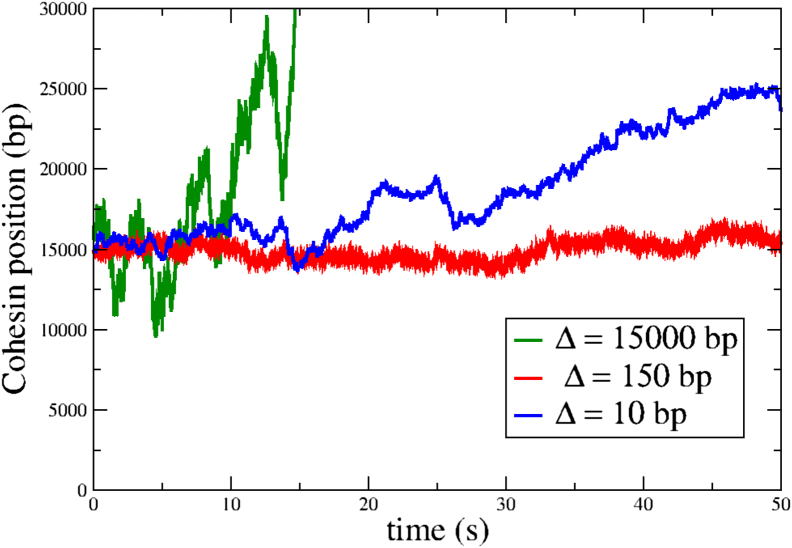
To visually represent the slowing down of cohesin trajectories when the mean linker length approaches the size of the nucleosome, we plot representative trajectories of one cohesin subunit for three different linker lengths. This is shown in Fig. 3 for Δ = 10 (blue), 150 (red), and 1500 bp (green) over a time of 50 s. When the linker length is comparable to the nucleosome size, the trajectory appears effectively frozen, with the cohesin position virtually unchanged over this time window. In contrast, there is discernible motion when nucleosomes are present at a greater density (Δ = 10 bp), which is reflective of the nonmonotonic nature of the looping times and shows how denser nucleosome configurations can result in faster cohesin motion as compared with the case when the linker length and nucleosome size are comparable. Note that in the fully packed limit, as the linker length becomes very small (Δ → 2), the cohesin can only jump over the barriers, and hence, the problem reduces to a free diffusion problem with a smaller diffusion coefficient and simultaneously over a smaller lattice length. The measure of the slowdown in this case compared with the no-nucleosome limit is provided by the ratio qd²/pa² (∼0.28) and explains why the looping time is only one order of magnitude larger in this limit compared to the empty lattice.

Figure 3.

Snapshots of representative trajectories of a cohesin ring on a 30 kbp lattice for three different linker lengths, Δ = 15 kbp, Δ = 150 bp, and Δ = 10 bp. The trajectory corresponding to the maximal looping time, Δ = d = 150 bp, appears stationary over this timescale. A denser configuration of nucleosomes (Δ = 10 bp) results in more mobile cohesin trajectories. To see this figure in color, go online.

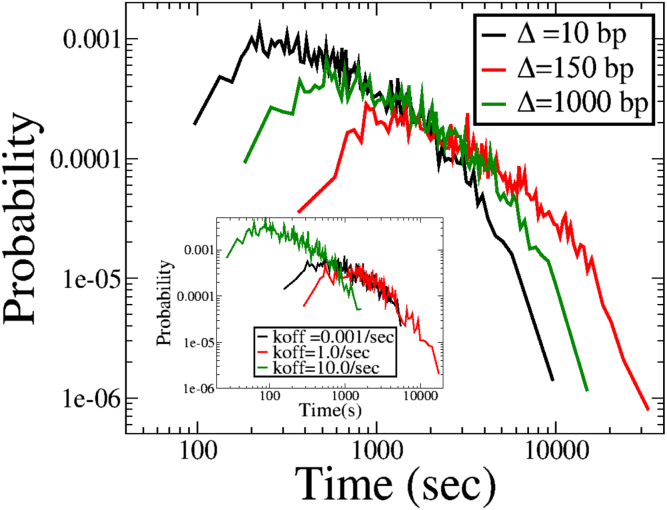
In addition to the mean loop formation time, we also calculate distributions of looping times. The distributions are shown in (Fig. 4) for three different values of the linker length. The looping time distribution is unimodal, with a peak at a finite looping time, and falls off exponentially as t → ∞. The nonmonotonic nature of the mean looping times is also reflected in the full distribution, with the peak of the distribution being shifted to the right when the linker length becomes comparable to the size of the nucleosome, as can be seen for the case of Δ = 150 bp in Fig. 4 (red curve). For linker lengths either smaller or larger than the nucleosome size, the distribution shifts to the left, commensurate with the observation of smaller loop formation times in these cases. This is a generic feature for this problem of 1D random walks with extended barriers in one dimension and continues to hold true for a single random walker.

Figure 4.

Distributions of loop formation times for three different values of internucleosome spacing for the case of static nucleosomes for two RWs on a lattice of L = 30 kbp. The distribution for Δ = d is the broadest, consistent with the mean t_loop being the highest in this case. The inset shows the distributions for the case of dynamic nucleosomes for three different unbinding rates, and again, the distribution for k_off = 1/s is the broadest. To see this figure in color, go online.

Nucleosome unbinding kinetics can decrease loop formation times

We now turn to the case of dynamic nucleosomes, which can stochastically bind and unbind to the DNA lattice. Inside the nucleus, nucleosomes are dynamic and can regulate their binding and unbinding rates in response to gene activity. It hence becomes important to estimate the loop formation times by cohesin in the context of dynamic nucleosomes.

The loop formation times for the case of dynamic nucleosomes are consistently smaller than that obtained for static nucleosomes, and the first passage time can be reduced by as much as two orders of magnitude. For different values of k_off, we obtain the mean linker length Δ. Higher values of k_off correspond to lower nucleosome densities and hence larger mean linker lengths (Fig. S5). We show the variation of the loop formation time with this mean linker length for dynamic nucleosomes in Fig. 2 (red curve). The nonmonotonicity of the loop formation time persists, as in the case of static nucleosomes. However, the peak of the first passage time curve is now shifted to smaller values of Δ, with the maximal loop formation time occurring around Δ $\simeq$ 79 bp. This shift in the peak loop formation time can be qualitatively understood by considering the full distribution of linker lengths at a given unbinding rate (Fig. S6). At k_off = 4/s ($\langle \Delta \rangle$ = 150 bp), the contributions from linker lengths both above and below this mean value sharply decrease the looping time relative to the static case. In contrast, for the case k_off = 1.0/s ($\langle \Delta \rangle$ = 79 bp), which corresponds to the peak for the dynamic nucleosome case, although the distribution is very similar for smaller linker lengths, there is a much smaller contribution from larger linker lengths (Δ $\gtrsim$ 200 bp), which leads to a comparatively larger looping time at this unbinding rate. The mean looping time drops sharply as the k_off (or equivalently, mean Δ) is increased and approaches the empty lattice value for mean separations as small as Δ ≈ 200 bp.

The distributions of looping times are also consistent with the nonmonotonic nature of the mean looping. The inset of Fig. 4 shows the looping time distribution for three different values of k_off. The distribution is broader for k_off = 1/s (red curve) than it is for unbinding rates both smaller (k_off = 0.001/s, black curve) and larger (k_off = 10/s, green curve) than this value. We note that there is a wide range of nucleosome turnover rates depending on the location along the DNA and the context. The turnover rate has been shown to be high near boundary elements (66, 67, 68, 69) and also depends on the state of the cell cycle (70). There have also been multiple experimental studies showing that linker lengths (and hence turnover rates) depend on the activity of the gene (71,72). For example, in human CD4⁺ T cells, the linker lengths for active promoters and active genes in the euchromatin region have been shown to be around ∼30–40 bp, whereas for heterochromatin regions, the linker lengths are around ∼50–60 bp (71). Our analysis shows that even such small variations in linker lengths can affect loop formation times in active genes compared to inactive regions.

Statistical positioning of nucleosomes can marginally accelerate looping

It is well known that the stochastic binding and unbinding of nucleosomes results in an oscillatory occupancy profile from the start of the transcription start site (TSS) (73, 74, 75, 76, 77). We assume, consistent with several experimental studies, that the TSSs are correlated to the CTCF markers, which define the endpoints of the loop (30,36, 37, 38, 39). This oscillatory profile can be interpreted as an effective potential landscape in which the cohesin random walker executes its diffusive dynamics.

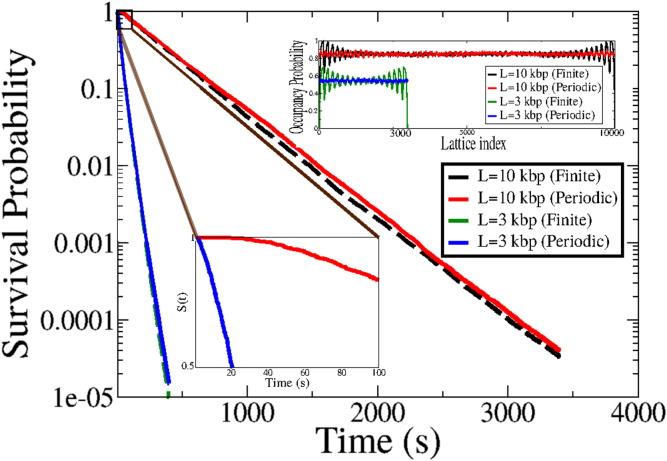
To determine whether the dynamic nature of the nucleosomes itself or the effective potential landscape imposed by the spatial variations of nucleosomal occupancy profiles ahead of a TSS is responsible for the predicted increase in the effective diffusivity, we investigate the variations of loop formation times on a lattice with periodic boundary conditions. The characteristic oscillatory profile of nucleosomal occupancy arises because of the finite boundaries at the ends of the lattice (CTCF markers), and hence is absent for the case of periodic lattice. This was explicitly verified for dynamic nucleosomes on a ring, where the nucleosomal occupancy shows a flat profile without any oscillations (see Fig. 5, inset).

Figure 5.

The effect of statistical positioning on mean looping times. Shown are the plots of the survival probabilities for a finite lattice (with statistical positioning, dashed lines) and a periodic lattice (no statistical positioning, solid lines), for two different lattice sizes, L = 3 kbp and L = 10 kbp. The unbinding rate is k_off = 0.01/s. The zoomed view illustrates the deviation of the survival probability from a single exponential for short looping times. The inset shows the nucleosomal occupancy probability as a function of the lattice site for the finite and periodic lattices. The plots for L = 3 kbp have been vertically shifted so as to avoid overlap with the L = 10 kbp plots. As expected, the periodic lattice shows no effect of statistical positioning. To see this figure in color, go online.

We plot the survival probability S(t), defined as the probability that at least one of the two cohesin subunits survives till time t, as a function of time for a finite lattice and for a periodic lattice for two different lattice sizes (L = 3000 bp and L = 10,000 bp) for a nucleosome unbinding rate of k_off = 0.01/s. We plot the survival probabilities using an ensemble cloning scheme (see Materials and Methods for details) to reliably access the tails of the distributions. As shown in Fig. 5, the difference in the survival probability distributions in the presence and absence of statistical positioning is relatively minor, showing that the nucleosome kinetics is primarily responsible for the small looping times for dynamic nucleosomes. However, the distribution for the case of periodic boundary conditions (in which there is no effect of statistical positioning) consistently lies above the curve for the finite lattice. The mean looping times can be derived from the survival probability as t_loop = $\langle t\rangle ={\int }_0^{\infty }S\left(t\right)dt$. This gives $t_{loop}^{fin,3\mathrm{k}\mathrm{b}\mathrm{p}}$ = 29.7 s and $t_{loop}^{per,3\mathrm{k}\mathrm{b}\mathrm{p}}$ = 30.8 s, whereas for the 10 kbp lattice, we obtain, $t_{loop}^{fin,10\mathrm{k}\mathrm{b}\mathrm{p}}$ = 338.4 s and $t_{loop}^{per,3\mathrm{k}\mathrm{b}\mathrm{p}}$ = 354.8 s, which also shows that the mean time for the periodic case is marginally higher than for the finite lattice. This implies that although the bulk of the speedup observed in the case of dynamic nucleosomes is due to the binding and unbinding of nucleosomes on the DNA backbone, statistical positioning can have a subtle effect in speeding up the formation of loops, and this can possibly become important for larger loop sizes.

Loop formation time grows diffusively on loop length

We now turn to the question of how mean looping times scale with the size of the loop (lattice size) and the related question of how to characterize mean looping speeds. Previous analysis suggests that cohesin can spread diffusively on DNA over distances of 7 kb in 1 h (33).

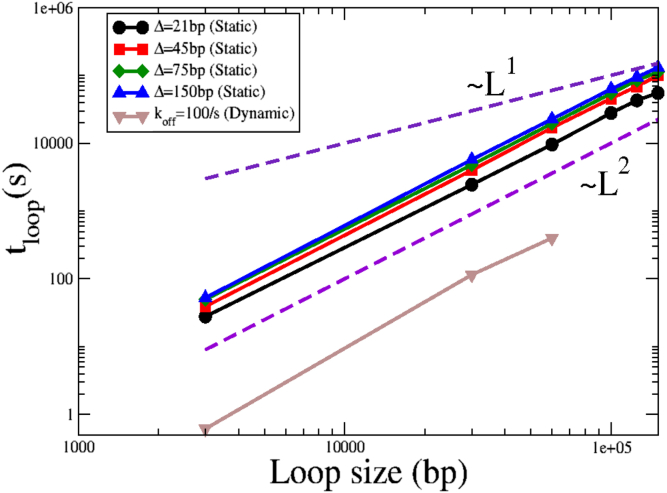
Although our work suggests that looping time scales nonmonotonically with the mean internucleosome spacing (or equivalently, with k_off for dynamic nucleosomes), for a fixed value of Δ (or k_off), the mean loop formation time scales with the lattice size as L², as expected from diffusive transport. This is shown in Fig. 6 for different values of Δ for static nucleosomes and for k_off = 100/s for dynamic nucleosomes. Based on this analysis, we can now estimate looping speeds as predicted by this barrier-mediated diffusion model. For the case of static nucleosomes, at a mean nucleosome spacing of Δ = 20 bp, our analysis predicts that cohesin would form a 30 kbp loop in a mean time of 2447 s, corresponding to an effective looping speed of around 45 kbp in 1 h. For loop sizes of L = 100 kbp, we obtain an effective looping speed of 13 kbp in 1 h. For dynamic nucleosomes, at k_off = 10/s and k_off = 0.01/s for a loop size of L = 30 kbp, we obtain a mean looping speed of 300 kbp per hour and 40 kbp per hour, respectively, a greater than 40-fold and sixfold speedup, respectively, as compared with the 7 kbp per hour speeds calculated earlier.

Figure 6.

Scaling of the loop formation time with loop size for different internucleosomal spacings for static and dynamic nucleosomes. The t ∝ L and t ∝ L² lines (dashed lines) are shown as guides to the eye. In all cases, the loop formation time grows diffusively with the size of the loop, consistent with the underlying diffusive dynamics. To see this figure in color, go online.

Discussion

We show that contrary to naive expectations of reduced diffusivities when cohesin faces a nucleosomal barrier, the true picture is far more nuanced. The macroscopic manifestation of extended microscopic barriers depends on the interbarrier separation, the mean linker length. Although the mean loop formation time initially increases with decreasing linker length, below a certain critical linker length (Δ $\lesssim$ d), this trend reverses, with the mean time now decreasing with decreasing linker lengths. At physiological nucleosome separations, this can lead to speedups of around two orders of magnitude compared with the diffusive speed estimated in previous studies. This counterintuitive result is due to the extended nature of the nucleosomal barriers, which introduces an additional length scale in the system that competes with the internucleosome spacing to give rise to this nonmonotonic behavior of the mean looping times. This nonmonotonic dependence of the looping time with linker length forms a testable prediction of our model. It is possible to design specific experiments to test our predictions. As an example, it is possible to design nucleosome arrays with specific linker lengths. For example, one may vary different linker DNA lengths with random sequences between 601 nucleosome positioning sequences and examine how the loop formation time varies as a function of linker length (78). One may also study looping times by varying nucleosome disassembly rates. By designing in vitro experiments with reconstituted chromatin having ATP-dependent remodeling enzyme at different concentrations, one may also modulate nucleosome disassembly rates (79). Further, it is known that histone modifications can also alter nucleosome disassembly rates (80,81) and offer another route to test the predictions of our model. An important consistency check can be made by comparing results with experimental observations of almost stationary cohesin at high nucleosome densities. These observations were made for a DNA strand of 48.5 kbp containing 10–50 nucleosomes (33). These correspond to mean linker lengths between ∼800 and 5000 bp, in which regime our model predicts extreme slowdown of cohesin diffusion, consistent with observations. To verify the nonmonotonic nature, we would need to observe an even higher density nucleosomal array, with $\gtrsim$200 nucleosomes on a 48.5 kbp DNA strand. Further, we illustrate how binding and unbinding of nucleosomes from the DNA backbone can speed up diffusion of cohesin by up to two orders of magnitude compared to the static case. There is widespread experimental evidence that cells can tune the binding-unbinding kinetics of nucleosomes in response to different signals, and in general, active genes are characterized by more dynamic nucleosomes (61,68,69,71,72,82). We show that this offers the cells a route to controlling the speed of loop formation by varying the nucleosome kinetics and hence linker length. This dependence of the looping time on the nucleosome kinetics also offers the tantalizing possibility of introducing directionality in the cohesin motion through an underlying asymmetry in the nucleosome positioning. Recent studies have opened the possibility of asymmetric nucleosome distributions near CTCF sites (83), and such an asymmetry can bias the underlying landscape in which cohesin performs its diffusive motion, leading to an effective drift term. In addition, sequence-dependent potentials may also play a role in determining looping times (84,85) Although we have not explicitly investigated the effect of such sequence specificity or asymmetry in the current work, our results in Fig. 2 suggest such an asymmetry can further decrease looping times in real biological scenarios. In addition to the effect of this extended barrier outlined in our work, several other factors may play a role in decreasing looping times. Experiments have found although the motion of cohesin on the DNA backbone is itself diffusive, cohesins can be transiently pushed along the DNA by other active DNA motor proteins such as FtSz (33). Although this active push is short lived because the FtSz protein changes direction, it can result in additional speedup of the loop formation process. Additionally, a recent theoretical proposal argues for a novel collective ratchet effect driven by a 1D osmotic pressure that favors the extrusion of larger loops (49, 50, 51). There have also been recent experimental reports of active directional extrusion by human cohesin (86,87), in contrast to earlier reports on yeast (33) and human (53) cohesin. This opens up the possibility of differing underlying mechanisms in different species, or even a combination of these passive versus active mechanisms under different conditions. The role of nucleosomal barriers in this case of active extrusion remains to be explored. However, we stress that the mechanism underlined in this work highlights the nontrivial role of the extended nucleosomal barriers. Other factors such as motor activity or collective effects would then serve to provide additional speedups to the estimates calculated in this work.

Our works opens up a tantalizing possibility for the case of binding site search on DNA by a generic DNA-binding protein (DBP). The question of how DBPs search for target sites has a long history, with the leading hypothesis being that of facilitated diffusion, a combination of three-dimensional and 1D diffusion (88, 89, 90, 91, 92, 93). During the phase of one-dimensional diffusion of the DBP on the DNA backbone, the proteins encounter nucleosomes. Although the specific topological association of cohesin on DNA may not be applicable to general proteins, one can imagine a DBP unbinding from the backbone and then reattaching past the nucleosome site, which would then correspond to an effective reduced barrier crossing rate in the context of our model. The same physical phenomenon as outlined in this work would then also be applicable, with the finite length of the nucleosomal barrier leading to effective speedups for certain linker lengths. This can result in faster 1D search, leading to lower effective search times.

In summary, our work highlights the nontrivial role of extended nucleosome barriers on the diffusion of cohesin on DNA. The extended barriers introduce an additional length scale that can reduce looping times beyond certain critical nucleosome densities. This nontrivial acceleration of DNA looping may serve to explain how cohesin forms large chromosomal loops even though it moves passively on the DNA backbone.

Author Contributions

M.K.M. and R.P. designed the research. A.M. carried out all simulations and analyzed data, under supervision from M.K.M. M.K.M., R.P., and A.M. wrote the article.

Editor: Tom Misteli.