Abstract
Assessing the structural properties of large proteins is important to gain an understanding of their function in, e.g., biological systems or biomedical applications. We propose a method to examine the mechanical properties of proteins subject to applied forces by means of multiscale simulation. Both stretching and torsional forces are considered, and these may be applied independently of each other. As a proof of principle, we apply torsional forces to a coarse-grained continuum model of the antibody protein immunoglobulin G using fluctuating finite element analysis and use it to identify the area of strongest deformation. This region is essential to the torsional properties of the molecule as a whole because it represents the softest, most deformable domain. Zooming in, this part of the molecule is subjected to torques and stretching forces using molecular dynamics simulations on an atomistically resolved level to investigate its torsional properties. We calculate the torsional resistance as a function of the rotation of the domain while subjecting it to various stretching forces. From this, we assess how the measured twist-torque profiles develop with increasing stretching force and show that they exhibit torsion stiffening, in qualitative agreement with experimental findings. We argue that combining the twist-torque profiles for various stretching forces effectively results in a combined force-torque spectroscopy analysis, which may serve as a mechanical signature for a biological macromolecule.
Significance
In this work, we propose a multiscale numerical approach to assess the mechanical properties of macromolecules such as proteins. We perform a combined force-torque spectroscopy analysis on the mechanically most relevant domain to compute the response signature of the spatial structure of the macromolecule. This information may lead to a better understanding of molecular structure and function in biological context and may be used toward diagnostic and sensing applications in the biomedical field.
Introduction
Proteins fulfill numerous different roles in organisms, such as providing rigidity, transporting cargo through cells, or catalyzing reactions. The functioning of a protein arises from the folding of its intrinsic structure, a linear chain of amino acids, into a higher-order hierarchical structure. Its final folded structure consists of a certain shape with one or more active sites, which facilitate the protein’s function (1). One type of protein in particular, the antibody or immunoglobulin, plays an important role in the mammalian immune system by specifically binding to foreign structures in the body. The fact that its binding to a particular molecule is very specific makes the antibody protein an excellent candidate to be employed for analyte detection in a so-called immunoassay (2). In an immunoassay, the analyte is targeted by an antibody molecule equipped with, e.g., a fluorescent or radioactive label. This label can, in turn, be detected using conventional detection methods.
To make immunoassays a viable method for point-of-care diagnostics in medical applications, however, not only the analysis but also all of the sample preparation, transportation, and mixing steps should be included in a “lab-on-a-chip” device. One proposed method for the integration is making use of magnetic particles within the device (3,4). Not only can these particles serve as labels for the analytes, but upon actuation with magnetic fields, they can be actively manipulated and used to, e.g., mix fluids within the sensor. In addition, the magnetic particles may act as magnetic tweezers to exert forces on the molecules (4, 5, 6). This experimental method is used to study the structural properties and unfolding of molecules such as proteins, DNA, and RNA (7, 8, 9, 10, 11) and may be employed side by side with atomic force microscopy (12, 13, 14, 15, 16) and optical tweezers (17, 18, 19, 20, 21, 22) experiments to assess the mechanical properties of molecules.
In recent years, van Reenen et al. (5) investigated the torsional resistance of immunoglobulin protein complexes using magnetic tweezers experiments. They showed that it is possible to distinguish between different torsion profiles for different proteins, a quality that may eventually be employed to, e.g., identify the nature of the binding (to be either specific or nonspecific) in immunoassays. This suggests that the ability to compute or even predict the response of a given biological macromolecule to torsional loading might permit the identification of that molecule using a torsional probe.
This work addresses this need for a predictive model. We introduce a multiscale numerical approach to analyze the mechanical properties of large molecules such as proteins. The method serves to gain more insight into the relation between the intrinsic structure of a molecule and its mechanical properties. As a proof of concept, we investigate an immunoglobulin molecule, which we subject to externally applied forces. Because investigating such large molecules (∼105 Da) as a whole on an atomistic level is too costly from a computational point of view, we examine the molecule on a coarse-grained mesoscopic level using fluctuating finite element analysis (FFEA) (23, 24, 25). FFEA considers the overall shape of the molecule and regards it as a continuum material internally. This allows for a fast evaluation of the molecule subject to thermal and/or external forces at the expense of the loss of information on the internal structure. Using FFEA, we can identify the area in which immunoglobulin deforms the most during torsion, which is presumably an essential region for the molecule’s torsional properties; it constitutes a weak link in the rigidity of the molecule.
Using molecular dynamics simulations, we subsequently perform a combined force-torque spectroscopy analysis on this domain on a microscopic, full-atom level; we investigate the torsional resistance of the molecule as a function of the rotation while a stretching force is exerted on the structure. We extract the resulting twist-torque profile of the molecule and learn how it develops as the stretching force increases. This gives us information on structural properties of the molecule, such as the preferred rotation direction and the strain-induced stiffening of the structure.
The remainder of this work is organized as follows. In the Methods, we describe the subject molecule of this work—immunoglobulin G (IgG)—in more detail. We briefly describe the FFEA and molecular dynamics (MD) methods that we use in our simulations. In the Results and Discussion, we present the results from the FFEA simulations, which we use to define the domain of interest. We discuss our results from the atomistic MD simulations of this relevant domain, in which we subject it to external forces and torques. In the Conclusions, we summarize our findings and draw our conclusions.
Methods
Force-torque spectroscopy on IgG
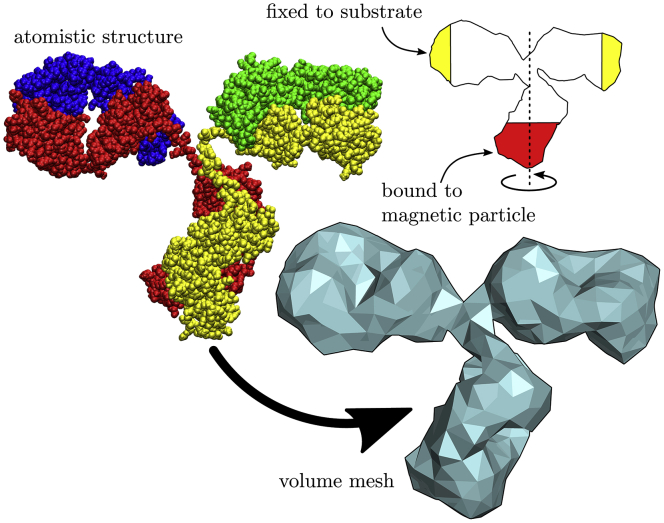
Our subject molecule is an antibody protein, IgG, of which an atomistic structure was found by x-ray diffraction (mouse IgG, PDB: 1IGT) (26); see Fig. 1 (top left). The protein consists of two structurally identical heavy chains (red and yellow) and two identical light chains (blue and green), with a total mass of ∼150 kDa. The four chains combined form three bulky domains (the three branches of the typical “Y” shape) connected by a thin linker, a feature shared by all isotypes of immunoglobulin (27).
Figure 1.
The overall shape of the atomistic structure (top left) of IgG is converted into a volume mesh (bottom right). Schematic (top right): the torsional force is exerted on the molecule at the bottom (red shaded area), and the protein is fixed at the ends of the top branches (yellow shaded areas) to mimic the fixation to a substrate. The torsion axis and rotation direction are indicated. To see this figure in color, go online.
The IgG molecule was the subject of experimental work by van Reenen et al. (5), who investigated the torsional properties of a protein complex formed by either two IgG molecules or an IgG and a protein G molecule. They sandwiched the complex between a glass substrate and a magnetic particle and found that the different protein complexes respond differently to exerted torques and that they stiffen for increasing torsion angles; they exhibit a torsion-stiffening behavior. We note that in practice, in addition to the torsional forces, a stretching force may be exerted on a protein complex by applying a second magnetic field that pulls the magnetic particle away from the substrate. However, stretching forces are already inherently present in the experimental situation because of the gravitational forces that work on the magnetic particle and the forces that arise from the direct interaction between the magnetic particle and the substrate to which the protein complex is bound.
Considering the addition of such stretching forces in the torsion experiments allows for a second, independent axis to exert forces on the molecules. Arguably, both the conventional stretching and torsional rigidities of a molecule depend in fact simultaneously on both the amount of stretching and the amount of torsion (28, 29, 30). This creates a direct coupling between the stretching and the torsion in such a combined force-torque spectroscopy analysis and may result in a more complex mechanical “signature” of a certain structure.
As a proof of principle, we aim to numerically investigate the mechanical properties of a single IgG molecule and to calculate the twist-torque profile of part of IgG under the influence of stretching forces. To that end, we first identify our region of interest on a mesoscopic level using FFEA. We briefly discuss the method below.
Mesoscopic simulation using FFEA
FFEA is a general biomolecular simulation tool for modeling large interacting macromolecules with continuum mechanics (23,24,31, 32, 33, 34). An extension of FFEA to include one-dimensional rods has been developed with a view to modeling DNA, cytoskeletal networks, the kinetochore machinery, and potentially chromatin (35). The FFEA method treats large molecules such as proteins as a continuum material to simulate their behavior on a mesoscopic scale (23,31). The underlying principle is that the overall shape of such a molecule determines its function and that the intrinsic structure of the molecule is of lesser importance at mesoscopic length and timescales: it can be represented by system-dependent macroscopic parameters to be described below. Because FFEA operates in the continuum limit, it is unable to capture atomically detailed processes such as selective interactions between proteins and small drug molecules or protein folding. We presume that the dynamics of such a material is described by the Cauchy momentum equation,
| (1) |
where u denotes the velocity at any point in the material, ρ is the mass density of the material, and σ is the total stress exerted by the continuum material. Although multiple choices for the elastic material model are possible, we employ the Mooney-Rivlin model: a general nonlinear viscoelastic model that allows us to go to finite strains locally, leading to a total stress σ that may be expressed as the sum of elastic, viscous, and thermal stress terms,
| (2) |
As stated, the elastic stress σe is computed using the Mooney-Rivlin hyperelastic model (36,37), a model often used for rubber-like materials at finite strains, which is described in more detail in the Appendix. This continuum model generalizes discrete approaches to protein mechanics such as those implemented by elastic network models. For the expressions for the viscous and thermal stresses, we refer the reader to (23) because these are of secondary importance for the purpose of this study. The protein’s material properties are parameterized using continuum material parameters such as the mass density ρ, the bulk modulus K, and the shear modulus G, and we parameterize the molecule homogeneously—that is, we ignore any structural differences between different parts of the protein. To directly measure experimentally the values for these parameters is not straightforward, although estimations can be made by considering experimental data on the density of proteins (roughly 1.5 g/cm3) (38,39), their internal viscosity (∼1 mPa s) (40), and their elastic modulus (order 107–108 Pa) (40,41). We note that in principle, different parameters may be chosen for different areas within the molecule, as demonstrated by Hanson et al. (33). However, this requires additional information or assumptions made on the structure, which we do not need for this proof-of-concept study. Nevertheless, as we shall see below, it turns out that even for a homogeneously parameterized structure, we find a distinct region that is torsionally sensitive. For the structural details of this area, we rely on atomistic simulations.
We create the volume mesh for the molecule by considering the atomistic model, converting it to an electron density map and meshing its surface (31), as illustrated in Fig. 1. We coarsen the surface until the shortest edge is 7 Å while maintaining the volume (40) and create the volume mesh using the Netgen open source software package (42). We investigate the IgG molecule in numerical torsion simulations by exerting an external torque on the bottom branch of the molecule (see Fig. 1). To mimic the fixation to a substrate, we immobilize the ends of the top two branches. We note that we do not exert stretching forces on the molecule in these FFEA simulations, in contrast to the molecular dynamics simulations described below.
We exert the torque by adding an additional torsion force to all the mesh nodes within the red shaded area in Fig. 1, where the magnitude depends on the distance to the torsion axis. The choice for this area is based on the experimental situation, in which the torque is exerted by a magnetic particle bound to the bottom region of the molecule (5). The size of the area is chosen such that the forces on the individual nodes do not become so strong that they cause an inversion of the elements. We point out that the extent of the region appears to be not all that important because (as we shall see) the strongest deformations occur in the thin linker region, outside of the forced area of Fig. 1. For definiteness, we disregard the thermal stresses in the material and focus instead on the viscoelastic response of the structure to the external torque. To that end, we set the thermal stresses in our simulations to zero.
By studying the internal stresses in the molecule during torsion using FFEA, we find the domain of interest for this protein. We isolate the domain and analyze it using molecular dynamics simulations, which we briefly describe below.
Atomistic simulation using MD
We perform MD simulations on the relevant domain of the molecule using the GROMACS software package (43). The simulations are performed using an implicit solvent model (generalized Born formalism, Onufriev-Bashford-Case (OBC) method (44)), at 100 mM monovalent salt, using a Langevin thermostat with a high friction constant γ = 5 ps−1 to ensure a strongly damped dynamics. This is prudent to suppress the influence of the high rotation rate (as discussed below) and to minimize inertial effects in our analysis of the mechanical response. We note that in reality, the solvent properties (e.g., surfactants) affect the torsional properties of proteins. As Gutiérrez-Mejía et al. (6) show, the presence of surfactants does not significantly affect the proteins’ structure; it may, however, induce a local denaturation near a binding site. Because our domain of interest is not near a binding site, we assume that it is not significantly affected by the presence (or absence) of a surfactant. We employ the Amber ff99SB-ILDN force field for the parameterization of the interactions in the atomistic representation of the protein (45).
By simultaneously exerting a stretching force f and a torque τ on the structure, we are able to explore its mechanical properties in this combined force-torque spectroscopy analysis (46). We exert various stretching forces f on the molecule, ranging from 0 to 3200 kJmol−1 nm−1 (∼5.3 nN). This is strong (equivalent to about 100 kBT, with kB Boltzmann’s constant and T the absolute temperature) from the perspective of a single covalent bond (typically 40 kBT (47)). Typical forces applied in protein unfolding studies range up to ∼2.5 nN (14,16). We note, however, that we investigate the mechanical response of a domain without inherent folding (i.e., the domain does not undergo a structural change) and that the stretching force is effectively distributed over the domain. A strong stretching force may help elucidate details in the structure that are important in the twist-torque response.
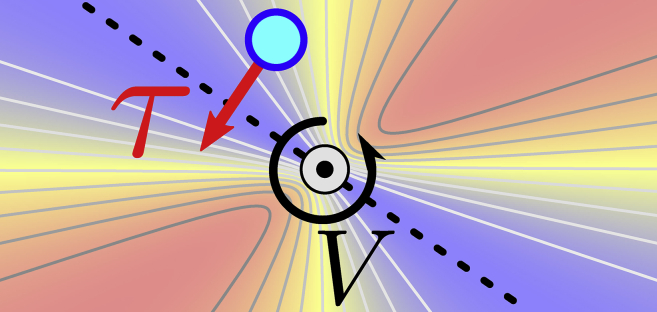
We initially exert the stretching force f without applying a torque to equilibrate the extension of the chains along the torsion axis. Subsequently, we exert the torque τ on the molecule by rotating a harmonic potential well V around the central axis of the molecule, which the forced residues of the structure are pulled into (GROMACS: Vrm2 (48)); see Fig. 2. The potential minimum is indicated by the dashed line, and the blue and red colors represent low and high potential energy, respectively. The rotation rate is 100° ns−1. We are aware that this is rather fast from an experimental perspective, which is why we choose a high friction coefficient γ in the simulations to suppress part of the inertial effects. The magnitude of the torque depends on the positions of the residues, as well as the spring constant k associated with the potential well. k ranges from 0 to 3000 kJmol−1 nm−2 (∼5 Nm−1) in our simulations, resulting in torques τ up to ∼2000 kJmol−1 (∼3300 pN nm). For reference, in the experiments by (5), the maximal exerted torques are of the order of 4000 pN nm.
Figure 2.
Schematic of the potential well V, which rotates in a counterclockwise direction with a rate of 100° ns−1. Blue indicates low potential energy, and red indicates high potential energy. The potential minimum is indicated by the dashed line. The forced residue, indicated by the blue circle, is pulled toward the bottom of the well, resulting in the torque τ. The central axis (the gray dashed line in Fig. 4) is indicated by . To see this figure in color, go online.
Next, we present our results on the mesoscopic FFEA simulations to identify the domain of interest in the molecule. We isolate this area and perform full-atom MD simulations on it, subjecting it to external forces and torques. We analyze the torque as a function of the torsion of the molecule and the exerted stretching force, resulting in a combined force-torque spectroscopy analysis of the domain.
Results and Discussion
Mesoscopic FFEA simulations
We perform mesoscopic simulations of the IgG molecule subject to torsional forces using FFEA while applying torques with various magnitudes up to 598 pN nm. Although FFEA can in principle be used to study the dynamics of large molecules such as proteins, for this proof-of-concept study, we are mainly interested in the viscoelastic response of the protein to externally applied torques to identify the torsionally most sensitive domain. Using FFEA to perform a full analysis of the torsional rigidity of the molecule turns out to not be possible within our simulation setup; for high values of the torsion angle ϕ (resulting from high values of the torque τ), the molecule relaxes its internal stresses by twisting back the linker region and thereby moving through its own surface, which is a nonphysical phenomenon. Although our method is very well suited to model large-scale deformations of macromolecules, incorporating steric surface-surface interactions to prevent such unphysical late-time configurations is challenging. Instead, we take care to run our simulations only up until times when such errors occur, making sure that only physically admissible configurations are included in our analyses.
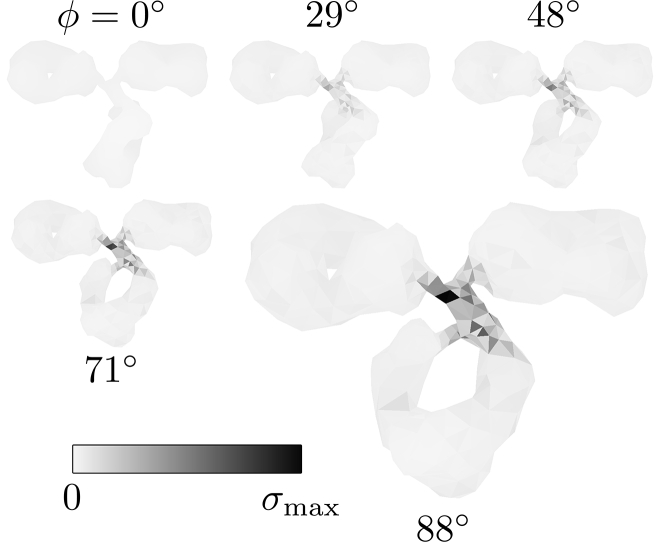
In Fig. 3, we show snapshots of a typical torsion simulation for various values of the torsion angle ϕ. An example FFEA simulation can be found in Video S1. We measure the stress at each position in the molecule and shade the stressed regions in gray. The shade of gray indicates the amount of stress, which is normalized to the maximal stress in the simulation σmax = 1.0 GPa. We note that this translates to ∼10 kBT per element, which contains multiple (on the order of five) atoms. This implies that the energy per atom or covalent bond is well below the bond breaking energy, which is typically >40 kBT (47). For different magnitudes of the applied torque (up to 598 pN nm), we find qualitatively similar results.
Figure 3.
Snapshots of a typical FFEA torsion simulation of the IgG molecule for various torsion angles ϕ, for a total torque τ = 299 pN nm. The surface elements shaded in gray indicate the areas in which the total stress is relatively high. The intensity of the shade of gray is scaled to the maximal stress magnitude in the simulation σmax = 1.0 GPa. The areas of high stress indicate strong deformations.
We find that for increasing torsion angles ϕ, the stress in the linker area between the three bulky domains strongly increases. The high stress indicates a strong deformation in this area, which hints at this region being critical for the torsional resistance of the molecule as a whole: it constitutes the softest area in the structure. We note that in this particular case this is not entirely surprising, considering that it is a relatively thin linker in the otherwise bulky geometry of the molecule. However, we argue that in general, this need not be the case. The use of the FFEA continuum model to assess the magnitude of the stress as a function of position within a molecule enables us to select which region is necessary to consider for more detailed analysis using atomistic simulations, which account for the internal structure of the protein.
We further investigate the linker domain and its mechanical properties on a microscopic level: we isolate the linker region and subject it to torques and stretching forces in molecular dynamics simulations to extract its twist-torque profile for various stretching forces. We discuss the results below.
Atomistic MD simulations
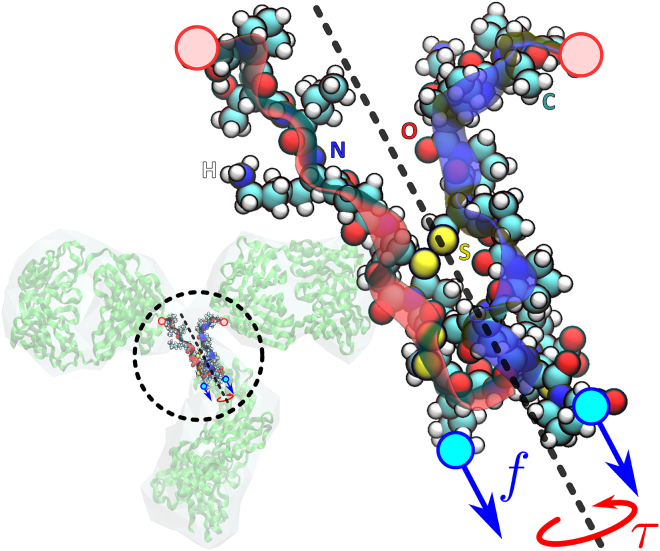
The flexible linker region of the IgG molecule consists of two identical peptide chains with 13 residues each, running from residue number 229–243 from chains B and D in the Protein Data Bank (PDB) file by Harris et al. (26), interconnected by three disulfide bonds (see Fig. 4). Note that only two of the disulfide bonds (indicated in yellow) are clearly visible in the figure.
Figure 4.
The linker region, consisting of two identical protein chains (indicated by the red and blue ribbons), in a full-atom representation. The central axis of the molecule is indicated (gray dashed line), as well as the direction of the torque τ and the pulling forces f. The residues at the top (red circles) are fixed to their position, and the torque and force are exerted on the residues at the bottom (blue circles). To see this figure in color, go online.
By way of initialization, we first perform an energy minimization and subsequently an NVT MD simulation while keeping the ends of the chains immobilized to equilibrate the molecule. After that, we perform a molecular dynamics simulation while subjecting the molecule to a stretching force f along its central axis in the absence of a torque. We fix the top residues (indicated in red in the figure) in place to mimic the fact that in reality, they are connected to the rather bulky top two branches of the molecule. For the initial stretching, we allow the bottom residues (indicated in blue in the figure) to only move strictly in the direction of the stretching force because this serves as an equilibration for the extension of the chains along the torsion axis. As we briefly discuss below, the extension of the chains is connected to the amount of twist in the structure. After the initial stretching, the bottom residues are released, and a torque τ is exerted on them along the molecule’s central axis, which causes the structure to rotate.
Directly calculating the rotation angle ϕ of the bottom residues around the torsion axis is only sensible if the molecule remains reasonably stretched during the torsion. Because of the double-chain nature of the structure, however, exerting a strong torque on the molecule not only results in a rotation around the torsion axis but also causes additional coiling of the central axis of the molecule. This coiling is not accounted for if we directly measure ϕ. To capture all of the torsion in the structure, we consider the twist Tw of the backbones of the chains in the linker region as a measure for the amount of rotation contained in the molecule. The twist is a quantity of a mathematical ribbon, independent of an external reference axis, that describes the winding of the ribbon around itself with respect to the ribbon axis (49). We note that the value for Tw becomes negative if we move along the ribbon in the opposite direction. We construct the ribbon by considering the pairs of corresponding atoms between the backbones of the two identical chains, from the lowest disulfide bond up to the top residues. We define the ribbon axis as the average positions of each pair of atoms, and the ribbon boundary consists of one of the two peptide chains. The protocol to calculate the twist, as well as the notion that using the writhe as an alternative measure of the torsion of the molecule turns out to not be viable, are discussed in detail in the Appendix.
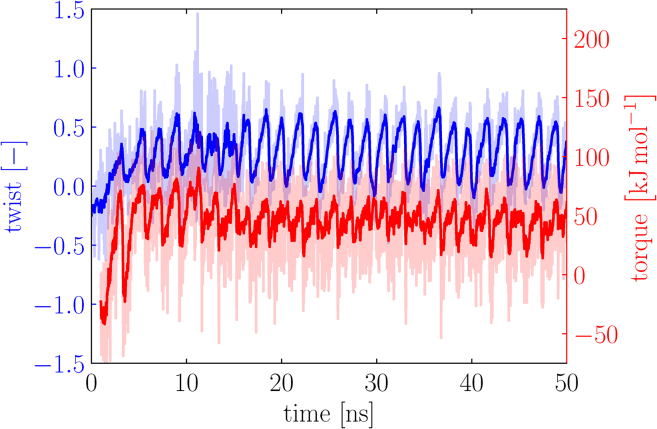
In our torsion simulations, we calculate the twist Tw of the structure for each snapshot of the simulation and track the exerted torque τ. We perform a single simulation per combination of force and torque; however, as we shall see below in Figs. 6 and 7, we do combine multiple simulations into one twist-torque profile per applied force. Fig. 5 shows the data from a typical simulation, for which we arbitrarily set the stretching force f = 800 kJmol−1 nm−1 and the spring constant k = 50 kJmol−1 nm−2, which results in a regularly oscillating behavior. An example MD simulation can be found in Video S2. We show the data for the twist Tw in blue and the torque τ in red. The light color represents the original data, and the darker color shows a weighted running average of the data over time to highlight the trends. The weighted running average at a point in time i is calculated by taking 2N data points surrounding i and weighing them by the inverse distance to the point,
| (3) |
where xi is the original data at the point in time i. For the trends in Fig. 5, we set N = 30. Note that this choice for N is arbitrary. However, because the terms are weighed with the inverse distance to the point, the exact value of N is irrelevant as long as it is sufficiently large.
Figure 6.
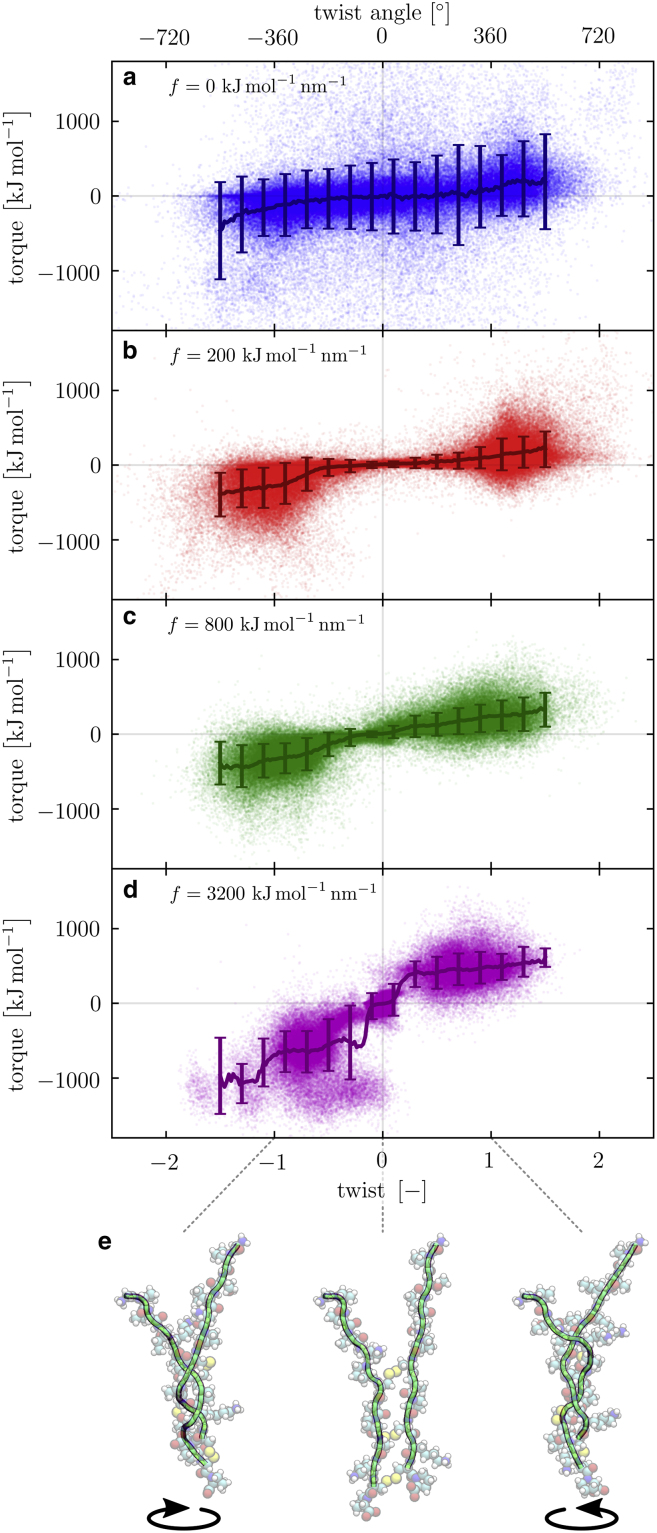
The development of the twist-torque profile for increasing stretching force; the exerted torque τ is shown as a function of the twist Tw for various stretching forces f: (a) 0, (b) 200, (c) 800, and (d) 3200 kJmol−1 nm−1. The points in the graphs are individual data points. The darker lines are averages and the error bars represent the standard deviation around the averages. (e) Snapshots of the torsion simulation are shown, illustrating the conformation of the molecule at specific values of the twist Tw = −1, 0, 1 for f = 3200 kJmol−1 nm−1. To see this figure in color, go online.
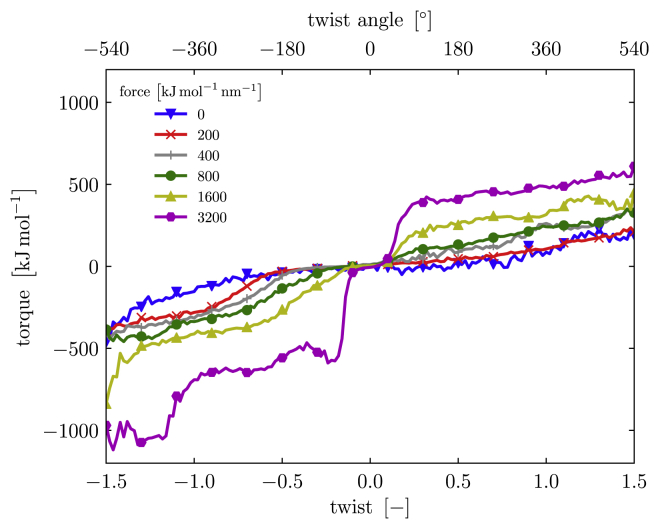
Figure 7.
The trends (averages) of the combined force-torque spectroscopy profile of the IgG linker region; the exerted torque τ is shown as a function of the twist Tw for various values of the stretching force f. For clarity, the individual data points and the standard deviations are not shown. To see this figure in color, go online.
Figure 5.
The twist Tw (blue) and applied torque τ (red) for a single simulation as a function of time, for a stretching force f = 800 kJmol−1 nm−1 and a spring constant k = 50 kJmol−1 nm−2. The light color represents the original data, and the darker color shows a weighted running average of the data over time, calculated using Eq. 3, to show the trends. To see this figure in color, go online.
We see that the data for both the twist and the torque strongly fluctuate as a result of the Brownian motion of the molecule, but that overall, the twist and torque show coherent behavior. At very short times (t < 100 ps), we see a fairly constant value for Tw, and no torque τ is exerted. This corresponds to the equilibration of the extension of the chains, in which we stretch the molecule using a force f without exerting a torque. Subsequently, we release the bottom residues and rotate the potential well V. As a result, we see an increase of both Tw and τ in time. After a while, the molecule reaches a state of oscillatory motion as both Tw and τ reach a maximal value, after which the molecule partially relaxes to a less strained state. Parenthetically, the same trend shows up in the extension of the chains along the torsion axis; they shrink as they coil around each other and extend back to a more relaxed state as the molecule relaxes its twist.
The process repeats for each (half-)cycle of the rotating potential well; as long as the rotated residues remain near the potential minimum, hardly any torque is exerted. Upon further rotation, however, the torsional resistance increases, and a torque is exerted on the residues to enforce the rotation. As the torsional resistance of the molecule then becomes too strong for the potential well to overcome, the residues move out of the well, and the structure is allowed to partially relax until the rotating potential catches up to it again. Because the potential well is symmetric with respect to the central axis (as is schematically shown in Fig. 2), this results in a period for the oscillatory motion of half a rotation of the well, corresponding to 1.8 ns for a rate of 100° ns−1.
We repeat the torsion simulations for various values of the spring constant k for the rotating potential well V. We track the twist Tw and the torque τ during the simulations and combine the results into a single twist-torque profile for a given stretching force f; we show the exerted torque τ as a function of the twist Tw of the molecule. In Fig. 6, we show the twist-torque profiles for various values of the stretching force f: (Fig. 6 a) 0, (Fig. 6 b) 200, (Fig. 6 c) 800, and (Fig. 6 d) 3200 kJmol−1 nm−1. All individual data points are shown with 5% opacity, which effectively results in a configuration density plot of the molecule in twist-torque space. The darker lines are trends, which we calculate by averaging the torques τ for twists Tw between −1.5 and 1.5, in steps of ΔTw = 0.02. The error bars shown are the standard deviations around the averages of the torque. Fig. 6 e shows typical snapshots of the simulations for specific values of the twist Tw = −1, 0, 1 for f = 3200 kJmol−1 nm−1.
From Fig. 6, we can make a few observations that we discuss in more detail below, giving us mechanical information about the structure of the protein at hand. Let us first focus on the point clouds and disregard the trend lines, which we discuss later:
-
1)
the slope of the torque versus twist curve at Tw = 0 increases with f;
-
2)
the range with a quasilinear dependence of τ on Tw decreases with increasing f;
-
3)
the spread increases with increasing Tw;
-
4)
the spread seems to depend nonmonotonically on f; and
-
5)
the twist-torque profiles are asymmetric for positive and negative twist.
Let us now discuss these observations point by point. First, the slope at zero twist increases with increasing stretching force. This indicates that the torsional resistance of the structure increases as the structure is stretched more strongly. If we consider that pulling on the two chains brings the individual residues and atoms closer together, we would indeed intuitively expect the torsional resistance to increase with a stronger stretching force f. In addition, the individual bonds between the atoms become more stretched, which limits their extensibility during the rotation, likely leading to a higher torsional resistance.
The second point closely relates to this because the more strongly we pull the chains together, the less space the atoms have to move around in. If the structure is subsequently twisted, the chains collide at lower values of the twist Tw. The increase in the torsional resistance likewise occurs for smaller values of Tw. The torsional stiffening behavior we report agrees qualitatively with the experimental results of van Reenen et al. (5), which show that the torsional resistance of an IgG-IgG complex starts out fairly constant but rises strongly as it is rotated. Note that the stiffening of biopolymers under strain is seen in many biological materials (50). In the experiments of (5), the stiffening is found at larger torsion angles, from ∼200°, compared with ∼40–200° in our simulations, depending on the stretching force f. We note, however, that in our study, we examine a small domain in IgG, in contrast to the full IgG-IgG protein complex studied in the experiments. The combination of multiple proteins arguably leads to a higher flexibility because multiple “torsional springs” are joined in series. Interestingly, in our analysis, for even greater rotations, the twist-torque profile appears to flatten off. We return to this in our discussion of Fig. 7.
The third observation that we would like to point out is that the spread in the data increases as the twist increases. This hints at the fact that the structure visits different conformations when twisting, such that the amount of torque needed to reach a certain twist varies significantly. The spread of the data indicates a variation in conformations of the structure at a certain value for the twist. For small twists, the structure has not been deformed so much, and therefore, the structural conformation is of lesser importance for the required torque. In general, twisting the molecule may unlock conformations that correspond to local minima in the free energy but are not thermally accessible from the untwisted ground state.
Fourth, the spread in the data seems to depend nonmonotonically on the stretching force f. We find that for f = 0, in Fig. 6 a, the spread is relatively large. This is likely to be caused by the circumstance that the molecule may become strongly supercoiled and the configuration of the molecule regularly becomes inverted, i.e., the bottom residues end up above the top residues because of the strong internal stresses caused by the exerted torque and the absence of a stretching force. As a result, the torque needed to reach a certain twist varies rather strongly.
Consequently, we expect the spread to decrease with increasing f because thermal energy becomes subdominant in comparison to the energy associated with the mechanical deformation. Indeed, in Fig. 6 b, the spread in the data is significantly smaller than in Fig. 6 a. For stronger stretching forces, however, it appears to increase again, most notably in Fig. 6 d. We presume that although the thermal forces become less relevant for stronger stretching forces f, the detailed conformation of the structure actually becomes more important; if we pull on the chains strongly, we effectively “lock” the structure in a particular configuration as it is twisted. This may be an explanation for the variable shapes in the point clouds in Fig. 6 d.
The fifth and last observation we discuss here is the asymmetry in the twist-torque profiles. For all values for the stretching force f in Fig. 6, we find that stronger torques are needed to reach a certain negative twist than the equivalent positive value. This hints at a preferred rotation direction for the molecule, which may indicate that the helicity of the structure is slightly right-handed.
To further illustrate the dependence of the twist-torque profile of the structure on the stretching force, we combine the trend lines for different stretching forces, as shown in Fig. 6, a–d, without error bars, into one graph (see Fig. 7). We emphasize that the full twist-torque profile point clouds contain more detailed information about the structure than the trend lines alone. The trend lines, however, allow for a more transparent comparison between the profiles for different forces.
From Fig. 7, we learn that the molecule indeed gradually stiffens as the stretching force f increases. It exhibits a torsional stiffening behavior for small twists, after which the resistance flattens off and the torsional resistance remains approximately constant. Geometrically speaking, given the double-chain structure of the molecule, we may in fact expect the profiles to show an additional torsional stiffening for even greater values of |Tw|. As the chains coil around each other, the structure becomes supercoiled. If it is twisted further, this supercoiled structure may in turn coil around itself, resulting in a second torsional stiffening. However, we have not investigated greater rotations. Note that the flattening off and “second stiffening” in the twist-torque profiles are not observed in the experiments (5). We speculate that this may be due to the torsion angles reached in experiments not being sufficiently large. Alternatively, the detailed mechanical response of a subdomain of the protein may not explicitly show up in experiments on a protein complex made up of two molecules.
Fig. 7 indicates that the end of the torsion-stiffening regime, represented by the inflection point of the twist-torque curve, gradually shifts to smaller values of |Tw| as f increases. This is likely related to the second observation with Fig. 6, in which the quasilinear regime shrinks as the chains are pulled closer together by the stretching force. This leads to a build-up in the torque at smaller values of the twist. In addition, the asymmetry between the magnitude of the exerted torques for positive and negative twists is apparent.
We argue that the twist-torque profiles (as shown in Fig. 6) and their dependence on the stretching force (Fig. 7) compose a mechanical signature for a molecule. Hence, our method may facilitate the development of an automated multiscale simulation procedure for the characterization of proteins, protein complexes, or other large molecules for which we can predict and/or explain the mechanical response by performing this numerical force-torque spectroscopy analysis. The ability to identify and isolate the most deformable domains allows for a detailed study of a molecule’s mechanical response.
This concludes the discussion of our results. Next, we summarize our main findings and draw our conclusions.
Conclusions
We put forward a multiscale molecular simulation method to perform a combined force-torque spectroscopy analysis of large molecules such as proteins; we analyze the mechanical response of a molecule when subjected to external torques and stretching forces. We combine 1) FFEA simulations with 2) MD simulations that incorporate external forces. In our proof-of-concept study, we find that using FFEA, we are able to indicate the region within an IgG molecule that is crucial for its torsional rigidity; while subjecting the molecule to torques, we locate the area of strongest deformation, suggesting that this linker domain is likely to be the most flexible. We subsequently isolate the relevant domain and investigate its torsional properties using MD simulations while subjecting it to stretching forces and torques. We make five observations on the twist-torque profile for the linker domain and how it develops as the stretching force increases: 1) the slope at zero twist increases with the force, 2) the regime with a quasilinear dependence of the torque on the twist decreases in size with increasing force, 3) the spread in the data increases with increasing twist, 4) the spread in the data appears to depend nonmonotonically on the force, and 5) the profiles are asymmetric for positive and negative twist angles.
We find that the linker region exhibits a torsion-stiffening behavior, a result that is in qualitative agreement with experimental results on IgG-IgG complexes by van Reenen et al. (5). For stronger rotations, the exerted torque flattens off and the torsional resistance remains approximately constant. Combining the twist-torque profiles for different stretching forces effectively results in a combined force-torque spectroscopy analysis of the molecule, and we argue that this composes a mechanical signature for the examined structure. Our method sheds light on molecular properties such as the location of a molecule’s most deformable domains, strain stiffening behavior, maximal rotation and/or extension, helicity, and so on.
In conclusion, our study serves as a proof of concept for an efficient numerical evaluation of the mechanical response of a large molecule. This method facilitates the automation of the multiscale procedure for a high-throughput computational analysis of multiple proteins subject to stretching and torsional forces. If the atomistic structure of such a molecule is known, we may disregard the domains less relevant to the torsional stiffness and focus on the softest areas from the perspective of the torsional rigidity, aided by the FFEA method. Bulky domains within the molecule that consist of many atoms and are likely to be relatively rigid do not need to be taken into account explicitly. This is a considerable advantage for the atomistic molecular dynamics simulation that is subsequently used to investigate the torsional properties of the relevant domain in more detail.
Author Contributions
T.W.G.v.d.H. performed simulations, analyzed the results, and wrote the manuscript. D.J.R., O.G.H., and S.A.H. developed the FFEA simulation method. T.W.G.v.d.H., P.v.d.S., S.A.H., and C.S. designed the research and interpreted the results. All authors contributed to the manuscript.
Acknowledgments
Molecular images were produced using the VMD software package (51). The authors thank Ben Hanson, Fabiola Gutiérrez-Mejía, and René de Bruijn for fruitful discussions. T.W.G.v.d.H. thanks the University of Leeds, where part of this work was executed, for their hospitality.
Editor: Markus Buehler.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.09.039.
Appendix
The elastic stress
The elastic energy of the molecule is based on a Mooney-Rivlin hyperelastic model for the stress (36), with an adaptation proposed by Gent (37) to introduce a maximal deformation for the structure. The strain energy density function W is as follows:
| (4) |
with G and K the shear and bulk moduli, respectively, and I1 and J two invariants of the deformation gradient tensor F:
| (5) |
and
| (6) |
with V and V0 the instantaneous and initial volumes, respectively. Im is the maximal value for I1 for the structure. In our analysis, to strongly limit the deformations and to emphasize the stressed regions, we set Im = 3.1. F describes the deformation for a mapping of a position X to a new position x, X x(X):
| (7) |
The elastic stress tensor is derived from the strain energy density function as follows:
| (8) |
which results in
| (9) |
with I the identity matrix.
Calculating the twist
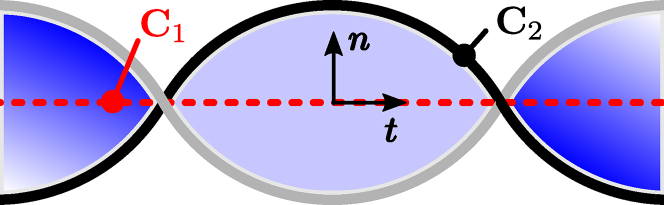
The twist of a ribbon indicates the amount of (right-handed) winding of the ribbon around itself, along the central axis. We can define a ribbon by considering the central axis C1 and the boundary C2 (see Fig. 8).
Figure 8.
A ribbon with central axis curve C1 and boundary curve C2. The unit tangent to the central axis t and the unit normal vector n pointing from C1 to C2 are indicated. This particular ribbon contains a twist Tw = 1. To see this figure in color, go online.
We indicate the unit tangent to the central axis t(s) and the normal unit vector n(s) perpendicular to t, pointing from C1 to C2. They share a common arc length parameter s. The twist Tw of the ribbon can be calculated as (49)
| (10) |
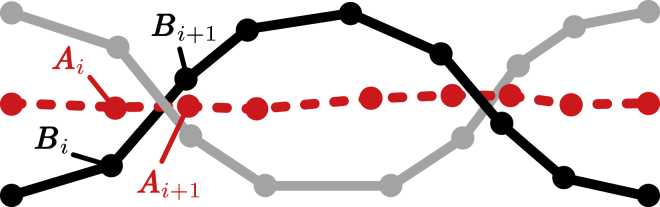
To calculate the twist contained in the linker region (see Fig. 4), we first need to transform this region to a ribbon representation. We consider only the backbones (consisting of carbon and nitrogen atoms) from the lowest disulfide bond up to the top. These are the atoms corresponding to the green ribbons in Fig. 6 e. Taking into account the dangling ends at the bottom of the two chains in the twist calculation would result in overestimations of the intrinsic twist of the protein because these are hindered less by the two-chain structure. Because the two chains are structurally identical, it is prudent to connect the corresponding atoms to form a ribbon. We define the central axis Ai as the average positions of the connected atoms in each chain,
| (11) |
where rj,i denotes the position of the i-th atom in chain j. The discrete ribbon is now defined by the central axis Ai and the boundary Bi r1,i (see Fig. 9).
Figure 9.
A discrete ribbon with central axis positions Ai and boundary positions Bi. To see this figure in color, go online.
We calculate the twist Tw of the discrete ribbon as
| (12) |
where
| (13) |
| (14) |
| (15) |
and AiAi + 1 indicates the segment from position Ai to Ai + 1 (49). The factor αi accounts for the direction of the twist, i.e., whether the respective segments cause a positive or negative contribution to the total twist.
Considering the writhe
In our analysis of the rotation of the molecule, we also considered using the writhe of the structure. To calculate the writhe, we construct a closed loop consisting of the two backbones of the chains, the lowest disulfide bond connecting the two chains, and an artificial connection between the top two residues. The writhe is a quantity of a closed loop, which means that it is independent of any external reference axis or orientation. However, it turns out that the writhe is rather sensitive to fluctuations in the positions of the atoms. This results in uncertainties and inaccuracies in determining the rotation of the molecule and we therefore deem it unsuitable for our analysis.
References
- 1.Bourne P.E., Weissig H. Wiley-Liss; Hoboken, NJ: 2003. Structural Bioinformatics. [Google Scholar]
- 2.John R., Sheehan C., He J. Fourth Edition. Elsevier; Amsterdam, the Netherlands: 2013. The Immunoassay Handbook - Theory and Applications of Ligand Binding, ELISA and Related Techniques. [Google Scholar]
- 3.van Reenen A., de Jong A.M., Prins M.W.J. Integrated lab-on-chip biosensing systems based on magnetic particle actuation--a comprehensive review. Lab Chip. 2014;14:1966–1986. doi: 10.1039/c3lc51454d. [DOI] [PubMed] [Google Scholar]
- 4.Moerland C.P., van IJzendoorn L.J., Prins M.W.J. Rotating magnetic particles for lab-on-chip applications - a comprehensive review. Lab Chip. 2019;19:919–933. doi: 10.1039/c8lc01323c. [DOI] [PubMed] [Google Scholar]
- 5.van Reenen A., Gutiérrez-Mejía F., Prins M.W.J. Torsion profiling of proteins using magnetic particles. Biophys. J. 2013;104:1073–1080. doi: 10.1016/j.bpj.2013.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gutiérrez-Mejía F.A., van IJzendoorn L.J., Prins M.W.J. Surfactants modify the torsion properties of proteins: a single molecule study. N. Biotechnol. 2015;32:441–449. doi: 10.1016/j.nbt.2015.02.005. [DOI] [PubMed] [Google Scholar]
- 7.Smith S.B., Finzi L., Bustamante C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 8.Schemmel A., Gaub H.E. Single molecule force spectrometer with magnetic force control and inductive detection. Rev. Sci. Instrum. 1999;70:1313–1317. [Google Scholar]
- 9.Gosse C., Croquette V. Magnetic tweezers: micromanipulation and force measurement at the molecular level. Biophys. J. 2002;82:3314–3329. doi: 10.1016/S0006-3495(02)75672-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Neuman K.C., Nagy A. Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods. 2008;5:491–505. doi: 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Long X., Parks J.W., Stone M.D. Mechanical unfolding of human telomere G-quadruplex DNA probed by integrated fluorescence and magnetic tweezers spectroscopy. Nucleic Acids Res. 2013;41:2746–2755. doi: 10.1093/nar/gks1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rief M., Gautel M., Gaub H.E. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 1997;276:1109–1112. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- 13.Oesterhelt F., Rief M., Gaub H.E. Single molecule force spectroscopy by AFM indicates helical structure of poly(ethylene-glycol) in water. New J. Phys. 1999;1:6.1–6.11. [Google Scholar]
- 14.Rief M., Grubmüller H. Force spectroscopy of single biomolecules. ChemPhysChem. 2002;3:255–261. doi: 10.1002/1439-7641(20020315)3:3<255::AID-CPHC255>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 15.Puchner E.M., Gaub H.E. Force and function: probing proteins with AFM-based force spectroscopy. Curr. Opin. Struct. Biol. 2009;19:605–614. doi: 10.1016/j.sbi.2009.09.005. [DOI] [PubMed] [Google Scholar]
- 16.Scholl Z.N., Li Q., Marszalek P.E. Single molecule mechanical manipulation for studying biological properties of proteins, DNA, and sugars. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2014;6:211–229. doi: 10.1002/wnan.1253. [DOI] [PubMed] [Google Scholar]
- 17.Nishizaka T., Miyata H., Kinosita K., Jr. Unbinding force of a single motor molecule of muscle measured using optical tweezers. Nature. 1995;377:251–254. doi: 10.1038/377251a0. [DOI] [PubMed] [Google Scholar]
- 18.Kellermayer M.S., Smith S.B., Bustamante C. Folding-unfolding transitions in single titin molecules characterized with laser tweezers. Science. 1997;276:1112–1116. doi: 10.1126/science.276.5315.1112. [DOI] [PubMed] [Google Scholar]
- 19.Tskhovrebova L., Trinick J., Simmons R.M. Elasticity and unfolding of single molecules of the giant muscle protein titin. Nature. 1997;387:308–312. doi: 10.1038/387308a0. [DOI] [PubMed] [Google Scholar]
- 20.Wang M.D., Yin H., Block S.M. Stretching DNA with optical tweezers. Biophys. J. 1997;72:1335–1346. doi: 10.1016/S0006-3495(97)78780-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bennink M.L., Leuba S.H., Greve J. Unfolding individual nucleosomes by stretching single chromatin fibers with optical tweezers. Nat. Struct. Biol. 2001;8:606–610. doi: 10.1038/89646. [DOI] [PubMed] [Google Scholar]
- 22.Wen J.-D., Manosas M., Tinoco I., Jr. Force unfolding kinetics of RNA using optical tweezers. I. Effects of experimental variables on measured results. Biophys. J. 2007;92:2996–3009. doi: 10.1529/biophysj.106.094052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Oliver R.C., Read D.J., Harris S.A. A stochastic finite element model for the dynamics of globular macromolecules. J. Comput. Phys. 2013;239:147–165. [Google Scholar]
- 24.Richardson R.A., Papachristos K., Harris S.A. Understanding the apparent stator-rotor connections in the rotary ATPase family using coarse-grained computer modeling. Proteins. 2014;82:3298–3311. doi: 10.1002/prot.24680. [DOI] [PubMed] [Google Scholar]
- 25.Hanson B., Richardson R., Harris S. Modelling biomacromolecular assemblies with continuum mechanics. Biochem. Soc. Trans. 2015;43:186–192. doi: 10.1042/BST20140294. [DOI] [PubMed] [Google Scholar]
- 26.Harris L.J., Larson S.B., McPherson A. Refined structure of an intact IgG2a monoclonal antibody. Biochemistry. 1997;36:1581–1597. doi: 10.1021/bi962514+. [DOI] [PubMed] [Google Scholar]
- 27.Janeway C.A., Jr., Travers P., Shlomchik M.J. Fifth Edition. Garland Science; New York: 2001. Immunobiology: The Immune System in Health and Disease. [Google Scholar]
- 28.Lipfert J., Kerssemakers J.W.J., Dekker N.H. Magnetic torque tweezers: measuring torsional stiffness in DNA and RecA-DNA filaments. Nat. Methods. 2010;7:977–980. doi: 10.1038/nmeth.1520. [DOI] [PubMed] [Google Scholar]
- 29.Yamaoka H., Adachi T. Coupling between axial stretch and bending/twisting deformation of actin filaments caused by a mismatched centroid from the center axis. Int. J. Mech. Sci. 2010;52:329–333. [Google Scholar]
- 30.Nomidis S.K., Skoruppa E., Marko J.F. Twist-bend coupling and the statistical mechanics of the twistable wormlike-chain model of DNA: perturbation theory and beyond. Phys. Rev. E. 2019;99:032414. doi: 10.1103/PhysRevE.99.032414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Solernou A., Hanson B.S., Harris S.A. Fluctuating finite element analysis (FFEA): a continuum mechanics software tool for mesoscale simulation of biomolecules. PLoS Comput. Biol. 2018;14:e1005897. doi: 10.1371/journal.pcbi.1005897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lee S.C., Collins R., Dafforn T.R. Nano-encapsulated Escherichia coli divisome anchor ZipA, and in complex with FtsZ. Sci. Rep. 2019;9:18712. doi: 10.1038/s41598-019-54999-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hanson B.S., Iida S., Harris S.A. Continuum mechanical parameterisation of cytoplasmic dynein from atomistic simulation. Methods. 2020 doi: 10.1016/j.ymeth.2020.01.021. S1046-2023(19)30244-0. Published online January 30, 2020. [DOI] [PubMed] [Google Scholar]
- 34.Richardson R.A., Hanson B.S., Harris S.A. Exploring the dynamics of flagellar dynein within the axoneme with fluctuating finite element analysis. Q. Rev. Biophys. 2020;53:e9. doi: 10.1017/S0033583520000062. [DOI] [PubMed] [Google Scholar]
- 35.Welch R., Harris S.A., Read D.J. KOBRA: a fluctuating elastic rod model for slender biological macromolecules. Soft Matter. 2020;16:7544–7555. doi: 10.1039/d0sm00491j. [DOI] [PubMed] [Google Scholar]
- 36.Shontz S.M., Vavasis S.A. A robust solution procedure for hyperelastic solids with large boundary deformation. Eng. Comput. 2012;28:135–147. [Google Scholar]
- 37.Gent A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996;69:59–61. [Google Scholar]
- 38.Fischer H., Polikarpov I., Craievich A.F. Average protein density is a molecular-weight-dependent function. Protein Sci. 2004;13:2825–2828. doi: 10.1110/ps.04688204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Quillin M.L., Matthews B.W. Accurate calculation of the density of proteins. Acta Crystallogr. D Biol. Crystallogr. 2000;56:791–794. doi: 10.1107/s090744490000679x. [DOI] [PubMed] [Google Scholar]
- 40.Oliver R.C. University of Leeds; 2013. A stochastic finite element model for the dynamics of globular proteins. PhD thesis. [Google Scholar]
- 41.Voss A., Dietz C., Stark R.W. Quantitative measurement of the mechanical properties of human antibodies with sub-10-nm resolution in a liquid environment. Nano Res. 2015;8:1987–1996. [Google Scholar]
- 42.Egger H., Gopalakrishnan J., Zaglmayr S. Netgen. https://ngsolve.org/
- 43.Abraham M.J., Murtola T., Lindahl E. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. [Google Scholar]
- 44.Onufriev A., Bashford D., Case D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 45.Lindorff-Larsen K., Piana S., Shaw D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Parker A., Ravikumar K., Cox D. Molecular dynamics-based strength estimates of beta solenoid proteins. Soft Matter. 2017;13:6218–6226. doi: 10.1039/c7sm01070b. [DOI] [PubMed] [Google Scholar]
- 47.Israelachvili J. Third Edition. Elsevier; Amsterdam, the Netherlands: 2011. Intermolecular and Surface Forces. [Google Scholar]
- 48.Abraham M., Hess B., Lindahl E. 2012. GROMACS reference manual, version 5.1.2. [Google Scholar]
- 49.Au C.K. The geometric interpretation of linking number, writhe and twist for a ribbon. Comput. Model. Eng. Sci. 2008;29:151–162. [Google Scholar]
- 50.Storm C., Pastore J.J., Janmey P.A. Nonlinear elasticity in biological gels. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 51.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38, 27–28. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.