Abstract
Background
Alzheimer's Disease (AD) is a neurodegenerative disease characterized by progressive loss of memory and general decline in cognitive functions. Multi-modal imaging such as structural MRI and DTI provide useful information for the classification of patients on the basis of brain biomarkers. Recently, CNN methods have emerged as powerful tools to improve classification using images.
New Method
In this paper, we propose a transfer learning scheme using Convolutional Neural Networks (CNNs) to automatically classify brain scans focusing only on a small ROI: e.g. a few slices of the hippocampal region. The network's architecture is similar to a LeNet-like CNN upon which models are built and fused for AD stage classification diagnosis. We evaluated various types of transfer learning through the following mechanisms: (i) cross-modal (sMRI and DTI) and (ii) cross-domain transfer learning (using MNIST) (iii) a hybrid transfer learning of both types.
Results
Our method shows good performances even on small datasets and with a limited number of slices of small brain region. It increases accuracy with more than 5 points for the most difficult classification tasks, i.e., AD/MCI and MCI/NC.
Comparison with Existing Method(s)
Our methodology provides good accuracy scores for classification over a shallow convolutional network. Besides, we focused only on a small region; i.e., the hippocampal region, where few slices are selected to feed the network. Also, we used cross-modal transfer learning.
Conclusions
Our proposed method is suitable for working with a shallow CNN network for low-resolution MRI and DTI scans. It yields to significant results even if the model is trained on small datasets, which is often the case in medical image analysis.
Keywords: Alzheimer's Disease, Magnetic Resonance Imaging (MRI), Diffusion Tensor Imaging (DTI), Multi-modality, Image classification, Convolutional Neural Network (CNN), Transfer learning, Applied computing, Applied computing in medical science, Computing methodology, Artificial intelligence, Signal processing, Image processing, Medical imaging
Alzheimer's Disease; Magnetic Resonance Imaging (MRI); Diffusion Tensor Imaging (DTI); Multi-modality; Image classification; Convolutional Neural Network (CNN); Transfer learning; Applied computing; Applied computing in medical science; Computing methodology; Artificial intelligence; Signal processing; Image processing; Medical imaging
1. Introduction
Alzheimer's disease (AD) is a major worldwide public health priority [1], it is a progressive degeneration that devastates cells in the human brain, and causes dementia for elderly individuals, mostly for people aged 65 or older. Alzheimer's patients suffer from short-term memory loss, deterioration of mood, behavior, and ability to continue daily activities. Globally, there are around 44 million people who have been diagnosed with AD in the world [2], and this number may reach to 131.5 million people in 2050 [3]. In USA 5.7 million individuals are living with AD in 2018, and this number will approximately triplicate by 2050 [1]. Recent statistical studies estimate 900.000 persons diagnosed with AD in France [2]. Mild Cognitive Impairment (MCI) is considered as the transitional stage where subjects have the risk to convert to AD [4]. There is no known cure for AD, however specific treatments including occupational individual therapy can make it easier for people to live with the disease [5], and that is why it is very important to diagnose and detect affected patients in the early stage of MCI before progression of the disease. MCI patients may remain stable, regress to a normal condition (s-MCI), or may develop dementia due to AD considered converters (c-MCI).
Monitoring and observing brain structural changes in AD subjects has been well studied, for a long time the structural magnetic resonance imaging (sMRI) has been the most used imagery technique for diagnostics and analysis of progressive brain deterioration. It permits tracking structural changes in the brain and measuring the inevitable atrophy caused by the neurodegenerative aspect of the AD pathology [5]. Most studies use the structural MRI to explore the deterioration process of some Regions-of-Interest (ROIs) in the brain, known to be affected by AD such as the hippocampus. The latter is very sensitive to be affected first [6], [7]. Temporal and cingulate gyri, and precuneus are amongst other affected structures [8], [9].
However, sMRI scans have insufficient contrast to delineate micro-structural changes due to AD. For an accurate measuring of the white matter integrity, diffusion Tensor Imaging (DTI) is an MRI technique based on the motion of water molecules in brain tissues. It quantifies the random water diffusion in cerebral gray and white matter tracts. The interpretation of diffusion tractography of water infers the tissue architecture continuity of the fiber bundles in brain from voxel to voxel [10], [11]. For diagnostic tasks, Mean Diffusivity (MD) and Fractional Anisotropy (FA) are the main density maps derived from DTI data. MD describes the magnitude of self-diffusion of water regardless of direction, while FA is used to characterize the degree of anisotropy of the diffusion [11]. In the AD patients studies, the computed DTI maps have shown an abnormal increase of MD values and decrease of FA values both in gray and white matter, and in some regions including Hippocampus. Quantifying the neuro-degeneration in the Hippocampus area leads to measure the pathological atrophy changes and discriminate AD subjects from those with Mild Cognitive Impairment (MCI) or those in Normal Control (NC) [12].
Deep learning approaches, and specifically Convolutional Neural Networks (CNN) have recently emerged as a powerful analysis approach for Computer-Aided Diagnosis (CAD) systems. Various CNN-based frameworks have been used in medical image analysis for disease classification, segmentation, detection and shape modeling problems [13]. Due to their remarkable performances, there exists a wide range of applications for AD classification using multi-modal imaging [14]. However, they require a large number of data samples to well train a network. If the training dataset is not sufficiently large, then the over-fitting phenomena occurs [15]. This happens because the depth of the dataset is not representative of the variability of brain structures, and consequently the classification results on train set are better while on the test set are not, whereas they should be the same when the over-fitting is absent. Specific data augmentation and regularization methods such as Dropout can solve the problem of insufficiency of samples [15], [16]. An alternative approach called “Transfer Learning” can battle the overfitting phenomena, which consists in reusing the weights of a trained model implemented for different application domain. This approach achieves good results compared to those trained only with an arbitrary initialization of network parameters (“from scratch”) [17]. Hence, numerous works use models pretrained on large publicly available datasets, such as LeNet [18], AlexNet [19], VGGNet [20], GoogleNet [21], and ResNet [22] which were built for various image classification tasks. For example, cross-domain transfer learning using the AlexNet architecture has been reported in various medical applications, resulting an improved performance [23], [24]. Nevertheless, they remain limited in case of considerably small datasets as it is the case in AD studies: merely few scans from both sMRI and DTI modalities are available for numerous cohorts in a public ADNI dataset [25] or in particular cohorts such as “Bordeaux-3City cohort” [26].
This paper is an extension of previous works [16], [27], [28] where we proposed a method that combines sMRI and DTI-MD imaging modalities focusing only on the hippocampal region. Moreover, we presented a fusion framework based on the concept of using multiple sources, including cross transfer learning approach. The method was much more promising, not only in improving the accuracy of classification, but also reducing the problem of overfitting. The originality of the approach allows to measure improvements of various techniques on small datasets. Moreover, the dataset is even smaller since we use just few 2D slices from a reduced region of the brain - the hippocampus. These double constraints lead us to deal with this challenge by combining various techniques, cross-modality being the one in focus in this paper.
In the present work we propose an adapted transfer learning scheme based on two processes: first, we implement an inter-modal approach using naturally similar dataset (sMRI and DTI-MD). Second, we carry out the knowledge transfer between two different datasets with non medical data, and use a pretrained model which is very similar to ours. As result, we show that such a transfer learning between close domains, even with a limited number of samples in source domain and shallow network, is more efficient than a plain cross-domain learning when the domains are too different.
The remainder of this paper is organized as follows: In section 2, we review related work, next in section 3, we describe the data preprocessing and our proposed approach in details. Then in section 4, we present the experimental results, and finally we conclude our work and outline its perspectives.
2. Related work
An improved classification performance of famous CNN models such as AlexNet, VGGNet, GoogleNet, and ResNet with transfer learning has been reported in various applications in medical domain. There are some recent related works relevant to our methodologies using the 2D-based CNN classification instead of working with the 3D or 4D imaging. In the follow-up, we focus on the works which use these known networks and adapt them to the medical image classification, and on the application of transfer learning method as a solution for the limited volume of datasets.
2.1. Works based on popular CNN networks
In [29], [30], [31] the authors presented an adaptive pipeline approach for Alzheimer's Disease binary classification. They used the structural and functional magnetic resonance imaging (sMRI, fMRI) modalities from the ADNI dataset project. They have designed and adopted architectures based on the famous networks LeNet [18] and GoogleNet [21] and adjusted them to binary classification problem for medical imaging data. In the case of sMRI modality, they converted the images from 3D data to a stack of 2D slices and resized them to pixels to match the input to LeNet network. The average accuracy for 2-Way (AD/NC) classification was 96.85%. In the second setup, they used the adopted GoogleNet model for binary classification, and the highest overall accuracy rate achieved was 98.84%. With the same concept of reusing an efficient architecture, authors in [32] used a modified version of VGGNet [20] network called DemNet that takes 2D images as input. It was composed of 13 convolutional layers and of three fully connected layers with dropout after each pooling layer, to reduce the over-fitting. The neural network took as an input a 2D slice from MRI data with resolution for both 2-way and 3-way classification problems. The authors selected 20 slices for each brain, classified each of them and measured the accuracy. The results showed that the first and the last two slices (111, 129, and 130) had significantly lower accuracy than the average accuracy per slice. They have achieved an overall accuracy of 98.33% for AD/NC classification. In [33], the authors used two networks, a baseline single-layer CNN and a pretrained ResNet network, they used a single 2D axial slice per subject (median slice from the 3D volume) as an input, the baseline CNN network was composed of only one convolutional layer and two FC layers. They studied the impact of transfer learning from RestNet trained on ImageNet, and the data augmentation in a real time, at training phase, they conclude that the ResNet architecture successfully fits to the MRI domain, and pretraining with data augmentation improves the prediction. In a recent study, Lee et al. [34] used a modified AlexNet network which is known as a high-performance pretrained model. The architecture is composed of five layers for convolution computation and a last FC layer with two outputs for binary classification AD/NC, or three outputs for 3-way classification (AD/MCI/NC). Due to the presence of some noisy in the dataset, they proposed a data permutation scheme with outlier rejection, and slice selection methods by removing pixels to eliminate interfering data. All 2D slices (obtained by permutation from axial, sagittal, and coronal planes) were used for training the network, and finally the network was fine-tuned using OASIS and ADNI datasets. They achieved 98.74%, and 95.35% accuracy in AD/NC classification task, respectively on the OASIS and ADNI datasets. For 3-way classification their method achieved 98.06% on ADNI 3T dataset.
2.2. Works based on a transfer learning approach
Overall, the more the architecture is deep the more it needs huge data, and consequently a considerable time for training. The crucial issue here is that, in general, data in medical area are not sufficiently available. For this reason, numerous research works have used transfer learning approach, whether based on popular networks or on novel methods to address the lack of data.
In [35] authors used AlexNet architecture pretrained on a general purpose large-scale ImageNet dataset to fine-tune last layers in the model on target sMRI and PET modalities. In the conclusion of their work, the authors state that as neuroimaging data differs significantly from the source domain data, such a transfer method is not optimal. Indeed, the accuracy values achieved for classification of AD/NC on sMRI modality are rather low (around 66%) and even worse when AD/MCI/NC classification problem is addressed. Another study [36] employs the transfer learning on the same kind of images, such as brain scans from the same modality (sMRI) but with the source database different from target data to deal with the limited target data to recognize MCI on MRI images. Here two different datasets OASIS2 and LIDC3 have been used for the pretraining stage. They achieved best performance with accuracy of 90.6% for MCI/NC. [37] integrates a method called Multi-Domain Transfer Feature Selection (MDTFS) to select discriminant features for classification of AD/NC. In their case, an auxiliary domain corresponds to classification problem on the same data but for different target classes. When classifying AD/NC they consider s-MCI/c-MCI and MCI/NC. Their experiments have been conducted on ADNI-1 sMRI and classification accuracies achieved were of 95.2% and 82.1% for AD/NC, and MCI/NC respectively. The DTI image maps are often seen as a good modality for the detection of Alzheimer's disease. Thus the authors in [38] have compared the NC, AD and MC using MD and FA maps. Their results showed that MD was a better indicator of brain atrophy than FA. In a recent work, Ahsan et al. [39] proposed multiple deep 2D neural networks for binary AD/NC classification. They introduced two architectures that use the transfer learning approach based on the InceptionV3 and Xcepetion models whose weights are pretrained on Imagenet LSVRC. In addition, a custom CNN network is built with the help of separable convolutional layers. They used 96 central 2D-slices from each subject's brain by ignoring the first and the last 40 outer slices. They used three datasets with different settings from the OASIS project, which are composed of 416 T1-weighted MRI scans. The two datasets are respectively (i) a balanced with 180 and (ii) unbalanced sets with 114 subjects. The third dataset is the one used in the work of [40]. The authors used different configurations of fold cross-validation over the three datasets for the experiments. They achieved an average accuracy of 64% on the first dataset, 82.79% on the second dataset, and 99.45% on the third dataset for AD/NC classification. The latter is doubtful as they used the dataset from [40], and it was mentioned that there could be a problem of leakage in this dataset [41]. They concluded that the transfer learning approaches outperform non-transfer learning-based approaches. This demonstrates the effectiveness of these approaches for the binary AD classification task.
Contrarily to all these approaches we propose a transfer learning scheme from one modality to another, on the same dataset. Indeed the sMRI modality shows good discrimination performance for AD diagnosis in brain atrophy analysis, it is our source modality. The supplementary modality is of the same nature, it is the DTI-MD modality which represent our target domain. Otherwise, in our previous work [28] we have shown that multimodal approach increases performances, hence it is interesting to explore if the fusion framework can be more efficient with a transfer learning. We remain using a shallow CNN-based architecture with only a small number of convolutional/pooling layers since the input region definition is rather low (28×28×28).
The contributions of the paper are as follows:
-
•
we transfer knowledge between sMRI and DTI modalities using a shallow architecture specifically designed for our “2-D+ε” approach.
-
•
we use a similar architecture, LeNet trained on a large set (60K) of images from MNIST4 which has (28×28) resolution as input, i.e. the same size as of our Hippocampal region-of-interest, and then fine-tune this model on ADNI dataset.
Hence in both cases we perform the “cross” transfer, therefore in the first case, it is a cross-modality transfer. The modalities are similar as the target pathology is expressed by the same image deformations yet in the opposite luminance. In the second case, it is a cross-domain transfer. The domains are different; character images (MNIST) have nothing to do with MRI scans except the fact that they are not colored. In the next section we present our approaches.
3. Methodology and approach
3.1. Acquisition method and data selection
We work with two brain imaging modalities: sMRI and DTI. We briefly describe these modalities, and we also present our selected ADNI dataset that we use in the preparation of this work.
3.1.1. Structural MRI and DTI modalities
For a long time, the structural MRI remains a popular technique for examining the anatomy and the pathology of the brain, it is a widely used imaging technique in research as well as in clinical practice. This modality provides information describing the shape, size, enhancement patterns and integrity of gray and white matter. In AD diagnosis, High-resolution T1-weighted sequences are used to distinct the anatomical boundaries and to detect structural changes in the brain [5]. Diffusion Tensor Imaging (DTI) is another modality used in AD studies, it is a recent imaging technique that is able to track and quantify water diffusion along fiber bundles, to detect and describe the anisotropy on surrounding tissue micro-structure [42]. Three eigenvalues (, and ) and eigenvectors are calculated from water's molecular motion tensor in a three-dimensional space to represent the main diffusion directions [42]. Fractional anisotropy (FA) and mean diffusivity (MD) are the two most common measures (scalar maps) derived from the diffusion tensor imaging. In case of the brain degeneration related to AD, the cerebro-spinal fluid fills-in the cavities and these effects are perceived both in FA and MD maps as the motion of water molecule becomes chaotic.
-
•Mean diffusivity: Mean diffusivity is an inverse measure of membrane density. It represents the average magnitude of molecular displacement by diffusion, as it informs on the microstructure of (WM) being sensitive to cell density, axon size, and quantities of water. MD is the average of the three eigenvalues . A higher MD value reflects more isotropy of the tissue.
(1) -
•Fractional anisotropy: Fractional anisotropy is a measure of the degree of diffusion anisotropy. It reflects the directions of molecular motion in a certain voxel. FA is calculated from the standard formula:
(2)
Where is the mean diffusivity (MD). The values of FA vary between 0, which means the voxel space is totally isotropic, and 1, which means infinite anisotropic diffusion. In CSF, the value of FA is zero due to the equality of the diffusion in all directions.
3.1.2. Brain imaging data: ADNI dataset
Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD).
Since we work with multimodal imaging, we consider two subsets of the whole data from ADNI. The first one is the data that were selected from the ADNI-1 screening baseline with only anatomical MRI T1-weighted sequences, in this set all subjects underwent whole-brain MRI scanning on 1.5 Tesla at 14 acquisition sites. It is the same dataset as used in [16]. With the same demographic information for each of the diagnosis groups (NC, AD and MCI), the data sample consists of 815 structural MRIs including 188 Alzheimer's Disease (AD) patients, 228 cognitively normal (NC) and 399 subjects with Mild Cognitive Impairment (MCI). The second subset includes images of subjects screened with both structural MRI and DTI modalities. It is a union of data from the ADNI-2&Go, and ADNI-3. The Table 1 presents demographic characteristics of subjects, including age, gender, and the Mini Mental State Examination (MMSE) score. The age of different groups ranges between 54 and 95 years old, and the proportions of male and female are close in AD/NC groups while the proportions of male are higher than female in MCI groups. We carried out a visual checking step of all sMRI images and DTI-MD maps to ensure the data quality, and exclude scans with excessive motion and/or artifacts. The Mini-Mental State Examination (MMSE) was used to provide a global measure of cognitive status [43].
Table 1.
Demographic description of the ADNI dataset group. Values are reported as mean and ± standard deviation (* Subjects with both modalities).
| Classes | # Subjects | Age [range] / μ(θ) | Gender (#F/ #M) | MMSE [range] / μ(θ) | |
|---|---|---|---|---|---|
| ADNI-1 | AD | 188 | [55.18, 90.99] / 75.37 ± 7.52 | 99/89 | 23.3 ± 2.03 |
| MCI | 399 | [54.63, 89.38] / 74.89 ± 7.30 | 256/143 | 27.0 ± 1.78 | |
| NC | 228 | [60.02, 89.74] / 75.98 ± 5.02 | 118/110 | 29.1 ± 1.00 | |
| ADNI-2/Go | AD | *48 | [55.73, 90.87] / 75.60 ± 8.63 | 28/20 | 23.0 ± 2.42 |
| MCI | *108 | [55.33, 93.62] / 74.40 ± 7.47 | 66/42 | 27.4 ± 1.99 | |
| NC | *58 | [59.91, 93.25] / 74.91 ± 5.90 | 28/30 | 28.9 ± 1.18 | |
| ADNI-3 | AD | *16 | [55.26, 86.10] / 74.63 ± 9.92 | 4/12 | - |
| MCI | *165 | [55.88, 95.93] / 75.01 ± 7.91 | 71/94 | - | |
| NC | *341 | [55.79, 95.39] / 73.52 ± 7.82 | 209/132 | - |
3.2. Image preprocessing
Different imaging modalities of the same subject have to refer to the same physical structures in the brain. For this we need to align and normalize them, but an important preliminary step is noise removal which has not been fulfilled on all subsets of ADNI data we use.
3.2.1. Noise correction
Depending on the equipment used in the data acquisition, the multimodal imaging data are recorded as raw, unprocessed, unthresholded, and noisy. Resulting images usually have artifacts caused by the magnetic susceptibility in biological tissues. According to the ADNI project, in the ADNI-3 phase two main preprocessing steps are to be completed for each subject, the eddy current and N4 Bias Field correction, while in ADNI-GO and ADNI-2, this correction has been already performed. We shortly describe these steps. The DTI scans were first corrected from the proprietary scanner formats, by using the eddy current (Foucault currents) correction tool of FSL (Version 5.0, FMRIB, Oxford, UK5). This correction consists in compensating non-linear susceptibility [44] and eddy-current distortions induced by head motion [45]. Then the mean of the non-diffusion-weighted (b0) volumes was used to create the DTI brain mask via the FSL “BET” utility [46]. Fitting of diffusion tensors to the data with “DTIfit” module of the Software Library FSL was the last step to generate MD maps [47].
Regarding MRI scans, bias field correction was performed to minimize the influence of the bias field signal obscuring gray/white matter boundaries [48]. Here N4ITK correction methodology has been used from the Advanced Normalization Tools (ANTs) [49], [50]. Note that in ADNI-3, and due to the modern MRI scanners, there is no need to provide MPRAGE / IRFSPGR prepossessing.6
3.2.2. Alignment and normalization
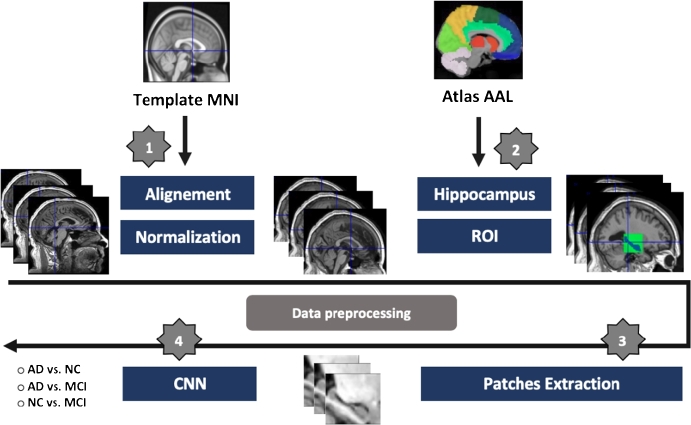
We work on AD biomarker, i.e. the hippocampal region. To select it in the brain scans, we need to superimpose on the anatomical atlas AAL [51]. Thus we need to align sMRI modality on the common template MNI [52] constructed at Montreal Neurological Institute (MNI) which corresponds to AAL. The MNI template is built by averaging 152 scans of normal subjects. Thus each T1-weighted anatomical (sMRI) scan was spatially aligned with MNI as illustrated in Fig. 1 (step 1) [16]. The alignment with MNI template is realized with a 3D affine transformation [53].
Figure 1.
Schematic diagram of dataset preprocessing: 1) registration of all MRI scans on MNI space, followed with intensity normalization. 2) ROI selection process using the Atlas AAL for both hippocampal regions. 3) 2D-slice extraction from selected 3D-volume. 4) feeding the CNN networks.
The process is based on the search for 12 affine deformation parameters ( to ) of the matrix M which performs the homogeneous transformation. The goal is to estimate these parameters for a given image (f) to fit a template image (g), including translation, rotation, scaling and shearing deformations [54]. In order to guide finding appropriate parameters, the algorithm relies on using objective function to minimize transformation error, e.g. (MSE) mean square error criterion.
The matrix M is decomposed as product of four matrices, translation, rotation, scaling and shearing.
| (3) |
| (4) |
We have used the sum of squared differences (SSD) as objective function to minimize the error between the subject (f) and the template images (g) which is the (MNI). The optimization method is the Gauss-Newton algorithm [55]. An additional parameter w is added to the function to correct the difference scale that can be produced in images. The function to minimize is then:
| (5) |
where is the position in the image (f), and is the target in (g), we refer this mapping equation as , where M is the mapping matrix.
Finally, as the scanners provide images in different scale of the intensity, we performed intensity normalization along the whole dataset. We used the algorithm developed by “Nyul and Udupam” [56], which is based on the use of the image histogram. In order to have similar intensities for similar structures, the method trains a standard histogram through the whole dataset, and makes deformation for the histogram of each image to obtain a correspondence of intensities of this image with the standard histogram. The process was done using the software SPM8 (Wellcome Trust Centre for Neuroimaging at UCL, London, UK)7 to fulfill the registration and the normalization [57].
3.2.3. Co-registration for DTI-MD
We aim to extract patches related to the same ROI as in sMRI from the DTI-MD map. Therefore, both modalities have to be co-registered [58]. This means sMRI and DTI-MD images for each subject must be comparable. The co-registration between sMRI and MD consists in estimating transformation parameters using mutual information criterion in some specific areas to fit the standard space (MNI). Thus we affinely co-register MD image to the coordinate system of its corresponding sMRI scan. The co-registration algorithm uses brightness of voxels. In order to avoid distortions which may be induced by bright skull voxels, skull stripping task has to be performed to pull out only the brain from the sMRI modality (see Fig. 2) [59]. The process of skull removal was performed with SPM8 software. The brain scans were segmented into gray matter (GM), white matter (WM) and Cerebro-Spinal Fluid (CSF). Merging these three maps we can subtract skull region from original sMRI scans. Thus, for each patient there is an sMRI and MD-DTI aligned images of the same definition of and each voxel has a spatial resolution of .
Figure 2.
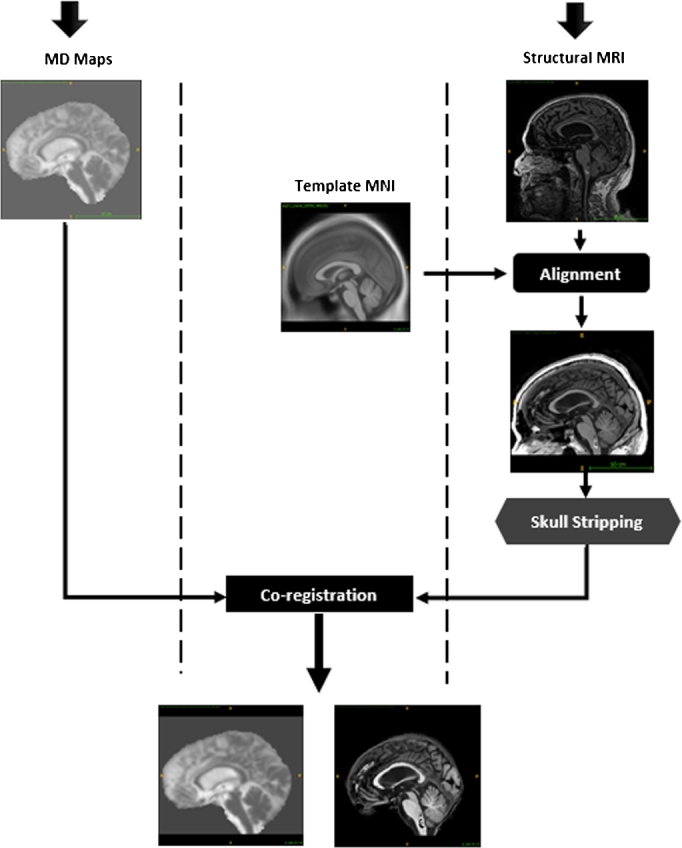
Illustration of the co-registration process includes spatial normalization and skull stripping.
3.2.4. Selection of the region of interest (ROI)
The next step is the selection of the hippocampal region which is convinced to be the first region in the brain affected by AD [6], [7]. So, after alignment of sMRI modality on MNI template and co-registration of MD-DTI to same space, the ROI can be selected on the automated anatomical labeling Brain atlas (AAL) [51]. By selecting voxels labeled as Hippocampal region in AAL and computing their 3D bounding boxes we get a sub-volume of the whole 3D scan which encircles Hippocampus in both modalities sMRI and DTI as presented in Fig. 1 (step 2). Hippocampus is a symmetrical anatomical structure in the brain consisting of two regions. To get only one ROI for a given patient we calculate the mean of the two regions when flipping the left hippocampal region on the right . Note that the resolution of normalized sMRI and MD volumes is quite low (121×145×121, see above), thus the hippocampal ROI occupies a small amount of voxels (28×28×28). Finally, we extract 2D-slice of 28 × 28 resolution from the computed 3D-volume to feed the CNN classifier (Fig. 1 step 3 & 4).
3.3. Domain-specific data augmentation strategy
Basically, deep networks need a sufficient dataset for training the model by optimizing network parameters, such as synaptic weights. However, we designed a specific domain data augmentation (DA) approach to increase the number of images introduced in [16], [60]. The method consists in applying a number of geometric transformations to the original image including random translation and Gaussian blur. For the Gaussian blur filter (Formula (6)), the scale sigma-value σ of the kernel varied randomly from 0.1 to 1.2 with a step 0.1. Then for each sigma-value, random translation for each dimension was performed with voxel step size in the interval from -2 to 2 in each dimension.
| (6) |
The final hippocampal region is then computed as:
| (7) |
Where is the flipping operator, and δx, δy and δz are the shifts between left and right regions, and are left and right hippocampal regions respectively.
3.4. Convolutional Neural Network approach
3.4.1. The 2-D+ε network architecture
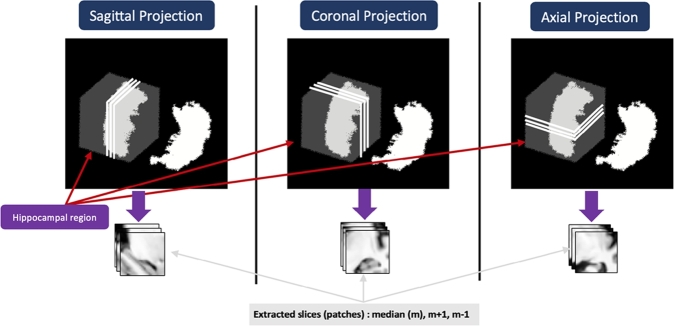
In our previous work we have proposed the so-called “2-D+ε” approach for ROI classification [16]. We use a 2D convolution in a CNN architecture feeding it with three neighboring slices for each projection Sagittal, Axial, and Coronal. The median slice of Hippocampal ROI and its two neighbors have been selected (see Fig. 3). Then the classification results of all three projections were fused. The choice of the depth of the CNN architecture depends on the resolution of input data. The CNN we proposed in [16] is relatively shallow. Indeed, due to the low resolution (28×28) of the ROI in each projection, the optimal architecture consisted of two convolutional layers followed by a max pooling layer for each one, and a fully connected layer. We get three networks associated with each modality, for the Sagittal, Axial and Coronal projections. Different tested fusion schemes resulted in application of the (best) late fusion with majority vote fusion operator [28] on the six binary classification tasks AD/NC, NC/MCI, and MCI/AD on three projections. We use the same fusion scheme in the present work.
Figure 3.
Illustration of the 2-D+ε Approach from each projection.
3.4.2. Transfer learning for brain image
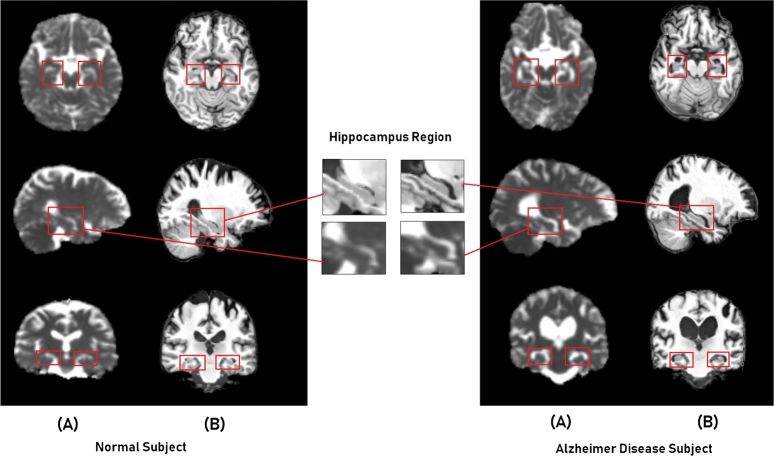
Transfer learning [17] is a popular way of dealing with limited volumes of training datasets. Actually, the CNN models can be either learned from scratch with random initialization of parameters or with the fine-tuning approach from pretrained models. From the domain knowledge of medical research, we retain that the shrinkage of hippocampal ROI which accompanies the development of AD is observable on both modalities sMRI and MD. Fig. 4 illustrates this phenomenon, it presents two examples of subjects: for the left a normal control (NC) subject, and the right an (AD) subject, with both modalities; the (A) is the MD map, and (B) is sMRI scan. It shows the hippocampal region from different projection views. From the top to the bottom, also the Axial, Sagittal, and Coronal planes respectively.
Figure 4.
Example of the hippocampal region with different projections for two Subjects: (A) - MD and (B) - sMRI.
As we can observe from the illustrative figure, the atrophy of the hippocampus can be recognized from both modalities by conserving the same shape, but in inverted representation. This means the signal spawned from CSF flows surrounding the Hippocampus portion can be interpreted by a dark area in sMRI scans, while it is bright in MD maps. For this reason, we could adopt a transfer learning strategy between these two types of data, from designing trained models in the source domain of sMRI towards the target domain MD called cross-modal transfer learning.
In the framework of learning CNN parameters, we can formally define the transfer learning strategy from the source modality (sMRI) to target MD as follows:
| (8) |
Where is the best trained model on the large sMRI dataset, we initialize the training with the parameters of , and fine-tune all or some layers of the used architecture. F is the optimization scheme.
In this work, we fine-tune only FC layer of our proposed architecture. We use Stochastic Gradient Descent with Nesterov momentum as in [19], and as a cost function 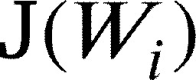 to minimize we used cross-entropy loss as in [16]. The weights update formula are defined as follows:
to minimize we used cross-entropy loss as in [16]. The weights update formula are defined as follows:
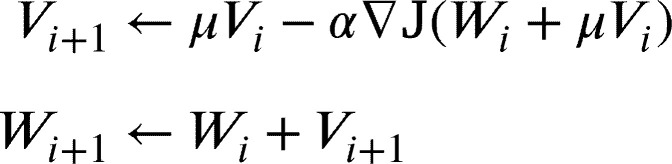 |
(9) |
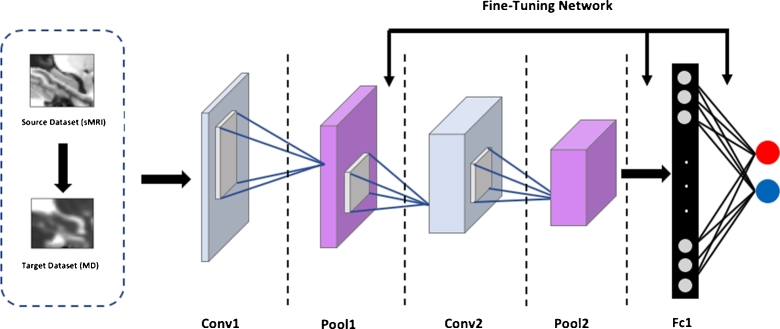
where are the parameters of each layer at iteration i, α is the learning rate, μ is the momentum and is the velocity. The transfer of the parameters in our CNN architecture is illustrated in Fig. 5. The arrows depict initialization of optimization process for each convolutional and fully connected layer.
Figure 5.
The scheme of Transfer Learning for parameters optimization from sMRI to MD-DTI modality. In the figure, an example of the proposed architecture for 2-way classification.
3.4.3. Adapted cross transfer learning schemes
It is believed that transfer learning improves classification performance, especially when the source and the target domains are awfully close. In order to validate our proposed scheme of intra-domain, we compare the classification efficiency across two different domains by using both known pretrained model and dataset. We have selected the LeNet network owing to similarity at the design level [18]. It takes the same input definition 28×28 as ours, and almost the same depth of layer except the fully connected layers. In this view, we take this model which it is already pretrained on MNIST dataset, and apply it to our brain image data DTI-MD and sMRI. Nevertheless, the model has been modified in FC layers and adapted to 2-way classification problem instead of ten. We freeze the two first convolutional layers which are already captured the universal features, and then we fine-tune it on the Alzheimer's disease dataset by optimizing weights only in the two FC layers of the model.
We evaluate the approach through two mechanisms as follows:
One-level transfer scheme: In this first approach, we realize the transfer using our LeNet-like model for both modalities from MNIST to sMRI and from MNIST to DTI-MD followed by our fusion scheme (Majority vote).
Two-level transfer scheme: In this second approach, we multiply the transfers; it is applied as MNIST-DTI-MD across sMRI. We first use the LeNet-like model trained on MNIST dataset. This model is used as the basis for training of sMRI classification model. Next from sMRI model we transfer to the DTI-MD images of the same domain. After that, we built our fusion framework from this model combined with the model we obtained from the cross-modal transfer (sMRI to DTI).
4. Experiments and results
4.1. Learning setup parameters and metrics
Data augmentation parameters: In order to sufficiently increase our dataset size, we applied the data augmentation strategy as presented in (see Section 3.3). Thus, we have set an augmentation factor F upon which the calculations are based. Indeed, we have proposed an approach to increase the data in an equitable manner. The method consists in setting the factor (a multiplication coefficient) for the most represented class, and by multiplying this factor to the cardinal of this class we obtain large enough class (this one). The next step of the approach is increasing all other classes to reach the same size of the first one. In this way we obtain a balanced dataset.
Hence, we defined the factor F to 100 for the both datasets: The subset “1” and subset “2” as introduced in Section 3.1.2. However, the factor was set for MCI class in subset “1” since it is the most represented class, in the same way, NC class was selected for subset “2” as well. The max shift was set to 2 slices (note that two slices of sagittal axis for example represent about 7.4% of the Hippocampus 3D Bounding Box) and the maximum scale parameter of smoothing Gaussian Blur was set to 1.2 (See Algorithm 1). Indeed, the original signal on both modalities is blurred and a stronger blurring would destroy the structure of the ROI. The parameters were generated randomly and selected to avoid similar augmentation for the same brain scan. Table 2 describes the split of samples before and after the augmentation process. Data are divided into Training, Validation, and Test subsets.
Algorithm 1.
DA pseudo algorithm.
Table 2.
Number of subjects for each class, with its corresponding augmentation, (⁎ Both modalities).
| Before augmentation |
After augmentation |
||||||
|---|---|---|---|---|---|---|---|
| AD | MCI | NC | ADa | MCIa | NCa | ||
| Dataset 1 | Train | 146 | 482 | 446 | 48200 | 48200 | 48200 |
| Valid | 42 | 126 | 117 | 12600 | 12600 | 12600 | |
| Test | 64 | 64 | 64 | 640 | 640 | 640 | |
| 252 | 672 | 627 | 61440 | 61440 | 61440 | ||
| Dataset 2⁎ | Train | 31 | 198 | 299 | 29900 | 29900 | 29900 |
| Valid | 13 | 55 | 80 | 8000 | 8000 | 8000 | |
| Test | 20 | 20 | 20 | 200 | 200 | 200 | |
| 64 | 273 | 399 | 38100 | 38100 | 38100 | ||
Metrics: To evaluate single and fusion binary classification tasks, we considered the metrics widely used in medical statistics. We denote tp, tn, fp, and fn respectively True positives, True negatives, False positives, and False negatives. The metrics used are as follows:
| (10) |
| (11) |
| (12) |
Finally, balanced accuracy (BAcc) measure, which is the average of sensitivity and specificity is defined as:
| (13) |
Hardware configuration: The experiments were conducted on a GPU-based high-performance computing platform featuring an Intel(R) Xeon(R) CPU E5-2680 v2 @2.80GHz processor, 187 Gb of RAM, equipped with two Nvidia TESLA P-100 graphic cards with 16 GB dedicated memory. The computational time for one epoch at the training step with batch-size of 64 samples takes 2.03 seconds in average.
Optimization settings: To pick the best learning parameters, we have trained our basic 2-D+ε network on the sMRI dataset. The choice of appropriate hyper-parameters was achieved using various training setups. Thus we finally use the exponential learning rate decay policy, , where is the initial value of learning rate, and . In our case we set γ to 0.95, and = 0.0001, and we use the Gradient Descent with Nesterov Momentum method (See Formula (9)). The batch-size set to 64 as mentioned above. After several iterations, the stabilization of the training is observed around the 30th epoch. The network was implemented with “Caffe” Deep learning Framework [61].
4.2. 2-D+ε single and fusion architecture
We use the “2-D+ε” network (see Section 3.4.1) we proposed in our previous work [16], [28] on sMRI data, It was shown that further improvements can be achieved through the fusion approach in particular the majority vote. Likewise, in this section of this work we use only sMRI data but with a larger number of subjects compared to the previous work. In addition, the best fusion method the “Majority Vote” as used in [28] is adopted here. We base our classification on two different models: single network for each projection (Axial, Coronal, and Sagittal), and a late fusion which is designed to improve and enhance classification performances.
We have designed two architectures to perform the classification: (i) 3-way classification (AD/MCI/NC) and (ii) 2-way classification (AD/MCI, AD/NC, and MCI/NC) as the most works in the literature. We built a 3-way classification baseline model, and accuracies of 60.23%, 58.71%, 56.84%, and 66.49% for Sagittal, Coronal, Axial, and fusion, respectively, were obtained. We found that the 3-way model performs somewhat faintly. However, we considered only the 2-way classification in our work since the application domain requires only to test positive or negative for the AD diagnosis. Besides, most of the related works provide only binary classification results with which we can make the comparison. Hence, we performed our method as presented above, and Table 3 presents an overview of the 2-Way classification results.
Table 3.
Classification results for each single projection and fusion by majority vote on sMRI dataset.
| Tasks | Projection | Acc (%) | Sen (%) | Spe (%) | BAcc (%) |
|---|---|---|---|---|---|
| AD vs. NC | Sagittal | 82.92% | 85.72% | 79.84% | 82.78% |
| Coronal | 81.04% | 83.20% | 78.63% | 80.41% | |
| Axial | 79.81% | 81.31% | 77.65% | 79.48% | |
| fusion ⁎ | 91.86% | 93,90% | 89.88% | 91.89% | |
| AD vs. MCI | Sagittal | 66.73% | 68.52% | 63.91% | 66.21% |
| Coronal | 67.61% | 71.25% | 61.88% | 66.56% | |
| Axial | 65.55% | 66.60% | 61.57% | 64.08% | |
| fusion ⁎ | 69.95% | 73.41% | 68.22% | 70.81% | |
| MCI vs. NC | Sagittal | 65.51% | 61.64% | 69.48% | 65.56% |
| Coronal | 66.45% | 60.27% | 65.11% | 62.69% | |
| Axial | 63.89% | 59.15% | 64.57% | 61.86% | |
| fusion ⁎ | 68.52% | 65.59% | 70.15% | 67.87% |
On average, the single network on the sagittal projection shows better results than other projections, but the fusion method with majority vote achieves the best results for each classification tasks in terms of accuracy. For example, for the AD/NC classification we obtain 82.92% of accuracy for the single sagittal network, while with the fusion we get 91.86%. For the classification tasks involving MCI class (e.g., AD/MCI, and MCI/NC), we can notice that the accuracy is lower than AD/NC, we have 69.65% for AD/MCI, and 68.52% for MCI/NC. This class is a special class, as it includes two subclasses: The early MCI (e-MCI), and the late MCI (l-MCI). We completely grasp that (l-MCI) have more similarity of the atrophy with AD in our ROI, making it difficult to distinguish between subjects in MCI and AD classes. The same conclusion can be derived from the MCI/NC classification.
4.3. Evaluation of transfer learning
In order to evaluate the efficiency of our method, different adaptive transfer learning schemes were adopted, in this section we provide experimental results on the two proposed approaches: the cross-modal and cross-domain.
4.3.1. Transfer learning from sMRI to DTI-MD with the 2-D+ε approach
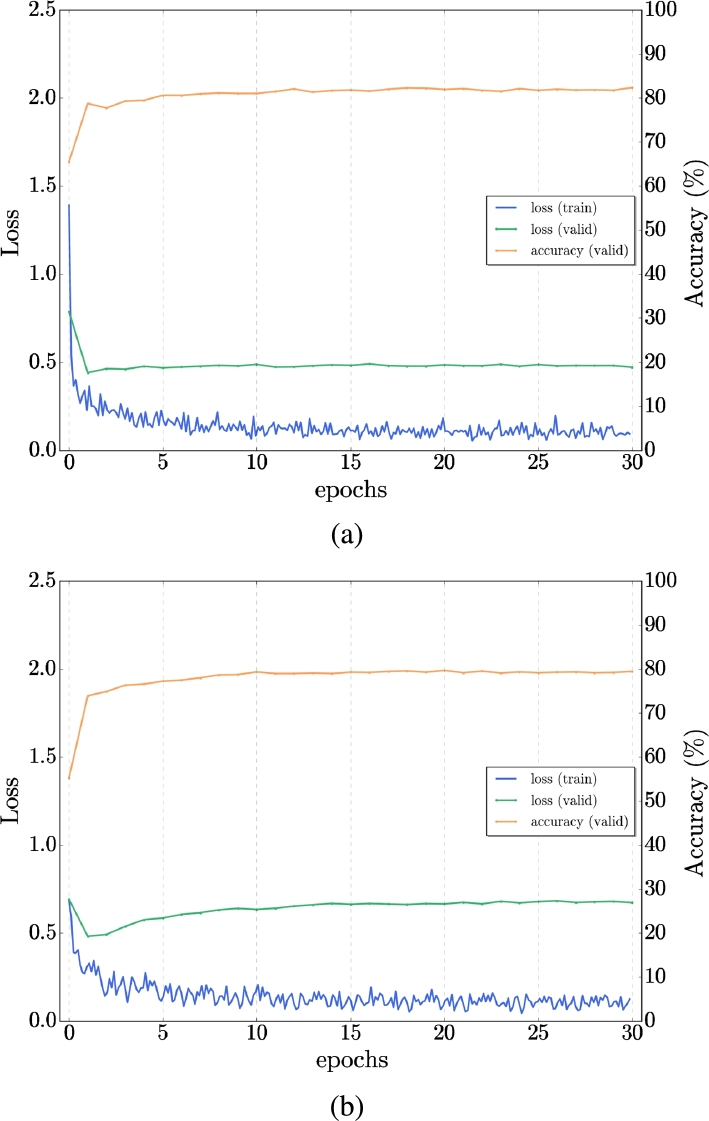
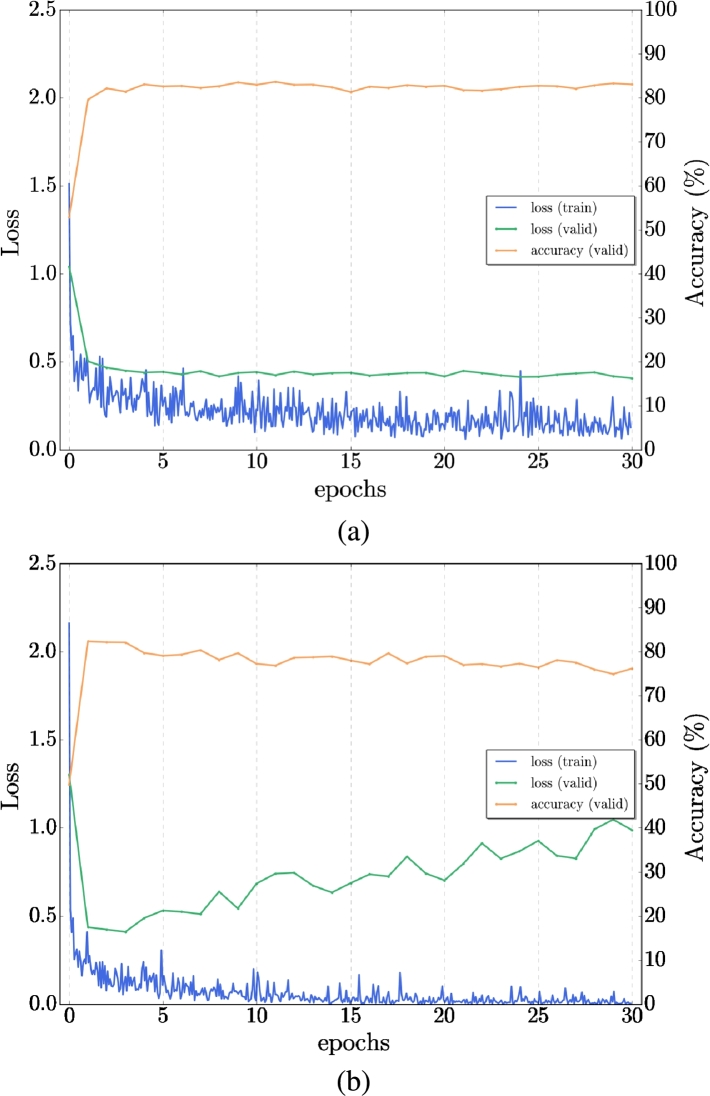
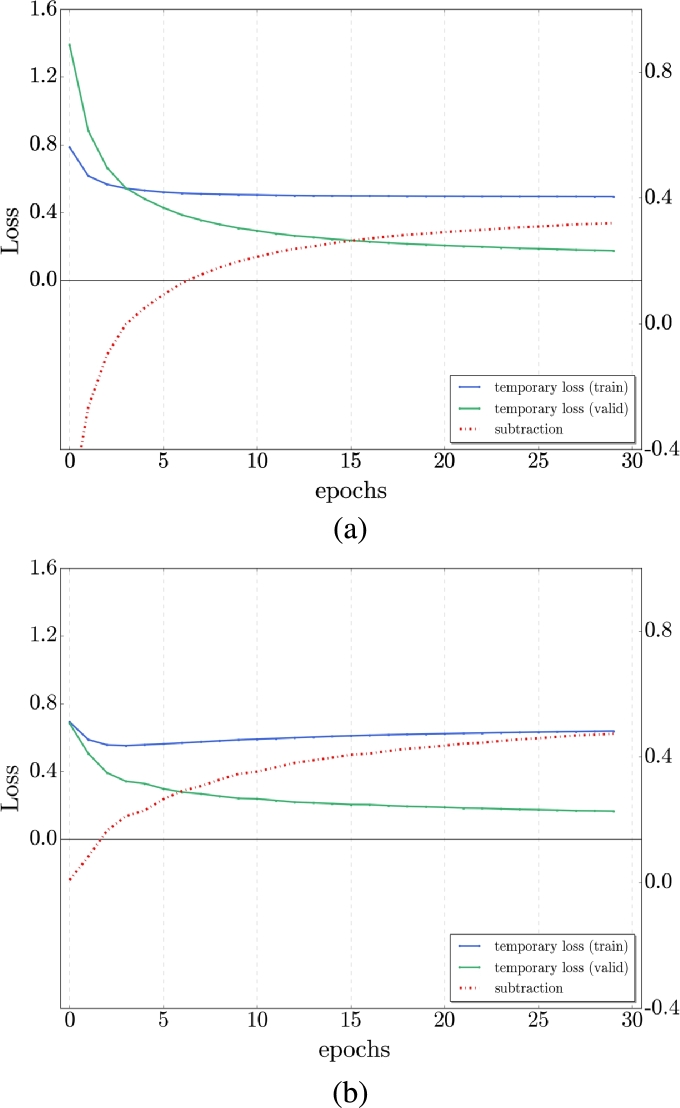
With the similarity between the structural MRI and DTI-MD, we proposed a cross-modal transfer learning from sMRI dataset as a source to the DTI-MD dataset, which is considered the target dataset. The model was first trained on the sMRI dataset and then fine-tuned with the DTI-MD dataset. Obviously, with the experiments, the cross-modal method yields slightly better results than the training from scratch (by random initialization of network parameters). We can see the difference of the behavior in training (loss) and validation (loss and accuracy) in Figs. 6, 7 for AD/NC and AD/MCI respectively. We get improved accuracy at the final 30th epoch with transfer learning, and the loss is lower on both sets along training epochs. Fig. 8 illustrates that with the transfer from sMRI to DTI-MD the overfitting is slightly reduced (a) compared to training from scratch (b). Table 4 presents the final results of cross-modal transfer learning for each projection and with the late fusion by majority vote. Compared with the results from Table 3, we have clearly augmentation of all metrics up to 5% for the most challenging classes AD/MCI and MCI/NC.
Figure 6.
Example of Transfer learning for single network - comparison of AD/NC: a) Transfer from sMRI to MD-DTI, b) Training from scratch on MD-DTI Dataset.
Figure 7.
Example of Transfer learning - comparison of AD/MCI: a) Transfer from sMRI to MD-DTI, b) Training from scratch on MD-DTI Dataset.
Figure 8.
Temporal loss curves comparison for AD/NC classification: a) From sMRI to MD-DTI transfer learning with reduced over-fitting - b) Training from scratch with little over-fitting.
Table 4.
Binary classification results with Transfer Learning from sMRI to MD-DTI data and fusion (* both modalities).
| Tasks | Modalities | Projection | Acc (%) | Sen (%) | Spe (%) | BAcc (%) |
|---|---|---|---|---|---|---|
| AD vs. NC | MD | Sagittal | 84.93% | 86.07% | 81.23% | 83.65% |
| Coronal | 80.62% | 81.15% | 79.75% | 80.45% | ||
| Axial | 79.50% | 81.91% | 78.04% | 79.97% | ||
| Fusion (*) | 92.11% | 94.53% | 90.02% | 92.27% | ||
| AD vs. MCI | MD | Sagittal | 65.12% | 72.25% | 68.44% | 70.34% |
| Coronal | 72.87% | 76.58% | 71.93% | 74.25% | ||
| Axial | 64.79% | 69.14% | 66.28% | 67.71% | ||
| Fusion (*) | 74.41% | 80.13% | 76.02% | 78.07% | ||
| MCI vs. NC | MD | Sagittal | 65.59% | 66.48% | 69.32% | 67.90% |
| Coronal | 69.14% | 67.97% | 70.82% | 69.39% | ||
| Axial | 64.98% | 67.71% | 71.06% | 69.38% | ||
| Fusion (*) | 73.91% | 76.79% | 79.63% | 78.21% |
4.3.2. From MNIST knowledge to sMRT and DTI cross-domain learning
In this part of the experiment, we apply our second proposed method for cross-domain transfer learning as presented. We construct the LeNet-like model, and perform the experiences as follows:
One-level transfer scheme: The transfer is realized for both modalities from MNIST to sMRI and from MNIST to DTI-MD followed by our fusion scheme. Table 5 presents an overview of results for both experiments and also results for the fusion. Analyzing the table, we obtain accuracies around 3% in average lower than the previous results for each classification task. For AD/NC as example, we passed from 82.92% to 80.02% for sMRI, and from 84.93% to 81.85% for DTI-MD on the sagittal projection. For the other classification tasks, the situation is pretty much the same. The results are lower than those for cross-modal transfer in the same domain, see Table 4.
Table 5.
Classification results with One-level scheme Transfer Learning: From MNIST to SMRI & From MNIST to DTI-MD data.
| Tasks | Modalities | Projection | Acc (%) | Sen (%) | Spe (%) | BAcc (%) |
|---|---|---|---|---|---|---|
| AD vs. NC | SMRI | Sagittal | 80.02% | 81.95% | 79.26% | 80.60% |
| Coronal | 79.94% | 80.59% | 78.18% | 79.38% | ||
| Axial | 79.11% | 81.05% | 79.42% | 80.23% | ||
| MD | Sagittal | 81.85% | 83.24% | 79.49% | 81.36% | |
| Coronal | 79.22% | 83.01% | 78.56% | 80.78% | ||
| Axial | 78.69% | 82.44% | 79.71% | 81.07% | ||
| Fusion (*) | 86.83% | 90.94% | 87.14% | 89.04% | ||
| AD vs. MCI | SMRI | Sagittal | 65.32% | 66.81% | 64.52% | 65.66% |
| Coronal | 64.57% | 65.63% | 63.74% | 64.68% | ||
| Axial | 61.74% | 63.05% | 59.88% | 61.46% | ||
| MD | Sagittal | 64.95% | 70.19% | 66.45% | 68.32% | |
| Coronal | 68.60% | 72.51% | 67.96% | 70.23% | ||
| Axial | 62.36% | 68.24% | 62.47% | 65.35% | ||
| Fusion (*) | 71.45% | 78.66% | 73.16% | 75.91% | ||
| MCI vs. NC | SMRI | Sagittal | 64.75% | 62.35% | 66.72% | 64.53% |
| Coronal | 60.49% | 58.62% | 63.40% | 61.01% | ||
| Axial | 60.15% | 59.14% | 62.63% | 60.88% | ||
| MD | Sagittal | 63.59% | 63.18% | 66.93% | 65.05% | |
| Coronal | 67.14% | 64.24% | 69.86% | 67.05% | ||
| Axial | 64.98% | 63.91% | 68.55% | 66.23% | ||
| Fusion (*) | 69.85% | 70.46% | 75.73% | 73.10% |
Two-level transfer scheme: In this setting we perform the experiments using the scheme as explained in 3.4.3. Table 6 presents the results. We can notice that the use of the Two-level transfer scheme, may clearly give better results which we will analyze in the following section.
Table 6.
Classification results with Two-level scheme Transfer Learning: From MNIST to DTI-MD crossed sMRI data.
| Tasks | Modalities | Projection | Acc (%) | Sen (%) | Spe (%) | BAcc (%) |
|---|---|---|---|---|---|---|
| AD vs. NC | MD | Sagittal | 85.14% | 87.95% | 84.14% | 86.04% |
| Coronal | 82.57% | 84.55% | 80.84% | 82.69% | ||
| Axial | 81.21% | 84.26% | 81.10% | 82.68% | ||
| Fusion (*) | 92.30% | 93.95% | 90.65% | 92.30% | ||
| AD vs. MCI | MD | Sagittal | 70.84% | 77.25% | 73.51% | 75.38% |
| Coronal | 76.53% | 78.39% | 76.64% | 77.51% | ||
| Axial | 69.21% | 73.08% | 68.52% | 70.8% | ||
| Fusion (*) | 79.16% | 82.72% | 78.36% | 80.54% | ||
| MCI vs. NC | MD | Sagittal | 71.09% | 70.15% | 74.95% | 72.55% |
| Coronal | 75.34% | 72.41% | 76.39% | 74.40% | ||
| Axial | 70.21% | 69.10% | 73.64% | 71.37% | ||
| Fusion (*) | 78.48% | 77.72% | 81.44% | 79.58% |
4.4. Discussion and comparison with literature review
Hence, we experienced three knowledge transfer types: cross-modal with LeNet-like designed architecture and cross-domain one-level and two-level transfer using LeNet Architecture. Comparing the results presented in Tables 4, 5, and 6, we can conclude the following. The cross-domain transfer, which is a very popular transfer learning scheme, performs the worst even on very distinct classes such as AD and NC. Hence definitely, the cross-modal transfer in the same domain (sMRI and DTI in our case) is a better solution. When multiplying transfers such as in the two-level cross-domain transfer scheme, we manage to get slightly better results for the most difficult classification tasks.
Indeed with the transfer from MNIST to sMRI and then DTI, we get a nearly 5% accuracy increase in the classification AD/MCI and MCI/NC. We note that in other metrics, such as Specificity, Sensitivity, and BAcc, the methods perform similarly. Thus, the two-level transfer increases the metrics by more than 5% for the most difficult classification tasks, which is an interesting result. Indeed, the transfer from a pre-trained model does not cost too much; hence the first step of it can be done from a different domain using publicly available trained models such as LeNet on MNIST. Although further transfer in the same domain is needed to improve the result.
Now we will compare our best results with methods from literature, see Table 7. We have to note that an exact comparison in the medical image domain is not possible, as different ADNI databases are used in each work. To illustrate this, we show the number of analyzed brain scans for AD, MCI, and NC subjects in the first three columns of this table. The authors of [62], [63], [64] use 3D convolutions. The authors of [31], [32], [33], [65] use the whole brain scans. Our method remains “light” in the sense that we focus only on one ROI, which is the biomarker of AD, the Hippocampal ROI. Afterward, we do not use the 3D volume entirely, but only a light version of it, such as three slices. Even with this lightweight method, we get quite decent results, namely in the separation of AD/NC.
Table 7.
Comparison of classification performances reported in the literature.
| Study | Subjects |
Classifier | Modality | Approach | Accuracy |
||||
|---|---|---|---|---|---|---|---|---|---|
| AD | MCI | NC | AD vs. NC | AD vs. MCI | MCI vs. NC | ||||
| Sarraf et al. [31] | 52 | - | 92 | CNN - LeNET-5 | sMRI | 2D slice-level | 97.88% | - | - |
| 211 | - | 91 | CNN - GoogleNet | sMRI | 2D slice-level | 98.74% | - | - | |
| Khvostikov et al. [64] | 53 | 228 | 250 | CNN | sMRI+DTI | 3D ROI-based | 93.3% | 86.7% | 73.3% |
| Gupta et al. [65] | 200 | 411 | 232 | CNN | sMRI | 2D slice-level | 93.80% | 86.30% | 83.30% |
| Billones et al. [32] | 53 | 228 | 250 | CNN - VGG-Net | sMRI | 2D slice-level | 98.33% | 93.89% | 91.67% |
| Lee et al. [34] | 192 | 398 | 229 | CNN - Alexnet | sMRI | 2D slice-level | 98.74% | - | - |
| 100 | - | 316 | CNN - Alexnet | sMRI | 2D slice-level | 95.35% | - | - | |
| Valliani et al. [33] | 188 | 243 | 229 | CNN - ResNet | sMRI | 2D slice-level | 81.3% | - | - |
| Cheng et al. [63] | 199 | - | 229 | CNN | sMRI | 3D subject-level | 83.88% | - | - |
| Glozman et al. [35] | 200 | 132 | 221 | CNN - AlexNet | sMRI | 2D slice-level | 66.51% | - | - |
| Hon et al. [40] | 100 | - | 100 | CNN - VGG-Net | sMRI | 2D slice-level | 92.30% | - | - |
| - | CNN - Inception V4 | sMRI | 2D slice-level | 96.25% | - | - | |||
| Payan et al. [62] | 755 | 755 | 755 | CNN | sMRI | 3D subject-level | 95.39% | 86.84% | 92.13% |
| Lian et al. [67] | 358 | - | 429 | H-FCN | sMRI | 3D patch-level | 90,00% | - | - |
| Proposed cross-modal transfer (1) | 252 | 672 | 627 | CNN | sMRI+DTI | 2D ROI-based | 92.11% | 74.41% | 73.91% |
| Cross-domain One-level transfer (2) | 64 | 273 | 399 | CNN - LeNet | sMRI+DTI | 2D ROI-based | 86.83% | 71.45% | 69.85% |
| Proposed Two-level transfer (3) | 64 | 273 | 399 | CNN - LeNet | sMRI+DTI | 2D ROI-based | 92.30% | 79.16% | 78.48% |
However, for the most challenging classifications MCI/NC and AD/MCI, even though we earn some accuracy points, the results remain slightly weaker compared to AD/NC. This leads to the investigation of other brain structures and regions or even implies the entire brain for this study. Indeed, as our models focus on the hippocampus atrophy for the discrimination task, working on the hippocampus's limbus can involve more advantages to improve performances, where it encompasses the outermost surface of the hippocampus, which seems to be the most affected by the passage of the MCI stage. Going back to our approach “2-D+ε”, we take only three slices where only a fraction of that surface, i.e., “the limbus” intersects, which could explain why MCI/AD and NC/MCI discrimination scores relatively low compared to a method that would be full 3D. Therefore, at the resolution at which we operate, the disease's characterization could be better determined at the hippocampus limbus level than with its whole internal structure [66].
Despite our classification results still need to be improved by introducing other regions of interest or additional information, as mentioned above, the proposed cross-modal transfer learning definitely yields increased performances. It can thus be re-used in combination with other methods of classification, as those using whole brain or full 3D information. Specifically, in such a field as medical image analysis and classification where large corpora of annotated data are not available, proposed transfer learning will help in circumventing the lack of training data. The cross-domain transfer learning method presents good results in applications on natural images. On the contrary, cross-domain transfer from natural images to medical image domain remains limited as our results show. This is due to the large difference in terms on content between natural and medical images. In this work, we have shown the efficiency of implementing a cross-modal transfer in medical diagnostic applications. We hope that this finding will be successfully used by the research community for medical image classification tasks.
5. Conclusion
In this paper, we have shown that intelligently initializing the network parameters, through transfer learning, allows to obtain better classification of AD stages by more than 5 points in some classification tasks (MCI/AD and NC/MCI). We compared various transfer learning schemes: cross-modal transfer learning using sMRI and DTI-MD brain images, cross-domain transfer learning from non-medical data to medical brain scans and a combination of both using a shallow LeNet network. Our approach remains light-weight in the sense that we used the “2-D+ε” scheme we previously developed on the hippocampal region, avoiding both 3D convolutions and full-brain usage. As an interpretation of our results, filters trained on a modality have similar geometrical characteristics that need a small adaptation when transferred to another modality. We think that this is due to the fact that underlying structures of the hippocampus present similar geometrical patterns, visual markers, on both modalities that characterize the progression of the disease. We think that proposed multi-modal transfer learning approach can be useful in other classification tasks on medical images.
Declarations
Author contribution statement
Karim Aderghal: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Karim Afdel, Gwénaëlle Catheline: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Jenny Benois-Pineau: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This work was supported by The Franco-Moroccan TOUBKAL Research Grant AlClass, Project Code N∘BK/16/23, and the LaBRI, University of Bordeaux/ CNRS / Bordeaux-INP.
Data availability statement
Data included in article/supplementary material/referenced in article.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer's Association; Alzheimer's Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (ww.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
References
- 1.A. Association 2018 Alzheimer's disease facts and figures. Alzheimer's Dement. 2018;14(3):367–429. [Google Scholar]
- 2.Lane C.A., Hardy J., Schott J.M. Alzheimer's disease. Eur. J. Neurol. 2017;25(1):59–70. doi: 10.1111/ene.13439. [DOI] [PubMed] [Google Scholar]
- 3.2016. https://www.alz.co.uk/research/WorldAlzheimerReport2016.pdf/ Alzheimer's Disease International (AZ) World Alzheimer Report 2016, Alzheimer's Disease International, London, UK.
- 4.Minati L., Edginton T., Grazia Bruzzone M., Giaccone G. Reviews: current concepts in Alzheimer's disease: a multidisciplinary review. Am. J. Alzheimer's Dis. Other Dement. 2009;24(2):95–121. doi: 10.1177/1533317508328602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Frisoni G.B., Fox N.C., Jack C.R., Jr., Scheltens P., Thompson P.M. The clinical use of structural MRI in Alzheimer disease. Nat. Rev. Neurol. 2010;6(2):67. doi: 10.1038/nrneurol.2009.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Deweer B., Lehericy S., Pillon B., Baulac M., Chiras J., Marsault C., Agid Y., Dubois B. Memory disorders in probable Alzheimer's disease: the role of hippocampal atrophy as shown with MRI. J. Neurol. Neurosurg. Psychiatry. 1995;58(5):590–597. doi: 10.1136/jnnp.58.5.590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dickerson B.C., Goncharova I., Sullivan M., Forchetti C., Wilson R., Bennett D., Beckett L.A., deToledo Morrell L. MRI-derived entorhinal and hippocampal atrophy in incipient and very mild Alzheimer's disease. Neurobiol. Aging. 2001;22(5):747–754. doi: 10.1016/s0197-4580(01)00271-8. [DOI] [PubMed] [Google Scholar]
- 8.Braak H., Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol. 1991;82(4):239–259. doi: 10.1007/BF00308809. [DOI] [PubMed] [Google Scholar]
- 9.Jack C.R., Petersen R.C., Xu Y.C., O'Brien P.C., Smith G.E., Ivnik R.J., Boeve B.F., Waring S.C., Tangalos E.G., Kokmen E. Prediction of AD with MRI-based hippocampal volume in mild cognitive impairment. Neurology. 1999;52(7):1397–1403. doi: 10.1212/wnl.52.7.1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Le Bihan D., Johansen-Berg H. Diffusion MRI at 25: exploring brain tissue structure and function. NeuroImage. 2012;61(2):324–341. doi: 10.1016/j.neuroimage.2011.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Le Bihan D. Looking into the functional architecture of the brain with diffusion MRI. Nat. Rev. Neurosci. 2003;4(6):469. doi: 10.1038/nrn1119. [DOI] [PubMed] [Google Scholar]
- 12.Mielke M.M., Kozauer N., Chan K., George M., Toroney J., Zerrate M., Bandeen-Roche K., Wang M.-C., Pekar J., Mori S. Regionally-specific diffusion tensor imaging in mild cognitive impairment and Alzheimer's disease. NeuroImage. 2009;46(1):47–55. doi: 10.1016/j.neuroimage.2009.01.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dolz J., Desrosiers C., Ayed I.B. 3D fully convolutional networks for subcortical segmentation in MRI: a large-scale study. NeuroImage. 2018;170:456–470. doi: 10.1016/j.neuroimage.2017.04.039. [DOI] [PubMed] [Google Scholar]
- 14.Liu J., Pan Y., Li M., Chen Z., Tang L., Lu C., Wang J. Applications of deep learning to MRI images: a survey. Big Data Min. Anal. 2018;1(1):1–18. [Google Scholar]
- 15.Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014;15(1):1929–1958. [Google Scholar]
- 16.Aderghal K., Boissenin M., Benois-Pineau J., Catheline G., Afdel K. International Conference on Multimedia Modeling. Springer; 2017. Classification of sMRI for AD diagnosis with convolutional neuronal networks: a pilot 2D+ε study on ADNI; pp. 690–701. [Google Scholar]
- 17.Yosinski J., Clune J., Bengio Y., Lipson H. Advances in Neural Information Processing Systems. 2014. How transferable are features in deep neural networks? pp. 3320–3328. [Google Scholar]
- 18.LeCun Y., Bottou L., Bengio Y., Haffner P. Gradient-based learning applied to document recognition. Proc. IEEE. 1998;86(11):2278–2324. [Google Scholar]
- 19.Krizhevsky A., Sutskever I., Hinton G.E. Advances in Neural Information Processing Systems. 2012. Imagenet classification with deep convolutional neural networks; pp. 1097–1105. [Google Scholar]
- 20.Simonyan K., Zisserman A. Very deep convolutional networks for large-scale image recognition. In: Bengio Y., LeCun Y., editors. 3rd International Conference on Learning Representations; ICLR 2015, San Diego, CA, USA, May 7-9, 2015; 2015. [Google Scholar]
- 21.Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015. Going deeper with convolutions; pp. 1–9. [Google Scholar]
- 22.He K., Zhang X., Ren S., Sun J. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016. Deep residual learning for image recognition; pp. 770–778. [Google Scholar]
- 23.Sivaranjini S., Sujatha C. Deep learning based diagnosis of Parkinson's disease using convolutional neural network. Multimed. Tools Appl. 2019:1–13. [Google Scholar]
- 24.Tajbakhsh N., Shin J.Y., Gurudu S.R., Hurst R.T., Kendall C.B., Gotway M.B., Liang J. Convolutional neural networks for medical image analysis: full training or fine tuning? IEEE Trans. Med. Imaging. 2016;35(5):1299–1312. doi: 10.1109/TMI.2016.2535302. [DOI] [PubMed] [Google Scholar]
- 25.Jack C.R., Jr, Bernstein M.A., Fox N.C., Thompson P., Alexander G., Harvey D., Borowski B., Britson P.J., Whitwell J.L., Ward C. The Alzheimer's disease neuroimaging initiative (ADNI): MRI methods. J. Magn. Reson. Imaging. 2008;27(4):685–691. doi: 10.1002/jmri.21049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pelletier A., Periot O., Dilharreguy B., Hiba B., Bordessoules M., Pérès K., Amieva H., Dartigues J.-F., Allard M., Catheline G. Structural hippocampal network alterations during healthy aging: a multi-modal MRI study. Front. Aging Neurosci. 2013;5:84. doi: 10.3389/fnagi.2013.00084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Aderghal K., Khvostikov A., Krylov A., Benois-Pineau J., Afdel K., Catheline G. 2018 IEEE 31st International Symposium on Computer-Based Medical Systems (CBMS) IEEE; 2018. Classification of Alzheimer's disease on imaging modalities with deep CNNs using cross-modal transfer learning; pp. 345–350. [Google Scholar]
- 28.Aderghal K., Benois-Pineau J., Afdel K., Catheline G. Proceedings of the 15th International Workshop on Content-Based Indexing. ACM; 2017. FuseMe: classification of sMRI images by fusion of deep CNNs in 2D+ε projections; p. 34. [Google Scholar]
- 29.Sarraf S., Tofighi G. 2016 Future Technologies Conference (FTC) 2016. Deep learning-based pipeline to recognize Alzheimer's disease using fMRI data; pp. 816–820. [Google Scholar]
- 30.Sarraf S., Tofighi G. Classification of Alzheimer's disease structural MRI data by deep learning Convolutional Neural Networks. arXiv:1607.06583 CoRR.
- 31.Sarraf S., Danielle D. D., Anderson J., Tofighi G. DeepAD: Alzheimer's Disease Classification via Deep Convolutional Neural Networks using MRI and fMRI. 2017. bioRxiv:10.1101/070441v4 Biorxiv preprint.
- 32.Billones C.D., Demetria O.J.L.D., Hostallero D.E.D., Naval P.C. DemNet: a convolutional neural network for the detection of Alzheimer's disease and mild cognitive impairment. 2016 IEEE Region 10 Conference (TENCON); Singapore; 2016. pp. 3724–3727. [Google Scholar]
- 33.Valliani A., Soni A. Deep residual nets for improved Alzheimer's diagnosis. Proceedings of the 8th ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics; ACM-BCB '17; Association for Computing Machinery; 2017. p. 615. [Google Scholar]
- 34.Lee B., Ellahi W., Choi J.Y. Using deep CNN with data permutation scheme for classification of Alzheimer's disease in structural magnetic resonance imaging (sMRI) IEICE Trans. Inf. Syst. 2019;E102.D(7):1384–1395. [Google Scholar]
- 35.Glozman T., Liba O. 2016. Hidden Cues: Deep Learning for Alzheimer's Disease Classification; pp. 1–8. CS331B project final report. [Google Scholar]
- 36.Wang S., Shen Y., Chen W., Xiao T., Hu J. International Conference on Artificial Neural Networks. Springer; 2017. Automatic recognition of mild cognitive impairment from MRI images using expedited convolutional neural networks; pp. 373–380. [Google Scholar]
- 37.Cheng B., Liu M., Shen D., Li Z., Zhang D., Initiative A.D.N. Multi-domain transfer learning for early diagnosis of Alzheimer's disease. Neuroinformatics. 2017;15(2):115–132. doi: 10.1007/s12021-016-9318-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nowrangi M.A., Lyketsos C.G., Leoutsakos J.-M.S., Oishi K., Albert M., Mori S., Mielke M.M. Longitudinal, region-specific course of diffusion tensor imaging measures in mild cognitive impairment and Alzheimer's disease. Alzheimer's Dement. 2013;9(5):519–528. doi: 10.1016/j.jalz.2012.05.2186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tufail A.B., Ma Y.-K., Zhang Q.-N. Binary classification of Alzheimer's disease using sMRI imaging modality and deep learning. J. Digit. Imaging. 2020;33(5):1073–1090. doi: 10.1007/s10278-019-00265-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hon M., Khan N.M. 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) IEEE; 2017. Towards Alzheimer's disease classification through transfer learning; pp. 1166–1169. [Google Scholar]
- 41.Wen J., Thibeau-Sutre E., Diaz-Melo M., Samper-González J., Routier A., Bottani S., Dormont D., Durrleman S., Burgos N., Colliot O. Convolutional neural networks for classification of Alzheimer's disease: overview and reproducible evaluation. Med. Image Anal. 2020;63 doi: 10.1016/j.media.2020.101694. [DOI] [PubMed] [Google Scholar]
- 42.Basser P.J., Mattiello J., LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66(1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Harrell L.E., Marson D., Chatterjee A., Parrish J.A. The Severe Mini-Mental State Examination: a new neuropsychologic instrument for the bedside assessment of severely impaired patients with Alzheimer disease. Alzheimer Dis. Assoc. Disord. 2000;14(3):168–175. doi: 10.1097/00002093-200007000-00008. [DOI] [PubMed] [Google Scholar]
- 44.Smith S.M., Jenkinson M., Woolrich M.W., Beckmann C.F., Behrens T.E., Johansen-Berg H., Bannister P.R., De Luca M., Drobnjak I., Flitney D.E. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 45.Andersson J.L., Sotiropoulos S.N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage. 2016;125:1063–1078. doi: 10.1016/j.neuroimage.2015.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Smith S.M. Fast robust automated brain extraction. Hum. Brain Mapp. 2002;17(3):143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jenkinson M., Beckmann C.F., Behrens T.E., Woolrich M.W., Smith S.M. Fsl. NeuroImage. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- 48.Juntu J., Sijbers J., Van Dyck D., Gielen J. Computer Recognition Systems. Springer; 2005. Bias field correction for MRI images; pp. 543–551. [Google Scholar]
- 49.Avants B.B., Tustison N., Song G. Advanced normalization tools (ANTS) Insight. 2009;2:1–35. [Google Scholar]
- 50.Tustison N.J., Avants B.B., Cook P.A., Zheng Y., Egan A., Yushkevich P.A., Gee J.C. N4ITK: improved N3 bias correction. IEEE Trans. Med. Imaging. 2010;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tzourio-Mazoyer N., Landeau B., Papathanassiou D., Crivello F., Etard O., Delcroix N., Mazoyer B., Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- 52.Frisoni G., Testa C., Sabattoli F., Beltramello A., Soininen H., Laakso M. Structural correlates of early and late onset Alzheimer's disease: voxel based morphometric study. J. Neurol. Neurosurg. Psychiatry. 2005;76(1):112–114. doi: 10.1136/jnnp.2003.029876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ashburner J., Neelin P., Collins D., Evans A., Friston K. Incorporating prior knowledge into image registration. NeuroImage. 1997;6(4):344–352. doi: 10.1006/nimg.1997.0299. [DOI] [PubMed] [Google Scholar]
- 54.Ashburner J., Friston K. Multimodal image coregistration and partitioning—a unified framework. NeuroImage. 1997;6(3):209–217. doi: 10.1006/nimg.1997.0290. [DOI] [PubMed] [Google Scholar]
- 55.Friston K.J., Ashburner J., Frith C.D., Poline J.-B., Heather J.D., Frackowiak R.S. Spatial registration and normalization of images. Hum. Brain Mapp. 1995;3(3):165–189. [Google Scholar]
- 56.Nyúl L.G., Udupa J.K., Zhang X. New variants of a method of MRI scale standardization. IEEE Trans. Med. Imaging. 2000;19(2):143–150. doi: 10.1109/42.836373. [DOI] [PubMed] [Google Scholar]
- 57.Friston K. Brain Mapping: the Methods. 1996. Statistical parametric mapping and other analyses of functional imaging data; pp. 363–396. [Google Scholar]
- 58.Cherubini A., Péran P., Spoletini I., Di Paola M., Di Iulio F., Hagberg G.E., Sancesario G., Gianni W., Bossu P., Caltagirone C. Combined volumetry and DTI in subcortical structures of mild cognitive impairment and Alzheimer's disease patients. J. Alzheimer's Dis. 2010;19(4):1273–1282. doi: 10.3233/JAD-2010-091186. [DOI] [PubMed] [Google Scholar]
- 59.Balbastre Y., Rivière D., Souedet N., Fischer C., Hérard A.-S., Williams S., Vandenberghe M.E., Flament J., Aron-Badin R., Hantraye P. Primatologist: a modular segmentation pipeline for macaque brain morphometry. NeuroImage. 2017;162:306–321. doi: 10.1016/j.neuroimage.2017.09.007. [DOI] [PubMed] [Google Scholar]
- 60.Khvostikov A., Aderghal K., Benois-Pineau J., Krylov A., Catheline G. 3D CNN-based classification using sMRI and MD-DTI images for Alzheimer disease studies. arXiv:1801.05968 [abs] CoRR.
- 61.Jia Y., Shelhamer E., Donahue J., Karayev S., Long J., Girshick R., Guadarrama S., Darrell T. Caffe: convolutional architecture for fast feature embedding. arXiv:1408.5093 arXiv preprint.
- 62.Payan A., Montana G. Predicting Alzheimer's disease: a neuroimaging study with 3D convolutional neural networks. arXiv:1502.02506 [abs] CoRR.
- 63.Cheng D., Liu M., Fu J., Wang Y. Classification of MR brain images by combination of multi-CNNs for AD diagnosis. Ninth International Conference on Digital Image Processing; ICDIP 2017; International Society for Optics and Photonics; 2017. p. 1042042. [Google Scholar]
- 64.Khvostikov A., Aderghal K., Krylov A., Catheline G., Benois-Pineau J. 3D inception-based CNN with sMRI and MD-DTI data fusion for Alzheimer's disease diagnostics. arXiv:1809.03972 CoRR.
- 65.Gupta A., Ayhan M.S., Maida A.S. Proceedings of the 30th International Conference on International Conference on Machine Learning (ICML) vol. 8. 2013. Natural image bases to represent neuroimaging data; pp. 987–994. (ICML'13). [Google Scholar]
- 66.Morra J.H., Tu Z., Apostolova L.G., Green A.E., Avedissian C., Madsen S.K., Parikshak N., Hua X., Toga A.W., Jack C.R., Jr Automated 3D mapping of hippocampal atrophy and its clinical correlates in 400 subjects with Alzheimer's disease, mild cognitive impairment, and elderly controls. Hum. Brain Mapp. 2009;30(9):2766–2788. doi: 10.1002/hbm.20708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lian C., Liu M., Zhang J., Shen D. Hierarchical fully convolutional network for joint atrophy localization and Alzheimer's disease diagnosis using structural MRI. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2020;42(4):880–893. doi: 10.1109/TPAMI.2018.2889096. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supplementary material/referenced in article.