Abstract
This study represents the investigation of earth-abundant and non-toxic CZTSSe absorber materials in kesterite solar cell by using the Finite Element Method (FEM) with (1) electrical, and (2) optical approaches. The simulated results have been validated with the experimental results to define guidelines for boosting the cell performance. For improving the cell efficiency, potential barrier variations in the front contact, and the effect of different lattice defects in the CZTSSe absorber layer have been examined. Controlling the defects and the secondary phases of absorber layer have significant influence on the cell performance improvement. Previous studies have demonstrated that, synthesis of CZTSSe:Na nanocrystals and controlling the S/(S + Se), Cu/(Zn + Sn), and Zn/Sn ratios (stoichiometry) have significant effects on the reduction of trap-assisted recombination (Shockley–Read–Hall recombination model). In this work, a screening-based approach has been employed to study the cell efficiency over a wide range of defect densities. Two categorized defect types including benign defects ( cm−3 , Nt defines trap density) and harmful defects cm−3) in the absorber bandgap in the CZTSSe solar cell, by analyzing their position changes with respect to the electron Fermi level (Efn) and the Valence Band Maximum positions have been identified. It is realized that, the harmful defects are the dominant reason for the low efficiency of the kesterite solar cells, therefore, reducing the number of harmful defects and also total defect densities lead to the power conversion efficiency record of 19.06%. This increment makes the CZTSSe solar cells as a promising candidate for industrial and commercial applications.
Subject terms: Electronics, photonics and device physics; Photonic devices; Electronic structure
Introduction
Thin-film photovoltaic (PV) solar cell, known as one of the great promises and flexible means for renewable energy science, has attracted tremendous research interests among scientists to develop it with high-efficiency absorbers to harness the solar energy1–7. Due to the mechanism of the solar cell, the two most essential reasons for choosing a material as an absorber layer are (1) the capability in absorbing light as much as possible to excite electrons to higher energy states and (2) the ability to move those excited electrons from the solar cell into an external circuit. Besides, as an essential point, choosing a non-toxic, environmentally friendly, and air-stable materials play a crucial role in manufacturing thin-film solar cells6,8–10.
In comparison to other photovoltaic solar cells, chalcopyrite Cu(In,Ga)(S,Se)2 (CIGS) and CdTe solar cells have attained great power conversion efficiencies (PCEs) of 22.6%11 and 22.1%12,13, respectively. Toxicity of Cadmium (Cd) and supply limitations for Indium (In) are barriers for the large-scale production of these solar cells. Therefore, the need for a non-toxic and earth-abundant material is the most critical standard to ensure an extensive low-cost PV solar cell development. Kesterite based materials including Cu2ZnSnS4 (CZTS), Cu2ZnSnSe4 (CZTSe), and Cu2ZnSn(S,Se)4 (CZTSSe), emerge as potential replacements for the chalcopyrite and CdTe absorbers2,14–16. Kesterite Cu2ZnSn(S,Se)4 (CZTSSe) solar cells have been seriously studied owing to their relatively high power conversion efficiency (PCE) with non-toxic and low-cost earth-abundant constituent elements. CZTSSe has been recognized as a prospective alternative absorber material due to its controllable bandgap (Eg) (1.0 to 1.5 eV) and high absorption coefficient (more than 104 cm−1). It should be noted that the bandgap (Eg) of the CZTSSe absorber can be controlled by varying S/(S + Se) ratio from ~ 1.0 eV of Cu2ZnSnSe4 (CZTSe) to ~ 1.5 eV of Cu2ZnSnS4 (CZTS)17–21. Besides, variation of mixed powder of S/Se not only causes bandgap variation, but also changes the electron affinity (χ), absorption coefficient, and series resistance (the higher series resistance decreases the fill factor)20,22–24. The last confirmed PCE of 12.6% has been recorded for CZTSSe-based solar cell by using hydrazine based non-vacuum process15, and the PCE of 12.3% has been certified from vacuum-based process20. Recently, D.H. Son et al. recorded the PCE of 12.62% by studying the effect of solid-H2S gas reactions on the CZTSSe thin-film25. Cationic disorder and the presence of intrinsic defects are directly affecting the carrier concentration, electrical conductivity, elemental non-stoichiometry (which leads to the formation of unwanted defects and defect complexes) and other properties of CZTS, CZTSe, and CZTSSe films, as well as the performance of PV devices. Intrinsic point defects in kesterite structure may form during the CZTSSe thin-film/bulk crystal growth including vacancies (VCu, VZn, VSn, and VS(e)), antisites (CuZn, ZnCu, CuSn, SnCu, ZnSn, and SnZn), and interstitials (Cui, Zni, Sni, and S(e)i). Besides, the donor and acceptor defects may attract each other and form defect clusters or complexes (VCu + ZnCu, 2CuSn + ZnSn, ZnSn + 2ZnCu, 2CuZn + SnZn…) because of their lower formation energy than antisite defects. To restrain high concentration of CuZn antisite defects, which is a deep one, CZTSSe films have been developed with Cu-poor and Zn-rich (Cu/(Zn + Sn) ≈ 0.8 and Zn/Sn ≈ 1.2) phases. According to the similar ionic size (Cu, Zn ≈ 1.35 Å) and small chemical difference between Cu and Zn, the cation disorder is formed with the lowest formation energy. This cation disorder can induce electrostatic band fluctuation which leads a phenomenon called “VOC-deficit” which is the key factor that limits the cell efficiency2,26–39. For resolving this crucial problem, the crystallinity of the absorber layer, which depends on the annealing temperature, annealing time and sulfurization should be improved because impurity of crystallinity results shallow and deep defect levels within the bandgap, which is a detrimental effect on the cell efficiency17,40–42. Just like defects, the formation of complex secondary phases like Zn(S,Se) and Cu2Sn(S,Se)3 should be prevented because they all lead to structural inhomogeneity, local fluctuations of open-circuit voltage (VOC), and high recombination of photogenerated carriers in CZTSSe films, which negatively affect the efficiency of CZTSSe-based solar cells. All secondary phases have detrimental effects on the device performance because the lower optical bandgap of them reduces the open-circuit voltage (VOC) and fill factor (FF); while the higher bandgap may increase the series resistance and reduce the fill factor (FF) and short circuit current (JSC)30, 43–47. Also, a non-Ohmic back contact between the absorber layer and Mo causes high electron–hole recombination, which leads to notable open-circuit voltage (VOC) loss, and reduces the cell efficiency2, 23, 48. Therefore, (1) improving the crystallinity of the absorber layer, (2) preventing the formation of secondary phases, and (3) improving the quality of Mo/CZTSSe interface leads to impurity-free and phase-controlled CZTSSe thin films. These result an increment in the open-circuit voltage (VOC) and short-circuit current density (Jsc), and with all these taken into account, it would be possible to record a better efficiency for the cell30.
A well-controlled heterojunction interface with fewer defects and secondary phases is an essential point to enhance the device performance, therefore, we try to take defects and unwanted phases under control by the simulation to improve the cell PCE. Characteristics of harmful defects can be altered by double cation substitution which is a feasible strategy to reduce the negative effects of the defects. The effects of double cation substitution by partially substituting of Cu with Ag and Zn with Cd have been explored on Cu2ZnSnS4 (CZTS) devices with 10.1% efficiency by Hadke49. It is shown that in substitution of Cd and Ag, Cd improves the cell performance by altering the defect characteristics of acceptor states close to the valence band, and Ag reduces non-radiative bulk recombination49. Recently, in order to reduce cation disorder in CZTSSe, isoelectronic cation substitution of Cd for Zn37 Ba for Zn50,51, Ag for Cu52,53, and Sn with Ge54,55 have been conducted. The isoelectronic cation substitution with larger ionic size, mismatching between cations, presents an approach, reducing cationic disorder with fewer defects leads improved solar cell performance56. To control the absorber defects, some approaches have been proposed, including: (1) synthesizing CZTSSe:Na nanocrystals57, (2) controlling the S/(S + Se), Cu/(Zn + Sn) and Zn/Sn ratios (Control Stoichiometry)24,36,58. Moreover, we propose adding Graphene59 and Graphyne to the absorber precursors in order to enhance the conductivity which improves the total mobility and reduces the defects.
In this study, the device simulations are examined using the Finite Element Method (FEM) in a 2D symmetric cylindrical coordinate. The simulated results have been validated with the experimental results to define guidelines for boosting the cell performance. Also, the cell efficiency has been investigated by studying the potential barrier effect in front contact and the connected semiconductor layer. In the next step, by identifying harmful defects in bandgap, we suggest a profitable way for improving the cell performance by analyzing defect position changes, monitoring the electron Fermi level (Efn) and the Valence Band Maximum (VBM) positions.
According to the results, the farther position of the defect from the electron Fermi level (Efn) records a better cell efficiency (19.06%, which is remarkable efficiency in comparison with other calculations). Besides, minimizing defects density causes an improvement in cell performance. Identifying the harmful and benign defects, and reduction in defect density helps us to record the PCE of 19.06%.
Results and discussion
Cell structure
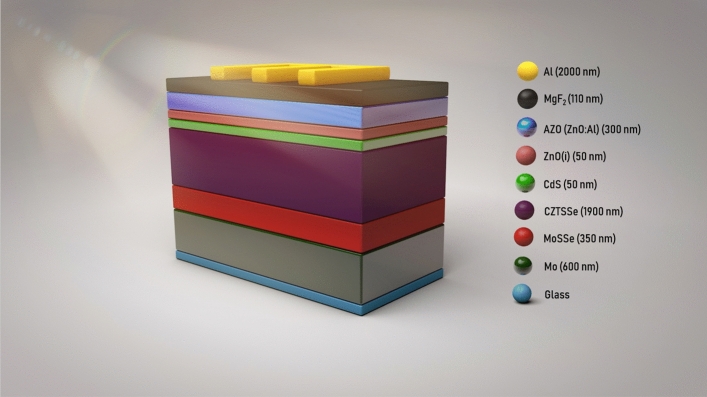
Based on the experimental model, the solar cell structure has been demonstrated in Fig. 1.
Figure 1.
Schematic image of CZTSSe solar cell layers.
Table S1 (supporting information) represents electrical and optical properties of simulated layers in grading mode using for the simulation of the CZTSSe-based solar cell. Likewise, the basic data for defect concentration, the defect properties at the interface of graded CZTSSe/CdS, and for graded absorber layer are available in Tables S2, S3, and S4 in the supporting document, respectively.
Defects and secondary phases control
Synthesizing CZTSSe:Na Nanocrystals
The presence of undesirable defects in the absorber layer during the deposition process, and formation of secondary phases, limit the cell performance by reducing open-circuit voltage (VOC). Synthesizing CZTSSe:Na nanocrystals is a method to overcome this problem. In fact, Na ions reduce concentration of deep level recombination, which results enhancement in the carrier concentration and open-circuit voltage (VOC), as well as the device performance30,57.
-
(2)
Controlling the S/(S + Se), Cu/(Zn + Sn) and Zn/Sn ratios (Control Stoichiometry)
As we mentioned above, the CZTSSe bandgap is controllable by varying S/(S + Se) ratio from ~ 1.0 eV of CZTSe to ~ 1.5 eV of CZTS. The greater bandgap demonstrates more S/(S + Se) ratio in the film. The graded bandgap implies that different S/(S + Se) ratios of the absorber are formed by different sulfo-selenization temperatures. Higher sulfo-selenization temperature leads to more S17. Moreover, the Cu-poor, Zn-rich, Cu/(Zn + Sn) ≈ 0.80, and Zn/Sn ≈ 1.20, conditions are desirable for higher device performance. The high concentration of defect clusters or complexes results a notable non stoichiometry, which leads to lower device performance. Sulfurization at high temperature during the post-deposition helps to control the stoichiometry24,36,58.
Numerical modeling
In this work, the CZTSSe solar cell has been investigated using the Finite Element Method (FEM), and validated by the experimental results. The simulation contains (1) electrical, and (2) optical sections, in a two-dimensional cylindrical coordinate based on charge carrier transport equations. In the provided structure, there is no nanoparticle, and due to the morphological properties of the absorber, the Beer–Lambert law has been employed to study the optical properties of the cell. The study of the electrical properties is divided into three parts, in which two parts are based on the Drift–Diffusion equations describing charge carriers with respect to the effect of diffusion and drift carriers, and also recombination rate. Furthermore, the third part is the electrostatic potential based on the Poisson equation60–63. The generation rate is calculated in optical part, which is available in the supporting.
Charge carrier transport equations in two-dimensional symmetrical cylindrical coordinate (3D form with symmetry in the angular direction)
The Poisson and charge carrier transport equations were used for validation of the experimental kesterite solar cell case. Three-dimensional form of these equations are represented below:
| 1 |
| 2 |
| 3 |
where and are concentration of electrons and holes, and are electron and hole diffusion coefficients. and are electron and hole mobilities, is the Boltzmann constant, is temperature is electronic charge. is the electrostatic potential, χ is the electron affinity, Eg is the bandgap of the semiconductor, and are effective density of states of the conduction and the valence band, is the Planck constant, and are effective mass of states of the conduction and the valence band. is the generation rate of charge carriers, λ is wavelength, and is the recombination rate of charge carriers. Moreover, and are vacuum and relative permittivity, is the impurity density.
The equation depicts the sum of Shockley–Read–Hall, radiative, and the Auger recombination terms which described as:
| 4 |
, , and define as:
| 5 |
| 6 |
| 7 |
where and are electron and hole lifetimes, and are electron and hole concentrations of the trap state. It should be noted that the strongest occurs when . The is the intrinsic carrier concentration, is the coefficient of bimolecular radiative recombination , and and are electron and hole Auger coefficients. The Auger and radiative recombination are neglected due to their low effect on the kesterite cell performance32,64. In this study, defect distribution is investigated based on Explicit Trap Distribution (ETD), which is close to Shockley–Read–Hall (SRH) recombination statistics. The equations are written as:
| 8 |
| 9 |
| 10 |
where is the ETD recombination rate, and are recombination rate of electrons and holes, is defect carrier density, is degeneracy factor, and and are electron and hole trap probabilities, which can be derived from following equations:
| 11 |
| 12 |
where and are electron and hole trap cross sections, and are thermal velocity of electrons and holes, and as we mentioned above, and are concentration of electrons and holes, which can be calculated with the following equations:
| 13 |
| 14 |
where and constants are related to the Maxwell–Boltzmann distribution function, and we assume they are equal to one ( = = 1). Also, and are electron and hole Fermi level energy respectively, and is the inherent density, which is calculated by:
| 15 |
also, subscript “i” in Eq. 5 and Eq. 6, is related to the defect’s charge, which is categorized in the Table 1 below:
Table 1.
| Trap type | Trapped species | Occupied charge | Unoccupied charge | |
|---|---|---|---|---|
| Donor trap | Electron | 0 | + | |
| Acceptor trap | Hole | 0 | − | |
| Neutral electron trap | Electron | − | 0 | |
| Neutral hole trap | Hole | + | 0 |
It should be noted that, the defect energy difference is calculated by the following equation:
| 16 |
where is the reference energy, based on our assumption, it is . (valence band position).
The final changing rate of trapped electrons derived by the following equation:
| 17 |
where and are calculated by:
| 18 |
| 19 |
Experimental validation
We studied the effect of optimization of various parameters for boosting the cell efficiency. Table 2 represents pervious reported performance parameters of Cu2ZnSn(S,Se)4 (CZTSSe) based solar cells with Cu/(Zn + Sn) and Zn/Sn ratios, which have been described as variable chemical components.
Table 2.
reported performance parameters (VOC, JSC, FF, and η) of Cu2ZnSn(S,Se)4 (CZTSSe) based solar cells with Cu/(Zn + Sn) and Zn/Sn ratios, which described as variable chemical components.
| Component | Cu/(Zn + Sn) | Zn/Sn | VOC (V) | JSC (mA/cm2) | FF (%) | η (%) |
|---|---|---|---|---|---|---|
| Cu2ZnSn(S,Se)466 | 0.925 | 1.0 | 0.622 | 15.87 | 60.0 | 5.90 |
| Cu2ZnSn(S,Se)467 | 0.79 | 1.11 | 0.420 | 30.40 | 52.70 | 7.20 |
| Cu2ZnSn(S,Se)468 | 0.90 | 1.10 | 0.497 | 20.0 | 54.32 | 5.40 |
| Cu2ZnSn(S,Se)469 | 0.80 | 1.22 | 0.5627 | 24.07 | 60.0 | 8.13 |
| Cu2ZnSn(S,Se)470,71 | 0.80 | 1.20 | 0.516 | 28.60 | 65.0 | 9.66 |
| Cu2ZnSn(S,Se)433 | 0.80 | 1.20 | 0.517 | 30.80 | 63.70 | 10.10 |
| Cu2ZnSn(S,Se)424 | – | – | 0.4598 | 34.50 | 69.80 | 11.10 |
| Cu2ZnSn(S,Se)4 (experimental case-this work) | 0.80 | 1.20 | 0.501 | 35.34 | 65.62 | 11.62 |
Furthermore, optimized parameters have been investigated in the following sections.
At first, for demonstrating the accuracy of simulated results, the comparison between the reported experimental data and the simulated one has been made. CZTSSe solar cell has been simulated using data listed in Tables S1–S4. The current–voltage characteristics (J–V) of the cell (Fig. 2a) indicates a good agreement between the experimental and simulation results.
Figure 2.

(a) Current density versus voltage curves for experimental and simulation results. (b) The C–V charge densities (NCV) in the CZTSSe absorber layer at temperature of 300 K and frequency of 100 kHz.
The C–V charge densities (NCV) in the CZTSSe absorber layers at a temperature of 300 K and a frequency of 100 kHz has been measured (Fig. 2b). The depletion width (Wd) at Vbias = 0 V was 0.149 µm for CZTSSe cell. By fitting the NCV, carrier density and epsilon of the CZTSSe layer have been extracted from experimental measurement.
Optimization of the potential barrier effect in front contact
Figure 3 indicates the effect of the potential barrier on performance of the simulated cell, which is derived by:
| 20 |
where is the potential barrier in the front contact, is the metal work function of the front contact, and is the electron affinity of the connected semiconductor layer to the front contact. According to Fig. 3, the lower the value of , the higher the open-circuit voltage (VOC) and the short-circuit current density (JSC), so the result would be increased in the cell PCE. As one can see in Fig. 4, the better efficiency at eV with work function of 4.1 eV is recorded.
Figure 3.

Current density versus voltage curves of the cell by optimization the potential barrier effect in front contact.
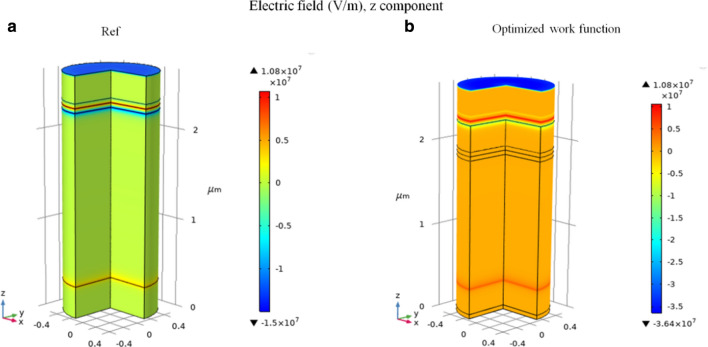
Figure 4.
The electric field along the z component for (a) validated (Ref), and (b) simulated model (optimized work function).
Moreover, Fig. 4 depicts the comparison between the electric field (along z component) of the validated and simulated case, after optimization of the work function. As one can notice, the electric field has been improved from − 1.50 × 107 to − 3.64 × 107 (V/m), and this leads to higher open-circuit voltage (VOC) and short-circuit current density (JSC), as well as the device performance.
Investigation of the cell performance based on the different possible defects and varying defect densities
The simulated results are based on the existence of possible defects and their energy level. Table 3 shows the defect position of (a) CZTS, and (b) CZTSe. Since CZTSSe absorber layer is considered based on the S/(S + Se) ratio, all types of defects could be possible for this layer. (+) and (−) denote donor and acceptor defects with their charges respectively.
Table 3.
The energy level position of acceptor and donor lattice defects (inside the bandgap with respect to the VBM positions) for CZTS (left column), and CZTSe (right column) layers based on the Density Functional Theory (DFT) calculations36.
| CZTS | CZTSe | ||
|---|---|---|---|
| Defect | Edefect (meV) | Defect | Edefect (meV) |
| VCu (−/0) | 30 | VCu (−/0) | 40 |
| VZn (2−/−) | 260 | VZn (2−/−) | 230 |
| VZn (−/0) | 120 | VZn (−/0) | 130 |
| VSn (4−/3−) | 900 | VSn (4−/3−) | 550 |
| VSn (3−/2−) | 600 | VSn (3−/2−) | 400 |
| VSn (2−/−) | 370 | VSn (2−/−) | 260 |
| VSn (−/0) | 180 | VSn (−/0) | 170 |
| CuZn (−/0) | 146 | CuZn (−/0) | 105 |
| CuSn (3−/2−) | 590 | CuSn (3−/2−) | 440 |
| CuSn (2−/−) | 440 | CuSn (2−/−) | 300 |
| CuSn (−/0) | 210 | CuSn (−/0) | 170 |
| ZnSn (2−/−) | 280 | ZnSn (2−/−) | 170 |
| ZnSn (−/0) | 140 | ZnSn (−/0) | 90 |
| ZnCu (0/+) | 1390 | ZnCu (0/+) | 920 |
| SnCu (0/+) | 1520 | SnCu (0/+) | 1100 |
| SnCu (+/3+) | 380 | SnCu (+/3+) | 430 |
| SnZn (0/+) | 500 | SnZn (0/+) | 670 |
| SnZn (+/2+) | 500 | SnZn (+/2+) | 550 |
| Cui (0/+) | 1400 | Cui (0/+) | 940 |
| Zni (0/+) | 1020 | Zni (0/+) | 700 |
| Zni (+/2+) | 870 | Zni (+/2+) | 680 |
| VS (0/2+) | 760 | VSe (0/2+) | 350 |
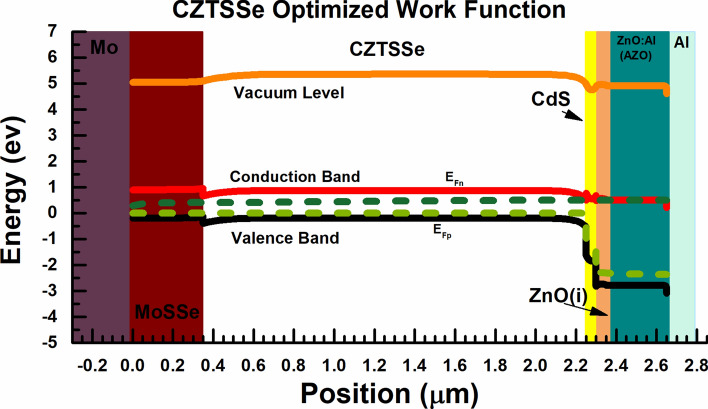
Moreover, Fig. 5 represents the band diagram of the CZTSSe-based solar cell under the standard source of illumination AM 1.5 (at the VOC voltage). According to Fig. 5, by optimizing the value of work function, the conduction and valence band have been changed, and this enhances the carrier transfer from absorber layer to back contact, so an increment in open-circuit voltage (VOC) and the cell efficiency has been recorded.
Figure 5.
Band diagram of CZTSSe solar cell with optimized value of the work function.
Optimization of defect energy and density
The value of 1.02 eV is the maximum value that the bandgap could attain as illustrated in Table 3. So, we ought to choose defects energies less than or equal to this value. The average value of the electron Fermi level (Efn) energy is 0.6 eV above the Valence Band Maximum (VBM) of the absorber layer. The effect of acceptor defects in the absorber layer [in the range of (1) 0.03 eV to 0.6 eV (Fig. 6a), and (2) 0.6 eV to 0.9 eV (Fig. 6b)] on the current density versus voltage (J-V) has been investigated. As indicated in Fig. 6a, acceptor defects with energy of eV record higher VOC and Jsc, which improve the cell PCE. Therefore, eV is the optimum energy value for the acceptor defect, and we used that as a defect energy value for simulating our device to find out the optimum value for donor defect energy. Moreover, the investigation of donor defects positions has been done in range of (1) 0.35 eV to 0.55 eV (Fig. 6c), and (2) 0.55 eV to 1.02 eV (Fig. 6d). Consequently, we recorded an increment in open-circuit voltage (VOC) and Jsc when the donor defect energy is eV. In a nutshell, we were able to claim that eV and eV are optimum energy values for acceptor and donor defects, respectively.
Figure 6.
The effect of the absorber bulk defects positions on the current density versus voltage in range of (a) 0.03 eV to 0.6 eV (acceptor defect), (b) 0.6 eV to 0.9 eV (acceptor defect), (c) 0.35 eV to 0.55 eV (donor defect), and (d) 0.55 eV to 1.02 eV (donor defect) (the choice of ranges was based on Density Functional Theory (DFT) calculations36).
As the next step, to find the optimum density value, acceptor densities in the range of 1.0 × 1012 cm−3 to 1.0 × 1018 cm−3 and donor defects densities in the range of 1.0 × 1012 cm−3 to 1.0 × 1017 cm−3 have been investigated. As seen in Fig. 7a, cm−3 (acceptor defect density) with higher short-circuit current density (Jsc), and open-circuit voltage (VOC) is the best density value for the acceptor density. Hence, we have simulated the device with cm−3 as an optimum defects density value to find the optimum density for donor defects. So, based on our calculations, cm−3 (donor defect density) is the optimum carrier density of donor defects (Fig. 7b). Subsequently, we can assert that cm−3 are optimum parameters for acceptor and donor defects. Thus, by having optimized values of energies and carrier densities of defects, we are able to simulate a CZTSSe solar cell with higher efficiency (19.06%) than previous works. Also, in Table 4 we present harmful and benign defects for the device performance. As a critical point, closer defects to the electron Fermi level (Efn) position or ~ Eg/2 (related equations are available in Part S2 in supplementary) cause the absorber electrical conductivity deterioration, which increases the recombination rate, and reduces the open-circuit voltage (VOC), short-circuit current density (Jsc) and PCE. Also, the increment of acceptor and donor defect densities increases the possibility of electron-trapping in the bandgap, and this leads to a reduction in the absorber electrical conductivity and PCE.
Figure 7.

The effect of the absorber bulk defects position on the Current density versus voltage curves in range of (a) 1.0 × 1012 cm−3 to 1.0 × 1018 cm−3 (acceptor defect density), and (b) 1.0 × 1012 cm−3 to 1.0 × 1017 cm−3 (donor defect density) (the choice of ranges was based on Density Functional Theory (DFT) calculations36).
Table 4.
Harmful and benign defects based on their influence on the cell performance.
| Defects | Approximate Et (eV) | Effect on the cell performance in | |
|---|---|---|---|
| in CZTS | in CZTSe | ||
| VCu (−/0) | VCu (−/0) | 0.030 | Benign |
| VZn (−/0), CuZn (−/0), ZnSn (−/0) | VZn (−/0), CuZn (−/0), ZnSn (−/0) | 0.10 | Benign |
| VSn (−/0), CuSn (−/0) | VZn ((2−/−), CuZn (−/0), ZnSn (2−/−) | 0.20 | Benign |
| VZn (2−/−), ZnSn (2−/−) | VSn (2−/−), CuSn (2−/−) | 0.30 | Harmful |
| VSn (2−/−) | VSe (0/2+) | 0.35 | Harmful |
| SnCu (+/3+) | VSn (3−/2−) | 0.40 | Harmful |
| CuSn (2−/−) | CuSn (3−/2−), SnCu (+/3+) | 0.45 | Harmful |
| SnZn (0/+), SnZn (+/2+) | – | 0.50 | Harmful |
| – | VSn (4−/3−), SnZn (+/2+) | 0.55 | Harmful |
| VSn (3−/2−), CuSn (3−/2−) | – | 0.60 | Harmful |
| – | SnZn (0/+) | 0.65 | Harmful |
| – | Zni (0/+), Zni (+/2+) | 0.70 | Harmful |
| VS (0/2+) | – | 0.75 | Harmful |
| – | – | 0.80 | Harmful |
| Zni (+/2+) | – | 0.85 | Harmful |
| VSn (4−/3−), Zni (+/2+) | ZnCu (0/+) | 0.90 | Benign |
| – | Cui (0/+) | 0.95 | Benign |
| Zni (0/+) | SnCu (0/+) | 1.020 | Benign |
Figure 8 represents the final optimized J–V characteristics of the cell in comparison with the experimental data. Obviously, this comparison indicates that the simulation results are in good agreement with experimental data, as it shows an impressive increment in the cell performance.
Figure 8.
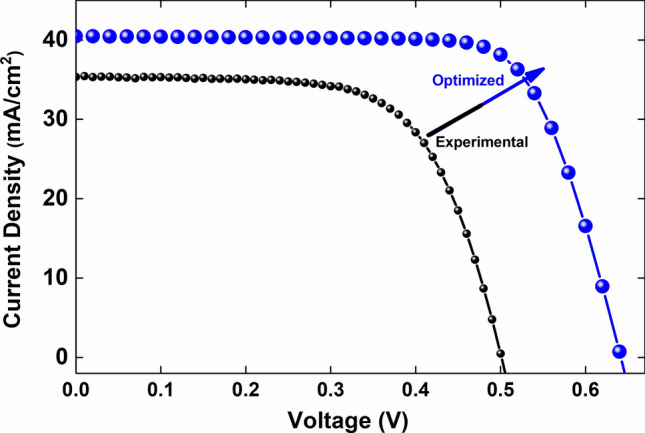
Optimized J–V characteristics of the cell in comparison with the experimental data.
Investigation of the device performance according to the recombination rate distribution
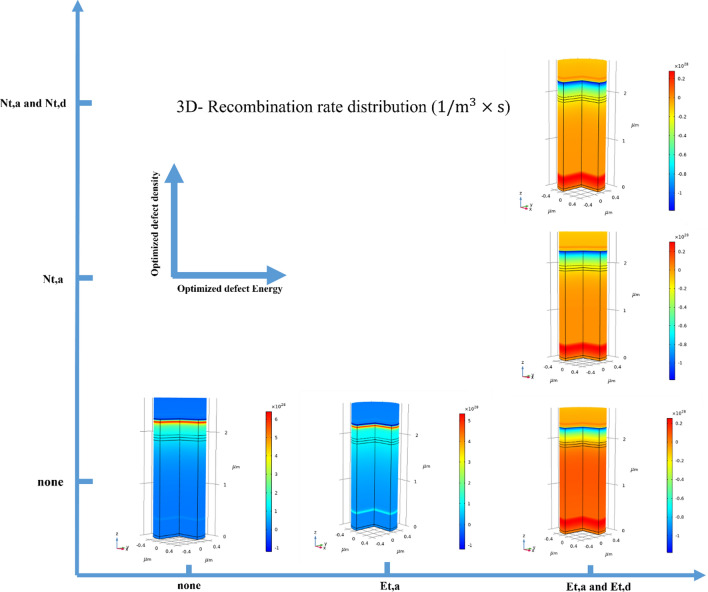
It is a crucial point to reduce recombination rate for enhancing the cell performance. So, Fig. 9 illustrates the optimized defect energy and density values along the z-component. As shown in Fig. 9, we introduce a 2-D coordinate system, where the x-component depicts optimized defect energy, and the y-component demonstrates optimized defect density. The ( value shows the recombination rate without the optimization of the defect energy and the defect density. Optimizing the acceptor defect energy () with non-optimized acceptor defect density (), causes lower recombination rate than the previous part in ( mode. The next step for reducing the recombination rate is optimizing without the optimization of the . Also, optimization of with reduces the recombination rate, but the best device performance has been recorded when we optimized the , and the , which shows a dramatic reduction in the recombination rate with the applied voltage of 0.9 V.
Figure 9.
The recombination rate of distribution (1/m3 × s) for different cases (optimized Eta,d, Nta,d and non-optimized).
Characterization harmful and benign defects (based on their effects on the cell efficiency)
All of the defects have been formed in the CZTSSe layer are not harmful, and there are benign defects in the CZTSSe absorber layer, and recognition of harmful or benign defects is based on their influence on the cell performance. Benign defects reduce carrier recombination on the grain boundary by their segregation. For example, ZnSn (as a benign defect) provides deep levels in the CZTSSe absorber by breaking or weakening bonds, and also create barrier for holes and easy transport of electrons through the grain boundaries30,72,73. Our evaluation for harmful and benign defects was based on the investigation of available defects in CZTS and CZTSe, and their energy Et (eV) with respect to the Valence Band Maximum (VBM) of the absorber layer. According to the Table 4, benign defects have no negative effect on the cell performance, in contradict, harmful defects cause the cell PCE deterioration. As a crucial point, defects with density () higher than 1016 (1/cm3) are harmful for the cell efficiency, even if they are far from the electron Fermi level (Efn) energy. It should be noted that, defects with the position higher than the Conduction Band Minimum (CBM) are not considered because they are meaningless (ZnCu (0/+), SnCu (0/+), Cui (0/+)).
Conclusion
Controlling the defects and secondary phases of CZTSSe absorber layer have significant influence on the in kesterite solar cell performance improvement. Previous studies have demonstrated that, synthesis of CZTSSe:Na nanocrystals and controlling the S/(S + Se), Cu/(Zn + Sn), and Zn/Sn ratios (Stoichiometry) have a significant effect on the reduction of trap-assisted recombination (Shockley–Read–Hall recombination model). Moreover, adding Graphene and Graphyne to the absorber precursors in order to enhance the conductivity might also improve the total mobility and reduces the recombination. In this paper, the CZTSSe absorber materials in kesterite solar cell by using the Finite Element Method (FEM) with (1) electrical, and (2) optical approaches has been investigated and simulation outcomes have been validated by the experimental data. We first optimized the potential barrier effect in the front contact and the connected semiconductor layer. It is found that the lower the value of eV leads the higher the open-circuit voltage (VOC) and PCE. In the next step, a screening-based approach has been employed to study the cell efficiency over a wide range of defect densities. Two categorized defect types including benign defects ( cm−3, Nt defines trap density) and harmful defects cm−3) in the absorber bandgap in the CZTSSe solar cell, by analyzing their position changes with respect to the electron Fermi level (Efn) and the Valence Band Maximum (VBM) positions have been recognized. The optimum values of = 0.03 eV, = 1.02 eV and cm−3 for accepter and donor have been obtained, respectively. Optimization of potential barrier effect in front contact (), classifying the harmful and benign defects, and reduction in defects densities helps us to record the PCE of 19.06%, which is a remarkable increment in comparison with other results and makes the CZTSSe solar cells as a promising candidate for industrial and commercial applications.
Methods
The precursor metal films have been deposited on a Soda Lime Glass (SLG) substrate, which has been coated with a 600 nm-thick Mo. Zn and Sn layers have been consecutively deposited by co-sputtering with the Cu layer. It should be noted that a single layer of Cu was finally deposited to control the Cu composition. Cu/Cu–Sn/Cu–Zn/Mo/Glass is the stack structure of the deposited precursor. The layers were deposited under sputtering powers of 150 W, 300 W, and 300 W for the Cu, Zn and Sn targets, respectively, at a working pressure of 1 mTorr at Ar atmosphere. It is worth mentioning that, the metal precursors were reacted and annealed in a furnace. The CZTSSe absorption layer was synthesized through a sulfo-selenization process and heat-treated in a Se Shot and Ar/H2S gas atmosphere. Also, 480 °C was the final temperature of the heat treatment, and lasted for 10 min. Cu2ZnSn(S,Se)4 (CZTSSe) absorber layer was coated with a 50 nm CdS buffer layer by chemical bath deposition to fabricate the solar cell,. Afterward, a 50 nm intrinsic ZnO (ZnO(i)) layer and a 300 nm Al-doped ZnO (AZO (ZnO:Al)) layer were deposited by RF sputtering. At last, a 2 µm Al grid, and a 110 nm MgF2 were deposited by the e-beam evaporator. It should be noted that, the MgF2 layer was deposited as an antireflection coating layer. Figure S1 in the supporting file illustrates the cross section FESEM image of the cell. It should be noted that, the substrate temperature and deposition time play a crucial role in determining the quality and composition of kesterite films. The current–voltage characteristics were measured under a simulated air mass 1.5 global (AM 1.5 G) spectrum in an illumination of 100 mW/cm2 (1 sun) using a solar simulator (Newport Co., model 94022A). The grading composition of S/S + Se ratio has been shown in Figure S3.
Supplementary information
Acknowledgements
We thank Dae-Ho Son and Dae-Hwan Kim for their contributions toward this work. This work was supported by the “Technology Development Program to Solve Climate Change of the National Research Foundation (NRF) funded by the Ministry of Science and ICT”, Republic of Korea (2016M1A2A2936781).
Author contributions
M.M. designed the Simulations, wrote the manuscript, prepared all the figures, and interpreted the simulation findings, visualization, data analyzing; and supervised the studies; A.G. simulation, wrote the manuscript, and visualization; E.Y. wrote the manuscript and supervised the studies. A.A.K. wrote the manuscript. A.H. helped in simulation, writing - review & editing, resources, software, Validation. All authors have approved the final version of the manuscript.
Data availability
The data that support the findings of this study are available from the corresponding author (M.M. and E.Y.), upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Mehran Minbashi, Email: mehran.minbashi@modares.ac.ir.
Elnaz Yazdani, Email: elnaz.yazdani@modares.ac.ir.
Supplementary information
is available for this paper at 10.1038/s41598-020-75686-2.
References
- 1.Müller J, Rech B, Springer J, Vanecek M. TCO and light trapping in silicon thin film solar cells. Sol. Energy. 2004;77:917–930. doi: 10.1016/j.solener.2004.03.015. [DOI] [Google Scholar]
- 2.Wallace SK, Mitzi DB, Walsh A. The steady rise of kesterite solar cells. ACS Energy Lett. 2017;2:776–779. doi: 10.1021/acsenergylett.7b00131. [DOI] [Google Scholar]
- 3.Polman A, Knight M, Garnett EC, Ehrler B, Sinke WC. Photovoltaic materials: Present efficiencies and future challenges. Science. 2016;352:aad4424. doi: 10.1126/science.aad4424. [DOI] [PubMed] [Google Scholar]
- 4.Tao J, et al. Solution-processed SnO2 interfacial layer for highly efficient Sb2Se3 thin film solar cells. Nano Energy. 2019;60:802–809. doi: 10.1016/j.nanoen.2019.04.019. [DOI] [Google Scholar]
- 5.Asim N, et al. A review on the role of materials science in solar cells. Renew. Sustain. Energy Rev. 2012;16:5834–5847. doi: 10.1016/j.rser.2012.06.004. [DOI] [Google Scholar]
- 6.Minbashi M, Ghobadi A, Ehsani MH, Rezagholipour Dizaji H, Memarian N. Simulation of high efficiency SnS-based solar cells with SCAPS. Sol. Energy. 2018;176:520–525. doi: 10.1016/j.solener.2018.10.058. [DOI] [Google Scholar]
- 7.Otoufi MK, et al. Enhanced performance of planar perovskite solar cells using TiO2/SnO2 and TiO2/WO3 bilayer structures: Roles of the interfacial layers. Sol. Energy. 2020;208:697–707. doi: 10.1016/j.solener.2020.08.035. [DOI] [Google Scholar]
- 8.Cui Y, et al. Over 16% efficiency organic photovoltaic cells enabled by a chlorinated acceptor with increased open-circuit voltages. Nat. Commun. 2019;10:1–8. doi: 10.1038/s41467-018-07882-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ge J, et al. Oxygenated CdS buffer layers enabling high open-circuit voltages in earth-abundant Cu2BaSnS4 thin-film solar cells. Adv. Energy Mater. 2017;7:1601803. doi: 10.1002/aenm.201601803. [DOI] [Google Scholar]
- 10.Ghobadi A, et al. Simulating the effect of adding BSF layers on Cu2BaSnSSe3 thin film solar cells. Opt. Mater. (Amst) 2020;107:109927. doi: 10.1016/j.optmat.2020.109927. [DOI] [Google Scholar]
- 11.Jackson P, et al. Effects of heavy alkali elements in Cu(In,Ga)Se2 solar cells with efficiencies up to 22.6% Phys status solidi (RRL)-Rapid Res. Lett. 2016;10:583–586. doi: 10.1002/pssr.201600199. [DOI] [Google Scholar]
- 12.Green MA, et al. Solar cell efficiency tables (version 54) Prog. Photovolt. Res. Appl. 2019;27:565–575. doi: 10.1002/pip.3171. [DOI] [Google Scholar]
- 13.Poplawsky JD, et al. Structural and compositional dependence of the CdTexSe1–x alloy layer photoactivity in CdTe-based solar cells. Nat. Commun. 2016;7:1–10. doi: 10.1038/ncomms12537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Katagiri H, et al. Preparation and evaluation of Cu2ZnSnS4 thin films by sulfurization of E–B evaporated precursors. Sol. Energy Mater. Sol. Cells. 1997;49:407–414. doi: 10.1016/S0927-0248(97)00119-0. [DOI] [Google Scholar]
- 15.Wang W, et al. Device characteristics of CZTSSe thin-film solar cells with 12.6% efficiency. Adv. Energy Mater. 2014;4:1301465. doi: 10.1002/aenm.201301465. [DOI] [Google Scholar]
- 16.Liu X, et al. The current status and future prospects of kesterite solar cells: A brief review. Prog. Photovolt. Res. Appl. 2016;24:879–898. doi: 10.1002/pip.2741. [DOI] [Google Scholar]
- 17.Kim S, et al. Limiting effects of conduction band offset and defect states on high efficiency CZTSSe solar cell. Nano Energy. 2018;45:75–83. doi: 10.1016/j.nanoen.2017.12.031. [DOI] [Google Scholar]
- 18.Katagiri H, et al. Development of CZTS-based thin film solar cells. Thin Solid Films. 2009;517:2455–2460. doi: 10.1016/j.tsf.2008.11.002. [DOI] [Google Scholar]
- 19.Walsh A, Chen S, Wei S, Gong X. Kesterite thin-film solar cells: Advances in materials modelling of Cu2ZnSnS4. Adv. Energy Mater. 2012;2:400–409. doi: 10.1002/aenm.201100630. [DOI] [Google Scholar]
- 20.Yang K-J, et al. A band-gap-graded CZTSSe solar cell with 12.3% efficiency. J. Mater. Chem. A. 2016;4:10151–10158. doi: 10.1039/C6TA01558A. [DOI] [Google Scholar]
- 21.Minbashi M, Omrani MK, Memarian N, Kim D-H. Comparison of theoretical and experimental results for band-gap-graded CZTSSe solar cell. Curr. Appl. Phys. 2017;17:1238–1243. doi: 10.1016/j.cap.2017.06.003. [DOI] [Google Scholar]
- 22.Hironiwa D, Murata M, Ashida N, Tang Z, Minemoto T. Simulation of optimum band-gap grading profile of Cu2ZnSn(S,Se)4 solar cells with different optical and defect properties. Jpn. J. Appl. Phys. 2014;53:71201. doi: 10.7567/JJAP.53.071201. [DOI] [Google Scholar]
- 23.Omrani MK, Minbashi M, Memarian N, Kim DH. Improve the performance of CZTSSe solar cells by applying a SnS BSF layer. Solid State Electron. 2018 doi: 10.1016/j.sse.2017.12.004. [DOI] [Google Scholar]
- 24.Todorov TK, et al. Beyond 11% efficiency: Characteristics of state-of-the-art Cu2ZnSn(S,Se)4 solar cells. Adv. Energy Mater. 2013;3:34–38. doi: 10.1002/aenm.201200348. [DOI] [Google Scholar]
- 25.Son D-H, et al. Effect of solid-H2S gas reactions on CZTSSe thin film growth and photovoltaic properties of a 12.62% efficiency device. J. Mater. Chem. A. 2019;7:25279–25289. doi: 10.1039/C9TA08310C. [DOI] [Google Scholar]
- 26.Bourdais S, et al. Is the Cu/Zn disorder the main culprit for the voltage deficit in kesterite solar cells? Adv. Energy Mater. 2016;6:1502276. doi: 10.1002/aenm.201502276. [DOI] [Google Scholar]
- 27.Chen S, Yang J-H, Gong X-G, Walsh A, Wei S-H. Intrinsic point defects and complexes in the quaternary kesterite semiconductor Cu2ZnSnS4. Phys. Rev. B. 2010;81:245204. doi: 10.1103/PhysRevB.81.245204. [DOI] [Google Scholar]
- 28.Zhai Y-T, et al. Structural diversity and electronic properties of Cu2SnX3 (X= S, Se): A first-principles investigation. Phys. Rev. B. 2011;84:75213. doi: 10.1103/PhysRevB.84.075213. [DOI] [Google Scholar]
- 29.Giraldo S, et al. Progress and perspectives of thin film kesterite photovoltaic technology: A critical review. Adv. Mater. 2019;31:1806692. doi: 10.1002/adma.201806692. [DOI] [PubMed] [Google Scholar]
- 30.Kumar M, Dubey A, Adhikari N, Venkatesan S, Qiao Q. Strategic review of secondary phases, defects and defect-complexes in kesterite CZTS–Se solar cells. Energy Environ. Sci. 2015;8:3134–3159. doi: 10.1039/C5EE02153G. [DOI] [Google Scholar]
- 31.Chen S, Gong XG, Walsh A, Wei SH. Defect physics of the kesterite thin-film solar cell absorber Cu2ZnSnS4. Appl. Phys. Lett. 2010;96:4–7. [Google Scholar]
- 32.Haghighi M, Taghavinia N, Kim D-H, Mahdavi SM, Kordbacheh AA, Minbashi M. A modeling study on utilizing SnS2 as the buffer layer of CZT(S,Se) solar cells. Sol. Energy. 2018;167:165–171. doi: 10.1016/j.solener.2018.04.010. [DOI] [Google Scholar]
- 33.Barkhouse DAR, Gunawan O, Gokmen T, Todorov TK, Mitzi DB. Device characteristics of a 10.1% hydrazine-processed Cu2ZnSn(Se,S)4 solar cell. Prog. Photovolt. Res. Appl. 2012;20:6–11. doi: 10.1002/pip.1160. [DOI] [Google Scholar]
- 34.Shin D, Saparov B, Mitzi DB. Defect engineering in multinary earth-abundant chalcogenide photovoltaic materials. Adv. Energy Mater. 2017;7:1602366. doi: 10.1002/aenm.201602366. [DOI] [Google Scholar]
- 35.Chen S, Wang L-W, Walsh A, Gong XG, Wei S-H. Abundance of CuZn + SnZn and 2CuZn + SnZn defect clusters in kesterite solar cells. Appl. Phys. Lett. 2012;101:223901. doi: 10.1063/1.4768215. [DOI] [Google Scholar]
- 36.Chen S, Walsh A, Gong X, Wei S. Classification of lattice defects in the kesterite Cu2ZnSnS4 and Cu2ZnSnSe4 earth-abundant solar cell absorbers. Adv. Mater. 2013;25:1522–1539. doi: 10.1002/adma.201203146. [DOI] [PubMed] [Google Scholar]
- 37.Su Z, et al. Cation substitution of solution-processed Cu2ZnSnS4 thin film solar cell with over 9% efficiency. Adv. Energy Mater. 2015;5:1500682. doi: 10.1002/aenm.201500682. [DOI] [Google Scholar]
- 38.Mutter D, Dunham ST. Calculation of defect concentrations and phase stability in Cu2ZnSnS4 and Cu2 ZnSnSe4 from stoichiometry. IEEE J. Photovolt. 2015;5:1188–1196. doi: 10.1109/JPHOTOV.2015.2430015. [DOI] [Google Scholar]
- 39.Zhang Y, et al. Structural properties and quasiparticle band structures of Cu-based quaternary semiconductors for photovoltaic applications. J. Appl. Phys. 2012;111:63709. doi: 10.1063/1.3696964. [DOI] [Google Scholar]
- 40.Sun R, et al. High-sulfur Cu2ZnSn(S,Se)4 films by sulfurizing as-deposited CZTSe film: The evolutions of phase, crystallinity and S/(S + Se) ratio. J. Alloys Compd. 2017;695:3139–3145. doi: 10.1016/j.jallcom.2016.11.335. [DOI] [Google Scholar]
- 41.Franckevičius M, et al. Efficiency improvement of superstrate CZTSSe solar cells processed by spray pyrolysis approach. Sol. Energy. 2019;185:283–289. doi: 10.1016/j.solener.2019.04.072. [DOI] [Google Scholar]
- 42.Han J, Shin SW, Gang MG, Kim JH, Lee JY. Crystallization behaviour of co-sputtered Cu2ZnSnS4 precursor prepared by sequential sulfurization processes. Nanotechnology. 2013;24:95706. doi: 10.1088/0957-4484/24/9/095706. [DOI] [PubMed] [Google Scholar]
- 43.Hergert F, Hock R. Predicted formation reactions for the solid-state syntheses of the semiconductor materials Cu2SnX3 and Cu2ZnSnX4 (X= S, Se) starting from binary chalcogenides. Thin Solid Films. 2007;515:5953–5956. doi: 10.1016/j.tsf.2006.12.096. [DOI] [Google Scholar]
- 44.Erkan ME, Chawla V, Repins I, Scarpulla MA. Interplay between surface preparation and device performance in CZTSSe solar cells: Effects of KCN and NH4OH etching. Sol. Energy Mater. Sol. Cells. 2015;136:78–85. doi: 10.1016/j.solmat.2015.01.006. [DOI] [Google Scholar]
- 45.Xie H, et al. Impact of Sn(S,Se) secondary phases in Cu2ZnSn(S,Se)4 solar cells: A chemical route for their selective removal and absorber surface passivation. ACS Appl. Mater. Interfaces. 2014;6:12744–12751. doi: 10.1021/am502609c. [DOI] [PubMed] [Google Scholar]
- 46.Kim S-Y, et al. Void and secondary phase formation mechanisms of CZTSSe using Sn/Cu/Zn/Mo stacked elemental precursors. Nano Energy. 2019;59:399–411. doi: 10.1016/j.nanoen.2019.02.063. [DOI] [Google Scholar]
- 47.Son D-H, et al. Growth and device characteristics of CZTSSe thin-film solar cells with 8.03 percent efficiency. Chem. Mater. 2015;27:5180–5188. doi: 10.1021/acs.chemmater.5b01181. [DOI] [Google Scholar]
- 48.Qi Y-F, et al. Engineering of interface band bending and defects elimination via a Ag-graded active layer for efficient (Cu,Ag)2ZnSn(S,Se)4 solar cells. Energy Environ. Sci. 2017;10:2401–2410. doi: 10.1039/C7EE01405H. [DOI] [Google Scholar]
- 49.Hadke SH, et al. Synergistic effects of double cation substitution in solution-processed CZTS solar cells with over 10% efficiency. Adv. Energy Mater. 2018;8:1802540. doi: 10.1002/aenm.201802540. [DOI] [Google Scholar]
- 50.Xiao Z, Meng W, Li JV, Yan Y. Distant-atom mutation for better earth-abundant light absorbers: A case study of Cu2BaSnSe4. ACS Energy Lett. 2017;2:29–35. doi: 10.1021/acsenergylett.6b00577. [DOI] [Google Scholar]
- 51.Shin D, et al. Earth-abundant chalcogenide photovoltaic devices with over 5% efficiency based on a Cu2BaSn(S,Se)4 absorber. Adv. Mater. 2017;29:1606945. doi: 10.1002/adma.201606945. [DOI] [PubMed] [Google Scholar]
- 52.Gershon T, et al. Photovoltaic materials and devices based on the alloyed kesterite absorber (AgxCu1–x)2ZnSnSe4. Adv. Energy Mater. 2016;6:1502468. doi: 10.1002/aenm.201502468. [DOI] [Google Scholar]
- 53.Guchhait A, et al. Enhancement of open-circuit voltage of solution-processed Cu2ZnSnS4 solar cells with 7.2% efficiency by incorporation of silver. ACS Energy Lett. 2016;1:1256–1261. doi: 10.1021/acsenergylett.6b00509. [DOI] [Google Scholar]
- 54.Khadka DB, Kim J. Band gap engineering of alloyed Cu2ZnGexSn1–xQ4 (Q= S, Se) films for solar cell. J. Phys. Chem. C. 2015;119:1706–1713. doi: 10.1021/jp510877g. [DOI] [Google Scholar]
- 55.Hages CJ, et al. Improved performance of Ge-alloyed CZTGeSSe thin-film solar cells through control of elemental losses. Prog. Photovolt. Res. Appl. 2015;23:376–384. doi: 10.1002/pip.2442. [DOI] [Google Scholar]
- 56.Lie S, et al. Reducing the interfacial defect density of CZTSSe solar cells by Mn substitution. J. Mater. Chem. A. 2018;6:1540–1550. doi: 10.1039/C7TA09668B. [DOI] [Google Scholar]
- 57.Zhou H, et al. Rational defect passivation of Cu2ZnSn(S,Se)4 photovoltaics with solution-processed Cu2ZnSnS4: Na nanocrystals. J. Am. Chem. Soc. 2013;135:15998–16001. doi: 10.1021/ja407202u. [DOI] [PubMed] [Google Scholar]
- 58.Yang K-J, et al. Effects of the compositional ratio distribution with sulfurization temperatures in the absorber layer on the defect and surface electrical characteristics of Cu2ZnSnS4 solar cells. Prog. Photovolt. Res. Appl. 2015;23:1771–1784. doi: 10.1002/pip.2619. [DOI] [Google Scholar]
- 59.Das S, Sa K, Alam I, Mahanandia P. Synthesis of CZTS QDs decorated reduced graphene oxide nanocomposite as possible absorber for solar cell. Mater. Lett. 2018;232:232–236. doi: 10.1016/j.matlet.2018.08.074. [DOI] [Google Scholar]
- 60.Anderson TH, Civiletti BJ, Monk PB, Lakhtakia A. Coupled optoelectronic simulation and optimization of thin-film photovoltaic solar cells. J. Comput. Phys. 2020;407:109242. doi: 10.1016/j.jcp.2020.109242. [DOI] [Google Scholar]
- 61.Sze SM, Ng KK. Physics of Semiconductor Devices. New York: Wiley; 2006. [Google Scholar]
- 62.Swinehart DF. The Beer–Lambert law. J. Chem. Educ. 1962;39:333. doi: 10.1021/ed039p333. [DOI] [Google Scholar]
- 63.Markowich PA, Ringhofer CA, Schmeiser C. Semiconductor Equations. Berlin: Springer; 2012. [Google Scholar]
- 64.Yousefi M, Minbashi M, Monfared Z, Memarian N, Hajjiah A. Improving the efficiency of CZTSSe solar cells by engineering the lattice defects in the absorber layer. Sol. Energy. 2020;208:884–893. doi: 10.1016/j.solener.2020.08.049. [DOI] [Google Scholar]
- 65.Shockley W, Read WT. Statistics of the recombinations of holes and electrons. Phys. Rev. 1952;87:835–842. doi: 10.1103/PhysRev.87.835. [DOI] [Google Scholar]
- 66.Timmo K, et al. Sulfur-containing Cu2ZnSnSe4 monograin powders for solar cells. Sol. Energy Mater. Sol. Cells. 2010;94:1889–1892. doi: 10.1016/j.solmat.2010.06.046. [DOI] [Google Scholar]
- 67.Guo Q, et al. Fabrication of 7.2% efficient CZTSSe solar cells using CZTS nanocrystals. J. Am. Chem. Soc. 2010;132:17384–17386. doi: 10.1021/ja108427b. [DOI] [PubMed] [Google Scholar]
- 68.Redinger A, Berg DM, Dale PJ, Siebentritt S. The consequences of kesterite equilibria for efficient solar cells. J. Am. Chem. Soc. 2011;133:3320–3323. doi: 10.1021/ja111713g. [DOI] [PubMed] [Google Scholar]
- 69.Todorov T, et al. Progress towards marketable earth-abundant chalcogenide solar cells. Thin Solid Films. 2011;519:7378–7381. doi: 10.1016/j.tsf.2010.12.225. [DOI] [Google Scholar]
- 70.Todorov TK, Reuter KB, Mitzi DB. High-efficiency solar cell with earth-abundant liquid-processed absorber. Adv. Mater. 2010;22:E156–E159. doi: 10.1002/adma.200904155. [DOI] [PubMed] [Google Scholar]
- 71.Mitzi DB, Gunawan O, Todorov TK, Wang K, Guha S. The path towards a high-performance solution-processed kesterite solar cell. Sol. Energy Mater. Sol. Cells. 2011;95:1421–1436. doi: 10.1016/j.solmat.2010.11.028. [DOI] [Google Scholar]
- 72.Persson C, Zunger A. Anomalous grain boundary physics in polycrystalline CuInSe2: The existence of a hole barrier. Phys. Rev. Lett. 2003;91:266401. doi: 10.1103/PhysRevLett.91.266401. [DOI] [PubMed] [Google Scholar]
- 73.Yan Y, et al. Electrically benign behavior of grain boundaries in polycrystalline CuInSe2 films. Phys. Rev. Lett. 2007;99:235504. doi: 10.1103/PhysRevLett.99.235504. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author (M.M. and E.Y.), upon reasonable request.