Gender stereotypes can explain the gender-equality paradox

Significance

Recent research has found that the strong underrepresentation of women in math-related fields is more pronounced in more egalitarian and more developed countries. This pattern has been called the “gender-equality paradox.” We show that stereotypes relating math primarily to men are actually stronger in more egalitarian and more developed countries and that they mediate the link between development and segregation across fields of study. The mechanisms connecting socioeconomic development to the strengthening of these stereotypes and the gendering of math-related fields are discussed. Results suggest that gender occupational segregation can be reduced but will not decrease by itself as societies become more developed. Appropriate policies are therefore needed to limit this segregation or its impact on gender inequality.

Abstract

The so-called “gender-equality paradox” is the fact that gender segregation across occupations is more pronounced in more egalitarian and more developed countries. Some scholars have explained this paradox by the existence of deeply rooted or intrinsic gender differences in preferences that materialize more easily in countries where economic constraints are more limited. In line with a strand of research in sociology, we show instead that it can be explained by cross-country differences in essentialist gender norms regarding math aptitudes and appropriate occupational choices. To this aim, we propose a measure of the prevalence and extent of internalization of the stereotype that “math is not for girls” at the country level. This is done using individual-level data on the math attitudes of 300,000 15-y-old female and male students in 64 countries. The stereotype associating math to men is stronger in more egalitarian and developed countries. It is also strongly associated with various measures of female underrepresentation in math-intensive fields and can therefore entirely explain the gender-equality paradox. We suggest that economic development and gender equality in rights go hand-in-hand with a reshaping rather than a suppression of gender norms, with the emergence of new and more horizontal forms of social differentiation across genders.

Although women nowadays outnumber men in higher education, they remain strongly underrepresented in math-intensive fields (1, 2). This underrepresentation is a source of concern for two main reasons: It contributes substantially to gender inequality in the labor market, and it represents a loss of potential talent that could in particular help meeting the growing demand of skills related to the development of information technology and artificial intelligence (1–6).

Despite these concerns, the underrepresentation of women in math-intensive fields has remained constant or even increased in most developed countries during the past two decades (7). This underrepresentation is also more pronounced in more developed countries (8–10) and in countries that are more gender equal in terms of economic and political opportunities and rights (10), a pattern that has been named the “gender-equality paradox” (10).

Similar cross-country paradoxical relationships have been found with a large range of other gender gaps: more gender-egalitarian (in the sense of the Global Gender Gap Index [GGGI], which essentially captures “vertical” or “traditional” gender equality; see details below), and wealthier countries also experience higher gender gaps in basic preferences measured through laboratory experiment (11), cognitive abilities such as spatial visualization (12), self-reported personality traits (13), basic human values (14), self-esteem (15), subjective well-being (16), or depression (17). These associations have led scholars to question gender socialization theories and the gender stratification model (9, 18) according to which gender gaps in interest, performance, and choices are mainly the result of gender gaps in status and opportunities. It has been argued in particular that the gender stratification model fails to account for the fact that countries renowned for gender equality show some of the largest sex differences in interest in and pursuit of science, technology, engineering, and mathematics (STEM) degrees (19).

A common explanation put forward in some recent literature for the gender-equality paradox is that in more equal and developed countries, girls and boys have more freedom and ease to express their intrinsically distinct inner preferences and interests (10–12). This explanation gets its theoretical foundations from the tradition of evolutionary psychology, which posits the existence of innate gender differences in, e.g., personality or interests (20).

In this contribution, in line with a strand of research in sociology, initiated by Charles and coworkers, relating horizontal educational and occupational segregation to gender essentialism (8, 9, 21, 22), we show that the gender-equality paradox could also be explained by differences across countries in culturally constructed gender identities. To this aim, we build a country-level measure of the gender essentialist norm that “math is not for girls,” we show that this measure is larger in more developed and more egalitarian countries, and we establish that it can mediate the paradoxical relationship between economic development or traditional gender equality and the underrepresentation of women in math-related fields.

To discuss the mechanisms connecting socioeconomic development or traditional gender equality to gender essentialism, we rely on previous research that highlights the multidimensional nature of gender equality (9, 23–26) and allows us to suggest possible explanations for the fact that more developed countries that are more gender egalitarian in terms of rights (as measured by the GGGI) can exhibit stronger gender norms, as well as gender inequalities in dimensions such as female representation in math-related fields. We focus primarily on mathematics, as the underrepresentation of women in STEM is large mostly in math-related fields (mathematics, physics, computer science, and engineering).

Materials and Methods

Our main data source is the 2012 Program for International Student Assessment (PISA2012), an every-3-y international assessment of the knowledge and skills of about half a million 15-y-old students in mathematics, reading, and science. PISA2012 takes place in the 34 mostly developed countries belonging to the Organization for Economic Co-operation and Development (OECD) in 2012 and an additional 30 developing countries (SI Appendix), covering in total students from 80% of the world economy. It focuses primarily on math and includes several measures of students’ attitudes to math. We complete PISA2012 with several country-level measures of socioeconomic development, extent of (gender) equality, gender segregation across fields of study, and gender norms or stereotypes (SI Appendix). Empirical analyses presented in the paper rely primarily on country-level correlations and multivariate regressions with a few competing explanatory variables. In robustness checks, we also present student-level regressions that control for some observable students’ characteristics.

A Measure of the Stereotype That “Math Is Not for Girls”

Measuring social norms or stereotypes is prone to many challenges. A direct approach consists in aggregating people’s responses to explicit questions such as “do you think that math is more for boys than for girls?” However, individuals’ explicit statements can be biased by social desirability (27), which can vary across countries depending on, e.g., the salience of gender issues. For this reason, the direct approach is usually considered not satisfactory (28).

An alternative strategy is to use the Implicit Association Test (IAT) (29, 30). It is however not entirely clear that the IAT measures social norms regarding what individuals from different social groups should do rather than perceptions of what they actually do (28, 31, 32). Two other more practical difficulties with the IAT are that results are available on nonrepresentative populations of individuals who volunteer for the test and that it focuses on science in general whereas gender segregation and stereotypes concern primarily math-related fields (e.g., math, physics, and computer sciences rather than biology or chemistry).

Our proposed measure of the importance of stereotypes associating math to males (hereafter GMS for Gender-Math Stereotype) is an attempt to limit as much as possible the problems described above. It is based on systematic differences in subjective norms or perceived control in math between representative girls and boys that have a similar level of ability in math. First, considering a gender gap in response to questions that do not explicitly mention gender is a way to ensure that our measure is not biased by social desirability concerns. Second, controlling for girls’ and boys’ abilities in math ensures that our measure does not capture gender differences in this variable that is likely to affect students’ attitudes to math but may arguably not be entirely the product of social norms.

More specifically, GMS is a country-level standardized index based on average differences between boys’ and girls’ beliefs that “doing well in math is completely up to them” (B1) and that “their parents think that math is important for their career” (B2), conditional on their math ability. B1 should be more affected by gender stereotypes regarding aptitudes for math, and B2 by stereotypes regarding appropriate educational and career choices. GMS is a valid measure of these stereotypes under the assumption that systematic differences in beliefs between girls and boys with similar measured ability are the product of social norms regarding gender roles in math. In this case, GMS recovers indirectly country-level social norms from the extent to which they are internalized by 15-y-old girls and boys.

We estimate GMS using PISA2012. The gender gaps in B1 and B2 are obtained from linear regression models that control for students’ ability for math and are fitted country by country (SI Appendix, Table S1). Across the 64 countries for which we compute it, the gender gap in B1 conditional on math ability averages to 0.10 SD of B1 and vary substantially, from −0.13 SD in Kazakhstan to 0.33 SD in the Netherlands (SI Appendix, Table S2). This gender gap is about three times larger on average among OECD than among non-OECD countries. It is positive (negative) and significantly different from zero in 29 (1) OECD countries and not significantly different from zero in the 4 remaining countries. Similar patterns are observed for the gender gap in B2 and for GMS, which is the gender gap in the arithmetic average of B1 and B2 conditional on math ability (SI Appendix, Table S2).

We retrieved from ref. 33 average respondents’ results at the Gender-Science IAT (SI Appendix) in 50 of the 64 countries in the PISA sample and checked that GMS is positively correlated with this alternative measure of stereotypes (r = 0.64, n = 50 countries, SI Appendix, Table S3). Using a similar strategy to the one used for GMS, we built alternative measures of the gender-math stereotypes from PISA using survey questions aimed at capturing students’ subjective norms or perceived self-responsibility for failing in math. Reassuringly, these measures are strongly correlated with GMS (SI Appendix, Table S3).

Gender-Math Stereotypes and the Gender-Equality Paradox

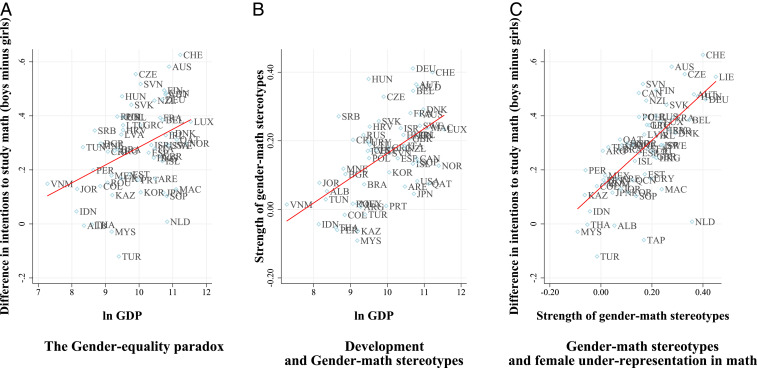
Gender-math stereotypes captured by GMS are positively correlated with the two main measures we use to capture countries’ development: The correlation is 0.47 with gross domestic product (GDP) (n = 61, Fig. 1B) and 0.65 with the Human Development Index (n = 61), which incorporates measures of education and life expectancy on top of economic wealth (row a of Table 1). GMS is also positively correlated with various measures of equality, such as the opposite of the GINI index of income inequality (r = 0.46, n = 56) or the opposite of the coefficient of Human Inequality, which incorporates measures of inequality in terms of education and life expectancy on top of economic inequality (r = 0.68, n = 54). Finally, GMS is also positively correlated with the GGGI (r = 0.43, n = 59), which is a leading composite index used to capture gender equality in the labor market, education, health, or political representation. Regarding the labor market, the index includes gender gaps in labor market participation, wage equality for similar work, and access to higher-rank occupations, but, importantly, it excludes horizontal segregation across jobs or fields of study.

Fig. 1.

Relationships between economic development, GMS, and female underrepresentation in math-related fields. The figure shows scatter plots and linear fits of the relationships between the logarithm of GDP and the gender gap in intentions (A), between the logarithm of GDP and gender-math stereotypes (B), and between gender-math stereotypes and the gender gap in intentions (C).

Table 1.

Relations between gender-math stereotypes (GMS), women’s underrepresentation in math-related fields, and countries’ development or equality

	Measure X of countries’ development or equality
	GDP	Human Development Index	Income equality (opposite of GINI index)	“Human equality” (opposite of coefficient of Human Inequality)	Gender equality (GGI)
a) Correlation of GMS with measures X of countries' development and economic, human, or gender equality	0.468***	0.649***	0.460***	0.680**	0.434***
Comparing the explanatory power of countries' GMS versus countries' development or equality measures X to predict gender gaps in students' intentions to pursue math-related studies or careers (Y)
b) Marginal effect of GMS on Y (regression of Y on GMS when X is available)†	0.677***	0.711***	0.706***	0.689***	0.699***
c) Marginal effect of X on Y (regression of Y on X)	0.326**	0.498***	0.300**	0.545***	0.402***
d) Marginal effect of X on Y controlling for GMS (regression of Y on X and GMS)	0.0116	0.0633	−0.0320	0.141	0.121
e) Marginal effect of GMS on Y controlling for X (regression of Y on X and GMS)	0.672***	0.670***	0.721***	0.593***	0.646***
No. of countries	61	61	56	54	59

All variables are standardized before each correlation or regression to have a mean equal to 0 and a SD equal to 1 on the sample of analysis. See SI Appendix for details on the construction of GMS and the sources of country-level measures of development or equality. ***P < 0.01, **P < 0.05, *P < 0.1.

^†Estimates from linear regression models with one (univariate) or two (horse race) regressors. Y = gender gap (boys minus girls) in intentions to study math or pursue a math career (standardized index).

In our main analysis, we capture female underrepresentation in math-related fields indirectly from the difference between boys’ and girls’ intentions to study math or pursue careers in relation to math (“math intentions”). This approach is validated by the fact that educational or occupational plans in high school have already been shown to be a strong predictor of actual educational plans (34–36). To show that gender-math stereotypes measured with GMS are a good candidate to explain the “gender-equality paradox,” we construct the gender gap in math intentions for a large set of countries using PISA2012 (see SI Appendix for detail and ref. 34) and regress it on either or both GMS and one of our five main measures of development or equality.

All variables used in a specific (linear) regression model have been systematically restandardized so that they have a SD of one on the regression sample. This allows us to compare the magnitude of the effect of our different explanatory variables.

We make three main points from these simple regression models. First, the importance of gender-math stereotypes in a country measured with GMS is positively associated with the gender gap in math intentions (r = 0.45, n = 64, Fig. 1C). In specifications with no additional control variable, a 1 SD increase in GMS is associated with an increase of 0.68–0.71 SD in the gender gap in math intentions, depending on the sample of countries used for the analysis (P < 0.0001 in all models, see row b of Table 1). Second, we do find evidence of a “gender-equality paradox” when we use math intentions to capture female underrepresentation in math-related fields (Fig. 1A). When no additional covariate is included as control variable, the marginal effects of our measures of development or equality on the gender gap in math intentions are always positive and statistically significant (row c of Table 1). These effects are however systematically lower than that of GMS, ranging from 0.30 for income equality (P = 0.025) to 0.55 for human equality (P < 0.0001).

The third point is that when GMS is included as a control, all of the relationships between development or equality and math intentions disappear: The estimated associations become close to zero in magnitude (below 0.15) and are no longer statistically significant (row d of Table 1). In contrast, when a measure of countries’ development or equality is included as a control, the association between GMS and the gender gap in math intentions is virtually unchanged and still statistically significant (row e of Table 1). This simple mediation analysis (see SI Appendix for more formal tests) shows that the “gender-equality paradox” could be explained by the fact that more developed or (gender) egalitarian countries have stronger norms regarding women and math rather than by differences in (innate) preferences that are more easily expressed in the latter countries.

To back up this conclusion, we run a number of robustness checks. First, our main results are not driven by a specific set of developed or developing countries as they hold when we restrict the analysis to either OECD or non-OECD countries (SI Appendix, Table S4). Second, they are not driven either by our indirect measure of female underrepresentation in math-related fields as they also hold when we use instead measures of actual gender segregation across fields of study or occupations (at the cost of reducing sample size, SI Appendix, Table S5). Third, they are not driven by the choice of specific questions to measure gender-math stereotypes as they hold when we use other relevant questions available in PISA2012 (SI Appendix, Table S7 A and B). Fourth, they are not driven either by gender differences in preferences that could be of noncultural origin and affect our measure of stereotypes. To show this, we construct a variant of GMS from the gender gaps in B1 and B2 conditional on both students’ ability in math and their declared interest for math. We then check that our conclusions remain with this more conservative measure of stereotypes (SI Appendix, Table S6).

Finally, our main conclusions are not driven by differences in students’ socioeconomic status, family background, or school attitudes across countries that could affect girls and boys differentially, hence explaining the gender gap in intentions to study math. To show this, we run the student-level counterparts of our main regression models on samples of 120,000–300,000 students and verify that all results are robust to controlling for students’ characteristics (Table 2 for GDP and GMS, SI Appendix, Tables S8–S11 for other results which are discussed in detail).

Table 2.

Stereotypes mediate the “gender-equality paradox,” microlevel evidence

	Dependent variable is standardized intentions to study math or pursue a math career
Girl	−0.269***	−0.253***	−0.191***	−0.198***
SE	(0.0152)	(0.0147)	(0.0138)	(0.0147)
Girl*GDP	−0.000134	−1.06e−05	0.0173	0.0259*
SE	(0.0127)	(0.0127)	(0.0129)	(0.0136)
Girl*GMS	−0.101***	−0.0969***	−0.0811***	−0.0828***
SE	(0.0157)	(0.0155)	(0.0147)	(0.0158)
No. of observations	293,782	293,782	292,395	133,808
Country fixed effects	Yes	Yes	Yes	Yes
Control for math ability	No	Yes	Yes	Yes
Control for math preferences	No	No	Yes	Yes
Other individual controls	No	No	No	Yes

The table displays the results from student-level regression models. All models include country fixed effects, so that the marginal effect of GDP or GMS cannot be estimated. Other individual controls include the level of education of the student’s parents, measured both in years and kind of diploma obtained, grade repetition, an index of economic, social and cultural status of the household, a measure of home educational resources, and a measure of attitude toward school. SEs have been clustered at the country level. Regressions are weighted by “senate” weights which sum to one in each country. See SI Appendix for details on the various measures and on the empirical models. ***P < 0.01, **P < 0.05, *P < 0.1.

Why do More Developed or (Gender) Equal Countries Exhibit Stronger Internalized Gender Stereotypes regarding Math?

At first sight, the fact that more developed or (gender) equal countries exhibit stronger gender norms regarding math may look counterintuitive. There are however good theoretical foundations to explain this pattern. Prominent theories of social norms indeed consider them as a way for dominant social groups to distinguish themselves (37). According to evolutionary psychologists, social differentiation can also be a way to achieve more cooperation between individuals by creating smaller subgroups with clear boundaries (38). Both of those lines of research highlight the processes and natural forces by which norms regarding the attributes, abilities, or appropriate behaviors of different social groups emerge and maintain themselves. Those theories do not exclude that political activism or targeted institutional changes can be efficient to eliminate some types of cultural norms. However, the eliminated sources of social differentiation are likely to be replaced by other type of norms. In particular, the elimination of the traditional gender roles implied by the male breadwinner model does not prevent and can even encourage the emergence of other forms of gender differentiation.

This interpretation is also supported by recent research in sociology focusing specifically on gender norms (8, 9, 39–43). This strand of research examines gender attitudes in several distinct domains and their evolution over time. In particular, it underlines the importance of distinguishing between two dimensions of gender ideology—gender essentialism and male primacy—the first representing men and women as fundamentally different, but not necessarily unequal, and the second representing men as hierarchically superior. Male primacy declined in all countries where it has been examined during the past decades, but it was replaced by distinct varieties of egalitarianism, which are characterized by different mixtures of essentialist and individualistic beliefs, with no country having eliminated gender essentialism (43).

A central reason that may explain why some gender essentialist norms (regarding math or other domains) are more pronounced in wealthier and more egalitarian countries could be that these countries have also developed more emancipative, individualistic, and progressive values (SI Appendix, Table S12) that give a lot of importance to self-realization and self-expression. Such countries tend to “give citizens greater space to fall back on an old, deeply ingrained cultural frame as they try to make sense of themselves and others and organize their choices and behaviors accordingly” (44). To express themselves, individuals in these countries need to make sense of who they are, and to do so, they will fall back on primary identities, including gender (22, 44). This can explain that essentialist gender norms can be more easily internalized in such countries, as these norms will give individuals a cultural background on which they can fall back when facing the need to express their selves.

Instead of limiting the mechanism described above, the larger extent of gender equality in terms of rights (as measured by the GGGI for example) in more individualistic countries can actually reinforce it. This is because the free expression of gender ideals as part of individuals’ gender performance is more likely to be societally approved in gender egalitarian contexts (45). Also, more gender egalitarian countries have de facto more limited gender differences in some well-identified domains such as labor market or political participation. This may exacerbate a need for differentiation on other, and perhaps less salient, dimensions in which individuals would like to perform their gendered identities.

Turning now more specifically to gender norms regarding math, we highlight a few specific mechanisms that could connect them to socioeconomic development. First, math has less instrumental value in wealthier countries since students in these countries need less to study in math-related fields to have good career prospects and guarantee their material security. This can explain that the choice of a field of study and a future professional activity takes a large place in the expression of students’ inner identities in wealthier countries. In these countries, educational or career interests and choices are probably one of the most important domains in which girls and boys have the opportunity to express their gendered selves (45). This combination of low economic constraints binding students’ educational choices and individualistic or emancipative values making these choices a direct expression of students’ “true selves” gives room for gender norms regarding fields of study and career choices to develop. Interestingly, the fact that choices are less economically constrained in wealthier countries is the argument usually given to explain that “deeply rooted” or innate gender differences can be expressed more easily in these countries (10, 11). Here, consistent with the line of research in sociology described above, we argue instead that less economic constraints can also give more room for gender stereotypes to be internalized and affect choices. This interpretation is backed up by empirical evidence at the household level, as in a developed country like the United States, we find that students’ gender essentialist norms captured by GMS are stronger among high-income households than among low-income households.

Second, more developed and egalitarian countries tend to have higher levels of math performance, that are likely to be associated with higher internalized gender math stereotypes. Indeed, research in sociology (46) has shown that stronger country performance implies more difficult curricula, higher performance standards, and greater competition, all of which heighten gender essentialist ideas about math and science. Consistent with this idea, we find that GMS is positively correlated with countries’ average performance in math (SI Appendix, Table S12).

Third, high-income parents spend more time and money on their children, they invest in more stereotypical activities, and they are more involved with their children’s educational choices (47). This could explain that parents in more developed countries transmit earlier, and to a larger extent, gender norms regarding educational aptitudes and choices, resulting in particular in larger gender-math stereotypes (48).

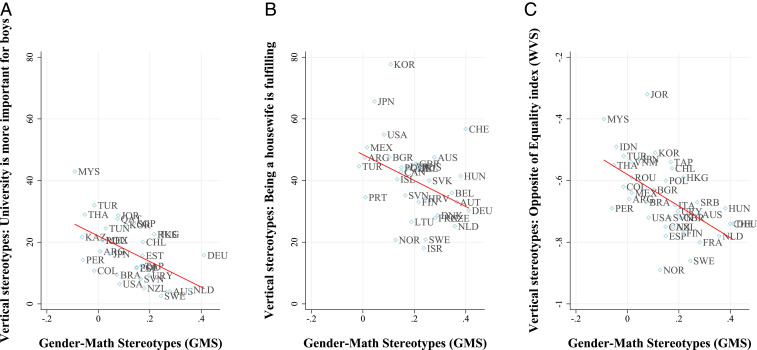
We provide two pieces of evidence broadly consistent with the theoretical arguments above. The first is that across countries, gender-math stereotypes are negatively correlated with traditional gender norms regarding, e.g., the fact that being a housewife is fulfilling or that going to university is less important for women (Fig. 2, Table 3, and SI Appendix, Table S12). In contrast, they are positively correlated with, on the one hand, individualistic and emancipative values, and, on the other hand, gender gaps in gender-stereotyped personality traits and values, as well as other country-level indicators of socially constructed gendered identities (see Table 3 and all details in SI Appendix). This means that countries that have eliminated the most the male-primacy ideology or “vertical gender norms” regarding women access to the labor market or even leadership positions are also countries that have developed more “horizontal essentialist norms” regarding women’s and men’s appropriate skills, behaviors, or emotions. The second piece of evidence is based on alternative measures of gender-math stereotypes that can be constructed both in 2003 and 2012 using questions available in PISA both of those years, making possible a study of the joint evolution of these stereotypes and other outcomes. Most of the relationships between the country-level evolutions of stereotypes and economic development or inequalities are small and not statistically significant over the period 2003–2012, likely because this period is too short to induce substantial changes in the measured outcomes. However, the few relationships that are significant provide some support for our main interpretation as we find that countries that grew the most between 2003 and 2012 in terms of GDP also developed more than others horizontal gender norms (SI Appendix, Table S13 and its discussion).

Fig. 2.

Relation between GMS and three measures capturing traditional gender roles. The figure shows measures of traditional gender roles (“vertical stereotypes”) against our measure of GMS. Measures of traditional gender roles are based on the ISSP survey of 2012 and the World Value Surveys (2005-2009 and 2010–2014). The first two graphs correspond to the share of men and women agreeing with the statements that “University is more important for a boy than a girl” (A) and “being a housewife is fulfilling” (B). C shows the value of the opposite of the equality index by country. See the data section in SI Appendix for details on the construction of the GMS and other measures of gender stereotypes.

Table 3.

Correlation of GMS with some country-level measures of essentialist gender attributes, traditional gender roles, and liberal values

	GMS
Essentialist gender attributes (“horizontal” stereotypes):
Gender gap in feminine extraversion (49)	0.763***
Gender gap in feminine openness (49)	0.698***
Gender gap in the share of individuals agreeing with the statement that family is important (WVS 2010–2014)	0.738***
Traditional gender roles (“vertical” stereotypes): belief by women and men that…
“Women should take care of their home and children” (ISSP 2012)	−0.386**
“Being a housewife is fulfilling” (ISSP 2012)	−0.392**
“University is more important for boys than girls” (WVS 2010–1014)	−0.532***
Index of traditional gender norms (opposite of Equality index, WVS 2005–2009)	−0.559***
“Liberal values”:
Individualism (33)	0.611***
Emancipative values (WVS 2005–2009)	0.621***

The table shows the correlation between our measure of GMS and a series of country-level variables. See SI Appendix for details on the construction of GMS and the other variables. ***P < 0.01, **P < 0.05, *P < 0.1.

Conclusion

The theory and results above reinforce the idea that gender segregation across fields of study or occupations will not decrease by itself as societies become more developed and egalitarian (24, 45). Appropriate policies are needed to induce such a change, or at least to limit the extent to which gender segregation generates inequality on the labor market. Similar conclusions are likely to be reached regarding gender differences in personality traits, values, or behaviors such as willingness to compete or risk aversion: These differences, which can also contribute to economic inequalities between women and men, are likely to remain even when countries become more developed. This is not because they are innate, but because they are the product of new forms of social differentiation between women and men that have replaced the male primacy ideology.

Data Availability.

Anonymized, publicly available data have been deposited in https://www.openicpsr.org/openicpsr/project/123361/version/V1/view.