Layer and rhythm specificity for predictive routing

Significance

An established theoretical model, predictive coding, states that the brain is constantly building models (signifying changing predictions) of the environment. The brain does this by forming predictions and signaling sensory inputs which deviate from predictions (“prediction errors”). Various hypotheses exist about how predictive coding could be implemented in the brain. We recorded neural spiking and oscillations with laminar resolution in a network of cortical areas as monkeys performed a working memory task with changing stimulus predictability. Predictability modulated the patterns of feedforward/feedback flow, cortical layers, and oscillations used to process a visual stimulus. These data support the theory of predictive coding but suggest an alternate model for its neural implementation: predictive routing.

Abstract

In predictive coding, experience generates predictions that attenuate the feeding forward of predicted stimuli while passing forward unpredicted “errors.” Different models have suggested distinct cortical layers, and rhythms implement predictive coding. We recorded spikes and local field potentials from laminar electrodes in five cortical areas (visual area 4 [V4], lateral intraparietal [LIP], posterior parietal area 7A, frontal eye field [FEF], and prefrontal cortex [PFC]) while monkeys performed a task that modulated visual stimulus predictability. During predictable blocks, there was enhanced alpha (8 to 14 Hz) or beta (15 to 30 Hz) power in all areas during stimulus processing and prestimulus beta (15 to 30 Hz) functional connectivity in deep layers of PFC to the other areas. Unpredictable stimuli were associated with increases in spiking and in gamma-band (40 to 90 Hz) power/connectivity that fed forward up the cortical hierarchy via superficial-layer cortex. Power and spiking modulation by predictability was stimulus specific. Alpha/beta power in LIP, FEF, and PFC inhibited spiking in deep layers of V4. Area 7A uniquely showed increases in high-beta (∼22 to 28 Hz) power/connectivity to unpredictable stimuli. These results motivate a conceptual model, predictive routing. It suggests that predictive coding may be implemented via lower-frequency alpha/beta rhythms that “prepare” pathways processing-predicted inputs by inhibiting feedforward gamma rhythms and associated spiking.

The brain exploits predictability. It makes cortical processing more efficient. Visuomotor integration, visual/auditory speech perception, and visual perception all benefit when sensory inputs are predictable (1–3). The brain has an arsenal of mechanisms to tamp down and improve processing of familiar, repeated, or predictable inputs. One example is stimulus-specific adaptation. All over cortex, there is less spiking and smaller blood-oxygen-level-dependent (BOLD) responses when a stimulus is repeated (4–9). Responsiveness is recovered if the stimulus is changed or a pattern is violated (i.e., to “oddballs”) (10, 11). This can lead to fewer activated neurons but finer-tuned, more robust representations (8).

But the brain does more than adapt to repeated inputs. A wide variety of evidence indicates that it makes mental models of the world that actively generate predictions, a process known as predictive coding (12–14). Moment-to-moment predictions are used to inhibit processing of expected inputs which, because they were expected, are not informative. Unexpected sensory inputs that deviate from a prediction, are “prediction errors” (PEs). They are informative and thus not inhibited, fed forward, processed, affect behavior, and are used to update the prediction models.

Much of the work on the neural mechanisms of prediction and its violation has focused on spiking activity (2, 15–17). But there is mounting evidence that oscillatory dynamics play a role in regulating cortical processing and thus can also play a role, especially the gamma (40 to 90 Hz) and alpha/beta (10 to 30 Hz) bands (1, 18–25). A key observation is that, all across cortex, gamma power (>35 Hz)/spiking is higher during bottom-up sensory inputs. They are anticorrelated with alpha/beta (8 to 30 Hz) power (26–29), which is higher under conditions of top-down control (e.g., attention and response inhibition) (30–34). This suggests that top-down alpha/beta help regulate the processing of bottom-up inputs served by gamma and spiking. The idea is that alpha/beta carries the top-down predictions that inhibit the gamma/spiking that process expected inputs. This is consistent with gamma power being higher in the superficial, feedforward, cortical layers, and alpha/beta power being higher in the deep, feedback, cortical layers (26, 35–40). Indeed, superficial cortical layers have been hypothesized to be specialized for computing PEs and feeding PEs forward at gamma frequency (1, 19). In addition, computational modeling studies have shown the plausibility of superficial gamma circuits to engage in prediction error computations (38, 41, 42). Direct evidence for alpha/beta and gamma in predictive coding per se comes from observations of increased gamma power to stimuli that are prediction errors (22, 24, 25).

How these rhythms (and their relation to spiking) differ with stimulus repetition/predictability as well as their stimulus specificity is not well known. Most neurophysiological studies of the effects of stimulus predictability have focused on spiking activity, often in a single area. And none of them to date have examined and compared activity in different cortical layers. We recorded local field potentials (LFPs) and spiking using multiarea, multilaminar recordings from a visual area (V4) and higher-order cortical areas (posterior parietal cortex and prefrontal cortex [PFC]) simultaneously. Area V4 was selected as previous studies have shown this area to be a target of top-down signals such as attention (43, 44). Frontoparietal cortex was targeted because of its well-established role in top-down attention and working memory, cognitive processes that are engaged in the task employed here (30, 31). We manipulated the predictability of objects used in a working memory task. This revealed layer and frequency-specific associations with stimulus repetition/predictability as well as evidence for the direction of flow of these signals. The findings suggest an update of neural models of prediction and predictive coding.

Results

Task, Behavior, and Neurophysiological Recordings.

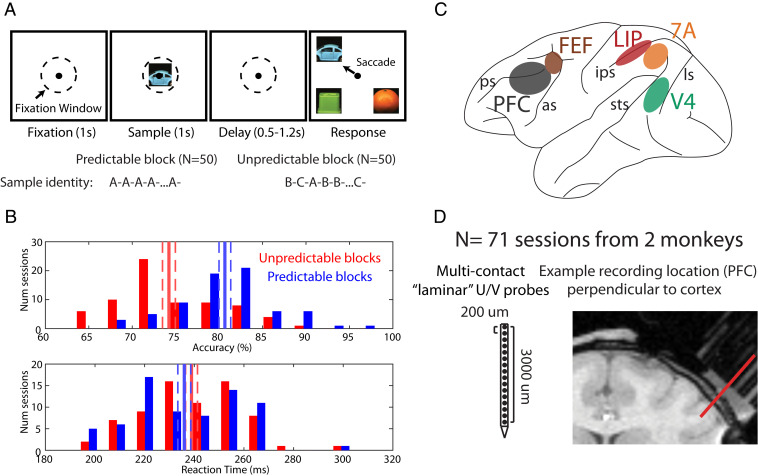
Monkeys performed a delayed match to sample (DMS) task (Fig. 1A). The task was performed in one of two modes: 1) unpredictable blocks, where one of three objects was chosen randomly as a sample on each trial for a block of 50 trials; and 2) predictable blocks, where the same object was used as a sample for 50 consecutive trials. The purpose of the DMS task was to ensure that animals were always engaged and attending to the stimuli.

Fig. 1.

Task design, recordings, and behavior. (A) Task design: after a 1-s fixation interval, a sample stimulus (one of three pictures) was shown for 1 s. After a variable delay, the sample reappeared at one of four locations (always randomized). Monkeys saccaded to the sampled stimulus. The sample identity was either randomized (unpredictable blocks) or held constant (predictable blocks). (B) Behavioral performance across 71 sessions. (Upper) Accuracy on the task during predictable vs. unpredictable blocks. (Lower) Same, but for reaction time. Solid red/blue bars denote the mean performance and dashed bars denote the mean ± SEM across sessions. (C) Recorded brain areas. PFC: prefrontal cortex, FEF: frontal eye fields, LIP: lateral intraparietal area, 7A: posterior parietal area 7A, V4: visual area 4. (D) Multielectrode 16 channel Plexon U/V probes with 200 μm site-to-site spacing. MRIs were used to select grid locations for laminar (perpendicular) access in areas located on cortical gyri: V4, 7A, and PFC. An example penetration in PFC is shown.

Choosing the match was more accurate and faster when the sample, seen 0.5 to 1.2 s before, had been predictable. Fig. 1 B, Upper shows the distribution of average performance across sessions and monkeys for predictable vs. unpredictable blocks. Average performance during predictable blocks was 80.6% vs. 74.2% for unpredictable blocks (sign test across sessions, P < 1E-8). Fig. 1 B, Lower shows the corresponding distribution for reaction time (RT). Although the RT effect size was small, the match was found significantly more quickly during predictable vs. unpredictable blocks (mean RT predictable: 236 ms; mean RT unpredictable: 239 ms; sign test across sessions, P = 0.017).

We recorded spiking and LFPs using multilaminar electrodes (Fig. 1D) in five cortical areas spanning sensory (V4), posterior parietal (lateral intraparietal area [LIP] and posterior parietal area 7A), and PFC and frontal eye fields [FEFs] (Fig. 1C) in two monkeys over 71 sessions. For areas on cortical gyri (V4, 7A, and PFC), we introduced the electrodes perpendicular to cortex (Fig. 1D) to resolve recordings into superficial layers (2/3) vs. deep layers (5/6). Data were aligned to the top of cortex as this was the most robust metric with minimal assumptions (SI Appendix, Experimental Procedures). Areas FEF and LIP are located in sulci. Recordings there were not layer resolved.

Neurophysiological analysis focused on the 1 s of fixation before the sample (presample interval) and the 1 s of sample presentation (sample interval). During the presample interval, monkeys could have an expectation of the forthcoming sample during predictable blocks. Once the sample appeared (sample interval), predictions about the sample could be confirmed or violated.

Neuronal Spiking Was Greater to Unpredictable than Predictable Samples.

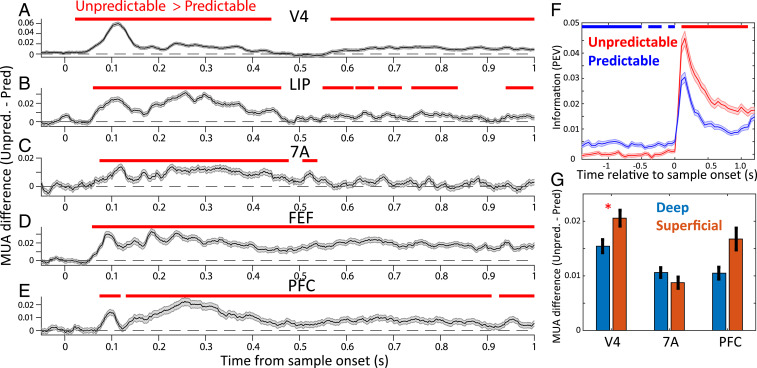
During the sample interval, spike rates were higher if the sample was unpredictable compared to when it was predictable. The black lines in Fig. 2 A–E show the average multiunit activity (MUA) for unpredictable minus predictable blocks (see SI Appendix, Experimental Procedures for data preprocessing steps; for MUA response to unpredictable vs. predictable without subtraction, see SI Appendix, Fig. S1). Positive numbers mean more spiking during unpredictable than predictable blocks. MUA in all areas showed greater spiking (Fig. 2 A–E, red bars, cluster-based randomization testing, P < 0.05) to unpredictable than predictable samples. Further, analysis of single neurons (SI Appendix, Experimental Procedures) confirmed that, during sample presentation, spikes also carried more information when the sample was unpredictable (P < 0.05 cluster-based randomization test, Fig. 2F). V4 spiking carried more sample information than other areas (SI Appendix, Fig. S3A, Wilcoxon rank sum test, V4 vs. all individual areas, all comparisons P < 0.01). Further, the increase in spiking to unpredictable samples was stronger in superficial than deep layers (Fig. 2G) in area V4 but not in 7A or PFC (Wilcoxon rank sum test for MUA difference, unpredicted minus predicted, in superficial vs. deep at 0.1 to 0.5 s postsample onset, P < 0.05).

Fig. 2.

Spiking to unpredictable vs. predictable samples. (A–E) MUA of unpredictable minus predictable blocks. Mean across all available MUAs per area (N = 1,664, 736, 704, 880, and 1,472 for V4, LIP, 7A, FEF, and PFC, respectively), ±1 SEM across MUAs. Horizontal bars denote significance at P < 0.05 for unpredictable vs. predictable, corrected for multiple comparisons (SI Appendix, Experimental Procedures). (F) Mean information ± SEM, quantified with percent explained variance (PEV) (see Experimental Procedures) in thresholded single units across all areas about the sample during predictable (blue line) vs. unpredictable (red line) blocks. Horizontal blue bars indicate significant (P < 0.05, corrected for multiple comparisons) unpredictable < predictable information. Horizontal red bars indicate significant (P < 0.05, corrected for multiple comparisons) unpredictable > predictable information. (G) Unpredictable minus predictable MUA for deep layers (5/6) vs. superficial layers (2/3), averaged between 0.1 and 0.5 s postsample onset. Mean ± SEM across MUAs in superficial (N = 575, 215, 397 for areas V4, 7A, and PFC) vs. deep layers (N = 615, 248, and 468 for areas V4, 7A, and PFC). Red asterisk denotes significant differences.

As expected, given randomly drawn samples during unpredictable blocks, spiking during the presample interval carried no information about the identity of the forthcoming sample. It did during predictable blocks in all areas (P < 0.05 cluster-based randomization test, Fig. 2F). PFC carried more information about the identity of the forthcoming sample than area V4 (SI Appendix, Fig. S3B, Wilcoxon rank sum test, V4 vs. PFC, P < 1E-4). In addition, we analyzed whether the difference in neural information between unpredictable and predictable blocks was stronger in superficial vs. deep layers. In the sample interval this positive difference (more neural information in unpredictable blocks) was stronger in superficial layers compared to deep layers (SI Appendix, Fig. S3C, Right subpanel, Wilcoxon rank sum test, P < 0.01). In the presample interval this negative difference (more neural information in predictable blocks) was stronger in deep layers compared to superficial layers (SI Appendix, Fig. S3C, Left subpanel, Wilcoxon rank sum test, P < 1E-8).

Predictability Changed the LFP Power Balance.

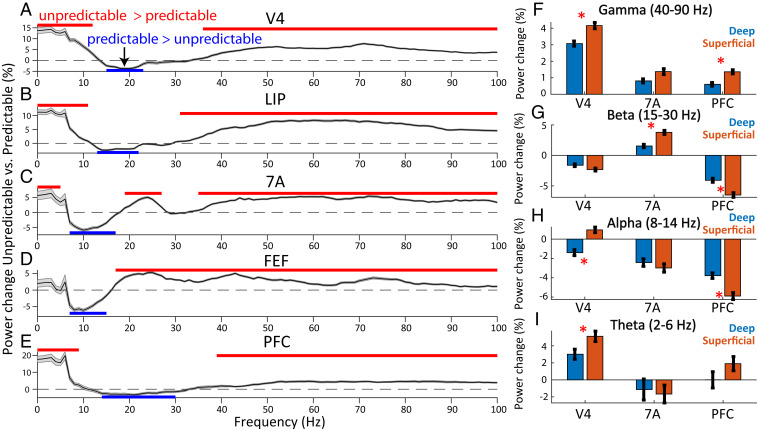
Sample predictability had different effects on different oscillatory bands/layers/areas. For each frequency, we calculated percent change in LFP power for unpredictable vs. predictable blocks (Fig. 3 A–E). During the sample interval, gamma-band power (∼40 to 90 Hz) was higher to unpredictable samples in all areas. In all areas except FEF, theta-band power (∼2 to 6 Hz) was higher to unpredictable than predictable samples (red lines in Fig. 3 A–E indicate significantly more power during unpredictable samples, P < 0.05, cluster-based randomization test). The alpha (8 to 14 Hz) and beta (15 to 30 Hz) bands generally showed the opposite effect (blue lines in Fig. 3 indicate significantly more power during predictable samples, P < 0.05, cluster-based randomization test). It was generally higher to predictable than unpredictable samples. The one exception was posterior parietal area 7A where there was higher power in a high-beta band (∼20 to 27 Hz) during unpredictable samples (Fig. 3C, but note that in 7A, power in a lower frequency band, 6 to 14 Hz, was higher for predictable samples). The differences in power between predictable vs. unpredictable blocks remained to a large extent significant even after equating for the time between repetitions of the same sample in the two block types (SI Appendix, Supplemental Results and Fig. S5).

Fig. 3.

LFP power for unpredictable vs. predictable samples. (A–E) Unpredictable vs. predictable percent change in LFP power from 0 to 100 Hz during the 1-s sample processing interval. Mean across all available bipolar derivations of LFPs per area (N = 1,483, 666, 650, 793, and 1,358 for V4, LIP, 7A, FEF, and PFC, respectively), ±1 SEM across LFPs. Horizontal red bars denote significance at P < 0.05 for power in unpredictable > predictable blocks, blue bars for power in predictable > unpredictable blocks (corrected for multiple comparisons). (F–I) Percent change in LFP power for unpredictable vs. predictable samples for deep vs. superficial layers in different bands. (F) Gamma band (40 to 90 Hz), (G) beta band (15 to 30 Hz), (H) alpha band (8 to 14 Hz), (I) theta band (2 to 6 Hz). Mean ± SEM across LFPs in superficial (N = 564, 227, and 410 for areas V4, 7A, and PFC) vs. deep layers (N = 586, 245, and 480 for areas V4, 7A, and PFC). Red asterisk denotes significant (P < 0.05) differences.

The strength of these power differences varied as a function of layer. Areas V4 and PFC showed a greater increase in superficial-layer than deep-layer gamma power during unpredictable samples (Fig. 3F, Wilcoxon rank sum test comparing power modulation in superficial vs. deep layers, P < 0.05) as did theta in area V4 (Fig. 3I). The PFC showed a greater increase in superficial layer than deep alpha (8–14 Hz) and beta (15 to 30 Hz) during predictable samples (Fig. 3 G and H, Wilcoxon rank sum test, P < 1E-3 for both alpha and beta). Area 7A showed a greater increase in superficial layer than deep beta (15–30 Hz) during unpredictable samples (Fig. 3G, Wilcoxon rank sum test, P < 1E-4). In area V4 in the alpha band (8–14 Hz), superficial and deep layers had different signs of modulation with respect to sample predictability. V4 deep-layer alpha increased with predictable samples but superficial-layer alpha increased to unpredictable samples (Fig. 3H, Wilcoxon rank sum test comparing power modulation in superficial vs. deep layers, P < 1E-8).

In, general, the sites with strong MUA modulation (unpredictable vs. predictable) were also sites with strong LFP gamma power modulation (unpredictable vs. predictable, SI Appendix, Supplemental Results and Fig. S2). The positive relationship between MUA and LFP gamma-power modulation was consistently strongest in superficial as compared to deep layers (SI Appendix, Fig. S2B, Wilcoxon rank sum test comparing correlation between MUA and gamma-power modulation in superficial vs. deep layers, P < 1E-4 for all areas). By contrast, in area V4 the negative relationship between MUA and LFP alpha- and beta-power modulation were consistently strongest in deep as compared to superficial layers (SI Appendix, Fig. S2 C and D, Wilcoxon rank sum test comparing correlation between MUA and alpha- and beta-power modulation in superficial vs. deep layers, P < 0.05 for both alpha and beta).

The increase in gamma and theta power was greater in V4 compared to higher areas (SI Appendix, Fig. S3 D and G). V4 showed the greatest increase in gamma and theta power during unpredictable samples while PFC/7A showed the smallest. In contrast, in the alpha band (8 to 14 Hz), LIP, PFC, and 7A had the strongest power modulation to predictable samples. The strength of alpha-band power modulation in all higher-order areas was stronger than in V4 (SI Appendix, Fig. S3F, V4 alpha-band power modulation vs. all other areas, Wilcoxon rank sum test, P < 1E-2). In the beta band (15 to 30 Hz) PFC had the strongest power modulation to predictable samples of any area (SI Appendix, Fig. S3E, PFC beta-band power modulation vs. all other areas, Wilcoxon rank sum test, P < 1E-16 for all comparisons).

Sample predictability also modulated LFP power during the presample interval but the effects were weaker and sparser. There was greater gamma/high-beta power during unpredictable than predictable blocks in V4, LIP, and 7A and reduced alpha/beta power in V4, 7A, and FEF (P < 0.05, SI Appendix, Fig. S4 A–E). During the presample interval, power modulation did not differ between superficial vs. deep layers (all comparisons, P > 0.05).

Violation of Predictions and Time Course of Prediction.

During predictable blocks, a strong expectation of a specific sample object could build. Then, when there was a switch to an unpredictable block, that expectation was violated for at least the first few trials. We examined the LFP power as a function of the number of trials since a switch from a predictable to an unpredictable block. This revealed strong gamma increases in all areas that were maximal within the first few trials of such a “violation” of expectation (SI Appendix, Supplemental Results and Fig. S6A).

We next analyzed the trial-by-trial power change in predictable blocks relative to the switch from an unpredictable block. For this analysis, each trial’s power on predictable trials compared to the average of all trials during an unpredictable block. In the gamma band, responses to predictable samples gradually reduced, reaching their minimum response at different trials in different areas. This followed a hierarchical progression with V4 reaching its minimum earliest at trial 19 (reflecting 18 repetitions), LIP at trial 35, 7A at trial 46, and both FEF and PFC at trial 49 (SI Appendix, Fig. S7A). In the alpha and beta bands, sample repetition caused power to increase. This plateaued after a number of repetitions. There was no clear hierarchical progression, with different areas reaching their maximum alpha/beta power in a wide variety of repetitions (range in areas LIP, 7A, FEF, and PFC: trials 12 to 47, SI Appendix, Fig. S7B). These increases in beta power and decreases in theta/gamma power tracked the animals’ behavioral improvement within predictable blocks (SI Appendix, Supplemental Results and Fig. S8).

Stimulus Specificity of Spiking and LFP Power Modulation.

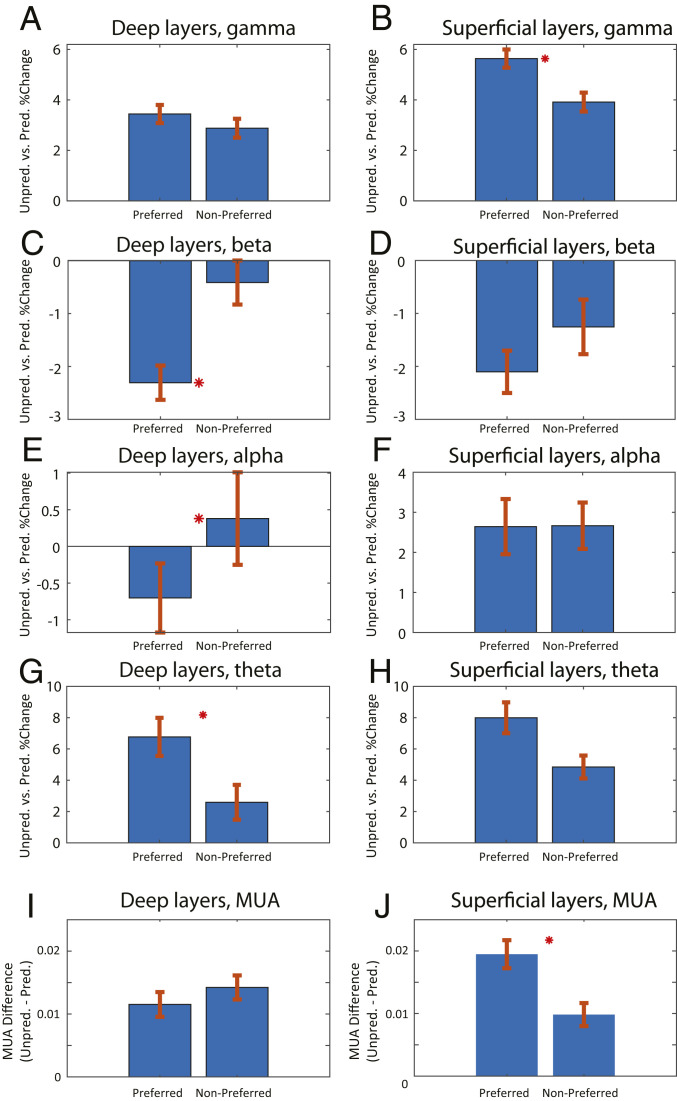
We next investigated whether the effects of predictability were stimulus specific. We tested whether the modulation of LFP power was strongest at recording sites that preferred (showed higher spiking to) the specific stimulus that is being predicted. We addressed this in V4 because its spiking showed the strongest spiking selectivity for the identity of the sample objects (SI Appendix, Fig. S3A).

We first analyzed each V4 site’s MUA activity for sample object specificity. For each V4 site, the sample that produced the highest MUA activity was defined as the “preferred” sample. The sample object that produced the least MUA activity was the “nonpreferred” sample. We calculated differences in power during unpredictable vs. predictable blocks for the preferred and nonpreferred samples separately.

Power modulation was stimulus specific. It was higher for the recording site’s preferred than nonpreferred sample object. During the sample interval, LFP gamma power and MUA modulation (unpredictable > predictable) was greater to the preferred sample in superficial cortical layers (P < 0.01, Wilcoxon rank sum test comparing each site’s preferred vs. nonpreferred power modulation) but not in deep layers (Fig. 4 A and B for LFP gamma and Fig. 4 I and J for MUA). An ANOVA testing for interaction between factors preference and layer on neural modulation by predictability revealed a significant interaction for MUA (P < 0.05 for MUA, P = 0.056 for gamma). Alpha- and beta-power modulation (predicted > unpredicted) was stronger to the preferred object in deep cortical layers (Fig. 4 C and E, P < 0.05, Wilcoxon rank sum test comparing each site’s preferred vs. nonpreferred power modulation) but not superficial (Fig. 4 D and F, P > 0.05, Wilcoxon rank sum test). Theta-power modulation (unpredictable > predictable) was significantly greater for preferred vs. nonpreferred samples only in deep layers (P < 0.05, Wilcoxon rank sum test comparing each site’s power modulation for preferred vs. nonpreferred sample objects, Fig. 4G). ANOVAs testing for interactions between factors preference and layer on neural modulation by predictability were not significant for theta, alpha, or beta (P > 0.05). Similar selectivity effects on LFP power were found in the presample interval (SI Appendix, Supplemental Results and Fig. S4).

Fig. 4.

Pathway specificity of LFP power and MUA modulation. (A–H) Unpredicted vs. predicted percent change in LFP power for the preferred and nonpreferred stimulus. (A) Deep layers in the gamma band (40 to 90 Hz), (B ) superficial layers in the gamma band, (C) deep layers in the beta band (15 to 30 Hz), (D) superficial layers in the beta band, (E) deep layers in the alpha band (8 to 14 Hz), (F) superficial layers in the alpha band, (G) deep layers in the theta band (2 to 6 Hz), (H) superficial layers in the theta band. (I) MUA modulation of deep cortical layers in area V4, unpredictable minus predictable during the sample interval, (J) same as I, but for superficial layers. Mean ± SEM. Red asterisk denotes significant (P < 0.05) differences between neural modulation of preferred vs. nonpreferred samples.

Network Interactions for Predictability.

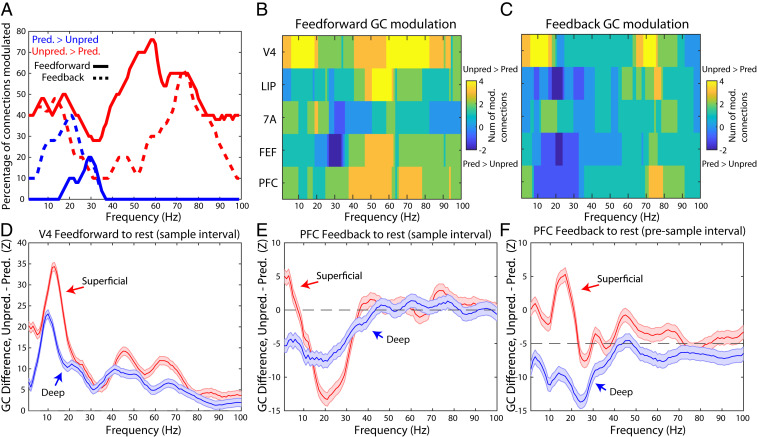
We first examined network interactions using coherence analysis between LFPs recorded in each pair of areas. During the sample interval, this confirmed coherence networks involving theta and gamma for unpredictable samples and alpha and beta for predictable samples (SI Appendix, Supplemental Results and Figs. S9 and S10, for presample coherence, see SI Appendix, Fig. S11). We next examined the direction of interactions between areas. We used nonparametric Granger causality (GC), which separately measures the impact of area A to B vs. B to A at each frequency from 1 to 100 Hz (45). To assess feedforward vs. feedback flow, we assumed the following cortical hierarchy (from lower to higher): V4, LIP, 7A, FEF, and PFC (46). We first focused on the sample interval. Fig. 5A shows the percentage of significantly modulated connections (cluster-based randomization test, P < 0.05) for both feedforward (solid lines) and feedback (dotted lines) directions (modulation of Granger causality for all individual area pairs is shown in SI Appendix, Fig. S12). The red line indicates unpredictable > predictable GC while the blue line shows the opposite (cluster-based randomization test, P < 0.05). Fig. 5 B and C show the sums of modulated connections per area as a function of whether connections into and out of the area were feedforward or feedback, respectively.

Fig. 5.

Granger causal networks for unpredicted vs. predicted samples. (A) Percentage of interareal functional connections with significant (P < 0.05, corrected for multiple comparisons) task modulation (red lines: unpredictable > predictable; blue lines: unpredictable < predictable), separately for feedforward (solid lines) and feedback (dotted lines). (B) Number of feedforward functional connections into and out of each area that are modulated as a function of frequency (yellow colors represent number of functional connections with more unpredictable > predictable Granger causality; blue lines represent number of functional connections with more unpredictable < predictable Granger causality). (C) Same as B, but for feedback Granger causality. (D) Granger causal z-score difference, unpredictable minus predictable, from V4 to other areas (feedforward functional connections) during the sample interval for superficial (red lines) vs. deep (blue lines). Mean ± SEM. (E) Granger causal z-score difference, unpredictable minus predictable, from PFC to other areas (feedback functional connections) during the sample interval for superficial (red lines) vs. deep (blue lines). Mean ± SEM. (F) same as E, but for the presample interval.

The strength and sign of modulation of GC by predictability depended on frequency and directionality. In the feedforward direction, unpredictable > predictable GC modulation peaked in the gamma-frequency range (Fig. 5A, solid red lines). Although the feedback direction was also positively modulated (Fig. 5A, dotted red lines), the percentage of modulated connections was lower than feedforward gamma (χ² test for percentage of positive modulation across the gamma band, 40 to 90 Hz, in the feedforward vs. feedback directions, 0.57 vs. 0.33, P < 1E-13). In the theta band (2–6 Hz), an approximately equal percentage of both feedforward and feedback connections had positive task modulation (unpredicted > predicted GC).

Notably, virtually all directed functional connections with greater GC during predictable than unpredictable samples were in the alpha and beta bands (blue lines in Fig. 5A). And they were mostly feedback connections. The percentage of feedback direction GC that was greater for predictable than unpredictable samples was higher than those in feedforward direction for alpha (χ² test for percentage of negative modulation across the alpha band, 8 to 14 Hz, in the feedforward vs. feedback directions, 0% vs. 29%, P < 1E-5), beta (χ² test for percentage of negative modulation across the beta band, 15 to 30 Hz, in the feedforward vs. feedback directions, 10% vs. 30%, P < 1E-5), and theta (χ² test for percentage of negative modulation across the theta band, 2 to 6 Hz, in the feedforward vs. feedback directions, 0% vs. 10%, P < 0.05). There was no predictable > unpredictable GC modulation in the gamma band in either direction. In short, feedforward functional connections were enhanced during unpredictable samples, especially in the gamma range, whereas feedback functional connections were enhanced during predictable samples with a peak at alpha/beta frequencies.

To determine the layer specificity of these effects, we focused on the two areas at the bottom and top of the hierarchy: V4 and PFC. The rationale was that GC interactions from V4 to the other areas are all feedforward, and interactions from PFC to the other areas are all feedback. The modulation of these feedforward and feedback functional connections by layer is shown in Fig. 5D (for V4) and Fig. 5E (for PFC) during the sample interval, and for PFC during the presample interval in Fig. 5F.

During the sample interval, feedforward connections from V4 to the rest of the areas were greater during unpredictable samples. This modulation was greater in superficial layers than deep layers in theta, alpha, beta, and gamma bands (Fig. 5D, Wilcoxon rank sum test comparing modulations for all feedforward channel pairs in superficial vs. deep layers, P < 1E-3 for theta, P < 1E-14 for alpha, P < 1E-8 for beta, and P < 1E-3 for gamma). By contrast, in PFC feedback, GC was greater during predictable samples, especially in the beta band (Fig. 5E). This effect was stronger in superficial than deep layers (Fig. 5E, Wilcoxon rank sum test comparing task modulations for all feedback channel pairs in superficial vs. deep, P < 1E-16 for the beta band, not significant for the alpha band). In the theta band, PFC feedback GC in deep layers was significantly stronger during predictable samples compared to superficial layers (Fig. 5E, Wilcoxon rank sum test comparing task modulations for all feedback channel pairs in superficial vs. deep, P < 1E-5 for the theta band).

During the presample interval, PFC feedback was different depending on whether it arose from superficial vs. deep layers. Superficial-layer PFC feedback was greater during unpredictable blocks but deep-layer PFC feedback was greater during predictable blocks (Fig. 5F). The differences between layers was significant for theta, alpha, and beta (Fig. 5F, Wilcoxon rank sum test comparing modulations for all feedback channel pairs in superficial vs. deep layers, P < 0.01 for the theta band, P < 1E-7 for the alpha and beta bands).

Higher Order Cortex Modulates Spiking and Gamma in V4.

Finally, we analyzed whether oscillations in higher-order areas (LIP, 7A, FEF, and PFC) couple to, and potentially inhibit, spiking and gamma in area V4. We used a general linear modeling (GLM) framework (see Experimental Procedures) to test whether MUA and gamma in V4 could be explained by power in higher-order cortex. We performed this GLM with laminar-resolved regressors in PFC and 7A. We attempted to explain trial-by-trial variance in superficial and deep layers of V4. Higher-order cortex inhibition of V4 would be reflected in a regression coefficient with a negative sign.

MUA in deep layers of V4 was negatively coupled to theta in superficial and deep layers of 7A, alpha in LIP and deep layers of PFC, and beta in LIP, FEF, and superficial layers of PFC (SI Appendix, Fig. S13, sign test for average regression coefficient across sessions, P < 0.05 for all comparisons). MUA in superficial layers of V4 was not significantly coupled to trial-by-trial variations in higher-order cortex power. Gamma in deep layers of V4 was negatively coupled to beta in superficial and deep layers of PFC and alpha in superficial layers of PFC. In addition to these negative regression coefficients, we also found positive coefficients. Beta in superficial and deep layers of area 7A positively coupled to gamma in superficial and deep layers of V4 (SI Appendix, Fig. S13C, sign test for average regression coefficient across all available sessions, P < 0.05). Gamma in all areas except LIP positively coupled to V4 gamma (SI Appendix, Fig. S13D, sign test for average regression coefficient across all available sessions, all comparisons, P < 0.05).

Discussion

Our results show differences in oscillatory dynamics between cortical layers as animals switch between two different modes of processing. In the “bottom-up” mode, a new sensory input had to be processed on every trial. In the other, “top-down” mode the same stimulus was used on every trial and thus there was no need to fully process new bottom-up inputs. In bottom-up mode, gamma power and feedforward Granger causality predominated. By contrast, in top-down mode, alpha/beta power and feedback Granger causality predominated.

This could be due to a variety of processes that differ between the two modes. One is habituation/adaptation due to stimulus repetition. To examine this, we measured effects as a function of the time between repetitions of the same sample object. This revealed that short-term adaptation alone did not explain the results. Longer-term stimulus repetition could have contributed. Passive adaptation effects tend to reach their maximum after just a single repetition (47). In our study repetition effects took dozens of trials to reach their maximum and correlated with the behavioral time course of improvement. This suggests that the animals were exploiting the increasing familiarity due to repetition. This is not surprising. Repetition is a foundation of predictability. Most, if not all, forms of prediction likely depend on repetition whether the repetition was from past experience or generated in the recent past (seconds to minutes).

In addition, the neurophysiological signatures of prediction and passive stimulus repetition are divergent. In previous studies where stimulus repetition was not behaviorally relevant, gamma-band power and synchronization in visual cortex increased with repetition, whereas we observed decreases (48, 49). In our study, repetition was used by the animals to perform the task. Here, we have used repetition as an initial tool to elicit predictions and top-down processing. In future paradigms, we will test more cognitive forms of prediction, such as learned associations.

In bottom-up mode, new inputs needed to be fully attended, processed, and temporarily held in working memory. In top-down mode, less attention could be paid to the repeating stimulus; it could be stored in and recalled from long-term memory. Such differences can be captured under the umbrella of predictive coding theory.

Relation to Predictive Coding Models.

Many predictive coding models share common elements. Prediction (PD) units anticipate forthcoming sensory inputs. They inhibit prediction error (PE) units when inputs match predictions. A mismatch due to an unpredictable input disinhibits the PE units. They feedforward the unpredicted input which updates the internal models that generate the predictions. Models differ on the details of the implementation in the brain. Some models (50) propose that prediction error signals act locally in each cortical area to update models. Predictions flow between areas in both feedforward and feedback directions. Other models (12, 14) instead suggest that predictions come from higher cortical areas that act on lower cortical (sensory) areas to gate the feeding forward of prediction errors. Of special note, many current models of predictive coding emphasize that prediction errors can be modulated by precision weighting, for example, by increasing attention or sensory evidence (12, 51, 52). Here, we have used a task that did not set out to explicitly modulate the precision of sensory samples in the unpredicted vs. predicted blocks. Sensory samples were always presented at full contrast; and in both block types, monkeys were required to attend to the samples in order to perform an attentional search. Therefore, we did not explicitly consider the issue of precision weighting of prediction errors.

A distinct class of models goes further in proposing a neurophysiological implementation involving distinct oscillations. “Rhythm-based” models suggest that superficial cortical layers (layers 2 and 3) feedforward prediction errors using gamma. Deep-layer cortex (layers 5 and 6) feedback predictions using alpha/beta (1, 19). Our results are more consistent with the rhythm-based models. We showed differences between areas, with higher areas contributing more to prediction, and rhythmic- and laminar-based differences between areas. Below, we summarize and discuss these effects.

The Contribution of Cortical Rhythms to Predictive Processing.

Alpha/beta and gamma have properties that suggest a general role in gating and control. They are common and anticorrelated across cortex. Gamma power is high during sensory inputs; alpha/beta power is high when they are ignored. In visual cortex, gamma power is high and alpha low during sensory stimulation. When a stimulus needs to be filtered or ignored, gamma power is low and alpha is high (43, 53–55). Further, alpha/beta oscillations in deep cortical layers are anticorrelated with superficial-layer gamma associated with spiking carrying sensory inputs (26, 27). The balance between alpha/beta and gamma reflect the encoding, maintenance, and read-out of working memory (56). The general idea is that top-down signals are fed back through alpha/beta in deep cortical layers. They inhibit and thus gate the expression of gamma in superficial layers that help feed forward and maintain the spiking carrying sensory inputs.

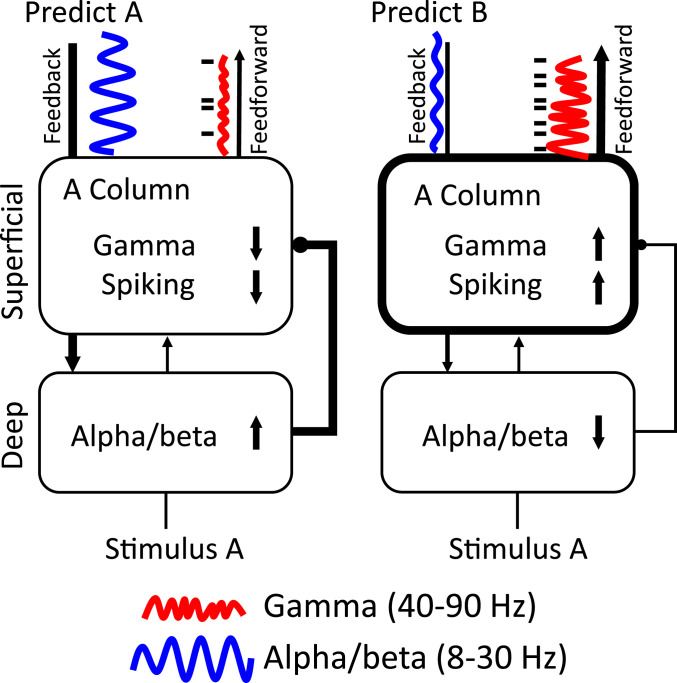
Extrapolating from the rhythm-based models of predictive coding (1, 19), this suggests a framework we call predictive routing (PR) (Fig. 6). In PR, there are not specialized circuits that compute prediction errors and send them feedforward. Rather, PR uses the same cortical circuitry used for other functions (sensory processing, attention, maintenance/control of working memory, etc.). Predictions act by alpha/beta preparation that actively inhibit the specific pathways in sensory cortex that would process the predicted input. As a result, there is less gamma and spiking to predicted inputs (and less feedforward output as a result). In other words, prediction errors do not result from a comparison between predictions and inputs via a specialized circuit. They result from the feed-forward passing of unexpected inputs because their pathways have not been prepared (functionally inhibited).

Fig. 6.

Predictive routing model. Arrows and connections represent functional (not anatomical) connections between areas/layers. Thick lines represent effective connections with increased influence; thin lines represent effective connections with decreased influence. The Upper boxes represent superficial layers (1 to 4) and the Lower boxes represent deep layers (5/6). (Left subpanel) Sensory cortex is dynamically prepared to process its preferred stimulus, stimulus A, by feedback which inhibits MUA and enhances alpha/beta in deep layers. Enhanced deep-layer alpha/beta functionally inhibits superficial-layer processing of stimulus A by reducing spiking and gamma, reducing feedforward outputs. (Right subpanel) When a strong prediction for stimulus B is present and stimulus A is presented (as in the first few trials of an unpredictable block after a predictable block where “B” was the repeated/predicted sample), there is less feedback alpha/beta inhibition to the A column. Deep-layer to superficial-layer inhibition is weak or absent. The A column is more excitable and responds to stimulus A with more gamma/spiking and enhanced feedforward output from superficial layers (a prediction error). Although we hypothesize this mechanism occurs at the level of cortical columns, it could apply to any pathway that processes the specific predicted stimulus. We also hypothesize that this mechanism can be graded to reflect varying strengths of prediction.

This does not mean that alpha/beta (or gamma) have the exact same roles all over cortex. For example, in prefrontal cortex, beta has been modeled as an inhibitory–excitatory network but with slower time constants than what would produce a gamma (57). By contrast, modeling suggests that in parietal cortex, there is a distinction between beta-1 (14 to 20 Hz) and beta-2 (24 to 30 Hz) (58) and that parietal beta-1 may act as a memory buffer activated by strong cortical inputs that feeds forward violations to the PFC (59). Indeed, we found in this study, that in parietal cortex (area 7A) beta was unique and beta was functionally excitatory (positively correlated with violations and local spiking) unlike the other areas. Below, we elaborate on how our results support different models of predictive coding.

Theta-band coherence and Granger causal interactions were stronger during unpredictable stimuli in the sample interval. These interactions were strongest between superficial layers of V4 and the other members of the network. Theta-band interactions were not previously proposed as candidates for processing unpredictable stimuli. However, theta is well known to be a slow rhythm in which faster rhythms such as gamma, can nest (60–62) and aid long-range communication (63). In addition, a previous study identified theta as a carrier for feedforward interactions in the visual system (30). In predictive routing, whatever mechanisms are already in place for feedforward processing are enhanced during unpredictable processing. Therefore, it makes sense that theta (and gamma) from V4 to higher-order cortex is enhanced during unpredicted stimuli, because this reflects an up-regulation of the feedforward channel.

Unpredicted Stimuli Enhance Spiking in Superficial Layers.

At each level of the cortical hierarchy tested, neurons spiked more to, and carried more information about, unpredictable compared to predicted stimuli. Neurons in superficial cortical layers (L2/3) of V4 showed stronger effects than deep layers. In addition, only superficial layers had unpredicted spiking selective to the predicted stimulus. Superficial layers 2/3 contain the majority of feedforward projecting cells. This laminar specificity suggests that unpredicted inputs are preferentially processed in superficial layers and fed forward.

Spiking Reflects an Upcoming Predictable Stimulus.

We found that during trial blocks in which the monkeys could predict the upcoming stimulus, all cortical areas we recorded carried information about it before it appeared. PFC contained the most prestimulus information. In addition, we found that deep layers held more information about the upcoming sample than superficial layers. This is consistent with hierarchical models that propose that generating predictions is primarily a function of higher than sensory cortex and deep layers.

Modulation of Rhythms by Prediction Are Layer Dependent.

In all areas studied, unpredictable stimuli evoked more gamma (40 to 90 Hz) power and less alpha/beta (8 to 30 Hz) power compared to predictable stimuli (beta in area 7A was an exception). These effects were strongest in the first few trials when transitioning from a predictable block to an unpredictable block, potentially reflecting a violation, or prediction error. This effect and the positive correlation between gamma and spiking (SI Appendix, Fig. S2) were stronger in superficial than deep cortical layers. There was generally more alpha/beta power to predictable than unpredictable stimuli but layer differences varied by area. This generally supports rhythm-based models positing that gamma transmits prediction errors and alpha/beta transmits predictions.

Modulation of Rhythms by Prediction Are Stimulus Specific.

The increases in gamma power (and spiking) with unpredicted stimuli and the increased alpha/beta with predicted stimuli were stimulus specific. Effects were larger at recoding sites where spiking preferred (was greater to) the specific stimulus that was predicted. For spiking, this selectivity occurred only in superficial layers. For gamma, this selectivity was only significant in superficial layers, and for alpha and beta, this selectivity was only significant in deep layers. Therefore, rhythmic modulation of power by predictability is stimulus specific. This supports the view that oscillations can be modulated in a representationally specific way (64), rather than only in a nonspecific way across wide areas of cortex. The specificity is a central feature of predictive routing, where alpha/beta inhibits the pathways that process the specific predicted stimulus and the increased gamma/spiking occurs because the pathways processing other stimuli were not inhibited.

Networks and Directionality.

Both coherence and Granger causality analysis showed that rhythmic interactions were modulated by stimulus predictability at several frequencies. Gamma-band coherence within and between areas was higher with unpredictable than predictable stimuli. This effect was largest for coherence between superficial layers of areas V4 and PFC. Granger causality analysis further showed that the increase in gamma-band coherence with unpredictable stimuli was stronger in the feedforward than feedback direction. In V4, this was more prominent in superficial layers. There was overall greater alpha/beta coherence with predictable stimuli. The strongest effects involved PFC and were stronger in the feedback compared to feedforward direction. In the presample interval, the enhanced Granger causality during predictable stimuli was strongest between deep layers of PFC to the rest of the network. These results are in line with hierarchical and rhythms models where (gamma-based) prediction errors primarily feed forward flow up the cortical hierarchy and (alpha/beta-based) predictions flow down the cortical hierarchy. They suggest that modulation of interareal synchronization at distinct frequencies is a central mechanism in communicating specific (predicted vs. unpredicted) information (65–68). In addition, prefrontal control over behavior is thought to be mediated by dynamic patterns of neuronal functional connectivity (69).

Higher-Order Cortex Inhibition of V4.

Trial-by-trial beta power in all higher-order areas except 7A negatively coupled to both spikes and gamma power in V4. Interestingly, this corticocortical top-down inhibition of V4 spiking was found only in deep layers, despite the fact that anatomically, top-down feedback targets both superficial and deep layers of V4 (46). In contrast, the actual effects of prediction on spiking and gamma were stronger in superficial layers. This suggests distinct layers for transmitting top-down prediction signals (in deep layers of V4) vs. bottom-up routing of unpredicted information (in superficial layers of V4). It also suggests a local circuit mechanism in visual cortex where deep layers functionally inhibit activity of superficial layers (70).

Summary.

Our results suggest a hierarchical layer and frequency-specific framework for top-down vs. bottom-up processing related to stimulus predictability. We interpret the results in a framework we call predictive routing (Fig. 6). Unpredictable stimuli evoked stronger feedforward- superficial-layer gamma/spiking (and theta), especially when they violated a previous prediction: the hallmark of a prediction error signal. Superficial-layer parietal area 7A high beta also signaled violations in both feedforward and feedback directions, which could engage working memory update mechanisms to process and hold unpredicted information online. Coherence and feedback connectivity were enhanced in the alpha/beta band when a stimulus was predictable. In the presample interval this enhanced feedback connectivity during predictable stimuli originated in deep layers of PFC. Alpha/beta power in higher-order cortical areas LIP, FEF, and PFC negatively modulated spiking in deep layers of V4. The modulatory effects of stimulus predictability on alpha/beta and on gamma/spiking modulation was strongest at the sensory cortical sites that preferred the predicted stimulus. Spiking/gamma in sensory cortex was only selective to the predictive stimulus in superficial layers. Alpha/beta was only selective to the predicted stimulus in deep layers. These results are consistent with the predictive routing model, which states that there need not be specialized circuits for extracting prediction error. Rather, when stimuli are predictable, these rhythmic, layer-specific mechanisms prepare and inhibit columns in sensory cortex that process the predicted stimulus. In the absence of these pathway-specific prediction signals, sensory samples receive stronger processing, causing enhanced spiking and feedforward gamma. Together, these results suggest that predictive coding may stem from rhythmic interactions between lower frequency rhythms in deep cortical layers that signal predictions and inhibit the superficial-layer gamma and spiking in the sensory pathways that match those predictions.

Experimental Procedures.

We performed multilaminar recordings using linear array U and V probes (Plexon). We recorded spiking and LFP activity in visual area V4, parietal, and prefrontal cortices of two macaque monkeys (Macaca mulatta) while the animals performed a delayed match to sample task. All surgical and animal care procedures were approved by the Massachusetts Institute of Technology (MIT)’s Committee on Animal Care and were conducted in accordance with the guidelines of the National Institute of Health and MIT’s Department of Comparative Medicine. Additional details of the study’s methodology are provided in SI Appendix, Experimental Procedures.

Behavioral Training and Task.

Monkeys were trained to sit comfortably in a primate chair inside a sound attenuating behavioral testing booth. They were seated 50 cm away from a LCD monitor with a 144-Hz refresh rate (ASUS, Taiwan). Using positive reinforcement, we trained monkeys to perform a visual search task (Fig. 1A). Monkeys fixated on a point at the center of the screen (fixation window radius: 2 to 3 visual degrees) for a duration of 1 s, were presented with one of three cue objects for a duration of 1 s, and were required to maintain fixation over a delay (between 0.5 and 1.2 s). A search array then appeared that consisted of the cued item together with either one or two distractors presented at the same eccentricity (3° to 8°), but different visual quadrants as the cued object. The position of the cued object and the distractors were always randomly chosen. Monkeys were rewarded with a few drops of diluted juice if they performed a saccade toward the cued item. Behavioral performance was high for each of the monkeys (monkey S: 77% over 41 sessions, monkey L: 75% over 30 sessions). Monkeys were trained on this task using a library of 22 sample images. For recordings, we used a subset of these images (12), choosing a total of 3 per session. Most sessions (65 out of 71) used the 3 objects depicted in Fig. 1: an orange, a green block, and a blue car.

To manipulate prediction, the task was performed either with unpredictable or predictable cuing. During unpredictable cuing, samples were randomly drawn on each trial. In block cuing/sampling, the sample was held constant for the duration of the block. The trial-by-trial and blocked modes each lasted for 50 trials before switching block modes. The starting order was randomized over sessions. The task design is schematized in Fig. 1A.

Neurophysiological Recordings.

All of the data were recorded through Blackrock headstages (Blackrock Cereplex M), sampled at 30 kHz, band passed between 0.3 Hz and 7.5 kHz (first order Butterworth high pass and third order Butterworth low pass), and digitized at a 16-bit, 250 nV/bit. All LFPs were recorded with a low-pass 250-Hz Butterworth filter, sampled at 1 kHz, and alternating current (AC) coupled.

We implanted the monkeys with a custom-machined carbon PEEK chamber system with three recording wells placed over visual/temporal, parietal, and frontal cortex. The process for making the chambers was based on design principles outlined previously (71). Briefly, we first took an anatomical MRI scan (0.5 mm^3 voxel size) and/or computed tomography (CT) scan to extract the bone and coregister the skull model with the brain tissue. We designed the center of each chamber to overlie the primary recording area of interest and to have an optimal angle for perpendicular recordings relative to the cortical folding. Postoperatively, after the recording chambers were implanted, MRIs were taken with the recording grid in place, filled with water, which created a marker to coregister each possible electrode trajectory with the animal’s anatomy, and to confirm trajectories that were as close to perpendicular as possible.

The areas where we could achieve perpendicular recordings (for laminar sampling) on the overlying gyrus were V4 (foveal and parafoveal representations), parietal cortex (area 7A), and prefrontal cortex (area 8A, ventro and dorsal lateral prefrontal cortex [VLPFC/DLPFC]). The areas where we recorded without laminar alignment (due to their location in sulci) were areas FEF and LIP.

We recorded a total of 71 sessions with laminar probes. In each session, we inserted between 1 and 3 laminar probes (“U probes” and “V probes” from Plexon) into each recording chamber with either 100- or 200-μm intersite spacing and either 16 or 32 total electrodes per probe. This gave a total linear sampling of 3.0 to 3.1 mm on each probe. Between three and seven probes in total per session were used, with a total channel count ranging between 48 and 128 electrodes per session. The recording reference was the reinforcement tube, which made metallic contact with the entire length of the probe (total probe length from connector to tip was 70 mm). Some U/V probes had noisy channels (average power greater than 2 SDs above the mean of all channels, this occurred on less than 5% of all channels), which were interpolated based on nearest neighbors prior to analysis.

Multiunit Activity Extraction and Spike Sorting.

For the analysis of the analog MUA we band-pass filtered the raw, unfiltered, 30-kHz sampled data into a wide band between 500 and 5,000 Hz, the power range dominated by spikes. The signal was then low-pass filtered at 250 Hz and resampled to 1,000 kHz. The advantage of this signal is that it captures all nearby units, including those with low signal-to-noise ratio that would not be captured with a strict threshold. For the analysis of thresholded spikes, we manually sorted spikes using a Plexon offline sorter. For additional details please see SI Appendix, Experimental Procedures.

Local Field Potential Power, Coherence, and Granger Causality Analysis.

All analyses were performed with customized MATLAB scripts and with Fieldtrip software (72). Bipolar derivation is a recommended prestep prior to Granger causality and coherence analysis, as the presence of a common reference can lead to spurious results (73, 74). In addition, bipolar derivation enhances the spatial localization of LFP signals and removes the common reference and any common noise or volume conduction in the signal (75). Here, we computed the sample-by-sample bipolar differences by subtracting contacts that were at a distance of 400 μm: next-nearest neighbors for the laminar probe data spaced at 200 μm between contacts, and next-next-nearest neighbors for the probe data spaced at 100 μm between contacts.

We then estimated power, coherence, and Granger causality on these bipolar derivations. We estimated power at all frequencies from 0 to 250 Hz using multitaper spectral estimation (smoothing window of 5 Hz), leading to nine tapers per spectral estimate, using window sizes of 1 s (0 to 1 s relative to sample onset is the period of visual stimulation, −1 to 0 s relative to sample onset is the prestimulus fixation interval) per trial. These Fourier coefficients were then used to calculate the cross-spectral density matrix, from which we derived coherence and nonparametric spectral Granger causality (45).

Neural Information Analysis with Percent Explained Variance.

We quantified the amount of variance in the task (sample identity) that could be explained by the spike rate of neurons using an unbiased statistic called the omega squared (76). For each point in time relative to sample onset, the amount of variance that firing rate of a given neuron across trials explained about the sample was measured. This was done separately for predictable and unpredictable blocks. We used nonparametric cluster-based statistics to assess differences in neural information during predictable vs. unpredictable blocks.

General Linear Model Analysis.

We assessed whether trial-by-trial fluctuations in LFP power during the sample interval in LIP, 7A, FEF, and PFC could explain variance in gamma power and MUA activity (averaged between 0.05 and 0.4 s postsample onset) in V4. We used a GLM with higher-order power (which had laminar resolution in PFC and 7A) as the regressors (77). We ran separate GLMs per session and then combined coefficients across sessions. We then used a sign test to assess whether the median sign of these regressors was significantly positive or negative (reflecting functional inhibition of V4 neural activity by higher-order cortex power).

Statistical Testing.

We computed whether the MUA, power, coherence, and Granger causality was systematically different between conditions (predictable vs. unpredictable). To do this, we calculated either the mean difference or percent change for each channel or interareal channel pair of predictable vs. unpredictable sampling. We then quantified whether this raw difference or percent change was significant by performing a cluster-based nonparametric randomization test (78). For additional details on statistical testing, please see SI Appendix, Experimental Procedures.

Data Availability.

Data are available on request by contacting Earl Miller (ekmiller@mit.edu).