Characterization, stability, and application of domain walls in flexible mechanical metamaterials

Significance

Mechanical metamaterials are an interesting platform to reproduce atomistic-scale phenomena at the macroscale and to exploit them to achieve additional functionalities. An interesting feature of many ordered solid-state materials is the formation of domain walls that separate different phases. While these interfaces have been reproduced in a variety of mechanical materials, the understanding of how to control them is still poor owing to their structural complexity. Here, we use a combination of experimental, numerical, and theoretical tools to engineer the domain walls emerging upon uniaxial compression in a mechanical metamaterial based on the rotating-squares mechanism. Our study reveals additional territories in the mechanical metamaterials design space which could unlock more tools for information encryption, stiffness tuning, and wave guiding.

Abstract

Domain walls, commonly occurring at the interface of different phases in solid-state materials, have recently been harnessed at the structural scale to enable additional modes of functionality. Here, we combine experimental, numerical, and theoretical tools to investigate the domain walls emerging upon uniaxial compression in a mechanical metamaterial based on the rotating-squares mechanism. We first show that these interfaces can be generated and controlled by carefully arranging a few phase-inducing defects. We establish an analytical model to capture the evolution of the domain walls as a function of the applied deformation. We then employ this model as a guideline to realize interfaces of complex shape. Finally, we show that the engineered domain walls modify the global response of the metamaterial and can be effectively exploited to tune its stiffness as well as to guide the propagation of elastic waves.

The coexistence of two or more phases plays a central role in many ordered solid-state materials, including ferroelectrics (1–3), ferromagnets (4, 5), ferroelastics (6, 7), shape memory alloys (7, 8), and liquid crystals (9). Despite being intrinsically different, these materials all share the emergence of domain walls—a type of topological defect that separates regions of different phases (10). Such interfaces are crucial for the control of many material properties, including coercivity, resistance, and/or fatigue (11), and have also been exploited to enable logic operations (12), racetrack memory (13), and line scanners for reading optical memories (14). Inspired by the recent advancements in domain walls control strategies at the atomistic scale, researchers have designed a variety of nonlinear mechanical structures to support these interfaces (15–25). Domain walls engineered at the structural scale have facilitated the control of elastic pulses (16, 17, 19, 25), the encryption of information (23), and the realization of deployable structures (20) as well as of phase-transforming metamaterials (15, 18). However, due to the structural complexity of mechanical metamaterials, no analytical solution has been proposed that fully describes the physics of such domain walls. This limits their systematic application in the design of smart structures and devices and hinders the discovery of additional functionalities.

Here, we use a combination of experiments and analyses to study the domain walls emerging in a mechanical metamaterial based on the rotating-squares mechanism. We start by introducing defects into the system to locally impose nucleation of one of the two supported buckling-induced rotated phases upon compression. Importantly, when such defects lead to the coexistence of two phases within the specimen, domain walls form, across which the angle of individual squares switches from one direction of rotation to the other. We establish an analytical model that fully describes the emerging domain walls, including their profile and position as a function of the applied deformation. Guided by our model, we then introduce pinning defects to reshape the energy landscape of the system and, therefore, engineer domain walls along arbitrary complex paths. Based on our findings we foresee the exploitation of domain walls in the realm of mechanical metamaterials to realize additional functionalities, as we hereby demonstrate by achieving stiffness tuning and reconfigurable elastic wave guiding.

Flexible Mechanical Metamaterial Based on the Rotating-Squares Mechanism

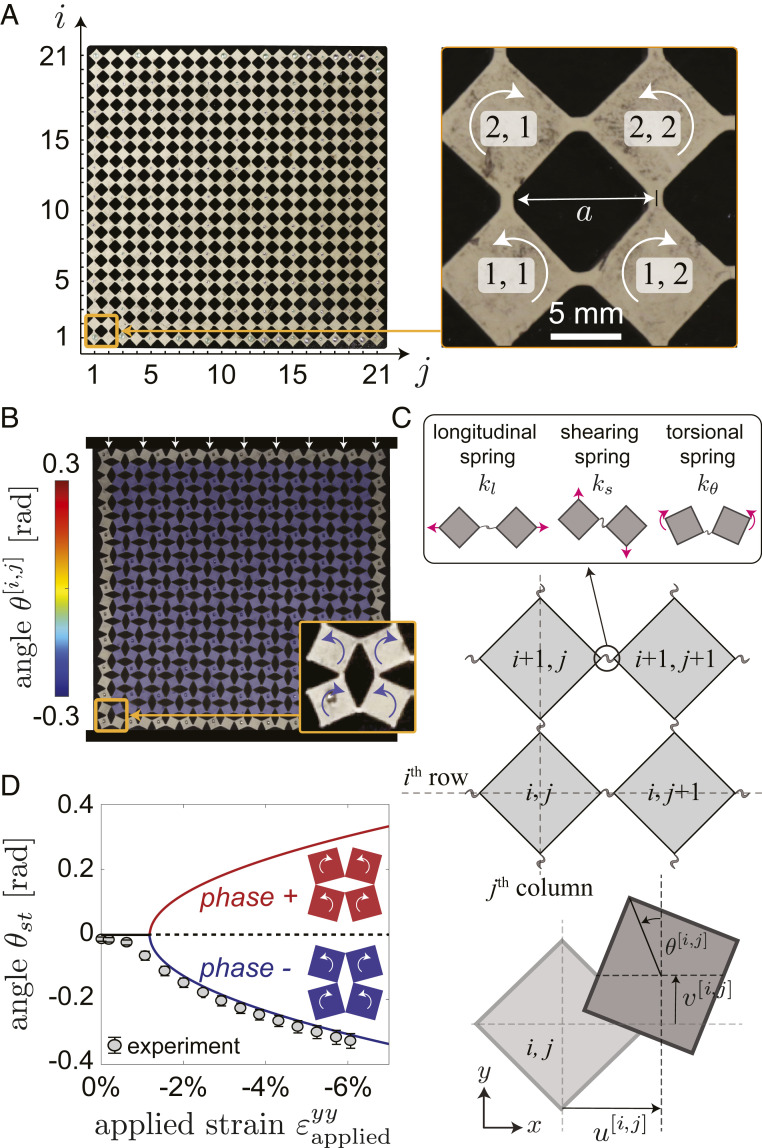
We consider an elastomeric structure of thickness $t=3$ mm comprising an array of $21\hspace{0.17em}\times \hspace{0.17em}21$ squares with center-to-center distance $a=10$ mm, connected at their vertices by ligaments with width and length of 1 mm (see Fig. 1A and SI Appendix, section S1 for fabrication details). In all our tests we uniaxially compress the structure by applying a vertical displacement ${\mathrm{\Delta }}_{\text{stage}}$ to the top edge (which results in a nominal longitudinal strain ${\epsilon }_{\text{applied}}^{yy}={\mathrm{\Delta }}_{\text{stage}}/\left(21a\right)$), while using a transparent acrylic plate to prevent its out-of-plane deformation. The deformation of the sample is captured with a camera (SONY RX100), and the position and rotation of the squares are tracked via image processing conducted in Matlab (see SI Appendix, section S2 for testing details). Under the applied compression, one of the beam-like ligaments in the sample buckles first, because of immeasurable small imperfections introduced during fabrication. This provides a unique nucleation site that leads to the formation of a uniform buckling pattern in which all squares alternately rotate in clockwise and counterclockwise directions (Fig. 1B and Movie S1). Note that to facilitate the analysis, we define the positive direction of rotation alternately for neighboring squares. Specifically, we choose the square at the bottom left corner to be unit $\left[\mathrm{1,1}\right]$ and define a counterclockwise rotation of the [i, j]th square (i.e., the square located on the ith row and jth column) positive if $i+j$ is an even number and negative if $i+j$ is odd (Fig. 1A). Using these definitions, we find that in our sample, buckling induces a negative rotation of all squares. On the other hand, if the ligament that acts as a nucleation site had buckled in the opposite direction, all units would have experienced a positive rotation.

Fig. 1.

(A) The system consists of a network of 21$\times$21 square domains connected by thin ligaments. The positive direction of rotation alternates for neighboring squares: A counterclockwise rotation of the [i, j]th square (the square located on the ith row and jth column) is defined positive if $i+j$ is an even number and negative if $i+j$ is odd. (B) Deformation of the sample when subjected to ${\epsilon }_{\text{applied}}^{yy}=-4\%$. The color indicates the rotation of the squares. (C) We model the system as an array of rigid squares connected at their vertices by elastic springs. (D) Evolution of ${\theta }_{st}$ as a function of ${ϵ}_{\text{applied}}^{yy}$ as predicted by Eq. 5 (solid lines) and measured in our experiment (circles).

The nonlinear behavior of our system can be captured using a discrete model comprising rigid squares connected at their vertices by a combination of springs (Fig. 1C) (26–30). Three degrees of freedom are assigned to the $\left[i,j\right]$th rigid square: 1) the displacement in the $x$ direction, $u^{\left[i,j\right]}$; 2) the displacement in the $y$ direction, $v^{\left[i,j\right]}$; and 3) the rotation around the $z$ axis, ${\theta }^{\left[i,j\right]}$. As for the ligaments, their longitudinal and shearing response is captured by linear springs with stiffness $k_l$ and $k_s$, respectively, whereas their bending behavior is modeled by using a nonlinear hardening rotational spring with linear and cubic terms that exert a torque $M=k_{\theta }\left(\mathrm{\Delta }\theta +\gamma \mathrm{\Delta }{\theta }^3\right)$, where $\mathrm{\Delta }\theta$ is the relative rotation between the connected squares, $k_{\theta }$ is the bending stiffness, and $\gamma$ is a dimensionless parameter (SI Appendix, section S3.1). Note that for the structure considered in this study $k_l=\mathrm{1,080}$ N/m, $k_s=239$ N/m, $k_{\theta }=1.62\times 10^{-4}$ N$\cdot$m, and $\gamma =0.5$ (SI Appendix, section S3.5) and that, to facilitate the analysis, we assume that the longitudinal and shearing springs are always parallel either to the $x$ or to the $y$ axis (an assumption which is valid only for small global rotations of the system). When adopting such a discrete model, the response of a structure comprising $N_x\times N_y$ units can be obtained by numerically solving the 3$N_x{N}_y$ coupled nonlinear equations derived by imposing force equilibrium at each square. Further, a deeper insight can be achieved by deriving analytical solutions. To this end, we assume small rotation of the squares and take the continuum limit of the discrete equilibrium equations to obtain (SI Appendix, section S4)

$$k_l{\partial }_{xx}u+k_s{\partial }_{yy}u+k_l\theta {\partial }_x\theta =0,$$ [1a]

$$k_l{\partial }_{yy}v+k_s{\partial }_{xx}v+k_l\theta {\partial }_y\theta =0,$$ [1b]

$$-a^2\left(k_s{a}^2-4k_{\theta }\right){\nabla }^2\theta +32k_{\theta }\theta +4\left(k_l{a}^2+32\gamma k_{\theta }\right){\theta }^3+4k_l{a}^2\left(\theta -{\theta }^3/6\right)\left({\partial }_{x}u+{\partial }_{y}v\right)=0,$$ [1c]

where ${\partial }_{\alpha }f=\partial f/\partial \alpha$; ${\nabla }^2={\partial }_{xx}+{\partial }_{yy}$; and $u$, $v$, and $\theta$ are three continuum functions that interpolate the discrete variables $u^{\left[i,j\right]}$, $v^{\left[i,j\right]}$, and ${\theta }^{\left[i,j\right]}$ as

$$\begin{array}{cc}\hfill & u\left(x=a\hspace{0.17em}j,y=a\hspace{0.17em}i\right)=u^{\left[i,j\right]},\hfill \\ \hfill & v\left(x=a\hspace{0.17em}j,y=a\hspace{0.17em}i\right)=v^{\left[i,j\right]},\hfill \\ \hfill & \theta \left(x=a\hspace{0.17em}j,y=a\hspace{0.17em}i\right)={\theta }^{\left[i,j\right]}.\hfill \end{array}$$ [2]

The uniaxial compression loading considered in our experiments is then modeled by imposing

$$v\left(y=a\hspace{0.17em}{N}_y\right)-v\left(y=a\right)=a\left(N_y-1\right){\epsilon }_{\text{applied}}^{yy},$$ [3]

and

$${\partial }_{x}u+{\theta }^2/2=0,$$ [4]

where Eq. 4 is obtained by requiring the longitudinal forces in all horizontal ligaments to vanish (since the vertical edges of the structure are traction-free).

For the case of a homogeneous deformation (as shown in Fig. 1B), both the rotation of the squares and the longitudinal strain in the $y$ direction are spatially constant (i.e., $\theta ={\theta }_{st}$ and ${\partial }_{y}v={\epsilon }_{st}^{yy}$, where ${\theta }_{st}$ and ${\epsilon }_{st}^{yy}$ are the constant rotation and longitudinal strain). It follows that, when substituting Eq. 4 into Eqs. 1, Eqs. 1a and 1b vanish, whereas Eq. 1c becomes

$$\left(1-\frac{\left(24\gamma +1\right){\epsilon }_{cr}^{yy}}{3}\right){\theta }_{st}^3+2\left({\epsilon }_{st}^{yy}-{\epsilon }_{cr}^{yy}\right){\theta }_{st}=0,$$ [5]

where ${\epsilon }_{cr}^{yy}=-8k_{\theta }/k_l{a}^2$. Further, Eq. 3 reduces to ${\epsilon }_{st}^{yy}={\epsilon }_{\text{applied}}^{yy}$. Eq. 5 can be solved to obtain the rotation of the squares, ${\theta }_{st}$, as a function of the strain ${\epsilon }_{st}^{yy}$ as

$${\theta }_{st}=\left\{\begin{array}{cc}0,\hfill & {\epsilon }_{st}^{yy}>{\epsilon }_{cr}^{yy}\hfill \\ \pm \sqrt{\frac{-6\left({\epsilon }_{st}^{yy}-{\epsilon }_{cr}^{yy}\right)}{3-\left(24\gamma +1\right){\epsilon }_{cr}^{yy}}},\hfill & {\epsilon }_{st}^{yy}<{\epsilon }_{cr}^{yy}.\hfill \end{array}\right.$$ [6]

Eq. 6 defines the pitchfork-shape bifurcation diagram shown in Fig. 1D. At ${\epsilon }_{\text{cr}}^{yy}$ the initially stable solution (${\theta }_{st}=0$) bifurcates into two new stable branches that correspond to positive and negative rotation of the squares and, therefore, to the two buckling-induced phases supported by the system (which we refer to as phase+ and phase−). Note that the evolution of the average rotation of the squares as a function of ${\epsilon }_{\text{applied}}^{yy}$ extracted from the experiments (Fig. 1 D, circles) nicely follows the phase− branch, confirming the validity of our model.

Phase-Inducing Defects and Domain Walls

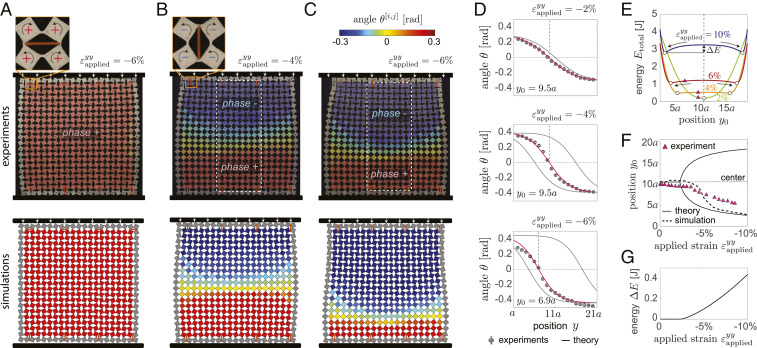
While in our sample the emerging buckling-induced phase is determined by unavoidable small imperfections introduced during fabrication, one can impose a prescribed phase by placing stiff plastic plates with length $l_d=1.2a$ into selected holes to act as phase-inducing defects (Fig. 2A and SI Appendix, Fig. S2). Such plates fully determine the buckling direction of the ligaments to which they are connected and, therefore, depending on their position and orientation, can induce the formation of either phase+ or phase−. To demonstrate our approach, we evenly distribute eight of such defects in the holes next to the horizontal boundaries. We find that when the eight defects are located and oriented as shown in Fig. 2A (see SI Appendix, Fig. S3 for details), they overcome the imperfections introduced during fabrication and make phase+ appear upon buckling (Fig. 2A and Movie S2). Further, by simply rotating the defects next to the top boundary by 90° (SI Appendix, Fig. S3), we can get phase− to propagate from the top boundary and phase+ from the bottom one (Fig. 2B). This leads to the coexistence of two phases within the specimen and to the formation of a horizontal domain wall in which the angles of individual squares switch from positive to negative values. For ${\epsilon }_{\text{applied}}^{yy}=-4\%$ such a domain wall is located near the center of the specimen. However, when the applied compression is increased to ${\epsilon }_{\text{applied}}^{yy}=-6\%$, it shifts toward the bottom (Fig. 2C and Movie S2).

Fig. 2.

(A) Deformation at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ of a sample with eight phase-inducing defects arranged to induce nucleation of phase+. (B and C) Deformation at (B) ${\epsilon }_{\text{applied}}^{yy}=-4\%$ and (C) ${\epsilon }_{\text{applied}}^{yy}=-6\%$ of a sample with eight phase-inducing defects arranged to induce nucleation of phase+ near the bottom boundary and phase- near the top one. Experimental and numerical snapshots are shown at Top and Bottom, respectively. The color corresponds to the rotation of the squares. Zoom-ins of the defects are also shown. (D) Comparison between analytically predicted (solid lines) and experimentally extracted (circles) evolution of the squares’ rotation $\theta$ across the sample for different values of applied strain. (E) Analytically predicted evolution of the total energy of the structure as a function of domain wall position $y_0$ for different values of applied strain. (F) Evolution of the domain wall position $y_0$ as a function of the applied strain ${\epsilon }_{\text{applied}}^{yy}$ as predicted by theory (solid line) and numerical simulations (dashed line) and extracted from experiments (triangles). (G) Evolution of the energy barrier $\mathrm{\Delta }E$ as a function of applied strain ${\epsilon }_{\text{applied}}^{yy}$.

To ensure that the phenomena observed in the experiments are not artifacts introduced by friction or unavoidable imperfections, we next conduct discrete simulations in which we model the phase-inducing defects as stiff springs with stiffness $k_d\gg k_l$ and length at rest $l_d$ (SI Appendix, section S3.2). We find a very good agreement between the numerical and experimental results (Fig. 2 A–C), with the simulations capturing both the deformation-induced shifting and thinning of the domain walls (see Movie S2 and SI Appendix, Figs. S12–S18 for simulation results conducted on larger $51\times 51$ structures). Having confirmed that our experimental observations emerge because of the bulk properties of the medium (rather than friction or geometrical imperfections), we then seek analytical solutions to describe both the profile and position of the emerging domain walls. To this end, since both our experiments and discrete simulations indicate that gradients of deformation along the domain wall are negligible (Fig. 2 B and C), we assume that ${\partial }_x\left(\cdot \right)=0$ (SI Appendix, section S4.1). It follows that Eqs. 1 and 4 reduce to

$$d_{yy}v+\theta d_y\theta =0,$$ [7a]

$$-a^2\left(k_s{a}^2-4k_{\theta }\right)d_{yy}\theta +32k_{\theta }\theta +2\left(k_l{a}^2+64\gamma k_{\theta }\right){\theta }^3+4k_l{a}^2\left(\theta -{\theta }^3/6\right)d_{y}v=0.$$ [7b]

Next, we integrate Eq. 7a to obtain

$$d_{y}v=-{\theta }^2/2+C,$$ [8]

where $C$ is an integration constant that can be determined by assuming homogeneous deformation inside each phase (i.e., far away from the domain wall). Specifically, by imposing

$${\left.{\partial }_{y}v\right|}_{phase\pm }={\epsilon }_{st}^{yy},{\left.\theta \right|}_{phase\pm }=\pm {\theta }_{st},$$ [9]

and using Eq. 5 to connect ${\epsilon }_{st}^{yy}$ and ${\theta }_{st}$, $C$ is determined as

$$C={\epsilon }_{cr}^{yy}\left[1+\frac{\left(24\gamma +1\right){\theta }_{st}^2}{6}\right].$$ [10]

Finally, by substituting Eqs. 8 and 10 into Eq. 7b we obtain

$$d_{yy}\theta =\frac{16k_{\theta }\left(1+24\gamma \right)}{3a^2\left(k_s{a}^2-4k_{\theta }\right)}\hspace{0.17em}\theta \left(\theta -{\theta }_{st}\right)\left(\theta +{\theta }_{st}\right).$$ [11]

Eq. 11 has the form of the Klein–Gordon equation with quadratic and cubic nonlinearities and has been shown to admit analytical solutions of the form (24, 31, 32)

$$\theta ={\theta }_{st}\tanh \frac{y-y_0}{w},$$ [12]

where $y_0$ denotes the position of the domain wall and

$$w=\frac{a}{{\theta }_{st}}\sqrt{\frac{3\left(k_s{a}^2-4k_{\theta }\right)}{8k_{\theta }\left(1+24\gamma \right)}}$$ [13]

indicates its characteristic width. Having determined $\theta$, the solution for the displacement field $u\left(x,y\right)$ and $v\left(x,y\right)$ is then calculated by integrating Eqs. 4 and 8 and ${\theta }_{st}$ is determined as a function of ${\epsilon }_{\text{applied}}^{yy}$ by imposing Eq. 3 (note that because of the existence of the domain wall, ${\epsilon }_{st}^{yy}\ne {\epsilon }_{\text{applied}}^{yy}$) (SI Appendix, section S4.1). At this point, it is worth noting that by multiplying both sides of Eq. 11 by $d_y\theta$ and integrating with respect to $y$, its effective Lagrangian (from which Eq. 11 can be retrieved by imposing $d_y\mathcal{L}=0$) is obtained as

$$\mathcal{L}=\frac{1}{2}{\left(d_y\theta \right)}^2-\frac{1}{w^2}\left[\frac{{\theta }^4}{2{\theta }_{st}^2}-{\theta }^2\right].$$ [14]

Remarkably, Eq. 14 is identical to the Lagrangian of the ${\varphi }^4$ mode—a well-known model established to describe second-order phase transitions and domain walls in solid-state materials (33). Next, we verify the validity of our analytical solution by comparing the evolution of the squares’ rotation across the sample as recorded in our tests and predicted by Eq. 12 (Fig. 2D). When choosing $y_0$ to best match the experimentally observed location of the domain wall (magenta lines in Fig. 2D), we find an excellent agreement between analytical and experimental results, with the analytical solution nicely capturing the deformation-induced thinning of the domain wall. However, it is important to note that $y_0$ can also be calculated by minimizing the total energy of the system, $E_{\text{total}}$ (SI Appendix, sections S3.3 and S4.2). As shown in Fig. 2E, we find that initially (i.e., for ${\epsilon }_{\text{applied}}^{yy}>-2.3\%$) $E_{\text{total}}$ is a convex function with a minimum located at the center of the specimen (i.e., at $y_0=11\hspace{0.17em}a$). However, as the applied compression is increased, it gradually turns into a multiwelled landscape with a local maximum at the center and two minima that progressively move toward the horizontal boundaries. Therefore, since the structure always seeks to minimize its total energy, our model indicates that for ${\epsilon }_{\text{applied}}^{yy}<-2.3\%$ the domain wall tends to shift toward one of the horizontal boundaries (solid line in Fig. 2F). While such shifting of the domain wall is present in both our experiments and simulations, it is found to start for larger values of applied deformation in simulations (triangles and dashed line in Fig. 2F). Such discrepancy is attributed to the small energy barrier $\mathrm{\Delta }E$ for moderate levels of applied strain (Fig. 2G), which makes the shifting very sensitive to imperfections and friction. However, despite this discrepancy, the results of Fig. 2 indicate that our analytical model captures all of the experimentally observed salient features of the emerging domain walls.

Pinning Defects and Stable Domain Walls

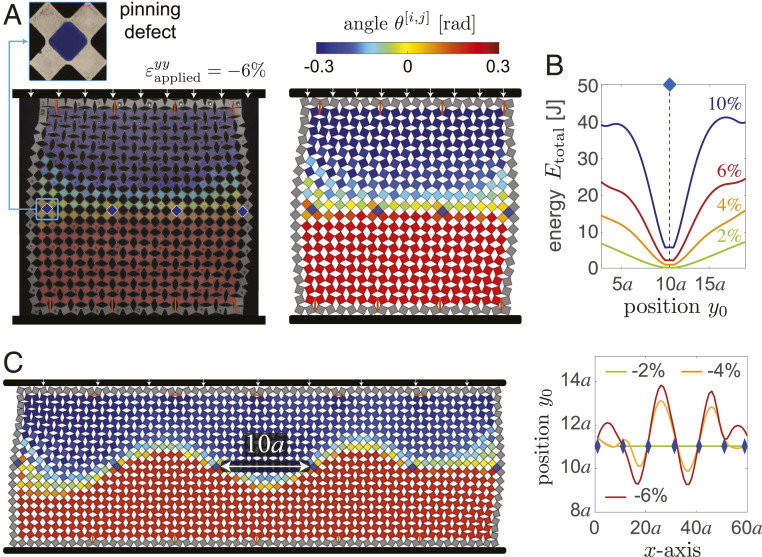
As shown in Fig. 2, by carefully arranging a few phase-inducing defects in the metamaterial we can induce the formation of a domain wall, whose location varies as a function of the applied deformation. To program the position of the domain wall, one can prevent the rotation of selected squares by introducing pinning defects consisting of square-shaped rigid plates (with size $0.95a\times 0.95a$) placed into neighboring holes (SI Appendix, Fig. S2). In Fig. 3A we present results for a sample with four pinning defects equally spaced along a horizontal line (see SI Appendix, Fig. S4 for details), in addition to the previous eight phase-inducing defects arranged as in Fig. 2 B and C. We find that in this case the location of the domain wall is fully determined by the square defects that act as pinning sites (see Fig. 3A for ${\epsilon }_{\text{applied}}^{yy}=-6\%$ and Movie S3). This is due to the pinning defects that modify the total energy of the system and make it convex for any value of applied deformation, with a clear minimum at the defects’ locations (see Fig. 3B and SI Appendix, Figs. S19 and S20 for additional results). Moreover, we find that the density of the pinning defects plays an important role. For example, it is possible to create a wavy domain wall by increasing the spatial separation between defects. In Fig. 3C and Movie S3, we show a 60 $\times$ 21 sample (larger width to minimize boundary effects) with pinning defects separated by 10 holes instead of 5. The competition between the pinning sites and the tendency of the domain wall to shift toward the boundary to minimize the total energy both cooperate in the formation of an undulating phase separation (see SI Appendix, Figs. S21–S23 for additional results). Finally, while in Fig. 3 we considered pinning defects positioned on the central line, the location of the domain wall can be programmed at any location in the sample (see SI Appendix, Fig. S19 for additional results).

Fig. 3.

(A) Deformation at ${\epsilon }_{\text{applied}}^{yy}=-6\%$ of a sample with four pinning defects and eight phase-inducing defects arranged as in Fig. 2 B and C. Experimental and numerical snapshots are shown on Left and Right, respectively. The color corresponds to the rotation of the squares. A zoom-in of a pinning defect is also shown. (B) Analytically predicted evolution of the total energy of the structure as a function of domain wall position $y_0$ for different values of applied strain. (C) Numerically predicted deformation at ${\epsilon }_{\text{applied}}^{yy}=-6\%$ of structures comprising $21\times 60$ squares with pinning defect separated by 10 holes. The domain wall becomes wavy for large enough values of applied compression.

Domain Walls with Arbitrary Orientations

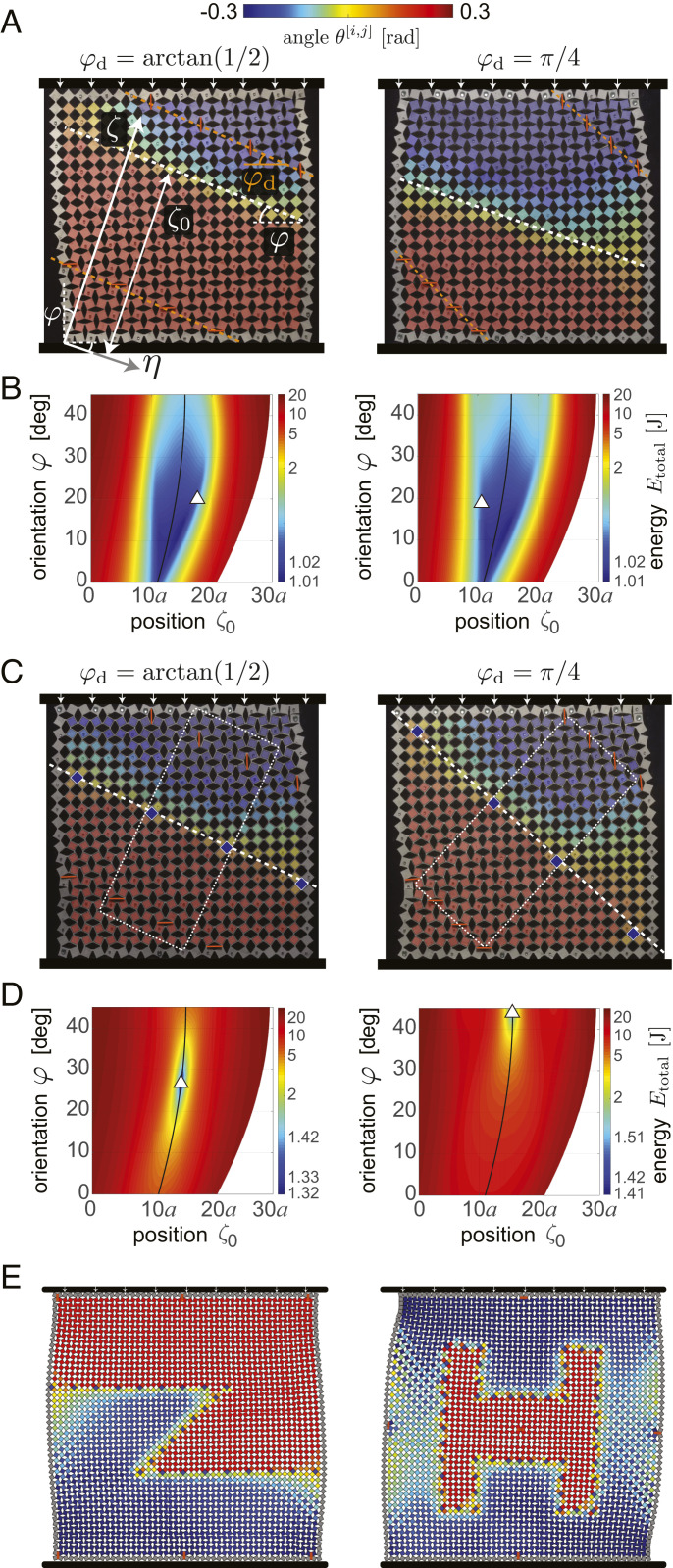
The domain wall’s orientation can be easily varied by arranging the defects along lines that form an angle ${\phi }_d$ with the horizontal axis. In Fig. 4A we show samples with eight phase-inducing defects linearly arranged and angled at ${\phi }_{\text{d}}=\arctan \left(1/2\right)$ and $\pi /4$ to induce opposite phases across the joining line (see SI Appendix, Fig. S3 for details on the arrangement of the defects). We find that at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ not only are the emerging domain walls shifted from the center of the region defined by the line of defects, but also they have a very different orientation from that prescribed by the defects (i.e., the domain wall forms an angle $\phi \hspace{0.17em}=$ 0.37 and 0.33 radians with the horizontal axis for ${\phi }_{\text{d}}=\arctan \left(1/2\right)$ and $\pi /4$, respectively; Movie S4). To understand this behavior, we extend our model to domain walls with $\phi \ne 0$ by introducing the local coordinates (Fig. 4A)

$$\zeta =x\sin \phi +y\cos \phi ,\hspace{0.17em}\eta =x\cos \phi -y\sin \phi .$$ [15]

When we neglect the variation of deformation along the domain wall (i.e., we assume ${\partial }_{\eta }\left(\cdot \right)=0$), we find that the profile of the domain wall is described by (SI Appendix, section S4.1)

$$\theta ={\theta }_{st}\tanh \frac{\zeta -{\zeta }_0}{w},$$ [16]

where ${\zeta }_0$ denotes the position along the $\zeta$ axis of the domain wall and

$$w=\frac{a}{{\theta }_{st}}\sqrt{\frac{3\left(k_s{a}^2-4k_{\theta }\right)}{8k_{\theta }\left(1+24\gamma \right)+\frac{3k_s{k}_l{a}^2{\sin }^2\phi }{k_s{\sin }^2\phi +k_l{\cos }^2\phi }}}.$$ [17]

Using the analytical solution given by Eq. 16, we then calculate the total energy of the system as a function of the orientation $\phi$ and position ${\zeta }_0$ of the domain wall. As shown in Fig. 4B, we find that the domain walls observed in our experiments minimize $E_{\text{total}}$ (SI Appendix, Figs. S24 and S25). However, once again the position and orientation of the domain walls can be controlled by introducing a few square pinning defects to reshape the energy landscape of the structure. For example, by placing four pinning defects along a line which runs parallel to those defined by the phase-inducing defects (Fig. 4C and Movie S4), we can manipulate $E_{\text{total}}$ to assume a single-welled landscape with a minimum at $\phi ={\phi }_d$ and ${\zeta }_0=21a/\cos {\phi }_d$ (Fig. 4D). Hence, given this energy landscape, the domain walls form exactly along the lines defined by the pinning defects (Fig. 4C). Further, by arranging the pinning defects along complex paths and carefully placing a few phase-inducing defects to initiate phase+ and phase− at desired locations, information in the form of arbitrary images can be encoded into the system, which can be revealed upon the application of a large enough compressive load (Fig. 4E and Movie S4).

Fig. 4.

(A) Deformation at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ of a sample with eight phase-inducing defects arranged along two lines that form an angle ${\phi }_{\text{d}}=\arctan \left(1/2\right)$ and $\pi /4$ with the horizontal axis. (B) Analytically predicted evolution of $E_{\text{total}}$ at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ as a function of ${\zeta }_0$ and $\phi$. The triangle corresponds to the configuration of the experimentally observed domain wall. (C) Deformation at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ of a sample with four pinning defects in addition to eight phase-inducing defects arranged as in A. (D) Analytically predicted evolution of $E_{\text{total}}$ at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ as a function of domain wall position ${\zeta }_0$ and orientation $\phi$. The triangle corresponds to the configuration of the experimentally observed domain wall. (E) Numerically predicted deformation at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ for $51\times 51$ structures with the pinning defects arranged along complex paths (in addition to phase-inducing defects to initiate phase+ and phase− at desired locations). The color in all snapshots corresponds to the rotation of the squares.

Applications

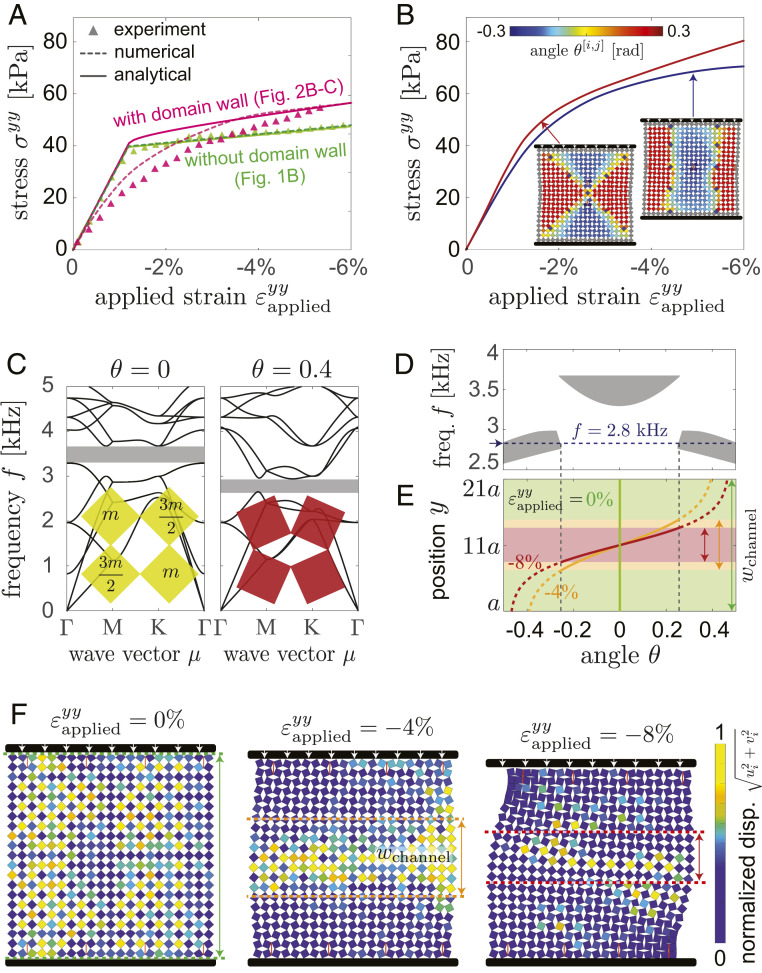
Having demonstrated that domain walls can be engineered by arranging a few defects in selected locations, we then explore how these can be harnessed to enhance the static and dynamic behavior of the system. To begin with, we focus on the effect of the domain walls on the nonlinear stress–strain response of the material. If we assume that near the horizontal boundaries of the structures (i.e., far away from the domain wall) the deformation is homogeneous (i.e., $\theta ={\theta }_{st}$ and $\partial v/\partial y={\epsilon }_{st}^{yy}$), the averaged normal stress in the $y$ direction can be analytically obtained by taking the continuum limit of the longitudinal forces acting on the vertical hinges as (SI Appendix, section S4.3)

$${\sigma }^{yy}=\frac{k_l}{t}\left({\epsilon }_{st}^{yy}+\frac{{\theta }_{st}^2}{2}\right).$$ [18]

In the absence of domain walls (i.e., for the case of homogeneous deformation), ${\epsilon }_{st}^{yy}={\epsilon }_{\text{applied}}^{yy}$ and ${\theta }_{st}$ can be determined as a function of ${\epsilon }_{\text{applied}}^{yy}$ using Eq. 5. Differently, in the presence of a domain wall ${\theta }_{st}$ and ${\epsilon }_{st}^{yy}$ are simultaneously determined as a function of ${\epsilon }_{\text{applied}}^{yy}$ by imposing Eqs. 3 and 5. In Fig. 5A we report the stress–strain curves predicted by Eq. 18 for systems with and without domain walls. We find that the structures become stiffer when a domain wall arises and the two opposite phases interact. Moreover, in Fig. 5A we compare the stress–strain curves predicted by our analytical model with those numerically calculated and the ones measured experimentally in $21\times 21$ structures with 1) no defects (green line) and 2) eight phase-inducing defects arranged as in Fig. 2 B and C (magenta line). The good agreement between all sets of data shows that our analytical model has potential to complement numerical tools for the design of systems with a targeted mechanical response. In its current form the model can capture only the response of systems with a single domain wall. However, we show in Fig. 5B that this stiffening effect can be amplified by the interactions of multiple domain walls. Therefore, our future work will aim at improving the current analytical model to predict more complex scenarios with multiple domain walls.

Fig. 5.

(A) Experimentally measured (triangles), numerically calculated (dashed lines), and theoretically predicted (solid lines) stress–strain curves for $21\times 21$ structures without a domain wall (structure considered in Fig. 1B) and with a horizontal domain wall (structure considered in Fig. 2 B and C). Note that the numerical and analytical predictions for the structure without a domain wall match perfectly, so that the green solid and dashed lines overlap. (B) Numerically calculated stress–strain curve for $21\times 21$ structures with two vertical domain walls (blue line) and two perpendicular domain walls at $\phi =\pi /4$ (red line). The corresponding deformations are shown as Insets. (C) Dispersion relations for planar elastic waves in the undeformed ($\theta =0$) and compressed ($\theta =0.4$) configurations. (D) Evolution of the band gap frequency, $f$, as a function of the squares rotation $\theta$. (E) Evolution of $\theta$ along the $y$ direction for a $21\times 21$ sample with an horizontal domain wall at ${\epsilon }_{\text{applied}}^{yy}=0\%$, $-4\%$, and $-8\%$. (F) Modal displacement fields at ${\epsilon }_{\text{applied}}^{yy}=0\%$ ($f=\mathrm{2,811}$ Hz), $-4\%$ ($f=\mathrm{2,812}$ Hz) and $-8\%$ ($f=\mathrm{2,779}$ Hz).

Next, we study the effect of the domain walls on the propagation of small-amplitude elastic waves. To this end, we consider a metamaterial with alternating light (with mass $m$) and heavy (with mass $3m/2$) squares and numerically calculate its dispersion relations as a function of ${\theta }_{st}$, assuming a state of homogeneous deformation (Fig. 5D and SI Appendix, section S3.6). We find that for $\theta =0$ (i.e., for unrotated squares) a complete band gap exists at frequency $f=\mathrm{3,293}\text{to}\mathrm{3,674}$ Hz (highlighted as the gray-shaded area in Fig. 5C), so that waves within this frequency range are not expected to propagate in the system. However, as the rotation of the squares is increased, this band gap shifts to a lower-frequency range ($f=\mathrm{2,652}\text{to}\mathrm{2,941}$ Hz; Fig. 5 C and D). Importantly, since $\left|\theta \right|\sim 0$ within the domain wall and $\left|\theta \right|>0$ in the surrounding compressed medium, such shifting can be harnessed to guide elastic waves along the paths defined by the domain walls. Our analytical model can be used to predict the width of the propagating channels, $w_{\text{channel}}$, at a given frequency $f$. To demonstrate this, we focus on $f=\mathrm{2,800}$ Hz—a frequency for which waves can propagate only if $-0.25<\theta <0.25$ (Fig. 5D). In Fig. 5E we report the evolution of $\theta$ predicted by Eq. 12 along the $y$ direction for a 21 $\times$ 21 sample at three different deformation levels ${\epsilon }_{\text{applied}}^{yy}=0\%$, $-4\%$, and $-8\%$. The width of the propagating channels can be easily determined by identifying the region in which $-0.25<\theta <0.25$. For this specific case we find that $w_{\text{channel}}=21a$ (entire structure), $8.0a$, and $5.5a$ at ${\epsilon }_{\text{applied}}^{yy}=0$, −4$\%$, and −8$\%$, respectively. Next, to verify these predictions, we report the eigenmodes associated to the frequency of $f\sim \mathrm{2,800}$ kHz at ${\epsilon }_{\text{applied}}^{yy}=0$, −4$\%$, and −8$\%$ for a system with defects arranged to form a horizontal domain wall (Fig. 5F and SI Appendix, section S3.6). As predicted by our continuum model, we find that, when the system is undeformed (i.e., for ${\epsilon }_{\text{applied}}^{yy}=0\%$), the vibrations are spread through the entire structure. Differently, at ${\epsilon }_{\text{applied}}^{yy}=-4\%$ and −8$\%$ they are confined near the domain wall, in a prescribed region. Importantly, the width of this region is very close to the one predicted by our analytical model $w_{\text{channel}}$. As such, our results indicate that domain walls generated by localized defects can be exploited to tune global properties of the system such as stiffness and wave guiding and that our analytical model can be leveraged to guide the design of functional systems.

Conclusions

To summarize, we have shown that in a rotating-squares–based mechanical metamaterial domain walls across which the rotation of the squares varies from positive to negative values can be formed by carefully arranging a few phase-inducing defects that control the nucleation of the two rotated buckling-induced phases. We have established an analytical model that explicitly describes the spatial profile of the domain walls for different orientations and predicts their evolution as a function of the applied deformation. Further, guided by this model, we have shown that domain walls of arbitrary shapes can be engineered by introducing a few pinning defects to modify the energy landscape of the structure. Importantly, since the considered defects can be easily placed and removed (the deformation is purely elastic), our platform can be used to efficiently explore how the shape and orientation of the emerging domain walls affect the mechanical properties of the material. Moreover, our study indicates that the metamaterial creates long-range interactions between the local defects, which may generate domain walls and ultimately affect the material’s global mechanical properties. We envision the exploitation of domain walls in order to encode additional modes of functionality in mechanical systems, including information encryption, stiffness tuning, and wave guiding.

Materials and Methods

Details of fabrication are described in SI Appendix, section S1. The protocol for experiments is provided in SI Appendix, section S2. The discrete model used to investigate the response of the system and additional numerical results are presented in SI Appendix, section S3. Details of the continuum model are presented in SI Appendix, section S4.

Data Availability.

All study data are included in this article and SI Appendix.