scTenifoldNet: A Machine Learning Workflow for Constructing and Comparing Transcriptome-wide Gene Regulatory Networks from Single-Cell Data

Summary

We present scTenifoldNet—a machine learning workflow built upon principal-component regression, low-rank tensor approximation, and manifold alignment—for constructing and comparing single-cell gene regulatory networks (scGRNs) using data from single-cell RNA sequencing. scTenifoldNet reveals regulatory changes in gene expression between samples by comparing the constructed scGRNs. With real data, scTenifoldNet identifies specific gene expression programs associated with different biological processes, providing critical insights into the underlying mechanism of regulatory networks governing cellular transcriptional activities.

Graphical Abstract

Highlights

• •scTenifoldNet is a machine learning tool for comparative single-cell network analysis
• •It is built upon PC regression, tensor decomposition, and manifold alignment
• •It constructs and compares gene regulatory networks from scRNA-seq data
• •It accurately identifies differentially regulated genes between single-cell samples

The Bigger Picture

Understanding the functions of genes requires the investigation of the structure of their regulatory networks of interactions. Single-cell RNA sequencing (scRNA-seq) brings new challenges and opportunities to the study of such networks. Here, we present a machine learning tool for constructing and comparing single-cell gene regulatory networks. Our algorithm, scTenifoldNet, can be used to identify differentially regulated genes between two scRNA-seq samples. It complements and enhances the commonly used differential expression analysis by revealing differences between samples in the regulatory relationships among genes, rather than the expression level. We anticipate that, by deciphering the complexity of data that surpasses human interpretative ability, scTenifoldNet can help achieve breakthroughs in understanding regulatory mechanisms underlying cell behaviors.

scTenifoldNet is a machine learning workflow built upon principal-component regression, low-rank tensor approximation, and manifold alignment. It uses single-cell RNA sequencing data to construct single-cell gene regulatory networks (scGRNs) and compares scGRNs of different samples to identify differentially regulated genes. Real-data applications demonstrate that scTenifoldNet accurately detects specific signatures of gene expression relevant to the cellular systems tested.

Introduction

A gene regulatory network (GRN) is a graph depicting the intricate interactions between transcription factors (TFs), associated proteins, and their target genes, reflecting the physiological condition of the cells in question. The analysis of GRNs promotes the interpretation of cell states, cell functions, and regulatory mechanisms that underlie the dynamics of cell behaviors. Multiple methods have been developed to build GRNs from data of gene expression.1, 2, 3, 4 It is important to compare GRNs constructed using datasets from different samples because the comparison may reveal regulatory mechanisms leading to transcriptomic changes. In particular, the comparison results may help us understand what is the most significant shift in regulatory mechanisms between samples, as well as how genetic and environmental signals are integrated to regulate a cell population's physiological responses and how cell behavior is affected by various perturbations. All of these are key questions in the study of the functional participation of given GRNs. Despite the critical importance of comparative GRN analysis, relatively few methods have been established to compare GRNs.⁵

Single-cell RNA-sequencing (scRNA-seq) technology has been revolutionizing the biomedical sciences in recent years. New research provides an unparalleled degree of precision in analyzing transcriptional regulation, cell history, and cell interactions with rich knowledge. It transforms previous entirely tissue-based assays into transcriptomic single-cell measurements and greatly enhances our understanding of cell development, homeostasis, and disease. Current scRNA-seq systems (e.g., 10× Genomics) can profile transcriptomes for thousands of cells per experiment. The sheer number of measured cells can be leveraged to construct GRNs. Advanced computational methods can facilitate such an effort to reach unprecedented resolution and accuracy, revealing the network state of given cells.6, 7, 8 Furthermore, comparative analyses among GRNs of different samples will be extremely powerful in revealing fundamental changes in regulatory networks and unraveling the transcriptional programs that govern the behaviors of cells. Since our ability to generate scRNA-seq data has outpaced our ability to extract information from it, there is a clear need to develop effective computational algorithms and novel statistical methods for analyzing and exploiting information embedded within GRNs.⁹

Constructing single-cell GRNs (scGRNs) using data from scRNA-seq and then effectively comparing constructed scGRNs presents significant analytical challenges.^9,10 A meaningful comparison of scGRNs first requires a robust construction of a GRN from scRNA-seq data. Comparing scGRNs built via an unstable solution would cause misleading results and inappropriate conclusions. The vast number of different cellular states in a sample and the technical and biological noise, as well as the sparsity of scRNA-seq data, complicate the process of scGRN construction. Often, the expression of a gene is governed by stochastic processes and also influenced by transcriptional activities of many other genes. Thus, it is difficult to tease out subtle signals and infer true connections between genes. Furthermore, a direct comparison between two scGRNs is difficult; e.g., comparing each edge of the graph between scGRNs would be ill powered when scGRNs involve thousands of genes. Taken together, the key challenge in conducting comparative scGRN analysis is to extract meaningful information from noisy and sparse scRNA-seq data, since the information is deeply embedded in the differences between highly complex scGRNs of two samples.

In this paper, we introduce a workflow for constructing and comparing scGRNs using data from scRNA-seq of different samples. The workflow, which we call scTenifoldNet, is built upon several machine learning algorithms, including principal-component (PC) regression, low-rank tensor approximation, and manifold alignment. Through several examples, we show that scTenifoldNet is a sensitive tool to detect specific changes in gene expression signatures and the regulatory network rewiring events. The input of scTenifoldNet is a pair of expression matrices from scRNA-seq of two different samples. For instance, one sample may come from a healthy donor and the other from a diseased donor. In scTenifoldNet, the two input expression matrices are simultaneously processed through a multistep procedure. The final output is a list of ranked genes, sorted according to the differential regulation level of each gene. The ranked gene list can be used to perform functional enrichment analysis to detect the enriched molecular functions and involved biological processes. The constructed scGRN can also be used to identify functionally significant modules, i.e., subsets of tightly regulated genes.

scTenifoldNet includes an innovative method for comparing two scGRNs. We are not aware of any prior work using a similar design to achieve the same analytical goal. scTenifoldNet overcomes several methodological challenges, resulting in an effective and efficient scGRN comparison method. Here, we first benchmark and demonstrate the utility of scTenifoldNet across synthetic datasets and then apply scTenifoldNet to real datasets. Our real data analyses showed scTenifoldNet's power in identifying significant genes and network modules whose regulatory patterns shift greatly between samples. Some of these findings have not been reported in the respective original studies in which the datasets were generated.

Results

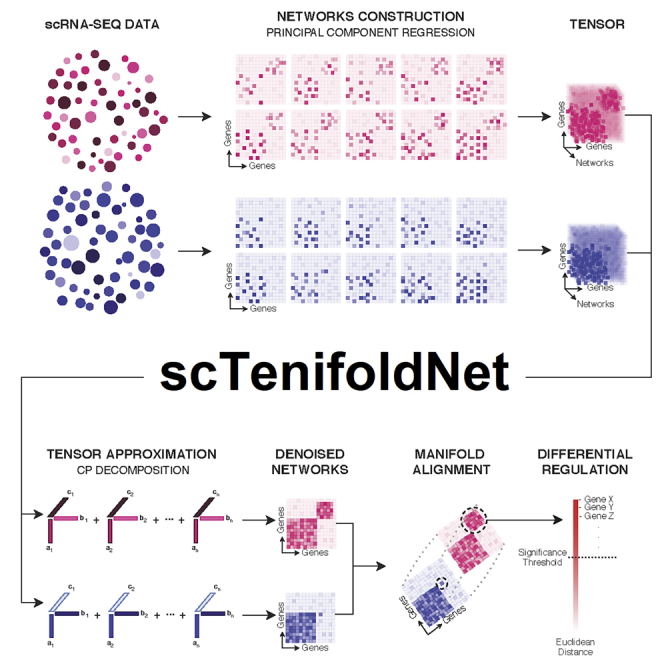
The scTenifoldNet Architecture

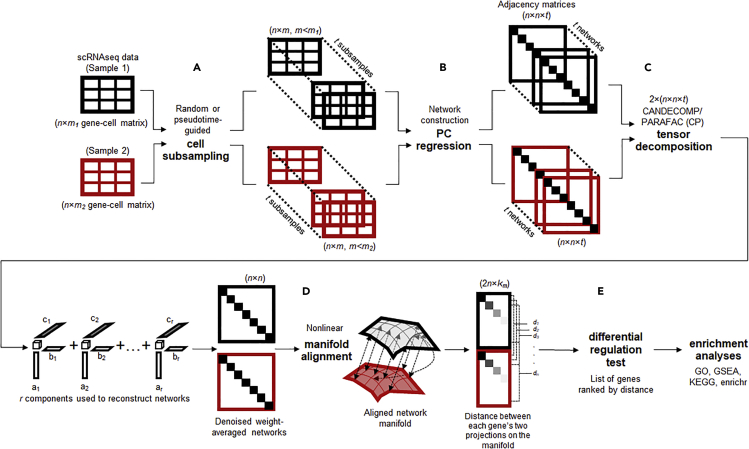
To enable comparative scGRN analysis in a robust and scalable manner, we base our method on a series of machine learning methods. A key challenge of our comparative analysis is to extract meaningful differences in regulatory relationships between two samples from noisy and sparse data. Specifically, we seek to contrast scGRNs constructed from different scRNA-seq expression matrices. Figure 1 shows the main components of scTenifoldNet architecture. The whole workflow contains five key steps: subsampling cells, constructing multilayer scGRNs, denoising, manifold alignment, and differential regulation (DR) test. To produce biologically meaningful results, we made dedicated design decisions for the task in each of these steps. Next, we briefly describe the numerical methods implemented in scTenifoldNet. More technical details are presented in the Experimental Procedures.

Figure 1.

Overview of the scTenifoldNet Workflow

scTenifoldNet is a machine learning framework that uses a comparative network approach with scRNA-seq data to identify regulatory changes between samples. scTenifoldNet is composed of five major steps.

(A) Cell subsampling. scTenifoldNet starts with subsampling cells in the scRNA-seq expression matrices. When two samples are analyzed, each of the two samples is subsampled either randomly or following a pseudotime trajectory of cells. The subsampling is repeated multiple times to create a series of subsampled cell populations, which are subject to network construction and form a multilayer scGRN.

(B) Network construction. PC regression is used for scGRN construction; each scGRN is represented as a weighted adjacency matrix.

(C) Tensor denoising. Two samples produce two multilayer GRNs and form two three-order tensors, which are subsequently decomposed into multiple components. The top components of tensor decomposition are then used to reconstruct two denoised multilayer scGRNs. Then, two denoised multilayer scGRNs are collapsed by taking the average weight across layers.

(D) Manifold alignment. The two single-layer average scGRNs are then aligned with respect to common genes using a nonlinear manifold alignment algorithm. Each gene is projected to a low-rank manifold space as two data points, one from each sample.

(E) Differential regulation test. The distance between the two data points is the relative difference of the gene in its regulatory relationships in the two scGRNs. Ranked genes are subject to tests for their significance in differential regulation between scGRNs.

Numerical Methods

The numerical methods used to construct and compare scGRNs involve the following five steps:

Step 1. Pre-processing Data and Subsampling Cells

The input data are two scRNA-seq expression data matrices, X and Y, containing expression values for n genes in m₁ and m₂ cells from two different samples. Next, m cells in X and Y are randomly sampled to form X′ and Y′. This subsampling process is repeated t times to create two collections of subsampled cells, $\left\{{\mathit{X}}_i^{\prime }\right\}$ and$\left\{{\mathit{Y}}_i^{\text{′}}\right\}$, where $i=1,2,\dots ,t$.

Step 2. Constructing Initial Networks

For each ${\mathit{X}}_i^{\prime }\in \left\{{\mathit{X}}_i^{\prime }\right\}$, $i=1,2,\dots ,t$, PC regression is used to construct a GRN. The constructed GRN from ${\mathit{X}}_i^{\text{′}}$ is stored as a weighted graph represented with an n × n weighted adjacency matrix ${\mathit{X}}_i^{\text{′}}$. Similarly, for each ${\mathit{Y}}_i^{\text{′}}\in \left\{{\mathit{Y}}_i^{\text{′}}\right\}$, $i=1,2,\dots ,t$, we construct a GRN and represent it with an n × n weighted adjacency matrix ${\mathit{W}}_i^y$. Diagonal values of each adjacency matrix are set to zeros, and other values are normalized by dividing by their maximal absolute value. Each normalized adjacency matrix is then filtered by retaining only the top 5% of edges ranked using the absolute edge weight, resulting in a sparse adjacency matrix.

Step 3. Denoising

Tensor decomposition¹¹ is used to denoise the adjacency matrices obtained in Step 2. The collection of $t$ scGRNs for each sample, $\left\{{\mathit{W}}_i^x\right\}$ or $\left\{{\mathit{W}}_i^y\right\}$, is processed separately as a third-order tensor, denoted as ${\mathfrak{T}}^x$ or ${\mathfrak{T}}^y$, each containing n × n × t elements. The CANDECOMP/PARAFAC (CP) decomposition is applied to decompose ${\mathfrak{T}}^x$ and ${\mathfrak{T}}^y$ into components. Next, ${\mathfrak{T}}^x$ and ${\mathfrak{T}}^y$ are reconstructed using the top r components to obtain denoised tensors: ${\mathfrak{T}}_d^x$ _and ${\mathfrak{T}}_d^y$. Denoised $\left\{{\mathit{W}}_i^x\right\}$ and $\left\{{\mathit{W}}_i^y\right\}$ in ${\mathfrak{T}}_d^x$ and ${\mathfrak{T}}_d^y$ are collapsed by taking the average of edge weights for each edge to form two denoised, averaged matrices, ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$, which are subsequently normalized as in step 2 and then symmetrized.

Step 4. Aligning Genes onto a Manifold

The weighted adjacency matrices ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ are regarded as two similarity matrices for a nonlinear manifold alignment procedure. The alignment is done by solving an eigenvalue problem with a Laplacian matrix derived from the joint matrices, $\mathit{W}=\left[{\mathit{W}}_d^x,\lambda \mathit{I}/2;\lambda {\mathit{I}}^T/2,{\mathit{W}}_d^y\right]$, where $\lambda$ is a tuning parameter and I is the identity matrix that reflects the binary correspondence between genes in the samples, X and Y. As the result of manifold alignment, all genes in the samples, X and Y, are projected on a shared, low-dimensional manifold with a dimension k_m ≪ n. The projections of each gene $j$ from the samples, X and Y, are two k_m-dimensional vectors, $F_j^x$ and $F_j^y$.

Step 5. Ranking Genes

For each gene j, let d_j be the Euclidean distance between the gene's two projections $F_j^x$ and $F_j^y$ on the shared manifold: one is from the sample X, and the other is from the sample Y. Genes are sorted according to this distance. The greater the distance, the greater the regulatory shift.

In the following sections, we explain the rationale behind each step of scTenifoldNet, as well as the selection of machine learning algorithms and implementation details.

Subsampling of Cells

The rationale for randomly subsampling cells is close to that of ensemble learning. Ensemble learning is a technique where multimodel decisions are merged to improve overall performance. Similarly, instead of attempting to build a single scGRN, scTenifoldNet randomly samples subsets of cells from the given scRNA-seq expression matrix and builds a series of “low-precision” scGRNs with the subsampled datasets. These low-precision scGRNs are then combined to obtain a “high-precision” scGRN. As mentioned above, current scRNA-seq technology can produce the transcriptome profiles of thousands of cells from each sample. It is fundamentally challenging to process high-dimensionality and large-scale scRNA-seq data, especially since there can be a substantial variation among cells. This happens even in a group of highly homogeneous cells of the same type.¹² The presence of so-called outlying cells, i.e., cells showing profiles of expression that deviate from those of most other cells, may influence the construction of high-precision scGRNs. Therefore, subsampling offers promise as a technique for handling the noise in the input datasets. When the number of cells is small, the input data matrix may be resampled with replacement.¹³

Constructing scGRNs Using PC Regression

Although many GRN construction methods have been developed,^1,2,4 it is unclear which one is suitable for constructing multiple large scGRNs from the subsampled data.⁹ When dealing with multiple sets of input data, both the accuracy and the computational efficiency of these algorithms have to be considered. After conducting a thorough review of existing methods, we opted to adopt PCNet,⁵ a method of network construction using PC regression.¹⁴ The PC regression method extracts the first few (e.g., k = 3) PCs and then uses these components as the predictors in a linear regression model fitted using ordinary least squares. The values of the transformed coefficients of genes are treated as the strength and regulatory effect between genes to generate the network. The utilization of PC regression in scTenifoldNet lies in its ability to surpass the multicollinearity problem that arises when two or more explanatory variables are linearly correlated.

Denoising via Low-Rank Tensor Approximation

Removing the noise from constructed scGRNs is an important step of scTenifoldNet. Here the term “noise” is used in a broad sense to refer to any outlier or interference that is not the quantity of interest, i.e., the true regulatory relationship between genes. For each sample, the multilayer scGRN constructed from multiple subsampled datasets is regarded as a rank 3 tensor. To reduce the noise in the multilayer scGRN, we decompose the tensor and reconstruct the multilayer scGRN using leading components. The idea is similar to that of denoising using truncated singular value decomposition (SVD). After cutting a larger portion of the noise spread over the lowest singular value components, the reconstructed data matrix based on the truncated SVD would, therefore, represent the original data with reduced noise. Indeed, tensor decomposition has been used in video data analyses for denoising and information-extracting purposes.¹⁵ It has also been used to impute missing data.¹⁶ Using the CP algorithm,¹⁷ we factorize the two multilayer scGRNs separately and regenerate all adjacency matrices using leading components. The number of components used for reconstruction can be specified and is set to 3 by default. In the real data applications, we find the tensor GRN regeneration serves two purposes, denoising and enhancing, i.e., making main signals stronger and making less important signals weaker.

Manifold Alignment of Two scGRNs

For a gene, its position in one of the two scGRNs (i.e., denoised adjacency matrices from the two samples) is determined by its regulatory relationships with all other genes. Here we regard each gene as a data point in a high-dimensional space where components of the data point are the features, i.e., weights between the gene and all other genes in the scGRN adjacency matrix. To compare the same gene's positions in the two scGRNs, we first align the two scGRNs. To do so, we take a popular and effective approach for processing high-dimensional data, intuitively modeling the intrinsic geometry of the data as being sampled from a low-dimensional manifold, commonly referred to as the manifold assumption.¹⁸ This assumption essentially means that local regions in the data can be mapped to low-dimensional coordinates, while the nonlinearity and high dimensionality in the data come from the curvature of the manifold. Manifold alignment produces projections between sets of data, given that the original datasets lie on a common manifold.19, 20, 21, 22 Manifold alignment matches the local and nonlinear structures among the data points from multiple sources and projects them to the same low-dimensional space while maintaining their local manifold structure of each source. The ability to flexibly learn and accurately represent the structure in the data with manifold alignment has been demonstrated in applications in automatic machine translation, face recognition, and so on.^23,24 Here, we use manifold alignment to match genes in the two denoised scGRNs, one from each sample, to identify cross-network linkages. Consequently, the information of genes stored in two scGRNs is aligned, meaning points close together in the low-dimensional space are more similar than points that are farther apart.

Ranking Genes and Reporting Differentially Regulated Genes

To identify genes whose regulatory status differs between the two samples, we calculate the distance between projected data points in the manifold alignment subspace. For each gene, if the gene appears in scGRNs of both samples, there are two data points for the same gene, one from each sample. We compute the Euclidean distance between the two data points of the gene and use the distance to measure the dissimilarity in the gene's regulatory status in two scGRNs.²⁵ We do this for all genes shared between two samples and then rank the genes by the distance. The larger the distance, the more different the gene in two samples. In this way, we obtain a list of ranked genes. These ranked genes are subject to functional annotation, such as by using the pre-ranked gene set enrichment analysis (GSEA)²⁶ to assess the enriched functions associated with top genes. To avoid choosing the number of selected genes arbitrarily, we compute p values for genes using χ² tests, adjust the p values with a multiple testing correction, and select significant genes using a 5% false discovery rate (FDR) cutoff.

Benchmarking the Performance of scTenifoldNet Using Simulated Data

Precision and Recall of the Network Construction Method Adopted in scTenifoldNet

PC regression is the method we adopted for scTenifoldNet to construct scGRN. It is important to ensure that scTenifoldNet/PC regression is an effective and efficient network construction method for our purpose.

To this end, we conducted a systematic comparison between network construction algorithms using a published evaluation tool package called BEELINE.¹⁰ We benchmarked scTenifoldNet/PC regression and compared it with 11 other algorithms (see Experimental Procedures). We chose to reuse a reference dataset called the gonadal sex determination (GSD) in the BEELINE package to perform the benchmarking. In the BEELINE package, GSD is the largest curated reference dataset, and it contains 19 genes and 2,000 cells. We compared different algorithms jointly using the area under the precision-recall curve (AUPRC), area under the receiver operating characteristic curve (AUROC), and computation time, and found that scTenifoldNet/PC regression and partial information decomposition and context (PIDC)²⁷ outperformed other algorithms (see Figure S1 for details).

We also simulated scRNA-seq data using a parametric method with a predefined scGRN model (see Experimental Procedures for details).²⁸ With the simulated data, which contain 100 genes and up to 3,000 cells, we compared constructed scGRNs against the ground truth (i.e., the simulated scGRN) to estimate the accuracy of reconstruction. We tested the accuracy of scTenifoldNet/PC regression against methods based on Spearman’s correlation coefficient (SCC) and mutual information (MI)¹ and on GENIE3.² The SCC and MI methods are computationally efficient, whereas GENIE3 is not, but GENIE3 is the top-performing method for network inference in the DREAM challenges.³ For each method, their performance in recovering gene regulatory relationships was compared with the ground-truth interactions between genes, which were generated according to pre-setting parameters. We found that scTenifoldNet/PC regression produced more specific (better accuracy) and more sensitive (better recall) scGRNs than other methods (Figure 2A). This is true across a wide range of settings of cell numbers in input scRNA-seq expression matrices. scTenifoldNet/PC regression is also much faster than GENIE3 (running time information is available in Table S1).

Figure 2.

Benchmarking the Performance of scTenifoldNet Using Simulated Data

(A) The accuracy and recall of scGRN construction using different methods, PC regression, SCC, MI, and GENIE3, as functions of the number of cells used in the analysis. Error bar is the SD of the computed values after 10 bootstrapped evaluations. PCR, PC regression; SCC, Spearman’s correlation coefficient; MI, mutual information; GENIE3, a random-forest-based network construction method.

(B) Visualization of the effect of tensor denoising on accuracy and recall of multilayer scGRNs. Each subpanel is a heatmap of a 100 × 100 adjacency matrix constructed using PC regression over the counts of 500 randomly subsampled cells. Gray scale indicates the relative strength of regulatory relationships between genes. Top part includes networks before tensor denoising (adjacency matrices in heatmap with red box); bottom part includes corresponding networks after tensor denoising (adjacency matrices in heatmap with green box). In each part, adjacency matrices of networks of 10 subsamples (10 small heatmaps) and their average adjacency matrix (one large heatmap) are shown.

(C) Evaluation of the sensitivity of scTenifoldNet in identifying punctual changes in the regulatory profiles. Top: evaluation of the original data matrix against itself. Bottom: evaluation of the original matrix against the perturbed matrix. Significant genes identified using the differential regulation test (FDR <0.1, B-H correction) are indicated in red. All significant genes are perturbed in simulation and thus are expected to be identified.

A limitation of our simulation-based evaluation is that simulated scGRNs are much simpler than GRNs in reality, which may contain hundreds or thousands of genes. It is a challenge to simulate such a realistic GRN and, for GRN inference algorithms, to figure out the key regulators and their targets. In this study, we chose to apply our method directly to real datasets and evaluate the biological relevance of results, rather than explore the impact of the size and diversity of synthetic GRNs on the results.

Effect of Denoising with Tensor Decomposition

To show the effect of tensor denoising, we simulated scRNA-seq data (see Experimental Procedures) and processed the data using the first two steps of scTenifoldNet, i.e., cell subsampling followed by the construction of scGRNs using PC regression. We subsampled 500 cells each time and generated 10 scGRNs. The 10 scGRNs were treated as a multilayer network or a tensor to be denoised. For each scGRN, we kept the top 20% of the links. The presence and absence of links in each scGRN were compared with those in the simulated, ground-truth scGRN to estimate the accuracy of recovery and the rate of recall. Figure 2B contains the heatmaps of adjacency matrices of the 10 scGRNs before and after denoising (small heatmaps). We also show two collapsed scGRNs (Figure 2B, large heatmaps), which were generated by averaging link weights across the 10 scGRNs before and after denoising. These results illustrate the ability of scTenifoldNet to denoise multilayer scGRNs. For instance, tensor denoising improves the recall rate of regulatory relationships between genes by 25%. This simulation study suggests that tensor denoising could be useful for removing the impacts of random dropout and other noise issues affecting the scGRN construction using scRNA-seq data.

Detecting Power Illustrated with a Simulated Dataset

We used simulated data to show the capability of scTenifoldNet in detecting differentially regulated genes. We first used the negative binomial distribution to generate a sparse synthetic scRNA-seq dataset (an expression matrix including 67% zeros in its values). This toy dataset includes 2,000 cells and 100 genes. We called it sample 1. We then duplicated the expression matrix of sample 1 to make sample 2. We modified the expression matrix of sample 2 by swapping expression values of three randomly selected genes with those of another three randomly selected genes. Thus, the differences between samples 1 and 2 are restricted in these six genes. Using scTenifoldNet with the default parameter setting, we compared the originally generated expression matrix (sample 1) with itself (sample 1 versus sample 1) and also with the manually perturbed version (sample 1 versus sample 2). As expected, when comparing the original matrix against itself, none of the genes was identified to be significant. However, when samples 1 and 2 were compared, the six genes whose expression values were swapped were identified as significant differentially regulated genes (Figure 2C, FDR <0.1). These results are expected and support the sensitivity of scTenifoldNet in identifying subtly shifted gene expression programs.

Real Data Analyses

Practical Considerations of Real Data Analysis Using scTenifoldNet

First of all, we address several practical questions regarding the application of scTenifoldNet to real scRNA-seq data. (1) What are the input expression matrices to be compared? The input to scTenifoldNet is two matrices of gene expression values (e.g., unique molecular identifier [UMI] counts) as measured in two samples to be compared. In each matrix, columns represent cells, and rows represent genes. We assume that each input matrix contains a sizable number of cells. For example, a typical input matrix may contain UMI counts for 5,000 genes and 2,000 cells. Whether a gene is expressed among cells can be determined by examining if this gene has a nonzero UMI count in more than 5% of cells. Scaling normalization (e.g., the library size normalization) of the input UMI count matrix does not seem to affect the construction of scGRNs (Figure S2). In contrast, imputing the UMI count matrix using an imputation algorithm (e.g., MAGIC)²⁹ may have an impact on the performance of scTenifoldNet (Figure S3). (2) How does scTenifoldNet handle cell heterogeneity? Heterogeneity in expression among cells is inevitable. scTenifoldNet is designed to tolerate a certain level of such heterogeneity as long as the cells are of the same type. scTenifoldNet is not a data preparation tool. It also does not perform any clustering analysis for cells; it does not assign cells to cell types. We assume all cells in both input matrices are of the same type. Otherwise, the results would be difficult to interpret. To solve this problem, a specific tool (to prioritize cell types most responsive to biological perturbations) has been developed elsewhere.³⁰ (3) What if the number of cells is too small? We expect that each input matrix contains a sizable number of cells (e.g., n > 2,000). If this is the case, the jackknife method (subsampling without replacement) is adapted by default: m = 500 cells are subsampled each time. Alternatively, an m-out-of-n bootstrap method (subsampling with replacement) can be used.¹³ When the number of cells is small (e.g., n = 500), a full bootstrap method can be used, i.e., resampling 500 cells each time out of 500 given cells with replacement.^13,31 scTenifoldNet is robust against unbalanced cell numbers in the two samples for comparison (Figure S4). (4) What is the relationship between scTenifoldNet analysis and differential expression (DE) analysis? scTenifoldNet analysis should be used as a complementary analysis method in addition to DE analysis, rather than replacing DE analysis. DE analysis (using, e.g., MAST,³² edgeR,³³ or SCDE)³⁴ is still a widely used method for understanding the difference between two scRNA-seq samples.³⁵ scTenifoldNet is designed based on a principle different from that underlying DE analysis. Thus, the results of scTenifoldNet analysis and DE analysis are not supposed to be compared side by side. It is not uncommon that scTenifoldNet and DE analyses report the same genes to be significant. This is because the change in the regulatory pattern of a gene in scGRNs may be associated with the change in the gene's expression level. To evaluate the influence of gene expression level on scGRN construction, we calculated the correlation between the average gene expression level and the average weighted degree of nodes in scGRNs, which are constructed using scTenifoldNet/PC regression and other algorithms in the BEELINE package.¹⁰ If the weighted degree of nodes in an scGRN constructed using a method is correlated with the expression level of genes, then it indicates that the method is likely to be biased toward highly expressed genes during the process of scGRN construction. We found that all evaluated algorithms produced results showing a certain level of such a correlation (Figure S5). However, compared with all other algorithms, scTenifoldNet/PC regression produced the smallest correlation value and thus is most robust against the bias toward highly expressed genes.

Analysis of Transcriptional Responses of Neurons to Acute Morphine Treatment

To illustrate the use of scTenifoldNet, we first applied scTenifoldNet to an scRNA-seq dataset from Avey and colleagues³⁶ This is a study on transcriptional responses of mouse neural cells to morphine (Figure 3A). In the study, Avey and colleagues performed scRNA-seq experiments with the nucleus accumbens of mice after 4 h of morphine treatment and used mice treated with saline as mock controls. Single-cell expression data were obtained for 11,171 and 12,105 cells from four morphine- and four mock-treated mice, respectively.³⁶ The measured cells were clustered to identify neurons (7,972 and 8,912 from morphine- and mock-treated samples, respectively); the identified neurons were then subgrouped into 11 clusters, including major clusters of D1 and D2 medium spiny neurons (MSNs), comprising ~95% of the neurons in the nucleus accumbens. Using DE analysis implemented in SCDE,³⁴ Avey et al. identified several hundred genes that are differentially expressed between morphine- and mock-treated samples (Table S2 of Avey et al.).³⁶ Although this result is intriguing, we argue that it seems that when so many genes are identified as “significant players,” it is difficult to interpret the result and to pinpoint the specific regulatory mechanism underlying the true response. Indeed, instead of functional enrichment analysis with identified differentially expressed genes, the subsequent analyses in the study of Avey and coworkers³⁶ were refocused on a tiny portion of D1 MSNs, called activated MSNs. It was only when activated MSNs were compared with all other D1 MSNs that 256 differentially expressed genes were identified (SCDE, p < 0.001, Table S2 of Avey et al.).³⁶ These genes were then found to be associated with several terms related to opioid addiction, including morphine dependence and opioid-related disorders (Table S3 of Avey et al.).³⁶ In the morphine-treated sample, less than 4.5% of D1 MSNs were activated MSNs; in the mock-treated sample, less than 2% (see Figure S2B of Avey et al.).³⁶ In view of this, we point out here that while relevant signals can be detected using traditional DE analysis, the analytical method involves extensive human intervention; i.e., an iterative clustering procedure is needed to identify a final population of cells (in this case, activated MSNs). The cell population size is small, making the analysis result potentially variable.

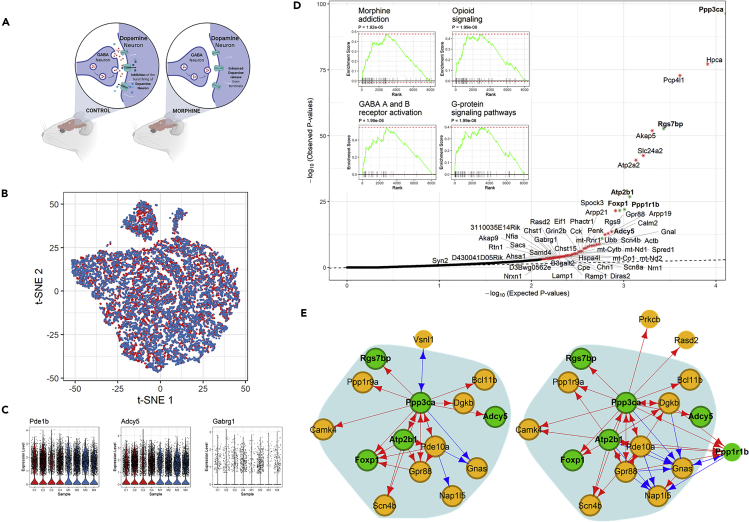
Figure 3.

Analysis of Transcriptional Responses to Morphine in Mouse Cortical Neurons

(A) Illustration of experimental design and data collection of the morphine response study.³⁶

(B) t-SNE plot of 7,972 and 8,912 neurons from morphine-treated (blue) and mock-treated (red) mice, respectively.

(C) Violin plots showing the log-normalized expression levels of representative differentially regulated and/or differentially expressed genes in four (M) morphine- and four (C) mock-treated mice.

(D) Quantile-quantile (Q-Q) plot for observed and expected p values of the 8,138 genes tested. Genes (n = 65) with FDR <0.1 are shown in red; genes (n = 56) with FDR <0.05 are labeled with an asterisk. Inset shows results of the GSEA for genes ranked by their distances in manifold aligned scGRNs from morphine- and mock-treated mice.

(E) The module enriched with differentially regulated genes and the corresponding subnetworks in two scGRNs. For illustrative purposes, the module is centered on the differentially regulated gene Ppp3ca. Significantly differentially regulated genes (FDR <0.05) in the module are highlighted in green. Edges are color-coded: red indicates a positive association, and blue indicates negative. Weak edges are filtered out by thresholding for clear visualization, and the background shadow indicates the shared portion of the module in the two scGRNs.

We were motivated by these considerations and set out to reanalyze the data. We first reproduced the results of the DE analysis. We found that the mock- and morphine-treated neurons indeed exhibited a striking similarity. For example, mock- and morphine-treated neurons are indistinguishable in a t-distributed stochastic neighbor embedding (t-SNE) plot (Figure 3B); expression levels of several known morphine-responsive genes, e.g., Adcy5, Ppp1r1b, and Ppp3ca, show no difference (Figure 3C). Thus, a direct comparison of gene expression between neurons using the DE method may have limited power to identify relevant genes involved in the morphine response.

Next, using scTenifoldNet, we identified 56 genes showing significant differences in their transcriptional regulation between mock- and morphine-treated neurons (Table S2). Compared with other genes, these genes have a significantly greater distance between their positions in two scGRNs aligned into the manifold (FDR <0.05, χ² test with Benjamini-Hochberg (B-H) multiple test adjustment, see Experimental Procedures for details). GSEA showed that these differentially regulated genes are enriched for opioid signaling, signaling by G protein-coupled receptors, reduction of cytosolic calcium levels, and morphine addiction (Figure 3D, inset, see also Table S3). It is known that morphine binds to the opioid receptors on the neuronal membrane. The signal is then transmitted through the G-protein-signaling system, inhibiting the adenylyl cyclase in the cytoplasm and decreasing the levels of cAMP and calcium-channel conduction.37, 38, 39 Furthermore, 21 of 56 (38%) identified differentially regulated genes were found to be targets of RARB (adjusted p < 0.01, Enrichr enrichment test based on the chromatin immunoprecipitation sequencing [ChIP-seq] data).⁴⁰ RARB plays a role in synaptic transmission in dopaminergic neurons and the adenylate cyclase-activating dopamine receptor signaling pathway.^41,42 Thus, these enriched functions are relevant to the morphine stimulus, which is known to induce the disinhibition of dopaminergic neurons by GABA transmission, enhance dopamine release, and cause addiction.^43,44 Using the constructed scGRN, we were able to trace differentially regulated genes back to their topological positions in the network and examine their interacting genes. Figure 3E shows such a network module, including multiple differentially regulated genes.

In this case, scTenifoldNet was used as an unsupervised tool, which needs no human interference to operate. This feature is critical when referring to this specific set of data because where the signal is limited to rare types of cells, there is a chance that a less sensitive approach would miss the signal, especially when human interference is not provided. It is ideal to have an unsupervised tool that is sensitive to signals and, at the same time, robust to variation between cells. We note that scTenifoldNet is a tool different from conventional DE analysis tools: —scTenifoldNet reported fewer differentially regulated genes, in terms of the number of genes, compared with differentially expressed genes identified in the original study.³⁶ Among the 56 differentially regulated genes that scTenifoldNet detected, 11 (Actb, Adcy5, Akap9, D430041D05Rik, Eif1, Pcp4l1, Penk, Phactr1, Rasd2, Scn4b, and Ubb) are among the 256 differentially expressed genes reported in Table S2 of Avey and colleagues³⁶ The number of overlapping genes is not significantly higher than expected by random according to a hypergeometric test (p = 0.29) with a total of 1,432 genes (from Table S2 of Avey et al.)³⁶ included in the test. Figure 3C shows expression levels of three representative genes, Pde1b, Adcy5, and Gabrg1, in neurons from mock- and morphine-treated mice. All three genes are known to be involved in the morphine response,45, 46, 47 but only when DE and DR tests were applied jointly were all three genes identified: Pde1b is a differentially expressed but not a differentially regulated gene, Adcy5 a differentially regulated and a differentially expressed gene, and Gabrg1 a differentially regulated but not a differentially expressed gene.

Analysis of Transcriptional Responses of a Carcinoma Cell Line to Cetuximab

To further illustrate the power of scTenifoldNet in identifying genes associated with specific perturbations, we applied scTenifoldNet to another published set of scRNA-seq data.⁴⁸ In this study,⁴⁸ Kagohara et al. use scRNA-seq to study mechanisms underlying the development of resistance to cetuximab in head and neck squamous cell carcinoma (HNSCC) (Figure 4A). Cetuximab is a human-murine chimeric monoclonal antibody used to treat metastatic colorectal cancer, metastatic non-small cell lung cancer, and head and neck cancer. In conjunction with radiotherapy, cetuximab improves the objective response rate in first-line treatment of recurrent or metastatic squamous cell carcinoma of the head and neck.⁴⁹ Cetuximab binds to the extracellular domain of the epidermal growth factor receptor (EGFR) on both normal and tumor cells.⁵⁰ EGFR is overexpressed in many cancers. Competitive binding of cetuximab to EGFR blocks the phosphorylation and activation of receptor-associated kinases and their downstream targets, e.g., MAPK, PI3K/Akt, and Jak/Stat pathways,⁵¹ thereby reducing their effects on cell growth and metastatic spread. It is known that blocking EGFR activation also affects cellular processes such as apoptosis, cell growth, and vascular endothelial growth factor production.⁵² Cetuximab is also known to cause degradation of the antibody-receptor complex and the downregulation of EGFR1 expression.⁵³

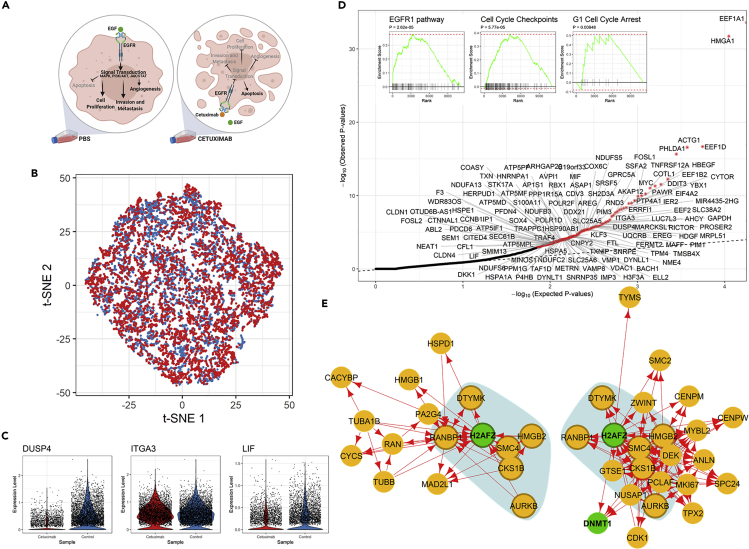
Figure 4.

Analysis of Transcriptional Responses of a Carcinoma Cell Line to Cetuximab

(A) Illustration of experimental design, including sample groups and the known mechanism of drug action, in the study of cetuximab resistance of HNSCC cell lines.⁴⁸

(B) t-SNE plot of 5,217 and 4,507 HNSCC-SCC6 cells treated with cetuximab (red) and PBS (blue), respectively.

(C) Violin plots showing the log-normalized expression levels of selected differentially regulated genes in SCC6 cells with and without cetuximab treatment.

(D) Q-Q plot for observed and expected p values of the 7,503 genes tested. Genes (n = 25) with FDR <0.05 are labeled with an asterisk. Inset shows the results of the GSEA for genes ranked by their distances in manifold aligned scGRNs from young and old mice.

(E) A representative module with differentially regulated genes and corresponding subnetworks in two scGRNs. The module is enriched with differentially regulated genes and the corresponding subnetworks in two scGRNs. For illustrative purposes, the module is centered on the differentially regulated gene H2AFZ. The colors, edges, and marks are presented as in Figure 3E.

Kagohara et al. sequenced the transcriptome profile of cells before and after cetuximab treatment for 120 h in three different HNSCC cell lines: SCC1, SCC6, and SCC25.⁴⁸ They found that SCC6 is the most sensitive to the cetuximab treatment, reporting 8,389 genes as differentially expressed (including 4,166 upregulated and 4,223 downregulated ones with p < 0.05; Table S4 of Kagohara et al.).⁴⁸ Such a large number of differentially expressed genes makes it difficult to identify genes directly associated with the molecular mechanism through which cetuximab acts.

We extracted scRNA-seq data for 4,507 and 5,217 SCC6 cells treated with and without cetuximab, respectively (Figure 4B). Expression levels of three genes, DuSP4, TIGA3, and LIF, in cells of two treatment groups are shown in Figure 4C. All three genes are in the EGFR pathway. We used scTenifoldNet to reanalyze the data and identified 125 differentially regulated genes (FDR <0.05, Figure 4D and Table S4). These genes are enriched with those (39 of 125) that are under the regulation of TFs: SMAD2 and SMAD3. GSEA showed that these differentially regulated genes are associated with the EGFR1 pathway, regulation of apoptosis, cell-cycle checkpoints, G1 cell-cycle arrest, and regulation of apoptosis (Figure 4D inset, Table S5). Once again, scTenifoldNet identified a much smaller set of significant genes compared with those reported in the original paper:⁴⁸ 125 differentially regulated genes versus 8,389 differentially expressed genes. Nevertheless, functional analyses show that scTenifoldNet identified a more specific gene set relevant to cetuximab's mechanism of action. Further scrutinization of enriched molecular functions of these differentially regulated genes will help to identify more regulatory targets induced by cetuximab in HNSCC cells.

Analysis of Transcriptional Responses of Alveolar Type 1 Cells to Nkx2-1 Gene Knockout

In the third example, we applied scTenifoldNet to another published set of scRNA-seq data from type 1 alveolar (AT1) cells.⁵⁴ AT1 cells are responsible for gas exchange, the physiological function of the lung.⁵⁵ Little et al. found that NK homeobox 2-1 (Nkx2-1) is expressed in AT1 cells and thought Nkx2-1 might be essential to the development and maintenance of AT1 cells.⁵⁴ To determine the function of NKX2-1 during the development of AT1 cells, they performed scRNA-seq experiments to obtain the transcriptome profile of cells from the lungs of Nkx2-1^CKO/CKO; Aqp5^Cre/+ mutant mice (i.e., knockout [KO] mice) and littermate controls (i.e., wild-type [WT] mice). They used early infant mice (postnatal day 10, P10), because P10 represents an intermediate time point when individual AT1 cells in the mutant lung are expected to collectively feature the full range of transcriptomic phenotypes. They reported 3,622 differentially expressed genes (2,105 upregulated and 1,517 downregulated, Supplementary Dataset S1 of Little et al.)⁵⁴ between the KO and the WT mice. Their analyses suggest that, without Nkx2-1, developing AT1 cells lose their molecular markers, morphology, and cellular quiescence, leading to aberrant expression of gastrointestinal (GI) genes, alveolar simplification, and lethality (Figure 5A).

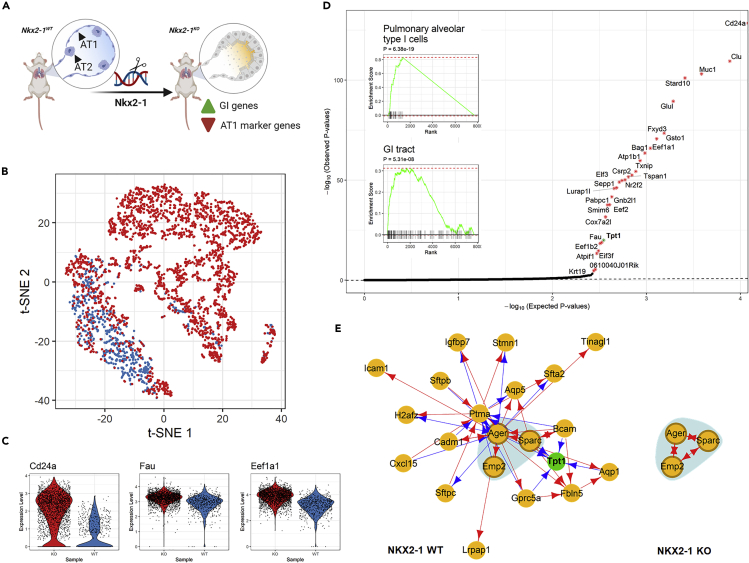
Figure 5.

Analysis of Transcriptional Responses of Alveolar Type 1 Cells to Nkx2-1 Gene Knockout

(A) Illustration of experimental design and data collection of the KO experiment.⁵⁴

(B) t-SNE plot of 2,397 and 638 AT1 cells from Nkx2-1 KO mice (red) and WT mice (blue).

(C) Violin plots showing the log-normalized expression levels of selected differentially regulated genes in KO (red) and WT (blue) mice.

(D) Q-Q plot for observed and expected p values of tested genes. Genes (n = 29) with FDR <0.05 are labeled with an asterisk. Inset shows the results of GSEA for genes ranked by their distances in manifold aligned scGRNs.

(E) A representative module that contains the differentially regulated gene Tpt1 in the WT mice. Most parts of the module disappear in the KO mice. The colors, edges, and marks are presented as in Figure 3E.

To evaluate the power of scTenifoldNet in identifying regulatory changes caused by gene KO, we reanalyzed the transcriptional profiles of 2,397 mutant AT1 cells from the Nkx2-1^CKO/CKO; Aqp5^Cre/+ mice and 638 AT1 cells from the WT mice (Figure 5B). Expression levels of Cd24a, Fau, and Eef1a1 in AT1 cells of KO and WT mice are shown in Figure 5C. Cd24a is a marker gene for AT1 cells; Fau and Eef1a1 are GI genes, known to be highly expressed in the GI tissues. Using scTenifoldNet, we identified 29 genes exhibiting significant difference in their regulation between the two samples: KO versus WT (FDR <0.05, Figure 5D). These 29 genes are Cd24a, Clu, Muc1, Stard10, Glul, Fxyd3, Gsto1, Eef1a1, Bag1, Atp1b1, Txnip, Csrp2, Tspan1, Nr2f2, Elf3, Sepp1, Pabpc1, Lurap1l, Gnb2l1, Eef2, Smim6, Cox7a2l, Tpt1, Fau, Eef1b2, Eif3f, Atpif1, 0610040J01Rik, and Krt19. Targets of Sox2 are highlighted in bold.⁵⁶ As reported,⁵⁴ this gene list is enriched with genes highly expressed in the intestine. Using GSEA, we showed the significant enrichment of GI marker genes (Figure 5D, insets),⁵⁷ which confirmed the effect of Nkx2-1 KO on the cellular identity of AT1 cells.

Analysis of Transcriptional Responses of Human Dermal Fibroblasts to a Double-Stranded RNA Stimulus

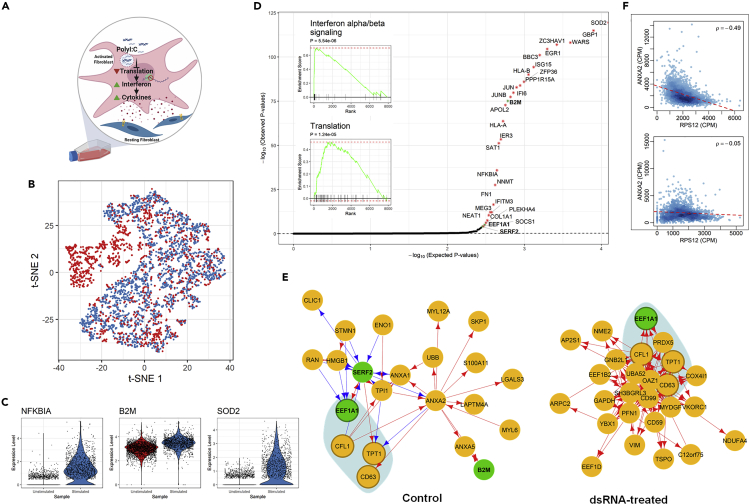
Next, we show the use of scTenifoldNet on an scRNA-seq dataset from human dermal fibroblasts.⁵⁸ In the original paper, Hagai et al. focused on single-cell transcriptional responses induced by the stimulus of polyinosinic-polycytidylic acid (polyI:C), a synthetic double-stranded RNA (dsRNA) (Figure 6A).⁵⁸ They obtained and compared the transcriptomes of 2,553 unstimulated and 2,130 stimulated cells and identified 875 differentially expressed genes (Table S3 of Hagai et al.).⁵⁸ These differentially expressed genes include IFNB, TNF, IL1A, and CCL5, encoding antiviral and inflammatory gene products, and are enriched for inflammatory response, positive regulation of immune system process, and response to cytokine, among many other biological processes and pathways. We found that the original scRNA-seq data have a batch effect between two samples, but the global batch effect can be removed using Harmony,⁵⁹ as shown in the t-SNE plot of cells of two samples (Figure 6B). Nevertheless, the differences in the expression levels between samples can still be detected in selected genes with Harmony-processed data (Figure 6B).

Figure 6.

Analysis of Transcriptional Responses of Human Dermal Fibroblasts to a Double-Stranded RNA Stimulus

(A) Illustration of experimental design and tested mechanism of transcriptional responses.⁵⁸

(B) t-SNE plot of human dermal fibroblasts before (blue) and after (red) dsRNA stimulus.

(C) Violin plots showing the log-normalized expression levels of selected differentially regulated genes before (blue) and after (red) stimulus.

(D) Q-Q plot for observed and expected p values of tested genes. Genes (n = 29) with FDR <0.05 are labeled with an asterisk. Inset shows the results of GSEA for genes ranked by their distances in manifold aligned scGRNs.

(E) Comparison of a representative module that contains three differentially regulated genes in the control sample. The colors, edges, and marks are presented as in Figure 3E.

(F) Scatterplots showing the correlation between TPT1 and ANXA2 before (top) and after (bottom) dsRNA stimulus.

Applying scTenifoldNet to the processed data, we identified 29 differentially regulated genes: SOD2, GBP1, WARS, ZC3HAV1, EGR1, BBC3, ISG15, HLA-B, ZFP36, PPP1R15A, JUN, IFI6, JUNB, B2M, APOL2, HLA-A, IER3, SAT1, NFKBIA, NNMT, FN1, IFITM3, MEG3, NEAT1, COL1A1, PLEKHA4, EEF1A1, SOCS1, and SERF2 (Figure 6D, Table S6). Among them, 14 (highlighted in bold) are targets of RELA (48%, adjusted p < 0.01, enrichment test by Enrichr).⁶⁰ These differentially regulated genes are functionally enriched for interferon signaling, immune system, interleukin-1 regulation of extracellular matrix, and others (Table S7).

Once again, scTenifoldNet reports fewer genes than DE analysis does in the original paper.⁵⁸ By comparing the differentially regulated genes with the differentially expressed genes, we found that enriched functions of differentially expressed genes reflect the differences between unstimulated cells and cells that have completed an initial response to a dsRNA stimulus and reached a final phase of the response, whereas the enriched functions of differentially regulated genes reflect ongoing activities associated with regulatory changes and immune responses to the stimulus. In this sense, differentially regulated genes are valuable for informing about mechanisms through which the dsRNA acts to induce immunological responses.61, 62, 63 For example, it is known that dsRNA inhibits the translation of mRNA to proteins⁶² and leads to the synthesis of interferon, which induces the synthesis of ribosomal units that are able to distinguish between cell mRNA and viral RNA.⁶³ Interferon also promotes cytokine production that activates the immune response and induces inflammation.⁶¹ To further illustrate the changes in the regulatory patterns between samples, we plotted the GRN module around EEF1A1. It can be seen that, before and after the dsRNA treatment, the interacting partnership of the genes is changed substantially (Figure 6E). Two scatterplots show the change in correlation between TPT1 and ANXA2, as an example (Figure 6F). The negative correlation between the two genes' expression among cells disappears after the dsRNA treatment and, thus, the two genes are not linked in the scGRN constructed using the after-treatment data.

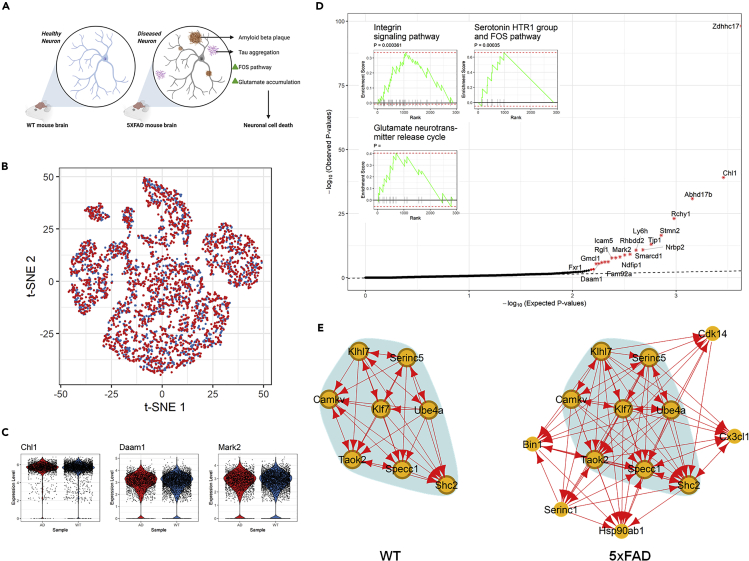
Analysis of Transcriptional Responses of Mouse Neurons in Alzheimer Disease

Last, we applied scTenifoldNet to scRNA-seq data of isolated single nuclei from the brains of the WT and 5xFAD mice.⁶⁴ The 5xFAD strain recapitulates the major features of Alzheimer disease amyloid pathology. The genotype of these mice contains several familial Alzheimer disease (FAD) mutations in APP and PSEN1, causing the overexpression of mutant human amyloid-β (Aβ) precursor protein and human presenilin 1. The 5xFAD model rapidly develops amyloid pathology, with high levels of intraneuronal Aβ accumulation beginning around 1.5 months of age and extracellular Aβ deposition beginning around 2 months.⁶⁵

In the original paper,⁶⁴ Zhou et al. compared scRNA-seq data between 6-month-old WT mice with 6-month-old 5xFAD mice. They found that neurons show limited responses to Aβ peptides: compared with microglia and oligodendrocytes, neurons show minimal transcriptional changes (149 differentially expressed genes) between WT and 5xFAD mice. To test whether scTenifoldNet can detect genes whose expression is differentially regulated between WT and 5xFAD mice, we decided to apply our method to these scRNA-seq data exclusively in neurons. We downloaded expression data matrices from the GEO database using accession no. GSE140511 and extracted expression data of neurons from two samples: WT2 (GSM4173505) and WT_5XFAD2 (GSM4173511) (Figure 7A).

Figure 7.

Analysis of Transcriptional Responses of Neurons to Aβ Peptides in 5xFAD Mice, a Model of Alzheimer Disease

(A) Illustration of experimental design and data collection of the 5xFAD mouse study.⁶⁴ (B) t-SNE plot of neurons of the 5xFAD (red) and WT (blue) mice.

(C) Violin plots showing the log-normalized expression levels of selected differentially regulated genes in neurons of the 5xFAD (red) and WT (blue) mice.

(D) Q-Q plot for observed and expected p values of tested genes. Genes (n = 18) with FDR <0.05 are labeled with an asterisk. Inset shows the results of the GSEA for genes ranked by their distances in manifold aligned scGRNs.

(E) Comparison of a representative module that contains top-ranked differentially regulated genes between the two scGRNs. The colors, edges, and marks are presented as in Figure 3E.

After reanalyzing the data using scTenifoldNet, we identified 18 differentially regulated genes: Zdhhc17, Chl1, Abhd17b, Rchy1, Stmn2, Tjp1, Nrbp2, Ly6h, Smarcd1, Rhbdd2, Ndfip1, Mark2, Icam5, Fam92a, Rgl1, Gmcl1, Daam1, and Fxr1 (FDR <0.05, Figure 7D). For functional enrichment analysis, we relaxed the significant-gene cutoff to include 57 additional genes with FDR ≥0.05 but nominal p < 0.05. These additional genes include Apoe and Bin1. Bin1 encodes bridging integrator 1 (also known as amphiphysin 2), which is the second most important risk locus (after Apoe) for late-onset Alzheimer disease.^66,67 Apoe and Bin1 rank 25th and 61th, respectively, in the list of 75 significant genes (18 genes with FDR <0.05 followed by 57 genes with nominal p < 0.05), and both play a role in negative regulation of amyloid precursor protein catabolic process and tau protein binding. Enrichr analysis reported the following top gene ontology terms: regulation of neuron projection development, positive regulation of cell projection organization, phosphatidylserine metabolic process, protein acylation, potassium channel activity, and methylation-dependent protein binding. GSEA showed that regulatory changes are associated with integrin signaling pathway, serotonin HTR1 group and FOS pathway, and glutamate neurotransmitter release cycle (Figure 7D, insets).

Discussion

We present scTenifoldNet, a robust, unsupervised machine learning workflow that streamlines comparative GRN analyses with data from scRNA-seq. The key feature of scTenifoldNet is to apply comparative network analysis with scRNA-seq data. It detects differences in the cell population's state between two samples in a sensitive and scalable manner. It provides the function of DR analysis, which can be used to reveal subtle regulatory shifts of genes.

Today, DE analysis is still the primary method for the purpose of comparative analysis between scRNA-seq samples (see Avey et al., Hagai et al., Ximerakis et al.).^36,58,68 As scRNA-seq datasets are becoming widely available, there will be more and more interest in comparing samples. The scTenifoldNet-based DR analysis is expected to be adapted in more scenarios wherever DE analysis is applicable. scTenifoldNet learns and contrasts high-dimensional features of genes in scGRNs by examining global interactions between the genes. scTenifoldNet is more suitable for comparing highly similar samples, such as two populations of cells of the same type. scTenifoldNet is built as a robust, sensitive tool that can capture signals that are even confined to rare cell types.

To achieve technical requirements, we overcome several analytical barriers in developing scTenifoldNet. First, constructing scGRN from scRNA-seq data, which consists of cells in many different states, is challenging at present. It is also difficult to control for technical noise in the data. To address these issues, we let scTenifoldNet begin with random cell subsampling. It is worth noting that not only can random cell subsampling help in dealing with the problem of cell heterogeneity, but additional information of cells can be incorporated into subsampling schema. More specifically, in addition to the random subsampling using jackknife and bootstrap methods, we can adapt a semirandom subsampling schema, if cells in an input matrix are sorted according to pseudotime.[69] These cells can be subsampled using a pseudotime-guided method, with which sorted cells are sampled along the pseudotime trajectory. In such a way, the subsamples contain pseudotime information, and the multilayer scGRN constructed from these subsamples will contain the pseudotime-series information. In machine learning, many multilayer network analysis algorithms have been proposed.70, 71, 72 With our pseudotime-series scGRN data, these algorithms will be relevant and applicable. Second, regulatory relationships between genes from scRNA-seq data are difficult to establish, even though the data may theoretically capture a complete picture of the regulatory gene landscape. We consider PC regression to stand out as a crucial method of building scGRNs. PC regression significantly outperforms the other GRN construction algorithms in all aspects of methodology metrics, including specificity, sensitivity, computational efficiency, and the required minimum number of cells. Importantly, PC regression explicitly projects thousands of gene expression measurements into a low-dimensional space to capture much of the observed variation. PC regression, therefore, establishes the relationship for each pair of genes after controlling for the most important background interactions. Third, in scTenifoldNet, the tensor denoising procedure effectively smooths edge weights across all networks in multilayer scGRNs. Fourth, scTenifoldNet performs nonlinear manifold alignment to align two networks. As such, two networks can be contrasted directly, and differentially regulated genes could be detected using distance in new coordinates of data in a low-dimensional space.

We validate the power of scTenifoldNet using real datasets coming from various studies and demonstrate that scTenifoldNet is sensitive to signals. Five real scRNA-seq datasets are involved (Table 1). These five datasets have one thing in common: they all have two sets of scRNA-seq data: one from a treated group and the other from a control/untreated group. More importantly, in all five cases, we have sufficient prior knowledge about the biological system from which the data were collected. Therefore, we have hypotheses about what transcriptional changes we are expected to see before doing the analysis. For example, in the morphine response analysis, the causal factor of transcriptional responses, i.e., the morphine stimulus, is known, and thus, we know what should be recovered through the analysis. Similarly, we had some clues in the examples of cetuximab and fibroblasts about what transcriptional changes we might be able to retrieve. By compiling all the findings from scTenifoldNet applications, we tested scTenifoldNet and showed that scTenifoldNet provides findings that are precise, specific, and relevant to the biological systems and questions in the test. This is of significance to building a specific and sensitive tool like scTenifoldNet for the purpose of molecular mechanism studies using scRNA-seq. This is because causal factors and their target genes remain unknown in many biological systems studied. If this is the case, it is crucial to apply a sensitive approach like scTenifoldNet, which may be in addition to the DE analysis, to unveil more gene candidates. Only then will we be able to scrutinize identified genes further to learn the mechanisms behind their actions in the whole system. We face such a challenge in many studies from unknown factors that cause a disorder. It is therefore critical that we adopt tools such as scTenifoldNet, instead of relying solely on conventional DE analysis, to tackle this big data analysis problem.

Table 1.

Summary of Real-Data Applications of scTenifoldNet Analysis

Study	Reference	Species	Cell Type	Perturbation Type	Number of Genes Included in Analysis	Number of Cells in Two Groups	Number of Differentially Regulated Genes	Enriched Functions of Differentially Regulated Genes
1	Avey et al.36	mouse	neurons	morphine	8,138	mock-treated 8,912; morphine-treated, 7,972	56	opioid signaling; signaling by G-protein-coupled receptors; reduction of cytosolic calcium levels; morphine addiction
2	Kagohara et al.48	human	carcinoma cell line	cetuximab	11,140	untreated, 5,217; treated, 4,507	125	EGFR1 pathway; regulation of apoptosis; cell-cycle checkpoints; G1 cell-cycle arrest, regulation of apoptosis
3	Little et al.54	mouse	lung alveolar cells	Nkx2-1 gene KO	7,842	WT, 638; KO, 2,397	29	gastrointestinal marker genes; Sox2 target genes
4	Hagai et al.58	human	dermal fibroblasts	dsRNA immune stimulus	7,904	unstimulated, 2,553; stimulated, 2,130	29	interferon signaling; immune system; interleukin-1 regulation of extracellular matrix
5	Zhou et al.64	mouse	neurons	Alzheimer disease	2,869	WT, 4,561; 5xFAD, 2,423	18	Apoe and Bin1; regulation of neuron projection development; positive regulation of cell projection organization; phosphatidylserine metabolic process; protein acylation; potassium channel activity; methylation-dependent protein binding; integrin signaling pathway; serotonin HTR1 group and FOS pathway; glutamate neurotransmitter release cycle

In summary, scRNA-seq enables the study of cellular and molecular components and the dynamics of complex biological systems at single-cell resolution. To unravel the regulatory mechanisms underlying cell behaviors, novel computational methods are essential for understanding the complexity in scRNA-seq data (e.g., scGRNs) that surpasses human interpretative ability. We anticipate that, when applied to real scRNA-seq data, our machine learning workflow implemented in scTenifoldNet can help achieve breakthroughs by deciphering the full cellular and molecular complexity of the data by constructing and comparing scGRNs.

Experimental Procedures

Resource Availability

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, James J. Cai (jcai@tamu.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

scTenifoldNet has been implemented in R. The source code is available at https://github.com/cailab-tamu/scTenifoldNet, which also includes the code of the benchmarking method, auxiliary functions, and example datasets (including the simulated data used to generate Figure 2). The scTenifoldNet R package is available at the CRAN repository: https://cran.r-project.org/web/packages/scTenifoldNet/.

The scTenifoldNet Workflow

The scTenifoldNet workflow takes two scRNA-seq expression matrices as inputs. The two matrices are supposed to be obtained from two samples of the same type of cell, such as those of different treatments or from diseased and healthy subjects. The purpose of the analysis is to identify genes whose transcriptional regulation is shifted between the two samples. The whole workflow consists of five steps: cell subsampling, network construction, network denoising, manifold alignment, and module detection.

Cell Subsampling

Instead of using all cells of each sample to construct a single GRN, we randomly subsample cells multiple times to obtain a set of subsampled cell populations. This subsampling strategy is to ensure the robustness of results against cell heterogeneity in samples. Subsampling of each sample is performed as follows: assuming the sample has M cells, m cells (m < M) are randomly selected to form a subsampled cell population. The process is repeated with cell replacement t times to produce a set of t subsampled cell populations.

Network Construction

For a given expression matrix, a PC-regression network construction method⁵ is adopted to construct scGRN. PC regression is a popular multiple regression method, where the original explanatory variables are first subjected to a PC analysis (PCA) and then the response variable is regressed on the few leading PCs. By regressing on $M$ PCs (M ≪ n, where n is the total number of genes in the expression matrix), PC regression mitigates the overfitting and reduces the computation time. To build an scGRN, each time we focus on one gene (referred to as the target gene) and apply the PC-regression method, treating the expression level of the target gene as the response variable and the expression levels of other genes as the explanatory variables. The regression coefficients from PC regression are then used to measure the strength of the association of the target gene and other genes and to construct the scGRN. We repeat this process n times, each time with one gene as the target gene. At the end, the interaction strengths between all possible gene pairs are obtained and an adjacency matrix is formed. The details of applying the PC-regression method to a scRNA-seq expression data matrix are described as follows.

More specifically, suppose $\mathit{X}\in {\mathbb{R}}^{n\times p}$ is the gene expression matrix with n genes and p cells. The ith row of X, denoted by $X_i\in {\mathbb{R}}^p$_, represents the gene expression level of the ith gene in p cells. We construct a data matrix, ${\mathit{X}}_{-i}\in {\mathbb{R}}^{\left(n-1\right)\times p}$_, by deleting X_i from X. To estimate the effects of the other n − 1 genes to the ith gene, we build a PC-regression model for X_i. First, we apply PCA to ${\mathit{X}}_{-i}^T$ and take the first M leading PCs to construct ${\mathit{Z}}^i=\left(Z_1^i,\cdots ,Z_M^i\right)\in {\mathbb{R}}^{p\times M}$, where $Z_m^i\in {\mathbb{R}}^p$ is the mth PC of ${\mathit{X}}_{-i}^T,m=1,2,\dots ,M$. Mathematically, ${\mathit{Z}}^i={\mathit{X}}_{-i}^T{\mathit{V}}^i$, where ${\mathit{V}}^i\in {\mathbb{R}}^{\left(n-1\right)\times M}$ is the PC loading matrix for the first M leading PCs, satisfying ${\left({\mathit{V}}^i\right)}^T{\mathit{V}}^i={\mathit{I}}_M$. Second, the PC-regression method regresses X_i on Zⁱ and solves the following optimization problem:

$${\hat{\beta }}^i=\arg mi{n}_{{\beta }^i\in R^M}{\mathit{X}}_i-{\mathit{Z}}^i{{\beta }^i}_2^2\text{.}$$

Then, ${\hat{\alpha }}^i={\mathit{V}}^i{\hat{\beta }}^i\in {\mathbb{R}}^{n-1}$ quantifies the effects of the other $n-1$ genes to the ith gene. After performing PC regression on each gene, we collect ${\left\{{\widehat{\text{α}}}^i\right\}}_{i=1}^n$ together and construct an n × n weighted adjacency matrix W of the gene-gene interaction network. The ith row of W is ${\widehat{\text{α}}}^i$, and the diagonal entries of W are all 0. Then we retain interactions with the top α% (= 5% by default) absolute value in the matrix to obtain the scGRN adjacency matrix.

Tensor Decomposition

For each of the $t$ subsamples of cells obtained in the cell subsampling step, we construct a network using PC regression, as described above. Each network is represented as an $n\times n$ adjacency matrix; the adjacency matrices of the t networks can be stacked to form a third-order tensor, $\mathfrak{T}\in {\mathbb{R}}^{\left(n\times n\times t\right)}$. To remove the noise in the adjacency matrices and extract important latent factors, the CP tensor decomposition is applied. Similar to the truncated SVD of a matrix, the CP decomposition approximates the tensor by a summation of multiple rank 1 tensors.¹¹ More specifically, for our problem:

$$\mathfrak{T}\approx {\mathfrak{T}}_d=\sum _{r=1}^d{\text{λ}}_r{a}_r\circ b_r\circ c_r\text{,}$$

where $\circ$denotes the outer product, $a_r\in {\mathbb{R}}^n,b_r\in {\mathbb{R}}^n$ and $c_r\in {\mathbb{R}}^t$ are unit-norm vectors, and ${\text{λ}}_r$ is a scalar. In the CP decomposition, ${\mathfrak{T}}_d$ is the denoised tensor of $\mathfrak{T}$, which assumes that the valid information of $\mathfrak{T}$ can be described by $d$ rank 1 tensors, and the remaining part $\mathfrak{T}-{\mathfrak{T}}_d$ is mostly noise.

We use the function cp in the R package “rTensor” to do the CP decomposition. For each sample, the reconstructed tensor ${\mathfrak{T}}_d$ includes $t$ denoised scGRNs. We then calculate the average of associated $t$ denoised networks to obtain the overall stable network. We further normalize entries by dividing them by their maximum absolute value to obtain the final scGRNs for the given sample. For later use, we denote the denoised adjacency matrices for the two samples as ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$.

Manifold Alignment

${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ are then compared to identify changes in regulatory relationships among genes and identify significantly affected genes. Instead of directly comparing these two n × n adjacency matrices, manifold alignment is applied to match the local and non-linear structures among the data points of ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$, project them to the same low-dimensional space, and build comparable low-dimensional features. These features between two samples can then be compared while maintaining the structural information of the two scGRNs. Specifically, ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ serve as the input for a manifold alignment algorithm to find the low-dimensional projections ${\mathit{F}}^x\in {\mathbb{R}}^{n\times d}$ and ${\mathit{F}}^y\in {\mathbb{R}}^{n\times d}$ of genes from each sample, where d ≪ n. In terms of the underlying matrix representation, we use $F_i^x\in {\mathbb{R}}^d$ and $F_i^y\in {\mathbb{R}}^d$ to denote the ith row of ${\mathit{F}}^x$ and ${\mathit{F}}^y$ that reflect the features of the ith gene in X and Y, respectively.

We note that ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ may include negative values, which means genes are negatively correlated. When an adjacency matrix contains negative edge weights, the properties of the corresponding Laplacian are not entirely well understood.⁷³ To mitigate this problem, we add 1 to all entries in ${\mathit{W}}_d^x\text{ and }{\mathit{W}}_d^y,$ transforming the range of ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ from [−1,1] to [0,2]. As a result, all original negative relationships have a transformed value in [0,1) and all original positive relationships have a transformed value in (1,2]. The projected features of two genes with a positive correlation will be closer than those with a negative correlation. For convenience, we still use ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ to denote the transformed similarity matrices of two datasets.

Now we propose a specific manifold alignment method to find appropriate low-dimensional projections of each gene. Our manifold alignment should trade off the following two requirements: (1) the projections of the same ith gene in two samples should be relatively close in the projected space and (2) if the ith gene and jth gene in sample 1 are functionally related, their projections $F_i^x$ and $F_j^x$ should be close in the projected space, and the same is true for sample 2. We minimize the following loss function:

$$Loss\left({\mathit{F}}^x,{\mathit{F}}^y\right)=\text{λ}\sum _{i=1}^n{\Vert F_i^x-F_i^y\Vert }_2^2+\sum _{i,j=1}^n{\Vert F_i^x-F_j^x\Vert }_2^2{W}_{i,j}^x+\sum _{i,j=1}^n{\Vert F_i^y-F_j^y\Vert }_2^2{W}_{i,j}^y\text{,}$$

where $W_{i,j}^x$ and $W_{i,j}^y$ denote the (i, j) entry of ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$_, respectively. The first term of the loss function requires the similarity between corresponding genes across two samples; the second and third terms are regularizers preserving the local similarity of genes in each of the two networks. $\text{λ}$ is an allocation parameter to balance the effects of two requirements.

One way to minimize the loss function is by using an algorithm similar to Laplacian eigenmaps,⁷⁴ which requires the adjacency matrix to be symmetry, but in our case both ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ are asymmetric. Notice that if we symmetrize ${\mathit{W}}_d^x$ and ${\mathit{W}}_d^y$ by ${\mathit{W}}^x=\frac{1}{2}({\left({\mathit{W}}_d^x\right)}^T+{\mathit{W}}_d^x)$ and ${\mathit{W}}^y=\frac{1}{2}\left({\left({\mathit{W}}_d^y\right)}^T+{\mathit{W}}_d^y\right)$, and again denote $W_{i,j}^x$ and $W_{i,j}^y$ as the (i, j) entry of ${\mathit{W}}^x$ and${\mathit{W}}^y$, then the value of the loss function will not be changed. Thus, minimizing the loss function based on the symmetrized adjacency matrices, ${\mathit{W}}^x$ and${\mathit{W}}^y$, is equivalent to using the original adjacency matrices, ${\mathit{W}}_d^x$ and${\mathit{W}}_d^y$. Based on this observation, using linear algebra, we can write the loss function into the matrix form as $Loss\left({\mathit{F}}^x,{\mathit{F}}^y\right)=2trace\left({\mathit{F}}^T\mathit{LF}\right)$, where $\mathit{F}=\left[\begin{array}{c}{\mathit{F}}^x\\ {\mathit{F}}^y\end{array}\right]$, $\mathit{L}=\frac{1}{2}\left(\mathit{D}-\mathit{W}\right)$, $\mathit{W}=\left[\begin{array}{cc}{\mathit{W}}^x& \frac{\lambda }{2}\mathit{I}\\ \frac{\lambda }{2}\mathit{I}& {\mathit{W}}^y\end{array}\right]$, and $\mathit{D}$ is a diagonal matrix with $D_{ii}=\sum _i{W}_{ij}$. $\mathit{L}$ is called a graph Laplacian matrix. The default selection of $\lambda$ is 0.9 times the mean value of the row sums of ${\mathit{W}}^x$ and ${\mathit{W}}^y$. By further adding the constraint ${\mathit{F}}^T\mathit{F}=\mathit{I}$ to remove the arbitrary scaling factor, minimizing $Loss\left({\mathit{F}}^x,{\mathit{F}}^y\right)$ is equivalent to solving an eigenvalue problem. The solution for $\mathit{F}=\left[f_1,f_2,\cdots ,f_d\right]$ is given by $d$ eigenvectors corresponding to the $d$ smallest nonzero eigenvalues of L.⁷⁵

Determination of the p Value of Differentially Regulated Genes

With $\mathit{F}=\left[\begin{array}{c}{\mathit{F}}^x\\ {\mathit{F}}^y\end{array}\right]=\left[f_1,f_2,\cdots ,f_d\right]$ obtained in manifold alignment, we calculate the distance d_j between projected data points of two samples for each gene. One may declare significant genes according to the ranking of d_j’s. To avoid arbitrariness in deciding the number of selected genes, we propose to use χ² distribution to determine the significance of genes.⁷⁶ Specifically, $d_j^2$ is derived from the summation of squares of differences of projected representations of gene j for two samples, whose distribution could be approximately χ². To adjust the scale of the distribution, we compute the scaled fold change defined as $df\cdot d_j^2/\overline{d^2}$ for each gene j, where f denotes the average of $d_j^2$ among all the tested genes. The scaled fold change approximately follows χ² distribution with the degree of freedom df if the gene does not perform differently in the two samples. By using the upper tail (P[X > x]) of the χ² distribution, we assign p values for genes and adjust them for multiple testing using B-H FDR correction.⁷⁷ To determine df, since the number of the significant genes will increase as df increases, we use df = 1 to make a conservative selection of genes with high precision.

Functional Enrichment Analyses

Functional enrichment analysis of gene sets was performed using Enrichr,^78,79 which is a web-based, integrative enrichment analysis application based on more than 100 curated gene set libraries. The test of enriched TF targets was performed using the ChIP-X enrichment analysis⁴⁰ based on comprehensive results from ChIP-seq studies. Finally, predefined gene sets from the REACTOME, BioPlanet, and KEGG databases were tested for enriched functions using the pre-ranked GSEA.²⁶

Simulations of scRNA-Seq Data and Benchmarking of Network Methods

A systematic evaluation of state-of-the-art algorithms for inferring scGRNs was performed using BEELINE.¹⁰ We applied scTenifoldNet/PC regression and other scGRN inference algorithms to a dataset called GSD, which is derived from a curated Boolean model.⁸⁰ These methods include PIDC,²⁷ PPCOR,⁸¹ LEAP,⁸² GRNBOOST2,⁸³ GENIE3,² SCINGE,⁸⁴ SINCERITIES,⁸⁵ GRISLI,⁸⁶ SCODE,⁸⁷ GRNVBEM,⁸⁸ and SCNS.⁸⁹ Due to compatibility issues, Scribe⁹⁰ was not included in the comparison. We processed the dataset through the uniform pipeline provided by BEELINE, including (1) data pre-processing, (2) generation of Docker containers for scTenifoldNet/PC regression and the 11 above-mentioned algorithms, (3) parameter estimation, and (4) post-processing and evaluation. Throughout the analysis, no information on TF-target relationships was given to any tested algorithm. We compared algorithms based on their average performance among three different metrics: AUROC, AUPRC, and time of computing. AUROC shows the performance of a tested algorithm by presenting the trade-off between true positive rate TP/(TP + FN) and false positive rate FP/(FP + TN) across different decision thresholds, while AUPRC shows the area under the precision TP/(TP + FP)-recall TP/(TP + FN) curve computed for different decision thresholds between 1 and 0 using $\sum _i\left(R_i-R_{i-1}\right)P_i$, where P_i and R_i are the precision and recall at the ith threshold, summarizing a weighted mean of precisions achieved at each threshold with the increase in recall from the previous threshold used as the weight. TP stands for true positive, TN true negative, FP false positive, and FN false negative.

We generated our own synthetic datasets using SERGIO, a single-cell expression simulator guided by GRNs.²⁸ SERGIO allows for the simulation of scRNA-seq data while considering the linear and non-linear influences of regulatory interactions between genes. SERGIO takes a user-provided GRN to define the interactions and generates expression profiles of genes in steady state using systems of stochastic differential equations derived from the chemical Langevin equation. The time course of mRNA concentration of gene i is modeled by:

$$\frac{\partial X_{\text{i}}}{\partial t}=P_i\left(t\right)-{\text{λ}}_i{x}_i\left(t\right)+q_i\left(\sqrt{P_i\left(t\right)\text{α}}\right)\text{,}$$

where x_i is the expression of gene i; P_i is its production rate, which reflects the influence of its regulators as identified by the given GRN; λ_i is the decay rate; q_i is the noise amplitude in the transcription of gene i; and α is an independent Gaussian white noise process. To obtain the mRNA concentrations as a function of time, the above stochastic differential equation is integrated for all genes as follows:

$${\left(X_i\right)}_t={\left(X_i\right)}_{t_0}+\underset{t_o}{\overset{t}{\int }}\left(P_i\left(t\right)-{\text{λ}}_i{x}_i\left(t\right)\right)\partial t+\underset{t_0}{\overset{t}{\int }}{q}_i\left(\sqrt{P_i\left(t\right)}\right)\partial W_{\text{α}}\text{.}$$

The simulation was focused on testing and comparing the performance of PC regression and several other methods (SCC, MI, GENIE3) using sparse data without imputation. The relationships between 100 genes were simulated as they belong to two major modules containing 40 and 60 genes, respectively. Each module is under the influence of one TF. We used the steady-state simulations to synthesize data to generate expression profiles of 100 genes, according to the parameter setting for two modules.

For each of the tested methods, we randomly selected n = {10, 50, 100, 500, 1,000, 2,000, 3,000} cells from the simulated data 10 times and built 10 scGRNs. For each $n$, relevance measurements (accuracy and recall) were evaluated for each of the 10 networks using the match of the sign of the relationships between genes to compute the following formulas: accuracy = (TP + TN)/(TP + TN + FP + FN) and recall = TP/(TP + FN). For the MI and GENIE3 methods that provide only positive values, the median value was used as the center point, and then the values were scaled to [−1,1] by dividing them over the maximum absolute value.

Published: November 5, 2020