A deep learning-based algorithm for detection of cortical arousal during sleep

Abstract

Study Objectives

The frequency of cortical arousals is an indicator of sleep quality. Additionally, cortical arousals are used to identify hypopneic events. However, it is inconvenient to record electroencephalogram (EEG) data during home sleep testing. Fortunately, most cortical arousal events are associated with autonomic nervous system activity that could be observed on an electrocardiography (ECG) signal. ECG data have lower noise and are easier to record at home than EEG. In this study, we developed a deep learning-based cortical arousal detection algorithm that uses a single-lead ECG to detect arousal during sleep.

Methods

This study included 1,547 polysomnography records that met study inclusion criteria and were selected from the Multi-Ethnic Study of Atherosclerosis database. We developed an end-to-end deep learning model consisting of convolutional neural networks and recurrent neural networks which: (1) accepted varying length physiological data; (2) directly extracted features from the raw ECG signal; (3) captured long-range dependencies in the physiological data; and (4) produced arousal probability in 1-s resolution.

Results

We evaluated the model on a test set (n = 311). The model achieved a gross area under precision-recall curve score of 0.62 and a gross area under receiver operating characteristic curve score of 0.93.

Conclusion

This study demonstrated the end-to-end deep learning approach with a single-lead ECG has the potential to be used to accurately detect arousals in home sleep tests.

Statement of Significance.

Using a deep learning algorithm, this study demonstrates that it is feasible to use a single-lead electrocardiography to detect cortical arousals with a high level of accuracy. This technology has potential for clinical applications in home sleep testing, long-term in-home healthcare, emergency care, and intensive care units.

Introduction

The arousal index is an important indicator describing the quality of sleep during diagnostic polysomnography (PSG). Frequent cortical arousals during sleep can cause sleep fragmentation, poor sleep quality, and insufficient sleep [1–4]. Furthermore, they are associated with a wide range of negative outcomes, such as daytime sleepiness, obesity, cardiovascular dysfunction, and hypertension [5–8]. Additionally, sleep-disordered breathing (SDB) and periodic leg movements increase the frequency of cortical arousal [9–11].

Arousal scoring is particularly important in the identification of hypopnea events observed with SDB. According to the American Academy of Sleep Medicine (AASM), the recommended definition of a hypopnea requires a 3% oxygen desaturation from pre-event baseline or associated cortical arousal [12]. Home sleep testing (HST) is increasingly used for the evaluation of possible SDB. However, most Type III sleep monitor systems commonly used for HST cannot detect arousals because they do not monitor the electroencephalogram (EEG); AASM scoring rules define an arousal as an abrupt change in EEG frequency that lasts at least 3 s [12]. Therefore, most HST systems potentially underestimate the apnea–hypopnea index resulting in some falsely negative studies.

Cortical arousals are associated with autonomic nervous system activation that is reflected by changes in blood pressure and heart rate [1, 13–18]. Based on this physiologic variability, several autonomous arousal detection algorithms have been developed. Pillar et al. proposed algorithms using the peripheral arterial tonometry (PAT) signal to detect arousal [19, 20]. Basner et al. developed an electrocardiographic (ECG)-based algorithm which used heart rate to detect cortical arousal [21]. Recently, Olsen et al. proposed a machine learning algorithm that used 25 features to detect autonomic arousal and used cortical arousal annotations as ground truth labels [22]. Compared with EEG sensors, ECG sensors are more suitable for in-home use because ECG data acquisition is convenient and highly reliable. However, the development of these previous ECG-based algorithms was based on the controlled environment that characterizes in-laboratory PSG studies. In contrast, data collection at home is complicated by external factors and may have larger variations in the data. Therefore, these algorithms may not be valid for use in home-based sleep testing.

In the past two decades, the deep learning approach has been increasingly utilized to analyze healthcare data. A deep neural network consists of multiple layers. Each layer includes multiple filters that are designed to extract features at different levels. In a classification task, higher-level layers amplify aspects of the inputs that are important for discrimination and suppress irrelevant variations [23]. Compared with human-designed filters, a deep neural network discovers intricate patterns in large data sets by using backpropagation algorithms to indicate how a network should change its filter weights [23]. A review article of deep learning in healthcare has been published [24]. In general, there are two intrinsic characteristics of such an approach. First, the performance of deep learning algorithms can be improved by providing increasing amounts of data [24]. Second, the algorithms do not need complicated preprocessing procedures. Instead, they can directly learn features from raw input and discover unrecognized patterns in high-dimensional data [25]. These characteristics make a deep learning approach ideal for analyses of complex nonlinear, multidimensional biomedical data. Convolutional neural networks (CNN) [26], a type of deep neural networks, have been evaluated for identifying biomedical images [24, 27, 28] and detecting arrhythmias on a single-lead ECG signal [29]. Deep learning approaches are being used to analyze electrophysiologic signals from sleep studies as well. Zhang et al. used a deep learning approach with spectrograms to score sleep stages from EEG, electrooculogram (EOG), and electromyogram (EMG) signals [30]. Howe-Patterson et al. employed a deep learning approach with EEGs, EOG, chin EMG, oxygen saturation, respiratory airflow, abdominal EMG, and chest EMG to detect cortical arousals and was awarded the best performance prize in the PhysioNet Challenge 2018 competition [31, 32]. However, all existing deep learning-based arousal detection algorithms rely on multichannel electrophysiologic signals, which are not necessarily available from conventional home sleep tests.

In this study, we developed and evaluated an end-to-end deep learning approach for its ability to detect cortical arousals during sleep using a one-night single-lead ECG signal. Our end-to-end deep learning-based cortical arousal detection (DeepCAD) model combines both CNN and recurrent neural networks (RNN) [26]. It has the ability to extract spatiotemporal features from raw 256 Hz ECG data to detect arousals with 1-s resolution. We developed and evaluated the DeepCAD model using a large manually scored dataset of home acquired PSG, the Multi-Ethnic Study of Atherosclerosis (MESA). To evaluate the generalizability of the algorithm, we also applied the DeepCAD model to another dataset of home acquired PSG, the Sleep Heart Health Study (SHHS).

Methods

Source and evaluation databases

We used the MESA database to develop and test the DeepCAD model. MESA is a multicenter longitudinal cohort study sponsored by the National Heart Lung and Blood Institute (NHLBI) [33–35]. Its overall goals are to investigate the characteristics of subclinical cardiovascular disease and their progression to overt disease [35]. Between 2010 and 2012, 2,237 of the original 6,814 participants were enrolled in a Sleep Exam, which included full overnight unattended PSG, 7-day wrist-worn actigraphy, and a sleep questionnaire.

The database of the SHHS was used to evaluate the generalizability of the algorithm. SHHS was a multicenter longitudinal cohort study sponsored by the NHLBI to determine whether obstructive sleep apnea (OSA) was a risk factor for the development of cardiovascular disease [36]. During the second exam cycle of the SHHS, between 2001 and 2003, 3,295 participants had full overnight PSG performed in the home. Both the sleep MESA and SHHS databases are publicly accessible at the National Sleep Research Resource (NSRR) [34].

Unattended polysomnogram

In the MESA Sleep Exam, all participants underwent home PSG. The PSG records were recorded using the Compumedics Somte System (Compumedics Ltd., Abbotsford, Australia) that included a single-lead ECG, three EEG derivations, two EOG derivations, chin EMG, thoracic, and abdominal respiratory inductance plethysmography, airflow, leg movements, putative snoring, and finger pulse oximetry. The sampling frequencies of ECG, EEGs, EMG, and EOGs were 256 Hz.

In the SHHS, home PSG was recorded using the Compumedics P Series System (Compumedics Ltd.) that included a single-lead ECG, two EEG derivations, two EOG derivations, chin EMG, thoracic, and abdominal respiratory inductance plethysmography, airflow, and finger pulse oximetry [36]. In contrast to MESA, the sampling frequencies of the ECG and EEG were 250 and 125 Hz, respectively.

EEG arousal scoring

For both Mesa and SHHS, certificated scorers manually scored cortical arousal events on Compumedics software based on the AASM criteria [37]. Cortical arousals were scored separately from sleep stages. The AASM defines cortical arousal as an abrupt shift in EEG frequency, which may include alpha and/or theta waves and/or delta waves and/or frequencies greater than 16 Hz lasting at least 3 s and starting after at least 10 continuous seconds of sleep. In rapid eye movement sleep, an increase in the EMG signal is also required.

Development and test datasets

The public accessible MESA data included 2,056 raw PSG records from 2,056 unique participants. We excluded PSG records which had less than 50% ECG signal available during the time spent asleep. We also excluded records that were only scored sleep/wake, were labeled as having unreliable arousal scoring, or did not have cortical arousal annotations. Thus, there were 1,547 records available for analysis. We randomly separated the 1,547 PSG records into two sets: a training set (n = 1,236 records) and a test set (n = 311 records). Table 1 describes the characteristics of the training set and the test set. The training set was further randomly divided into a training set (n = 1,112 records) and a validation set (n = 124 records) for development. We labeled each second of data as arousal “present/not present” based on the NSRR cortical arousal annotation. The binary labels were used as ground truth. To minimize the influence of unreadable signals, we extracted the segment starting from the 30 s before the first positive ground truth arousal label of the one-night record to the 30 s after the last positive ground truth arousal label of the one-night record for this study (Appendix A).

Table 1.

Characteristics of the datasets

	MESA		SHHS
	Training set (n = 1,236)	Test set (n = 311)	Training set (n = 1,176)	Test set (n = 785)
% Female	51.62	57.56	55.5%	54.6%
	Mean ± SD	Mean ± SD	Mean ± SD	Mean ± SD
Age	69.02 ± 8.94	69.06 ± 8.83	66.92 ± 10.09	67.53 ± 10.20
AHI	19.89 ± 17.97	18.34 ± 15.82	13.81 ± 13.39	14.80 ± 15.29
Total record time (min)	636.94 ± 86.15	634.44 ± 93.52	596.50 ± 65.93	601.48 ± 64.33
Total sleep time (min)	361.14 ± 81.06	364.00 ± 82.71	377.13 ± 66.01	377.42 ± 68.40
Number of arousals	158.76 ± 80.99	158.09 ± 81.78	131.18 ± 67.29	133.84 ± 63.16
Total arousal duration (s)	1,679.64 ± 883.81	1,671.89 ± 928.80	1,328.35 ± 649.49	1,360.37 ± 637.43

The number of arousals and arousal duration were based on the manually scored annotations. AHI, Apnea-Hypopnea Index≥ 4%: number of all apneas and hypopneas with ≥ 4% oxygen desaturation or arousal per hour of sleep.

The public accessible second examination SHHS data included 2,651 raw PSG records from 2,651 unique subjects. After excluding the scoring unreliable PSG records, we split the dataset (n = 1,961) to a training set (n = 1,176 records) and a test set (n = 785 records). We further split the training set to a training set (n = 1,058 records) and a validation set (n = 118 records). The identification of the presence of arousals was performed identically to the procedure used for the MESA datasets.

Preprocessing ECG data

We intended to minimize the complexity of preprocessing and use less expert knowledge about the relationships between ECG signals and cortical arousals in development. Therefore, in the preprocessing stage, we only standardized each one-night ECG signal using the Scikit-learn’s robust scaler which removed the median and divided each sample by the interquartile range [38].

Models development

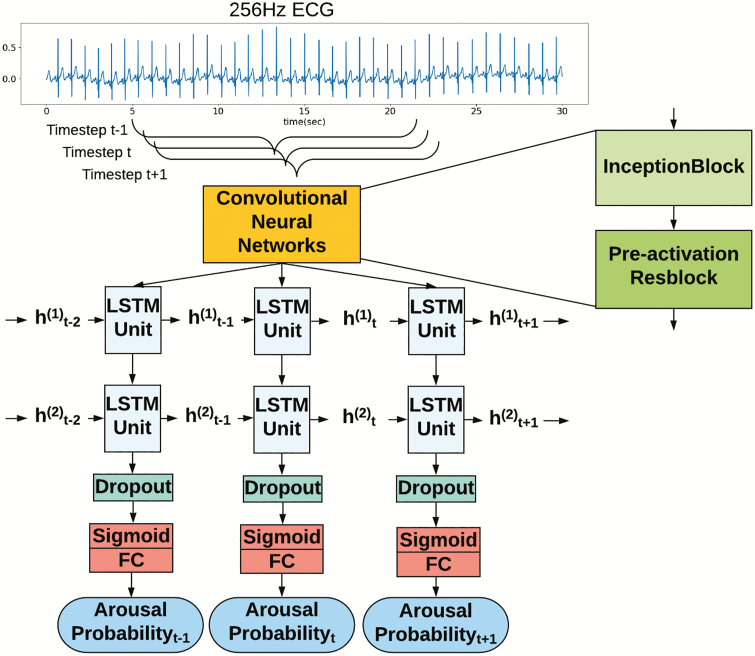
We developed an end-to-end learning model to detect arousals. It used raw ECG signal as input; the model produced a new output (arousal probability) every one second. The architecture of the proposed DeepCAD model is shown in Figure 1 and the hyper-parameters are listed in Appendix B. It consists of 33 convolutional layers, 2 long short-term memory (LSTM) layers, and a fully connected layer. The convolutional layers are effective feature extractors with filters and moving windows that are able to learn relevant features from the ECG data. We used batch normalization [39] and a rectified linear unit activation function [40] after each convolutional layer. To increase the flexibility of the model and ability to extract information on multiple time scales, as described by Szegedy et al. [41] and Roy et al. [42], we used multiple filters with various filter sizes as the first CNN layer to extract information from the raw ECG signal. The first layer structure was termed the inception block [41]. Similar to the architecture employed by Hannun et al. [29], we used pre-activation residual blocks (ResBlocks) to extract spatial features from the raw 256 Hz ECG and to downsample the input to 1 Hz before it was passed into the LSTM layers. The concept of ResBlocks was introduced by He et al. for solving the training problem of deep neural networks and improving generalization [43, 44]. The LSTM is a specialized type of RNN, including memory cells, that can learn long-range dependencies [45, 46]. An unfolded LSTM layer includes multiple weight-shared LSTM units. The number of units is equal to the number of seconds of the 1 Hz input (Figure 1). The two inputs of each LSTM unit of the first layer are the outputs of the previous LSTM unit and the ECG features which were extracted by CNN. We used a dropout layer atop the highest LSTM layer to reduce overfitting [47]. It was followed by a fully connected layer with a sigmoid activation function for producing probability of arousal. Appendix B includes a detailed description of the model architecture. For evaluating the importance of individual components, multiple alternative network architectures were also developed with the training set including a spectrogram and LSTMs model, an inception block and LSTMs model, a two-layer LSTM model, a ResBlocks and LSTMs model, and an inception block and ResBlocks model (Appendix C). Model development was performed using PyTorch.

Figure 1.

Model architecture. The input is a sequence of 256 Hz ECG signal. The CNN includes two main blocks: inception block and pre-activation residual block (Resblock). The CNN are applied to extract spatial features from ECG signal by filters and moving windows. The extracted features are passed into LSTMs layer, where t indicates timestep and h indicates the hidden cells which pass the information from one timestep to the next timestep. The output of the model is a sequence of the probability of presence arousal.

We used the cross-entropy loss as the loss function (Equation (1)), where y is the ground truth label denoted by {0, 1}, ŷ is the arousal probability [0, 1], n is the sample index, and N is the total number of samples in one batch. We trained the models using truncated backpropagation-through-time [48] with a depth of 90 and an Adam algorithm [49] (β₁=0.9, β₂=0.999) with L2 weight decay (λ=1e−5) on the training set. We set a minibatch size of 30 and initialized a learning rate to 1e⁻⁴. In each epoch, we used the validation set to evaluate the performance of the model and reduced the learning rate by a factor of 10 when the performance stopped improving for four consecutive epochs. When the performance of the model on the validation dataset stopped improving within the error, we stopped the training process.

$${\displaystyle \begin{array}{l}{\displaystyle \mathcal{L}=-\frac{1}{N}{\displaystyle \underset{n=1}{{\displaystyle \sum ^N}}}[y_n\cdot \log {{\displaystyle \widehat{y}}}_n+(1-y_n)\cdot \log (1-{{\displaystyle \widehat{y}}}_n)]}\end{array}}$$ (1)

Because the model development included a number of hyper-parameters, we used a random search method with manual tuning to set their values. Generally, we set a search space and searched the learning rate, number of layers, the size and number of filters per layer, minibatch size, pooling method, etc. Then, we selected the model with the highest gross area under the precision-recall curve (AUPRC) as the best model for our final DeepCAD model. This model had an AUPRC of 0.65 on the validation set. We also selected a decision threshold of 0.4 to classify each output as arousal “present/not present” based on the precision-recall curve of the DeepCAD model on the validation set.

Algorithm evaluation

We evaluated the models on a holdout test set (n = 311). We performed three types of evaluation: gross sequence level evaluation, event level evaluation, and record-wise evaluation. The gross sequence level AUPRC and area under receiver operating curve (AUROC) (vide infra for definitions) were calculated for the entire test set which consisted of the concatenated output probability sequence of each PSG record together as one sequence. Then, we compared the sequence against the ground truth labels for computing gross sequence level metrics. For event-level evaluation, we used the selected decision threshold to classify each second to presence/no presence of an arousal. A set of continuous positive labels was considered as one arousal event. We recognized that the changes in the ECG signal may not have occurred simultaneously with changes in the EEG during a cortical arousal. Therefore, if the ground truth arousal and predicted arousal had overlap, we considered the predicted arousal as true positive. We also performed a record-wise evaluation in which we computed the AUPRC and AUROC for each PSG record. In addition, we correlated the number of detected arousal events with the number of ground truth arousal events for each PSG record. To determine whether all components of the DeepCAD model were essential to its optimum performance, we also performed a series of ablation experiments (Table 2) where various components were omitted, and the respective AUPRC and AUROC were recalculated.

Table 2.

Performance of DeepCAD and alternative models

Models	AUPRC	AUROC
DeepCAD (InceptionBlock+ ResBlocks+LSTMs)	0.62	0.93
ResBlocks + LSTMs	0.61	0.92
InceptionBlock + LSTMs	0.48	0.86
InceptionBlock + ResBlocks	0.46	0.87
LSTMs	0.39	0.82
Spectorgram + LSTMs	0.37	0.81

DeepCAD, deep learning-based cortical arousal detection; ResBlocks, pre-activation residual blocks; LSTMs, Long short-term memory.

In order to assess the generalizability of the algorithm, we applied the DeepCAD model on a subset of SHHS 2 data which was acquired by home PSG using different hardware filters and sampling rates (Tables 1 and 3) [36, 50, 51]. Because the ECG sampling frequency of SHHS was 250 Hz, we used the NumPy one-dimensional interpolation method to resample the ECG signal to 256 Hz before applying the robust scaler [38, 52]. As shown in Table 4, we conducted four experiments for evaluating the algorithm on the SHHS data. In all experiments, we did not change any hyper-parameters of DeepCAD model. In the first experiment, we directly applied the pretrained DeepCAD model (pretrained on MESA training set) on the SHHS test set (n = 785). In the second experiment, we trained a random initialized DeepCAD model on the SHHS training set (n = 1,058) and tested it on the SHHS test set (n = 785). In the third experiment, we used the DeepCAD model (pretrained on the MESA training set) and performed additional training on a small subset of the SHHS training set (n = 105) before applying it to the SHHS test set (n = 785). In the fourth experiment, we used the DeepCAD model (pretrained on the MESA training set) and performed additional training on the full SHHS training set (n = 1,058) before applying it to the SHHS test set (n = 785).

Table 3.

Montage and sampling rate comparison

MESA			SHHS
Channel and channel derivation	Sampling frequency (Hz)	Hardware filters (Hz)	Channel and channel derivation	Sampling frequency (Hz)	Hardware filters (Hz)
ECG	256	–	ECG	250	High pass 0.15
EEG (Fz/Cz)	256	Low pass 100	EEG (C3/A2)	125	High pass 0.15
EEG (Cz/Oz)	256	Low pass 100	EEG (C4/A1)	125	High pass 0.15
EEG (C4/M1)	256	Low pass 100

MESA, Multi-Ethnic Study of Atherosclerosis; SHHS, Sleep Heart Health Study.

Table 4.

Generalizability of the algorithm

Experiments			AUPRC	AUROC
Training set	Test set	Pretrained on MESA
Pretrained on MESA	SHHS (n = 785)	–	0.39	0.86
SHHS (n = 1,058)	SHHS (n = 785)	No	0.54	0.91
SHHS (n = 105)	SHHS (n = 785)	Yes	0.52	0.91
SHHS (n = 1,058)	SHHS (n = 785)	Yes	0.54	0.92

MESA, Multi-Ethnic Study of Atherosclerosis; SHHS, Sleep Heart Health Study.

Statistical analysis

Arousal detection has a high-class imbalance problem as the arousal events are relatively rare during the sleep period. Therefore, we used the AUPRC as a metric to evaluate performance. The precision-recall curve is a curve of precision versus recall/sensitivity with variance probability thresholds. The AUPRC is more informative of performance of the model because it only evaluates the performance of true positives [53]. In this study, we used Scikit-learn’s average precision method to compute the AUPRC [38]. We also reported the AUROC. The receiver operating curve is a curve of true positive rate (sensitivity) versus false-positive rate (1—specificity) with variance probability thresholds. Differences between the AUPRC and AUROC are documented by Davis et al. [53] In the record-wise evaluation, we report the Pearson correlation between the number of detected arousal events and the number of ground truth arousal events. We also compared the difference between the two methods by a Bland–Altman plot [54]. Analyses were performed using Python package Scikit-learn v0.20.1 and Scipy v1.3.0.

Results

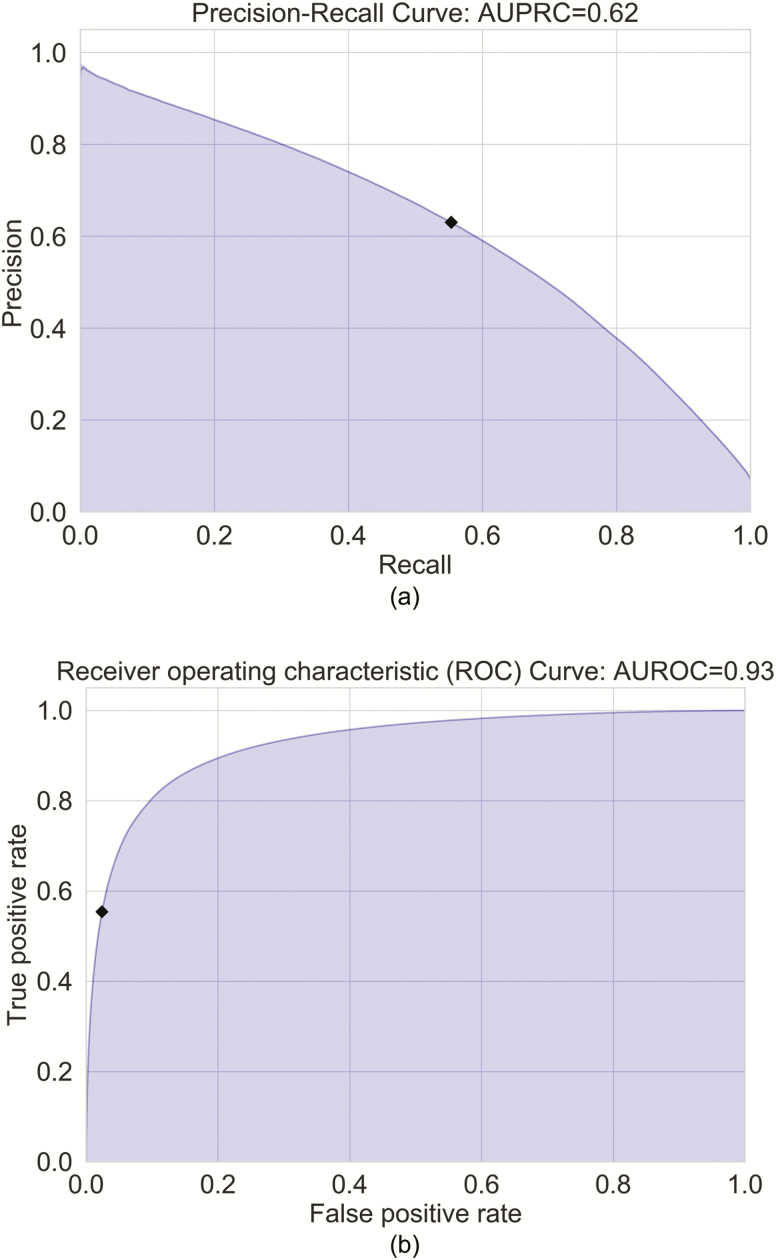
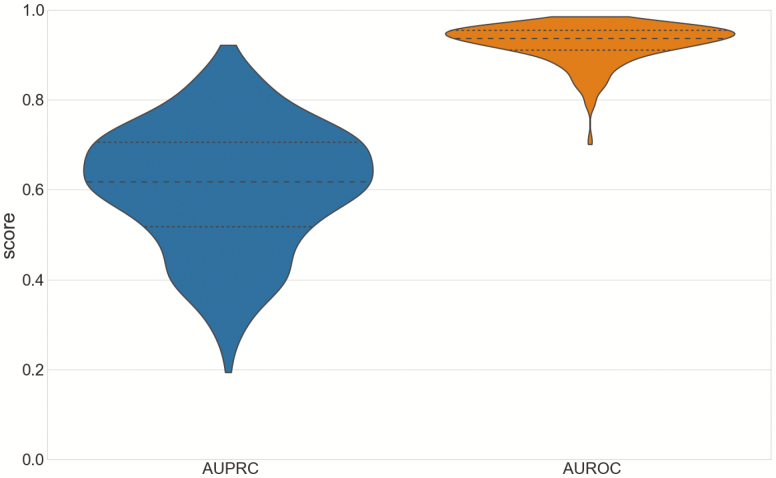
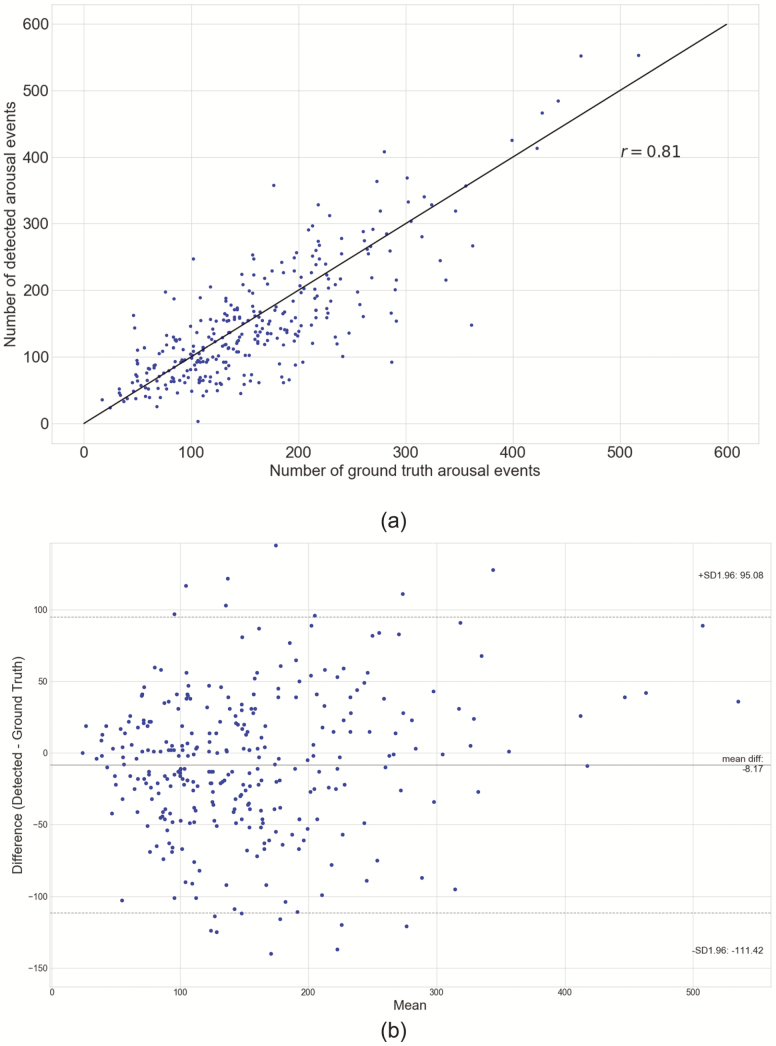
The DeepCAD model with the AUPRC score of 0.65 on the validation set and the five alternative models were evaluated on the test set (n = 311) for measuring the performance of the models. We report gross AUPRC and gross AUROC scores of the DeepCAD model and five alternative models in Table 2. The precision-recall curve and receiver operating characteristic curve of the DeepCAD model are shown in Figure 2, A and B, respectively. Compared with the other five alternative models, the DeepCAD model had consistently better performance in terms of AUPRC and AUROC scores. The DeepCAD model also demonstrated similar performance during different sleep stages (Appendix D). In the event level evaluation, with the selected decision threshold of 0.4, the DeepCAD model had a 0.69 precision, and 0.65 sensitivity on the test set. Figure 3 represents the record-wise AUPRC and AUROC. Although the AUPRC scores varied widely across test records (Min: 0.19, Max: 0.92), the distribution representing the AUPRC scores is concentrated in the center. Additionally, Figure 3 shows that over 80% of the records had AUROC scores higher than 0.9. Figure 4, A represents the scatterplot of the number of detected arousal events versus the number of ground truth arousal events. The Pearson correlation between the number of detected arousal events and the number of ground truth arousal events was 0.81 (p<0.0001). Figure 4, B represents the Bland–Altman plot that compares the difference between the automatic detection method and the ground truth. With the selected decision threshold of 0.4, the automatic detection method slightly underestimated the total number of arousal events (mean difference = −8.17). The difference slightly widens as the average of number arousal events increases.

Figure 2.

Precision-recall curve and receiver operating characteristic curve. (A) Precision-recall curve. In the figure, the black diamond corresponds to the selected decision threshold of 0.40. The area under precision-recall curve (AUPRC) is 0.62. (B) Receiver operating characteristic curve. In the figure, the black diamond corresponds to the selected decision threshold of 0.40. The area under receiver operating characteristic curve (AUROC) is 0.93.

Figure 3.

Record-wise area under precision-recall curve (AUPRC) and area under receiver operating characteristic curve (AUROC). The violin plots represent the record-wise AUPRC and AUROC. The black lines in the box correspond to the 25 percentile, 50 percentile, and 75 percentile. The shape shows the distributions of record-wise AUPRC and AUROC.

Figure 4.

Comparison between detected arousal events and ground truth arousal events. (A) Pearson’s correlation plots. (B) Bland–Altman plot. The solid horizontal line shows the mean of the difference between the two methods, and the dotted horizontal lines show the upper and lower 95% limits of agreement.

Table 4 shows the gross AUPRC and AUROC scores of the four experiments for evaluating generalizability. Although the two models trained on full SHHS dataset (n = 1,058) exhibited the same AUPRC score of 0.54, the training time of the pretrained model is only one-sixth of the model without pretraining. Additionally, the pretrained model that was trained on full SHHS training set (n = 1,058) exhibited the highest AUROC score of 0.92. The pretrained model that was additionally trained on a small SHHS training set (n = 105) had the closest performance with the two models that were trained on full SHHS training set (n = 1,058). The record-wise performances of four evaluation experiments are shown in Appendix E; these results show the same rankings as gross sequence-level evaluation.

Illustrative examples/source code

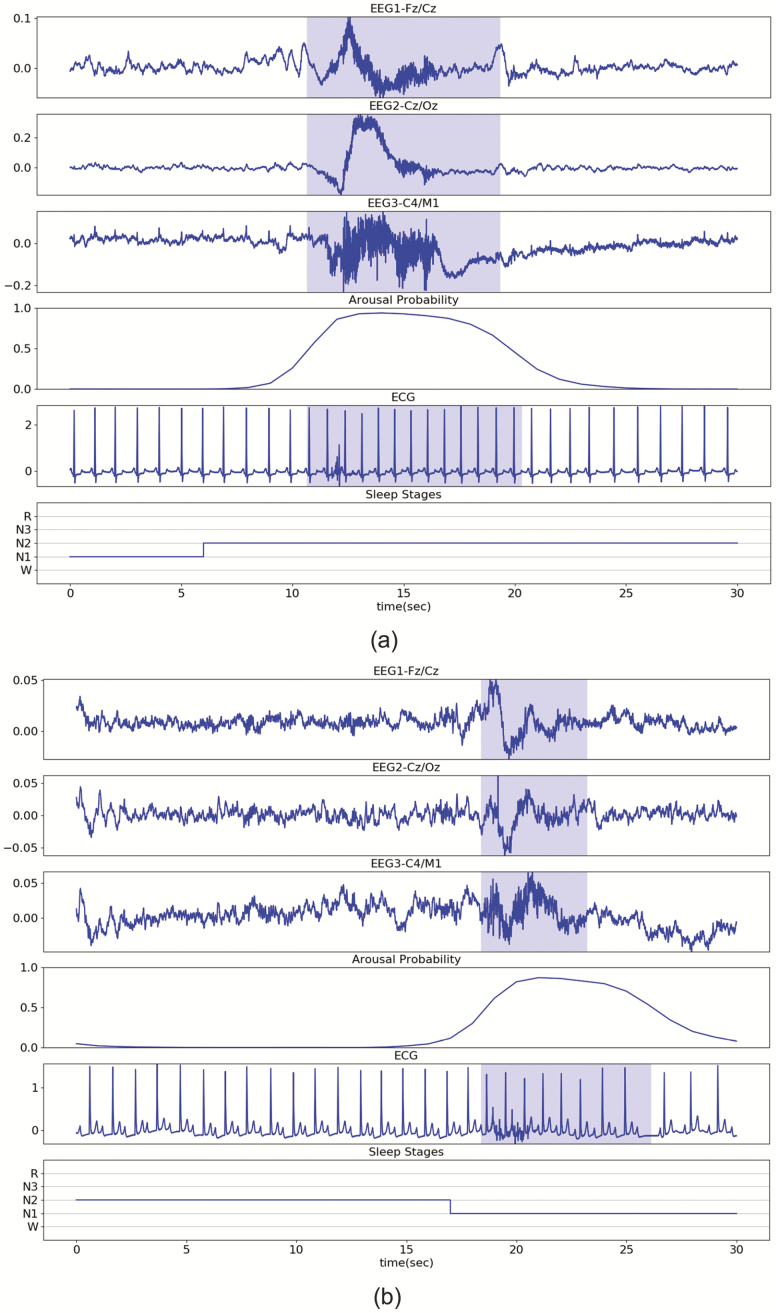
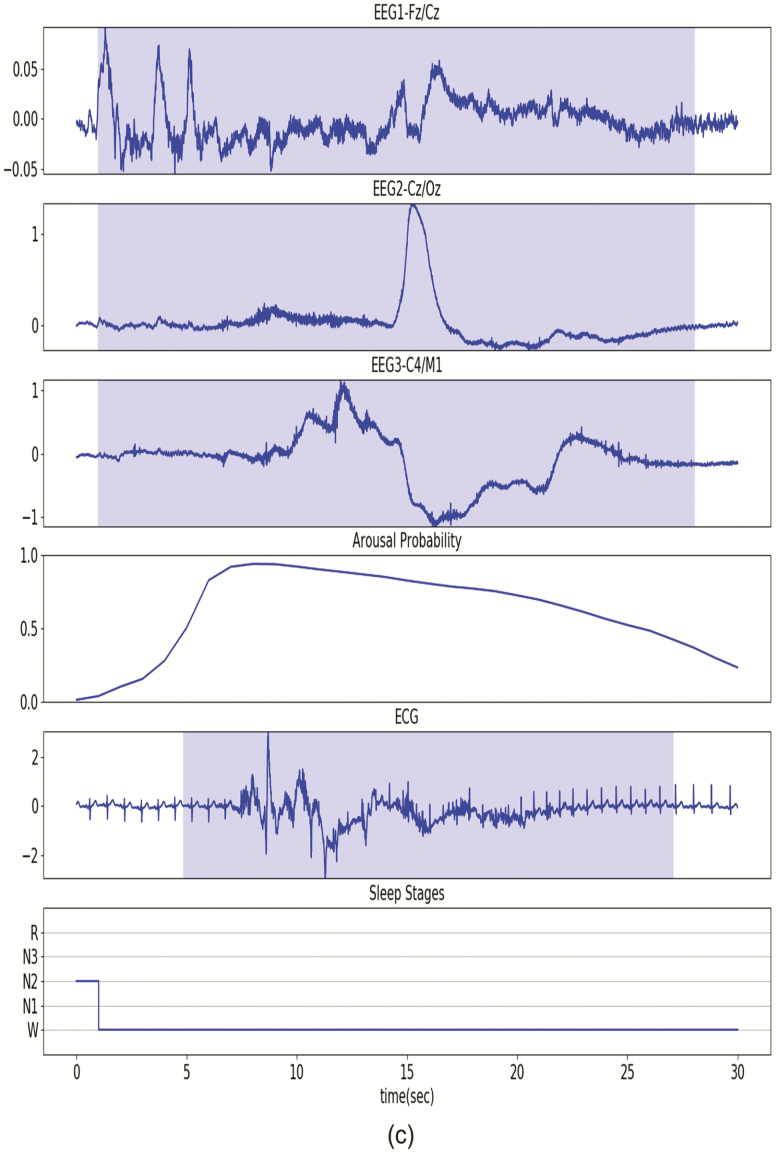
Figure 5, A illustrates the detection of a typical arousal event. Figure 5, B illustrates the detection of a short arousal event (<5 s) in a participant with a heart rate abnormality (e.g. second- or third-degree block). Figure 5, C illustrates the detection of a long arousal event (>15 s) from a participant whose ECG signal included multiple types of noise. In the three illustrative examples, the probability of an arousal event is continuous; gradually increasing and gradually decreasing at the start and end of the event. Additionally, in the high arousal probability (>0.4) segment, the most noticeable ECG change is the shorter RR intervals. Source code for our DeepCAD model is available at https://github.com/leoaoli1/DeepCAD

Figure 5.

Illustrative examples. The blue shadows on EEG derivations indicate manually scored ground truth arousal. The arousal probability indicates the outputs of the DeepCAD model. The blue shadow on the ECG signal indicates detected arousal with a decision threshold of 0.4. (A) Short arousal (<5 s) event from a participant with heart block. (B) Long arousal (>15 s) from a different participant. The ECG signal includes multiple types of noise (e.g. motion artifacts and EMG noise).

Discussion

In this study, we developed and tested a deep learning model that can automatically detect cortical arousals using a single-lead ECG signal. The model was trained and tested on PSG records from a large database of unattended PSGs recorded from a diverse adult population. It was further evaluated using records from another large database of unattended PSGs. The deep learning model consisted of CNN, RNN, and a fully connected layer and was capable of directly extracting features from a raw ECG signal and learning long-range dependencies in the extracted features. Compared to manually scored cortical arousal events as ground truth, the model attained a high level of accuracy.

Attempts to automate the detection of arousals have been made by others [19–22, 31]. Recently, Howe-Patterson et al. used a deep learning model to detect target arousals [31]. The inputs of their model included 6 derivations of EEGs, EOG, chin electromyography (EMG), oxygen saturation, respiratory airflow, abdominal EMG, and chest EMG, but not ECG. Their model produced a 0.57 gross AUPRC and 0.93 gross AUROC on the test set that included 994 in-laboratory PSG records.

In another study, Olsen et al. proposed an algorithm that used a shallow neural network and 25 features including heart rate variability (HRV) features, Hjorth parameters, and sleep stage features (from EEG) to detect autonomic arousal from in-laboratory PSG records [22]. They used an expanded window from 2 s before a cortical arousal event to 10 s after the event to link the events and acquired 72% precision and 63% sensitivity on arousal detection [22]. However, the detection network heavily depended on the accuracy of manual hand-tuning features (e.g. HRVs). Additionally, the HRV features may not be accurately extracted when the ECG signal includes arrhythmia or high noise, and sleep stage features are required. These issues may limit the applicability of this algorithm.

As an alternative to employing PSG signals, Pillar et al. used the PAT signal and heart rate (derived from PAT) to detect autonomic arousal [19, 20]. They observed correlations of 0.82¹⁹ and 0.87²⁰ between the model calculated arousal index and the PSG arousal index in studies of a mixture of OSA and healthy subjects. However, this method relies on the PAT signal that is currently available only on a proprietary type IV sleep monitor.

Previously, Basner et al. developed a single-lead ECG-based automatic arousal detection method that uses consecutive RR intervals to compute arousal probability [21]. Their algorithm identified 69.2% of 2,273 arousals which were scored on 30 laboratory nights of 10 subjects [21]. Importantly, their algorithm was developed using externally stimulated arousals on only a small number of healthy subjects. Its performance may be different when used to identify arousals in both normal and clinical populations.

The DeepCAD model has significant advantages over a RR interval-based algorithm. Such an algorithm needs a carefully designed preprocessing method for accurate annotation of R peaks. In contrast, our DeepCAD model learned to extract a large number of features from raw ECG signals. It required minimal data preprocessing and increased its precision as greater amounts of data were presented. It has the ability to handle ectopy and variability in arousal duration. Importantly, our algorithm can be applied to new data collected by different instruments.

Our DeepCAD model performed well in predicting arousals from a single-lead ECG. It obtained a 0.62 gross AUPRC on our test set (n = 311) and a 0.81 correlation between the number of detected arousal events and the number of ground truth arousal events in a record-wise comparison. We also compared the model with several alternative models and demonstrated that the performance of the DeepCAD model was superior. Additionally, in the ablation study, we found the ResBlocks and LSTMs are the two components that were responsible for the biggest performance gain. By comparing the performance between the DeepCAD model and the model without LSTMs (InceptionBlock + ResBlocks), we believe capturing long-term ECG changes is an important capability for an accurate arousal detection model. Moreover, our end-to-end DeepCAD model can function without requiring experts’ knowledge and derivations of the ECG signal. By utilizing the raw ECG signal as input, our method removed the pre-processing step that potentially loses useful information and introduces inconsistency to the final detection result. The four generalizability experiments using SHHS data further demonstrated that it was possible to replicate the performance of the DeepCAD model by simply training the model on new data without any hyper-parameter tuning. Compared with the directly applied DeepCAD model, the pretrained DeepCAD model only needed to be trained on a small dataset (10% of the full training set) to obtain a competitive performance. Additionally, training a pretrained model took significantly less time than training a random initialized model for achieving similar performance on SHHS data. These characteristics allow the DeepCAD model to have wider clinical applicability.

There are several caveats and limitations to our approach. First, although we excluded PSG records that were labeled as unreliable arousal annotation by scorers, the arousal annotation is only moderately reliable [55]. Systematic differences existing in arousal scoring could have decreased the performance of the deep learning model. Second, reporting exact event-level sensitivity and precision is difficult because the detected arousal events on ECG and the cortical arousal on EEG signals may not always be synchronous. Third, we acknowledge that our deep learning model may have difficulty differentiating arousals from prolonged wakefulness and may identify arousals during epochs scored as wake. However, circumstances where there are repetitive transitions between wake and sleep are commonly scored as wake because sleep never constitutes more than 50% of any epoch. In these situations, the model will appropriately identify arousals in these epochs. In the future, it may be feasible to identify sleep/wakefulness and arousal using a single-lead ECG and a deep learning model that incorporates multitask learning [56, 57]. Additional investigation will be required. Fourth, we did not classify the arousal events based on their etiology (e.g. respiratory or spontaneous). It is unclear whether a single-lead ECG signal contains sufficient information to make this differentiation. However, combining the DeepCAD model with an additional commonly used signal (e.g. pulse oximeter signal) may allow differential classification. Fifth, we acknowledge that the training time of our deep learning model is very long. However, the inference time is short. On average it needed less than 1.5 s to process one PSG record on an Nvidia RTX 2080Ti graphics card. Sixth, the presence of large amounts of ectopy on the ECG signal may adversely affect performance because of greater RR interval variability. However, our dataset did contain studies with ectopy which partially mitigated this source of error. The use of a training set with a larger number of studies with ectopy will further increase the accuracy of the model. Finally, although we have demonstrated that it is feasible to use the arousal probability to identify cortical arousals from a single-lead ECG, conceptualizing the mid-level features of the deep learning model is challenging; the mid-layers’ filters yield large amounts of output that are difficult to visualize. In the current study, we have attempted to present an example of one of our mid-layer outputs in Appendix Figure 3. Notwithstanding the aforementioned caveats, several methods recently have been proposed to explain the mid-level results of deep learning models [58, 59]. However, this area remains unsettled and is actively being investigated.

Although the new algorithm has several limitations, our study has several strengths. Most importantly, the DeepCAD model only needs a single-lead ECG signal as input. Because a single ECG lead is easy to record in all environments, there is potentially wide applicability in a variety of clinical scenarios (e.g. home, intensive care, and step down). In particular, it could be easily incorporated into the interpretation algorithms for Level III HST to facilitate identification of hypopneas associated only with arousals. The proposed end-to-end learning model also does not need complicated pre-processing and post-processing stages, has better generalizability, and has higher robustness. The DeepCAD model exhibited a competitive performance when tested on a large unattended PSG dataset, one that was recorded in a field type environment. As was shown in Figure 5, the end-to-end learning model has the ability to capture the ECG pattern changes and detected arousal with arrhythmia and noisy ECG signals. Additionally, the DeepCAD model produced arousal probability can be used to assist scorers in manual scoring as well. Furthermore, the generalizability experiments demonstrate that the DeepCAD model is applicable to new data collected by different hardware filters and sampling rates.

In conclusion, to our knowledge, this study was the first to use a deep learning model to detect cortical arousal on unattended PSG records using a single-lead ECG. The performance of the DeepCAD model was highly competitive with the performance demonstrated by other related approaches, and has wider potential clinical applicability.

Funding

This research is supported by the National Science Foundation under Grant No. 1918797, and partially supported by the National Science Foundation under Grant No. 1433185. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. During the conduct of this study, Dr Quan was partially supported by P01 AG009975 from the National Institute of Aging.

Conflict of interest statement

Financial disclosure: Dr Quan reports personal fees from Jazz Pharmaceuticals, personal fees from Best Doctors, grants from the National Institutes of Health, personal fees from American Academy of Sleep Medicine, outside the submitted work. A patent application is in process.

Non-financial disclosure: None