Genotype and sex-based host variation in behaviour and susceptibility drives population disease dynamics

Abstract

Host heterogeneity in pathogen transmission is widespread and presents a major hurdle to predicting and minimizing disease outbreaks. Using Drosophila melanogaster infected with Drosophila C virus as a model system, we integrated experimental measurements of social aggregation, virus shedding, and disease-induced mortality from different genetic lines and sexes into a disease modelling framework. The experimentally measured host heterogeneity produced substantial differences in simulated disease outbreaks, providing evidence for genetic and sex-specific effects on disease dynamics at a population level. While this was true for homogeneous populations of single sex/genetic line, the genetic background or sex of the index case did not alter outbreak dynamics in simulated, heterogeneous populations. Finally, to explore the relative effects of social aggregation, viral shedding and mortality, we compared simulations where we allowed these traits to vary, as measured experimentally, to simulations where we constrained variation in these traits to the population mean. In this context, variation in infectiousness, followed by social aggregation, was the most influential component of transmission. Overall, we show that host heterogeneity in three host traits dramatically affects population-level transmission, but the relative impact of this variation depends on both the susceptible population diversity and the distribution of population-level variation.

1. Introduction

Individual heterogeneity in host traits affecting disease transmission has major consequences for the predictability and severity of outbreaks of infectious disease, and in extreme cases can lead to ‘superspreaders’ or ‘supershedders’ of infection [1–3]. An individual's transmission potential can be described as a function of: (1) its rate of contact with susceptible individuals, (2) the likelihood of that contact resulting in infection and (3) the length of time that individual remains infectious [4,5]. It is, therefore, important to understand how common sources of variation, such as host genetic background and sex, may contribute to the variance in these traits and how individual variation may scale up to population level disease dynamics [4,6,7].

Disease dynamics may be disproportionately driven by individuals with extreme behavioural and physiological traits including social aggregation, pathogen shedding or in the host's ability to resist or tolerate the infection. For example, sex differences in immunity [8] or nutritional and thermal effects on host behaviours [9,10] can lead to differences in hosts' ability to tolerate infection and consequently increase transmission rates. Similarly, there are also examples of genetic differences driving the extent of pathogen shedding [11] and behaviours that mediate contact between infected and susceptible individuals [12,13]. Quantifying these relevant behavioural, physiological and immune traits and their interactions remains tremendously challenging, particularly in wild or natural disease settings [4].

One potentially useful approach is experimentally infecting model systems under controlled laboratory settings in order to quantify the roles of physiological and behavioural host heterogeneity on pathogen transmission [12,14,15]. This experimental approach offers the advantage of providing an experimentally tractable framework to partition the variance in individual transmission among a range of behavioural, physiological and immune phenotypes [4], while minimizing environmental variation and allowing highly replicated measurements of individual host traits. However, such studies may be limited in their ability to extrapolate the effects of measured heterogeneity at the level of individual hosts to population-level epidemic dynamics. Mathematical modelling is a useful tool to efficiently test different hypotheses and infer patterns across scales [16], but many theoretical studies often rely on assumptions about the level of heterogeneity in host traits, in the absence of empirical data [4,5]. A helpful approach is therefore to use mathematical modelling of epidemiological dynamics where as many parameters as possible are informed by experimental data measured on individual hosts in controlled laboratory settings.

Here, we combine experimental data and a simulation approach to test how population-level disease transmission dynamics are affected by experimentally measured levels of variation in pathogen shedding, lifespan following infection and social aggregation. We previously measured individual-level variation in behavioural and physiological traits that are relevant to pathogen transmission in the fruit fly (Drosophila melanogaster) when infected with its viral pathogen Drosophila C virus (DCV) [13,17]. DCV is a horizontally transmitted ssRNA virus of Drosophila. While relatively little is known about DCV dynamics in the wild, it appears to be common as a low-level persistent infection with apparently little pathology among several species of Drosophila [18,19]. Following what is presumably a predominantly faecal–oral route of transmission, DCV replicates in the fly's reproductive and digestive tissues leading to intestinal obstruction, lower metabolic rate and reduced locomotor activity [20–22]. Some experimental work has also shown that cannibalism of infectious fly cadavers is a viable route of transmission, but it is unknown how common this transmission route is in the wild [23]. Previously, we observed sex-based and genetic-based variation in both locomotor activity and social aggregation following DCV infection [13]. We also showed that fly genetic background, sex and female mating status significantly influenced infected lifespan, viral growth, virus shedding and viral load at death [17]. These experiments leveraged genetic and sex-specific sources of variation in three traits that likely affect individual transmission potential of DCV: the degree of group-level social aggregation (as an indicator of potential contact rate); how much DCV each individual sheds into its environment (as a proxy measure of infectiousness); and mortality rate (which defines the duration of infection).

In the present study, we explore the interactions of social aggregation, viral shedding and mortality on pathogen transmission when we: (1) vary population means of these traits; (2) vary the individual traits of the index case; and (3) constrain the variance of these traits in the population at large. First, we asked if genetic and sex-specific variation in the population means of social aggregation, virus shedding and duration of infection—as measured in a lab setting—would result in different predicted epidemics in theoretical populations. By comparing simulated epidemics in host populations comprised of a single sex and one genetic background, we isolated genetic and sex-specific sources of variation in disease transmission. Second, to test the relative importance of the index case versus group composition, we simulated epidemics in populations where the index case's traits were sampled from a larger phenotypic distribution, including males and females from all 10 genetic backgrounds. Third, to test the relative importance of variation in specific host traits on epidemic dynamics, we compared epidemic dynamics of populations exhibiting experimentally measured levels of variation in social aggregation, viral shedding and mortality, to populations where we constrained variation in these traits to the population mean.

2. Methods

(a). Simulation model

We developed an individual-based, stochastic, discrete time model that tests how experimentally measured variation in host social aggregation, mortality and viral shedding in D. melanogaster translates to differences in disease dynamics. The simulated contact networks underlying this model were generated from degree distributions derived from experimental measurements of social aggregation specific to the sex (σ) and genetic line (g) present in the simulated population. Using a susceptible–infected–removed (SIR) process, we simulated direct transmission of DCV in a closed population with no births and where only infected individuals die [24]. We did not include background (i.e. non-disease related) mortality. Note that these transmission processes are consistent with other agent-based models that encompass contact heterogeneity [25].

Let the time step be equal to 1 day, S(t) equal the number of susceptible hosts at time t and I(t) equal the number of infectious hosts at time t. The total number of hosts, N(t), in the population at time t is represented by: $N(t)=S(t)+I(t)$. The number of susceptible (S) and infected (I) individuals at the next time step is given by

$$S(t+1)=S(t)-\sum _{i=1}^{S(t)}\sum _{\hspace{0.17em}j=1}^{I(t)}{\beta }_{ij}(t)s_i(t)i_j(t)\hspace{0.17em}$$

and

$$I(t+1)=I(t)+\sum _{i=1}^{S(t)}\sum _{\hspace{0.17em}j=1}^{I(t)}{\beta }_{ij}(t)s_i(t)i_j(t)-{\alpha }_j(\sigma ,g)i_j(t).$$

Here, s_i(t) is a vector of susceptible individuals at time t, and i_j(t) is a vector of infected individuals at time t. Therefore, the summations in both equations above iterate over individuals and not time steps.

The processes of mortality α_j(σ, g) and transmission (β_ij) were individual-specific reflecting the covariates of sex (σ) genetic line (g). More specifically, the transmission between a susceptible individual (s_i) and infectious host (i_j) is given by

$${\beta }_{ij}(t)={\kappa }_j(\sigma ,\hspace{0.17em}g)\eta \tau x_{ij}(t),$$

where κ_j(σ, g) represents the infectiousness of infectious host i_j and x_ij represents whether or not an edge exists in the network between individuals s_i and i_j $(x_{ij}(t)=\hspace{0.17em}\left\{\begin{array}{c}1\\ 0\end{array}\right\})$. Because of the uncertainty surrounding the DCV transmission process, we also include scaled infectiousness (η) and transmission efficiency of the pathogen (τ) as components of β_ij(t), which we discuss in further detail below.

For each susceptible individual s_i at each time step, transmission was a stochastic process governed by a Bernoulli draw based on the value of β_ij(t). Likewise, for each infectious individual i_j, mortality was a stochastic process stochastic processes based on a Bernoulli draw for the value of α_j(σ, g). Individuals removed during the mortality process no longer contributed to transmission dynamics.

(b). Experimental data distributions: measuring social aggregation, viral shedding and mortality rate in infected D. melanogaster

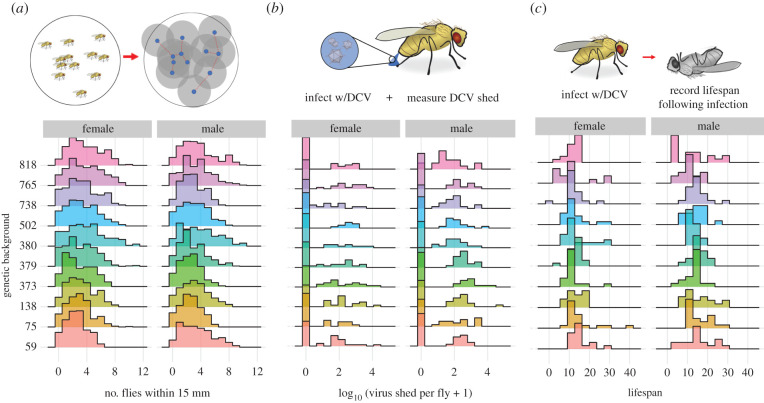
We used experimental measurements of host social aggregation, mortality and viral shedding from D. melanogaster infected with DCV (figure 1a–c; note the heterogeneity among genotypes) to test how the sex-specific and genetic variation translates to differences in disease dynamics. An in-depth analysis of these experimental data has been carried out previously, showing substantial genotype-by-sex interactive effects on each of these traits [13,17]. Briefly, we established systemic infections with DCV in males and females of 10 lines (table 1) from the Drosophila Genetic Resource Panel (DGRP) [26] and measured a number of traits including social aggregation [20], the infected lifespan and the viral shedding of each line-by-sex combination [17].

Figure 1.

The epidemiological model was parameterized by sampling frequency distributions of experimental data collected from 10 Drosophila Genetic Reference Panel lines for both male and female flies infected with DCV published previously [13,17]. Here, we provide a qualitative description of these data. (a) Social aggregation: the average number of neighbouring flies present within a 15 mm radius of each focal fly; (b) infectiousness: the number of viral copies shed per fly within the first 3 days following infected, as measured by DCV-specific qPCR; (c) the day of death of each individual infected fly. Detailed analysis showing extensive line-by-sex interactive effects are reported in [13,17]. (Online version in colour.)

Table 1.

Parameters used to simulate outbreaks of infectious disease in simulations 1–3. Simulation 1 tested the effect of genetic and sex-specific variation in social aggregation, viral shedding and susceptibility on population-level disease dynamics. Simulation 2 tested the effect of susceptible host diversity on disease transmission potential. Simulation 3 tested the effect of variation in social aggregation, infectiousness and infection duration on population-level disease transmission dynamics. We conducted 500 replicates per parameter set with 1000 individuals in the network. Simulations were allowed to run for 1000 time steps.

parameter	levels	simulation 1	simulation 2	simulation 3
population genetic background	RAL-59, RAL-75, RAL-138, RAL-373, RAL-379, RAL-380, RAL-502, RAL-738, RAL-765, RAL-818	X
population sex	female, male	X
index genetic background	RAL-59, RAL-75, RAL-138, RAL-373, RAL-379, RAL-380, RAL-502, RAL-738, RAL-765, RAL-818		X
index sex	female, male		X
threshold radius (r)	10 mm, 15 mm, 20 mm	X	X	X
pathogen transmission efficiency (τ)	0.1, 0.5, 1	X	X	X
scaled infectiousness (η)	1, 2	X	X	X
vary social aggregation	true, false			X
vary infectiousness	true, false			X
vary infection duration	true, false			X

Here, we focus on the frequency distributions of these data for each fly line and sex (figure 1), as the simulations described below were parameterized using these experimentally derived distributions. Of particular, note is the distribution of viral shedding (figure 1b), which showed substantial zero-inflation, due to many flies not shedding DCV in detectable quantities despite being infected.

(c). Social aggregation and contact network degree distribution

Social aggregation was measured by calculating the nearest neighbour distance (NND) from a photograph of groups of 10 to 12 flies of the same genetic background, sex and infection status, in 55 mm Petri dishes [13]. In accordance with other studies of D. melanogaster social aggregation [27], photos were taken of fly groups in Petri dishes following 30 min of acclimation to ensure minimal fly activity. Social aggregation was measured in n = 14–16 replicate groups of 12 flies for every combination of genetic background and sex (580 groups of flies in total).

The dynamics of faecal–oral DCV transmission are poorly understood [19,28], but the virus readily proliferates through laboratory stocks of Drosophila [18]. To account for this uncertainty in transmission mode and to assess the relative importance of possible direct transmission routes, we considered three threshold radii (10, 15 or 20 mm) for feasible transmission. For each of these thresholds, the qualifying neighbours for each focal individual was calculated using the coordinates of each fly generated with the ImageJ multipoint tool.

To generate a simulated contact network reflecting contact rates of different phenotypes, we started by creating empirical contact networks where an individual (node) shared an edge in the network if they appeared within the prescribed threshold radius of the focal fly. Importantly, using social aggregation as a proximate measure of contact rate assumes the likelihood of contact with DCV is proportional to an individual's proximity to an infected fly. Using the number of neighbours within this radius for each fly (i.e. unweighted degree centrality), we derived an empirical degree distribution for each genetic line and sex combination. From this empirical degree distribution, we sampled 1000 times with replacement to generate a larger degree distribution representing more individuals. To produce a random graph with this given degree sequence, we then used the samp_degseq function from the igraph package [29]. Note that we resampled if the degree sequence summed to be odd. This produced a network where the mean degree (rather than network density) was maintained between experimental and simulated populations.

(i). Infectiousness

We estimated infectiousness (κ_j) for any given infected individual, j, from our experimental measurements of viral shedding [17]. Viral shedding was measured by housing single infected flies in 1.5 ml Eppendorf tubes for 24 h, removing the fly, washing out the tube with 50 µl of TRI-reagent to preserve viral RNA, and freezing this sample at −70°C to await RT-PCR and qPCR. Each combination of sex and genetic background consisted of a minimum of 20 replicate flies, with most combinations consisting of 32–38 shedding samples [17].

The untransformed distribution of these data was highly skewed and zero-inflated, with some rare flies shedding exceedingly high viral titres (i.e. supershedders)—over two orders of magnitude greater than the population mean—and others not shedding any virus at all (within the technical limit of detection). To account for this disparity, we used the natural log to transform our viral load shed distribution and then normalized values by the greatest amount of virus shed. This transformation yielded a distribution constrained between 0 and 1 with a median value of 0 and a mean value of 0.23. With this transformed distribution, only extreme supershedders at the upper end of the distribution would ensure a high probability transmission, with all other individuals had a probability much less than one.

Since the amount of virus needed to ensure DCV transmission is unclear, we also considered a ‘scaled infectiousness' (η) parameter to explore what would happen if average or non-zero shedders could also shed enough to ensure infection. This scenario was implemented by multiplying our measure of infectiousness (κ_j) by 2. This step expanded the range of the transformed experimental distribution from 0 to 2. Note that for the Bernoulli trial determining whether a transmission event had occurred, the final transmission probability (β_ij(t)) was than capped at a maximum value of 1.

Finally, because the dosage and viability of DCV in the environment remain unclear, we included a transmission efficiency (τ) parameter in our model to account for this uncertainty. The three levels, τ = 0.1, 0.5 or 1, altered infectiousness and correspond to 10, 50 and 100% probability of transmission given contact. Both scaled infectiousness (η) and transmission efficiency (τ) were held constant in simulations unless specifically mentioned.

(ii). Mortality rate

DCV results in death for infected flies, making our experimental measurement of the time between inoculation and death an ideal measure of mortality rate. Infected lifespan was measured by housing single flies in standard Lewis medium vials following systemic DCV infection and monitored daily until death. For 18 of 20 sex and genetic background combinations, the lifespan following infection was measured for n = 17–20, two combinations consisted of n = 13 and n = 15 flies [17]. For simulations, we calculated mortality rate, α_j(σ, g), as the inverse of experimentally measured disease-related mortality for a given sex and genetic background.

(d). Simulation factorial design

The effects of all parameters on outbreak dynamics were tested in a full-factorial design. For each parameter set, 500 simulations were conducted for a population of 1000 individuals over the course of 1000 time steps (table 1). A wide variety of outbreaks of infectious disease were produced by different combinations of these parameters. To avoid datasets becoming predominated by fadeout, we have presented the outbreaks in populations defined by a set of parameters (r = 15 mm, τ = 1, η = 2). Key metrics to measure outbreak dynamics included: fadeout probability, maximum number of infected individuals, outbreak duration and time to maximum number of infected individuals. Fadeout probability represents the probability of an outbreak stochastically dying out [30]; in this case, we define it as the proportion of simulations where DCV fails to spread beyond the index case. We use R₀ as a measure of the number of secondary cases of infection caused by the index case for the duration of the simulation. Code to conduct these simulations was written in R (v. 3.4.4) and is available at: https://doi.org/10.5281/zenodo.4139408 [31].

(e). Random forest analysis

Parsing out the effects of individual variables in simulation modelling can be challenging because of collinear effects and sensitivity of frequentist measures of significance to sample size. To further a descriptive discussion of our simulation results, we have used random forest analysis—a machine learning method that can handle complex, nonlinear relationships between model inputs and outputs, as well as potential collinearity between covariates [32]. Random forest analysis is a recursive partitioning method that combines the predictions from numerous fittings of classification or regression trees to the same set of data [32,33]. A higher mean decrease in accuracy correlates with higher variable importance, i.e. more predictive power is lost if this variable is excluded from the analysis. For all three simulation experiments, we analysed outputs of: fadeout probability (whether the infection spread beyond initially infected individual), maximum prevalence, outbreak duration and R₀ (the number of secondary cases resulting from a single infectious individual in an entirely susceptible population). A detailed description of the analyses can be found in electronic supplementary material, information and figures S1–S3.

3. Results

(a). Simulation results

Overall, our findings were robust to changes in various parameter combinations (table 1). Threshold radius had strong effects on maximum prevalence but was not as strong predictor of a predictor of outbreak likelihood (electronic supplementary material, figures S1–S4). Here, we present results for a threshold radius of 15 mm, a transmission efficiency of 1, and a scaled infectiousness of 2, which were generally representative of most parameter spaces. Summary figures for every parameter combination are presented in electronic supplementary material, figures S4–S15.

(b). Theoretical simulation no. 1

We scaled-up the experimental degree distributions for males and females of our 10 genetic backgrounds to a theoretical population size of 1000. In each simulated population, flies were of the same sex and genetic background. We allowed infectiousness, duration of infection and social aggregation to vary based on experimental measurements for each combination of sex and genetic background (table 1). For each individual simulation, we generated a new network from the scaled-up degree distribution, and randomly selected an individual from the network to start as the index case.

(c). Individual variation in host infectiousness, social aggregation and mortality rate produced variation in population-level, pathogen transmission dynamics

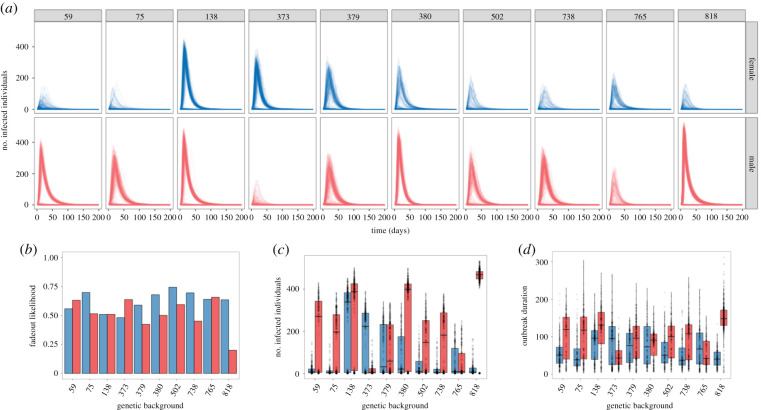
The variation in experimental treatment groups produced distinct outbreaks of infectious disease in populations comprised solely of one genetic background and sex (figure 2a–d). This finding held true when comparing both genetic lines and sexes. For example, the median outbreak size for line 373 females was approximately 200 flies compared to approximately one fly for line 373 males. By contrast, the median outbreak size for line 818 females was approximately one fly, but approached approximately 500 flies for line 818 males. Random forest analysis suggested that the two top predictors for outbreak likelihood were genetic and sex-specific variation (electronic supplementary material, figure S1). Given a successful outbreak, host genetic and sex-specific variation also affected the maximum number of infected individuals at any given time step (figure 2c; electronic supplementary material, figure S1) and outbreak duration (figure 2d; electronic supplementary material, figure S1). However, host genetic background and sex were less important than the threshold radius used to derive social network degree distribution for both outcomes (electronic supplementary material, figure S1) and less important than transmission efficiency for predicting the maximum number of infected individuals (electronic supplementary material, figure S1).

Figure 2.

(a) Simulation time courses of populations comprised of either male (red) or female (blue) individuals of the same sex and genetic background (columns) for simulation experiment no. 1. Across all of these simulations, parameters outside of host genetic background and sex are fixed; threshold radius (r) = 15 mm, transmission efficiency (τ) = 1 and scaled infectiousness (η) = 2. (b–d) Summary statistics of simulations of populations comprised of male (red) or female (blue) individuals of the same genetic background (x-axis) for (b) the proportion of simulations that resulted in fadeout; and, in the subset of simulations where fadeout did not occur and disease spread from the index case; (c) the maximum number of infected individuals at any given time step; and (d) the number of time steps infected by the index case. Shown for threshold radius (r) = 15 mm, transmission efficiency (τ) = 1 and scaled infectiousness (η) = 2. A random forest analysis was used to determine the relative importance of genetic background and sex to each summary statistic used to describe outbreak dynamics (electronic supplementary material, figure S1). (Online version in colour.)

(d). Theoretical simulation no. 2

Many natural host populations have highly variable levels of genetic diversity which can significantly affect host–pathogen dynamics [34]. To test the relative importance of trait differences among potential index cases, we simulated populations where males and females of all 10 genetic backgrounds were combined in equal proportion. More specifically, the simulated, scaled-up populations of 1000 individuals were comprised of 20 sub-populations each containing 50 sampled individuals drawn from the larger experimental distribution for each respective line/sex combination. Individuals maintained their respective experimentally measured distributions for aggregation, infectiousness, and duration of infection according to their genetic background and sex combination. A connected network of these sub-populations was created by sampling an expected degree for each node based on its subpopulation traits and then using the samp_degseq function from the igraph package to create a random graph with the given degree sequence as described in the Methods [29]. Thus, flies with different covariate traits (as simulated from sampling from their respective experimental data distributions) could be connected in the network. These simulated populations therefore reflect a relatively diverse population. We then varied which genetic background and sex combination served as the index case (table 1). We conducted 500 replicates per index case type. For each recorded replicate, the traits of the simulated population were resampled, and a new network was generated.

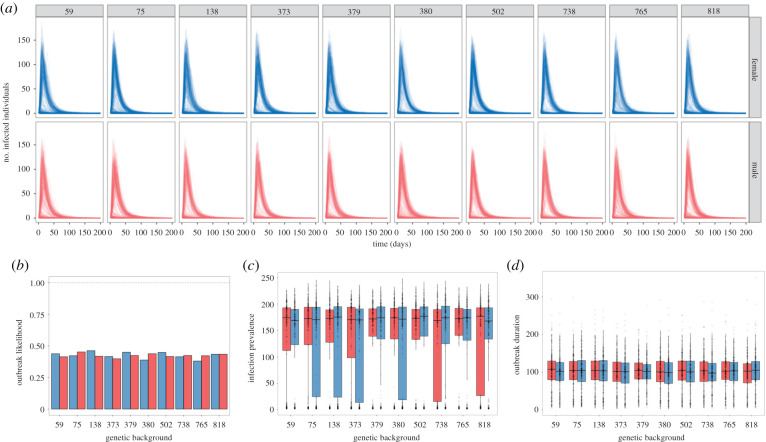
(e). Effects of the index case were outweighed by heterogeneity in the susceptible population

The genetic background or sex of the index case did not alter outbreak dynamics in diverse populations where 20 experimental treatment groups (all genotype by sex combinations) were equally sampled to create a heterogeneous population (figure 3; electronic supplementary material, figure S2). This was true for all outbreak parameters (figure 3; electronic supplementary material, figure S2). Based on the random forest analysis, threshold radius and transmission efficiency were the top two predictors for fadeout probability, maximum number of infected individuals, outbreak duration and R₀ (electronic supplementary material, figure S2).

Figure 3.

Simulation time courses of populations comprised of all 10 genetic backgrounds and males (red), and females (blue) in equal proportion, where the index case of an outbreak is an individual of a specific genetic background and sex (simulation experiment no. 2). Across all of these simulations, other parameters are fixed: threshold radius (r) = 15 mm, transmission efficiency (τ) = 1 and scaled infectiousness (η) = 2. A random forest analysis was used to determine the relative importance of genetic background and sex to each summary statistic used to describe outbreak dynamics (electronic supplementary material, figure S2). (Online version in colour.)

(f). Theoretical simulation no. 3

To determine the relative importance of experimentally observed variation in social aggregation, viral shedding and disease-related mortality on disease transmission in a heterogeneous population, we simulated heterogeneous populations derived from the variation seen across all genetic backgrounds and both sexes. To determine the effect of population-level variation, we iteratively constrained the variation in each three host traits to the population's mean. During these simulations, the unconstrained traits were free to vary according to their experimentally determined distributions (table 1). For example, to understand at the effect of variation in social aggregation in isolation, we constrained social aggregation to take on the experimentally determined mean degree distribution of the entire heterogeneous population but allowed viral shedding and mortality rate to vary according to their experimentally measured distributions across all genetic backgrounds and both sexes. In the case of degree of the network, we rounded this value to ensure a whole number, which is essential for contact network formation (e.g. an individual cannot have 2.5 contacts). We also considered interactions between variability of these three traits (table 1).

(g). Variation in infectiousness increased fadeout probability and decreased maximum prevalence of successful outbreaks, but increased outbreak duration

Constraining the infectiousness of a population to the mean (0.23, 0.46 for scaled infectiousness (η) levels 1 and 2, respectively) of the experimentally measured distribution increased the outbreak severity (figure 4a), made outbreaks twofold more likely (figure 4b), more than doubled the maximum prevalence (figure 4a,c), and persisted in the population for longer (figure 4a,d). Limiting variation in infectiousness also made outbreaks more predictable, reducing the variance of the time taken to reach the maximum number of infected individuals (figure 4d). According to the random forest analysis, variation in infectiousness was the top predictor for whether or not an outbreak spread beyond the initially infected individual (electronic supplementary material, figure S3).

Figure 4.

(a) Simulation time courses of populations where aggregation, infectiousness and duration variation are derived from the entire population's variation rather than for a single genetic line and sex combination (simulation experiment no. 3). In each panel, the variation of a particular set of components is confined to the population's mean. Across all of these simulations, parameters outside of host genetic background and sex are fixed: threshold radius = 15 mm, transmission efficiency = 1 and scaled infectiousness = 2. (b–d) Summary statistics of time course simulations where individual variation is determined by the variation seen across all genetic backgrounds and sexes (simulation experiment no. 3). The x-axis of all panels sees variation in aggregation (A), infectiousness (I) and mortality rate (D), and all their combinations fixed to the population mean. Outbreak metrics include: (b) the proportion of simulations that resulted in fadeout; (c) the maximum number of individuals infected during the simulation; and (d) the time until maximum prevalence was reached. A random forest analysis was used to determine the relative importance of genetic background and sex to each summary statistic used to describe outbreak dynamics (electronic supplementary material, figure S3).

(h). Variation in social aggregation did not influence fadeout probability but made outbreaks more severe

When social network degree distribution of simulated populations was confined to the mean of the experimental data (2, 3 and 4 for threshold radii of 10, 15 and 20 mm, respectively), outbreaks became less severe (figure 3a) compared to simulations based on the complete degree distribution. Simulated DCV spread to fewer individuals (figure 4c) and was quicker to die-out than in simulations where infectiousness, social aggregation and mortality varied freely (figure 4d).

(i). Variation in disease-related mortality did not affect epidemic outcomes

When constrained to the mean of the experimental data (13.6 days), we found disease-related mortality had little to no effect on any aspect of disease outbreak (figure 4). This is supported by the random forest analysis which identified variation in mortality rate as the least important predictor across outbreak metrics (electronic supplementary material, figure S3).

(j). Variation in infectiousness, followed by social aggregation, was the most influential component of transmission

An increase in the maximum number of infected individuals was only seen when variation in infectiousness was constrained. Interestingly, the same effect was seen in simulations where other traits are constrained alongside virus shedding, despite this differing substantially from the effects of social aggregation and mortality rate when constrained alone (figure 4; electronic supplementary material, figure S3). A similar, overruling effect was seen when social aggregation and mortality rate were constrained simultaneously, and virus shedding varied freely; outbreak dynamics were similar to the cases where only aggregation is constrained (figure 4; electronic supplementary material, figure S3).

4. Discussion

Here, we investigated how host genetic background and sex may contribute to the variance in social aggregation, infectiousness and mortality and how this variation may scale up to population level disease dynamics. We found substantial between-individual differences in pathogen transmission, constituting genetic and sex-specific variation in transmission potential. Crucially, in relatively homogeneous populations comprised of single sex and genotype combinations, heterogeneity in the index case produced major differences in population-level outbreak dynamics, including making outbreaks more likely, broader reaching and longer lasting. However, variation in the index case's transmission potential exerted little influence over population-level outbreak dynamics in diverse host populations. We also found that population-level variation in social aggregation, virus shedding and disease-related mortality affected outbreak dynamics in starkly contrasting ways. This effect appeared to be linked to the population-level distribution of each respective host trait, with factors such as skewness and zero-inflation influencing how variation in each trait affected outbreak dynamics.

In simulation experiment no. 1, males from the RAL-818 genetic background were not only more likely to start an outbreak of infectious disease, but these outbreaks were also more severe than in other populations. This suggests these males represent a class of individuals with a high transmission risk. Interestingly, high-risk males are seen in a number of host–pathogen systems [35,36]. While high-risk male classes can be produced by a range of traits pertaining to sex-specific ecology or physiology, their occurrence across systems is likely driven by sexual selection shaping male traits affecting transmission [37]. For example, in the yellow-necked mouse, Apodemus flavicollis, males are thought to be a high-risk class due to a range of sex differences in their immune response, home range and contact rates [35]. Moreover, as male Drosophila exhibit a number of other traits with the potential to alter their transmission potential, such as male–male fighting [38], the transmission risk of RAL-818 males could increase further. Focussing on classes of high-risk individuals is a more pragmatic approach to reducing the effect of heterogeneity in transmission potential, requiring less intensive monitoring protocols [4]. Additionally, as classes of individuals are identified using ranges of physiological or behavioural traits, classes are potentially more generalizable to other host–pathogen systems (e.g. sex, social dominance). Many studies of transmission heterogeneity in natural systems focus on using either behavioural or physiological traits to infer transmission dynamics and identify high-risk individuals [2,4]. Our results highlight the importance of disentangling the relative contributions made by behavioural and physiological traits together in order to infer variation in transmission potential.

High-risk individuals, such as superspreaders, present a challenge to current methods of disease control because they are capable of starting outbreaks of infectious disease that are difficult to predict and amplifying them once transmission begins [39,40]. Pre-emptively identifying high-risk individuals is therefore a major aim of epidemiology and disease ecology. However, in the second theoretical experiment we conducted, we found that starting outbreaks with individuals that differed in transmission potential did not affect outbreak dynamics when susceptible populations are genetically diverse. Our results therefore suggest outbreaks are not solely driven by the traits of rare, high-risk individuals, but are also affected by the traits of the susceptible population. High-risk individuals were unable to cause explosive outbreaks of infectious disease when surrounded by low-risk individuals as presumably, once infected, low-risk individuals failed to transmit disease to the rest of the population. Similar transmission dynamics have also been observed in laboratory populations of the social spider, Stegodyphus dumicola, where transmission of a bacterial pathogen was affected by the boldness of the index case and the individuals it interacted with [14], but ultimately traits of the index case did not alter transmission dynamics compared to the collective traits of the susceptible population. Together with our results, these findings do not suggest diversity in the susceptible population is a universal buffer to the effects of between-individual heterogeneity in disease transmission. Instead, this work highlights the necessity to characterise population diversity in the context of social interactions and networks as these may determine the relevance of this diversity. Population-level diversity is particularly important in host–pathogen systems where behavioural changes occur following infection. In populations of the guppy, Poecilia reticulata, for example, male, but not female, sociality has been shown to increase following infection. As a result, females social males are more likely to interact with, and infect, females [12]. There are many traits across species that bias social interactions, such as sexual receptivity or personality type [41]. Should these traits bias contact between transmission classes, this may explain why social and transmission networks rarely match.

Extreme phenotypes often play a key role in between-individual heterogeneity in disease transmission. However, being a relative term, ‘extreme’ phenotypes are defined by population-level variation. Constraining population-level variation in the amount of virus shed following infection to the population mean increased outbreak likelihood and severity. This was likely a result of the huge zero-inflation of the distribution of virus shedding, where many infected individuals did not shed virus. These individuals, previously termed ‘supersponges’ [42], represent the left-most extreme of the population distribution, and bore no transmission risk. While some of the individuals that do not transmit infection may simply not get any transmission opportunity, others may be supersponges and therefore incapable of transmitting disease. The presence of supersponges also demonstrates the importance of measuring variation in both behavioural and physiological traits when seeking to understand heterogeneity in disease transmission. Characterising extreme forms of population-level variation, particularly in natural systems where experiments are less controlled, should certainly be prioritised in order to understand individual heterogeneity in disease transmission.

An important caveat of our results is that because we did not measure social aggregation, virus shedding and lifespan simultaneously we cannot account for how they might covary within individuals. We, therefore, allow them to co-occur in hosts randomly, which may not reflect associations produced in nature or potential combinations of traits that are not likely due to physiological or evolutionary constraints. This is particularly true for how we estimated contact behaviour from social aggregation arenas containing 10–12 flies and measuring 55 mm wide. For our simulations, we scaled-up these smaller populations to create theoretical populations of 1000 individuals. This approach was required by the experimental demands of measuring social aggregation, although it is known that social aggregation changes may change with population size and sex ratio [43,44].

Threshold radius was a singularly important parameter across our theoretical experiment. Understanding how distance affects pathogen transmission or definitions of what constitutes a contact remains poorly described in many host–pathogen systems [7]. Moreover, real networks may have different structures not accounted for here, such as a modular structure which has been shown to facilitate or prevent the spread of disease [27,44]. As our social aggregation data come from Petri dishes containing only males or females from a single genetic background, we cannot account for how aggregation might change in more diverse and larger populations [43].

Our work bears a number of consequences for understanding how between-individual heterogeneity in disease transmission is determined and how it could affect outbreak dynamics. We show that variation in key individual traits can dramatically affect population-level transmission, surmounting to genetic and sex-specific variation in transmission potential. Importantly, the influence of this variation is dramatically affected by susceptible population diversity and the distribution of population-level variation. These results support the observations of other systems that suggest the traits of susceptible individuals can exert significant influence over transmission. This is particularly relevant to populations with low genetic diversity, such as agricultural monocultures, as this lack of diversity increases the risk of explosive outbreaks [45]. Our work posits the merits of integrating data collected in highly controlled laboratory experiments with simulations capable of extrapolating this information to larger populations.

Data accessibility

Code to conduct these simulations was written in R (v. 3.4.4) and is available at: https://doi.org/10.5281/zenodo.4139408 [31]. An earlier preprint is available from the biological preprint server bioRxiv at: https://doi.org/10.1101/735480 [46].

Authors' contributions

All authors conceived the study. J.S.J. carried out experimental work. L.A.W. wrote the model. J.S.J. and L.A.W. analysed the data. J.S.J. and L.A.W. drafted the manuscript. All authors contributed to writing the final version of the manuscript. All authors contributed funding and materials. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

J.A.S.-J. was funded by a NERC E3 DTP PhD studentship awarded to the University of Edinburgh. L.A.W. was funded by the National Science Foundation (nos. GRFP-00039202 and DEB-1701069), the University of Minnesota Informatics Institute, and the National Socio-Environmental Synthesis Center (SESYNC) under funding received from the National Science Foundation DBI-1639145. J.A.S.-J. and L.A.W. received funding for a research exchange from the Infectious Disease Evolution Across Scales RCN funded by NSF. M.E.C. was funded by National Science Foundation (nos. DEB-1413925, 1654609 and 2030509). The authors acknowledge the Minnesota Supercomputing Institute (MSI) at the University of Minnesota for providing resources that contributed to the research results reported within this paper. URL: http://www.msi.umn.edu. P.F.V. was supported by a Branco Weiss fellowship (https://brancoweissfellowship.org/) and a Chancellor's Fellowship (School of Biological Sciences, University of Edinburgh).