Diradical Character of Neutral Heteroleptic Bis(1,2-dithiolene) Metal Complexes: Case Study of [Pd(Me₂timdt)(mnt)] (Me₂timdt = 1,3-Dimethyl-2,4,5-trithioxoimidazolidine; mnt^2– = 1,2-Dicyano-1,2-ethylenedithiolate)

Abstract

The reaction of the bis(1,2-dithiolene) complex [Pd(Me₂timdt)₂] (1; Me₂timdt^•– = monoreduced 1,3-dimethyl-2,4,5-trithioxoimidazolidine) with Br₂ yielded the complex [Pd(Me₂timdt)Br₂] (2), which was reacted with Na₂mnt (mnt^2– = 1,2-dicyano-1,2-ethylenedithiolate) to give the neutral mixed-ligand complex [Pd(Me₂timdt)(mnt)] (3). Complex 3 shows an intense solvatochromic near-infrared (NIR) absorption band falling between 955 nm in DMF and 1060 nm in CHCl₃ (ε = 10700 M^–1 cm^–1 in CHCl₃). DFT calculations were used to elucidate the electronic structure of complex 3 and to compare it with those of the corresponding homoleptic complexes 1 and [Pd(mnt)₂] (4). An in-depth comparison of calculated and experimental structural and vis–NIR spectroscopic properties, supported by IEF-PCM TD-DFT and NBO calculations, clearly points to a description of 3 as a dithione-dithiolato complex. For the first time, a broken-symmetry (BS) procedure for the evaluation of the singlet diradical character (DC) of heteroleptic bis(1,2-dithiolene) complexes has been developed and applied to complex 3. The DC, predominant for 1 (n_DC = 55.4%), provides a remarkable contribution to the electronic structures of the ground states of both 3 and 4, showing a diradicaloid nature (n_DC = 24.9% and 27.5%, respectively). The computational approach developed here clearly shows that a rational design of the DC of bis(1,2-ditiolene) metal complexes, and hence their linear and nonlinear optical properties, can be achieved by a proper choice of the 1,2-dithiolene ligands based on their electronic structure.

Short abstract

The reaction of [Pd(Me₂timdt)₂] (1; Me₂timdt^•− = monoreduced 1,3-dimethyl-2,4,5-trithioxoimidazolidine) with Br₂ yielded [Pd(Me₂timdt)Br₂] (2), which was reacted with Na₂mnt (mnt²⁻ = 1,2-dicyano-1,2-ethylenedithiolate) to give [Pd(Me₂timdt)(mnt)] (3), showing an intense solvatochromic near-infrared (NIR) absorption band. The singlet diradical character (DC), predominant for 1, provides a remarkable contribution to the ground states of 3 and 4. A rational design of the DC of bis(1,2-dithiolene) complexes can be achieved by a proper choice of the 1,2-dithiolene ligands.

Introduction

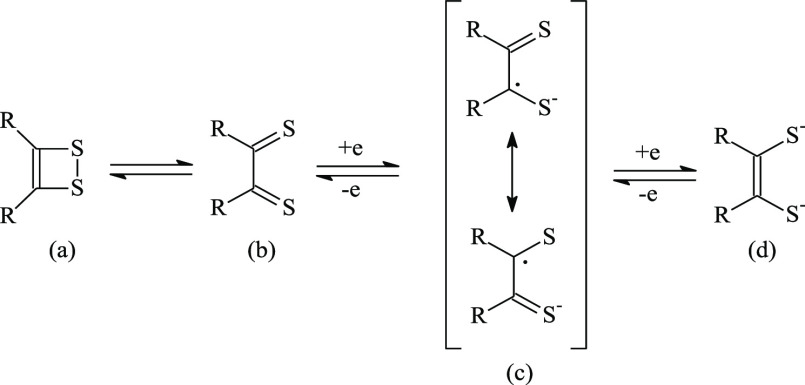
The interest of the scientific community toward bis(1,2-dithiolene) metal complexes has been continuously increasing during the past few decades,¹⁻⁶ accompanied by a growing number of applications relying on the superconducting,⁷⁻¹² photoconducting,¹³⁻¹⁷ magnetic, and linear and nonlinear optical properties¹⁸⁻²² of this class of compounds. Bis(1,2-dithiolene) complexes [M(R₂C₂S₂)₂]^q− of d⁸ metal ions M^x+, such as Ni^II, Pd^II, Pt^II, and Au^III, feature peculiar properties,^5,23 such as molecular planarity and the ability to exist in well-defined oxidation states q typically ranging between x – 4 and x – 2,²⁴⁻²⁶ also assuming fractional charges in nonintegral oxidation state (NIOS) salts.^9,12 The redox noninnocence of the 1,2-dithiolene ligands (Scheme 1) renders it difficult to partition the charge of the complexes between the ligands L and the central metal ion M^x+.^27,28

Scheme 1. Redox Noninnocence of 1,2-Dithiolene Ligands: Neutral 1,2-Dithiete (a) and 1,2-Dithione (b), Radical 1,2-Dithiolene Anion (c), and Dianionic Ene-1,2-dithiolate (d).

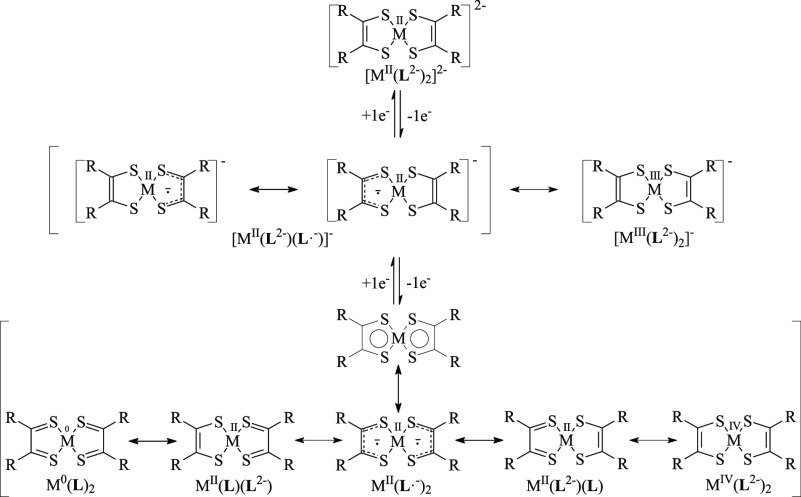
The typical redox steps accessible to bis(1,2-dithiolene) complexes of group 10 metals (M = Ni, Pd, Pt) are summarized in Scheme 2. Dianionic bis(1,2-dithiolene) complexes [ML₂]^2– are diamagnetic species, which can be isolated as stable anions in salts such as (Ph₄P)₂[Ni(mnt)₂] (mnt^2– = maleonitrile-1,2-dithiolate, 1,2-dicyano-1,2-ethylenedithiolate).²⁹ These species are fully described as [M^II(L^2–)₂]^2– complexes, featuring the ene-1,2-dithiolato form L^2– of the ligands (d in Scheme 1). Paramagnetic monoanionic 1,2-dithiolene complexes [ML₂]⁻ can be represented as [M^III(L^2–)₂]⁻ compounds^30,31 or by two resonance forms showing the dianionic ligand L^2– (d in Scheme 1) and a monoanionic radical ligand L^•– (c in Scheme 1): i.e., [M^II(L^•–)(L^2–)]⁻.²⁷ In diamagnetic neutral complexes [ML₂], the central metal ion can carry formal charges varying between 0 and +4, while the ligands can assume a neutral, monoanionic, or dianionic charge (Scheme 2), indicating a large degree of π-electron delocalization involving the metal as well as the L ligands (metalloaromaticity).³² Spectroscopic and theoretical results suggest that the complexes are better described as formed by the metal dication M^II, whatever the charge on the complex.^27,33 Therefore, the oxidation/reduction steps leading from [ML₂]^2– to [ML₂] are mainly located on the ligands,³³⁻³⁵ analogously to what has been reported for [Au^III(Ar-edt)₂]^0/– complexes (Ar-edt^2– = arylethylene-1,2-dithiolate; Ar = phenyl, 2-naphthyl, 2-pyrenyl).³⁶ Hence, the neutral M^II complexes can be described as diamagnetic singlet species formed by two antiferromagnetically coupled monoanionic radical ligands, [M^II(L^•–)₂].^33,37 Indeed, neither the closed-shell (CS) restricted delocalized nor the localized singlet diradical description represents reliably the ground state (GS) of neutral bis(1,2-dithiolene) complexes, so that an index n_DC of the diradical character (DC) can be calculated to evaluate the relative weight of the diradical singlet description.³⁷⁻³⁹ Notably, different optical properties in the visible–near-infrared (vis–NIR) region are associated with the differently charged forms of bis(1,2-dithiolene) complexes (electrochromism).^16,40,56 Neutral complexes [ML₂] show a peculiar intense absorption in the region above 800 nm.^2,5,30 This band, attributed to a π–π* HOMO → LUMO (H → L) one-electron excitation,^5,6 is shifted to lower energies and lowered in intensity in the corresponding monoreduced forms [ML₂]⁻,⁴¹ while the dianions [ML₂]^2– do not show any vis–NIR absorption. In this context, for a few decades, some authors have been investigating the [M(R′₂timdt)₂]^q– class of photoconducting⁴²⁻⁴⁴ complexes (R′₂timdt^•– = monoreduced 1,3-disubstituted imidazoline-2,4,5-trithione; M = Ni, Pd, Pt; q = 0, 1, 2; Chart S1).⁴⁵⁻⁵² Neutral [M(R′₂timdt)₂] complexes show a strikingly intense absorption at about 1000 nm (molar extinction coefficient ε as large as 120000 M^–1 cm^–1 in toluene),⁴⁸ whose energy can be fine-tuned by a proper choice of the metal M and the substituents R′.^46,48 The corresponding reduced forms show a NIR absorption falling at about 1450 nm for M = Ni, Pt and at about 1700 nm for M = Pd.⁵¹

Scheme 2. Differently Charged Species and Resonance Forms of Bis(1,2-dithiolene) Metal Complexes (M = Ni, Pd, Pt; q = 0, 1, 2).

Mixed-ligand bis(1,2-dithiolene) complexes [M(L)(L′)] have been much less investigated than homoleptic complexes^48,53 and are often prepared by metathesis reactions.⁵⁴⁻⁵⁶ The synthetic way of obtaining [M(L)(L′)] complexes by replacement of halides in MLX₂ complexes has been previously reported in a few cases.⁴⁸ In these complexes, most often containing a Ni^II ion,^31,57−61 the most electron withdrawing “pull” ligand L tends to assume the ene-1,2-dithiolate form L^2– (d in Scheme 1), with shorter C–C and longer C–S bond distances, while the other “push” ligand (L′) assumes a 1,2-dithione form (b in Scheme 1), with longer C–C and shorter C–S distances, so that the complex is generally described as the dithione-dithiolato species [M^II(L^2–)(L′)]. The electronic structure of these complexes in their neutral state, reminiscent of that of diimine-dichalcogenolato complexes,⁶²⁻⁶⁴ shows the HOMO featuring a larger contribution from the “pull” ligand L^2– and the LUMO from the “push” ligand L′. The peculiar visible–near-IR (vis–NIR) electron transition of the neutral species assumes a partial charge-transfer (CT) character from the 1,2-dithiolato L^2– ligand to the 1,2-dithione L′ (LL′CT), testified by a remarkable negative solvatochromism of the resulting absorption band.⁵⁴ In comparison to homoleptic complexes, the DC of heteroleptic bis(1,2-dithiolene) complexes has not been investigated, implicitly accepting that the GS configuration of these complexes is fully defined by the dithione-dithiolato CS description.⁴⁸ Nevertheless, it is conceivable that a continuous variation from ideally pure open-shell singlet diradicals [M^II(L^•–)(L′^•–)] to CS dithione-dithiolato complexes [M^II(L)(L′^2–)] occurs as the difference in the donor properties of the L and L′ ligands increases. Therefore, we have considered as a case study the mixed-ligand 1,2-dithiolene Pd^II complex featuring the well-known mnt “pull” ligand coupled to the “push” ligand Me₂timdt. Herein, we report an experimental and theoretical investigation on the resulting complex [Pd(Me₂timdt)(mnt)], in comparison with the relevant parent complexes [Pd(Me₂timdt)₂] and [Pd(mnt)₂], aimed at evaluating the role of the electronic structure of the ligands in tailoring the DC in homoleptic and heteroleptic bis(1,2-dithiolene) palladium complexes.

Experimental Section

Materials and Methods

Reagents were purchased from Honeywell, Alfa Aesar, and Sigma-Aldrich and used without further purification. Solvents (reagent grade) were purchased from Honeywell, VWR, and Merck and dried by using standard techniques when required. Manipulations were performed using standard Schlenk techniques under a dry dinitrogen atmosphere. Elemental analyses were performed with a CHNS/O PE 2400 series II CHNS/O elemental analyzer (T = 925 °C). FT-IR spectra were recorded with a Thermo-Nicolet 5700 spectrometer at room temperature: KBr pellets with a KBr beam splitter and KBr windows (4000–400 cm^–1, resolution 4 cm^–1) were used. Absorption spectra were recorded at 25 °C in a quartz cell of 10.00 mm optical path with either a Thermo Evolution 300 (190–1100 nm) spectrophotometer or an Agilent Cary 5000 UV–vis–NIR (190–2000 nm) dual-beam spectrophotometer. Absorption spectra were decomposed into their constituent Gaussian peaks using the Specpeak 2.0⁶⁵ and Fityk 1.3.1⁶⁶ programs. The Crystallographic Structural Database was accessed by using CCDC ConQuest 2020.1.⁶⁷

X-ray Diffraction Measurements

Single-crystal X-ray diffraction data were collected with a Rigaku MM007/Mercury diffractometer with Mo Kα radiation. The structure was solved by direct methods with SHELXS-97⁶⁸ and refined on F² by using SHELXL-97.⁶⁹

Synthesis

1,3-Dimethyl-2-thioxoimidazolidine-4,5-dione and complex 1 were prepared according to a previously reported procedure (yield 86%).^45,46,70

Synthesis of [Pd(Me₂timdt)Br₂] (2)

[Pd(Me₂timdt)₂] (1; 35.4 mg; 7.27 × 10^–2 mmol) was reacted with an excess of molecular dibromine in an Aldrich pressure tube using 30 mL of a CHCl₃/CH₃CN (2/1) solvent mixture. The glass vessel was heated to 130 °C for 15 min and slowly cooled to room temperature. The precipitate was filtered and washed with petroleum ether (brown solid; yield 32.1 mg, 97%). Mp: >230 °C. FT-IR (4000–400 cm^–1): ν 1477 (s), 1399 (s), 1360 (m), 1345 (m), 1291 (s), 1080 (s), 1032 (mw), 548 cm^–1 (w). Anal. Calcd for C₅H₆Br₂N₂PdS₃: C, 14.10; H, 0.76; N, 8.11. Found: C, 14.86; H, 0.33; N 9.02.

Synthesis of [Pd(Me₂timdt)(mnt)] (3)

Complex 2 (30.2 mg; 6.61 × 10^–2 mmol) and a molar excess of sodium 1,2-dicyanoethylene-1,2-dithiolate (21.5 mg; 0.115 mmol) were suspended in CH₃CN (30 mL) in an Aldrich pressure tube. The mixture was heated to 130 °C for 30 min and slowly cooled to room temperature. The product was isolated as black needles by filtration, washed with water, and dried under vacuum (yield 8.3 mg, 29%). Mp: >230 °C. FT-IR (4000–400 cm^–1): ν 2925 (w), 2204 (m), 1459 (m), 1397 (ms), 1285 (s), 1150 (m), 1079 (ms), 864 (m), 551 (mw), 500 cm^–1 (mw). Anal. Calcd for C₉H₆N₄PdS₅: C, 24.74; H, 1.38; N, 12.82. Found: C, 24.68; H, 0.45; N, 13.07.

Theoretical Calculations

Quantum-chemical calculations were carried out on [Pd(Me₂timdt)₂]^q− (1^q–; Chart S2 for q = 0), [Pd(Me₂timdt)Br₂] (2; Chart S2), [Pd(Me₂timdt)(mnt)]^q− (3^q–; q = 0, 1, 2; Chart S2 for q = 0), [Pd(mnt)₂]^q− (4^q–; q = 0, 1, 2; Chart S2 for q = 0), [Pt(phen)(tdt)] (phen = 1,10-phenanthroline; tdt^2– = 3,4-toluenedithiolate; Chart S2),⁷¹ and [Ni(bdt)₂] (bdt^2– = benzene-1,2-dithiolate)^33,37 and the compounds (Me₂timdt)₂ (Chart S2), Li(R′′₂timdt)·2THF (R′′ = 2,6-diisopropylphenyl; 5; Chart S2),^72,73 and Me₂timdt(SPh)₂ (7; Chart S2)⁷⁴ at the density functional theory (DFT)⁷⁵ level with the commercial suite Gaussian 16.⁷⁶ The computational setup was validated as previously described for the strictly related [Ni(Me₂timdt)₂] complex and derivatives,⁵² and it took into account three hybrid functionals (B3LYP,⁷⁷ mPW1PW,⁷⁸ and PBE0⁷⁹) and six basis sets with relativistic effective core potentials (RECPs)^80,81 for the central metal ion (LANL08(f),⁸² SBKJC,⁸³ Stuttgart 1997 RC,⁸⁴ CRENBL,⁸⁵ LANL2DZ,⁸⁶ and LANL2TZ⁸²). DFT calculations were eventually carried out with the hybrid mPW1PW functional,⁷⁸ including a modified Perdew and Wang (PW) exchange functional coupled with the PW correlation functional.^87,88 Schäfer, Horn, and Ahlrichs double-ζ plus polarization (pVDZ)⁸⁹ all-electron basis sets for light atomic species (C, H, N, S) and CRENBL basis sets⁸⁵ with RECPs for heavier atomic species (Pd and Br) were used. Basis sets and RECPs were obtained from Basis Set Exchange and Basis Set EMSL Library.⁹⁰ Dianionic bis(1,2-dithiolene) complex species were modeled according to a closed-shell (CS) restricted description (RDFT), monoanionic paramagnetic species within an unrestricted formalism (UDFT), while neutral species were investigated (a) in their triplet ground state (2S + 1 = 3, two unpaired electrons), (b) in the closed-shell singlet state (2S + 1 = 1), or (c) as antiferromagnetically coupled singlet diradicals in a broken-symmetry (DFT-BS) approach. The last description was obtained by starting from the triplet state, with the two antiparallel electrons attributed to the two 1,2-dithiolene ligands (Chart S3 in the Supporting Information). The BS electron density guess was obtained through a fragment approach (guess = fragment = 3, the three fragments being the Pd^II ion and the two monoanionic 1,2-dithiolene radical ligands), eventually allowing optimization (opt) of the geometry of the complex (BS1 solution). Finally, only in the case of 1, the guess of the electron density of the lowest BS singlet excited state (ES) was used to reoptimize the geometry of the GS electronic structure of the complex, giving an alternative minimum for the BS GS configuration (BS2), degenerate with respect to the BS1 description (|Δε_BS2–BS1| ≈ 8 × 10^–4 hartree).

For all compounds, tight SCF convergence criteria and fine numerical integration grids (grid = ultrafine) were used. In order to evaluate the singlet diradical contribution to the GS in the BS approach, the differences between the total electronic energy of the singlet state (ε_S), the BS-singlet state (ε_BS), and the triplet (ε_T) states were considered:^38,91,92

1

2

The effective electron exchange integrals J_ab(93) were calculated as follows:

3

where ⟨S²⟩_T and ⟨S²⟩_BS represent the spin expectation values^94,95 determined at the optimized geometry for the triplet and broken-symmetry GSs, respectively, after verification of the wave function stability (stable = opt). The singlet–triplet energy gap Δε_ST^SC = ε_S – ε_T, accounting for the effect of spin contamination to the energy of the singlet GS,⁹⁵ corresponding to a mixing of the singlet and triple state, was calculated as

Therefore, the ε_S^SCvalue was obtained:

4

The diradical character index n_DC can be directly calculated from ⟨S²⟩_BS:^17,37

5

A complete natural population analysis (NPA) was carried out with a natural bonding orbital (NBO)⁹⁶ partitioning scheme (pop = nboread, with boao and bndidx keywords in the NBO section of the input file) in order to investigate the charge distributions and Wiberg bond indexes.⁹⁷ Absorption vertical transition energies and oscillator strengths were calculated at the time-dependent (TD) DFT level.^98,99 TD-DFT calculations were carried out at the optimized geometry in the gas phase and in a selection of solvents (CHCl₃, CH₂Cl₂, DMF, THF, acetonitrile), implicitly taken into account by means of the polarizable continuum model in its integral equation formalism (IEF-PCM),¹⁰⁰ describing the cavity of the complexes within the reaction field (SCRF) through a set of overlapping spheres. Oscillator strength values calculated at the TD-DFT level along with experimental full width at half maximum (FWHM) values of the NIR band were used to evaluate the molar extinction coefficients ε.¹⁰¹ Experimental FWHM values on an energy scale (eV) were evaluated from the corresponding values w determined in nm from the experimental NIR spectra:

The one-photon absorption oscillator strength f_0n for each transition 0 → n is¹⁰²

where m_e and e are the mass and the charge of the electron, ν_0n is the frequency (s^–1) of the transition between the states 0 and n, μ_0n is the transition dipole moment, and h is Planck’s constant. f_0n is related to the experimental intensity of each absorption band:

where ε is the molar extinction coefficient (M^–1 cm^–1) and ϖ is the frequency (cm^–1). By adoption of Gaussian curve shapes for the absorption bands

where the width parameter θ is related to W by

Therefore, the equation

6

allows evaluating the molar extinction coefficients of the NIR transition at the TD-DFT level. Calculated molar extinction coefficients were scaled on experimental available data to give a corrected ε_calc^corr value.

The nature of the minima of each structure optimized at the DFT and DFT-BS levels was verified by harmonic frequency calculations (freq = raman), including the determination of thermochemistry parameters (zero-point energy (ZPE) corrections and thermal corrections to enthalpy and Gibbs free energy) and the calculation of FT-Raman frequencies. Gibbs free energies were used to calculate absolute reduction potentials at 298 K (E_Abs^298K) according to the following equation:^103−106

7

where ΔG_neutral^298K and ΔG_anion are the free energy values calculated at 298 K and ΔG_e^°/F represents the potential of the free electron (−0.03766 eV at 298 K; ΔG_neutral is calculated on the most stable neutral form).¹⁰⁷E_Abs^298K values were also referenced to the Fc⁺/Fc couple, taken into account at the same level of theory.

The total static (i.e., under zero frequency)¹⁰⁸ second-order (quadratic) hyperpolarizability (the first hyperpolarizability)¹⁰⁹ β_tot was calculated as previously described.¹¹⁰

Throughout all this work, molecules in their optimized standard orientation were rotated in order to align the main symmetry axis (bisecting C–C 1,2-dithiolene bonds and passing through the central metal ion) with the z axis and lie on the yz plane. Molden 6.2¹¹¹ and GaussView 6.0.16¹¹² were used to analyze Kohn–Sham (KS) molecular orbital (MO) compositions and energies. GaussSum 3.0¹¹³ and Chemissian 4.54¹¹⁴ were used to evaluate the atomic orbital contributions to KS-MOs and to analyze TD-DFT data.

Results and Discussion

Synthesis

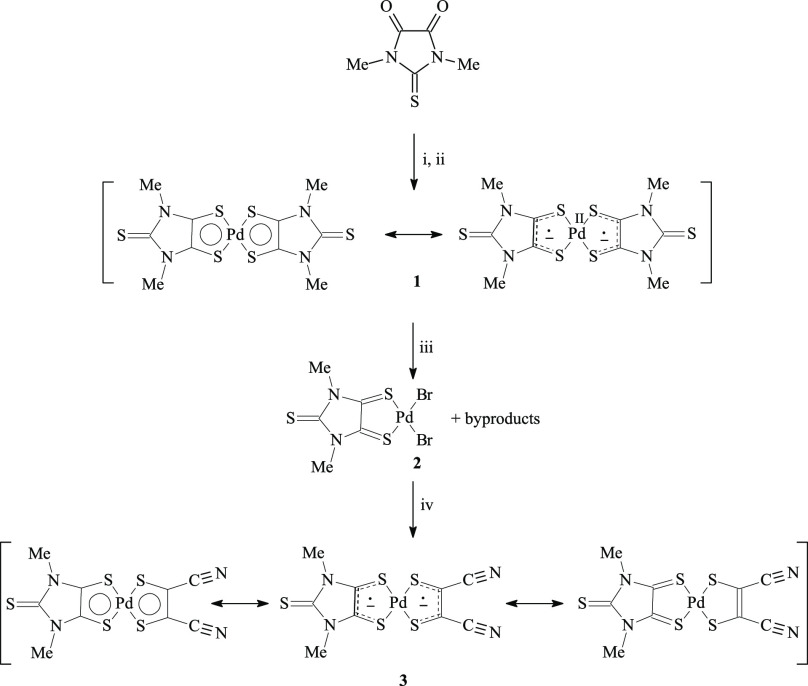
The synthesis of [Pd(R′₂timdt)₂] neutral complexes can be achieved by direct sulfuration with Lawesson’s reagent (2,4-bis(4-methoxyphenyl)-1,3,2,4-dithiadiphosphetane-2,4-disulfide)¹¹⁵ of the corresponding 1,3-disubstituted 2-thioxoimidazolidine-4,5-diones, followed by addition of PdCl₂ (reactions i and ii in Scheme 3).^45,46 The reaction of a suspension of [Pd(Me₂timdt)₂] (1) in a 2/1 CHCl₃/CH₃CN solvent mixture with a molar excess of molecular dibromine in a high-pressure tube at 130 °C yielded the neutral complex [Pd(Me₂timdt)Br₂] (2; reaction iii in Scheme 3), which was successively made to react with sodium 1,2-dicyanoethylene-1,2-dithiolate (Na₂mnt) in CHCl₃ at 130 °C to give the mixed-ligand neutral complex [Pd(Me₂timdt)(mnt)] (3; reaction iv in Scheme 3).

Scheme 3. Reaction Pathways for the Synthesis of 3.

Legend: (i) Lawesson’s reagent, refluxing toluene, N₂; (ii) PdCl₂; (iii) Br₂, CHCl₃/CH₃CN 2/1, 130 °C; (iv) Na₂mnt, CH₃CN, 130 °C.

X-ray Diffraction Studies

Tiny needle crystals of 3, suitable for a structural characterization by X-ray diffraction analysis (Figure 1, Tables S1–S6, and Figures S1 and S2), were isolated from the reaction mixture. The structural features of 3 (Figure 1) closely resemble those determined previously for [Pd(Et₂timdt)(mnt)].⁴⁸ The molecule is planar except for the methyl substituents, with the central Pd ion coordinated by the two 1,2-dithiolene ligands in a pseudo-square-planar fashion, with unbalanced Pd–S bond distances (Pd–S(1), 2.314(2); Pd–S(4), 2.258(2) Å). The C(1)–C(1)ⁱ bond length within the Me₂timdt ligand (1.454(16) Å) is longer than that previously reported for [Pd(Et₂timdt)₂] (1.397(9) Å),⁴⁵ while the C(1)–S(1)/C(1)ⁱ–S(1)ⁱ distances (1.660(8) Å) are shorter (corresponding average value in [Pd(Et₂timdt)₂] 1.689(8) Å), suggesting a larger character of ene-1,2-dithiolate of the Me₂timdt ligand in 3 as compared to the Et₂timdt ligands in [Pd(Et₂timdt)₂]. When the two C₂S₂Pd metallacycles in 3 are compared, the C(4)–C(4)ⁱ length in the mnt unit (1.364(16) Å) is shorter than that in the Me₂timdt unit, while the C–S distances are longer in the mnt ligand (C(4)–S(4) 1.724(8) Å). The C–C distance in the Me₂timdt ligand of 3 (1.454(16) Å) is intermediate between the corresponding distance in [Pd(Et₂timdt)Br₂] (1.474(10) Å; Chart S2),⁴⁸ featuring an authentic neutral Et₂timdt ligand, and that of Li(5, R″ = 2,6-diisopropylphenyl, Chart S2; 1.417(4) Å), featuring the R″₂timdt^•– radical monoanion.^72,73 Analogously, the C(4)–C(4)ⁱ distance in 3 (1.364(16) Å) is shorter than that found in [Pd(mnt)₂] (4; 1.39(2) Å; Chart S2)¹¹⁶ and the average value for 4^– monoanions (1.377(24) Å)¹¹⁷ but slightly larger than the average value found in salts of the complex 4^2– (1.359(19) Å).¹¹⁸ This suggests that the Me₂timdt ligand in 3 should be considered to carry a partial negative charge and that the GS of 3 should include a partial DC. The unit cell contains pairs (Z = 2) of symmetry-related complex molecules, each forming slipped stacks along the a vector (Figures S1 and S2 in the Supporting Information) with an interplanar distance of 3.619 Å, very close to that featured by the stacks found in the crystal structure of [Pd(Et₂timdt)₂] (3.6 Å).⁴⁵ Along the stacks, the terminal thione groups of the Me₂timdt ligands weakly interact with the π-system of the imidazoline ring (C(1)^ii/iii–S(2) 3.420 Å; (ii) −1 + x, y, z; (iii) −1 + x, 1/2 – y, z; Figure S1). Weak contacts between the methyl substituents at the Me₂timdt ligands and the terminal N atoms of the mnt ligands (H(3A)···N(5)^iv 2.644 Å; (iv) −1 + x, y, 1 + z) are responsible for the interactions between adjacent stacks aligned along the c direction. Notably, the crystal packing is sensibly different from that found in [Pd(Et₂timdt)(mnt)], where the complex molecules are stacked in an alternate head-to-tail disposition, allowing for shorter interplanar distances (3.570 Å).⁴⁸

Figure 1.

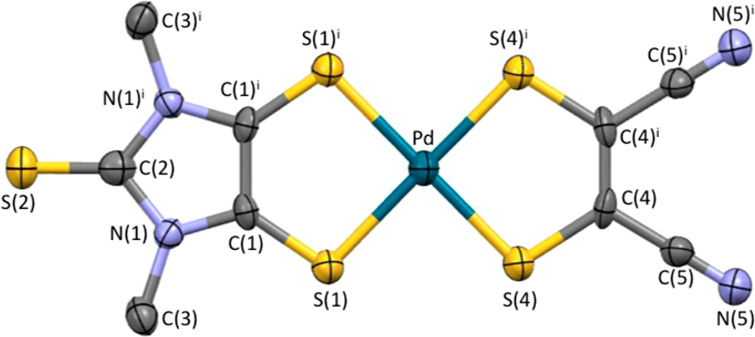
ORTEP view of complex 3 with the adopted labeling scheme. Selected bond distances (Å) and angles (deg): Pd–S(1) 2.314(2), C(1)–S(1) 1.660(8), C(1)–C(1)ⁱ 1.454(16), C(1)–N(1) 1.342(9), N(1)–C(3) 1.454(10), N(1)–C(2) 1.401(10), C(2)–S(2) 1.603(13), Pd–S(4) 2.258(2), C(4)–S(4) 1.724(8), C(4)–C(4)ⁱ 1.364(16), C(4)–C(5) 1.423(11), N(5)–C(5) 1.139(10) Å; S(1)–Pd–(S1)ⁱ 91.53(12), S(1)–Pd–(S1)ⁱ 90.61(12), S(1)–Pd–S(4) 88.92(8), C(1)–S(1)–Pd–S(4) 179.6(2), S(1)–Pd–S(4)–C(4) 177.3(2). Displacement ellipsoids are drawn at the 30% probability level. Hydrogen atoms are omitted for clarity. Symmetry operation: (i) x, 1/2 – y, z.

Absorption Spectroscopy

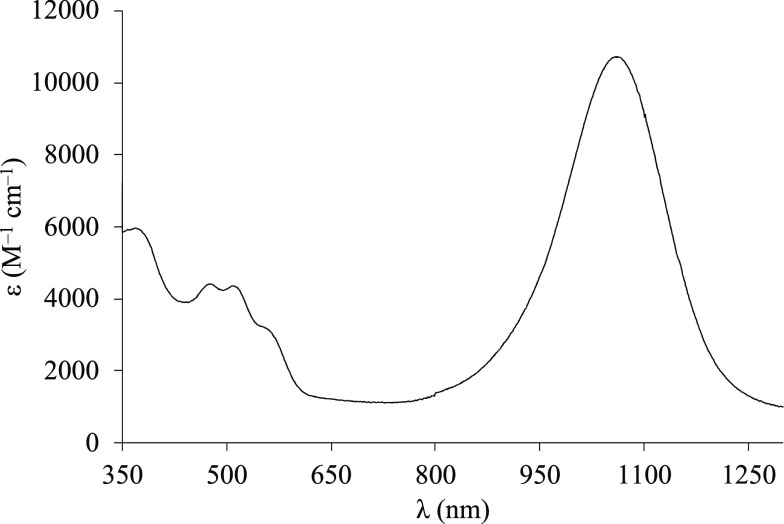
Neutral [Pd(R′₂timdt)₂] bis(1,2-dithiolene) complexes featuring alkyl R substituents show a peculiar, intense NIR absorption falling at about 1010 nm, with molar extinction coefficients ε as high as 70000 M^–1 cm^–1 in CH₂Cl₂.^45,46 The UV–vis–NIR absorption spectrum of a CH₂Cl₂ solution of 1 shows a NIR absorption maximum falling at 1008 nm (full width at half-maximum (FWHM) w = 131 nm; Figure S3). Notably, the NIR peak shows at least three Gaussian components (λ₁ = 1004.8 nm, w₁ = 121.9 nm, integral ratio 74.5%; λ₂ = 890.3 nm, w₂ = 93.5 nm, 6.6%; λ₃ = 1120.2 nm, w₃ = 155.4 nm, 18.9%; Figure S3),⁶⁵ in agreement with the spectral decomposition reported for [Pd(2,4-^tBu₂C₆H₂S₂)₂], for which a series of d–d transitions with different spin couplings to the open-shell ligands were envisaged.³³ Complex 3 shows a well-defined intense NIR peak at 1060 nm in CHCl₃ (ε = 10700 M^–1 cm^–1; Figure 2), in perfect agreement with the spectral features shown by [Pd(Et₂timdt)(mnt)] in the same solvent (λ_max = 1061 nm, ε = 12500 M^–1 cm^–1).⁴⁸ The NIR band can be decomposed into two main peaks, each accounting for about half the area of the band (λ₁ = 1066.2 nm, w₁ = 140.6 nm, 51.6%; λ₂ = 1025.1 nm, w₂ = 249.5 nm, 48.4% in CHCl₃; Figures S4 and S5). The NIR band displays a remarkable negative solvatochromism, with absorption maxima wavelengths ranging between 955 nm in DMF and 1060 nm in CHCl₃ (Table 1). When the solvent polarity is increased, the change in the experimental spectral shapes (Figure S6) suggests that the relative weight and the energy difference between the red component and the main peak of the solvatochromic NIR band increases, so that a greater polar nature should be attributed to the higher energy peak as compared to the main peak.

Figure 2.

UV–vis–NIR absorption spectrum (350–1300 nm) of 3 in CHCl₃ solution.

Table 1. Experimental NIR Absorption Maximum Wavelengths λ (nm), Energies E (eV), and FWHM Values w on a Wavelength Scale (nm) Recorded for 3, in Comparison with the Corresponding Values λ_calc and E_calc Calculated at the TD-DFT IEF-PCM Level (CS GS) and Calculated Oscillator Strengths f, Extinction Coefficients ε_calcd^corr (M^–1 cm^–1), and HOMO–LUMO Energy Gaps ΔE_H–L (eV) in Selected Solvents.

	λ	λcalc	E	Ecalc	w	f	εcalccorr	ΔEH–L
CHCl3	1060	876.0	1.167	1.416	180	0.385	10700	1.68
CH2Cl2	1020	863.8	1.216	1.436	151	0.368	11895	1.73
THF	1011	864.4	1.226	1.435	168	0.368	10675	1.71
CH3CN	966	843.9	1.284	1.469	236	0.340	6630	1.77
DMF	955	851.8	1.298	1.456	217	0.356	7712	1.77

Theoretical Calculations

During the past few decades, DFT calculations have been used successfully to investigate the structural features and the redox and spectroscopic properties of homoleptic and heteroleptic complexes containing 1,2-dithiolene ligands.^{36−39,48,50,52,62,64,72} DFT calculations were applied here on Me₂timdt^q–, mnt^q– (q = 0, 1, 2), and related compounds and the relevant neutral, monoanionic, and dianionic homoleptic and heteroleptic Pd complexes.

Ligands

The relative stability of the variously charged forms of 1,2-dithiolene ligands (Scheme 1) depends on the nature of the R substituents. The mnt ligand is generally encountered in its 1,2-dithiolate form, and the corresponding neutral species is unreported. In fact, neutral 1,2-dithiolene species are generally unstable,⁶ but depending on the R substituents they can be found as either 1,2-dithiones (Scheme 1, b), for instance embedded in 1,2-dithioxamides,¹¹⁹ or stabilized as 1,2-dithietes (Scheme 1, a).^120−122 Since vicinal dithioxamides in five-membered rings are reportedly unstable,¹²³ R′₂timdt ligands cannot be isolated as neutral 2,4,5-trithiones and the sulfuration of disubstituted 2-thioxomidazolidine-4,5-diones leads to tetrasubstituted 4,5,6,7-tetrathiocino[1,2-b:3,4-b′]diimidazolyl-2,9-dithione or 4,5,9,10-tetrathiocino[1,2-b:5,6-b′]-2,7-dithione (a and b in Chart S4 in the Supporting Information, respectively), the latter type of compounds being the final product of the Br₂ oxidation of [Pd(R′₂timdt)₂] complexes (R′ = Et).¹²⁴ The only example of an authentic radical monoanion R″₂timdt^•– has been isolated in compound 5.⁷² Neutral 1,2-dithiolene ligands stabilized in the form of 3,4-disubstituted 1,2-dithietes have been characterized in few cases (R = CF₃,¹²⁰ COOCH₃,¹²¹ 1-adamantyl¹²²). An examination of the ZPE-corrected total electronic energies ε_ZPE⁰ of the neutral 1,2-dithiolene ligands in the dithione and dithiete forms (Table 2) shows that the dithiete form is more favored for the mnt ligand in comparison to the Me₂timdt ligand (ε_ZPE = 16.28 and −42.58 kcal/mol, respectively). A comparison of the C–C bond distances calculated for Me₂timdt^q– (d_C–C = 1.500, 1.434, and 1.394 Å for q = 0, 1, and 2, respectively; Table 2) can be made with the corresponding bond distances determined structurally in [Pd(Et₂timdt)Br₂] (average d_C–C value 1.47(1) Å; q = 0; Chart S2), 5 (d_C–C = 1.417(4) Å, q = 1; Chart S2),⁴⁸ [6·2Br]²⁺(Br₂)₂(Br₂)₃ (6 = 4,5,9,10-tetrathiocino[1,2-b:5,6-b′]-1,3,6,8-tetraethyldiimidazolyl-2,7-dithione; d_C–C = 1.37(2) Å, q = 2; Chart S2), and 1,3-dimethyl-4,5-bis(phenylsulfanyl)-1,3-dihydro-2H-imidazole-2-thione (7, d_C–C = 1.361(6) Å, q = 2; Chart S2).⁷⁴ As expected, on passing from dianions to the corresponding neutral species the C–C bond lengths increase and the C–S distances decrease. It is worth noting that mnt^q– and Me₂timdt^q– (q = 0, 1, 2) share closely related frontier MO compositions (Figures S7 and S8). For both ligands, the KS-HOMO-1 and KS-HOMO of neutral species L are nonbonding molecular orbitals (NBMOs) built up from the in-phase and out-of-phase combinations, respectively, of the sulfur 3p AOs lying on the ligand plane. The LUMO is a π-in-nature MO derived from the combination of C 2p_z and S 3p_z AOs of the ene-1,2-dithiolate system, bonding with respect to the C–C bond and antibonding with respect to the C–S bonds. The LUMO of neutral L ligands becomes the SOMO and the HOMO in monoanionic L^•– and dianionic L^2– species, respectively (Figures S7 and S8). The absolute reduction potential^105,125,126E_Abs^298K (eq 7) of the redox step L/L^•– increases on passing from Me₂timdt to mnt (2.245 and 3.014 V, respectively), indicating that the mnt ligand displays the largest tendency to reduction. The difference in the E_Abs values for the L/L^•– and L’/L′^•– couples, which only depends on the choice of the substituents R at the ene-1,2-dithiolate, can be considered a useful parameter to evaluate the “push” and “pull” nature^48,54 of 1,2-dithiolene ligands in heteroleptic mixed-ligand metal complexes [M(L)(L′)].

Table 2. Optimized C–C and C–S Bond Distances (d_C–C and d_C–S, Å) within the 1,2-Dithiolene Moiety and Corresponding Wiberg Bond Indices (WBI_C–C and WBI_C–S), Variations in ZPE Corrected Total Electronic Energies (ε_ZPE⁰ = ε⁰ + ZPE, kcal mol^–1), Sum of Electronic Energies and Thermal Enthalpies (H_corr, kcal mol^–1), and Free Energies (G_corr, kcal mol^–1) Calculated for the 1,2-Dithiolene Ligands mnt^q– and Me₂timdt^q– (q = 0, 1, 2).

	q	dC–C	dC–S	WBIC–C	WBIC–S	ΔεZPE0	Δ(ε0 +Hcorr)c	Δ(ε0+Gcorr)d
mnta	0	1.501	1.625	1.018	1.787
mntb	0	1.371	1.756	1.501	1.100	–16.28e	–16.58e	–15.46e
Me2timdta	0	1.500	1.629	1.007	1.712
Me2timdtb	0	1.343	1.765	1.538	1.061	42.58e	41.28e	45.27e
mnt–	1	1.431	1.681	1.397	1.235	–84.47f	–84.58f	–84.09f
Me2timdt–	1	1.434	1.675	1.217	1.423	–51.33f	–51.35f	–50.90f
mnt2–	2	1.406	1.736	1.365	1.178	–34.75f	–34.87f	–33.87f
Me2timdt2–	2	1.394	1.738	1.453	1.201	13.09f	13.07f	14.23f

^a1,2-Dithione form.

^b1,2-Dithiete form.

^cSum of electronic and thermal enthalpies.

^dSum of electronic and thermal free energies.

^eRelative energy difference between the 1,2-dithiete and the 1,2-dithione form: .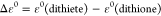

^fRelative energy difference between reduced and neutral species: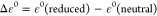

Diradical Character (DC) in Bis(1,2-dithiolene) Complexes

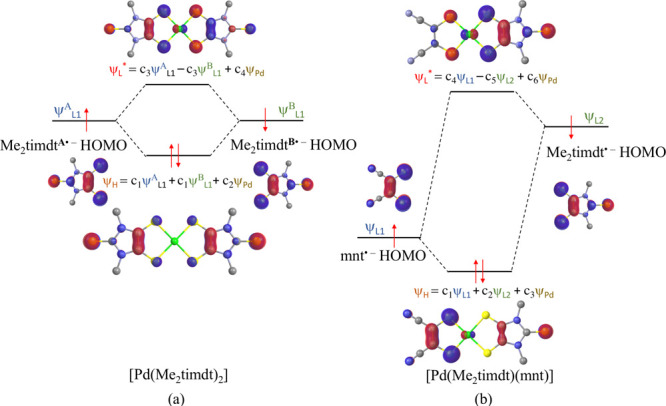
The ground state (GS) of neutral bis(1,2-dithiolene) complexes is characterized by a significant degree of DC,³³⁻³⁷ due to the very narrow HOMO–LUMO energy gap ΔE_H–L that renders the singlet and triplet GSs very close in energy. In a pure diradical the nonbonding molecular orbitals (NBMOs) ψ_a and ψ_b hosting the two electrons at the highest energy are degenerate, being localized on the two different ligands in bis(1,2-dithiolene) metal complexes,¹²⁷ and they have consequently a negligible overlap integral S_ab = ⟨ψ_a|ψ_b⟩. Under these conditions, the two possible spin states, i.e. singlet (2S + 1 = 1) and triplet (2S + 1 = 3), are degenerate, their energy difference Δε_ST = ε_S – ε_T being related to the exchange interaction J = 1/2(ε_S – ε_T) = 1/2Δε_ST.⁹¹ When S_ab is not negligible and the two NBMOs are quasi-degenerate, the triplet configuration is the most stable (ε_S > ε_T) and J assumes positive values in the so-called diradicaloids or diradical-like compounds. Wirz proposed discriminating between diradicals and diradicaloids depending on the singlet–triplet energy gaps (Δε_ST ≤ 10 and 100 kJ mol^–1 for diradicals and diradicaloids, respectively).¹²⁸ When the energy difference between the two involved MOs is larger and a significant gap exists, the energy stabilization competes with the electron–electron exchange interaction, and the CS singlet GS becomes progressively more stable. The theoretical evaluation of the GS in diradical and diradicaloid species is a challenging task, which requires the evaluation of the stability of the triplet and singlet GSs of the investigated compound. The triplet GS can generally be calculated by theoretical methods with unrestricted wave functions, such an unrestricted HF (UHF) or density functional theory (UDFT). The modeling of open-shell singlet diradicals requires multireference approaches: for instance, multireference coupled-cluster calculations, such as Mk-CCSD(T),¹²⁹ complete active-space self-consistent field (CASSCF),⁹⁴ or the complete-active-space second-order perturbation theory (CASPT2).¹³⁰ In fact, although they are computationally very efficient, DFT calculations cannot accurately describe open-shell singlet states of diradicals, so that Δε_ST and hence J values are largely uncertain. The broken-symmetry (BS) DFT (DFT-BS) spin-unrestricted reference configuration with antiparallel spins has been proposed as a compromise to extend UDFT calculations to diradical species,^91,131−135 by correcting J and Δε_ST for spin contamination^94,133,134 that affects the expectation value of the total spin ⟨S²⟩ with respect to ⟨S(S + 1)⟩.^94,95,136 In different studies, the DC index n_DC of homoleptic bis(1,2-dithiolene) complexes was evaluated. A comparison of n_DC calculated at different levels of theory suggests that the DFT-BS approach underestimates the DC of bis(1,2-dithiolene) metal complexes. In fact, the DC of the neutral complex [Ni(bdt)₂] (bdt^2– = benzene-1,2-dithiolate) was calculated to be as large as 69.1% at the CASSCF level,³⁷ 32% at the ZORA-SORCI level (ZORA = zeroth-order regular approximation; SORCI = spectroscopy oriented configuration interaction),³³ and 17.2% at the DFT-BS level. The DC depends not only on the 1,2-dithiolene ligand but also on the nature of the central metal ion. In the series of complexes of M^II ions derived from the 3,5-di-tert-butyl-1,2-benzene-dithiolato ligand, the n_DC values were calculated to be 32%, 50%, and 30% for M = Ni, Pd, Pt, respectively,³³ suggesting that Pd^II species may show particularly stable singlet diradicals in comparison to the corresponding Ni^II/Pt^II analogues.

Homoleptic Bis(1,2-dithiolene) Complexes

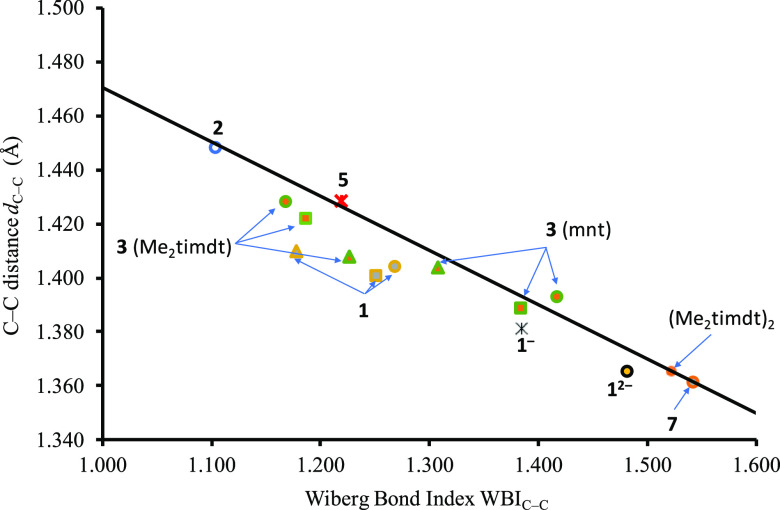
Members of the class of complexes [M(R′₂timdt)₂]^q− (M = Ni, Pd, Pt; q = 0, 1, 2) are mostly stable as neutral species, and quite severe conditions are needed to achieve a reversible chemical or electrochemical reduction to the corresponding monoanionic radical species.^16,46,48,52 With regard to M = Pd, while the crystal structures of [Pd(Et₂timdt)₂] and the CT adduct [Pd(Et₂timdt)₂]·I₂·CHCl₃ have long since been published,⁴⁵ no anionic complexes [Pd(R′₂timdt)₂]^−/2– have been structurally characterized so far. Conversely, neutral [M(mnt)₂] complexes (M = Ni, Pd, Pt) are extremely rare, and (perylene)₂(4) is the only compound characterized structurally incorporating the neutral species 4,¹¹⁶ while to date 37 examples of compounds incorporating the anions 4^–/2– have been deposited with the Cambridge Crystallographic Database.¹³⁷ Accordingly, 1 is calculated to be sensibly more stable to reduction in the gas phase and in CH₂Cl₂ than 4 (E_Abs^298K = 3.057 and 4.349 eV for complex 1 and 4.786 and 5.752 eV for complex 4, in the gas phase and in CH₂Cl₂, respectively). In Table 3, the metric parameters optimized for the bis(1,2-dithiolene) complexes 1^q– and 4^q– (q = 0, 1, 2) are summarized. In the case of neutral complexes (q = 0), the geometry was optimized (i) for the singlet CS (RDFT), (ii) for the triplet open-shell (UDFT), and (iii) for the singlet diradical (DFT-BS) GS configurations. The total electronic energy ε_T of the ³B_1u triplet state is calculated to be lower by about 2.4 kcal mol^–1 (10 kJ mol^–1) in comparison to that (ε_S) of the uncorrected singlet ¹A_g GS (ε₂ < 0, eq 2), thus classifying 1 as a diradical species.¹²⁸ In fact, the DFT-BS GS of 1 shows a large ⟨S²⟩_BS value (0.80, Table 4), indicating a considerable spin contamination from the triplet state.⁹⁴ An evaluation of the total electronic energy of the BS GS shows that it is the most stable configuration in comparison to both the triplet and CS-singlet configurations (eq 1), reflected by the diradical character n_DC = 55.4% (Table 4, eq 5). The singlet GS calculated for 4 is sensibly lower in energy in comparison to the relevant triplet state (Table 4), indicating a diradicaloid character. Accordingly, the singlet diradical configuration is only slightly more stable than the uncorrected CS singlet state and has an ⟨S²⟩_BS value smaller than 0.5. In fact, the spin-contamination corrected state (eq 4) was found to be the most stable state with only a partial diradical character (n_DC = 27.5%, Table 4). A comparison between structural and DFT-optimized bond distances for complexes 1 and 4 shows that the Pd–S and C–C distances are slightly overestimated, while C–S bond lengths are very close. Pd–S bond lengths are very sensitive to the GS configuration and follow the trend Pd–S (triplet) > Pd–S (CS singlet) ≥ Pd–S (singlet diradical) > Pd–S (structure). The C–S bond distances optimized for the singlet diradical GSs of 1 and 4 (1.699 Å; Table 3) are very close to those calculated for the hypothetical free Me₂timdt^•– and mnt^•– radical anions (1.681 and 1.675 Å, respectively) but remarkably different from those calculated for the relevant 1,2-dithiones and 1,2-dithiolates (Table 2). This supports the description of neutral homoleptic complexes as [Pd(L^•–)₂] for both classes of complexes. Although the agreement between structural and optimized C–C distances is less accurate in comparison to C–S bond lengths, the former values are affected very greatly by the charge on the ligands. In Figure 3, the optimized C–C distances and the corresponding Wiberg bond indices (WBIs)⁹⁷ are compared for a variety of R′₂timdt derivatives showing a C=C double bond, as in 4,5,9,10-tetrathiocino[1,2-b:5,6-b′]diimidazolyl-1,3,6,8-tetramethyl-2,7-dithione (Me₂timdt)₂ and compound 7,⁷⁴ or a single bond, as in the neutral complex 2 and in compound 5 (Chart S2).^72,73 For these compounds, a clear correlation (R² = 0.99) holds between the optimized C–C bond distance d_C–C within the R₂timdt ring and the corresponding WBI_C–C values. This clearly shows that WBIs calculated at the optimized distances represent a reliable parameter for evaluating the charge distribution and hence the oxidation state of noninnocent 1,2-dithiolene ligands. When 1,2-dithiolene complexes 1^q– (q = 0, 1, 2) are considered, the d_C–C and WBI_C–C data, while not exactly fitting the correlation, point out that complex 1^2– falls in the area of C=C double bonds, very close to (Me₂timdt)₂ and compound 7, therefore confirming the 2-thioxoimidazoline-4,5-dithiolate nature of the ligands in the dianionic complex. Complexes 1 (whatever the approach adopted for describing its GS) and 1^– fall in the central area of the graph, indicating an intermediate character of the C–C bond between a single and a double bond.

Table 3. Optimized Pd–S, C–C, and C–S Bond Lengths (d, Å) and Wiberg Bond Indices (WBI) within the 1,2-Dithiolene Ligands L and L′ of [Pd(L)(L′)]₂^q– Complexes (L = L′ = Me₂timdt for 1^q–; L = Me₂timdt, L′ = mnt for 3^q–; L = L′ = mnt for 4^q–; q = 0, 1, 2)^a.

			L						L′
	GS	symmb	dPd–S	dC–C	dC–S	WBIC–C	WBIC–S	dPd–S	dC–C	dC–S	ΔdC–Cc	WBIC–C	WBIC–S
1	triplet	3B1u	2.351	1.410	1.698	1.177	1.378
	singlet	1Ag	2.314	1.404	1.697	1.269	1.276
	BS		2.307	1.401	1.699	1.251	1.274
[Pd(Et2timdt)2] (structural data)d,e			2.295(2)	1.397(9)	1.689(8)
1–	doublet	2B2g	2.337	1.381	1.717	1.385	1.192
12–	singlet	1Ag	2.376	1.365	1.739	1.482	1.126
3	triplet	3B1	2.359	1.408	1.700	1.226	1.267	2.305	1.404	1.701	0.004	1.307	1.098
	singlet	1B1	2.342	1.428	1.674	1.168	1.397	2.263	1.393	1.725	0.035	1.417	1.098
	BS	–	2.344	1.422	1.682	1.186	1.354	2.273	1.389	1.717	0.033	1.384	1.098
3 (structural data)f			2.314(2)	1.454(16)	1.660(8)			2.258(2)	1.364(16)	1.724(8)	0.090
3–	doublet	2A1	2.369	1.397	1.697	1.290	1.276	2.286	1.376	1.740	0.021	1.451	1.138
32–	singlet	1B1	2.384	1.364	1.737	1.477	1.131	2.323	1.381	1.744	–0.017	1.424	1.130
4	triplet	3B1u	2.325	1.410	1.696	1.277	1.329
	singlet	1Ag	2.275	1.403	1.701	1.325	1.305
	BS		2.289	1.451	1.699	1.311	1.312
4–	doublet	2B2g	2.295	1.386	1.725	1.405	1.195
42–	singlet	1Ag	2.332	1.380	1.743	1.428	1.131
4 (structural data)e,g			2.263(7)	1.39(2)	1.71(1)

^aFor neutral species (q = 0), the distances in the open-shell paramagnetic triplet, CS diamagnetic singlet, and singlet diradical (BS) configurations are reported.

^bGS-symmetry representations are referenced to the D_2h (1, 4) and C_2v (3) point groups, with the complex molecule laying on the yz plane and the main axis being coincident with z.

^cΔd_C–C = difference in d_C–C values calculated within the two ligands Me₂timdt^–q/2–1 and mnt^–q/2–1 in 3^q–.

^dReference (45).

^eAverage value.

^fThis work.

^gIsolated in (perylene)₂(4). Reference (116).

Table 4. Energy Differences (kcal mol⁻¹) between the Singlet and the Broken–Symmetry Configurations (ε₁), the Singlet and the Triplet Configurations (ε₂), the Spin Contamination Corrected Singlet and the Triplet Configurations (Δε_ST^SC), Expectation Value of the Spin Contaminant ⟨S²⟩_BS for the Singlet Diradical Configuration, Effective Electron Exchange Integrals J_ab and Diradical Characters n_DC (%) Calculated for Complexes 1, 3, and 4.

	1	3	4
ε1	–4.325	–0.789	–1.015
ε2	–2.404	5.817	6.197
ΔεSTSC	3.986	–7.420	–8.096
⟨S2⟩BS	0.801	0.436	0.474
|Jab|	1.579	4.175	4.664
nDC (%)	55.4	24.9	27.5

Figure 3.

Correlation between optimized C–C bond distances (d_C–C) and Wiberg bond indices (WBI_C–C) within the 1,2-dithiolene ligand calculated for selected systems (circle, singlet; star, doublet; triangle, triplet; square, singlet diradical).

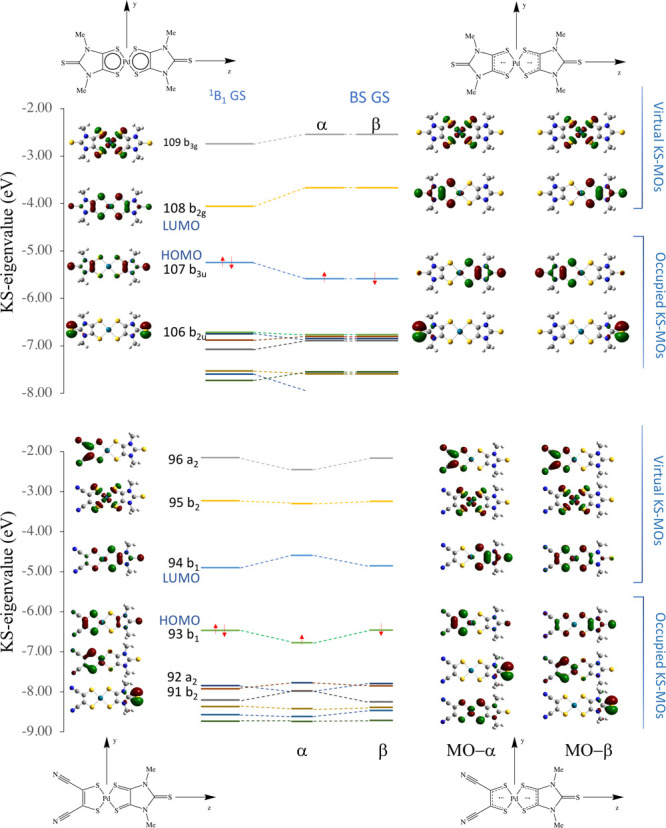
An examination of the frontier KS-MOs composition shows that, according to the CS description of the GS of 1, the KS-HOMO and the KS-LUMO are π-MOs represented by the b_3u in-phase and b_2g out-of-phase combinations of the singly occupied molecular orbitals (SOMOs) of the two Me₂timdt^•– ligands (Figure 4a and Figure S8). In fact, the b_3u KS-HOMO (MO 107 according to a progressive labeling based on an energy scale) is mainly made up of the four 3p_x AOs of the four donor S atoms, perpendicular to the molecular yz plane, and the four C 2p_x AOs taken with opposite phases. The terminal S atoms also participate in this MO, while the contribution from the central Pd ion is very poor (4%). The 108 b_2g KS-LUMO involves the same atomic species as the HOMO with a larger contribution from the bonding sulfur atoms, but the contributions from the two ligands are opposite in phase. In the KS-LUMO, the metal ion is only marginally involved (5%) as well through its 3d_yz AOs. In the singlet diradical DFT-BS GS configuration, the α- and β-HOMOs show the same composition as the HOMOs of the constituent 1,2-dithiolene Me₂timdt^•– ligands, analogously to what was previously reported for different Ni and Pt bis(1,2-dithiolene) metal complexes,⁵² the central Pd ion participating to both α and β MOs (3%). Notably, the DFT-BS approach results in a stabilization of the KS-HOMO and destabilization of the KS-LUMO with respect to the restricted CS solution, thus increasing the ΔE_H–L gap (Figure 5, top). The CS description of complex 1 features a single allowed NIR one-electron excitation calculated at the TD-DFT level. This corresponds to the ¹A_g → ¹B_1u transition, involving almost exclusively (97%) the one-electron HOMO–LUMO (H → L) excitation. This is calculated to fall at 963.0 nm (oscillator strength f = 0.436) in the gas phase and 1068.3 nm (f = 0.581) in CH₂Cl₂. The oscillator strength calculated at the TD-DFT level along with the experimental FWHM value of the NIR band were used to evaluate the molar extinction coefficient ε for 1 (eq 6).¹⁰¹ The symmetric and antisymmetric combinations of the α-107 → α-108 and β-107 → β-108 excitations (H,H → L,L double exciton states) are calculated as BS-GS → ES 1 and BS-GS → ES 2 transitions. Double exciton states have been reported for conjugated chromophores with open-shell diradical character,¹²⁷ such as polyenes^138,139 and quinoidal oligothiophenes.¹⁴⁰ The double exciton state is one-photon forbidden, and it has been observed as a weak band at lower energies in comparison to the main absorption band due to the one-photon allowed single exciton state.¹²⁷ The symmetry-allowed transition BS-GS → ES 2 falls at wavelength values lower (E = 1.487 eV, λ_max = 833.6 nm, f = 0.310) than those predicted for the singlet GS (see above). The complex envelope of the NIR absorption band of neutral [M(R,R′timdt)₂] bis(1,2-dithiolene) complexes can be attributed to the contribution of doubly excited states to the main single exciton states, thus possibly accounting for the unusually high molar extinction coefficients observed for the NIR absorption in this class of bis(1,2-dithiolene) complexes.^46,49 The forbidden BS-GS → ES 1 transition (1.142 eV, λ_max = 1085.6 nm) may provide a low-energy weak contribution¹³⁸ to the NIR absorption due to the vibronic coupling with the B_1u antisymmetric combination of the stretching Pd–S vibrations, calculated at 294.1 and 293.2 cm^–1 at the RDFT and DFT-BS levels, respectively.

Figure 4.

Qualitative MO diagram showing the contributions of the HOMOs of the 1,2-dithiolene ligands to the HOMO and LUMO of complex 1 (a; c₁ 48%, c₂ 4%; c₃ 47.5%, c₄ 5%) and complex 3 (b; c₁ 61%, c₂ 31%, c₃ 8%; c₄ 24%, c₅ 70%, c₆ 6%) in the CS GS description. In the KS-MO drawings hydrogens have been omitted for clarity. Cutoff value: 0.05 |e|.

Figure 5.

Frontier KS-MO energy diagram (−2 to −8 eV) showing the energy and MO drawing in the restricted (CS GS, left) and singlet diradical (BS GS, right) descriptions for 1 (top) and 3 (bottom). Cutoff value: 0.05 |e|.

Electronic Structure of [Pd(Me₂timdt)(mnt)] (3)

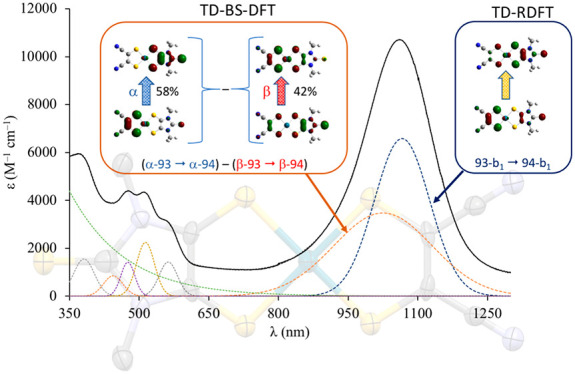
The GS geometry for 3 (E_Abs^298K = 3.784 and 4.872 eV in the gas phase and CH₂Cl₂, respectively) was optimized in its singlet CS (¹B₁), triplet open shell (³B₁), and singlet diradical (BS) configurations. The triplet–singlet energy gap classifies 3 as a diradicaloid (Table 4).^91,128 While the ³B₁ state is sensibly less stable than the singlet state, the singlet diradical BS (⟨S²⟩_BS = 0.436) and the ¹B₁ CS singlet configurations differ by less than 1 kcal mol^–1 (Table 4). The singlet configurations calculated at the RDFT and DFT-BS levels show very close optimized Pd–S, C–C, and C–S bond distances, only very slightly overestimated (by less than 0.03 Å) in comparison to the relevant structural distances (Table 3). The difference Δd_C–C between the C–C bond distances d_C–C of the two 1,2-dithiolene ligands (corresponding to the C(1)–C(1)ⁱ and C(4)–C(4)ⁱ structural bond lengths in Figure 1 for the Me₂timdt and mnt ligands, respectively) is evaluated correctly (C(1)–C(1)ⁱ > C(4)–C(4)ⁱ), but it is slightly underestimated, so that the calculated dithione-dithiolato character is less pronounced than expected on the basis of the structural data (Table 3). The DFT-BS description of the GS provides a lower Δd_C–C value in comparison to the CS description. Accordingly, while the charge Q_Pd on the central Pd ion in the CS and in the singlet diradical GSs is essentially unchanged (ΔQ_Pd = 0.024 |e|), the difference in the charges calculated on the two 1,2-dithiolene ligands at the NBO level is sensibly larger in the former (0.514 and 0.390 |e|, respectively). In the RDFT approach, the optimized values for the C–C distances of the Me₂timdt and mnt ligands correspond to noticeably different WBIs (1.168 and 1.417 in the ¹B₁ CS GS) and clearly fall in different regions of the d_C–C vs WBI_C–C correlation (Figure 3). Therefore, a comparison between structural and DFT-optimized data indicates that the CS description is more suitable than the singlet diradical description in modeling the GS of the mixed-ligand complex 3. Notably, the value of the C–C bond lengths within the mnt ligand in 3 (1.393 Å, Table 3) is even shorter than the value calculated for the free mnt^2– ligand (1.406 Å, Table 2). On passing from 3 to the radical anion 3^•– and the dianion 3^2–, only minor differences (lower than 0.02 Å) are observed on the mnt ligand, while the Me₂timdt ligand is more greatly affected, the d_C–C distance being progressively shortened (d_C–C = 1.428, 1.397, and 1.364 Å within the Me₂timdt ligand for 3, 3^–, and 3^2–, respectively; Table 3). In summary, a comparison between calculated and experimental data supports the hypothesis that the GS of 3 can be better described as a dithione-dithiolato [Pd^II(Me₂timdt)(mnt^2–)] complex with a minor contribution from the singlet diradical [Pd^II(Me₂timdt^•–)(mnt^•–)] description. Accordingly, the diradical character n_DC = 24.9% (eq 5) is calculated for complex 3 (Table 4).¹⁴¹ The KS-HOMO and KS-LUMO in the CS description (MOs 93 and 94, respectively) are π-in-nature MOs mainly located on the mnt (61%) and Me₂timdt (70%) ligands, respectively, with only minor contributions from the 4d_xz AO of the Pd central atom (6% and 8%, respectively; Table S7). Hence, KS-HOMO and KS-LUMO in the heteroleptic complex can be considered as being derived from the in-phase and out-of-phase combinations of the SOMOs of the constituent ligands mnt^•– and Me₂timdt^•– (Figure 4b and Figures S7 and S8). The former (“pull” electron-withdrawing ligand, HOMO at lower energy) contributes mostly to the KS-HOMO of 3 and assumes a larger character of 1,2-dithiolate, while the latter (“push” ligand, HOMO at higher energy) contributes mostly to the KS-LUMO of 3 and assumes a larger character of 1,2-dithione, in agreement with the structural data discussed above. In the DFT-BS description, the eigenvalues of the corresponding α- and β-MOs are remarkably unequal, reflecting their different compositions (Figure 5 (bottom) and Figure S9). In particular, the α-MO 93 is located on the mnt ligand (76%; Table S8 and (a) in Figure S9), while the β-MO 93 is less stable and is located largely on the Me₂timdt ligand (63%; Table S8 and (c) in Figure S9). Conversely, the α-MO 94 is located almost entirely on the Me₂timdt ligand (91%; Table S8 and (b) in Figure S9), while the β-MO 94 shows contributions from both ligands (mnt 54%, Me₂timdt 36%; Table S8 and (d) in Figure S9).

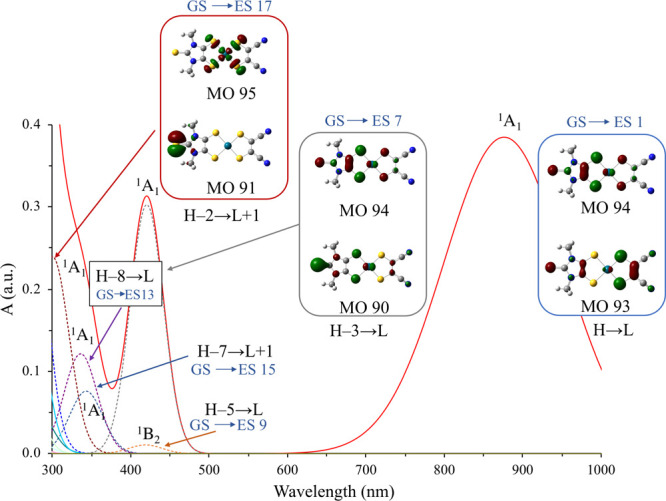
Therefore, both the RDFT and DFT-BS approaches agree in attributing an LL′CT character to the lowest energy transition, from the mnt “pull” ligand to the Me₂timdt “push” ligand. TD-RDFT calculations show, in excellent agreement with experimental data (Figure 2 and Figure S3 in the Supporting Information), three main spectral regions, namely (i) an overlap of intense transitions in the UV region (λ < 280 nm), (ii) a band in the visible region (300 ≤ λ ≤ 500 nm), and (iii) a single very intense NIR transition (λ > 800 nm). In Figure 6, the UV–vis–NIR spectrum of 3 in CHCl₃ solution, simulated on the basis of singlet IEF-PCM TD-RDFT calculations (Table 5), is depicted. The absorption bands in the UV region are due to the overlap of several peaks involving the frontier orbitals, with intraligand (GS → ES 9), interligand (GS → ES 13), or ligand-to-metal (GS → ES 15 and GS → ES 17) character. The absorption in the visible region is mainly due to the GS → ES 7 intraligand transition, involving mainly the KS-HOMO-3 and KS-LUMO, centered on the Me₂timdt ligand and the Pd^II ion. A single intense transition is calculated in the NIR region, falling at 1.489 eV (Table 5). This transition involves almost exclusively (88.4%) the one-electron excitation from the KS-HOMO (MO 93) to the KS-LUMO (MO 94). Notably, the oscillator strength f calculated for the NIR transition (0.315) is sensibly lower than that calculated for 1 (f = 0.436, see above), in agreement with the experimental values determined for the corresponding molar extinction coefficients. TD-RDFT calculations were carried out at the IEF-PCM level of theory in the same solvent systems experimentally adopted to record UV–vis–NIR spectra. The calculated NIR transition energies are generally overestimated but are linearly correlated to the experimental energies (R² = 0.88; E_calc (eV) = 0.374; E_exp + 0.979; Table 1 and Figure S10). Both in the gas phase and in the solvents considered at the IEF-PCM level, the NIR transition is attributed exclusively to the H → L one-electron excitation. Accordingly, a linear correlation holds between the calculated transition energies in the NIR region and the ΔE_H–L energy gap evaluated in each of the examined solvents (Table 1; R² = 0.92). Along the series CHCl₃, CH₂Cl₂, THF, CH₃CN, and DMF the contribution of the mnt fragment to KS-HOMO and KS-LUMO slightly increases (68% to 70%) and decreases (16% to 13%), respectively (Table S7). The contribution of the Me₂timdt fragment to the KS-HOMO and to the KS-LUMO decreases (23% to 20%) and increases (78% to 82%), respectively. Therefore, on passing to CHCl₃ to DMF, the NIR transition assumes a larger LL′CT character, and the ΔE_H–L energy gap increases from 1.68 eV in CHCl₃ to 1.77 eV in DMF and CH₃CN, in agreement with the experimental trend of NIR absorption energies (Table 1). Calculated oscillator strengths f fall between 0.356 and 0.385 in DMF and CHCl₃, respectively (Table S9). Oscillator strength values calculated at the TD-DFT level have been used along with experimental full widths at half-maximum (FWHM, w) to evaluate the ratio between the extinction coefficient in each solvent and that in CHCl₃ solution. The resulting scaled calculated extinction coefficients ε_calc^corr (Table 1) progressively decrease with an increase in the transition energies. TD-DFT calculations were carried out on 3 in the singlet diradical electron configuration. Since the two α-93 → α-94 and β-93 → β-94 (H → L) excitations are not degenerate (Figure 5, bottom), the α-excitation contributes mainly (58.1%) to the symmetry-allowed transition at higher energy (0.853(α-93 → α-94) – 0.464(β-93 → β-94); E = 1.629 eV, λ = 761 nm, f = 0.267 in the gas phase), while the β-excitation contributes to the transition at lower energy (0.486(α-93 → α-94) + 0.881(β-93 → β-94); E = 0.746 eV, λ = 1663 nm, f = 0.033), forbidden in the C_2v point group. Although the contribution of the singlet diradical description to the GS of 3 is limited, it is conceivable that the former transition, corresponding to a double exciton state, can provide a high-energy component to the NIR transition. Notably, due to its nature, the double exciton transition is predicted to show remarkable solvatochromic effects, thus accounting for the different spectral shapes observed on varying the solvent (Table 1 and Figure S6).

Figure 6.

UV–vis–NIR spectrum of 3 simulated on the basis of IEF-PCM TD-RDFT calculations in CHCl₃. FWHM w = 90 nm for the ¹A₁ (H → L) transition, and w = 25 nm for the UV–vis bands. Cutoff value: 0.05 |e|.

Table 5. Energies E (eV), Wavelengths λ (nm), and Oscillator Strengths f of the Main (f ≥ 0.005) UV–vis–NIR Electronic Transitions Calculated for 3 in the Gas Phase and in CH₂Cl₂ and CHCl₃ at the IEF-PCM TD-RDFT Level^a.

		gas phase			CHCl3			CH2Cl2
ESb	symm	E	λ	f	E	λ	f	E	λ	f	main contribution
1	1A1	1.489	832.6	0.315	1.415	876.0	0.385	1.436	863.8	0.368	H(93) → L(94) (100%)
7	1A1	2.931	423.0	0.153	2.950	420.3	0.303	2.974	416.9	0.324	H-3(90) → L(94) (91%)
9	1B2	2.983	415.7	0.009	2.962	418.6	0.011	2.966	418.0	0.008	H-5(88) → L(94) (92%)
13	1A1	3.586	345.8	0.096	3.691	335.9	0.121	3.719	333.4	0.122	H-8(85) → L(94) (91%)
15	1B2	3.787	327.4	0.046	3.616	342.9	0.076	3.583	346.1	0.076	H-7(86) → L+1(95 (15%), H(93) → L+2(96) (75%)
17	1A1	4.133	300.1	0.121	4.135	299.9	0.240	4.132	300.1	0.250	H-2(91) → L+1(95) (96%)
20	1B2	4.364	284.2	0.005	4.294	288.8	0.007	4.274	290.1	0.006	H-13(80) → L+1(95) (19%), H-9(84) → L+1(95) (65%)

^aKS-HOMO (H) = MO 93; KS-LUMO (L) = MO 94.

^bExcited state (ES) numbering taken from gas-phase calculations.

Finally, the lack of an inversion center in the title complexes suggests a possible application of heteroleptic bis(1,2-dithiolene) complexes as second-order nonlinear optical (SONLO) materials. Prompted by the results obtained at TD-DFT level, since small geometrical differences can determine large differences in NLO properties,^38,39 we calculated static dipole moments (μ) and static first (quadratic) hyperpolarizabilities (β_tot) for 3 in the gas phase and in CH₂Cl₂ and CHCl₃ solutions (Table S10).¹⁰⁹ Calculations were also carried out at the DFT-BS level (Table S10) in the gas phase. For the sake of comparison, the same calculations were also undertaken, at the same level of theory, on [Pt(phen)(tdt)] (phen = 1,10-phenanthroline; tdt^2– = 3,4-toluenedithiolate; Chart S2), a neutral diimine-dithiolate Pt complex showing a very large hyperpolarizability value among those investigated experimentally by means of EFISH measurements (λ_max = 583 nm; β_μ = −28 × 10^–30 esu with ω = 1.569 × 10¹¹ GHz; zero-frequency β₀ = −16 × 10^–30 esu).⁷¹ In agreement with the charge distribution within complex 3, the μ vector lies along the molecular z axis and β shows only tensor z components. As previously observed for different heteroleptic metal complexes containing 1,2-dithiolato ligands,⁶² a dramatic increase in β_tot was calculated when solvation is taken into account (|β_tot| = 37.6 × 10^–30, 475.6 × 10^–30, and 330.5 × 10^–30 esu in the gas phase, CH₂Cl₂, and CHCl₃, respectively). In addition, when the diradical character of 3 is evaluated at the DFT-BS level, the β_tot value dramatically increases (177.4 × 10^–30 esu in the gas phase), reaching the same order of magnitude computed for [Pt(phen)(tdt)].

Conclusions

DFT calculations have been exploited to investigate the structural and spectroscopic features of the heteroleptic mixed-ligand neutral complex Pd^II bis(1,2-dithiolene) 3, to highlight the differences between the homoleptic related complexes 1 and 4 and to develop sound structure–property relationships. The closed-shell (CS) description is only partially suitable to describe the electronic structure of bis(1,2-dithiolene) complexes, and—whatever the nature of the ligands—the singlet diradical character (DC) must be taken into account. The broken-symmetry (BS) approach within DFT, although itself a dramatic approximation underestimating the DC of bis(1,2-dithiolene) metal complexes, is a useful tool in supplementing the description of the ground state (GS). A few general conclusions can be drawn

• (1)The nature of the 1,2-dithiolene ligand is responsible for the relevance of diradical character (DC) in the GS of 1,2-dithiolene complexes. In homoleptic neutral bis(1,2-dithiolene) complexes, on passing from complex 4 to complex 1, the n_DC index is roughly doubled. This can be related to the capability of the ligands mnt^•– and Me₂timdt^•–, respectively, to stabilize the unpaired electron. In heteroleptic mixed-ligand complexes, the absolute one-electron-reduction potentials E_Abs^298K calculated for the L/L^•– and L′/L′^•– couples can be used to evaluate the nature of the [Pd^II(L)(L′)] complex. The 1,2-dithiolene ligand displaying the largest reduction potential (“pull” ligand) features its π-NBMO at lower energy and contributes largely to the KS-HOMO of the heteroleptic complex, while that with the lowest potential (“pull” ligand) contributes to the KS-LUMO. As a consequence, it is conceivable that the difference ΔE_Abs in the absolute reduction potentials of the ligands L and L′ can be adopted as a useful parameter to estimate the push–pull nature of the resulting heteroleptic neutral complexes [Pd^II(L)(L′)] and the different localizations of the KS-HOMO and KS-LUMO. A larger push–pull character points to a larger dithione-dithiolato nature and a lower DC of the complex. This implies that the DC is the largest in homoleptic bis(1,2-dithiolene) complexes [Pd^II(L)₂] with ligands L featuring low values of E_Abs^298K, such as Me₂timdt, and decreases in heteroleptic complexes [Pd^II(L)(L′)] in dependence on ΔE_Abs.
• (2)Several authors have observed that metal–sulfur bond lengths optimized at the DFT level are slightly overestimated in comparison to structural bond distances. This can be attributed to the use of RDFT calculations in complexes featuring a significant DC. The DFT-BS approach leads to bond distances closer to the structural distances. It can be deduced that, in the case of complexes with a large DC, such as complex 1, the difference between CS-optimized distances and the relevant experimental metric parameters increases with the DC of the complex.
• (3)The spectral shape of the NIR band of neutral bis(1,2-dithiolene) metal complexes has been indicated to be a complex envelope resulting from a series of d–d transitions with different spin couplings to the open-shell ligands. The intensity of this band, peculiar to metal bis(1,2-dithiolene) complexes, may be attributed not only to the very large oscillator strength f calculated for the HOMO–LUMO one-electron excitation within a CS description but also to the contribution of double exciton states typical of diradical species. To a lower extent, double exciton states are possible also in heteroleptic bis(1,2-dithiolene) complexes and can be related to the spectral shapes observed for the NIR band in different solvents.
• (4)The intrinsic optical nonlinearity of heteroleptic bis(1,2-dithiolene) complexes is enhanced by their DC, providing a further criterion, in addition to the lack of an inversion center and large electric dipole moment values, for the rational design of NLO materials active in the vis–NIR region.

Summarily, this investigation shows that the DC of bis(1,2-dithiolene) metal complexes can be extensively modulated by means of the choice of the substituents R at the 1,2-dithiolene core, allowing for the rational design of the linear and nonlinear optical properties of the resulting complexes and hence the possibility of applying them in fields as varied as nonlinear optics, photoconductivity, and electrochromism.

Further studies are ongoing in our laboratory to investigate in detail the role of the central metal ion and to generalize the limited findings described here for the Pd^II complexes with the mnt and Me₂timdt ligands to other homoleptic and heteroleptic bis(1,2-dithiolene) complexes differing in the nature of the central metal ions and 1,2-dithiolene ligands.

Glossary

Abbreviations

BS

broken symmetry

CS

closed shell

DC

diradical character

GS

ground state

MO

molecular orbital

HOMO

highest occupied molecular orbital

KS

Kohn–Sham

LUMO

lowest unoccupied molecular orbital

NBMO

nonbonding molecular orbital

NLO

nonlinear optics

SONLO

second-order nonlinear optics.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.0c02696.

• Details on theoretical calculations, molecular schemes for the compound discussed in the paper, crystallographic data and packing details for complex 3, experimental UV–vis–NIR spectra decomposed into their component Gaussian peaks, NIR spectra in MeCN, DMF, THF, CH₂Cl₂, and CHCl₃, KS frontier MO drawings calculated for Me₂timdt^q–, mnt^q– (q = 0, 1, 2), and complex 3, RDFT, DFT-BS, and (IEF-PCM) TD-DFT data for 1 and 3, and calculated second-order hyperpolarizabilities β and dipole moments μ (PDF)

Accession Codes

CCDC 2027023 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.

Author Contributions

The manuscript was written through contributions of all authors.

The authors declare no competing financial interest.