Abstract
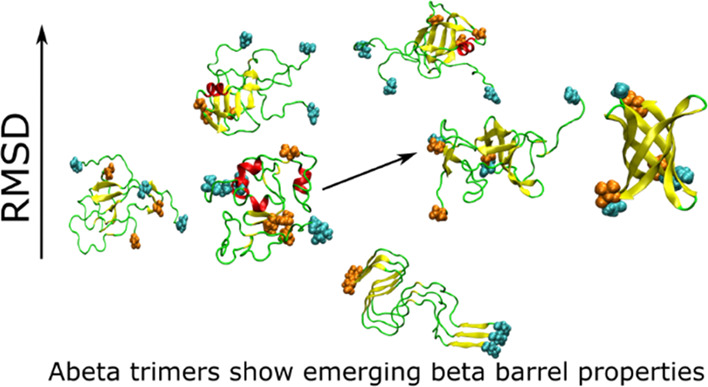
Amyloid-β (Aβ) peptides form assemblies that are pathological hallmarks of Alzheimer’s disease. Aβ oligomers are soluble, mobile, and toxic forms of the peptide that act in the extracellular space before assembling into protofibrils and fibrils. Therefore, oligomers play an important role in the mechanism of Alzheimer’s disease. Since it is difficult to determine by experiment the atomic structures of oligomers, which accumulate fast and are polymorphic, computer simulation is a useful tool to investigate elusive oligomers’ structures. In this work, we report extended all-atom molecular dynamics simulations, both canonical and replica exchange, of Aβ(1–42) trimer starting from two different initial conformations: (i) the pose produced by the best docking of a monomer aside of a dimer (simulation 1), representing oligomers freshly formed by assembling monomers, and (ii) a configuration extracted from an experimental mature fibril structure (simulation 2), representing settled oligomers in equilibrium with extended fibrils. We showed that in simulation 1, regions with small β-barrels are populated, indicating the chance of spontaneous formation of domains resembling channel-like structures. These structural domains are alternative to those more representative of mature fibrils (simulation 2), the latter showing a stable bundle of C-termini that is not sampled in simulation 1. Moreover, trimer of Aβ(1–42) can form internal pores that are large enough to be accessed by water molecules and Ca2+ ions.
Introduction
The extracellular accumulation of amyloid-β (Aβ) peptide is the main pathological hallmark of Alzheimer’s disease (AD).1−4 Recently, among aggregation forms of Aβ, small soluble oligomers have been determined as the most neurotoxic species rather than mature fibrils.2,5,6 Experimental evidence revealed that oligomers can cause neurotoxicity,6−8 induce membrane disorder and pores,8,9 and inhibit hippocampal long-term potentiation.2 Therefore, characterizing the assembly process of Aβ peptides into oligomers is crucial to get insight into the early steps of AD.
Oligomers are soluble aggregation forms of Aβ that consist of 2 to about 32 monomers.7 In contrast to mature fibrils, oligomers are partially disordered,10,11 but not as ordered as fibrils,12,13 which suggests that a radically structural change occurs in the transition from oligomers to fibrils. Therefore, the study of the oligomerization process is important to understand not only neurotoxicity, but also how the fibril forms. Structural studies of Aβ oligomers by experiment are difficult due to their transient nature, since they occur as intermediates along the aggregation pathways. Therefore, stabilization of oligomers inhibiting the progression to fibrillar structures requires either chemical modifications14,15 or specific solvent conditions.16 In this situation, molecular dynamics (MD) simulation becomes a useful tool for obtaining the molecular structures of oligomers with no constraints, oligomerization pathways, and the relevant physicochemical properties. Replica exchange MD (REMD)17 show that the content of secondary and tertiary structural elements strongly depends on the force field, water model, and sampling.18−24 However, most of computational studies20,21,23,25 have reached a general consensus that, in agreement with recent NMR26 and FRET27 experiments, Aβ monomers adopt random coil structures at physiological conditions. The smallest Aβ aggregates associated with neurotoxicity are dimers28 whose structures have been extensively studied using MD simulations.29−33 There are variations between the results reported by different groups, but in general, the dimer structure is more compact with much lower β content compared to mature fibrils. The Aβ42 tetramer was studied using a multiscale approach, where the most representative structures, obtained by coarse-grained REMD simulations, were refined by all-atom simulations.34 Polymorphic stable structures were obtained providing an insight into various pathways of Aβ aggregation. The computational models comprise the outer and core chains and, therefore, they are significantly different from the structure of mature fibrils.34 Moreover, the interaction with the water solvent is the reason why the tetramer is more compact and less dry inside than fibrils.
Truncated Aβ(17–42) trimers in solution were investigated using OPEP coarse-grained model and REMD,35 while all-atom models were applied to study binding of protofibrillar Aβ(17–42) trimers to lipid bilayer surface.36 As a toxic agent, the full-length Aβ(1–42) trimer plays an important role in understanding the cause of AD10,37−39 and Aβ aggregation,40 but its structure has not been investigated using all-atom REMD simulation, which is considered the most accurate sampling technique. Moreover, in previous works, REMD simulation of small oligomers was started with protofibrillar structures,36,41,42 and it remains unclear to what extent the initial configuration affects the result, since this matters even for Aβ monomers.43 To assess how the initial structures affect the results for trimers, in this article, we study the Aβ(1–42) trimers using the CHARMM36m force field and TIP3P water model (see the Material and Methods section) using two sets of simulations: in simulation 1, the initial structure includes three random chains preassembled according to docking methods, while in simulation 2, the REMD run started with a fibrillar structure. Simulation 1 models the behavior of a trimer formed by early events in molecular association, while simulation 2 models events closer to dissociation of a stabilized trimer.
The issue of occurrence of a barrel structure in Aβ oligomers has been widely debated, as it may be related with the formation of an ion channel in a lipid bilayer,44 which would lead to the penetration of Ca2+ ions into the cell, causing toxic effects. Combining ion-mobility mass spectrometry, electron microscopy, atomic force microscopy, and computational modeling, Eisenberg et al. demonstrated45 that Aβ fragments with a length of 11 residues (residues 24–34, 25–35, 26–36) can form cylindrin-like barrels of tandem repeats held together by two glycine residues. To check whether a similar structure can occur in the full-length Aβ oligomers, Xi et al.46 built barrel-shaped structures consisting of β2-turn-β3 domains (residues 27–42) and showed that they are stable in Aβ(1–42) trimers and tetramers after at least 200 ns of all-atom MD simulations. Preformed tetrameric Aβ(1–40) and Aβ(1–42) β-barrel structures made of eight antiparallel β-strands covering residues 9–40/42 with two distinct β-hairpin types and an inner pore diameter of 0.7 nm were transiently populated in an extensive REMD simulation with four atomistic force fields and an aqueous solution.47 Therefore, the question of whether we can observe the barrel structure in MD simulations starting from the initial configuration without preformed cylindrin-like barrels remains open. Note that porelike conformations but not barrels were sampled in Aβ(1–40) and Aβ(1–42) oligomers obtained using MD simulation with random initial conformations.48
Our results showed some similarities and differences between the structures obtained in the two sets of simulations. In both simulations, Aβ(1–42) trimers are compact and much less structured than mature fibrils. Consistent with Voelker et al.,48 they form pores with a radius of 1.7–2.1 Å, suggesting molecules like water and Ca2+ ions can pass through them. In simulation 1, where the simulation began with random configurations, for the first time, we obtained trimer structures containing small β-barrels, but no barrels were found in simulation 2.
The C-terminus of the structures obtained in simulation 2 is more rigid than in simulation 1. But in both simulations, the C-terminus is more stable than other regions, which implies that aggregation may initiate from this terminus. Summing up, with limited simulation time, the initial conformations can affect the structure of Aβ oligomers and caution should be used in interpreting the simulation results.
Early detection of toxic oligomers is a goal of prevention in Alzheimer’s disease, and structural models of early species are required to understand all of these efforts. For instance, Raman spectroscopy was used to explore the structure and mechanism of formation of Aβ(1–42) fibrils49,50 and to detect Aβ(1–40) isoform in various conformational states.51 Tip-enhanced Raman spectroscopy was utilized to distinguish between the nontoxic and toxic forms of oligomers of misfolded HypF-N protein, which indicates a significantly higher content of hydrophobic aromatic residues on the surface of the toxic form compared with the nontoxic one.52 Moreover, solvent exposure of Tyr10 in toxic Aβ oligomers has been proven greater than that in nontoxic oligomeric forms53 as well as in mature fibrils,54 paving a way to use this effect to probe the structural differences between various forms of Aβ aggregates. Our simulations showed that, in agreement with the experiment, in the fibrillary state, aromatic amino acid residues are shielded from solvent to a greater extent than in the oligomeric state. Since in this work we are dealing with the full-length Aβ(1–42), for clarity, Aβ42 will be used instead of Aβ(1–42).
Material and Methods
Simulation Protocol
We performed two independent REMD simulations using, respectively, two different initial structures (Figure 1). For one simulation, we used the lowest-energy structure obtained by docking Aβ42 dimer structure from Zhang et al.30 and nine monomer configurations of Aβ42 from Yang et al.55 The trimer structure with the lowest energy was chosen as the initial structure (simulation 1, hereafter). For the second simulation, we extracted chains ABC from the fibril structure of Aβ4212 (PDB code 2NAO) as the initial Aβ42 trimer structure (simulation 2, hereafter).
Figure 1.
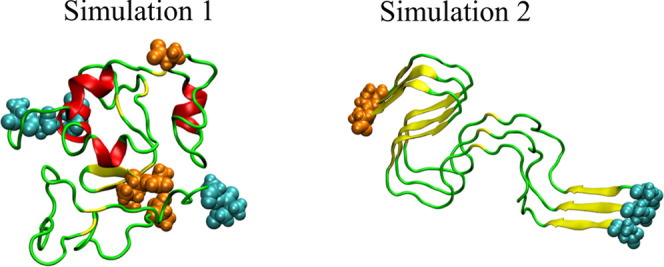
Initial structures for REMD simulations 1 (left) and 2 (right). The N-termini and C-termini atoms are shown as cyan and orange spheres, respectively.
The simulations were performed with GROMACS56 2018.2 package. The force field CHARMM36m57 was used for peptides parameterization. The force field has been demonstrated as a good representation for intrinsically disordered proteins.57 The initial structures of trimer were solvated in dodecahedral box of TIP3P58 water with the minimum distance between solute trimer and the box edge 1.8 nm. The concentration of Aβ42 was about 8 mM. The minimal amount of counterions was added to the solvated systems for neutralization. The systems were relaxed by steepest descent algorithm. Then, the systems were equilibrated in the NVT ensemble for 1 ns at the temperature T = 300 K followed by 5 ns NPT ensemble simulation at the pressure P = 1 atm. The temperature and pressure of systems were kept constant by v-rescale59 and Parrinello–Rahman60 algorithms, respectively. The cutoff for Coulomb interactions was 1.2 nm, and the particle-mesh Ewald (PME) algorithm61 was used for long-range interactions. As for van der Waals interactions, we used a cutoff switching between 1.0 and 1.2 nm. After the systems were equilibrated, REMD simulations were carried out with 72 replicas. Temperature was assigned to replica62 choosing values in the range of 299.00 to 410.30 K. Exchange between adjacent replicas was attempted every 1000 steps, and temperatures were slightly adjusted to have an exchange rate of about 20–25%. The time step was 2 fs, and the bond length between H atoms and non-H atoms were kept rigid with the LINCS algorithm.63 The simulation time for each replica was 600 ns. Configurations were saved every 20 ps, and the last 15 000 configurations (300 ns) were used for analysis.
We also performed one trajectory of conventional MD simulation at 300 K using the same initial structure as in REMD simulation for three chains of 2NAO. To preserve the fibril conformation, we applied restrains to Cα atoms with spring constant k = 1000 kJ/mol/nm. The setup parameters are the same as REMD simulations, except that the time length of simulation is 20 ns. The RMSD of Cα is about 0.08 nm, indicating that the system changes insignificantly. In this work, we used the last 10 ns of the simulation for data analysis.
Structural Analysis
A contact is assumed when the distance between centers of mass of two side chains is smaller than or equal to 6.5 Å. The STRIDE algorithm64 was used to calculate the secondary structure of peptide conformations. The hydrophobic solvent-accessible surface area (hSASA) is the surface area of hydrophobic residues. In this work, hydrophobic residues are glycine (Gly), alanine (Ala), valine (Val), leucine (Leu), isoleucine (Ile), proline (Pro), phenylalanine (Phe), methionine (Met), and tryptophan (Trp). The gmx sasa65 module of the GROMACS package was used to calculate hSASA.
To measure shape anisotropy,
trimer Aβ42 structures were approximated as an ellipsoid with
semiaxes a, b, and c. When c < a, the ellipsoid
is an oblate spheroid, while when c > a, it is a prolate spheroid. The eccentricity is calculated
from equation  when c < a and
when c < a and 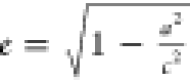 when c > a. The semiaxes are calculated from the three
eigenvalues, I1, I2, and I3, of the inertia tensor,
according to
when c > a. The semiaxes are calculated from the three
eigenvalues, I1, I2, and I3, of the inertia tensor,
according to
| 1 |
The trimer mass m = 13518 g/mol. The height of the trimer is twice the smallest semiaxis. To represent molecular anisotropy, we also calculated the ratio between the smallest and the largest inertia eigenvalues. This ratio is multiplied by 10 and rounded to the nearest integer to provide an anisotropy index (RI) between 1 and 10.
The molecular dipole is calculated with the point charges of the force field, using the center of mass of the trimer as the reference for atomic positions and the inertia principal axes as reference frame.34 The dihedral angles of trimer Aβ42 are analyzed by the dihedral principal component analysis (dPCA) method.66 Then, the free-energy surface is constructed from the first two components. The free energy is defined as
| 2 |
with P the probability and Pmax the maximal probability of the point in the two-dimensional space.
We used the k-means method for clustering structures,67 and the number of basins of the two-dimensional free-energy landscape (FEL) was obtained by the silhouette method.68 These methods are implemented in RStudio software.
The MOBCAL software69,70 was used to estimate the collision cross section (CCS), which characterizes the ion mobility of Aβ42 trimer using the trajectory method (TM) with the effects of ion-induced interactions included. Theoretical CCS values are very useful for the comparison with experimental results, though they are difficult to interpret independently.71
Assembly Structure and Water Penetration
To determine and calculate the size of pores in trimer configurations, we used the MOLE software.72 Parallel disks are drawn at the entrance and exit of cavities. A segment is drawn connecting the centers of the disks. The radius of the pore is the distance from the segment connecting disks and the nearest atom.
The β barrel was assigned using the method proposed by Murzin et al.73,74 Aβ barrel is formed when at least one β-strand of the barrel does not have side-chain contacts with one of its neighbors. The shear number S is calculated by rotating the barrel around an axis perpendicular to the strands until the original coordinates of the first strand (strand 1) are overlapped. The absolute value of the difference between the terminal and initial residues of strand 1 is the shear number S.
To measure water penetration, we built a convex hull in trimer configurations using quick hull algorithm.40,75 Then, based on the built convex hull, we constructed a concave hull by an algorithm proposed by Park and Oh using threshold 5.76 The water molecules inside this concave hull are counted as internal water molecules.
The hydropathy index of each residue is obtained from the study of Kyte and Doolittle.77 A comparison between collected configurations and some reference structures was performed calculating root-mean-square deviation (RMSD). Fibril structures used as reference are 5OQV,785KK3, 2MXU,792NAO,12 and 2BEG.80 The atoms used in RMSD calculations are the backbone atoms of corresponding sequences in three chains of Aβ42 fibrils. In twofold symmetry structures, we extracted three chains from one side of the structure, i.e., from the asymmetric unit. To calculate RMSD between our trimer and the barrel structure 3SGO,81 we used regions 15–25 and 30–40 for structural alignment because these regions display the most structured β-strands. In the 3SGR case,81 we used region 16–40 for structural alignment for the same reason.
Results and Discussion
Difference in the Initial Conformations
We remind (see the Material and Methods section) that we performed REMD simulations 1 and 2 using, respectively, two different initial structures: (i) the first one obtained from a docking protocol and (ii) the second one obtained from three chains (ABC) in the fibrillar structure of Aβ42 (PDB ID 2NAO). We calculated the secondary structures and interchain contact maps of initial structures to investigate the structural difference between them. The secondary structure of initial conformations (Table 1) indicates that trimer Aβ42 structures from 1 and 2 are significantly different. The β-structure of 1 is low (8.73%), while in 2, it is high (37.30%), which is consistent with the fact that 2NAO has no helix domains, while in docking conformation, the helix structure has significant population (15.08%). Furthermore, the extent of the turn in 1 is larger than that in 2.
Table 1. Secondary Structure (%) of Initial and Average (T = 300.38 K) Aβ42 Trimer Conformations. Errors (within Parentheses) Are Standard Deviations.
| simulation 1 |
simulation 2 |
|||
|---|---|---|---|---|
| structure | initial | average | initial | average |
| β | 8.73 | 24.87 (1.97) | 37.30 | 25.14 (2.39) |
| helix | 15.08 | 2.72 (0.30) | 0.00 | 1.45 (0.26) |
| turn | 53.17 | 23.95 (1.39) | 29.37 | 25.30 (1.73) |
| coil | 23.02 | 48.45 (1.70) | 33.33 | 48.11 (2.20) |
Similar to the secondary structure, the interchain contact map of initial configurations (Figure S1) shows that the three chains in 1 arrange differently from the three chains of 2NAO (in 2). In the case of docking structure 1, the distribution of contacts is sparse. The regions showing mutual interactions are 10–20 and 30–40 (residue numbers). On the contrary, in the three chains of 2NAO, the contacts concentrate along the diagonal and between 15–28/25–35. This result comes from the ordered arrangement of chains in the fibril structure (Figure 1), in which the chains align parallel to each other because of extended hydrogen bonds between backbone atoms in flanking β-strand regions. The total hydrophobicity index of residues that form interchain contacts of 1 and 2 are, respectively, 153.4 and 169.3. This result indicates that the interface between chains in 2NAO is more hydrophobic than in docking structure, which is reasonable because chains in a fibrillar structure as 2NAO are arranged in a stable state, with optimal attractive interactions, while the docking structure represents an initial not yet stable encounter complex.
Convergence of the Simulations
To investigate the convergence of the REMD simulations, we calculated the configurational entropy for replicas in two time windows, 300–600 and 450–600 ns. The result (Figure S2) shows that the difference of entropy between these time windows is negligible, which indicates that the simulations converged. Furthermore, the calculation of heat capacity in two time windows (Figure S3) also indicates that there is no change after 300 ns. We also constructed FEL for two time windows. Their structures differ in some details, but overall they look quite similar (results not shown), which indicates that we have reached at least quasi-equilibrium. Therefore, in this work, we used configurations in the time window 300–600 ns for data analysis and T = 300.38 K.
Secondary Structures of Aβ42 Trimer
A comparison between the extents of the secondary motifs obtained by simulations (Table 1) indicates that, within errors, the secondary structure displays a small difference between REMD simulations 1 and 2. Therefore, despite the difference displayed by the initial structures (Table 1 and Figure 1), the average secondary structure of the trimer in water solution is not significantly affected by initial conditions. The β-strand content in both systems (Figure 2) is high in regions 15–20 and 30–40. However, in 1, the β-structure of chains is different from that in 2 (Figure 2): the C-terminus of the trimer obtained from 2NAO has sharp peaks in the distribution, while in the docking case, the peaks are curly. Both systems display a low extent of helix. The total average of β-strand and helix structure (≃27%) is lower than the total amount of disordered motifs (turn and coil, ≃73%) in both REMD simulations (Table 1), which indicates that Aβ42 trimer is mostly in disordered state. This result is consistent with experimental data10 as well as with computational studies for other low-weight Aβ oligomers.34,82 Moreover, the secondary structure of the two REMD simulations differs mostly in the C-terminal region, suggesting the high persistence of this terminal in the structure of the Aβ42 trimer, once a bundle of the C-termini is formed, as in the 2NAO structure or in other mature fibrillar structures.
Figure 2.
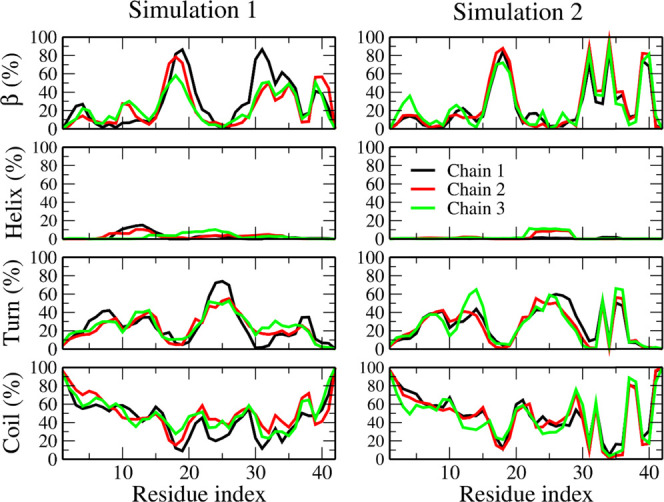
Distribution of secondary structures of chains of Aβ42 trimer at 300.38 K, averaged in the last 300 ns of simulations.
Shape of Trimeric Structures
Because the distribution of secondary structures is similar between the two REMD simulations 1 and 2, we investigated the shape of trimer structures using the anisotropy index RI (see the Material and Methods section). The structure is defined as compact when RI > 5 and as an extended conformation when RI ≤ 5. The ratio of compact conformations from simulation 1 is 0.77 ± 0.06, while for 2, it is 0.66 ± 0.02, which means that the trimer structures obtained from simulation 1 are more compact than the structures obtained from three chains of 2NAO (2). The eccentricity values are 0.81 ± 0.09 (a > c) and 0.83 ± 0.08 (a > c) for 1 and 2, respectively, indicating that Aβ42 trimers have a oblate spheroid shape. These eccentricity values are equivalent to cluster 3 of the Aβ42 tetramer obtained from UNRES model,34 suggesting that the Aβ42 trimers and tetramers have a similar discoidal shape.
Hydrophobic Solvent-Accessible Surface Area (hSASA) and Raman Spectroscopy
The hSASA values in both simulations are equivalent within the error bars (Table 2), suggesting that the compaction of hydrophobic residues in the two systems is the same. The hSASA of trimeric structures is similar to the hSASA of Aβ42 tetramer in the OPLS force field but less than that in the AMBER force field from our previous simulation.34 Thus, hSASA is highly dependent on the choice of force field. However, the hSASA of trimer structures in this work is smaller than or equivalent to the tetramer in the AMBER and OPLS force fields because the number of chains in the trimer is smaller than in the tetramer.
Table 2. Average hSASA, Height, and CCS of Aβ42 Trimer Obtained at T = 300.38 K.
| simulation 1 | simulation 2 | |
|---|---|---|
| hSASA (nm2) | 38.91 (2.91) | 36.46 (3.08) |
| height (nm) | 2.15 (0.22) | 2.03 (0.23) |
| CCS (nm2) | 18.15 (1.03) | 17.96 (1.10) |
Errors (within parentheses) are standard deviations.
To compare the solvent exposure of residues in the Aβ42 trimer and in fibrils, we calculated the ratio between the SASA values of the residues in the trimer, fibrils (2NAO), and free amino acids. In the fibril case, we considered only residues in the core chains, neglecting the first and the last chains because in a real fibril the number of core chains increases with the fibril size. Residues in the trimer have a larger solvent exposure than fibrils (Figure 3), with the exception of Tyr 10, Gly 9, and Ala 21. This result is reasonable since we calculated SASA for the core chain of fibrils. In fibrils, residues Phe 19, Phe 20, Gly 29, Ala 30, Ile 31, Ile 32, Gly 33, and Val 39 are completely shielded from solvent access (Figure 3), which is a consequence of assembly of chains into a hydrophobic core.
Figure 3.
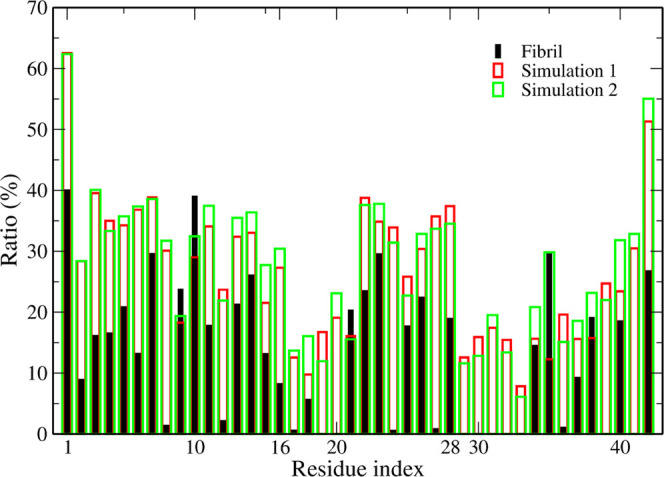
Ratio between SASA of residues and free amino acid molecules (see the Material and Methods section). Aβ42 trimer simulation 1 (green); Aβ42 trimer simulation 2 (red); three chains of 2NAO structure (black).
Because the binding sites of metal ions, such as Zn(II) and Cu(II), are mainly in the N-terminal region,83,84 the low solvent exposure of residues in fibril suggests that the binding of these ions to the fibril is more difficult than to oligomer. Aran et al. observed that in Aβ42 oligomers and monomers, Tyr10 is more solvent-exposed than in fibrils.54 Furthermore, using Raman spectroscopy, Yamamoto et al. determined the hydrogen bonding between tyrosine residues and the solvent.85 Based on the information of the network of hydrogen bonds, it is possible to find out whether tyrosine residues are buried or exposed to solvent. They found that tyrosine residues in the amyloid fibril formed by insulin are less solvent-accessible than in native insulin, which is in line with the Aβ result.54 However, these results are inconsistent with our results, which is probably a consequence of a smaller number of chains compared to experimental oligomer samples. To investigate this possibility, we calculated the SASA ratios for the Aβ42 tetramer using the simulation data from our previous work34 and for fibrils made of four chains extracted from the 2NAO structure (Figure S4).
The 2NAO fibril, previously studied,34 does not have a core chain since it consists of two branches with two chains per branch. Therefore, we calculated the average SASA ratio for four chains in the tetrameric and fibrillar systems. In both force fields, the fibril system has no region that is shielded from solvent access (Figure S4), which is reasonable because there is no core chain in this structure. Nevertheless, the solvent exposure of Tyr10 in the fibril case is slightly smaller than that of a tetramer with the AMBER force field, and this residue is significantly screened from water access in fibrils with the OPLS force field. These results indicate that, as expected, the SASA ratio of residues depends on the number of chains and conformation of fibrils. We expect that as the number of chains extracted from fibrils to model oligomers increases (i.e., larger oligomers are modeled), the result for the computational SASA ratio will be more consistent with experiments.
Height, Collision Cross Section (CCS), and Intermolecular Nonbonded Interactions
The average height of trimers is about 2 nm in both simulations, which is consistent with experimental observation.86 In addition, the height of the Aβ42 tetramer obtained from the MD simulations is also about 2 nm,34 which indicates that low-order Aβ oligomers, like trimers and tetramers, have an equivalent height. This may be due to the fact that both trimers and tetramers are compact.
Within the error bars, both REMD simulations gave the same values of about 18 nm2 for CCS (Table 2). Although CCS of the trimer has not been experimentally determined, our result is reasonable as it falls between the values obtained by mass spectroscopic measurements for the Aβ42 dimers (≈12.5 nm2) and tetramers (≈23.3 nm2).39
We calculated the nonbonded interaction energies between the chains in the trimer (Table 3). In both cases, the electrostatic interaction dominates the van der Waals (vdW) interaction. This result differs from the Aβ42 tetramer,34 in which vdW interactions play a dominant role. Although the force fields used in this and the previous study are different, the number of chains probably decides which interaction is more important, but not the choice of force field. A smaller number of chains in the trimer allows monomers to more easily organize their mutual orientation and interactions. As a result, the electrostatic energy in the trimer can take a more negative value than in the tetramer.
Table 3. Average Interchain Interaction Energy (kcal/mol) for Different Components of the Aβ42 Trimer Obtained at T = 300.38 Ka.
| simulation 1 | simulation 2 | three chains of 2NAO with restrained Cα atoms | |
|---|---|---|---|
| electrostatic | –217.08 (66.90) | –347.30 (88.20) | –334.75 (0.28) |
| van der Waals | –126.42 (22.60) | –155.89 (20.75) | –202.63 (5.17) |
| total | –343.50 (89.50) | –503.19 (108.95) | –537.38 (55.45) |
Errors (within parentheses) are standard deviations.
As in the mechanism of aggregation that we proposed,34 the lower the weight of the oligomer, the easier it is to minimize the electrostatic repulsion between the chains at physiological pH, where the charge of Aβ42 is −3. Therefore, the lower electrostatic energy achieved by the trimer configurations compared to the tetramer is reasonable. Moreover, lower values of the intermolecular interaction between the monomers in the trimer than in the tetramer suggest that higher-order oligomers have stronger electrostatic repulsion, which is compensated by strong vdW attraction. This leads to a limited chance of organizing low-order oligomers before electrostatic repulsion between the monomers destroys the oligomer. The interaction in the 2NAO case, simulation 2 (−503.19 ± 108.95 kcal/mol), is lower than that of the trimeric structures from simulation 1 (−343.50 ± 89.50 kcal/mol) with t-test p < 0.0001, which is considered as statistically significant (Table 3). The difference comes from the electrostatic energy in 2NAO being lower than that in the docking case, while the vdW energies are the same in both REMD simulations. Furthermore, the interaction between three 2NAO chains with restrained Cα atoms is equivalent to that of the structures from simulation 2 within errors. This result indicates that the initial structure extracted from 2NAO is already stable. Intermolecular interactions of these cases are favorable, which indicates that the ordered arrangement in the Aβ42 fibril minimizes the electrostatic interaction, leading to stabilization of the assembled structure and allowing further fibril elongation. The conformation of the three chains used in this work was extracted from one side of 2NAO, while in our previous simulation,34 the tetramer extracted from 2NAO was made of two compartments that form a fibrillar unit along its elongation axis, with two chains per compartment. Thus, the intermolecular interactions in the trimer and tetramer with restrained Cα atoms are different, which caused a topological difference in the assembly of monomers into small oligomers.
C-Terminal of the Trimer Obtained in Simulation Using the Fibrillar Structure as the Initial Configuration Is Stable
Intrachain contacts around the turn region (residues 25–29, as displayed by Figure 4) are more extended in simulation 1 than in simulation 2. This extension is accompanied by an increase in the number of contacts between residues in the N-terminus (residues 1–16) compared to 2. On the other hand, a few long-range intrachain contacts that are displayed by simulation 2 and that stabilize the C-terminus are demolished in simulation 1.
Figure 4.
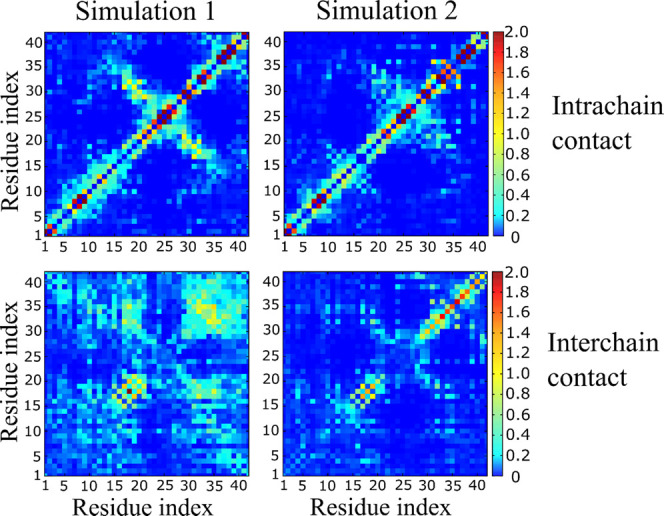
Intrachain (top) and interchain (bottom) contact map of the Aβ42 trimer at T = 300.38 K.
In terms of interchain contacts, 1 displays three regions with significant interactions: 30–42/30–42, 10–20/10–20, and 10–20/30–40. Especially, 30–35/30–35 and 15–20/15–20 regions display a large number of contacts. This map is similar to that displayed by the initial structure (Figure S1, left), but with more residues involved. This result is consistent with our previous work on Aβ42 tetramer34 and the results of Urbanc et al.87 and Barz et al.82 and confirms the importance of these interactions as emerging in early oligomers. In the case of 2, only the regions 15–20/15–20 and 30–42/30–42 have a significant number of interchain contacts, indicating that these regions are more stable compared to other regions. A much higher propensity for interactions in 15–20/15–20 and 30–42/30–42 regions, together with a lower probability of 10–20/30–40 contacts in 2 compared to 1 (Figure 4), is consistent with an important role of the persistent C-terminus and hydrophobic core in stabilization of Aβ42 fibrils. The above interpretation of the contact map is supported by the time dependence of RMSD of the trimer with respect to the initial structure (Figure 5). The sequence of Aβ42 is divided into three regions: the N-terminus of residues 1–15; central region, residues 16–29; and the C-terminus, residues 30–42. The total hydropathy indexes (see the Material and Methods section) of these regions are −25.3, −0.3, and 34.2, for the N-terminus, center, and C-terminus, respectively, indicating that the C-terminus is the area with the strongest hydrophobicity. Simulation 1 shows that all three regions have equivalent RMSD values (Figure 5) and the corresponding structures change dramatically during the simulation.
Figure 5.
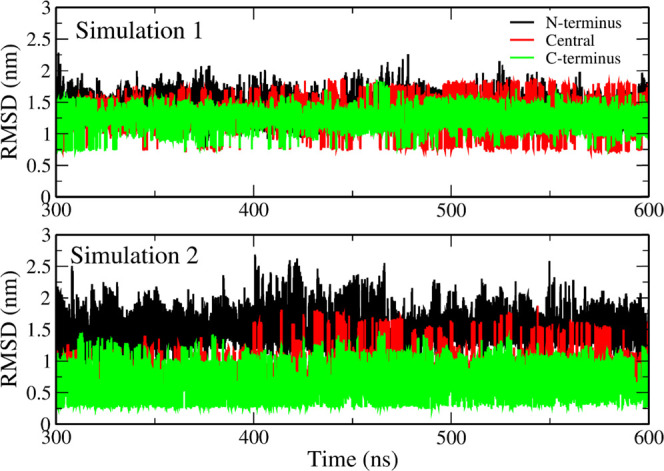
RMSD as a function of time (t) of the N-terminal (black curve), central (red), and C-terminal (green) regions of Aβ42 trimer at T = 300.38 K. The reference structures are initial conformations.
However, the C-terminus of the three chains in simulation 2 has a lower RMSD than the other regions (Figure 5), and the N-terminus has the highest RMSD. Therefore, the C-terminal region in three chains of 2 tends to keep the initial structure intact, which is different from the behavior in simulation 1. Since the hydropathy index of C-terminus is the highest, the hydrophobic interaction between residues strongly stabilizes this region. Furthermore, the initial three chains extracted from 2NAO (Figure 1) have a high interchain contact probability (Figure S1) and the structure of C-terminus bundle in the trimer simulated in 2 is stable.
We calculated a nonbonded interaction map of regions in various chains, including the N-terminus, center, C-terminus, and solvent (Figure 6, Tables S2, and S3). In both simulations, the interaction between the C-terminus and the solvent is the weakest, while the N-terminus has the strongest interaction with the solvent. This result is consistent with the hydropathy of the C-terminus, which is the highest, while the N-terminus is the most hydrophilic region. The interactions between the N-terminus and other components (Figure 6) are similar in both REMD simulations, suggesting that the initial structure has a negligible effect on the behavior of the N-terminus region. The total energy for the interaction between the central regions of the different chains in 2 is lower than that in 1, but the nonbonded interaction between the central and C-terminal regions in 2 is higher than that in 1.
Figure 6.
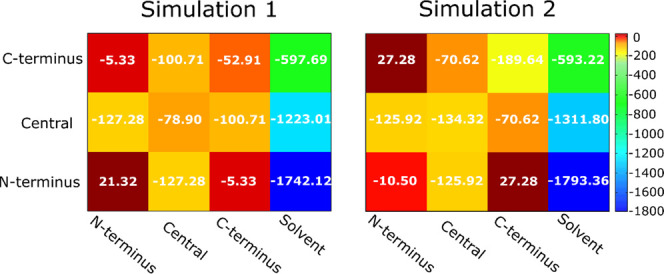
Sum of electrostatic and van der Waals energy (kcal/mol) for regions of different chains and solvent at T = 300.38 K. The numbers within the squares are the average values, while the color coding indicates the scale. The values of electrostatic and van der Waals components and their standard deviations are reported in Tables S2 and S3.
In both REMD simulations, nonbonded interactions between the central and N-terminal regions are equivalent. The interactions between the C-termini of the various chains in simulation 2 are much stronger than that in 1 (Figure 6). The vdW interaction between the C-termini in 2 is less than those in all other cases. These results are consistent with the highest hydropathy index, and consequently the weakest interaction with water, of the Aβ42 C-terminus, which favors self-interaction. Taken together, in simulation 2, the C-termini extracted from the fibrillar structure are stable due to the strong interactions between them and their weak interaction with water.
Free-Energy Landscape of Aβ42 Trimer: Emergence of Barrel Motif
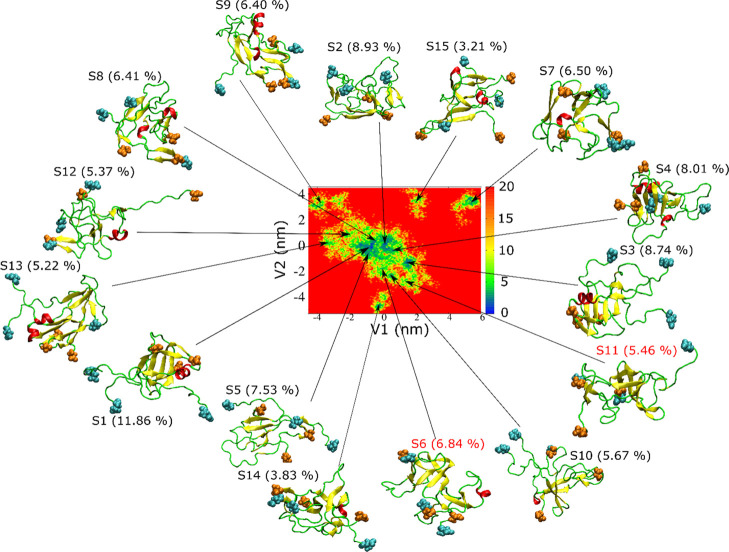
Using the dPCA method (see the Material and Methods section), we constructed FEL for the Aβ42 trimer in two simulations (Figures 7 and 8). FEL is complex and consists of 15 and 12 basins for 1 and 2, respectively. In simulation 1, all characteristic structures are in disordered conformations. β-Strands are present in most representative structures, but they are not long enough to form a cross β-structure as in mature fibrils.13
Figure 7.
Free-energy landscape of the Aβ42 trimer and representative structures obtained from REMD simulation 1. The N-terminal and C-terminal residues are shown as cyan and orange spheres, respectively. V1 and V2 are the first two dPCA eigenvectors (see the Material and Methods section). A β-barrel is present in S6 and S11 (red).
Figure 8.
A barrel-shaped structure was experimentally observed in an oligomer of αB crystallin81 and hexamer of Aβ C-terminal fragments.45 Shafrir and co-workers presented the Aβ42 hexamer in the barrel form with a C-terminus in the core of the barrel.88 Serra-Batiste et al. found that the Aβ42 oligomer forms a barrel in a membrane-mimicking environment.89 These results indicate that a barrel motif is accessible to low-weight oligomers. The stability of preformed barrel structures in full-length Aβ trimers and tetramers was computationally probed.46,47 We again emphasize that the barrel-shaped structure was never observed in previous computational studies, where simulation was started with conformations without barrels.
Interestingly, we found that the structures S6 and S11 obtained in simulation 1 (Figure 7) have a β-barrel-like structure (Figure 9). To investigate whether these structures satisfy the criteria of β-barrel, we used the definition described in the Material and Methods section. The number of strands in β-barrels is six for both structures S6 and S11, while the shear number S = 8 for clusters 6 and 11 (Figure 9). Therefore, structures S6 and S11 have the same class of β-barrels. However, the barrel displayed by structure S6 is partially open, while the barrel in S11 is closed. The residues involved in these two β-barrel structures are shown in Table S4. The average diameter of β-barrel formed in simulation 1 is 12.2 ± 2.2 Å; thus, it is smaller than that reported by Jang et al., 17–25 Å.42,90,91 This difference is due to the larger number of monomers (16–24) in previous studies90,91 compared to our work. The average β-barrel diameter obtained in this work is slightly larger than the inner pore diameter of 7 Å observed by Serra-Batiste et al.,89 but this difference arises from a different definition: in this work, we calculated the mean diameter of barrel using interatomic distances, while in ref (89), the inner diameter of the space inside the barrel was calculated. Thus, a difference of about 2 vdW radii is reasonable.
Figure 9.
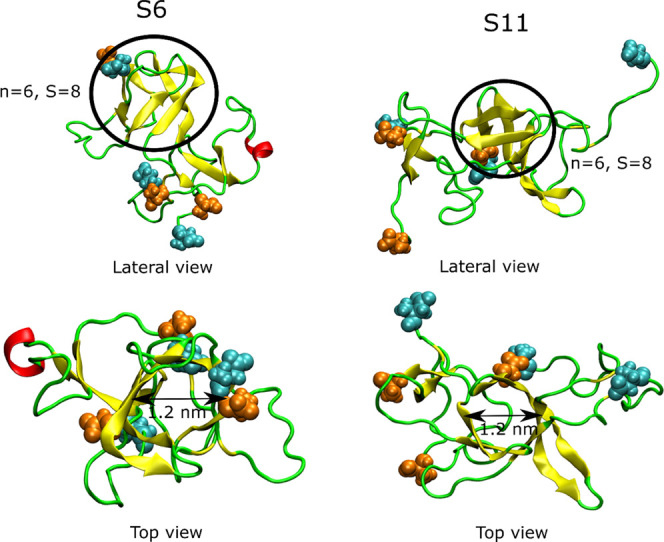
β-Barrel in clusters S6 and S11 of simulation 1, n is the number of β-strand in barrel, and S is the shear number. The atoms of the N-terminal and C-terminal residues are in cyan and orange, respectively.
Although the population of each cluster 6 and 11 is smaller than that of cluster 1, the total population of the former two clusters is 12.30%, which is greater than that of cluster 1 (11.86%). Therefore, the probability of the presence of β-barrel in the trimer structures obtained from simulation 1 is significant. The nonbonded interaction energies of structures S6 and S11 are not the lowest among all structures, indicating S6 and S11 as the local minima of potential energy.
The formation of the β domain is facilitated by the formation of a β-turn-β hairpin motif with intrachain contact between the N- and C-termini of each chain, together with the formation of interchain contacts between the N- and C-termini. Consequently, the C-terminus bundle in the 2NAO structure, which is mainly due to interactions between the parallel C-termini of different chains, is broken in simulation 1, while it is kept in simulation 2 (Figure 5). This happens in our model construction, that is, the choice of initial configurations: the docking selection of the monomer and the dimer, mimicking a first-encounter trimer, has more chances to mutually orient the N- and C-termini of each chain to form a seed of β hairpin motifs that evolves into trimers resembling a small β-barrel structure (Figure 7 compared to Figure 8).
The fibrillar bundle of parallel C-termini evolves in a draft of parallel C-termini intercalated by antiparallel N-termini, that is, the topology proposed in ref (89) for Aβ42. A good agreement of barrel diameter between our work and ref (89) is consistent with the convergence of both models toward the same-chain arrangement. In our work, we show that three chains can be the minimum number to allow the appearance of this kind of topology and trigger an assembly pathway alternative to fibrillar aggregation.
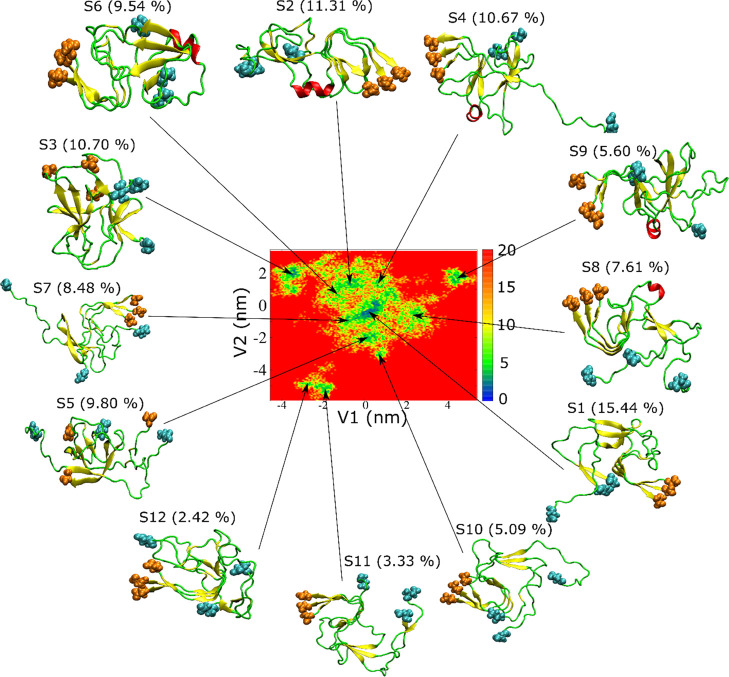
In the case of the Aβ42 trimer obtained from REMD simulation 2, the range of V1 and V2 is not as wide as in 1 (compare Figures 8 to 7). We obtained 12 basins from clustering FEL from 2. The characteristic structures displayed in Figure 8 are more disordered than the initial structure (Figure 1, right), which is a consequence of the release of interactions present in the fibril during the simulation. This release is mainly due to the extraction of three chains from the infinite-length fibril. As in simulation 1 (Figure 7), the characteristic structures have multiple short β-strands and only five clusters have short helices (S2, S4, S6, S8, S9). The β-strands in the C-terminus of structures S1, S2, S4, S6, S7, S8, S9, S10, S11, and S12 have a similar conformation to the C-terminus of initial structure (Figure 1, right).
We calculated the RMSD relative to the initial 2NAO structure for three regions, the N-terminus, central region, and C-terminus, of the Aβ42 trimer for representative structures. Residues in the C-terminus of structures S1, S2, S4, S6, S7, S8, S9, S10, S11, and S12 have the lowest RMSD compared to other regions (Table S1). Therefore, the characteristic structures also show that the C-terminus of the initial structure is more stable, while the conformation of other regions changes rapidly and sharply during simulation 2.
Contrary to simulation 1, we did not observe a β-barrel structure in simulation 2. We calculated the RMSD of all collected configurations using several PDB structures as reference, including the typical β-barrel structures reported in the PDB. The backbone atoms were used in the structural comparison. In Figure 10, we show RMSD with respect to PDB structures 3SGR and 3SGO,81 together with the comparison to some typical fibril structures (2NAO,122MXU,132BEG,805KK3, and 5OQV(79)). All of these fibril structures consist of parallel β-strands.
Figure 10.
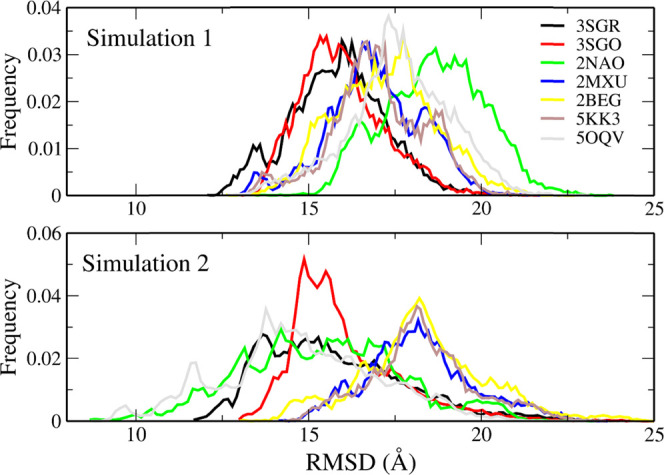
RMSD of backbone atoms for the Aβ42 trimer with reference from several β-barrel structures (3SGO, 3SGR) and Aβ fibril structures (2NAO, 2MXU, 2BEG, 5KK3, 5OQV).
The transition from parallel to antiparallel fibrillar aggregates was observed with a single-point mutation D22N (Iowa variant).92,93 Thus, this mutation shows that a small change in intramolecular interactions, namely, the release of the Asp22-Lys28 salt bridge, allows both fibrillar architectures to be sampled. In fibrillar conformations, only 2NAO and 5OQV have a β-strand at the N-terminus. 2NAO has β-strands in regions 2–6, 15–18, 26–28, 30–32, and 38–42. In 5OQV, the β-rich regions are 2–9, 11–21, 25–36, and 39–42. The 2MXU structure has three β-strands: 12–20, 27–32, and 36–41. 5KK3 has β-strands in regions 15–18, 26–28, 30–32, and 39–42. In 2BEG, β regions cover residues 18–26 and 31–42. It can be noted that there is a significant population for the smallest RMSD with respect to 3SGR in both simulations. This population is also present in simulation 2, but most of the configurations are “attracted” to the fibrillar structures that were selected as the initial configurations. In simulation 1, the maxima of the RMSD distribution are found at lower RMSD values for 3SGR and 3SGO than for all fibrillar structures, thus showing that the structural similarity is higher for β-barrel structures than for all fibrillar structures, although the RMSD values of the maximum populations have high values (1.3–1.5 nm) (Figure 10). In 1, the structural deviation from typical β-barrel motifs is, on average, less than that from fibril structures. Comparing the RMSD distributions for 1 and 2 (top and bottom panels of Figure 10, respectively), we can see that the β-barrel motif is an intermediate state along the transition from 2NAO/5OQV structures to other fibril states.
As mentioned above, one of the possible mechanisms for Aβ-induced neurotoxicity is that Aβ peptides can form a channel in the membrane that allows metal ions such as Ca2+ to transport through it, resulting in toxicity to cells. This has encouraged a lot of theoretical44,94 as well as experimental95−97 research. Since in previous computational works94,98 Aβ channels were prebuilt and inserted into the membrane, it would be interesting to check whether the barrels identified in our simulations can serve as stable pores. For clarity, barrels obtained from clusters 6 and 11 (Figure 9) will be referred to as barrel 6 and barrel 11, respectively. Similar to the 3SGR barrel, barrels 6 and 11 are expected to be stable within the membrane because they have more hydrophobic residues than hydrophilic residues (Table S5 and Figure S6). We can demonstrate, for example, that barrel 6 can span the DDPC membrane, but not barrel 11 due to its low height (Table S5). However, our preliminary results show that even when the barrel cannot cover the membrane, the channel formed by the barrel and lipid molecules surrounding the void due to lipid removal above and below the cylinder can be stable. The presence of such a channel is important as ions can pass through it into the cell. This interesting problem will be discussed in the forthcoming publication.
Aβ42 Trimers Can Form Water-Permeable Pores
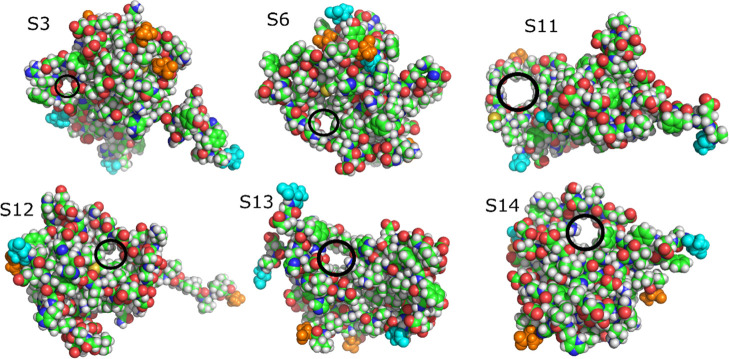
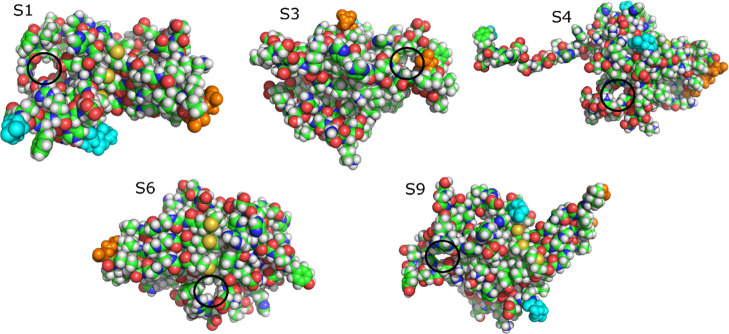
We observed pores (see the Material and Methods section) in the structures representing clusters in the free-energy landscapes of both REMD simulations (Tables 4 and 5). All observed pores are at least 5 Å in diameter. The results show that pores are populated in clusters 3, 6, 11, 12, 13, and 14 in simulation 1 and clusters 1, 3, 4, 6, and 9 in simulation 2 (Figures 11 and 12). The average radius of pores is 1.7–2.1 Å, which is consistent with the observation for the trimer from ref (48). In the latter study, pores with a radius in the range of 1.5–2.5 Å were detected in the Aβ42 trimer, but no β-barrel structure was found. The reason that β-barrels were found in our simulation but not in ref (48) is probably related to various modeling protocols. In this work, we used the all-atom model and performed REMD simulation with 72 replicas of 600 ns each. On the other hand, Voelker et al.48 applied the multiscale MD method, where REMD simulation was first performed for a coarse-grained model, and then the stability of coarse-grained representative structures was tested using a 200 ns all-atom conventional MD simulation. Thus, from the point of view of all-atom simulation, we provided better sampling than Voelker et al., explaining why we observed both β-barrels and pores, but they found only pores in all-atom structures.
Table 4. Characteristic Structures Obtained by Free-Energy Landscape Partition of REMD Simulation 1 at T = 300.38 Ka.
| interchain
interaction energy (kcal/mol) |
secondary
structure (%) |
|||||||
|---|---|---|---|---|---|---|---|---|
| cluster | population of cluster (%) | electrostatic | van der Waals | pore radius (Å) | β | helix | turn | coil |
| S1 | 11.86 | –309.15 | –142.93 | N/A | 24.60 | 6.35 | 19.84 | 49.21 |
| S2 | 8.93 | –276.09 | –129.70 | N/A | 23.02 | 0.00 | 24.60 | 52.38 |
| S3 | 8.74 | –299.18 | –143.11 | 1.82 (0.25) | 20.64 | 6.35 | 22.22 | 50.79 |
| S4 | 8.01 | –202.60 | –104.30 | N/A | 22.22 | 8.73 | 28.57 | 40.48 |
| S5 | 7.53 | –217.78 | –143.59 | N/A | 24.61 | 0.00 | 22.22 | 53.17 |
| S6 | 6.84 | –240.83 | –168.83 | 1.93 (0.43) | 34.92 | 3.18 | 33.33 | 28.57 |
| S7 | 6.50 | –209.34 | –110.78 | N/A | 24.60 | 2.38 | 27.78 | 45.24 |
| S8 | 6.41 | –351.66 | –141.56 | N/A | 26.19 | 4.76 | 25.40 | 43.65 |
| S9 | 6.40 | –324.57 | –136.95 | N/A | 31.75 | 7.94 | 26.98 | 33.33 |
| S10 | 5.67 | –201.56 | –85.13 | N/A | 20.64 | 2.38 | 17.46 | 59.52 |
| S11 | 5.46 | –203.38 | –131.23 | 2.05 (0.45) | 34.13 | 0.00 | 26.98 | 38.89 |
| S12 | 5.37 | –406.86 | –162.50 | 1.81 (0.25) | 17.46 | 4.76 | 19.84 | 57.94 |
| S13 | 5.22 | –171.73 | –128.02 | 2.16 (0.56) | 32.54 | 7.94 | 14.29 | 45.24 |
| S14 | 3.83 | –388.68 | –148.07 | 1.82 (0.23) | 29.37 | 2.38 | 26.98 | 41.27 |
| S15 | 3.21 | –92.53 | –124.36 | N/A | 27.78 | 6.34 | 14.29 | 51.59 |
N/A in pore radius represents no determined pore. Errors (within parentheses) are standard deviations.
Table 5. Same as Table 4, but for Simulation 2.
| interchain interaction energy (kcal/mol) |
secondary structure (%) |
|||||||
|---|---|---|---|---|---|---|---|---|
| cluster | population of cluster (%) | electrostatic | van der Waals | pore radius (Å) | β | helix | turn | coil |
| S1 | 15.44 | –681.59 | –187.84 | 1.87 (0.22) | 32.54 | 0.00 | 6.35 | 61.11 |
| S2 | 11.31 | –655.46 | –207.55 | N/A | 27.78 | 5.55 | 26.19 | 40.48 |
| S3 | 10.70 | –288.29 | –146.26 | 1.89 (0.27) | 34.13 | 0.00 | 17.46 | 48.41 |
| S4 | 10.67 | –229.88 | –157.30 | 1.70 (0.23) | 22.22 | 4.76 | 15.87 | 57.15 |
| S5 | 9.80 | –381.51 | –162.76 | N/A | 24.60 | 0.00 | 21.43 | 53.97 |
| S6 | 9.54 | –479.34 | –186.41 | 1.98 (0.34) | 30.16 | 5.56 | 26.98 | 37.30 |
| S7 | 8.48 | –237.10 | –135.33 | N/A | 28.57 | 0.00 | 33.33 | 38.10 |
| S8 | 7.61 | –546.31 | –168.60 | N/A | 24.60 | 2.38 | 21.43 | 51.59 |
| S9 | 5.60 | –531.05 | –183.49 | 1.93 (0.20) | 23.82 | 4.76 | 26.98 | 44.44 |
| S10 | 5.09 | –386.39 | –159.77 | N/A | 22.22 | 0.00 | 24.60 | 53.18 |
| S11 | 3.33 | –465.62 | –170.44 | N/A | 25.40 | 0.00 | 30.16 | 44.44 |
| S12 | 2.42 | –338.33 | –158.81 | N/A | 26.98 | 0.00 | 19.05 | 53.97 |
Figure 11.
Pores in representative structures of Aβ42 trimer obtained from simulation 1. The black circles indicate the pores. The atoms of N-terminal and C-terminal residues are emphasized as cyan and orange spheres, respectively. C, green; N, blue; O, red; H, white.
Figure 12.
Our result indicates that even low-order oligomers can form pores in water with no lipid bilayer, although the shape of pores is random. The pores that we observed in representative structures have enough space for water molecules and Ca2+ ions to pass through because the radius of the water molecule and Ca2+ ion is about 1.4 Å. The pore radii in our trimer structures are equivalent to the radii of the narrowest region of ion channels, which are about 2 Å.99−101 Our analysis suggests that although the shapes of pores are random and not fully settled into barrels or ion channels,88,89 pores in the Aβ42 trimer have a size in the range of the possible channel. Note that in one model, the β-barrel and water-permeable pore are clearly separated from each other (Figure S5).
Water Molecules in Aβ42 Trimer
The existence of water molecules inside Aβ fibrils has been debated for many years. Contrary to the old experiment,102 in which no water molecules were found in the fibril core, recent solid-state NMR experiments confirmed their presence.103,104 This conclusion was also supported by all-atom MD simulation105 using experimental and computational models of fibrils. Utilizing the multiscale MD approach, it was found that the density of water inside the Aβ42 tetramer is higher than that of mature fibrils.34 Therefore, it seems that the water density tends to decrease with increasing size of Aβ aggregate, and we want to check this point. In addition, the importance of this problem is related to the fact that water leakage may be associated with increased neurotoxicity of oligomers in comparison to mature fibrils.
We built a concave hull for the Aβ42 trimeric structures in both REMD simulations (see the Material and Methods section). Water molecules were selected as inside the trimer if they locate inside this hull. To better compare trimeric structures with fibrils, we performed the conventional MD simulation for three and four chains of 2NAO, starting with the same structure shown in Figure 1 (right), at T = 300 K for 20 ns. To preserve the initial fibrillar conformation, we applied position harmonic restraints to Cα atoms with a harmonic constant of 1000 kJ/mol/nm. The structures of simulation 1 have the highest water concentration inside the hull, 3.3 M (Table 6).
Table 6. Molar Concentration (M) of Water for Trimer Structures of REMD Simulations and Conventional MD Simulation with Restrained C-α Atomsa.
| trimer |
tetramer |
||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1a | 1b | 3a | 3b | |
| molar concentration | 3.3 (0.1) | 1.4 (0.1) | 0.6 (0.1) | 2.5 (0.2) | 2.4 (0.2) | 0.8 (0.1) | 0.9 (0.1) |
| average molar concentration per chain | 1.1 | 0.5 | 0.2 | 0.6 | 0.6 | 0.2 | 0.2 |
Errors are standard deviations. 1, simulation 1 (REMD); 2, simulation 2 (REMD); 3, 3 chains of 2NAO with restrained Cα (CMD); 1a, Aβ42 tetramer, AMBER force field, CMD;34 1b, Aβ42 tetramer, OPLS force field, CMD;34 3a, 4 chains of 2NAO with restrained Cα, AMBER force field, CMD; 3b, 4 chains of 2NAO with restrained Cα, OPLS force field, CMD.
The trimer from simulation 2 (0.5 M per chain) is less soaked than 1 (1.1 M) (Figure S6) and tetramer (0.6 M34). However, as expected, the difference between the Aβ42 tetramer and trimer structures from 2NAO is negligible (Table 6). Both the restrained three and four chains of 2NAO have the same molar concentration of water (0.2 M per chain) and are drier than the Aβ42 trimer and tetramer. These results reinforce the observation from our previous simulations of tetramers, where oligomers were found to be more soaked than mature fibrils. The trimer obtained from the PDB structure 2NAO by a 20 ns CMD simulation with Cα atoms restrained contains the same number of water molecules per chain (0.2 M) but not more than that of the tetrameric partner (0.2 M), since the tetramer has two compartments, allowing more water molecules to be located between them (Figure S7). Under the same simulation condition, i.e., starting with random configurations, the tetramer (0.6 M) is drier than the trimer (1.1 M) (Table 6). Therefore, in the aggregation process, water molecules are ejected out of the oligomer.
Impact of Initial Structure on the Obtained Oligomers
We calculated the angles between the dipole and each of the three components of the inertia moment of the trimer (Figure S8). The trimer dipole in both cases is more isotropic than that of the mature fibril, consistently with the simulation of the tetramer.34 Together with the oblate ellipsoid (discoidal) shape of the trimer observed in this work (see above) and for the tetramer,34 these results strengthen our picture, where the shape of soluble Aβ42 oligomers is spheroidal, while protofibrils are rod-shaped. The arrangement of the monomers in fibrils screens the electrostatic repulsion by optimizing the vdW attraction between the monomers, while in soluble oligomers, the vdW attraction is looser.
This explains why the C-terminus is more stable in the case of REMD simulation 2, started with three 2NAO chains than in simulation 1. The C-terminal region is the most hydrophobic and pre-formed interactions between the C-termini of various monomers maximize the vdW attraction. As we pointed out in the previous work,34 the structure of fibril must have a rodlike shape to minimize the electrostatic repulsion, and the arrangement of monomers becomes highly ordered due to sealing by backbone hydrogen bonds. Consequently, the arrangement of monomers in the fibril becomes preferred in the long mature fibril. The oligomeric structures obtained from mature fibrils are biased by fibrillar conformations, as it can be observed from the results presented above on the characteristic structures, contact map, and interchain interaction energy.
Conclusions
Using the all-atom model and the REMD method with two different initial structures, we report on the structural properties of the Aβ42 trimer. The trimer models obtained by simulation with different initial conformations, on average, have a similar secondary structure and shape. The Aβ42 trimer is dominated by disordered structure with a disklike shape.
The hydrophobic C-terminus is more stable than the N-terminus and the peptide center. Due to the strong interaction between the chains in the bundle formed by the C-termini, the latter do not change significantly when the initial configuration is extracted from the fibrils. This result shows that the C-terminus plays an important role in the stabilization of mature fibril and, therefore, in the late stages of aggregation, when fibril-like assemblies are sealed. On the contrary, once the C-terminus bundle is demolished, by choosing a different initial configuration resembling a trimer, just formed by a monomer and a dimer, many different structural features emerge during simulation.
In an aqueous medium, the Aβ42 trimer can form pores with size that is large enough for the passage of water molecules and Ca2+ ions. This result strengthens the experimental and simulated observations that oligomers can act as ion channels. Furthermore, barrel structures can be formed more easily in a trimer representing freshly formed oligomers than in trimers representing mature fibrils, which suggests that the formation of channel structures is a transient event that is hindered by fibril formation. We showed that hydrophobic residues, such as Tyr 10, Gly 9, and Ala 21, have a greater solvent exposure in oligomers than in fibrils, which can serve as the basis for using tip-enhanced Raman spectroscopy to distinguish toxic forms from the nontoxic ones.
The Aβ42 trimeric structures are more soaked than the mature fibril in both simulations, consistently with the Aβ42 tetramer case.34 Therefore, the interaction between oligomers and solvent plays a crucial role in the accumulation process of Aβ-soluble species before the formation of mature and less soluble aggregated forms becomes dominant. Our computational models may be useful for constructing higher-order oligomers and structure-based drug design for AD.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c05508.
RSMD (nm) of regions of characteristic structures from FEL of Aβ42 trimer from simulation 2 at 300.38 K; nonbonded interaction energy between solvent, N-terminus, central, and C-terminus regions of different chains; residues in the barrels of S6 and S11 from simulation 1; interchain contact maps of initial structures; configurational entropy of trimer Aβ42 in two time windows [300–600 ns] and [450–600 ns]; heat capacity of trimer Aβ42 and solvent in two time windows [300–600 ns] and [450–600 ns]; SASA ratio of residues in the Aβ42 tetramer, four chains of 2NAO and free amino acids; location of β-barrel and pore in S1 and S6; characteristics of barrels 6, 11, and 3SGR; water molecules inside trimers and tetramers; and the angles between three components of inertia moment and dipole (PDF)
Author Contributions
M.S.L. conceived the in silico experiments. H.L.N. conducted the experiment. H.L.N., G.L.P., and M.S.L. analyzed the results. M.S.L., H.L.N., G.L.P., and P.M. wrote the paper. All authors reviewed the manuscript.
The work was supported by Narodowe Centrum Nauki in Poland (grant no. 2019/35/B/ST4/02086), the Department of Science and Technology, Ho Chi Minh City, Vietnam (grant 02/2018/D2/HĐ-KHCNTT), PLGrid Infrastructure (Poland), the bilateral project Cnr(I)-PAN(PL) “The role of copper ions in neurodegeneration: molecular models”, and the Domestic Master/Ph.D. Scholarship Programme of Vingroup Innovation Foundation, Vietnam. P.M. thanks the European Community and the Italian Ministry of Education, University and Research within the EuroNanoMed3 ERANET cofund SPEEDY project (ID 221).
The authors declare no competing financial interest.
Supplementary Material
References
- Masters C. L.; Simms G.; Weinman N. A.; Multhaup G.; McDonald B. L.; Beyreuther K. Amyloid plaque core protein in Alzheimer disease and Down syndrome. Proc. Natl. Acad. Sci. U.S.A. 1985, 82, 4245–4249. 10.1073/pnas.82.12.4245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh D. M.; Klyubin I.; Fadeeva J. V.; Rowan M. J.; Selkoe D. J. Amyloid-beta oligomers: their production, toxicity and therapeutic inhibition. Biochem. Soc. Trans. 2002, 30, 552–557. 10.1042/bst0300552. [DOI] [PubMed] [Google Scholar]
- Masters C. L.; Selkoe D. J. Biochemistry of Amyloid β-Protein and Amyloid Deposits in Alzheimer Disease. Cold Spring Harbor Perspect. Med. 2012, 2, a006262 10.1101/cshperspect.a006262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esparza T. J.; Zhao H.; Cirrito J. R.; Cairns N. J.; Bateman R. J.; Holtzman D. M.; Brody D. L. Amyloid-beta oligomerization in Alzheimer dementia versus high-pathology controls. Ann. Neurol. 2013, 73, 104–119. 10.1002/ana.23748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacor P. N.; Buniel M. C.; Chang L.; Fernandez S. J.; Gong Y.; Viola K. L.; Lambert M. P.; Velasco P. T.; Bigio E. H.; Finch C. E.; Krafft G. A.; Klein W. L. Synaptic Targeting by Alzheimer’s-Related Amyloid β Oligomers. J. Neurosci. 2004, 24, 10191–10200. 10.1523/JNEUROSCI.3432-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glabe C. G.; Kayed R. Common structure and toxic function of amyloid oligomers implies a common mechanism of pathogenesis. Neurology 2006, 66, S74–S78. 10.1212/01.wnl.0000192103.24796.42. [DOI] [PubMed] [Google Scholar]
- Benilova I.; Karran E.; De Strooper B. The toxic Aβ oligomer and Alzheimerʼs disease: an emperor in need of clothes. Nat. Neurosci. 2012, 15, 349–357. 10.1038/nn.3028. [DOI] [PubMed] [Google Scholar]
- Kayed R.; Lasagna-Reeves C. A. Molecular mechanisms of amyloid oligomers toxicity. J. Alzheimer’s Dis. 2012, 33, S67–S78. 10.3233/JAD-2012-129001. [DOI] [PubMed] [Google Scholar]
- Lal R.; Lin H.; Quist A. P. Amyloid beta ion channel: 3D structure and relevance to amyloid channel paradigm. BBA, Biochim. Biophys. Acta, Rev. Biomembr. 2007, 1768, 1966–1975. 10.1016/j.bbamem.2007.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ono K.; Condron M. M.; Teplow D. B. Structure–neurotoxicity relationships of amyloid β-protein oligomers. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 14745–14750. 10.1073/pnas.0905127106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breydo L.; Kurouski D.; Rasool S.; Milton S.; Wu J. W.; Uversky V. N.; Lednev I. K.; Glabe C. G. Structural differences between amyloid beta oligomers. Biochem. Biophys. Res. Commun. 2016, 477, 700–705. 10.1016/j.bbrc.2016.06.122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wälti M. A.; Ravotti F.; Arai H.; Glabe C. G.; Wall J. S.; Böckmann A.; Güntert P.; Meier B. H.; Riek R. Atomic-resolution structure of a disease-relevant Aβ (1–42) amyloid fibril. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, E4976–E4984. 10.1073/pnas.1600749113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colvin M. T.; Silvers R.; Ni Q. Z.; Can T. V.; Sergeyev I.; Rosay M.; Donovan K. J.; Michael B.; Wall J.; Linse S.; Griffin R. G. Atomic resolution structure of monomorphic Aβ42 amyloid fibrils. J. Am. Chem. Soc. 2016, 138, 9663–9674. 10.1021/jacs.6b05129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller-Schiffmann A.; Andreyeva A.; Horn A. H. C.; Gottmann K.; Korth C.; Sticht H. Molecular Engineering of a Secreted, Highly Homogeneous, and Neurotoxic Aβ Dimer. ACS Chem. Neurosci. 2011, 2, 242–248. 10.1021/cn200011h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Nuallain B.; Klyubin I.; Mc Donald J. M.; Foster J. S.; Welzel A.; Barry A.; Dykoski R. K.; Cleary J. P.; Gebbink M. F. B. G.; Rowan M. J.; Walsh D. M. A monoclonal antibody against synthetic Aβ dimer assemblies neutralizes brain-derived synaptic plasticity-disrupting Aβ. J. Neurochem. 2011, 119, 189–201. 10.1111/j.1471-4159.2011.07389.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klyubin I.; Betts V.; Welzel A. T.; Blennow K.; Zetterberg H.; Wallin A.; Lemere C. A.; Cullen W. K.; Peng Y.; Wisniewski T.; Selkoe D. J.; Anwyl R.; Walsh D. M.; Rowan M. J. Amyloid β Protein Dimer-Containing Human CSF Disrupts Synaptic Plasticity: Prevention by Systemic Passive Immunization. J. Neurosci. 2008, 28, 4231–4237. 10.1523/JNEUROSCI.5161-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Ball K. A.; Phillips A. H.; Nerenberg P. S.; Fawzi N. L.; Wemmer D. E.; Head-Gordon T. Homogeneous and heterogeneous tertiary structure ensembles of amyloid-β peptides. Biochemistry 2011, 50, 7612–7628. 10.1021/bi200732x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y. S.; Pande V. S. Effects of familial mutations on the monomer structure of Abeta(4)(2). Biophys. J. 2012, 103, L47–49. 10.1016/j.bpj.2012.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenman D. J.; Connors C. R.; Chen W.; Wang C.; García A. E. Aβ Monomers Transiently Sample Oligomer and Fibril-Like Configurations: Ensemble Characterization Using a Combined MD/NMR Approach. J. Mol. Biol. 2013, 425, 3338–3359. 10.1016/j.jmb.2013.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linh N. H.; Thu T. T. M.; Tu L.; Hu C.-K.; Li M. S. Impact of Mutations at C-Terminus on Structures and Dynamics of Abeta40 and Abeta42: A Molecular Simulation Study. J. Phys. Chem. B 2017, 121, 4341–4354. 10.1021/acs.jpcb.6b12888. [DOI] [PubMed] [Google Scholar]
- Coskuner O. Divalent copper ion bound amyloid-β(40) and amyloid-β(42) alloforms are less preferred than divalent zinc ion bound amyloid-β(40) and amyloid-β(42) alloforms. J. Biol. Inorg. Chem. 2016, 21, 957–973. 10.1007/s00775-016-1392-5. [DOI] [PubMed] [Google Scholar]
- Krupa P.; Huy P. D. Q.; Li M. S. Properties of monomeric Aβ42 probed by different sampling methods and force fields: Role of energy components. J. Chem. Phys. 2019, 151, 055101 10.1063/1.5093184. [DOI] [Google Scholar]
- Lincoff J.; Sasmal S.; Head-Gordon T. The combined force field-sampling problem in simulations of disordered amyloid-β peptides. J. Chem. Phys. 2019, 150, 104108 10.1063/1.5078615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carballo-Pacheco M.; Strodel B. Comparison of force fields for Alzheimerʼs A: A case study for intrinsically disordered proteins. Protein Sci. 2017, 26, 174–185. 10.1002/pro.3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roche J.; Shen Y.; Lee J. H.; Ying J.; Bax A. Monomeric Aβ1–40 and Aβ1–42 Peptides in Solution Adopt Very Similar Ramachandran Map Distributions That Closely Resemble Random Coil. Biochemistry 2016, 55, 762–775. 10.1021/acs.biochem.5b01259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng F.; Bellaiche M. M. J.; Kim J.-Y.; Zerze G. H.; Best R. B.; Chung H. S. Highly Disordered Amyloid-β Monomer Probed by Single-Molecule FRET and MD Simulation. Biophys. J. 2018, 114, 870–884. 10.1016/j.bpj.2017.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta U.; Nilson A. N.; Kayed R. The Role of Amyloid-β Oligomers in Toxicity, Propagation, and Immunotherapy. EBioMedicine 2016, 6, 42–49. 10.1016/j.ebiom.2016.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huy P. D. Q.; Vuong Q. V.; La Penna G.; Faller P.; Li M. S. Impact of Cu(II) Binding on Structures and Dynamics of Aβ42 Monomer and Dimer: Molecular Dynamics Study. ACS Chem. Neurosci. 2016, 7, 1348–1363. 10.1021/acschemneuro.6b00109. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Hashemi M.; Lv Z.; Lyubchenko Y. L. Self-assembly of the full-length amyloid Aβ42 protein in dimers. Nanoscale 2016, 8, 18928–18937. 10.1039/C6NR06850B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Man V. H.; Nguyen P. H.; Derreumaux P. High-Resolution Structures of the Amyloid-β 1–42 Dimers from the Comparison of Four Atomistic Force Fields. J. Phys. Chem. B 2017, 121, 5977–5987. 10.1021/acs.jpcb.7b04689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das P.; Chacko A. R.; Belfort G. Alzheimer’s Protective Cross-Interaction between Wild-Type and A2T Variants Alters Aβ42 Dimer Structure. ACS Chem. Neurosci. 2017, 8, 606–618. 10.1021/acschemneuro.6b00357. [DOI] [PubMed] [Google Scholar]
- Sharma B.; Ranganathan S. V.; Belfort G. Weaker N-Terminal Interactions for the Protective over the Causative Aβ Peptide Dimer Mutants. ACS Chem. Neurosci. 2018, 9, 1247–1253. 10.1021/acschemneuro.7b00412. [DOI] [PubMed] [Google Scholar]
- Nguyen H. L.; Krupa P.; Hai N. M.; Linh H. Q.; Li M. S. Structure and Physicochemical Properties of the Aβ42 Tetramer: Multiscale Molecular Dynamics Simulations. J. Phys. Chem. B 2019, 123, 7253–7269. 10.1021/acs.jpcb.9b04208. [DOI] [PubMed] [Google Scholar]
- Chebaro Y.; Jiang P.; Zang T.; Mu Y.; Nguyen P. H.; Mousseau N.; Derreumaux P. Structures of Aβ17–42 Trimers in Isolation and with Five Small-Molecule Drugs Using a Hierarchical Computational Procedure. J. Phys. Chem. B 2012, 116, 8412–8422. 10.1021/jp2118778. [DOI] [PubMed] [Google Scholar]
- Dong X.; Sun Y.; Wei G.; Nussinov R.; Ma B. Binding of protofibrillar Aβ trimers to lipid bilayer surface enhances Aβ structural stability and causes membrane thinning. Phys. Chem. Chem. Phys. 2017, 19, 27556–27569. 10.1039/C7CP05959K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Townsend M.; Shankar G. M.; Mehta T.; Walsh D. M.; Selkoe D. J. Effects of secreted oligomers of amyloid β-protein on hippocampal synaptic plasticity: a potent role for trimers. J. Physiol. 2006, 572, 477–492. 10.1113/jphysiol.2005.103754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shankar G. M.; Li S.; Mehta T. H.; Garcia-Munoz A.; Shepardson N. E.; Smith I.; Brett F. M.; Farrell M. A.; Rowan M. J.; Lemere C. A.; Regan C. M.; Walsh D. M.; Sabatini B. L.; Selkoe D. J. Amyloid-β protein dimers isolated directly from Alzheimerʼs brains impair synaptic plasticity and memory. Nat. Med. 2008, 14, 837–842. 10.1038/nm1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein S. L.; Dupuis N. F.; Lazo N. D.; Wyttenbach T.; Condron M. M.; Bitan G.; Teplow D. B.; Shea J.-E.; Ruotolo B. T.; Robinson C. V.; Bowers M. T. Amyloid-β protein oligomerization and the importance of tetramers and dodecamers in the aetiology of Alzheimer’s disease. Nat. Chem. 2009, 1, 326–331. 10.1038/nchem.247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumura S.; Shinoda K.; Yamada M.; Yokojima S.; Inoue M.; Ohnishi T.; Shimada T.; Kikuchi K.; Masui D.; Hashimoto S.; Sato M.; Ito A.; Akioka M.; Takagi S.; Nakamura Y.; Nemoto K.; Hasegawa Y.; Takamoto H.; Inoue H.; Nakamura S.; Nabeshima Y.-i.; Teplow D. B.; Kinjo M.; Hoshi M. Two Distinct Amyloid β-Protein (Aβ) Assembly Pathways Leading to Oligomers and Fibrils Identified by Combined Fluorescence Correlation Spectroscopy, Morphology, and Toxicity Analyses. J. Biol. Chem. 2011, 286, 11555–11562. 10.1074/jbc.M110.181313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngo S. T.; Hung H. M.; Truong D. T.; Nguyen M. T. Replica exchange molecular dynamics study of the truncated amyloid beta (11–40) trimer in solution. Phys. Chem. Chem. Phys. 2017, 19, 1909–1919. 10.1039/C6CP05511G. [DOI] [PubMed] [Google Scholar]
- Jang H.; Connelly L.; Teran Arce F.; Ramachandran S.; Kagan B. L.; Lal R.; Nussinov R. Mechanisms for the Insertion of Toxic, Fibril-like β-Amyloid Oligomers into the Membrane. J. Chem. Theory Comput. 2013, 9, 822–833. 10.1021/ct300916f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C.; Zhao W.; Xing X.; Shi H.; Kang B.; Liu H.; Li P.; Ai H. An Original Monomer Sampling from a Ready-Made Aβ(42) NMR Fibril Suggests a Turn-β-Strand Synergetic Seeding Mechanism. ChemPhysChem 2019, 20, 1649–1660. 10.1002/cphc.201801137. [DOI] [PubMed] [Google Scholar]
- Jang H.; Teran Arce F.; Ramachandran S.; Kagan B. L.; Lal R.; Nussinov R. Disordered amyloidogenic peptides may insert into the membrane and assemble into common cyclic structural motifs. Chem. Soc. Rev. 2014, 43, 6750–6764. 10.1039/C3CS60459D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do T. D.; LaPointe N. E.; Nelson R.; Krotee P.; Hayden E. Y.; Ulrich B.; Quan S.; Feinstein S. C.; Teplow D. B.; Eisenberg D.; et al. Amyloid β-protein C-terminal fragments: Formation of cylindrins and β-barrels. J. Am. Chem. Soc. 2016, 138, 549–557. 10.1021/jacs.5b09536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi W.; Vanderford E. K.; Hansmann U. H. E. Out-of-Register Aβ42 Assemblies as Models for Neurotoxic Oligomers and Fibrils. J. Chem. Theory Comput. 2018, 14, 1099–1110. 10.1021/acs.jctc.7b01106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen P. H.; Campanera J. M.; Ngo S. T.; Loquet A.; Derreumaux P. Tetrameric Aβ40 and Aβ42 β-Barrel Structures by Extensive Atomistic Simulations. II. In Aqueous Solution. J. Phys. Chem. B 2019, 123, 6750–6756. 10.1021/acs.jpcb.9b05288. [DOI] [PubMed] [Google Scholar]
- Voelker M. J.; Barz B.; Urbanc B. Fully Atomistic Aβ40 and Aβ42 Oligomers in Water: Observation of Porelike Conformations. J. Chem. Theory Comput. 2017, 13, 4567–4583. 10.1021/acs.jctc.7b00495. [DOI] [PubMed] [Google Scholar]
- VandenAkker C. C.; Schleeger M.; Bruinen A. L.; Deckert-Gaudig T.; Velikov K. P.; Heeren R. M. A.; Deckert V.; Bonn M.; Koenderink G. H. Multimodal Spectroscopic Study of Amyloid Fibril Polymorphism. J. Phys. Chem. B 2016, 120, 8809–8817. 10.1021/acs.jpcb.6b05339. [DOI] [PubMed] [Google Scholar]
- Kurouski D.; Van Duyne R. P.; Lednev I. K. Exploring the structure and formation mechanism of amyloid fibrils by Raman spectroscopy: a review. Analyst 2015, 140, 4967–4980. 10.1039/C5AN00342C. [DOI] [PubMed] [Google Scholar]
- Chou I. H.; Benford M.; Beier H. T.; Coté G. L.; Wang M.; Jing N.; Kameoka J.; Good T. A. Nanofluidic Biosensing for β-Amyloid Detection Using Surface Enhanced Raman Spectroscopy. Nano Lett. 2008, 8, 1729–1735. 10.1021/nl0808132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DʼAndrea C.; Foti A.; Cottat M.; Banchelli M.; Capitini C.; Barreca F.; Canale C.; de Angelis M.; Relini A.; Maragò O. M.; Pini R.; Chiti F.; Gucciardi P. G.; Matteini P. Nanoscale Discrimination between Toxic and Nontoxic Protein Misfolded Oligomers with Tip-Enhanced Raman Spectroscopy. Small 2018, 14, 1800890 10.1002/smll.201800890. [DOI] [PubMed] [Google Scholar]
- Banchelli M.; Cascella R.; DʼAndrea C.; Cabaj L.; Osticioli I.; Ciofini D.; Li M. S.; Skupień K.; de Angelis M.; Siano S.; Cecchi C.; Pini R.; La Penna G.; Chiti F.; Matteini P. Nanoscopic insights into the surface conformation of neurotoxic amyloid β oligomers. RSC Adv. 2020, 10, 21907–21913. 10.1039/D0RA03799K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aran Terol P.; Kumita J. R.; Hook S. C.; Dobson C. M.; Esbjorner E. K. Solvent exposure of Tyr10 as a probe of structural differences between monomeric and aggregated forms of the amyloid-beta peptide. Biochem. Biophys. Res. Commun. 2015, 468, 696–701. 10.1016/j.bbrc.2015.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang M.; Teplow D. B. Amyloid β-protein monomer folding: free-energy surfaces reveal alloform-specific differences. J. Mol. Biol. 2008, 384, 450–464. 10.1016/j.jmb.2008.09.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1-2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Huang J.; Rauscher S.; Nawrocki G.; Ran T.; Feig M.; de Groot B. L.; Grubmüller H.; MacKerell A. D. Jr. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71. 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Jenson C. Temperature dependence of TIP3P, SPC, and TIP4P water from NPT Monte Carlo simulations: Seeking temperatures of maximum density. J. Comput. Chem. 1998, 19, 1179–1186. . [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Patriksson A.; van der Spoel D. A temperature predictor for parallel tempering simulations. Phys. Chem. Chem. Phys. 2008, 10, 2073–2077. 10.1039/b716554d. [DOI] [PubMed] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Frishman D.; Argos P. Knowledge-based protein secondary structure assignment. Proteins 1995, 23, 566–579. 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- Eisenhaber F.; Lijnzaad P.; Argos P.; Sander C.; Scharf M. The double cubic lattice method: efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J. Comput. Chem. 1995, 16, 273–284. 10.1002/jcc.540160303. [DOI] [Google Scholar]
- Mu Y.; Nguyen P. H.; Stock G. Energy landscape of a small peptide revealed by dihedral angle principal component analysis. Proteins 2005, 58, 45–52. 10.1002/prot.20310. [DOI] [PubMed] [Google Scholar]
- Lloyd S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. 10.1109/TIT.1982.1056489. [DOI] [Google Scholar]
- Rousseeuw P. J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. 10.1016/0377-0427(87)90125-7. [DOI] [Google Scholar]
- Mesleh M.; Hunter J.; Shvartsburg A.; Schatz G.; Jarrold M. Structural information from ion mobility measurements: effects of the long-range potential. J. Phys. Chem. A 1996, 100, 16082–16086. 10.1021/jp961623v. [DOI] [Google Scholar]
- Shvartsburg A. A.; Jarrold M. F. An exact hard-spheres scattering model for the mobilities of polyatomic ions. Chem. Phys. Lett. 1996, 261, 86–91. 10.1016/0009-2614(96)00941-4. [DOI] [Google Scholar]
- May J. C.; Morris C. B.; McLean J. A. Ion mobility collision cross section compendium. Anal. Chem. 2017, 89, 1032–1044. 10.1021/acs.analchem.6b04905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sehnal D.; Svobodová Vařeková R.; Berka K.; Pravda L.; Navrátilová V.; Banáš P.; Ionescu C.-M.; Otyepka M.; Koča J. MOLE 2.0: advanced approach for analysis of biomacromolecular channels. J. Cheminf. 2013, 5, 39. 10.1186/1758-2946-5-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murzin A. G.; Lesk A. M.; Chothia C. Principles determining the structure of β-sheet barrels in proteins I. A theoretical analysis. J. Mol. Biol. 1994, 236, 1369–1381. 10.1016/0022-2836(94)90064-7. [DOI] [PubMed] [Google Scholar]
- Murzin A. G.; Lesk A. M.; Chothia C. Principles determining the structure of β-sheet barrels in proteins II. The observed structures. J. Mol. Biol. 1994, 236, 1382–1400. 10.1016/0022-2836(94)90065-5. [DOI] [PubMed] [Google Scholar]
- Barber C. B.; Dobkin D. P.; Huhdanpaa H. The quickhull algorithm for convex hulls. ACM Trans. Math. Software 1996, 22, 469–483. 10.1145/235815.235821. [DOI] [Google Scholar]
- Park J.-S.; Oh S.-J. A new concave hull algorithm and concaveness measure for n-dimensional datasets. J. Inf. Sci. Eng. 2012, 28, 587–600. 10.6688/JISE.2012.28.3.10. [DOI] [Google Scholar]
- Kyte J.; Doolittle R. F. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982, 157, 105–132. 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- Gremer L.; Schölzel D.; Schenk C.; Reinartz E.; Labahn J.; Ravelli R. B. G.; Tusche M.; Lopez-Iglesias C.; Hoyer W.; Heise H.; Willbold D.; Schröder G. F. Fibril structure of amyloid-β(1–42) by cryo–electron microscopy. Science 2017, 358, 116–119. 10.1126/science.aao2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao Y.; Ma B.; McElheny D.; Parthasarathy S.; Long F.; Hoshi M.; Nussinov R.; Ishii Y. Aβ (1–42) fibril structure illuminates self-recognition and replication of amyloid in Alzheimer’s disease. Nat. Struct. Mol. Biol. 2015, 22, 499. 10.1038/nsmb.2991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lührs T.; Ritter C.; Adrian M.; Riek-Loher D.; Bohrmann B.; Döbeli H.; Schubert D.; Riek R. 3D structure of Alzheimer’s amyloid-β (1–42) fibrils. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 17342–17347. 10.1073/pnas.0506723102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laganowsky A.; Liu C.; Sawaya M. R.; Whitelegge J. P.; Park J.; Zhao M.; Pensalfini A.; Soriaga A. B.; Landau M.; Teng P. K.; Cascio D.; Glabe C.; Eisenberg D. Atomic View of a Toxic Amyloid Small Oligomer. Science 2012, 335, 1228–1231. 10.1126/science.1213151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barz B.; Liao Q.; Strodel B. Pathways of Amyloid-beta Aggregation Depend on Oligomer Shape. J. Am. Chem. Soc. 2018, 140, 319–327. 10.1021/jacs.7b10343. [DOI] [PubMed] [Google Scholar]
- Alies B.; Conte-Daban A.; Sayen S.; Collin F.; Kieffer I.; Guillon E.; Faller P.; Hureau C. Zinc(II) Binding Site to the Amyloid-beta Peptide: Insights from Spectroscopic Studies with a Wide Series of Modified Peptides. Inorg. Chem. 2016, 55, 10499–10509. 10.1021/acs.inorgchem.6b01733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Barrio M.; Borghesani V.; Hureau C.; Faller P.. Chapter 14 - Metal-Binding to Amyloid-β Peptide: Coordination, Aggregation, and Reactive Oxygen Species Production. In Biometals in Neurodegenerative Diseases; White A. R.; Aschner M.; Costa L. G.; Bush A. I., Eds.; Academic Press, 2017; pp 265–281. [Google Scholar]
- Yamamoto S.; Watarai H. Raman optical activity study on insulin amyloid- and prefibril intermediate. Chirality 2012, 24, 97–103. 10.1002/chir.21029. [DOI] [PubMed] [Google Scholar]
- Ahmed M.; Davis J.; Aucoin D.; Sato T.; Ahuja S.; Aimoto S.; Elliott J. I.; Van Nostrand W. E.; Smith S. O. Structural conversion of neurotoxic amyloid-β 1–42 oligomers to fibrils. Nat. Struct. Mol. Biol. 2010, 17, 561. 10.1038/nsmb.1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urbanc B.; Betnel M.; Cruz L.; Bitan G.; Teplow D. Elucidation of amyloid β-protein oligomerization mechanisms: discrete molecular dynamics study. J. Am. Chem. Soc. 2010, 132, 4266–4280. 10.1021/ja9096303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shafrir Y.; Durell S. R.; Anishkin A.; Guy H. R. Beta-barrel models of soluble amyloid beta oligomers and annular protofibrils. Proteins 2010, 78, 3458–3472. 10.1002/prot.22832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serra-Batiste M.; Ninot-Pedrosa M.; Bayoumi M.; Gairi M.; Maglia G.; Carulla N. Abeta42 assembles into specific beta-barrel pore-forming oligomers in membrane-mimicking environments. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 10866–10871. 10.1073/pnas.1605104113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jang H.; Arce F. T.; Ramachandran S.; Capone R.; Lal R.; Nussinov R. β-Barrel Topology of Alzheimer’s β-Amyloid Ion Channels. J. Mol. Biol. 2010, 404, 917–934. 10.1016/j.jmb.2010.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jang H.; Teran Arce F.; Ramachandran S.; Capone R.; Lal R.; Nussinov R. Structural Convergence Among Diverse, Toxic β-Sheet Ion Channels. J. Phys. Chem. B 2010, 114, 9445–9451. 10.1021/jp104073k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgourakis N. G.; Yau W.-M.; Qiang W. Modeling an In-Register, Parallel “Iowa” Aβ Fibril Structure Using Solid-State NMR Data from Labeled Samples with Rosetta. Structure 2015, 23, 216–227. 10.1016/j.str.2014.10.022. [DOI] [PubMed] [Google Scholar]
- Qiang W.; Yau W.-M.; Luo Y.; Mattson M. P.; Tycko R. Antiparallel β-sheet architecture in Iowa-mutant β-amyloid fibrils. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 4443–4448. 10.1073/pnas.1111305109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strodel B.; Lee J. W. L.; Whittleston C. S.; Wales D. J. Transmembrane Structures for Alzheimer’s Aβ1–42 Oligomers. J. Am. Chem. Soc. 2010, 132, 13300–13312. 10.1021/ja103725c. [DOI] [PubMed] [Google Scholar]
- Quist A.; Doudevski I.; Lin H.; Azimova R.; Ng D.; Frangione B.; Kagan B.; Ghiso J.; Lal R. Amyloid ion channels: A common structural link for protein-misfolding disease. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 10427–10432. 10.1073/pnas.0502066102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bode D. C.; Baker M. D.; Viles J. H. Ion Channel Formation by Amyloid-β42 Oligomers but Not Amyloid-β40 in Cellular Membranes. J. Biol. Chem. 2017, 292, 1404–1413. 10.1074/jbc.M116.762526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Österlund N.; Moons R.; Ilag L. L.; Sobott F.; Gräslund A. Native Ion Mobility-Mass Spectrometry Reveals the Formation of β-Barrel Shaped Amyloid-β Hexamers in a Membrane-Mimicking Environment. J. Am. Chem. Soc. 2019, 141, 10440–10450. 10.1021/jacs.9b04596. [DOI] [PubMed] [Google Scholar]
- Ngo S. T.; Nguyen P. H.; Derreumaux P. Stability of Aβ11–40 Trimers with Parallel and Antiparallel β-Sheet Organizations in a Membrane-Mimicking Environment by Replica Exchange Molecular Dynamics Simulation. J. Phys. Chem. B 2020, 124, 617–626. 10.1021/acs.jpcb.9b10982. [DOI] [PubMed] [Google Scholar]
- Jojoa-Cruz S.; Saotome K.; Murthy S. E.; Tsui C. C. A.; Sansom M. S.; Patapoutian A.; Ward A. B. Cryo-EM structure of the mechanically activated ion channel OSCA1.2. Elife 2018, e41845 10.7554/eLife.41845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan J.; Li J.; Zeng B.; Chen G.-L.; Peng X.; Zhang Y.; Wang J.; Clapham D. E.; Li Z.; Zhang J. Structure of the mouse TRPC4 ion channel. Nat. Commun. 2018, 9, 3102 10.1038/s41467-018-05247-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James Z. M.; Borst A. J.; Haitin Y.; Frenz B.; DiMaio F.; Zagotta W. N.; Veesler D. CryoEM structure of a prokaryotic cyclic nucleotide-gated ion channel. Proc. Natl. Acad. Sci. U.S.A. 2017, 114, 4430–4435. 10.1073/pnas.1700248114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petkova A. T.; Yau W.-M.; Tycko R. Experimental Constraints on Quaternary Structure in Alzheimer’s β-Amyloid Fibrils. Biochemistry 2006, 45, 498–512. 10.1021/bi051952q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y. S.; Liu L.; Axelsen P. H.; Hochstrasser R. M. 2D IR provides evidence for mobile water molecules in β-amyloid fibrils. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 17751–17756. 10.1073/pnas.0909888106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T.; Jo H.; DeGrado W. F.; Hong M. Water Distribution, Dynamics, and Interactions with Alzheimer’s β-Amyloid Fibrils Investigated by Solid-State NMR. J. Am. Chem. Soc. 2017, 139, 6242–6252. 10.1021/jacs.7b02089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi W. H.; Hansmann U. H. E. Ring-like N-fold Models of A beta(42) fibrils. Sci. Rep. 2017, 7, 6588 10.1038/s41598-017-06846-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.