Testing small study effects in multivariate meta-analysis

Summary:

Small study effects occur when smaller studies show different, often larger, treatment effects than large ones, which may threaten the validity of systematic reviews and meta-analyses. The most well-known reasons for small study effects include publication bias, outcome reporting bias and clinical heterogeneity. Methods to account for small study effects in univariate meta-analysis have been extensively studied. However, detecting small study effects in a multivariate meta-analysis setting remains an untouched research area. One of the complications is that different types of selection processes can be involved in the reporting of multivariate outcomes. For example, some studies may be completely unpublished while others may selectively report multiple outcomes. In this paper, we propose a score test as an overall test of small study effects in multivariate meta-analysis. Two detailed case studies are given to demonstrate the advantage of the proposed test over various naive applications of univariate tests in practice. Through simulation studies, the proposed test is found to retain nominal Type I error rates with considerable power in moderate sample size settings. Finally, we also evaluate the concordance between the proposed test with the naive application of univariate tests by evaluating 44 systematic reviews with multiple outcomes from the Cochrane Database.

1. Introduction

Meta-analysis is a statistical procedure that combines the results of multiple scientific studies. In meta-analysis, small study effects (SSE) is a well-known critical and challenging issue that may threaten the validity of the results (Sutton et al., 2000). “Small-study effects” is a generic term for the phenomenon that smaller studies sometimes show different, often larger, treatment effects than large ones (Sterne and Egger, 2001). One of the most well-known reason for SSE is publication bias (PB), in which case the chance of a small study being published does not depend on its quality, but on its effect size, significance or direction. A possible reason is that authors tend to report significant or positive results or journals tend to publish studies with significant or positive results. Besides PB, outcome reporting bias (ORB) and clinical heterogeneity (i.e. variability in the participants, interventions and outcomes) in small studies are also important sources for SSE. It is worth mentioning that small trials or the large effect sizes coming from small studies themselves are not problematic, and provide valuable information. However, selective publication of the results from smaller studies may be more common than those from larger studies.

SSE (including PB) is arguably the greatest threat to the validity of meta-analysis (Schwarzer et al., 2015). Erroneous conclusions can arise from a meta-analysis if SSE is not properly accounted for. For example, conclusions from several meta-analyses were later found to be contradicted by mega-trials (Egger and Smith, 1995). In the last two decades, a great deal of effort has been devoted to better reporting protocols, risk of bias evaluation, and statistical methods to detect and correct for SSE based on reported studies (Bürkner and Doebler, 2014).

Among the many statistical methods on this issue, funnel plots have been commonly used to study SSE. Statistical tests based on funnel plot symmetry have been developed, including the rank correlation test (Begg and Mazumdar, 1994) and regression-based tests (Egger et al., 1997; Harbord et al., 2006). Using the symmetry of funnel plots, Duval and Tweedie (2000) further developed the nonparametric “Trim and Fill” method for imputing missing studies in a meta-analysis. Recently, Lin and Chu (2018) proposed a method to quantify the magnitude of publication bias in univariate meta-analysis based on the skewness of the standardized deviates. Similar to Egger’s regression test, the measure proposed by Lin and Chu describes the asymmetry of the distribution of individual studies.

Multivariate meta-analysis (MMA), which jointly analyzes multiple and possibly correlated outcomes, has recently received a great deal of attention (Jackson et al., 2011a). By borrowing information across outcomes, MMA improves estimation of both pooled effects and between-study variances. However, to the best of our knowledge, statistical tests that quantify the evidence of SSE for multivariate meta-analysis have not been developed. In fact, there are several unique challenges in MMA that need to be properly addressed in developing a sensible test to study SSE in MMA.

The first challenge comes from various scenarios of SSE. Unlike univariate meta-analysis, some studies may have only part of their outcomes selectively reported, known as outcome reporting bias (ORB) (Chan and Altman, 2005). More recently, an investigation of the impact of ORB in reviews of rheumatoid arthritis from the Cochrane Database of Systematic Reviews (hereinafter refer to as the “Cochrane Database”) suggests that ORB has the potential to affect the conclusion in meta-analysis (Frosi et al., 2015). Therefore, a measure to quantify SSE needs to include both PB and ORB scenarios. The second challenge is to fully account for the multivariate nature of MMA. With multiple outcomes, a common practice is to apply a univariate test, such as the Egger’s test, to each of outcomes and report PB for outcomes with small p-values (Kavalieratos et al., 2016). The problem of multiple testing is often ignored, which may cause excessive false positive findings. In the effort of studying SSE in MMA, we shall aim to apply the strength of MMA by combining information across outcomes. The third challenge is that within-study outcome correlations, typically required by MMA methods, are often not reported and are difficult to obtain even on request (Riley et al., 2008; Chen et al., 2015). As a consequence, the standard likelihood involves unknown within-study correlations, which makes the traditional likelihood based tests (e.g., Wald, score and likelihood ratio tests) not applicable.

In this paper, we propose a score test to study the overall evidence of SSE. To the best of our knowledge, this is the first test for SSE in MMA setting. The proposed test has the following properties. First, by combining evidence of SSE across multiple outcomes, the proposed test can detect SSE due to PB and/or ORB. Secondly, by jointly modeling multivariate outcomes, the proposed test fully accounts for the multivariate nature of MMA, which avoids the separate investigations of individual outcomes. We demonstrate the superior power of the proposed test as compared to the simple procedure of separate investigation of outcomes. Furthermore, the proposed test is based on a pseudolikelihood of MMA in the same spirit as Chen et al. (2014). A key advantage is that within-study correlations are not required. Lastly, the test statistic has a closed-form formula and a simple approximated distribution.

2. Method

In this section, we introduce notation for the multivariate random-effects meta-analysis and review the existing funnel-plot-based methods for detecting SSE, including Egger’s regression test and two of its variations, Begg’s rank test and the Trim and Fill method.

2.1. Notations for multivariate random-effects meta-analysis

We consider a meta-analysis with m studies where a common set of J outcomes are of interest. For the ith study, let Y_ij and s_ij denote, respectively, the summary measure for the jth outcome and the associated standard error, both assumed known, for i = 1, … , m and j = 1, … , J. Each summary measure Y_ij is an estimate of the true effect size θ_ij. To account for heterogeneity in effect size across studies, we assume θ_ij to be independently drawn from a common distribution with overall effect size β_j and between-study variance ${\tau }_J^2$, j = 1, … , J. Under the assumption of a normal distribution for Y_ij and θ_ij, a multivariate random-effects model is often taken to be

$$\left(\begin{array}{c}{Y}_{i1}\\ ⋮\\ Y_{iJ}\end{array}\right)~N\left(\left(\begin{array}{c}{\theta }_{i1}\\ ⋮\\ {\theta }_{iJ}\end{array}\right),{\mathbf{\Delta }}_i\right),{\mathbf{\Delta }}_i=\left(\begin{array}{ccc}{s}_{i1}^2& \dots & s_{i1}{s}_{iJ}{\rho }_{{\text{W}}_{i(1J)}}\\ ⋮& \ddots & ⋮\\ s_{iJ}{s}_{i1}{\rho }_{{\text{W}}_{i(1J)}}& \cdots & s_{iJ}^2\end{array}\right),$$ (1)

$$\left(\begin{array}{c}{\theta }_{i1}\\ ⋮\\ {\theta }_{iJ}\end{array}\right)~N\left(\left(\begin{array}{c}{\beta }_1\\ ⋮\\ {\beta }_J\end{array}\right),\mathbf{\Omega }\right),\mathbf{\Omega }=\left(\begin{array}{ccc}{\tau }_1^2& \dots & {\tau }_1{\tau }_J{\rho }_{\text{B}(1J)}\\ ⋮& \ddots & ⋮\\ {\tau }_J{\tau }_1{\rho }_{\text{B}(1J)}& \dots & {\tau }_J^2\end{array}\right),$$ (2)

where Δ_i and Ω are J × J study-specific within-study and between-study covariance matrices, respectively, and ρ_Wi(jk) and ρ_B(jk) are the respective within-study and between-study correlations between the jth and kth outcomes (Jackson et al., 2011a). When the within-study correlations ρ_Wi(jk) are known, inference on the overall effect sizes (β₁, … , β_J) can be based on the marginal distribution of (Y_i1, … , Y_iJ), i.e.,

$$\left(\begin{array}{c}{Y}_{i1}\\ ⋮\\ Y_{iJ}\end{array}\right)~N\left(\left(\begin{array}{c}{\beta }_1\\ ⋮\\ {\beta }_J\end{array}\right),{\mathbf{\text{V}}}_{\mathbf{i}}\right),{\mathbf{\text{V}}}_{\mathbf{i}}={\mathbf{\Delta }}_{\mathit{i}}+\mathbf{\Omega }.$$ (3)

We note that the variance of Y_ij is partitioned into two parts ($s_{iJ}^2$ and ${\tau }_J^2$) as in analysis of variance (ANOVA) for univariate random-effects models, and the covariance is also partitioned into two parts as the sum of within- and between-study covariances, i.e., cov(Y_ij, Y_ik) = s_ijs_ikρ_Wi(jk) + τ_jτ_kρ_B(jk). However, study-specific within-study correlations ρ_Wi(jk) among multiple outcomes are generally unknown (Riley et al., 2008; Chen et al., 2014).

2.2. A score test for multivariate meta-analysis

In this subsection, we propose a score test for SSE under MMA. The proposed test can be considered as a multivariate extension of Egger’s regression test, which fully accounts for the multivariate nature of MMA, and does not require within-study correlations. We refer to our test as the Multivariate Small Study Effect Test (MSSET) hereinafter. Specifically, we calculate each component of the pseudolikelihood (Gong and Samaniego, 1981) using the estimated residuals in the regression model of the univariate Egger’s test and then employ the idea of composite likelihood (Lindsay, 1988) to combine individual pseudolikelihoods together. For the jth outcome of the ith study, define the standardized effect size as ${\text{SND}}_{ij}=Y_{ij}{\left(s_{ij}^2+{\tau }_j^2\right)}^{-1/2}$ and the precision as ${\text{P}}_{ij}={\left(s_{ij}^2+{\tau }_j^2\right)}^{-1/2}$. We have

$${\text{SND}}_{ij}=a_j+b_j{\text{P}}_{ij}+{\epsilon }_{ij},$$ (4)

where a_j is the intercept that measures the asymmetry, b_j is the slope indicating the size and direction of effect, ε_ij is a standard normal random variable. Let ${\tilde{\tau }}_j^2$ denote a consistent estimator of ${\tau }_j^2$ (e.g., a moment estimator). By substituting ${\tilde{\tau }}_j^2$ into model (4), we obtain the log pseudolikelihood

$$\text{log}{L}_p^j\left(a_j,b_j\right)=-\frac{1}{2}{\sum _{i=1}^m\left({\widetilde{\text{SND}}}_{ij}-a_j-b_j{\tilde{P}}_{ij}\right)}^2,$$ (5)

where ${\widetilde{\text{SND}}}_{ij}$ and ${\tilde{P}}_{ij}$ are simply SND_ij and P_ij with ${\tau }_j^2$ replaced by ${\tilde{\tau }}_j^2$. We note here that the regression coefficients (a_j, b_j) (in particular a_j) are parameters of interest, while the heterogeneity ${\tau }_j^2$ is a nuisance parameter. Replacing the nuisance parameter by its estimate can reduce its impact and offer a simple inference procedure. Such an idea was originally proposed by Gong and Samaniego (1981), where the uncertainty associated with the estimated nuisance parameters is properly accounted for, and it was later studied by Liang and Self (1996) and Chen and Liang (2010) in various settings.

To combine the signal for SSE from multivariate outcomes, we propose the following pseudolikelihood by synthesizing individual pseudolikelihoods across outcomes:

$$\text{log}{L}_p(a,b)=\sum _{j=1}^J\text{log}{L}_p^j\left(a_j,b_j\right),$$ (6)

where a = (a₁, … , a_J)^T and b = (b₁, … , b_J)^T. By simply adding together the log pseudo-likelihoods for the various outcomes, we avoid the use of within-study correlations. This idea is similar to the composite likelihood (Lindsay, 1988) or independence likelihood (Chandler and Bate, 2007), where (weighted) likelihoods are multiplied together whether or not they are independent. An important distinction here is that each component in logL_p(a, b) is a pseudolikelihood (instead of a likelihood), and its score function is not an unbiased estimating equation. Using a similar argument as in the proofs of Lemma 2.1 and Theorem 2.2 in Gong and Samaniego (1981), for the jth outcome, we have shown the asymptotic consistency and normality of the maximum pseudolikelihood estimator in Appendices A and B of the Supporting Information.

With the pseudolikelihood in equation (6), testing SSE in MMA can be carried out by simply testing H₀ : a = 0, where a = (a₁, … , a_J)^T. We propose the following procedure, where the calculation at each step has a closed-form expression.

1. Calculation of the pseudo-score function

   The maximum pseudolikelihood estimator under a_j = 0 can be calculated as

   $${\tilde{b}}_j(0)={\left(\sum _{i=1}^m{\tilde{P}}_{ij}^2\right)}^{-1}\left(\sum _{i=1}^m{\widetilde{\text{SND}}}_{ij}{\tilde{P}}_{ij}^2\right).$$

   The pseudo-score function w.r.t. a under the null can be calculated as $U_a\left\{0,\tilde{b}(0),{\tilde{\tau }}^{\text{2}}\right\}={\left({\sum }_{i=1}^m{\widetilde{\text{SND}}}_{i1}-{\text{R}}_1,\dots ,{\sum }_{i=1}^m{\widetilde{\text{SND}}}_{ij}-{\text{R}}_J\right)}^T$. For notation simplicity, we use $U_a\left\{0,\tilde{b}(0)\right\}$ to denote $U_a\left\{0,\tilde{b}(0),{\tilde{\tau }}^{\text{2}}\right\}$ hereafter.

2. Calculation of information matrices

   The negative Hessian of the log pseudolikelihood function evaluated at $\left(0,\tilde{b}(0)\right)$ is calculated as

   $$I_0=\left(\begin{array}{cc}{I}_{0_{\text{aa}}}& I_{0_{\text{ab}}}\\ I_{0_{\text{ab}}}{}^T& I_{0_{\text{bb}}}\end{array}\right),$$

   where $I_{0_{\text{aa}}}=\text{diag}(m,\dots ,m)$ is a J-dimensional diagonal matrix with m as its diagonalelements, $I_{0_{\text{ab}}}=\text{diag}\left({\sum }_{i=1}^m{P}_{i1},\dots ,{\sum }_{i=1}^m{P}_{ij}\right)$ is a J-dimensional diagonal matrix with ${\sum }_{i=1}^m{P}_{ij}$ as its j th element, and $I_{0_{\text{bb}}}=\left({\sum }_{i=1}^m{P}_{i1}^2,\dots ,{\sum }_{i=1}^m{P}_{iJ}^2\right)$ is a J-dimensional diagonal matrix with ${\sum }_{i=1}^m{P}_{iJ}^2$ as its jth element. The J ×J submatrix of the inverse of I₀ with respect to a, denoted by $I_0^{aa}$, can be calculated as $\left(I_{0_{\text{aa}}}-I_{0_{\text{aa}}}{I}_{0_{\text{bb}}}^{-1}{I}_{0_{\text{ab}}}\right){}^{-1}$.

3. Calculation of the test statistic

   Let Σ_aa denote the asymptotic variance of $\sqrt{m}\left(\widehat{a}-a_0\right)$. The calculation of Σ_aa requires properly accounting for the additional uncertainty in ${\tilde{\tau }}^2$, as we described in Appendix C of the Supporting Information. Let $\overline{\lambda }$ denote the arithmetic mean of the eigenvalues of ${\left(I_0^{aa}\right)}^{-1}{\sum }_{\text{aa}}$. The proposed MSSET test is constructed by

   $$\text{MSSET}={(m\overline{\lambda })}^{-1}{U}_a{\{\mathbf{0},b(0)\}}^T{I}_0^{aa}{U}_a\{\mathbf{0},b(0)\}.$$ (7)

   The test statistic is compared with the ${\chi }_J^2$ distribution to obtain a p-value.

A proof of the asymptotic distribution of the score test is provided in Appendix C of the Supporting Information. We note that instead of constructing the test following the traditional score test for composite likelihood (e.g., the pseudo-score statistics defined on page 193 in Molenberghs and Verbeke (2005)), the above test is constructed for better computational stability. Finally, the proposed test reduces to the traditional Egger’s test for univariate meta-analysis when the number of outcomes is one (i.e., J = 1). The above steps for obtaining the MSSET and p-value will be illustrated in Section 4.1. In addition to MSSET multivariate meta-analysis for continuous outcomes, we also developed a modified version of MSSET for binary outcomes. The details are provided in Appendix D of the Supporting Information.

3. Two case studies

In this section, we consider two case studies: 1) structured telephone support or non-invasive tele-monitoring for patients with heart failure and 2) prognostic value of MYCN and Chromosome 1p in patients with neuroblastoma.

3.1. Structured telephone support or non-invasive tele-monitoring for patients with heart failure

Heart failure is a complex, debilitating disease. To improve clinical outcomes, and reduce healthcare utilization, specialized disease management programs are conducted, such as structured telephone support and non-invasive home telemonitoring. Over the last decade, trials have been conducted to examine the effects of these programs. To compare structured telephone support or non-invasive home tele-monitoring interventions with standard practice, Inglis et al. (2016) conducted a systematic review including 41 randomized clinical trials. Primary outcomes included all-cause mortality, and both all-cause and heart failure-related hospitalizations. Other outcomes included length of stay, health-related quality of life, heart failure knowledge and self-care, acceptability and cost.

We revisit the systematic review conducted by Inglis et al. (2016), and use the primary outcome (all-cause mortality) and the secondary outcome (mental quality of life) to illustrate the proposed method. We analyze the 35 trials that reported either of the two outcomes. Among the 35 trials, 11 reported both outcomes; 34 reported the primary; and 12 reported the secondary outcome.

A detailed step-by-step illustration of the calculation of proposed MSSET is provide in Appendix E of the Supporting Information. The upper panel in Figure 1 displays the funnel plots of all-cause mortality and mental quality of life of 35 trials. The funnel plots of both all-cause mortality and quality of life suggest severe asymmetry. Such an observation is confirmed by univariate tests of SSE (Egger’s test). When we apply Eggers test to the two outcomes separately, both are marginally significant (p=0.06 and 0.09). But after Bonferroni correction, both are not significant. In contrast, the proposed test yields statistically significant result with smaller p-values (p=0.03). We use this example to highlight a limitation of univariate tests: the loss of power after adjusting for multiple testing. In contrast, the proposed MSSET test is better in identifying SSE by combining signals of SSE from multiple outcomes.

Figure 1.

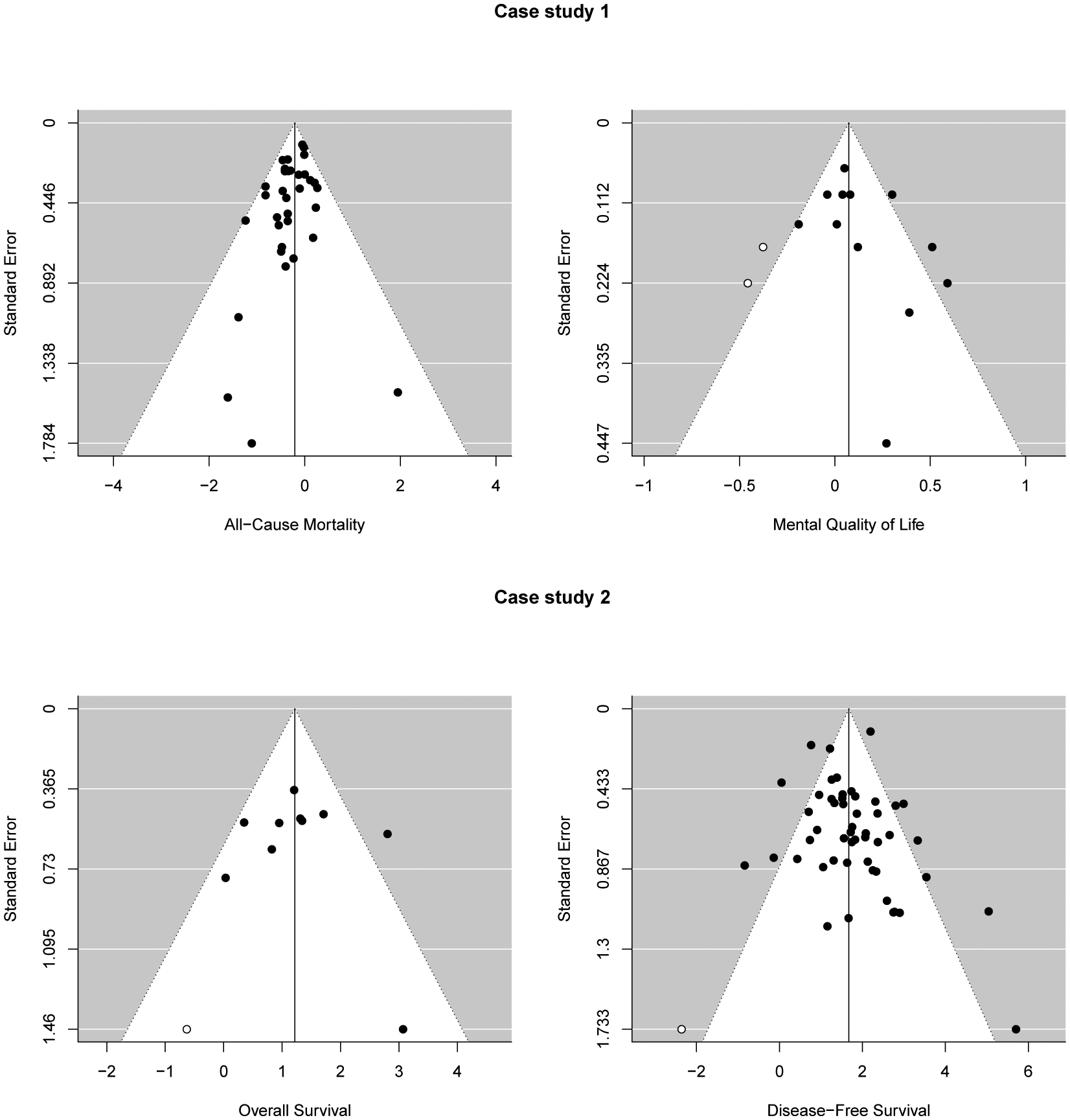
Funnel plots for Case study 1 in Section 4.1 (upper panels) and Case study 2 in Section 4.2 (lower panels).

3.2. MCYN and Chromosone 1p in patients with neuroblastoma

Neuroblastoma, a type of cancer that starts in early nerve cells, is a common extracranial solid tumor of childhood. Studies have been conducted to assess whether amplified levels of MYCN and deletion of chromosome 1p, Ch1p, are associated with survival outcomes in children with neuroblastoma. Jackson et al. (2011b) conducted a meta-analysis to examine the association of the two factors (MYCN and Chromosome 1p) with overall and disease-free survival. Seventy-three studies assessing the prognostic values of MYCN and Chromosome 1p, in patients with neuroblastoma are included in this meta-analysis. Up to four estimates of effect are provided by the individual studies, including an estimated unadjusted log hazard ratio of survival, either of the high relative to the low level group of MYCN, or Chromosome 1p deletion to its presence.

We study the SSE for overall survival and disease free survival using Egger’s test and the proposed MSSET test. The lower panel in Figure 1 displays the funnel plots of the two outcomes. For the overall survival, we observe a certain degree of asymmetry, while for the disease-free survival, we do not observe such evidence. Similarly, applying univariate methods for SSE to outcomes separately only lead to the detection of SSE for overall survival (p=0.01 and 0.58). The proposed MSSET test suggests a statistically significant evidence of overall SSE for bivariate outcomes (p=0.02).

4. Simulation studies and an empirical evaluation using 44 systematic reviews

In this section, we evaluate the performance of the proposed MSSET test through fully controlled simulation studies, and study the empirical impact of our new MSSET.

4.1. Simulation studies

In our simulation studies, we compare the proposed MSSET test with the commonly used Egger’s regression test and Begg’s rank test. The data are generated from MMA with a common set of two outcomes as specified by model (1). To cover a wide spectrum of scenarios, we vary the values of several factors that are considered important in practice: 1) To reflect the heterogeneity in the standard error of the summary measure across studies, we sample $s_{ij}^2$ from the square of the distribution N(0.3, 0.5), which leads to a mean value of 0.33 for $s_{ij}^2$. 2) The size of the within-study variation relative to the between-study variation may have a substantial impact on the performance of the methods. To this end, we let the between-study variances ${\tau }_1^2={\tau }_2^2$ range from 0.1 to 0.6 to represent the random-effects model with relatively small to large random effects. 3) For within-study and between-study correlations, we consider ρ_Wi to be constant with value −0.5, 0, or 0.5 and ρ_B to be constant with value −0.5, 0, or 0.5. 4) The number of studies n is set to 10, 25, 50, or 100 to represent meta-analysis of small to large numbers of studies. We consider the Type I error setting where the selection (i.e., the decision of whether to publish a particular study or report a particular outcome) does not depend on the effect sizes. We also consider the power settings where the selection depends on the effect sizes. We conduct 5000 simulations for the Type I error setting and 1000 simulations for the power settings. For the power settings, in order to obtain n published studies, we follow three steps: 1) N studies are simulated, where N is an integer greater than n (here we choose N = 3n to ensure there are enough studies before selection); 2) studies are excluded based on four different selection scenarios described in the following paragraph; and 3) n studies are sampled randomly from those that remain after the previous step.

4.1.1. Selection model scenarios.

To evaluate the performance of MSSET, it is critical to design and cover a wide range of publication/reporting scenarios. We consider four different scenarios for two types of SSE, including scenarios where studies are completely missing (Scenario C1, C2, and C3), and scenarios where studies are partially missing (Scenario P). For Scenarios C1–C3, the probability of a study being published depends on the p-values of both effect sizes of this study. For example, as shown in the upper left panel of Figure 2, a study is published if and only if the p-values of both effect sizes are less than 0.05. Although Scenarios C2 and C3 may be more common in practice, we include Scenario C1 as it was usually considered in the literature as a benchmark for sanity check of a procedure (Bürkner and Doebler, 2014). For Scenario P (P stands for partial reporting), as visualized in the lower-right panel of Figure 2, the probability of an outcome being reported depends on the p-value of its effect size. A brief description, as well as the data of obtaining this selection model are provided in Appendix F of the Supporting Information.

Figure 2.

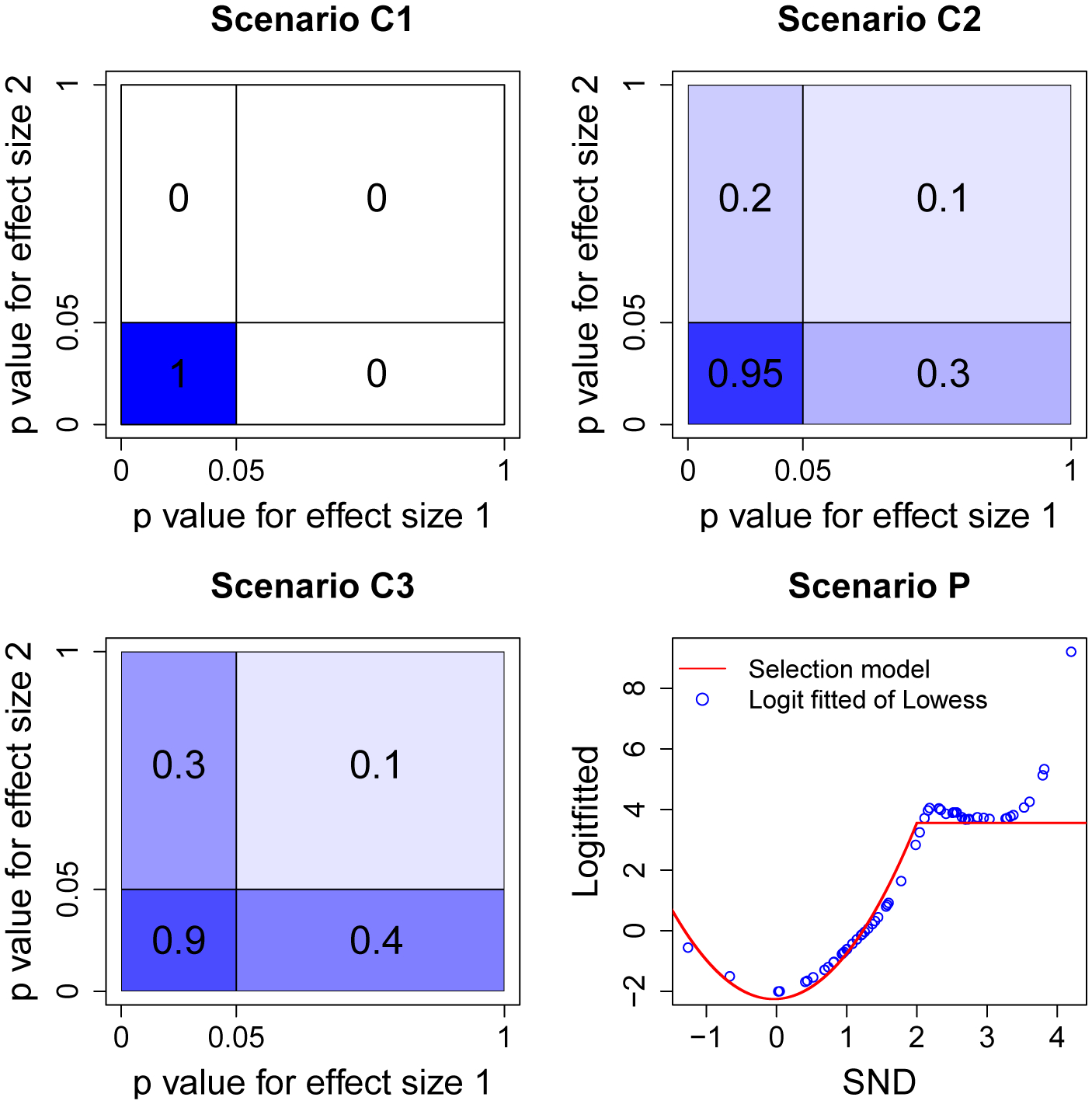
Probability of being published under Scenarios C1, C2, C3, and P. In Scenarios C1–C3, the probabilities are shaded from dark to light (i.e., the largest probability refers to the darkest shade). This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

4.1.2. Simulation results.

Table 1 summarizes the Type I errors rates at the 10% nominal level of the tests under comparison. The proposed MSSET test controls the Type I error rates well in all settings. The Egger’s regression test for one outcome only (Egger₁) or two outcomes separately with Bonferroni correction (Egger_BON) have slightly inflated Type I error rates when the sample size is small (n = 10), while other adjustment methods proposed by Holm (1979), Hochberg (1988), Benjamini and Hochberg (1995), and Benjamini et al. (2001) tend to produce conservative Type I error rates. We observe that the Type I error rates of Begg’s rank test are very conservative when the sample size is relatively small but inflated when it is relatively large. This observation is consistent with the literature, where investigators report that Begg’s rank test does not perform well in controlling Type I errors rates (Bürkner and Doebler, 2014).

Table 1.

Type I error rates (×100%), at the 10% nominal level, of Egger’s test (E), Begg’s test(B), and the proposed MSSET test. The univariate tests are conducted on the first outcome only, denoted as “test₁”, and the p value adjustment methods proposed by Bonferroni correction (bon), Holm, Hochberg (hoch), Benjamini & Hochberg (bh), Benjamini & Yekutieli (by) are used to combine the test results, denoted as “test”. The number of studies n is 10, 25, 50, 75, and 100, and the between-study heterogeneity τ² is 0.1, 0.9, and 1.9.

n	τ2	MSSET	E1	Ebon	Eholm	Ehoch	Ebh	Eby	B1	Bbon	Bholm	Bhoch	Bbh	Bby
10	0.1	12.9	14.7	15.8	8.7	9.0	9.0	6.6	2.4	2.1	1.1	1.1	1.1	0.4
	0.9	12.7	13.2	14.6	8.1	8.4	8.4	6.3	2.6	2.0	1.0	1.1	1.1	0.4
	1.9	11.9	13.1	15.0	8.2	8.4	8.4	6.3	2.3	1.6	0.8	0.9	0.9	0.3
25	0.1	11.3	11.9	13.0	7.0	7.3	7.3	5.1	17.8	22.4	12.6	13.0	13.0	10.4
	0.9	11.1	11.4	12.2	6.6	6.9	6.9	4.7	24.1	32.7	18.8	19.1	19.1	16.3
	1.9	10.9	11.3	12.0	6.5	6.9	6.9	4.3	24.6	33.7	19.4	19.8	19.8	17.0
50	0.1	10.4	10.7	10.9	5.9	6.2	6.2	4.2	38.1	51.8	32.8	33.3	33.3	29.2
	0.9	10.5	10.8	10.6	5.7	6.0	6.0	3.9	44.7	61.7	40.9	41.5	41.5	37.2
	1.9	10.4	10.9	10.6	5.7	6.0	6.0	3.8	45.5	62.8	41.9	42.4	42.4	38.4
75	0.1	10.0	9.8	9.8	5.3	5.6	5.6	3.5	48.2	65.5	44.3	44.8	44.8	40.4
	0.9	10.3	10.2	9.8	5.4	5.8	5.8	3.8	55.9	73.8	52.3	52.7	52.7	48.7
	1.9	10.1	10.5	10.2	5.6	5.9	5.9	3.8	56.6	74.8	53.4	53.8	53.8	49.6
100	0.1	9.9	9.9	9.6	5.2	5.5	5.5	3.7	55.4	72.1	50.3	50.9	50.9	46.7
	0.9	9.7	9.8	9.7	5.3	5.5	5.5	3.6	62.0	79.8	57.8	58.3	58.3	54.2
	1.9	9.7	10.2	9.6	5.1	5.4	5.4	3.4	63.0	80.7	58.9	59.4	59.4	55.5

Figure 3 summarizes the power of the tests under comparison. Clearly, the proposed MSSET test is the most sensitive under all the settings considered. Egger’s regression test on one outcome (Egger₁) and those on two outcomes with Bonferroni correction (Egger_BON) and Benjamini & Hochberg correction (Egger_BH) have substantial power loss compared with the proposed MSSET. There are several additional interesting findings from Figure 3:

1. For Scenarios C1–C3, we observe non-monotonic trends for the MSSET test and Egger’s regression test. A possible explanation for this non-monotonicity is due to the fact that both the MSSET test and Egger’s regression test assume the random-effects model and require the estimation of the between-study variance τ². However, when the between-study variance is close to zero, a fixed-effect model is more suitable than a random-effects model. Therefore, these two tests have lower power as heterogeneity is very small, as a consequence of lack of good fit assumed for the random-effect meta-analysis model.

2. Unlike in Scenarios C1–C3, the power curve in Scenario P is increasing. One possible explanation is that this scenario allows selective reporting of parts of multiple outcomes. Because the proposed test combines signals of SSE across multiple outcomes, the number of studies required to identify the same degree of heterogeneity is smaller than that required for the other scenarios.

3. We observe that there is a decreasing trend in power from Scenario C1 to Scenario C3 for all tests under comparison. This indicates that it is easier to detect SSE when selectivity is greater.

Figure 3.

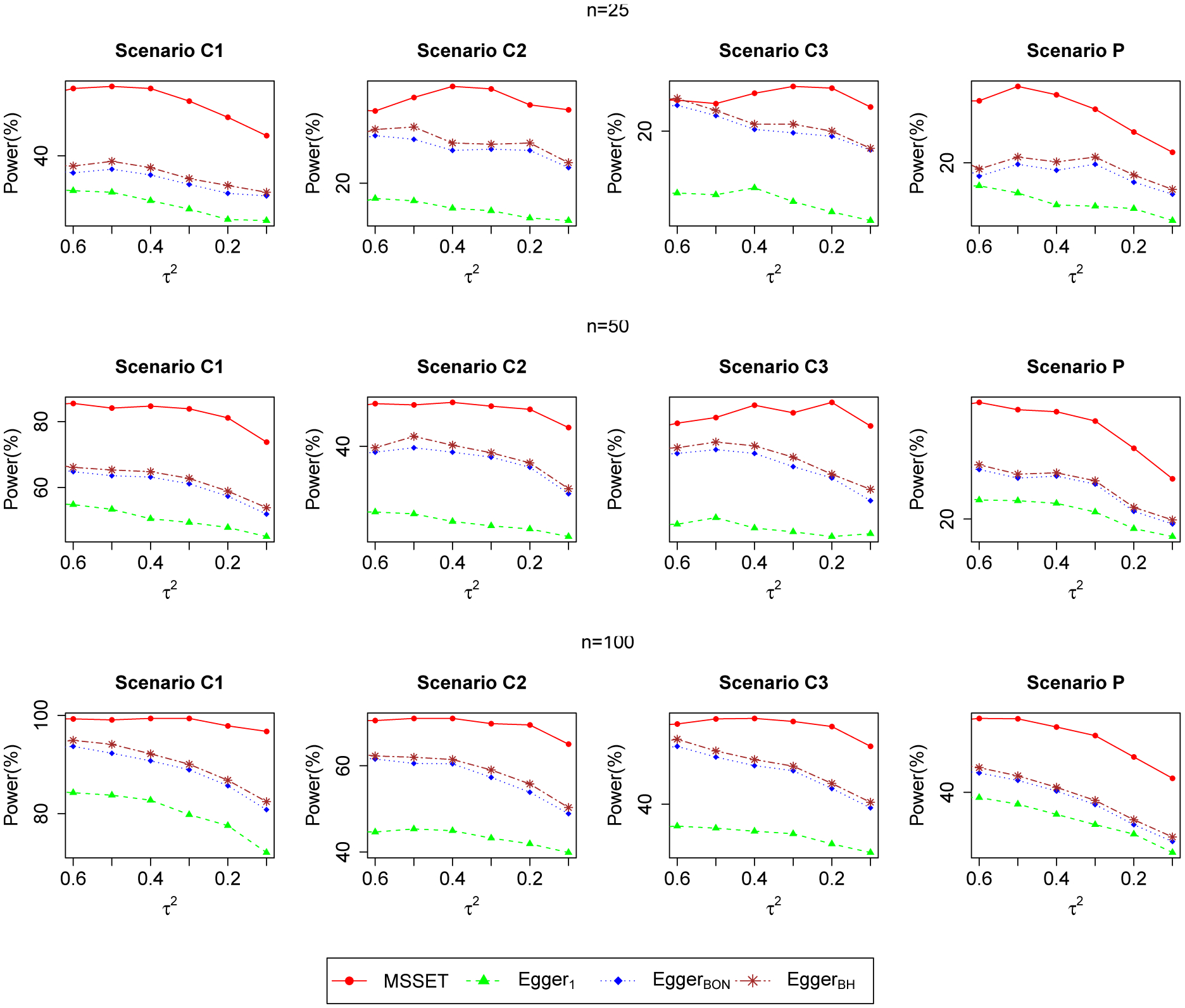
Power plots of the proposed MSSET test, Egger’s regression test on one outcome (Egger₁), and Egger’s regression test on two outcomes with Bonferroni correction (Egger_BON) and Benjamini & Hochberg correction (Egger_BH) at the 10% nominal level for sample sizes varying from 25 to 100 and between-study variances varying from 0.1 to 0.6. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

In addition, we evaluate the performance of the modified version of MSSET using smoothed within-study variance for binary outcomes as described in Appendix G. The observation is consistent with the literature, in that the correlated effect size and its variance will lead to false positive testing results of SSE. The MSSET and Egger’s tests using smoothed variance control the Type I errors rates better than those using naive variances.

4.2. An empirical evaluation using 44 systematic reviews from the Cochrane Database

To evaluate the practical impact of MSSET, we compare the results of MSSET with the results from univariate tests of SSE by applying MSSET and the Egger’s test to a large number of comparable meta-analyses obtained from the Cochrane Database of Systematic Reviews, an online collection of regularly updated systematic reviews and meta-analyses of medical studies. We do not include the Begg’s test for comparison, since our simulation study in the previous session indicated that Begg’s rank test does not perform well in controlling Type I error rates. We extracted 5320 out of 11401 available reviews from the database before July 2015 (6081 files were corrupt). Among these records, we identified 1675 meta-analyses that compare treatment to placebo or no treatment. The following criteria were then applied: a) the number of studies in a meta-analysis must be at least 10; b) all studies in a meta-analysis must contain a common set of two different outcomes; and c) in any meta-analysis, at least one study should report both outcomes. Similar criteria have been used in the literature (Trikalinos et al., 2014). After imposing the above quality control, we obtained 44 meta-analyses with bivariate outcomes.

We compare the results from MSSET with the results of the univariate Egger’s test on bivariate outcomes separately. Specifically, for each meta-analysis, we apply MSSET, the Egger’s test on outcome 1 (Egger₁), and the Egger’s test on outcome 2 (Egger₂). We then dichotomize the p-value at the level of 0.10, for MSSET test, Egger₁ and Egger₂. In addition, we use Bonferroni correction to combine the results from Egger’s test of bivariate outcomes (Egger_Bonferroni). We cross-tabulate the dichotomized results, comparing the MSSET test results with one of the univariate tests. Table 2 shows 2×2 tables of the number of meta-analyses that identified SSE via the MSSET test, versus one of the three Egger’s tests.

Table 2.

Contingency table of MSSET test vs. Egger’s regression based on outcome 1 (Egger₁) only and outcome 2 only (Egger₂), and Egger test using Bonferroni correction to combine the results from Egger’s test of bivariate outcomes (Egger_Bonferroni) (i.e., S=1 if p-value < 0.1; S=0 if p-value > 0.1).

	Egger1		Egger2		EggerBonferroni
MSSET	S=0	S=1	S=0	S=1	S=0	S=1
S=0	31	3	31	3	31	3
S=1	6	1	6	1	4	3

Among the 44 meta-analyses considered in the analysis, MSSET has identified 7 (16%) meta-analyses with SSE at the significance level of 0.10. Egger’s regression test has identified 4 (9%) meta-analyses having SSE for both outcome 1 and outcome 2. For both outcomes with Bonferroni correction, Egger’s regression test and Begg’s rank test has identified 6 (14%) meta-analyses having SSE. The percentage of SSE identified by the MSSET test is the highest among all tests, which is consistent with the simulation results showing that the MSSET test is the most powerful among all tests under comparison. In addition, MSSET is in a larger concordance with the Egger_Bonferroni test, by combining signals from both outcomes.

In summary, this “meta-meta” analysis of 44 reviews from the Cochrane Database demonstrates the practical implications of MSSET by comparing the test to the results of univariate tests. The MSSET has consistently detected more SSE than the univariate tests.

5. Discussion

In this paper, we have proposed a rigorous score test for studying overall evidence of SSE in MMA. To the best of our knowledge, the proposed test is the first effort to study SSE in an MMA setting. It can be thought of a multivariate extension of Egger’s regression test, which naturally is Egger’s test when the number of outcomes is one (i.e., J = 1). For more general settings (J ⩾ 2), the proposed test has the following advantageous properties, besides its simplicity. First, by combining signals of SSE across multiple outcomes (whether or not they are of different data types or on different scales), the proposed test can quantify SSE under different scenarios, and is consistently more powerful than univariate tests. Second, by jointly modeling multiple outcomes, the score test can fully account for the multivariate nature of MMA, which avoids the need of a Bonferroni correction for multiple testing. As a technique and practical advantage, the within-study correlations are not required in the proposed test, while the between-study correlations are properly accounted for in the testing procedure, by the theory of composite likelihood.

ORB had not received sufficient attention until recently. Dwan et al. (2013) reviewed the evidence from empirical cohort studies assessing ORB and showed that statistically significant outcomes are more likely to be selectively reported. Copas et al. (2014) suggested a likelihood-based model that reflects the empirical findings to estimate the severity of ORB. More recently, Frosi et al. (2015) suggested that the difference between the results from MMA and those from univariate meta-analysis indicates the presence of ORB. Designing a specific test for detecting ORB is a topic of future research. In addition, to the best of our knowledge, there is no literature investigating the relationship between ORB and study sizes. This question is critical and deserves future investigation.

In this paper, we construct a composite likelihood under a working independence assumption. It is worth mentioning that in some clinical trials, the measurement of secondary outcomes is not of quality comparable to the measurement of a primary outcome, so it is possible that when simply adding the two marginals together to form the composite likelihood, the uncertainty contained in the low-quality secondary/exploratory outcomes can dilute the information provided by the primary outcome.

One major motivation of the proposed method is that it does not require the knowledge of within-study correlations under the working independence assumption. However, it is of interest to investigate how within-study correlation affects the power in the scenario where the within-study correction is available. We have conducted additional simulation studies with results in Appendix H of the Supporting Information. We observed that the full-likelihood based score test (FLST) with known within-study correlations tends to have inflated Type I error rates when number of studies are relatively small (n < 50). A possible reason is that the model complexity is increased by introducing more correlation parameters. On the other hand, the proposed model under the working independence assumption retains the model parsimony by avoiding estimating the within-study correlation parameters. A full investigation of the FLST and the development of methods to correct its small-sample bias will be a future topic of interest.

The choice of numbers of outcome is an essential question in the multivariate meta-analysis. A unified protocol is usually developed by the investigator team, where outcomes of interests (multiple outcomes) are pre-specified. The choice of the multiple outcomes is usually developed through discussions among clinicians and systematic reviewers based on their clinical knowledge. For example, in an investigation of heart failure the multiple outcomes could include all-cause mortality, heart failure related hospitalization, health-related quality of in the protocol. Studies do not report those outcomes (but with these outcomes in their protocols) may be subject to outcome reporting bias. In addition, one advantage of the proposed method is under the working independence assumption it is doable for many outcomes without introducing more correlation parameters, thus retains the model parsimony and simplicity. It would be of interest to investigate the empirical performance of the proposed test in settings with more than two outcomes.

One limitation of the proposed method is the asymptotic test distribution holds only when number of studies are at least moderately large. Based on our simulation studies, the number of studies should be greater than or equal to 10 to guarantee a good performance of the proposed method. The use of the asymptotic distribution in settings where the number of studies in a meta-analysis is small needs more investigation. Theory such as high order asymptotics could be applied here to enhance the small sample performance of the proposed test. Another limitation of the proposed method is that it only detects for SSE and does not correct for it. An important extension is to develop a robust procedure to correct for SSE by jointly analyzing multivariate outcomes. Another interesting extension of the proposed test is to network meta-analysis, where multiple treatments are compared jointly in clinical trials but each trial may compare only a subset of all treatments. In addition, a common limitation of the Egger’s regression test and its extensions is they only account for the shape of deviates (skewness). Following a similar strategy as in Lin and Chu (2018), an interesting future topic is to extend the proposed multivariate test based on skewness or kurtosis and other distribution test.

To summarize, we have developed a simple and useful test to detect SSE in a multivariate meta-analysis setting. As a natural extension of the univariate Egger’s regression test, our test has the advantage of combining signals across outcomes without requiring within-study correlations. We have found that the proposed test is substantially more powerful than the univariate tests and has a practical impact on real applications, calling for more attention on potential SSE or PB during research synthesis. We believe this test is a useful addition for tackling the problem of SSE and PB in comparative effectiveness research.