Differential emergence and stability of sensory and temporal representations in context-specific hippocampal sequences

Abstract

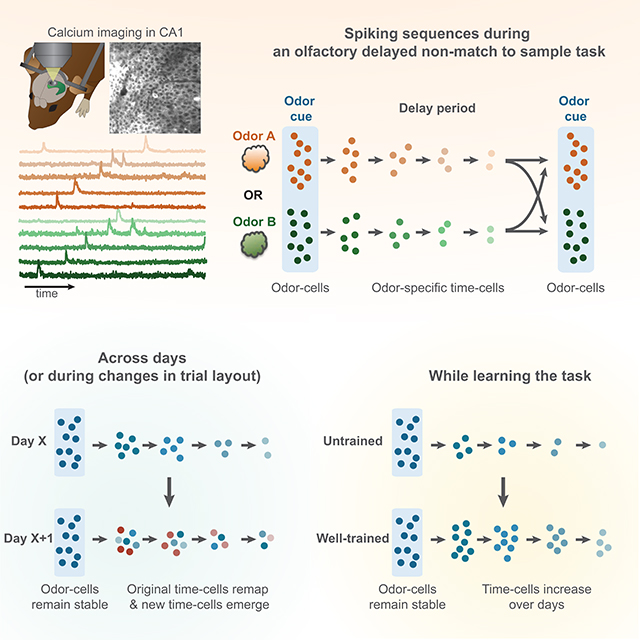
Hippocampal spiking sequences encode external stimuli and spatiotemporal intervals, linking sequential experiences in memory, but the dynamics controlling the emergence and stability of such diverse representations remain unclear. Using two-photon calcium imaging in CA1, while mice performed an olfactory working-memory task, we recorded stimulus-specific sequences of ‘odor-cells’ encoding olfactory stimuli, followed by ‘time-cells’ encoding time-points in the ensuing delay. Odor-cells were reliably activated and retained stable fields during changes in trial structure and across days. Time-cells exhibited sparse and dynamic fields that remapped in both cases. During task training, but not in untrained task exposure, time-cell ensembles increased in size whereas odor-cell numbers remained stable. Over days, sequences drifted to new populations with cell activity progressively converging to a field and then diverging from it. Therefore, CA1 employs distinct regimes to encode external cues versus their variable temporal relationships which may be necessary to construct maps of sequential experiences.

eTOC

Taxidis et al. demonstrate that odor-specific spiking sequences in the hippocampus combine robust and stable encoding of olfactory stimuli with highly dynamic temporal codes that increase during learning of a working memory task. This combination allows linking fixed external elements and their variable temporal relationships in memory space.

Graphical Abstract

INTRODUCTION

The hippocampus forms representations of the external world, as well as internal representations of space and time (Buzsáki and Moser, 2013; Buzsáki and Llinas, 2017; Eichenbaum, 2017). Cell assemblies encoding such information generate spiking sequences which link temporally related experiences to form maps in memory space (Buzsáki and Tingley, 2018; Eichenbaum, 2014). Yet little is known about how such sequences combine sensory and internal information, how they emerge, evolve and stabilize when a context is learned or how they adapt to changes in that context.

External representations are formed via neurons that selectively respond to sensory stimuli, including visual (Kamiński et al., 2017), auditory (Aronov et al., 2017), olfactory cues or combinations of those (Terada et al., 2017). Olfactory responses are particularly prominent in the mouse hippocampus (Eichenbaum et al., 1987; Igarashi et al., 2014; Manns et al., 2007; Wood et al., 1999). Hippocampal networks receive olfactory information through the lateral entorhinal cortex (LEC; Li et al., 2017; Woods et al., 2020) and project back to olfactory cortex (Aqrabawi and Kim, 2007), playing an important role in odor-discrimination (Martin et al., 2007), odor-rule learning (Zelcer et al., 2005) or odor-sequence memory (Fortin et al., 2002).

Internally generated representations involve temporal codes. Neuronal ensembles in area CA1 form spiking sequences of ‘time-cells’, typically observed in delayed-response tasks involving working memory. These cells encode elapsed time during the delay period (Itskov et al., 2011; MacDonald et al., 2011) and can be specific to the remembered stimulus or ensuing response (MacDonald et al., 2013; Pastalkova et al., 2008). Such sequences have also been reported in CA3 (Salz et al., 2016) and cortical regions (Harvey et al., 2012; Tiganj et al., 2016).

The dynamics governing sensory and internal representations have mostly been studied separately, often yielding contradictory conclusions. For example, both stable encoding (Gonzalez et al., 2019; Kinsky et al., 2018; Tonegawa et al., 2015) and dynamic spatial (Mankin et al., 2012; Ziv et al., 2013) and contextual representations (Cai et al., 2016) have been reported, and stability can vary between hippocampal areas (Hainmueller et al., 2018). But to combine fixed sensory inputs as well as their shifting temporal relationships, hippocampal networks may need to employ multiple encoding regimes in parallel. Are sensory and temporal representations encoded with similar reliability, long-term stability and adaptability or with distinct dynamics? Do they pre-exist in the network or emerge and evolve as a context is learned?

To disentangle these alternatives we studied multi-modal representations and compared their dynamics during and after learning a behavioral context. Using in vivo two-photon calcium imaging we recorded activity from thousands of pyramidal cells in the CA1 pyramidal layer of head-fixed mice, over multiple days during and after mice learned to perform an olfactory delayed non-match-to-sample task (Liu et al., 2014), as well as during changes in the trial structure. Our findings reveal distinct representational regimes, intermixed within CA1 neural networks; a robust and stable sensory code followed by a sparse and dynamic temporal code shaped by learning. This combination allows hippocampal networks to encode both fixed elements of the external world as well as their changing temporal relationships to construct maps of sequential experiences in memory space.

RESULTS

Two-photon calcium imaging in dorsal CA1 during an olfactory working-memory task

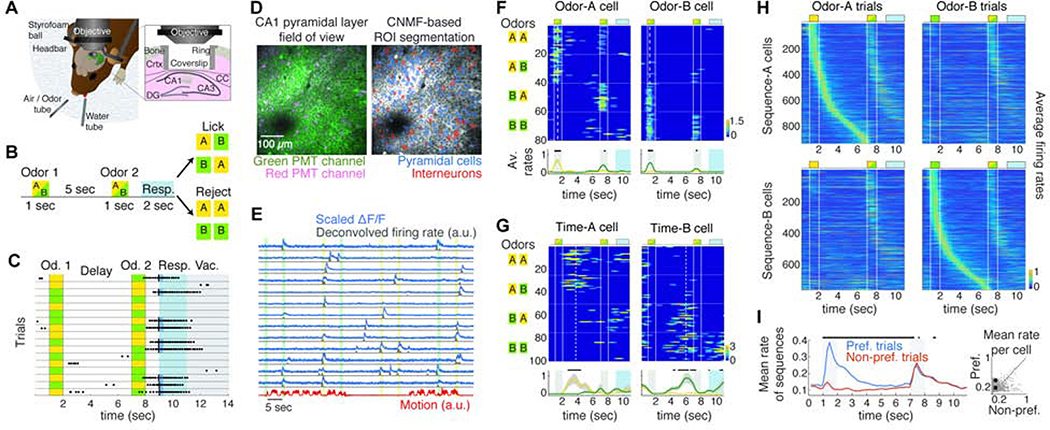
Adult mice (N = 17), expressing tdTomato in GABAergic interneurons, were injected with AAV1-Syn-GCAMP6f virus in the right dorsal CA1 area (dCA1) and were implanted with a titanium ring with glass coverslip over the corpus callosum after surgical aspiration of the overlying cortex (Figure 1A). During water-deprivation they were trained to perform an olfactory delayed non-match-to-sample task (DNMS) involving working memory (Liu et al., 2014), while head-fixed on a spherical treadmill (Figure 1A). Each trial consisted of an odor cue presented for 1 sec followed by a second one after a 5 sec delay. Mice were trained to lick the lickport to release a water reward if the two odors did not match and refrain from licking when they matched (Figure 1B). Cues were either isoamyl acetate (‘odor-A’) or pinene (‘odor-B’). Each session comprised of typically 5 trial-blocks (and always between 4–8) of 20 trials each, with randomly distributed odor-combinations (Figure 1C). Performance was quantified as the ratio of summed correct hits and correct rejections over all trials in each trial block.

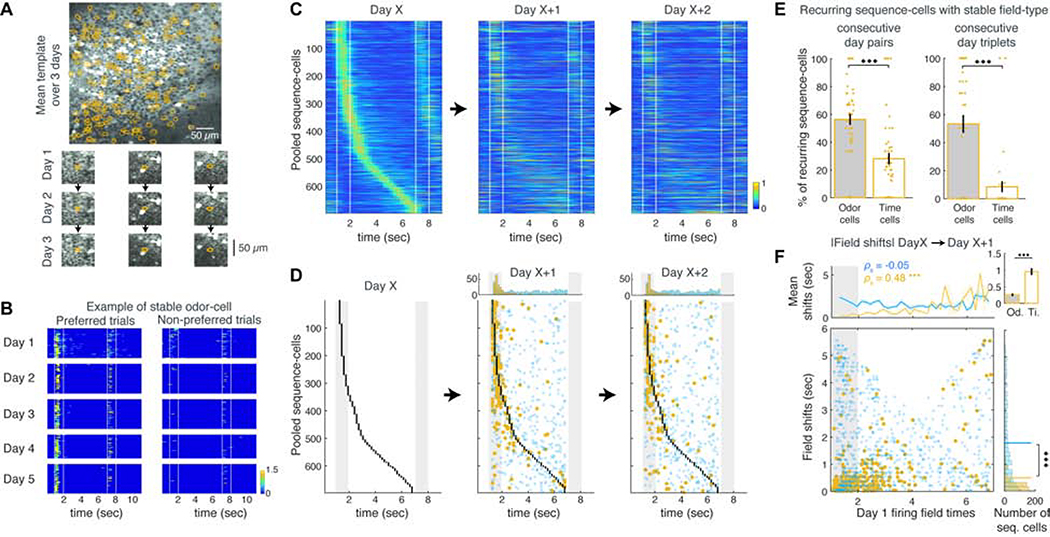
Figure 1: Odor-specific spiking sequences in dCA1 encode cues and delay time in a DNMS task.

A. Behavioral and experimental set-up. CC: corpus callosum. B. Schematic of the DNMS trial. Licking is assessed during a 2 sec response window (blue). C. Example trial-block. Dots indicate licks. The first lick in the response window (black lines) triggers a water drop (blue) only in non-match trials. Vac: vacuum applied at trial end to clear the water tube. D. Left: Example FOV in dCA1 pyramidal layer, recorded in green and red PMT channels, from a Gad2Cre:Ai9 mouse expressing GCaMP6f (green). Interneurons express tdTomato (magenta). Right: Same FOV after ROI segmentation. E. Example ΔF/F traces (scaled by their maximum value), binned deconvolved spiking probability (‘firing rates’) and motion on treadmill during 4 DNMS trials. Color bars: odor delivery. F. Firing rates of example ‘odor-cells’ encoding odor-A and odor-B during a session, with trials (rows) stacked in blocks (horizontal lines) according to odor combination (left). Trial layout shown on top. Vertical lines: odor delivery. Dashed lines: firing field time-bin. Bottom: Mean rate over odor-A (yellow) and odor-B trials (green). Dots: P < 0.05, Wilcoxon test (WT); FDR-corrected over all time-bins (FDR). G. Same as F for two ‘time-cells’ with fields during the delay after a specific odor. H. Average rates of sequence-A (odor-A and time-A cells; top) and sequence-B (bottom) over odor-A (left) and odor-B (right) trials, pooled over mice and well-trained sessions. The second odor in a trial can be either A or B. I. Average rate of pooled sequence-cells over trials starting with their corresponding preferred odor versus the opposite one. Bars: P < 0.05; WT; FDR. Right: Average rate of each cell across the odor-delay interval over preferred versus non-preferred trials. Square: Mean across cells is higher for preferred trials (* P < 0.001; right-tailed paired sample t-test). Throughout all figures, gray bars indicate odor delivery, color-bars refer to all relevant panels in a group, error-bars indicate standard error and all sequence-cell firing rates are normalized by the cell’s average rate at its field.

We recorded activity in the dCA1 pyramidal layer, using two-photon calcium imaging in vivo, while animals performed the DNMS task. Calcium imaging movies, recorded on green and red PMT-channels to segregate pyramidal and GABAergic activity (Figure 1D), were motion-corrected and active regions of interest (ROI) were segmented and split into pyramidal cells and interneurons, using custom-written software based on an extended version of the CNMF algorithm (Giovannucci et al., 2019; Pnevmatikakis et al., 2016). Extracted calcium signals were deconvolved to yield a measure of time-binned spiking probability for each ROI (Figure 1E) which we used as proxy of spiking activity and refer to as ‘firing rate’ for simplicity. Imaging sessions (N = 160 in total) yielded 191.7 ± 121.3 pyramidal cells (mean ± SD) and 45.1 ± 14.9 interneurons (75.8 ± 14.1% and 24.4 ± 14.1% of all ROI respectively). Only 2.5 ± 2.2% of all CNMF-detected ROI were interneurons, as calcium traces from these cells did not meet CNMF criteria (Methods). All interneurons were removed from analysis. A combination of rotating stages ensured that the same field of view (FOV) per mouse was recorded in every session. FOVs were aligned across days, and registered cells were tracked for multiple days. Locomotion on the treadmill was also monitored (Figure 1E).

Control experiments confirmed that mice relied on working memory to perform the DNMS task (Figure S1): i) Task participation stopped when odors where turned off, excluding the use of auditory cues from valves. ii) Airflow values were identical for the two odors to exclude relying on them to perform DNMS. Performance was also unaffected by randomly varying airflows for the two odors. iii) Odor mixture during the second odor presentation in non-match trials was prevented by minimizing the common tube-path for the two odors (~4cm), confirmed by photo-ionization detector measurements. iv) To test whether mice detected lingering odors during the delay, 3 animals were trained on a non-match-to-long-duration-sample task (Liu et al. 2014) where a 5 sec-long odor-stimulus was followed by a 1 sec matching or non-matching odor. Mice had to lick for reward only in non-match trials. Mean performance dropped to chance levels when the odorant concentration of the long stimulus was reduced to 0.01%. Based on this threshold, odorants were undetectable within 1 sec of odor offset in DNMS. v) Performance declined over increased delay durations (N = 4 mice), corroborating that working memory was employed during DNMS.

Odor-specific spiking sequences encode the presented stimulus and the ensuing delay time

Focusing on the first odor cue and the ensuing delay period (‘odor-delay interval’) in each trial in well-trained sessions (average daily performance ≥90%; N = 8 mice, 32 sessions), we found ‘odor-cells’ whose activation was significantly coupled to the presentation of a specific odor (Figure 1F), as well as odor-specific ‘time-cells’ that tended to fire during specific time bins in the ensuing delay (Figure 1G). These neurons fired in a continuum forming two distinct sequences: ‘Sequence-A’ comprised of ‘odor-A’ and ‘time-A’ cells, spiking during odor-A and its ensuing delay, and ‘Sequence-B’ for odor-B accordingly (Figure 1H). We collectively refer to these neurons as ‘sequence-cells’ and their fields refer to the time-bin of their statistically significant, average activity peak. We note that the naming ‘odor-cells’ and ‘time-cells’ is purely operational and used for semantic simplicity, since we analyzed them separately throughout the text, and for consistency with previous studies. However, as shown in the rest of the study, the two cell groups have radically different short- and long-term dynamics.

Sequences were observed in all mice, covering parts or the entire odor-delay interval in individual sessions (Figure S2). 22.6 ± 7% of detected (active) pyramidal cells per well-trained session were classified as sequence-cells. 5 ± 2% and 8.3 ± 3.7% of all cells were odor-A and time-A cells respectively; 5.5 ± 2.2% and 5.3 ± 2.8% were odor-B and time-B cells respectively. They exhibited higher firing rates during their preferred- than non-preferred odor trials (Figure 1I) and fired mostly within their field, retaining similar activity throughout a session’s trials (Figure S2). 93.8 ± 6.1% of these neurons belonged to a single sequence while 6.2 ± 6.1% had significant fields in both sequences, with 28.6 ± 23.1% of those having the same field (those were assigned to the sequence where they exhibited higher average peak activity). 86 ± 31% of cells in this latter subgroup were odor-cells that responded to both odors early during their presentation, encoding trial-onset (Figure S2).

The same sequences were also triggered by the second odor (Figure 1H), though behavioral and reward variations confounded activity after its presentation. During the second stimulus, odor-cells showed a small reduction in activation probability, in firing rates during activated trials and in selectivity to their preferred odor compared to the first odor (Figure S2). These effects were not driven by early licking during the second odor, since removing those trials did not affect results. Odor-cells exhibited similar activation probability during the second odor in match and non-match trials (Figure S2) though 34.1 ± 24.6% and 24.3 ± 15.8% odor-cells were >2x more likely to be activated if the second odor was preceded by a matching or a non-matching odor respectively. Moreover, 6.2% ± 5% of non-sequence-cells encoded a specific odor combination during and after the second odor, while 3 ± 2.6% and 3.3 ± 2.8% were preferentially activated by match or by non-match trials respectively (Figure S2).

Control experiments confirmed that sequences encoded the identity of the olfactory stimulus (Figure S3): i) Sequence-cells did not encode odorant concentration, potentially waning throughout the delay from lingering odorant. If each cell encoded a particular concentration, reducing the delivered odorant would silence odor-cells and shift time-cells earlier in the trial. Sequences remained robust when the odorant concentration was reduced. ii) Sequences did not encode locomotion on the ball, since individual animals had different locomotion patterns during trials and there were no differences in activity between trials with immobility versus trials with highest locomotion. iii) Sequences were not triggered by auditory stimuli from air valves, since turning the air supply off while retaining all valves on silenced sequence-cells.

Sequence-cells were intermixed and randomly distributed throughout the pyramidal layer (Figure S4). Spatial proximity of two cells was not correlated with their preferred odor, since odor-cells and time-cells of the same sequence were similarly distributed to those of opposite sequence. Distances between time-cells of the same sequence were also not correlated with the temporal intervals between their fields.

Therefore, uniformly distributed pyramidal cells in dCA1 pyramidal layer form stimulus-specific spiking sequences during the DNMS task, triggered by the identity of the odor cue and tiling the odor presentation and ensuing delay, corroborating findings in head-fixed rats (MacDonald et al., 2013).

Odor and timing information monotonically decreases throughout the delay

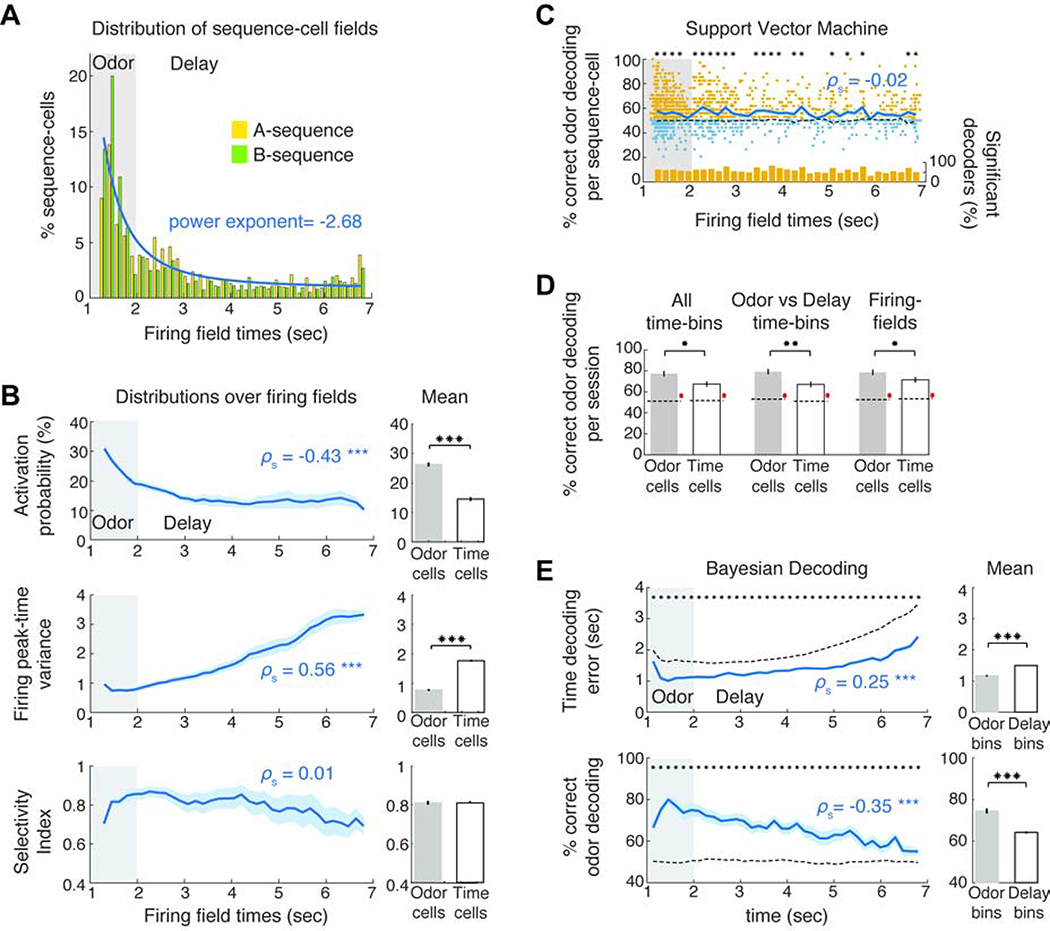
How efficiently are odor and time encoded by sequence-cells throughout the odor-delay interval? Even though odor presentation was encoded by many odor-cells, time-fields were sparse with decreasing density throughout the delay that could be fitted by a power law (Figure 2A; P < 0.01 for goodness of fit based on random sampling), supporting theoretical predictions of logarithmic reduction in field density (Liu et al., 2019). Sparser fields were not due to any inability to detect late time-cells since the mean ΔF/F amplitude of sequence-cells did not change across the trial (Figure S5).

Figure 2: Robust odor-cell activation is followed by progressive information loss by time-cells.

A. Field distribution for the two sequences and mean power-law fit (blue) of distribution. B. Mean activation probability (% preferred trials where each cell spiked at its field), variance of each cell’s peak-activity time-bin per trial and selectivity index as a function of field (ρ_s: Spearman correlation throughout the text). Right: Average over odor- and time-cells. C. Mean odor-decoding accuracy (blue) by SVM classifiers, trained on each cell’s average activity over the odor-delay interval, as function of its field. Yellow dots: classifiers with significantly higher accuracy than chance (P < 0.05, WT, FDR). Blue: non-significant ones (small random noise added for plotting clarity). Bottom: ratio of significant decoders in each field. D. Odor-decoding accuracy by SVM classifiers trained on odor- or time-cell activity averaged over the denoted temporal intervals in each trial. Accuracies were significantly higher than chance (red *). E. Mean time-decoding error (absolute values) and odor-decoding accuracy as a function of time from Bayesian decoders trained on all sequence-cells per session. Right: Average over odor- and time-bins. Dashed lines in panels: Chance baseline. * P < 0.05, ** P < 0.01, *** P < 0.001. SPT for all spearman correlations and WT for distribution comparisons or comparisons to chance baseline per time-bin, FDR corrected over corresponding tests or time-bins accordingly.

Furthermore, the activation probability of sequence-cells during their preferred trials decreased across the delay and their variability in activation time increased (P < 0.001, Spearman rank correlation permutation distribution test, ‘SPT’ henceforth), so that time-cells spiked in less trials and with noisier activation than odor-cells (P < 0.001; WT). This variability resulted in increasing field sizes along the delay, in agreement with electrophysiological (MacDonald et al., 2011) and theoretical studies (Howard et al., 2014) though it may be driven by an increase in peak firing rates over trial-time (Figure S5). Interestingly, the mean selectivity index (SI) of sequence-cells did not change across the trial (P > 0.05, SPT; FDR across 3 tests), indicating a similar selectivity for all cells to their preferred odor (Figure 2B).

Is odor information retained in single cells throughout the delay? Binary support vector machine (SVM) classifiers, trained on each sequence-cell’s average activity over the odor-delay interval, decoded odor-identity significantly better than chance on average (Figure 2C; P < 0.05 vs chance baseline; WT, FDR) and a uniform ratio of these classifiers per time-bin performed better than chance (P > 0.05, SPT) mirroring the stable odor-selectivity across the delay. To assess olfactory information in the ensemble activity of odor or time-cells, we trained SVM classifiers on the collective firing rates of either cell group, averaged over the odor-delay interval, the odor presentation or delay period respectively, or at the specific field of each cell (Figure 2D). All three intervals yielded similar odor-decoding accuracy that was better than chance for both groups (P < 0.001 WT versus shuffled data; FDR), but was lower for time-cells than odor-cells in all cases (P < 0.05).

Is olfactory and temporal information collectively retained throughout the delay period of a trial? Principal component (PC) analysis over trials initiated by the two odors, yielded average trajectories that deviated during odor presentation but intermingled as delay progressed (Figure S5) due to averaging across trials with variable cell activation. To decode timing by ensemble activity along individual trials, we trained Bayesian decoders on all sequence-cells) and decoded time-points along a doubled odor-delay interval, representing time and odor-information (Methods). Errors in time-decoding increased across the delay and the accuracy of odor-decoding decreased (P < 0.001, SPT) though both variables were decoded better than chance in all time-bins (P < 0.05, WT over shuffled data; FDR; Figure 2E).

Therefore, a robust odor presentation code is followed by a sparse and noisy temporal code with odor and timing information retained throughout the delay but monotonically degrading, supporting theoretical and computational models of scale invariant sequences (Howard et al., 2014; Liu et al., 2019).

Odor-cells remain relatively stable while time-fields are remapped during changes in trial configuration

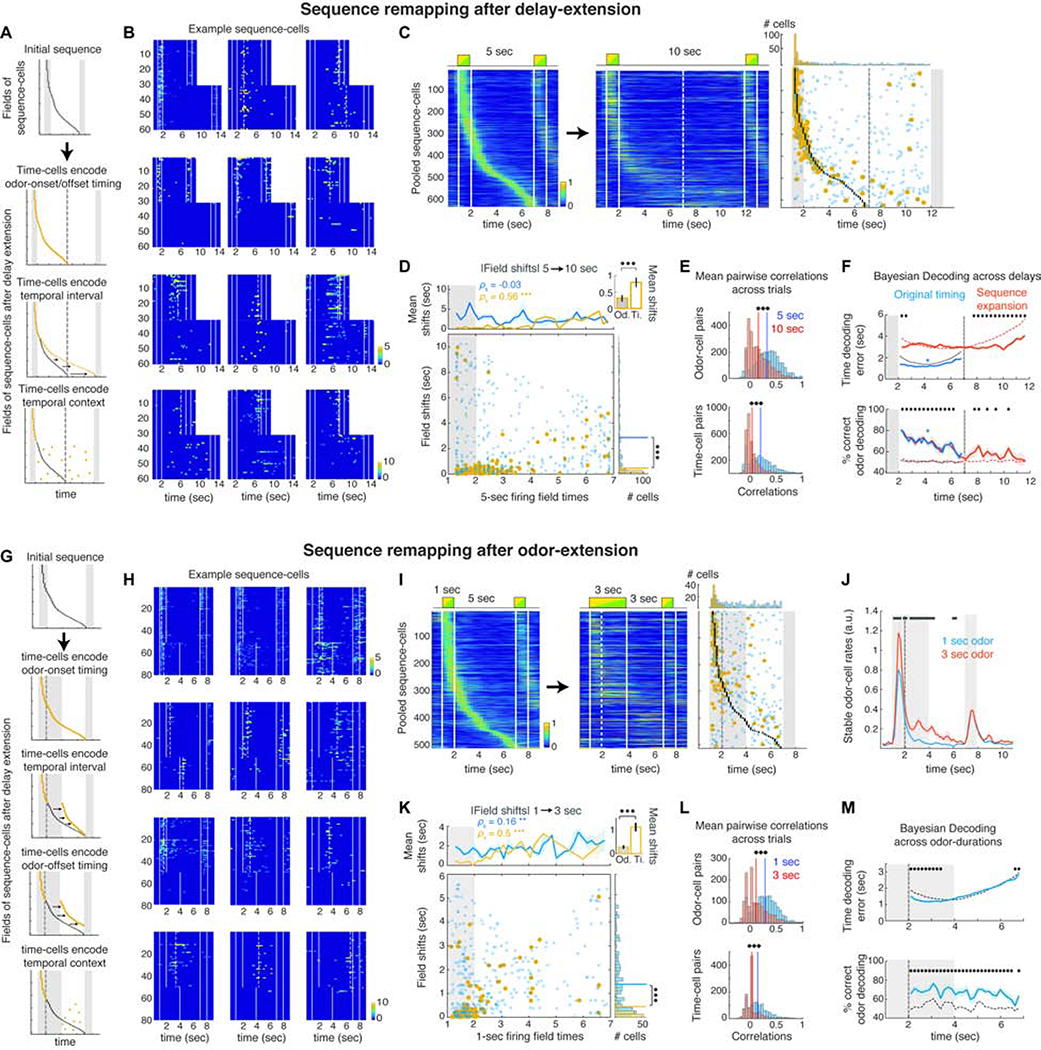
How do these sequences adapt to changes in the DNMS trial? If spiking sequences encode specific behavioral contexts (Buzsáki and Tingley 2018; Eichenbaum 2014, 2017), time-cell sequences should get reconfigured if the delay duration is changed, independently of preceding odor-cell activity. Alternatively, if time-cells are passively triggered by odor-cells, sequences will persist irrespective of the ensuing trial structure (‘feedforward chain model’; Eichenbaum 2014). Finally, if sequences are shaped solely by the delay duration, any change to it should be mirrored in the sequence expanding or contracting accordingly (Figure 3A).

Figure 3: Odor-cells retain their activity whereas time-fields remap when the delay or odor-delivery is extended.

A. Sequence-remapping under different encoding models when the delay period is doubled. Dashed line: Default delay offset. B. Activity across all 5 sec and 10 sec delay trials in example cells that retain a field near the same time-bin, become silent or sparsely activated, exhibit disorganized activation or shift activation to the added delay. Dashed lines: significant fields. C. Pooled sequence-cells mean activity over preferred trials in default and extended delays. Right: Black dots depict fields of the initial sequence. Circles depict the time-bin of each cell’s peak rate in the 10 sec delay trials. Blue: Non-significant peaks. Yellow: Significant fields. Dashed lines: 5 sec delay offset. Top: Distributions of significant and non-significant peaks. D. Absolute time-shifts of peak activation in the extended trials as a function of their initial field. Top: Mean shifts for stable (yellow) and unstable cells (blue). *** P < 0.001, SPT. Inset: Mean shifts of stable odor- and time-cells (P < 0.001, WT). Right: Histogram of field shifts. Lines: distribution means (P < 0.001, two-sample Kolmogorov-Smirnov test). E. Average pairwise correlations for odor and time-cells before and after delay extension. Solid lines: Distribution means (*** P < 0.001; paired t-test). F. Mean time-decoding error (absolute values) and odor decoding accuracy, using Bayesian decoders trained on the original time-cell activity and decoding either the first 5 sec of the extended trials (blue) or the entire 10 sec delays under a ‘sequence-expansion’ model (Methods; red). Dashed curves: Chance baseline (* P < 0.05; blue *: P < 0.05 for all time-bins; WT; FDR). G. Sequence-remapping schemes when odor delivery is extended over the delay. Dashed line: Offset of default odor delivery. H. Example cells during default and extended-odor trials, as in B. Top row: Cells retaining or expanding their field over the prolonged odor. Rest: Examples of field shifts, disorganized or sparse activation. I. Pooled sequence-cells over the default and prolonged-odor trials as in C. J. Mean rates of stable odor-cells during default and prolonged-odor trials (black bars: P < 0.05, WT, FDR). K. Time-shifts of peak activity during the prolonged-odor trials, plotted as in D. L. Pairwise correlations before and after odor-prolongation, as in E. M. Time decoding error and odor decoding accuracy in prolonged-odor trials with Bayesian decoders trained on original time-cell activity, plotted as in F (* P < 0.05; WT; FDR).

To disentangle these alternatives, we extended the delay period from 5 to 10 sec within consecutive trial blocks (N = 5 mice; 10 sessions). Mice had not been exposed to extended delays previously but their performance exhibited only a minor reduction (from 96 ± 7% to 88.3 ± 14.8%; P < 0.01; WT). During extended delays, roughly half of odor-cells (55.1 ± 13.7%) retained significant fields (‘stable cells’) which remained odor-fields in their majority (96.7 ± 4.6% of significant fields). In ‘unstable’ odor-cells (i.e. not retaining a significant field anywhere in the odor-delay interval) 61.8 ± 27.5% shifted their peak activity to the delay, 32.8 ± 27.1% retained it in the odor-presentation and 5.4 ± 2.3% became inactive (Figure 3B). In contrast, few ‘stable’ time-cells retained a field (25.3 ± 13%; P < 0.001; WT compared to odor-cells). Those were mostly early time-cells (83.4 ± 15.4% had initial field < 4 sec) whose fields did not shift considerably (85.8 ± 13.1% of those shifted by < 1 sec). Consequently, the fields of stable time-cells covered less delay time than the original sequence (Figure S6). Most time-cells did not retain a significant field and their peak activity shifted in time (57.4 ± 12.8% non-significant peaks were shifted > 1 sec), supporting previous studies (MacDonald et al., 2011). Even though the activation probability of 51.8 ± 21% time-cells anywhere in the extended odor-delay interval increased, their timing of activation became disorganized (83.3 ± 5.3% time-cells with increased peak-activity timing variance; Figures 3B–C). Unstable cells shifted their peak-activation more than stable ones (P < 0.001; Kolmogorov-Smirnov test) whose shifts increased as a function of their initial field (P < 0.001 SPT) as stable time-cells yielded larger shifts than odor-cells (P < 0.001; WT) and late time-cells remapped more than early ones (Figure 3D). Interestingly, 41.7 ± 25.2% of late time-cells (initial field > 4 sec) versus 14.2 ± 11.8% of early ones, shifted their peak activity to the added delay (Figure 3B).

The sequence disorganization was reflected in significantly reduced pairwise correlations between odor-cells and more so between time-cells (Figure 3E; P < 0.001; paired t-test). Many time-cells started remapping as soon as the delay was extended (Figures 3B, S6) yielding reduced per-trial correlations from the first extended trial onwards, while the de-correlation of odor-cells was more gradual (Figure S6). However, Bayesian decoders trained on time-cell activity during the default trials, performed better than chance in decoding the first 5 sec of the extended delay (Figure 3F; P < 0.05 versus chance; WT; FDR) suggesting that timing information was partially retained. When decoding across the entire extended delay (assuming sequence expansion, with late time-cells shifting forward more than early ones; see Methods), only the first ~1 sec and the final ~4 sec of added delay could be decoded better than chance (Figure 3F; P < 0.05 versus chance; FDR), supporting a sequence expansion mostly for the late time-cells. Odor-identity could be decoded efficiently, but less so over the additional delay period (Figure 3F).

In parallel, new sequences emerged across the 10 sec-delay trials, from the first trial block onwards, comprising of a similar percentage of time-cells as the original ones (Figure S6), 82.1 ± 7.8% of which were new cells. In default trials, these were often sparsely active or with disorganized activation, lower pairwise correlations and peak activity distributed across the 5 sec delay (Figure S6). 64.2 ± 10.8% of new time cells with < 5 sec fields had peak activation < 1 sec away in the original trials but not reaching significance, and late time-cells covering the added delay spiked during late parts of the initial delay as well (Figure S6). Moreover, 56.3 ± 15.7% of new odor-cells spiked during the delay in default trials, 35.8 ± 13.9% were active during odor-presentation but not reaching significance and 7.8 ± 3% were completely inactive. Bayesian decoders trained on the new sequence activity and decoding time in the original delay (reversing the sequence expansion scheme) performed better than chance, particularly during early and late parts of delay (Figure S6), suggesting that new sequences partially emerged by the extension of non-significant timing activity in the original trials.

Our findings favor the context-representation model but also indicate partial retainment of initial timing as well as sequence-expansion. To disassociate these alternatives further, we asked if time-cells remap when the trial structure is changed but its duration is not. In a different set of mice (N = 9 mice; 22 sessions) we extended the first odor delivery from 1 to 3 sec in consecutive trial-blocks and shortened the delay to 3 sec, retaining an odor-delay interval of 6 sec total. If time-cell sequences encode time-since-odor-onset or offset they would remain intact or shift forward respectively, whereas if they are shaped explicitly by the delay interval they would be compressed (Figure 3G). Odor prolongation yielded qualitatively similar results to delay extension. Again we found more odor-cells than time-cells retaining significant fields (34 ± 25.2% versus 17.2 ± 23.8%; P < 0.05, t-test; Figures 3H–I, S7). Interestingly, stable odor-cells and some early time-cells significantly increased their mean activity throughout the added odor delivery (Figures 3H, 3J, S7; P < 0.05; WT; FDR), corroborating that odor-cells encode stimulus delivery. Time fields radically remapped and their activation became sparser or disorganized from the first altered trial block onward (Figures 3H, 3L, S7). Peak activation of stable and unstable cells shifted as before (Figure 3K). New sequences tiled the extended-odor trials, comprised of similar percentage of odor-cells, with the extended odor-delivery represented by its own sequence with markedly different field distribution than the new time-cell sequence (Figure S7). Bayesian decoders trained on time-cells during the initial delay, performed better than chance only when decoding time over the extended odor delivery (Figure 3I; P < 0.05; WT; FDR; similar for reverse time-decoding using the new sequence, Figure S7), reflecting the activity extension of early time-cells combined with a radical remapping of late time-cells.

Collectively, during alterations in trial structure, odor-cells largely retained their activity compared to time-cells that were readily reconfigured and partly replaced by new ones, supporting a ‘temporal context’ model for spiking sequences.

The number of time-cells increases during DNMS learning but not during passive exposure to trials

Little is known about how hippocampal representations emerge when a context is learned. Are odor-specific sequences present in dCA1 before the animal is exposed to DNMS trials or do they emerge through learning the context of the task?

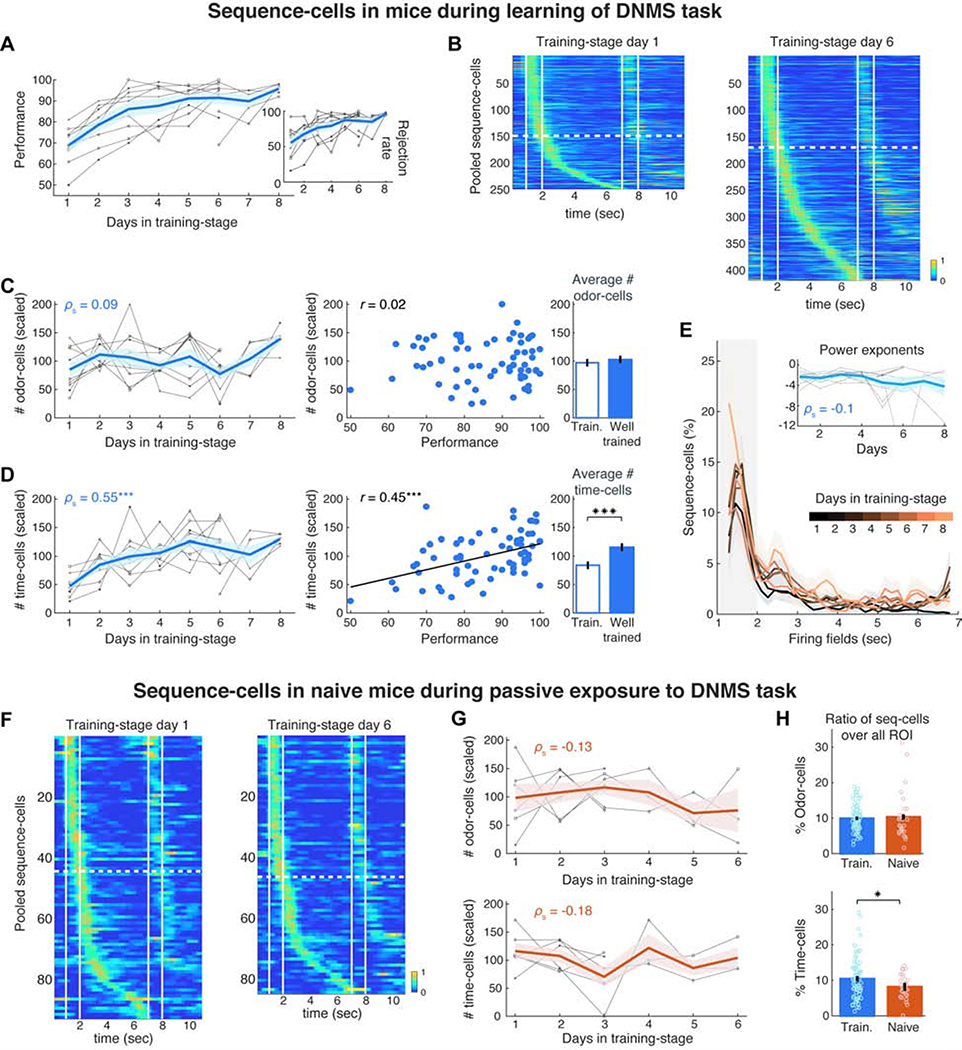
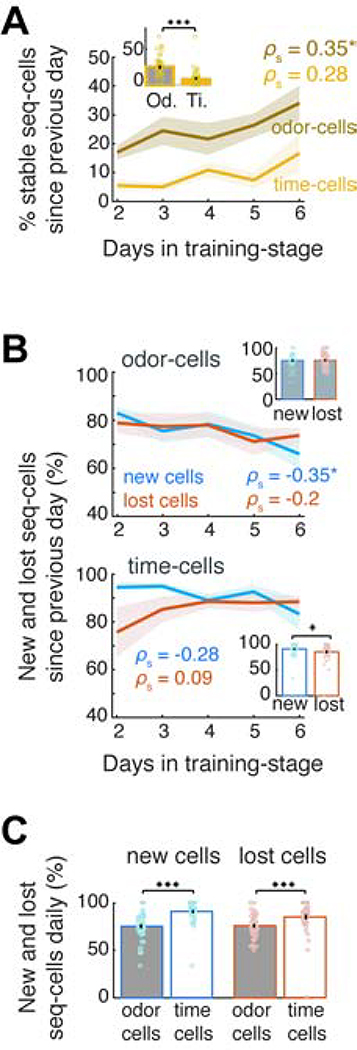
We performed calcium imaging in mice (N = 11) while they were learning the full DNMS task. In a pre-training stage not requiring working memory, these animals had only been exposed to non-match-trials where they learned to always lick after the second odor to release a reward. Imaging started when they were introduced to the full DNMS task where they learned to reject match-trials over days while retaining a high hit rate in non-match trials. Together with the rejection rate, performance increased rapidly, reaching well-trained level within 3–6 days (>90% mean daily performance; Figure 4A). 9 mice were imaged from the first day of the full-DNMS training-stage and 2 mice from its 6th day onwards.

Figure 4: Time-cells selectively increase in number during DNMS learning, but not during passive exposure to trials.

A. Mean performance (blue) of individual mice (grey) over DNMS training days. Inset: Rejection rate for match trials. B. Pooled sequence-cell rates in preferred trials on Day 1 and 6 of training-stage (same 9 mice). Dashed lines separate odor-cells from time-cells. C. Left: Number of odor-cells per day, scaled for each mouse by their mean number across all days (in %), plotted as in A. Middle: Scaled number of odor-cells versus mean performance daily. r: Pearson correlation. Right: Mean scaled number of odor-cells during all days at ‘training level’ (<90%) versus ‘well-trained’ level (≥90% daily performance; P > 0.05, WT). D. Same as in C for number of time-cells, scaled as before. Time-cells increased over days (P < 0.001, SPT) and were correlated with performance (P < 0.01, Pearson permutation test; FDR over the two cell types; Black line: least-squares linear fit) with lower average number in training than in well-trained sessions (P < 0.001; tailed two-sample t-test). E. Distribution of fields per day, scaled by the mean distribution for each animal and averaged across animals. Inset: Exponent of power law fit of each day’s distribution per animal (one outlier truncated for clarity). F. Pooled sequence-cell rates in 3 untrained animals on Day 1 and 6 of passive exposure to DNMS trials. G. Same as panels C-D (left) for scaled number of odor- and time-cells in untrained animals (N = 6) exposed to the full DNMS task (P > 0.05, SPT). H. Mean ratio of odor- and time-cells over all ROI daily, in trained versus naive mice (* P < 0.05, right-tailed WT).

We tracked the number of sequence-cells throughout DNMS learning. Since our fixed FOV per mouse contained an overall stable set of neurons, compared to the variable number of CNMF-detected (active) cells daily, we focused on the actual number of sequence-cells daily (as opposed to ratios over ROI). Even though the number of odor-cells did not change substantially during training and was uncorrelated to performance (P > 0.05, Spearman and Pearson correlation permutation tests respectively), the number of time-cells increased over time (Figure 4B) and was significantly correlated with days in training and with mean daily performance (Figures 4C–D; P < 0.001, same tests; FDR over the two cell-types), resulting in more time-cells in well-trained days than training days (Figure 4D). Interestingly, the distribution of time-fields did not change over time, retaining a similar power-law profile daily (Figure 4E).

This increase was not confounded by any overall changes in activity since there were no trends across days in: i) the total number of ROI daily, ii) their mean firing rate or iii) their inter-spike intervals during each trial. The number of daily trials or locomotion on the treadmill also did not change. The same held for imaging conditions and GCaMP6f expression since no trends existed in: i) ΔF/F amplitudes during cell activation, ii) the standard deviation of these amplitudes, or iii) the baseline fluorescence of cells (Figure S8). The decay time of calcium transients minimally increased over days (~50 ms), similarly for odor- and time-cells (P > 0.05, two-sample t-test, FDR), precluding it can affect the size of any particular cell group (Figure S8). Limiting analysis to days with high relative-correlation of FOV with the template FOV of Day 1 in each mouse also did not affect results, excluding any small changes in FOV as confounds (Figure S8). Finally, switching to ratios over all detected cells daily yielded similar results (Figure S8). The spiking properties of individual sequence-cells were also stable during learning since we found no correlations of the SI, activation probability or peak-activity time variance with days or performance (Figure S8). Odor-cells also showed no changes in odor selectivity and activation probability during the second odor in a trial, or in selectivity to first versus second odor (Figure S8).

Do time-cells emerge over DNMS learning or are they present before the animal is exposed to any trials? We imaged 6 mice that were water deprived and habituated to head-fixation but were naive to the DNMS task, with no previous exposure to the odors or any lick-training. Mice were imaged for 3 or 6 days, while passively exposed to a similar number of DNMS trials daily as trained mice. Even though these animals did not yield a behavioral output or receive any reward, sequences similar to trained mice existed (Figure S9). Cells were often already tuned to a particular field from the first trials of DNMS exposure onwards even though the olfactory cues were novel. Within a few trial-blocks, sequences were similar to those of Day 1 in training mice and had similar field distributions and spiking properties (Figure S9). Therefore, pre-existing cell assemblies get quickly associated with novel odors, supporting previous observations of place-cell ‘preplay’ before novel navigation (Dragoi and Tonegawa, 2011).

Could the increase in time-cells be driven by the repeated activation of odor-cells over days of stimulation, independently of DNMS learning? Sequences on Day 1 were similar to those on Day 6 of passive DNMS exposure in naïve mice and the size of neither odor-cell nor time-cell ensembles changed across days (Figures 4F–G; P > 0.05; same for ratios over all cells daily, Figure S9). As a result, the two mouse groups had a similar percentage of odor-cells over all ROI but naive mice had a significantly lower percentage of time-cells compared to trained mice (Figure 4H; P < 0.01, WT, FDR).

The increase in time-cells led to increased information. Using independent Bayesian decoding daily, the decoded-time error significantly decreased during training, anti-correlated with performance, and decoded-odor accuracy increased over days (Figure S10). In contrast, decoding accuracy in naive mice was better than chance but did not change across days (Figure S10).

Collectively, olfactory and temporal representations exist even in naive animals passively exposed to trials, but time-cell ensembles selectively increase during learning the DNMS task, but not in passive trial exposure, whereas odor-cells remain stable.

Odor-cells retain their fields across days whereas time-fields are remapped

Is there a fixed sequence-cell ensemble from training onset with new time-cells added daily? Or do temporal representations shift to new, larger ensembles daily? Non-stimulus-specific time-cells during locomotion are dynamic across days (Mau et al., 2018) but non-spatial multi-modal representations are under-explored.

We aligned the stable FOVs of each mouse between each pair of days, registering cells appearing in both days and detecting those that belonged to the same sequence (‘stable cells’; Figures 5A, S11). The same sessions as before were analyzed (N = 11 mice) and findings were similar in training and well-trained sessions. The number of matched cells and the ratio of matched over all sequence-cells decreased with distance between days (Figure S11), suggesting a progressive drift in ensemble activity over time. The number of common odor-cells also decreased the further apart two days were but remained higher than that of time-cells, up to 4 days apart (Figure S11). In fact, odor-cells often retained a significant field in their preferred trials for multiple days (Figure 5B), whereas few time-cells were stable for > 2 consecutive days. As a result, pooled odor-cells of any Day X that were matched to cells on the next two days remained overall stable whereas time-cells mostly lost their field or shifted their activity (Figures 5C–D). Thus, more stable odor-cells existed between 2 or 3 consecutive days than time-cells (Figure 5E) and odor-fields shifted significantly less than time-fields (Figure 5F). Again, the initial field of a stable cell was correlated with its shift the next day (Figure 5F; P< 0.001; SPT). A minority of cells transitioned between odor and time-encoding across days, and even fewer cells switched preferred odor across days (Figure S11).

Figure 5: Odor-cells retain their activity whereas time-fields remap across days.

A. Example FOV averaged over 3 consecutive days. Contours: cells registered across all days. Bottom: Example registered cells on each day. B. Firing rate of an example stable odor-cell over all preferred and non-preferred trials during 5 consecutive days. C. Pooled sequence-cell rates from any Day X and their activity during the next two days, stacked in the same order (only cells matched over all 3 days included). D. Same as panel C, showing the original fields of Day X (black dots) and their peak activity time-bins in following days. Stable and unstable cells shown as before (blue and yellow respectively). Top: Distributions of significant and non-significant fields each day. E. Mean ratio of stable odor- versus time-cells between two or three consecutive days. *** P < 0.001, t-test). F. Absolute time shifts of sequence-cells over consecutive days as a function of their initial field, plotted as in Figure 3D.

Any cell mis-registration from small deviations in parts of the FOV across days did not underlie time-cell instability since including only day with high relative FOV correlation (65% of all continuous pairs and 37.5% of continuous day triplets) yielded similar results (Figure S11).

Therefore, spiking sequences combine stable olfactory representations with highly dynamic temporal ones.

Turnover in odor-cell and time-cell ensembles during learning

Given the differential stability of odor- and time-cells, is there a relatively fixed set of odor-cells from the onset of training and a new, expanding set of time-cells daily?

Focusing only on mice that were recorded from Day 1 of DNMS training (N = 9), we examined the sequence-cell turnover across the first 6 training days. From Day 2 onwards, we computed separately for odor- and time-cells the ratios of (i) ‘stable’ cells retaining a field in the same sequence as the previous day, (ii) ‘new cells’ that did not have a significant field the previous day and (iii) ‘lost cells’, i.e. previous day’s cells that did not retain a field on the current day. Stable odor-cells increased significantly over days (Figure 6A; P < 0.05, SPT) whereas the inflow of new odor-cells decreased (P < 0.05; SPT) and, on average, remained similar to the outflow of lost ones daily (Figure 6B; P > 0.05 WT). In contrast, stable time-cells did not increase substantially (P > 0.05) and were less than odor-cells (Figure 6A; P < 0.001; WT), corroborating their instability. The inflow of new time-cells was higher than the outflow of lost ones daily, particularly during the initial days of learning (P < 0.05; WT; Figure 6B) and neither one changed significantly over days (P > 0.05 SPT). Finally, the turnover of time-cells was higher than odor-cells (Figure 6C; P < 0.001; WT; FDR).

Figure 6: Higher daily inflow of new cells than outflow of lost ones.

A. % odor- and time-cells daily that retained a field in the same sequence from the previous day (‘stable’). * P < 0.05, SPT, FDR over two cell groups. Inset: Mean across days. *** P < 0.001; WT. B. Inflow of new odor-cells and time-cells (blue) versus outflow of lost ones daily (red; see text for definition). Insets as in A. * P < 0.05, paired t-test. C. Mean daily inflow of new versus outflow of lost sequence-cells. *** P < 0.001, WT, FDR.

Interestingly, the co-activation and cross-correlation between pairs of stable odor- or time-cells was significantly higher than corresponding pairs of new cells daily, indicating that neurons which retained their field across days formed more synchronously active ensembles, though overall population synchrony did not significantly increase over days (Figure S12).

Therefore, the fixed number of odor-cells is maintained by a slow accumulation of stable neurons and a decreasing, balanced cell turnover. In contrast, time-cell ensembles expand through a higher cell turnover with more cells added than lost daily.

Sequence-cells gradually converge to and diverge from their field time-bin over days

How did neurons spike before they became a new odor- or time-cell? Does the activity of a sequence-cell contain timing-information on days before it acquires a field or after it has lost it?

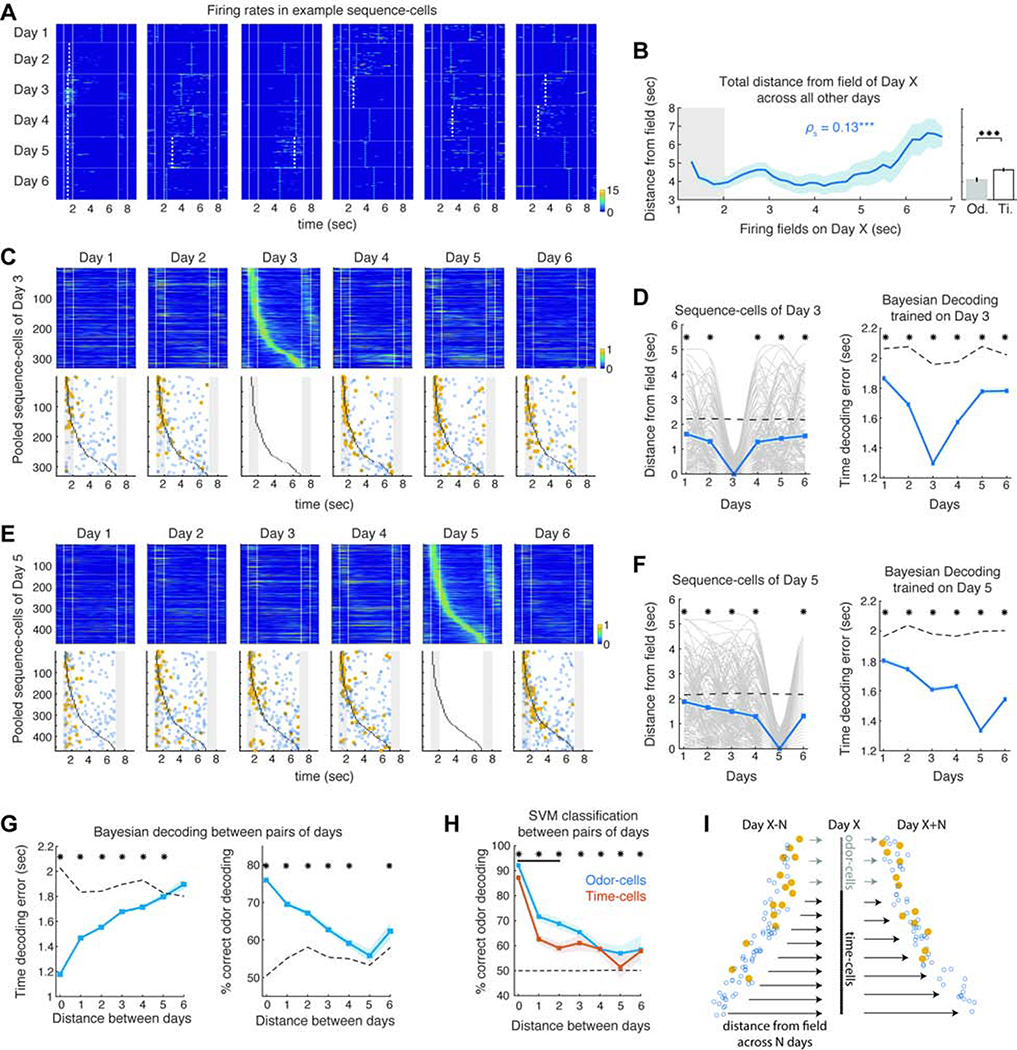
For each sequence-cell of any day, we traced its peak activation time-bin on previous and subsequent days (first 6 days of DNMS training used as before; N = 9 mice), over trials starting with its preferred odor. Odor-cells of any Day X tended to spike near or within the odor delivery interval early on, often yielding a stable field that they retained throughout most days (Figure 7A). As expected, the peak activation of many time-cells shifted along the delay before and after Day X, mostly without a significant field. The total distance across all days between a cell’s peak time-bin daily and its field time-bin on Day X increased as a function of that field (Figure 7B; P < 0.05 SPT) and time-cells fluctuated around their field on other days more than odor-cells (P < 0.001; WT).

Figure 7: Timing of sequence-cell activation gradually converges to and diverges from their firing fields over days.

A. Activity over all preferred trials across 6 days, for example sequence-cells of any Day X. Dashed lines: significant fields (white) and non-significant peak activity time-bins (blue) daily. B. Summed distance between the fields of Day X sequence-cells and their peak activation on all other days, as a function of each cell’s field. *** P < 0.001; SPT. Right: Mean across odor-cells versus time-cells (P < 0.001, WT). C. Pooled Day 3 sequence-cells (top) and their peak activity time-bins (bottom; plotted as before), during their preferred trials over each day (cells stacked in the same order). D. Left: Distance between peak-activation time-bin and field on Day 3 across all days, for each sequence-cell of Day 3 (grey; smoothed) and mean over all sequence-cells (blue). Dashed line: chance baseline from shuffled rates. * P < 0.05; WT; FDR. Right: Mean time-decoding error per day, from Bayesian decoders trained on sequence-cells on Day 3 (*P < 0.001; right-tailed WT; FDR; Day 3 not included in tests). E-F. Same as C-D for sequence-cells of Day 5. G. Mean time-decoding error and odor-decoding accuracy from Bayesian decoders trained on sequence-cells of Day X and decoding their activity on Day Y, as function of distance between days. Dashed lines: Chance baselines. * P < 0.05; tailed WT; FDR. H. Same for mean odor-decoding accuracy with SVM classifiers on odor- or time-cells. Black bar: Days with significantly better decoding from odor-cells than time-cells (P < 0.05; WT; FDR). Dashed line: Chance baseline (identical for both groups). * P < 0.05; tailed WT; FDR. I. Sketch of drift dynamics and increase of sequence-cells. Arrow density: inflow/outflow of cells. Arrow length: distance between peak activity of cells on previous/following days and field on Day X. Odor-cells of Day X attain a significant field (yellow) earlier on and retain it for more days, yielding lower cell turnover and shorter activity trajectories. Time-cells follow longer trajectories around their field, with higher turnover and mostly non-significant firing peaks (blue) outside Day X. During learning, more time-cells enter the sequence daily than leave it, increasing their number.

Interestingly, the peak activation of many sequence-cells on days outside Day X did not shift randomly across time-bins. On days before Day X, their activation progressively approached their eventual field and on days after Day X it deviated away from it (Figure 7A). Thus, closer to Day X, their collective activity gradually approached their Day X sequence, particularly for stable fields (Figures 7C,E), while on days further away, peak activation was more randomly distributed and with fewer stable fields. Indeed, the distance between each cell’s peak activity at a day and its field on Day X decreased the closer the two days were and remained, on average, lower than random (Figures 7D,F; P < 0.05, WT; FDR). As a result, Bayesian decoders trained on sequence-cells of Day X decoded time through the same cells with increasing errors away from Day X, but better than chance (Figures 7D,F; P < 0.05; WT; FDR).

These findings were similar for all 6 days of DNMS (as well as for later days in 3 mice that were imaged longer). For example, activity of Day 1 sequence-cells drifted away from their fields on following days, while Day 6 sequence-cells monotonically approached their fields over the preceding days (Figure S13). This population drift holds for both odor- and time-cells but, on average, odor-cell peak activation was significantly closer to their Day X field than chance across all days, whereas peak-activation of time-cells became randomly distributed within 2–3 days before or after Day X (Figure S13). As a result Bayesian decoders trained on sequence-cells of any Day X performed increasingly worse in decoding time or odor through the same cells on days further apart from X, but better than chance up to 5 days apart (Figure 7G; P < 0.05, WT; FDR). To quantify odor-information independently of timing, we repeating this analysis with SVM classifiers, separately for odor- and time-cells, which yielded similar results, with odor-cells performing better than time-cells when decoding activity up to 2 days apart (Figure 7H; P < 0.05).

Therefore, cells that comprise the sequences of any Day X converge to their field and then diverge from it over days, resulting in a constant population drift (Figure 7I) and in the collective information decreasing away from Day X. Odor-cells attain their field faster and for longer than time-cells.

Sequence-cell activity does not predict trial outcome

Time-cell activity has been reported to correlate with trial outcome in working-memory based tasks (MacDonald et al., 2013; Pastalkova et al., 2008). However, odor-specific sequences were not predictive of trial outcome (Figure S14). Their activity was similar in correct (correct hits and rejections) and error trials (false alarms and misses). No differences existed in: i) the average activation probability of cells, ii) the activation probability of odor-cells during the second (preferred) odor in a trial or iii) their firing rate during its presentation, though a minimal reduction of SI existed in error trials. SVM classifiers trained on correct trials performed similarly when decoding odors in correct versus error trials (P > 0.05; WT). The same held when using only the ‘stable’ or ‘new’ sequence-cells of each day, as well as for classifiers trained only on correct non-match trials and decoding odors in correct rejection versus false alarm (match) trials. Finally, SVM classifiers trained on trial outcomes (instead of odors) yielded chance accuracy of outcome-prediction which did not improve with DNMS learning.

DISCUSSION

Hippocampal networks generate cell assemblies encoding space, time, sensory or contextual information. Their sequential activation is thought to organize temporally related experiences in memory space (Buzsáki and Llinas 2017; Buzsáki and Tingley 2018; Eichenbaum 2014, 2017). However, sensory and internal representations have mostly been studied separately and the dynamics governing the emergence, stability and information content of multi-modal representations remain unclear. Taken together, our findings reveal a rich repertoire of population dynamics in CA1 where continuous spiking sequences combine stable and reliable sensory representations with sparse and highly dynamic temporal ones, with distinct relationships to learning of a context. Stable representations can reliably convey information downstream while flexible activity patterns allow for a larger pool of information and quick adaptation to perturbations (Rabinovich et al., 2008). Therefore, this combined stability and flexibility allows CA1 circuits to encode both fixed elements of the external world as well as their changing temporal relationships, to construct maps of temporally related experiences.

Under different conditions, hippocampal activity has been found to yield both stable encoding (Gonzalez et al., 2019; Tonegawa et al., 2015) as well as dynamic representations (Cai et al., 2016; Mankin et al., 2012; Ziv et al., 2013) drifting to different neuronal assemblies over days. This drift can be a gradual global remapping or a more coherent reorienting of representations to different external cues (Kinsky et al., 2018). Our findings support a gradual global remapping since, even though most time-cells quickly lose their field, temporal and stimulus information is partially retained in the same population for days, also seen in non-stimulus-specific time-cells during locomotion (Mau et al., 2018). How new ensembles are selected during such a drift is unclear. Place fields in CA1 may be shaped by the interplay of dendritic inputs on a pyramidal neuron (Sheffield and Dombeck, 2015) and active dendritic plateau potentials can generate a stable field within single trials (Bittner et al., 2015, 2017). Our findings suggest that time-fields are shaped over days, with the spiking activity of a cell becoming progressively tuned to a time-point and later diverging away from it.

The stability of odor fields is analogous to that of cortical sensory (Peron et al., 2015) or CA1 and dentate gyrus (DG) spatial representations (Gonzalez et al., 2019; Hainmueller et al., 2018). Anatomically, only few synapses separate the olfactory bulb (OB) from CA1, with OB projections reaching LEC even directly (Igarashi et al., 2012) which outputs to CA1 (Vanderwolf, 1992). Anatomical and functional LEC-CA1 connectivity is involved in olfactory-guided behavior (Igarashi et al., 2014) and associative learning (Li et al., 2017). LEC-DG projections are also important for olfactory representations and associative learning (Woods et al., 2020). Therefore, stable odor-fields in CA1 pyramidal cells may be shaped by direct or indirect LEC projections.

The sequential time-cell activation may be initiated by cortical inputs that propagate within the hippocampus through internal feedforward excitation (‘chain model’). Alternatively, time-cells may be driven by continuously changing cortical activity so that each time-cell represents a given moment in cortical states and the sequence encodes a specific temporal context (Buzsáki and Tingley 2018; Eichbaum 2014, 2017). In the chain model, odor-cells would initiate the sequence irrespective of the duration or structure of the ensuing trial. Even though we did find partial retention of the original temporal information when the delay was extended, the rapid, radical remapping of most time-fields favors the ‘temporal context’ model. Similar dynamic remapping was reported in non-stimulus-specific time-cells in rats (MacDonald et al., 2011) and in spatial representations in expanded environments (Diba and Buzsáki, 2008). The decreasing information and field density throughout the delay also support the scale invariance feature of the ‘temporal context’ model (Howard et al., 2014; Liu et al., 2019). Finally, the selective increase of time-cells during learning suggests these sequences are shaped by processes involved in learning, attention or working memory (WM) activation, rendering a passive chain model more unlikely.

The shaping of time-cell sequences may occur within recurrent CA3 networks which can sustain multiple stimulus-specific assemblies (Liu and Buonomano, 2009) and form behaviorally relevant spiking sequences (Holtmaat and Caroni, 2016) and temporal codes (Salz et al., 2016). However, CA3 spatial maps are relatively stable (Hainmueller et al., 2018; Mankin et al., 2012) suggesting that CA3 assemblies may not adapt to context alterations fast enough to drive the observed instability in CA1. Alternatively, time-cells may be shaped by medial entorhinal cortex (MEC) where sequences have been observed during treadmill running (Kraus et al., 2013) and timed immobility (Heys and Dombeck, 2018) and since inactivating MEC output disrupts non-specific CA1 time-cells and WM performance (Robinson et al., 2017; but see Sabariego et al., 2019) but not olfactory learning (Li et al., 2017). LEC is another candidate since it generates firing-rate-based temporal codes (Tsao et al., 2018). Finally, either MEC or LEC outputs are expected to function in coordination with CA3 activity.

Our observations support a link between CA1 dynamics and WM: i) The collective activity retains significant stimulus information throughout the delay when WM is active. ii) The encoding of matching/non-matching odors or specific odor combinations by cells is related to WM manipulation. iii) The selective increase of time-cells during learning but not in passive task exposure corroborate that temporal coding develops in conjunction with temporally structured memories (Modi et al., 2014). On the other hand, the lack of correlation between sequence activity and trial outcome, unlike previous studies (MacDonald et al., 2011; Pastalkova et al., 2008) and the stable firing properties of time-cells throughout learning indicate that WM performance was not reflected in how these cells spiked. Sequences may thus be reflective of WM activation but not directly involved in performing the task. Stimulus-information carried by time-cells may instead be important for downstream processing through projections to the OB (VanGroen and Wyss, 1990), olfactory cortex (Aqrabawi and Kim, 2007) or to mPFC which is involved in DNMS learning (Liu et al., 2014) and exhibits temporal codes (Tiganj et al., 2016). Expanding time-cell ensembles would increase information sent out to such areas during learning.

The existence of time-cells in untrained animals supports observations of hippocampal sequences even in the absence of external cues (Villette et al., 2015). These may be composed of pre-existing cell assemblies, activated in sequence, that quickly get associated with novel cues, as in ‘preplays’ of place-cell sequences before exposure to a novel navigation task (Dragoi and Tonegawa 2011; Grosmark and Buzsáki, 2016; Liu et al., 2018). In this case, high correlations between sequence-cells in naïve mice would be observed even before the novel exposure of the animal to odors, which remains to be tested.

STAR METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to the Lead Contact, Peyman Golshani (pgolshani@mednet.ucla.edu).

Materials Availability

All unique resources generated in this study are available from the Lead Contact with a completed Materials Transfer Agreement.

Data and Code Availability

The data and analysis code generated in this study are available upon reasonable request to the corresponding authors.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animals

A total of 23 adult male mice (11–31 weeks old) were used for in vivo two-photon calcium imaging experiments: 7 Gad2-Cre:Ai9 mice (Gad2^tm2(cre)Zjh/J crossed with B6.Cg-Gt(ROSA)26Sor^{tm9(CAG-tdTomato)Hze}/J), 14 Gad2-Cre:Ai14 (Gad2^tm2(cre)Zjh/J crossed with B6.Cg-Gt(ROSA)26Sor^{tm14(CAG-tdTomato)Hze}/J) and 2 Gad2-Cre mice. An additional 10 adult male mice (13–25 weeks) were used for behavioral control experiments: 2 Gad2-Cre:Ai32 (Gad2^tm2(cre)Zjh/J crossed with B6;129S-Gt(ROSA)26Sor^{tm32(CAG-COP4*H134R/EYFP)Hze}/J), 2 Gad2-Cre:Ai9 and 6 C57B/6J. All animals were experimentally naïve. All animals were acquired from The Jackson Laboratory and were group housed (2–5 per cage) on a 12 h light/dark cycle. All experimental protocols were approved by the Chancellor’s Animal Research Committee of the University of California, Los Angeles, in accordance with NIH guidelines.

METHOD DETAILS

Surgical Procedures

Mice were anaesthetized with isoflurane (3–5% induction, 1.5% maintenance), their scalp was shaved and they were placed into a stereotactic frame (David Kopf Instruments, Tujunga, CA) on a feedback-controlled heating pad (Harvard Apparatus) to maintain body temperature at 37^oC. Eyes were protected from desiccation using artificial tear ointment. The scalp was sterilized with betadine and infiltrated with lidocaine (2%; Akorn, Lake Forest, Illinois) as a local anesthetic. An incision was made to expose the skull from bregma to lambda. Fascia was removed by applying hydrogen peroxide and the skull was stereotactically aligned. A small burr hole was made on the right hemisphere (−2mm posterior and 1.8 mm lateral to bregma), using a dental drill. Using a Nanoject II microinjector (Drummond Scientific), 1500 nl of 1:10 saline-diluted AAV1.Syn.GCaMP6f.WPRE.SV40 virus (diluted immediately prior to surgery; titre: 4.65 × 1013 GC/mL; Penn Vector Core) were injected into dorsal CA1 (1.3 mm ventral from dura) at a 50–100 nl per minute. 60 minutes after the termination of viral injection, a circular craniotomy (3mm diameter) was made around the injection site. Dura over the exposed brain surface was removed and the cortical tissue above the dorsal CA1 was carefully aspirated using a 27 gauge blunt needle. Buffered artificial cerebrospinal fluid (7.888g NaCl, 0.372g KCl, 1.192g HEPES, 0.264g CaCl2, 0.204g MgCl2 per 1000 ml milipore water) was constantly applied throughout the aspiration to prevent desiccation of the tissue. The aspiration ceased after partial removal of the corpus callosum and bleeding terminated, at which point a 3-mm titanium ring with a glass coverslip attached to its bottom was implanted into the aspirated area and its circular flange was secured to the skull surface using vetbond (3M). A custom-made lightweight metal head holder (headbar) was attached to the skull posterior to the implant. Cyanoacrylate glue and black dental cement (Ortho-Jet, Lang Dental) were used to seal and cover the exposed skull. Mice that were used for behavioral experiments were only implanted with a headbar and were not given a craniotomy or aspiration. During recovery (~7 days) mice were administered carprofen (5 mg per kg of body weight) for 3 days as a systemic analgesic and amoxicillin antibiotic (0.25 mg ml⁻¹ in drinking water) through the water supply for 5 days. Their weight was monitored daily.

Experimental Setup

The treadmill consisted of an 8-inch Styrofoam ball (Graham Sweet) suspended through a metal axis, allowing for 1D rotation. It was housed within a dark enclosure. Mice were headfixed on the treadmill by attaching the implanted headbar to a custom-made metal holder. Locomotion was recorded as an independent analog signal, using a custom printed circuit board based on a high sensitivity gaming mouse sensor (Avago ADNS-9500), connected to a microcontroller (Atmel Atmega328) sending data to a dual channel digital-to-analog converter at 100 Sps.

A constant stream of clear air (~1 L/min) was transferred to the behavioral rig via Tygon PVC clear tubing and was supplied to the mouse through a custom-made lickport. During odor stimulation a dual synchronous 3-way valve (NResearch), placed ~6 cm away from the mouse, would switch from the clear air stream to the odorized one for 1 sec. Odorized air was created using a 4-ports olfactometer (Rev. 7c; Biology Electronics, Caltech), supplying air to either of two glass vials containing liquid isoamyl acetate (70% isoamyl acetate basis, FCC; Sigma Aldrich) or pinene ((−)-α-Pinene, ≥97%, FCC; Sigma Aldrich) odorants, diluted in mineral oil at 5% concentration (unless stated otherwise). For the non-match-to-long-duration-sample task (NMLS) experiments, all 4 ports were connected to odor vials (see below). Odorized air from each vial would reach the behavioral rig through separate Tygon tubing each leading to a 3-way solenoid valve (Lee Company). For olfactory stimulation, the corresponding olfactometer port started supplying air to its attached odor vial 1 sec prior to actual stimulation to allow for odorized air to travel through the tubing and reach its corresponding solenoid valve. During the 1 sec stimulation, that solenoid turned on allowing the corresponding odorized air to enter a short common path for both odorants (~4cm) ending at the dual synchronous 3-way valve and from there being released to the mouse through the lickport (~10 cm total common path for the two types of odorized air). At the offset of the stimulus, the solenoid turned off and the dual 3-way valve switched the airstream back to clear air, ensuring a constant flow of air to the mouse and a quick clearing of the odorant from the air around the mouse. The odorized and clean air were set to similar airflow values (~1 lt/min), measured with a flowmeter (AWM3300; Honeywell).

Odorant concentration in open air was measured through a mini photoionization detector (PID; 200B mini PID; Aurora Scientific), located at the distance of the mouse snout from the air-delivering lickport. Lower ionization threshold for pinene (odor-B) lead to higher deflections in the PID signal during its presentation compared to isoamyl acetate (odor-A). Therefore, potential odor lingering in the small common tube path, during the delay, and mixing with the second odor would result in a larger PID deflection during the second odor in B-A trials (lingering pinene molecules mixing with isoamyl acetate) than in A-A trials (lingering isoamyl acetate mixing with itself). This was observed when creating a very long common path length, but not in our default set up (Figure S1), indicating that no odor mixing is created during the second odor.

Licking was detected using a battery operated, custom-made, printed circuit board operating as a lickometer (Slotnick, 2009). One end of the circuit was attached to the metal headbar on the mouse and the other to the metal tube delivering water. Whenever the mouse would lick the tube, an electrical circuit would close, creating a voltage drop that was recorded as a continuous RSE analog signal. Water droplets (~10 μl) were released by a 3-way solenoid valve (Lee Company) and delivered to the mouse through a metal tube on the lickport. At the end of each trial, after the response window, vacuum was applied for 3 sec, through a metal tube underneath the water delivering tube, to clear any lingering water and assist in removing any odorized air.

The behavioral rig was controlled with custom written software (Matlab) and through a data acquisition board (USB-6341; National Instruments).

Behavioral training and recording protocol

After the recovery period, mice were briefly handled for two days and water restriction was initiated. They were provided with 1–1.5ml of water daily, either throughout or post training. Their weight was maintained at around 85% of their final weight pre-water restriction initiation. Mice were initially habituated to head fixation on the spherical treadmill for 3 consecutive days. On the second day, the lickport was placed in its normal position for habituation to the metal ports and air flow. Mice were given water drops through the lickport on the third day of habituation.

DNMS training consisted of 3–4 days of ‘shaping-stage’ (Liu et al., 2014) where mice were presented with trial-blocks (20 trials each) of non-match trials and the water reward was delivered automatically at the start of the response window in each trial. This was followed by a ‘pre-training’ stage for 2–4 days where mice were presented with non-match trials but had to actively lick the lickport during the response window to release the water drop. They were moved to the final training stage once they performed at >85% hit trials per day. In the ‘training stage’, mice were presented with the full task in a series of trial-blocks per day. Each block again consisted of 20 trials and match trials were intermingled with non-match ones with each group of 4 consecutive trials containing all possible 4 combinations of odors in random order. Mice were not punished if they licked at match trials but no reward was presented. Within ~2–5 days they learned to refrain from licking during match-trials. During training, mice gradually refrained from licking during the delay period as well, and well-trained mice would typically initiate licking during or right after the second odor. Responses were assessed based on licking during the response window only. If any licking occurred during that window, the trial was a hit (non-match trials) or false alarm (match trials) accordingly. In the opposite case, they were labeled as miss or correct rejection respectively. Performance over each trial-block, was quantified as the percentage of hits and correct rejections over the 20 trials. Daily performance was the corresponding ratio over the total number of trials (all blocks) during that day. Mice were typically presented with 5–7 blocks daily.

Two-photon imaging sessions for mice under training started as soon as they were ready to move from the ‘pre-training’ stage to ‘training stage’ (N = 9 mice), at ~2–3 weeks post-surgery. 3 mice were first imaged on their first day in ‘training stage’ and 6 mice were first imaged for 2 days while performing ‘pre-training’ trial-blocks (non-match trials only). 3 of them received 3 ‘pre-training’ blocks followed by 3 training blocks on their second day of imaging. The other 3 received 5 pre-training trial-blocks on their second imaging day and were moved to training blocks on their third day of imaging. Finally, 2 mice were imaged only after they had received 5 days of training stage (not having reached well-trained level yet) and they were only imaged at training stage.

Some mice (N = 6) were imaged while naive to the task. Only the 3 days of habituation were applied (without any water droplets delivered on day 3 of habituation) before onset of calcium imaging, upon which they were presented with normal DNMS trials for 3 or 6 consecutive days (N = 3 in each case), same as with trained mice. 5/6 naive mice never licked the lickports for a reward. One naive mouse kept licking the tubes and received a series of water rewards, but only early sessions (3 days) where the mouse had not grasped the task were included here. These animals were imaged 2–3 weeks post-surgery to match the time the trained animals were imaged and to allow for GCamp6f to be expressed.

Behavioral control experiments

Non-match-to-long-duration-sample task training (NMLS; N = 3 mice) consisted of the same training steps as DNMS, but the first odor was presented throughout a 5-sec period and was immediately followed by the second odor. Varying odorant concentration vials were used only for the first odor whereas the second odor was delivered by different olfactometer ports connected with 5% odorant vials. For experiments with odors turned off, the olfactometer ports were deactivated, halting any flow of odorized air, but trials were otherwise normal. For experiments with variable airflow, the airflow for both odor-ports on the olfactometer was altered randomly for each port at the beginning of each trial-block, between ~0.4 −1 lt/min, measured by the flowmeter.

In vivo two-photon imaging

A resonant scanning two-photon microscope (Scientifica) was used for calcium imaging, recording 512×512 pixel frames at 30.9 Hz, with a 16× 0.80 NA objective (Nikon) yielding a 500×500 μm field of view. Excitation light was delivered with a Ti:sapphire excitation laser (Chameleon Ultra II, Coherent), operated at 920 nm. GCamp6f and Td-Tomato fluorescence were recorded with green and red channel gallium arsenide photomultiplier tubes respectively (GaAsP PMTs; Hamamatsu). Microscope control and image acquisition were performed using LabView-based software (SciScan). Imaging and behavioral data were synchronized by recording TTL pulses, generated at the onset of each imaging frame, as well as olfactory stimulation digital signals at 1 kHz, using the WinEDR software (Strathclyde Electrophysiology Software).

A single fixed field of view was imaged every day for each mouse. To ensure that the same neurons were tracked every day, each day’s field of view was overlaid to that of the first day of imaging for each mouse. The reference and live fields of view were aligned using the recording software before recording was initiated. This fixed template reference avoided deviations from the correct z-plane or any slow drifts across days. Moreover, a combination of rotating stages was used to allow tilting of the objective over two degrees of freedom as well as adjusting the mouse head-angle, to fine-tune the alignment of the live field of view to its reference template.

Imaging sessions were performed separately for each trial-block, allowing laser power and PMT adjustments in between to ensure optimal imaging conditions and signal-to-noise ratio as well as fine-tuning of the field of view position during the recording session. Time breaks of ~1min were given between trial-blocks to prevent brain heating or photo-toxicity. Laser power was kept to a minimum and no photo-bleaching was observed.

QUANTIFICATION AND STATISTICAL ANALYSIS

Calcium imaging data processing

Data was pre-processed in MATLAB using a custom-built pipeline based on the CaImAn package (Giovannucci et al., 2019) for large scale calcium imaging data analysis. To reliably track neurons over multiple days in the presence of changes in the field of view, active neurons were extracted separately for each day and were then registered against each other.

Motion correction and source extraction

Datasets from each day where corrected for motion artifacts using online piecewise rigid registration (Pnevmatikakis and Giovannucci, 2017), where the template obtained during motion correction of trial-block X was used to align data from trial-block X+1. For 3 animals with low signal-to-noise ratio, motion correction took place on spatially downsampled videos and shifts were interpolated and applied on the original recordings. Data from all the trial-blocks each day was then concatenated and downsampled in time by a factor of 5 to increase the signal-to-noise ratio. The spatial footprints of the active sources (ROI) were then extracted from the downsampled data using an implementation of the CNMF algorithm in spatial patches (Giovannucci et al., 2019). Spatial and temporal correlation thresholds for ROI detection were set to 0.6 and 0.8 respectively, acceptable ROI size was limited to 50–150 pixels, and an ROI eccentricity threshold was set at 0.97 to avoid elongated ROI that were axodendritic segments. These values were determined after examination of the relationship between these thresholds and the final accepted ROI spatial footprints and temporal traces, using a custom graphical user interface on a set of our recordings. The spatial footprints were then used to obtain the traces at the original frame rate by solving a non-negative regression problem. The computed traces were first transformed in ΔF/F units and were then deconvolved using the OASIS algorithm for fast nonnegative deconvolution (Friedrich et al., 2017), separately for each trial-block, to correct for variations of laser power between those or any possible bleaching artifacts. Noise levels were computed for each ROI using a power spectral method, and spike thresholds were set to 3 x noise level, except for 4 animals with lower signal-to-noise ratio and sparse activity, were the threshold was lowered to 1.5 and 2 respectively (N = 2 for each). Finally, the deconvolved traces were binned in time using 50% overlapping 320 ms time bins. This signal is used as a proxy of spiking activity per unit of time and is referred to as ‘spiking rate’ throughout the text. This pipeline generated a set of spatial footprints and temporal traces (both in ΔF/F unit and in deconvolved neural activity) for each animal at each day of recordings.

Calcium transients decay time, mean ΔF/F amplitudes and baseline fluorescence

The decay time of each ROI’s calcium transient during spiking was estimated through the CNMF algorithm (Pnevmatikakis et al., 2016). Under the assumption that the spiking signal comes from a homogeneous Poisson process, the discrete-time calcium concentration dynamics c(t) at time-bin t were approximated using a stable autoregressive process of order p = 2, as:

$$c(t)=g_{1}c(t-1)+g_{2}c(t-2)+s(t)$$

with s(t) a noise component. The discrete-time calcium transient in response to a spike is thus modeled by two exponential functions with the time constant of the slower function yielding an approximation of the continuous calcium signal’s decay time τ₂. This is computed as:

$${\tau }_2=\Delta t/log\left(r_2\right),$$

where Δt is the signal’s time-bin width and r₂ is the smallest of the two roots of the polynomial:$x^2-g_{1}x-g_2=0$. The decay time parameter was computed separately for each trial-block (20 trials) and was averaged across all blocks in a day.

To estimate an ROI’s ΔF/F mean amplitude and SD during its activation we isolated the ΔF/F traces during each spiking segment (i.e. continuous set of non-zero values in the deconvolved signal) and used the maximum ΔF/F value at each segment as a measure of the ΔF/F amplitude during that segment. The average and the SD of these maximal values across all spiking segments in a session were computed.

Baseline fluorescence of each ROI was computed as the mode value of the raw fluorescence (the weighted average fluorescence from all the pixels in the ROI after removing overlapping components and neuropil contamination and prior to the ΔF/F transformation), separately in each trial-block, and averaged over all blocks of the session. Since cells were activated very sparsely, this mode value corresponded to their baseline, which we confirmed via visual inspections.

Inhibitory neuron detection and removal

Inhibitory neurons were identified based on their static Td-Tomato fluorescence recorded for 500 frames at the beginning of each imaging day on the red-channel PMT, together with the functional (green) channel. The red channel was first aligned to the green one by using the motion displacement field that was estimated during the motion correction of the green channel. Then the average of the red channel was computed and the resulting image was segmented to obtain contour plots of the inhibitory neurons. The segmentation was performed by using adaptive thresholding (to model different illumination levels within the field of view), with a threshold at each location computed as the Gaussian weighted average of a small neighborhood around the location. The resulting thresholded image was segmented using connected components. For each connected component, the corresponding part in the mean image was then thresholded at 75% of its maximum value, and after this thresholding and another round of connected components analysis, components of small size (<30 pixels) or odd shape (>0.95 eccentricity) were removed. The remaining components identified the locations and spatial extent of the inhibitory neurons within the field of view. These components were then registered with the CNMF identified components from the functional channel using the procedure described above. Components that were matched corresponded to inhibitory neurons that were active during this imaging session, whereas mismatched components corresponded to inhibitory neurons that were either silent or whose activity did not meet detection criteria by CNMF (slow traces potentially due to prolonged high-frequency spiking). Matched components were removed from the final pool of ROI, so that only pyramidal cell activity from the green channel was analyzed further.

Pairwise Registration

To register components across two different days we followed the following procedure: First the ROI from both days were aligned to the same FOV, by computing a motion transformation between the templates from day 1 to day 2 and using this transformation to align the components from day 1 to the FOV of day 2. Let ${\alpha }_1^1,{\alpha }_2^1,\dots ,{\alpha }_{N_1}^1$ and ${\alpha }_1^2,{\alpha }_2^2,\dots ,{\alpha }_{N_2}^2$ be the set of (aligned) spatial footprints from the two sessions. The components were first transformed into binary masks $m_1^2,m_2^2,\dots ,m_{N_2}^2$ and $m_1^2,m_2^2,\dots ,m_{N_2}^2$ respectively, by thresholding each component at the 10% of its maximum value. An intersection over union metric was used to quantify the distances between the footprints from the different days:

$$d_{i,j}=1-\frac{\left|m_i^1\cap m_j^2\right|}{\left|m_i^1\cup m_j^2\right|}$$

Based on this metric a matrix of pairwise distances was constructed. Distances between components where the one was a subset of the other (>60% pixels of smallest of the 2 ROIs overlapping with those of the largest) were set to zero, whereas high distances d_i,j > 0.98 were set to infinity. Components were then registered to each other using the Hungarian algorithm (a polynomial time algorithm for solving the linear assignment problem). Setting weakly overlapping components to have infinite distance prevented false pairings between components which were instead left unmatched between these two particular sessions.

Calcium and Behavioral Data Analysis

All analysis was performed on the binned spiking rate traces from all pyramidal cells each recording day, using custom written analysis software (Matlab).

Sequence-cell detection and analysis

Whether each cell had an odor or time-field was determined separately over all trials of a session initiated by odor-A or odor-B, respectively, through the following process: First we computed the cell’s average firing rate for the corresponding group of trials within the ‘odor-delay interval’ (from first odor onset up to second odor onset). Only if the cell spiked within that interval at least in 10% or 3 (whichever was greatest) trials of the corresponding type was considered further. The maximum average rate was computed and the time-bin it occurred in was considered the cell’s potential field. Its firing rate trace over the odor-delay interval was then circularly shifted by a random interval up to ± 1/2 x odor-delay interval, separately for each trial and the maximum mean firing rate over the shifted trials was computed. This process was repeated 1000 times, generating a distribution of maximal rate values. The cell was considered to have a significant firing field if its maximum mean firing rate at that time-bin was larger than the 95^th percentile of the shuffled distribution (see additional SI condition below). The time bin of that maximal rate was considered the cell’s field time-point. If it was during the odor stimulation, it was considered an ‘odor-cell’, otherwise a ‘time-cell’.

For the three mice receiving a combination of 3 ‘pre-training’ and 3 ‘training-stage’ trial-blocks on their second imaging day (see above), sequence-cell detection was performed separately for each training stage. For experiments where the odors were turned off after the initial trial-blocks, the sequence-cells were computed using only the trials with the odors on. For trials with variable odorant concentrations, they were computed based on all trials. Finally, for imaging days with multiple delays, sequence cells were detected separately over trials of each delay duration.

To estimate a cell’s field size, its mean firing rate over preferred trials, from the odor onset to the delay offset, was lowpass filtered (< 1 Hz) and its baseline was approximated by its mode value. We then detected the two time-bins in either side of the field where the filtered rate dropped below a threshold of baseline + 1/2 standard deviation. The time interval between these points was used at the field size. If either of these thresholds was not crossed throughout the whole interval then the odor onset or delay offset were used accordingly. Field sizes longer than 4 sec were disregarded. We note however that, since firing rates here refer to binned deconvolved calcium traces, they do not accurately depict actual levels of activity. Therefore, field sizes should be considered as an approximation of the time interval where the cell had the highest activation probability relative to the rest of the trial, and as such its length represents the variability in activation time for the cell.

We computed the selectivity index (SI) of each sequence cell as:

$$SI=\frac{R_f^i-R_f^j}{R_f^i+R_f^j}$$

Where $R_f^i$ is the cell’s mean firing rate at its firing field f over all i-trials, whereas $R_f^j$ is its mean firing rate at the same time bin but over the opposite type of trials j (with i and j representing odor-A or odor-B accordingly). Cells with a negative SI over the trial type under consideration were discarded from the corresponding sequence (as preferring opposite trials). Therefore, if a cell had a field at the same time-bin during both trial-types, it was assigned to the sequence where its field-rate was highest (positive SI). This condition was removed for analysis of multi-field cells in Figure S2D (the total number of sequence-cells was only increased by 7.6%), but was applied in all other cases.

A sequence-cell’s SI over correct or error trials was computed using the above formula but for the corresponding trials only. The cell was included in analysis only if there were at least 10% error preferred-trials and 10% error non-preferred-trials in the session, to allow for adequate sample size and fair comparison of SI over both outcome-types. Cells that were never active in any correct trial, of either odor-type were also removed and the same for those that were never active in any error trials (though including these cells did not alter our results).

An odor-cell’s SI at the second odor stimulus was computed using the above formula as well, but for the time-bin that corresponds to its field transferred over the second-odor in a trial. For Figure S11, it was computed with the same formula but using the cell’s mean firing rate over the two trial types, summed over all time-bins of the second odor. The SI over the first versus the second odor was computed similarly, as:

$$S{I}_{1-2}=\frac{R_m^1-R_m^2}{R_m^1+R_m^2}$$

where $R_m^1$ is the cell’s mean firing rate summed over all time-bins of the first odor and $R_m^2$ is the corresponding summed rate over the second odor time-bins. Only trials with preferred first or second odor, respectively, were included.

The activation probability of a cell in its field was quantified as the percentage of preferred trials where it had a nonzero firing rate inside its firing field. The same holds for the computation over correct or error trials only (again using only sessions where a cell’s preferred trials contained at least 10% errors). Activation probability at the first versus second odor stimulus for an odor-cell was the percentage of trials with nonzero $R_m^1$ and $R_m^2$ respectively. Activation probability at match or non-match trials was computed by computing $R_m^2$ over the corresponding trial groups. Spiking variance was quantified as the variance in the time bin containing a cell’s maximal firing rate at each trial over all trials of a given type.

To detect cells encoding match or nonmatch trials or specific odor-combinations, the SI over match versus nonmatch trials was computed for each cell (excluding all cells with an odor or time-field):

$$S{I}_{match}=\frac{R_{match}-R_{nonmatch}}{R_{match}+R_{nonmatch}}$$

where R_match and R_nonmatch is each cell’s average firing rate across match or non-match trials respectively, summed over all time-bins covering the second odor and the ensuring 1 sec interval, before the response window (to avoid any effects from the water reward in nonmatch trials). Cells with SI_match > 0.2 were considered potential match and those with SI_match < −0.2 were potential non-match cells. Neurons that spiked within that interval less than 10% or 3 (whichever was greatest) trials of the corresponding type were discarded. For potential match cells, their SI over the same interval was computed for A-A versus B-B trials with the same formula, and for potential non-match cells their SI was computed for A-B versus B-A trials. Potential match cells with SI > 0.5 were considered A-A cells and those with SI < −0.5 were B-B. Similarly, A-B and B-A cells were selected out of all potential non-match cells. The remaining cells with |SI| < 0.5 were the final match and non-match cells accordingly.

For plotting, mean firing rates of each sequence cell were normalized by their maximal firing rate at their firing field. The same normalization was applied for both trial types.

For spatial distribution analysis, the centroid of each sequence-cell’s spatial footprint was computed. All pairwise centroid Euclidean distances were measured as well as pairwise time distances between firing fields for all time-cells.

Place-field distributions were approximated by a two-term power law distribution:

$$f(x)=b\ast x^a+c$$

using the trust region reflective algorithm (fit function in Matlab). The goodness of fit was assessed by creating random sampled distributions from this power law, of equal size to the original, with 2500 repetitions, fitting each sampled distribution with the same algorithm, and comparing the Kolmogorov-Smirnov (KS) statistic of the original distribution with those from the random sampling (Clauset et al., 2009). The P-value corresponds to the ratio of distributions with KS statistic lower than the default distribution.

Motion Analysis

The locomotion signal had its baseline removed (mode value), was binned in the same manner as for the deconvolved calcium traces and its summed value across the odor-delay interval in each trial was computed. For Figure S3, trials with total motion < 30 (a.u.) during that interval were considered “immobility trials”. Visual inspection of locomotion traces supported this threshold, allowing only some sparse brief motion bouts. An equal number of trials with highest total motion were also selected in each session. The mean firing rates of each sequence-cell during its preferred trials from the two trial groups were compared.

Analysis Across Multiple Days

ROI were matched across all pairs of imaging days per mouse. ‘Stable sequence-cells’ were defined as two matched ROI that had a significant field in the same sequence both days. Across a series of days, ‘stable sequence-cells’ were detected using the final day’s sequence cells as reference and tracking those that had a match with a cell belonging to the same sequence each other day. To compute field shifts across two consecutive days (Day 1 and 2), we took all sequence cells from Day 1 that were matched to an ROI on Day 2 and computed the maximal firing rate time bin of that matched ROI across the corresponding trials of Day 2 (along the odor-delay interval as usual). Field shifts of recurring sequence-cells were those where the matched ROI was a sequence cell for that trial type as well. If the matching ROI never spiked on Day 2 in the corresponding trials, the cells were discarded from field-shift analysis. When color-plotting average sequence firing rates across days, each cell’s rate was normalized by its mean rate in its field on Day 1.

To quantify the FOV alignment quality between two days, we computed a ‘relative correlation’ ${\overline{\rho }}_{ij}$ between the FOVs of days i and j defined as:

$${\overline{\rho }}_{ij}=\frac{{\rho }_{ij}}{\sqrt{{\rho }_i\ast {\rho }_j}}$$

where ρ_ij. is the correlation between the mean FOVs of the two days across all recorded videos and ρ_x is the correlation between the mean FOV of the first half of all videos of day x with the second half. The denominator provides an intra-session stability baseline for comparing the inter-session cross-correlation ρ_ij. Most pairs of days had high relative correlations with a mean of $\langle {\overline{\rho }}_{ij}\rangle =0.85$ across all pairs per animal. For Figure S11, we set $\langle {\overline{\rho }}_{ij}\rangle$ as a threshold for relative correlation and any continuous pair of days under that limit (or day triplet that contained at least one such pair) was removed from analysis (35% of day pairs and 62.5% of triplets removed). For Figure S13 any day that yielded ${\overline{\rho }}_{ij}<\langle {\overline{\rho }}_{ij}\rangle$ with the first imaging day of an animal (initial template day), was removed from calculating the number of odor/time cells per day (36% of imaging days removed).

Analysis Across Multiple Delays and Odor Durations

A set of well-trained mice (N = 5) was imaged during both 5 and 10 sec trial-blocks on the same day. Typically, they received a set of 2–3 trial blocks with 5 sec delay followed by the same number of blocks with 10 sec delays. Each animal was exposed to extended delays for 2–3 days in total. For two animals the delay was reduced back to 5 sec after the extension to 10 sec (during 1 day for one animal and 2 days for the other). Removing these imaging days where the delay was reduced again, did not affect our results.

A different set of mice (N = 9) was imaged during both 1 sec and 3 sec odor-stimulations on the same day. The delays were set to 5 sec and 3 sec respectively to keep the trial duration constant. Each animal was exposed to extended odors for 2–4 days in total (only 1 day for one animal) and received a set of 4–5 trial blocks with 1 sec delay followed by 3 trial-blocks of extended odor.

Separate sequence-cells were detected each day over the 5 sec-delay and the 10 sec-delay trials or the 1 sec-odor and 3 sec-odor trials respectively. ‘Stable cells’ refer to those that have a significant firing field in the same sequence in both delays (though not necessarily in the same time bin), whereas ‘unstable’ cells refer to cells that have a field in one delay but not the other. As in multi-day analysis, for unstable cells we use their maximal average firing rate location over their preferred trials as proxy of a field. If a sequence-cell never spiked in the opposite delay/odor-duration trials it was discarded from field-shift analysis. When color-plotting average sequence firing rates, each cell’s rate was normalized by its mean rate in its default delay (or odor-duration).

Analysis over Training Days

Performance was calculated separately for each trial-block (20 trials) and was averaged over all blocks per imaging day. Rejection rate was quantified as the ratio of match-trials where the mouse did not lick and is only defined for the training-stage trials (full DNMS). To pool individual mice, data from each mouse (number of cells, control measures, Bayesian decoding measures etc.) were normalized over their mean number across all training-stage days, and are plotted as percentages.

Mean total rate was computed by summing the deconvolved calcium trace of each cell over all time-bins during each trial, and averaging over all trials and all cells. Mean motion was computed by summing the motion signal (see above) over all time bins of each trial and averaging over all trials. Inter-spike intervals (ISI) were computed at each trial by making the deconvolved calcium trace of each cell binary (turned to 1 for any value > 0) and computing the time interval between two consecutive 1s following 0s. Mean ISI was computed by averaging each cell’s ISI over each trial, and taking the mean over all trials and all cells.

The inflow of new odor- or time-cells in a sequence at any training day d was computed as the ratio of odor- or time-cells, respectively, of day d that did not exhibit a significant field in the same sequence on day d-1. Stable cells are defined as the complement set of new ones, i.e. the ratio of all odor- or time-cells of day d that also had a field in the same sequence on day d-1. The outflow of lost odor- or time-cells at any training day d was computed as the ratio of odor- or time-cells, respectively, of day d-1 that did not retain a significant field in the same sequence on day d.

Cross-correlation between pairs of odor-cells (stable or new ones accordingly) or time-cells in each session was computed as the average Pearson’s correlation between their rates over all preferred trials. Since cells fired at different timepoints, correlations were computed for lag equal to the interval between the time fields of each cell pair. Co-activation ‘C_ij’ of cells i and j was defined as:

$$C_{ij}=\frac{a_{ij}}{\sqrt{a_i\ast a_j}}$$

where a_ij is the number of preferred trials where both cells were active (i.e. non zero rates anywhere over the odor/delay interval) and a_x is the number of preferred trials where cell x was active. Therefore, this definition does not consider the timing of activation but only its co-occurrence between two cells over the odor/delay interval.

Since ROI segmentation is activity-dependent and cross-day registration is done pairwise, to discern how the sequence-cells of any training Day X spiked maximally on all other days, we traced the matched ROI for each sequence-cell of Day X in every other day. Sequence-cells of Day X that were not matched to another cell on another day, were considered inactive there (zero firing rate). For each matched cell of a Day X sequence-cell, its mean firing rate over trials starting with the same odor as the one on Day X was computed separately for each day. The time-bin within the odor-delay interval yielding the peak mean rate was detected. If the cell was also detected as sequence-cell over those trials that day, this time-bin corresponded to its field location. Otherwise it was considered a non-significant peak location. If a cell was inactive during the odor-delay interval on a day, that data point was ignored. On each day, the absolute time-distance between the corresponding peak rate time-bin and the field location on Day X was computed. Time-distance baseline was computed by shuffling each cell’s firing rate over the odor-delay interval in each trial, just as for significant field detection, computing the new mean rate peak time-bin and repeating the above process. This was done separately for 1000 shuffle repetitions and the mean baseline was computed by averaging over all cells and repetitions.

Principal Components Analysis

Principal component analysis (PCA) was applied to the collected firing rates of sequence-cells in each imaging day. Each cell’s rate was z-scored over all trials of a given odor and the PCA scores were computed. The explained variances for each PC were computed and PCs explaining >80% mean cumulative variance were kept, separately for each trial type. If that threshold was never reached, then all PCs were kept. The minimum number of the two PC limits was finally applied to both trial types. Trajectories along the multidimensional space of those PCs were computed for each trial and the mean trajectories over the two trial types were kept. The Euclidean distance between those was computed and smoothed with a 0.65 sec-window moving average. Baseline distances were computed for each session by circularly shifting the rates of sequence-cells along time by a random interval up to ± 1/2 x trial duration with 100 repetitions and repeating the PCA analysis for each repetition.

Plotted PCA trajectories were smoothed over the 3 PC space with spline interpolation and color coded using linear interpolation over time.

Bayesian Decoding

A Bayesian decoder was used to assess how well can collective sequence-cell activity predict time during the trial, as well as trial-type (Zhang et al., 1998). A separate decoder was constructed for each imaging day, using the firing rates of all sequence-cells (both sequences pooled), over the odor-delay time interval. For well-trained sessions, only correct trials out of the first 2/3 of all trials of the day were used for training the decoder and the last 1/3 trials were used for decoding. Both correct and error trials were decoded, unless otherwise stated.

Each cell’s mean firing rate over each trial-type was smoothed using 1sec-window moving average. In order to decode the trial-type (odor presented), we considered time space to be 2 x odor-delay interval (12 sec long in total). We thus concatenated along the time axis, each cell’s mean rate over the two trial-types. The decoder, trained by these concatenated firing rates (mean rate over odor-A-initiated trials followed by mean rate over odor-B-initiated trials) would thus predict a time point along the doubled time interval 0–12 sec. If the time point was within the first half (0–6 sec) it corresponded to that time point of an A-trial, whereas if it was within the second half (6–12 sec) it corresponded to the analogous time point of a B-trial.

Assuming Poisson distributed spiking and statistical independence of sequence cells, the decoded time point ${\widehat{T}}_t$ from activity at time bin t is given by:

$${\widehat{T}}_t=\underset{t}{argmax}\left(K\left(\prod _{c=1}^N\tau R_m{(c,t)}^{\tau R(c,t)}\right)exp\left(-\tau \sum _{c=1}^N{R}_m(c,t)\right)exp\left(\frac{{\left|t-{\widehat{T}}_{t-1}\right|}^2}{2{\sigma }^2}\right)\right)$$

where c = 1,…,N are the pooled sequence-cells and R_m(c,t) is the mean firing rate of cell c at time bin t (with bins concatenated over both trial types, spanning 12 sec) over all training trials. R(c,t) is the corresponding firing rate at the decoded trial, τ is the bin duration and K is the probability of being at time bin t of a particular trial type which is a constant, proportional to the ratio of trials of that type over all training trials (Zhang et al., 1998). The last term functions as a continuity constraint, limiting the decoded time bin to be in a relative proximity to the previous one⁵, with σ = 3 sec. Time bins with no activity from any sequence cell were not decoded. Chance baselines were computed by randomly shuffling the cell identities for each decoded trial with 1000 repetitions and decoding the shuffled cells for each repetition. Time prediction error refers to the mean absolute time distance between a given timepoint from either trial-types and the decoded one:$\langle \left|t-{\widehat{t}}_t\right|\rangle$, and does not take the trial-type into account. It thus functions as a measure of the time-information carried by the sequence-cells. Odor prediction accuracy refers to the percentage of correct trial-type decoding at any given timepoint (i.e. correct half of extended time-axis) and functions as a measure of the information on the odor identity carried by the sequence cells. Both measures were averaged over pooled trials from all analyzed sessions, for each decoded time point separately.

For cross-days analysis, we applied the Bayesian decoder on the firing rates of the recurring sequence-cells between each pair of days. Day pairs with no common sequence cells were not processed. All correct trials from Day 1 were used to train the decoder and all trials of Day 2 were decoded. Baseline was created separately for each day pair, by randomly shuffling the identities of the recurring cells in Day 2, with 1000 repetitions, and applying to decoder at each repetition. Decoded-time errors over each time point were computed for each day pair, concatenated for both trial types. Errors from all day pairs of any given distance were pooled together and their mean value for that given day distance was computed and plotted. The same process was applied to odor-decoding accuracy as well as the corresponding baselines for both measures. Data points from zero distance between days correspond to decoding all trials from a single day using the same trials (subset of correct trials) for training the decoder.

For multi-delay analysis, the Bayesian decoder was trained only with the firing rates of 5 sec-trials time-cells and was used to decode odor/time through the activity of these cells during the 10 sec trials. All correct 5 sec delay trials were used for training and all 10 sec trials for decoding. Only the delay time bins were used. The same method was used for extended odor-duration analysis. Using both correct and error trials for training the decoders did not alter our results. In order to account for the difference in length between training and decoding delays, every other time-bin was decoded, so that firing rates for training and decoding had the same number of time-points. E.g. the 2^nd time-bin in the extended delay was decoded through activity on the 1^st time-bin in the original delay whereas the 10^th time-bin in the extended delay would be decoded by the 5^th time-bin. This scheme inherently assumes that sequences rescale by a constant factor, with late time-cells shifting forward more than early ones. If time-cells are randomly shuffled in the extended delay, this scheme is not expected to yield significant decoding accuracy at any time bin. The opposite approach was used when decoding short delays based on sequences of the extended delays. Baseline was created by randomly shuffling the identities of the cells in the 10 sec delay trials (or the 3 sec extended-odor trials accordingly), with 1000 repetitions and applying to decoder at each repetition.

To compute the progress in decoding efficacy over training days, Bayesian decoders were built as before, with all first 2/3 trials per day used for training the decoder and all final 1/3 trials of each day used for decoding. Both correct and error trials were used to avoid sample sizes increasing with behavioral improvement. In naive mice, the same process was followed. To compute the progress in decoding efficacy with a fixed set of cells, a Bayesian decoder was trained on the activity of a subset of sequence-cells of training day 6 that were active in all previous days as well (see above). The decoder was then applied to the activity of the same cells in all previous days. All trials of the pair of days were used for training and decoding respectively. In both cases, baseline was created for each mouse each training day, following the same shuffling procedure as before. Mean baselines were computed by averaging across mice each day. For each day, significance over baseline was extracted by comparing pooled Bayesian data points from all mice with pooled chance values from each shuffling iteration in each mouse.

Support Vector Machine

A binary support vector machine (SVM) classifier was used to assess the odor stimulus in a trial based on the collective activity of all odor or time-cells. The same method as in Bayesian decoding was used to split trials into the training set and prediction set. All trials were split into two groups based on their odor identity. Again, only the correct trials were used from the training pool, whereas all trials from the decoding pool were decoded. Only sessions with at least 3 training trials of each odor were analyzed. The decoder was applied on the collective firing rates of all sequence cells, averaged either over the entire odor-delay interval, or the odor presentation timepoints or delay timepoints accordingly, or only over the firing field time point of each cell. The corresponding mean rate of each cell was z-scored over all trials. The classifier was trained using a radial basis function kernel with scale σ = 11 and box constrain parameter C = 15505. These values were acquired by Bayesian optimization of the SVM classifier over the two parameters, using the odor-cell firing rates over odor time-bins from one imaging session and a 10-fold cross-validation partition for data. Odor-prediction accuracy refers to the percentage of correct odor-predictions over all predicted trials and is averaged over all imaging days analyzed. Chance baselines were computed by randomly shuffling the cell identities for each predicted trial with 1000 repetitions and applying the SVM classifier on the shuffled data for each repetition.

The same classifier parameters and method were applied when using SVM on individual sequence-cells instead of collective sequence-cell groups. Chance baseline for each cell was computed by shuffling the identity of both training and predicted trials with 50 repetitions and applying the SVM classifier on each repetition.

For cross-days analysis, we applied the SVM classifier on the firing rates of the recurring sequence-cells between each pair of days, following the same process as with Bayesian decoding (see above). The classifier was applied separately on recurring cells that were odor-cells on Day 1 and those that were time-cells, irrespective of their field on Day 2. Baseline was created by randomly shuffling the odor identity of trials on Day 2, with 1000 repetitions and applying to decoder at each repetition. Decoded-odor accuracy by either cell group was pooled over all day pairs of a given distance and their mean value was computed and plotted.

For odor-decoding over correct or error trials, SVM classifiers were trained with the correct trials (correct hits and rejections) out of the first 2/3 trials in a session and either the remaining 1/3 correct trials or all the error trials (false alarms and misses) were decoded using firing rates of only odor-cells or time-cells averaged over the entire odor-delay interval. Due to low number of errors, even in training stages, this resulted in a similar sample size for both decoded outcomes (881 correct versus 773 error trials decoded in total). To decode odors in correct versus error match-trials only, SVM classifiers were trained over all the correct hit trials in a session and either correct rejection or false alarm trials were used for decoding. The same number of correct rejection and false alarm trials were decoded in each session, by randomly downsampling the largest trial group to match the smallest (491 trials total).

For SVM outcome-prediction, all trials were split into two groups based on their outcome (correct vs error). Classifiers were trained on 2/3 of error trials and an equal amount of correct trials, chosen randomly, and the outcome of all remaining trials was decoded using firing rates of only odor-cells or time-cells averaged over the entire odor-delay interval. Chance baselines were computed as before in all these cases.

Statistical Analysis

Unless otherwise stated, most statistical tests between distribution averages were performed under the Wilcoxon median test (‘WT’) if the corresponding distributions were not sufficiently close to normality under the Lillieform normality test (p > 0.05). Otherwise, a paired t-test was used. Significance of increasing or decreasing trends in distributions was assessed by a permutation distribution test of the Spearman rank correlation (‘SPT’) between x- and y-axis. P-values were corrected for multiple comparisons wherever necessary. ‘FDR’ across the text refers to FDR-correction. Statistical tests are mentioned in the main text or figure legends. No statistical methods were used to determine sample sizes but those were comparable to sizes used in similar publications.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
AAV1.Syn.GCaMP6f.WPRE.SV40	Penn Vector Core	100837-AAV1
Experimental Models: Organisms/Strains
Mouse: B6.Cg-Gt(ROSA)26Sortm9(CAG-tdTomato)Hze/J	Jackson Laboratories	007909
Mouse: B6.Cg-Gt(ROSA)26Sortm14(CAG-tdTomato)Hze/J)	Jackson Laboratories	007914
Mouse: Gad2tm2(cre)Zjh/J	Jackson Laboratories	010802
Mouse: B6;129S-Gt(ROSA)26Sortm32(CAG-COP4*H134R/EYFP)Hze/J	Jackson Laboratories	012569
Mouse: C57B/6J	Jackson Laboratories	000668
Software and Algorithms
Matlab 2016b	https://www.mathworks.com/products/matlab.html	N/A
CaImAn (modified version)	Giovannucci et al., 2019	https://github.com/flatironinstitute/CaImAn-MATLAB
NoRMCorre	Pnevmatikakis and Giovannucci, 2017	https://github.com/flatironinstitute/NoRMCorre
Custom written code for data processing and analysis	This paper	N/A

Highlights.

Spiking sequences in CA1 encode odor-stimuli and delay time in a working memory task

Odor-fields are stable whereas time-fields remap across days and trial alterations

Time-cell numbers increase during learning the task, not when passively exposed to it

Cell activity progressively converges to a field and then diverges from it over days