Kinetic modeling of stem cell transcriptome dynamics to identify regulatory modules of normal and disturbed neuroectodermal differentiation

Abstract

Thousands of transcriptome data sets are available, but approaches for their use in dynamic cell response modelling are few, especially for processes affected simultaneously by two orthogonal influencing variables. We approached this problem for neuroepithelial development of human pluripotent stem cells (differentiation variable), in the presence or absence of valproic acid (signaling variable). Using few basic assumptions (sequential differentiation states of cells; discrete on/off states for individual genes in these states), and time-resolved transcriptome data, a comprehensive model of spontaneous and perturbed gene expression dynamics was developed. The model made reliable predictions (average correlation of 0.85 between predicted and subsequently tested expression values). Even regulations predicted to be non-monotonic were successfully validated by PCR in new sets of experiments. Transient patterns of gene regulation were identified from model predictions. They pointed towards activation of Wnt signaling as a candidate pathway leading to a redirection of differentiation away from neuroepithelial cells towards neural crest. Intervention experiments, using a Wnt/beta-catenin antagonist, led to a phenotypic rescue of this disturbed differentiation. Thus, our broadly applicable model allows the analysis of transcriptome changes in complex time/perturbation matrices.

INTRODUCTION

Early cell fate commitment towards the neural lineage is accompanied by highly dynamic and large-scale transcriptome changes (1–6). Disturbances during this process can alter developmental trajectories permanently. Accordingly, key transcription factors as well as large transcriptome modules, such as gene ontologies and constituents of regulatory circuits, are strongly affected (7–12).

Pluripotent stem cells (PSC) are good models to mimic the in vivo processes during neurodevelopment. Human embryonic stem cells (hESC) or induced pluripotent stem cells (iPSC) are of particular interest, as this allows experimental access to the development of neuroectodermal and later nervous system structures in man. Such neurodevelopmental processes have many species specific features (13–16) and they could hardly be studied in a systematic way prior to the advent of stem cell technology. Examples for human specific aspects of brain development range from transposon activity (17), to largely differing time scales and relative steps of wave-like gene activation patterns (18–21).

Prior to the classical neurodevelopmental stages, leading from neural stem cells to brain tissue formation and regional specialization (16,22), early differentiation processes lead from initially pluripotent cells to neuroepithelial progenitor cells (NEP) and various types of neural stem cells (23). Such steps occur in fetuses during the formation and initial folding/closure of the neural plate (24,25). In vitro, the NEP cells form neural rosettes, a correlate of the neural tube (26). A highly standardized method (STOP-tox_(UKN) assay) has been developed to track early neural development and its disturbances via analysis of transcriptome changes, epigenome alterations and the capacity to self-organize in rosettes (8,9,12,23,27–29).

Disturbances of the regulatory networks that control the spatio-temporal expression of genes can lead to severe congenital malformations (e.g. spina bifida, anencephaly) (30,31), and they may contribute to neuropsychiatric disorders such as attention deficit/hyperactivity disorder (ADHD), autism spectrum disorders (ASD) or schizophrenia (32,33). Such disturbances can be induced by genetics (34), stress experiences during fetal and early childhood development (35) and environmental influences (drugs, environmental and industrial chemicals, malnutrition) (33,34). Little is known about the biochemical mechanisms that underlie these neurodevelopmental disorders, and how and when transient perturbations, such as by drugs, alter differentiation in a pathological way.

Valproic acid (VPA) may be used to establish bona fide models of clinically-relevant neurodevelopmental disorders. It is an anticonvulsant drug that is administered in epilepsy and mood disorders and it is well known to increase the risk for congenital malformation such as neural tube closure defects and craniofacial malformations (30,31,36–38). Extensive clinical data exist on VPA’s developmental neurotoxicity effects (39), and the relevant plasma concentrations in fetal and maternal blood are known (40,41).

The impact of developmental disturbances depends strongly on the time of onset and duration of the disturbance. In this sense, thalidomide (best known under the brand name Contergan) gained notoriety as there were very small time windows of in utero exposure identified that determined the kind of malformation (42). Therefore, in order to investigate the molecular mechanisms of such disturbances by using differentiating human PSC, it is important to get a better understanding of how these perturbations propagate to dysregulated gene activities and cellular phenotypes.

Mathematical models have been very instrumental to disentangle the complexity of regulatory networks in general, and of gene regulation in the context of stem cell differentiation more specifically. Models have been applied to analyze networks on multiple layers. For stem cells, most models focused on the network of key regulators and the long-term dynamics of cell fate decisions (43,44). Those models were able to disentangle the network topology of small networks of key pluripotency factors and have helped to define the logic that governs the stability and exit from pluripotency or other cell identity transitions (45–47). Such detailed mechanistic models build on extensive mechanistic knowledge and often integrate detailed data from different sources and studies. In contrast, a number of data-driven modeling approaches have been used to model transcriptome changes on a genome-wide scale. Broadly, these models were either used to infer quantitative information about mRNA processing and turnover to describe the response of the transcriptome to acute stimulations, or they have been used to infer hidden variables like transcription factor activity from transcriptome time series data (48–52). So far, these models were only applicable to describe the transcriptome dynamics to immediate stimuli or the effect of individual transcription factor on gene expression. Neither detailed mechanistic approaches nor the current transcriptome-wide modeling approaches are optimally suited to disentangle the transcriptome dynamics of a differentiation program, such as the transition from pluripotency to neural progenitor cells. As these transitions occur in a cascade of steps and lead to waves of gene expression, models are needed that consider the dynamic changes under control conditions to evaluate modulations by stressors/toxicants. Moreover, they need to be simple enough to be parameterized from sparse data, such as transcriptome time series. We therefore developed a coherent modeling framework that allows us to describe and model transcript dynamics during differentiation and to disentangle the effects of perturbation on the transcriptome dynamics. Our model allows to describe time-dependent gene expression in differentiating cells, and it is sufficiently coarse-grained to be applied transcriptome-wide. Using this model, we analyze differences between untreated and disturbed differentiation, where we study the influence of VPA on transcript dynamics as an example. We show that our kinetic model correctly predicts gene expression kinetics at concentrations of VPA not used for training. Additionally, the model provides a mechanistic basis to explain experimentally observed non-monotonic concentration-response relations that were non-intuitive at first. Finally, the model allows us to identify perturbed regulatory modules with high resolution in the time/compound concentration space. With this approach, we find that treatment with VPA leads to a transient upregulation of Wnt signaling which in turn causes the upregulation of neural crest genes. Our work shows that genome-wide models of transcriptome dynamics during stem cell differentiation may not only help to understand organogenesis/embryogenesis, but will also shed new light on developmental disturbances due to genetic and environmental stressors.

MATERIALS AND METHODS

Materials

Gelatine, putrescine, sodium selenite, progesterone, apotransferrin, glucose, insulin, ascorbic acid, valproic acid and ICRT3 were obtained from Sigma (Steinheim, Germany). Accutase was from PAA (Pasching, Austria). FGF-2 (basic fibroblast growth factor), FGF-8b, Sonic hedgehog and noggin and were obtained from R&D Systems (Minneapolis, MN, USA). Y-27632, SB-43154, CHIR99021 and dorsomorphin dihydrochloride were from Tocris Bioscience (Bristol, UK). MatrigelTM was from BD Biosciences (Massachusetts, USA). All cell culture reagents were from Gibco/Invitrogen (Darmstadt, Germany) unless otherwise specified.

Neuroepithelial and rosette differentiation

Human embryonic stem cells (hESC) (H9 from WiCells, Madison, WI, USA) were differentiated according to the protocol published by Chambers and colleagues (24) with modifications established in (8,25). Instead of using 500 μM noggin we used the combination of 35 μM noggin and 600 nM dorsomorphin together with 10 μM SB-431642 for dual SMAD inhibition as described earlier. This was used to prevent BMP and TGF-β signaling, and thus to achieve a highly selective neuroectodermal lineage commitment. For handling details, see supplemental material as decribed by Balmer et al. (8). Beginning on DoD4, KSR medium was gradually replaced by N2 medium (DMEM/F12 medium with 1% Glutamax, 0.1 mg/ml apotransferrin, 1.55 mg/ml glucose, 25 μg/ml insulin, 100 μM putrescine, 30 nM selenium and 20 nM progesterone), supplemented with the same amounts of noggin, dorsomorphin and SB-431642 as KSR. All differentiations were performed in six-well plates containing 2 ml of medium per well. For some experiments, cells were further differentiated until they formed neural rosettes. In detail, cells were differentiated until DoD10 as described above or in Chambers et al. (24). On DoD11, cells were detached using Accutase, and seeded at a density of 150 000 cells/cm² onto Matrigel-coated 96-well plates or glass cover slips. Cells were grown in N2S medium supplemented with 20 ng/ml FGF2, 100 ng/ml FGF8, 20 ng/ml sonic hedgehog, 20 μM ascorbic acid and 10 μM ROCK inhibitor Y-27632. On DoD13 ROCK inhibitor was removed. Cells were fixed for immune staining at DoD15 after rosettes had formed (26).

Experimental exposure

Developing cells were treated from DoD0–DoD6 with different concentrations of valproic acid (0.025, 0.15, 0.35, 0.45, 0.55, 0.65, 0.8 and 1mM) or the Wnt activator CHIR99021 (2 μM). For rescue experiments with the β-catenin Inhibitor iCRT3 (Sigma) cells were (co)treated from DoD2–DoD6.

Immunostaining

For immunostaining, cells were fixed on DoD6 or DoD15 in 4% paraformaldehyde and 2% sucrose prior to permeabilization in 0.3% Triton X-100 in PBS. After blocking in PBS containing 5% bovine serum albumin and 0.1% Tween-20 for 1 h, primary antibodies (Supplementary Figure S1) were incubated for 1 h, at room temperature (RT). After washing, secondary antibodies were applied for 45 min at RT. DNA was stained with Hoechst H-33342, and cover slips were mounted in FluorSaveTM reagent (Calbiochem, Merck).

Rosette formation assay

Rosette formation assay was performed in 96 well plates. Number of rosettes was assessed in six technical replicates for control and three technical replicates for treatments. The immune cytochemistry staining of golgi matrix protein (GM130), zona occludens 1 (ZO1) and the DNA with Hoechst H-33342 was used to identify rosettes. ZO1 is located in the centre of a rosette, surrounded by GM130. Images of the whole well were taken by Cellomcis (Thermo Fisher Scientific) automated microscope. Using Konstanz information miner software (KNIME) (53), rosettes were detected and counted. The number of rosettes per well was normalized to the total nuclear area. Data is always displayed relative to an untreated control (Described in detail in (26)).

Sample preparation for microarray analysis and quantitative PCR

Cells were lysed in Trizol reagent (Quiagen) at the indicated time points. mRNA was isolated as advised by the manufacturers protocol and an aliquot of 1μg reverse transcribed in a reaction mix of 20 μl (iScript, Biorad: the cDNA synthesis kit works with high sensitivity in this range. Standard curve r = 0.998, efficiency = 96.5%). The reaction mix was diluted 1:5 in water. Quantitative PCR was performed in 10 μl samples using EVAGreen SsoFastTM mix (5 μl EVAGreen mix, 3.6 μl water, 0.4 μl primer (final concentration: 200 nM), 1 μl cDNA (0.01 μg)) on a BioRad Light Cycler (Biorad, Germany). For quantification, qPCR threshold cycles were normalized to reference genes [tatabox binding protein (TBP) and ribosomal protein L13 (RPL13A)] (Primer list: Supplementary Figure S2A). Data was either displayed relative to expression in stem cells or cells treated with chemicals were then expressed relative to transcript levels of untreated control cells (which had been grown and differentiated for the same amount of time). For this normalization, the 2^–ΔΔC(T) method was used (54). Primer specificity was assessed by agarose gel electrophoresis and melting curves are provided (Supplementary Figure S2B). A standard curve was generated for each pair of primers and efficiency was measured (Supplementary Figure S2 A and C).

Affymetrix chip-based DNA microarray analysis (Human Genome U133 plus 2.0 arrays) was performed exactly as described earlier (12,55). Expression kinetics for unperturbed differentiation were measured in quadruplicates at the following 12 time points: 0, 6, 10, 16, 24, 36, 48, 60, 72, 96, 120, 144 h. Expression kinetics at 0.6 mM VPA were obtained in quadruplicates at the time points 72 and 144 h and in duplicates at 24, 48 and 96 h. Transcriptomes at 144 h were obtained for the window treatments with 0.6 mM VPA as follows. For treatment from 24 to 72 h in triplicates, for treatment from 24 to 9 6h in quadruplicates and for treatment from 72h to 144h in triplicates. One sample for the window treatment from 72 to 144 h had to be removed because of apparent mislabeling. Concentration dependent transcriptomes were obtained at 144 h in triplicates at eight VPA concentrations (0.025, 0.15, 0.35, 0.45, 0.55, 0.65, 0.8 and 1 mM) and were published earlier (27).

Data preparation

Gene expression data was normalised using bioconductor and rma as described in (12). For each condition, we computed the mean expression of each gene. Empirical Bayesian estimates of the standard deviations were computed using the ebayes function in the R package limma for each condition separately. These estimates were subsequently divided by the square root of the number of replicates for each condition to obtain the standard error of the mean.

Batch effect correction

As the untreated kinetics and the kinetics obtained from cells treated with 0.6 mM VPA were obtained in different batches (first and second batch), we performed batch effect corrections. For this, we used untreated samples at the time points 0, 72 and 144 h, where we computed the difference in expression between batches for each gene at the three time points. These differences were linearly interpolated to obtain b(t), the time dependent batch correction. Finally, for each gene and time point, expression in the VPA-treated kinetic samples was transformed according to

where expr(t) denotes the measured gene expression at time point t and expr′(t) is the batch corrected gene expression.

Selection of regulated genes

First, genes present on the microarray were restricted to protein coding genes using the Ensembl database (Ensembl 84 from March 2016) through the R package biomaRt. To identify regulated genes, the variation of the replicates of single time points was compared to the variation with respect to time using the Hotelling T2 statistic obtained with the mb.long function from the R package timecourse (www.bioconductor.org). For a description of the Hotelling T2 statistic see Tai and Speed (56). The four replicates for each of the 12 time points of the untreated kinetic served as input to mb.long. The 1500 genes with the top T2 statistic were labeled as regulated.

Model and cost function

The dynamic model consists of a linear chain of n states with transition rates g_on and g_off. The rate g_on is the on-rate of each state and the off-rate of its preceding state. Only the final state n has a different off-rate, g_off. This model can be analytically solved (see supplemental text S1 for details) to obtain the quantity Act(t,n,g_on,g_off), the fraction of cells in the active state. To model gene expression kinetics, we also introduce a time shift dt and the parameters A and B as the expression in states 0…n − 1 and n, respectively. Then the gene expression E_p is given by E_p(t, A, B, g_on, g_off, n, dt) = A + B Act(t + dt, n, g_on, g_off). To prevent non-defined values when computing the logarithm, 1 + E_p is used instead of E_p in the cost function. This amounts to a redefinition of the parameter A.

To model the dependency of the rates g_on (VPA) and g_off (VPA) on VPA, we use Hill functions of the form g(VPA,k,n) = g + (g’ −g)*VPAⁿ/(VPAⁿ + kⁿ) for both rates. The full model thus contains the additional parameters g_on', g_off', k₁, k₂, n₁ and n₂.

For each gene and each condition i, we compute the mean E_m,i of the measured expression and the standard error of the mean S_i as well as E_p,i, the expression predicted by the model for condition i. The cost function used for fitting the parameters is obtained by summing (E_m,i− E_p,i)²/S_i² over all data points from the untreated and treated kinetic indexed by i. For the concentration-response data at t = 144 h the sum (F_m,i − F_p,i)²/S_i² over all data points indexed by i is computed. Here, F_m,i is the measured fold change with respect to the time point 144 h in the untreated kinetic and F_p,i is the predicted fold change with respect to the predicted expression for time 144 h, untreated. The overall cost function is the sum of both contributions.

Parameter estimation

We estimated the parameters by optimizing the difference between data and model simulations weighted by the standard-deviation (see above). Because of the sensitivity of optimization results with respect to starting parameters, the often shallow cost landscape and the influence of the details of the optimization algorithm, optimization is performed in three iterations. In the first iteration, the microarray data with the original expression standard deviation computed with the limma package is used. In the second and third iteration, the standard deviation is corrected by a factor determined from the residuals of the first iteration fits. The first and second iteration each start with fitting only the data from untreated cells and subsequently fitting the full data set to improve convergence of the optimizer in the 12-dimensional parameter space of the full model. The third iteration employs different optimization algorithms to improve on the fit determined in the second iteration. We used the analytical solution computed for the model for all optimization algorithms and the analytical gradient function for algorithms that make use of a gradient (see supplemental text S1 and S2 for details).

For all fits, optimization parameters are restricted to the intervals 10⁻⁵ < g_on' < 10, 10⁻⁵ < g_off' < 10, 10⁻² < k₁ <2, 1 < n₁ < 4, 10⁻² < k₂ < 2, 1 < n₂ < 4, 1 < A < 6 × 10⁴, 1 < B < 10⁵, 10⁻⁵ < g_on < 3, 10⁻⁵ < g_off < 3, 1 < n < 20, 10⁻² < dt < 100. In the following we list the optimization algorithms and starting values used for the different iterations.

First iteration, fit of parameters A, B, n, g_on, g_off, dt to untreated data: optimizer GenSA from the R package GenSA with initial values A = min(e), B = max(e), g_on = 0.1, g_off = 0.01, n = 1, dt = 0, where e is the vector of expression values in linear units for the respective gene and optimizer option max.time = 200. Second iteration, fit of all parameters to the full data set: optimizer L-BFGS-B from the R package optim with 1000 sets of random starting parameters and optimizer options fnscale = 1, factr = 1e7, maxit = 1000. Random parameters are generated in the interval (1/5⋅par,5⋅par), where par is the optimized parameter from the untreated fits using the latin hypercube sampling implemented in the function randomLHS from the package lhs. The parameters g_on', g_off ‘, k₁, k₂, n₁ and n₂ that are not determined in the first iteration, are either randomly drawn from the entire allowed interval (k₁, k₂, n₁, n₂) or drawn from the interval determined by g_on and g_off, respectively (g_on’, g_off ').

Second iteration, fit of parameters A, B, n, g_on, g_off, dt to untreated data with rescaled standard deviation: as in the first iteration but with option max.time = 1000.

Second iteration, fit of all parameters to the full data set with rescaled standard deviation: as in the first iteration with 1000 sets of random start parameters but with options fnscale = 1e6, factr = 1e2, maxit = 2e4.

Third iteration, fit of all parameters to the full data set with rescaled standard deviation: optimization algorithms GenSA and L-BFGS-B as described above as well as LM (package minpack.lm) and NMKB (package dfoptim) are used with 100 random starting parameters. Random parameters are picked form the interval (0.999 par, 1.001 par). Optimizer options are set as follows. GenSA: max.time = 200, L-BFGS-B: fnscale = 1e6, factr = 1e2, maxit = 2e4, LM: ftol = 1e–25, ptol = 1e–16, gtol = 1e–15, maxiter = 2e4 and standard options for NMKB.

Finally, if a set of parameters yielding a better fit of the model to the data was encountered for a gene during the profile likelihood analysis (see below), then this set was adopted.

Parameter identifiability

To analyse parameter identifiability, we performed profile likelihood (PL) as described in Kreutz et al. (57). First, optimal parameter sets were reoptimized using the L-BFGS-B method to ensure a local optimum as start of the PL procedure. Parameters were increased and decreased starting from the optimal value with a fixed step size until the cost was increased by more than 95%-quantile of the χ²-distribution with one degree of freedom or until the upper or lower parameter boundary was reached. The minimal and maximal parameter values determined in this way yield the 95% parameter confidence interval. Further details of the PL procedure are described in the supplemental information (supplemental text S3).

GSEA

GSEA was performed using the HTSAnalyzeR package for R. As reference gene sets for the GSEA we used gene sets from the MSigDB v6.0 (gsea-msigdb.org), containing manually curated gene sets from pathway databases as well as published experiments (all curated sets, c2.all.v6.0.entrez.gmt and KEGG sets, c2.cp.kegg.v6.0.entrez.gmt). For all curated sets and KEGG sets, we used a minimum gene set overlap of 20 genes for computing significance. The FDR for each gene set was computed from 10 000 permutations. The GSEA exponent was set to 1.

Pathway gene sets

Gene sets for Figure 4C–F were obtained as follows. Neural crest signature genes were taken from the MSigDB (see above) gene set named ‘LEE_NEURAL_CREST_STEM_CELL_UP’. TGFbeta pathway genes were taken from the MSigDB gene set named ‘KEGG_TGF_BETA_SIGNALING_PATHWAY’.

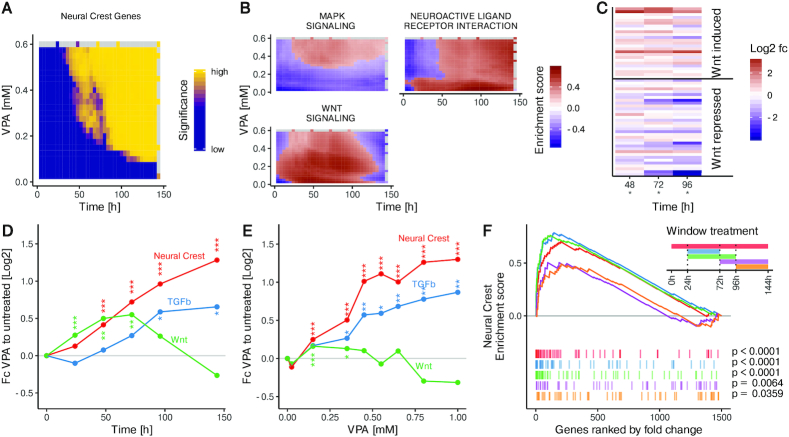
Figure 4.

Up-regulation of Wnt and TGFbeta pathway genes in cells exposed early in the differentiation time course to VPA. (A) GSEA using curated gene sets from the MsigDB on the fold change between VPA-treated and untreated cells at the indicated time points and concentrations. The significance of enrichment is shown as a heatmap for the top enriched term ‘Neural crest stem cell up’ (q < 10⁻⁴) The fold change data were measured for different VPA concentrations at the time point 144 h and for different time points at the concentration of 0.6 mM VPA (grey indicates no measurement available). Fold changes for all other times and concentrations are model predictions. (B) GSEA as in A using KEGG pathway gene sets available in the MsigDB. The enrichment scores are shown as heatmaps for the three top enriched pathways (q < 0.05), with red indicating enrichment and blue indicating de-richment (grey indicates no measurement available). (C) The fold change between cells treated with 0.6 mM VPA and untreated cells is shown as a heatmap for Wnt-induced and Wnt-repressed genes separately at the indicated time points. Significance is indicated below the time point (*P< 0.05, Fisher's test) (D) The average fold change between cells treated with 0.6 mM VPA and untreated cells is shown for the following groups of genes: Genes up-regulated in neural crest cells (Neural crest), genes induced by Wnt signaling (Wnt) and genes annotated as being part of the TGFbeta pathway (TGFb). The symbols indicate the significance of the up-regulation at the respective time point (*P< 0.05; **P< 0.01; ***P< 0.001, Wilcoxon rank sum test) (E) Average concentration-response curves at the differentiation endpoint (t = 144 h) for gene groups from D are shown. The symbols indicate significance as in (D). (F) H9-hPSC were differentiated towards neuroepithelial cells and treated with 0.6 mM VPA during different time windows. Two early windows, 24–72 h (blue) and 24 h-96 h (green) as well as two late windows, 72–144 h (magenta) and 96–144 h (orange) were compared to the continuous treatment 0–144 h (red). GSEA on the fold change of VPA treated cells compared to untreated cells for neural crest up-regulated genes for different treatment windows: Coloured lines indicate the enrichment score for the respective treatment window and coloured vertical bars indicate the fold change rank of all neural crest up-regulated genes with respect to the fold change of all genes for the respective treatment window.

Wnt pathway target genes were obtained from (58) through the GEO database (GSE45223). Robust estimates of the standard deviation were derived using an error model that was parameterised as follows. The empirical standard deviation for each gene and time point was computed using replicates. The data was then divided into 15 equally sized bins based on mean expression, and the average empirical standard deviation was computed within each of the 15 bins. For bins with expression <10, the standard deviation was set to the maximal value. The resulting values were then interpolated using the R function loess with a span of 0.75. Wnt induced genes were obtained using the fold change between samples ‘WA09 embryonic stem cells, NC, day 3’ and ‘WA09 embryonic stem cells, DSi, day 3’ with a z-value threshold of 3.5. Wnt repressed genes were obtained using the fold change between samples ‘WA09 embryonic stem cells, DSi, day 3’ and ‘WA09 embryonic stem cells, NC, day 3’ with a z-value threshold of 3.5. The z-value was defined as mean expression divided by the loess interpolated standard deviation.

Gene ordering in heatmaps

In order to sort genes by the time of peak expression, gene expression values were interpolated to a resolution of 0.1 h using the R function loess with a span of 0.8. Subsequently, the time point of the maximum value of the interpolated expression was determined for each gene.

UMAP

Dimensional reduction of the transcriptome data for the 1500 top regulated genes was performed using the umap R package with parameters n_neighbors = 4, n_epochs = 4000 and random_state = 798395.

RESULTS

Heterogeneity of gene regulation during early neural differentiation

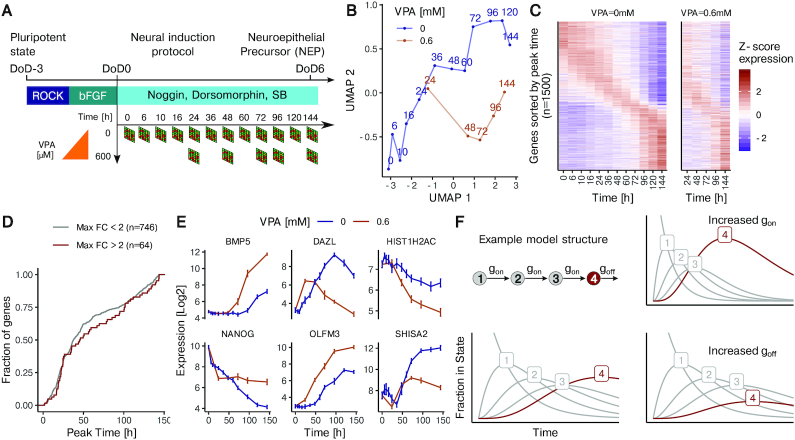
We used an in-vitro system where human pluripotent stem cells (hPSC) are differentiated according to the double SMAD inhibition neural induction protocol to analyze gene expression dynamics. We first obtained transcriptome profiles at twelve time points during the first six days of differentiation. To trigger a defined developmental disturbance (8,9,12,59), we treated cells with 0.6 mM VPA and obtained the transcriptome samples after 1, 2, 3, 4 and 6 days (Figure 1A). A 2D Uniform Manifold Approximation and Projection (UMAP) representation was chosen to visualize transcriptome changes over time. The progressive gene expression changes over time were clearly visualized by this approach. Compared to the trajectory of unperturbed cells, VPA-treated cells were clearly offset (Figure 1B). As first overview of gene expression dynamics on the individual gene level the 1500 top regulated transcripts were ordered by the time of their peak expression. The gene expression heatmap clearly showed that many genes had their highest expression at the start or end of differentiation, but that also a sizeable number peaked at intermediate times (n = 810) (Figure 1C). The sequential peaking of groups of genes is typical for a highly coordinated sequence of neurodevelopmental steps. It may be explained by waves of gene activation programs.

Figure 1.

The effect of HDAC inhibition on gene expression kinetics in spontaneously differentiating hPSC. (A) Time-resolved transcriptome data was obtained during the differentiation of hPSC from the pluripotent state to the neuroepithelial stage (DoD6), using an established double SMAD inhibition protocol to direct cell fate. Data were obtained for 12 time points (between 0 and 144 h) during undisturbed differentiation (VPA = 0 mM, n = 4 independent differentiations), and for five time points in the presence of 0.6 mM VPA (n = 2–4). (B) Presentation of dimensionality reduced (UMAP method) transcriptome data (time series for the 1500 most strongly regulated genes during undisturbed differentiation) to probe differences between normal and VPA-affected differentiation. Numbers indicate the time (in h) after initiation of differentiation. (C) Heatmap of gene expression (row-wise z-normalized) over time for unperturbed differentiation (left) and cells treated with 0.6 mM VPA (right). Expression is shown for the 1500 most strongly regulated genes, sorted by the time of peak expression. (D) The distribution of the time point of peaking is shown for a subset of the 1500 genes from C that have their peak expression at a timepoint after day 0 or before day 6. Genes were grouped as strongly affected by VPA (red, n = 64) or little affected by VPA (blue, n = 746). (E) Examples of expression kinetics for genes with different behavior in the case of undisturbed differentiation and differentiation in the presence of VPA. Data are means ± standard deviation. (F) Schematic of the structure of the kinetic model, based on the assumption that differentiation proceeds via a sequence of discrete cellular states (e.g. stages 1–4), and that the speed of transition can be described by the transition rates g_on and g_off. A gene is assumed to be expressed only in a single cellular state (here in state 4, red). For a given gene all transition rates between cell states are assumed to be the same (g_on).The decay rate of the final state (here: state 4) can differ (g_off). Variations of g_on/g_off are exemplified in a 4-state model. The fraction of cells in a given state is shown as a function of time. The model assumes all cells to be in state 1 at t = 0. The fraction of cells expressing the gene of interest (being in state 4) increases with time. The two panels on the right show the effects of increasing either g_on (top) or g_off (bottom).

The observed pattern is also consistent with the sequential occurrence of cell states that express particular genes. We observed that the timing of peak expression remained broadly unaltered in VPA-treated cells, although a detailed comparison of the patterns showed individual genes that shifted their time course of expression (Figure 1C). To follow up on the latter finding, we examined whether VPA-affected genes generally peaked later or earlier than genes not significantly affected by VPA. However, transcripts most strongly affected by the drug (log fold changes > 2) showed a peak time distribution that did not differ from little-affected genes (Figure 1D). This suggests that VPA does not selectively affect genes induced at a specific time point in development. The above analysis of the overall expression pattern showed that VPA-affected genes are not peaking at a particular point in time and that the number of genes peaking at a given time is not affected by the drug. However, for individual genes we noticed that VPA treatment can cause dramatic changes in the expression concerning the timing as well as the extent of regulations (Figure 1E). The complexity of the transcriptome modulation by VPA treatment was our incentive to develop a mathematical model of gene expression dynamics that would reflect the observed expression changes over time. Our model assumes that each cell transits through different states during differentiation, and that each gene is expressed only in one specific state (Figure 1F). Application of the model to cell population averages implies that the gene expression data it predicts are determined by how many cells are in a state where the gene is in the ‘switched-on’ state. To make the model mathematically tractable, we based it on three assumptions. (i) For each gene, the cell has to transit through n prior states before it enters the state n + 1 where the gene is activated. (ii) Cells transit through the first n states with a rate g_on, and they leave the active state with a rate g_off. (iii) For each gene, the parameters n, g_on and g_off can be different, i.e. each gene is modeled separately (Figure 1F). The basic working of the model may be exemplified for an n = 3 situation, in which the gene of interest is expressed in state 4 (final state) (Figure 1F, bottom, left). On the population level, an increase of g_on in this situation would lead to earlier and more peaked gene expression (Figure 1F, top, right). An increase of g_off would lead to an overall attenuated expression (Figure 1F, bottom, right). An intuitive explanation for this is that few cells ever occupy state 4 at the same time, because the off-rate g_off is high compared to the on-rate g_on. To allow the model to fit also genes that decrease monotically in expression, we additionally introduced a time shift parameter dt. This parameter shifts the peak to the left so that the data can exclusively be fitted to the decreasing flank of the peak.

Modeling of dynamic transcriptome disturbances by VPA

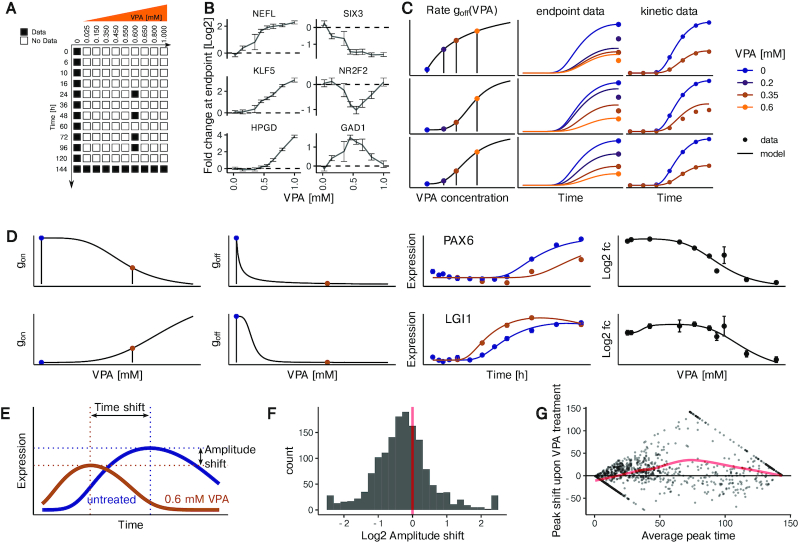
In order to extend the model to VPA-treated cells, additional data were required. We used transcriptome data published earlier (28), in which the effect of eight additional VPA concentrations (from 25 μM to 1 mM) was measured after 6 days of differentiation (Figure 2A). When we inspected concentration-response curves for different genes in this data set, we noticed a high heterogeneity: for example gene expression was perturbed at different VPA concentration thresholds (NEFL is very sensitive while HPGD is only perturbed at high concentrations of VPA). Also, we found the deregulation to reach a saturation (SIX3) or not (KLF5). Finally, we noticed that some genes showed a non-monotonic concentration-response (e.g. GAD1 or NR2F2) (Figure 2B).

Figure 2.

Establishment of a mathematical gene expression model of VPA-disturbed neurogenesis. (A) Data matrix used to fit the combined kinetic and VPA effect model. For each condition marked in black, data from two to four microarrays were used. All numbers refer to independent differentiations. (B) Curves exemplifying various types of concentration-response behavior of individual genes (means ± standard deviation, n = 3). Data for the effect of eight VPA concentrations on day 6 (t = 144 h) are shown. (C) Exemplification of the VPA effect model constraints (for g_off and an example gene down-regulated by VPA): It is assumed that the two rate constants of the kinetic model (g_on and g_off) depend on the concentration of VPA, and can be described by a Hill model (shown in the first column). The Hill function ‘g_off (VPA)’ is parametrized in such a way that the multi-step model fits both the endpoint data (expression levels for different VPA concentrations measured at 144 h, column 2) and the kinetic data (measurements of gene expression at different times ≤ 144 h, column 3). Three examples illustrate how the combination of constraints by endpoint and kinetic data lead to model optimization for g_off (VPA). Upper panel: the kinetics are correctly fitted but the endpoint is wrong for small concentrations because the Hill curve is not steep enough. Middle panel: both the endpoint and kinetic data (after VPA treatment) are not correctly fitted because the turning point of the Hill function is at too high VPA concentrations. Bottom panel: correct function g_off (VPA), fitting both the endpoint and the kinetic data. (D) Example fits for the genes PAX6 (top) and LGI1 (bottom). The left two panels show the fits for the Hill model, with the blue and brown points indicating the VPA concentrations of 0 and 0.6 mM, respectively. The third panel shows data and fit for the gene expression kinetics in the absence (blue) or presence of VPA (0.6 mM, brown). The fourth panel shows the data for the 9 VPA concentrations and one untreated sample at the endpoint (144 h) of the differentiation together with the fit line from the model. (E) Amplitude shift and time shift with respect to fitted gene expression kinetics are indicated by the offset of brown and blue dotted lines. (F) Distribution of genes with respect to the amplitude shift triggered by 0.6 mM VPA compared to the untreated differentiation. (G) MA-plot for the change in peak time triggered by 0.6 mM VPA compared to the untreated differentiation. For each gene that peaks after day 0 or before day 6, the change in peak time is plotted against the mean of the peak time in the treated and untreated conditions. The red line indicates a loess interpolation with span 0.75.

In order to set up a model for the VPA effect that reflects the molecular features of the neurodevelopmental program, we reasoned that VPA was unlikely to affect the number of cell states. We assumed the drug to alter the parameters g_on and g_off. Therefore, we made g_on and g_off monotonic functions of the VPA concentration (modelled using a Hill function). The resulting model was then fitted (i) to the expression data at t = 144 h for different VPA concentrations and (ii) to the time series data for unperturbed differentiation and differentiations at 0.6 mM VPA (Figure 2C). This procedure was applied for each gene, i.e. training each model with 12 parameters on data from 86 samples for 25 conditions. Example fits are shown for the genes PAX6 and LGI1 (Figure 2D). The plots for the input functions for g_on and g_off illustrate how different concentration dependencies of the rates g_on and g_off can lead to distinct concentration-response behavior at the endpoint. We found that the multi-step model with VPA concentration-dependent rates correctly described the observed changes in gene expression amplitude and timing caused by VPA treatment (Figure 2D).

To judge the general ability of the model to fit the kinetic and concentration-response data, we computed the correlation between data and fits. We found a correlation coefficient larger than 0.9 for 88% of the 1500 fitted genes for the unperturbed differentiation. For the concentration-response data, we compared the fits to the data for genes with a minimum log₂ fold change of 1 at the endpoint. For this group of 557 genes, 95% had a correlation coefficient higher than 0.9. We concluded that the model correctly describes expression patterns for the large majority of regulated genes in the presence and absence of VPA.

Since the model describes peaked gene expression kinetics, parameter identifiability will in general depend on the peak location. For montonically decreasing or increasing genes, where the peak is outside of the observed time frame, we expect g_on and g_off to be less identifiable than for genes peaking at intermediate times. To analyse parameter identifiability, we performed a profile likelihood analysis which allows to compute parameter confidence intervals (57), exemplified for the gene POU4F1 in Supplementary Figure S6. As expected, g_on,g_off, dt and n are best defined for genes peaking at intermediate times (Supplementary Figure S7). The considerable uncertainty in these parameters even for genes with a clearly defined peak is also due to structural non-identifiabilities. For instance, a shift in the peak location to earlier times by increasing g_on can be offset by increasing n. Peak times, which are computed from a combination of parameters, are better identifiable (Supplementary Figure S8). For genes peaking at intermediate times, the uncertainty in the peak time is comparable to the time resolution determined by the transcriptome samples.

In order to characterize the overall effect of VPA on regulated genes, we computed the change in peak-to-trough expression (amplitude shift) and the change in peak timing (time shift) (Figure 2E) from the model fits. We observed a bias towards a decreased amplitude upon VPA treatment (68% of all regulated genes) (Figure 2F). This bias was retained when restricting the analysis to genes with a significant change in amplitude (Supplementary Figure S9). When plotting the change in peak timing against the average of the peak time in the untreated and VPA-treated conditions, we noticed an average peak time shift towards later times for genes that peak intermediately (Figure 2G). When restricting the analysis to genes with a significant peak time shift, the average delay became more pronounced (Supplementary Figure S10). The model fits thus indicate that expression changes over time are mostly attenuated and delayed by VPA. Taken together, we established computational models for hundreds of genes that capture gene expression kinetics during differentiation and model the influence of VPA on the kinetics.

Explanation of non-monotonic concentration-response curves by the gene expression model.

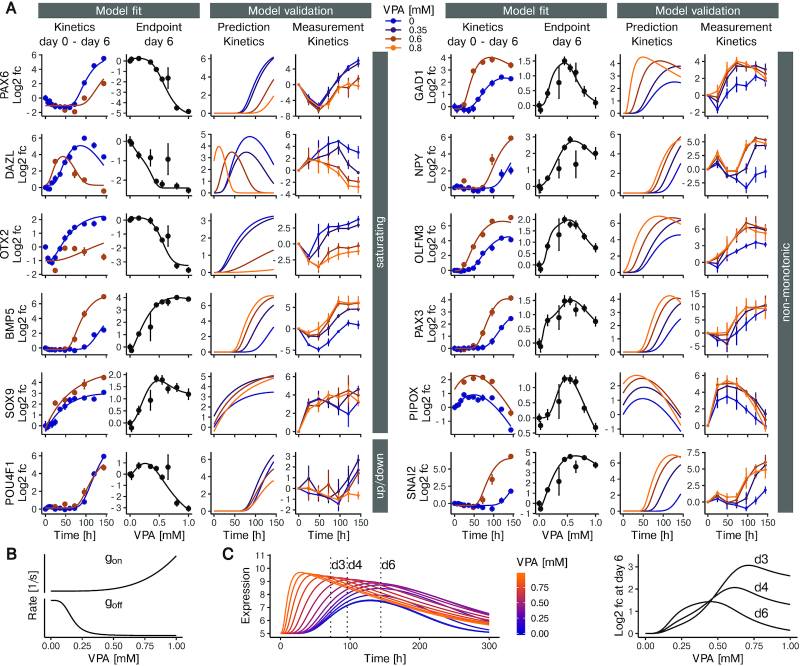
We set out to validate the gene expression kinetics predicted by the model by generating additional kinetic data at VPA concentrations that have not been used for model fitting. Gene expression kinetics for 12 genes were measured at 0.35, 0.6 and 0.8 mM VPA using quantitative RT-PCR. We selected these 12 genes to cover a broad range of qualitatively different concentration-response curves with respect to VPA at t = 144 h (Figure 3A). Saturating concentration-responses were exemplified by three genes (PAX6, DAZL, OTX2) that are down-regulated and two genes (BMP5, SOX9) that are up-regulated by VPA. POU4F1 was included as a gene that shows a slight increase in expression at low concentrations, and a pronounced decrease at high concentrations. Most importantly, we also selected genes that show a pronounced non-monotonic behavior, where expression is either reduced or increased at intermediate, but not at high concentration (Figure 3A, right column). Using the model fits, we simulated expression kinetics for the three different VPA concentrations (0.35, 0.6 and 0.8 mM VPA). The model predicted that treatment with VPA can dramatically alter the amplitude of peak expression (see e.g. OTX2), as well as timing of peak expression (see e.g. DAZL). BMP5 exemplified the case of changes in both peak expression and peak timing. When comparing the peak timing and changes in amplitude observed in the RT-PCR data, we observed good qualitative agreement with the model predictions (Figure 3A, rightmost panel for each gene). Quantitatively, the 12 tested genes have an average correlation between predicted and measured expression values of 0.85 (Pearson's r). Our observation that non-monotonic concentration-response curves were predicted with high accuracy was surprising, given the fact that the model represents the effect of VPA as monotonic functions (g_on(VPA) and g_off(VPA)). We therefore analyzed the model simulations with regard to the question how such behavior can occur. An intuitive understanding of this model feature can be obtained from a detailed examination of the GAD1 gene (Figure 3B/C). In this example, g_on increases with increasing concentration and g_off decreases with increasing concentration. This leads to an increase in amplitude and earlier peaking times as the VPA concentration is increased (Figure 3C). However, because g_off is more sensitive to changes in concentration than g_on, the increase in amplitude precedes the change in timing. This explain why, at t = 144 h expression is first increased, then decreased. We concluded that the gene expression model we developed correctly predicts differentiation kinetics at VPA concentrations on which the model was not trained. It furthermore helps to explain non-monotonic concentration-response curves, as monotonic changes in activation and de-activation kinetics can in combination lead to non-monotonic fold change at a given timepoint (e.g. t = 144 h), while peak time and maximal expression change monotonically.

Figure 3.

Multi-state model-based predictions of gene expression under the influence of VPA. (A) Model fit and experimental validation for genes with different types of concentration-response behavior. The left panel shows examples of genes with largely monotonic concentration-response behavior. The right panel exemplifies non-monotonic responses. For each gene, the first column (from left to right) shows the experimental data (means ± standard deviation) together with the model fit for the time-dependent expression in the presence of 0 (blue) or 0.6 mM (brown) VPA. Next, the concentration-response data for 6 days of VPA exposure are shown together with the model fit. The third column indicates the model predictions for gene expression kinetics at VPA concentrations of 0, 0.35, 0.6 and 0.8 mM. The fourth column shows expression kinetics data from a validation experiment using RT-PCR (means ± SD, n = 3). The concentrations were 0, 0.35, 0.6, 0.8 mM (blue to orange). (B, C) Detailed exemplification of non-monotonic concentration-response behavior predicted by the model for the GAD1 gene. The graphs in B show how the VPA concentration affects the production rate (g_on) and the decay rate (g_off). Both rates change monotonically with the VPA concentration. (C) The left plot shows the computed model prediction of gene expression over time, at VPA concentrations increasing from blue to orange (range: 0–1 mM). The peak concentration not only increases with increasing VPA concentration, but also moves to earlier time points. The plot to the right shows fold changes in gene expression based on the data on the left, for a time of 72, 96 and 144 h and for various VPA concentrations versus control.

Identification of Wnt signaling as major driver for divergent differentiation

Due to non-monotonic and transient effects of VPA, analyses of single time points or at single concentrations might be misleading. We therefore used our gene expression model to predict gene expression for various times and VPA concentrations, and used these predictions to ask which cellular processes are perturbed by VPA during differentiation. Specifically, we predicted fold changes for regulated genes at densely spaced time points (0–144 h) and VPA concentrations (0–600 μM). Subsequently, we performed gene set enrichment analysis (GSEA) on the predicted fold changes. The term with the maximum enrichment score was ‘Neural Crest Stem Cell up (NCSC)’. For the VPA concentration of 0.6 mM, a concentration well within the therapeutic range of VPA as an anticonvulsant drug (60,61), and associated with clinical birth defects (28,60–63), neural crest stem cell (NCSC) signature genes were enriched from about 50 h onwards. Even at much lower drug concentrations (down to 0.1 mM), enrichment was found, but it occurred at later time points (Figure 4A).

The model predictions were further used to identify possible mechanisms by which VPA induces NCSC genes. We found only 7 KEGG pathways showing a sufficient overlap with our set of regulated genes to compute meaningful p-values. Three of them were significantly enriched: neuroactive ligand receptor interaction, MAPK signaling and Wnt signaling. The time-concentration matrix of the enrichment scores of neuroactive ligand receptor interaction indicated activation of this pathway at minimal VPA concentrations, and increasing the concentration did not enhance this effect. For MAPK signaling, 300 μM VPA led to an up-regulation, which persisted until at least 144 h. The regulation of Wnt-associated genes was particularly interesting, with only a transient up-regulation that ended between 100 and 120 h. Increased VPA concentrations shifted the time frame of up-regulation towards earlier times, so that it was not enriched for at the 144 h data points (Figure 4B).

The predicted up-regulation of Wnt signaling is remarkable, because together with TGFβ signaling, it is known to play a role in neural crest development (64,65). To further investigate the connection between Wnt/TGFβ signaling and NCSC induction, we derived a Wnt target gene signature (Supplemental Table S1) from a transcriptome study in human embryonic stem cells (58). When examining the VPA-induced fold changes for these genes at the relevant time period (48–96 h), we observed that Wnt induced genes tended to be up-regulated by VPA, while Wnt-repressed genes were rather down-regulated. Additionally, the majority of TGFβ pathway genes were upregulated by VPA (Supplementary Figure S11). This trend is consistent with an activation of Wnt signaling by VPA (Figure 4C).

To confirm this activation hypothesis, we used a more robust approach: average fold-changes caused by VPA treatment for Wnt-activated genes, for TGFβ pathway genes, and NCSC signature genes were calculated for measured time points and VPA concentrations. This data showed that VPA treatment indeed lead to a transient response for Wnt-induced genes. In contrast, NCSC signature genes and TGFβ pathway genes showed increased up-regulation over time (Figure 4D).

Predictions from our model suggested that NCSC signature genes were induced already at very low VPA concentrations (Figure 4E). A steep increase in regulation by VPA was observed in the 200–400 μM range, while the average fold change hardly increased at concentrations above 0.5 mM. Such data are of high interest for systems pharmacology models and toxicity prediction algorithms. With respect to our model, it was also very interesting to observe that Wnt signaling target genes were not significantly altered, when analyzed at the usual model endpoint (144 h) (Figure 4E). They were only clearly identified by modeling of data for earlier time points. This re-emphasizes the need to provide and analyze kinetic data.

The transient activation of Wnt signaling targets could mean that differentiating cells are susceptible to altered Wnt signaling only for a limited duration. This would explain the frequent observation in developmental toxicology of particular windows-of-sensitivity (9,26). To investigate this further, we treated cells with VPA at different times and with variable treatment duration and reanalyzed a published dataset (26,27) (Figure 4F). GSEA for NCSC genes showed a marked difference between early and late treatment windows, with late treatments failing to efficiently upregulate NCSC genes. Brief early treatments led to a very similar up-regulation as continuous treatment. This implies that differentiation disturbances by VPA are most efficient/toxic during early neurodevelopmental periods (Figure 4F). Taken together, these applicability tests of our mathematical gene expression model show that this form of data analysis can unveil complex regulation patterns, exemplified here by a transient dysregulation in Wnt signaling associated with a permanent up-regulation of the NCSC fate.

Altered VPA-induced neural crest formation by interference with Wnt signaling

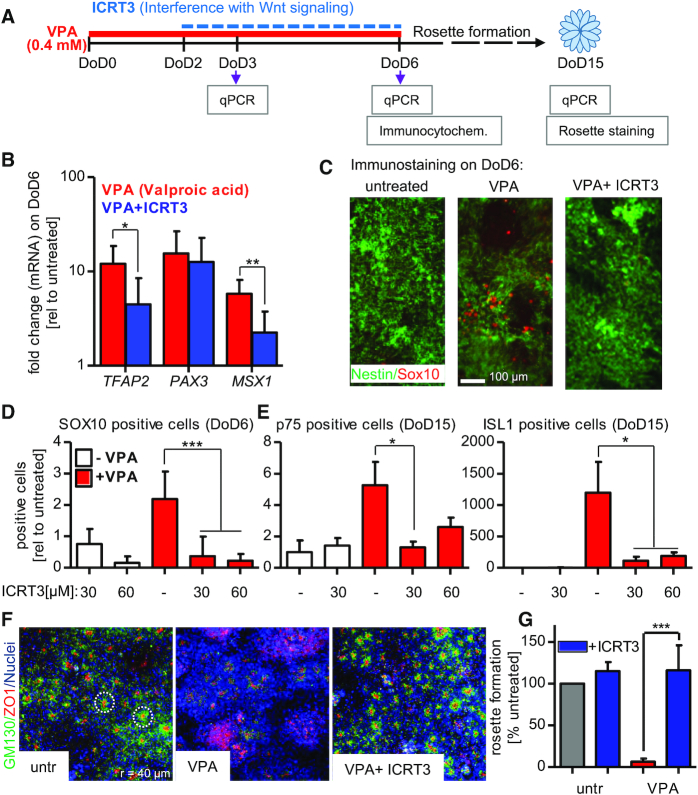
Finally, we tested in how far the toxicant-induced shift of differentiation from neuroepithelial cells towards neural crest cells may be prevented by interference with Wnt signaling. First, a diverse set of Wnt target genes relevant for early neurodevelopment (DACT, SP5, SIX3, GAD) was analyzed to compare the response to VPA with the one triggered by the well-established Wnt activator CHIR (CHIR99021; a specific inhibitor of glycogen synthase kinase-3) (9,66). The analysis was performed after three days of differentiation (DoD3), a time period relevant to fate switching. Both VPA and CHIR triggered similar response patterns (Supplementary Figure S3A). Moreover, analysis of the established neuroepithelial test endpoints (expression of PAX6 and of OTX2) on DoD6 confirmed that Wnt activation during the differentiation process by CHIR indeed disturbed the correct differentiation. The drug attenuated the up-regulation of PAX6 and of OTX2; in other words, CHIR triggered a relative downregulation of the neuroepithelial markers compared to untreated control cells (Supplementary Figure S3B).

Having established that Wnt signaling may disturb neuroepithelial differentiation in our experimental system, we used the beta-catenin inhibitor ICRT3 as tool to attenuate this pathway. In a proof-of-concept experiment we found that ICRT3 attenuated the expression of typical neural crest genes (TFAP2, PAX3, MSX1) in cells treated with CHIR (Supplementary Figure S4A). Thus, we proceeded to a series of experiments investigating the effect of ICRT3 on cells treated with VPA (Figure 5A). On the gene expression level, 30 μM of ICRT3 already attenuated the VPA-induced up-regulation of TFAP2 and MSX1, but not PAX3 (Figure 5B); at higher concentrations (60 μM), ICRT3 had pronounced attenuating effects on all three neural crest marker genes (Supplementary Figure S4B). More importantly, the beta-catenin inhibitor also prevented protein expression of the neural crest master regulator SOX10 in the presence of either 400 μM (Figure 5C) or 600 μM VPA (Supplementary Figure S5A). This phenotypic effect was persistent, as the intermittent treatment with ICRT3 (from DoD2–DoD6) also prevented the up-regulation of neural crest marker proteins ISL1 and p75 (also named TNFRSF16, CD271, p75NTR) at DoD15 (Figure 5D, Supplementary Figure S5B). These data strongly suggest that the intermittent up-regulation of Wnt pathway genes contributes to the differentiation switch away from neuroepithelial cells and towards neural crest. The rescue from disturbed neuro-differentiation by ICRT3 was further investigated in a rosette formation assay (26,27). Self-organized formation of rosettes is a hallmark of the neuroepithelial phenotype, and has been considered as functional correlate of neural tube formation (8,67). The cells generated by our standard protocol (26) showed extensive formation of neural rosettes, which was completely disturbed in cells exposed to VPA during the pivotal differentiation period of DoD0–DoD6 (Figure 5F). Co-treatment with ICRT3 (from DoD2-DoD6) fully restored the rosette formation capacity of the cells (Figure 5F, G). Thus, interference with Wnt signaling at a critical period of differentiation prevented the neurodevelopmental phenotype triggered by VPA.

Figure 5.

Interference with toxicant-induced Wnt activation and neural crest formation. (A) Pluripotent stem cells were differentiated within 6 days to neuroectodermal precursor cells; in some experiments, these were further differentiated until DoD15, when they formed neural rosettes. The developing cells were either exposed to valproic acid (VPA; 400 μM; from DoD0–DoD6) or they were co-treated with VPA + ICRT3 (beta-catenin inhibitor; 30/60 μM; from DoD2-6). For analysis, gene expression was measured by quantitative real-time PCR (qPCR), marker proteins were evaluated by immunocytochemistry or rosette formation was quantified by immunostaining followed by automated imaging. (B) The mRNA levels of three neural crest marker genes (TFAP2, PAX3, MSX1) was measured after treatment with VPA alone or VPA + ICRT3. Data is shown as fold change relative to the untreated control. (C) Cells were fixed and immunostained for SOX10 and nestin, after treatment with VPA or VPA + ICRT3 (30 μM). (D) Quantification of SOX10 staining in DoD6 cells. Stained cultures were imaged and SOX10-positive pixel were counted. They were normalized to the nuclear area (H-33342-positive pixels). (E) Cells were differentiated and treated as described in A until DoD15. Immunostaining was performed for ISL1 and p75, and quantification was performed as in D. Data is shown relative to untreated controls. (F) Cells were treated as described in A until DoD15. Then, the tight junction marker ZO1 (zona occludens 1; red), the golgi marker GM130 (Golgi matrix protein 130 kDa; green) and nuclei (blue, H-33342 DNA-intercalating dye) were stained, and rosette formation was quantified. The left images show untreated cells that form neural rosettes. Each red dot surrounded by a green halo represents one rosette. The two dashed white rings (80 μm diameter) indicate exemplary rosettes. (G) The neural rosette formation assay (RoFA) software was used to quantify rosettes (normalized to the number of cells in a well). Data are given relative to the untreated control. All data are means ± SD of at least three replicates, *P < 0.05; **P < 0.01; ***P < 0.001.

DISCUSSION

Analyzing perturbations of differentiating cells is particularly difficult compared to similar approaches in more or less static cell cultures. For instance, a matrix of time- and concentration-resolved data needs to be analyzed. Here, we used interpolation of a limited amount of data by a kinetic model to make such an analysis feasible. The modeling principle may be applied to any other differentiation process in cell biology and organism development that is affected by an additional factor (signaling molecule, drug or gene dose). Previous genome-wide modeling was mainly focused on the description of gene expression dynamics in terms of RNA production and turnover rates (e.g. (52)). This allowed excellent modeling of transcriptome changes triggered by defined signaling events in static cell cultures. Extensions of these models allowed very precise predictions of kinetic rates, particularly when combined with metabolic labeling (68–70). Recent progress also allowed definition of cell trajectories in single cell data (71). A major principle that distinguishes our current work from previous transcriptome descriptions is our model assumption of distinct cellular states in which particular genes are expressed, and that the transition between these states is slow relative to gene expression kinetics. This feature allowed us to model long time series as typically observed during differentiation of human cells. An important finding of the model applications was that a small set of simple assumptions (e.g. monotonic modeling of g_on and g_off) can lead to predictions of complex behavior, such as non-monotonic concentration-response curves. Another important conclusion is that few experimental samples may be used to predict unobserved points in a relatively large data matrix. Vice versa, the model may be used in the future to predict the most efficient experimental design to allow robust predictions in particular sub-areas of the differentiation-disturbance matrix.

With the help of model simulations, we studied the effect of VPA on differentiating stem cells during the first six days of a well-established neural induction protocol. This model was chosen to exemplify processes where dynamic natural transcriptome changes are overlaid with those triggered by an external stimulus (2-dimensional response matrix). This particular biological model was also used as it is supported by robust clinical data (72,73). The use of VPA during pregnancy can lead to a complex phenotype, often described as fetal valproate syndrome. Notably, different windows of exposure need to be distinguished. If the drug is given during the period of neural network formation (pregnancy months 2–3 onwards), an autism-related phenotype may arise. This is associated with the endophenotype of altered neurite connectivity, and it has recently been shown to be related to the down-regulation of the cytoskeletal/microfilament regulator MARCKSL1 (59). Drug exposure during earlier phases of development (about 4 weeks after conception) is better documented, and it leads to neural tube defects and alterations related to neural crest function (e.g. cleft palate) (72,73). Spina bifida and hydrocephalus are the clinically best-documented malformations in this case, and the test system used here (STOP-tox_(UKN)) refers to this neuro-teratological problem (8). Interestingly, the upstream signaling disturbances triggered by VPA may be similar in early and late phases: HDAC inhibition and block of GSK-3 activity. The activation of the Wnt pathway, and a related shift from central neural development to neural crest development was found here as a main pathological pathway for early-stage drug exposure.

In exposed rats, it was shown that VPA induced beta-catenin and phospho-GSK3 in brain tissue (74,75). Although such studies suggest that VPA treatment affects Wnt signaling, an exact molecular explanation is still lacking. VPA itself is a poor inhibitor of GSK3, and other molecules that trigger similar responses as VPA (e.g. trichostatin A) do not affect this kinase at all. Possibly, the main primary target of VPA is a broad spectrum inhibition of HDACs (excluding HDAC6), which then leads indirectly to a Wnt response (40,76). It has been shown that the direct effects of VPA on histone acetylation have an indirect, but permanent effect on methylations (9). In line with this, it has been suggested that VPA increases the expression of Wnt target genes in prenatally exposed rats by altering demethylation state of Wnt-activators (77). Dissecting the transcriptional changes by which VPA affects Wnt signaling is complicated by the dynamic nature of the problem. The initial signaling phase is quickly followed by secondary effects, and signaling pathways often contain feedbacks that limit signal duration. Thus, the timing of the observations after a perturbation can be critical when trying to identify direct effects on signaling, and concentration-dependent effects complicate the analysis. Our approach tries to overcome these limitations by augmenting the limited experimental resolution in time–concentration space using a dynamic model.

Further insights could be gained in the future by combining the model with single cell transcriptome data. This would allow anchoring of the model states to transcriptome states that are observed in cells during differentiation (78–81). Under such conditions, we would be able to use the same states and their transition rates for all genes, instead of using independent state models for each gene. This would further constrain the parameters and thus provide robustness and interpretability of the model. Consequently, the transition rate parameters could yield typical half lifes of transcriptome states that are currently inaccessible by models using a single cell snapshot. It would also complement pseudotime reconstruction algorithms that lack absolute time scales (82,83).

Taken together, our modeling framework allowed us to model the effect of a perturbation on a complex developmental transition and helped us to unveil the molecular pathway that mediates dysregulation due to the perturbation. We believe that this framework is broadly applicable to the analysis of transcriptome changes in complex differentiation processes that are subjected to perturbations.

DATA AVAILABILITY

The R scripts to generate Figures 1–4 are publicly available in the GitHub repository https://github.com/johannesmg/kinetic_modeling_stem_cell_transcriptome_dynamics. The R scripts used for fitting the dynamic model are also publicly available in the GitHub repository https://github.com/johannesmg/BatemanDiff.

The raw CEL files of the Affymetrix chips that have been used are publicly available in the Gene Expression Omnibus (GEO) database under the accession number GSE147270.

Notes

Present address: Tanja Waldmann, trenzyme GmbH, Byk-Gulden-Str.2, D-78467 Konstanz.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

BMBF [031L0117A-D]; EFSA; DK-EPA [MST-667-00205]; DFG (Konstanz Research School of Chemical Biology; KoRS-CB); European Union's Horizon 2020 research and innovation programme [681002 to EU-ToxRisk, 825759 to ENDpoiNTs]. Funding for open access charge: Funding provided by the German Research Foundation (DFG) and the Open Access Publication Fund of Charité – Universitätsmedizin Berlin.

Conflict of interest statement. None declared.