Double-stranded RNA bending by AU-tract sequences

Abstract

Sequence-dependent structural deformations of the DNA double helix (dsDNA) have been extensively studied, where adenine tracts (A-tracts) provide a striking example for global bending in the molecule. However, in contrast to dsDNA, sequence-dependent structural features of dsRNA have received little attention. In this work, we demonstrate that the nucleotide sequence can induce a bend in a canonical Watson-Crick base-paired dsRNA helix. Using all-atom molecular dynamics simulations, we identified a sequence motif consisting of alternating adenines and uracils, or AU-tracts, that strongly bend the RNA double-helix. This finding was experimentally validated using atomic force microscopy imaging of dsRNA molecules designed to display macroscopic curvature via repetitions of phased AU-tract motifs. At the atomic level, this novel phenomenon originates from a localized compression of the dsRNA major groove and a large propeller twist at the position of the AU-tract. Moreover, the magnitude of the bending can be modulated by changing the length of the AU-tract. Altogether, our results demonstrate the possibility of modifying the dsRNA curvature by means of its nucleotide sequence, which may be exploited in the emerging field of RNA nanotechnology and might also constitute a natural mechanism for proteins to achieve recognition of specific dsRNA sequences.

INTRODUCTION

Double-stranded RNA (dsRNA) plays a central role in a number of biological processes. For instance, dsRNA molecules are involved in the regulation of gene expression by RNAi (1), or in the host responses to dsRNA encoded by viruses (2). In addition, dsRNA helices perform key functions as an essential part of tertiary RNA structures, including tRNA and riboswitches (3,4), and of macromolecular RNA-protein complexes such as ribosomal subunits and the spliceosome (5–7).

Many of the biological processes involving dsRNA exploit the conformational flexibility of dsRNA helices in order e.g. to achieve folding of the RNA into complex 3D structures (8–10) or in dsRNA:protein interactions (11–13). Therefore, a quantitative understanding of the physical properties of dsRNA can provide novel insights on these processes, and also, can aid the design of RNA nanostructures for biotechnological applications (14). Motivated by these considerations, immense research efforts have characterized the effect of helical imperfections, such as bulges or internal loops, on dsRNA conformations (15,16). However, the question of how the nucleotide sequence impacts the overall structure of canonical, Watson–Crick base-paired dsRNA helices remains largely unanswered (17).

In contrast to dsRNA, the sequence-dependent structure of the canonical DNA double-helix (dsDNA) has been characterized in great detail. A prime example of such sequence-dependent features are the so-called A-tracts, runs of adenines and thymines without a TpA step that, when in phase with the helical pitch yield a significant global curvature of the dsDNA (18,19). Besides their bending character, A-tracts show a peculiar conformation at the molecular level, with a characteristic narrow minor groove (20,21). Remarkably, both the curvature induced by A-tracts and the molecular conformation of these sequences are thought to have biological relevance. The former seems to stabilize DNA tertiary structures, such as loops and supercoils (22,23), whereas the latter is used by proteins to achieve binding specificity (24). Moreover, the DNA bending induced by A-tracts has aided the design of DNA rings as part of nanotechnological devices (25).

Scattered experimental evidence suggests the existence of sequence-induced curvature in a Watson–Crick base-paired RNA duplex. Early crystallographic works reported helical kinks in the structure of an RNA duplex consisting of alternating adenines and uracils (26,27). However, this bent conformation was stabilized by the intermolecular interactions among the molecules forming the crystal and, therefore, bending could not be attributed to the RNA duplex alone. In parallel, analysis of structural databases and theoretical methods, such as molecular dynamics (MD) simulations, have provided valuable insight on sequence-dependent dsRNA conformations (17,28–31). In particular, recent MD studies have predicted strong sequence effects on the dsRNA shape (29,30) and flexibility (31), which could potentially lead to sequence-induced bending. Such simulation techniques hold great potential in deciphering the sequence-dependent dsRNA conformational landscape, provided that the computational predictions are thoroughly tested against experimental measurements. However, such comparison remains challenging due, in part, to the limited availability on high-resolution dsRNA experimental structures and the number of artifacts that are often found, e.g. in crystal structures (17).

Here, we present a procedure that led us to the direct experimental observation of single dsRNA molecules bent only by their nucleotide sequence. We combined MD simulations and atomic force microscopy (AFM) experiments; a technique especially suited for studying dsRNA bending, as demonstrated by AFM measurements of the dsRNA persistence length (32,33). We first performed a systematic analysis of how the sequence affects the structure of dsRNA using MD simulations. Our simulations predicted that a sequence motif, that we named AU-tract, would cause a bend in the RNA double-helix. We then synthesized long dsRNA molecules containing AU-tracts in phase with the helical pitch. Analysis of AFM images of these molecules revealed that they were indeed significantly more bent than control dsRNA molecules of arbitrary sequence. Finally, we propose a molecular mechanism for AU-tract bending based on a large propeller twist at A:U base pairs. Our work unveils the phenomenon of sequence-induced curvature in dsRNA, challenging the traditional picture of dsRNA as an invariant double helix.

MATERIALS AND METHODS

Molecular dynamics simulations

Simulation details are similar to the ones from (34), only excluding the external force. RNA duplexes were placed in an approximately cubic box of 110 Å edge size and filled with water and sodium counterions to balance the phosphate charges. Only sodium ions were included in the simulations. The systems were heated up to 300 K and equilibrated in the isobaric-isothermal (NPT) ensemble (P = 1 atm, T = 300 K) for 20 ns. Production simulations were run in the NVT ensemble using as input coordinates the ones from the last configuration of the NPT equilibration. All simulations were extended to ∼1 μs time.

We used the AMBER14 software suite with NVIDIA GPU acceleration (35,36). For the modeling of dsRNA molecules we resorted to the Cornell ff99 force field (37) with the parmbsc0 (38) refinement and the χOL3 modification (39). The ions were described according to the Joung/Cheatham (40) parametrization; and the TIP3P model (41) was used for water molecules. Periodic boundary conditions and Particle Mesh Ewald (with standard defaults and a real-space cutoff of 9 Å) were used to account for long-range electrostatics interactions. The same real space cutoff was used to truncate van der Waals forces. SHAKE algorithm was used to constrain bonds containing hydrogen atoms, thus allowing us to use an integration step of 2 fs. Coordinates were saved every 1000 steps. Average structures were computed using the cpptraj software of the AMBER14 suite. Helical, base pair step parameters and groove dimensions were computed using Curves+ (42) and 3DNA (43) and helical bending was calculated using Curves+ (42). The four base pairs adjacent to the termini of the molecules were excluded from the analysis.

Production of dsRNA molecules

In order to study the mechanical properties of AU-tracts at the single-molecule level, we produced dsRNA molecules that contain periodic repetitions of alternating AU nucleotides. We named them ExpAU-4 or ExpAU-5 depending on the length of four or five nucleotides of the AU-tract. These molecules were produced by hybridizing two long complementary ssRNAs. To fabricate these, the sequence of interest was cloned after the T7 RNA polymerase promoter between two KpnI sites. In this way, the fragment could be digested and ligated in the opposite orientation, allowing us to synthesize the two complementary ssRNA chains. In addition, a SmaI site was introduced at the end of the sequence, enabling the linearization of the plasmid vector to limit the length of the transcripts.

dsRNA molecules were synthesized according to a previously described protocol (33,44) with slight modifications to increase yield for single-molecule manipulation purposes. Once each pair of plasmids were obtained, plasmid vectors used as transcription templates were linearized with SmaI followed by purification (QIAGEN). Afterwards, in-vitro transcription using the commercial HiScribe™ T7 High Yield RNA Synthesis Kit (NEB) gave rise to two complementary ssRNAs without any non-complementary nucleotides at their ends. After 3 h at 42°C, EDTA was added to a final concentration of 30 mM, and both strands were subsequently hybridized by heating 1 h at 65°C and slowly cooling to room temperature at a 1.2°C/5 min rate up to 25°C. This resulted in dsRNA molecules without any single-stranded overhangs. Transcription products were then cleaned with RNeasy MinElute Cleanup Kit (QIAGEN) followed by treatment for 1 h at 37°C with 2.5 units of RNase-free DNase I (NEB). The sample was once again cleaned with RNeasy MinElute Cleanup Kit before applying on a 1% agarose gel for gel extraction and purification with QIAGEN gel extraction kit and elution with RNase free H₂O. dsRNA constructs were stored at 4°C in RNase free H₂O. The final sequences are shown in Supplementary Table S1. Further details on the synthesis of the dsRNA molecules can be found in the Supplementary Material (see section 1, Supplementary Table S3 and Supplementary Figure S12).

Atomic force microscopy measurements

Imaging conditions and data analysis were similar to those employed in a previous work (33). A 10 μl solution containing 0.5 nM dsRNA, 2.5 mM NiCl₂, 25 mM TrisAc pH 7.5, 2.5 mM MgOAc and 100 mM NaCl was deposited onto freshly cleaved mica. After ∼60 s, the sample was washed using Milli-Q water and dried using air nitrogen. Images were taken in tapping mode in air, using an AFM from Nanotech Electronica S.L. with PointProbePlus tips (PPP-NCH Nanosensors). Contour lengths were obtained using the WSxM software (45). Persistence lengths were computed using the tracing routine from (46,47). Traces of 170 nm were obtained with a point-to-point separation of 2.5 nm.

RESULTS AND DISCUSSION

The dsRNA sequence affects the width of the major groove, the extension, and twist of dsRNA

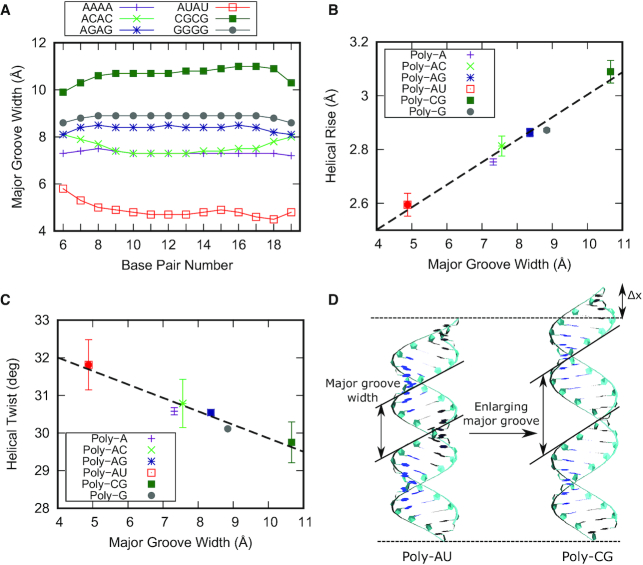
In order to explore how the nucleotide sequence affects the dsRNA structure, we first analyzed a set of six MD simulations from a previous work (31). These simulations had been performed on benchmark dsRNA sequences of the form G₄(NN)₈G₄, with NN = AA, AC, AG, AU, CG, GG (Table 1), where the G₄ regions in the termini had been included to prevent edge fraying and were excluded from the analysis. We measured the size of the grooves of these benchmark sequences using the software Curves+ (42) and found that the major groove width was highly dependent on the sequence, being able to change by as much as 6 Å. This is shown in Figure 1A, where we represent the values of the major groove width along the helical axis for the benchmark molecules. Notice that, because these sequences consist of repeating dinucleotides, their major groove should be regular along the helical axis, as manifested by the flat lines of Figure 1A. In contrast, the minor groove dimensions as well as the major groove depth did not significantly change with the sequence (Supplementary Figure S1).

Table 1.

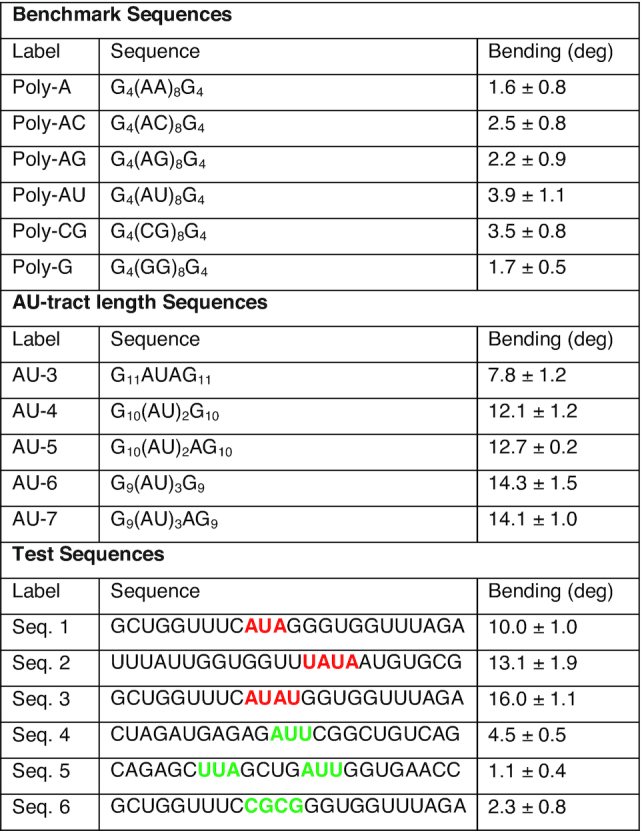
dsRNA sequences studied in this work by MD simulations. dsRNA sequences are represented in abbreviated form without the complementary strand and written from the 5′ end to the 3′ end. Benchmark sequences were selected from a previous work (31). These sequences consisted of eight repetitions of dinucleotides flanked on both sides by G₄. AU-tract length sequences were of approximately the same size (24 or 25 bp, depending on whether the AU-tract comprised an even or odd number of base pairs) and contained an AU-tract exactly at the center of the sequence. These centered AU-tracts were of varying lengths from three (AU-3) to seven (AU-7) base pairs. Test sequences were designed to include AU-tracts in different contexts (highlighted in red, Seqs. 1-3) and to contain other potential bending motifs, such as AUU, UUA or CGCG (highlighted in green, Seqs. 4–6). In order to calculate the bending angle, we split the trajectory into five windows of 200 ns and obtained the average structure of each window. We then computed the bending angle of these average structures using Curves+ and neglecting four base pairs in each of the termini of the molecule. The final value of the bending angle is the mean of the measurements of these windows and the error is the standard deviation

Figure 1.

The major groove width modulates the overall structure of the dsRNA helix. (A) Values of the major groove width measured along the helix for the benchmark sequences (Table 1). The average structures over the simulation time were computed for the benchmark molecules using the software AmberTools. These structures were then analyzed with the software Curves+ (42) to obtain the values of the major groove width along the sequence. (B) Mean helical rise and (C), helical twist of the benchmark molecules measured as a function of the major groove width. Values of the helical rise and helical twist were obtained for each base pair step from the average structures of the benchmark molecules using the software Curves+ (42). These values, together with the major groove width values from panel a, were then averaged over the 15 central base pair steps. Error bars are the standard error of the mean. X-axis error bars are within the symbols. The dotted line represents a fit of the data to a linear function. (D) Average structures of the poly-AU and poly-CG over the simulation time. These structures illustrate how the sequence induces an elongation in the molecule by enlarging the major groove.

Notably, the major groove width was primarily responsible for modulating the extension and number of turns of the molecules. This was quantified by means of the helical rise and helical twist parameters, which were highly correlated (R = 0.987) and anticorrelated (R = –0.974), respectively, with the major groove width (Figure 1B, C). These results suggested that the nucleotide sequence could simultaneously induce an elongation and unwinding of the dsRNA by expanding the major groove. Conversely, contraction of the major groove resulted in shrinkage and overwinding of the double-helix. This mechanism is illustrated in Figure 1D, where we computed the average structures over the 1 μs simulation time of the two sequences with extreme values of major groove width: the poly-AU and the poly-CG. The former was the most compact sequence with a very narrow major groove. As the major groove was enlarged, the molecule approached a stretched and unwound conformation, which was maximal with the poly-CG sequence. The helical rise of the poly-CG and the poly-AU molecule was ±10% of the canonical value of the extension per base pair of dsRNA, which is ∼2.9 Å (48). Similar results for the sequence dependence of the major groove width and the high correlation (anticorrelation) with the helical rise (twist) were obtained when analyzing our data with the alternative 3DNA software (43) (Supplementary Figures S2 and S3). In addition to the helical rise, other structural parameters such as inclination and roll were found to be highly negatively correlated with the major groove width (Supplementary Figures S4 and S5). Finally, our results are in line with previous MD works performed on similar dsRNA benchmark sequences, although the poly-CG molecule presents certain variability attending to the water model and ionic conditions used (29,30) (see Supplementary Table S2).

AU-tracts induce a curvature in dsRNA by local compression of the major groove

We have shown that the sequence of homogeneous dsRNA molecules modulates the major groove size, with the poly-AU sequence leading to a significant compaction of the major groove width. Compaction of the minor groove in DNA A-tracts has been linked with the intrinsic bending induced by these sequences (18). Motivated by the DNA case, we next explored if major groove narrowing could lead to bent structures in dsRNA. In order to do so, the poly-G sequence, which showed standard values of the structural parameters (Figure 1), was modified to include a stretch of alternating A's and U's, hereafter AU-tract. We thus simulated five different sequences with AU-tracts of lengths varying from three to seven base pairs, which were denoted as AU-3 to AU-7 (Table 1). All sequences were designed to be similar in length (24 or 25 bp) and to contain the AU-tract exactly in the center of the duplex.

Our results revealed a localized compression of the major groove at the position of the AU-tract. This can be seen in Figure 2A–C, where we represented the major groove width profiles of the poly-G (same as Figure 1A), AU-4 and AU-6 sequences. The homogeneous major groove width of the poly-G molecule (Figure 2A) contrasted with the abrupt drop found when a 4 bp-long AU-tract is introduced (Figure 2B). As the length of the AU-tract increased, the reduction of the major groove width was more pronounced, reaching lower values and extending over longer distances along the duplex. This effect can be appreciated in the major groove profile of AU-6, which presented a deeper and wider drop than that of AU-4, reaching a minimum value lower than 5 Å (Figure 2C). Notice that a short 3 bp-long AU-tract was enough to induce major groove narrowing, although the effect was amplified in longer AU-tracts (Supplementary Figure S6).

Figure 2.

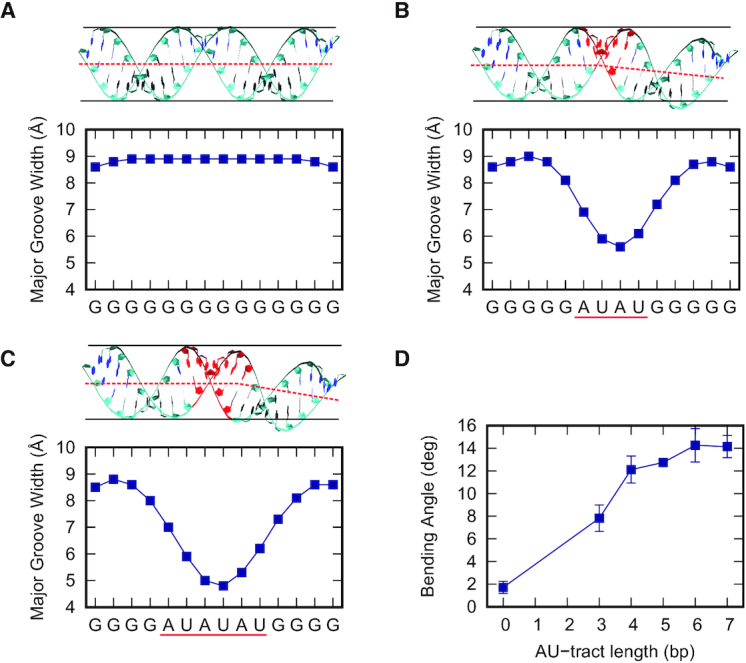
AU-tracts produce a bend when inserted in poly-G dsRNA molecules. Average structure and major groove width profiles of the poly-G (A), AU-4 (B) and AU-6 (C) sequences. The AU-tracts are highlighted in red. The black lines represent a cylinder, which is unable to embed highly bent molecules, namely AU-4 and AU-6. An approximate helical axis was drawn in red dotted line to guide the eye. Major groove width profiles were computed and represented as in Figure 1A. Localized drops in these profiles are found in the AU-tracts (underscored in red) which coincide with the bending region of the molecule structure (on top). (D) Bending was computed for the AU-tracts of different lengths (values of the AU-tract length sequences are shown in Table 1). We divided the trajectories into five 200 ns-long windows and we then computed the average structure over each of these sub-trajectories. The bending angle of these average structures was then obtained using the curvilinear helical axis from the software Curves+ (42) and neglecting four base pairs on each terminal of the molecule. The plotted points are the mean values of the five time windows and the errors are the standard deviations. A line connecting the points was drawn to guide the eye.

Interestingly, compression of the major groove by AU-tracts resulted in bent dsRNA structures. This can be noticed by visual inspection of the computed average structures of the molecules throughout the simulation time. The average structures of AU-4 and AU-6 presented a bend at the position of the AU-tract and were therefore unable to be embedded inside a virtual cylinder. The same reasoning applies to the other AU-tracts, namely AU-3, AU-5 and AU-7 (see Supplementary Figure S6). On the contrary, the poly-G was straight and, therefore, could be fitted inside a cylinder (see Figure 2A). In order to provide a quantitative description of this bending we resorted to the curvilinear axis definition of Curves+ (42). We first divided our μs-long simulations into five windows of 200 ns and computed the average structure of these subtrajectories. For each of these structures, we computed the bending angle, discarding the four base pairs adjacent to each molecule's termini. We then averaged over these five measurements for each of the sequences. This bending angle was plotted as a function of the AU-tract length in Figure 2D, where we also included the poly-G homopolymer, which can be considered as a zero-length AU-tract. These measurements corroborated the bending effect of AU-tracts that we inferred from visual inspection of the dsRNA structures. The poly-G sequence, which lacks AU-tracts, was found to be essentially straight, as quantified by a very small bending angle of ∼2°. Interestingly, the shortest AU-tract considered, which was only 3 bp long, already induced a significant bending of ∼8° in the RNA duplex. This value increased with the AU-tract length, saturating at ∼14° with AU-tracts of 6 bp or longer.

AU-tracts are a major source of bending in arbitrary dsRNA sequences

The homogeneous sequences—repeating dinucleotides or mononucleotides—studied so far have allowed us to unveil the phenomenon of AU-tract bending and to relate the length of the tract with the magnitude of the bending. We next explored whether AU-tract bending occurs in the context of heterogeneous sequences by performing a new set of simulations of 24 bp-long arbitrary dsRNA sequences containing an AU-tract (Table 1, highlighted in red) as well as other potential bending motifs (Table 1, highlighted in green). As in previous sections, simulations were extended to 1 μs time and bending was evaluated from the average structures discarding the four terminal base pairs from each side.

Importantly, only those sequences containing AU-tracts, namely Seqs. 1–3, were significantly bent, showing values of the bending angle larger or equal than 10° (Figure 3). Among these three sequences, Seq. 1, which has the shortest AU-tract—3 bp long—scored the lowest bending angle, but still substantially larger than any of the sequences lacking AU-tracts (Seqs. 4–6). Consistently, Seq. 1 presented a less pronounced drop in the major groove width compared with Seq. 2 and Seq. 3, which contain a longer AU-tract comprising four base pairs. Seq. 4 and Seq. 5 contained no AU-tract, but other motifs rich in A's and U's, namely AUU and UUA. Contrary to AU-tracts, these motifs produced very modest variations in the major groove width and, consequently, Seq. 4 and Seq. 5 were nearly straight (Figure 3). Seq. 6 presented a CG-tract that locally enlarged the major groove, in line with the results from Figure 1A. However, this effect was not translated into an enhanced bending of the duplex.

Figure 3.

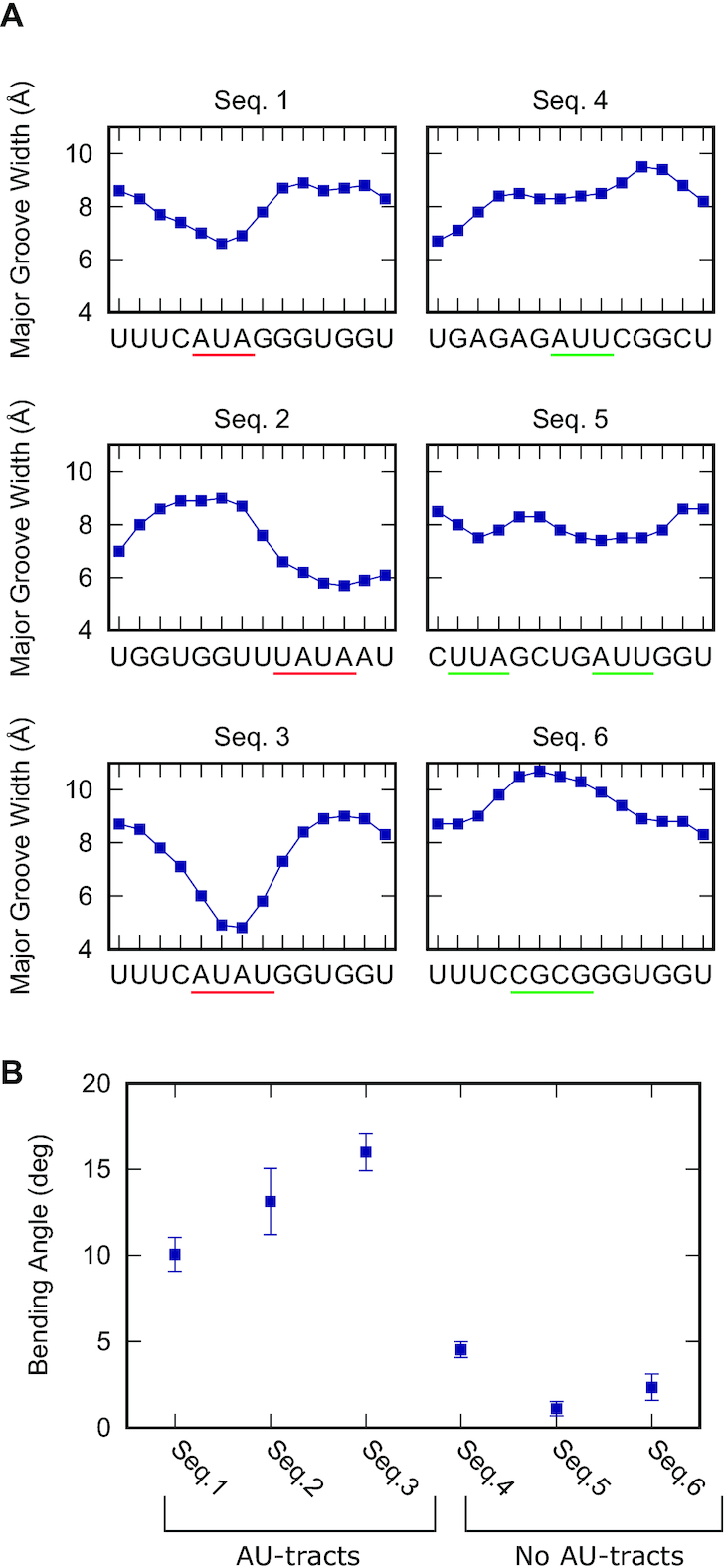
AU-tracts bend arbitrary dsRNA sequences. (A) Major groove width profiles of the test sequences (see Table 1) were computed and represented as done in Figure 1A. AU-tracts are highlighted in red and other tested motifs, such as AUU or CGCG, are highlighted in green. (B) The bending angle was measured for the arbitrary sequences as done in Figure 2D. Only Seqs. 1–3, which contain an AU-tract, scored a bending angle larger or equal than 10°.

These results are in line with crystallographic studies reporting a bend in duplexes containing a central AU-tract (26,27,49). However, crystal packing can induce spurious bending in nucleic acids (50) and, indeed, the bent helices observed in the AU-tract structures were partly attributed to intermolecular interactions among different duplexes of the crystal (26,27). In the following section we experimentally demonstrate that AU-tracts promote the formation of bent dsRNA structures at the single-molecule level.

Atomic force microscopy imaging shows that phased AU-tracts induce a macroscopic curvature in dsRNA

Motivated by our simulation findings, we performed atomic force microscopy (AFM) imaging to experimentally test the effect of AU-tracts on dsRNA bending. We hypothesized that AU-tracts located in phase with the dsRNA helical pitch would amplify their bending, similar to the case of A-tracts in hyperperiodic DNA sequences (19,46,52,51). Therefore, we synthesized two dsRNA constructs that contained phased repetitions of an AU-tract with a periodicity of 11 bp. The first of these constructs was 612 bp-long and contained a periodic AU-tract of 4 bp; the second one, comprised 624 bp and the periodic AU-tract was 5 bp in length. These molecules were correspondingly denoted as ExpAU-4 and ExpAU-5 (see Table 2 and Supplementary Material). As control, we considered an arbitrary dsRNA sequence of 612 bp and GC-content of ∼50% (see Supplementary Table S1). Figure 4A–C shows representative AFM images of control and AU-tracts dsRNA molecules. From the AFM images, we measured the contour length of the molecules and obtained a value of 179 nm for the three constructs, with an error (standard error of the mean) of 3 nm for the control and 4 nm for both AU-tracts molecules (see Table 2). These values yielded a ratio of 2.9 Å/bp, which coincides with crystallographic data of dsRNA (48) and with our MD simulations (Figure 1B). Further details on the preparation of dsRNA molecules and AFM imaging conditions can be found in the Materials and Methods section.

Table 2.

Experimental AFM measurements on AU-tract dsRNA bending. The control was an arbitrary dsRNA sequence of 612 bp; ExpAU-4 and ExpAU-5 sequences consisted on periodic repetitions of a 4 bp-long and a 5 bp-long AU-tract, respectively. The letter N denotes an arbitrary nucleotide. Sequences are written from the 5′ to the 3′ end, omitting the complementary strand. The full sequences can be found in Supplementary Table S1. The contour length showed a similar value for the three molecules. Curvature standard deviations (columns 4, 5) were obtained from Gaussian fits to the curvature distributions data sets shown in Figure 5C, D. Errors are the error of the fit

Label	Sequence	Contour length	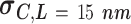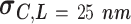(nm−1)	(nm−1)	Number of molecules
Control	Arbitrary, 612 bp	179±3	0.0332 ± 0.0002	0.0251 ± 0.0003	202
ExpAU-4	N7 (AUAU N7)55	179±4	0.0404 ± 0.0004	0.0331 ± 0.0006	127
ExpAU-5	N7 (UAUAU N6)56N	179±4	0.0467 ± 0.0006	0.0422 ± 0.0011	195

Figure 4.

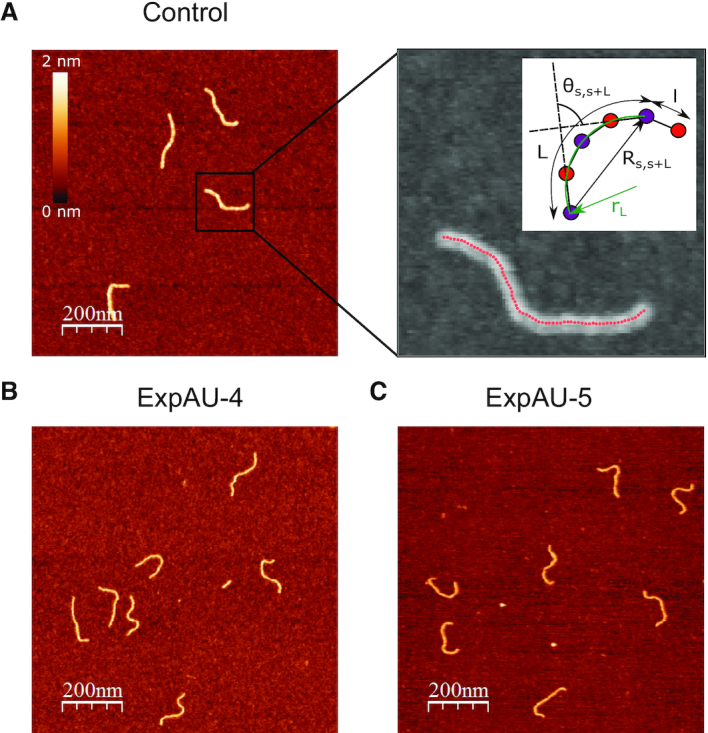
AFM images of control and AU-tract dsRNA sequences. (A) Representative AFM image of control molecules with a zoom-in image of the marked region showing an example of a typical trace. Additional AFM images are shown in Supplementary Figure S7. Inset, cartoon depicting a segment of a trace. In black, we represented the end-to-end distance, 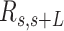, between two points separated by a contour distance 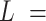15 nm and the angle defined by the tangents at those points,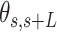. Those same points are considered together with a third, middle point located at 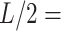7.5 nm from each of them (purple points) to fit a circle of radius 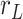(in green). The distance between two adjacent points of the trace is 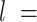2.5 nm. (B) Representative AFM images of ExpAU-4 and (C), ExpAU-5 molecules. Z-scale is the same as in A.

By visual inspection of Figure 4A–C and Supplementary Figure S7 one can already notice that AU-tracts molecules are more bent than the control. In order to quantitatively assess the bendability of the control and AU-tracts dsRNA molecules, we first obtained traces of points separated by 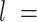2.5 nm that follow the trajectory of the molecules (19,47) (Figure 4A, right). From these traces, we computed the end-to-end distance, 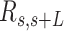, between two points separated by a given contour length 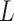, and the angle, 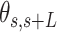, defined by the tangents to the trajectory at those points (inset in Figure 4A, right). We then computed the square of 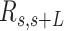and the cosine of  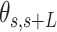and averaged over all the points of a trace and over all the measured traces. The resulting mean squared end-to-end distance,  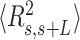and mean cosine of the tangents,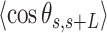, allowed us to study the mechanical properties of dsRNA in the context of polymer physics models, concretely the widely used worm-like chain (WLC) model:

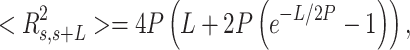(1)

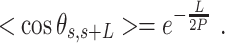(2)

In these equations, 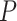is the persistence length, which is directly proportional to the bending rigidity (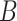) of the polymer 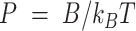(where 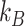is the Boltzman constant and 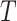is the temperature).

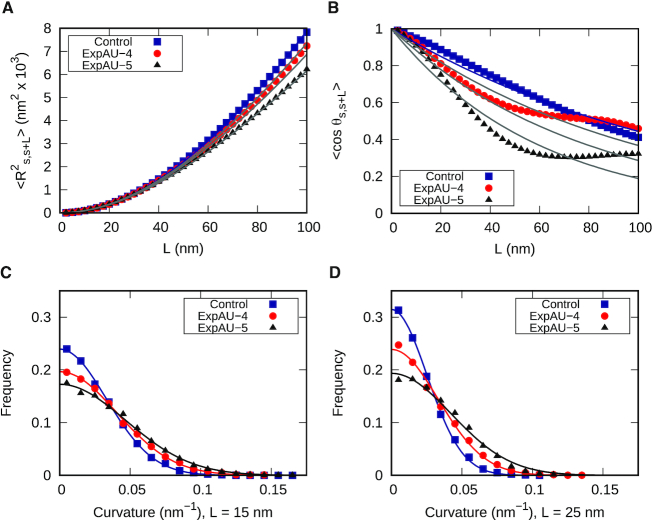
The control dsRNA data nicely fitted to the WLC model (Figure 5A, B). When fitted to Equation (1), the 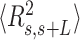data of the control dsRNA yielded a persistence length of 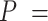66 ± 1 nm, consistent with previous single-molecule experiments on arbitrary dsRNA sequences (32,33,53) (Figure 5A). A fit of the 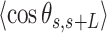control data to Equation (2) resulted in a persistence length of 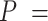62 ± 1 nm, slightly lower, but consistent with the value obtained using  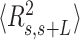(Figure 5B). Importantly, these measurements prove that adsorption conditions preserve equilibrium conformations of the polymer.

Figure 5.

Experimental quantification of dsRNA bending induced by AU-tracts. Mean squared end-to-end distance (A) and mean cosine of the tangents (B) plotted as a function of the contour distance between two points. The blue solid line is a fit of the control data to the WLC equations (Equation (1) for panel A, and Equation (2) for panel B), which yielded 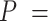66 ± 1 nm and 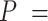62 ± 1 nm for the 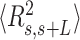and 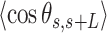data, respectively. To guide the eye, theoretical WLC curves are included with persistence lengths of 30, 40 and 50 nm (bottom-up in both panels). Histograms of curvature distributions for fixed contour lengths of 15 nm (C) and 25 nm (D), showing the relative frequency of different curvature values. The distributions were fitted to Gaussian functions (solid lines). The standard deviation parameters obtained from these Gaussian fits are presented in Table 2.

Contrary to the control, the AU-tracts data were not well captured by the WLC model. The inadequacy of the WLC to describe the AU-tracts data is evident from the 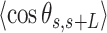plot (Figure 5B), where both ExpAU-4 and ExpAU-5 molecules presented clear deviations from Equation (2). These deviations from the WLC behavior are particularly significant for the ExpAU-5 molecule, which showed a local minimum of 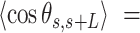0.3 at around 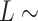60 nm. The fact that the WLC could not capture the flexibility of AU-tracts molecules is indicative of the existence of an additional bending that is not contemplated by purely entropic models. Such extra bending should also reduce the end-to-end distance of the molecules, making them more compact. Consistent with this idea, we found that  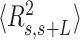values were shorter for the AU-tracts when compared to the control molecule (Figure 5A). Notice that as the length of the periodic AU-tract was increased from 4 to 5 bp, the molecules showed shorter  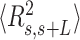values and larger deviations from Equation (2) in the 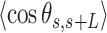data, suggesting that longer AU-tracts induce more pronounced bending.

The analysis of our data in the context of the WLC model indicated the presence of extra bending in the AU-tract sequences. In order to provide a more direct characterization of this AU-tract bending, we calculated the curvature of the molecules, following the procedure described in (46). We considered two points of the trace separated by a contour distance 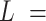15 nm; and a third, middle point located at a contour distance of 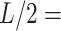7.5 nm from the other two. We then fitted a circle to the arc described by these three points and computed the curvature, 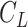, as the inverse of the radius, 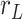, of that circle (see Figure 4A, right). This calculation was performed for all the points of the trace and for all the traces, yielding a distribution of curvature values for each of the molecules studied. We repeated the same procedure for a contour distance of 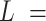25 nm.

The resulting curvature distributions strongly support the idea of AU-tract induced bending (Figure 5C, D). Indeed, curvature distributions were systematically wider for AU-tract molecules than for the control (see Figure 5C, D). This effect was quantified by fitting the data sets to a Gaussian function and extracting the standard deviation, 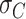, which provides a measurement of the width of the distributions (see Table 2). The 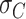values obtained for the ExpAU-5 molecule were systematically larger than the 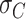values of ExpAU-4, which, in turn, were larger than those of the control. This finding indicates that AU-tract molecules were more prone to adopt highly curved conformations when compared to the control. Moreover, this effect was more pronounced for the ExpAU-5 molecule, supporting that the magnitude of AU-tract bending increases with the AU-tract length, as predicted by our MD simulations (Figure 2D).

AU-tracts: similarities and differences with DNA A-tracts

Sequence-dependent bending is known to take place in dsDNA by means of A-tracts: sequences of at least four A·T base pairs without a TpA step. When several A-tracts are located in phase with the helical pitch they produce a macroscopic curvature in the DNA (18). This curvature can be directly observed using AFM or electron microscopy (19,46,54,55), or can be inferred from gel electrophoresis experiments (51). In addition, A-tracts display a particular conformation at the molecular level, which differs from that of canonical B-DNA (18,20). In the following, we compare these well-known features of dsDNA A-tracts – macroscopic curvature and molecular conformation – with our findings on dsRNA AU-tracts.

Previous AFM works have provided a detailed picture of bending deformations in dsDNA molecules with A-tract-induced curvature. These experiments showed that, as a consequence of that curvature, the structural properties of dsDNA sequences with phased A-tracts exhibit significant deviations from the WLC model (46). This effect was also observed for the dsRNA AU-tracts (see Figure 5A, B). Although our AU-tracts 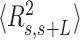data showed no clear discrepancy with respect to the WLC prediction, such deviations only appeared in the A-tracts for contour lengths greater than ∼120 nm length (19,46), which are beyond the range studied here (<100 nm). The 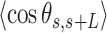of the A-tracts, on the contrary, deviated from the WLC behavior at shorter contour lengths (∼50 nm) and is, therefore, a better indicator of the existence of intrinsic curvature. Consistent with the presence of intrinsic bending, our AU-tracts also presented significant deviations from the WLC in the 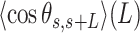data. Moreover, the shape of the 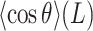plot for the phased AU-tract studied here is remarkably similar to an intrinsically-bent A-tract dsDNA that we recently reported (19).

We then turned our attention to the molecular structure of A-tracts and AU-tracts. We compared the structural features of the dsRNA AU-tract from Seq. 3 (see Table 1) with the DNA A-tract from a high-quality NMR structure of the Drew-Dickerson Dodecamer (DDD) (56). The DDD is the most extensively characterized DNA duplex and contains a central A-tract: CGCGAATTCGCG. As expected, the central region of the DDD shows the standard features of A-tracts, which are a highly negative propeller twist, a narrowing of minor groove and a negative roll (18) (Figure 6). Moreover, the major groove width showed little variation and all the plots were symmetric, a consequence of the palindromic sequence of the DDD.

Figure 6.

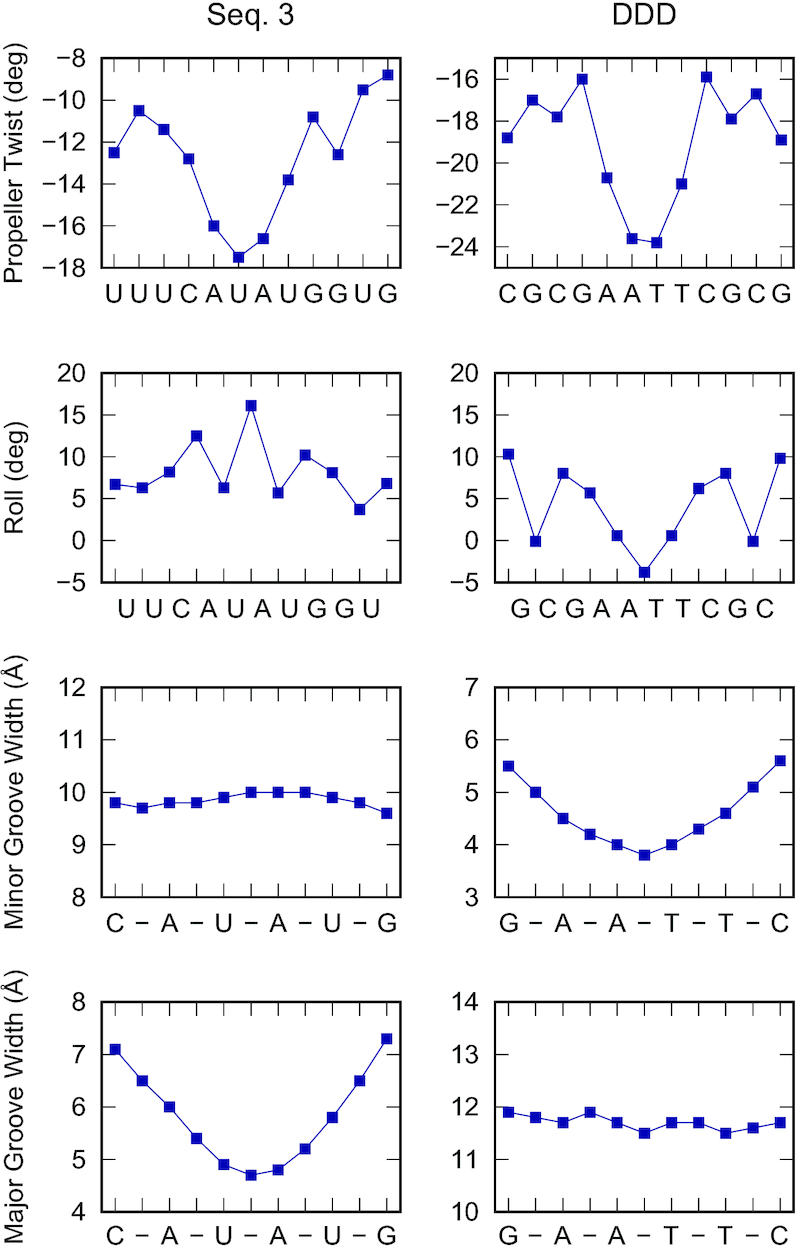
Comparison of the structural parameters of a dsRNA AU-tract (left) and a dsDNA A-tract (right). The average structure of the simulated Seq. 3 and a recent NMR (56) structure of the Drew Dickerson Dodecamer (DDD) were taken, respectively, as representative examples of a dsRNA AU-tract and a dsDNA A-tract structure. The analysis was performed using Curves+ (42). In addition to the major groove width, the structural parameters propeller twist, roll and minor groove width, which are typically used in the characterization of A-tracts (18) were computed.

The comparison of the most relevant structural parameters revealed intriguing similarities and differences between A-tract and AU-tract bending (Figure 6). In both structures, a large negative propeller twist was observed. Similar to what has been proposed for DNA A-tracts (18), a highly propeller twisted base pairs could stabilize the structure of AU-tracts, e.g. by favoring interstrand and intrastrand stacking interactions (see below) or by promoting the formation of non-canonical hydrogen bonds (Supplementary Figure S8). In contrast to the propeller twist, the roll parameter presented very different trends in the two molecules. In the AU-tract case, roll exhibited a zig-zag pattern with a maximum located at the UpA step of the AU-tract, whereas in the A-tract case the roll parameter presented a drop with a minimum at the center of the A-tract (Figure 6). This difference in roll can be associated to the changes observed in the dimensions of the grooves. Positive roll values are attributed to bending towards the major groove and, therefore the large roll found at the UpA step is consistent with the compression of the major groove observed in the AU-tracts (Figure 2 and Figure 3A). Conversely, the high negative roll found in A-tracts can be associated with their narrow minor groove, a well-known feature of these sequences (18). Furthermore, notice that only one of the grooves showed a significant sequence variation, that is, the minor groove of the AU-tract and the major groove of the A-tract were approximately homogeneous. Consistently, similar trends of these structural parameters were obtained with the alternative analysis software 3DNA (Supplementary Figure S9). Moreover, a structural analysis of three additional AU-tract motifs from sequences AU-5, AU-7 and Seq. 2—yielded similar results to the ones from Figure 6, confirming that a highly negative propeller twist and a zig-zag roll pattern with maxima at UpA steps are conserved features of AU-tracts (Supplementary Figure S10).

The structural features of AU-tracts discussed above are consistent with previous findings on sequence-dependent dsRNA structure. Zig-zag patterns of high and low roll values are known to occur at sequences consisting of alternating purines and pyrimidines, and have been proposed to stabilize intrastrand stacking interactions at purine-pyrimidine steps and interstrand stacking at pyrimidine-purine steps (57). Inspection of the trajectories of Seq. 3 suggests that in AU-tracts those stacking interactions (Figure 7 motion #1, Supplementary Figure S8) are further stabilized by means of extensive propeller-twisting (Figure 7 motion #2). By doing so, the uracils are able to maintain their intrastrand stacking interactions with their adjacent (intrastrand) adenine, while the opposing adenines in the UpA step engage in interstrand stacking (Figure 7 bottom, dotted lines; and Supplementary Figure S8). This propeller twist motion would then propagate along the AU-tract (Figure 7, motion #3), creating a region of highly negative propeller twist, in line with the data from Figure 6 and Supplementary Figure S10. It is important to note that such large propeller twisting motions are less favorable in G:C base pairs, where the three hydrogen bonds hinder rotation of the bases with respect to the base pairing axis. Consistently, other alternating purine-pyrimidine sequences that contain G:C base pairs presented a less pronounced propeller twisting than the poly-AU (Supplementary Figure S11). We propose that the combination of these two phenomena—zig-zag roll characteristic of alternating purine–pyrimidine and large propeller as a result of low GC content—make AU-tracts particularly effective at inducing groove distortion and curvature.

Figure 7.

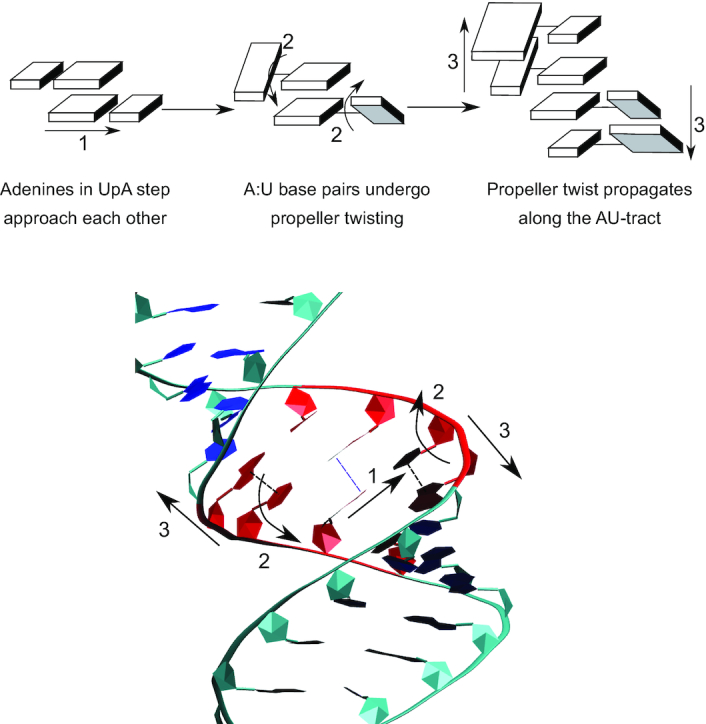
Proposed mechanism for AU-tract induced bending. AU-tract bending is illustrated using rigid blocks representation (top) and a snapshot of the trajectory of Seq. 3 (bottom, AU-tract is marked in red). 1) Adenines in UpA steps come together in close proximity; 2). A:U base pairs undergo propeller twisting, potentially stabilizing both interstrand (bottom, dotted purple line) and intrastrand (bottom, dotted black line) stacking interactions; 3) propeller twist propagates along the AU-tract resulting in major groove compression and dsRNA bending.

Potential implications on dsRNA sequence recognition

dsRNA structures are ubiquitous in cells, and together with dsRNA-binding proteins are central players in cellular processes, such as mRNA biogenesis and editing, microRNA processing and function, as well as anti-viral defense (58,59). In some of these processes, dsRNA-binding proteins can be rather selective in their target RNA sequences, although the recognition mechanism is not completely understood (60). Interestingly, these protein–dsRNA complexes sometimes present bent dsRNA structures. For example, dsRNA bending was observed in the crystal structure of an RNA duplex in complex with MDA5 (11) or OAS1 (13). Moreover, bending was predicted to occur in dsRNA upon the interaction with RIG-I (61) or Dicer (12,62). One can thus speculate that the dsRNA curvature at the AU-tracts observed in the present study might play a role in specific target recognition by dsRNA-binding proteins. Namely, it is conceivable that AU-tracts sequences will be preferred in protein–dsRNA interactions that require dsRNA bending. Finally, the narrow major groove characteristic of AU-tracts might also contribute to achieve dsRNA sequence specificity, as occurs with the minor groove in dsDNA A-tracts (24). This would add to other mechanisms of dsRNA sequence recognition, such as the recently proposed contacts through the minor groove (60,63). Future works should address the question of whether the structural features of AU-tracts here described play a role in protein:dsRNA sequence recognition.

In summary, we have investigated how the nucleotide sequence affects the dsRNA structure. We found that the sequence not only affects fine, local features of the double-helix, as previously reported, but it can also impact its global shape, inducing a macroscopic curvature. Our molecular dynamics simulations of repeating dinucleotide sequences revealed that the poly-AU sequence adopted a characteristic conformation with a narrow major groove. By inserting AU-tracts of different lengths inside a poly-G homopolymer, we found that a 3 bp-long AU-tract was enough to induce a bend, but longer AU-tracts resulted in larger bending. This finding was confirmed by studies of AU-tracts located in arbitrary sequences. Our simulation results guided the design of dsRNA constructs suitable for measuring the effect of AU-tract bending in AFM experiments. Using AFM imaging, we found that these AU-tract molecules exhibited higher curvature than control dsRNA's of arbitrary sequence, confirming the prediction of our simulations. A molecular mechanism for AU-tract bending is proposed, where extensive propeller twisting of the A:U base pairs induce major groove compression.

Intrinsic bending induced by dsDNA A-tracts has been linked to multiple biological functions such as nucleosome positioning, localization of supercoils or germ-line gene silencing. It is therefore expected that the sequence-dependent bending reported here for dsRNA might also have important biological implications. On one hand, the bent structure of the AU-tracts could be exploited in the formation of tertiary contacts in the process of RNA folding. On the other hand, AU-tracts might provide a mechanism for sequence recognition based on dsRNA shape. Finally, our finding that the global dsRNA structure is sequence dependent might be relevant in the field of RNA nanotechnology. Future works might explore how this effect can be exploited in the design of complex RNA nanostructures.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Spanish MINECO [MAT2017-83273-R (AEI/FEDER, UE) to R.P., BFU2017-83794-P (AEI/FEDER, UE to F.M.-H.) and Comunidad de Madrid (Tec4Bio – S2018/NMT-4443 and NanoBioCancer – Y2018/BIO-4747 to F.M.-H.]; R.P. acknowledges support from the Spanish Ministry of Science and Innovation, through the ‘María de Maeztu’ Programme for Units of Excellence in R&D [CEX2018-000805-M]; F.M.-H. acknowledges support from European Research Council (ERC) under the European Union Horizon 2020 research and innovation [681299]; J. G. V. acknowledges funding from a Marie Sklodowska-Curie Fellowship within the Horizons 2020 framework (DLV-795286) and the Swiss National Science Foundation (grant number CRSK-2 190731/1). Alberto M.-G. acknowledges support from the International PhD Program of ‘La Caixa-Severo Ochoa’ as a recipient of a PhD fellowship; U.F.G. acknowledges support from the Swiss National Science Foundation [31003A_179256/1]; Alejandro M.-G. and MM-B acknowledge support from the Spanish Ministry of Competitiveness and Industry as a recipients of a FPI fellowship [REFs BES-2015-071244, PRE2018-083464, respectively]. Funding for open access charge: European Research Council (ERC) [681299].

Conflict of interest statement. None declared.