Abstract
Blood-brain barrier (BBB) permeability of a compound determines whether the compound can effectively enter the brain. It is an essential property which must be accounted for in drug discovery with a target in the brain. Several computational methods have been used to predict the BBB permeability. In particular, support vector machine (SVM), which is a kernel-based machine learning method, has been used popularly in this field. For SVM training and prediction, the compounds are characterized by molecular descriptors. Some SVM models were based on the use of molecular property-based descriptors (including 1D, 2D, and 3D descriptors) or fragment-based descriptors (known as the fingerprints of a molecule). The selection of descriptors is critical for the performance of a SVM model. In this study, we aimed to develop a generally applicable new SVM model by combining all of the features of the molecular property-based descriptors and fingerprints to improve the accuracy for the BBB permeability prediction. The results indicate that our SVM model has improved accuracy compared to the currently available models of the BBB permeability prediction.
Keywords: Blood-brain barrier permeability, molecular descriptor, fingerprint, physical property, modeling
INTRODUCTION
The blood-brain barrier (BBB) is a highly selective semipermeable membrane barrier that isolates the central nervous system (CNS) from the circulating blood and, thus, maintains the brain homeostasis. As targeting the brain represents an important challenge in pharmaceutical research (1), BBB penetration property (permeability) is a critical character of a compound in chemical toxicological studies and drug discovery. The transferring ability of small-molecule compounds into the brain is dependent on a variety of complex factors, such as passive permeation through the BBB, uptake and efflux by transporter (carrier-mediated transport and receptor-mediated transcytosis), and binding to plasma proteins (2). Unfortunately, it is still challenging for the BBB permeability screening to develop a truly reliable in vitro model capable of accounting for all of these complex factors (3).
To date, a lot of in silico models for BBB permeability prediction have been developed and thoroughly reviewed (4-13). These models could be roughly classified into two types, i.e. quantitative and qualitative models. Qualitative and quantitative BBB permeability prediction models are very different in many aspects including dataset selection, training/regression methodology, prediction precision, and scope of the practical application. Quantitative BBB permeability prediction models are trained to predict the LogBB (Logarthm of the ratio of total steady-state concentration in brain to that in blood at a given time point) or LogPS (Logarithm of the permeability surface area product), providing prediction of the quantitative characteristics for the BBB permeability of compounds. Multiple statistical methods, such as multiple linear regression (MLR) (4, 15-17), nonlinear regression (18, 19), and partial least squares (PLS) (9, 20, 21), were used to construct quantitative BBB prediction models. A qualitative BBB permeability prediction model may be considered as a simplified characterization of the BBB permeability, because it only provides the binary classification prediction concerning whether a compound can penetrate the BBB or not. Machine learning methods, such as linear discriminant analysis (LDA) (14), recursive partitioning (RP) (9, 22), genetic algorithms (GA) (23), decision tree (DT) (9), k nearest-neighbor (kNN) (2, 24, 25), artificial neural network (ANN) (23, 26, 27), and support vector machine (SVM) (24, 25, 28-31), are usually used for training qualitative BBB permeability prediction models. In general, a quantitative BBB permeability model provides more detailed prediction of the BBB permeability of compounds, compared to the simple classification prediction from a qualitative BBB permeability model. However, the accuracy of the machine learning or statistical model is heavily dependent on the quantity (dataset size), diversity, and accuracy of the input data within the available dataset. As available compounds with quantitative experimental data of LogBB or/and LogPS are far less than compounds with the BBB permeability classification data, a qualitative model trained with the BBB permeability classification data can be expected to achieve a higher accuracy in the qualitative BBB permeability classification prediction. In many cases, particularly early-stage screening stage of a drug discovery effort, a binary classification prediction of BBB permeability is sufficient for quickly screening a large number of compounds. Therefore, in the present work, we only focus on constructing a reliable qualitative BBB permeability prediction model. Among all of the commonly used methods in training a qualitative BBB permeability prediction model, SVM, which was originally developed by Vapnik and coworkers (32), is a superior method compared to other machine learning methods. The SVM method has been used extensively in drug discovery and related fields (33, 34).
In general, SVM is a supervised learning method used for classification and regression analysis (35-37). For a classification problem such as predicting BBB penetration, each compound in training dataset is marked as BBB+ or BBB− (indicating BBB penetration and BBB non-penetration, respectively); see below for the detailed classification of BBB+ and BBB−. With the SVM algorithm, the known training dataset is used to build a model that can assign unclassified new compounds to BBB+ or BBB−, making it a non-probabilistic binary linear classifier. SVM model represents each compound as a point mapping into a high-dimensional space according to its descriptors, so that these data points with different BBB penetration properties can be separated by a clear gap (depicted by a hyperplane) that is as wide as possible. Each new compound can be mapped into the same high-dimensional space for predicting its BBB penetration property based on the side of the gap they fall. Technically, the SVM algorithm uses a kernel function to map input descriptors (input space; each descriptor represents a dimension) into the high-dimensional space (feature space). A radial basis function (RBF) (38) (Equation 1) was used in this study:
| (1) |
| (2) |
such that yif(xi) ≥ 1 − εi, εi ≥ 0. Equation 2 means to minimize the function. In these equations, yi indicates the classification (BBB+ or BBB−) of compound i, f(x) presents the function of hyperplane, xi and xj are the training vectors (i ≠ j, xi ≠ xj) corresponding to compounds i and j, respectively, w = Σ αixixi, αi is the Lagrange multiplier (0 ≤ αi ≤ C), and εi is the slack variable. C is the penalty parameter for the SVM model and γ is the coefficient for the RBF kernel function. In fact, the RBF is the most commonly used kernel function due to its better generalization, small number of parameters, and relatively less numerical computing difficulty (39). Using the RBF kernel, the performance of SVM model is dependent on two parameters, i.e. C and γ. As the best values for these two parameters are unknown beforehand, it is necessary to carry out a systematic search for the parameter values in constructing a reliable SVM model.
Both molecular property-based descriptors (including 1D, 2D, and 3D descriptors) and fragment-based descriptors (known as the fingerprints of a molecule) are commonly used in training a SVM model. The property-based descriptors mainly contain the overall and statistical information of compounds, whereas the fingerprints (fragments descriptors) focus on the information of substructure pattern and atom connectivity. Usually, the property-based descriptors might be more likely related to the passive diffusion, and the fingerprints might be more likely related to specific interactions, such as uptake, efflux, and protein binding. Hence, it might be reasonable to combine these two types of descriptors to construct a more generally applicable model for BBB permeability prediction. Besides, due to the high complex nature of the BBB system, one may expect that the quality of a BBB permeability prediction model can be improved when the training is performed with more data, as long as the model is not over-trained. We demonstrate, in this study, that a combined use of molecular property-based descriptors and fingerprints led us to obtain an SVM model capable of accurate prediction of the BBB permeability.
METHODS
Generating molecular descriptors
Molecular property-based descriptors.
Molecular property-based descriptors can be generated based on the molecular formula (1D descriptors), atom connection table (2D descriptors), and molecular shape (3D descriptors). Each of the property-based descriptors represents a certain feature of molecule, such as constitution, topology, geometry, electrostatic, polarizability, or refractivity. As each property-based descriptor only depicts a specific character of molecule, combination of a large number of property-based descriptors would provide more information. In this study, a total of 1441 1D/2D and 431 3D descriptors calculated by the PaDel-descriptor (40) were employed to represent each compound in the dataset. Then we combined all these 1874 property-based descriptors together into an array denoted as P.
Fragment-based descriptors (fingerprints).
The fragment-based descriptors were represented as a Boolean array indicating existence of the corresponding fragments in a molecule. If a certain pattern was found in the structure, the corresponding bit in the fragment-based descriptor array was set to “true”; otherwise, the bit was set to “false”. Generally speaking, a fragment could be defined by either a substructure pattern or a path-based pattern. Substructure patterns are usually a predefined dictionary containing a SMARTS list and, thus, the use of substructure patterns is a more intuitive way to describe the components of a molecule. Path-based patterns index small fragments of the structure based on linear segments of multiple atoms, which is more sensitive to the local atom connections in a molecule. In this study, the performances of multiple fragment-based descriptors were compared, including the Klekota-Roth fragment pattern (4860 bit, denoted as F1), CDK extended fragment pattern (1024 bit, denoted as F2), PubChem fragment pattern (881 bit, denoted as F3), 2D atom path pattern (780 bit, denoted as F4), and OpenBabel FP4 fragment pattern (307 bit, denoted as F5). All these 5 types of fragment-based descriptors were generated by the PaDEL-descriptor (40).
Preparation of the training and test sets
Two datasets were used in this study. Dataset A contained 1593 compounds (including 1283 BBB+ and 310 BBB− compounds), which was originally reported by Adenot et al. (21) and refined by Zhao et al. (9). Notably, the classification of BBB+ and BBB− in dataset A was based on the use of the well-known Anatomical Therapeutic Chemical (ATC) classification system. According to their classification system (21), the compounds assigned as BBB+ must have a sufficiently large BB ratio (i.e. the ratio of total steady-state concentration in brain to that in blood) because all of these compounds have been known as therapeutic agents or under clinical development for diseases in nervous systems, and the compounds assigned as BBB− must have a negligibly small BB ratio because all of these compounds have been known not to cross the BBB. Dataset B, as an extension of dataset A, was composed of all compounds in dataset A and additional 397 compounds (including 267 BBB+ with the BB ratio ≥ 0.1 and 130 BBB− compounds with the BB ratio < 0.1), reported originally by Li et al. (24) and refined by Zhao et al. (9). So, dataset B contained a total of 1990 compounds, including 1550 BBB+ (with the BB ratio ≥ 0.1) and 440 BBB− compounds (with the BB ratio < 0.1).
The datasets were downloaded in the SMILES format and then converted to the SDF format using the OpenEye toolkit (41). The 3D conformations of the compounds were generated and optimized using the Omega2 module of the OpenEye toolkit (41), and the protonation or deprotonation states of compounds in pH 7.4 were calculated using the Fixpka module of the OpenEye toolkit (41).
The quality of model constructed by machine learning methods is usually very susceptible to the way of training set selection. To decrease the biases introduced by training set selection, Kennard-stone (KS) algorithm (42) was used to divide the dataset into the training and test sets. With the KS algorithm, the compounds in the center of the chemical space (according to the Euclidean distance based on the property-based descriptors calculated using the method mentioned above) was selected as the starting point, then the farthest compound from the selected compound was selected. This process continued until reaching the required selection number for the training set. Then the remaining compounds were collected into the test set; the BBB+ and BBB− compounds were processed separately to ensure that these two classes of compounds have the same proportion in the training set and test set. As a result, the training set selected by the KS algorithm was expected to uniformly cover the property distribution space of the whole dataset, which may be considered as an ideal representative subset of the original dataset. However, the KS algorithm provided only one option for the training set selection, which may still carry the risk that the trained model may be highly dependent on the training set selection. Therefore, the random selection (RS) method was used to generate five independent training/test set pairs that were likely to be unevenly distributed in the chemical space (the BBB+ and BBB− compounds were processed separately). Finally, to examine the correlation between the prediction accuracy and the size of the training set, we selected the training set with four different percentages from the whole dataset, i.e. 80%, 75%, 67%, and 50%. That is, a total of eight pairs of different training/test sets were generated from the datasets A and B (Table 1).
Table 1.
Number of compounds in each training/test set pair
| Proportion of Training Set |
Compounds in Training Set | Compounds in Test set | |||||
|---|---|---|---|---|---|---|---|
| BBB+ | BBB− | Total | BBB+ | BBB− | Total | ||
| Dataset A | 80% | 1026 | 248 | 1274 | 257 | 62 | 319 |
| 75% | 962 | 232 | 1194 | 321 | 78 | 399 | |
| 66% | 846 | 205 | 1051 | 437 | 105 | 542 | |
| 50% | 641 | 155 | 796 | 642 | 155 | 797 | |
| Dataset B | 80% | 1240 | 352 | 1592 | 310 | 88 | 398 |
| 75% | 1162 | 330 | 1492 | 388 | 110 | 498 | |
| 66% | 1023 | 290 | 1313 | 527 | 150 | 677 | |
| 50% | 775 | 220 | 995 | 775 | 220 | 995 | |
Training the SVM model
Input vector.
The input vector for each compound in the training set was composed of the property-based descriptors array and/or fragment-based descriptors (fingerprints) array. To examine the influence of descriptor selection on the quality of the SVM model (see Figure 1), we compared the performance of 11 different input vectors formed by property-based descriptors (P), five different types of fragment descriptors (F1, F2, F3, F4, or F5), or the combinations of property-based and fragment-based descriptors (P+F1, P+F2, P+F3, P+F4, or P+F5). The values of property-based descriptors were scaled into the range of [−1,1] by using the SVM-scale module of the LibSVM (43), as we did in other artificial intelligence analyses (44-48). The values of fragment-based descriptors array were not scaled because they are Boolean arrays.
Figure 1.
Work flowchart of the SVM training and validating.
Parameter search.
Parameter C of the SVM training controls the tradeoff between the training error and model complexity. A too large value of C could lead to overfitting of the model, because the model would tend to use unnecessarily more support vectors to avoid the high penalty for non-separable points. On the other hand, a too small value of C may result in under fitting of the model. Parameter γ in the RBF controls the amplitude of the RBF kernel and, therefore, controls the generalization ability of the SVM model. Parameter γ may be considered as the inverse of the radius of influence for support vectors in the SVM model. A too large value of γ could also lead to the model overfitting, because the support vectors would only influence a small region nearby on this occasion. On the other hand, a too small value of γ could constrain the model and impair its ability of adopting information from input data, which could make the model under fitting. To obtain the best combination of parameters C and γ, the “grid search” strategy was used for the parameter optimization, which systematically traversed all the C and γ parameter pairs in a rational numeric range (C = 2−5, 2−4.5, …, 215, and γ = 23, 22.5, … , 2−15). To avoid overfitting of the SVM model, 5-fold cross-validation was used in the training steps. With the 5-fold cross-validation, the training set was first divided into five subsets with an equal size, then each subset was examined with the classifier trained based on the remaining four subsets.
Training SVM model.
For both the datasets A and B, four different training sets with different sizes (80%, 75%, 67%, and 50% of the whole dataset) were used to train the SVM model. Each training set was represented by 11 different types of vector (P, F1, F2, …, F5, P+F1, P+F2, …, P+F5). There were six training/test set pairs (five from the RS method and one from the KS method) for each dataset. As a result, a total of 2 × 4 × 11 × 6 = 528 SVM models were trained with its own best C and γ parameter pairs by using the SVM-train module of the LibSVM (43).
Validating the performance of SVM model
Predicting BBB permeability of compounds in the test set.
The input vector for test set was prepared in the same way as preparing input vector for training set mentioned above. Then the obtained 528 SVM models were used to predict the BBB permeability of the compounds in their corresponding test sets and examine the performance of the models.
Measurement for the quality of the SVM model.
A variety of approaches have been proposed in the literature to evaluate the quality of classification models (49). In this study, the quality of the SVM models was estimated by the overall prediction accuracy Q (Equation 3). Furthermore, the sensitivity of the model was defined as SE (Equation 4), which represents the prediction accuracy for the positives, and the specificity of the model was defined as SP (Equation 5), which represents the prediction accuracy for the negatives. In addition, the Matthews correlation coefficient (MCC) (Equation 6) was calculated to measure the performance of the binary classification.
| (3) |
where TP is the counts of the true positives, TN the true negatives, FN the false negatives, and FP the false positives, respectively.
| (4) |
| (5) |
| (6) |
RESULTS
Performances of our SVM models
The BBB+ and BBB− prediction accuracies for the training and test sets (selected by the KS method) for both datasets A and B are listed in Tables 2 and 3, respectively. The more detailed data, including those for the training/test set pairs selected by the random method (RS method), are listed in Tables S1 to 4 as the supplementary materials. The accuracy for the training set was the average accuracy from the 5-fold cross-validation with optimized C and γ parameter pair. The accuracy for the test set was obtained by using the SVM model trained by using the corresponding training set with the optimized C and γ parameter pair.
Table 2.
Overall accuracy of the SVM model with different descriptor vectors based on dataset A. The training set was selected by the KS method.
| Descriptor Vector |
Training Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|
| SE (%) | SP (%) | Q (%) | MCC | SE (%) | SP (%) | Q (%) | MCC | |
| P | 100.0 | 96.5 | 99.2 | 0.977 | 97.9 | 88.0 | 95.6 | 0.876 |
| F1 | 99.9 | 99.3 | 99.8 | 0.993 | 97.9 | 92.0 | 96.5 | 0.904 |
| F2 | 99.9 | 98.9 | 99.7 | 0.991 | 98.3 | 92.0 | 96.8 | 0.912 |
| F3 | 99.9 | 98.2 | 99.5 | 0.986 | 98.3 | 88.0 | 95.9 | 0.885 |
| F4 | 99.9 | 98.6 | 99.6 | 0.989 | 97.1 | 82.7 | 93.7 | 0.822 |
| F5 | 99.9 | 96.5 | 99.1 | 0.975 | 97.9 | 86.7 | 95.3 | 0.867 |
| P+F1 | 99.9 | 99.6 | 99.8 | 0.995 | 98.8 | 93.3 | 97.5 | 0.930 |
| P+F2 | 99.9 | 98.2 | 99.5 | 0.986 | 99.2 | 90.7 | 97.2 | 0.920 |
| P+F3 | 99.9 | 98.9 | 99.7 | 0.991 | 99.2 | 89.3 | 96.8 | 0.912 |
| P+F4 | 99.9 | 93.3 | 98.4 | 0.954 | 99.2 | 84.0 | 95.6 | 0.876 |
| P+F5 | 100.0 | 98.6 | 99.7 | 0.991 | 98.8 | 89.3 | 96.5 | 0.903 |
Table 3.
Overall accuracy of the SVM model with different descriptor vectors based on dataset B. The training set was selected by the KS method.
| Descriptor Vector |
Training Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|
| SE (%) | SP (%) | Q (%) | MCC | SE (%) | SP (%) | Q (%) | MCC | |
| P | 98.8 | 97.4 | 98.4 | 0.962 | 93.7 | 90.7 | 92.9 | 0.826 |
| F1 | 99.2 | 98.2 | 98.9 | 0.974 | 93.4 | 91.7 | 92.9 | 0.828 |
| F2 | 99.2 | 97.6 | 98.7 | 0.969 | 93.0 | 90.7 | 92.4 | 0.816 |
| F3 | 99.0 | 97.8 | 98.6 | 0.968 | 93.7 | 93.5 | 93.7 | 0.847 |
| F4 | 99.2 | 96.0 | 98.2 | 0.958 | 94.4 | 88.9 | 92.9 | 0.824 |
| F5 | 98.8 | 95.2 | 97.7 | 0.946 | 94.4 | 85.2 | 91.9 | 0.796 |
| P+F1 | 98.5 | 97.6 | 98.2 | 0.959 | 95.8 | 93.5 | 95.2 | 0.881 |
| P+F2 | 99.2 | 98.0 | 98.8 | 0.972 | 95.8 | 94.4 | 95.4 | 0.888 |
| P+F3 | 99.4 | 98.0 | 98.9 | 0.975 | 96.2 | 94.4 | 95.7 | 0.894 |
| P+F4 | 99.3 | 98.2 | 98.9 | 0.975 | 96.2 | 91.7 | 94.9 | 0.873 |
| P+F5 | 98.8 | 95.8 | 97.9 | 0.950 | 96.5 | 93.5 | 95.7 | 0.893 |
Unlike a simple physicochemical property such as oil/water partition coefficient or solubility, the BBB permeability of a compound is affected by a variety of complicated factors. Therefore, the use of comprehensive descriptors was expected to improve the quality and generality of the SVM model. In this study, a large number of descriptors were used to retain information as much as possible for the BBB permeability prediction. Meanwhile, we wanted to make sure that the SVM model was not overfitted. In addition to the use of the cross-validation method in the training steps, we also checked whether the prediction accuracies on the training sets would be dramatically different from those on independent test sets (that were never used in the training). For an overfitted SVM model, the performance of the prediction for compounds in the training set is expected to be significantly better than the performance of the prediction for compounds in the test set. As shown in Tables 2 and 3 (and also Tables S1 and S2 for more detailed data), for both the smaller dataset (dataset A) and the larger dataset (dataset B), the overall prediction accuracies for compounds in the training set and for compounds in the test set are always similar, suggesting that these SVM models were unlikely overfitted.
To know how good the SVM models are, the BBB permeability classification prediction based on the correlation with LogD (octanol/water distribution coefficient at pH 7.4) may be used a baseline for comparison with the SVM models. The LogD values of compounds in datasets A and B were calculated by using the Calculator Plugin in Marvin suite of ChemAxon (http://www.chemaxon.com). The larger LogD means the higher hydrophobicity and, thus, suggests that the compound can more likely penetrate BBB. For dataset A, the MCC of the BBB+/BBB− classification using LogD achieves the maximal of 0.572 when the cutoff LogD is −1.81 (i.e. BBB+ when LogD ≥ −1.81). For dataset B, the MCC of the BBB+/BBB− classification using LogD achieves the maximal of 0.484 when the cutoff LogD is −1.42 (i.e. BBB+ when LogD ≥ −1.42). Comparing with the simple LogD-based classification model, all of the SVM models discussed below have much improved performance as they have much larger MCC values.
As the SVM method usually does not adopt all input data into the model, only part of unique or representative data used to form the “supporting vector” are effective for constructing the model. So, using the KS method to select the training set is expected to achieve a better performance than using the RS method, because the compounds selected by the KS method are more likely to be the representative compounds that may be used as the “supporting vector”. As seen in Tables 2 and 3, the results obtained from the MCC with the KS method are systematically better than the results with the RS method (Tables S3 and S4 in Supplementary Materials), regardless of the descriptors used in training the SVM model. The property distribution for compounds in the training set selected by the RS method might be biased. However, most of the standard deviations regarding the overall accuracy of the model trained by the five independent training/test set pairs are less than 1%, suggesting that these models are better in terms of the robustness and generality.
Further, the SVM models trained with different sizes of the training set (80%, 75%, 67%, and 50% of the whole dataset) were compared. According to the overall accuracy data listed in Tables 2 and 3, the performances of the SVM models were not sensitive to the size of the training set. Results from the RS method also support that the size of the training set did not significantly influence the performance of the SVM model. All of these data suggest that our SVM models were not overfitted, which gives us more confidence for using these SVM models in predicting the BBB permeability of various compounds.
According to Tables 2 and 3, the prediction accuracies for the SVM models using only molecular property-based or fragment-based descriptors were in the range of 93.7% to 96.8% and 91.9% to 93.7% for datasets A and B, respectively, for the compounds within the respective datasets. As noted above, all compounds in dataset A have either a sufficiently large BB ratio or a negligibly small BB ratio (<< 0.1). Dataset B includes extra compounds with the BB ratio values between the two extremes, in addition to all compounds in dataset A. So, the SVM models obtained with dataset B should be more reliable in general BBB permeability prediction applications.
Interestingly, according to the data summarized in Tables 2 and 3, the SVM model with the fragment-based descriptors has better prediction performance than the corresponding SVM model with the property-based descriptors for both datasets A and B. So, the fragment-based descriptors (fingerprints) provide more important information relevant to the BBB permeability, compared to the property-based descriptors, for all of the compounds in a given dataset (A or B). As most of the BBB+ compounds in the dataset are supposed to penetrate BBB through passive diffusion (although the dataset does not provide the information about the BBB penetration mechanisms), the better performance of the model with the fragment-based descriptors suggests that the “fragment” information is also important for the BBB penetration through passive diffusion, in addition to the BBB penetration through the aforementioned “structure-specific” ways (e.g. selective transporters).
Further, the combined use of the property-based descriptors and fingerprints has improved the prediction accuracies to the range of 95.6% to 97.5% and 94.9% to 95.7% for datasets A and B, respectively. Figure 2 showed the significant performance improvement for the combined use of the property-based descriptors and fingerprints, indicating that information contained in property-based descriptors and fingerprints can complement to each other. The data associated with both the KS and RS methods (Figure 2B and D) consistently indicate that the best outcomes came from the combined use of the property-based descriptors and fingerprints. Notably, although the performances of the SVM models trained with different types of descriptors were significantly different, the performances of the SVM models trained with different combinations of the descriptors were very similar, further suggesting that the combination of the property-based descriptors with fingerprints can be used to improve the SVM model for BBB permeability prediction.
Figure 2.
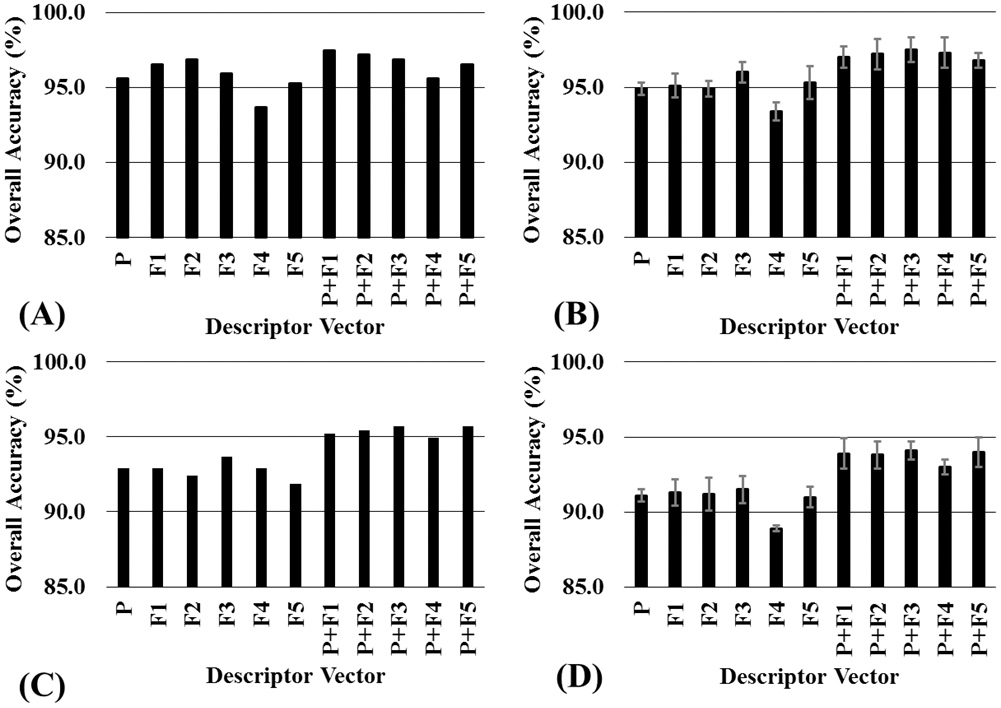
Comparison of the quality of the SVM models with different descriptor vectors in the prediction for the test set. (A) Training set included 80% compounds selected from dataset A by the KS method, and the test set included the remaining 20% compounds from dataset A. (B) Training set included 80% compounds selected from dataset A by the RS method, and the test set included the remaining 20% compounds from dataset A. The average prediction accuracy and standard deviation were caclulated from 5 independent training sets generated by the RS method (containing 80% compounds of the whole dataset). (C) Training set and test sets were selected from dataset B with the KS method. (D) The training set and test sets were selected from dataset B with the RS method.
DISCUSSION
Generally speaking, from the perspective of training a predictive model for practical use, one would like to use a dataset as large as possible because the model trained with a larger dataset is expected to be more reliable in practical predictions for any new compounds that are currently unknown. However, due to the high diversity of accessible chemical space associated with a larger dataset and the high complexity of the BBB permeability problem, the model trained with a larger dataset often shows lower accuracy (for the compounds within the dataset) compared to a specialized model trained with a smaller dataset. For this reason, large datasets were rarely used in previous computational studies. It should be noticed that the specialized models trained with smaller datasets indeed provide high-accuracy predictions for a portion of compounds, but these models are usually not practical due to their relatively low coverage of chemical diversity which is essential for practical prediction. Therefore, we trained our models with the largest available dataset (dataset B). In addition, we also trained the models with a relatively smaller dataset (dataset A), in order to compare our methods with previously reported models using the same dataset (Table 4).
Table 4.
Comparison of the performances of various computational models for the BBB permeability predictions.
| Number of Compounds in Dataset |
Study | Descriptors Used | SE(%) | SP(%) | Q(%) | MCC |
|---|---|---|---|---|---|---|
| 1593 (Dataset A)c | Zhao et al.a | Property-based Descriptors | 98.2 | 87.8 | 97.2 | 0.844 |
| Shen et al.b | Fingerprints | 99.6 | 85.7 | 98.2 | 0.895 | |
| This work | Property-based Descriptors | 97.9 | 88.0 | 95.6 | 0.876 | |
| Fingerprints | 98.3 | 92.0 | 96.8 | 0.912 | ||
| Both Property-based Descriptors and Fingerprints | 100.0 | 93.2 | 98.7 | 0.958 | ||
| 1990 (Dataset B)c | Zhao et al.a,d | Property-based Descriptors | 88.8 | 66.5 | 80.1 | 0.575 |
| This work | Property-based Descriptors | 93.7 | 90.7 | 92.9 | 0.826 | |
| Fingerprints | 93.7 | 93.5 | 93.7 | 0.847 | ||
| Both Property-based Descriptors and Fingerprints | 96.2 | 94.4 | 95.7 | 0.894 |
Using dataset A, two research groups (9, 30) developed BBB permeability classification prediction models using molecular property-based descriptors and fingerprints, respectively, as indicated in Table 4. The performances of these two models were comparable with our SVM models constructed by using the same type of descriptors (property-based descriptors or fingerprints). Compared to the models reported by Shen et al. (30) and Zhao et al. (9), our SVM model using the same type of descriptors had a slightly lower sensitivity (SE) and a slightly higher specificity (SP). Here, the sensitivity represents the prediction accuracy for the positives, and the specificity refers to the prediction accuracy for the negatives. Since the ratio of the number of the positive samples to the number of negative samples in the dataset was about 4 : 1 (which is true for both the training and test sets), indicating that the dataset was unbalanced. Hence, the accurate prediction for the negatives, i.e. the higher SP in this case, should have a larger weight in the assessment for the overall performance of the models. For the same reason, the overall accuracy (Q) would be biased for evaluating the models in the present work because Q is more suitable for measuring models with a balanced dataset. Matthews correlation coefficient (MCC) is widely used in measuring the performance of binary classification, because MCC is generally regarded as a balanced measure and can be used even if the classes are of very different sizes. So, MCC index, instead of Q, was used to evaluate the quality of various models in the present work. According to the data in Table 4, the MCC of our models using the property-based descriptors (MCC = 0.876) and fingerprints (MCC = 0.912) were slightly higher than the respective models reported by Shen et al. (30) (property-based descriptors, MCC = 0.844) and Zhao et al. (9) (fingerprints, MCC = 0.895). So, our SVM model using the same type of descriptors (property-based descriptors or fingerprints) is slightly better due to the detailed difference in the training protocol, but the improvement is not significant, which reflects the ceiling in improving the BBB model using only one type of descriptors (molecular property-based descriptors or fingerprints). Interestingly, our SVM model with the combined use of both the property-based descriptors and fingerprints has a significantly improved performance (MCC = 0.958) in comparison with previously reported models; all indexes including MCC, SE, SP, and Q are better than the previous models constructed with only the property-based descriptors or fingerprints, as seen in Table 4.
Further, we are interested in a more generalized SVM model using the largest possible dataset (dataset B). Using dataset B, all of our SVM models are significantly better than the previous models, as seen in Table 4. The best SVM model is also associated with the combined use of both the molecular property-based descriptors and fingerprints, because the combined use of both the property-based descriptors and fingerprints for the extraction of information from the compounds would be more complete.
In general, this research suggests that a combined use of the property-based descriptors and fingerprints may also help to improve the accuracy of other SVM models to be developed for other molecular activities/functions in the future.
CONCLUSION
It is critically important for the development of a predictive machine-learning model, such as SVM, to appropriately select the descriptors of compounds. We have demonstrated that the combined use of both the property-based descriptors and fingerprints can lead to significant improvement of the SVM models compared to the corresponding SVM models using the property-based descriptors or fingerprints alone. Hence, through the combined use of both the property-based descriptors and fingerprints, we have developed a generally applicable SVM model to more reliably predict the BBB permeability classification of compounds. Compared to current available methods, our new SVM model has a significantly improved accuracy in the BBB permeability prediction, suggesting that future development of other machine-learning models for other molecular activities/functions may also be based on a combined use of the property-based descriptors and fingerprints for improving the accuracy of the computational predictions.
Supplementary Material
Acknowledgments
This work was supported in part by the National Science Foundation (NSF grant CHE-1111761) and the National Institutes of Health (NIH grants UH2/UH3 DA041115, R01 DA035552, R01 DA032910, R01 DA013930, R01 DA025100, and UL1TR001998). The authors also acknowledge the Computer Center at the University of Kentucky for supercomputing time on a Dell Supercomputer Cluster consisting of 388 nodes or 4,816 processors.
Footnotes
REFERENCES
- 1.George A. The design and molecular modeling of CNS drugs. Current opinion in drug discovery & development. 1999;2(4):286–92. [PubMed] [Google Scholar]
- 2.Puzyn T, Leszczynski J, Cronin MT. Recent advances in QSAR studies: methods and applications: Springer Science & Business Media; 2010. [Google Scholar]
- 3.Bicker J, Alves G, Fortuna A, Falcão A. Blood–brain barrier models and their relevance for a successful development of CNS drug delivery systems: a review. European Journal of Pharmaceutics and Biopharmaceutics. 2014;87(3):409–32. [DOI] [PubMed] [Google Scholar]
- 4.Abraham MH. The factors that influence permeation across the blood–brain barrier. European journal of medicinal chemistry. 2004;39(3):235–40. [DOI] [PubMed] [Google Scholar]
- 5.Rose K, Hall LH, Kier LB. Modeling blood-brain barrier partitioning using the electrotopological state. Journal of chemical information and computer sciences. 2002;42(3):651–66. [DOI] [PubMed] [Google Scholar]
- 6.Crivori P, Cruciani G, Carrupt P-A, Testa B. Predicting blood– brain barrier permeation from three-dimensional molecular structure. Journal of medicinal chemistry. 2000;43(11):2204–16. [DOI] [PubMed] [Google Scholar]
- 7.Ooms F, Weber P, Carrupt P-A, Testa B. A simple model to predict blood–brain barrier permeation from 3D molecular fields. Biochimica et Biophysica Acta (BBA)-Molecular Basis of Disease. 2002;1587(2):118–25. [DOI] [PubMed] [Google Scholar]
- 8.Gerebtzoff G, Seelig A. In silico prediction of blood– brain barrier permeation using the calculated molecular cross-sectional area as main parameter. Journal of chemical information and modeling. 2006;46(6):2638–50. [DOI] [PubMed] [Google Scholar]
- 9.Zhao YH, Abraham MH, Ibrahim A, Fish PV, Cole S, Lewis ML, et al. Predicting penetration across the blood-brain barrier from simple descriptors and fragmentation schemes. Journal of chemical information and modeling. 2007;47(1):170–5. [DOI] [PubMed] [Google Scholar]
- 10.Lanevskij K, Japertas P, Didziapetris R. Improving the prediction of drug disposition in the brain. Expert opinion on drug metabolism & toxicology. 2013;9(4):473–86. [DOI] [PubMed] [Google Scholar]
- 11.Mehdipour AR, Hamidi M. Brain drug targeting: a computational approach for overcoming blood–brain barrier. Drug discovery today. 2009;14(21):1030–6. [DOI] [PubMed] [Google Scholar]
- 12.Nagpal K, Singh SK, Mishra DN. Drug targeting to brain: a systematic approach to study the factors, parameters and approaches for prediction of permeability of drugs across BBB. Expert opinion on drug delivery. 2013;10(7):927–55. [DOI] [PubMed] [Google Scholar]
- 13.Di L, Kerns EH, Carter GT. Strategies to assess blood–brain barrier penetration. Expert opinion on drug discovery. 2008;3(6):677–87. [DOI] [PubMed] [Google Scholar]
- 14.Vilar S, Chakrabarti M, Costanzi S. Prediction of passive blood–brain partitioning: straightforward and effective classification models based on in silico derived physicochemical descriptors. Journal of Molecular Graphics and Modelling. 2010;28(8):899–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zah J, Terre'Blanche G, Erasmus E, Malan SF. Physicochemical prediction of a brain–blood distribution profile in polycyclic amines. Bioorganic & medicinal chemistry. 2003;11(17):3569–78. [DOI] [PubMed] [Google Scholar]
- 16.Young RC, Mitchell RC, Brown TH, Ganellin CR, Griffiths R, Jones M, et al. Development of a new physicochemical model for brain penetration and its application to the design of centrally acting H2 receptor histamine antagonists. Journal of medicinal chemistry. 1988;31(3):656–71. [DOI] [PubMed] [Google Scholar]
- 17.Dagenais C, Avdeef A, Tsinman O, Dudley A, Beliveau R. P-glycoprotein deficient mouse in situ blood–brain barrier permeability and its prediction using an in combo PAMPA model. European Journal of Pharmaceutical Sciences. 2009;38(2):121–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lanevskij K, Japertas P, Didziapetris R, Petrauskas A. Ionization-specific prediction of blood–brain permeability. Journal of pharmaceutical sciences. 2009;98(1):122–34. [DOI] [PubMed] [Google Scholar]
- 19.Lanevskij K, Dapkunas J, Juska L, Japertas P, Didziapetris R. QSAR analysis of blood–brain distribution: The influence of plasma and brain tissue binding. Journal of pharmaceutical sciences. 2011;100(6):2147–60. [DOI] [PubMed] [Google Scholar]
- 20.Luco JM. Prediction of the brain− blood distribution of a large set of drugs from structurally derived descriptors using partial least-squares (PLS) modeling. Journal of chemical information and computer sciences. 1999;39(2):396–404. [DOI] [PubMed] [Google Scholar]
- 21.Adenot M, Lahana R. Blood-brain barrier permeation models: discriminating between potential CNS and non-CNS drugs including P-glycoprotein substrates. Journal of chemical information and computer sciences. 2004;44(1):239–48. [DOI] [PubMed] [Google Scholar]
- 22.Mente* S, Lombardo F. A recursive-partitioning model for blood–brain barrier permeation. Journal of computer-aided molecular design. 2005;19(7):465–81. [DOI] [PubMed] [Google Scholar]
- 23.Shen J, Du Y, Zhao Y, Liu G, Tang Y. In silico prediction of blood–brain partitioning using a chemometric method called genetic algorithm based variable selection. Molecular Informatics. 2008;27(6):704–17. [Google Scholar]
- 24.Li H, Yap CW, Ung CY, Xue Y, Cao ZW, Chen YZ. Effect of selection of molecular descriptors on the prediction of blood– brain barrier penetrating and nonpenetrating agents by statistical learning methods. Journal of Chemical Information and Modeling. 2005;45(5):1376–84. [DOI] [PubMed] [Google Scholar]
- 25.Zhang L, Zhu H, Oprea TI, Golbraikh A, Tropsha A. QSAR modeling of the blood–brain barrier permeability for diverse organic compounds. Pharmaceutical research. 2008;25(8):1902. [DOI] [PubMed] [Google Scholar]
- 26.Jung E, Kim J, Kim M, Jung DH, Rhee H, Shin J-M, et al. Artificial neural network models for prediction of intestinal permeability of oligopeptides. BMC bioinformatics. 2007;8(1):245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Garg P, Verma J. In silico prediction of blood brain barrier permeability: an artificial neural network model. Journal of chemical information and modeling. 2006;46(1):289–97. [DOI] [PubMed] [Google Scholar]
- 28.Hou T, Wang J, Li Y. ADME evaluation in drug discovery. 8. The prediction of human intestinal absorption by a support vector machine. Journal of chemical information and modeling. 2007;47(6):2408–15. [DOI] [PubMed] [Google Scholar]
- 29.Fröhlich H, Wegner J, Sieker F, Zell A. Kernel Functions for Attributed Molecular Graphs–A New Similarity-Based Approach to ADME Prediction in Classification and Regression. Molecular Informatics. 2006;25(4):317–26. [Google Scholar]
- 30.Shen J, Cheng F, Xu Y, Li W, Tang Y. Estimation of ADME properties with substructure pattern recognition. Journal of chemical information and modeling. 2010;50(6):1034–41. [DOI] [PubMed] [Google Scholar]
- 31.Golmohammadi H, Dashtbozorgi Z, Acree WE. Quantitative structure–activity relationship prediction of blood-to-brain partitioning behavior using support vector machine. European Journal of Pharmaceutical Sciences. 2012;47(2):421–9. [DOI] [PubMed] [Google Scholar]
- 32.Vapnik V. The nature of statistical learning theory: Springer science & business media; 2013. [Google Scholar]
- 33.Trotter MWB. Support vector machines for drug discovery: University of London; 2007. [Google Scholar]
- 34.Geppert H, Vogt M, Bajorath Jr. Current trends in ligand-based virtual screening: molecular representations, data mining methods, new application areas, and performance evaluation. Journal of chemical information and modeling. 2010;50(2):205–16. [DOI] [PubMed] [Google Scholar]
- 35.Collobert R, Bengio S. SVMTorch: Support vector machines for large-scale regression problems. Journal of machine learning research. 2001;1(February):143–60. [Google Scholar]
- 36.Smola AJ, Schölkopf B. A tutorial on support vector regression. Statistics and computing. 2004;14(3):199–222. [Google Scholar]
- 37.Gunn SR. Support vector machines for classification and regression. ISIS technical report. 1998;14:85–6. [Google Scholar]
- 38.Chung K-M, Kao W-C, Sun C-L, Wang L-L, Lin C-J. Radius margin bounds for support vector machines with the RBF kernel. Neural computation. 2003;15(11):2643–81. [DOI] [PubMed] [Google Scholar]
- 39.Hsu C-W, Chang C-C, Lin C-J. A practical guide to support vector classification. 2003.
- 40.Yap CW. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. Journal of computational chemistry. 2011;32(7):1466–74. [DOI] [PubMed] [Google Scholar]
- 41.Toolkits O. OpenEye Scientific Software, Santa Fe, NM. 2015. [Google Scholar]
- 42.Kennard RW, Stone LA. Computer aided design of experiments. Technometrics. 1969;11(1):137–48. [Google Scholar]
- 43.Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST). 2011;2(3):27. [Google Scholar]
- 44.Zheng F, Bayram E, Sumithran SP, Ayers JT, Zhan C-G, Schmitt JD, et al. QSAR modeling of mono- and bis-quaternary ammonium salts that act as antagonists at neuronal nicotinic acetylcholine receptors mediating dopamine release. Bioorg Med Chem. 2006;14:3017–37. [DOI] [PubMed] [Google Scholar]
- 45.Zheng F, McConnell MJ, Zhan C-G, Dwoskin LP, Crooks PA. QSAR study on maximal inhibition (Imax) of quaternary ammonium antagonists for S-(−)-nicotine-evoked dopamine release from dopaminergic nerve terminals in rat striatum. Bioorg Med Chem. 2009;17:4477–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zheng F, Zheng G, Deaciuc AG, Zhan C-G, Dwoskin LP, Crooks PA. Computational neural network analysis of the affinity of lobeline and tetrabenazine analogs for the vesicular monoamine transporter-2. Bioorg Med Chem. 2007;15:2975–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zheng F, Zheng G, Deaciuc AG, Zhan C-G, Dwoskin LP, Crooks PA. Computational neural network analysis of the affinity of N-n-alkylnicotinium salts for the alpha4beta2* nicotinic acetylcholine receptor. J Enzyme Inhib Med Chem. 2007;24:157–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ring JR, Zheng F, Haubner AJ, Littleton JM, Crooks PA. Improving the inhibitory activity of arylidenaminoguanidine compounds at the N-methyl-D-aspartate receptor complex from a recursive computational-experimental structure-activity relationship study. Bioorg Med Chem. 2013;21:1764–74. [DOI] [PubMed] [Google Scholar]
- 49.Baldi P, Brunak S, Chauvin Y, Andersen CA, Nielsen H. Assessing the accuracy of prediction algorithms for classification: an overview. Bioinformatics. 2000;16(5):412–24. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


