Improvement of d-d interactions in Density Functional Tight Binding for Transition Metal Ions with a Ligand Field Model: Assessment of a DFTB3+U model on Nickel coordination compounds

Abstract

To improve the description of interactions among the localized d, f electrons in transition metals, we have introduced a ligand-field motivated contribution into the Density Functional Tight Binding (DFTB) model. Referred to as DFTB3+U, the approach treats the d, f electron repulsions with rotationally invariant orbital-orbital interactions and a Hartree-Fock model; this represents a major conceptual improvement over the original DFTB3 approach, which treats the d, f -shell interactions in a highly averaged fashion without orbital level of description. The DFTB3+U approach is tested using a series of nickel compounds that feature Ni(II) and Ni(III) oxidation states. By using parameters developed with the original DFTB3 Hamiltonian and empirical +U parameters (F^0/2/4 Slater integrals), we observe that the DFTB3+U model indeed provides substantial improvements over the original DFTB3 model for a number of properties of the nickel compounds, including the population and spin polarization of the d-shell, nature of the frontier orbitals, ligand field splitting and the energy different between low and high spin states at OPBE optimized structures. This proof-of-concept study suggests that with self-consistent parameterization of the electronic and +U parameters, the DFTB3+U model can develop into a promising model that can be used to efficiently study reactive events involving transition metals ion condensed phase systems. The methodology can be integrated with other approximate QM methods as well, such as the extended tight binding (xTB) approach.

Graphical Abstract

DFTB3+U for Transition Metal Systems

I. Introduction

Transition metal ions play important roles in chemistry and biology,^1–8 thus it is important to describe their electronic structure and coordination geometry with a high degree of accuracy in computational studies.^9–12 Due to the localized nature of the valence shell in transition metals (e.g., 3d), electron correlation effects are significant and need to be well treated for an accurate description.^9,11,12 In fact, both static and dynamic correlation effects are significant for transition metal (TM) ions, making them challenging to study using quantum mechanical (QM) methods.^9,11–13 Progress in quantum chemistry has seen the development of various Density Functional Approximations (DFAs),^13–16 or different methodologies such as DMRG,^17–22 and Multi-Configuration Pair-Density Functional Theory^23,24, followed very recently by including DMRG (DMRG-PDFT).²⁵ These developments have generated promising results¹⁴ for transition metal systems, including multi-metal clusters.^20,26–32 Nevertheless, such calculations remain computationally expensive and therefore not readily applicable to problems where extensive sampling of the configurational space is crucial.³³ An exciting and emerging direction is to develop machine learning (ML) potentials based on high-level QM methods,^34–40 yet application of ML potentials to condensed phase systems is not as straightforward and remains an active area for research.⁴¹ Semi-empirical QM methods^42–45 can potentially fill the gap between highly accurate quantum chemistry methods and empirical or numerical (e.g., machine learning) potentials. As described below in more detail, while these techniques generally provide reasonable geometries, most current approaches lack accuracy with respect to energetics and electron distribution particularly when comparing different electronic (magnetic) states in transition metal compounds. Here we show a possible solution to this problem by enhancing Density Functional Tight Binding (DFTB) with an explicit description of electron-electron interactions inside the d,f-shell of a transition metal with orbital resolution.

DFTB has attracted much attention in recent years due to its computational efficiency and reasonable accuracy for many applications.^42–44 The DFTB2⁴⁵ approach has been parameterized for the first row of transition metal ions by Morokuma and co-workers;⁴⁶ the method was found to give reasonable structures, while energetics, especially spin state splittings, often have large errors on the order of at least tens of kcal/mol.⁴⁶ The third-order variant of DFTB (DFTB3)⁴⁷ has been parameterized for several transition metal ions such as zinc,⁴⁸ copper⁴⁹ and nickel⁵⁰ within the framework of the 3OB parameterization. Obtained structures are general fairly robust, but the metal-ligand binding interactions may exhibit large errors, especially for charged ligands; the robustness of the structures was demonstrated by the much improved metal-ligand interaction energies in single point calculations at higher level theories (e.g., G3B3 or B3LYP). Investigation of the bonding structure in the context of Natural Bonding Orbital analysis⁵¹ suggested that the DFTB3/3OB model generally provides physically sound descriptions of metal-ligand interactions, including (pseudo) Jahn-Teller effects,^49,50 although the degree of ligand-to-metal charge transfer and certain orbital interactions can be grossly overestimated. Specifically, for nickel, the first parameterization had to resort to distinct Hubbard charge derivatives for different oxidation states to capture reliable structural and energetic properties for the respective oxidation state, and larger errors were observed for the spin state splittings.⁵⁰

More recently, the xTB model^52,53 of Grimme and co-workers has been developed for the entire periodic table, including all transition metal ions. The model has been shown to give impressive structural properties for many transition metal compounds, including transition state structures for organometallic catalysis.⁵⁴ Similar to DFTB3/3OB, however, the energetics are generally less satisfactory, due in part to the fact that the xTB model was parameterized based on structure and vibrational frequencies.⁵²

Therefore, it is evident that additional development is worthwhile to improve the energetic properties of transition metal compounds at the semi-empirical QM level. In this work, we address the problem of strong d-electron correlation by augmenting the DFTB3 approach with a ligand field (LF) ^9,55–58 motivated model to specifically treat the d-d interactions with resolved magnetic quantum numbers (m_l). The idea of using LF theory is not new; LF model has been incorporated into force fields for transition metal ions, ⁵⁹ and it has been integrated with Density Functional Theory^60,61 and ab initio wavefunction methods for the interpretation of electronic structure and spectroscopies of metal compounds.⁶² The philosophy of treating the d and f electrons in transition metal ions separately is also the basis for the DFT+U method in the materials science community. ^63–66 Therefore, we expect that introducing the LF motivated model into DFTB3 can improve the latter’s description of transition metal compounds. Indeed, using a set of nickel compounds as exploratory examples, we find that including the additional term into DFTB3 Hamiltonian with 3OB improves many properties related to the electronic structure of both Ni(II) and Ni(III) compounds, such as the occupancy of metal d orbitals and spin-state splitting. While further adjustment in the 3OB parameterization is clearly required since the DFTB3 Hamiltonian is modified, the current findings suggest that the augment DFTB3 with a LF type of model for the d electrons, referred below as DFTB3+U, has the potential to become an effective approach for describing transition metal systems.

In the following, we first present the integration of the LF inspired model with DFTB3, leading to the DFTB3+U. This is followed by the analysis of computational results for nickel ions and a set of Ni(II)/Ni(III) compounds to illustrate the impact of including the new term into DFTB3 Hamiltonian. We end by a few concluding remarks.

II. Theory and Computational Methods

In this section, we will give a short overview of DFTB3 methods, and the interested reader is pointed to the literature.^{33,43–45,47,67,68}

II.1. Density Functional Tight Binding (DFTB) Model

The DFTB energy is obtained as an approximation of DFT by replacing the electron density, ρ, by the sum of the reference density ρ⁰, which is obtained as a sum of precalculated atomic densities and a density fluctuation Δρ,

$$\begin{array}{c}\rho ={\rho }^0+\mathrm{\Delta }\rho .\#\end{array}$$ (1)

Expanding the total energy in a Taylor series in Δρ, and following a set of additional approximations,⁶⁹ the following energy expression is obtained at the third order,

$$\begin{array}{c}E=\stackrel{DFT{B}^3}{\overbrace{\stackrel{DFT{B}^2}{\overbrace{\stackrel{DFT{B}^1}{\overbrace{E^{H0}+E^{rep}}}+E^{\gamma }}}+E^{\mathrm{Г}}}}=\\ =\sum _{iab}\sum _{\mu \in a}\sum _{v\in b}{n}_i{c}_{\mu i}{c}_{vi}{H}_{\mu v}^0+E^{rep}+\frac{1}{2}\sum _{ab}{\gamma }_{ab}\mathrm{\Delta }{q}_a\mathrm{\Delta }{q}_b+\frac{1}{3}\sum _{ab}{\mathrm{Г}}_{ab}\mathrm{\Delta }{q}_a^2\mathrm{\Delta }{q}_b\#\end{array}$$ (2)

As the first order term depends only on the reference density, the generalized eigenvalue problem needs to be diagonalized only once, while for DFTB2 and DFTB3 it needs to be solved self-consistently.⁶⁷ DFTB1 is a good approximation when there is no large density fluctuation relative to atoms during bond formation, i.e., for non-polar molecules. For more complex molecules, DFTB2/3 are needed for computing the changes in the electron-electron interactions relative to the reference, as represented in the third and fourth terms of the energy expression. Third order terms involve, Г_ab, which is the charge derivative of the second order term, γ_ab. ⁶⁷ Spin-polarization^49,68,70,71 and l-dependence of the Hubbard parameters⁷⁰ have also been incorporated.

II.2. Augment DFTB with a Ligand Field Type of Model for the d,f Electrons

DFTB2 and DFTB3 approaches make strongest approximations when treating electron-electron interactions. In particular these methods only deal with the average interaction among the electrons localized on the atoms. However, for the d or f shells in transition or rare-earth metals, electrons are highly localized and more detailed orbital-orbital interactions are necessary. ^9,58 Despite these difficulties, Morokuma and co-workers produced DFTB2 parameters for several first-row transition metals,⁴⁶ including Fe and Ni while Grimme and co-workers developed a tight-binding model (xTB) for the entire periodic table.⁵² Both models provided satisfactory results for geometries but not for energetics. Even though their work was certainly a step forward, it is now apparent that further developments are necessary to fully capture the rich chemistry of these systems involving a full register of magnetism, spin-states and other orbital-dependent phenomena like the Jahn-Teller effect.

At the simplest level, the interaction of electrons within d or f shells can be written using the Hartree-Fock method, ⁷²

$$\begin{array}{c}{E}^{ee}=\sum _{\sigma }\sum _{\alpha \beta {\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}\left(P_{\alpha \beta }^{\sigma }{P}_{{\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}^{-\sigma }+P_{\alpha \beta }^{\sigma }{P}_{{\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}^{\sigma }\right)⟨{\chi }_{\alpha }{\chi }_{{\alpha }^{\mathrm{\text{'}}}}|\frac{1}{\left|r-r^{\mathrm{\text{'}}}\right|}|{\chi }_{\beta }{\chi }_{{\beta }^{\mathrm{\text{'}}}}⟩\\ -\sum _{\sigma }\sum _{\alpha \beta {\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}{P}_{\alpha \beta }^{\sigma }{P}_{{\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}^{\sigma }⟨{\chi }_{\alpha }{\chi }_{{\alpha }^{\mathrm{\text{'}}}}|\frac{1}{\left|r-r^{\mathrm{\text{'}}}\right|}|{\chi }_{{\beta }^{\mathrm{\text{'}}}}{\chi }_{\beta }⟩\#\end{array}$$ (3)

where α, β, α’, and β’ are indices that run over all the spatial orbitals of the highly localised atomic shell, represented by a basis function χ_α; σ represents the spin (up or down) and $P_{\alpha \beta }^{\sigma }$ is the corresponding density matrix element. Many classical texts, like that of Griffith,⁵⁸ show that, when we confine the interactions within a particular shell, and under spherical symmetry, the four-center integrals can be written in term of the Slater integrals (F⁰, F², F⁴ for d-shells and F⁰, F², F⁴ and F⁶ for f-shells)

$$\begin{array}{c}⟨{\chi }_{\alpha }{\chi }_{{\alpha }^{\mathrm{\text{'}}}}|\frac{1}{\left|r-r^{\mathrm{\text{'}}}\right|}|{\chi }_{\beta }{\chi }_{{\beta }^{\mathrm{\text{'}}}}⟩=\sum _{k=\mathrm{0,2},4}{\alpha }_k\left(\alpha ,\beta ,{\alpha }^{\mathrm{\text{'}}},{\beta }^{\mathrm{\text{'}}}\right)F^k\#\end{array}$$ (4)

where α_k can be expressed as a product of Clebsch-Gordan coefficients. Slater integrals are simply related to Racah parameters (A, B and C) commonly used in the ligand field theory, and to parameters U and J in DFT+U:

$$F^0=A+\frac{7}{5}C=U;F^2=49B+7C\approx \frac{5390}{637}J;F^4=\frac{441}{35}C\approx \frac{3528}{637}J$$

$$A=F^0-{\frac{49}{441}F}^4;B={\frac{1}{49}F}^2-{\frac{5}{441}F}^4;{C=\frac{35}{441}F}^4$$

In these transformations, we follow the usual approximation that fixes the the ratio F⁴/F² to a value of 0.625. It is important to note that, in this work where the spin constants W_lal’a have been fixed to values from a previous work,⁵⁰ the effect of using different F⁴/F² values, as well as their ratio, is found to be negligible.

In this work, we propose to add this rotationally invariant ligand-field term to the DFTB3 energy to describe detailed orbital-orbital interactions when active d or f electrons are present in the system. This is a similar prescription to the DFT+U model commonly used in the materials science community. A convenient energy expression can be reached making use of the total density matrix, $P_{\alpha \beta }^U=1/2\left(P_{\alpha \beta }^{\uparrow }+P_{\alpha \beta }^{\downarrow }\right),$ and spin-polarization density matrix $P_{\alpha \beta }^I=1/2\left(P_{\alpha \beta }^{\uparrow }-P_{\alpha \beta }^{\downarrow }\right),$

$$\begin{array}{c}{E}^{ee}=\sum _{\alpha \beta {\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}{P}_{\alpha \beta }^U{P}_{{\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}^U\left(⟨{\chi }_{\alpha }{\chi }_{{\alpha }^{\mathrm{\text{'}}}}|\frac{1}{\left|r-r^{\mathrm{\text{'}}}\right|}|{\chi }_{\beta }{\chi }_{{\beta }^{\mathrm{\text{'}}}}⟩-⟨{\chi }_{\alpha }{\chi }_{{\beta }^{\mathrm{\text{'}}}}|\frac{1}{\left|r-r^{\mathrm{\text{'}}}\right|}|{\chi }_{\beta }{\chi }_{{\alpha }^{\mathrm{\text{'}}}}⟩\right)\\ -\sum _{\alpha \beta {\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}{P}_{\alpha \beta }^I{P}_{{\alpha }^{\mathrm{\text{'}}}{\beta }^{\mathrm{\text{'}}}}^I⟨{\chi }_{\alpha }{\chi }_{{\beta }^{\mathrm{\text{'}}}}|\frac{1}{\left|r-r^{\mathrm{\text{'}}}\right|}|{\chi }_{{\beta }^{\mathrm{\text{'}}}}{\chi }_{\alpha }⟩\#\end{array}$$ (5)

In this way the first term can be used in simulations in absence of spin polarization while the second term can be added to include magnetic effects.

Comparing the approach taken here to the usual DFT+U⁷³ it is clear that we do not include the correction to avoid double counting d-d interactions. This is partially justified as DFTB is a semi-empirical method where we aim to examine the inclusion of the extra ligand-field or +U term on the description of the spin state splitting with existing basis. Clearly much room for improvement remains with a full reparameterization of the basis, excluding the average d-d/f-f interactions existing in DFTB3 and relying solely on the more detailed description given by the ligand field terms.

III. Results and Discussion

III.1. Atomic Systems: Ni(II) and Ni(III) ions

To examine the impact of the +U contribution on the electronic structure of metal ions, the natural place to start is the atomic systems since they lack the complications due to mixing with the ligand orbitals. Here we focus on both Ni(II) and Ni(III).

The first question we aim to answer is how the increase of interelectronic repulsion influences the energies of the spin states individually as well as the spin state splitting (ΔE_LS-HS). To this end, we vary the three Slater integral parameters, F⁰ F² and F⁴ individually. As electron-electron repulsion favours the high spin state, it is natural to expect that the general bias of DFTB3 (and many DFT functionals) toward the low spin state will be somewhat counteracted.

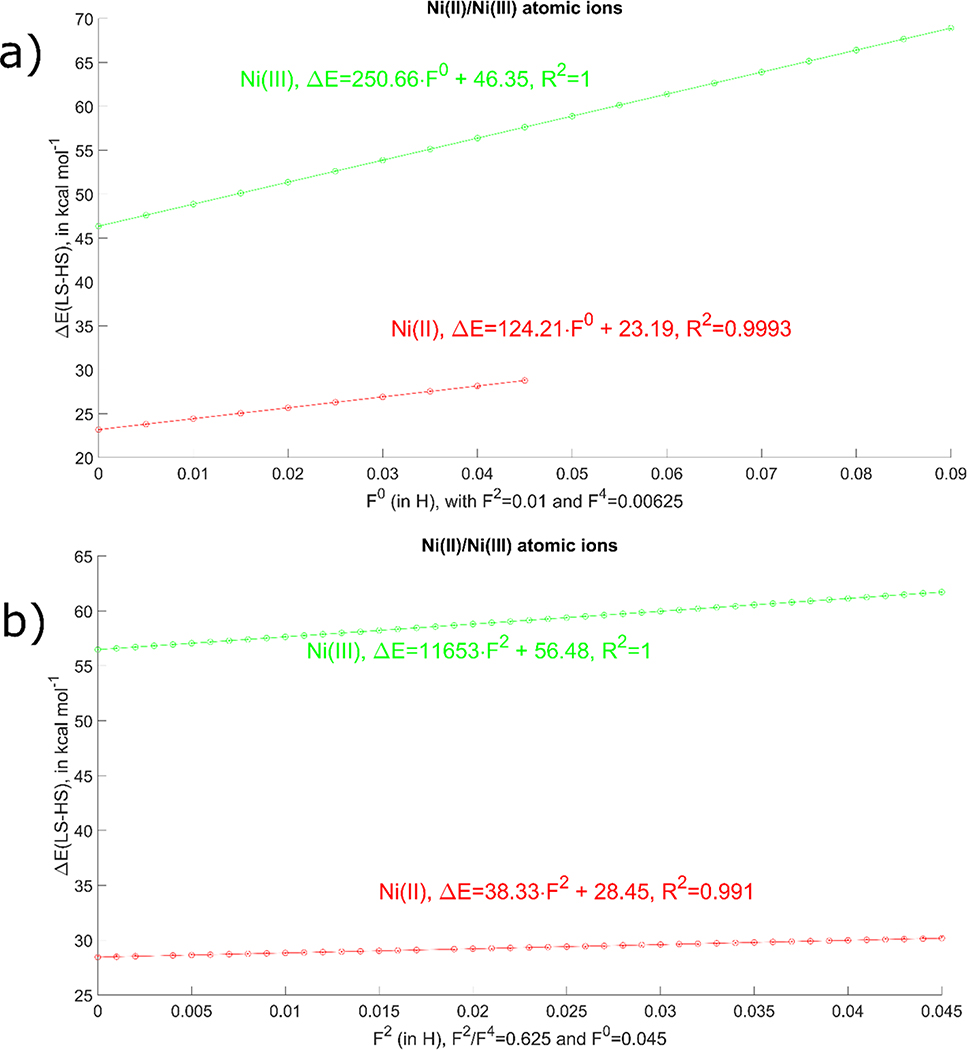
As shown in Figure 1 this is, indeed, what is observed in the actual calculations. As expected from LF theory⁵⁸, it is found that the energies of the spin states, as well as their difference (ΔE_LS-HS), show perfect linear dependence on the F²/F⁴ parameters and the high spin state becomes more favoured when the electron-electron repulsion is increased, Figure 1. Somewhat surprisingly, ΔE_LS-HS also exhibits a linear dependence on F⁰, which is not the result expected from pure ligand field theory where the difference in energy between the low and high spin states is not dependent on F⁰. This somewhat surprising result comes from the fact that the ligand-field theory found in classical books like the one by Griffith⁵⁸ expresses the atomic wavefunction as a combination of multiple Slater determinants while in our case we use a mean-field approach distilled into Eq. 3 where the atomic orbital occupations are fractional. Using Eq. 3, and substituting the four-center integrals using Eq. 4 and setting F²=F⁴=0 we can show (see SI.docx) that the energy difference between high and low spin states in Ni(III) is twice as large as that for Ni(II), as found numerically in our calculations shown in Figure 1.

Figure 1.

Dependence of ΔE_LS-HS on the F⁰ electron repulsion parameter (a), and F² electron repulsion parameter (b), for Ni(II) and Ni(III) atomic systems.

Regarding the spin state energetics, the best results in comparison to available experimental data are obtained with F⁰=0.05–0.055 Hartree with a mean-absolute-error (MAE) of ~13 kcal/mol for both Ni(II) and Ni(III) oxidation states; we need to bear in mind that the double counting of d-d interaction has not been explicitly taken out in this work, thus our value (around 1.3 eV) is very small compared to the usual value of F⁰ in atoms (tens of eV)⁷⁴ or the value in solids (around a few (7–9) eV for Ni)^75,76. This obtained MAE is competitive with the best DFT results (see Table S5); for example, the MAE is 37 kcal/mol for PBE0 and 8 kcal/mol for OPBE (which showed the best performance out of all used DFAs). However, from a practical point of view using these values of F⁰ in molecular calculations leads to convergence problems in SCF cycles. While for atomic ions we detect that SCF problems start after F⁰≥0.05 for Ni(II) and F⁰>0.1 for Ni(III), we found that robust SCF behaviours for molecules are observed for up to F⁰=0.035 Hartree. With this F⁰ value, the average spin-state splitting error becomes 19.3 kcal/mol, in comparison to the range of 8–38.5 kcal/mol for DFT methods (see SI.xlsx, Table S5). Given that standard DFTB3 has a MAE of 32.0 kcal/mol, it is clear that the +U model leads to a significant improvement in the description of the spin state splitting. Finally, it should be noted that the notion of MAE used in this section is not optimal, since we have only two values, the error for Ni(II) and the error for the Ni(III) ion. Since we need the functional with the lowest error for Ni(II) and Ni(III), together, the MAE was used for our general discussion. We will just mention that GGAs have much larger errors for Ni(II), hybrids for Ni(III), while meta-GGAs can show any behaviour; the detailed errors are included in the SI.xlsx.

III.2. Electronic structure of molecular systems: Ni(II)/Ni(III) compounds

Choice of Ni(II) and Ni(III) coordination compounds

To examine the impact of the +U term on the electronic structure of molecular compounds, 85 Ni(II) and 69 Ni(III) compounds have been examined (for details, see SI.xlsx). These include small molecule ligands coordinated using O, C, N, P and S heteroatoms (H₂O, OH⁻, NH₃, NH₂⁻, en, AcO⁻, CN⁻, NC⁻, NCS, CO, PH₃, PH₂⁻, SH₂ and SH⁻) with varying coordination numbers (CN=1–6). The structures were taken from our previous work⁵⁰ and were optimized at the PBE/TZP level of theory. We performed single point DFTB3+U energy calculations at the corresponding PBE geometries, which were optimized for each spin state; the same procedure was utilized for various DFT functionals. This choice was made since the centre of the attention in this work revolves around capturing the energetics and the correct electron distribution around the transition metal site rather than the geometry. As discussed in the introduction, DFTB and other approaches (see e.g. Refs. 52, 53) already perform quite adequately for structures and we would like to remove this degree of freedom as a source of error when determining purely electronic properties. A comparison between the geometries of DFTB3+U and DFT is provided in the SI, showing that DFTB3+U has similar performance as DFTB3, despite the fact that most parameters for the DFTB3+U model in this work were optimized previously for the DFTB3 Hamiltonian. Finally, due to the small size of the model ligands, we do not include empirical dispersion when comparing DFTB3(+U) and DFT results. This is supported by the observation that reoptimizing the structures at the PBE+D3 level lead to only small changes in structure and energetics; for example, the impact on the spin-state splitting has a root-mean-square value of 0.48 kcal/mol among all the model compounds studied (see SI). In realistic applications to systems that include large ligands, we expect that including empirical dispersion in DFTB3(+U) is important.

Before discussing the results, we note that the spin states in Ni(II) with most stable and most abundant coordination environments are not always straightforward to compare since they involve different coordination numbers, or, at least, completely different arrangements around the central metal ion. For Ni(III), which has d⁷ occupation, there is very high metal oxidative power (low energy empty orbitals), resulting in very few known complexes in the CCDC crystal structure database. Despite all these complications, the list of small molecule systems is useful for testing the performance of the DFTB3+U Hamiltonian in comparison to the original DFTB3 approach that does not explicitly treat d-d interactions at the orbital level.

Regarding the choice of F⁰/F²/F⁴ parameters, a thorough examination of the influence of F²/F⁴ parameters (with the fixed F²/F⁴ ratio) indicates only a small effect on the overall MAE, while F⁰ has a substantially larger impact. This is in accordance with their relative magnitude^9,58 and the portion of e-e interaction that is taken into account by F⁰ vs. F²/F⁴ parameters. Therefore, we use a fixed ratio of F²/F⁴, as often done in the literature. The highest values (in Hartree) that do not lead to SCF problems have been selected: F⁰=0.035, F²=0.01 and F⁴/F² = 0.625. To minimize SCF convergence issues, all calculations have been done with an electronic temperature of 2000K; results with a lower electronic temperature, wherever available, are also included in the SI.

The effect of +U on d-orbital population and spin density

The first set of properties that should be examined includes the d-shell occupation, the total number of d electrons and the number of unpaired d electrons. As seen from Table 1, in an octahedral environment, Ni(II) is expected to have the d⁸ configuration with 2 unpaired electrons in the high spin (HS) and no unpaired electrons (S=0) in the low spin (LS) state. In the case of Ni(III), in the same octahedral environment, 3 unpaired electrons are expected in the HS state and 1 in the LS state.

Table 1.

$d^n$ configuration ${(d}_{\alpha }^{occ}+d_{\beta }^{occ})$ and number of unpaired electrons in d-shell $(d_{\alpha }^{occ}-d_{\beta }^{occ})$ obtained by Mulliken population analysis for DFTB3, DFTB3+U (F⁰=0.035) and OPBE, together with atomic values. ^a

number of electrons in d-shell
	${\mathit{d}}^{\mathit{n}}={\mathit{d}}_{\mathit{\alpha }}^{\mathit{o}\mathit{c}\mathit{c}}+{\mathit{d}}_{\mathit{\beta }}^{\mathit{o}\mathit{c}\mathit{c}}$				$\mathit{u}\mathit{n}\mathit{p}\mathit{a}\mathit{i}\mathit{r}\mathit{e}\mathit{d}\mathit{e}\mathit{l}\mathit{e}\mathit{c}.={\mathit{d}}_{\mathit{\alpha }}^{\mathit{o}\mathit{c}\mathit{c}}-{\mathit{d}}_{\mathit{\beta }}^{\mathit{o}\mathit{c}\mathit{c}}$
	Ni(II)		Ni(III)		Ni(II)		Ni(III)
	HS	LS	HS	LS	HS	LS	HS	LS
atomic values	d8	d8	d7	d7	2	0	3	1
DFTB3	d8.9	d9.0	d8.7	d8.8	1.0	0	1.2	0.4
xTB	d8.6	d8.7	d8.4	d8.4	1.3	0	1.6	0.6
DFTB3+U	d7.8	d8.0	d7.5	d7.7	1.7	0	2.2	0.9
OPBE	d8.3	d8.5	d8.2	d8.2	1.3	0	1.5	0.8

^aThe values are averages for all Ni(II) and Ni(III) compounds studied here; for individual molecules, see SI (Tables S1, S2). Mulliken population analysis is used for all methods.

With the original DFTB3 Hamiltonian and Mulliken population analysis, the population of the d-shell is overestimated while the degree of spin polarization (the number of unpaired d electrons) is underestimated. For both Ni(II) and Ni(III), the d shell population is close to 9.0, and the spin polarization is underestimated by ~1 for Ni(II) and ~1.8/0.6 for HS/LS Ni(III). With the xTB model, which treats the d-shell in a similar fashion as DFTB3, the deviations from the expected values are smaller in magnitude yet still significant; for example, for Ni(III), the d shell population is ~8.4 rather than 7, and the spin polarization is underestimated by ~1.4 and 0.4 for the high spin and low spin states, respectively. In fact, these values are close to those observed for the OPBE functional (for results for other functionals, see SI.xlsx, Table S3 and Table S4).

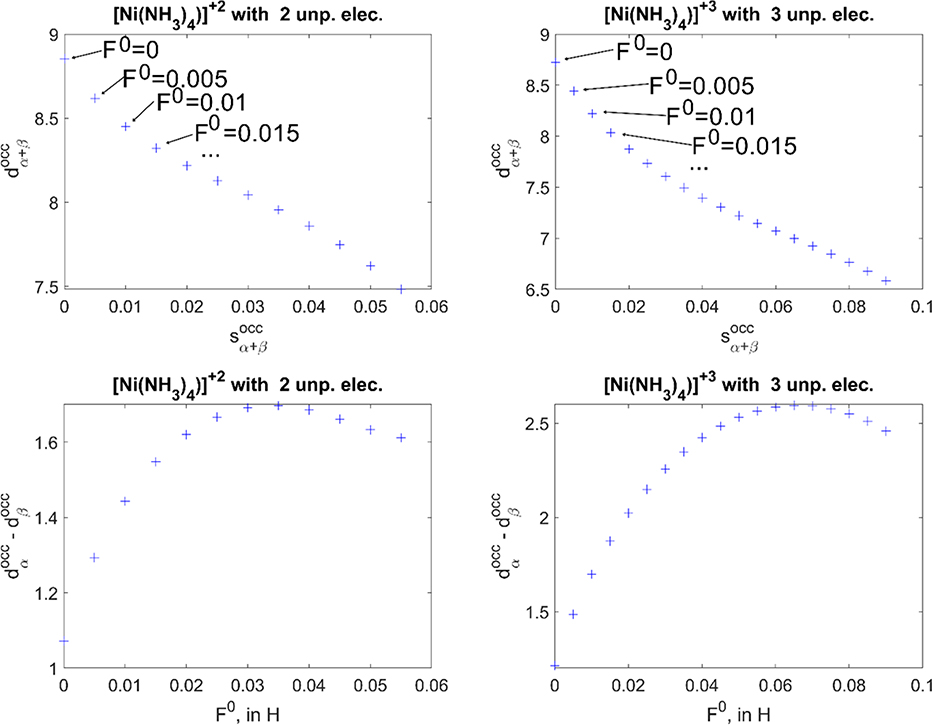
With the DFTB3+U Hamiltonian and a F⁰ value of 0.035 Hartree, the results represent a major improvement: both the overall population of the d-shell and the spin polarization are closer to the expected values compared to DFTB3, xTB or OPBE (see Table 1). To better illustrate the impact of the +U contribution, we monitor the populations of the metal d/s shells as functions of the F⁰ parameter, holding F²/F⁴ fixed. After examining all the systems, for both oxidation and spin states, we confirm that the total d-population generally decreases as F⁰ increases, due to a combination of increased s occupancy and larger charge transfers to the ligands. For the example of the HS state of [Ni(NH₃)₄]²⁺ in Figure 2 b, for example, the d/s-populations are ~8.85/0.61 for DFTB3, and they change to ~7.96/0.67 for F⁰=0.035 Hartree, and to ~7.62/0.79 for F⁰=0.050 Hartree. This general trend is expected, as increased d-d repulsions lead to delocalization of the d electrons to both the metal s orbital and ligand orbitals. Since F^0/2/4 parameters also contribute to exchange interactions, d-spin population generally increases with F⁰, until reaching a maximum and then decreases (see the examples for the HS state of [Ni(NH₃)₄]^2+/3+ in a); the value of F⁰ that corresponds to the maximum in the d-spin population varies significantly among the different systems.

Figure 2.

Population redistribution between the d and s shells, on Ni centre (with increasing F⁰ for every subsequent point) for HS state of [Ni(NH₃)₄]^2+/3+and change of spin density on d-shell with F⁰

MOs contours and ligand field splitting

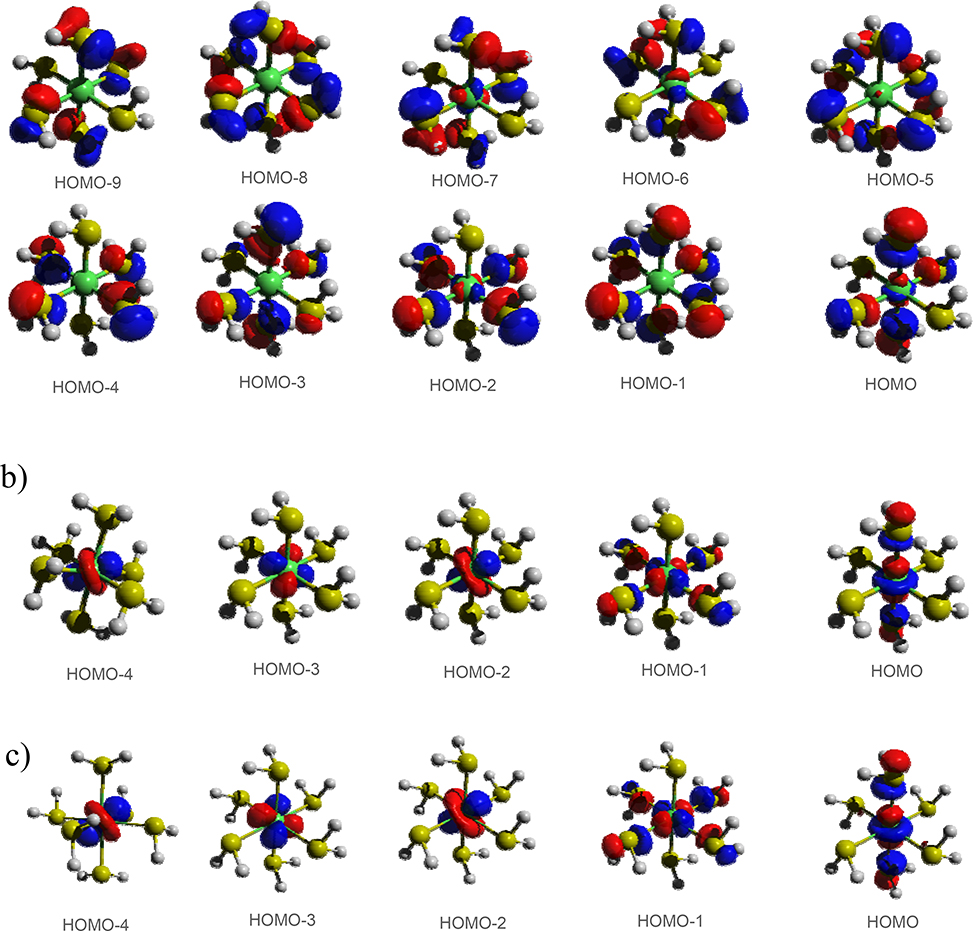
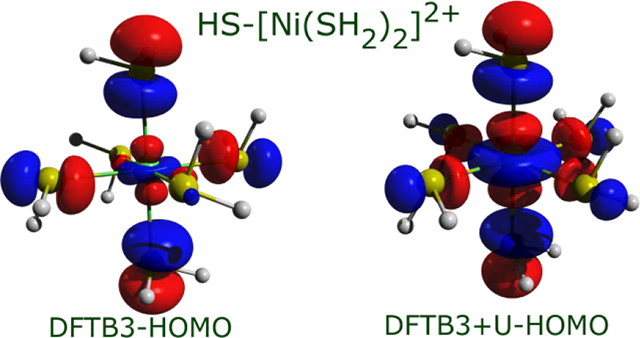
An important aspect of transition metal electronic structure is the localized molecular orbitals (MOs) with dominant d-characters, which are responsible for the peculiar reactivity, optical and magnetic properties of coordination compounds. In the previous paper,⁵⁰ we have shown that reasonable orbitals and somewhat larger ligand field splittings (LFS) were obtained for Ni(II) octahedral complexes at DFTB3/3OB level of theory. In this work, we have also analysed the +3 oxidation state, and, the low spin state. It turns out that qualitatively expected shape of MOs can be obtained with DFTB3 only for rare cases. The example of HS-[Ni(SH₂)₆]²⁺ is given in Figure 3a, which shows that the frontier MOs are largely localized to the ligands. As shown in Figure 3b, the +U Hamiltonian corrects this behaviour and produces the five metal d-orbitals as frontier orbitals.

Figure 3.

An illustration of frontier MOs (isovalue 0.05 a.u.) in HS-[Ni(SH₂)₆]²⁺, with a) DFTB3, b) DFTB3+U (F⁰=0.035 Hartree) and c) DFT-OPBE.

Regarding LFS, it is not straightforward to extract even from (unrestricted) DFT calculations: highest MOs in α-spin usually do not have significant d-contribution and orbitals in β-spin include virtual ones, making the energy predictions difficult, and specialized procedures are often used for estimating LFS.⁷⁷

Since experimental data for simple octahedral complexes of Ni(III) are not available, we use the [Ni(H₂O)₆]²⁺ and [Ni(NH₃)₆]²⁺ as examples. As shown in Table 2, DFTB3+U significantly improves the LFS and shows even better performance than OPBE. Experimental results, obtained by fitting the experimental spectra to a LF model, give Δ_o (10Dq) to be 1.05eV and 1.34 eV for these complexes, respectively.⁷⁸ Using orbitals in β-spin from the OPBE calculations, values almost twice as the experimental ones are obtained; the same holds for DFTB3. With DFTB3+U, we observe a monotonic decrease in splitting with increasing F⁰; with F⁰=0.035, the estimated LFS values are 1.24 eV for [Ni(H₂O)₆]²⁺ and 1.38 eV for [Ni(NH₃)₆]²⁺, which are in very good agreement with experimental data.

Table 2.

Ligand Field Splitting (LFS) for two octahedral Ni(II) complexes. All energies are given in eV.

Source	OPBE	DFTB3	DFTB3+U	Experiment70
Δo(10Dq) for [Ni(H2O)6]2+	1.98	1.50	1.24	1.05
Δo(10Dq) for [Ni(NH3)6]2+	2.32	2.70	1.38	1.34

III.3. Spin State Splitting for Ni(II)/Ni(III) compounds

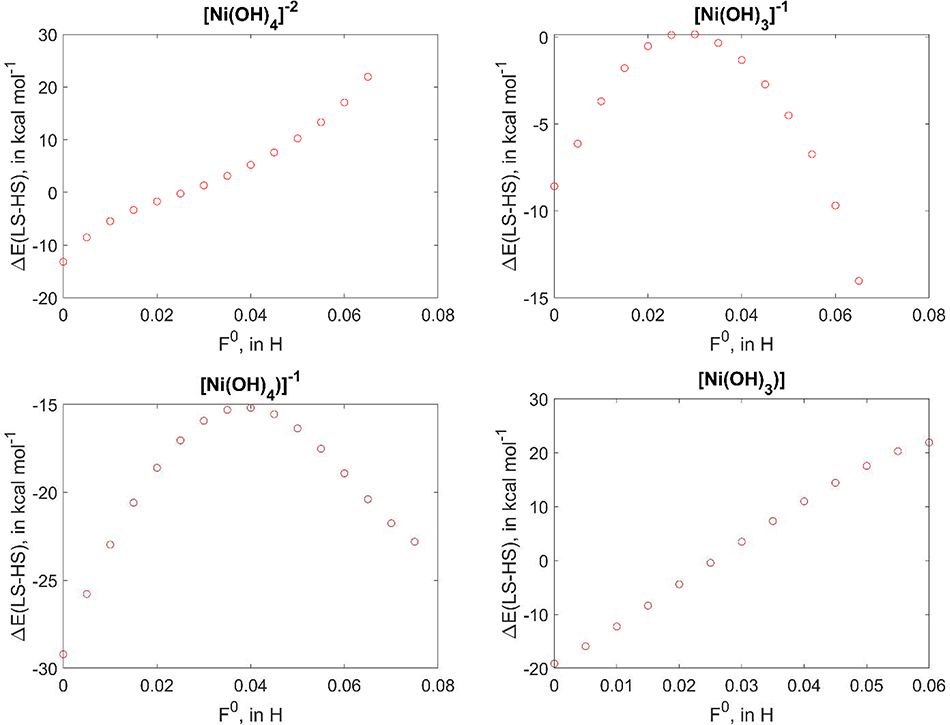
Before discussing the errors in spin splitting, we note that computed ΔE_LS-HS with DFTB3+U often exhibits non-monotonic dependence on the F⁰ value; the ΔE_LS-HS vs F⁰ dependence for all the examined systems is summarized in SI.xlsx, Table S6 and Table S7. As illustrations, representative DFTB3+U computed ΔE_LS-HS results for Ni(II)/Ni(III) compounds with OH⁻ ligands are shown in Figure 4. While [Ni(OH)₄]^2- and [Ni(OH)₃] exhibit a linear dependence on F⁰, other compounds show clear non-monotonic behaviours between ΔE_LS-HS and F⁰. In general, although total energies of different spin states show a linear dependence on F⁰, small deviations from linearity are sufficient to make a large impact on their difference since ΔE_LS-HS are several orders of magnitude smaller than the total energies of both spin states.

Figure 4.

Dependence of ΔE_LS-HS of F⁰ electron repulsion parameter; monotonic, almost linear dependence for [Ni(OH)₄]^2- and [Ni(OH)₃] and plot with non-monotonic regions for [Ni(OH)₃]⁻ and [Ni(OH)₄]⁻.

Table 3 and Table 4 summarize the Mean Absolute Errors (MAE) for all Ni complexes with tight binding-based and DFT methods, respectively (for specific systems see SI.xlsx, Table S6, Table S7, Table S10, Table S11, Table S12 and Table S13). All errors are calculated relative to the OPBE functional, which has been shown to be fairly accurate for spin state energetics.^79–81

Table 3.

Variation of MAE in spin-state splitting (ΔE_LS-HS, in kcal/mol) as the F⁰ parameter (in Hartree) increases in DFTB3+U; also shown is the MAE for xTB. ^a

M	F0	0	0.005	0.01	0.015	0.02	0.025	0.03	0.035	0.04	0.045	0.05	xTB
Ni(II)	MAE	21.8	19.9	18.4	15.8	14.6	14.2	13.9	13.8	14.0	14.9	16.8	18.7
Ni(III)	MAE	17.3	16.6	15.5	13.9	12.7	11.5	9.9	9.0	8.6	8.9	9.4	19.6

^a.The reference value is OPBE/TZP.

Table 4.

Variation of MAE in spin-state splitting (ΔE_LS-HS, in kcal/mol) for various DFT functionals.^a

	M	GGA	metaGGA		HYBRID					metaHYBRID
			TPSS	M06-L	B3LYP	PBE0	X3LYP	B1LYP	B3LYP*	TPSSH	M06
MAE	Ni(II)	1.1–2.0	1.6	6.9	15.2	8.5	7.0	8.9	4.0	4.6	3.8
	Ni(III)	1.4–2.9	2.6	4.1	5.1	5.5	4.8	5.8	3.1	3.5	4.7

^a.The reference value is OPBE/TZP.

For Ni(II) complexes, the MAE of 21.8 kcal/mol for DFTB3 is reduced to 13.8 kcal/mol for DFTB3+U with F⁰=0.035 Hartree. For Ni(III) systems, the corresponding MAE values are 17.3 kcal/mol and 9.0 kcal/mol, respectively, again supporting the value of the +U contribution. In general, the errors for Ni(III) are smaller than for Ni(II) systems; this is to be expected considering the problems with ligand dissociation and complicated LS state with Ni(II). This provides optimism that results for other transition metal ions, which have simpler spin states (than Ni(II)) and better separated metal d-orbitals (than Ni(III)), will be more satisfactory with DFTB3+U. Compared to the DFTB3 methods, the xTB approach gives spin splittings closer to the original DFTB3; this is expected due to the similar approximations for treating the d-d interactions in these methods.

To put the errors of the tight binding methods in perspective, Table 4 presents MAE for various DFT functionals. All GGA functionals have small errors, which is not surprising since we used a GGA level of theory (OPBE) as the reference. It is interesting to note that B3LYP has a similar level of MAE as DFTB3+U. We note that care needs to be exercised when interpreting these errors. Spin-state splittings in transition metal compounds are difficult to treat properly with any computational method, as post-Hartree-Fock methods strongly depend on the choice of active space, and DFT methods suffer from the unclear choice of the exchange-correlation functionals.¹⁴ With electronic spectroscopy of transition metal ions, it is often necessary to calculate the spin forbidden bands (vertical spin state energy difference). It is accepted that transitions with errors up to 2–3000cm⁻¹ (8.5kcal/mol) are considered acceptable, even with the most sophisticated post-HF ab initio methods.82

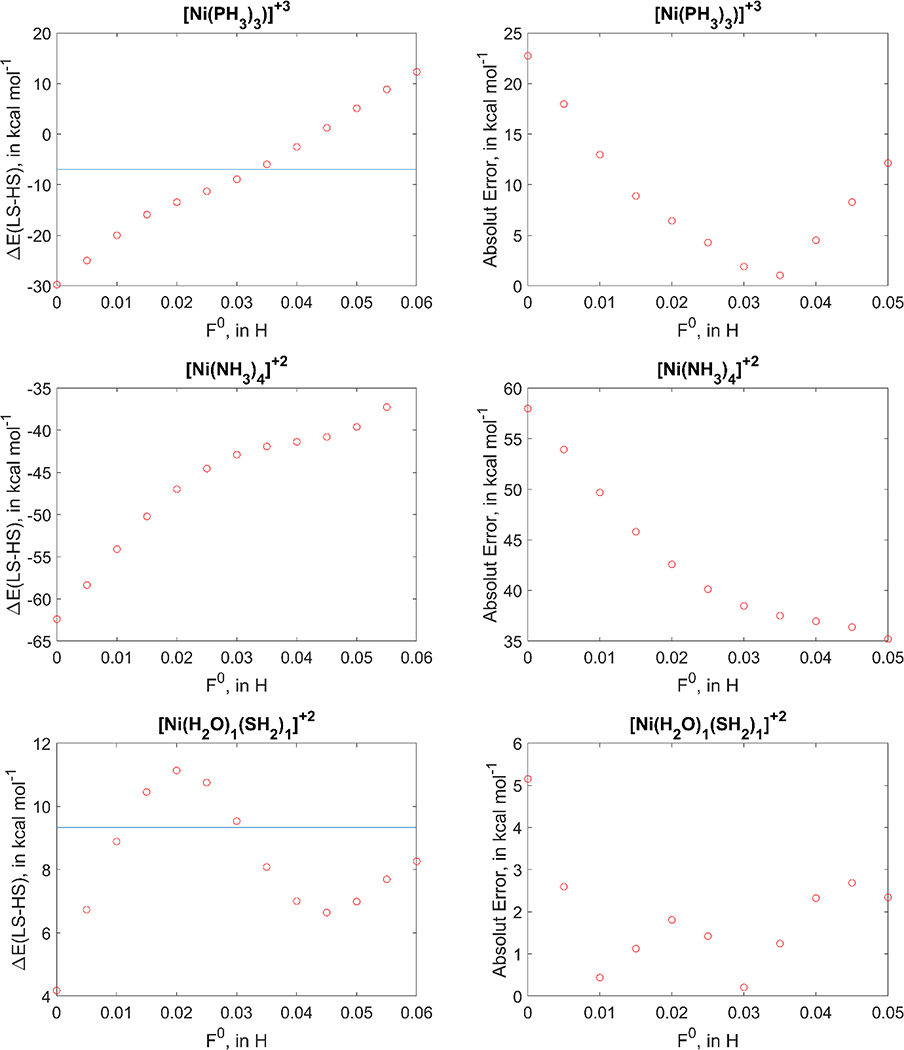
Attempts to search for simple rationalizations of trends based on, for example, ligand type and polarizability, π-donors and π-acceptors, coordination number, do not lead to any straightforward explanation for the error trends in spin splitting. Furthermore, the non-monotonic behaviour of spin splitting with respect to F⁰ (Figure 4) is not easily connected with changes in the electronic structure or orbital occupations (as is with atomic systems). Therefore, we illustrate the distinct error vs F⁰ trends using three examples: [Ni(PH₃)₃]³⁺, [Ni(NH₃)₄]²⁺ and [Ni(H₂O)(SH₂)]²⁺. These complexes cover cases with large, medium and small DFTB3 errors, as well as monotonic and non-monotonic ΔE_LS-HS vs F⁰ dependence.

For [Ni(PH₃)₃]³⁺, the DFTB3 error is ~23 kcal/mol; with F⁰=0.035 in DFTB3+U, the error is reduced to only 1 kcal/mol. From Figure 5, we observe that ΔE_LS-HS depends largely linearly on F⁰, with decreasing errors until the point F⁰=0.035 is reached (the closest point to the OPBE value, horizontal blue line); the error then enlarges as F⁰ increases.

Figure 5.

Dependence of ΔE_LS-HS (left side) and absolute error relative to OPBE (right side) on the F⁰ electron repulsion parameter in DFTB3+U for [Ni(PH₃)₃]³⁺, [Ni(NH₃)₄]²⁺ and [Ni(H₂O)(SH₂)]²⁺.

For [Ni(NH₃)₄]²⁺, the DFTB3 error is 58 kcal/mol, and it remains significant (38 kcal/mol) for DFTB3+U with F⁰=0.035. Finally, [Ni(H₂O)(SH₂)]²⁺ does not show a monotonic ΔE_LS-HS vs F⁰ behaviour, resulting in irregular relations of error vs F⁰; the magnitude of error, however, is modest for all F⁰ values.

In short, we observe that for systems with medium DFTB3 errors (10–15 kcal/mol), the DFTB3+U model can significantly reduce the error in spin splitting; the ones with too high DFTB3 errors (50–60 kcal/mol), the +U contribution leaves still significant (30–40 kcal/mol) errors even with a reasonable F⁰ value; and finally, there are ~10% of systems with modest and comparable DFTB3/DFTB3+U errors.

Conclusions

To enable extensive sampling of transition metal containing systems, such as metalloenzymes, it is valuable to develop semi-empirical QM methods. This, however, has remained a major challenge in the area of quantum chemistry for many decades. Motivated by the success of ligand field theory and DFT+U models, we have implemented a DFTB3+U approach to treat the d-d/f-f interactions and tested it using a series of nickel compounds. This should be considered as a proof of concept study as we have used the 3OB set of parameters developed with the original DFTB3 Hamiltonian; moreover, the parameters in the +U contribution (F^0/2/4 parameters) are considered empirical since the averaged d-d interactions in the original DFTB3 model have not been excluded. Nevertheless, we see that the DFTB3+U model provides substantial improvements over the original DFTB3 model for a number of properties of the nickel compounds, including the population and spin polarization of the d-shell, nature of the frontier orbitals, ligand field splitting and the energy different between low and high spin states. For some of the properties, the DFTB3+U model can give results that are competitive with some of the best DFT results. On the other hand, there are also cases where the errors at the DFTB3 level are so large (e.g., for the spin splitting) that with a +U model, the magnitude of error remains significant.

The results obtained so far suggest that it is worthwhile further developing the DFTB3+U model by reparameterizing the DFTB3 electronic parameters together with the +U parameters. In particular, the valence basis set and spin-spin coupling parameters should be optimized in the framework of the +U model, with the double-counting d-d/f-f interactions properly excluded. Considering that Ni(II) and Ni(III) represent challenging cases for spin splittings, we anticipate that the DFTB3+U model will lead to more favorable results for other transition metal ions important in biology, such as Mn(II) and Co(II). Finally, we note that while the +U term is entirely an on-site contribution, it can have an impact on the molecular structure indirectly by perturbing the nature of metal-ligand interactions, such as the degree of charge transfer between metal and ligands. Therefore, with further parameterization, the DFTB3+U can potentially provide improved description of structural and energetic properties of transition metal containing complexes over existing semi-empirical QM methods and become a useful tool for efficiently exploring reactive processes involving transition metals in the condensed phase. The methodology can also be integrated with other approximate QM methods such as the extended tight binding approach, which already appears to provide rather reliable structures and frequencies for many transition metal systems.