ABSTRACT
This paper presents the design and analysis of a newly proposed form of care delivery called an integrated practice unit (IPU) in which a multi-disciplinary team of providers and staff work together to cover the full care cycle for a given condition. In an IPU, the different providers circulate among the patients, according to the need for their expertise, while patients remain in a single location once they check-in. From the patient’s perspective, the benefits of such an arrangement should be self-evident. For payers and providers there will also be benefits as the fee-for-service market gives way to structured payments for each episode of care. Before setting up an IPU, it is necessary to gain an understanding of how available resources will limit patient flow and system performance. Treating resources such as providers, imaging equipment, and rooms parametrically, the primary goal of our work is to determine the number of patients that can be seen per day in an IPU while trying to constrain overtime, length of stay, and waiting time to best practice targets. Discrete-event simulation serves as our analytic tool.
While we are involved in the design of a comprehensive suite of musculoskeletal IPUs, we illustrate our approach with an extensive computational study of one: a Lower Extremity Joint Pain IPU. Using the simulation methodology, we are not only able to determine the number of patients that can be scheduled for an in-clinic visit each day, but also the daily number of follow-up patients that can be served virtually through telemedicine with no additional resources and minimal impact on IPU performance. These results assisted the Department of Surgery at the Dell Medical School at The University of Texas in the optimal design of its first IPU, which opened in the fall of 2017.
KEYWORDS: Outpatient clinic, integrated practice unit, patient scheduling, simulation, patient-centred care, virtual medicine
1. Introduction
As the focus of healthcare shifts from how much “doctoring” is provided to maximising value and patient health, many aspects of current delivery models will change. The concept of an Integrated practice unit (IPU) – a co-located, multi-disciplinary team of providers who treat the full care cycle (Koenig, Keswani, & Bozic, 2016; Porter, 2010) – has been suggested as a patient-centred approach to the management of chronic illnesses such as osteoarthritis, cardiomyopathy, and diabetes. To successfully implement a model that places the patient at the centre of the process, a new paradigm for scheduling and resource utilisation of outpatient services must be developed. In an IPU, the providers move around the patient rather than the patient moving to and from the providers. The beauty of this system is the “built-in” nature of communication between different providers and disciplines, which should yield untold efficiencies compared to the siloed, fragmented current state. The problem is how to operationalise the complex interaction between the parties efficiently while achieving a favourable patient experience. Speedy throughput is a key performance measure for outpatient practices. Surveys have shown that waiting time is one of the top differentiators for “best practice” facilities, so reducing delays can offer a competitive advantage when patients have a choice (Cartwright & Windsor, 1993; McCarthy, McGee, & O’Boyle, 2000).
As envisioned, IPUs should lead to improved patient outcomes, more efficient use of patient time, and better use of resources, which translates into more providers working at the “top of their license”. They also have the potential to align with new reimbursement schemes (e.g., bundled payments based on condition) and information systems aimed at data sharing and coordination across multiple services (Koenig & Bozic, 2015; Koenig et al., 2016). These concepts have self-evident value in light of the current economic climate in which market changes are driving care delivery systems towards value-based models. Nevertheless, without more sophisticated management tools, the increased complexity of operating an IPU has the potential to elevate healthcare delivery costs and decrease the value achieved when compared to traditional outpatient clinics.
Several institutions, including MD Anderson Cancer Center in Houston and Virginia Mason Medical Center in Seattle (Porter & Lee, 2013, October), along with The Dell Medical School (DMS) at the University of Texas at Austin, have begun trials with co-located, multi-disciplinary teams to treat a variety of conditions. One of the purposes of this paper is to describe the methods and analysis used to help set up a cluster of musculoskeletal IPUs at the DMS. Our presentation concentrates on the Lower Extremity Joint Pain IPU (or simply, Joint Pain IPU), but we have conducted similar studies to date for Upper Extremity, Back Pain, Fracture Care, Sports Injury, and Work Life IPUs using the same approach. As a result of this experience, we believe that the methodology is generalisable to all such multi-provider clinics as well as to a range of other venues such as home health where home-bound patients must be seen by several specialists in a day.
The work was done over 10-month period and was primarily aimed at determining the number of patients that can be seen in-clinic during an 8-hour working day as a function of patient mix, the numbers and types of providers and support staff available, and the number of exam rooms in the facility. An additional objective was to estimate the number of virtual medicine (VM) patients that can be accommodated by the schedule. Although patient outcomes are the primary means by which a healthcare system is evaluated, there is often a trade-off between outcomes and costs. To address managerial concerns, it was necessary to consider more detailed metrics at the operational level including patient length of stay, resource utilisation, provider idle time, and IPU closing time. In systems like this where uncertainty abounds, we found that maximising performance could only be achieved by tightly coordinating provider and patient flow.
In generic terms, an IPU can be viewed as an extended combination of a flexible flow shop and an open shop (Pinedo, 2016), where different types of patients (jobs) arrive, perhaps according to a given schedule, and require individualised levels of service from a subset of providers (machines) but not necessarily in a given order. Extensions include the need for additional resources as well as constraints on system performance measures like maximum length of stay and makespan. In practice, patients in an IPU are stationary and the providers move from one to another, but from a modelling point of view this detail is inconsequential. Which providers see which patients during their visit, depends on the patient’s medical condition, its severity, and whether the visit is the first for a particular patient or a follow-up. Leeftink, Bikker, Vliegen, and Boucherie (2018) provide a thorough review of the health care multi-disciplinary planning literature. According to their classification scheme, the IPUs we consider are flexible mixed-shop (i.e., combination of flow and open shops) systems with multiple appointments for each patient scheduled on a single day. The stochastic elements include arrivals, appointment durations, and care pathways. Since we use the results for clinic design, the scheduling problem is offline.
What complicates the modelling of an IPU compared to a flexible flow shop is the fact that some resources like surgeons and physical therapists must be scheduled in sequence, while others, such as rooms and translators, must be scheduled concurrently. In addition, the order in which patients see some of the providers is not fixed. When arrival and service time uncertainties are taken into account, optimisation formulations for determining patient and resource flows become intractable. Solutions to exact models are limited to only a handful of patients and providers, even without the additional complications (e.g., see Anand & Panneerselvam, 2015). As an alternative, we have built a discrete-event simulation model in Simio (www.simio.com) that has allowed us to capture all of the critical components of a generic IPU along with the system-level uncertainties. Simulation has long been used to investigate policies and procedures in healthcare delivery (e.g., see Braly, 1995), and offers many modelling advantages over mathematical programming. While it is straightforward to account for room availability in a simulation model, for example, we are unaware of any equivalent open shop or job shop models that include the equivalent of this restriction.
The primary contributions of this research centre on the introduction of a prototypical IPU and the analysis that accompanied its implementation. Specifically,
We define an IPU and develop a generic simulation model that can serve as a blueprint for a variety of musculoskeletal conditions including lower and upper extremity joint pain, back pain, fracture care, sports injuries, and foot care.
We determine the maximum number of patients that can be treated each day in the Joint Pain IPU at DMS along with performance metrics for a given set of resources.
We also determine the daily number of follow-up patients that can be treated virtually via telemedicine by the Joint Pain IPU providers with no additional resources and without sacrificing clinic performance.
We develop near-optimal patient appointment schedules and provider assignments as a function of resource availability through the use of simulation and designed experiments.
We quantify the benefit of scheduling patients with smaller processing time means or variances first.
We provide managerial insights into provider and resource utilisation, the effectiveness of various scheduling schemes, and other measures of system performance.
To be sure, a multi-disciplinary approach to diagnosis and treatment has been relatively common for certain conditions for decades. There are two main factors, however, that distinguish an IPU from a more general multi-disciplinary clinic. The first is that the usual “multi-disciplinary care” model involves moving patients around a circle of appointments with individual clinicians not all necessarily in the same location. This can provide a wide range of perspectives and can sometimes foster conversations between the disciplines, but the interdisciplinary approach is not “built in” to each patient visit. It is probably more efficient on a “per provider” basis but does not foster the interdisciplinary approach in the same way as an IPU. Our model does not pre-suppose which providers will be needed for a given patient, but rather allows us to customise each visit on an as needed basis. The second difference is that many multi-disciplinary teams are not set up to purposefully manage the full care cycle of a condition from mild to severe. They are usually focused on a certain episode within the cycle (often the most severe stage, such as the need for surgery or transplant). An IPU is designed to efficiently manage all aspects of a condition.
In the next section, we review the relevant literature on patient scheduling, multi-disciplinary clinics, and the use of simulation in healthcare delivery. In Section 3, we summarise the design approach to musculoskeletal IPUs and highlight some of their perceived benefits. This is followed in Section 4 by a discussion of patient and provider flow in an IPU and a description of our simulation model. The analysis of the Joint Pain IPU is contained in Section 5 along with the experimental design. We end in Section 6 with a series of observations obtained from the research and some suggestions for future work.
2. Literature review
In the fee-for-service environment, scheduling and capacity management models have largely focused on a single clinic or service. This is true both in practice and in the academic literature (Berg & Denton, 2012; Chakraborty, Muthuraman, & Lawley., 2013; Gupta & Denton, 2008; Millhiser, Veral, & Valenti, 2012). A property of many healthcare systems is heavy congestion that can lead to excessive delays or even bring flow to a halt (Jenkins & Gisler, 2012). In part, this is due insufficient attention paid to patient flow issues but also to the financial structure of healthcare (Savin, 2006). For appointment scheduling systems, the goal is to balance patient waiting time, provider idle time, and overtime, but the emphasis more often than not, is on the latter two components. Highly congested queueing systems, like an emergency centre or ambulatory clinic, may find themselves in a perpetual state of dysfunctional equilibrium, which degrades their ability to deliver quality care. Crowding in waiting rooms and treatment areas, loss in privacy, delays in accessing needed equipment, and delays in providing medication can all add to patient anxiety and suffering. In addition, the need to shuttle patients in and out of treatment rooms as they wait for test results or resources reduces everyone’s productivity.
Due to arrival time and service time variation, patients often end up waiting despite the fact that they have reserved time slots. Moreover, it is common practice at many outpatient clinics to overbook the day, in part, to ensure that patients are always available to see their provider (Noon et al. 2003). Many related issues are presented by Gupta and Denton (2008) who give an overview of common rules for constructing schedules and responding to disruptions in real time.
2.1. Use of simulation and optimisation for patient flow analysis
The use of simulation to analyse and improve healthcare delivery has a long history, especially in efforts to reduce patient waiting times and length of stay (e.g., see Braly, 1995). In an early study, Klassen and Rohleder (1996) used discrete-event simulation to address the problem of how to schedule patients as they call for appointments, absent of an accounting for future requests. Their main goal was to compare various scheduling rules aimed at minimising a combination of patient waiting time and provider idle time. Swisher, Jacobson, Jun, and Balci (2001) were one of the first to build a model using an object-oriented simulation package with graphical capabilities. They studied a family practice facility with the goal of maximising a combination of clinic profit, and patient and staff satisfaction. Results were based on a fractional factorial design that included the number of mid-level practitioners, the number of nurses, the number of medical assistants, the number of check-in rooms, the number of examination rooms, and the number of specialty rooms.
Applying a combination of simulation and optimisation, Woodall, Gosselin, Boswell, Murr, and Denton (2013) investigated patient flow at the Duke Cancer Institute. They first developed a discrete-event simulation model (in Arena) to predict patient waiting times and resource utilisation across various parts of the centre, and showed that nurse unavailability during oncology treatment caused a serious bottleneck. Next, they developed a mixed-integer programming model to relieve the bottleneck by optimising the weekly and monthly schedules of the different types of nurses. Gartner and Kolisch (2014) looked at the problem of planning elective surgeries at a hospital under constrained resources with the objective of maximising the contribution margin. As in our case, it was necessary for them to schedule patients around multiple resources. Their first step was to define a set of the most prevalent care pathways to assess provider, staff, equipment, and laboratory needs for each patient type. They then developed two integer programming models to determine when patients should be scheduled for surgery over the planning horizon. Oh, Muriel, Balasubramanian, Atkinson, and Ptaszkiewicz (2013) investigated a less complex problem in which both provider and staff needs were considered when scheduling patients in a primary care environment. Both acute and chronic cases where included in the analysis, as well as the uncertain time spent with each resource. Their objective was to minimise a weighted measure of provider idle time and patient wait time. Key model features included an empirically based classification scheme to accommodate different chronic and acute conditions, adequate coordination of patient time with a nurse and physician, and strategies for introducing slack in the schedule to counter the effects of variability in service times.
Morrice et al. (2014) developed a patient-centered surgical home (PCSH) based on concepts proposed by the American Society of Anesthesiologists to streamline perioperative care. A key feature of a PCSH is to have an anaesthesiology pre-operative assessment clinic (APC) serve as the system coordinator and information integrator prior to surgery. Using statistical analysis and discrete-event simulation the authors were able to demonstrate how this can be accomplished by overcoming improper triaging of patients and patient information deficiencies by ensuring that the APC sees the right patients and has the right information. In a related study conducted at a family health clinic, Bard et al. (2016) investigated changes to current scheduling rules and operating procedures with the goal of reducing length of stay, minimising overtime and queue lengths, and maximising resource utilisation. Discrete-event simulation was again used to establish a baseline and to evaluate a variety of scenarios associated with appointment scheduling and managing early and late arrivals. In part, the results indicated that by carefully adjusting appointment times, up to an 8% reduction in patient length of stay is achievable without noticeably affecting the other metrics.
Also using discrete-event simulation, Baril et al. (2014) studied the performance of a traditional outpatient orthopaedic clinic in which each orthopaedist is scheduled to see 40–50 patients per day. Their objective was to determine the relationships and interactions between patient flows, resource capacity (number of consulting rooms and number of nurses), and appointment scheduling rules. The experimental design evaluated the assignment of consulting rooms and nurses to each orthopaedist under four appointment scheduling rules and three patient flows. Testing showed that system performance, as measured by patient length of stay, provider utilisation, and average overtime, was highly dependent on adapting the scheduling rules to the different patient trajectories. For more discussion on the use of simulation to model and design healthcare systems, see Brailsford, Harper, Patel, and Pitt (2009) and Günal and Pidd (2010).
Research on job shop scheduling is mostly limited to the use of heuristics. This is not surprising since all but the simplest versions of the problem are strongly NP-hard for n jobs and m machines, even without sequence dependent setup times. The problem is a bit easier when the sequence of jobs (patients) is given but exact solutions are still out of reach. In our case, we face an open shop scheduling problem in which determining the sequence is part of the decision (Pinedo, 2016). Anand and Panneerselvam (2015) classify open shop problems by performance measure, such as makespan, weighted sum of completion times, and weighted sum of tardy (or late) jobs, and cite much of the relevant literature by category. In the vast majority of cases, metaheuristics have been used to find solutions. Simplifications of the general problem, though, have led to a few polynomial-time exact algorithms. For example, Dror (1992) studied an open shop problem with the objectives of minimising the makespan and minimising the mean flow time. For the former case with n ≥ m, he derived an optimal algorithm with complexity O(mn); however, for n < m but ≥3 he proved that the problem is NP-hard. For the case when the objective is to minimise the mean flow time, he developed an optimal algorithm with complexity O(n).
2.2. Multi-disciplinary clinics
A multi-disciplinary approach to care refers to caring for a patient through the work of multiple practitioners, and creating a consolidated plan that considers the recommendations of all team members (Horvath et al., 2010). Strasser et al. (2004) compare the performance of a new, one-stop multi-disciplinary palliative care clinic with a traditional pain and symptom management clinic run by a physician and a nurse. The former offers standardised multi-disciplinary assessment, specific care recommendations, patient and family education, and on-site counselling. The authors retrospectively showed that the multi-disciplinary approach led to significantly greater patient satisfaction and improved outcomes. Romero et al. (2013) also developed a “one-stop shop”, but for treating basal cell carcinoma. Using a deterministic model and then simulation, they observed a significant improvement in the average waiting time that a patient spends between diagnosis and treatment. Their study focused on the identification of factors that influence the average throughput time of patients from a logistic perspective. One of their goals was to provide schedules for all the clinicians for the day and to assure that each patient was seen by all indicated providers during a single visit.
Also considering the logistics of patient visits, Mutlu, Benneyan, Terrell, Jordan, and Turkcan (2015) introduced a co-availability scheduling problem that arises in various healthcare settings in which personnel from different disciplines work together as care teams. Synchronisation of their availability proved to be the most important factor in improving system performance. To coordinate treatment, they developed an integer programming model to create schedules that maximise the amount of co-available time across the scheduling templates of the desired team members, while still satisfying each of their clinic coverage requirements, preferences, and outside responsibilities. Applying the model to breast surgery at MD Anderson Cancer Center indicated that team co-availability increased by 94% over the study period without negatively affecting operating room utilisation and surgery start times.
Hyer, Wemmerlov, and Morris (2009) consider an integrated trauma centre in which multiple resources are brought to bare on the care of trauma patients. Since the centre was within a hospital, the authors refer to it as a focused hospital unit (FHU). They empirically studied the performance of the FHU using a pre- and post-analysis finding no change in the mortality rate, a moderately decrease in length of stay, and a substantial increase in the net operating margins. Beyond the pre- and post-analysis, the paper does not consider any other design or re-design issues to improve system performance.
In work similar to ours, Leeftink, Vliegen, and Hans (2017) designed blueprint schedules for multi-disciplinary appointment planning that take into account uncertainties in patient routing. The modelling and analysis centred on cancer diagnosis where each patient gets two consultations during a visit. The first is generally with a nurse practitioner who provides the diagnosis. The second is with a clinician who explains more about the proposed treatment. Stochastic integer programming was used to derive the schedules with the goal of optimising a combination of patient waiting time, clinician idle time, and clinician overtime. Solutions were found using sample average approximation. Although there is no universally accepted model of multi-disciplinary care a number of cancer centres worldwide have established multi-disciplinary clinics that aim to deliver a one-stop experience. This has been the case in particular for women with newly diagnosed breast cancer. Being able to see the appropriate specialists at the same location on the same day partially eases the anxiety that comes with the diagnosis. Some cancer centres hold treatment planning meetings that include all relevant specialists as well as the woman herself (e.g., see Horvath et al., 2010; Leeftink et al., 2018; Zorbas, Barraclough, Rainbird, Luxford, & Redman, 2003). They may also provide medical information and psychosocial support.
2.3. Capacity planning
Though a staple in manufacturing, capacity planning in healthcare organisations has mainly focused on matching supply with demand in hospital departments such as wards, critical care units, surgery suites, and emergency centres. Utley and Worthington (2012) have defined this process as determining the amount of beds, staff, consulting rooms, equipment, and other resources that is sufficient to enable an organisation to meet demand for one or more packages of care while achieving specified service standards. For a colonoscopy suite, Berg et al. (2010) showed that there is a positive linear relationship between the number of patients examined and the number of procedure rooms. Using simulation, they tested ratios of one and two rooms per physician and found that with the higher ratio, more auxiliary personnel (nurses, secretaries) are needed to improve performance. They also concluded that a better appointment schedule could increase the number of patients seen without adding resources.
Although there are few IPUs in existence and no published studies on capacity planning and scheduling, there are several hospital units that share common characteristics. For example, multiple providers treat multiple patients in emergency centres each day. Similarly, operating suites must juggle the schedules of multiple surgeons, nurses, and staff when scheduling patients and estimating capacity. Nevertheless, the analysis described in the literature on emergency centres (e.g., see Marmor, Golany, Israelit, & Mandelbaum, 2012; Sinreich and Marmor (2005) and operating suites (e.g., see; M’Hallah & Al-Roomi, 2014; Samudra et al., 2016) does not extend to configuring and scheduling IPUs.
2.4. Multiple patient types and scheduling rules
There have been numerous studies that demonstrate improved clinic performance when patients are divided into cohorts and their visits sequenced in a manner that takes these cohorts into account. Vanden Bosch and Dietz (2000), for example, considered three classes of patients based on the number of chronic complaints, each with a distinctive service time distribution. They showed in an outpatient setting that there is no easy rule that can be derived from this stratification that determines an optimal sequence; however, referring to their previous work, they indicated that if service times are exponential, the horizon is zero, and the goal is to minimise a weighted combination of the physician idle time and the sum of expected waiting times, then the optimal sequence orders patients by their service means. Because none of these conditions held in the clinic that they investigated, they proposed a simple heuristic that found the optimal sequence more than 85% of the time.
Cayirli, Veral, and Rosen (2006) worked with an ambulatory clinic in a New York metropolitan hospital that sees about 300,000 patients a year. Using discrete-event simulation, they investigated six different appointment scheduling rules and six different appointment sequencing rules with the goal of minimising a combination average waiting time, the physician’s average idle time per patient, and average overtime per patient. Patients were classified as either new or returning with a 40–60% fixed division, and with a service time ratio of 2:1. Their results showed that patient sequencing had a greater effect on system performance than the choice of an appointment rule but there was no definitively superior combination of the two. The most they could say about sequencing was that first-come, first served gave uniformly poor results, and that combining the scheduling of short-consultation patients in the beginning of the session with the 2BEG rule was one of the best performing approaches.
What is common to the clinic environment that Vanden Bosch and Dietz, Cayirli et al. and virtually all their predecessors modelled is that only the primary consultation service is considered, and then only as a single-server, single phase queueing system. In practice, outpatient clinics are multi-stage processes in which a variety of resources affect patient flow and system performance. In work closely related to ours, White, Froehle, and Klassen (2011) developed an empirically based discrete-event simulation that incorporates various common resource components and operational elements that go beyond the single provider. They examine the interactions between patient appointment policies and capacity allocation policies (i.e., the number of available examination rooms) and how they jointly affect resource utilisation, patient waiting time, and other performance measures. Data were gathered from an outpatient orthopaedic clinic with two different patient types, five registrars, two radiology technicians, and a single physician. Sixty per cent of the patients required x-rays regardless of type, but otherwise the flow was sequential through registration, chart prep, and nurse prep, ending with the physician consultation. In the study environment, available rooms proved to be the bottleneck but had no effect on physician utilisation beyond a certain threshold. As expected, when the number of rooms dropped too low, patient throughput suffered severely. Their findings also suggested that scheduling shorter, low variance appointments, usually associated with follow-up or returning patients, early in a session produced the greatest reduction in patient waiting and clinic overtime without affecting physician utilisation, given adequate facility capacity. Such a policy provided the lowest waiting time, the smallest mean clinic duration, and the highest physician utilisation, and is consistent with the single-server system studied by Cayirli et al. (2006).
Using a stochastic optimisation model, Oh et al. (2013), similarly investigated scheduling and sequencing rules for ambulatory care with the objective of minimising a weighted measure of provider idle time and patient wait time. From their preliminary work with a Massachusetts three-provider family medicine clinic, they found that service times varied significantly depending on the nature of the patient’s ailment. This led them to propose the following easy-to-apply patient classification scheme: high complexity (HC), which has the longest average service time and consists of routine physical exams, well-child check-ups, diabetes and chronic condition management; low complexity (LC), which has the shorted average service time; and urgent, same-day appointments (SD). During a visit, a patient first checks in and then is seen by a nurse and physician in that order. For testing purposes, Oh et al. examined a range of scenarios with an even mix of patients per half-day session per provider. The patient distribution was HC = 3, LC = 3, and SD = 4, and appointment slots were set at 15-minute intervals. With respect to sequencing, they found it best to follow the shortest processing time rule with respect to the provider’s average processing time and to mix patient types with the HC patients last, e.g., SD/LC/HC. This is opposed to assigning strings of identical patient types. To account for longer service times, they assigned an empty slot after the HC patients, which is equivalent to allowing 30 rather than 15 min for each of them. For all sequences examined, they also observed that it was best to double-book the first slot, which is essentially a TwoBeg schedule. A final relevant observation was that placing an HC appointment first reduced system performance by almost 50%.
The IPU that we are investigating differs substantially in resource requirements and patient flow when compared to previous research on outpatient scheduling. In particular, recall that an IPU is defined by multiple provider types, multiple providers of the same type, multiple supplementary services, and multiple pathways through the system. Additionally, previous literature considered a much higher proportion of shorter, low variance appointments usually associated with follow-up patients. For example, White et al. (2011) assume a ratio of 3:1 short-to-long appointments. Our ratio is the opposite, i.e., 1:3 follow-up (short) to new (long) appointments. Therefore, it was not at all clear that the previously reported results on patient sequencing would carry over to an IPU, so we felt obliged at least to explore the possibilities in Section 5.3.
3. Designing a musculoskeletal IPU
The effectiveness of any system designed to provide outpatient care depends heavily on how its resources are managed. Murray and Berwick (2003) offer three high-level recommendations for improving the alignment of demand and supply in a clinical setting; namely, (1) enforce continuity of care by scheduling patients only with their primary care providers, (2) increase the effectiveness of each appointment, and (3) reduce the demand for face-to-face patient-physician contact. IPUs have been conceived to achieve the latter two objectives. In the remainder of this section, we summarise the steps for designing a musculoskeletal IPU but believe that they can be similarly applied to designing IPUs for virtually all chronic conditions. For the most part, the discussion here is taken from Keswani, Koenig, and Bozic (2016).
The first step is to choose a condition or patient segment. This might sound simple but being too inclusive will dilute the team’s ability to provide focused, high-value care; in contrast, picking a condition that is too rare or narrow makes it difficult to justify the upfront investment in resources. To be successful, an IPU must lend itself to management by a multi-disciplinary team of providers (e.g., mid-level provider, orthopaedic surgeon, nutritionist, physical therapist, and social worker for a joint pain IPU). An opportunity for value improvement must also exist, which would be the case, for example, with lower extremity pain because the condition can be debilitating and the cost of care is high.
The second step is to define the team of providers and staff who will be held jointly accountable for managing the condition. This requires distinguishing between a physical IPU (i.e., co-located providers under one roof) versus a “virtual” IPU, which includes any and all services delivered throughout the cycle of care. One must also apply principles of high-value care in defining the various roles on the team. For a lower extremity joint pain IPU – the basis of this paper – all patients are evaluated and initially managed by well-trained orthopaedic mid-level providers (generally, nurse practitioners or physician’s assistants), while surgeons are available to provide clinical “backup” for complex cases, and to offer surgery to those patients who are appropriate candidates. This is an example of “downstreaming care”. Additional examples include patient-risk stratification, needs assessment prior to the visit, and shared-decision making.
The final step concerns process improvement and the identification of opportunities to add value to both the patient experience and care delivery. This includes ensuring appropriate use of diagnostic and therapeutic interventions, addressing holistic patient needs to improve overall health, reducing the use of low-value health services, and maintaining greater patient engagement through unhindered communication with the care team. For operative patients, additional benefits that are expected to accompany realignment of incentives towards value include greater opportunity to modify pre-operative risk factors, higher rates of patients discharged to their homes, fewer unplanned readmissions, and fewer reoperations (Iorio et al., 2016).
4. IPU process and model development
Patients entering an IPU will require a variety of resources including exam rooms, physicians and other providers, support staff, and equipment for medical tests and procedures. From an operational point of view, patient flow can be thought of as movement between a series of activities, each requiring a unique set of resources and consuming time. It is common to portray the collective process as a network in which nodes represent the healthcare components and arcs indicate movement between them. This is the view taken in developing our mathematical models. Figure 1 contains a process flow diagram showing the interaction of patients, providers, and information in the envisioned Joint Pain IPU.
Figure 1.
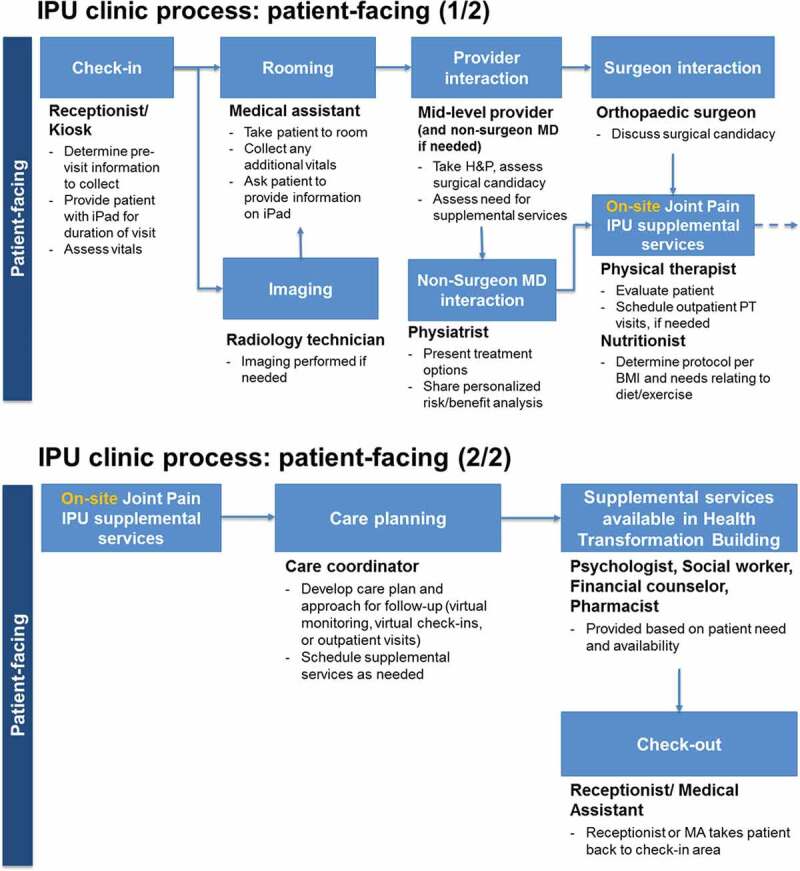
Process flow diagram of the prospective Joint Pain IPU
4.1. Simulation model
Using the information and processes indicated in Figure 1, combined with provider requirements and corresponding service times, we have implemented a discrete-event simulation model for both initial and follow-up type visits. The model is shown in Figure 2 and was built in Simio, a commercial package with a strong graphical user interface. Four different general types of patients are included (mild, moderate, and severe osteoarthritic, and surgical candidates), each with unique clinical requirements and a different pathway through a subset of providers.
Figure 2.
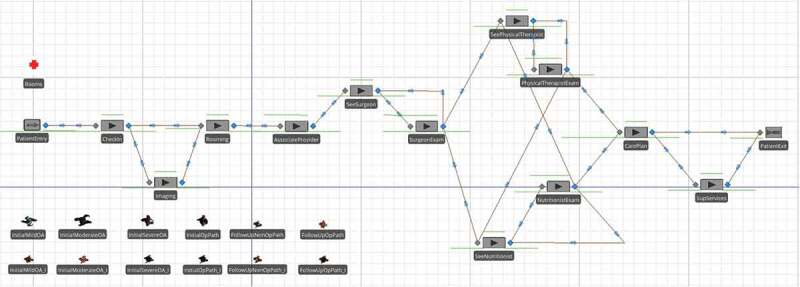
High-level simulation model of Joint Pain IP
Following the process flow given in Figure 1 (as modelled by Simio in Figure 2), when a patient enters the clinic, he or she checks in at a kiosk and is given a room assignment. If imaging is required, the patient first goes to the lab where a radiology technician takes x-rays, and then heads to the exam room. The patient occupies a room (denoted by the red cross symbol with the label “Rooms” in Figure 2) starting at the “Rooming” stage until just before exiting the IPU at the “CarePlan” stage. For those patients that need help navigating the facility, a medical technician is available. The first provider that all patients see is a nurse practitioner or physician assistant. In the IPUs at DMS, these clinicians are referred to as associate providers. The remaining providers visit each patient in accordance with the probabilities given in Table 1. These probabilities are based on estimates by the third author and other providers from the DMS Department of Surgery who had experience with the patient population at other clinics prior to the formation of the Joint Pain IPU. They represent population level estimates based on care paths for different types of patients. For example, an initial mild osteoarthritic (OA) patient has a 5% probability of requiring x-rays during the initial visit, but in all cases is seen by an associate provider at the first stage of care. Additionally, this type of patient receives follow-ups from a surgeon, physical therapist, and a nutritionist in 25%, 50%, and 40% of the cases, respectively. It is common to model patient inputs in this manner in the literature (e.g., Dobson, Tezcan, & Tilson., 2013; Lahiri & Seidmann, 2012; Saghafian, Hopp, Van Oyen, Desmond, & Kronick, 2014; Zonderland, Boer, Boucherie, de Roode, & van Kleef, 2009), even when simulation is used (Swisher et al., 2001; White et al., 2011).
Table 1.
Osteoarthritic patient probabilities for initial and follow-up visits
| Patient typea | Patient mix | Imaging | Surgeon | Physical therapist | Nutritionist | Sup servicesb |
|---|---|---|---|---|---|---|
| Initial Mild OA | 0.198 | 0.05 | 0.25 | 0.5 | 0.4 | 0.2 |
| Initial Moderate OA | 0.1935 | 0.05 | 0.5 | 0.5 | 0.4 | 0.2 |
| Initial Severe OA | 0.03375 | 0.05 | 0.9 | 0.7 | 0.4 | 0.2 |
| Initial Op Path | 0.02475 | 0.05 | 1 | 0.9 | 0.4 | 0.2 |
| Initial Mild OA (I) | 0.132 | 0.05 | 0.25 | 0.5 | 0.4 | 0.2 |
| Initial Moderate OA (I) | 0.129 | 0.05 | 0.5 | 0.5 | 0.4 | 0.2 |
| Initial Severe OA (I) | 0.0225 | 0.05 | 0.9 | 0.7 | 0.4 | 0.2 |
| Initial Op Path (I) | 0.0165 | 0.05 | 1 | 0.9 | 0.4 | 0.2 |
| Follow-up nonOp Path | 0.1125 | 0 | 0.3925 | 0.4875 | 0.378 | 0.05 |
| Follow-up Op Path | 0.0375 | 0.5 | 1 | 0.5 | 0 | 0.05 |
| Follow-up nonOp Path (I) | 0.075 | 0 | 0.3925 | 0.4875 | 0.378 | 0.05 |
| Follow-up Op Path (I) | 0.025 | 0.5 | 1 | 0.5 | 0 | 0.05 |
aPatient types with “Initial” and “Follow-up” are initial and follow-up visits, respectively, “OA” are osteoarthritic, “Op Path” are surgical candidates on an operative pathway, and “(I)” require an interpreter.
bSupplementary services including psychologist, social worker, financial advisor, pharmacist co-located with IPU.
The patient/provider interaction probabilities in Table 1 are implemented in the Simio network model in Figure 2 by the nodes (or stations) with labels that start with “See” (e.g., “SeeSurgeon”). Following each of these nodes, the path that leads to an exam represented by a node with a label that ends in “Exam” (e.g., “SurgeonExam”) is selected with the probability corresponding to the patient/provider types in Table 1. The other path that bypasses the exam is selected with one minus this probability. The order in which the patient sees the physical therapist and nutritionist is arbitrary but the simulation requires logic to direct the flow. We use a smallest workload rule: if the patient is to see both providers, then he or she is channelled first to the one with the shorter queue plus number in service. In the case of ties, the nutritionist, who has lower utilisation than the physical therapist, is chosen first. Implementing this endogenous decision rule leads to some complex logic as shown Figure 2. More details are provided in Section 4.2.
After each patient encounter, the associate provider, surgeon, physical therapist, and nutritionist spend an average of 3–5 min wrapping-up the visit depending on the type of patient. This involves writing notes in the electronic medical records system on the patient’s condition, on the course of recommended treatment, and whether there is a need for follow-up. Provider wrap-ups are common in medical practice, but they require logic not found in standard queueing models. More specifically, during a provider wrap-up, the current patient can advance to the next step in the process, but since the provider is still occupied, the next patient cannot be examined until the wrap-up is complete. As a result, modelling wrap-ups in Simio required some extra logic that will be discussed in Section 4.2.
At the end of the visit, all patients see the care coordinator who develops a follow-up plan that may call for virtual check-ups or visits, and schedules supplementary services as needed. A small percentage of patients then visit one (or more) specialists, such as a psychologist, financial counsellor, pharmacist, or social worker after they leave the IPU (see Figure 1). These are grouped together under the heading “Sup services” in Table 1, and are treated as a single resource in the simulation model with unlimited capacity. These services are modelled as one step because they are “pooled” services for multiple IPUs and do not need to be modelled in detail. We include them to get a more accurate estimate of total patient flow time from clinic entry to exit.
The second column in Table 1 lists the patient mix. Based on past experience of the third author it was estimated that 75% are new (or initial visit) patients and 25% are follow-ups. This new to follow-up patient ratio was derived from the demographics of the patient population and was not expected to change in the foreseeable future. There are 12 different types of patients. The first eight correspond to the initial visit of the aforementioned four general types, with and without the need for an interpreter. The bottom four entries in Table 1 correspond to the four classes of follow-up patients – those on an operative pathway and those that aren’t, as well as those that require an interpreter. All operative follow-up patients are seen by the surgeon, 50% are seen by the physical therapist, and none are seen by the nutritionist. The probabilities are different for the non-surgical patients.
The third column in Table 1 indicates that many new patients come to the IPU with imaging from other sources. Prior to arrival, the IPU team spends time gathering that imaging. This is why most patients do not need additional imaging as part of the visit, regardless of the severity of their condition.
Interpreters are required by roughly 40% of the patients who are generally poor and living in immigrant communities. This is often the situation for urban clinics served by medical school faculty and residents. The Joint Pain IPU at the DMS falls in this category. Its affiliated hospital provides a safety net for the poor and vulnerable populations in Austin. The most common way to handle interpreters in a simulation model is to treat them as a resource and assign them as needed. However, because they are not physically present in the facility or limited in number, we have taken an alternative approach. Recognising that they are mostly available on demand from a tele-service with perhaps a small delay, they are modelled by increasing the provider service times, including wrap-up, by 20%. This allows us to account for the initial delay as well as the delay in provider–patient communications. It is important to note that there is an increase in wrap-up time because a document is produced at the end of every exam during wrap-up discussing the care plan for the patient. If this document has to be translated, it requires extra time.
4.2. Modelling issues
As Figure 2 illustrates, IPUs are complex queueing networks, making them impossible to study using analytical techniques prevalent in queueing theory, which is why we resort to simulation. In the Joint Pain IPU, the patients can be divided into 12 different types depending on the severity level of their condition, whether the patient is on an initial or a follow-up visit, and whether or not an interpreter is needed. Further, patients of the same type may take different pathways through the clinic seeing a different mix of providers based on population percentages. We modelled these pathways using probabilistic routing.
Routing patients to the physical therapist and nutritionist in any order based on an endogenous decision rule (in our case, the decision is based on the smallest workload) further complicates the modelling and analysis. On the modelling side, once a patient has been visited by one of these two providers, a flag must be set in the simulation logic so that the patient will not visit the same provider again. With a fixed routing sequence, no such flag is necessary. Incidentally, to determine which rule gave the best results, we compared the smallest workload rule to two others: shortest average processing time and completely random assignment (i.e., a 50–50 routing probability). In our model, the shortest average processing rule results in always having the nutritionist visit a patient before the physical therapist. Based on clinic closing time, total patient waiting time, and resource utilisation, we found that the smallest workload rule performed slightly better than the other rules. Additionally, it was the preferred rule by the clinic director and other IPU providers.
Wrap-up times are another complicating factor when modelling healthcare clinics. During the wrap-up time, a provider is unavailable to see the next patient, but the current patient may proceed to the next step in the process. This has the potential to shorten the flow time for a patient who needs to see multiple providers and represents a distinct advantage of the IPU over single provider clinics that a patient must visit separately. For the latter, wrap-up times are simply lost in the patient transit times between the separate clinics.
To demonstrate, consider the simple clinic structure given in Figure 3 with two providers in tandem. We are interested in the flow time for a patient to be seen by both providers. The parameters used in this illustration are representative of the Joint Pain IPU analysed in Section 5. Patients enter the clinic according to an exponential distribution with a mean interarrival time of 15 (i.e., Exponential(15)). Patients are served by Provider 1, followed by Provider 2 and then exit the clinic. We assume the service times at Provider 2 are Exponential(S), where 0 ≤ S < 15. For Provider 1, we consider two service scenarios. Scenario 1 is intended to represent an IPU in which the providers are co-located at the same clinic. Provider 1 has Exponential(S) service times and wrap-up times of Exponential(f × S), where 0 ≤ f < 1. During the wrap-up, the current patient can proceed to Provider 2 when Provider 1 is wrapping-up. In Scenario 2, we assume that Provider 1 takes Exponential(S) + Exponential(f × S) time with each patient. Since Provider 1 is busy for the same amount of time for each patient in both scenarios, the two are comparable. However, in the second scenario, the patient loses the benefit of being able to move on to Provider 2 during the wrap-up stage. Hence, the comparison of these two scenarios on the basis of flow time is intended to provide a conservative illustration of the benefit of co-locating two complementary providers in IPU clinic structure. It is conservative because if the two providers were not co-located in the same clinic, the transit times between the two would likely be much greater than lost wrap-up time.
Figure 3.

Simple clinic structure with two providers in tandem
To quantify the differences in patient flow time, we simulated 24 design points in our illustration. For the average total service time for Provider 1 (including wrap-up), we used 12 and 14, representing moderately high (0.8) and high (0.933) traffic intensities. Average wrap-up times for Provider 1 considered include 2 (low), 4 (moderate), and 6 (high). Finally, we used average service times of 6, 9, 12, and 14 for Provider 2 to represent low to high congestion at the second stage. The factor levels were chosen to reflect the clinic setting in which time spent at the first stage where an initial evaluation occurs tends to be longer than most of the subsequent stages. However, since subsequent stages can involve relative short to relatively long service times, we considered a broader range of times for the second stage. To imitate the clinic setting further, each simulation replication represented a day in which 30 patients are served. To get high precision, we simulated 5000 days at each design point. The sample size of 5000 was chosen to get the coefficient of variation of all average flow times to be less than 1%.
Figure 4 shows the results for the design point triplets (average total time for Provider 1, average wrap-up times for Provider 1, average service times for Provider 2). The bars are 95% t-confidence intervals for the difference between the mean flow times of Scenario 2 and Scenario 1 (Law & Kelton, 1991, Section 10.2.2). The results clearly show that there is tangible benefit in terms of reduced average flow time when the patient is able to proceed to the next stage during wrap-up. This follows because the confidence interval either covers or exceeds the average wrap-up time for each design point. The results appear to be robust even for the high traffic intensity cases. Since the clinic in Figure 3 represents the simplest IPU imaginable with only one provider engaged in wrap-up, benefits in an IPU where patients can visit three to five providers with wrap-ups are multiplied. Shorter flow time not only leads to increased patient satisfaction (Huang, 1994), it also allows the clinic to service more patients each day.
Figure 4.
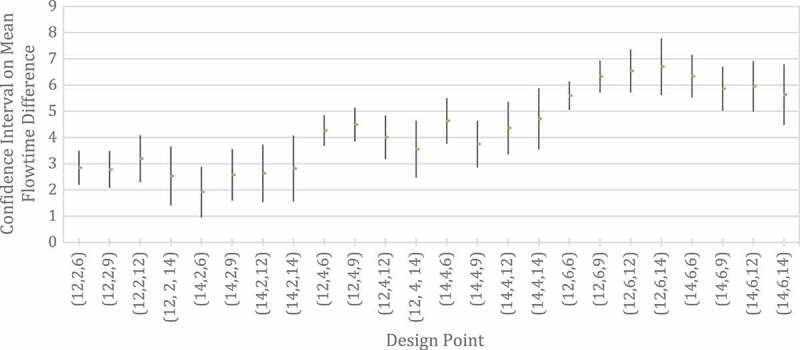
Ninety-five per cent t-confidence intervals for the difference between the mean flow times of Scenario 2 and Scenario 1. The design point triplets are (average total time for Provider 1, average wrap-up times for Provider 1, average service times for Provider 2)
It is important to note that in this illustration we chose to use exponential interarrival and service times because the exponential distribution is fairly noisy (the coefficient of variation is equal to 1). Hence, results obtained for less noisy distributions will likely be robust as well. Additionally, we chose to simulate both scenarios even though steady state analytic results exist for Scenario 2 (Gross & Harris, 1985, Section 4.5). However, every day each clinic starts empty, serves 30 patients, and completes service of all patients before it closes. Therefore, these clinics never achieve steady state and must be modelled as transient systems (Law & Kelton, 1991, Chapter 9), for which there are no analytic results.
Based on these benefits, wrap-up times must be modelled distinctly and carefully in the IPU setting. We modelled them by creating a “phantom” job (or entity) at the end of each patient exam. The phantom job, representing the patient wrap-up time, is assigned a higher priority than the next patient exam and is instantaneously inserted at the beginning of the provider queue. Thus, the provider always performs a wrap-up for the current patient before examining the next patient. While there may be other ways to model wrap-ups times in Simio, we found this to be the way that best facilitates designed experiments in which we consider different numbers of providers (e.g., associate providers) at a given station in the model.
A patient handoff involving multiple providers represents another complication often found in IPUs. Handoffs result from a consultation between the provider who is finishing with a patient and the provider whom the patient will see next. This involves having the patient “seize” or occupy the time of more than one provider at a time, which is a relatively straightforward thing to do in a simulation language like Simio. However, coordination of multiple resources over numerous stages in the clinic process and must be modelled with great care to accurately reflect protocols used in practice. For example, it is best to avoid having a very expensive resource (e.g., surgeon) waiting on a less valuable resource (e.g., associate provider) to consult over a specific patient. While the Joint Pain IPU in Figure 2 does not involve a handoff, two other clinics that we are modelling, Back Pain and Upper Extremity Pain, do.
5. Experiment design and computational results
The primary aim of our analysis was to determine the number of patients that can be seen each day in the Joint Pain IPU as a function of resource availability. A secondary aim was to determine the number of VM patients that could be treated without noticeably disrupting the in-clinic schedule. Table 2 lists all 12 patient types and the corresponding processing time distributions for each IPU resource. It also lists resources for each activity in the base case. Check-in and imaging follow normal distributions while all encounters with providers follow triangular distributions with various parameter values. For example, the processing time for an initial visit by a mild osteoarthritic patient at check-in is modelled as a normal distribution with mean 5 and standard deviation 1. The rooming time is modelled as a triangular distribution with a lower bound of 1 min, a mode of 3 min, and an upper bound of 5 min (abbreviated as Tri(1,3,5)), giving a mean of 3 min. Most activities have a single resource. Although self-check-in is planned, two medical assistants will be available to help those who are having difficulty with the kiosk screens. They will also escort patients to the various examination rooms if necessary. For the base case, there are six rooms and two associate providers available.
Table 2.
Processing time probability distributions by patient type and number of resources for the base case at each activity
| Patient type | Check-in (min) |
Rooming (min) |
Imaging (min) |
Associate provider (min) |
Surgeon (min) |
Physical therapist (min) |
Nutritionist (min) |
Care planner (min) | Sup services (min) |
|---|---|---|---|---|---|---|---|---|---|
| Initial Mild OA | Norm(5,1) | Tri(1,3,5) | Norm(15,3) | Tri(15,20,30) | Tri(7,10,20) | Tri(10,15,25) | Tri(10,15,25) | Tri(5,10,20) | Tri(15,30,45) |
| Initial Moderate OA | Norm(5,1) | Tri(1,3,5) | Norm(15,3) | Tri(15,20,30) | Tri(7,10,20) | Tri(10,15,25) | Tri(10,15,25) | Tri(5,10,20) | Tri(15,30,45) |
| Initial Severe OA | Norm(5,1) | Tri(1,3,5) | Norm(15,3) | Tri(15,20,30) | Tri(7,10,20) | Tri(10,15,25) | Tri(10,15,25) | Tri(5,10,20) | Tri(15,30,45) |
| Initial Op Path | Norm(5,1) | Tri(1,3,5) | Norm(15,3) | Tri(15,20,30) | Tri(7,10,20) | Tri(10,15,25) | Tri(10,15,25) | Tri(5,10,20) | Tri(15,30,45) |
| Initial Mild OA (I) | Norm(6,1) | Tri(1.2,3.6,5) | Norm(18,3) | Tri(19,25,37) | Tri(8.4,12,24) | Tri(13,19,31) | Tri(13,19,31) | Tri(6,12,24) | Tri(18,36,54) |
| Initial Moderate OA (I) | Norm(6,1) | Tri(1.2,3.6,5) | Norm(18,3) | Tri(19,25,37) | Tri(8.4,12,24) | Tri(13,19,31) | Tri(13,19,31) | Tri(6,12,24) | Tri(18,36,54) |
| Initial Severe OA (I) | Norm(6,1) | Tri(1.2,3.6,5) | Norm(18,3) | Tri(19,25,37) | Tri(8.4,12,24) | Tri(13,19,31) | Tri(13,19,31) | Tri(6,12,24) | Tri(18,36,54) |
| Initial Op Path (I) | Norm(6,1) | Tri(1.2,3.6,5) | Norm(18,3) | Tri(19,25,37) | Tri(8.4,12,24) | Tri(13,19,31) | Tri(13,19,31) | Tri(6,12,24) | Tri(18,36,54) |
| Follow-up nonOp Path | Norm(5,1) | Tri(1,3,5) | Norm(15,3) | Tri(7,12,17) | Tri(4,5,10) | Tri(10,15,20) | Tri(6,8,12) | Tri(5,10,20) | Tri(15,30,45) |
| Follow-up Op Path | Norm(5,1) | Tri(1,3,5) | Norm(15,3) | Tri(7,12,17) | Tri(2.8,4,8) | Tri(6,8,12) | 0.0 | Tri(5,10,20) | Tri(15,30,45) |
| Follow-up nonOp Path (I) | Norm(6,1) | Tri(1.2,3.6,5) | Norm(18,3) | Tri(9,15,21) | Tri(4.8,6,12) | Tri(12,18,24) | Tri(7.2,9.6,14.4) | Tri(6,12,24) | Tri(18,36,54) |
| Follow-up Op Path (I) | Norm(6,1) | Tri(1.2,3.6,5) | Norm(18,3) | Tri(9,15,21) | Tri(3.36,4.8,9.6) | Tri(7.2,9.6,14.4) | 0.0 | Tri(6,12,24) | Tri(18,36,54) |
| No. of resources* | 2 | 6 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
*For the base case.
There are two other important stochastic elements in the simulation not listed in Table 2: wrap-up time and early/late patient arrivals from their scheduled appointment times. For the three providers that require a wrap-up time, we use a Tri(2,5,8) distribution for initial visit patients and a Tri(2,3,4) for follow-up patients. Since follow-up patients have already visited the clinic, they tend to take less clinic time and require less wrap-up time. Empirical evidence suggests that patients tend to arrive early (Blanco White & Pike, 1964; White et al., 2011). Thus, we use a Tri(−30,0,20) to represent arrival time deviations for patients off of their scheduled appointment times. Note that we do not consider no-shows because our aim is to discern the maximum number of patients that can be accommodated in the design of the clinic.
The parameter values for the distributions used in the simulation were estimated from the experience of the third author in conjunction with other providers in the DMS Department of Surgery who staff the IPUs. In the absence of historical data, anecdotal evidence suggests that the time to undergo medical procedures in an outpatient setting can be modelled using minimum, maximum and modal times (e.g., see Swisher et al., 2001). These three parameters lead directly to a triangular distribution, which we use for most processes. As an aside, when the Joint Pain IPU opened in the fall of 2017, subsequent analysis over a 3-month period showed that the estimated distributions in Tables 1 and 2 were highly accurate.
The performance of the system is measured by average values for (i) closing time of the clinic, (ii) total patient waiting time, and (iii) resource utilisation. Minimum average requirements were specified by the third author, the IPU director, and are as follows:
Patient waiting time for a room of no more than 5 min
No less than 25 patients per day
Patient time in a room of no more than 90 min
Patient time in the clinic of no more than 150 min.
5.1. Base case and variations
The base case configuration consisted of the resources and distributions identified in Table 2, coupled with 25 patients, 15-minute time slots in the schedule, and random sequencing (each patient type is scheduled in a slot with a probability equal to the patient mix fractions in Table 1). The 15-minute time slot corresponds to a bit more than half the average processing plus wrap-up time for an associate provider. Even with two resources, the associate provider tends to limit the flow since all patients must see the associate provider and it has the longest service times. Assuming an 8-h day starting at 8:00 am, this means that the last patient arrives at 2:15 pm, or 1 h and 45 min before the tentative closing time. To determine the number of replications for each scenario, we ran the base case for 100, 200, and 500 trials and concluded that there was no significant statistical difference in the results for 200 and 500 replications, so we settled on 200. Note that each replication is an independent trial, implying that there is no autocorrelation in the output data. We then compared the base case, known as IBFI (individual block/fixed interval), with several scheduling rules commonly found in the literature (Bard et al., 2016; Cayirli et al., 2006; Cayirli, Yang, & Quek, 2012; Milhiser et al. 2012). These included TwoBeg (two patients are scheduled at time zero and one patient every 15 min thereafter), multiple block/fixed interval, where two patients are scheduled every 30 min, and DOME, where patients scheduled early and late in the day are spaced closer together than those scheduled in the middle of the day. We also tried a number of variations on these rules. In summary, no single rule was dominant so we decided to use IBFI, which generally performed well for the first set of experiments with respect to patient waiting time and clinic closing time.
In designing the IPU, we were able to alter five factors: number of rooms, number of patients scheduled, the length of patient schedule time slots, the number of associate providers, and the sequencing of patients by appointment status (initial versus follow-up visit). We looked at perturbations of the base case that included scenarios defined by combinations of the following parameter values: rooms {6, 7, 8}; patients {25, 30, 35, 40}, schedule time slots {10 min, 12 min, 15 min}, associate providers {2, 3} and patient sequencing {random, follow-ups at beginning of the day, follow-ups at end of day, follow-ups at the beginning of each session}. Scenarios that did not meet the minimum performance requirements were omitted. The results allowed us to narrow down the values of the parameters to a reasonable number for the purposes of conducting a second set of experiments.
In the second phase of the analysis, we extended the day to 9 hours and approximated a 1-hour lunch break starting at 11:30 am. This was achieved by scheduling the last patient in the morning session at around 11:15 am, depending on the number of patients and the schedule time slots used. The first patient in the afternoon session was scheduled at 12:30 pm. Clinic operations exceeding 540 min or 9 h triggered overtime.
Allowing for the lunch break, the results for the base case and several variations are given in Table 3. For each statistic, we report the mean and 95% confidence interval halfwidth. While most statistics are self-explanatory, a few require additional discussion. “Clinic closing time” refers to how many minutes the clinic stayed open on any given day to service all the patients. “Patient time in clinic” is the total time in the clinic across all patient types. “Patient total wait time” is the total time a patient spent waiting for service in the clinic. Additional statistics for total time in the clinic by patient type and waiting times for specific resources are contained in Table A1 in Appendix A. Note that patient total wait time is not merely the sum of the other wait times listed in Table A1 because patients take different paths through the clinic. Additionally, some waiting time statistics are omitted because they were not statistically different form zero, i.e., for Check-in, Imaging, and Sup Services.
Table 3.
Average statistics (all times in minutes; all utilisations in percentages) for 2 associate providers, 15-minute schedule time slot, random sequencing, 25 and 30 patients, and 6 and 7 rooms
| 25 Patients |
30 Patients |
|||||||
|---|---|---|---|---|---|---|---|---|
| 6 Rooms |
7 Rooms |
6 Rooms |
7 Rooms |
|||||
| Statistics | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth |
| Clinic closing time | 523.41 | 3.64 | 523.03 | 3.45 | 597.67 | 3.58 | 600.25 | 3.45 |
| Patient time in room | 74.24 | 1.01 | 75.39 | 1.15 | 75.15 | 0.93 | 76.93 | 1.11 |
| Patient time in clinic | 87.61 | 1.22 | 88.16 | 1.27 | 88.71 | 1.12 | 89.73 | 1.25 |
| Patient wait time for room | 0.65 | 0.14 | 0.08 | 0.05 | 1.02 | 0.18 | 0.15 | 0.05 |
| Patient total wait time | 15.51 | 0.72 | 15.90 | 0.79 | 16.91 | 0.70 | 17.50 | 0.78 |
| Associate provider utilisation | 61.59 | 0.56 | 61.56 | 0.54 | 64.60 | 0.53 | 64.33 | 0.50 |
| Surgeon utilisation | 35.59 | 1.16 | 35.56 | 1.17 | 37.57 | 1.07 | 37.00 | 1.06 |
| Nutritionist utilisation | 38.55 | 1.43 | 38.45 | 1.46 | 40.18 | 1.39 | 40.42 | 1.37 |
| Physical therapist utilisation | 56.09 | 1.45 | 57.33 | 1.59 | 58.44 | 1.37 | 59.72 | 1.50 |
| Care planner utilisation | 59.96 | 0.63 | 60.34 | 0.63 | 62.89 | 0.57 | 63.08 | 0.56 |
| Room utilisation | 59.16 | 0.78 | 51.53 | 0.79 | 62.90 | 0.73 | 54.94 | 0.74 |
The first observation from the results in Table 3 is that adding a 7th room has no noticeable effect on performance. Although some statistics improve with the extra room, their values overlap the 95% halfwidths and so we cannot conclude that they are different. A second observation is that all minimum requirements are met for both the 25- and 30-patient scenarios; however, the clinic closing time for the 30-patient case extends to approximately 598 min on average, implying 58 min of overtime with either six or seven rooms. Also notice that the total patient time in the room is between 74 and 77 min across all scenarios and that the longest a patient spends in the clinic is roughly 124 min, on average (operative path patient needing an interpreter, 7 rooms, 25 patients – see Table A1).
Looking at the remaining statistics, we see that total patient waiting time, a critical determinant in patient satisfaction, remains in the range of 15–17.5 min, on average. Utilisation for rooms and associate providers top out at 62.9% and 64.6%, respectively. Statistically, the associate provider has the highest utilisation of all resources indicating that it is a potential bottleneck. Although this resource utilisation is not especially high compared to other studies (e.g., see Bard et al., 2016; Morrice et al., 2014; White et al. 2011), it can be explained by the fact that associate providers are often idle towards the end of the day after they have seen all their patients and the system empties out.
To reduce patient waiting time it would be necessary to either increase the number of associate providers thereby reducing their utilisation, or increase the patient schedule time slots. The former option is explored in the next section; the latter was seen to produce excessive overtime in initial testing and hence abandoned as a scheduling option. The relatively lower utilisation of the other providers is not a critical concern at this point because each will have other responsibilities within the clinic and within the medical school that will occupy most of their unfilled patient-facing time. Moreover, in the current fee-for-service model it is understood that placing the patient at the centre of the IPU will inevitably incur additional costs, at least in the short term. Another option being considered to increase the utilisation of the surgeon, the physical therapist, and the nutritionist is to schedule virtual visits at the beginning of the day before the clinic fills up and at the end of the day when the clinic is emptying out. These visits are done virtually by telemedicine with follow-up patients who do not need a physical exam in the clinic. Results for this option are included in Section 5.4.
The simulation results for 25 and 30 patients, 6 and 7 rooms, 2 associate providers, but now with 12-minute schedule time slots are presented in Table 4 (Table A2 in Appendix A contains additional statistics). Not surprisingly, clinic closing times decrease to less than 9 h in all cases, while the waiting time statistics increase due to more congestion in the clinic with the tighter patient time slots in the schedule. For the base case (25 patients, 6 rooms), for example, the closing time drops from an average of 523.41–455.91 min while the patient time in room increases from 74.24 to 81.95 min on average. Furthermore, patient total waiting time, almost doubles. Similar results for all metrics were observed for the other scenarios and seen to be statistically significant based on the non-overlapping 95% confident intervals as implied by the halfwidths.
Table 4.
Average statistics (all times in minutes; all utilisations in percentages) for 2 associate providers, 12-minute schedule time slot, random sequencing, 25 and 30 patients, and 6 and 7 rooms
| 25 Patients |
30 Patients |
|||||||
|---|---|---|---|---|---|---|---|---|
| 6 Rooms |
7 Rooms |
6 Rooms |
7 Rooms |
|||||
| Statistics | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth |
| Clinic closing time | 455.91 | 3.68 | 451.26 | 3.18 | 529.05 | 4.11 | 524.43 | 3.47 |
| Patient time in room | 81.95 | 1.04 | 84.62 | 1.18 | 82.58 | 0.96 | 86.27 | 1.08 |
| Patient time in clinic | 103.45 | 2.04 | 100.29 | 1.62 | 105.27 | 2.05 | 102.30 | 1.51 |
| Patient wait time for room | 8.91 | 1.00 | 3.17 | 0.44 | 10.09 | 1.13 | 3.35 | 0.43 |
| Patient total wait time | 31.35 | 1.56 | 28.71 | 1.18 | 33.29 | 1.65 | 30.40 | 1.12 |
| Associate provider utilisation | 70.70 | 0.65 | 71.32 | 0.66 | 72.98 | 0.60 | 73.53 | 0.61 |
| Surgeon utilisation | 40.43 | 1.29 | 40.38 | 1.38 | 41.84 | 1.24 | 41.49 | 1.27 |
| Nutritionist utilisation | 43.33 | 1.72 | 43.50 | 1.70 | 45.22 | 1.47 | 45.25 | 1.64 |
| Physical therapist utilisation | 64.03 | 1.56 | 63.08 | 1.60 | 65.41 | 1.49 | 66.01 | 1.58 |
| Care planner utilisation | 69.60 | 0.75 | 69.74 | 0.68 | 71.66 | 0.72 | 71.89 | 0.65 |
| Room utilisation | 74.92 | 0.76 | 66.99 | 0.83 | 78.07 | 0.72 | 70.54 | 0.81 |
Similar to the results in Table 3, when the schedule time slot drops from 15 to 12 min, adding a 7th room does not seem to have much impact on clinic closing time, patient time in clinic, and patient total wait time (see Table 4). However, it does have significant impact on patient wait time for room and patient time in room. More specifically, increasing the number of rooms from 6 to 7 shifts the patient wait time for the room to the room. This is an important point because a minimum service requirement is to have the patient roomed in 5 min or less, which is violated for both 25 and 30 patients when only 6 rooms are available.
5.2. Factorial design experiment
To gain a better understanding of the effects of the various factors on the main performance measures of interest, we conducted a more detailed statistical analysis using StatTools (www.palisade.com) in the form of least squares regression. In particular, we ran a two-level factorial design experiment on the following four factors:
Number of associate providers (2, 3). We refer to this factor as “Num_AP”.
Number of rooms (6, 7). We refer to this factor as “Num_Room”.
Number of patients (25, 30). We refer to this factor as “Num_Pat”.
Patient schedule time slot (12 min, 15 min). We refer to this factor as Time_Int”.
Table 5 contains the 16 design points and their corresponding factor levels.
Table 5.
Design points and corresponding factor level
| Factors and their levels |
||||
|---|---|---|---|---|
| Design point | Num_AP | Num_Room | Num_Pat | Time_Int |
| 1 | 2 | 6 | 25 | 12 |
| 2 | 2 | 7 | 25 | 12 |
| 3 | 2 | 6 | 30 | 12 |
| 4 | 2 | 7 | 30 | 12 |
| 5 | 2 | 6 | 25 | 15 |
| 6 | 2 | 7 | 25 | 15 |
| 7 | 2 | 6 | 30 | 15 |
| 8 | 2 | 7 | 30 | 15 |
| 9 | 3 | 6 | 25 | 12 |
| 10 | 3 | 7 | 25 | 12 |
| 11 | 3 | 6 | 30 | 12 |
| 12 | 3 | 7 | 30 | 12 |
| 13 | 3 | 6 | 25 | 15 |
| 14 | 3 | 7 | 25 | 15 |
| 15 | 3 | 6 | 30 | 15 |
| 16 | 3 | 7 | 30 | 15 |
Each of these factors and their levels was chosen based on our initial analysis and observed system performance, which is partially reported in Tables 3 and 4 (the corresponding tables for three associate providers are available from the authors as are all the statistical results). In the experiments, we replicated each design point 200 times to get good estimates of the averages for each performance measure and to satisfy the standard regression assumptions. In the regression results to follow, all models satisfied the assumption of normality based on a Chi-Square test. We verified linearity and homoscedasticity by inspection of residual versus fitted plots. Independently seeded simulation runs guaranteed the independence assumption.
Table 6 contains regression models for the main performance measures: clinic closing time, patient total wait time, patient waiting time for room, patient time in room, and patient time in clinic. All models were generated using backward regression. Since all factors are qualitative, we converted them to dummy variables and included their high levels as explanatory variables in the regression analysis. Following the “sparsity of effects principle” (Myers, Montgomery, & Anderson-Cook, 2009, page 96), we only consider main effects and first order interaction effects, leaving the remaining degrees of freedom to estimate error. According to the Adjusted-R2 shown in the last row of the table, all models provided good fit to these data.
Table 6.
Regression model results for the two-level factorial design: *, ** and *** indicate model term coefficients are significant at the 5%, 1%, and 0.1% levels, respectively; empty cells indicate that term was excluded from the model by the backward regression procedure
| Model response (time in minutes) |
|||||
|---|---|---|---|---|---|
| Model term | Clinic closing time | Patient total wait time | Patient wait time for room | Patient time in room | Patient time in clinic |
| Constant | 453.75*** | 31.28*** | 9.09*** | 81.43*** | 103.10*** |
| Num_AP = 3 | −3.75* | −6.77*** | −2.33*** | −3.67*** | −6.18*** |
| Num_Room = 7 | −2.30*** | −5.81*** | 3.59*** | −2.22*** | |
| Num_Patient = 30 | 72.46*** | 1.61*** | 0.40 | 1.26*** | 1.67*** |
| Time_Int = 15 | 68.75*** | −15.55*** | −8.24*** | −7.17*** | −15.40*** |
| (Num_AP = 3) × (Num_Room = 7) | 0.96* | −0.96* | |||
| (Num_AP = 3) × (Num_Patient = 30) | |||||
| (Num_AP = 3) × (Time_Int = 15) | 3.68*** | 1.78** | 1.11* | 2.77** | |
| (Num_Room = 7) × (Num_Patient = 30) | |||||
| (Num_Room = 7) × (Time_Int = 15) | 2.13*** | 4.67*** | −2.53*** | 2.25* | |
| (Num_Patient = 30) × (Time_Int = 15) | 5.08* | ||||
| Adjusted-R2 | 0.999 | 0.997 | 0.986 | 0.994 | 0.994 |
All main effects impact the responses in the way expected. Increasing the number of associate providers reduces clinic closing time and all patient times. However, it tends to have more impact on patient waiting times. Increasing the number of rooms has no significant impact on clinic closing time confirming our initial observation in Section 5.1, but it does significantly affect all other responses, especially patient wait time for a room. While the positive influence on patient time in room seems counterintuitive, adding a room shifts the patient time waiting for a room to patient time in the room. Increasing the number of patients increases the workload on the clinic. Hence, almost all times in Table 6 increase, especially clinic closing time. It is important to note that we retained the Num_Patient term in the patient wait time for room model because its coefficient had a suggestive p-value (0.076) and it improved the Adjusted R2 by about half a percentage point. Lastly, making the patient schedule time slots larger spaces patients out more in the schedule. Consequently, clinic closing time sees a significant increase and congestion decreases significantly reducing all the patient times.
The interaction effects provide some interesting insights. There is a reinforcing interaction effect on clinic closing time when more patients are added to the schedule and the patient schedule time slots are lengthened. All the other interaction terms that include Time_Int in the rest of the models mitigate the main effects. In fact, the impact of increasing the number of rooms is largely diminished for all four patient time responses when Time_Int = 15 min, which coincides with our observations from Table 3. Similar alleviation happens to Num_AP, but to a lesser extent. The observed mitigations follow because there is less congestion and hence less waiting time when patients are spaced farther apart in the schedule. Therefore, adding rooms or associate providers has less impact. The interaction term that includes Num_AP and Num_Room in the model for patient wait time for room is also a mitigating effect reflecting that wait times are bounded below by zero and adding both resources at the same time cannot achieve proportionate improvement due to this constraint. The interaction term for Num_AP and Num_Room in the patient time in room model is in effect reinforcing because adding associate providers and rooms together reduces patient time in room more.
We gained one more important insight from the regression analysis. As the regression results indicate, increasing the number of associate providers has significant benefit on all the main performance measures. Table 7 contains the fitted values from the regression models for the design points at which there are 2 associate providers and 30 patients. All but design point 3 on patient wait time for room satisfies the minimum requirements set by the clinic director indicating that 3 associate providers may not be necessary. Thus, for the rest of the analysis, we will focus on strategies to improve configurations with 2 associate providers and 30 patients.
Table 7.
Fitted values from the five regression models for design points with 2 associate providers and 30 patients
| Design point | Fitted values (time in minutes) |
||||
|---|---|---|---|---|---|
| Clinic closing time | Patient total wait time | Patient wait time for room | Patient time in room | Patient time in clinic | |
| 3 | 526.21 | 32.89 | 9.49 | 82.69 | 104.77 |
| 4 | 526.21 | 30.59 | 3.68 | 86.28 | 102.55 |
| 7 | 600.04 | 17.34 | 1.25 | 75.53 | 89.37 |
| 8 | 600.04 | 17.17 | 0.10 | 76.59 | 89.40 |
5.3. Patient sequencing
The Joint Pain IPU has 12 patient types (see Table 2) but all that is known about them prior to their visit is that they can be classified as either new or follow-up (the need for an interpreter is not known). The experiments we performed involved shortening the schedule time slot of the follow-up patients to more closely match their service time with the associate provider, the bottleneck. In general, the average service time for follow-ups for each provider type is less than for new patients (Table 2), and except for imaging, the probability of seeing each type of provider is also smaller (Table 1). In the testing, we fixed the schedule time slot for the follow-ups patients at 10 min and all seven (25% of 30 patients) were scheduled at the beginning of the day. New patients were scheduled after the follow-ups on 12- or 15-minute time slots.
The results for the “12-minute time slot for new patients” given in Table 8 are best compared with the last two columns in Table 4 where all patients receive 12-minute time slots and are randomly sequenced. For these scenarios, there was no statistical difference for the closing time of the clinic although the values ranged from 524 to 529 min. For the 6-room case, the patient total waiting time dropped from 33.29 to 28.51 min, or 14.4%. The drop for the 7-room case was 9.1%. The reductions in the average time follow-up patients spend in the clinic were statistically significant as expected, but to some surprise, not the corresponding times for the new patients or the utilisation metrics (see also Appendix A for a comparison of the first two columns of Table A3 with the last two columns of Table A2). Notice that while sequencing patients in this manner does improve patient wait time for the room, 7 rooms are still necessary to achieve the minimum requirement of no more than 5 min waiting.
Table 8.
Average statistics (all times in minutes; all utilisations in percentages) for 2 associate providers, 6 and 7 rooms, 10-minute schedule time slots for 7 follow-up patients at beginning of day, and 12- and 15-minute schedule time slots for 23 new patients
| 12-minute time slot for new patients |
15-minute time slot for new patients |
|||||||
|---|---|---|---|---|---|---|---|---|
| 6 Rooms |
7 Rooms |
6 Rooms |
7 Rooms |
|||||
| Statistics | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth |
| Clinic closing time | 526.73 | 3.82 | 526.03 | 3.61 | 584.37 | 3.81 | 581.32 | 3.60 |
| Patient time in room | 81.29 | 0.78 | 85.19 | 0.92 | 76.47 | 0.83 | 77.29 | 0.94 |
| Patient time in clinic | 101.29 | 1.40 | 100.18 | 1.32 | 90.32 | 1.08 | 90.07 | 1.07 |
| Patient wait time for room | 6.75 | 0.65 | 2.09 | 0.32 | 1.40 | 0.24 | 0.22 | 0.08 |
| Patient total wait time | 28.51 | 1.04 | 27.64 | 0.94 | 18.28 | 0.70 | 17.95 | 0.66 |
| Associate provider utilisation | 73.91 | 0.54 | 73.69 | 0.51 | 66.60 | 0.49 | 66.79 | 0.45 |
| Surgeon utilisation | 42.31 | 1.12 | 43.81 | 1.25 | 38.41 | 1.21 | 39.10 | 1.10 |
| Nutritionist utilisation | 46.01 | 1.50 | 46.08 | 1.66 | 42.16 | 1.44 | 42.36 | 1.38 |
| Physical therapist utilisation | 66.57 | 1.52 | 66.54 | 1.43 | 60.16 | 1.44 | 59.49 | 1.39 |
| Care planner utilisation | 71.81 | 0.70 | 71.49 | 0.62 | 64.49 | 0.57 | 65.03 | 0.56 |
| Room utilisation | 77.25 | 0.71 | 69.43 | 0.64 | 65.48 | 0.67 | 57.01 | 0.66 |
We can compare the results for the “15-minute time slot for new patients” given in Table 8 with the last two columns in Table 3 where patients are randomly sequenced and all received 15-minute time slots. For the 6 and 7 room cases, clinic closing times dropped significantly by 2.2% and 3.2%, respectively. Patient total waiting time, though, remained statistically similar at about 17 or 18 min.
This analysis suggests the following for 10-minute schedule time slots for follow-ups at the front of the sequence. When patients are scheduled with looser time slots (i.e., 15 min), segmenting and sequencing follow-up patients on shorter time slots first serves to reduce clinic closing time without helping or hindering total patient wait time because the clinic did not have much congestion to begin with. On the other hand, when the schedule time slots are relatively tight (i.e., 12 min) and the clinic experiences significantly higher congestion, segmenting and sequence follow-up patients on shorter time slots first results in a tremendous waiting time reduction for these patients that more than offsets any increase in patient waiting time experienced by the new patients. However, since patients are already slotted tightly in time, the closing time reduction is at best marginal. These results are in line with what others have found; that is, scheduling patients with smaller processing time means or variances first can lead to improved system performance (see Cayirli et al., 2006; Oh et al., 2013; White et al. 2011). However, compared to previous literature, we show that the improvements are time-slot dependent. Additionally, we establish that they hold even under a more complex clinic structure and when the percentage of follow-up patients is relatively small.
Incidentally, we also tried sequencing the follow-up patients after the new patients using scenarios comparable to those found in Table 8. While the analysis yielded reductions in clinic closing time of up to 10% when compared with the results in Table 8, it also showed increases of patient time in clinic ranging from 13% to 27%. So while sequencing patients with smaller processing times at the beginning of the schedule can yield benefits on some performance measures without hindering others, the same does not appear to be true when those patients are placed at the end of the schedule.
5.4. Adding VM patients to the schedule
The simulation model allowed us to assess the potential for adding VM appointments to the clinic schedule. Some patients do not need to physically come to the clinic, but can interact directly with a single provider in the IPU using some form of telemedicine. Thus, VM patients can be inserted into a providers schedule during off-peak periods. This concept gives tremendous freedom to improve patient-level value through convenience and decrease costs of the typical care cycle by reducing unnecessary in-person visits. In the Joint Pain IPU, we considered VM patients for the surgeon, nutritionist, and physical therapist (see Figure B1 in Appendix B for the updated Simio model). Given a clinic in which these providers sit in the middle of the process steps, off-peak periods are likely to occur at the beginning and end of the day as the clinic is filling up and emptying out, respectively.
To illustrate, we consider the scenario in Table 8 when there are 2 associate providers, 7 rooms, 10-minute schedule time slots for 7 follow-up patients at beginning of day, and 12-minute schedule time slots for 23 new patients. The simulation results are given in Table 9 for the average starting and finishing times for the surgeon, nutritionist, and physical therapist. For example, the surgeon starts his first in-clinic patient and finishes his last in-clinic patient, 30.85 and 452.08 min after the clinic opens, respectively.
Table 9.
Average starting and finishing times for surgeon, nutritionist and physical therapist when there are 2 associate providers, 7 rooms, 10-minute time slots for 7 follow-up patients at beginning of day, and 12-minute time slots for 23 new patients
| Statistics (all in minutes) | Mean | Halfwidth |
|---|---|---|
| Surgeon starting time | 30.85 | 1.83 |
| Surgeon finishing time | 452.08 | 3.61 |
| Nutritionist starting time | 50.27 | 4.13 |
| Nutritionist finishing time | 466.43 | 5.21 |
| Physical therapist starting time | 38.35 | 2.36 |
| Physical therapist finishing time | 493.59 | 4.50 |
Table 10 contains the processing time probability distributions by for VM follow-up patients. Once again, the parameter values for the distributions used in the simulation were estimated from the experience of the third author in conjunction with other providers in the DMS Department of Surgery. Similar to other patients, the distributional parameters are increased by 20% for the 40% of patients requiring an interpreter. Since these are follow-up patients, a Tri(2,3,4) is used for wrap-up time for all providers. Finally, given the ease with which VM patients can connect with a provider, we assume they are prompt and show up.
Table 10.
Processing time probability distributions and patient mix for VM follow-up patients
| Patient type | Patient mix (%) | Surgeon (min) | Physical therapist (min) | Nutritionist (min) |
|---|---|---|---|---|
| VM follow-up | 60 | Tri(6,10,15) | Tri(12,15,20) | Tri(12,15,20) |
| VM follow-up (I) | 40 | Tri(7.2,12,18) | Tri(14.4,18,24) | Tri(14.4,18,24) |
Based on the results in Table 9 and the processing and wrap-up times for VM follow-up patients, we consider two schedules. In Schedule 1, the surgeon sees three VM follow-up patients at 0, 15, and 30 min, and the nutritionist, and physical therapist see three VM follow-up patients each at 0, 20, and 40 min. Schedule 2 extends Schedule 1 to also include two patients for the surgeon at the end of the day at times 485 and 500 min, and one patient each for the nutritionist and the physical therapist at 500 min. As such, these schedules respectively accommodate an additional 9 and 13 patients daily with no additional resources.
Table 11 provides the results for Schedules 1 and 2 (see Table A4 in Appendix A for more statistics), and may be compared with the results in the third column of Table 8. As expected, adding VM follow-ups to the surgeon, nutritionist, and physical therapist does increase their utilisations, but they are all still within acceptable ranges. Furthermore, while patient waiting times do increase, the minimum requirements are still satisfied for both scenarios. Clinic closing time for Schedule 1 does not increase significantly over the scenario in Table 8, likely because the VM follow-ups are processed at the beginning of the day and have little impact on the end of the day activities. Not surprisingly, Schedule 2 does have a statistically significant later closing time. However, it is the only statistic with a significant difference between Schedules 1 and 2. Hence, the impact of adding VM patients at the end of the day is quite limited. In summary, both schedules should be given serious consideration since they can accommodate an increase of about one third to almost one half more patients without any additional resources while meeting all the minimum requirements.
Table 11.
Average statistics (all times in minutes; all utilisations in percentages) for 2 associate providers, 7 rooms, 10-minute time slots for 7 follow-up patients at beginning of day, 12-minute time slots for 23 new patients, 9 VM patients at the beginning of the day for Schedules 1 & 2 plus 4 VM patients at the end of the day for Schedule 2
| Schedule 1 |
Schedule 2 |
|||
|---|---|---|---|---|
| Statistics | Mean | Halfwidth | Mean | Halfwidth |
| Clinic closing time | 528.89 | 4.13 | 539.17 | 3.27 |
| Patient time in room | 89.69 | 1.08 | 89.68 | 1.09 |
| Patient time in clinic | 106.89 | 1.69 | 106.86 | 1.69 |
| Patient wait time for room | 4.24 | 0.64 | 4.24 | 0.64 |
| Patient total wait time | 33.71 | 1.36 | 33.71 | 1.36 |
| Associate provider utilisation | 73.61 | 0.59 | 72.12 | 0.47 |
| Surgeon utilisation | 49.59 | 1.14 | 53.90 | 1.12 |
| Nutritionist utilisation | 56.85 | 1.53 | 59.50 | 1.49 |
| Physical therapist utilisation | 78.43 | 1.60 | 80.69 | 1.59 |
| Care planner utilisation | 72.07 | 0.67 | 70.45 | 0.60 |
| Room utilisation | 72.72 | 0.74 | 71.29 | 0.75 |
6. Discussion
Healthcare organisations worldwide find themselves under mounting pressure to improve the quality of care they offer while decreasing the cost of delivering it. These challenges are compounded by competition, declining reimbursement schedules, and an ageing, often chronically ill population. In this paper, we have tried to tackle one aspect of the healthcare delivery problem as it relates to outpatient services. Our goal has been to develop the tools needed to design and analyse a condition-based ambulatory clinic, known as an IPU, in which critical patient services are provided in a single location during a single visit.
Using discrete-event simulation, we built a parametric model of the DMS’s Joint Pain IPU to determine the relationships and trade-offs among the number of providers, the number of exam rooms, the number of patients, and appointment time slots. Performance was measured by the clinic closing time, the patient waiting time and resource utilisation. The analysis showed that up to 30 patients can be seen within an 8-hour working day with two associate providers (the bottleneck), 7 rooms and 12-min appointment slots, plus a single surgeon, nutritionist, physical therapist, and care planner. This configuration is well within the IPU budget and meets all its performance requirements.
To provide the clinic director with a simple means of evaluating the impact of changing any of the inputs or trying to schedule more patients, we performed a multiple regression analysis to establish the relationship between these factors and our five primary output measures. The derived relationships for the averages of clinic closing time, patient total waiting time, patient waiting time for a room, patient time in a room, and patient time in the clinic as a function of the number of associate providers, number of patients, number of rooms, and arrival time intervals are provided in Table 6. The regression analysis also provided valuable insights into how the main and interaction factor effects impacted each of the regression responses.
Additional analyses were conducted to determine whether improved performance could be achieved by sequencing the follow-up and new patients in various ways, and in assigning shorter appointment slots to follow-up patients who generally require less provider time. Analysis of two templates with follow-ups first, each with 10-minute appointment slots, and then the new patients, each with either 12 or 15-minute appointments slots showed improvements in either patient waiting times or clinic closing times. Similar results have been found in the literature and suggest that ordering patients by their processing time variance from smallest to largest reducing waiting times without affecting clinic closing time or vice versa.
Our final analysis addressed the idle time in the schedules of the surgeon, nutritionist, and physical therapist before the first patient arrives and after the last patient leaves. Using 10-minute and 12-minute time slots for follow-up and new patients, respectively, (30 in-clinic patients; see Table 8), we found it possible to schedule virtual visits for three additional follow-up patients for each of these providers at the beginning of the day, two additional follow-up patients for the surgeon at the end of the day, and one each for the other two providers at the end of the day. Thus, up to an additional 13 (or 43% more) patients can be seen daily without noticeably affecting the statistics of the 30 patients who visit the clinic.
The Lower Extremity Joint Pain IPU at DMS officially opened in November of 2017. During the first two months, the clinic operated at about 70% planned capacity in order for staff to gain more familiarity with the physical facilities and the IT systems, and to hone the workflows. After two months, the clinic began using a full 30-patient schedule recommended by the findings of this work. The clinic director found that the majority of the time estimates were accurate and that the schedule was running smoothly. In particular, the primary requirements that, on average, patients spend less than 5 min to be roomed, no more than 90 min in a room, and no more than 150 min in the clinic are being achieved. We are currently collecting additional data from time studies to use the simulation model for clinic operations decision support and to plan for future developments in the growing practice.
As future research, we plan to develop a two-stage stochastic programming model to determine the optimal appointment time slots as a function of resource limits and performance requirements. The templates derived from the optimisation model will be used to fix appointment times within the simulation model. Knowing the optimal schedule in advance will allow us to forgo the time-consuming process of trying to determine them through enumeration as we develop simulation models for five more orthopaedic IPUs at the DMS.
Appendix A.
Table A1.
Additional average statistics to Table 3 (all times in minutes; all utilisations in percentages) for 2 associate providers, 15-minute schedule time slot, random sequencing, 25 and 30 patients, and 6 and 7 rooms
| 25 Patients |
30 Patients |
|||||||
|---|---|---|---|---|---|---|---|---|
| 6 Rooms |
7 Rooms |
6 Rooms |
7 Rooms |
|||||
| Statistics | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth |
| Patient wait time for associate provider | 3.56 | 0.21 | 3.82 | 0.23 | 3.64 | 0.20 | 4.08 | 0.23 |
| Patient wait time for surgeon | 2.76 | 0.26 | 2.69 | 0.27 | 2.86 | 0.25 | 2.81 | 0.27 |
| Patient wait time for nutritionist | 3.55 | 0.42 | 3.61 | 0.43 | 3.76 | 0.40 | 3.87 | 0.42 |
| Patient wait time for physical therapist | 8.89 | 0.81 | 9.47 | 0.95 | 9.81 | 0.80 | 10.37 | 0.88 |
| Patient wait time for care planner | 4.80 | 0.30 | 4.94 | 0.34 | 5.25 | 0.28 | 5.69 | 0.34 |
| MildOAPatients time in clinic | 84.11 | 2.19 | 84.23 | 2.09 | 84.75 | 1.83 | 85.14 | 1.95 |
| ModOAPatients time in clinic | 89.06 | 2.22 | 88.41 | 2.12 | 89.08 | 2.01 | 90.44 | 1.93 |
| SevOAPatients time in clinic | 93.07 | 4.18 | 95.72 | 4.74 | 98.72 | 4.30 | 98.90 | 4.65 |
| OpPathPatients time in clinic | 102.92 | 4.38 | 105.20 | 5.32 | 103.73 | 4.11 | 106.06 | 4.62 |
| MildOAPatients (I) time in clinic | 96.89 | 2.72 | 97.77 | 2.80 | 97.59 | 2.43 | 99.68 | 2.64 |
| ModOAPatients (I) time in clinic | 100.75 | 2.65 | 102.71 | 3.00 | 102.57 | 2.37 | 103.76 | 2.71 |
| SevOAPatients (I) time in clinic | 116.43 | 5.45 | 119.72 | 6.01 | 118.29 | 5.46 | 119.53 | 5.30 |
| OpPathPatients (I) time in clinic | 119.33 | 6.31 | 124.45 | 7.41 | 120.62 | 6.14 | 123.39 | 7.38 |
| FollowupNonOpPath time in clinic | 66.24 | 2.50 | 66.94 | 2.51 | 67.49 | 2.37 | 68.72 | 2.50 |
| FollowupOpPath time in clinic | 69.32 | 3.96 | 68.97 | 4.15 | 72.68 | 3.91 | 71.24 | 3.85 |
| FollowupNonOpPath (I) time in clinic | 74.06 | 3.20 | 75.06 | 3.41 | 76.22 | 3.12 | 77.17 | 3.07 |
| FollowupOpPath (I) time in clinic | 80.38 | 4.85 | 80.25 | 4.53 | 81.22 | 4.03 | 81.84 | 4.11 |
Table A2.
Average statistics to Table 4 (all times in minutes; all utilisations in percentages) for 2 associate providers, 12-minute schedule time slot, random sequencing, 25 and 30 patients, and 6 and 7 rooms
| 25 Patients |
30 Patients |
|||||||
|---|---|---|---|---|---|---|---|---|
| 6 Rooms |
7 Rooms |
6 Rooms |
7 Rooms |
|||||
| Statistics | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth |
| Patient wait time for associate provider | 6.34 | 0.30 | 9.02 | 0.46 | 6.39 | 0.29 | 9.42 | 0.42 |
| Patient wait time for surgeon | 3.23 | 0.36 | 3.38 | 0.37 | 3.29 | 0.34 | 3.52 | 0.35 |
| Patient wait time for nutritionist | 4.36 | 0.49 | 4.35 | 0.51 | 4.84 | 0.47 | 5.04 | 0.61 |
| Patient wait time for physical therapist | 11.95 | 1.04 | 11.76 | 1.16 | 12.15 | 1.04 | 12.66 | 1.18 |
| Patient wait time for care planner | 7.54 | 0.47 | 8.15 | 0.54 | 8.09 | 0.43 | 8.43 | 0.52 |
| MildOAPatients time in clinic | 100.11 | 3.14 | 96.80 | 2.67 | 101.70 | 2.77 | 99.05 | 2.18 |
| ModOAPatients time in clinic | 102.15 | 3.03 | 101.61 | 2.79 | 104.59 | 2.74 | 102.66 | 2.54 |
| SevOAPatients time in clinic | 116.18 | 6.21 | 106.96 | 5.42 | 118.33 | 6.32 | 108.29 | 5.12 |
| OpPathPatients time in clinic | 118.55 | 6.59 | 120.40 | 6.18 | 121.70 | 6.69 | 122.61 | 6.48 |
| MildOAPatients (I) time in clinic | 113.26 | 3.49 | 108.75 | 2.95 | 114.82 | 3.26 | 111.04 | 2.88 |
| ModOAPatients (I) time in clinic | 115.63 | 3.45 | 111.99 | 3.12 | 117.21 | 3.29 | 114.59 | 2.92 |
| SevOAPatients (I) time in clinic | 126.32 | 7.90 | 120.52 | 6.93 | 129.44 | 6.48 | 124.27 | 7.01 |
| OpPathPatients (I) time in clinic | 134.03 | 7.67 | 134.57 | 7.43 | 136.56 | 6.38 | 133.58 | 7.01 |
| FollowupNonOpPath time in clinic | 81.59 | 3.42 | 80.21 | 3.17 | 83.62 | 3.17 | 82.66 | 2.80 |
| FollowupOpPath time in clinic | 84.90 | 5.07 | 90.18 | 5.84 | 90.80 | 5.27 | 92.85 | 5.49 |
| FollowupNonOpPath (I) time in clinic | 94.09 | 4.04 | 91.70 | 3.79 | 96.68 | 3.76 | 92.47 | 3.32 |
| FollowupOpPath (I) time in clinic | 94.77 | 6.52 | 94.26 | 5.95 | 96.56 | 5.67 | 93.62 | 5.47 |
Table A3.
Additional average statistics to Table 8 (all times in minutes; all utilisations in percentages) for 2 associate providers, 6 and 7 rooms, 10-minute schedule time slots for 7 follow-up patients at beginning of day, and 12- and 15-minute schedule time slots for 23 new patients
| 12-minute time slot for new patients |
15-minute time slot for new patients |
|||||||
|---|---|---|---|---|---|---|---|---|
| 6 Rooms |
7 Rooms |
6 Rooms |
7 Rooms |
|||||
| Statistics | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth | Mean | Halfwidth |
| Patient wait time for associate provider | 7.16 | 0.30 | 9.85 | 0.37 | 4.56 | 0.24 | 5.07 | 0.25 |
| Patient wait time for surgeon | 2.85 | 0.26 | 2.93 | 0.28 | 2.66 | 0.24 | 2.76 | 0.27 |
| Patient wait time for nutritionist | 4.88 | 0.56 | 4.93 | 0.57 | 4.15 | 0.47 | 4.35 | 0.49 |
| Patient wait time for physical therapist | 10.48 | 0.86 | 12.03 | 1.09 | 8.82 | 0.72 | 8.85 | 0.75 |
| Patient wait time for care planner | 6.78 | 0.33 | 6.86 | 0.35 | 5.66 | 0.30 | 6.03 | 0.34 |
| MildOAPatients time in clinic | 104.09 | 2.22 | 102.65 | 2.43 | 89.82 | 2.04 | 90.31 | 2.05 |
| ModOAPatients time in clinic | 106.39 | 2.56 | 105.36 | 2.46 | 91.00 | 2.17 | 91.36 | 2.05 |
| SevOAPatients time in clinic | 121.19 | 5.79 | 118.45 | 5.38 | 105.35 | 4.67 | 105.80 | 5.21 |
| OpPathPatients time in clinic | 113.43 | 5.25 | 121.91 | 5.50 | 109.55 | 5.10 | 107.18 | 4.71 |
| MildOAPatients (I) time in clinic | 118.29 | 2.89 | 112.43 | 2.66 | 100.26 | 2.84 | 99.48 | 2.68 |
| ModOAPatients (I) time in clinic | 116.43 | 2.84 | 116.72 | 2.73 | 106.30 | 2.71 | 105.14 | 2.66 |
| SevOAPatients (I) time in clinic | 131.00 | 6.24 | 131.30 | 6.78 | 114.94 | 5.95 | 113.99 | 5.97 |
| OpPathPatients (I) time in clinic | 139.24 | 6.79 | 134.42 | 7.75 | 123.85 | 6.37 | 125.24 | 5.66 |
| FollowupNonOpPath time in clinic | 61.73 | 1.83 | 61.73 | 1.76 | 60.50 | 1.87 | 60.00 | 1.74 |
| FollowupOpPath time in clinic | 67.47 | 2.95 | 67.18 | 2.89 | 70.17 | 3.50 | 68.54 | 3.24 |
| FollowupNonOpPath (I) time in clinic | 61.73 | 1.83 | 61.73 | 1.76 | 68.87 | 2.27 | 69.13 | 2.27 |
| FollowupOpPath (I) time in clinic | 67.47 | 2.95 | 67.18 | 2.89 | 76.68 | 4.20 | 75.91 | 3.79 |
Table A4.
Additional average statistics to Table 11 (all times in minutes; all utilisations in percentages) for 2 associate providers, 7 rooms, 10-minute time slots for 7 follow-up patients at beginning of day, 12-minute time slots for 23 new patients, 9 VM patients at the beginning of the day for schedules 1 & 2 plus 4 VM patients at the end of the day for schedule 2
| Schedule 1 |
Schedule 2 |
|||
|---|---|---|---|---|
| Statistics | Mean | Halfwidth | Mean | Halfwidth |
| Patient wait time for associate provider | 8.93 | 0.39 | 8.93 | 0.39 |
| Patient wait time for surgeon | 3.88 | 0.33 | 3.56 | 0.30 |
| Patient wait time for nutritionist | 5.61 | 0.49 | 5.36 | 0.48 |
| Patient wait time for physical therapist | 15.44 | 1.28 | 15.20 | 1.29 |
| Patient wait time for care planner | 8.04 | 0.51 | 8.01 | 0.51 |
| MildOAPatients time in clinic | 106.01 | 2.52 | 106.12 | 2.51 |
| ModOAPatients time in clinic | 111.94 | 2.86 | 111.40 | 2.72 |
| SevOAPatients time in clinic | 119.13 | 5.66 | 119.60 | 6.04 |
| OpPathPatients time in clinic | 131.96 | 6.22 | 131.78 | 6.16 |
| MildOAPatients (I) time in clinic | 117.16 | 3.01 | 117.11 | 3.03 |
| ModOAPatients (I) time in clinic | 121.92 | 3.55 | 122.07 | 3.50 |
| SevOAPatients (I) time in clinic | 137.80 | 7.36 | 136.77 | 7.10 |
| OpPathPatients (I) time in clinic | 150.82 | 7.98 | 150.50 | 8.22 |
| FollowupNonOpPath time in clinic | 72.20 | 2.68 | 72.20 | 2.68 |
| FollowupOpPath time in clinic | 80.19 | 4.36 | 80.19 | 4.36 |
| FollowupNonOpPath (I) time in clinic | 82.38 | 3.60 | 82.38 | 3.60 |
| FollowupOpPath (I) time in clinic | 89.22 | 5.22 | 89.22 | 5.22 |
Appendix B.
Figure B1.
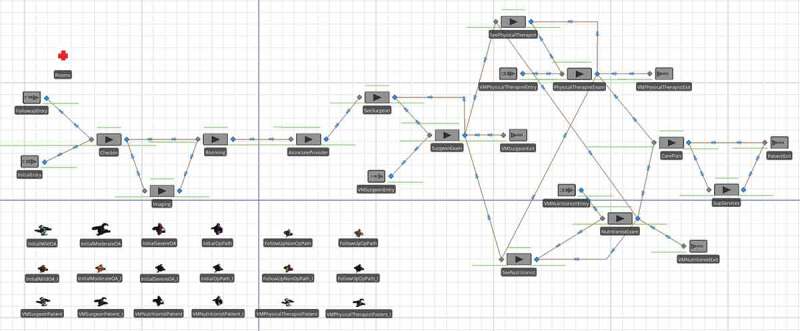
High-level simulation model of Joint Pain IPU with VM patients
Funding Statement
This work was supported by the Dell Medical School [Texas Health Catalyst Program]; Simio Academic Software Licence [Institution Grant]; McCombs School of Business, The University of Texas at Austin [Research Grant].
Disclosure statement
No potential conflict of interest was reported by the authors.
References
- Anand, E., & Panneerselvam, R. (2015). Literature review of open shop scheduling problems. Intelligent Information Management, 7(1), 33–52. [Google Scholar]
- Bard, J. F., Shu, Z., Morrice, D. J., Wang, D., Poursani, R., & Leykum, L. (2016). Improving patient flow at a family health clinic. Health Care Management Science, 19(2), 170–191. [DOI] [PubMed] [Google Scholar]
- Barli, C., Gascon, V., & Cartier, S. (2014). Design and analysis of an outpatient orthopaedic clinic performance with discrete-event simulation and design of experiments. Computers & Industrial Engineering, 78, 285–298. [Google Scholar]
- Berg, B., & Denton, B. T. (2012). Appointment planning and scheduling in outpatient procedure centers. In Hall R. (Ed.), Handbook of healthcare system scheduling (pp. 131–154). New York: Springer. [Google Scholar]
- Berg, B., Denton, B. T., Nelson, H., Balasubramanian, H., Rahman, A., Bailey, A., & Lindor, K. (2010). A discrete-event simulation model to evaluate operational performance of a colonoscopy suite. Medical Decision Making, 30(3), 380–387. [DOI] [PubMed] [Google Scholar]
- Blanco White, M. J., & Pike, M. C. (1964). Appointment systems in outpatients’ clinics and the effect on patients’ unpunctuality. Medical Care, 2(3), 133–145. [Google Scholar]
- Brailsford, S. C., Harper, P. R., Patel, B., & Pitt, M. (2009). An analysis of the academic literature on simulation and modelling in health care. Journal of Simulation, 3, 130–140. [Google Scholar]
- Braly, D. (1995). Seek alternatives via simulation software. Health Management Technology, 16(13), 13–15. [PubMed] [Google Scholar]
- Cartwright, A., & Windsor, J. (1993). Outpatients and their doctors: A study of patients, potential patients, general practitioners and hospital doctors. London: H.M. Stationary Office. [Google Scholar]
- Cayirli, T., Veral, E., & Rosen, H. (2006). Designing appointment scheduling systems for ambulatory care services. Health Care Management Science, 9, 47–58. [DOI] [PubMed] [Google Scholar]
- Cayirli, T., Yang, K. K., & Quek, S. A. (2012). A universal appointment rule in the presence of no-shows and walk-ins. Production and Operations Management, 21(4), 682–697. [Google Scholar]
- Chakraborty, S., Muthuraman, K., & Lawley., M. (2013). Sequential clinical scheduling with patient no-show: The impact of pre-defined slot structures. Socio-Economic Planning Sciences, 47(3), 205–219. [Google Scholar]
- Dobson, G., Tezcan, T., & Tilson., V. (2013). Optimal workflow decisions for investigators in systems with interruptions. Management Science, 59(5), 1125–1141. [Google Scholar]
- Dror, M. (1992). Open shop scheduling with machine dependent processing times. Discrete Applied Mathematics, 39(3), 197–205. [Google Scholar]
- Gartner, E., & Kolisch, R. (2014). Scheduling the hospital-wide flow of elective patients. European Journal of Operational Research, 233(3), 689–699. [Google Scholar]
- Gross, D., & Harris, C. M. (1985). Fundamentals of queueing theory (2nd ed.). New York: John Wiley & Sons. [Google Scholar]
- Günal, M. M., & Pidd, M. (2010). Discrete-event simulation for performance modelling in health care: A review of the literature. Journal of Simulation, 4, 42–51. [Google Scholar]
- Gupta, D., & Denton, B. (2008). Appointment scheduling in health care: Challenges and opportunities. IIE Transactions on Operations Engineering, 40(9), 800–819. [Google Scholar]
- Horvath, L. E., Yordan, E., Malhotra, D., Leyva, I., Bortel, K., Schalk, D., … Huml, J. (2010). Multidisciplinary care in the oncology setting: Historical perspective and data from lung and gynecology multidisciplinary clinics. Journal of Oncology Practice, 6(6), e21–e26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, X. (1994). Patient attitude towards waiting in an outpatient clinic and its applications. Health Services Management Research, 7, 2–8. [DOI] [PubMed] [Google Scholar]
- Hyer, N. L., Wemmerlov, U., & Morris, J. A. (2009). Performance analysis of a focused hospital unit: The case of an integrated trauma center. Journal of Operations Management, 27, 203–219. [Google Scholar]
- Iorio, R., Clair, A. J., Inneh, I. A., Slover, J. D., Bosco, J. A., & Zuckerman, J. D. (2016). Early results of Medicare’s bundled payment initiative for a 90-day total joint arthroplasty episode of care. Journal of Arthroplasty, 31(2), 343–350. [DOI] [PubMed] [Google Scholar]
- Jenkins, J., & Gisler, P. (2012). Let my patients flow: Lean diminishes gridlock at central baptist hospital. Industrial Engineer, 44(5), 39–44. [Google Scholar]
- Keswani, A., Koenig, K. M., & Bozic, K. J. (2016). Value-based healthcare: Part i–Designing and implementing integrated practice units for the management of musculoskeletal disease. Clinical Orthopaedics and Related Research, 474, 2100–2103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klassen, K. J., & Rohleder, T. R. (1996). Scheduling outpatient appointments in a dynamic environment. Journal Of Operations Management, 14(2), 83–101. doi: 10.1016/0272-6963(95)00044-5 [DOI] [Google Scholar]
- Koenig, K. M., & Bozic, K. J. (2015). Orthopaedic healthcare worldwide: The role of standardization in improving outcomes. Clinical Orthopaedics and Related Research, 473(11), 3360–3363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig, K. M., Keswani, A., & Bozic, K. J. (2016, April 27). The role of integrated practice units in the treatment of musculoskeletal conditions. American Associate of Orthopaedic Surgeons, AAOS Now. Retrieved from http://www.aaos.org/AAOSNow/2016/Apr/Managing/managing1/?ssopc=1
- Lahiri, A., & Seidmann, A. (2012). Information hang-overs in healthcare service systems. Manufacturing & Service Operations Management, 14(4), 634–653. [Google Scholar]
- Law, A. M., & Kelton, W. D. (1991). Simulation modeling and analysis (2nd ed.). New York: McGraw-Hill, Inc. [Google Scholar]
- Leeftink, A., Vliegen, I., & Hans, E. (2017). Stochastic integer programming for multi-disciplinary clinic planning. Health Care Management Science. doi: 10.1007/s10729-017-9422-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leeftink, A. G., Bikker, I. A., Vliegen, I. M. H., & Boucherie, R. J. (2018). Multi-disciplinary planning in health care: A review. Health Systems, 1–24. doi: 10.1080/20476965.2018.1436909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- M’Hallah, R., & Al-Roomi, A. H. (2014). The planning and scheduling of operating rooms: A simulation approach. Computers & Industrial Engineering, 78, 235–248. [Google Scholar]
- Marmor, Y. N., Golany, B., Israelit, S., & Mandelbaum, A. (2012). Designing patient flow in emergency departments. IIE Transactions on Healthcare Systems Engineering, 2(4), 233–247. [Google Scholar]
- McCarthy, K., McGee, H. M., & O’Boyle, C. A. (2000). Outpatient clinic waiting times and non-attendance as indicators of quality. Psychology, Health & Medicine, 5, 287–293. [Google Scholar]
- Millhiser, W. P., Veral, E. A., & Valenti, B. C. (2012). Assessing appointment systems’ operational performance with policy targets. IIE Transactions on Healthcare Systems Engineering, 2, 274–289. [Google Scholar]
- Morrice, D. J., Wang, E., Bard, J. F., Leykum, L., Noorily, S., & Veerapaneni, P. (2014). A patient-centered surgical home to improve outpatient surgical processes of care and outcomes. IIE Transactions on Healthcare Systems Engineering, 4(3), 119–134. [Google Scholar]
- Murray, M., & Berwick, D. M. (2003). Advance access: Reducing waiting and delays in primary care. Journal of the American Medical Association, 289(8), 1035–1039. [DOI] [PubMed] [Google Scholar]
- Mutlu, S., Benneyan, J., Terrell, J., Jordan, V., & Turkcan, A. (2015). A co-availability scheduling model for coordinating multi-disciplinary care teams. International Journal of Production Research, 53(24), 7226–7237. [Google Scholar]
- Myers, R. H., Montgomery, D. C., & Anderson-Cook, C. M. (2009). Response surface methodology: Process and product optimization using designed experiments (3rd ed.). Hoboken, NJ: Wiley. [Google Scholar]
- Noon, C. E., Hankins, C. T., & Côté, M. J. (2003). Understanding the impact of variation in the delivery of healthcare services. Journal Of Healthcare Management, 48(2), 82–97. doi: 10.1097/00115514-200303000-00004 [DOI] [PubMed] [Google Scholar]
- Oh, H.-J., Muriel, A., Balasubramanian, H., Atkinson, K., & Ptaszkiewicz, T. (2013). Guidelines for scheduling in primary care under different patient types and stochastic nurse and provider service times. IIE Transactions on Healthcare Systems Engineering, 3(4), 263–279. [Google Scholar]
- Pinedo, M. L. (2016). Scheduling: Theory, algorithms, and systems (5th ed.). New York: Springer. [Google Scholar]
- Porter, M. E. (2010). What is value in health care? New England Journal of Medicine, 363(26), 2477–2481. [DOI] [PubMed] [Google Scholar]
- Porter, M. E., & Lee, T. H. (2013, October). The strategy that will fix health care. Harvard Business Review, 91(10), 50–70.23898735 [Google Scholar]
- Romero, H. L., Dellaert, N. P., van der Geer, S., Frunt, N. P., . M., Jansen-Vullers, M. H., & Krekels, G. A. M. (2013). Admission and capacity planning for the implementation of one-stop-shop in skin cancer treatment using simulation-based optimization. Health Care Management Science, 16(1), 75–86. [DOI] [PubMed] [Google Scholar]
- Saghafian, S., Hopp, W. J., Van Oyen, M. P., Desmond, J. S., & Kronick, S. L. (2014). Complexity-augmented triage: A tool for improving patient safety and operational efficiency. Manufacturing & Service Operations Management, 16(3), 329–345. [Google Scholar]
- Samudra, M., Van Riet, C., Demeulemeester, E., Cardoen, B., Vansteenkiste, N., & Rademakers, F. E. (2016). Scheduling operating rooms: Achievements, challenges and pitfalls. Journal of Scheduling, 19(5), 493–525. [Google Scholar]
- Savin, S. (2006). Managing patient appointments in primary care. In Hall R. W. (Ed.), Patient flow: Reducing delay in healthcare delivery (Chapter 5. pp. 123–150). New York: Springer. [Google Scholar]
- Sinreich, D., & Marmor, Y. (2005). Emergency department operations: The basis for developing a simulation tool. IIE Transactions on Operations Engineering, 37(3), 233–245. [Google Scholar]
- Strasser, F., Sweeney, C., Willey, J., Benisch-Tolley, S., Palmer, J. L., & Bruera, E. (2004). Impact of a half-day multidisciplinary symptom control and palliative care outpatient clinic in a comprehensive cancer center on recommendations, symptom intensity, and patient satisfaction: A retrospective descriptive study. Journal of Pain and Symptom Management, 27(6), 481–491. [DOI] [PubMed] [Google Scholar]
- Swisher, J. R., Jacobson, S. H., Jun, J. B., & Balci, O. (2001). Modeling and analyzing a physician clinic environment using discrete-event (visual) simulation. Computers & Operations Research, 28(2), 105–125. [Google Scholar]
- Utley, M., & Worthington, D. (2012). Capacity planning. In Hall R. (Ed.), Handbook of healthcare system scheduling (Chapter 2. pp. 11–30). New York: Springer. [Google Scholar]
- Vanden Bosch, P. M., & Dietz, D. C. (2000). Minimizing expected waiting in a medical appointment system. IIE Transactions on Operations Engineering, 32(9), 841–848. [Google Scholar]
- White, D. L., Froehle, C. M., & Klassen, K. J. (2011). The effect of integrated scheduling and capacity policies on clinical efficiency. Production and Operations Management, 20(2), 442–455. [Google Scholar]
- Woodall, J. C., Gosselin, T., Boswell, A., Murr, M., & Denton, B. T. (2013). Improving patient access to chemotherapy treatment at Duke Cancer Institute. Interfaces, 43(5), 449–461. [Google Scholar]
- Zonderland, M. E., Boer, F., Boucherie, R. J., de Roode, A., & van Kleef, J. W. (2009). Redesign of a university hospital preanesthesia evaluation clinic using a queuing theory approach. Anesthesia and Analgesia, 109(5), 1612–1621. [DOI] [PubMed] [Google Scholar]
- Zorbas, H., Barraclough, B., Rainbird, K., Luxford, K., & Redman, R. (2003). Multidisciplinary care for women with early breast cancer in the Australian context: What does it mean? Healthcare, 179, 528–531. [DOI] [PubMed] [Google Scholar]


