Abstract
Background
In reverse shoulder arthroplasties (RSA), osseous in-growth is promoted if glenoid micromotion does not exceed 150 μm. The purpose of this study was to determine whether the configuration of central fixation for RSA glenoid baseplates reduces implant micromotion or changes scapula bone stresses.
Methods
Using finite element analysis, glenoid baseplate fixation was tested in a cohort of 3 male and 2 female patients who were to undergo RSA. Computer models were created for 3 different RSA glenoid baseplate and 84 glenosphere designs, a central threaded peg (1 variant, D-TP), a central unthreaded peg (2 variants, I- 85 P(15) and I-P(25)), and a central peg with a screw (2 variants, A-PS and I-PS). A compressive and shear force of 756 N was distributed across the glenosphere with the scapula anchored.
Results
Displacement was within 20-130 μm at the glenosphere baseplate-bone interface for all baseplates. The glenospheres with unthreaded pegs had intermediate displacement values (I-P(15): median, 89 μm; range, 32-112 μm; and I-P(25): median, 93 μm; range, 31-109 μm). The von Mises stresses were 1.8-7.0 MPa within cortical bone and 0.6-1.6 MPa within trabecular bone. Cortical bone stresses were similar with unthreaded pegs (I-P(15): median, 4.2 MPa; range, 1.8-6.0 MPa; and I-P(25): median, 4.2 MPa; range, 1.8-6.1 MPa), whereas mean trabecular stresses were similar for all configurations.
Conclusions
All configurations yielded adequate stability, with micromotions being below 150 μm. The unthreaded pegged designs provided a valid alternative to the stable threaded pegged convex baseplates in terms of micromotions and bone stresses.
Keywords: RSA, glenoid baseplate, peg fixation, micromotion, finite element analysis
The number of reverse shoulder arthroplasties (RSA) performed is increasing4 especially for complex conditions.2 The most common primary diagnoses are osteoarthritis (45%), followed by rotator cuff arthropathy (35%) and fracture (15%).24 For primary RSA, the complication rates are typically around 13%-25%,2,4,9,35 whereas for revision RSA, the complication rates double or triple to 33% or 69%.2,4,35,36 Most revision procedures are performed to replace both the cup and glenosphere (22%), the humeral component only (20%), cup only (20%), and humeral head only (15%).24 The main complications in RSA include instability, infection, and notching, but albeit rare, loosening is the most common complication specific to the glenoid.2,4 The main risk factors for baseplate failure include the use of all 3.5 mm nonlocking peripheral screws and the use of a bone graft to address inadequate bony support beneath the glenoid baseplate.3
To promote osseous in-growth, glenoid micromotion should ideally be limited to 50 μm18,39 and should not exceed 150 μm.31,37 The magnitude of glenoid micromotion is, therefore, a key indicator of glenoid fixation potential. Factors that govern glenoid fixation in RSA are the length and diameter of the fixation screws,10,18 the inclination of the screws relative to the glenoid baseplate,10 inferior tilt of the baseplate,8,10 and the lateral offset of the glenosphere center of rotation.10,37,38
Finite element analysis (FEA) enables the modeling of the functional RSA glenoid baseplate/screw and osseous interface to estimate glenoid micromotion and stress distribution. Hopkins et al18 performed a parametric FEA to investigate the effects of screw size and orientation on glenoid fixation and found that glenoid micromotion was reduced by maximizing screw length, diameter, and inclination angle. Denard et al10 also performed an FEA study on RSA implanted in a polyurethane block and confirmed that divergent screws reduce stress and displacement. In a study using sawbones, Königshausen et al21 demonstrated that glenoid loading capacity increased when pegs were anchored deep in the bone stock. The purpose of this study was to use FEA to determine whether the configuration of central fixation RSA glenoid baseplates reduces implant micromotion or changes scapula bone stresses.
Material and methods
Anatomic models
The effect of glenoid baseplate fixation on micromotion and stress distribution was tested in a small cohort of 3 male and 2 female patients who were to undergo RSA (Table I). The scapular geometry of each patient was segmented from computed tomography (CT) scan data using VolView v3.2 (Kitware, Clifton Park, NY, USA). During segmentation, the scapula was isolated from the clavicle along the acromioclavicular joint through manual selection, after which the cortical and trabecular bone material properties were based on the CT Hounsfield units.6,14,29 The same CT scanner (SOMATOM Definition AS; Siemens Healthcare SAS, Saint-Denis, France) with standardized scanner parameters (281 mA; 120 kVp; B31s reconstruction kernel) was used for each patient. The segmented geometries were then imported into SolidWorks 2016 (Dassault Systèmes; SolidWorks Corporation, Waltham, MA, USA), before Young's moduli were assigned using the method described by Pomwenger et al.32 All patients had provided written informed consent for the use of their images and data for research and publishing purposes.
Table I.
Patient parameters
| Patient |
|||||
|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | |
| Patient cohort | |||||
| Sex | M | F | M | F | M |
| Side | Right | Right | Left | Left | Right |
| Age (yr) | 41 | 49 | 40 | 41 | 46 |
| Height (cm) | 193 | 163 | 170 | 168 | 182 |
| Weight (kg) | 105 | 47 | 85 | 74 | 98 |
| Retroversion (°) | 3 | 4 | 0 | 4 | 5 |
| Inclination (°) | 2 | 9 | 7 | 13 | 4 |
| Glenoid diameter (mm) | 70.2 | 60 | 68.8 | 70.6 | 68.2 |
| Cortical Young's modulus (MPa) | 4336 | 2633 | 1880 | 4259 | 2617 |
| Trabecular Young's modulus (MPa) | 305 | 33 | 43 | 68 | 144 |
| Mesh density (number of elements) | |||||
| Cortical bone | 76,000 | 60,000 | 44,000 | 35,000 | 75,000 |
| Trabecular bone | 72,000 | 50,000 | 37,000 | 37,000 | 63,000 |
| Baseplate | 30,000 | 30,000 | 30,000 | 30,000 | |
| Central screw | 15,000 | 15,000 | 15,000 | 15,000 | |
| Peripheral screw (per screw) | 4000 | 4000 | 4000 | 4000 | |
The bone density in each voxel was estimated by
| (1) |
with the bone density (g cm−3) per voxel, a subject-specific coefficient, and the Hounsfield unit value.The coefficient was calculated for each patient using
| (2) |
with 1.8 g cm−3 and the maximum Hounsfield unit value.
The cortical and trabecular boundaries in each slice were then differentiated using the thresholding (trabecular bone <20% of the maximum density) and manual selection tools of the segmentation software (VolView v3.2; Kitware). The mean cortical () and mean trabecular () densities were then calculated using
| (3) |
with cortical, trabecular, the current voxel number, and the total number of voxels in the cortical and trabecular slice.
The mean Young's modulus ( in Pa) could then be assigned using the following relationship:
| (4) |
The Poisson ratio was set at 0.3 for both cortical and trabecular bone.10 Young's moduli of the osseous geometries of the 5 anatomical models are shown in Table I.
Implant configurations
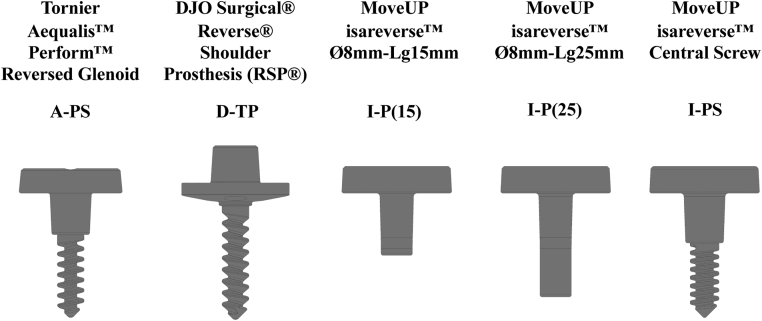
Computer models of 5 different RSA glenoid baseplate and glenosphere designs were created using SolidWorks 2016 (Dassault Systèmes; SolidWorks Corporation) (Table II, Fig. 1). Measurements were obtained from the manufacturer and, where unavailable, physically measured on implant models.
Table II.
RSA glenoid baseplate designation and properties
| Commercial name | Tornier Aequalis Perform Reversed Glenoid | DJO Surgical Reverse Shoulder Prosthesis (RSP) | MoveUP isareverse Ø8mm-Lg15mm | MoveUP isareverse Ø8mm-Lg25mm | MoveUP isareverse Central Screw |
|---|---|---|---|---|---|
| Designation | A-PS | D-TP | I-P(15) | I-P(25) | I-PS |
| Baseplate/bone interface | Flat | Convex | Flat | Flat | Flat |
| Central fixation configuration | Unthreaded peg with screw | Threaded peg | Unthreaded peg (15 mm) | Unthreaded peg (25 mm) | Unthreaded peg with screw |
| Baseplate diameter (mm) | 25 | 26 | 26 | 26 | 26 |
| Central screw diameter (mm) | 6.5 | – | – | – | 7 |
| Peg length (mm) | 10 | 30 | 15 | 25 | 12 |
| Peg diameter (mm) | 10 | 6.5 | 8 | 8 | 10 |
| Number of peripheral screws | 4 | 4 | 4 | 4 | 4 |
| Diameter of peripheral screws (mm) | 5 | 5 | 4.5 | 4.5 | 4.5 |
Figure 1.
Reverse shoulder arthroplasties glenoid baseplate designs (excluding peripheral screws).
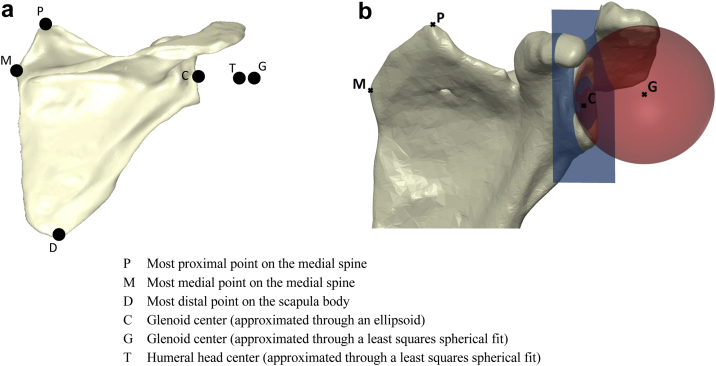
The implants were virtually positioned on each patient's scapula following the manufacturers' surgical guidelines and under the supervision of a senior surgeon (NB). A standard coordinate system was defined based on the anatomical landmarks on the scapula (Fig. 2, a), with its origin set at the glenoid center (G):
-
•
Step 1: Z-axis
-
•
Step 2: temporary X-axis
-
•
Step 3: Y-axis
-
•
Step 4: X-axis
with weighting factors between 0 and 1, where their sum is always equal to 1; the vector originating at point P in the direction of point D; and the vector cross product.
Figure 2.
(a) Definition of landmarks on the scapula for the formulation of the coordinate system. (b) Illustration of glenoid sizing, by means of a least-squares plane and sphere being fitted to the glenoid.
A least-squares plane was fitted to points on the glenoid surface to measure glenoid version and inclination in the newly defined coordinate system. In addition, the glenoid size was defined by a least-squares sphere, fitted to the glenoid surface (Fig. 2, b).
During positioning of the glenoid baseplates, 4 peripheral screws were added and kept parallel to the baseplate axis, and their lengths were adapted for each patient to ensure that they were bicortical in each scapula. For each patient, the lengths of the peripheral screws were then constant across the 5 baseplate designs, and they were modeled as locked screws. Central screws and long pegs were also bicortical. Glenosphere diameters between 36 and 42 mm were chosen for each patient under the supervision of a senior surgeon (JB), whereas the lateralization of the center of rotation remained constant within each patient for the different implants. The glenospheres were manufactured from CrCo28Mo (E, 220 GPa; Poisson, 0.3), and the glenoid baseplates and screws from Ti6Al4V-ELI (E, 112.4 GPa; Poisson, 0.34). Implants were positioned with up to ±5° of anteversion and 0° of downward inclination depending on patient morphology and kept constant for any given patient.
Finite element analysis
Tetrahedral volume meshes (10 nodes per element) were formulated from the 3-dimensional anatomic and implant models in Solidworks 2016 (Dassault Systèmes; SolidWorks Corporation). The mesh quality was set to a maximum of 0.05 mm difference between the segmented and the mesh 3-dimensional models. The approximate mesh density for each patient is provided in Table I.
A compressive and shear force of 756 N37 was distributed across the glenosphere, and the scapula was anchored at its medial aspect and at the acromial clavicular joint (Fig. 3). Eight contact interactions were defined between the model sections, with no penetration allowed between bodies in contact (Table III). Contacts between the cortical and trabecular bone, the glenosphere and baseplate, the baseplate and screws (central and peripheral), and the peripheral screws and bone (trabecular and cortical) were tied. A coefficient of friction of 0.7437,40 was applied between the bone (trabecular and cortical) and baseplate, and a coefficient of friction of 0.415,34 was applied between the bone and central screw to allow for relative movement between the baseplate and bone.
Figure 3.
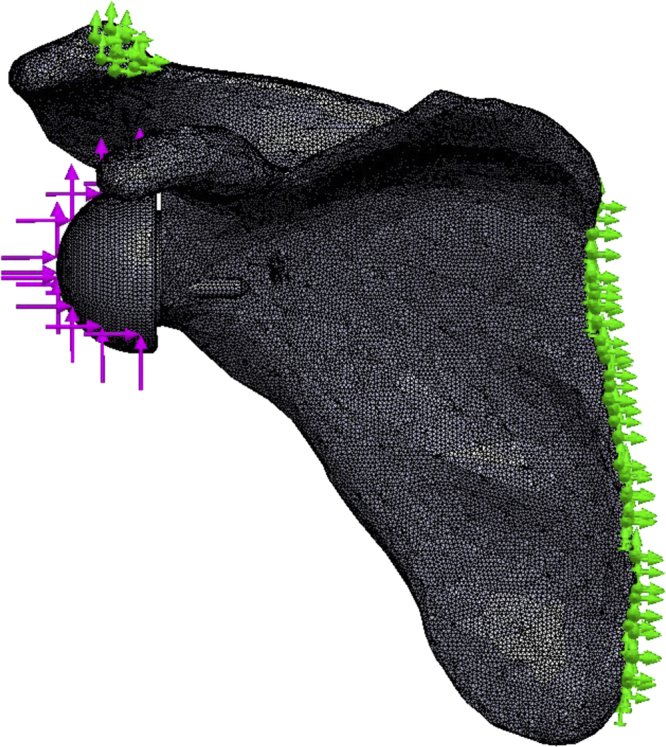
Schematic presentation of the application of the boundary conditions. The  indicate the compressive and shear force application points. The
indicate the compressive and shear force application points. The  indicate the anchoring points on the scapula.
indicate the anchoring points on the scapula.
Table III.
Contact interaction between the model sections
| Cortical Bone | Trabecular bone | Central screws | Peripheral screws | Glenosphere | |
|---|---|---|---|---|---|
| Trabecular bone | Tied | – | – | – | – |
| Central screws | μ = 0.4 | μ = 0.4 | – | – | – |
| Peripheral screws | Tied | Tied | – | – | – |
| Baseplate | μ = 0.74 | μ = 0.74 | Tied | Tied | Tied |
The displacement of the baseplate with respect to the bone was calculated by tracking the displacement of baseplate nodes from their respective closest neighbors on the bone at the baseplate/bone interface. The micromotion was then defined by calculating the mean resultant nodal displacements in superior-inferior, medial-lateral, and anterior-posterior directions. The bone stress distribution in the vicinity of the baseplate and screws was monitored.
An implicit linear static FEA was conducted in Solidworks 2016 (Dassault Systèmes; SolidWorks Corporation). Convergence was achieved with a displacement threshold of 1.0e-06 with the maximum allowable number of iterations set at 1.0e+07. All the analyses were run on a workstation with an Intel CORE i7-6700 @3.40GHz processor, 16 GB RAM, and an NVIDIA Quadro K420 graphics card. Wall times took an average of 60 minutes per simulation.
Model verification
A mesh convergence analysis was done for model P1 using implant I-PS. The criterion for convergence was defined as a change of less than 5% in the maximum displacement between mesh densities (Table IV). The mesh convergence analysis showed that the maximum and mean displacement would change by less than 0.05% when limiting maximum element edge lengths to 1 mm. The percentage change in the trabecular mean stress between mesh densities was below 12%, whereas the percentage change in cortical mean stress was below 0.05%. A final maximum element edge length of 1 mm was chosen.
Table IV.
Mesh convergence analysis on the I-PS glenosphere for patient P1
| Element length (mm) | 1 | 0.75 | 0.5 |
|---|---|---|---|
| Number of elements | 297,883 | 605,480 | 1,773,420 |
| Number of nodes | 432,390 | 864,595 | 2,485,387 |
| Mean displacement (μm) | 34.8 | 34.8 | 34.2 |
| Maximum displacement (μm) | 56.3 | 56.6 | 56.2 |
| Cortical—mean von Mises stress (MPa) | 2.35 | 2.36 | 2.36 |
| Trabecular—mean von Mises stress (MPa) | 0.95 | 0.89 | 0.83 |
Statistical analysis
Descriptive statistics were used to summarize the data. The means, medians, and ranges of the mean baseplate displacements and bone stresses were reported in text as well as boxplots using R version 3.3.3 (R Foundation for Statistical Computing, Vienna, Austria).
Results
Micromotion
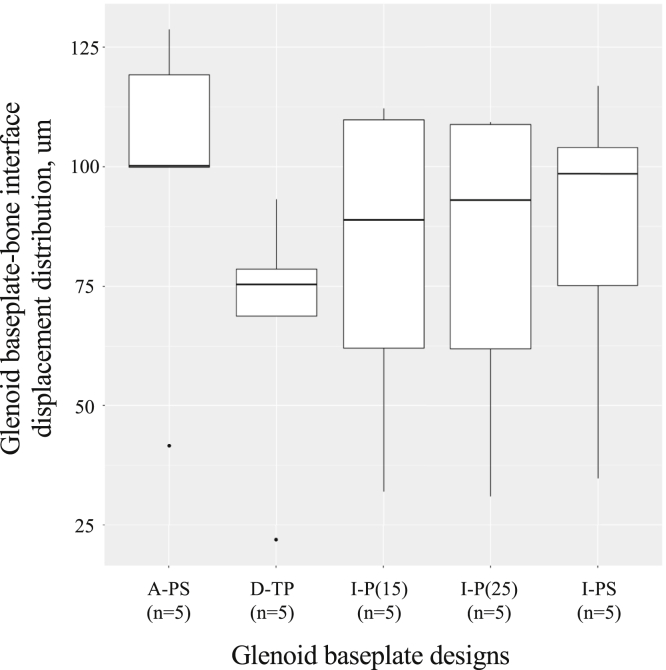
Using all anatomical models and implant configurations, the displacement was within 20-130 μm at the glenoid baseplate-bone interface (Fig. 4). The displacement was higher for glenoid baseplates with unthreaded central peg and screw fixation (A-PS: median, 100 μm; range, 42-129 μm; and I-PS: median, 98 μm; range, 35-104 μm) and lower for the glenoid baseplates with threaded central peg fixation (D-TP: median, 72 μm; range, 22-93 μm). The glenoid baseplates with unthreaded central peg fixation had intermediate displacement values (I-P(15): median, 89 μm; range, 32-112 μm; and I-P(25): median, 93 μm; range, 31-109 μm).
Figure 4.
Glenoid baseplate-bone displacement distribution.
Bone stresses
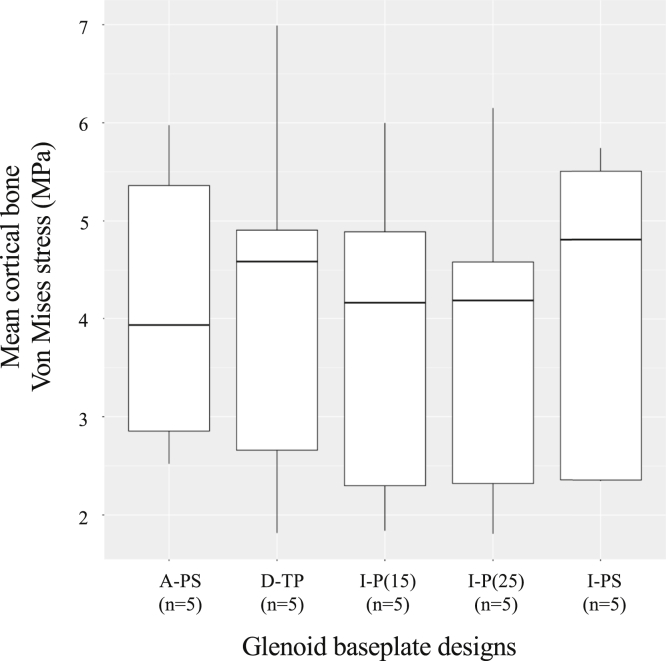
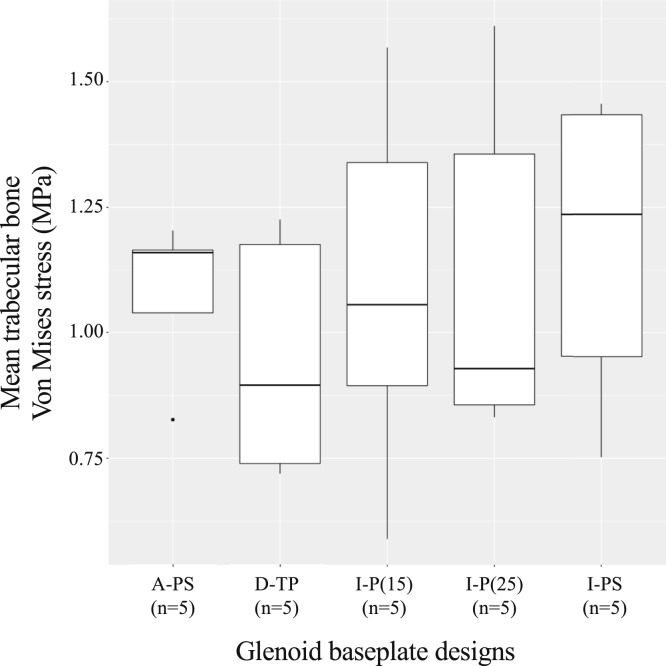
Using all anatomical models and implant configurations, von Mises stresses were 1.8-7.0 MPa within cortical bone and 0.6-1.6 MPa within trabecular bone (Figs. 5 and 6). The cortical stresses were higher for 1 glenoid baseplate with unthreaded central peg with screw fixation (I-PS: median, 4.8 MPa; range, 1.8-7.0 MPa) and the glenoid baseplate with threaded central peg fixation (D-TP: median, 4.6 MPa; range, 2.4-5.7 MPa). Cortical stresses were lower for the other glenoid baseplate with unthreaded central peg with screw fixation (A-PS: median, 3.9 MPa; range, 2.5-6.0 MPa). The cortical bone stresses were similar using glenoid baseplates with unthreaded central peg fixation (I-P(15): median, 4.2 MPa; range, 1.8-6.0 MPa; and I-P(25): median, 4.2 MPa; range, 1.8-6.1 MPa). The mean trabecular von Mises stresses were similar for all the fixation methods used (Fig. 6).
Figure 5.
Mean cortical bone von Mises stress distribution.
Figure 6.
Mean trabecular bone von Mises stress distribution.
Discussion
Glenoid baseplate fixation is facilitated through the baseplate geometry and peripheral screw arrangement. Stability will increase with peripheral screws that are divergent, longer, and thicker based on finite element studies.10,18 There is no scientific evidence eluding to a difference in stability or fixation between a screwed, keeled, single pegged, or double pegged baseplates.28
Although glenoid loosening after RSA is rare (<4%), it remains a burdensome complication.22 Factors associated with glenoid loosening include infection,27 poor bone stock,7 glenoid component design17 and fixation method,5 or excessive shear loading. In the present analysis, all the contemporary baseplate designs with peripheral locking screws exhibited adequate stability. These results are therefore in support of the clinical observations of reduced failure rates after the introduction of locking screws in the glenoid baseplate.26
Previous finite element studies and in vitro studies that investigated glenoid stability and load response were limited by their use of solid rigid polyurethane foam or sawbone blocks.10,13,16,18,21,25,30,37 Glenoid baseplate positioning and stability on the scapular geometry cannot be simulated accurately by a flat surface as is the case with polyurethane and sawbone blocks. Other studies that implemented scapular geometry in their models focused on bone remodeling,1,33 the role of inferior tilt on glenoid stability8 and stress distribution due to glenoid distalization,38,39 lateralization,12,23,38,39 and biograft thickness.38
In this study, we evaluated whether the configuration of central fixation for RSA glenoid baseplates reduces implant micromotion or changes scapular bone stresses. The use of real patient scapulae allowed for the inclusion of morphology and bone density variability and its role in the displacement and cortical and cancellous stress response, thus enabling better assessment of glenoid component stability in RSA. In comparison to mechanical testing techniques, the FEA provided a more detailed investigation of mean stress and micromotion, and it also enabled the application of repeatable boundary conditions to each specimen. On the basis of our results on the relative interfacial micromotion, all designs yielded adequate stability with micromotions being below 150 μm. The higher cortical bone von Mises stresses for 2 of the baseplates are likely due to medial contact between the central fixation end and the scapular cortex. None of the fixation configurations had a considerable effect on trabecular bone stresses, suggesting no potential deleterious effects.
The outcomes from this study indicated no discernible difference in displacement and stress response between the 2 pegged glenoid baseplates. This is in contrast to the findings from a previous study,25 which showed that a shorter central peg will lead to increased micromotions based on results from mechanical testing in a polyurethane block. A possible explanation for this contradiction in outcomes is the 4 peripheral screws that were added to all baseplates. Although 2 peripheral screws provide adequate stability,19 additional screws become important if the central peg depth is reduced.28 Our results indicate that the D-TP glenoid baseplate that has a spherical bone-baseplate interface had the smallest displacements. James et al20 have previously shown that convex backed glenoid baseplates also exhibit larger surface contact areas. However, in the same study, flat backed designs delivered better screw engagement, which was defined as the length from where the screw enters the bone until it begins to protrude from the bone, as well as less bone volume removal. Surprisingly, convex backed baseplates might also lead to more cortical bone loss, with increased difficulty to get a proper position and orientation. A possible explanation is that a convex baseplate keel might be larger than a flat baseplate post and that with these glenoids, a reamer for the convex baseplate will have a smaller radius of curvature than the actual glenoid curvature.20
The central fixation geometries in the A-PS, I-PS and D-TP were not defeatured, which allowed for relative comparison between the designs. Dharia et al11 showed in a parametric finite element study that predicted trends become inconsistent between comparable systems if the screws are defeatured and tied. In addition, defeaturing produced lower predicted values for micromotion.
Strengths and limitations
The results of this study must be interpreted in conjunction with the assumptions and simplifications made. First, the magnitude and application of the force boundary condition used in this study remained constant between anatomical models. Previous studies have used a variety of force magnitudes ranging from 0.6 BW to 1.3 BW,8 whereas the magnitude used in the present study has been used in 2 previous studies.18,37 The application of a compressive and shear force is a simplification of the force the humeral component will exert on the glenosphere, and therefore the simulated moment arm might be different to the physiological moment arm. Second, the peripheral screws were defeatured, which considerably reduced the computational load. Although a simplification, the authors believe that the effect will be negligible because at any given time at least 2 screws were bicortical. Third, the mechanics of baseplates with central compression screws were further simplified by not adding or correcting for the pre-tension that would account for added compression afforded by real screws. Fourth, bone mineral density was based on Hounsfield Units, for which the CT scanner settings were not calibrated using standard samples. The scans for each patient were obtained with the same CT scanner, for which scanning parameters and postprocessing settings were standardized and consistently applied. Fifth, the study analyzed computational results from a small cohort of only 5 shoulders. Because of the small sample size and therefore low statistical power, a comprehensive statistical analysis was not warranted, and the authors could also not perform additional analyses to investigate the effect of bone density on micromotion and bone stress distribution. Sixth, the material behavior of the cortical and trabecular bone was simulated with a linear-elastic material model that did not account for the anisotropic behavior of bone. Finally, the role of other biomechanical structures such as the capsule, stabilizing ligaments, and tendons was not considered. The anatomical models were, however, modeled from CT scans of patients who were to undergo RSA.
Conclusion
Our study demonstrates that all the considered designs will provide adequate stability. The unthreaded pegged designs provided a valid alternative to the more stable threaded pegged convex baseplates in terms of micromotions and bone stresses. The clinical relevance of these findings is that current RSA baseplates provide adequate stability to facilitate bone in-growth and therefore reduce the risk of loosening.
Acknowledgments
The authors are grateful to Paul Potel for his assistance with the finite element analyses. The authors are also grateful to Mo Saffarini for his assistance in manuscript preparation.
Disclaimer
Laurent Geais declares employment at Move-Up.
Jacobus Hendrik Müller declares employment at ReSurg.
Julien Berhouet declares receiving consulting fees from Move-Up.
The other authors, their immediate families, and any research foundations with which they are affiliated have not received any financial payments or other benefits from any commercial entity related to the subject of this article.
Footnotes
This basic science study did not require ethical approval.
References
- 1.Ahir S.P., Walker P.S., Squire-Taylor C.J., Blunn G.W., Bayley J.I. Analysis of glenoid fixation for a reversed anatomy fixed-fulcrum shoulder replacement. J Biomech. 2004;37:1699–1708. doi: 10.1016/j.jbiomech.2004.01.031. [DOI] [PubMed] [Google Scholar]
- 2.Barco R., Savvidou O.D., Sperling J.W., Sanchez-Sotelo J., Cofield R.H. Complications in reverse shoulder arthroplasty. EFORT Open Rev. 2017;1:72–80. doi: 10.1302/2058-5241.1.160003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bitzer A., Rojas J., Patten I.S., Joseph J., McFarland E.G. Incidence and risk factors for aseptic baseplate loosening of reverse total shoulder arthroplasty. J Shoulder Elbow Surg. 2018;27:2145–2152. doi: 10.1016/j.jse.2018.05.034. [DOI] [PubMed] [Google Scholar]
- 4.Boileau P. Complications and revision of reverse total shoulder arthroplasty. Orthop Traumatol Surg Res. 2016;102(1 Suppl):S33–S43. doi: 10.1016/j.otsr.2015.06.031. [DOI] [PubMed] [Google Scholar]
- 5.Boileau P., Watkinson D.J., Hatzidakis A.M., Balg F. Grammont reverse prosthesis: design, rationale, and biomechanics. J Shoulder Elbow Surg. 2005;14:S147–S161. doi: 10.1016/j.jse.2004.10.006. [DOI] [PubMed] [Google Scholar]
- 6.Cattaneo P.M., Dalstra M., Frich L.H. A three-dimensional finite element model from computed tomography data: a semi-automated method. Proc Inst Mech Eng H. 2001;215:203–213. doi: 10.1243/0954411011533760. [DOI] [PubMed] [Google Scholar]
- 7.Cazeneuve J., Cristofari D. Grammont reversed prosthesis for acute complex fracture of the proximal humerus in an elderly population with 5 to 12 years follow-up. Rev Chir Orthop Reparatrice Appar Mot. 2006;92:543. doi: 10.1016/j.otsr.2013.12.005. [DOI] [PubMed] [Google Scholar]
- 8.Chae S.W., Lee H., Kim S.M., Lee J., Han S.H., Kim S.Y. Primary stability of inferior tilt fixation of the glenoid component in reverse total shoulder arthroplasty: a finite element study. J Orthop Res. 2016;34:1061–1068. doi: 10.1002/jor.23115. [DOI] [PubMed] [Google Scholar]
- 9.Choi S., Bae J.H., Kwon Y.S., Kang H. Clinical outcomes and complications of cementless reverse total shoulder arthroplasty during the early learning curve period. J Orthop Surg Res. 2019;14:53. doi: 10.1186/s13018-019-1077-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Denard P.J., Lederman E., Parsons B.O., Romeo A.A. Finite element analysis of glenoid-sided lateralization in reverse shoulder arthroplasty. J Orthop Res. 2017;35:1548–1555. doi: 10.1002/jor.23394. [DOI] [PubMed] [Google Scholar]
- 11.Dharia M.A., Bischoff J.E., Schneider D. Impact of modeling assumptions on stability predictions in reverse total shoulder arthroplasty. Front Physiol. 2018;9:1116. doi: 10.3389/fphys.2018.01116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Elwell J., Choi J., Willing R. Quantifying the competing relationship between adduction range of motion and baseplate micromotion with lateralization of reverse total shoulder arthroplasty. J Biomech. 2017;52:24–30. doi: 10.1016/j.jbiomech.2016.11.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Favre P., Perala S., Vogel P., Fucentese S.F., Goff J.R., Gerber C. In vitro assessments of reverse glenoid stability using displacement gages are misleading—recommendations for accurate measurements of interface micromotion. Clin Biomech (Bristol, Avon) 2011;26:917–922. doi: 10.1016/j.clinbiomech.2011.05.002. [DOI] [PubMed] [Google Scholar]
- 14.Giambini H., Dragomir-Daescu D., Huddleston P.M., Camp J.J., An K.N., Nassr A. The effect of quantitative computed tomography acquisition protocols on bone mineral density estimation. J Biomech Eng. 2015;137:114502. doi: 10.1115/1.4031572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grant J.A., Bishop N.E., Götzen N., Sprecher C., Honl M., Morlock M.M. Artificial composite bone as a model of human trabecular bone: the implant-bone interface. J Biomech. 2007;40:1158–1164. doi: 10.1016/j.jbiomech.2006.04.007. [DOI] [PubMed] [Google Scholar]
- 16.Gutiérrez S., Walker M., Willis M., Pupello D.R., Frankle M.A. Effects of tilt and glenosphere eccentricity on baseplate/bone interface forces in a computational model, validated by a mechanical model, of reverse shoulder arthroplasty. J Shoulder Elbow Surg. 2011;20:732–739. doi: 10.1016/j.jse.2010.10.035. [DOI] [PubMed] [Google Scholar]
- 17.Harman M., Frankle M., Vasey M., Banks S. Initial glenoid component fixation in “reverse” total shoulder arthroplasty: a biomechanical evaluation. J Shoulder Elbow Surg. 2005;14:S162–S167. doi: 10.1016/j.jse.2004.09.030. [DOI] [PubMed] [Google Scholar]
- 18.Hopkins A.R., Hansen U.N., Bull A.M., Emery R., Amis A.A. Fixation of the reversed shoulder prosthesis. J Shoulder Elbow Surg. 2008;17:974–980. doi: 10.1016/j.jse.2008.04.012. [DOI] [PubMed] [Google Scholar]
- 19.James J., Allison M.A., Werner F.W., McBride D.E., Basu N.N., Sutton L.G. Reverse shoulder arthroplasty glenoid fixation: Is there a benefit in using four instead of two screws? J Shoulder Elbow Surg. 2013;22:1030–1036. doi: 10.1016/j.jse.2012.11.006. [DOI] [PubMed] [Google Scholar]
- 20.James J., Huffman K.R., Werner F.W., Sutton L.G., Nanavati V.N. Does glenoid baseplate geometry affect its fixation in reverse shoulder arthroplasty? J Shoulder Elbow Surg. 2012;21:917–924. doi: 10.1016/j.jse.2011.04.017. [DOI] [PubMed] [Google Scholar]
- 21.Königshausen M., Jettkant B., Sverdlova N., Ehlert C., Gessmann J., Schildhauer T.A. Influence of different peg length in glenoid bone loss: a biomechanical analysis regarding primary stability of the glenoid baseplate in reverse shoulder arthroplasty. Technol Health Care. 2015;23:855–869. doi: 10.3233/thc-151031. [DOI] [PubMed] [Google Scholar]
- 22.Lädermann A., Schwitzguebel A., Edwards T., Godeneche A., Favard L., Walch G. Glenoid loosening and migration in reverse shoulder arthroplasty. Bone Joint J. 2019;101:461–469. doi: 10.1302/0301-620X.101B4.BJJ-2018-1275.R1. [DOI] [PubMed] [Google Scholar]
- 23.Liou W., Yang Y., Petersen-Fitts G.R., Lombardo D.J., Stine S., Sabesan V.J. Effect of lateralized design on muscle and joint reaction forces for reverse shoulder arthroplasty. J Shoulder Elbow Surg. 2017;26:564–572. doi: 10.1016/j.jse.2016.09.045. [DOI] [PubMed] [Google Scholar]
- 24.Australian Orthopaedic Association National Joint Replacement Registry (AOANJRR) Hip, knee & shoulder arthroplasty: annual report 2018. https://aoanjrr.sahmri.com/annual-reports-2018 Accessed September 17, 2019.
- 25.Lung T.S., Cruickshank D., Grant H.J., Rainbow M.J., Bryant T.J., Bicknell R.T. Factors contributing to glenoid baseplate micromotion in reverse shoulder arthroplasty: a biomechanical study. J Shoulder Elbow Surg. 2019;28:648–653. doi: 10.1016/j.jse.2018.09.012. [DOI] [PubMed] [Google Scholar]
- 26.Markes A.R., Cheung E., Ma C.B. Failed reverse shoulder arthroplasty and recommendations for revision. Curr Rev Musculoskelet Med. 2020;13:1–10. doi: 10.1007/s12178-020-09602-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Melis B., DeFranco M., Lädermann A., Molé D., Favard L., Nérot C. An evaluation of the radiological changes around the Grammont reverse geometry shoulder arthroplasty after eight to 12 years. J Bone Joint Surg Br. 2011;93:1240–1246. doi: 10.1302/0301-620X.93B9.25926. [DOI] [PubMed] [Google Scholar]
- 28.Middernacht B., Van Tongel A., De Wilde L. A critical review on prosthetic features available for reversed total shoulder arthroplasty. Biomed Res Int. 2016;2016:3256931. doi: 10.1155/2016/3256931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Neal M.L., Kerckhoffs R. Current progress in patient-specific modeling. Brief Bioinform. 2010;11:111–126. doi: 10.1093/bib/bbp049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nigro P.T., Gutiérrez S., Frankle M.A. Improving glenoid-side load sharing in a virtual reverse shoulder arthroplasty model. J Shoulder Elbow Surg. 2013;22:954–962. doi: 10.1016/j.jse.2012.10.025. [DOI] [PubMed] [Google Scholar]
- 31.Pilliar R.M., Lee J.M., Maniatopoulos C. Observations on the effect of movement on bone ingrowth into porous-surfaced implants. Clin Orthop Relat Res. 1986:108–113. [PubMed] [Google Scholar]
- 32.Pomwenger W., Entacher K., Resch H., Schuller-Götzburg P. Need for CT-based bone density modelling in finite element analysis of a shoulder arthroplasty revealed through a novel method for result analysis. Biomed Tech (Berl) 2014;59:421–430. doi: 10.1515/bmt-2013-0125. [DOI] [PubMed] [Google Scholar]
- 33.Quental C., Fernandes P.R., Monteiro J., Folgado J. Bone remodelling of the scapula after a total shoulder arthroplasty. Biomech Model Mechanobiol. 2014;13:827–838. doi: 10.1007/s10237-013-0537-5. [DOI] [PubMed] [Google Scholar]
- 34.Razfar N., Reeves J.M., Langohr D.G., Willing R., Athwal G.S., Johnson J.A. Comparison of proximal humeral bone stresses between stemless, short stem, and standard stem length: a finite element analysis. J Shoulder Elbow Surg. 2016;25:1076–1083. doi: 10.1016/j.jse.2015.11.011. [DOI] [PubMed] [Google Scholar]
- 35.Saltzman B.M., Chalmers P.N., Gupta A.K., Romeo A.A., Nicholson G.P. Complication rates comparing primary with revision reverse total shoulder arthroplasty. J Shoulder Elbow Surg. 2014;23:1647–1654. doi: 10.1016/j.jse.2014.04.015. [DOI] [PubMed] [Google Scholar]
- 36.Villacis D., Sivasundaram L., Pannell W.C., Heckmann N., Omid R., Hatch G.F., III Complication rate and implant survival for reverse shoulder arthroplasty versus total shoulder arthroplasty: results during the initial 2 years. J Shoulder Elbow Surg. 2016;25:927–935. doi: 10.1016/j.jse.2015.10.012. [DOI] [PubMed] [Google Scholar]
- 37.Virani N.A., Harman M., Li K., Levy J., Pupello D.R., Frankle M.A. In vitro and finite element analysis of glenoid bone/baseplate interaction in the reverse shoulder design. J Shoulder Elbow Surg. 2008;17:509–521. doi: 10.1016/j.jse.2007.11.003. [DOI] [PubMed] [Google Scholar]
- 38.Yang C.C., Lu C.L., Wu C.H., Wu J.J., Huang T.L., Chen R. Stress analysis of glenoid component in design of reverse shoulder prosthesis using finite element method. J Shoulder Elbow Surg. 2013;22:932–939. doi: 10.1016/j.jse.2012.09.001. [DOI] [PubMed] [Google Scholar]
- 39.Zhang M., Junaid S., Gregory T., Hansen U., Cheng C.K. Effect of baseplate positioning on fixation of reverse total shoulder arthroplasty. Clin Biomech (Bristol, Avon) 2019;62:15–22. doi: 10.1016/j.clinbiomech.2018.12.021. [DOI] [PubMed] [Google Scholar]
- 40.Zhang Y., Ahn P.B., Fitzpatrick D.C., Heiner A.D., Poggie R.A., Brown T.D. Interfacial frictional behavior: cancellous bone, cortical bone, and a novel porous tantalum biomaterial. Indian J Orthop. 1999;3:245–251. [Google Scholar]