Compositional Tuning of Carrier Dynamics in Cs₂Na_1–xAg_xBiCl₆ Double-Perovskite Nanocrystals

Abstract

We devised a hot-injection synthesis to prepare colloidal double-perovskite Cs₂NaBiCl₆ nanocrystals (NCs). We also examined the effects of replacing Na⁺ with Ag⁺ cations by preparing and characterizing Cs₂Na_1–xAg_xBiCl₆ alloy NCs with x ranging from 0 to 1. Whereas Cs₂NaBiCl₆ NCs were not emissive, Cs₂Na_1–xAg_xBiCl₆ NCs featured a broad photoluminescence band at ∼690 nm, Stokes-shifted from the respective absorption by ≥1.5 eV. The emission efficiency was maximized for low Ag⁺ amounts, reaching ∼3% for the Cs₂Na_0.95Ag_0.05BiCl₆ composition. Density functional theory calculations coupled with spectroscopic investigations revealed that Cs₂Na_1–xAg_xBiCl₆ NCs are characterized by a complex photophysics stemming from the interplay of (i) radiative recombination via trapped excitons localized in spatially connected AgCl₆–BiCl₆ octahedra; (ii) surface traps, located on undercoordinated surface Bi centers, behaving as phonon-assisted nonradiative decay channels; and (iii) a thermal equilibrium between trapping and detrapping processes. These results offer insights into developing double-perovskite NCs with enhanced optoelectronic efficiency.

Nanocrystals (NCs) of lead halide perovskites have attracted significant interest in recent years and are promising candidate materials for various optoelectronic applications.¹⁻⁷ However, given the intrinsic toxicity of lead, which constrains the use of such materials in commercial devices, the scientific community is now seeking for alternative stable lead-free metal halide perovskite compounds with comparable optical properties.^8,9 The most promising candidates in this context are the so-called double perovskites (DPs), also termed elpasolites, having the general formula A₂B⁺B³⁺X_6, characterized by a 3D perovskite structure made of alternating [B⁺X₆] and [B³⁺X₆] corner-sharing octahedra with A⁺ ions occupying the voids in between.⁸⁻¹¹ The different combinations of possible A⁺, B⁺, and B³⁺ ions create a richness of structures, making the elpasolites family particularly interesting from a chemistry and a materials science point of view,¹⁰ as well as for technological applications in photovoltaics,¹²⁻¹⁴ artificial lighting, and photon management.¹⁵

In the last couple of years, various DP materials featuring interesting optical properties have been synthesized at the nanoscale, comprising Cs₂AgBiX₆ (X = Cl, Br, I), Cs₂AgInCl₆, Cs₂NaInCl₆, Cs₂NaBiCl₆, and Cs₂AgSbX₆ NCs (X = Cl, Br).¹⁶⁻²⁹ Unluckily, all these systems feature a weak PL emission because they have either an indirect band gap (Cs₂AgBiX₆, Cs₂AgSbX₆) or a direct band gap characterized by a parity-forbidden transition (Cs₂AgInCl₆) or by a parity-allowed transition albeit with a weak oscillator strength (Cs₂NaInX₆ and Cs₂NaBiX₆).^{9−11,24,30−32} As a result, the interplay between radiative and nonradiative processes makes the excitonic photophysics of these materials significantly more complex than for the case of lead halide perovskites. This calls for specific multidisciplinary investigations to trace rational guidelines for their optimization. In turn, the control and the design of highly performing DP materials has great technological implications, as it will enable us to reap the benefits of their intrinsically broad and largely Stokes-shifted luminescence that makes them particularly appealing for heavy-metal-free, single-component white light-emitting diodes¹⁵ and for transparent luminescent solar concentrators for building-integrated PV applications.³³

In order to enhance the photoluminescence (PL) of these compounds, different strategies have been already pursued which involved doping, alloying, or both. Doping Cs₂AgInCl₆ NCs with either Mn²⁺ or Bi³⁺ ions was observed to yield an orange emission with PL efficiency (Φ_PL) of ∼16% and 11%, respectively.^18,23 Different groups reported the doping of Cs₂AgInCl₆ NCs with rare earth (RE) ions, which led to a near-infrared (NIR) emission at ∼1000 nm with Yb³⁺ and ∼1537 nm with Er³⁺.^19,34 Chen et al. further extended Yb³⁺ and Mn²⁺ doping to Cs₂AgBiX₆ (X = Cl, Br) NCs.¹⁷ On the other hand, alloying strategies, mainly involving Bi³⁺, In³⁺, and Sb³⁺ as B³⁺ cations and Ag⁺ and Na⁺ as B⁺ cations, were exploited to induce an indirect-to-direct band gap transition in DPs with a consequent increase of their PL quantum yield.^{21,26,29,31,35−38}

For example, Luo et al. showed that simultaneous doping and alloying can boost the emission of Cs₂AgInCl₆: the use of a minimal amount of Bi³⁺ dopants (1%) together with Na⁺ cations resulted in Bi-doped Cs₂Ag_1–xNa_xInCl₆ powders with a Φ_PL as high as 86% for x = 0.4.¹⁵ Similarly, our group prepared Bi-doped Cs₂Ag_1–xNa_xInCl₆NCs with a bright and broad yellow emission which was maximum for x = 0.6 (Φ_PL = 22%).¹⁶ Our density functional theory (DFT) calculations revealed that the presence of both Bi³⁺ and Ag⁺ cations was essential to optimize the emission of the “host” Cs₂NaInCl₆ NCs: the introduction of Bi³⁺ dopants and the substitution of a low percentage of Na⁺ with Ag⁺ ions led to the formation of a localized BiCl₆ → AgCl₆ transition. Note that, differently from the common way of describing these materials, we consider the system with Na⁺ cations as the reference case, because it presents a wide band gap, with the Na⁺ ions acting as electronic barriers (vide infra).

Motivated by such results, and inspired by the recent paper by Lamba et al.,³⁰ we decided to systematically investigate the effects of replacing Na⁺ with Ag⁺ ions inside Cs₂NaBiCl₆ NCs. When the Na/Ag precursor ratio was tuned, a series of Cs₂Na_1–xAg_xBiCl₆ NCs were synthesized with an average size around 10 nm and a good size distribution (Scheme 1). These NCs had a broad PL emission around 1.85 eV, which was maximized (∼3% at room temperature) when replacing only a low percentage of Na⁺ cations with Ag⁺, that is, for the Cs₂Na_0.95Ag_0.05BiCl₆ composition. An in-depth spectroscopic and theoretical investigation of such NC system as a function of the Ag⁺ content and temperature revealed a complex photophysics, where the optical efficiency of the NCs results from the interplay between (i) a radiative recombination of trapped excitons (TE) localized in connected AgCl₆–BiCl₆ octahedra, (ii) their phonon-assisted nonradiative decay, and (iii) a thermal equilibrium between trapping and detrapping of electrons in an intragap defect. This defect is likely associated with surface traps located on undercoordinated Bi centers, whose energy depends on the Na⁺ content that ultimately determines the fraction of emissive NCs in the ensemble. Altogether, these processes result in a markedly different temperature dependence of the optical properties of Cs₂Na_1–xAg_xBiCl₆ NCs at various Ag⁺ content values, whose proper understanding offers useful materials design guidelines to maximize emission efficiency.

Scheme 1. Colloidal Synthesis of Cs₂Na_1–xAg_xInCl₆ NCs.

Cs₂Na_1–xAg_xBiCl₆ NCs were synthesized by a colloidal hot-injection approach in which metal carboxylates and carbonates were reacted with benzoyl chloride to trigger the nucleation and growth of the NCs (Scheme 1). Cs₂Na_1–xAg_xBiCl₆ NCs with different compositions (x = 0, 0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 1) were obtained by adjusting the Na/Ag metal precursors ratio, as revealed by both our scanning electron microscope-energy dispersive X-ray spectroscopy (SEM-EDS) and X-ray photoelectron spectroscopy (XPS) analyses (see Experimental Section, Table S1, and Figures S1 and S2 of the Supporting Information).

The X-ray diffraction (XRD) patterns of our NC products showed that they all crystallized in the double-perovskite crystal structure with XRD peaks positioned between those of bulk Cs₂AgBiCl₆ (ICSD number 291598) and Cs₂NaBiCl₆ (ICSD number 2738), with no presence of secondary phases (Figure 1a). Upon closer inspection, when the Ag⁺ content inside the Cs₂Na_1–xAg_xBiCl₆ NCs is increased the XRD peaks shifted toward higher 2θ angles, with pure Cs₂AgBiCl₆ NCs having lattice parameter of 10.78 Å and pure Cs₂NaBiCl₆ NCs of 10.84 Å (Figure 1b). These results indicated the formation of alloyed NCs when working at intermediate Na/Ag compositions. The high-resolution (HR) transmission elecectron microscopy (TEM) characterization of our samples evidenced that the NCs were monocrystalline and exhibited the expected DP structure (Figure 1c–h). The scanning TEM-EDS (STEM-EDS) elemental mapping further supported the formation of alloy NCs in which the different elements were uniformly distributed (Figure 1i).

Figure 1.

(a) XRD patterns of Cs₂Na_1–xAg_xBiCl₆ NCs (x = 0, 0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 1) together with the bulk reflections of Cs₂AgBiCl₆ (ICSD number 291598). (b) Magnification of the XRD patterns in the 30°–36° range. The black bars correspond to the bulk Cs₂AgBiCl₆ (ICSD number 291598) reflection, while the gray bars correspond to bulk Cs₂NaBiCl₆ (ICSD number 2738). (c–f) TEM images of Cs₂Na_1–xAg_xBiCl₆ NCs. (g) High-resolution TEM image of a Cs₂Na_0.95Ag_0.05BiCl₆ NC and (h) the corresponding Fast Fourier transform (FFT). (i) STEM-EDS elemental maps of (Cs₂Na_0.95Ag_0.05BiCl₆).

Theoretical Calculations. To provide a comprehensive picture of the photophysics of Cs₂Na_1–xAg_xBiCl₆ NCs, including the effect of both Na⁺ and Ag⁺ ions, we conducted a multilevel investigation by DFT calculations addressing the main structural and electronic features of these NCs, as well as nonradiative processes associated with structural defects on their surfaces. Initially, we focused on investigating atomistically the mechanism of photoemission, thus paving the way for our spectroscopic measurements of the next section. First, we computed the electronic structure of the cubic Cs₂NaBiCl₆ system which, as calculated by Meng et al.,³² is known to have a direct band gap with a parity-allowed transition. As illustrated in Figure 2a, at the valence band maximum (VBM) the Cs₂NaBiCl₆ states are localized on the 3p orbitals of chlorine ions while at the conduction band minimum (CBM) the edge states are mostly localized on the 6p orbitals of Bi ions, as expected. Because of the high ionicity of the bond, the edge-to-edge transition for this system is characterized by a poor spatial overlap, thus accounting for a weak transition dipole matrix element (this is also reported by others on similar systems).³² As a result, the oscillator strength for this lowest band transition is negligible.

Figure 2.

(a) Electronic structure of the Cs₂NaBiCl₆, Cs₂NaBiCl₆ doped with 1 Ag⁺ ion, and Cs₂AgBiCl₆ 2 × 2 × 2 supercells computed at the DFT/PBE level of theory on a large 2 × 2 × 2 supercell at the Γ point. Each orbital is represented in real space and decomposed according to each atom type. (b) CBM and VBM orbital plots in real space. The undoped materials present delocalized electron and hole wave functions, while the Ag-doped Cs₂NaBiCl₆ system exhibits localization of the wave function.

By introduction of one Ag⁺ cation (in substitution of one Na⁺) at the center of the Cs₂NaBiCl₆ supercell, two main changes were observed in the electronic structure: The first one involved the VB edge, with the formation of two topmost (quasi-degenerated) states composed of a heavily mixed configuration of Ag⁺ 4d orbitals (4d_z² and 4d_z²–y², respectively) and Cl^– 3p orbitals that interact in a σ* antibonding fashion. As illustrated in Figure 2b, the two VB edge states become mainly localized at the AgCl₆ octahedron, with only a small contribution of the neighboring BiCl₆ octahedra. Such spatial confinement of the hole wave function at the VB edge is ensured by the electropositive Na⁺ ions which behave as electronic barriers around the Ag⁺ center. Conversely, in pure Cs₂NaBiCl₆ the hole wave function is delocalized over the whole supercell. The second important change is the lowering in energy of the CBM state due to the contribution of the 5s orbital of Ag⁺. In the stabilized CB edge state, both the Ag⁺ 5s orbital and one of the 6p orbitals of the neighboring Bi³⁺ interact in a σ* antibonding fashion with the directional 3p orbital of the Cl^– ions that connect them spatially. This orbital mixing leads to a partial delocalization of the electron wave function over the six BiCl₆ octahedra surrounding the Ag⁺ center at the CBM. However, as revealed by the orbital plot in Figure 2b, a further delocalization of the wave function in the supercell is again prevented by the presence of Na⁺ ions. Therefore, in a Na-rich Cs₂Na_1–xAg_xBiCl₆ system, Ag⁺ ions act as centers that are able to localize both holes and electrons at the band edges, thus suggesting the presence of a sizable TE emission, which is compatible with the steady-state and time-resolved PL spectroscopic data shown in the next section.

Because these double-perovskite systems attain only moderate PL efficiency (∼3% at room temperature), we can speculate, also because of the experimental evidence presented in the next sections, that nonradiative processes take place at the surface of these NCs. Deep trap states can indeed emerge from an incomplete surface passivation after the synthesis, which leads to the formation of undercoordinated (dangling) ions at the surface.^35,39−41 To probe this effect, we performed DFT calculations by preparing cubic DP NCs model systems with a Cs₃₂₄(Ag+Na)₁₀₈Bi₁₀₈Cl₇₅₆ stoichiometry. This corresponds to a cube with a side of about 3.0 nm, which is both affordable computationally and relevant from an experimental standpoint (see also Computational Methodology in the Supporting Information for further details). Four different Cs₂Na_1–xAg_xBiCl₆ NC models with representative compositions were constructed, featuring x = 0, 0.05, 0.80, and 1, respectively. A survey of their electronic structure is presented in Figure S4. Notably, when their surface was fully passivated, their electronic structures presented either no traps or only shallow ones. On the other hand, when the surface was only partially passivated, then traps began to emerge. To further study this aspect, we analyzed the detachment of surface ions from the outermost surface. This situation was simulated by displacing a neutral CsCl ion pair from one (100) facet in all four NCs models, thus modifying the coordination numbers of some surface atoms. DFT calculations showed that, even after the structural relaxation, a deep trap state localized on a Bi penta-coordinated atom was formed (Figure 3a). The orbital density plot of this molecular orbital (Figure 3b) shows that for all four NC compositions, such a midgap state appeared and was primarily composed of a single Bi 6p atomic orbital localized on the under-coordinated Bi.

Figure 3.

(a) Electronic structures of 3 nm Cs₂Na_1–xAg_xBiCl₆ NCs models featuring x = 0, x = 0.05, x = 0.80, and x = 1 after the removal of one CsCl ion pair from the surface. Each line corresponds to a molecular orbital (MO). Each color indicates the contribution of a type of atom for a given MO. The black dotted circles evidence trap states below the CB for all the systems. The position of these electron trap states depends on the Na/Ag ratio of the NC. (b) Lowest unoccupied molecular orbitals (LUMO) plots. The electron wave function localization is more pronounced in the two Na-rich systems (x = 0 and x = 0.05) than in the two Ag-rich ones (x = 0.80 and x = 1).

This unoccupied MO within the band gap is therefore likely to behave as an electron trap. In Na-rich NCs, this state is very deep, because the surrounding Na⁺ ions confine it on the Bi 6p orbital only. Conversely, in Ag-rich systems the Bi 5c ion can be surrounded by AgCl₆ octahedra, which ensure a partial delocalization of the electron wave function. As a consequence, the energetic level associated to the detrimental state is closer to the CB edge and the trap is less deep (i.e., it is shallower). In summary, the presence of Na⁺ in Cs₂Na_1–xAg_xBiCl₆ DP NCs has the effect of isolating electronically the BiCl₆ octahedra. On the one hand, this confinement is essential to obtain a TE that can radiatively recombine at the Ag⁺ center. On the other hand, the Na⁺ ions increase the degree of localization of the surface trap states, making nonradiative processes more efficient. This result, as it will be shown in the next section, is in line with the temperature- and time-dependent PL measurements varying the Ag⁺ content.

Optical Properties of Cs₂Na_1–xAg_xBiCl₆ NCs. To investigate the implications of the substitution of Ag⁺ for Na⁺ cations in our DP NCs experimentally, we performed side-by-side spectroscopic studies as a function of composition and temperature. Upon increasing the fraction of Ag⁺ (x) from 0 to 1, the absorption peak linearly shifted from ∼3.8 to ∼3.3 eV (Figures 4a and S5). At intermediate Ag⁺ fractions (0 < x < 1), the absorption peak was broader than for the pure compounds (Cs₂NaInCl₆ and Cs₂AgInCl₆), as also observed in the respective PL excitation (PLE) spectrum reported in Figure S6. All PLE spectra were well reproduced by using a linear combination of the pure Cs₂NaBiCl₆ and Cs₂AgBiCl₆ excitation peaks, indicating the progressive conversion of pure Cs₂NaBiCl₆ into Cs₂AgBiCl₆.

Figure 4.

(a) Optical absorption (continuous lines) and PL (dashed lines) spectra of Cs₂Na_1–xAg_xBiCl₆ NCs with progressively increasing Ag⁺ content (from the blue bottom curve, corresponding to x = 0, to the red top curve, corresponding to x = 1). (b) PL quantum yield, Φ_PL (empty circles), and effective lifetime, τ (full circles), extracted by fitting the respective PL decay traces in panel c with stretched exponential functions. The stretching factors, β, are reported in the inset indicating gradually larger disorder with increasing x. All measurements were conducted at room temperature. The color scheme in all panels refers to the code in panel a.

Consistent with the negligible oscillator strength computed for Cs₂NaBiCl₆,²⁶ no PL emission was observed from these NCs. In contrast, Cs₂Na_1–xAg_xBiCl₆NCs with x > 0 featured a broad PL band (fwhm ∼550 meV at T = 300 K) with sub-band gap energy of ∼1.85 eV (Figures 4a). This, together with the red shift of the absorption peak resulted in the progressive decrease of the Stokes shift (Δ_SS) from ∼1.9 eV for x = 0.05 to ∼1.5 eV for x = 1 (Figure S5). The near invariance of the PL position regardless of the marked change of the band gap energy with varying x is indicative of a recombination mechanism mediated by TEs, in agreement with the DFT predictions. Upon increasing the Ag⁺ content, the PL peak underwent progressive broadening (Figure S5), and the PL efficiency, Φ_PL, dropped from over 3% for x = 0.05 to below 1% for x = 1 (Figure 4b). This is in agreement with the localization effect of Na⁺ ions on the electron and hole wave functions evidenced by the DFT study, which reduced inhomogeneous spectral broadening and lowered the probability for nonradiative decay in defect sites. Support to this interpretation was provided by time-resolved PL measurements shown in Figure 4c, where we report the PL decay traces of the Cs₂Na_1–xAg_xBiCl₆ NCs. Consistent with a dispersion of TE local configurations inside the NC lattice, all kinetics are well fitted by a stretched exponential function, 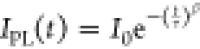, with stretching factor β slightly decreasing from 0.5 to 0.4 with increasing x, in agreement with the growing fwhm of the respective PL spectra. With increasing x, the PL dynamics progressively accelerated, with lifetime τ decreasing from ∼700 ns for x = 0.05 to τ ∼ 5 ns for x = 1. Importantly, the resulting τ versus x trend resembled quantitatively well the evolution of the Φ_PL with the Ag⁺ content (Figure 4c). This indicates that, at room temperature, the main effect of Na⁺ cations is to suppress nonradiative decay pathways competing with the radiative recombination of TEs on a similar time scale. Despite the beneficial shielding effect by the Na⁺ cations, Φ_PL was below 5% also in lightly Ag-substituted NCs (x = 0.05), which indicated that nonradiative processes likely associated with electron trapping in Bi³⁺ sites and phonon-mediated decay were still dominant over radiative recombination of the TE.

In order to probe the radiative PL decay kinetics and thereby evaluate the effects of Ag⁺ substitution on the oscillator strength of TEs, we performed time-resolved PL measurements at cryogenic temperatures. Cooling the NCs dramatically lengthened their PL dynamics that reached a plateau for T < 120 K (Figure S7), indicating that thermally assisted nonradiative channels were largely suppressed. As shown in Figure 5a, the PL decay curves at T = 77 K were well described by stretched exponential functions similar to the room-temperature kinetics, although with significantly larger β-factors than at 300 K (Figure S8), indicating reduced thermal disorder. We notice that also at 77 K the β-factor was slightly lower for larger x-values, consistent with the higher structural disorder already highlighted by the room-temperature data. The corresponding PL lifetimes were up to 3 orders of magnitude slower than at room temperature, and the corresponding radiative decay rates increased monotonically with increasing x (Figure 5b), suggesting that the addition of Ag⁺ cations gradually enhanced the oscillator strength of TE transition.

Figure 5.

(a) Normalized PL decay traces of the Cs₂Na_xAg_1–xInCl₆ NCs at 77 K. The fitting curves to stretched exponential functions are shown as black lines. The respective β values are shown in Figure S8. Inset: Enlargement of the first 110 ns of the PL decay, highlighting the emergence of the fast decay portion that is directly proportional to the fraction of dark NCs, D. (b) Radiative recombination rate, k, of the PL decay traces reported in panel a as a function of the Ag⁺ content. The black line is a guide for the eyes. (c) Oscillator strength of the TE recombination pathway (CBM → VBM transition) obtained by the DFT calculations as a function of the number of AgCl₆ octahedra surrounding a central BiCl₆ octahedron in a Cs₂NaBiCl₆ 2 × 2× 2 supercell. In the case of 2 and 4 Ag ions, the reported oscillator strengths are relative to the cis configurations (see the Supporting Information for further details). The black line is a guide for the eyes. (d) Static (η) and dynamic (φ) brightening factors and the product of φ × B as a function of x. The gray shading corresponds to y-axis <1. Inset: The term B = 1 – D representing the fraction of emissive TEs as a function of x. (e) Schematics of the energy diagram of the Cs₂Na_0.95Ag_0.05InCl₆ (top) and Cs₂Na_0.2Ag_0.8InCl₆ NCs (bottom). The same color scheme applies to all panels. All measurements were conducted using an excitation energy of 3.5 eV and a pulse frequency of 140 Hz. The color scheme in all panels refers to the code reported in Figure 4a.

To support this hypothesis, we computed the oscillator strength for TE transitions at the DFT/PBE level as a function of the number of Ag⁺ cations surrounding a central BiCl₆ octahedron (Figure 5c). This was done by gradually replacing Na⁺ ions with Ag⁺ ions around the chosen Bi³⁺ ion. The substitution of Na⁺ ions around one octahedron centered on a Bi ion either with 2 Ag⁺ or with 4 Ag⁺ leads to two possible configurations, cis or trans. In a random distribution of Na⁺ and Ag⁺ ions, the cis configuration is more plausible and is thus reported in Figure 5c. The oscillator strengths associated to the trans configurations are reported in Figure S9 for completeness. Overall, we observe that the oscillator strength increases at increasing amount of Ag⁺ ions comparing well with the monotonic increase of the radiative recombination rates observed experimentally (Figure 5b).

The low-temperature PL studies enabled us to gather deeper insights into the mechanism of carrier trapping that was found to correlate with the DFT-predicted role of Bi-related surface defects. Specifically, the lengthening of the PL dynamics suggested that the Φ_PL of all investigated systems was enhanced at cryogenic temperatures with respect to T = 300 K. This behavior is quantified by the dynamic brightening factor φ = τ^77K/ τ^300K reported in Figure 5d, which represents the relative increase of Φ_PL expected solely based on the lengthening of the PL decay traces at low T. Interestingly, while following a qualitatively similar trend with the Ag⁺ content, φ systematically exceeded by at least 10 fold the respective relative PL enhancement measured in continuous-wave (cw) conditions, expressed through the static brightening factor, η (extracted as the ratio between the PL efficiency at 77 and 300 K measured using cw excitation, Figure S10). This indicated that, at low temperature, the emission yield of our NCs was less than 10% of the respective intrinsic value represented by φ, suggesting that the population of emitting NC had dropped with respect to room temperature. For x = 0.05, η showed the minimum value of ∼0.3, indicating that for such NCs, Φ_PL was lower at T = 77 K with respect to T = 300 K, despite the respective lifetime had significantly lengthened (Figures 5a).

This surprising behavior suggested that the photophysical mechanism responsible for the optical properties of Cs₂Na_1–xAg_xBiCl₆ NCs was more complex than the mere competition between radiative recombination of TEs and their thermal-assisted nonradiative decay. This was revealed by the analysis of the initial fast component of the low-temperature PL decay curves shown in the inset of Figure 5a. At T = 77 K, all NCs showed a resolution-limited PL drop, whose relative intensity (indicated as D) with respect to the long-lived PL decay decreased with increasing x. In light of the DFT study suggesting the presence of electron-accepting sites associated to under-coordinated surface Bi atoms, we ascribe this decay to the rapid dissociation of TEs by nonradiative electron trapping, which rendered a fraction of our NCs nonemissive or dark. As a result of this process, with increasing Ag⁺ content, the complementary fraction of emissive (or bright, B) NCs in the ensemble, expressed as B = 1 – D, monotonically grew, as shown in the inset of Figure 5d. Consistent with this picture, by scaling the dynamic brightening factor for the evolution of the bright NC population at low temperature through the product φ × B, we reproduced the x-trend of η (Figure 5e), including the low-T drop of Φ_PL for x = 0.05.

Considering the whole body of spectroscopic data and DFT calculations, we model the effect of both temperature and Ag⁺ substitution on the recombination of TEs according to the scheme depicted in Figure 5e. For any x-value, at 300 K, the radiative recombination of the TE competes mostly with phonon-assisted nonradiative recombination likely associated to a combination of vibrational quenching and electron trapping in Bi-related surface defects. The latter effect is, however, compensated by efficient thermal electron detrapping. At low temperatures, on the other hand, the emission efficiency is determined by the interplay between the beneficial suppression of such a temperature-assisted nonradiative decay channel for TEs and the detrimental effect of reduced thermal detrapping of electrons trapped in surface defects. At a given temperature, the latter effect depends strongly on the depths of the electron trap. Consistently, NCs with low Ag⁺ content showed the largest trapping-related PL drop (hence lowest B-values), because in such NCs, electron traps associated to undercoordinated Bi atoms were deeper in the forbidden gap. One key consequence of this mechanism is that NCs with higher Ag⁺ content (showing relatively larger B-values at T = 77 K) approach the behavior of lightly Ag-substituted NCs, featuring shallow electron traps, upon lowering the temperature further. This is highlighted by the evolution of the spectral and dynamic properties of NCs featuring x = 0.05 and x = 0.8 from 300 to 3.5 K reported in Figures S11–S14 and discussed in detail in Supplementary Discussion 1. Importantly, such side-by-side experiments corroborate the theoretical findings and show that the activation energy for electron detrapping drops from ΔE_DT = 102 meV for x = 0.05 to ΔE_DT = 2 meV for x = 0.8.

In summary, we have developed a hot injection synthesis approach to prepare Cs₂NaBiCl₆ NCs which we systematically alloyed with Ag⁺ cations to form Cs₂Na_1–xAg_xBiCl₆ NCs. While pure Cs₂NaBiCl₆ NCs did not exhibit any PL emission, the incorporation of Ag⁺ cations, to form Cs₂Na_1–xAg_xBiCl₆ NCs, led to the emergence of a broad PL band (fwhm ≈ 550 meV) peaked at around 1.8 eV and characterized by a large Stokes shift (ranging from ∼1.9 eV for x = 0.05 to ∼1.5 eV for x = 1). The PL efficiency of these NCs was maximized for low amounts of Ag⁺ incorporated, reaching ∼3% for x = 0.05. These optical features were consistent with a trapped exciton emission mechanism. Indeed, our DFT calculations indicated that in a Na-rich (hence Ag-poor) Cs₂Na_1–xAg_xBiCl₆ system, Ag⁺ ions act as centers that are able to localize both holes and electrons at the band edges. On the other hand, the low Φ_PL for the whole batch of systems could be ascribed to the presence of nonradiative quenching mechanisms dominated by the presence of surface traps. In particular, undercoordinated Bi³⁺ ions, which are generated from an incomplete surface passivation after synthesis and/or washing, create an empty electronic trapping state below the conduction band, whose energy is modulated according to the Na/Ag ratio. The depth of such trap states was probed at various temperatures by measuring the PL emission efficiency, which confirmed that the trapping/detrapping rate increased with the concentrations of Ag. In practice, the system that shows the most efficient TE mechanism is also the one that has efficient concomitant nonradiative pathways, thus reducing the overall performance of the DP material. These results provide a gateway to design new materials to maximize their optoelectronic efficiency.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsenergylett.0c00914.

• XPS and SEM-EDS elemental analyses, TEM images and size distribution histograms of Cs₂Na_1–xAg_xBiCl₆ NCs, electronic structure of Cs₂Na_1–xAg_xBiCl₆ NC models, PLE curves, PL spectra at different temperatures, PL decay times, PL peak maximum, and fwhm of the PL peaks as a function of the temperature (PDF)

Author Present Address

^○ Z.D.: School of Materials, Sun Yat-sen University, Guangzhou, 510275, China.

Author Contributions

^∇ D.Z., J.Z., and V.P. contributed equally to this work.

The authors declare no competing financial interest.