Applicability assessment of a stent-retriever thrombectomy finite-element model

Abstract

An acute ischaemic stroke appears when a blood clot blocks the blood flow in a cerebral artery. Intra-arterial thrombectomy, a mini-invasive procedure based on stent technology, is a mechanical available treatment to extract the clot and restore the blood circulation. After stent deployment, the clot, trapped in the stent struts, is pulled along with the stent towards a receiving catheter. Recent clinical trials have confirmed the effectiveness and safety of mechanical thrombectomy. However, the procedure requires further investigation. The aim of this study is the development of a numerical finite-element-based model of the thrombectomy procedure. In vitro thrombectomy tests are performed in different vessel geometries and one simulation for each test is carried out to verify the accuracy and reliability of the proposed numerical model. The results of the simulations confirm the efficacy of the model to replicate all the experimental setups. Clot stress and strain fields from the numerical analysis, which vary depending on the geometric features of the vessel, could be used to evaluate the possible fragmentation of the clot during the procedure. The proposed in vitro/in silico comparison aims at assessing the applicability of the numerical model and at providing validation evidence for the specific in vivo thrombectomy outcomes prediction.

1. Introduction

An acute ischaemic stroke (AIS) occurs when an artery that supplies blood to the brain is blocked by a blood clot (thrombus), which is a solidified mass of blood cells, platelets, fibrin and other blood components occurring as a result of blood coagulation. Rarely, occlusive clots may also consist of non-thrombus components such as fat emboli, tumour tissue, calcifications and the like. In the majority of AIS cases, the clot is formed elsewhere and embolized to the vessel it eventually occludes, although in situ occlusive thrombi also occur. Red thrombi, red blood cell (RBC) dominant, are understood to form where the blood flow is slow and the fibrin network entraps the RBCs, while white thrombi, fibrin dominant, are generated under high shear flow and inflammatory conditions [1]. Mechanical properties of blood clot strongly depend on the clot composition [1]. Common origins of embolic thrombi are the heart, atherosclerotic plaques, or from vessel wall dissections.

Detection of the location of the intracranial occlusion must be done in a fast and accurate way to ensure an appropriate selection of treatment and its speedy delivery [2]. Treatment of AIS is aimed at restoring blood flow in the affected cerebral arteries as quickly as possible. Time is crucial in stroke—2 million neurons are lost every second without reperfusion [3]. The main diagnostic imaging techniques used to identify the clot location are computed tomography and magnetic resonance imaging.

There are currently two main therapies to treat an ischaemic stroke: (i) medical therapy using thrombolytic agents (thrombolysis) and (ii) interventional therapy to remove the clot using mechanical thrombectomy. The latter is indicated for large vessel occlusions of the neurovasculature. Thrombolysis became available recently and involves the administration of tissue plasminogen activator 3–4.5 h after the onset of a stroke. Most recently, intra-arterial mechanical thrombectomy has emerged as a widespread clinical intervention technique in the treatment of stroke [4]. Currently, a combined approach of thrombolysis and mechanical thrombectomy is recommended for the treatment of AIS involving large vessel occlusion. Mechanical thrombectomy interventions are carried out with the aid of angiography to ensure the correct positioning of the devices relative to the occluded vessel.

Thrombectomy device design has two classifications based on their mode of action: (i) aspiration catheters and (ii) stent-retrievers. Aspiration catheters may be used without stent-retrievers; however, stent-retriever use usually includes some element of aspiration, either through a guide catheter placed in the extracranial internal carotid artery (ICA) or using a distal access catheter which can be placed close to the occlusion in smaller intracranial vessels. The superiority of one approach over the other is an ongoing subject of debate among neurointerventionalists [5–7]. Effectiveness of the thrombectomy approach taken is measured in terms of speed of revascularization, reperfusion grade, patient outcome, ease-of-use and cost of the procedure. The revascularization of the affected vessels is strongly associated with improved clinical outcomes for patients [8].

Stent-retrievers rely on the mechanical removal of the thrombus by means of a nickel–titanium (NiTi) self-expandable stent at the end of a flexible wire, delivered in a crimped configuration in a microcatheter and positioned across the thrombus. Once in position, the stent-retriever is deployed by withdrawing the microcatheter (even at this stage, the expanded stent may restore the blood flow by compressing the clot between the stent-retriever and the arterial wall). After deploying the stent-retriever, the clot, trapped in the stent struts, is pulled along with the stent towards a receiving catheter. In many cases, this operation is performed under arrested flow conditions achieved by a balloon inflated in a guide catheter positioned at the ICA at the skull base. A number of stent-retriever device designs are currently being used in clinical practices [9], and a number of clinical trials are currently ongoing [8,10–12]. In this regard, the seminal MR CLEAN clinical trial [13], a multicentre randomized clinical trial of endovascular treatment for AIS in The Netherlands, confirmed the effectiveness and safety of stent-retriever thrombectomy devices and demonstrated their improved outcome when combined with best medical therapy compared to thrombolysis alone.

However, despite its increasing clinical application, thrombectomy may result in some adverse outcomes, such as thrombus embolization to distal vessels caused by disruption of the clot during crossing, deployment or retrieval [14], embolization of clot to new vascular territories, hemorrhagic events and vessel wall damage [15,16]. Procedural success also greatly depends on vascular geometry (tortuosity), clot characteristics or in cases involving atherosclerotic stenosis [6].

To date, a limited number of in vitro and in silico studies on the thrombectomy procedure have been reported. In vitro studies have investigated the mechanical behaviour and functioning of devices [17] and clots [18], and the stent–clot interaction [19,20]. In the few published in silico studies [21,22], the procedure was modelled as an electric circuit analogue and the clot as a spring–damper system, ignoring the mechanical nature of the stent–clot interaction.

In this regard, the increasing fascination of performing ‘virtual’ treatment in ‘virtual’ patients [23] makes necessary the development of accurate in silico models of the thrombectomy procedure. An in silico clinical trial of AIS incorporating a robust in silico thrombectomy model would enable evaluation of various hypotheses on the effectiveness of thrombectomy. In silico thrombectomy models in numerous vessel geometries and with different clot characteristics would allow the rapid evaluation of the feasibility of different thrombectomy treatment approaches for specific patients, and patient populations, resulting in the faster and safer introduction of new treatments or devices.

In this context, the objective of the current study is to develop an in silico finite-element model of the thrombectomy procedure and to demonstrate the ability of the model to replicate experimental thrombectomy tests using commercial stents-retriever and clot analogues. To the best of our knowledge, this is the first finite-element model of the thrombectomy procedure. In vitro tests are also performed to verify the accuracy and reliability of the numerical models. The proposed in vitro/in silico comparison aims at assessing the applicability of the numerical model and at providing validation evidence for the specific in vivo thrombectomy outcomes prediction, which constitutes the ultimate context of use (COU). In particular, finite-element models of the stent-retriever and the clot are developed and their mechanical behaviour is calibrated with experimental tensile and compression tests; in vitro bench-top tests in different cerebral-like vessel geometries (idealized and anatomically based) are performed—and a computational simulation of each in vitro test is implemented using the in silico thrombectomy modelling framework.

2. Method

2.1. Stent-retriever model

The EmboTrap II (CERENOVUS, Galway, Ireland) is a NiTi stent-retriever with a dual-layer design (figure 1a): the outer stent cage has large openings aimed at trapping the clot, while articulating leaflets maintain the contact with the arterial wall during retrieval, the inner channel formed by a closed-cell stent is aimed at trapping captured clot within the stent-retriever and restoring the blood flow through the clot upon deployment [24]. The device was approved for the use in EU in late 2013 under the CE mark. The CAD model (5 mm outer diameter and 33 mm length) was analysed by means of ANSA Pre Processor v19.0 (BETA CAE System, Switzerland) to extract the centreline of the frames (figure 1b). The resulting wire model was discretized with 4353 Hughes-Liu beam elements with a rectangular cross section and average length of 0.2 mm, following a rigorous mesh size sensitivity analysis. In particular, three different discretizations with an average element size of 0.4 mm, 0.2 mm and 0.1 mm were considered, with the resultant force and the axial stresses on selected elements in the central part of the device used as monitored variables for the convergence analysis. The difference in the monitored variables between the 0.2 mm and the 0.1 mm discretization was less than 3% during the crimping step of the simulations. The stent's cross sections were measured with a confocal laser scanning microscope (LEXT-OLS4100, Olympus) (figure 1c). A self-penalty hard contact between the struts of the stent was modelled in order to prevent inter-penetration of the inner parts of the retriever during the simulations.

Figure 1.

(a) EmboTrap II device and (b) its finite-element model, discretized with beam elements; (c) the stent section acquired with a confocal laser scanning microscope; (d) uniaxial tensile test and (e) the resultant force–displacement curve (dotted blue line), compared with the curve from the in silico model (solid red line).

The NiTi material parameters, provided by CERENOVUS (data not shown), were verified through a numerical–experimental coupling [25]: the stent was subjected to a uniaxial tensile test at an applied displacement rate of 0.05 mm min⁻¹ until its length is extended by 4.5 mm, in a temperature-controlled chamber with air at 37.0 ± 0.1°C (EnduraTEC ELF 3200, BOSE) (figure 1d). The experiment was then computationally simulated (figure 1e) and the NiTi material was modelled using the shape memory material constitutive formulation available in the commercial finite-element solver LS-DYNA Release 11.0 (ANSYS, Canonsburg, PA, USA) [26].

Crimping simulations of the device in a microcatheter with an inner diameter of 0.5 mm followed by unconstrained release were carried out to verify the crimping and release kinematic of the device. These simulations were used to determine the optimal system damping and mass scaling [27]. Internal, kinematic and dissipative energies were compared in order to guarantee quasi-static conditions during the simulation, i.e. a kinetic to internal energy ratio of less than 2%. The finite-element simulations were performed on 16 CPUs of an Intel Xeon64 with 64 GB of RAM memory using the commercial finite-element solver LS-DYNA Release 11.0 (ANSYS, Canonsburg, PA, USA).

2.2. Clot model

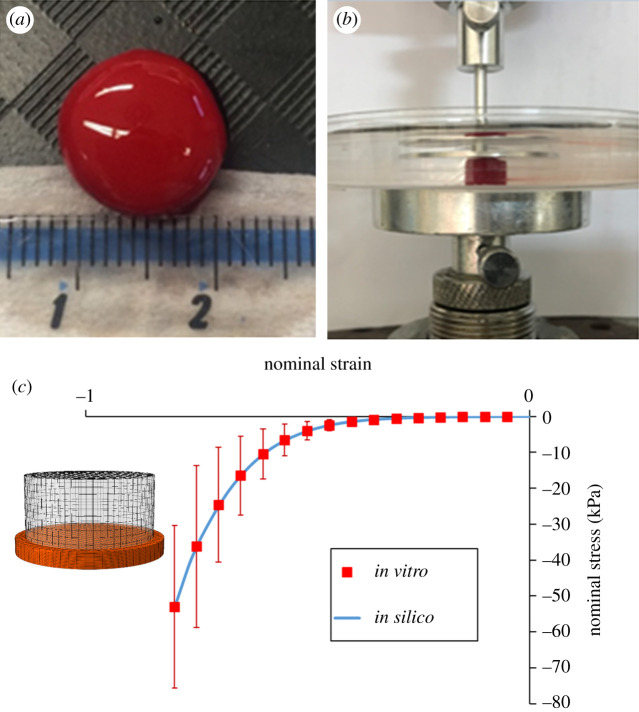
Clot analogues were obtained from venous whole ovine blood using a customized protocol [28,29] (figure 2a). Unconfined compression tests of synthetic clots in 0.9% saline were performed using a custom-built parallel plate experimental setup (figure 2b). Clots with a composition intermediate between red and white clots (ca 20% RBC) were subjected to confined compression up to 80% nominal compressive strain at an applied strain rate of 10% s⁻¹. The compressibility of the blood clot was also investigated by the processing of the images taken at different deformations during the compression test. The initial deformation of the clot at the start of the test leads to the calibration of a Poisson's ratio of 0.3.

Figure 2.

(a) Clot analogues from venous whole ovine blood; (b) unconfined compression test in saline solution; (c) the measured nominal stress–strain curve with standard deviation (dotted red line), compared with the curve from the in silico model (solid blue line).

The compression test was numerically reproduced using a simplified quasi-hyperelastic foam model defined by a single uniaxial load curve and an assumed Poisson's ratio [30]. The term quasi is used because there is really no strain energy function for determining the stresses. In this regard, the stress response mimics the gradient of the classical Hill–Ogden strain energy potential which for the case of a foam reads

$${\tau }_{ii}^E=f({\lambda }_i)-\hspace{0.17em}f\left(J^{-\frac{\nu }{1-2\nu }}\right),$$

where ${\tau }_{ii}^E$ are the principal components of the Kirchhoff stress, ν is the Poisson's ratio, ${\lambda }_i$ the principal stretches, with $J={\lambda }_1{\lambda }_2{\lambda }_3$ the relative volume change, and $f(.)$ a function determined directly from uniaxial test data as [30]

$$f(\lambda )=\lambda g(\lambda )+{\lambda }^{-\nu }g({\lambda }^{-\nu })+\cdots +{\lambda }^{{(-\nu )}^n}g({\lambda }^{{(-\nu )}^n}),$$

where $\tau =g(\lambda )$ corresponds to the experimental uniaxial curve. The formulation does not require an analytical expression for $f(.)$; this function consists of tabulated values of the principal stretch ratios and the input Poisson's ratio. The tabulated values are determined by LS-DYNA at the beginning of the computation in such a way that supplied data from uniaxial tension and compression tests are fitted within an arbitrarily small error, whereas linear interpolation is used to approximate the function between tabulated values. Figure 2c shows the performance of the model to replicate the unconfined compression tests.

2.3. In vitro thrombectomy tests

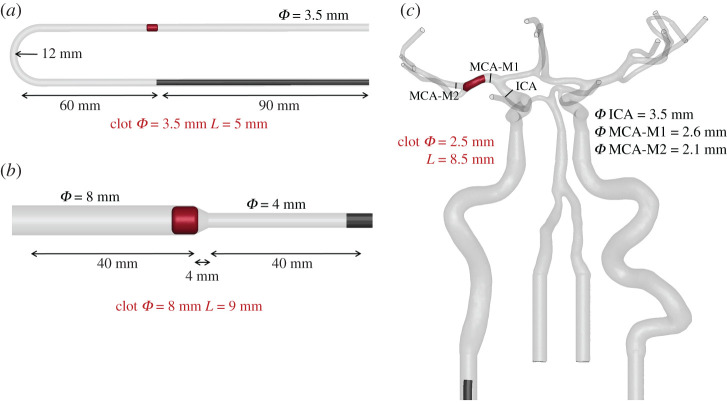
Three different functional bench tests were designed: (i) a glass U-bent vessel; (ii) a silicone funnel-shaped vessel; and (iii) a patient-like three-dimensional-printed silicone vascular branch. Vessel models were fabricated with physiological dimensions in order to realistically replicate the thrombectomy procedure. Clots with the same composition (ca 20% RBC) but different sizes were used. Figure 3 shows the dimensions of the different vessel models and clots considered in the study. The experiments were carried out with a stationary flow of saline solution heated at 37°C and each procedure was video recorded. Each test was performed three times in order to assure the repeatability of the outcomes.

Figure 3.

Geometry and dimensions of the three functional bench tests: (a) a glass U-bent vessel, (b) a silicone funnel-shaped vessel and (c) a patient-like three-dimensional-printed silicone vascular branch. Clots’ diameters and lengths are also pointed out (in red).

2.4. In silico thrombectomy tests

Different clot model geometries were generated in accordance with the dimensions of the tested clot analogues. Clot model geometries were discretized with tetrahedral elements with an average size of 0.2 mm. The mesh size for the clot was chosen to be similar to that of the stent to achieve optimal simulation of the contact between the stent and the clot. A mass proportional damping of 10 s⁻¹ was adopted for the clot in order to achieve stability without excessively constraining the maximum time-step [27]. The CAD models of the glass and silicone vessels were discretized with triangular rigid elements. The clots were positioned in the vessels at the same location as the in vitro tests. A selective mass scaling was adopted in order to have a constant time-step of 5 × 10⁻⁷ s.

The finite-element models were set up in ANSA Pre Processor v19.0 (BETA CAE System, Switzerland) and the simulations were performed on 40 CPUs of an Intel Xeon64 with 256 GB of RAM memory using the commercial finite-element solver LS-DYNA.

The simulation of the thrombectomy procedure consisted of four steps:

• (i)Stent crimping/catheter tracking—the stent-retriever is crimped in a 0.5 mm diameter rigid straight catheter in 1 s. A hard penalty contact is defined between the stent and the catheter; at the same time, the clot is deformed and pushed against the vessel wall by the catheter. Frictionless soft penalty contact is defined between the clot and the catheter, whereas a rough soft penalty contact is defined between the clot and the vessel wall, with a friction coefficient of 0.1 in the glass vessel and of 0.2 in the silicone vessels [31].
• (ii)Stent tracking—the crimped stent is positioned at the location of the clot by removing it along the centreline of the guide catheter at a velocity of 0.1 m s⁻¹.
• (iii)Deployment—the stent is released/unsheathed by sliding the crimping catheter from the stent at a velocity of 0.1 m s⁻¹. As the stent is released it comes into contact with the clot; a soft penalty contact is defined between the stent and the clot, whereas a hard contact is implemented where the stent contacts the rigid vessel wall.
• (iv)Retrieval—the clot trapped by the stent following release, and the stent and trapped clot are then pulled at a velocity of 0.05 m s⁻¹ along the catheter's centreline until an aspiration catheter is reached.

3. Results

Simulation of the crimping of the device in the catheter followed by an unconstrained release was carried out to verify the crimping and release kinematics predicted by the model. The stent model was successfully crimped in 1 s in a 0.5 mm diameter catheter without distortion of the beam elements, element inter-penetration or instability. In figure 4, the simulation of the crimping is compared against the actual crimping of the Embo Trap II device. The unconstrained release in 1 s was also successfully modelled, the stent recovered its nominal open configuration with no residual stresses or strains. The quasi-static condition in this simulation was achieved; a mass-weighted damping factor for the stent of 50 s⁻¹ and a constant time-step of 5 × 10⁻⁷ s with selective element mass scaling were identified as optimum parameters.

Figure 4.

Comparison between the real (left panel) and the modelled (right panel) crimping phase of the device in the microcatheter with an inner diameter of 0.5 mm.

Thrombectomy in vitro tests were performed and numerically reproduced. Comparison in terms of the kinematics (structure deformation) was performed, focusing in particular on the clot's position, deformation and motion. Evaluation over time of the von Mises (VM) stresses and Green von Mises (VM) strains, also known as effective stress and strain respectively, of the clot during all the steps of the simulations was performed. Maximum stress and strain are reported as the average of the 10 elements with the maximum value, instead of local maximum values to avoid possible spikes due to the contact of the clot with the stent or due to excessive distortion of the mesh.

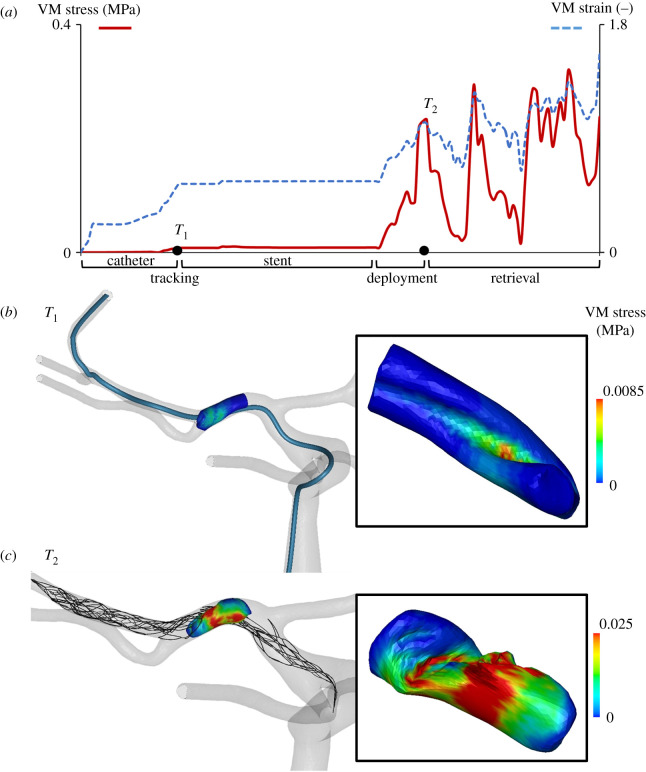
The first test was conducted in a glass U-bent vessel, with a positive thrombectomy outcome. The model consisted of 48 655 finite elements and the simulation lasted 17 h. The clot, trapped into the stent's struts, was retrieved along the bend of the vessel (figure 5, left panel). In this case, the simulation successfully replicated the procedure (figure 5, right panel): during the first step (stent crimping/catheter tracking) the stent was crimped and the catheter, following the centreline of the U-bent vessel, was positioned across the cot. At this point (T₁ in figure 6), the clot, pushed against the vessel wall, reached a maximum VM stress of 0.6 kPa and a VM strain of 0.25. In the stent tracking phase, the crimped stent was positioned across the clot following the centreline of the catheter, while nothing occurred on the clot, whose stress and strain values remained stable. In the deployment step, the stent was released by unsheathing the catheter. As the stent and the clot enter in contact, the stress and strain values in the clot increase dramatically. The maximum VM stress and strain once the stent was completely released (T₂ in figure 6) were 36.3 kPa and 0.72, respectively. In the third and final retrieval step, the clot is trapped between the inner and the outer layer of the stent and was retrieved following the centreline of the catheter. During the retrieval phase, the maximum effective stress and strain in the clot decreased as the retriever passed the U-bent to further stabilize at a constant value as the retriever reaches the straight part of the vessel. In this setting, the maximum effective stress and strain in the clot resulted in 36.5 kPa and 0.78, respectively (figure 6). The second test was conducted in a silicone funnel-shaped vessel, with a negative thrombectomy outcome. The model consisted of 50 518 finite elements and the simulation lasted 18 h. In this case, the clot is not trapped within the retriever's struts during the retrieval phase and the retriever is unable to pull the clot through the small vessel. Instead, the clot rolls up in the place where the larger vessel narrows (figure 7, left panel). The simulations, again, successfully replicated the procedure (figure 7, right panel). After the first stent crimping/catheter tracking step (T₁ in figure 8), the clot was pushed against the vessel wall reaching a maximum VM stress of 0.4 kPa and a VM strain of 0.23, values that were maintained during the second step. During the deployment step the stent went in contact with the clot, increasing the maximum effective stress and strain values to 4.3 kPa and 0.45, respectively (T₂ in figure 8). In the retrieval step, the clot, due to the significantly larger vessel to retriever diameter ratio that prevented an effective clot–stent interaction, started to roll up preventing the retriever from pulling the clot into a smaller vessel. In this step, the continuous rolling of the clot produced oscillating values of the effective stresses and strains with peaks of 15.4 kPa and 0.61, respectively. The third thrombectomy test was conducted in a patient-like three-dimensional-printed silicone vascular branch, with a positive outcome (figure 9, left panel). This last test is closer to the in vivo thrombectomy procedure. From a numerical point of view, the simulation was composed of the same four steps, but the tortuosity of the vessel increased the overall complexity of the solution. The model consisted of 144 760 finite elements and the simulation lasted 26 h. This simulation demonstrates the robustness of the thrombectomy numerical model as it successfully replicated the experiments in terms of the successful retrieval (figure 9, right panel). In the stent crimping/catheter tracking step (T₁ in figure 10), the clot was pushed against the vessel wall reaching maximum effective stress of 8.0 kPa and a maximum effective strain of 0.56, values that were maintained during the second step. During the deployment step the stent went in contact with the clot, increasing the maximum effective stress and strain values to 230 kPa and 1.02, respectively (T₂ in figure 10). As evidenced by these results, during the deployment phase of the retriever the clot undergoes large deformations and the stresses reach values way superior to those found in the other two experimental setups. During the retrieval phase, the clot remained trapped in the stent's struts all the way along the vessel. In this case, the open architecture of the EmboTrap II stent helped the insertion of the clot inside the stent struts [28]. During this final step, the effective stress and strain reached a maximum value of 320 kPa and 1.6, respectively.

Figure 5.

Comparison between the in vitro (left panel) and the in silico (right panel) thrombectomy test in the glass U-bent vessel. In both the results the clot, trapped in the stent, is successfully retrieved until reaching the aspiration catheter.

Figure 6.

(a) Maximum (averaged over 10 elements with the maximum values) von Mises (VM) stress and Green von Mises (VM) strain values over time during the catheter tracking, stent tracking, deployment and retrieval steps of the simulation in the glass U-bent vessel. Von Mises stress contours on the clot in two different views (b) at the end of the catheter tracking step (time T₁) and (c) at the end of the deployment step (time T₂).

Figure 7.

Comparison between the in vitro (left panel) and the in silico (right panel) thrombectomy test in the silicone funnel-shaped vessel. In both the results, the clot escaped from the stent by turning on itself.

Figure 8.

(a) Maximum (averaged over 10 elements with the maximum values) von Mises (VM) stress and Green von Mises (VM) strain values over time during the catheter tracking, stent tracking, deployment and retrieval steps of the simulation in the silicone funnel-shaped vessel. Von Mises stress contours on the clot in two different views (b) at the end of the catheter tracking step (time T₁) and (c) at the end of the deployment step (time T₂).

Figure 9.

Comparison between the in vitro (left panel) and the in silico (right panel) thrombectomy test in the silicone patient-like three-dimensionally-printed vascular branch. In both the results the clot, trapped in the stent, is successfully retrieved until reaching the aspiration catheter.

Figure 10.

(a) Maximum (averaged over 10 elements with the maximum values) von Mises (VM) stress and Green von Mises (VM) strain values over time during the catheter tracking, stent tracking, deployment and retrieval steps of the simulation in the silicone patient-like three-dimensional-printed vascular branch. Von Mises stress contours on the clot in two different views (b) at the end of the catheter tracking step (time T₁) and (c) at the end of the deployment step (time T₂).

4. Discussion

In the in silico trial arena, numerical models of clinical procedures are becoming an important tool. Even today, numerical modelling plays a decisive role in research and the development of biomedical products. In combination with patient-specific models, in silico models can be used to build in silico clinical trials in which virtual patients are treated with virtual treatments. On this line, in 2018, the US Food & Drug Administration published the ASME V&V 40 technical standard ‘Assessing Credibility of Computational Modeling through Verification and Validation: Application to Medical Devices' [32]. The credibility assessment begins with the statement of the COU of the proposed numerical model. In this case, the COU, or in other words the specific final goal of the model, is the prediction of the thrombectomy outcomes in an ischaemic stroke patient, if the clot will be removed or not, if, consequently, the blood flow will be restored in time or not. In this view, ‘would favourable validation results lead to trustworthy predictions in the COU?’ This is the question that the framework proposed by Pathmanathan et al. [33] sets out. In biomedical modelling, the issue to ‘strictly’ validate the numerical model is demanding due to ethical and/or technological problems. Proper validation of the thrombectomy procedure with in vivo measurements and images is at the moment impossible. The generation of evidence to explain the differences between the COU and the numerical model presented in this work is the cornerstone of the so-called applicability analysis.

In the thrombectomy procedure (our COU), the stent is crimped in a microcatheter with a diameter of 0.5 mm, deployed at the location of the clot in a way that, once the stent is released by unsheathing the catheter, it is in direct contact with the clot. The clot is pushed against the arterial wall and it should be trapped by the stent struts. Finally, both the stent and the clot are removed. However, the means of the removal varies considerably. An ever-increasing list of variants to the thrombectomy procedure is being reported. In some instances, the stent-retriever is pulled to a receiving guide catheter in the extracranial ICA; in other instances, a distal access catheter is advanced to the site of the clot and stent-retriever and they are withdrawn into the catheter at that point; in other cases still, the stent-retriever is used to partially pull the clot into a distally positioned catheter and the catheter, stent-retriever and clot are removed en bloc in that configuration. In all cases, aspiration through the receiving catheter is used to aid with clot capture. In the clinical reality, different parameters could vary and affect the outcomes: the choice of the stent-retriever design and size, the patient-specific morphology of the artery branches and the clot size, location and composition.

In accordance with the clinical procedure, the finite-element analysis of the COU models the crimping, the deployment, the release and the retrieval phases. The finite-element models of the most clinically used stent-retrievers in different sizes will be available, with an equivalent section derived from the microscope observation and material model calibrated with uniaxial tensile tests. The limited availability of NiTi stents prevented the performance of a statistically significant experimental campaign aimed at the model validation. Additional experiments, such as uniaxial, torsion and bending tests, should be performed to achieve a better degree of confidence in the model validation. Finite-element models of the clot with different sizes and compositions [1], and material behaviour calibrated with compression tests will be realized. The thrombectomy simulation will be set up with the same steps described in this work. The stent will be crimped in the 0.5 mm diameter catheter, deployed across the clot by following the centreline of the catheter. It will be released by unsheathing the catheter, and finally, pulled along the vessel following the catheter's centreline up to the location of the aspiration catheter.

The main differences between the in silico thrombectomy procedure (COU) and the numerical model described in this study are the assumptions that have been adopted, which generate some limitations of the work. First, the vessel is here considered rigid instead of deformable with a nonlinear behaviour. In this study, the glass and silicon vessels of the in vitro model can be reasonably modelled with rigid parts, an assumption that in the COU model will be withdrawn. Second, the finite-element model of the device is based on the discretization of the stent's centreline into beam elements, to which an equivalent section has been assigned. This represents a simplification which may be a source of discrepancies (in particular in terms of local strains). In addition, the dual-layer structure of the EmboTrap II stent-retriever introduces an additional difficulty to model the two parts linked together. In the current model, the two layers have been considered as a single part, contributing to stiffen the overall axial response of the in silico model with respect to the actual device. Moreover, the strongly nonlinear constitutive model, such as the super-elastic material herein discussed, may lead to an intensification of the hysteresis effect in the numerical model (figure 1e), which is attributable to those elements experiencing higher strains. In the future, more efforts should be made in a more realistic reconstruction of details of the stent geometry, in order to fully exploit the power of this computational tool for the investigation of local quantities, such as stress and strains. Third, the clot shape and material model are defined from analogues instead of from ex vivo clots. However, the methodology proposed by Duffy et al. [29] to replicate clot analogues with diverse compositions is reproducible and clot analogues, despite having a homogeneous composition, duplicate efficaciously ex vivo clots [18]. The clot is modelled with homogeneous compressible hyperelastic material, but different aspects such as viscoelasticity, porosity and adhesion behaviour on the vessel wall could be investigated in future studies.

Moreover, if the thrombectomy procedure is preceded by thrombolysis, the size and location of the clot, drug administration time and drug dose can affect the clot mechanical properties and, consequently, the prediction of the thrombectomy simulation. Fourth, in both the thrombectomy numerical model (COU) and the numerical model described in this work, there is no blood flow. In reality, even though the procedure is usually performed with a balloon which, before the stent-retriever retraction, is inflated to arrest the antegrade flow [14], there could be some secondary flow through the collateral circulation affecting the clot removal. Fifth, in the clinical procedure, it is common practice to wait for an embedding time during the thrombectomy to enforce the integration between clot and stent. This effect is been hypothesized to depend on the clot fibrin stretching during the stent release [28] and is not considered in both the in silico thrombectomy procedure (COU) and the numerical model described in this work.

The goal of a mechanical thrombectomy procedure is to completely remove a thrombus from a vessel, without loss of fragments, and the goal of the relative numerical model is to predict the procedure outcome. The comparison between the in vitro and their equivalent in silico models conducted in this study provides confidence that the numerical model is able to capture and replicate the interaction between the clot and the stent-retriever in both successful and unsuccessful procedures. Distinct validation studies were performed on the stent and the clot models, by replicating with in silico models the in vitro uniaxial tensile and unconfined compression tests. Moreover, stress and strain values from numerical models, which are impossible to obtain from in vivo or in vitro tests, can be used once coupled with a fracture model to predict the possibility of clot fragmentation, the most important complication after thrombectomy procedure. The different stress and strain fields obtained in the different vessel geometries tests allow in future studies to consider some correlation between geometric features of the vessel—such as tortuosity and diameter—and the stresses and strains on the clot.

5. Conclusion

The novel methodology developed shows the potential of our finite-element analysis to model all the steps of a thrombectomy procedure in an accurate way. In particular, this analysis can be used to predict potential revascularization outcomes, help to interpret adverse effects and to improve the understanding of the influence of individual patient anatomies. There is room for further improvement of the thrombectomy technique, which is generally considered the most important treatment for improving stroke treatment today. Another interesting issue is to use numerical modelling to better understand the complications of the treatment despite successful recanalization. There are still open questions about the treatments, such as the effect of the combination of thrombolysis and stent-retriever thrombectomy and the design of new, more effective devices. Consequently, there is still room for improvement in thrombectomy device technology and the thrombectomy procedure. With the introduction of new stroke treatments, many new clinical trials are planned and expected. As such a great opportunity for thrombectomy numerical investigations exists to expedite, optimize or even replace these resource-intensive trials.

Appendix A: INSIST investigators

Charles Majoie¹, Henk Marquering^1,2, Ed van Bavel², Alfons Hoekstra³, Diederik W.J. Dippel⁴, Hester L. Lingsma⁵, Aad van der Lugt⁶, Noor Samuels^4,5,6, Nikki Boodt^4,5,6, Yvo Roos⁷, Simon de Meyer⁸, Senna Staessens⁸, Praneeta Konduri^1,2, Nerea Arrarte², Bastien Chopard⁹, Franck Raynaud⁹, Remy Petkantchin⁹, Vanessa Blanc-Guillemaud¹⁰, Mikhail Panteleev^11,12, Alexey Shibeko¹¹, Francesco Migliavacca¹³, Gabriele Dubini¹³, Giulia Luraghi¹³, Jose Felix Rodriguez Matas¹³, Sara Bridio¹³, Patrick McGarry¹⁴, Kevin Moerman¹⁴, Behrooz Fereidoonnezhad¹⁴, Michael Gilvarry¹⁵, Ray McCarthy¹⁵, Sharon Duffy¹⁵, Anushree Dwivedi¹⁵, Stephen Payne¹⁶, Tamas Jozsa¹⁶, Wahbi El-Bouri¹³, Sissy Georgakopoulou², Victor Azizi³, Raymond Padmos³.

¹Department of Radiology and Nuclear Medicine, Amsterdam UMC, location AMC, Amsterdam, The Netherlands;

²Biomedical Engineering and Physics, Amsterdam UMC, location AMC, Amsterdam, The Netherlands;

³Computational Science Lab, Faculty of Science, Institute for Informatics, University of Amsterdam, Amsterdam, The Netherlands;

⁴Department of Neurology, Erasmus MC University Medical Center, PO Box 2040, 3000 CA Rotterdam, The Netherlands;

⁵Department of Public Health, Erasmus MC University Medical Center, PO Box 2040, 3000 CA Rotterdam, The Netherlands;

⁶Department of Radiology & Nuclear Medicine, Erasmus MC University Medical Center, PO Box 2040, 3000 CA Rotterdam, The Netherlands

⁷Department of Neurology, Amsterdam UMC, location AMC, Amsterdam, The Netherlands;

⁸Laboratory for Thrombosis Research, KU Leuven Campus Kulak Kortrijk, Kortrijk, Belgium;

⁹Computer Science Department, University of Geneva, CUI, 7 route de Drize, 1227 Carouge, Switzerland;

¹⁰Institut de Recherches Internationales Servier, Coubevoie Cedex, France;

¹¹Center for Theoretical Problems of Physicochemical Pharmacology RAS, Moscow, Russia;

¹²Dmitry Rogachev National Research Center of Pediatric Hematology, Oncology and Immunology, Moscow, Russia; Faculty of Physics, Lomonosov Moscow State University, Moscow, Russia;

¹³Department of Chemistry, Materials and Chemical Engineering ‘Giulio Natta’, Politecnico di Milano, Milan, Italy;

¹⁴College of Engineering and Informatics, National University of Ireland Galway, Ireland; National Centre for Biomedical Engineering Science, National University of Ireland Galway, Ireland;

¹⁵Cerenovus, Galway Neuro Technology Centre, Galway, Ireland;

¹⁶Institute of Biomedical Engineering, Department of Engineering Science, University of Oxford, Parks Road, Oxford OX1 3PJ, UK.

Data accessibility

This article has no additional data.

Authors' contributions

G.L. developed the finite-element thrombectomy models with the supervision of J.F.R.M. and the help of S.B.; G.D. helped supervise the research project; F.B. carried out the experimental tests on the device; S.D. and A.D. carried out the thrombectomy in vitro tests with the supervision of R.M.C.; B.F. carried out the experimental tests on the clot analogues with the supervision of P.M.G.; C.B.L.M.M. helped supervise the project from a clinical point of view, and F.M. was in charge of overall direction and planning. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

The authors declare the following potential conflicts of interest with respect to the research, authorship, and/or publication of this article: A.S., A.D. and R.M.C. report a financial relationship with Cerenovus outside the submitted work.

Funding

This project has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement no. 777072.