What processes must we understand to forecast regional-scale population dynamics?

Abstract

An urgent challenge facing biologists is predicting the regional-scale population dynamics of species facing environmental change. Biologists suggest that we must move beyond predictions based on phenomenological models and instead base predictions on underlying processes. For example, population biologists, evolutionary biologists, community ecologists and ecophysiologists all argue that the respective processes they study are essential. Must our models include processes from all of these fields? We argue that answering this critical question is ultimately an empirical exercise requiring a substantial amount of data that have not been integrated for any system to date. To motivate and facilitate the necessary data collection and integration, we first review the potential importance of each mechanism for skilful prediction. We then develop a conceptual framework based on reaction norms, and propose a hierarchical Bayesian statistical framework to integrate processes affecting reaction norms at different scales. The ambitious research programme we advocate is rapidly becoming feasible due to novel collaborations, datasets and analytical tools.

1. Overview

From systems biology [1] to ecosystem ecology [2], researchers claim that (1) prediction is an acid test of our understanding of biology and (2) the best predictions will come from models rooted in the processes that generate system-wide patterns. This is a growing emphasis among organismal biologists, who often argue that prediction of population- and species-level dynamics should be grounded in genetics, physiology and community ecology [3–7].

A key challenge facing contemporary organismal biologists is predicting or forecasting regional-scale population dynamics under environmental change. We use the terms ‘prediction’ and ‘forecast’ interchangeably, defined as expected states of nature in the future. Reliable predictions could guide biodiversity conservation under future environments [8–10]. For example, a model capable of predicting the dynamics of a threatened or invasive species across a large region could identify future critical habitat or help managers allocate resources for eradication. These predictions have been traditionally based on site-specific population models or large-scale, phenomenological distribution models [11]. However, these approaches are frequently criticized [9,12,13], whereas a number of prominent recent reviews have made the case for models based on lower-level mechanisms [3,5–7]. Phenomenological models are based on empirical correlations between environment and occurrence or abundance without explicit functions representing lower-level biological processes. By contrast, mechanistic approaches have explicit representations of how the environment interacts with genotypes, phenotypes or demography.

But which processes are essential? Many population biologists believe that useful forecasts are impossible without accounting for demographic mechanisms [14]. Evolutionary biologists argue that models must consider genetic variation and adaptation [3,15]. Community ecologists focus on species interactions [4,5]. Organismal ecologists argue that physiology [6,16–18] or behaviour [19,20] are essential. Must our models include all of these processes?

We suggest that this is an empirical question that can only be answered by making predictions with competing models and validating them with independent observations. However, testing the predictive value of so many processes requires a programme of data collection and integration that, to our knowledge, has never been completed for any system. Our purpose is to motivate and facilitate such an effort. We begin by reviewing the arguments for building multiple mechanisms into forecasts of regional-scale dynamics. We then develop a conceptual framework for integrating diverse mechanisms, and propose a statistical framework to test their impact on predictive skill while accommodating uncertainty.

2. Toward a process-oriented approach

(a). Shortcomings of a phenomenological approach

Population predictions based on a purely phenomenological representation of biological systems may lack fidelity under novel conditions or when the underlying drivers are high dimensional. In the first case, the functional form of responses to environment may change as organisms encounter conditions not previously experienced, or as individuals develop trait values and trait combinations not previously observed [21,22]. These novel conditions may arise in space (e.g. for an invasive species) or in future times (e.g. under climate change). Note that forecasts have specific temporal scales: many ecological forecasts apply to the next few years, or to the next few decades. A consideration of novel conditions may be particularly problematic for long-term forecasts as conditions with no contemporary analogue become more common.

In a variety of fields, such as epidemiology of infectious disease, fitting curves to past observations and extrapolating to predict the future has yielded poor results as conditions change [23,24]. In principle, mechanistic models avoid these problems by capturing the processes that lead to novel responses to environment. It is important to note that we focus on approaches that both model underlying processes and include lower-level data on these processes. Mechanistic approaches that lack such data may suffer from problems with identifiability, for example, when high-level abundance data can be reproduced by models with very different mechanisms [25,26]. Therefore, a crucial feature of the approach we present below is that mechanistic models are combined with data on underlying mechanisms.

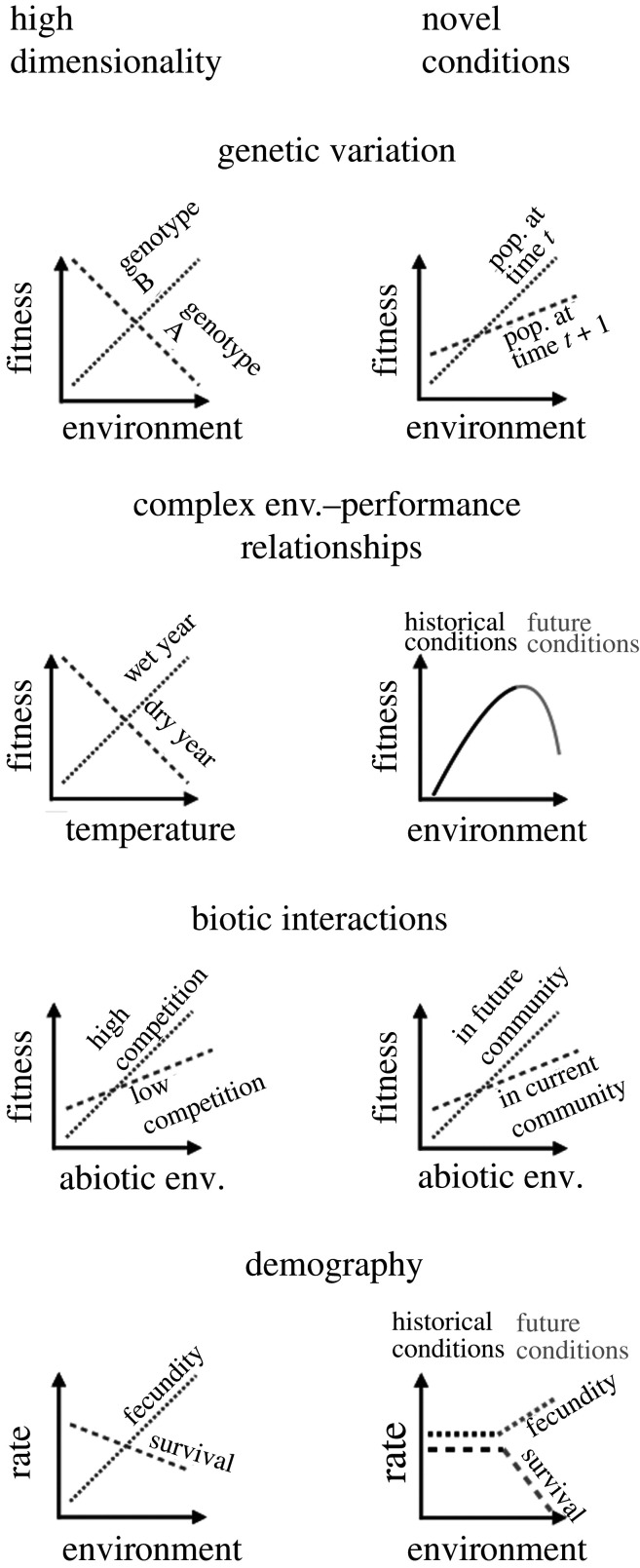
High-dimensionality limits the feasibility of data-driven phenomenological approaches to prediction. When true functional forms are unknown and there are many potentially important and interacting independent variables, it is difficult to collect sufficient high-quality data to describe the true, complex relationships driving regional population dynamics. When multiple population drivers have opposing effects or opposing patterns of variation in nature, observational studies can easily miss these signals. This dimensionality is especially problematic when observations are made at a scale where aggregation obscures the effects of important processes [27–29]. A mechanistic understanding can identify the most important aspects of organisms, environments and scales of observation. In the following sections, we describe examples of the potential benefits of process-oriented approaches, focusing on four categories of biological complexity that can confound regional population forecasts (figure 1): genetic variation, complex environment–performance relationships, biotic interactions and demography.

Figure 1.

Examples of how underlying biological complexity may confound regional population forecasting, due to high dimensionality of the systems or the systems entering novel conditions. For each example, ignoring the complexity shown here could lead to major inaccuracies in forecasts. In the ‘high dimensionality’ examples, relationships between environment and fitness are highly dimensional due to the four different categories of processes. In the ‘novel conditions’ examples, the relationship between environment and fitness observed in contemporary populations change under novel conditions related to the same four categories of processes.

(b). Genetic variation

Genetic variation within species is often overlooked in population, community and macro-ecology. Models and predictions of species range dynamics or regional population forecasts typically assume a single set of parameters for a species [30].

In reality, species often exhibit intraspecific genetic variation in response to their environment. Evolutionary biology offers numerous examples of genetic variation in trait and demographic responses to environmental variation, such as for abiotic stress response [31–33], host–pathogen interactions [34] and predator–prey interactions [35,36]. Spatially varying environments can favour different traits in different places and, as a result, much of the genetic variation in environmental responses is geographically structured. Thus, individual fitness and population growth rates often respond to the environment in different ways in different locations. Large-scale forecasts typically ignore these differences.

If populations differ genetically in environmental responses, then accurate regional population forecasts may require accounting for genetic variation, as well as genetic change over time (i.e. evolution; figure 1). For example, forecasts of regional population dynamics might assume individuals have as broad an environmental tolerance as the species in aggregate, while in reality locally adapted populations have narrower tolerances [30]. In this case, even though populations suited to future environments might exist within a species’ range, specific alleles may not occur in the location where they would be adaptive. As a result, forecasts under environmental change might be overly optimistic and underestimate the threat of extinction [37].

Researchers have begun to incorporate genetic variation into regional population prediction. Some researchers have fit models that identify genotypes associated with specific current environments, assuming local adaptation, and then used predicted future environments to assess mismatch between local genotypes and their future environments [38–41] (reviewed by Capblancq et al. [15]). Additionally, researchers have fitted environmental response models using geographically restricted subsets of populations, presumably accounting for geographic genetic variation, to project distributions under future conditions [42–44].

Without rigorous validation, predictions have unknown value. Important hurdles for predictions are success at out-of-sample prediction, and prediction into parameter space where data are sparse. After all, these models are being developed for prediction in a future of novel conditions. Recently, genetic models of environmental response and adaptation have been used in out-of-sample predictions of individual or population performance in response to environmental stressors in both wild and agricultural species [38,41,45–48]. These have generally had modest success, for example, in predicting relative genetic variation in change in performance [46,47] or population change [38] with accuracy (predicted versus observed correlation) ≈ 0.3. Messina et al. [48] were able to predict relative genetic variation in performance in novel (non-test) environments, using a combined genomic–physiological model, to r ≈ 0.6.

Incorporating genetic variation in regional population forecasts presents several challenges. First, statistical interactions among genetic loci can be important, but may be unknown a priori and too high-dimensional to discover with data-driven approaches. In crop systems, where there have been major advances in using genetics to predict environmental responses, models incorporating genetic variation have largely treated genetics as phenomenological [49]. Opportunities may exist to improve forecasts with largely phenomenological treatment of genetic effects, but focused on capturing some important aspects of the underlying genetic mechanism. For example, predictions may be based on subsets of genetic loci (e.g. gene regulatory loci) most likely to affect ecologically important traits and environmental responses [50–52].

Second, novel population genetic compositions will evolve through new mutations, gene flow, selection and drift. Some of these processes are particularly challenging to model [30]. For example, gene flow is often poorly observed, and can result in major shifts in genetic composition of populations, potentially alleviating maladaptation to future environments [53]. Predictive modelling of drift may require demographic data (see below). Given the rate of global environmental change and the high standing variation often observed in traits related to abiotic stress response [54], new mutations are likely to be of lesser importance for regional dynamics (although this may not be true at expanding range margins, due to drift) [55]. Selection can be modelled using experimental data relating fitness to genotype [33], although indirect approaches may be required for species not amenable to experimentation [56,57].

(c). Complex environment–performance relationships

Biologists often study how individuals, populations or species respond to a single environmental gradient, or perhaps a small set of environmental factors, along with their pairwise interactions or linear combinations [58,59]. But interactions among environmental drivers are more complex: precipitation, temperature and soil characteristics determine soil moisture; snow cover and air temperature determine winter soil temperature; solar radiation, albedo, wind and air temperature determine the energy balance of ectothermic plants and animals. Additional complexity arises as organismal trait changes in response to environment moderate the effects of potential stressors. For example, when the timing of developmental transitions (phenology) is sensitive to environmental thresholds, organisms can show sharp trait changes [60]. Animals can use behaviour to avoid thresholds beyond which abiotic conditions can become dangerous [6]. As a result, individual fitness responses to environment are often nonlinear and non-monotonic, as in mortality caused by freezing temperatures, rapid nonlinear declines in performance at high temperatures or hydraulic failure under moisture stress in plants [42,61].

It is difficult to detect thresholds and complex interactions among measured environmental variables, especially given the noisy relationships between those variables and abundance or fitness components. The potential model space to explore is large. While machine learning approaches have been used to predict species or genotype geographical distributions based on complex environmental interactions [62,63], they are not generative models and cannot be easily customized for specific studies, data types and questions. Machine learning approaches can sometimes excel at prediction when they are used in the exact setting they were designed for, but they lack the ability to formally incorporate mechanisms via thoughtfully developed simulation models (e.g. mathematical models, agent-based models, virtual ecologist models [64]). Furthermore, nonlinearities that only emerge under novel conditions may thwart extrapolations of phenomenological relationships. Forecasting models that do not account for thresholds and interactions might not predict large changes in populations moving across thresholds under future environments (figure 1).

Direct observation of individual responses to changing environments, especially under controlled conditions, may provide more precise information for building this complexity into predictive models [6,19,65]. Complexity may be partly captured in models by relating measured environmental parameters to conditions directly experienced by organisms, such as an organism’s body temperature (as opposed to the air temperature in most gridded datasets). Additionally, this complexity may be captured by modelling environmental effects based on developmental, physiological or behavioural first principles, such as energy budget [66] or stem hydraulics models [67]. A mechanistic understanding of these responses might allow prediction of responses to extreme events that are rarely observed even in long-term observational studies.

A major challenge is that these approaches require many detailed observations or background information on the most important aspects of the environment for organisms. For many species and populations this information currently does not exist and will require extensive study of phenology, physiology or behaviour. Even in crops, which are among the most well-studied systems from an ecophysiological and developmental perspective, models struggle to effectively predict across multiple dimensions of novel environmental conditions [49]. Additionally, the fine-scale data required to describe specific aspects of environment that impact fitness might be challenging to collect, model and predict at large scales [61].

(d). Biotic interactions

Studies of population response to the abiotic environment and forecasts of large-scale dynamics typically overlook biotic interactions even though they can have large effects on individual fitness and population growth. For example, species with strong interactions (e.g. host–parasite, predator–prey) might have tightly coupled population dynamics, obscuring the effects of fluctuating abiotic conditions. Additionally, a given species might show strong population responses to local gradients in community composition, as in the case of an early or late successional specialist. Biotic constraints such as resource competition may limit organisms’ ability to take advantage of favourable conditions, such as greater resource supply (e.g. higher rainfall for plants) [68,69]. Abiotic conditions may determine the nature of species interactions, such as when stress shifts the balance between competition and facilitation [70]. The effects of abiotic change on populations may be constrained and mediated by these biotic interactions.

Incorporating biotic interactions in predictive models is challenging because of the high dimensionality of community ecology (i.e. the number of species and higher-order interactions among them) and the potential for no-analogue future assemblages (figure 1). When species interactions have a strong influence on population growth, shifts in community composition caused by abiotic environmental change can offset or even overwhelm the direct effects of abiotic change [5,71,72]. Unravelling these direct and indirect effects would be straightforward if the effects of abiotic factors and biotic interactions on demographic rates were independent and additive, but we have good reasons to expect complex interactions. For example, abiotic change might reduce fitness of a superior competitor more than an inferior competing species, leading to a population increase of the inferior competitor despite less favourable abiotic conditions [73]. Studies often rely on interannual climate fluctuations to observe abiotic–biotic interactions, but when future abiotic conditions are novel, communities may also enter novel states, thwarting prediction of a focal species’s population dynamics based on recent observations (figure 1). Furthermore, direct human impacts on populations will generate novel communities and biotic interactions [74]. The potential for such interactions illustrates the need for experiments that manipulate both abiotic conditions and biotic interactions.

Some researchers have fit joint models of community members’ responses to abiotic conditions while including interactions among species [4,75,76]. However, such an approach requires large amounts of data, and it remains unclear how these efforts will succeed at forecasting under environmental change when models are fitted to noisy observational data [77,78]. A major reason there has been slow empirical progress in this area is the challenge in experimentally manipulating multiple community members (a problem of high dimensionality). Mechanistic models of species interactions are one potential way to include these interactions in predictive models [5,79]. Alternative approaches focus on forecasts of community- or ecosystem-wide responses to environmental change [2]. These aggregate over the many dimensions of community variation, but may offer little information about dynamics of individual species of interest.

(e). Demography

Simple, linear and phenomenological models that relate environment to abundance might work well for organisms with very simple life cycles. For organisms with more complex life cycles, ignoring differences in how individuals of different ages, life stages, sizes or sexes respond to the environment may be problematic (figure 1). When these sources of heterogeneity are important, models need to account for how individual vital rates (e.g. survival, growth and fecundity) vary as a function of both demographic state (e.g. age, size, sex) and the environment [80].

To appreciate why accounting for the interactive effects of population structure and the environment is important, consider a phenomenological approach that relates local abundance of a long-lived plant directly to an environmental driver. If the population is well established, it is likely to be dominated by large, mature individuals. Year-to-year variation in abundance will reflect the growth and mortality of these large individuals, and contributions from rare recruitment events will be small. If the mature individuals are stress-tolerant, we might find only a weak correlation between drought and population growth rate. Extrapolating this relationship to project the potential impacts of increasing aridity under climate change would predict minimal impacts on the population. But what if seedlings are less stress tolerant, and recruitment is limited to infrequent cool, wet years [81]? After disturbance of the established stand, the population might have difficulty recovering under future, more arid, conditions. By contrast, a model that accounts for interactions between size or stage structure and the environment could correctly predict both the limited impacts of increasing aridity on a population dominated by mature individuals, as well as a reduced ability of the population to recover following disturbance (when population growth depends most on recruitment). This hypothetical example shows how traditional demographic analyses, such as matrix population models [82] and integral population models [83], can handle both high dimensionality (interactions between the environment and multiple vital rates) and novel conditions (changes in stage structure and environment).

While the existing tools for modelling demography and population growth are sophisticated, they have almost always been applied to just one local population at a time. Scaling up to multiple populations along complex environmental gradients represents a much greater challenge. Fortunately, many demographers are now focused on this task, using approaches described as ‘landscape demography’ [84–86] or ‘dynamic range models’ [87–89]. These approaches incorporate differences among populations in environmental context and stage-structure, but have largely ignored genetic or phenotypic variation among populations and species interactions.

3. How do we determine which of these processes are most important for prediction?

(a). Including all processes in a model may not improve prediction

We have reviewed compelling arguments for why each of the processes described in §2 must be considered in a regional-scale population projection. However, a critical point that this body of the literature has ignored is that including all of these processes in a model may not improve prediction.

Uncertainty in predictive modelling can be divided into two components: bias, caused by incorrect and overly simple models, versus variance, due to low numbers of observations relative to the number of estimated parameters [90]. While it may appeal to biologists to create models that incorporate ever more processes in greater realism, increasing model complexity can increase errors resulting from poorly estimated parameters, lead to overfitting and decrease interpretability (making it harder to troubleshoot models). Optimal models for population prediction must balance bias against variance, and optimal models are often surprisingly simple [91,92]. These problems have already presented themselves in population forecasting, but there has not been a reckoning for the complex models that would be the logical extension of the current movement to incorporate all the processes in §2.

(b). Comparing models

Optimal predictive models are typically selected through empirical comparison or regularization (i.e. reducing complexity of a more general model [93]). While we may have extensive knowledge about some components of the system, we may lack empirical results to constrain certain model formulations. Thus, we must make predictions with a set of models that represent different processes, test those predictions using proper and local scores based on independent data (data not used for model fitting [94]), assess which model works best, and rigorously analyse uncertainties and biases [95].

To date, many efforts to predict species distributional changes or regional population dynamics have been conducted without out-of-sample validation. Without out-of-sample validation, we cannot determine how well predictions will fare under the novel conditions of the future. Experiments that manipulate environments to represent potential future conditions will provide important information. By testing model predictions locally (i.e. for specific locations in geographic or parameter space), we can begin to understand where and why models fail. This kind of validation and model comparison has yet to be performed for a regional-scale population model that incorporates all of the categories of processes described above, meaning that the relative importance of these processes is unknown, as is the utility of an integrative model.

(c). Reaction norms as a conceptual basis for integrative models

Traditionally, each of the important candidate processes described above has been studied separately. To test their relative value for predictions, we need new approaches for integrating information about different processes in statistical models. Without an integrative model, we cannot compare models incorporating more than one process, let alone consider interactions among these processes. For example, information about a genetic variant or a physiological threshold that affects organisms of a particular size class might be far more useful in a size-structured demographic model than in a model that simply tracks population density.

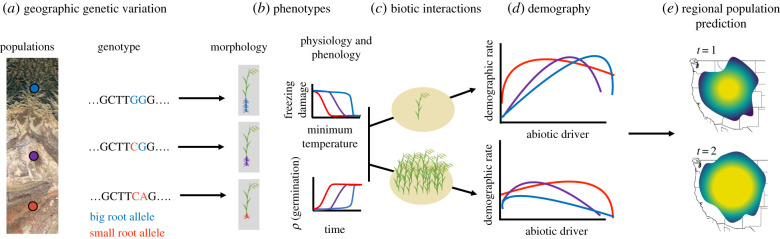
Reaction norms, which describe the change in a trait or performance across environments, provide a framework to integrate the processes discussed in the preceding sections. Reaction norms occupy a middle position in a hierarchy of biological complexity among the mechanisms we discussed, and thus they may be viewed as a nexus for integration (figure 2). It is the complexity of these reaction norms that unites the arguments for incorporating mechanism into population forecasts (§2, figure 1). We suggest that reaction norms are an intuitive concept that can be embedded in integrative population models. Genetic variation can be linked to reaction norms of lower-level traits like phenology, behaviour and physiology, which can then be linked to reaction norms for individual demographic rates and fitness (figure 2). However, previous research has described the response of one vital rate or trait to just one abiotic driver measured under controlled conditions. Such idealized reaction norms may be of little use for predicting population dynamics at a single location affected by many interacting environmental drivers, let alone for scaling up population models across a heterogeneous region containing genetically differentiated populations. The complexities we highlight require higher-dimensional reaction norms (figure 1).

Figure 2.

Reaction norms (figures with coloured curves) occupy a middle position in a hierarchy of biological complexity among the mechanisms discussed here. Thus, reaction norms can be viewed as a conceptual basis for building integrative models of regional population dynamics. We show a hypothetical plant example. Predicting regional dynamics (e) may require understanding (a) geographical patterns of genetic variation in environmental response, (b) the phenotypes involved and complex environment–performance relationships (such as physiological thresholds), (c) biotic interactions such as intraspecific density dependence or (d) individual demographic rate responses to environment. (Online version in colour.)

One benefit of shifting to models that include reaction norms for key traits is that population models are more easily linked to ecosystem processes. For example, if photosynthetic rates are built into population models of a plant, it is easier to build integrated population–ecosystem models that allow us to assess how environmental changes jointly impact both (e.g. as has been investigated in crop models [49]). The complexity of trait relationships with demography and ecosystem processes requires a substantial integration of underlying mechanisms into population–ecosystem models [96].

4. Integrative hierarchical framework

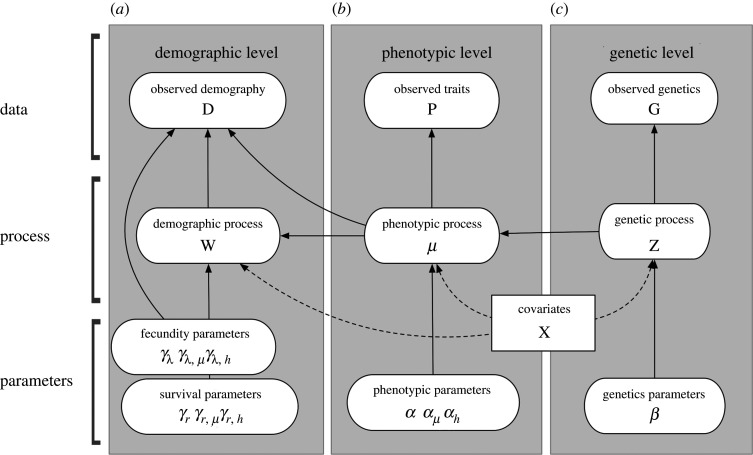
We propose a hierarchical Bayesian framework to construct an integrated reaction norm model with genetic, phenotypic and demographic components (figure 3). These components correspond to multiple types of experimental and observational data, including DNA sequences, phenotypes, vital rates and environmental conditions. The components of this model are linked by relationships that have been historically modelled separately. To account for and link the processes described above, an integrative model is required ([98], ch. 25). We propose straightforward extensions and generalizations of past efforts that enhance the power of our inferences and compare the importance of different components, and build on approaches developed for other integrated models that borrow strength from multiple data sources [99,100].

Figure 3.

The directed acyclic graph (e.g. [97]) for our integrated reaction norm model. Solid and dashed arrows indicate stochastic and deterministic connections, respectively. Parameter descriptions in full can also be found in electronic supplementary material, tables S1 and S2.

We briefly describe an integrated hierarchical model that comprises three levels (figure 3): genetic, phenotypic and demographic. We offer more detail in the following sections. Our example model connects the three levels using conditional stochastic models with latent processes that depend on each other. In this case, the natural scaling between levels implies the conditional structure with the demographic process depending on the phenotypic process, which in turn depends on the genetic process.

The genetic component allows allele frequencies to change in space and time as a function of underlying environmental selective gradients and gene flow. This part of our approach is similar to genotype–environment association models that identify loci locally adapted to specific environments [63,101], or spatial models of allele frequency turnover [102].

The genetic component is linked to a phenotypic model that determines how genotype and environment determine phenotypes. This part of the model captures processes usually studied by genetic mapping approaches that identify genetic loci causing trait variation [103], or genomic selection approaches that model the whole-genome contribution to quantitative trait variation [104], including models of trait variation across environments [45,48]. This part of the model also captures plastic trait responses to environment (trait reaction norms) that are often a topic in ecophysiology, behavioural ecology and functional ecology.

Finally, the demographic component determines how traits influence vital rates and ultimately fitness. This approach mirrors evolutionary ecology, quantitative genetic analyses of how trait variation is related to vital rates [105], changes in these relationships across environments (i.e. how traits mediate reaction norms of demography) [106,107], as well as how selection may change across life stages/vital rates [108]. These model components cover the processes discussed in §2 and their integration is described below.

(a). Modelling genetic processes based on environment and space

We start with an approach to model change in allele frequency along environmental gradients and in space in a way that facilitates prediction of allelic state at genetic markers (e.g. single-nucleotide polymorphisms, SNPs) for a given location. Obtaining the predictive distribution of allele frequencies allows us to make inference on changes in allele frequencies under changing environmental conditions or with gene flow [109]. Parametric models allow us to properly account for, and learn about, uncertainty in a way that can be correctly propagated through to other types of inference. To generalize the concept of genotype–environment associations in a way that accounts for individual-level variability and mechanistic sources of gene flow, we use a hierarchical modelling structure where the individual-based genotype data g_jil for individual i = 1, …, n_j in population j = 1, …, J and for genetic locus l = 1, …, L, arise stochastically as

$$g_{\hspace{0.17em}jil}\sim \text{Bern}(z_{\hspace{0.17em}jl}).$$ 4.1

The population-level allele frequency is modelled as

$$f(z_{\hspace{0.17em}jl})={\mathbf{x}}_{\hspace{0.17em}j}^{\prime }{\mathit{\beta }}_l+{\eta }_{\hspace{0.17em}jl},$$ 4.2

where x_j represent a set of covariates (e.g. topography, soil type, precipitation) and f is an appropriate link function. In this model (4.2), the coefficients ${\mathit{\beta }}_l$ connect the environmental variables to allele frequency at SNP l in a way that accounts for local adaptation.

In cases where we need to account for patterns of gene flow and population structure, the η_jl are random effects (e.g. spatially structured) [109–111] that we can model jointly as

$$\mathit{\eta }\sim \text{N}(\mathbf{0},\mathbf{\Sigma }),$$ 4.3

where the covariance matrix is parameterized as

$$\mathbf{\Sigma }={\sigma }^2\mathbf{R}.$$ 4.4

The J × J matrix R may be specified as an intrinsic conditional autoregressive (ICAR) [112] correlation matrix that depends on geographic information about the environment. Hanks & Hooten [109] showed that this type of ICAR formulation provides a formal statistical model for gene flow based on circuit theory. By allowing the random effects η_jl in (4.2) to be spatially structured, we can accommodate gene flow mechanisms such as isolation by barrier, distance and resistance [111]. Note that historical patterns of gene flow, especially during colonization when drift is strong, may differ from current gene flow and the model can be generalized to accommodate such processes.

In the presence of temporal data, the model could be formulated as

$$g_{\hspace{0.17em}jilt}\sim \text{Bern}(z_{\hspace{0.17em}jlt}),$$ 4.5

for time t = 1, …, T, where the time-specific population-level allele frequency is modelled as

$$f(z_{\hspace{0.17em}jlt})={\mathbf{x}}_{\hspace{0.17em}jt}^{\prime }{\mathit{\beta }}_{lt}+{\eta }_{\hspace{0.17em}jlt}.$$ 4.6

This extended model formulation explicitly accounts for changes in the environment over time to help us understand how environment aids in the prediction of genotypes. The model is generative and can be used to simulate genetic data to better understand the effects of future environments on genotypes.

This modelling framework can also be generalized to account for multilocus dependence explicitly. To do that, we introduce another random effect to the model in (4.2):

$$f(z_{\hspace{0.17em}jl})={\mathbf{x}}_{\hspace{0.17em}j}^{\prime }{\mathit{\beta }}_l+{\eta }_{\hspace{0.17em}jl}+{\xi }_{\hspace{0.17em}jl},$$ 4.7

where, jointly across loci, the random effects are assumed to be structured according to their linkage distance (if on the same chromosome), such that ${\mathit{\xi }}_{\hspace{0.17em}j}\sim \text{N}(\mathbf{0},{\mathbf{\Sigma }}_{\xi })$. Not accounting for multilocus associations when they exist can obscure our inference about the importance of physically linked loci. Furthermore, multilocus dependence could improve prediction of genotypes for cases where the genotype is only partially observable (e.g. because of limited resources and genetic markers).

(b). Incorporating phenotypes

We can integrate genotype–phenotype and environment–phenotype relationships into our model. Consider the measurement of p_jiq for trait q on individual i in population j. To connect the phenotype and genotype in a statistical model, let

$$p_{\hspace{0.17em}jiq}\sim {[p_{\hspace{0.17em}jiq}|{\mu }_{\hspace{0.17em}jiq},{\mathit{\theta }}_q]}_q,$$ 4.8

such that ${[p_{\hspace{0.17em}jiq}|{\mu }_{\hspace{0.17em}jiq},{\mathit{\theta }}_q]}_q$ is a trait-specific conditional data model with ${\mathit{\theta }}_q$ as trait-specific parameters. We let the trait data model vary to accommodate a variety of traits; for example, for binary traits, the distribution in (4.8) should be Bernoulli and ${\mathit{\theta }}_q=\mathrm{\varnothing }$.

We now introduce the first reaction norm presented in our model, describing plastic trait change across environments (e.g. figure 2, ‘phenotypes’), as well as a way to accommodate higher dimensionality due to genetic variation in reaction norms. The mean μ_jiq of the conditional trait distribution is modelled as

$$f({\mu }_{\hspace{0.17em}jiq})={\mathbf{x}}_{\hspace{0.17em}j}^{\prime }\mathit{\alpha }+{\mathbf{z}}_{\hspace{0.17em}ji}^{\prime }{\mathit{\alpha }}_{\mu }+h({\mathbf{x}}_{\hspace{0.17em}j},{\mathbf{z}}_{\hspace{0.17em}ji},{\mathit{\alpha }}_h)+{\epsilon }_{\hspace{0.17em}jiq},$$ 4.9

where f is a suitable link function and ${\mathbf{x}}_{\hspace{0.17em}j}^{\prime }\mathit{\alpha }$ accounts for phenotypic plasticity (i.e. environmental effects on traits), ${\mathbf{z}}_{\hspace{0.17em}ji}^{\prime }{\mathit{\alpha }}_{\mu }$ accounts for genetic effects on the trait, $h({\mathbf{x}}_{\hspace{0.17em}j},{\mathbf{z}}_{\hspace{0.17em}ji},{\mathit{\alpha }}_h)$ is a function (e.g. a set of interactions) that accounts for genetic variation in plasticity (i.e. reaction norms), and the error term is correlated by a relevant grouping structure due to genetic similarity among individuals or latent spatial structure, for example. The genetic component of traits changes in space and time due to changes in allele frequency as described in the previous section. Jointly across individuals and groups, the errors are modelled as

$${\mathit{\epsilon }}_q\sim \text{N}(\mathbf{0},{\sigma }_q^2\mathbf{I}+{\mathbf{\Sigma }}_y),$$ 4.10

where the variance component ${\sigma }_q^2$ may be set to zero as necessary for certain traits q.

Up to this point, we have described what might be termed an ‘integrated landscape genomic-reaction norm model’, following common usage of terms. We can generalize this model to account for temporally indexed trait data like the genotype model described in the previous section. Finally, the modular nature of the two models implies that we may be able to apply recursive Bayesian techniques to fit the model in a computationally efficient framework [113,114]. When genetic data are not available or desired, patterns of local adaptation in genetic trait–environment correlations can be accommodated in our framework by treating the genetic process in §4a as latent.

(c). Incorporating demography

We can learn about population dynamics using demographic models, the specific form of which will vary depending on the study system. For example, at site j we observe n_j individual-level survival outcomes (w_ij = 1) that we model as w_ij ∼ Bern(r_ij), where r_ij represents the survival probability of individual i. By specifying individual-level demography, we can link individual genotype and phenotype to environment and the effects on demography. Our approach is to build reaction norms of demographic vital rates that depend on (possibly latent) phenotype–environment interactions, where the phenotypes themselves are modelled as reaction norms as described in the previous section.

At the end of a reproductive season, we can model the number of offspring of a hermaphroditic individual i, d_ij, as arising from the zero-inflated distribution

$$d_{ij}\sim \{\begin{array}{cc}\text{Pois}({\lambda }_{ij})\text{, }& \hspace{0.17em}{w}_{ij}=1\\ 0\text{, }& \hspace{0.17em}{w}_{ij}=0,\end{array}$$ 4.11

where λ_ij represents the fecundity of individuals surviving to reproduction.

We seek to infer the effect of phenotype and environment on individual-level fecundity and survival at site j. Consider the latent process model for individual-level survival probability r_ij where

$$f(r_{ij})={\mathbf{x}}_{ij}^{\prime }{\mathit{\gamma }}_r+{\mathit{\mu }}_{ij}^{\prime }{\mathit{\gamma }}_{r,\mu }+h({\mathbf{x}}_{ij},{\mathit{\mu }}_{ij},{\mathit{\gamma }}_{r,h}),$$ 4.12

and the covariates and associated regression coefficients are specified in the same manner as in the genetic and phenotypic model components. This model allows us to account for multivariate phenotypic effects ${\mathit{\mu }}_{ij}$ on survival. When important traits are unknown or unmeasured (a common occurrence) we may use genotypes in place of or in addition to ${\mathit{\mu }}_{ij}$, to model selection on latent traits. We can specify a similar model for fecundity λ_ij as

$$\log ({\lambda }_{ij})={\mathbf{x}}_{ij}^{\prime }{\mathit{\gamma }}_{\lambda }+{\mathit{\mu }}_{ij}^{\prime }{\mathit{\gamma }}_{\lambda ,\mu }+h({\mathbf{x}}_{ij},{\mathit{\mu }}_{ij},{\mathit{\gamma }}_{\lambda ,h}).$$ 4.13

Biotic interactions (e.g. conspecific density dependence, parasitism) can be incorporated via x_ij. This model can be fitted from a hierarchical perspective (perhaps jointly with the previously described genetic and phenotypic components).

To review, we have a genetic model component connected to a phenotypic component, which is then linked to selection and demography. Note that the $h({\mathbf{x}}_{ij},{\mathit{\mu }}_{ij},{\mathit{\gamma }}_{\lambda ,h})$ function in (4.13) (and the similar function in (4.12)) and the ${\mathbf{x}}_{\hspace{0.17em}j}^{\prime }{\mathit{\beta }}_l$ term in (4.2) both represent changes in selection across environmental gradients x_ij, and the information on these changes in selection arises from both the distribution of alleles across environments, their effects on phenotypes and the changes in selection on these phenotypes across environments [115]. Together with the genetic and phenotypic model components, we can express the full integrated hierarchical genetic–phenotypic–demographic–environmental model as a directed acyclic graph (figure 3).

We can generalize the ecological model component by allowing for additional data sources when available. For example, we can fuse presence-only and occupancy (with no individual identification) data, as well as unmarked counts of individuals if replicates are available, by adapting (4.2) to include the point process, occupancy, or N-mixture model frameworks [98]. Furthermore, we can accommodate time series data by indexing the data with a t subscript as described in §4a.

(d). Resulting inference

The full hierarchical model in figure 3 is generative and can be used to simulate data to better understand the effects of future environmental regimes on populations, phenotypes and genotypes. For example, by comparing contemporary genotypes in a given location with genotypes under future environments, we can better understand sensitivity to changes in environment [15] and link this inference to spatio-temporal predictor variables and create maps of these sensitivities with uncertainty.

Each model component in figure 3 can be fitted individually to the relevant subset of data while conditioning on known or hypothesized elements from other components. However, the benefit of constructing a jointly specified integrated model is that we can fit the full hierarchical model and simultaneously learn about all the model quantities while allowing for feedbacks to occur among demographic, phenotypic and genetic processes. The full hierarchical model also allows the uncertainties to propagate among model components so that we can make valid conclusions about the relative importance of each process. We can also compare predictions from the full model with predictions from simpler models that ignore one or more components and the processes they represent. These comparisons will identify the optimal level of complexity for prediction. When implementing the model, if additional flexibility is needed, we can use basis function expansions of the environmental, genetic and phenotypic space [116] to account for nonlinearities in the relationships.

To optimize predictive ability, we can hold out data from a subset of sites (or time points) for model validation. We can use the integrated model to obtain the posterior predictions for the latent processes. The direct comparison of observed and predicted population growth is essential for quantifying sources of uncertainty in the model, an important step in guiding future research to improve the model.

(e). Feasibility

Fitting our integrated model will require an unprecedented, coordinated data collection effort. But unprecedented does not mean impossible. Annual plants may be a good starting point because their simple life cycles facilitate estimation of lifetime fitness, even in experimental settings. For example, existing knowledge and resources make the model annual plant Arabidopsis thaliana amenable [40,47]. We are leading a network of researchers tackling the goal of this paper using Bromus tectorum, a widely distributed annual grass invasive in western North America. Even some long-lived perennial plants have been studied using common gardens, demographic observations and genomic techniques (especially in species of economic value) [117,118]. While controlled field or lab experiments may even be possible for some small animals [119], for many species controlled experiments are extremely difficult. Additionally, the complexity of biological systems may resist our efforts to experiment, observe and build mechanistic models. In the face of such challenges, integrative regional forecasting models may be built with fewer of the processes described above, or with phenomenological components. The strength of our suggested approach is its ability to quantify the predictive value of any processes that can be feasibly modelled.

5. Conclusion

It is clear that a wide range of biological processes can be incorporated into large-scale forecasts of population dynamics under environmental change. But the route to accurate prediction might not involve building models of ever-increasing complexity. While the integrated model we describe does account for many underlying processes, we emphasize that this full model is intended for development and may not itself be the ideal model for prediction. To advance the field of regional population prediction, we need extensive empirical study and an iterative process of model improvement [120]. Which processes are important for good forecasting may depend on the time scale of the forecast (or forecast horizon) [121].

We presented a statistical framework to integrate these diverse processes in a model for use in prediction. This framework is novel because it formally unifies genetic, phenotypic and demographic components into an integrated reaction norm model and suggests general computational methods for fitting it. We can compare our methods with other existing, less integrated approaches and quantify the value added when formally borrowing strength across multiple sources of data in a single, cohesive hierarchical modelling framework. The answer to the question we posed, ‘what processes must we understand to forecast regional scale population dynamics?’, will be found only through careful study that generates the extensive multi-dimensional data discussed here combined with an integrative modelling approach.

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed to the development of the manuscript. J.R.L. led the writing and M.B.H. led the model development.

Competing interests

We declare we have no competing interests.

Funding

Funding was provided by NSF DEB grant nos. 1927177, 1927282 and 1927009.

Disclaimer

Any use of trade, firm or product names is for descriptive purposes only and does not imply endorsement by the US Government.