The thermodynamics of thinking: connections between neural activity, energy metabolism and blood flow

Abstract

Several current functional neuroimaging methods are sensitive to cerebral metabolism and cerebral blood flow (CBF) rather than the underlying neural activity itself. Empirically, the connections between metabolism, flow and neural activity are complex and somewhat counterintuitive: CBF and glycolysis increase more than seems to be needed to provide oxygen and pyruvate for oxidative metabolism, and the oxygen extraction fraction is relatively low in the brain and decreases when oxygen metabolism increases. This work lays a foundation for the idea that this unexpected pattern of physiological changes is consistent with basic thermodynamic considerations related to metabolism. In the context of this thermodynamic framework, the apparent mismatches in metabolic rates and CBF are related to preserving the entropy change of oxidative metabolism, specifically the O₂/CO₂ ratio in the mitochondria. However, the mechanism supporting this CBF response is likely not owing to feedback from a hypothetical O₂ sensor in tissue, but rather is consistent with feed-forward control by signals from both excitatory and inhibitory neural activity. Quantitative predictions of the thermodynamic framework, based on models of O₂ and CO₂ transport and possible neural drivers of CBF control, are in good agreement with a wide range of experimental data, including responses to neural activation, hypercapnia, hypoxia and high-altitude acclimatization.

This article is part of the theme issue ‘Key relationships between non-invasive functional neuroimaging and the underlying neuronal activity’.

1. Introduction: The challenge of interpreting metabolism and blood flow dynamics in terms of the underlying neural activity

Current functional non-invasive neuroimaging methods such as functional magnetic resonance imaging (fMRI), positron emission tomography (PET) and near-infrared spectroscopy (NIRS) do not measure neural activity directly, but instead are sensitive to metabolic and blood flow changes that accompany changes in neural activity [1]. Consequently, understanding the links between metabolism, flow and neural activity is an active goal of current neuroimaging research. Intuitively, we expect strong connections because neural activity is energetically costly [2–10]. To simplify a complex process, excitatory synaptic activity generates sodium currents from the extracellular to intracellular space, and in recovery from this activity neurons must then pump sodium back out of the cell against a steep thermodynamic gradient. This is accomplished by coupling sodium transport to the conversion of adenosine triphosphate (ATP) to adenosine diphosphate (ADP), a thermodynamically highly favourable reaction, within the sodium/potassium pump [11]. ATP, the ubiquitous energy currency of the cell, is then restored through glucose metabolism [8,12,13]. The first step is glycolysis in the cytosol, generating a small amount of ATP with the conversion of glucose to pyruvate (Pyr). Much more ATP is then generated by oxidative metabolism of Pyr in the mitochondria, consuming O₂ and producing CO₂. Blood flow delivers the O₂ and glucose and carries away the CO₂.

The simplest scenario we might have imagined for this net process would be a serial chain of events with each triggering the next: recovery from neural activity depletes ATP, reduced ATP stimulates glycolysis and oxidative metabolism, and increased metabolism stimulates blood flow. In addition to this simple chain of driving mechanisms, we might have anticipated proportional changes of the cerebral metabolic rate of glucose (CMRGlc), the cerebral metabolic rate of oxygen (CMRO₂) and cerebral blood flow (CBF), all matched to the degree of neural activity change. Instead, though, current research suggests a much more complicated picture (figure 1a), with several counterintuitive features, and it is the complexity of this process that currently presents a barrier to more quantitative interpretations of metabolism and flow dynamics in terms of the underlying neural dynamics.

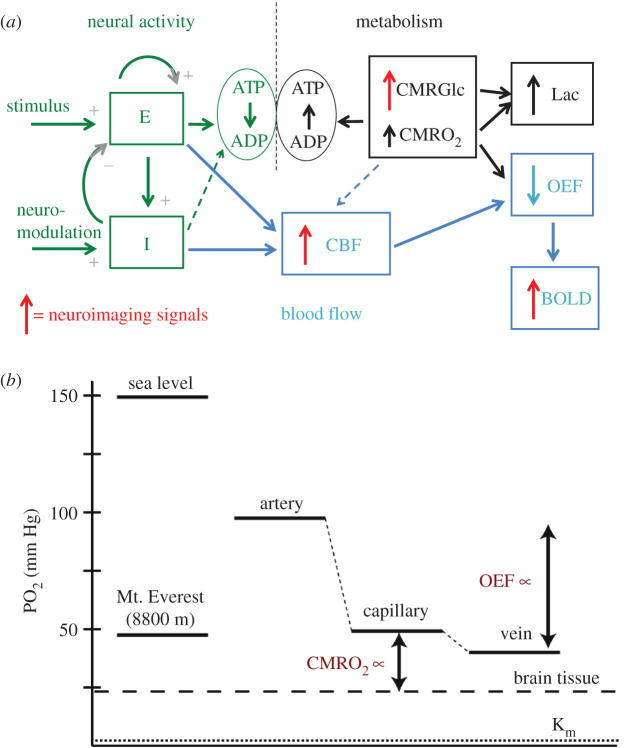
Figure 1.

(a,b) Schematic of the connections between neural activity, metabolism, blood flow and neuroimaging signals. (a) Input stimulus and neuromodulatory signals evoke activity of interacting excitatory (E) and inhibitory (I) neural populations (left, green), and ATP is consumed in recovery from that activity, primarily in restoring ion gradients. The ATP is restored through oxidative metabolism of glucose (right, black), with oxygen and glucose delivered by blood flow (middle, blue; CMRGlc = cerebral metabolic rate of glucose (glycolysis), CMRO₂ = cerebral metabolic rate of O₂, CBF = cerebral blood flow). Solid/dashed connecting arrows reflect strong/weak drivers, respectively, and the vertical arrows reflect the fractional increase of each rate. The larger increase of glycolysis than CMRO₂ leads to increased lactate production (Lac), and the larger increase of CBF than CMRO₂ leads to decreased oxygen extraction fraction (OEF), which produces the blood oxygenation level-dependent (BOLD) signal measured in fMRI. The sources for current neuroimaging signals (fMRI and PET) are indicated by red arrows. The seemingly paradoxical features addressed in this paper are: the mismatch of CMRGlc and CMRO₂, leading to increased Lac production despite the availability of O₂; the mismatch of CBF and CMRO₂, leading to the decreased OEF; and the presence of a strong feed-forward drive from the inhibitory neural population (I) to CBF, even though the I activity is likely to be only a small contribution to the ATP costs and thus CMRO₂. (b) Diagram of O₂ partial pressures, with atmospheric values on the left for comparison and physiological values on the right. To increase CMRO₂, the diffusion gradient of PO₂ between the capillary blood and the mitochondria (tissue) must increase. A consequence of increasing CBF more than CMRO₂ is that the OEF is reduced, raising capillary PO₂. In this way, the PO₂ gradient can be increased, supporting increased CMRO₂, while maintaining the tissue PO₂ at a constant level. The larger increase of CMRGlc than CMRO₂ may serve an analogous function by increasing cytosolic Pyr to increase the diffusion gradient to the mitochondria without reducing mitochondrial Pyr. In the context of the proposed thermodynamic framework, the large increases of CBF and CMRGlc serve the broader role of maintaining the entropy change of oxidative metabolism. For CBF, a key element is that it controls the tissue O₂/CO₂ level, and this has additional implications for the CBF response to hypercapnia and hypoxia.

The most striking departure from the simple picture described above is the apparent mismatch of the rates of different processes. The CMRGlc change with increasing neural activity is much larger than the CMRO₂ change [8,13–15], and some of the excess pyruvate created is converted to lactate [15,16]. The production of lactate is surprising given that there appears to be no lack of available oxygen, and this phenomenon has been called ‘aerobic glycolysis’ [8,13]. From the perspective of increasing ATP production, the added glycolysis has little impact because the ATP production from oxidative metabolism in the mitochondria is more than 15 times the ATP production from glycolysis alone. For example, even a 50% increase in glycolysis alone would increase ATP production by only about 3%. In short, even with this added glycolysis most of the needed increase in ATP production is owing to the increased oxidative metabolism, reflected in CMRO₂ [17,18].

Blood flow also increases much more than CMRO₂ [19–32], so that oxygen delivery to tissue is increased much more than the actual increase in the rate at which it is metabolized. A natural idea is that the large blood flow increase might be necessary to support the large change in CMRGlc, even though the function served by the large change in glycolysis is still unclear. However, studies limiting the increase of CBF nevertheless found normal increases of CMRGlc [33,34], indicating that the large change in CBF is not necessary to support CMRGlc.

The phenomenon of a much larger increase of CBF than CMRO₂ creates the seemingly paradoxical effect that the oxygen extraction fraction (OEF), the fraction of delivered oxygen that is extracted and metabolized, decreases with increased neural activity, and this effect is at the heart of the blood oxygenation level-dependent (BOLD) changes of the measured fMRI signal [35,36]. The physical origin of the BOLD effect is that deoxyhaemoglobin has paramagnetic properties that create magnetic field distortions and reduce the measured MR signal [37]. The reduction of OEF with increased neural activity then reduces those field distortions, creating a slight increase of the MR signal. Importantly, the magnitude of the BOLD signal depends on the degree of mismatch between CBF and CMRO₂, as well as the amount of deoxyhaemoglobin present in the baseline state, creating a critical challenge to any quantitative interpretation of the BOLD signal alone in neural terms [37,38]. In short, the mismatch of CBF and CMRO₂ makes possible BOLD-fMRI, but what function is served by this mismatch, and under what circumstances might the degree of mismatch change?

The primary idea for understanding this mismatch is that a larger CBF increase than the CMRO₂ increase tends to maintain the tissue O₂ level [39–42]. As CMRO₂ increases, the gradient of O₂ concentration from blood to tissue must increase to support a higher diffusive flux of O₂ to the mitochondria (figure 1b). In principle, this gradient could be increased by lowering the partial pressure of oxygen (PO₂) in tissue or by raising blood PO₂, and we made the early suggestion that tissue O₂ concentration is so low to begin with that the only option is to raise blood O₂ [43]. By reducing the OEF, the capillary PO₂ is increased, increasing the PO₂ gradient from blood to mitochondria. Later studies further developed this idea in the context of non-zero tissue PO₂ [44–48], with a less severe requirement for increased CBF if tissue PO₂ can drop. In addition, studies directly measuring tissue PO₂ indicate that the tissue O₂ level is reasonably high, about 25 mmHg [49,50], and until recently the dominant view was that oxygen metabolism is not affected until the tissue PO₂ is reduced significantly below 1 mmHg [51]. Why does the brain maintain such a high tissue PO₂ when it seems to be unnecessary, particularly because allowing PO₂ to drop with increased CMRO₂ would strongly reduce the need for a large CBF change? More recently, though, the work of Wilson [52] has been a strong challenge to previously held views about how oxygen concentration limits metabolism. The basic finding was that the oxygen metabolic rate can be maintained down to very low O₂ concentrations, but the phosphorylation potential that governs ATP energy metabolism in the cell begins to degrade at a much higher concentration, a partial pressure of about 12 mmHg [53]. This finding is a primary motivation for the thermodynamic framework developed in this paper.

Several other aspects of CBF also are puzzling. Even in the baseline state, OEF in grey matter is relatively low (approx. 40% [54]), so that the high baseline CBF is already delivering more oxygen than is needed, and OEF drops further with neural stimulation (to approx. 30% for a strong neural stimulus [55]). By contrast, heart muscle has a baseline OEF of about 70–80% that does not change much as O₂ metabolism increases [56], even though the rates of oxidative metabolism are roughly similar for the resting heart and grey matter. Why are the set points and dynamic behaviour of blood flow in these two organs so different? Another blood flow effect is that CBF increases strongly with inhaled CO₂, a phenomenon that has been recognized for more than a century [57], but it is not clear what function this serves.

Finally, the simple picture of serial mechanisms driving the metabolic and flow changes appears to be wrong, or at least a simple path like this is not the primary mechanism involved for CBF control during neural activation. Instead, the current picture is that aspects of neural activity drive CBF changes in a feed-forward way, essentially anticipating the upcoming need for increased metabolism, and this control is applied by a wide variety of mechanisms [58–74]. In this way CBF and CMRO₂ are driven in parallel by neural activity, and there is growing evidence that the aspects of neural activity that drive the CBF increase may not be the same aspects that entail the largest ATP cost and so account for most of the increased CMRO₂. As noted above, the primary ATP cost is in restoring ion gradients after neural signalling, primarily excitatory synaptic activity. By contrast, the inhibitory synaptic activity often involves opening chloride channels, and because the intracellular/extracellular concentrations are near equilibrium with the resting membrane potential there is little ionic current. As a result, the recovery from the inhibitory synaptic activity is likely to be less costly in terms of ATP than the recovery from excitatory activity. Although recovery from spiking of both excitatory and inhibitory neural populations also consumes ATP, estimates for the human brain are that excitatory synaptic activity dominates the overall ATP cost of neural signalling [3]. For this reason, we would expect excitatory activity to be a strong driver of CBF, and a number of studies support this [75]. Interestingly, though, some aspects of inhibitory activity also have a surprisingly strong effect on increasing CBF [62,65,66,76]. The release of nitric oxide (NO), a potent vasodilator, has been associated with the activity of inhibitory neurons [77], and adenosine, which often has an inhibitory neural effect, is also a strong vasodilator [78]. In a recent study using optogenetic methods to stimulate only inhibitory neurons, the positive CBF response was approximately the same size as with a more natural stimulus [63]. Why has evolution favoured a strong role of inhibitory neural activity to increase CBF?

This complicated picture of how different aspects of neural activity drive CMRO₂ and CBF suggests the possibility that the balance of changes in CBF and CMRO₂ may vary with the mix of underlying neural activity [38]. While this would create even more of a problem for any quantitative interpretation of the BOLD signal alone, it potentially opens the door for quantitative physiological fMRI, measuring the changes in CBF and CMRO₂ [26,79–88], to provide a deeper and more nuanced interpretation of the underlying neural activity. For this potential to be realized, though, we need a much better understanding of the connections between neural activity, metabolism and blood flow.

The goal of this paper is to lay a foundation for the theory that the puzzling aspects described above are consistent with thermodynamic limitations on oxygen metabolism [40]. Section 2 outlines the basic theory, describing the general thermodynamic foundations and how the preservation of the entropy change associated with oxidative metabolism is consistent with the observed physiological behaviour. A key result of this development is the importance of maintaining the tissue O₂/CO₂ concentration ratio, primarily by modulating CBF. Section 3 illustrates the implications of preserving tissue O₂/CO₂ with modelling studies based on a model of gas transport in blood and tissue, and a simple neural dynamics model of feed-forward drivers of CBF and CMRO₂, to develop predictions of the theory and compare the predictions with experimental data on CBF responses to neural activity, hypercapnia and hypoxia.

2. Proposed thermodynamic framework

(a). The role of entropy change

The central argument of the thermodynamic framework is that the apparent mismatches of the changes in CMRGlc and CBF compared to CMRO₂, as well as the CBF response to inhaled CO₂, can all be viewed as preserving the entropy change of oxidative metabolism in the mitochondria, and through that the oxidative metabolic rate. Entropy is directly related to the number of different molecular states—defined by the positions and velocities of all the particles—that are consistent with given macroscopic constraints. For chemical transformations, such as a chemical reaction or transport of an ion across a cellular membrane, the macroscopic constraint is the average concentrations of different molecules. The basic principles underlying the current theory are that for any transformation of such a system: (1) the net entropy change ΔS of all the processes involved in the transformation cannot be negative (Second Law of Thermodynamics); (2) the net entropy change ΔS has a simple mathematical form that depends on the concentrations of the molecules involved; and (3) the steady-state rate of the chemical transformation depends on both kinetic factors related to the process and on the entropy change ΔS, with that rate going to zero as ΔS goes to zero. All three of these effects follow in a general way from the basic equations of motion of the molecules, specifically that as the molecular states evolve over time they remain as distinct states and do not converge (this is developed in more detail in the electronic supplementary material, A: Thermodynamic Basis, based on work in the late twentieth century by Jaynes [89] and Bennett [90], and on the implications of the Fluctuation Theorem [91]).

Applying these ideas, for any chemical transformation in a cell the net entropy change cannot be negative. Cellular work involves processes with a negative entropy change, and for these processes to take place they must be coupled to another transformation with a positive entropy change with a larger magnitude. For many cellular processes, the coupled process with a positive entropy change is the breakdown of ATP to ADP and Pi (inorganic phosphate). Another important source of a positive entropy change is the movement of a sodium ion down its electrochemical gradient across the cellular membrane from outside to inside, often used for co-transport of other molecules (e.g. clearance of glutamate from the synaptic cleft by uptake into astrocytes [61]). The sodium gradient is then restored by the sodium/potassium pump, by coupling sodium transport to ATP consumption, and in the brain the activity of the sodium/potassium pump accounts for most of the ATP consumed [11]. The ATP is then restored, involving a negative entropy change, by coupling the process to oxidative metabolism, providing a stronger positive entropy change.

(b). Key relationships from thermodynamics

The electronic supplementary material contains an extended derivation and discussion of the thermodynamic ideas underlying the current theory, leading to the two principal results whose implications are developed below.

(i). Entropy change of a chemical process

The first thermodynamic result is the general form of the entropy change ΔS for a chemical transformation. Suppose that a chemical transformation involves the recombination of several reactants (R₁, R₂,…) to form several products (P₁, P₂,…) and consider one minimal instance of this molecular transformation (e.g. one molecule of R₁ plus one molecule of R₂) so that the overall concentrations are not significantly changed. The entropy change associated with this minimal transformation is:

$$\mathrm{\Delta }S=k_{\mathrm{B}}\ln \frac{\mathit{\Phi }}{{\mathit{\Phi }}_{\mathit{0}}},$$ 2.1

where k_B is Boltzmann's constant and the parameter Φ is the ratio of the reactants to the products of the chemical transformation:

$$\mathit{\Phi }=\frac{[R_1][R_2]\dots }{[P_1][P_2]\dots }.$$ 2.2

The parameter Φ₀ is the equilibrium value of Φ such that the chemical transformation involves no change of entropy: ΔS = 0. The value of Φ₀ depends on the specific context in which the chemical transformation occurs, including temperature, the energy change of the chemical system related to the different net binding energies of the reactants and products, environmental interactions such as those between the reactants and products with the surrounding water molecules or with pH, and the conditions under which the chemical transformation takes place (e.g. constant volume or constant pressure). In general, it is difficult to precisely quantify the value of Φ₀ in a biological setting, but the important result for the current theory is simply the mathematical form of equation (2.1).

(ii). Implications: net entropy change for a linked series of chemical transformations

If a net process contains several steps, such as oxidative metabolism, the net entropy change is the sum of the entropy changes for each step, each of the form of equation (2.1). Mathematically, the net entropy change will then depend on the products of the Φ terms for each step. If the linked steps involve an intermediate chemical that is a product of one step that is consumed as a reactant by the second step, the concentration of that intermediate drops out of the expression for the net entropy change. That is, the concentration of an intermediate will appear in the denominator of Φ₁ and the numerator of Φ₂, and the net entropy change will depend on Φ₁Φ₂. As a result, for an extended process of chemical transformations, the net entropy change depends only on the concentrations of molecules changed by the net process. However, the concentration of the intermediate can play a useful role in balancing the separate entropy changes of the sequential steps (e.g. increasing the concentration of the intermediate will reduce the entropy change of the first step but increase the entropy change of the second step, without altering the net entropy change), and this idea is further discussed in electronic supplementary material, A: Thermodynamic Basis.

(iii). Rate of a chemical process

The second important relationship, following from the Fluctuation Theorem (derived in electronic supplementary material, A: Thermodynamic Basis), is that the net rate of a chemical process can be expressed as:

$$R=R_0\left[1-\text{exp}\left(-\frac{\mathrm{\Delta }S}{k_{\mathrm{B}}}\right)\right].$$ 2.3

In this form, the rate of a process has a kinetic term R₀ and a thermodynamic term depending on the entropy change ΔS. We refer to the parameter R₀ as the kinetic rate, and it may depend on the reactant concentrations in a simple way for first-order kinetics, or in principle could be independent of the reactant concentrations and controlled by enzyme kinetics (see below). The rate R₀ is the rate a process will have if the entropy change is large, and as ΔS goes to zero, the net rate of the process also goes to zero.

(iv). Implications: kinetic and thermodynamic effects on the rate of a chemical process

Equation (2.3) suggests two ways in which the rate of a chemical process could be modified: a kinetic mechanism, changing R₀; or a thermodynamic mechanism, changing ΔS. This distinction is important both for considering how a chemical process can be controlled, and also for considering how a reduction of the concentration of a reactant, such as a reduction of the O₂ concentration in the mitochondria, can affect the rate of the process through both a kinetic and a thermodynamic limitation. In general, the kinetic term R₀ for a process will depend on the enzyme kinetics affecting the mechanics of the process. For example, with simple Michaelis−Menten enzyme kinetics R₀ has the form:

$$R_0=\frac{v_{\max }}{1+K_m/C}$$ 2.4

where C is the concentration of the reactant and v_max and K_m are parameters describing the enzyme kinetics. If C ≪ K_m the kinetics become first order, and R₀ is proportional to C. However, for C ≫ K_m the kinetic rate R₀ is v_max, independent of C. In this case, the rate could be controlled by modulating the enzyme kinetics (i.e. modulating v_max), with no change in C. However, the net rate of the process is fully determined by those enzyme kinetics only when the entropy change ΔS is large and positive, and as C is reduced ΔS also is reduced by equation (2.1). In principle, the reduction of C could begin to degrade the rate of the process by a thermodynamic limitation (reduced ΔS) even though the process is not kinetically limited because C is still larger than K_m.

(c). Oxidative metabolism in the brain

The oxidative metabolism of Pyr and generation of ATP is a complicated extended process consisting of a series of chemical transformations in which some of the products of one process are the reactants for the next process: (1) in the mitochondria, the tricarboxylic acid (TCA) cycle cycle metabolizes Pyr, coupled to the conversion of NAD⁺ to NADH and the production of CO₂; (2) the NADH contributes electrons to the electron transfer chain, which are eventually transferred to O₂ to produce water, and this electron transfer is coupled to the transport of hydrogen ions across the inner membrane of the mitochondria, creating a proton/potential gradient; and (3) movement of protons down the proton gradient is coupled to conversion of ADP plus Pi to ATP.

For the entropy changes involved, we can consider this extended process as two net processes based on the molecules that are changed (consumed or produced). From equation (2.1), the net entropy change associated with the consumption of Pyr and O₂ and the production of CO₂ depends on the ratio:

$${\mathit{\Phi }}_{\mathrm{OX}}=\frac{[\text{Pyr}]{[{\text{O}}_2]}^3}{{[\text{C}{\text{O}}_2]}^3}.$$ 2.5

This positive entropy change from oxidative metabolism of pyruvate must be larger than the negative entropy change associated with the conversion ADP + P_i → ATP, determined by the phosphorylation potential:

$${\mathit{\Phi }}_{\mathrm{ATP}}=\frac{[\text{ATP}]}{[\text{ADP}][P_i]}.$$ 2.6

If the tissue O₂ concentration begins to fall (e.g. by decreased O₂ delivery), Φ_OX will be reduced and the net entropy change ΔS will be reduced. The net positive entropy change can be maintained as Φ_OX falls, and CMRO₂ preserved, if Φ_ATP falls as well, as in the study of Wilson et al. [53]. In this scenario the metabolic rate is maintained, but at the expense of the entropy change available from ATP to drive cellular work. In the context of the proposed thermodynamic framework, this is interpreted as a distinction between kinetic and thermodynamic limits on metabolism. In this interpretation, the kinetic limit is not reached until [O₂] drops to a very low level, but the thermodynamic limit is reached at higher O₂ levels, marked by when Φ_ATP begins to degrade to maintain the metabolic rate.

(d). Preserving the entropy change of oxidative metabolism and the importance of the tissue O₂/CO₂ ratio

The core of the proposed thermodynamic framework is that the physiological changes described in §1 serve to preserve Φ_OX (equation (2.5)) and support the metabolic rate of oxygen. Preserving Φ_OX can be done by maintaining the tissue concentrations of O₂ and Pyr, and the physiological challenge of doing this is the need for transport of these molecules to the mitochondria by diffusion (figure 1b). Unlike enzymatically controlled processes, where in principle the rate of the process can be controlled by modulation of the enzyme activity with no change in the concentration of metabolic substrates, transport by diffusion necessarily involves concentration gradients. In order to increase the flux of O₂ to the mitochondria while preserving the mitochondrial O₂ concentration, the gradient can be increased by raising the O₂ concentration in blood, and that requires reducing the OEF by increasing CBF more than CMRO₂. Similarly, to increase the pyruvate flux from the cytosol to the mitochondria while preserving the mitochondrial pyruvate concentration, the pyruvate gradient can be increased by increasing CMRGlc to increase the cytosolic pyruvate concentration. In this context, the key roles of glycolysis and blood flow are their effects in modulating tissue concentrations of pyruvate and oxygen, respectively, to increase diffusion gradients while maintaining concentrations in the mitochondria. In short, even though empirically it appears that CMRO₂ may be a lesser player compared with CMRGlc and CBF, because the two latter processes are much more responsive to increased neural activity, within the proposed thermodynamic framework CMRO₂ is the key function that shapes the complex physiology.

Based on the thermodynamic arguments it is not necessary to preserve the individual concentrations that make up Φ_OX, but just to preserve Φ_OX itself. The role of glycolysis as the first metabolic step, modulating the Pyr concentration, is discussed in detail in the electronic supplementary material. In §3a–f, we focus on the implications of maintaining Φ_OX by maintaining the tissue O₂/CO₂ ratio under different conditions, including increased CMRO₂, hypercapnia and hypoxia.

3. Modelling results

The key result of the thermodynamic framework is the importance of the tissue O₂/CO₂ ratio to preserve Φ_OX and thus the entropy change of oxygen metabolism. The modelling studies in this section develop the quantitative implications of this idea, testing the effects of reduced tissue O₂/CO₂ and how it can be maintained by blood flow. A quantitative model for O₂ and CO₂ transport in blood and exchange with tissue (described in detail in electronic supplementary material, B: Oxygen Transport Model) was used to develop predictions based on the thermodynamic framework and compare the predictions to experimental results. Starting from an assumed normal baseline state, the model predicts the change in tissue O₂ and CO₂ concentrations as CBF, CMRO₂ and arterial blood gases are modulated.

(a). At what level does reduced tissue O₂/CO₂ begin to limit Φ_ATP?

To put the proposed thermodynamic framework on a more quantitative basis, the limiting O₂/CO₂ ratio when the ATP phosphorylation potential Φ_ATP begins to degrade was estimated by using the transport model to analyse the extensive data reported by Nioka et al. [92] in a study of different degrees of hypoxia in a canine model. Importantly, they measured changes in Φ_ATP as well as CBF, CMRO₂ and blood gases (figure 2a). When analysed with the transport model, Φ_ATP begins to degrade when the tissue O₂/CO₂ ratio is reduced to about 50% of the baseline value. Figure 2b shows the modelled tissue PO₂ when Φ_ATP begins to degrade, in good agreement with the earlier studies of Wilson in mitochondria preparations finding impairment when tissue PO₂ drops below about 12 mmHg [52].

Figure 2.

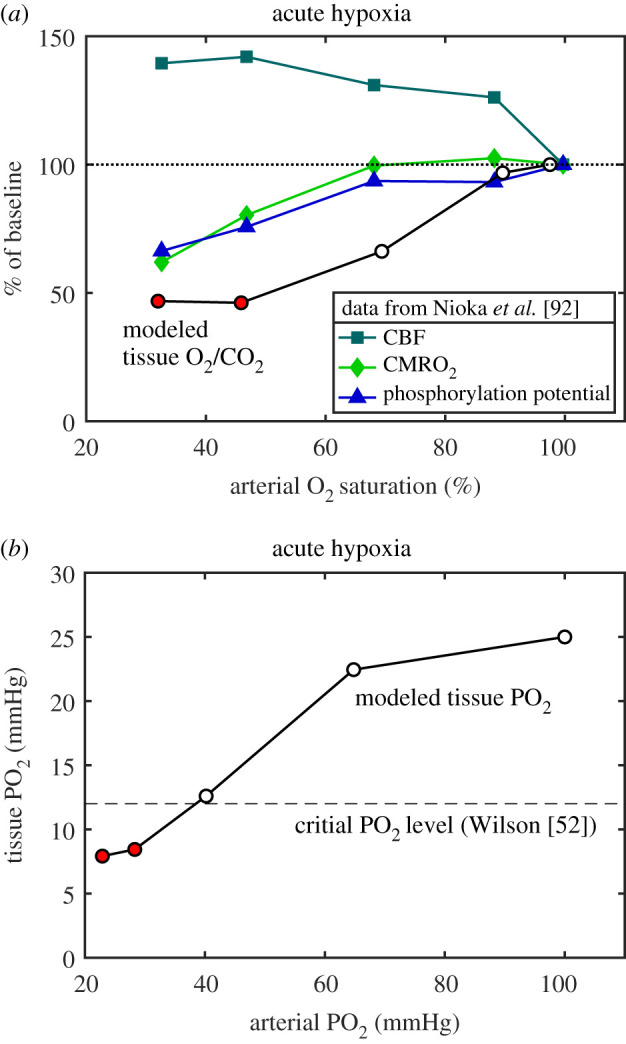
Modelling experimental data to determine the critical level of tissue O₂/CO₂. (a) Data from Nioka et al. [92] for several stages of hypoxic hypoxia in a canine model as arterial O₂–haemoglobin saturation was reduced, including measurement of the ATP phosphorylation potential, are plotted as a percentage of the normoxic value. The transport model was applied to these data to calculate the O₂/CO₂ ratio in tissue (circles). The ATP phosphorylation potential was degraded for the two most extreme hypoxic conditions, and for these states the tissue O₂/CO₂ ratio was reduced to about 50% of the normoxic baseline value (red circles). (b) For the same model, the calculated tissue PO₂ values are plotted as a function of the arterial PO₂ values. Based on a number of studies of mitochondria, Wilson [52] concluded that a PO₂ of about 12 mmHg was a critical threshold below which the ATP phosphorylation potential would degrade (dashed line), in good agreement with the data of Nioka et al. [92] analysed with the transport model.

(b). Effect of reduced O₂ delivery on tissue O₂/CO₂: different sensitivity to reduced flow and reduced arterial PO₂

Oxygen delivery to the capillary bed depends on both blood flow and the O₂ content of arterial blood. Because of the nonlinear O₂–haemoglobin binding curve, with O₂ delivery largely determined by haemoglobin saturation but O₂ transport to tissue determined by capillary PO₂, the degree of impairment of the tissue O₂/CO₂ ratio depends on which of the factors affecting O₂ delivery is reduced. Based on the transport model, the results are that the reduction of tissue O₂/CO₂ is more severe when the arterial PO₂ is reduced than when CBF is reduced (figure 3a). Importantly, when blood PO₂ is reduced and CBF is increased to restore O₂ delivery to the baseline level, this is not sufficient to restore the tissue O₂/CO₂ ratio (dotted curve in figure 3a). The consequences of reduced arterial PO₂ and reduced CBF are considered in more detail in the following two sections in the contexts of high-altitude acclimatization and stroke, respectively.

Figure 3.

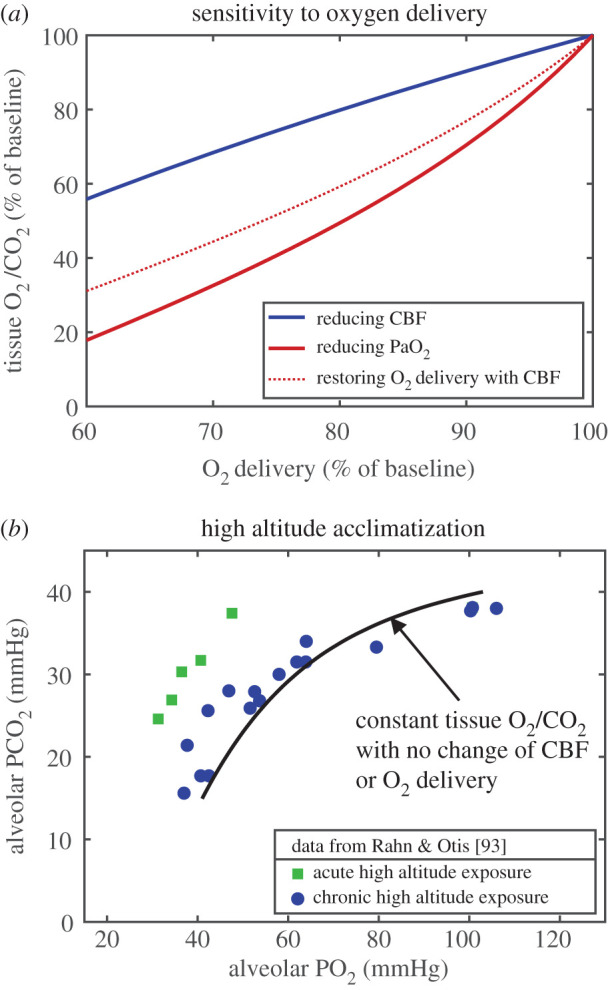
Implications of the thermodynamic framework for sensitivity to oxygen delivery. (a) Curves for the reduction of tissue O₂/CO₂ for two ways of reducing O₂ delivery: by reducing CBF (blue) or by reducing arterial PO₂ (PaO₂) (red). The brain is more sensitive to reduced O₂ delivery owing to reduced blood PO₂. Importantly, for the case of reduced arterial PO₂, restoring baseline O₂ delivery by increasing CBF does not restore tissue O₂/CO₂ (red dotted curve). (b) Classic data from Rahn & Otis [93] showing the effect of increased ventilation rate as a key element of successful acclimatization to the low inspired O₂ concentration at high altitude, reducing arterial CO₂ (PaCO₂) and increasing PaO₂, creating a shift diagonally to the right. The solid model curve shows the value of PaCO₂ needed to compensate for the reduced PaO₂ and maintain the tissue O₂/CO₂ ratio with no change in CMRO₂ or CBF from the normoxic baseline, and constant O₂ delivery. (An alveolar/arterial PO₂ difference of 3 mmHg was assumed in making the plot.).

(c). High-altitude acclimatization: increased ventilation to preserve tissue O₂/CO₂ by reducing tissue CO₂

Long-term exposure to high altitude involves a number of physiological changes, some of which, such as increased hematocrit, serve to restore O₂ delivery. In addition, though, a key response is an increased ventilation rate that lowers arterial CO₂, and this response helps to maintain tissue O₂/CO₂. For the calculations for the acclimatized state, as arterial PO₂ was lowered, hematocrit was increased so that O₂ delivery remained at the baseline level, and there was no change in CBF or CMRO₂. As in figure 3a, though, maintaining O₂ delivery, here by increasing the O₂ carrying capacity of blood, was not sufficient to preserve tissue O₂/CO₂. The model was then used to calculate the degree of reduction of arterial PCO₂ needed in addition to restore tissue O₂/CO₂ (figure 3b). Also plotted are the data reported in the classic study of Rahn & Otis [93], reporting alveolar PO₂ and PCO₂ for subjects acutely exposed to simulated altitude in a pressure chamber along with values reported from several studies of acclimatized individuals, showing the effect of increased ventilation rate with acclimatization. The model curve is consistent with the experimental data for acclimatized subjects, with the acute subjects falling above the model curve, corresponding to reduced tissue O₂/CO₂ if there is no increase of CBF. This too is consistent with other experiments finding increased CBF on acute exposure to high altitude that resolves back to baseline CBF over about a week as subjects acclimatize [94].

(d). Ischaemic stroke: reducing the fall of tissue O₂/CO₂ by reducing CMRO₂

Calculations with the transport model were used to consider the question of how much of the baseline O₂ metabolic rate can be maintained as CBF decreases so that the tissue O₂/CO₂ level remains above 70% of baseline, which from figure 2a is a level where the phosphorylation potential is still maintained. At this reduced level, and for a normal baseline OEF of 40%, CMRO₂ can be as high as approximately 65% of normal when CBF is reduced to approximately 30% of normal. Interestingly though, for a higher baseline OEF of 60%, the maximum CMRO₂ is reduced to approximately 50% of baseline. Note also that increased OEF by itself is not necessarily a sign of critical impairment: for this example with the normal baseline OEF of 40%, that level of maintained CMRO₂ is achieved with OEF rising to about 60%. These modelling results suggest that a full evaluation of stroke conditions should involve measurements of both CBF and CMRO₂, as a more modest reduction of CMRO₂ than the CBF reduction may be sufficient to maintain tissue O₂/CO₂ at a sufficient level to preserve the phosphorylation potential.

(e). Increased CMRO₂ owing to neural activation: CBF response needed to maintain tissue O₂/CO₂ while increasing the blood/tissue O₂ gradient

When CMRO₂ increases, the gradient of O₂ concentration between blood and tissue must increase, and this can be accomplished by increasing CBF more than CMRO₂ so that the O₂ concentration in blood rises (figure 1b). Based on the transport model, the CBF required to maintain the tissue O₂/CO₂ ratio as CMRO₂ increases is shown in figure 4a. The CBF/CMRO₂ coupling ratio n, defined as the fractional change in CBF divided by the fractional change in CMRO₂, varies from about 2 to about 3 as CMRO₂ increases, in good agreement with experimental studies (reviewed in [40]). Note that the large increase of CBF required is owing to the relatively low baseline OEF (40%), and if instead baseline OEF were larger, less of a CBF change would be needed to preserve tissue O₂/CO₂.

Figure 4.

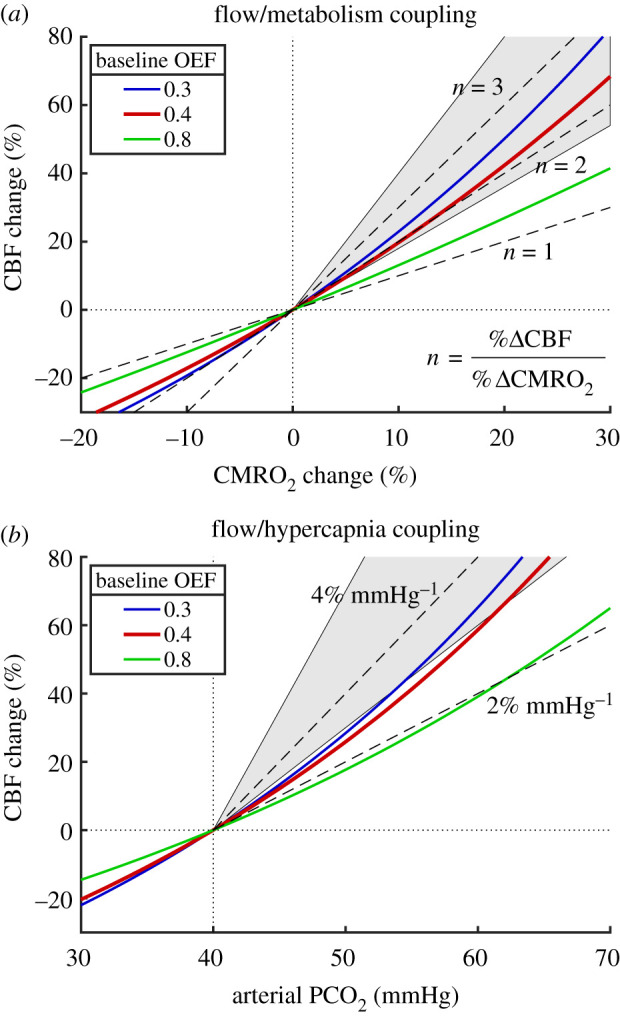
Modelled CBF responses needed to preserve the [O₂]/[CO₂] ratio in tissue in response to increased CMRO₂ and hypercapnia. (a) With increasing O₂ metabolism, the required CBF change is shown for three different values of the baseline OEF (the red line is the typical value for the brain). Dashed lines show constant coupling ratios n of the fractional CBF change to the fractional CMRO₂ change. The shaded area between n = 1.8 and n = 4 shows the approximate range of experimental results. (b) The required CBF change for increasing arterial CO₂ shown for the same values of baseline OEF, with dashed lines indicating constant slope values, and the shaded area between slopes of 3 and 7% mmHg⁻¹ approximates the range of reported experimental values.

(f). Increased tissue CO₂ with hypercapnia: CBF response needed to maintain tissue O₂/CO₂ by raising tissue O₂

Increased CBF, as a mechanism to raise tissue O₂, also may explain the function served by the strong sensitivity of CBF to hypercapnia. Breathing a gas with increased CO₂ content will increase arterial and tissue CO₂ levels, and increased CBF can raise tissue [O₂] to preserve the tissue O₂/CO₂ ratio. Figure 4b shows the CBF change needed to maintain tissue O₂/CO₂ when the partial pressure of CO₂ in arterial blood (PaCO₂) is raised by inhaling a gas mixture with elevated CO₂. Experimental measurements of the CBF response, expressed as % change per mmHg change in PaCO₂, vary widely, and the model prediction is consistent with the low end of the experimental results [95–99].

(g). Neural control of CBF: potential feed-forward mechanisms from both excitatory and inhibitory neural activity

Although the central argument here is that the function served by a large CBF change is to maintain tissue O₂/CO₂, there is not yet a known mechanism—an O₂ sensor—that could be the basis of a feedback system [40]. Instead, a growing body of evidence points to neural activity, both excitatory and inhibitory, driving the rapid control of CBF in a feed-forward way. By contrast, given the high entropy cost of excitatory activity owing to the associated sodium currents and required sodium transport in recovery, we earlier speculated that CMRO₂ is largely driven by excitatory neuronal activity [38]. This qualitative picture of CMRO₂ largely determined by excitatory (E) activity with both E and inhibitory (I) activity as feed-forward drivers of CBF, was used by Mullinger and colleagues [100] as a possible explanation for their finding of an altered CBF/CMRO₂ coupling ratio in a deactivation induced by transcallosal inhibition. In this case, the CBF drivers from increased I activity and the associated decreased E activity were in opposition, reducing the net degree of reduction of CBF. A simple example of the reverse effect, when both E and I activity increase—so that the two drivers of CBF change are in the same direction—is the effect of increasing stimulus intensity. Interestingly, an electrophysiology study concluded that while both E and I activity increased as the stimulus intensity increased, there was a growing dispersion between the two with the I activity continuing to increase while excitatory neuronal activity began to taper off [101]. We reported a study in humans [55] measuring BOLD and CBF responses as the contrast of a visual stimulus was increased, finding that the BOLD signal increased more than CBF, which was consistent with a gradual plateauing of the CMRO₂ response as CBF continued to increase with increasing contrast.

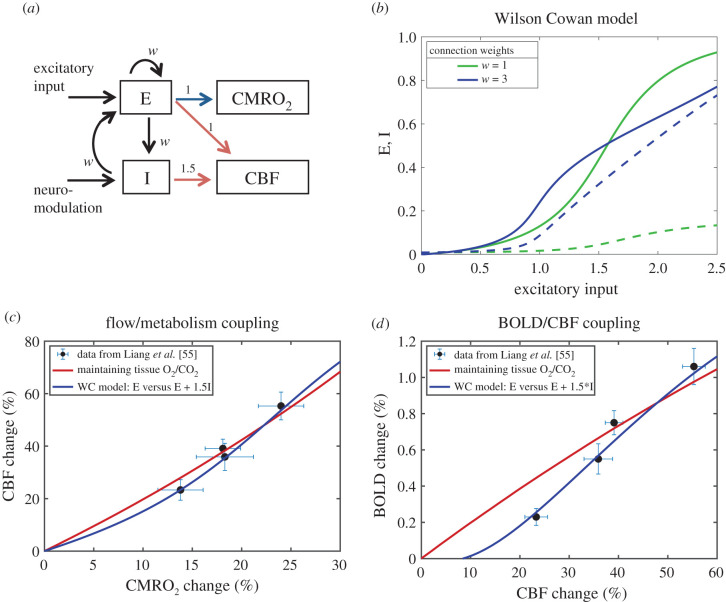
Here we implemented a simple quantitative model as an initial test of the feasibility of these ideas using a version of the Wilson–Cowan (WC) model [102] describing the interaction of excitatory (E) and inhibitory (I) populations of neurons as the stimulus to the E population increases. The model is described in detail in electronic Supplementary material, C: Neural Model, but the general structure is illustrated in figure 5a, and the behaviour of the E and I populations with increasing input is shown in figure 5b. Assuming that CMRO₂ is primarily owing to E activity and CBF is driven by a combination of E and I activities can create a CBF/CMRO₂ response curve that is a reasonably good approximation to the curve calculated to be necessary to maintain the tissue O₂/CO₂ ratio (figure 5c). The curve is not identical, though, with slight differences in the balance of CBF and CMRO₂, although these differences have little impact on the general preservation of the entropy change. The data from human visual cortex [55] are also plotted in figure 5c. Interestingly, because the BOLD signal is sensitive to the exact balance of CBF and CMRO₂ changes, when the BOLD signal is calculated for the WC model curve and for the curve calculated to maintain tissue O₂/CO₂ (figure 5d) the WC model gives a much better fit to the experimental data.

Figure 5.

A speculative mechanism for control of CBF through feed-forward signals from neural activity. (a) The Wilson–Cowan (WC) model [101] was used to model in a simple way the dynamics of interactions of excitatory (E) and inhibitory (I) neural populations driven by an increasing external excitatory input to the E population. The weights for the different interactions were taken to be the same value w. As a proof of concept, CMRO₂ was assumed to be driven by E (blue arrow) and CBF was assumed to be driven by both E and I (red arrows), with a higher weighting for inhibitory activity. (b) Curves of the activities of the E (solid lines) and I (dashed lines) populations as the input increases are shown for w = 1 and w = 3. For higher w, the E population is more sensitive to weaker input values, with activity rising faster owing to the increased self-excitation of the E population, and at higher input values E rises more slowly owing to a strong steady rise in I activity. (c) Data from Liang et al. [55] showing the estimated CMRO₂ changes and the measured CBF changes (mean ± s.e.m.) from a calibrated BOLD study of effects of increasing contrast of a visual stimulus in humans. The red curve is the curve calculated to preserve tissue O₂/CO₂ (from figure 2a). The blue curve is calculated from the WC model with w = 3 with the assumption that %ΔCMRO₂ ∼ E and %ΔCBF ∼ E + 1.5I, with the same proportionality constant for both chosen to make the largest input value for the curves in panel (b) correspond to %ΔCMRO₂ = 30%. (d) Measured BOLD and CBF responses from Liang et al. [55] and the predicted BOLD curves for the constant O₂/CO₂ model (red) and the WC model (blue). The WC feed-forward model gives a reasonably good approximation of the CBF/CMRO₂ coupling needed to preserve tissue O₂/CO₂ (panel c), but the BOLD sensitivity to subtle differences in the balance of CBF and CMRO₂ creates some divergence of the predictions of the BOLD signal for the two models, with the WC model providing a better fit to the experimental data (panel d).

4. Discussion

The goal of this work was to lay a foundation for a thermodynamic framework for understanding a number of aspects of blood flow and metabolism in the brain that have emerged from experimental studies over the past several decades. The central implication of the proposed thermodynamic framework is the importance of maintaining the tissue O₂ to CO₂ concentration ratio (tissue O₂/CO₂) to preserve the entropy change of oxidative metabolism. If this ratio falls, the risk is that the phosphorylation potential also will fall to decrease the entropy cost of converting ADP to ATP. While this could preserve the overall entropy change of oxidative phosphorylation and ATP production, and maintain the oxygen metabolic rate, the critical cost is the reduced entropy change available from ATP that is needed to drive nearly all cellular work. By modelling reported hypoxia data (figure 2), the phosphorylation potential begins to degrade when tissue O₂/CO₂ drops to about 50% of its normal value, corresponding to a tissue PO₂ of about 12 mmHg, in good agreement with the work of Wilson and colleagues [52,53].

In the context of maintaining tissue O₂/CO₂, blood flow can be thought of as doing more than simply delivering O₂; it also modulates capillary and tissue PO₂. The central apparent paradox is that it often appears that blood flow is delivering plenty of O₂ already, so why does CBF need to increase so much? In the context of the thermodynamic framework, the need for a CBF increase is to meet the central challenge of creating a sufficiently large O₂ gradient between capillaries and mitochondria to support CMRO₂ without letting the tissue O₂/CO₂ decrease. In response to increased CMRO₂, the large CBF increase serves to reduce OEF and raise capillary PO₂, creating the larger O₂ gradient from blood to tissue needed to support the higher CMRO₂ while preserving tissue O₂/CO₂. In response to hypercapnia, with an associated increase of tissue CO₂, the CBF increase serves to increase tissue PO₂ and again preserve tissue O₂/CO₂.

In exploring the quantitative implications of maintaining tissue O₂/CO₂, the use of a detailed transport model, such as the one used here (electronic supplementary material, B: Oxygen Transport Model), is critical because the results are not intuitively apparent, owing primarily to the nonlinear effects of the oxygen/haemoglobin binding curve and the factors that affect it. For example, tissue O₂/CO₂ is strongly altered by hypercapnia but much less so by hyperoxia, and it is more sensitive to reduced O₂ delivery when arterial PO₂ is reduced than when CBF is reduced. The transport model provides a novel way to evaluate the effect of hypoxia in the brain in different settings by calculating the effect on tissue O₂/PO₂, and the limited modelling done here makes predictions related to hypoxia that are in good agreement with experimental data. More work is needed, though, to understand the mechanisms involved and the full implications for high-altitude acclimatization, stroke, and other instances of hypoxia.

The modelling also illustrates the way the baseline OEF affects the preservation of tissue O₂/CO₂. As noted earlier, a typical OEF in the brain is about 40%, and yet for the heart muscle the OEF is typically much higher. At first glance, one might assume that the lower OEF in the brain allows for a greater dynamic range of O₂ metabolism, in some sense a larger buffer of unused capacity that could be accessed by increasing OEF. However, the dynamic range of O₂ metabolism in the heart is several times larger than in the brain, and with increased O₂ metabolism in the brain the OEF decreases, rather than increases. The somewhat counterintuitive result of the modelling (figure 4a) is that a given range of blood flow can maintain tissue O₂/CO₂ in support of a larger range of O₂ metabolism (as in the heart) when the baseline OEF is higher. However, with a higher baseline OEF the PO₂ difference between capillary and tissue is reduced if the tissue O₂ is maintained, and to create the same O₂ gradient to support O₂ metabolism the distance from capillary to mitochondrion must be reduced by increasing capillary density. Possibly the relatively low baseline OEF in the brain is the result of minimizing capillary density while retaining the capability to maintain tissue O₂/CO₂ over a limited range of O₂ metabolism. In addition, the low baseline OEF in the brain confers an advantage in ischaemia, and it is here that the ‘unused capacity’ can come into play to preserve a reduced level of CMRO₂ with increased OEF.

The thermodynamic framework addresses the question of why the physiology responds as it does in terms of the function served (i.e. why evolution might preserve these responses), but does not address the question of how this is accomplished—the specific mechanisms that drive CBF. Given this picture, with the central role of CBF being to maintain the tissue O₂/CO₂ ratio, we might expect that CBF would be strongly driven by an oxygen sensor in tissue, but there is currently no known mechanism that could operate in this way. In addition, O₂ dissolves so poorly in water that there is very little O₂ in tissue to serve as a buffer against a drop in O₂ concentration (we previously estimated that if blood flow stopped completely, the amount of O₂ dissolved in tissue would support grey matter CMRO₂ for only about 1 s, with the O₂ in trapped blood extending this to about 10 s, while in contrast the glucose in tissue provides a strong buffer, able to support normal levels of glycolysis for several minutes [40]). Given the lack of an O₂ sensor and the lack of a buffer of O₂, a feed-forward system with a CBF increase triggered by aspects of neural activity could increase O₂ delivery, and specifically the O₂ gradient driving O₂ flux to the mitochondria, in anticipation of the upcoming metabolic need and would help prevent a drop in tissue O₂ and thus a drop in Φ_OX. That is, the neural activity initiates sodium fluxes, and afterwards during recovery the sodium will be pumped back at the cost of ATP, and then oxygen metabolism will increase to restore the ATP. As a feed-forward signal, all aspects of neural activity could potentially be beneficial as drivers of CBF, and empirically many mechanisms linking neural activity to CBF have been found [58–74].

As a first test of modelling a neural feed-forward connection as the potential basis of such a mechanism, we assumed that the activities of both inhibitory and excitatory neural populations drive CBF, while CMRO₂ is driven primarily by ATP consumption related to recovery from the excitatory activity [3,38,62,65,66,75,76]. With this assumption, a simple Wilson–Cowan model of interacting excitatory and inhibitory neural populations was sufficient to explain experimental fMRI data for increasing stimulus amplitude [55]. In this model, the CBF driver from inhibitory activity produced a continuous rise in CBF as stimulus intensity increased even as excitatory activity tapered off, consistent with the data and with the modelled requirement to balance tissue O₂/CO₂. We should be cautious about over-interpreting this result, though—it is one experimental dataset and one implementation of the model. Nevertheless, it supports the feasibility of modelling the full connections between neural activity and the BOLD signal in a way that is consistent with the proposed thermodynamic framework. Continuing work on possible mechanisms linked to neural activity, both modelling and experimental, and a more detailed understanding of the timing of CBF and CMRO₂ responses, are needed to determine the full mechanisms involved.

Data accessibility

This work uses data only from the cited papers. Details of the modelling have been uploaded as part of the electronic supplementary material.

Competing interests

I declare I have no competing interests.

Funding

This work was supported by the National Institutes of Health grant nos. NS036722, MH111359, MH112969 and MH113295.