Directly modelling population dynamics in the South American Arid Diagonal using ¹⁴C dates

Abstract

Large anthropogenic ¹⁴C datasets are widely used to generate summed probability distributions (SPDs) as a proxy for past human population levels. However, SPDs are a poor proxy when datasets are small, bearing little relationship to true population dynamics. Instead, more robust inferences can be achieved by directly modelling the population and assessing the model likelihood given the data. We introduce the R package ADMUR which uses a continuous piecewise linear (CPL) model of population change, calculates the model likelihood given a ¹⁴C dataset, estimates credible intervals using Markov chain Monte Carlo, applies a goodness-of-fit test, and uses the Schwarz Criterion to compare CPL models. We demonstrate the efficacy of this method using toy data, showing that spurious dynamics are avoided when sample sizes are small, and true population dynamics are recovered as sample sizes increase. Finally, we use an improved ¹⁴C dataset for the South American Arid Diagonal to compare CPL modelling to current simulation methods, and identify three Holocene phases when population trajectory estimates changed from rapid initial growth of 4.15% per generation to a decline of 0.05% per generation between 10 821 and 7055 yr BP, then gently grew at 0.58% per generation until 2500 yr BP.

This article is part of the theme issue ‘Cross-disciplinary approaches to prehistoric demography’.

1. Introduction

The varying frequencies of archaeological samples through time are commonly represented using a summed probability distribution (SPD) of associated calibrated ¹⁴C dates, and such distributions of anthropogenic dates are widely used as a proxy to infer dynamics in human populations [1–8]. Prior to more recent simulation approaches (see below), the SPD curve was (and often continues to be) misinterpreted as a faithful representation of population dynamics despite its shape being influenced by other nuisance factors such as taphonomic loss, wiggles inherited from the calibration curve and ascertainment biases. Curves from very small datasets are dominated by the sporadic nature of small sample sizes, and the inevitable gaps between individual calibrated dates cannot be interpreted as population hiatuses [9–11]. In this paper, we use an available extended radiocarbon database [12] for the South American Arid Diagonal (SAAD) and develop an improved method to extract demographic signatures from archaeological data by combining continuous piecewise linear models and formal model comparison.

(a). The archaeological hypothesis: population troughs in the South American Arid Diagonal

The SAAD is a major climatic and biogeographic NW–SE band extending from northwestern Peru to southeastern Argentina, encompassing most of the arid and semiarid ecosystems of South America [13,14]. While spatially and temporally variable, the mid Holocene (8.2–4.2 kyr BP [15]) has been characterized as a period of enhanced aridity in these deserts [16,17]. Volcanic eruptions have also been suggested to have affected human occupations at local and regional scales in parts of the SAAD [18]. Based on this palaeoecological framework, there has been a growing archaeological debate on the possible existence of gaps in the archaeological record in different regions which may signal a demographic discontinuity during the mid-Holocene [2,19–24]. Previous analyses by some authors of this paper (R.B. and C.M.) used SPDs of radiocarbon dates to explore population dynamics and found evidence of synchronicity in fluctuations at different latitudes, allowing the formation of a hypothesis that there may have been two short population troughs in the SAAD driven by increasing aridification between 7.6–7.2 kyr BP and 6.8–6.4 kyr BP [2,24]. Here, we build on this previous work and apply a rigorous model comparison framework to test this hypothesis.

2. Current inferential methods

(a). Directly interpreting a summed probability distribution

As a thought experiment, we can consider a curve comprising just a single (calibrated) date of an organic sample. The sample has a single (point) true date of death, and the curve tells us how believable each possible date is. Neither the sample's existence nor the true date of its death waxes and wanes through time. Likewise, we cannot interpret the SPD of a small dataset across a narrow time period as representing the fluctuations of a population through time—instead, it represents how believable each year is, as possible point estimates for sample 1 or sample 2 or sample 3, etc. It is this ‘or’ component (the summing) that restricts the interpretation of the curve—the SPD is not the single best explanation of the data, nor even a single explanation of the data, but rather a conflation of many possible explanations simultaneously, each of which is mired by the artefacts inherited from the calibration wiggles.

We deliberately used the word explanation, since the SPD is merely a convolution of two datasets: the raw ¹⁴C/¹²C ratios with their errors, and the calibration curve with its error ribbon. Therefore, the SPD provides an excellent graphical representation of the data by compressing a large amount of information into a single plot, and its value in data representation should not be disparaged. However, the SPD is not a model and cannot be directly interpreted to draw reliable inferences about the population dynamics.

(b). Simulation methods to reject a null model

Recognizing the need for a more robust inferential framework, by 2013 methods were developed that moved away from mere data representation, and instead focused on directly modelling the population. An exponential (or any other hypothesized shape) null model could be proposed, and many thousands of simulated datasets could then be generated under this model and compared to the observed. The SPD was no longer the end product; instead, it was used to generate a summary statistic. The summary statistics from each simulated SPD (and the observed SPD) could then be compared, a p-value calculated and (if deemed significant) the hypothesized model could be rejected [25,26]. This approach was successful in directly testing a single hypothesized population history and was widely adopted [12,27–33] as the field moved towards a model-based inferential framework.

(c). Other approaches to directly modelling the population

The inferential limits of the SPD and the importance of directly modelling population fluctuations have been approached with various underlying model structures. The Oxcal program offers Kernel Density Models [34], while the R package Bchron [35] employs Bayesian Gaussian mixture models. Both approaches can provide models of the underlying population by performing parameter searches and are based on sound model likelihood approaches. However, Gaussian-based models (both mixture models and kernels) are by nature complex curves with constantly changing gradients. No doubt real population levels also fluctuate through time with complex and relentless change, but this leaves us with a model that can only be described graphically and cannot be easily summarized in terms of dating key demographic events.

Furthermore, these methods do not address how reasonable the model structure is in the first place. There are two approaches to achieve this. Firstly, a goodness-of-fit (GOF) test can establish if the observed data could have been reasonably produced by the model. This is essentially the approach taken by the simulation methods mentioned above where the p-value provides this GOF, and allows the model to be rejected if it is a poor explanation of the data. Secondly, a model selection process can be used to ensure unjustifiably complex models are rejected in favour of the simplest plausible model with the greatest explanatory power.

Goldberg et al. [36] and de Pablo et al. [32] also modelled population dynamics directly. They both used a piecewise model comprising various phases of logistic and/or exponential growth. However, neither study used a continuous model (the phases did not join) nor were the authors able to calculate likelihoods. As a result, Goldberg et al. misappropriate the Schwarz criterion (Bayesian information criterion: BIC) for use with their ‘proxy likelihoods’ and contradict their own modelling results that indicate a stable population size during the mid Holocene in favour of overinterpreting existing SPD simulation methods to infer oscillations of peaks and troughs. In the case of de Pablo et al. [32] and others [30], the modelling is even more problematic since they apply regression directly to the SPD. The graphical points on the SPD, however, correspond to the number of calendar years in the study period and are not the independent samples that formed it, i.e. the ¹⁴C dates (or more conservatively, the smaller number of phases can be considered independent samples). This renders their standard regression outputs (likelihoods, Akaike's information criterion - AIC - and BIC) meaningless.

Nevertheless, Goldberg et al. innovated an important contribution in two key respects. Firstly, their piecewise model is defined by a small number of discrete phases or periods. This brings the advantage of directly modelling the timing and intensity of population events (the date at which the model changed from one phase to the other), and a simple description of the population behaviour in each phase. Secondly and most importantly, the authors raised the point that a model comparison is required. They test various models, both simpler (one phase) and more complex (up to six phases) in various permutations of logistic and exponential phases. We build on this approach and overcome their shortcomings. We construct a continuous piecewise model, calculate likelihoods and use the BIC to select the most appropriate number of phases. Finally, we use a GOF test to show the data are plausible under the best model.

3. Continuous piecewise linear modelling

The goal in population modelling is usually to identify specific demographic events. Typically, the objective is to estimate the date of some event that marks a change in the trajectory of the population levels, such as the start of a rapid decline or increase in population levels (perhaps from disease, migration or changes in carrying capacity) and provide a simple description of the population behaviour between these events, such as a growth rate. A CPL model lends itself well to these objectives since its parameters are the coordinates of the hinge points, which are the relative population size (y) and timing (x) of these events.

4. Model selection using the Schwarz criterion

We choose the number of linear phases (or number of hinge points joining these phases) systematically as part of a model selection process. Given a ¹⁴C dataset, we find the maximum-likelihood (ML) continuous one-piece (or one phase) linear model (1-CPL), then the ML 2-CPL, etc. Although the likelihood increases with the number of parameters (the greater freedom allows the model to fit more closely to the data), we calculate the Schwarz criterion [37], otherwise commonly misnamed [38] the BIC, to naturally penalize for this increasing complexity. We favour this criterion over AIC [39] since the BIC provides a greater penalty for model complexity than does the AIC, ensuring conservative selection that avoids an overfit model. Indeed, we find the AIC typically favours an unjustifiably complex model, for example, when using toy data where the ‘true model’ is known. Therefore, we select the model with the lowest BIC as the best model. Model complexity beyond this provides incrementally worse BIC values, and as a result, the turning point in model complexity can be easily found, and superfluous computation for unnecessarily complex CPL models is thus avoided.

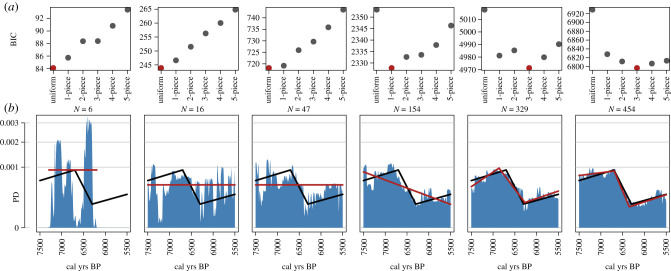
While a large database provides greater information content to justify a CPL model with many hinge points, it is worth considering the extreme case of fitting a CPL model to a tiny dataset. Figure 2 illustrates that the lack of information content naturally guards against overfitting, and a uniform distribution is always selected (a model with no demographic events and no population fluctuations) where sample sizes are low. This should make intuitive sense—in the light of such sparse evidence we should not infer anything more complex than a constant population.

Figure 2.

Model selection naturally guards against overfitting with small sample sizes since the lack of information content favours simple models. By contrast, the SPDs suggest interesting population dynamics that in fact are merely the artefacts of small sample sizes and calibration wiggles. (a) The best model (red) selected using BIC between a uniform distribution and five increasingly complex n-CPL models. (b) SPD (blue) generated from calibrated ¹⁴C dates randomly sampled from the same true (toy) population curve (black), and best CPL model PDF (red) constructed from ML parameters. Note, the slight bend in black and red lines are merely a consequence of the nonlinear y-axis used. (Online version in colour.)

Large ¹⁴C databases covering long time periods often exhibit a general long-term background increase through time, attributable to some combination of long-term population growth and some unknown rate of taphonomic loss of dateable material through time. Such a dataset may be better explained by a model of exponential growth (requiring just a single lambda parameter) than a CPL model. Therefore, for real datasets, the model selection procedure should also consider other non-CPL models such as an exponential model.

5. Calculating likelihoods

Theoretically, a calibrated date should be a continuous probability density function (PDF); however, in practice a date is represented as a discrete vector of probabilities corresponding to each calendar year, and is therefore a probability mass function (PMF). This discretization (of both a proposed model probability distribution and a calibrated date probability distribution) provides the advantage that numerical methods can be used to calculate likelihoods.

Hypothetically, if a calibrated date was available with such precision that it could be attributed with certainty to just a single calendar year the model likelihood would trivially be the model probability at that date. Similarly, if the data comprised just two such point estimates (at calendar time points A and B), the model's relative likelihood would trivially be the model probability at date A multiplied by the model probability at date B.

However, a single calibrated ¹⁴C date is not a point estimate, but rather a complex multimodal probability distribution, representing the probability of each possible year being the true date. Therefore, the probability of a single calibrated date given the model can be calculated as the model probability at year A, or the model probability at year B etc., for all possible years, weighted by how probable the calibrated ¹⁴C date is at each of those years. This can be calculated using the scalar product between model probabilities and calibrated date probabilities, and gives the probability of a single calibrated date under the model. This is repeated for every calibrated date, and the overall product gives the relative likelihood of the model, given the whole dataset.

This approach assumes each date is a fair and random sample, but where many dates are available from a single site-phase, it is sensible to first bin dates into phases. This is an important step in modelling population dynamics to adjust for the data ascertainment bias of some archaeological finds having more dates by virtue of a larger research interest/budget. This is achieved by first generating an SPD for each phase and normalizing. These phase-SPDs are then combined and normalized to create a final SPD. This procedure ensures phases with multiple dates are weighted to contribute the same overall pm as a phase with a single date. The probability of each phase-SPD can then be calculated in exactly the same way as the probability of a single calibrated date.

6. Avoiding edge effects

It is common for a research question to be targeted at a specific time range that spans only part of the overall calibrated date range of the ¹⁴C dataset being used. This is of no consequence if merely generating an SPD, as regions outside the range of interest can be ignored or truncated. Indeed, simulation approaches benefit from considering a slightly wider range by pushing any potential edge effects outside the target range. By contrast, any modelling approach that calculates likelihoods will be influenced by the entire dataset provided, including dates that fall well outside the modelled date range. These external dates must be excluded, since they can have a substantial and mischievous influence on the parameter search.

This influence can be attributed to the interesting behaviour of the tails of a Gaussian distribution, from which a calibrated date is derived. A calibrated date has a non-zero probability at all calendar dates, and as a consequence, a mostly external date still has a tiny tail within the model's date boundaries. However, despite the absolute probability values of this tail being extremely small, surprisingly the relative value increases hugely towards the model boundary (approximately exponentially). As a result, given a dataset where all/most dates are external to the date range of interest, the most likely model shape will have massive upticks at the boundaries. Overall, the likelihood of such a model will be extremely small, but it will be the best explanation given so much data are outside the date range.

Similarly, modelling population dynamics across a range wider than the available dates would be making the incorrect assumption that the absence of evidence at these edges provides evidence of absence, and this will influence the shape of the fitted model. There may be rare occasions where this is reasonable, for example, where humans are known to be absent from an island prior to (or after) some date, or where the archaeological sampling is so substantial that there is confidence that dates would have been recovered if there was a human presence.

Therefore, it is important to ensure the date range of the data and model are appropriate for each other, and to exclude dates from the dataset that do not reasonably fall within the modelled range. We achieve this with our real datasets by only including a date if more than 50% of its probability falls within the modelled date range—i.e. it is more probable that its true date is internal than external. Similarly, we achieve this with our extremely small toy dataset (N = 6) by constraining the modelled date range to exclude the negligible tails outside the calibrated dates.

7. Search algorithm for parameters

The CPL model is a PMF such that the probability outside the date range equals 0, and the total probability within the date range equals 1. The exact shape of this PMF is defined by the (x, y) coordinates of the hinge points. Therefore, there are various constraints on parameters required to define such a curve. For example, if we consider a 2-CPL model, only the middle hinge has a free x-coordinate parameter, since the start and end date are already specified by the date range. Of the three y-coordinates (left, middle, right hinges), only two are free parameters, since the total probability must equal 1. Therefore, a 2-CPL model has three free parameters (one x-coordinate and two y-coordinates) and an n-phase CPL model has 2n−1 free parameters.

We perform the search for the ML parameters (given a ¹⁴C dataset and calibration curve) using the differential evolution optimization algorithm DEoptimR [40]. A naive approach to this search would propose a set of values for all parameters in an iteration simultaneously, and reject the set if it does not satisfy the above constraints. However, this approach would result in the rejection of many parameter sets. Instead, our objective function considers the parameters in order, such that the next parameter is searched for in a reduced parameter space, conditional on the previous parameters. We achieve this by adapting the ‘stick breaking’ Dirichlet process to apply in two dimensions by sampling stick breaks on the x-axis using the beta distribution and y-coordinates using the gamma distribution. At each hinge, the length of the stick is constrained by calculating the total area so far between the first and previous hinge.

8. Estimating credible intervals using Markov chain Monte Carlo

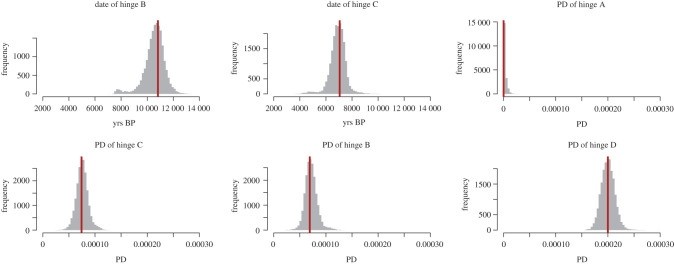
Having constructed a likelihood function that calculates the relative likelihood of any parameter combination, it can be used as the objective function in a parameter search to find the ML parameter estimates. However, we also use the likelihood function in a Markov chain Monte Carlo (MCMC) framework to estimate credible intervals of our parameter estimates. We achieve this using the Metropolis–Hastings algorithm [41] using a single chain of 100 000 iterations, discarding the first 2000 for burn-in, and thinning to every fifth iteration. The resulting joint posterior distribution can then be graphically represented in several ways, such as histograms of the marginal distributions (figure 6) or directly plotting the joint parameter estimates on a two-dimensional plot (figure 7).

Figure 6.

Grey: marginal posterior distributions of the parameters defining the four hinge points, estimated using MCMC. The dates of hinges A and D are not free parameters since they are fixed at 14 kyr BP and 2.5 kyr BP, respectively. Red: ML parameters estimated separately using the search algorithm. (Online version in colour.)

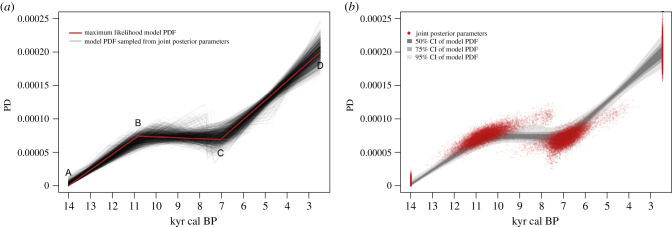
Figure 7.

Credible intervals of the 3-CPL model. (a) Model PDFs using the joint parameters of 1000 samples from the joint posterior parameter distribution (black) and ML parameters (red), hinge points marked A–D. (b) The 50%, 75% and 95% credible intervals (grey) of all model PDFs (grey), and parameter values (red), sampled from the joint posterior parameter distribution. (Online version in colour.)

9. Goodness-of-fit test

Once the best CPL model has been selected, its parameters found and the likelihood calculated, we generate 1000 simulated ¹⁴C datasets under this CPL model by ‘uncalibrating’ calendar dates randomly sampled under the model, taking care to ensure sample sizes exactly match the number of phases in the observed dataset. We then calculate the proportion of each calibrated simulated dataset outside the 95% CI, giving a distribution of summary statistics under our best CPL model. The p-value is then calculated as the proportion of these simulated summary statistics that are smaller or equal to the observed summary statistic. Conceptually, this is similar to the method of calculating p-values under existing simulation methods for testing a null model [12,25–33].

10. Demonstration of methods with toy data

(a). Testing continuous piecewise linear model for a typical sample size

To demonstrate our approach, we first generate a true (toy) population curve, which comprises a 3-CPL model PDF between 5.5 and 7.5 kyr BP. We then randomly sample N = 1500 dates under this true (toy) population curve, ‘uncalibrate’ these dates, apply an arbitrary ¹⁴C error of 25 years, then calibrate. We then conduct a parameter search for the best fitting 1-CPL, 2-CPL, 3-CPL, 4-CPL and 5-CPL models. The BIC is calculated using: ln(n) k − 2 ln(L), where k is the number of parameters (k = 2p − 1, where p is the number of phases), n is the number of ¹⁴C dates and L is the ML [37]. Table 1 gives the results of this model comparison and shows that the model fits closer to the data as its complexity increases. However, the BIC shows that the model is overfitted beyond a 3-CPL model. Therefore, the model selection process successfully recovered the 3-CPL model from which the data were generated.

Table 1.

The 3-CPL model is selected as the best, since it has the lowest BIC (italics). As the number of parameters in the model increases, the likelihood of the model given the data increases. However, the BIC shows that this improvement is only justified up to the 3-CPL model, after which the more complex models are overfit to the data.

model	parameters	maximum log likelihood	BIC
uniform	0	−9976.29	19952.58
1-CPL	1	−9862.86	19732.90
2-CPL	3	−9833.87	19689.26
3-CPL	5	−9792.05	19619.97
4-CPL	7	−9790.87	19631.97
5-CPL	9	−9790.40	19645.38

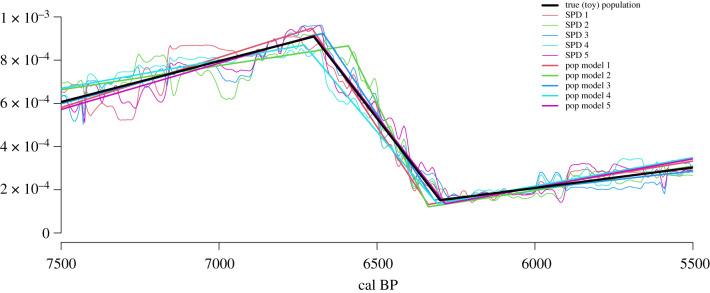
We then assess the accuracy of the parameter estimates by generating five more random datasets under our true (toy) population curve and apply a parameter search to each dataset. Figure 1 illustrates the best 3-CPL model for each dataset, which are all qualitatively similar to the true population curve. Each is the most likely model given the differences between their respective datasets, which are represented with SPDs.

Figure 1.

3-CPL models best fitted to five randomly sampled datasets of N = 1500 ¹⁴C dates. SPDs of each calibrated dataset illustrate the variation from generating random samples. This variation between random datasets is the underlying cause of the small differences between the hinge-point dates in each ML model. (Online version in colour.)

(b). Testing continuous piecewise linear model with small sample size

We continue with the same true (toy) population curve and test the behaviour of both the model selection and parameter estimation with smaller sample sizes. As before, N dates are randomly sampled under the population curve, ‘uncalibrated’, assigned an error and calibrated. Figure 2 shows that for N = 329 and N = 454 the 3-CPL model is successfully selected, and its shape is similar to the true population. For N = 154, the lack of information content favours a 1-CPL model which successfully avoids overfitting, and for N = 47 and smaller, the even simpler uniform model is selected. Fo N = 6, the modelled date range is reduced to only encompass the range of the data (see ‘Avoiding edge effects'). These results successfully demonstrate that this approach provides robust inferences of the underlying population dynamics, avoids the misinterpretation inherent in small datasets and approaches the true population dynamics as sample sizes increase.

11. R package ADMUR

To enable full transparency of our methods and aid other researchers in applying and further developing these methods, we provide an accompanying package in R [42] called ADMUR: Ancient Demography Modelling Using Radiocarbon (https://CRAN.R-project.org/package=ADMUR) and refer users to the vignette ‘guide’ which provides details of installation and use. All analysis and plots in this paper can be exactly replicated using the vignette ‘replicating-timpson-rstb.2020’.

12. Modelling population dynamics in the South American Arid Diagonal

(a). Data overview

For this analysis, we used a subset of the radiocarbon database compiled by Riris & Arroyo-Kalin [12] incorporating sites that fall within the geographically contiguous ‘Arid’ climatic categories of the SAAD as described in the World Köppen climate classification (figure 3) [44]. This provides a more relevant dataset to directly test previous hypotheses of demographic fluctuations in arid ecosystems [2,20–24] by not averaging widely diverse ecological settings (e.g. [12,36]).

Figure 3.

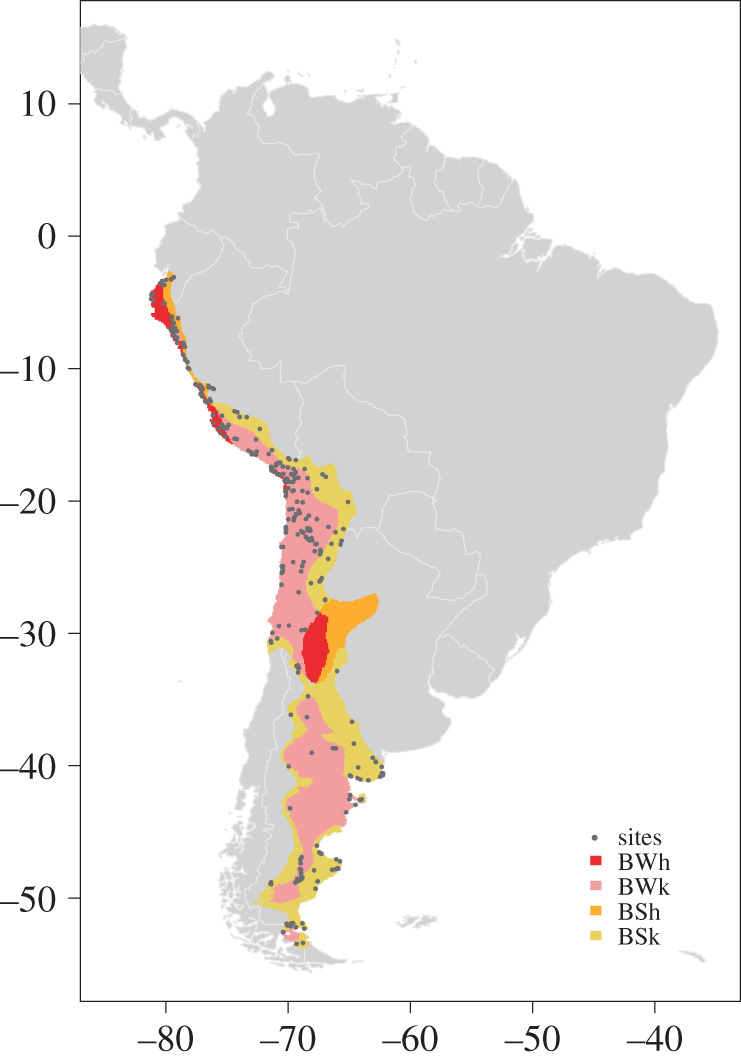
Site location of radiocarbon dates in SAAD. All sites are within the contiguous SAAD, the boundary of which is defined using four of the Koppen–Geiger climate classification zones using table 1 from Peel et al. [43]: BWh, arid hot desert, mean annual precipitation (MAP) < 5× P_threshold, mean annual temperature (MAT) ≥ 18°C; BWk, arid cold desert, MAP < 5× P_threshold, MAT < 18°C; BSh, arid steppe hot, MAP ≥ 5× P_threshold, MAT ≥ 18°C; BSk, arid steppe cold MAP ≥ 5× P_threshold, MAT < 18°C. (Online version in colour.)

(b). Summed probability distribution simulation method testing exponential model

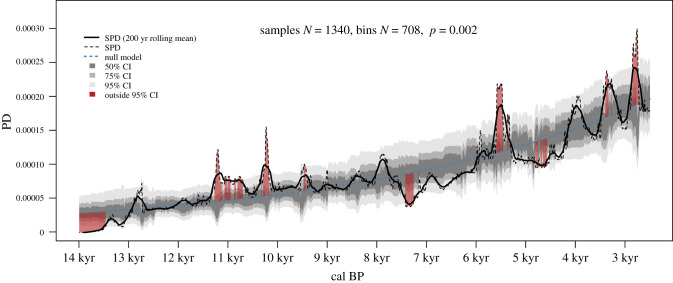
We generate an SPD from the dataset and test for significance using methods described in Shennan et al. [25]. Individual dates from a single site within 200 years of each other were first binned into site-phases, calibrated using SHCal20 [45], and summed and normalized to unity, to account for site-specific ascertainment bias. These distributions in each of the 708 phases were then summed and normalized to unity. Fluctuations in this observed SPD were tested for significance by generating 20 000 random datasets, each sampling 708 dates from a fitted exponential distribution. Dates were ‘uncalibrated’, assigned a random error and calibrated. p-values were calculated using a summary statistic of each SPD calculated as the proportion outside the 95% CI.

The highly significant p-value of 0.002 is the result of only 35 of the 20 000 simulated SPDs having more periods outside the 95% CI than the observed SPD. However, there are important interpretive limits to be respected. This p-value permits us to confidently reject the hypothesis that these data can be explained by an exponential model, but this does not offer us an alternative plausible population model. While we can interpret the sections outside the CI (highlighted red in figure 4) as possible periods where the population may have been unusually high or low relative to the null exponential, we cannot misappropriate this p-value to confidently validate these interpretations as genuine population dynamics, for two reasons. Firstly, due to random fluctuations, we can expect approximately 5% of each simulated SPD to sit outside the CI, so there is no way to identify which local sections are attributable to this random behaviour. Secondly, we still have the fundamental problem that the SPD is not a model of the population dynamics—it is merely a representation of the data being used as a proxy for the population dynamics. Nevertheless, we can successfully reject the simple exponential model, which permits us to explore alternative population models to better explain the data.

Figure 4.

SPD simulation approach illustrating the null hypothesis of steady exponential growth can be rejected. (Online version in colour.)

(c). Continuous piecewise linear modelling

We apply our CPL modelling methods to the same SAAD dataset. As before, the data are binned into 796 discrete site-phase bins, and this is reduced to 708 bins after the exclusion of dates mostly outside the date range (see ‘Avoiding edge effects'). We then apply four procedures. Firstly, model selection using the BIC establishes the 3-CPL model as best (figure 5a). Secondly, the ML parameters of this model are found using the parameter search (figures 6 and 7). Thirdly, the joint posteriors are estimated using MCMC. Fourthly, we apply the GOF test to this model, giving a p-value of 0.235, which establishes the dataset as a typical outcome of the model.

Figure 5.

(a) Model comparison between an exponential model and n-CPL models of varying complexity using the BIC establishes the 3-CPL model as best; (b) red line shows the shape of the best 3-CPL model estimated using the ML parameters; blue polygon shows the calibrated dataset as an SPD. (Online version in colour.)

13. Discussion

The three phases identified in table 2 can be contextually informed by the archaeological record from dry regions in South America. While there is recent debate surrounding some earlier human occupations in the Americas [30,46–49], 15/14 kyr BP represents a widely accepted range for the successful human exploration of the South American continent and of the SAAD in particular [50–52], based on both archaeological evidence and genomic data [30,53]. In the SAAD, the period extending between 14 000 and 10 821 yr BP is characterized by a remarkably high growth rate of 4.15% per 25 year generation. While current global population growth rates average ca 30% per generation (just over 1% per annum), this is a consequence of modern technological advances, and recent estimates on the prehistoric growth for human populations indicate a much smaller growth rate of 1% per generation (0.04% per annum) [54–56]. Therefore, the magnitude of population growth in this first phase is unusually high, and far greater than during any subsequent phase. This is likely due to the successful exploration and colonization of diverse and uncontested niches by early human societies [36,52,57] resulting in typical spread dynamics [56]. At 14.6 kyr BP, the Antarctic Cold Reversal (ACR) began, resulting in colder conditions that were similar to those attributed to the North Atlantic Younger Dryas (YD) stadial [58–61]. This colder climate was accompanied by glacial advances throughout South America and higher lake levels in the Altiplano, which, based on palynological and glacial geological studies, appear to be a result of precipitation increase over the Altiplano [62,63]. The amelioration of different ecological niches and richness in resident species such as megafauna would have increased the carrying capacity of the SAAD, leading to rapid human population growth and exploration of new landscapes. This population expansion would have had a significant ecological impact. In addition to climatic changes (discussed below), the increase in predation rates and niche displacement would ultimately have contributed to the extinction of the American megafauna [50,64]. The regional pace of this anthropogenic impact on megafauna extinction remains unclear in the SAAD given its sparse evidence in some areas, such as in north-central Chile [65].

Table 2.

Summary of the best 3-CPL model represented as ML dates of hinge points, and the growth rates of the three phases. 95% CI calculated using quantiles.

linear phase between hinges	start yrs BP (95% CI)	end yrs BP (95% CI)	gradient (×10−9 per year) (95% CI)	relative growth rate per 25 yr generation (95% CI)
1 (A–B)	14 000	10 821 (11 887 to 8265)	23.3 (15.4 to 28)	4.15% (1.12 to 5.32)
2 (B–C)	10 821 (11 887 to 8265)	7055 (8013 to 5421)	−1.3 (−61.3 to 7.3)	−0.05% (−1.96 to 0.25)
3 (C–D)	7055 (8013 to 5421)	2500	28.7 (20.1 to 42.5)	0.58% (0.42 to 0.81)

The second phase covers almost four millennia between 10 821 and 7055 yr BP and is associated with a slight population decrease (−0.05% per generation, table 2). It has previously been hypothesized that human populations experienced periodic fluctuations during the mid Holocene in response to climatic forces [2,36]. However, our analysis, using a refined dataset and improved method, does not support this hypothesis for the SAAD. Instead, the best model suggests a population that was failing to grow, despite the estimated population size relative to occupiable land still being very low (ca 200 000 people in South America) [36]. While ethnographic and theoretical studies demonstrate how a process of alternating growth and decline offers one possible mechanism that can give the long-term appearance of a stable plateau-like population trend [66,67], we are unable to identify these hypothesized fluctuations. Indeed, neither did the modelling results presented by Goldberg et al. [36], which, like our results, indicate little or no change in the population size ca 9–7 kyr BP. The question, therefore, remains as to what prompted such a significant shift from a rapidly growing population to one that was stagnating. Using the broader South American radiocarbon dataset, Riris & Arroyo-Kalin [12] propose three periods (8.4, 8.2 and 8.1 kyr BP) with exceptionally high frequency of climatic anomalies, which they correlate with an initial drop in relative population at and after 8.6 kyr BP and lasting until at least 6 kyr BP. Likewise, Goldberg et al. [36] identified two mid-Holocene dips from additional SPD simulation analysis. Indeed, a relatively abrupt onset of aridity is recorded in a number of continental and marine records across South America [58,68], and specifically the SAAD [17,31,69–71]. This landscape was, therefore, remarkably different from the one experienced by the first colonizers. Almost all the megafaunal species were either extinct or going extinct [72], forest cover significantly decreased, surface water availability decreased and temperatures were higher [57]. Importantly, a recent analysis at the scale of South America has identified demographic declines associated with climate change [12], thus substantiating the case for diverse demographic trajectories behind continent-wide patterns.

Finally, the third phase extends between 7055 and 2500 yr BP (table 2) and is characterized by a 0.58% increase per generation. It has been proposed that the mid-Holocene increase in population growth rates may have been driven by the development of regional intensification [73]. However, except for the central coast of Peru, most centres of New World crop development were outside the SAAD, such as in the lowlands of central America and the interior of the Amazon [74–76]. Furthermore, the timing of the introduction of domestic species in the SAAD is inconsistent with the start of this third phase. Large parts of the drylands incorporated domesticated plant species as staples only after 4 kyr BP [77,78]. Similarly, llamas appear to have been initially domesticated around 4.5–4 kyr BP in the South-Central Andes, although the full process of camelid domestication would have occurred independently at different times and places within the Andes [79,80]. Therefore, the shift from slight population decline to an upward growth rate of 0.58% per generation occurs 2.5–3 kyr prior to domestication in the SAAD so does not appear to be associated with the development of agropastoral economies.

Increased sedentism has also been proposed as an explanation for this late phase of growth [36], and while a decrease in residential mobility has been proposed in the Atacama desert of northern Chile around 7 kyr BP [81] coinciding with our observed population growth at 7055 yr BP, there also appears to be much regional heterogeneity in mobility and, for instance, there is little to no evidence of increased sedentism in large areas of the SAAD at this time, including Patagonia [50,82].

In contrast with these possible explanations, we note that a growth rate of 0.58% per generation (95% CI = 0.42–0.81) is not unusually high, and is instead broadly consistent with (indeed slightly lower than) the global estimates of 1% per generation (0.04% per year) for broadscale background Holocene population growth [54]. Zahid et al. [54] proposed that this background growth rate is a global phenomenon occurring irrespective of the local environment or subsistence strategy and is, therefore, intrinsic to our species, arguing that it is likely to be related to the global climate and/or endogenous biological factors.

14. Conclusion

While current SPD simulation methods provide a robust statistical framework to test a single null hypothesis, successfully rejecting the null offers the researcher little in the way of drawing an inference about true population dynamics, and this inferential vacuum is often filled with overinterpretation of peaks and troughs in SPDs. Furthermore, rejection of the simple exponential model of constant background growth has become so common that it is no longer tenable to use a classical hypothesis test that heavily favours this null. Instead, we argue that a model selection approach is more appropriate. By including the exponential in the model selection process, there is still the opportunity for this model to be selected, but unlike current simulation methods that can only reject (or fail to reject) an ‘assumed correct’ model, CPL modelling automatically provides a best explanation. The structure of the CPL model provides meaningful and useful date estimates of historic events, relative population levels and growth rates, avoids overfitting, and the GOF test quantitively checks if the data are reasonable, given the model. Together, these methods provide a solid inferential framework for evaluating prehistoric population dynamics from ¹⁴C datasets of any size, and naturally avoids the overinterpretation that is common with SPD analysis.

Our SAAD case study provides a demonstration of the need for this more robust inferential methodology. A substantial body of literature has grown to support a claim of mid-Holocene population fluctuations, based on the misinterpretation of the available ¹⁴C data and the misappropriation of a significant p-value when using SPD simulation methods. We show that based on the current data, this inference is unjustified, and that a steady population trajectory during this period is a better explanation of the data. Directly modelling population dynamics provides robust, justified and reasonable inferences. Our findings should not be misinterpreted as a claim that, in reality, there were no population fluctuations. Future larger datasets have the potential to support models of much greater complexity, and CPL modelling provides the basis and flexibility of fitting any number of hinges, offering detailed population histories of key events.

Data accessibility

To enable full transparency of our methods and aid other researchers in applying and further developing these methods, we provide an accompanying package in R [42] called ADMUR: Ancient Demography Modelling Using Radiocarbon. We refer users to the vignette ‘Guide’ from https://github.com/UCL/ADMUR which provides details of installation and use. All analysis and plots in this paper can be exactly replicated using the vignette ‘Replicating results’.

Authors' contributions

A.T. devised the methodology, performed the analyses, generated plots and co-wrote the paper. R.B., M.G.T., C.M. and KM co-wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

We are grateful for the Chilean support to C.M. from the ANID-FONDECYT no. 1170408 grant and Argentinean support to R.B. from PICT 2016-0062.